Investigation of the Relationships between Coat Colour, Sex, and Morphological Characteristics in Donkeys Using Data Mining Algorithms
Abstract
Simple Summary
Abstract
1. Introduction
2. Materials and Methods
2.1. Chi-Square Automatic Interaction Detection (CHAID)
2.2. Random Forest (RF) Algorithm
- From the initial training dataset, ntree bootstrap sample sets, or (i = bootstrap iteration, and its value was restricted to the range of [1, ntree]), were drawn at random with replacement. For that bootstrap sample set, the elements that are absent from Xi are referred to as out-of-bag data.
- Morphological features were randomly chosen at each node of each tree, and the feature with the lowest Gini Index that best partitioned those features was chosen.
- For each tree, until a predetermined stop condition was met, the data splitting process in each internal node of a rule was repeated from the root node.
2.3. Multivariate Adaptive Regression Spline (MARS)
2.4. Bootstrap Aggregating Multivariate Adaptive Regression Splines (Bagging MARS)
2.5. Automatic Linear Model (ALM)
3. Results
3.1. Descriptive Statistics
3.2. Correlation Matrix and Principal Component Analysis (PCA) Results
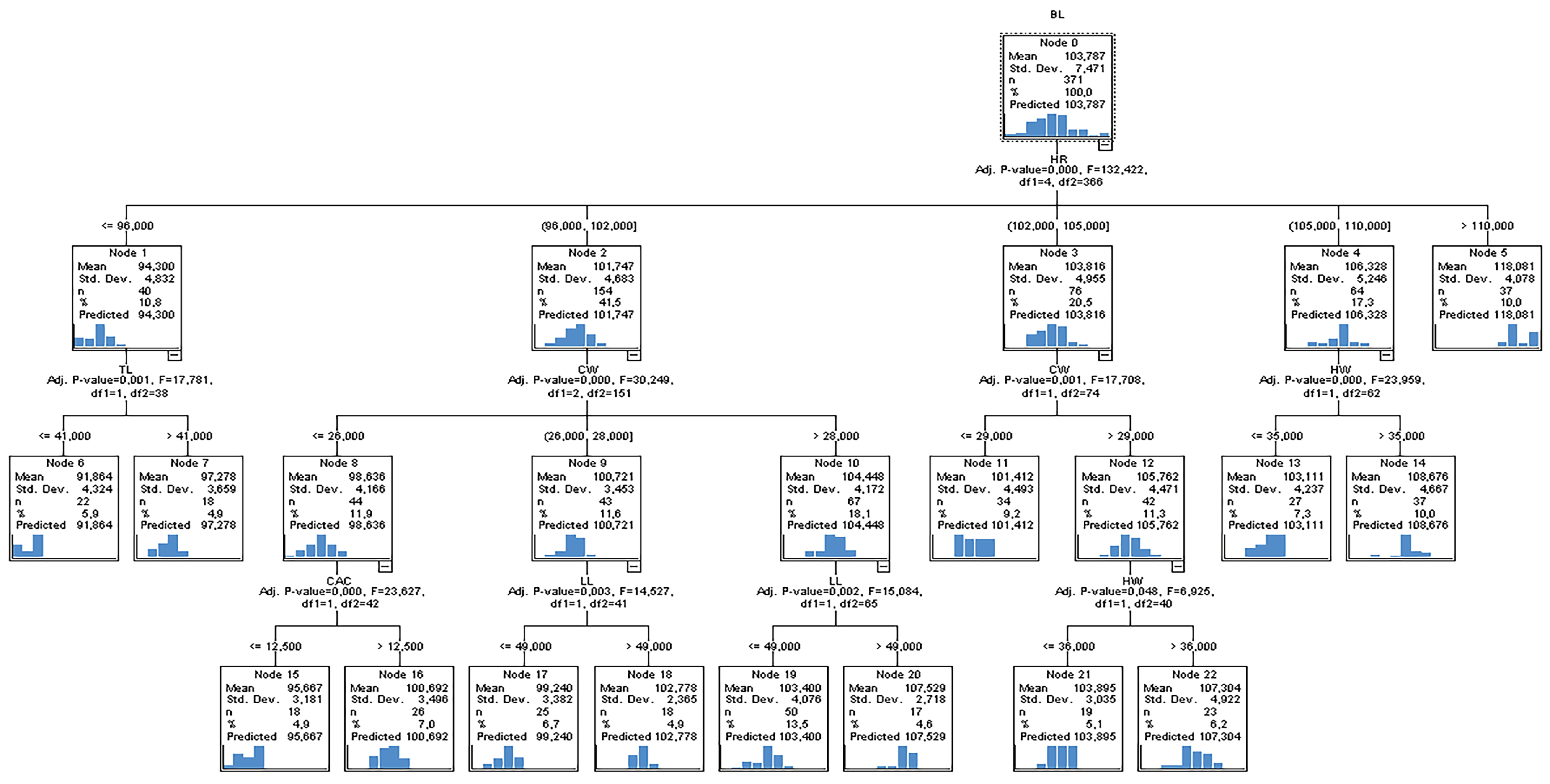
3.3. Result of the CHAID Algorithm
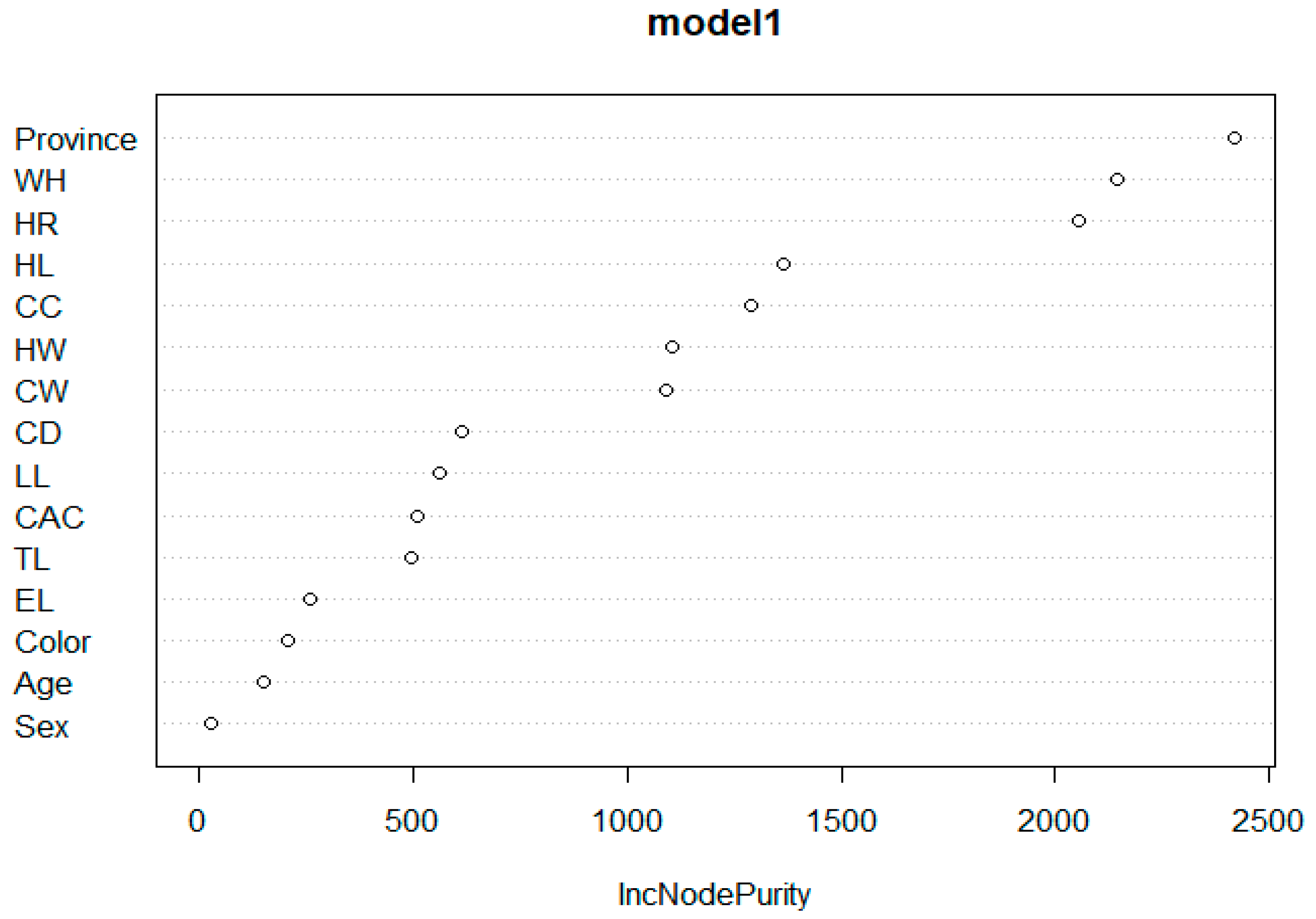
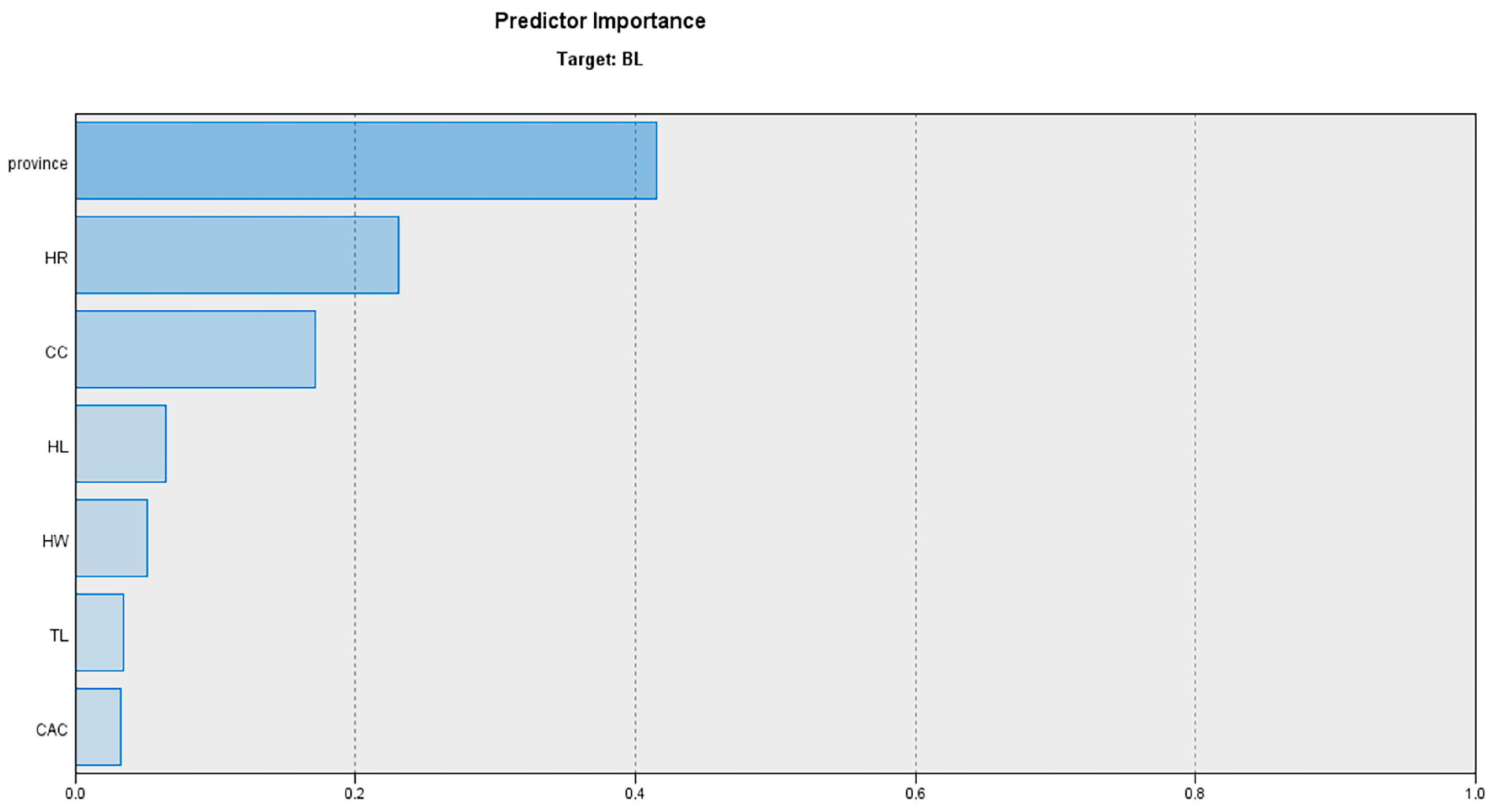
3.4. Random Forest (RF) Algorithm Results
- split, n, deviance, yval, * denotes terminal node(1) root 297 16845.50000 103.76430(2) HL < 60 255 8246.78400 101.72550(4) HR < 97.5 44 1127.90900s 94.95455(8) CC < 96.5 12 160.00000 90.00000 *(9) CC >= 96.5 32 562.87500 96.81250(18) CW < 28.5 23 185.21740 95.34783 *(19) CW >= 28.5 9 202.22220 100.55560 *(5) HR >= 97.5 211 4681.01400 103.13740(10) CW < 30.5 156 2869.91700 101.91670(20) LL < 49.5 102 1540.87300 100.42160(40) CAC < 14.25 95 1260.00000 100.00000(80) CW < 28.5 60 405.65000 98.65000 *(81) CW >= 28.5 35 557.54290 102.31430(162) Province = Artvin, Kars, Sanliurfa, Sirnak 7 76.85714 97.14286 *(163) Province = Ardahan, Balikesir, Erzurum, Hakkari, Igdir, Konya, Van 28 246.67860103.60710 *(41) CAC >= 14.25 7 34.85714 106.14290 *(21) LL >= 49.5 54 670.37040 104.74070(42) LL >= 51.5 20 140.55000 102.35000 *(43) LL < 51.5 34 348.26470 106.14710(86) CC < 112 12 50.00000 103.00000 *(87) CC >= 112 22 114.59090 107.86360 *(11) CW>= 30.5 55 919.20000 106.60000(22) HW < 38.5 45 424.31110 105.35560 *(23) HW >= 38.5 10 111.60000 112.20000 *(3) HL >= 60 42 1103.14300 116.14290(6) CD < 47.5 16 180.00000 111.50000 *(7) CD >= 47.5 26 366.00000 119.00000 *
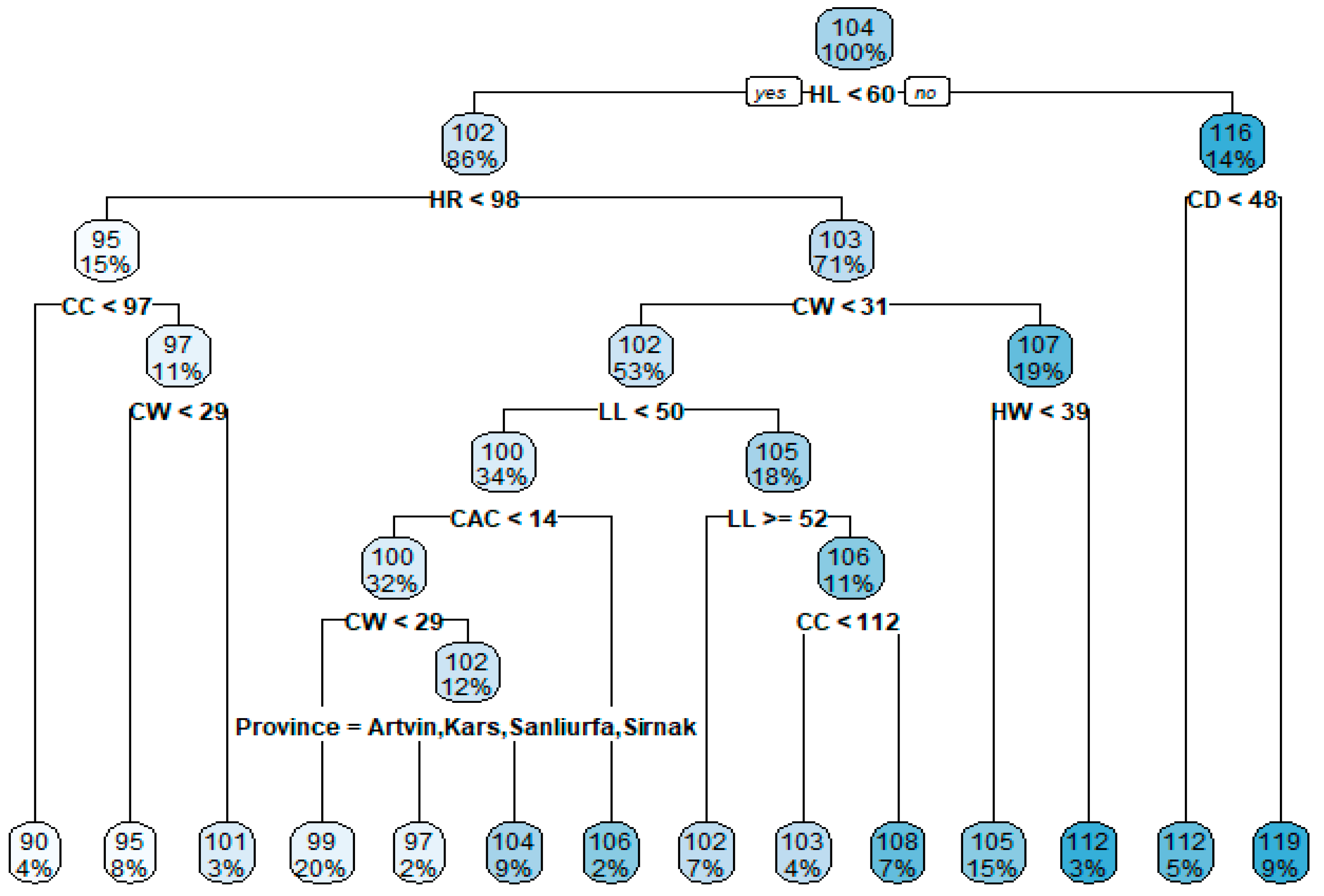
3.5. Automatic Linear Modelling (ALM) Results
3.6. MARS Algorithm Results
| BL | = 105.9362 − 1.063314 * max(0, 108 − HR) + 0.2863338 * max(0, HR − 108) + 4.494783 * max(0, CC − 115) − 8.182082 * max(0, CC − 116) + 0.9779915 * max(0, 118 − CC) + 13.99938 * max(0, CC − 118) − 7.825563 * max(0, CC − 119) − 1.210453 * max(0, 41 − HW) − 1.296884 * max(0, HW − 41) − 0.138144 * max(0, 51 − TL) + 0.4437916 * Province Mardin * max(0, WH − 106) − 0.06556272 * max(0, 98 − HR) * max(0, 118 − CC) + 0.1441603 * max(0, 108 − HR) * max(0, 36 − HW) + 0.906941 * max(0, 108 − HR) * max(0, CAC − 13.5) + 0.05564873 * max(0, 108 − HR) * max(0, LL − 45) + 0.04835515 * max(0, 108 − HR) * max(0, 45 - LL) + 0.9082933 * max(0, CC − 113) * max(0, 41 − HW) − 0.1116934 * max(0, 114 − CC) * max(0, 41 − HW) − 1.079222 * max(0, CC − 114) * max(0, 41 − HW) − 0.1164698 * max(0, CC − 118) * max(0, TL − 42) + 0.3044909 * max(0, CC − 118) * max(0, 42 − TL) + 0.2111183 * max(0, 41 − HW) * max(0, HL − 59) + 0.06125319 * max(0, 41 − HW) * max(0, 59 − HL) − 0.05277187 * Province Kars * max(0, 41 − HW) * max(0, 59 − HL) − 0.04979143 * max(0, 2 − Age) * max(0, 41 − HW) * max(0, 59 − HL) + 0.06762594 * max(0, 108 − HR) * max(0, CW − 25) * max(0, 13.5 − CAC) + 0.08863474 * max(0, 108 − HR) * max(0, 25 − CW) * max(0, 13.5 − CAC) + 0.5347178 * max(0, 108 − HR) * max(0, HW − 36) * max(0, CAC − 13) + 0.5566363 * max(0, 108 − HR) * max(0, HW − 36) * max(0, 13 − CAC) + 7.388817 * max(0, 108 − HR) * max(0, 46 − TL) * max(0, CAC − 13.5) − 0.3124338 * max(0, CC − 113) * max(0, 41 − HW) * max(0, 46 − LL) − 0.06662377 * max(0, 108 − HR) * CC * max(0, 46 − TL) * max(0, CAC − 13.5) − 0.01671139 * max(0, 108 − HR) * max(0, CC − 111) * max(0, HW36) * max(0, LL − 48) |
3.7. Bagging MARS Algorithm Results
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yilmaz, O.; Wilson, R.T. The domestic livestock resources of Turkey: Notes on donkeys. J. Anim. Plant Sci. 2013, 23, 651–656. [Google Scholar]
- Cozzi, M.C.; Valiati, P.; Cherchi, R.; Gorla, E.; Prinsen, R.T.M.M.; Longeri, M.; Bagnato, A.; Strillacci, M.G. Mitochondrial DNA genetic diversity in six Italian donkey breeds (Equus asinus). Mitochondrial DNA Part A 2018, 29, 409–418. [Google Scholar] [CrossRef] [PubMed]
- Clarence-Smith, W.G. Mules in the Indian Ocean world: Breeding and trade in the long nineteenth century, 1780s to 1918. In Early Global Interconnectivity across the Indian Ocean World; Palgrave Macmillan: Cham, Switzerland, 2019; Volume 2, pp. 295–317. [Google Scholar]
- Smith, D.G.; Burden, F.A. Practical donkey and mule nutrition. Equine Appl. Clin. Nutr. 2013, 1, 304–316. [Google Scholar]
- Yarkın, İ. Atçılık, 1st ed.; Ankara Üniversitesi Ziraat Fakültesi Yayınları: 40; Ankara Üniversitesi Basımevi: Ankara, Turkey, 1962. [Google Scholar]
- Jones, P. Donkeys for Development, 3rd ed.; Donkey Power/Animal Traction Network for Eastern and Southern Africa (ATNESA) and Agricultural Research Council of South Africa: Louis Trichardt, South Africa, 2007; ISBN 0-620-22177-1. [Google Scholar]
- Aganga, A.A.; Letso, M.; Aganga, A.O. Feeding donkeys. Livestock Res. Rural Develop. 2000, 12, 1–8. Available online: http://www.lrrd.org/lrrd12/2/agan122.htm (accessed on 12 June 2023).
- Kuger, W.; Grunenfelder, H.P.; Borxham, E. Donkey Breeds in Europe; Conservation Monitoring Institute for Rare Breeds: Zurich, Switzerland, 2008. [Google Scholar]
- Grinder, M.I.; Krausman, P.R.; Hoffmann, R.S. Equus asinus. Mamm. Species 2006, 794, 1–9. [Google Scholar] [CrossRef]
- Yılmaz, O.; Ertuğrul, M. The Morphologic Traits of Donkeys Raised in East and Southeast of Turkey. Hayvansal Üretim 2012, 53, 10–13. [Google Scholar]
- Yılmaz, O.; Ertuğrul, M. Eşeğin (Equus asinus) evcilleştirilmesi. Iğdır Üniversitesi Fen Bilim. Enstitüsü Derg. 2011, 1, 111–115. [Google Scholar]
- Yılmaz, O.; Ertuğrul, M. Türkiye’de yetiştirilen kimi tek tırnaklılara ait bazı morfolojik özellikler. Çanakkale Onsekiz Mart Üniversitesi Ziraat Fakültesi Derg. 2014, 2, 9–16. [Google Scholar]
- Gürcan, E.K.; Genç, S.; Kaplan, S.; Özdil, F.; Özkan Ünal, E.; Bulut, H.; Yatkın, S.; Arat, S.; Soysal, M.İ. Determination of the morphometric characteristics of donkey (Equus asinus) populations reared in Turkey. Turk. J. Vet. Anim. Sci. 2022, 46, 445–456. [Google Scholar] [CrossRef]
- Sargentini, C.; Tocci, R.; Lorenzini, G.; Gianangeli, B.; Martini, A.; Gallai, S.; Giorgetti, A. Morphological characteristics of Amiata donkey reared in Tuscany. Ital. J. Anim. Sci. 2009, 8, 721–723. [Google Scholar] [CrossRef]
- McLean, A.; Wang, W.; Heartfield, A.; Rodrigues, J. Measuring conformation in mules, hinnies, and donkeys (Equus asinus) from Spanish and Portuguese populations. J. Equine Vet. Sci. 2015, 35, 426–427. [Google Scholar] [CrossRef]
- Stanisic, L.; Aleksić, J.M.; Dimitrijevic, V.; Kovačević, B.; Stevanovic, J.; Stanimirovic, Z. Banat donkey, a neglected donkey breed from the central Balkans (Serbia). PeerJ 2020, 8, e8598. [Google Scholar] [CrossRef] [PubMed]
- Quaresma, M.; Bacellar, D.; Leiva, B.; Silva, S.R. Estimation of Live Weight by Body Measurements in the Miranda Donkey Breed. J. Equine Vet. Sci. 2019, 79, 30–34. [Google Scholar] [CrossRef]
- Martins-Bessa, A.; Quaresma, M.; Leiva, B.; Calado, A.; Navas González, F.J. Bayesian Linear Regression Modelling for Sperm Quality Parameters Using Age, Body Weight, Testicular Morphometry, and Combined Biometric Indices in Donkeys. Animals 2021, 11, 176. [Google Scholar] [CrossRef]
- Anonymous. Southeast Turkey-Google My Maps. 2016. Available online: www.googleearth.com (accessed on 19 February 2016).
- Anonymous. TÜRKİYE ENLEM ve BOYLAM TABLOSU. 2022. Available online: http://www.astroset.com/bilgi/astroloji/enlem.htm (accessed on 20 January 2022).
- Nilipour, A.H.; Butcher, C.D. Data collection is important in poultry integrations. Missed World Poult. 1997, 13, 19–20. [Google Scholar]
- Gürcan, E.K.; Tuna, Y.T.; Soysal, M.İ. Anadolu Mandalarının çeşitli vücut ölçülerine göre morfometrik karakterizasyonu. J. Tekirdağ Agric. Fac. 2011, 8, 143–152. [Google Scholar]
- Díaz-Pérez, F.M.; Bethencourt-Cejas, M.; Álvarez-González, J.A. The segmentation of Canary island tourism markets by expenditure: Implication for tourism policy. Tour. Manag. 2005, 26, 961–964. [Google Scholar] [CrossRef]
- Legohérel, P.; Hsu, C.H.C.; Daucé, B. Variety-seeking: Using the CHAID segmentation approach in analyzing the international traveler market. Tour. Manag. 2015, 46, 359–366. [Google Scholar] [CrossRef]
- Kass, G.V. An exploratory technique for investigating large quantities of categorical data. Appl Stat. 1980, 29, 119–127. [Google Scholar] [CrossRef]
- Duru, M.; Duru Arslan, A.; Karadas, K.; Eyduran, E.; Cinli, H.; Tariq, M.M. Effect of Carrot (Daucus carota) Leaf Powder on External and Internal Egg Characteristics of Hy-Line White Laying Hens. Pak. J. Zool. 2017, 49, 125–132. [Google Scholar] [CrossRef]
- Karadas, K.; Tariq, M.; Tariq, M.M.; Eyduran, E. Measuring predicting performance of data mining and artificial neural network algorithms for predicting lactation milk yield in indigenous Akkaraman sheep. Pak. J. Zool. 2017, 49, 1–7. [Google Scholar] [CrossRef]
- Milanović, M.; Stamenković, M. CHAID decision tree: Methodological frame and application. Econ. Themes 2016, 54, 563–586. [Google Scholar] [CrossRef]
- de Ville, B. Decision Trees for Business Intelligence and Data Mining: Using SAS Enterprise Miner; SAS Institute Inc.: Cary, NC, USA, 2006. [Google Scholar]
- Rokach, L.; Maimon, O. Data Mining with Decision Trees: Theory and Applications; World Scientific: New Jersey, NJ, USA, 2008. [Google Scholar]
- Nisbet, R.; Elder, J.; Miner, G. Handbook of Statistical Analysis and Data Mining Applications; Elsevier Inc.: Amsterdam, The Netherlands, 2009. [Google Scholar]
- Breiman, L. Random forests, machine learning. Kluwer Acad. Publ. 2001, 45, 5–32. [Google Scholar]
- Archer, K.J. Empirical characterization of random forest variable ımportance measure, computational statistical data analysis. Comput. Stat. Data Anal. 2008, 52, 2249–2260. [Google Scholar] [CrossRef]
- Breiman, L.; Cutler, A. Random Forest. 2015. Available online: https://www.stat.berkeley.edu/~breiman/RandomForests/cc_home.htm (accessed on 23 June 2015).
- Yang, S.; Brandeis, T.J.; Helmer, E.H.; Oatham, M.P.; Heartsill-Scalley, T.; Marcano-Vega, H. Characterizing height-diameter relationships for Caribbean trees using mixed-effects random forest algorithm. For. Ecol. Manag. 2022, 524, 120507. [Google Scholar] [CrossRef]
- Wright, M.N.; Ziegler, A. Ranger: A fast implementation of random forests for high dimensional data in C++ and R. J. Stat. Softw. 2017, 77, 1–17. [Google Scholar] [CrossRef]
- Friedman, J.H. Multivariate adaptive regression splines. Ann. Stat. 1991, 19, 1–67. [Google Scholar] [CrossRef]
- Deconinck, E.; Coomansb, D.; VanderHeyden, Y.J. Pharm. Biomed. Anal. 2007, 43, 119–130. [Google Scholar] [CrossRef]
- Jalali-Heravi, M.; Asadollahi-Baboli, M.; Mani-Varnosfaderani, A. Shuffling multivariate adaptive regression splines and adaptive neuro-fuzzy inference system as tools for QSAR study of SARS inhibitors. J. Pharm. Biomed. Anal. 2009, 50, 853–860. [Google Scholar] [CrossRef]
- Ju, X.; Chen, V.C.P.; Rosenberger, J.M.; Liu, F. Expert Systems with Applications. Expert Syst. Appl. 2021, 171, 114565. [Google Scholar] [CrossRef]
- Kornacki, J.; Cwik, J. Statistical Learning Systems (in Polish); WNT: Warsaw, Poland, 2005. [Google Scholar]
- Akin, M.; Eyduran, S.P.; Eyduran, E.; Reed, B.M. Analysis of macro nutrient related growth responses using multivariate adaptive regression splines. Pl. Cell Tissue Organ Cult. (PCTOC) 2020, 140, 661–670. [Google Scholar] [CrossRef]
- Naser, A.H.; Badr, A.H.; Henedy, S.N.; Ostrowski, K.A.; Imran, H. Application of Multivariate Adaptive Regression Splines (MARS) approach in prediction of compressive strength of eco-friendly concrete. Case Stud. Construct. Mater. 2022, 17, e01262. [Google Scholar] [CrossRef]
- Breiman, L. Bagging Predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef]
- Kunn, M.; Johnson, K. Applied Predictive Modeling; Springer: New York, NY, USA, 2013. [Google Scholar] [CrossRef]
- Kulekçi, M.; Eyduran, E.; Altın, A.Y.; Tariq, M.M. Usefulness of MARS and Bagging MARS Algorithms in Prediction of Honey Production in Beekeeping Enterprises from Elazig Province of Turkey. Pak. J. Zool. 2022, 54, 1087–1093. [Google Scholar] [CrossRef]
- Panneerselvam, B.; Muniraj, K.; Thomas, M. Identifying influencing groundwater parameter on human health associate with irrigation indices using the Automatic Linear Model (ALM) in a semi-arid region in India. Environ. Res. 2021, 202, 111778. [Google Scholar] [CrossRef]
- Yang, H. The case for being automatic: Introducing the automatic linear modeling (LINEAR) procedure in SPSS statistics. Mult. Linear Regres Viewpoints 2013, 39, 27–37. [Google Scholar]
- Yang, L.; Liu, S.; Tsoka, S.; Papageorgiou, L.G. A regression tree approach using mathematical programming. Exp. Syst. Appl. 2017, 78, 347–357. [Google Scholar] [CrossRef]
- Willmott, C.; Matsuura, K. Advantages of the mean absolute error (MAE) over the root mean square error (RMSE) in assessing average model performance. Clim. Res. 2005, 30, 79–82. [Google Scholar] [CrossRef]
- Liddle, A.R. Information criteria for astrophysical model selection. Month. Not. R. Astron. Soc. 2007, 377, L74–L78. [Google Scholar] [CrossRef]
- Takma, C.; Atil, H.; Aksakal, V. Comparison of multiple linear regression and Artificial neural network models goodness of fit to lactation milk yields. Kafkas Üniv. Veter. Fakültesi Derg. 2012, 18, 941–944. [Google Scholar]
- Chen, T.; Guestrin, C. XGBoost: A scalable tree boosting system. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining; ACM: New York, NY, USA, 2016; pp. 785–794. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing. (Version 4.1) [Computer Software]. (R Packages Retrieved from MRAN Snapshot 2022-01-01). 2021. Available online: https://cran.r-project.org (accessed on 12 April 2022).
- Eyduran, E. ehaGoF: Calculates Goodness of Fit Statistics. R Package Version 0.1.0. 2020. Available online: https://CRAN.Rproject.org/package=ehaGoF (accessed on 27 September 2022).
- IBM Corp. Released. IBM SPSS Statistics for Windows; Version 26.0; IBM Corp.: Armonk, NY, USA, 2019. [Google Scholar]
- Yılmaz, O.; Ertuğrul, M. Some morphological traits of donkeys raised in Iğdır, Turkey. Iğdır Univ. J. Inst. Sci. Technol. 2011, 1, 113–116. [Google Scholar]
- Nininahazwe, P.C.; Sow, A.; Roamba, R.C.; Kalandi, M.; Ahmed, H.D.; Ouédraogo, G.A.; Sawadogo, G.J. West African donkey’s live weight estimation using body measurements. Vet. World 2017, 10, 1221–1226. [Google Scholar] [CrossRef] [PubMed]
- Moreira, C.G.; Balieiro, J.C.C.; Menezes, M.L.; Ribeiro, G.; Nascimento, O.C.A.; Brandi, R.A. Estimated live weight of growing Pêga breed donkeys. Ciência Rural 2017, 47, e20161120. [Google Scholar] [CrossRef]
- Moreira, C.G.; Menezes, M.L.; Nunes, T.R.; Mota, T.P.; Balieiro, J.C.C.; Oliveira, C.A.A.; Brandi, R.A. Biometric parameters of adult and growing Pêga donkeys. Revista Brasileira de Zootecnia 2019, 48, e20180297. [Google Scholar] [CrossRef]
- ABCJPÊGA. Associação Brasileira de Criadores de Jumentos Pêga. Padrão da raça. 2016. Available online: http://www.jumentopegabrasil.com.br (accessed on 25 May 2023).
- Brum, P.P. Avaliação Morfométrica de Asininos Machos da Raça Pêga: Medidas Lineares e Determinação das Proporções Corporais. Dissertação de Monografia, Diploma Thesis, Pontifícia Universidade Católica de Minas Gerais, Betim, Brazil, 2010. [Google Scholar]
- Mariz, T.M.A.; Escodro, P.B.; Dittrich, J.R.; Souza Neto, M.; Lima, C.B.; Ribeiro, J.S. Padrão biométrico, medidas de atrelagem e índice de carga de equídeos de tração urbana do município de Arapiraca, Alagoas. Arch. Veter. Sci. 2014, 19, 1–8. [Google Scholar] [CrossRef]
- Pimentel, M.M.L.; Pinheiro, M.; Maia Filho, H.; Sakamoto, S.M.; Nobre, F.V.; Dias, R.V.C. Parâmetros biométricos de asininos (Equus asinus) utilizados em provas de corrida no estado do Rio Grande do Norte. Acta Veter. Brasil. 2014, 8, 136–143. [Google Scholar]
- Khaleel, A.G.; Lawal, L.A.; Mudassir, N.; Hassan, A.M.; Abdu, M.I.; Salisu, N.; Kamarudin, A.S. Morphometric Characterization of Donkeys (Equus asinus) in D/Kudu Kano State for Selective Breeding and Genetic Conservation. J. Agrobiotechnol. 2020, 11, 12–21. [Google Scholar] [CrossRef]


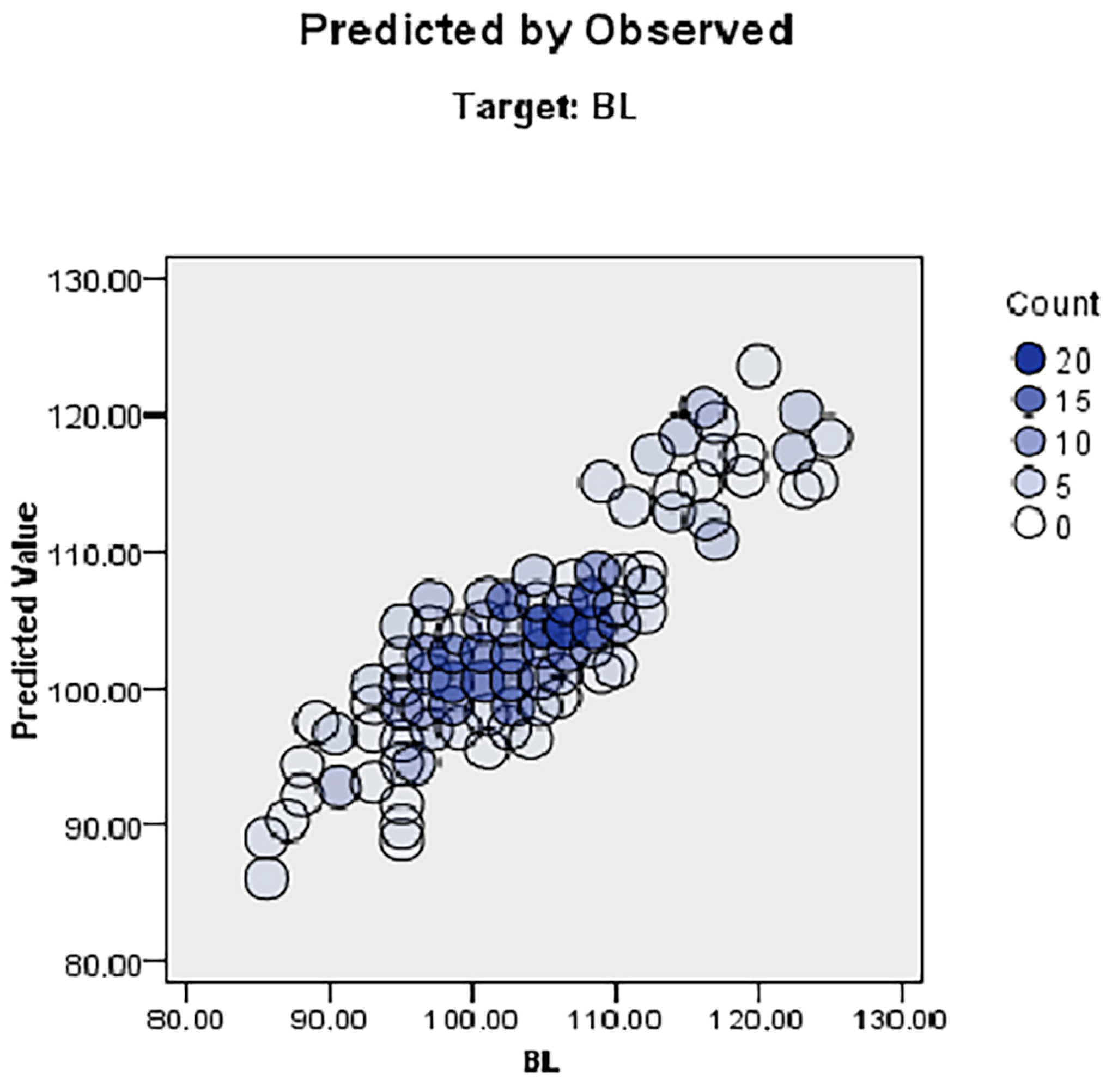
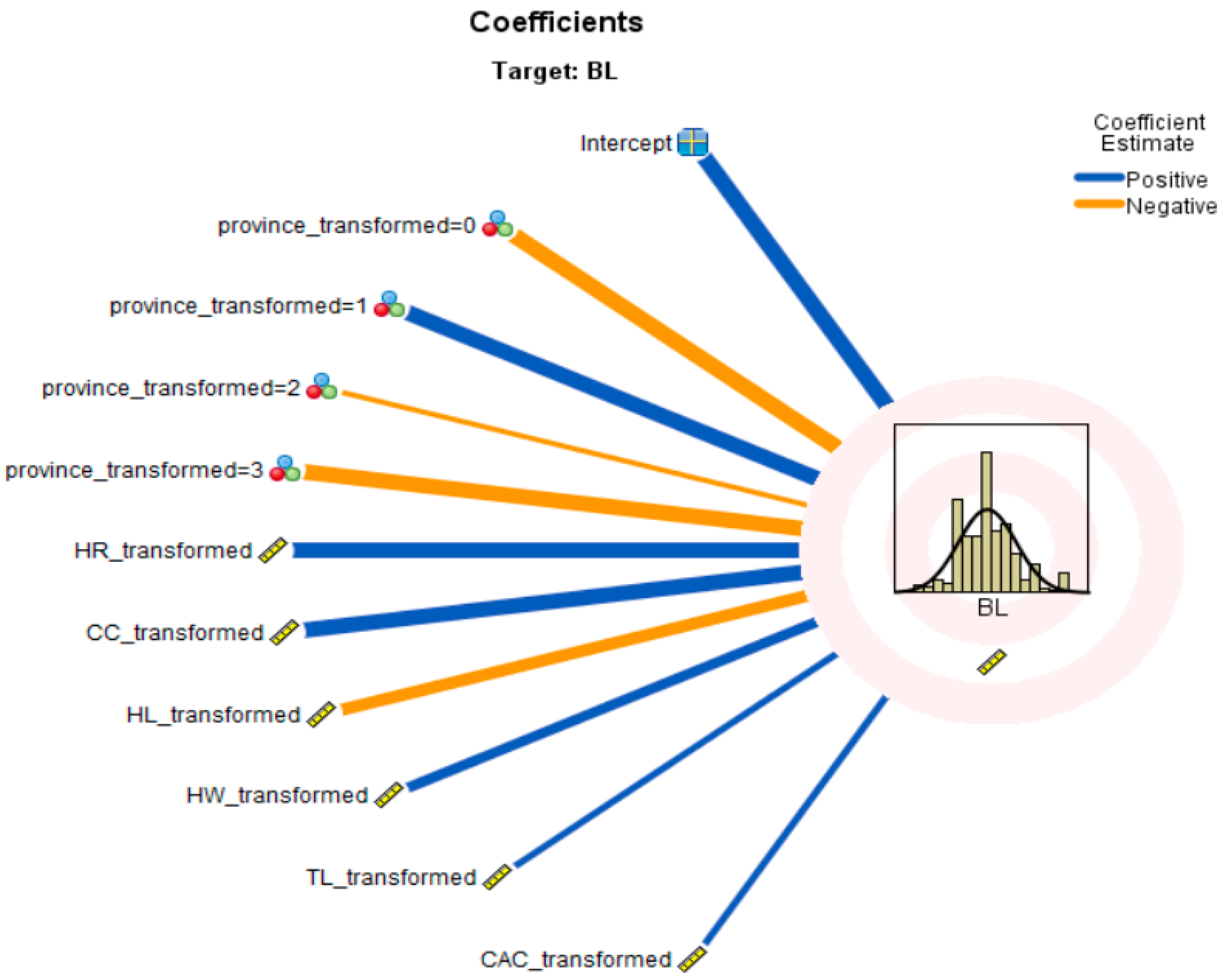
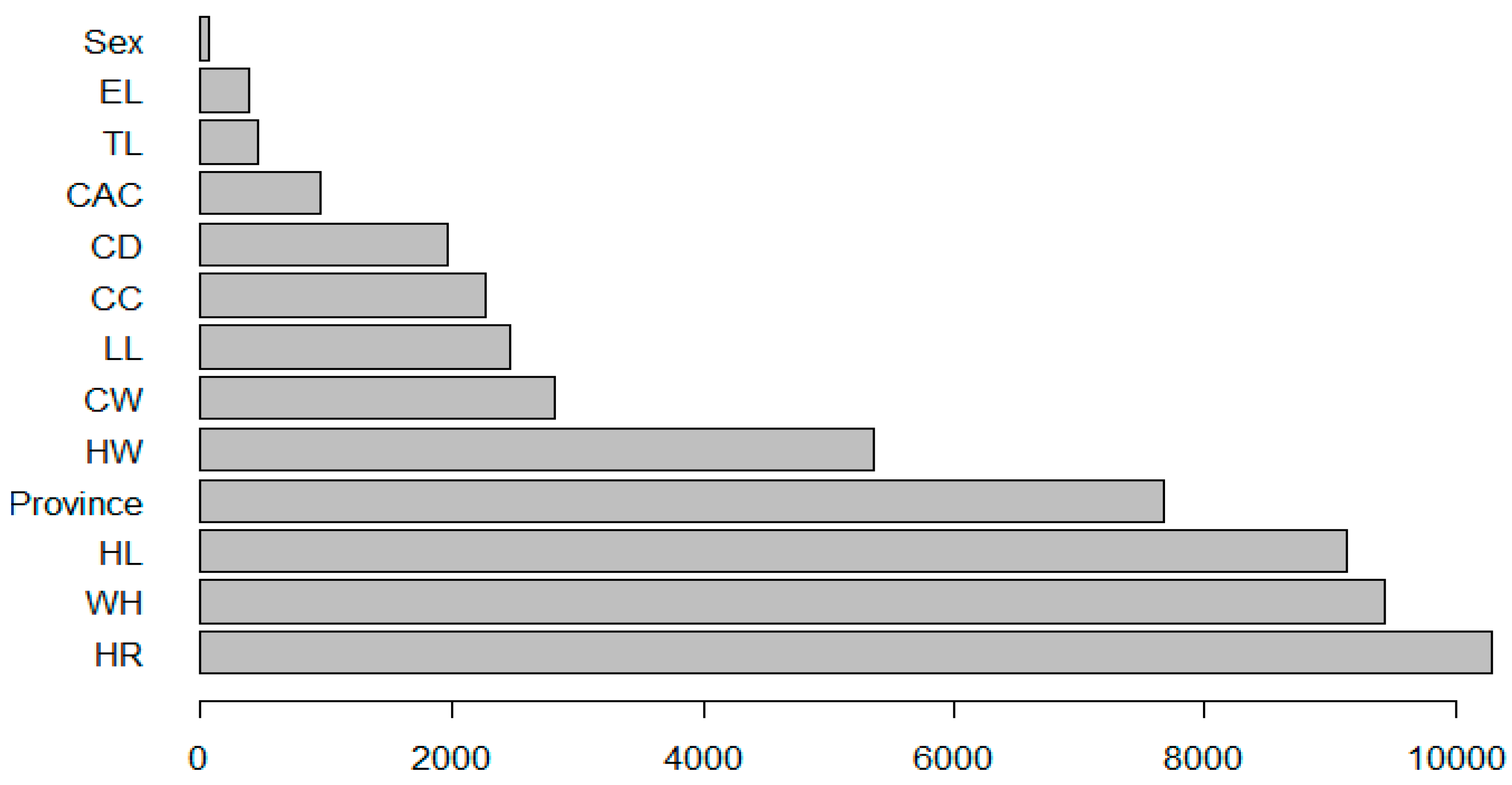
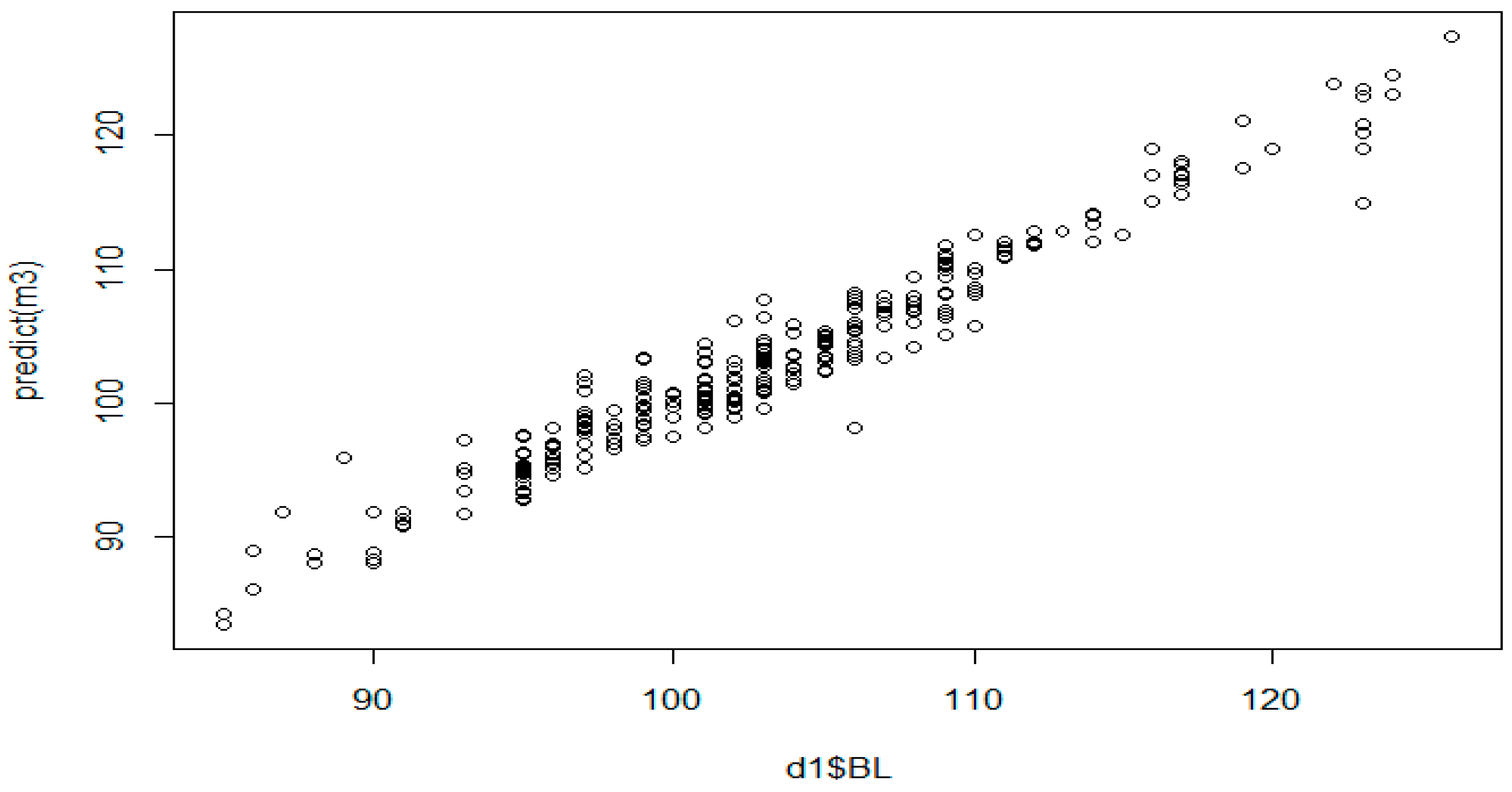
| Colour | Sex | BL | WH | HR | CC | CD | CW | HW | TL | HL | CAC | LL | EL | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| N | Brown | Male | 44 | 44 | 44 | 44 | 44 | 44 | 44 | 44 | 44 | 44 | 44 | 44 |
| Female | 26 | 26 | 26 | 26 | 26 | 26 | 26 | 26 | 26 | 26 | 26 | 26 | ||
| Grey | Male | 91 | 91 | 91 | 91 | 91 | 91 | 91 | 91 | 91 | 91 | 91 | 91 | |
| Female | 55 | 55 | 55 | 55 | 55 | 55 | 55 | 55 | 55 | 55 | 55 | 55 | ||
| Black | Male | 58 | 58 | 58 | 58 | 58 | 58 | 58 | 58 | 58 | 58 | 58 | 58 | |
| Female | 23 | 23 | 23 | 23 | 23 | 23 | 23 | 23 | 23 | 23 | 23 | 23 | ||
| White | Male | 59 | 59 | 59 | 59 | 59 | 59 | 59 | 59 | 59 | 59 | 59 | 59 | |
| Female | 15 | 15 | 15 | 15 | 15 | 15 | 15 | 15 | 15 | 15 | 15 | 15 | ||
| Brown | Male | 101 | 98.4 | 101 | 110 | 43.7 | 28.4 | 34.3 | 46.4 | 54.8 | 13.2 | 47.3 | 21.3 | |
| Female | 102 | 99.3 | 102 | 113 | 46.3 | 28.9 | 35.2 | 49.2 | 52.7 | 13.4 | 48.3 | 22.2 | ||
| Grey | Male | 103 | 100 | 102 | 113 | 45.3 | 28.9 | 35.5 | 47.9 | 54.8 | 13.5 | 49 | 22 | |
| Female | 103 | 98.5 | 101 | 113 | 45.7 | 28.7 | 34.6 | 48.4 | 52.9 | 13.1 | 48.1 | 22.1 | ||
| Black | Male | 103 | 101 | 103 | 113 | 45.6 | 29.4 | 35.4 | 49.3 | 55.1 | 13.6 | 49.2 | 22.8 | |
| Female | 102 | 99.4 | 102 | 112 | 45.9 | 28.1 | 34 | 48.5 | 53.5 | 13.2 | 48.7 | 22 | ||
| White | Male | 109 | 106 | 108 | 115 | 47.7 | 30.6 | 36.8 | 52.6 | 58.5 | 13.8 | 49.7 | 21.8 | |
| Female | 104 | 100 | 103 | 114 | 45.1 | 28.4 | 35.1 | 49.3 | 55.2 | 13.5 | 48.6 | 22.2 | ||
| General | 103.8 | 100.7 | 103.1 | 112.8 | 45.7 | 29.1 | 35.3 | 49 | 55 | 13.5 | 49 | 22 | ||
| Brown | Male | 1.18 | 0.88 | 0.79 | 1.27 | 0.65 | 0.5 | 0.52 | 1.5 | 0.71 | 0.15 | 0.58 | 0.32 | |
| Female | 1.07 | 0.64 | 0.76 | 1.02 | 0.62 | 0.56 | 0.43 | 1.75 | 0.58 | 0.14 | 0.53 | 0.25 | ||
| Grey | Male | 0.73 | 0.61 | 0.57 | 0.76 | 0.42 | 0.34 | 0.43 | 0.86 | 0.43 | 0.11 | 0.37 | 0.18 | |
| Female | 0.72 | 0.63 | 0.63 | 1.07 | 0.45 | 0.4 | 0.35 | 1.09 | 0.47 | 0.13 | 0.4 | 0.25 | ||
| Black | Male | 0.91 | 0.81 | 0.76 | 0.72 | 0.54 | 0.36 | 0.49 | 1.03 | 0.69 | 0.13 | 0.39 | 0.28 | |
| Female | 1.12 | 1.09 | 0.95 | 1.72 | 0.76 | 0.74 | 0.63 | 1.74 | 0.67 | 0.25 | 0.68 | 0.38 | ||
| White | Male | 1.19 | 1.15 | 1.09 | 0.93 | 0.66 | 0.57 | 0.5 | 1.05 | 0.75 | 0.16 | 0.39 | 0.24 | |
| Female | 2 | 1.96 | 1.88 | 1.8 | 0.75 | 0.69 | 0.89 | 1.89 | 1.53 | 0.25 | 0.58 | 0.44 | ||
| s | Brown | Male | 7.81 | 5.86 | 5.25 | 8.42 | 4.3 | 3.34 | 3.41 | 9.92 | 4.73 | 1 | 3.84 | 2.09 |
| Female | 5.45 | 3.29 | 3.85 | 5.19 | 3.15 | 2.88 | 2.19 | 8.92 | 2.96 | 0.7 | 2.68 | 1.29 | ||
| Grey | Male | 6.95 | 5.84 | 5.39 | 7.28 | 4.01 | 3.27 | 4.11 | 8.18 | 4.06 | 1 | 3.55 | 1.73 | |
| Female | 5.35 | 4.65 | 4.66 | 7.9 | 3.35 | 2.95 | 2.63 | 8.09 | 3.52 | 0.95 | 2.95 | 1.87 | ||
| Black | Male | 6.96 | 6.17 | 5.75 | 5.46 | 4.08 | 2.73 | 3.73 | 7.88 | 5.23 | 0.98 | 2.95 | 2.09 | |
| Female | 5.36 | 5.24 | 4.55 | 8.26 | 3.65 | 3.57 | 3 | 8.36 | 3.19 | 1.2 | 3.25 | 1.83 | ||
| White | Male | 9.12 | 8.83 | 8.35 | 7.14 | 5.1 | 4.39 | 3.86 | 8.1 | 5.77 | 1.21 | 3.01 | 1.82 | |
| Female | 7.75 | 7.6 | 7.27 | 6.98 | 2.9 | 2.67 | 3.44 | 7.34 | 5.91 | 0.97 | 2.26 | 1.7 |
| BL | WH | HR | CC | CD | CW | HW | TL | HL | CAC | LL | EL | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| BL | 1 | 0.762 ** | 0.767 ** | 0.614 ** | 0.541 ** | 0.642 ** | 0.584 ** | 0.444 ** | 0.581 ** | 0.515 ** | 0.532 ** | 0.233 ** |
| WH | 0.762 ** | 1 | 0.951 ** | 0.569 ** | 0.691 ** | 0.572 ** | 0.555 ** | 0.457 ** | 0.783 ** | 0.528 ** | 0.547 ** | 0.210 ** |
| HR | 0.767 ** | 0.951 ** | 1 | 0.586 ** | 0.649 ** | 0.590 ** | 0.571 ** | 0.444 ** | 0.755 ** | 0.533 ** | 0.551 ** | 0.240 ** |
| CC | 0.614 ** | 0.569 ** | 0.586 ** | 1 | 0.505 ** | 0.652 ** | 0.604 ** | 0.251 ** | 0.345 ** | 0.528 ** | 0.505 ** | 0.361 ** |
| CD | 0.541 ** | 0.691 ** | 0.649 ** | 0.505 ** | 1 | 0.378 ** | 0.337 ** | 0.186 ** | 0.096 | 0.344 ** | 0.432 ** | 0.280 ** |
| CW | 0.642 ** | 0.572 ** | 0.590 ** | 0.652 ** | 0.378 ** | 1 | 0.661 ** | 0.392 ** | 0.460 ** | 0.489 ** | 0.497 ** | 0.244 ** |
| HW | 0.584 ** | 0.555 ** | 0.571 ** | 0.604 ** | 0.337 ** | 0.661 ** | 1 | 0.438 ** | 0.472 ** | 0.411 ** | 0.481 ** | 0.333 ** |
| TL | 0.444 ** | 0.457 ** | 0.444 ** | 0.251 ** | 0.186 ** | 0.392 ** | 0.438 ** | 1 | 0.469 ** | 0.244 ** | 0.375 ** | 0.126 * |
| HL | 0.581 ** | 0.783 ** | 0.755 ** | 0.345 ** | 0.096 | 0.460 ** | 0.472 ** | 0.469 ** | 1 | 0.434 ** | 0.380 ** | 0.045 |
| CAC | 0.515 ** | 0.528 ** | 0.533 ** | 0.528 ** | 0.344 ** | 0.489 ** | 0.411 ** | 0.244 ** | 0.434 ** | 1 | 0.562 ** | 0.291 ** |
| LL | 0.532 ** | 0.547 ** | 0.551 ** | 0.505 ** | 0.432 ** | 0.497 ** | 0.481 ** | 0.375 ** | 0.380 ** | 0.562 ** | 1 | 0.312 ** |
| EL | 0.233 ** | 0.210 ** | 0.240 ** | 0.361 ** | 0.280 ** | 0.244 ** | 0.333 ** | 0.126* | 0.045 | 0.291 ** | 0.312 ** | 1 |
| Inc Node | Purity |
|---|---|
| Colour | 206.65191 |
| Province | 2418.43807 |
| Sex | 26.98572 |
| Age | 148.93556 |
| WH | 2147.68648 |
| HR | 2058.41290 |
| CC | 1286.96548 |
| CD | 611.77061 |
| CW | 1087.82828 |
| HW | 1102.90156 |
| TL | 497.52907 |
| HL | 1364.95827 |
| CAC | 510.62463 |
| LL | 561.35982 |
| EL | 261.88463 |
| Model Term | Coefficient | p-Value | Importance |
|---|---|---|---|
| Intercept | 23.554 | 0.000 | |
| Province = 0 | 5.964 | 0.000 | 0.415 |
| Province = 1 | 5.988 | 0.000 | 0.415 |
| Province = 2 | 1.231 | 0.000 | 0.415 |
| Province = 3 | 3.000 | 0.000 | 0.415 |
| HR | 0.425 | 0.000 | 0.231 |
| CC | 0.260 | 0.001 | 0.171 |
| HL | 0.260 | 0.001 | 0.065 |
| HW | 0.289 | 0.003 | 0.051 |
| TL | 0.072 | 0.015 | 0.034 |
| CAC | 0.635 | 0.017 | 0.033 |
| Sample ID | Value | Cook’s Distance |
|---|---|---|
| 323 | 97 | 0.043 |
| 219 | 97 | 0.041 |
| 28 | 126 | 0.034 |
| 209 | 97 | 0.032 |
| 45 | 123 | 0.028 |
| 50 | 102 | 0.022 |
| 55 | 95 | 0.021 |
| 292 | 124 | 0.020 |
| 282 | 117 | 0.016 |
| 303 | 117 | 0.016 |
| 54 | 108 | 0.015 |
| 3 | 97 | 0.012 |
| 240 | 95 | 0.012 |
| Variables | Coefficients |
|---|---|
| (Intercept) | 105.936153 |
| h(108-HR) | −1.063314 |
| h(HR-108) | 0.286334 |
| h(CC-115) | 4.494783 |
| h(CC-116) | −8.182082 |
| h(118-CC) | 0.977991 |
| h(CC-118) | 13.999379 |
| h(CC-119) | −7.825563 |
| h(41-HW) | −1.210453 |
| h(HW-41) | −1.296884 |
| h(51-TL) | −0.138144 |
| Province Mardin * h(WH-106) | 0.443792 |
| h(98-HR) * h(118-CC) | −0.065563 |
| h(108-HR) * h(36-HW) | 0.144160 |
| h(108-HR) * h(CAC-13.5) | 0.906941 |
| h(108-HR) * h(LL-45) | 0.055649 |
| h(108-HR) * h(45-LL) | 0.048355 |
| h(CC-113) * h(41-HW) | 0.908293 |
| h(114-CC) * h(41-HW) | −0.111693 |
| h(CC-114) * h(41-HW) | −1.079222 |
| h(CC-118) * h(TL-42) | 0.116470 |
| h(CC-118) * h(42-TL) | 0.304491 |
| h(41-HW) * h(HL-59) | 0.211118 |
| h(41-HW) * h(59-HL) | 0.061253 |
| Province Kars * h(41-HW) * h(59-HL) | −0.052772 |
| h(2-Age) * h(41-HW) * h(59-HL) | −0.049791 |
| h(108-HR) * h(CW-25) * h(13.5-CAC) | 0.067626 |
| h(108-HR) * h(25-CW) * h(13.5-CAC) | 0.088635 |
| h(108-HR) * h(HW-36) * h(CAC-13) | 0.534718 |
| h(108-HR) * h(HW-36) * h(13-CAC) | 0.556636 |
| h(108-HR) * h(46-TL) * h(CAC-13.5) | 7.388817 |
| h(CC-113) * h(41-HW) * h(46-LL) | −0.312434 |
| h(108-HR) * CC * h(46-TL) * h(CAC-13.5) | −0.066624 |
| h(108-HR) * h(CC-111) * h(HW-36) * h(LL-48) | −0.016711 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Çelik, Ş.; Yılmaz, O. Investigation of the Relationships between Coat Colour, Sex, and Morphological Characteristics in Donkeys Using Data Mining Algorithms. Animals 2023, 13, 2366. https://doi.org/10.3390/ani13142366
Çelik Ş, Yılmaz O. Investigation of the Relationships between Coat Colour, Sex, and Morphological Characteristics in Donkeys Using Data Mining Algorithms. Animals. 2023; 13(14):2366. https://doi.org/10.3390/ani13142366
Chicago/Turabian StyleÇelik, Şenol, and Orhan Yılmaz. 2023. "Investigation of the Relationships between Coat Colour, Sex, and Morphological Characteristics in Donkeys Using Data Mining Algorithms" Animals 13, no. 14: 2366. https://doi.org/10.3390/ani13142366
APA StyleÇelik, Ş., & Yılmaz, O. (2023). Investigation of the Relationships between Coat Colour, Sex, and Morphological Characteristics in Donkeys Using Data Mining Algorithms. Animals, 13(14), 2366. https://doi.org/10.3390/ani13142366





