Genomic Selection for Milk Production Traits in Xinjiang Brown Cattle
Abstract
Simple Summary
Abstract
1. Introduction
2. Materials and Methods
2.1. Data Source and Processing
2.2. Genotyping Data
2.3. Statistical Analysis
2.3.1. Estimation of Genetic Parameters of the Single-Trait Model
2.3.2. Estimation of Genetic Parameters of the Multitrait Model
2.3.3. Calculation of Heritability
2.3.4. Reliability of Breeding Value Estimation
3. Results
3.1. Descriptive Statistical Analysis of Each Trait
3.2. Estimation of the Genetic Parameters of Milk Production Traits
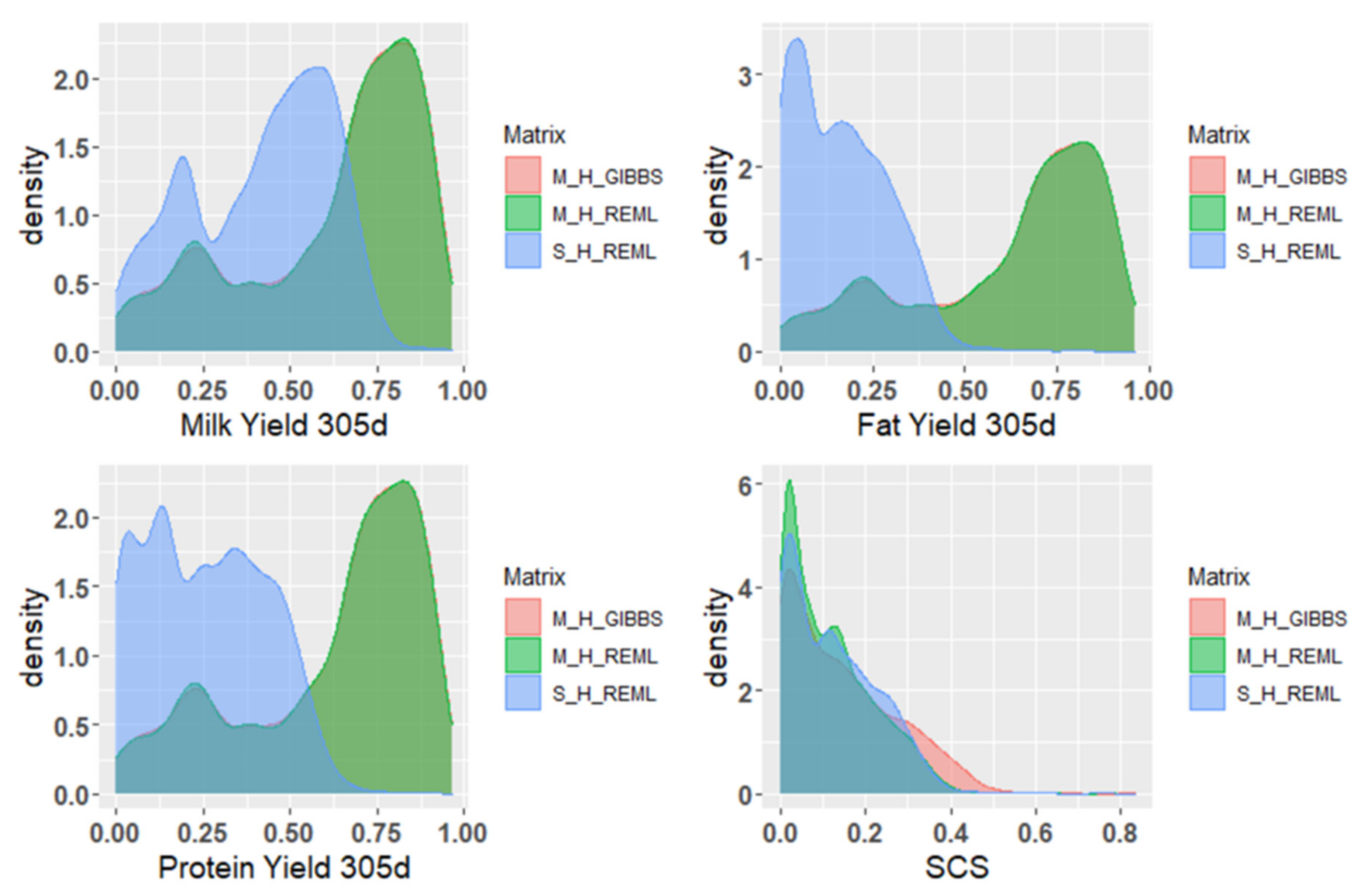
3.3. Reliability of Breeding Value Estimation of Milk Production Traits
4. Discussion
4.1. Analysis of Genetic Parameters of Milk Production Traits
4.2. Predictive Analysis of EBV and GEBV Reliability
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Xu, L. Estimates of Genetic Parameters and Total Performance Index Construction of Xinjiang Brown Cattle; Xinjiang Agricultural University: Urumqi, China, 2020. [Google Scholar]
- Zhou, J.; Li, P.; Liu, L.; Zhao, G. The present situation and the genetic improvement proposal of the Xinjiang Brown Cattle. Chin. J. Anim. Sci. 2017, 53, 38–43. [Google Scholar]
- Meuwissen, T.H.; Hayes, B.J.; Goddard, M.E. Prediction of total genetic value using genome-wide dense marker maps. Genetics 2001, 157, 1819–1829. [Google Scholar] [CrossRef] [PubMed]
- Hayes, B.J.; Bowman, P.J.; Chamberlain, A.J.; Goddard, M.E. Invited review: Genomic selection in dairy cattle: Progress and challenges. J. Dairy Sci. 2009, 92, 433–443. [Google Scholar] [CrossRef] [PubMed]
- Legarra, A.; Aguilar, I.; Misztal, I. A relationship matrix including full pedigree and genomic information. J. Dairy Sci. 2009, 92, 4656–4663. [Google Scholar] [CrossRef] [PubMed]
- Misztal, I.; Legarra, A.; Aguilar, I. Computing procedures for genetic evaluation including phenotypic, full pedigree, and genomic information. J. Dairy Sci. 2009, 92, 4648–4655. [Google Scholar] [CrossRef] [PubMed]
- Bolormaa, S.; Pryce, J.E.; Zhang, Y.; Reverter, A.; Barendse, W.; Hayes, B.J.; Goddard, M.E. Non-additive genetic variation in growth, carcass and fertility traits of beef cattle. Genet. Sel. Evol. 2015, 47, 26. [Google Scholar] [CrossRef] [PubMed]
- Su, G.; Madsen, P.; Nielsen, U.S.; Mäntysaari, E.A.; Aamand, G.P.; Christensen, O.F.; Lund, M.S. Genomic prediction for Nordi Red cattle using one-step and selection index blending. J. Dairy Sci. 2012, 95, 909–917. [Google Scholar] [CrossRef] [PubMed]
- Meuwissen, T.H.E. Accuracy of breeding values of ’unrelated’ individuals predicted by dense SNP genotyping. Genet. Sel. Evol. 2009, 41, 35. [Google Scholar] [CrossRef]
- Harris, B.L.; Johnson, D.L. Genomic predictions for New Zealand dairy bulls and integration with national genetic evaluation. J. Dairy Sci. 2010, 93, 1243–1252. [Google Scholar] [CrossRef]
- Su, G.; Ma, P.; Nielsen, U.S.; Aamand, G.P.; Wiggans, G.; Guldbrandtsen, B.; Lund, M.S. Sharing reference data and including cows in the reference population improve genomic predictions in Danish Jersey. Animal 2016, 10, 1067–1075. [Google Scholar] [CrossRef]
- Li, X.; Wang, S.; Huang, J.; Li, L.; Zhang, Q.; Ding, X. Improving the accuracy of genomic prediction in Chinese Holstein cattle by using one-step blending. Genet. Sel. Evol. 2014, 46, 66. [Google Scholar] [CrossRef][Green Version]
- Legarra, A.A.; Christensen, O.F.B.; Aguilar, I.C.; Misztal, I.D. Single Step, a general approach for genomic selection. Livest. Sci. 2014, 166, 54–65. [Google Scholar] [CrossRef]
- Misztal, I.; Vitezica, Z.G.; Legarra, A.; Aguilar, I.; Swan, A.A. Unknown-parent groups in single-step genomic evaluation. J. Anim. Breed. Genet. 2013, 130, 252–258. [Google Scholar] [CrossRef] [PubMed]
- Teissier, M.; Larroque, H.; Robert-Granié, C. Weighted single-step genomic BLUP improves accuracy of genomic breeding values for protein content in French dairy goats: A quantitative trait influenced by a major gene. Genet. Sel. Evol. 2018, 50, 31. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.Y.; Misztal, I.; Aguilar, I.; Tsuruta, S.; Meuwissen, T.H.E.; Aggrey, S.E.; Wing, T.; Muir, W.M. Genome-wide marker-assisted selection combining all pedigree phenotypic information with genotypic data in one step: An example using broiler chickens. J. Anim. Sci. 2011, 89, 23–28. [Google Scholar] [CrossRef] [PubMed]
- Yoshida, G.M.; Carvalheiro, R.; Rodríguez, F.H.; Lhorente, J.P.; Yáñez, J.M. Single-step genomic evaluation improves accuracy of breeding value predictions for resistance to infectious pancreatic necrosis virus in rainbow trout. Genomics 2019, 111, 127–132. [Google Scholar] [CrossRef]
- Guarini, A.R.; Lourenco, D.A.L.; Brito, L.F.; Sargolzaei, M.; Baes, C.F.; Miglior, F.; Tsuruta, S.; Misztal, I.; Schenkel, F.S. Use of a single-step approach for integrating foreign information into national genomic evaluation in Holstein cattle. J. Dairy Sci. 2019, 102, 8175–8183. [Google Scholar] [CrossRef]
- Chen, G.; Zhang, Q. Animal Genetic Principle and Breeding Method; China Agricultural Press: Beijing, China, 2009. [Google Scholar]
- Xu, C.; Wang, X.; Li, Z.; Xu, S. Mapping QTL for multiple traits using Bayesian statistics. Genet. Res. 2009, 91, 23–37. [Google Scholar] [CrossRef] [PubMed]
- Aguilar, I.; Misztal, I.; Tsuruta, S.; Wiggans, G.R.; Lawlor, T.J. Multiple trait genomic evaluation of conception rate in Holsteins. J. Dairy Sci. 2011, 94, 2621–2624. [Google Scholar] [CrossRef]
- Jia, Y.; Jannink, J. Multiple-Trait Genomic Selection Methods Increase Genetic Value Prediction Accuracy. Genetics 2012, 192, 1513–1522. [Google Scholar] [CrossRef]
- Miar, Y.; Plastow, G.S.; Moore, S.S.; Manafiazar, G.; Charagu, P.; Kemp, R.A.; Van Haandel, B.; Huisman, A.E.; Zhang, C.Y.; McKay, R.M.; et al. Genetic and phenotypic parameters for carcass and meat quality traits in commercial crossbred pigs. J. Anim. Sci. 2014, 92, 2869–2884. [Google Scholar] [CrossRef] [PubMed]
- Jiang, J.; Zhang, Q.; Ma, L.; Li, J.; Wang, Z.; Liu, J. Joint prediction of multiple quantitative traits using a Bayesian multivariate antedependence model. Heredity 2015, 115, 29–36. [Google Scholar] [CrossRef] [PubMed]
- Hayashi, T.; Iwata, H. EM algorithm for Bayesian estimation of genomic breeding values. BMC Genet. 2010, 11, 3. [Google Scholar] [CrossRef] [PubMed]
- Guo, G.; Zhao, F.; Wang, Y.; Zhang, Y.; Du, L.; Su, G. Comparison of single-trait and multiple-trait genomic prediction models. BMC Genet. 2014, 15, 30. [Google Scholar] [CrossRef]
- Henderson, C.R. Best linear unbiased estimation and prediction under a selection model. Biometrics 1975, 31, 423–447. [Google Scholar] [CrossRef] [PubMed]
- Aguilar, I.; Misztal, I.; Johnson, D.L.; Legarra, A.; Tsuruta, S.; Lawlor, T.J. Hot topic: A unified approach to utilize phenotypic, full pedigree, and genomic information for genetic evaluation of Holstein final score. J. Dairy Sci. 2010, 93, 743–752. [Google Scholar] [CrossRef] [PubMed]
- Dekkers, J.C.M. Prediction of response to marker-assisted and genomic selection using selection index theory. J. Anim. Breed. Genet. 2007, 124, 331–341. [Google Scholar] [CrossRef]
- Misztal, I.; Tsuruta, S. Manual for BLUPF90 Family of Programs; University of Georgia: Athens, Greece, 2015. [Google Scholar]
- Meyer, K.; Houle, D. Sampling based approximation of confidence intervals for functions of genetic covariance matrices. Proc. Assoc. Advmt. Anim. Breed. Genet. 2013, 20, 523–526. [Google Scholar]
- Meng, Q.; Hua, C.; Chun, Y.; Gang, Y.; Li, S.; Yuan, Z. Chinese and international situation, progresses and perspectives of breeding strategies in dual purpose cattle. China Dairy Cattle 2013, 13, 18–21. [Google Scholar]
- Zółkiewski, P.; Stanek, P.; Janus, E. Productivity of Simmental and Monbeliarde cows culled ub 2005–2006 taking into account the reasons for their culling. Acta Sci. Pol. Zootech. 2018, 17, 15–22. [Google Scholar] [CrossRef]
- Cesarani, A.; Gaspa, G.; Masuda, Y.; Degano, L.; Vicario, D.; Lourenco, D.A.; Macciotta, N.P. Variance components using genomic information for two functional traits in Italian Simmental cattle: Calving interval and lactation persistency. J. Dairy Sci. 2020, 103, 5227–5233. [Google Scholar] [CrossRef] [PubMed]
- Zhou, J.; Liu, L.; Chen, C.J.; Zhang, M.; Lu, X.; Zhang, Z.; Huang, X.; Shi, Y. Genome-wide association study of milk and reproductive traits in dual-purpose Xinjiang Brown cattle. BMC Genom. 2019, 20, 827. [Google Scholar] [CrossRef] [PubMed]
- Gibson, K.D.; Dechow, C.D. Genetic parameters for yield, fitness, and type traits in US Brown Swiss dairy cattle. J. Dairy Sci. 2018, 101, 1251–1257. [Google Scholar] [CrossRef]
- Dal Zotto, R.; De Marchi, M.; Dalvit, C.; Cassandro, M.; Gallo, L.; Carnier, P.; Bittante, G. Heritabilities and genetic correlations of body condition score and calving interval with yield, somatic cell score, and linear type traits in Brown Swiss cattle. J. Dairy Sci. 2007, 90, 5737–5743. [Google Scholar] [CrossRef] [PubMed]
- Loberg, A.; Dürr, J.W.; Fikse, W.F.; Jorjani, H.; Crooks, L. Estimates of genetic variance and variance of predicted genetic merits using pedigree or genomic relationship matrices in six Brown Swiss cattle populations for different traits. J. Anim. Breed. Genet. 2015, 132, 376–385. [Google Scholar] [CrossRef] [PubMed]
- Haile-Mariam, M.; Nieuwhof, G.J.; Beard, K.T.; Konstatinov, K.V.; Hayes, B. Comparison of heritabilities of dairy traits in Australian Holstein-Friesian cattle from genomic and pedigree data and implications for genomic evaluations. J. Anim. Breed. Genet. 2013, 130, 20–31. [Google Scholar] [CrossRef]
- Veerkamp, R.F.; Mulder, H.A.; Thompson, R.; Calus, M.P.L. Genomic and pedigree-based genetic parameters for scarcely recorded traits when some animals are genotyped. J. Dairy Sci. 2011, 94, 4189–4197. [Google Scholar] [CrossRef]
- Jensen, J.; Su, G.; Madsen, P. Partitioning additive genetic variance into genomic and remaining polygenic components for complex traits in dairy cattle. BMC Genet. 2012, 13, 44. [Google Scholar] [CrossRef]
- Powell, J.E.; Visscher, P.M.; Goddard, M.E. Reconciling the analysis of IBD and IBS in complex trait studies. Nat. Rev. Genet. 2010, 11, 800–805. [Google Scholar] [CrossRef] [PubMed]
- Calus, M.P.L.; Meuwissen, T.H.E.; de Roos, A.P.W.; Veerkamp, R.F. Accuracy of Genomic Selection Using Different Methods to Define Haplotypes. Genetics 2008, 178, 553–561. [Google Scholar] [CrossRef]
- Habier, D.; Fernando, R.L.; Dekkers, J.C.M. The Impact of Genetic Relationship Information on Genome-Assisted Breeding Values. Genetics 2007, 177, 2389–2397. [Google Scholar] [CrossRef]
- Daetwyler, H.D.; Villanueva, B.; Bijma, P.; Woolliams, J.A. Inbreeding in genome-wide selection. J. Anim. Breed. Genet. 2007, 124, 369–376. [Google Scholar] [CrossRef]
- Muir, W.M. Comparison of genomic and traditional BLUP-estimated breeding value accuracy and selection response under alternative trait and genomic parameters. J. Anim. Breed. Genet. 2007, 124, 342–355. [Google Scholar] [CrossRef]
- Forni, S.; Aguilar, I.; Misztal, I. Different genomic relationship matrices for single-step analysis using phenotypic, pedigree and genomic information. Genet. Sel. Evol. 2011, 43, 1. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, Q. Linear Model in Livestock and Poultry Breeding; Beijing Agricultural University Press: Beijing, China, 1993. [Google Scholar]
- Hossein-zadeh, N.G. Estimates of genetic parameters and genetic trends for production and reproduction traits in Iranian buffaloes (Bubalus bubalis). Anim. Prod. Sci. 2017, 57, 216–222. [Google Scholar] [CrossRef]
- Foroutanifar, S. Comparison of long-term effects of genomic selection index and genomic selection using different Bayesian methods. Livest. Sci. 2020, 241, 104207. [Google Scholar] [CrossRef]
- Gao, H. Comparison of Statistical Models for Genomic Prediction Based on Nordic Cow Population; China Agricultural University: Beijing, China, 2012. [Google Scholar]
- Vanraden, P.M.; Van Tassell, C.P.; Wiggans, G.R.; Sonstegard, T.S.; Schnabel, R.D.; Taylor, J.F.; Schenkel, F.S. Invited review: Reliability of genomic predictions for North American Holstein bulls. J. Dairy Sci. 2009, 92, 16–24. [Google Scholar] [CrossRef] [PubMed]
- Nordbø, Ø.; Gjuvsland, A.B.; Eikje, L.S.; Meuwissen, T. Level-biases in estimated breeding values due to the use of different SNP panels over time in ssGBLUP. Genet. Sel. Evol. 2019, 51, 76. [Google Scholar] [CrossRef] [PubMed]
- Ventura, R.V.; Miller, S.P.; Dodds, K.G.; Auvray, B.; Lee, M.; Bixley, M.; Clarke, S.M.; Mcewan, J.C. Assessing accuracy of imputation using different SNP panel densities in a multi-breed sheep population. Genet. Sel. Evol. 2016, 48, 71. [Google Scholar] [CrossRef] [PubMed]
- Casellas, J.A.; Piedrafita, J.B. Accuracy and expected genetic gain under genetic or genomic evaluation in sheep flocks with different amounts of pedigree, genomic and phenotypic data. Livest. Sci. 2015, 182, 58–63. [Google Scholar] [CrossRef]
- Liu, A. Estimation of Genetic Parameters and Genomic Prediction of Reproductive Traits in Dairy Cows; China Agricultural University: Beijing, China, 2018. [Google Scholar]
- Cesarani, A.; Gaspa, G.; Correddu, F.; Cellesi, M.; Dimauro, C.; Macciotta, N.P.P. Genomic selection of milk fatty acid composition in Sarda dairy sheep: Effect of different phenotypes and relationship matrices on heritability and breeding value accuracy. J. Dairy Sci. 2019, 102, 3189–3203. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.; Ekine-Dzivenu, C.; Vinsky, M.; John, B.; Jennifer, A.; Mike, E.R.D.; Carolyn, F.; Paul, S.; Li, C. Genome-wide association and genomic prediction of breeding values for fatty acid composition in subcutaneous adipose and longissimus lumborum muscle of beef cattle. BMC Genet. 2015, 16, 135. [Google Scholar] [CrossRef] [PubMed]
- Zhou, L.; Wang, Y.; Yu, J.; Yang, H.; Kang, H.; Zhang, S.; Wang, C.; Liu, J. Improving genomic prediction for two Yorkshire populations with a limited size using the single-step method. Anim. Genet. 2019, 50, 391–394. [Google Scholar] [CrossRef] [PubMed]
- Lund, M.S.; de Roos, A.P.; de Vries, A.G.; Druet, T.; Ducrocq, V.; Fritz, S.; Guillaume, F.; Guldbrandtsen, B.; Liu, Z.; Reents, R.; et al. A common reference population from four European Holstein populations increases reliability of genomic predictions. Genet. Sel. Evol. 2011, 43, 43. [Google Scholar] [CrossRef] [PubMed]
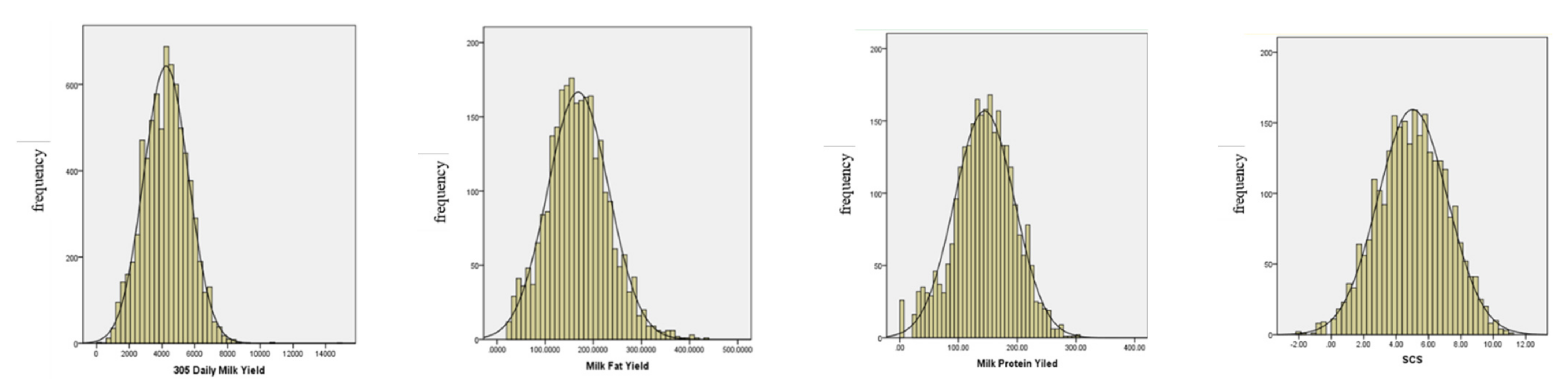
| Trait 1 | Number | Minimum | Maximum | Average | SD | CV |
|---|---|---|---|---|---|---|
| 305 dMY/kg | 7515 | 814 | 8444 | 4126.49 | 1405.71 | 34.07 |
| MFY/kg | 2655 | 21.6 | 431.55 | 168.53 | 68.29 | 40.52 |
| MPY/kg | 2655 | 20.3 | 302.72 | 143.71 | 51.42 | 35.78 |
| SCS | 2655 | −2.05 | 10.95 | 4.98 | 2.16 | 43.37 |
| PBLUP | ssGBLUP | ||||||
|---|---|---|---|---|---|---|---|
| Trait 1 | |||||||
| REML (single-trait model) | 305 dMY | 275,620 (21,393) | 922,930 (18,862) | 0.238 (0.016) | 276,960 (21,545) | 924,850 (18,869) | 0.239 (0.016) |
| MFY | 198.390 (67.272) | 2849.800 (95.395) | 0.065 (0.022) | 197.690 (63.325) | 2843.100 (93.252) | 0.065 (0.021) | |
| MPY | 233.960 (43.413) | 1427.100 (47.843) | 0.141 (0.025) | 230.860 (43.347) | 1429 (47.566) | 0.139 (0.025) | |
| SCS | 0.177 (0.076) | 4.0239 (0. 127) | 0.042 (0.018) | 0.15410 (0.073) | 4.047 (0.127) | 0.037 (0.017) | |
| REML (Multiple-trait model) | 305 dMY | 499,900 (30,746) | 803,200 (15,783) | 0.384 (0.016) | 507,300 (31,206) | 804,400 (15,803) | 0.387 (0.016) |
| MFY | 1341 (119.960) | 2138 (67.600) | 0.386 (0.024) | 1368 (121.450) | 2146 (67.735) | 0.389 (0.024) | |
| MPY | 937.500 (74.342) | 1026 (1.370) | 0.478 (0.023) | 961.400 (75.724) | 1028 (31.676) | 0.483 (0.027) | |
| SCS | 0.189 (0.077) | 4.015 (0.130) | 0.045 (0.018) | 0.164 (0.07362) | 4.040 (0.127) | 0.039 (0.017) | |
| Bayes (Multiple-trait model) | 305 dMY | 506,620 (26,877) | 803,370 (15,108) | 0.387 (0.014) | 503,920 (26,790) | 805,970 (15,165) | 0.385 (0.014) |
| MFY | 1368.800 (101.480) | 2142.800 (63.356) | 0.389 (0.020) | 1426.400 (100.910) | 2148.500 (63.497) | 0.399 (0.019) | |
| MPY | 932.260 (53.003) | 1031.300 (30.717) | 0.475 (0.017) | 987.080 (59.840) | 1032.300 (30.720) | 0.488 (0.018) | |
| SCS | 0.290 (0.080) | 3.978 (0.129) | 0.068 (0.018) | 0.273 (0.078) | 3.997 (0.129) | 0.065 (0.018) | |
| Whole Population | Genotyped Subpopulation | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Traits 1 | PBLUP | ssGBLUP | Δrel (%) | Correlation | PBLUP | ssGBLUP | Δrel (%) | Correlation | |
| REML (single-trait model) | 305 dMY | 0.404 (0.206) | 0.414 (0.201) | 1 | 0.98 ** | 0.491 (0.123) | 0.526 (0.108) | 3.5 | 0.89 ** |
| MFY | 0.148 (0.117) | 0.166 (0.126) | 1.8 | 0.89 ** | 0.213 (0.115) | 0.237 (0.115) | 2.5 | 0.73 ** | |
| MPY | 0.242 (0.172) | 0.258 (0.173) | 1.6 | 0.94 ** | 0.341 (0.154) | 0.377 (0.150) | 3.6 | 0.81 ** | |
| SCS | 0.115 (0.097) | 0.125 (0.106) | 1 | 0.87 ** | 0.161 (0.093) | 0.172 (0.095) | 1.1 | 0.76 ** | |
| REML (Multiple-trait model) | 305 dMY | 0.612 (0.265) | 0.620 (0.257) | 0.9 | 0.99 ** | 0.811 (0.092) | 0.825 (0.085) | 1.4 | 0.97 ** |
| MFY | 0.610 (0.265) | 0.619 (0.257) | 1 | 0.99 ** | 0.810 (0.092) | 0.824 (0.085) | 1.4 | 0.97 ** | |
| MPY | 0.611 (0.265) | 0.619 (0.257) | 0.9 | 0.99 ** | 0.810 (0.092) | 0.825 (0.085) | 1.5 | 0.97 ** | |
| SCS | 0.109 (0.099) | 0.119 (0.103) | 1 | 0.90 ** | 0.190 (0.095) | 0.199 (0.097) | 1 | 0.81 ** | |
| Bayes (Multiple-trait model) | 305 dMY | 0.614 (0.265) | 0.621 (0.258) | 0.8 | 0.99 ** | 0.813 (0.090) | 0.828 (0.083) | 1.5 | 0.97 ** |
| MFY | 0.610 (0.264) | 0.619 (0.257) | 1 | 0.99 ** | 0.809 (0.090) | 0.825 (0.083) | 1.6 | 0.97 ** | |
| MPY | 0.613 (0.265) | 0.621 (0.258) | 0.9 | 0.99 ** | 0.812 (0.090) | 0.827 (0.083) | 1.5 | 0.97 ** | |
| SCS | 0.133 (0.122) | 0.146 (0.128) | 1.3 | 0.91 ** | 0.235 (0.118) | 0.260 (0.119) | 2.5 | 0.79 ** | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, M.; Luo, H.; Xu, L.; Shi, Y.; Zhou, J.; Wang, D.; Zhang, X.; Huang, X.; Wang, Y. Genomic Selection for Milk Production Traits in Xinjiang Brown Cattle. Animals 2022, 12, 136. https://doi.org/10.3390/ani12020136
Zhang M, Luo H, Xu L, Shi Y, Zhou J, Wang D, Zhang X, Huang X, Wang Y. Genomic Selection for Milk Production Traits in Xinjiang Brown Cattle. Animals. 2022; 12(2):136. https://doi.org/10.3390/ani12020136
Chicago/Turabian StyleZhang, Menghua, Hanpeng Luo, Lei Xu, Yuangang Shi, Jinghang Zhou, Dan Wang, Xiaoxue Zhang, Xixia Huang, and Yachun Wang. 2022. "Genomic Selection for Milk Production Traits in Xinjiang Brown Cattle" Animals 12, no. 2: 136. https://doi.org/10.3390/ani12020136
APA StyleZhang, M., Luo, H., Xu, L., Shi, Y., Zhou, J., Wang, D., Zhang, X., Huang, X., & Wang, Y. (2022). Genomic Selection for Milk Production Traits in Xinjiang Brown Cattle. Animals, 12(2), 136. https://doi.org/10.3390/ani12020136







