Predicting Subclinical Ketosis in Dairy Cows Using Machine Learning Techniques
Abstract
:Simple Summary
Abstract
1. Introduction
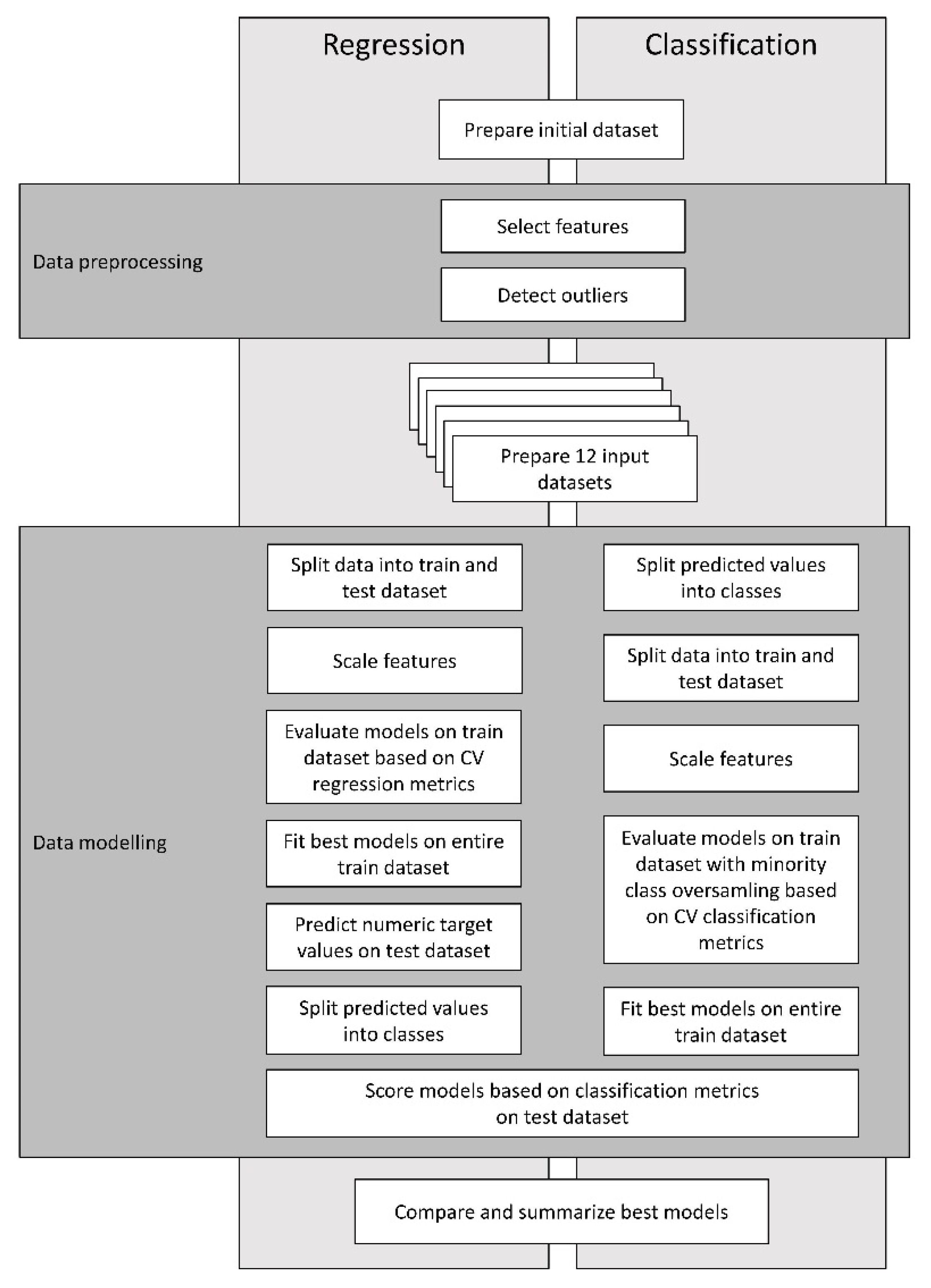
2. Materials and Methods
2.1. Initial Dataset
2.2. Approach
2.3. Data Pre-Processing for Machine Learning
2.3.1. Feature Selection
2.3.2. Outliers
2.4. Modeling Pipelines—Description and Validation of Models
2.4.1. Regression Pipeline
2.4.2. Classification Pipeline
2.4.3. Evaluation Metrics
3. Results
3.1. Number of Models
3.2. Performance of Classification Models
3.3. Performance of Regression Models
4. Discussion
4.1. The Use of Classification Models for Diagnosing Subclinical Ketosis
4.2. The Use of Regression Models for Diagnosing Subclinical Ketosis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Oetzel, G.R. Monitoring and testing dairy herds for metabolic disease. Vet. Clin. North Am. Food Anim. Pract. 2004, 20, 651–674. [Google Scholar] [CrossRef]
- LeBlanc, S.J. Monitoring metabolic health of dairy cattle in the transition period. J. Reprod. Dev. 2010, 56 (Suppl. 56), S29–S35. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- McArt, J.A.A.; Nydam, D.V.; Overton, M.W. Hyperketonemia in early lactation dairy cattle: A deterministic estimate of component and total cost per case. J. Dairy Sci. 2015, 98, 2043–2054. [Google Scholar] [CrossRef] [Green Version]
- Seifi, H.A.; LeBlanc, S.J.; Leslie, K.E.; Duffield, T.F. Metabolic predictors of post-partum disease and culling risk in dairy cattle. Vet. J. 2011, 188, 216–220. [Google Scholar] [CrossRef] [PubMed]
- LeBlanc, S.J.; Leslie, K.; Duffield, T. Metabolic predictors of displaced abomasum in dairy cattle. J. Dairy Sci. 2005, 88, 159–170. [Google Scholar] [CrossRef] [Green Version]
- Duffield, T.F.; Lissemore, K.; McBride, B.; Leslie, K. Impact of hyperketonemia in early lactation dairy cows on health and production. J. Dairy Sci. 2009, 92, 571–580. [Google Scholar] [CrossRef] [Green Version]
- Suthar, V.S.; Canelas-Raposo, J.; Deniz, A.; Heuwieser, W. Prevalence of subclinical ketosis and relationships with postpartum diseases in European dairy cows. J. Dairy Sci. 2013, 96, 2925–2938. [Google Scholar] [CrossRef] [Green Version]
- Liang, D.; Arnold, L.M.; Stowe, C.J.; Harmon, R.J.; Bewley, J.M. Estimating US dairy clinical disease costs with a stochastic simulation model. J. Dairy Sci. 2017, 100, 1472–1486. [Google Scholar] [CrossRef] [Green Version]
- Mostert, P.F.; Bokkers, E.A.M.; van Middelaar, C.E.; Hogeveen, H.; de Boer, I.J.M. Estimating the economic impact of subclinical ketosis in dairy cattle using a dynamic stochastic simulation model. Animal 2018, 12, 145–154. [Google Scholar] [CrossRef]
- Andersson, L.; Gustafsson, A.H.; Emanuelson, U. Effect of hyperketonaemia and feeding on fertility in dairy cows. Theriogenology 1991, 36, 521–536. [Google Scholar] [CrossRef]
- Walsh, R.B.; Walton, J.; Kelton, D.; LeBlanc, S.; Leslie, K.; Duffield, T. The effect of subclinical ketosis in early lactation on reproductive performance of postpartum dairy cows. J. Dairy Sci. 2007, 90, 2788–2796. [Google Scholar] [CrossRef] [Green Version]
- Andersson, L. Subclinical ketosis in dairy cows. Vet. Clin. North Am. Food Anim. Pract. 1988, 4, 233–251. [Google Scholar] [CrossRef]
- Benedet, A.; Manuelian, C.L.; Zidi, A.; Penasa, M.; De Marchi, M. Invited review: β-hydroxybutyrate concentration in blood and milk and its associations with cow performance. Animal 2019, 13, 1676–1689. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- van Haelst, Y.N.T.; Beeckman, A.; van Knegsel, A.T.M.; Fievez, V. Short communication: Elevated concentrations of oleic acid and long-chain fatty acids in milk fat of multiparous subclinical ketotic cows. J. Dairy Sci. 2008, 91, 4683–4686. [Google Scholar] [CrossRef] [PubMed]
- van der Drift, S.G.A.; Jorritsma, R.; Schonewille, J.T.; Knijn, H.M.; Stegeman, J.A. Routine detection of hyperketonemia in dairy cows using Fourier transform infrared spectroscopy analysis of β-hydroxybutyrate and acetone in milk in combination with test-day information. J. Dairy Sci. 2012, 95, 4886–4898. [Google Scholar] [CrossRef] [Green Version]
- Ruoff, J.; Borchardt, S.; Heuwieser, W. Short communication: Associations between blood glucose concentration, onset of hyperketonemia, and milk production in early lactation dairy cows. J. Dairy Sci. 2017, 100, 5462–5467. [Google Scholar] [CrossRef]
- Belay, T.K.; Svendsen, M.; Kowalski, Z.M.; Ådnøy, T. Genetic parameters of blood β-hydroxybutyrate predicted from milk infrared spectra and clinical ketosis, and their associations with milk production traits in Norwegian Red cows. J. Dairy Sci. 2017, 100, 6298–6311. [Google Scholar] [CrossRef]
- Chandler, T.L.; Pralle, R.S.; Dόrea, J.R.R.; Poock, S.E.; Oetzel, G.R.; Fourdraine, R.H.; White, H.M. Predicting hyperketonemia by logistic and linear regression using test-day milk and performance variables in early-lactation Holstein and Jersey cows. J. Dairy Sci. 2018, 101, 2476–2491. [Google Scholar] [CrossRef]
- Ospina, P.A.; Nydam, D.V.; Stokol, T.; Overton, T.R. Evaluation of nonesterified fatty acids and β-hydroxybutyrate in transition dairy cattle in the northeastern United States: Critical thresholds for prediction of clinical diseases. J. Dairy Sci. 2010, 93, 546–554. [Google Scholar] [CrossRef]
- Ospina, P.A.; Nydam, D.V.; Stokol, T.; Overton, T.R. Associations of elevated nonesterified fatty acids and β-hydroxybutyrate concentrations with early lactation reproductive performance and milk production in transition dairy cattle in the northeastern United States. J. Dairy Sci. 2010, 93, 1596–1603. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chapinal, N.; LeBlanc, S.J.; Carson, M.E.; Leslie, K.E.; Godden, S.; Capel, M.; Santos, J.E.P.; Overton, M.W.; Duffield, T.F. Herd-level association of serum metabolites in the transition period with disease, milk production, and early lactation reproductive performance. J. Dairy Sci. 2012, 95, 5676–5682. [Google Scholar] [CrossRef]
- Andersson, L. Concentrations of blood and milk ketone bodies, blood isopropanol and plasma glucose in dairy cows in relation to the degree of hyperketonemia and clinical signs. Zentralbl. Veterinarmed. A 1984, 31, 683–693. [Google Scholar] [CrossRef] [PubMed]
- van Knegsel, A.T.M.; van der Drift, S.G.A.; Horneman, M.; de Roos, A.P.W.; Kemp, B.; Graat, E.A.M. Short communication: Ketone body concentration in milk determined by Fourier transform infrared spectroscopy: Value for the detection of hyperketonemia in dairy cows. J. Dairy Sci. 2010, 93, 065–3069. [Google Scholar] [CrossRef] [PubMed]
- Vanholder, T.; Papen, J.; Bemers, R.; Vertenten, G.; Berge, A.C.B. Risk factors for subclinical and clinical ketosis and association with production parameters in dairy cows in the Netherlands. J. Dairy Sci. 2015, 98, 880–888. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kowalski, Z.M.; Plyta, A.; Rybicka, E.; Jagusiak, W.; Sloniewski, K. Novel model of monitoring of subclinical ketosis in dairy herds in Poland based on monthly milk recording and estimation of ketone bodies in milk by FTIR spectroscopy. ICAR Techn. Ser. 2015, 19, 25–30. [Google Scholar]
- Kotsiantis, S.B.; Zaharakis, I.; Pintelas, P. Supervised machine learning: A review of classification techniques. Informatica 2007, 31, 249–268. [Google Scholar]
- Gahegan, M. Is inductive machine learning just another wild goose (or might it lay the golden egg?). Int. J. Geogr. Inf. Sci. 2003, 17, 69–92. [Google Scholar] [CrossRef]
- Kamphuis, C.; Mollenhorst, H.; Feelders, A.J.; Pietersma, D.; Hogeveen, H. Decision-tree induction to detect clinical mastitis with automatic milking. Comput. Electron. Agric. 2010, 70, 60–68. [Google Scholar] [CrossRef]
- Ebrahimie, E.; Ebrahimi, F.; Ebrahimi, M.; Tomlinson, S.; Petrovski, K.R. Hierarchical pattern recognition in milking parameters predicts mastitis prevalence. Comput. Electron. Agric. 2018, 147, 6–11. [Google Scholar] [CrossRef]
- Ebrahimi, M.; Mohammadi-Dehcheshmeh, M.; Ebrahimie, E.; Petrovski, K.R. Comprehensive analysis of machine learning models for prediction of sub-clinical mastitis: Deep learning and gradient-boosted trees outperform other models. Comput. Biol. Med. 2019, 114, 103456. [Google Scholar] [CrossRef]
- Ebrahimie, E.; Mohammadi-Dehcheshmeh, M.; Laven, R.; Petrovski, K.R. Rule discovery in milk content towards mastitis diagnosis: Dealing with farm heterogeneity over multiple years through classification based on associations. Animals 2021, 11, 1638. [Google Scholar] [CrossRef]
- Miller, G.; Mitchell, M.; Barker, Z.; Giebel, K.; Codling, E.; Amory, J.; Michie, C.; Davison, C.; Tachtatzis, C.; Andonovic, I.; et al. Using animal-mounted sensor technology and machine learning to predict time-to-calving in beef and dairy cows. Animal 2020, 14, 1304–1312. [Google Scholar] [CrossRef]
- Bovo, M.; Agrusti, M.; Benni, S.; Torreggiani, D.; Tassinari, P. Random forest modelling of milk yield of dairy cows under heat stress conditions. Animals 2021, 11, 1305. [Google Scholar] [CrossRef] [PubMed]
- Becker, C.A.; Aghalari, A.; Marufuzzaman, M.; Stone, A.E. Predicting dairy cattle heat stress using machine learning techniques. J. Dairy Sci. 2021, 104, 501–524. [Google Scholar] [CrossRef] [PubMed]
- Biecek, P.; Burzykowski, T. Explanatory Model Analysis, 1st ed.; Chapman and Hall/CRC: New York, NY, USA, 2021. [Google Scholar]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning: Data Mining, Inference and Prediction, 2nd ed.; Springer: New York, NY, USA, 2009. [Google Scholar]
- Mower, J.P. PREP-Mt: Predictive RNA editor for plant mitochondrial genes. BMC Bioinform. 2005, 6, 96. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Matthews, B.W. Comparison of the predicted and observed secondary structure of T4 phage lysozyme. Biochim Biophys. Acta 1975, 405, 442–451. [Google Scholar] [CrossRef]
- Kayano, M.; Kataoka, T. Screening for ketosis using multiple logistic regression based on milk yield and composition. J. Vet. Med. Sci. 2015, 77, 1473–1478. [Google Scholar] [CrossRef] [Green Version]
- Denis-Robichaud, J.; Dubuc, J.; Lefebvre, D.; DesCoteaux, L. Accuracy of milk ketone bodies from flow-injection analysis for the diagnosis of hyperketonemia in dairy cows. J. Dairy Sci. 2014, 97, 3364–3370. [Google Scholar] [CrossRef]
- Duffield, T.F.; Kelton, D.F.; Leslie, K.E.; Lissemore, K.D.; Lumsden, J.H. Use of test day milk fat and milk protein to detect subclinical ketosis in dairy cattle in Ontario. Can. Vet. J. 1997, 38, 713–718. [Google Scholar]
- Krogh, M.A.; Toft, N.; Enevoldsen, C. Latent class evaluation of a milk test, a urine test, and the fat-to-protein percentage ratio in milk to diagnose ketosis in dairy cows. J. Dairy Sci. 2011, 94, 2360–2367. [Google Scholar] [CrossRef]
- Grohn, Y.T.; Erb, H.N.; McCulloch, C.E.; Saloniemi, H.S. Epidemiology of metabolic disorders in dairy cattle: Association among host characteristics, disease, and production. J. Dairy Sci. 1989, 72, 1876–1885. [Google Scholar] [CrossRef]
- Rasmussen, L.K.; Nielsen, B.L.; Pryce, J.E.; Mottram, T.T.; Veerkamp, R.F. Risk factors associated with the incidence of ketosis in dairy cows. Anim. Sci. 1999, 68, 379–386. [Google Scholar] [CrossRef]
| Item | Lactation 1 | Lactation 2 | Lactation 3 | Lactation ≥ 4 |
|---|---|---|---|---|
| Number of cows | 324 | 202 | 155 | 152 |
| bBHB (mmol/L) | 0.60 ± 0.45 | 0.83 ± 0.87 | 0.93 ± 0.90 | 0.93 ± 0.87 |
| Milk variables | ||||
| Milk (kg) | 31.5 ± 7.9 | 39.2 ± 10.3 | 39.1 ± 10.5 | 38.4 ± 10.9 |
| Fat (%) | 3.88 ± 0.72 | 4.14 ± 1.03 | 4.12 ± 1.00 | 4.30 ± 0.97 |
| Protein (%) | 3.07 ± 0.33 | 3.12 ± 0.34 | 3.06 ± 0.35 | 3.06 ± 0.37 |
| FPR | 1.27 ± 0.24 | 1.33 ± 0.32 | 1.35 ± 0.32 | 1.42 ± 0.34 |
| Lactose (%) | 4.96 ± 0.20 | 4.88 ± 0.21 | 4.85 ± 0.19 | 4.82 ± 0.23 |
| MU (mg/L) | 198 ± 60 | 202 ± 71 | 189 ± 75 | 177 ± 69 |
| SCS | 3.37 ± 1.93 | 2.86 ± 1.88 | 3.54 ± 2.17 | 3.80 ± 2.26 |
| Acetone (mmol/L) | 0.06 ± 0.09 | 0.09 ± 0.16 | 0.09 ± 0.14 | 0.10 ± 0.15 |
| mBHB (mmol/L) | 0.05 ± 0.05 | 0.07 ± 0.08 | 0.08 ± 0.08 | 0.09 ± 0.09 |
| Variable | Milk | Fat | Protein | FPR | ACE | mBHB | Lactose | MU | SCS | bBHB |
|---|---|---|---|---|---|---|---|---|---|---|
| Milk (kg) | 1 | −0.21 | −0.22 | −0.12 | −0.17 | −0.20 | 0.14 | 0.06 | −0.19 | −0.09 |
| Fat (%) | 1 | 0.30 | 0.86 | 0.49 | 0.56 | −0.36 | 0.01 | 0.14 | 0.43 | |
| Protein (%) | 1 | −0.22 | 0.05 | −0.04 | −0.27 | −0.01 | 0.17 | −0.01 | ||
| FPR | 1 | 0.46 | 0.59 | −0.23 | 0 | 0.05 | 0.44 | |||
| ACE (mmol/L) | 1 | 0.76 | −0.41 | −0.05 | 0.15 | 0.63 | ||||
| mBHB (mmol/L) | 1 | −0.40 | −0.11 | 0.16 | 0.62 | |||||
| Lactose (%) | 1 | 0.05 | −0.38 | −0.24 | ||||||
| MU (mg/L) | 1 | −0.05 | −0.07 | |||||||
| SCS | 1 | 0 | ||||||||
| bBHB (mmol/L) | 1 |
| Dataset Number | Feature Selection Method 1 | Outlier Detection Method 2 | Number of Observations | Independent Features Used for Modeling |
|---|---|---|---|---|
| 1 | Correlation | none | 833 | parity, DIM, FPR, ACE, mBHB, lactose |
| 2 | Correlation | IQR/SD | 783 | parity, DIM, FPR, ACE, mBHB, lactose |
| 3 | Correlation | LOF | 792 | parity, DIM, FPR, ACE, mBHB, lactose |
| 4 | RFE | none | 833 | ACE |
| 5 | RFE | IQR/SD | 776 | ACE |
| 6 | RFE | LOF | 811 | ACE |
| 7 | RFE | none | 833 | milk, fat, protein, FPR, ACE |
| 8 | RFE | IQR/SD | 776 | milk, fat, protein, FPR, ACE |
| 9 | RFE | LOF | 811 | milk, fat, protein, FPR, ACE |
| 10 | RFE | none | 833 | protein, ACE |
| 11 | RFE | IQR/SD | 776 | protein, ACE |
| 12 | RFE | LOF | 811 | protein, ACE |
| Dataset Number | bBHB Cut-Off | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 1.0 | 1.2 | 1.4 | |||||||
| No SCK | SCK | SCK Prevalence (%) | No SCK | SCK | SCK Prevalence (%) | No SCK | SCK | SCK Prevalence (%) | |
| 1 | 670 | 163 | 19.6 | 709 | 124 | 14.9 | 737 | 96 | 11.5 |
| 2 | 658 | 125 | 16.0 | 696 | 87 | 11.1 | 721 | 62 | 7.9 |
| 3 | 636 | 156 | 19.7 | 673 | 119 | 15.0 | 701 | 91 | 11.5 |
| 4 | 670 | 163 | 19.6 | 709 | 124 | 14.9 | 737 | 96 | 11.5 |
| 5 | 650 | 126 | 16.2 | 688 | 88 | 11.3 | 713 | 63 | 8.1 |
| 6 | 656 | 155 | 19.1 | 695 | 116 | 14.3 | 722 | 89 | 11.0 |
| 7 | 670 | 163 | 19.6 | 709 | 124 | 14.9 | 737 | 96 | 11.5 |
| 8 | 650 | 126 | 16.2 | 688 | 88 | 11.3 | 713 | 63 | 8.1 |
| 9 | 656 | 155 | 19.1 | 695 | 116 | 14.3 | 722 | 89 | 11.0 |
| 10 | 670 | 163 | 19.6 | 709 | 124 | 14.9 | 737 | 96 | 11.5 |
| 11 | 650 | 126 | 16.2 | 688 | 88 | 11.3 | 713 | 63 | 8.1 |
| 12 | 656 | 155 | 19.1 | 695 | 116 | 14.3 | 722 | 89 | 11.0 |
| Dataset Number | Model 1 | Scaler Method 2 | Oversampling Method 3 | Training (Mean ± SD) | Testing | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Sensitivity (TPR) | Specificity (TNR) | bACC | MCC | F2 | TPR | TNR | bACC | MCC | F2 | ||||
| 1 | SGD | MMS | BSMOTE | 0.72 ± 0.20 | 0.70 ± 0.19 | 0.71 ± 0.08 | 0.37 ± 0.14 | 0.60 ± 0.13 | 0.78 | 0.74 | 0.76 | 0.43 | 0.66 |
| 2 | LOG | STS | ADASYN | 0.66 ± 0.16 | 0.73 ± 0.07 | 0.69 ± 0.08 | 0.30 ± 0.12 | 0.54 ± 0.11 | 0.71 | 0.73 | 0.72 | 0.34 | 0.58 |
| 3 | SVC | RBS | ADASYN | 0.74 ± 0.14 | 0.73 ± 0.07 | 0.74 ± 0.07 | 0.40 ± 0.12 | 0.63 ± 0.11 | 0.57 | 0.72 | 0.65 | 0.25 | 0.50 |
| 4 | CAT | STS | BSMOTE | 0.67 ± 0.14 | 0.71 ± 0.10 | 0.69 ± 0.07 | 0.32 ± 0.12 | 0.57 ± 0.10 | 0.57 | 0.70 | 0.63 | 0.22 | 0.49 |
| 5 | LOG | NOR | SMOTE | 0.90 ± 0.09 | 0.14 ± 0.05 | 0.52 ± 0.05 | 0.04 ± 0.12 | 0.48 ± 0.05 | 0.87 | 0.18 | 0.52 | 0.05 | 0.48 |
| 6 | LOG | STS | BSMOTE | 0.64 ± 0.13 | 0.73 ± 0.06 | 0.69 ± 0.08 | 0.31 ± 0.13 | 0.55 ± 0.11 | 0.60 | 0.75 | 0.67 | 0.29 | 0.53 |
| 7 | SVC | none | SMOTE | 0.74 ± 0.12 | 0.50 ± 0.08 | 0.62 ± 0.07 | 0.20 ± 0.11 | 0.55 ± 0.08 | 0.61 | 0.53 | 0.57 | 0.11 | 0.47 |
| 8 | SVC | none | BSMOTE | 0.78 ± 0.16 | 0.38 ± 0.10 | 0.58 ± 0.09 | 0.12 ± 0.13 | 0.49 ± 0.09 | 0.87 | 0.28 | 0.57 | 0.12 | 0.51 |
| 9 | SVC | none | SMOTE | 0.75 ± 0.15 | 0.45 ± 0.10 | 0.60 ± 0.08 | 0.16 ± 0.12 | 0.53 ± 0.09 | 0.74 | 0.54 | 0.64 | 0.22 | 0.56 |
| 10 | SVC | STS | BSMOTE | 0.75 ± 0.11 | 0.63 ± 0.07 | 0.69 ± 0.06 | 0.31 ± 0.10 | 0.60 ± 0.08 | 0.76 | 0.61 | 0.68 | 0.29 | 0.59 |
| 11 | SVC | RBS | ADASYN | 0.63 ± 0.17 | 0.66 ± 0.08 | 0.65 ± 0.09 | 0.23 ± 0.14 | 0.49 ± 0.12 | 0.66 | 0.65 | 0.65 | 0.23 | 0.51 |
| 12 | KNN | NOR | ADASYN | 0.71 ± 0.14 | 0.60 ± 0.07 | 0.65 ± 0.08 | 0.24 ± 0.12 | 0.55 ± 0.10 | 0.66 | 0.54 | 0.60 | 0.16 | 0.50 |
| Dataset Number | Model 1 | Scaler Method 2 | Oversampling Method 3 | Training (Mean ± SD) | Testing | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Sensitivity (TPR) | Specificity (TNR) | bACC | MCC | F2 | TPR | TNR | bACC | MCC | F2 | ||||
| 1 | LOG | MMS | ADASYN | 0.73 ± 0.15 | 0.77 ± 0.06 | 0.75 ± 0.08 | 0.39 ± 0.12 | 0.60 ± 0.11 | 0.68 | 0.80 | 0.74 | 0.38 | 0.58 |
| 2 | LOG | MMS | ROS | 0.65 ± 0.17 | 0.74 ± 0.06 | 0.69 ± 0.09 | 0.27 ± 0.12 | 0.48 ± 0.12 | 0.77 | 0.76 | 0.76 | 0.36 | 0.57 |
| 3 | LOG | MMS | ADASYN | 0.74 ± 0.14 | 0.76 ± 0.06 | 0.75 ± 0.07 | 0.38 ± 0.12 | 0.60 ± 0.10 | 0.72 | 0.80 | 0.76 | 0.42 | 0.62 |
| 4 | LOG | NOR | SMOTE | 0.97 ± 0.06 | 0.15 ± 0.05 | 0.56 ± 0.04 | 0.12 ± 0.07 | 0.49 ± 0.03 | 0.86 | 0.17 | 0.52 | 0.03 | 0.45 |
| 5 | LOG | NOR | SMOTE | 0.90 ± 0.10 | 0.15 ± 0.05 | 0.53 ± 0.06 | 0.05 ± 0.10 | 0.39 ± 0.04 | 0.96 | 0.16 | 0.56 | 0.11 | 0.41 |
| 6 | LOG | NOR | SMOTE | 0.94 ± 0.08 | 0.14 ± 0.05 | 0.54 ± 0.04 | 0.08 ± 0.09 | 0.47 ± 0.04 | 0.94 | 0.19 | 0.57 | 0.12 | 0.48 |
| 7 | SVC | none | ADASYN | 0.77 ± 0.15 | 0.41 ± 0.09 | 0.59 ± 0.08 | 0.13 ± 0.13 | 0.47 ± 0.09 | 0.81 | 0.48 | 0.64 | 0.21 | 0.52 |
| 8 | SVC | none | ADASYN | 0.87 ± 0.14 | 0.30 ± 0.07 | 0.58 ± 0.07 | 0.12 ± 0.10 | 0.42 ± 0.06 | 0.69 | 0.19 | 0.44 | -0.09 | 0.31 |
| 9 | SVC | none | ADASYN | 0.83 ± 0.15 | 0.27 ± 0.07 | 0.55 ± 0.08 | 0.08 ± 0.13 | 0.45 ± 0.08 | 0.91 | 0.25 | 0.58 | 0.14 | 0.49 |
| 10 | SGD | MMS | BSMOTE | 0.68 ± 0.19 | 0.73 ± 0.19 | 0.71 ± 0.09 | 0.35 ± 0.17 | 0.55 ± 0.12 | 0.76 | 0.69 | 0.73 | 0.33 | 0.58 |
| 11 | KNN | MMS | ADASYN | 0.53 ± 0.18 | 0.67 ± 0.07 | 0.60 ± 0.09 | 0.13 ± 0.13 | 0.37 ± 0.12 | 0.54 | 0.68 | 0.61 | 0.15 | 0.38 |
| 12 | SGD | STS | BSMOTE | 0.66 ± 0.19 | 0.68 ± 0.17 | 0.67 ± 0.09 | 0.27 ± 0.15 | 0.50 ± 0.13 | 0.74 | 0.71 | 0.73 | 0.33 | 0.58 |
| Dataset Number | Model 1 | Scaler Method 2 | Oversampling Method | Training (Mean ± SD) | Testing | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Sensitivity (TPR) | Specificity (TNR) | bACC | MCC | F2 | TPR | TNR | bACC | MCC | F2 | ||||
| 1 | SGD | RBS | ADASYN | 0.73 ± 0.21 | 0.71 ± 0.13 | 0.72 ± 0.10 | 0.31 ± 0.14 | 0.52 ± 0.13 | 0.79 | 0.67 | 0.73 | 0.31 | 0.55 |
| 2 | KNN | STS | ADASYN | 0.58 ± 0.22 | 0.77 ± 0.06 | 0.67 ± 0.11 | 0.21 ± 0.14 | 0.39 ± 0.14 | 0.42 | 0.80 | 0.61 | 0.14 | 0.31 |
| 3 | LOG | STS | ADASYN | 0.75 ± 0.17 | 0.78 ± 0.06 | 0.76 ± 0.08 | 0.38 ± 0.12 | 0.58 ± 0.12 | 0.74 | 0.81 | 0.77 | 0.40 | 0.59 |
| 4 | LOG | NOR | SMOTE | 0.97 ± 0.07 | 0.17 ± 0.05 | 0.57 ± 0.04 | 0.12 ± 0.07 | 0.43 ± 0.04 | 0.97 | 0.13 | 0.55 | 0.10 | 0.42 |
| 5 | LOG | NOR | SMOTE | 0.98 ± 0.07 | 0.15 ± 0.05 | 0.56 ± 0.04 | 0.10 ± 0.06 | 0.33 ± 0.03 | 0.89 | 0.16 | 0.53 | 0.04 | 0.31 |
| 6 | LOG | NOR | SMOTE | 0.97 ± 0.07 | 0.15 ± 0.05 | 0.56 ± 0.04 | 0.11 ± 0.07 | 0.41 ± 0.03 | 0.96 | 0.17 | 0.57 | 0.12 | 0.41 |
| 7 | GNB | NOR | ADASYN | 0.77 ± 0.18 | 0.52 ± 0.10 | 0.65 ± 0.09 | 0.19 ± 0.11 | 0.46 ± 0.10 | 0.83 | 0.51 | 0.67 | 0.22 | 0.48 |
| 8 | SVC | none | ADASYN | 0.85 ± 0.15 | 0.33 ± 0.07 | 0.59 ± 0.08 | 0.11 ± 0.09 | 0.34 ± 0.06 | 0.68 | 0.38 | 0.53 | 0.04 | 0.29 |
| 9 | SVC | none | ADASYN | 0.79 ± 0.16 | 0.49 ± 0.08 | 0.64 ± 0.09 | 0.18 ± 0.11 | 0.44 ± 0.09 | 0.67 | 0.58 | 0.62 | 0.15 | 0.41 |
| 10 | KNN | none | ADASYN | 0.62 ± 0.20 | 0.73 ± 0.06 | 0.67 ± 0.10 | 0.24 ± 0.14 | 0.46 ± 0.14 | 0.66 | 0.71 | 0.69 | 0.25 | 0.48 |
| 11 | LOG | STS | SMOTE | 0.59 ± 0.23 | 0.71 ± 0.06 | 0.65 ± 0.11 | 0.18 ± 0.13 | 0.44 ± 0.13 | 0.79 | 0.78 | 0.78 | 0.35 | 0.54 |
| 12 | SVC | RBS | ADASYN | 0.74 ± 0.15 | 0.79 ± 0.07 | 0.77 ± 0.07 | 0.38 ± 0.11 | 0.58 ± 0.10 | 0.67 | 0.82 | 0.74 | 0.36 | 0.55 |
| Dataset Number | Model 1 | Scaler Method 2 | Training (Mean ± SD) | ||
|---|---|---|---|---|---|
| R2 | MAE | RMSE | |||
| 1 | SVR—linear | STS | 0.39 ± 0.26 | 0.34 ± 0.05 | 0.55 ± 0.12 |
| 2 | BayesianRidge | none | 0.14 ± 0.20 | 0.30 ± 0.04 | 0.44 ± 0.10 |
| 3 | SVR—linear | STS | 0.35 ± 0.15 | 0.35 ± 0.06 | 0.58 ± 0.15 |
| 4 | SVR—linear | none | 0.37 ± 0.26 | 0.35 ± 0.05 | 0.55 ± 0.10 |
| 5 | BayesianRidge | none | 0.08 ± 0.15 | 0.34 ± 0.05 | 0.50 ± 0.11 |
| 6 | SVR—linear | none | 0.21 ± 0.29 | 0.35 ± 0.05 | 0.56 ± 0.12 |
| 7 | SVR—linear | none | 0.37 ± 0.32 | 0.34 ± 0.05 | 0.55 ± 0.11 |
| 8 | SVR—rbf | MMS | 0.17 ± 0.14 | 0.31 ± 0.05 | 0.48 ± 0.12 |
| 9 | SVR—linear | MMS | 0.24 ± 0.24 | 0.34 ± 0.05 | 0.56 ± 0.13 |
| 10 | SVR—linear | none | 0.36 ± 0.27 | 0.35 ± 0.05 | 0.55 ± 0.10 |
| 11 | BayesianRidge | none | 0.08 ± 0.15 | 0.34 ± 0.05 | 0.50 ± 0.12 |
| 12 | SVR—linear | NOR | 0.21 ± 0.26 | 0.35 ± 0.06 | 0.56 ± 0.13 |
| Dataset Number | Model 1 | Scaler Method 2 | bBHB Cut-Off 1.0 | bBHB Cut-Off 1.2 | bBHB Cut-Off 1.4 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| TPR | TNR | bACC | MCC | F2 | TPR | TNR | bACC | MCC | F2 | TPR | TNR | bACC | MCC | F2 | |||
| 1 | SVR—linear | STS | 0.38 | 0.94 | 0.66 | 0.37 | 0.40 | 0.40 | 0.96 | 0.68 | 0.44 | 0.43 | 0.32 | 0.97 | 0.65 | 0.40 | 0.36 |
| 2 | BayesianRidge | none | 0.34 | 0.90 | 0.62 | 0.26 | 0.35 | 0.12 | 0.98 | 0.55 | 0.16 | 0.13 | 0.16 | 0.99 | 0.57 | 0.28 | 0.19 |
| 3 | SVR—linear | STS | 0.33 | 0.96 | 0.65 | 0.40 | 0.37 | 0.26 | 0.98 | 0.62 | 0.38 | 0.30 | 0.23 | 1.00 | 0.61 | 0.42 | 0.27 |
| 4 | SVR—linear | none | 0.25 | 0.94 | 0.60 | 0.25 | 0.28 | 0.26 | 0.96 | 0.61 | 0.30 | 0.29 | 0.19 | 0.98 | 0.59 | 0.27 | 0.22 |
| 5 | BayesianRidge | none | 0.38 | 0.95 | 0.66 | 0.37 | 0.40 | 0.20 | 0.97 | 0.58 | 0.20 | 0.21 | 0.08 | 0.99 | 0.53 | 0.12 | 0.10 |
| 6 | SVR—linear | none | 0.32 | 0.98 | 0.65 | 0.44 | 0.36 | 0.34 | 0.99 | 0.67 | 0.50 | 0.39 | 0.37 | 1.00 | 0.68 | 0.55 | 0.42 |
| 7 | SVR—linear | none | 0.33 | 0.94 | 0.63 | 0.33 | 0.36 | 0.29 | 0.96 | 0.62 | 0.33 | 0.32 | 0.23 | 0.96 | 0.59 | 0.26 | 0.25 |
| 8 | SVR—rbf | MMS | 0.28 | 0.96 | 0.62 | 0.32 | 0.31 | 0.20 | 0.98 | 0.59 | 0.24 | 0.22 | 0.25 | 0.98 | 0.62 | 0.30 | 0.27 |
| 9 | SVR—linear | MMS | 0.32 | 0.97 | 0.64 | 0.41 | 0.36 | 0.31 | 0.99 | 0.65 | 0.45 | 0.36 | 0.30 | 1.00 | 0.65 | 0.52 | 0.35 |
| 10 | SVR—linear | none | 0.21 | 0.94 | 0.57 | 0.21 | 0.23 | 0.26 | 0.96 | 0.61 | 0.30 | 0.29 | 0.19 | 0.98 | 0.59 | 0.27 | 0.22 |
| 11 | BayesianRidge | none | 0.34 | 0.95 | 0.65 | 0.35 | 0.37 | 0.20 | 0.98 | 0.59 | 0.24 | 0.22 | 0.08 | 0.99 | 0.54 | 0.15 | 0.10 |
| 12 | SVR—linear | NOR | 0.32 | 0.98 | 0.65 | 0.46 | 0.36 | 0.34 | 1.00 | 0.67 | 0.53 | 0.39 | 0.33 | 1.00 | 0.67 | 0.55 | 0.38 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Satoła, A.; Bauer, E.A. Predicting Subclinical Ketosis in Dairy Cows Using Machine Learning Techniques. Animals 2021, 11, 2131. https://doi.org/10.3390/ani11072131
Satoła A, Bauer EA. Predicting Subclinical Ketosis in Dairy Cows Using Machine Learning Techniques. Animals. 2021; 11(7):2131. https://doi.org/10.3390/ani11072131
Chicago/Turabian StyleSatoła, Alicja, and Edyta Agnieszka Bauer. 2021. "Predicting Subclinical Ketosis in Dairy Cows Using Machine Learning Techniques" Animals 11, no. 7: 2131. https://doi.org/10.3390/ani11072131
APA StyleSatoła, A., & Bauer, E. A. (2021). Predicting Subclinical Ketosis in Dairy Cows Using Machine Learning Techniques. Animals, 11(7), 2131. https://doi.org/10.3390/ani11072131






