Genomic Prediction in Local Breeds: The Rendena Cattle as a Case Study
Abstract
Simple Summary
Abstract
1. Introduction
2. Materials and Methods
2.1. Data Availability
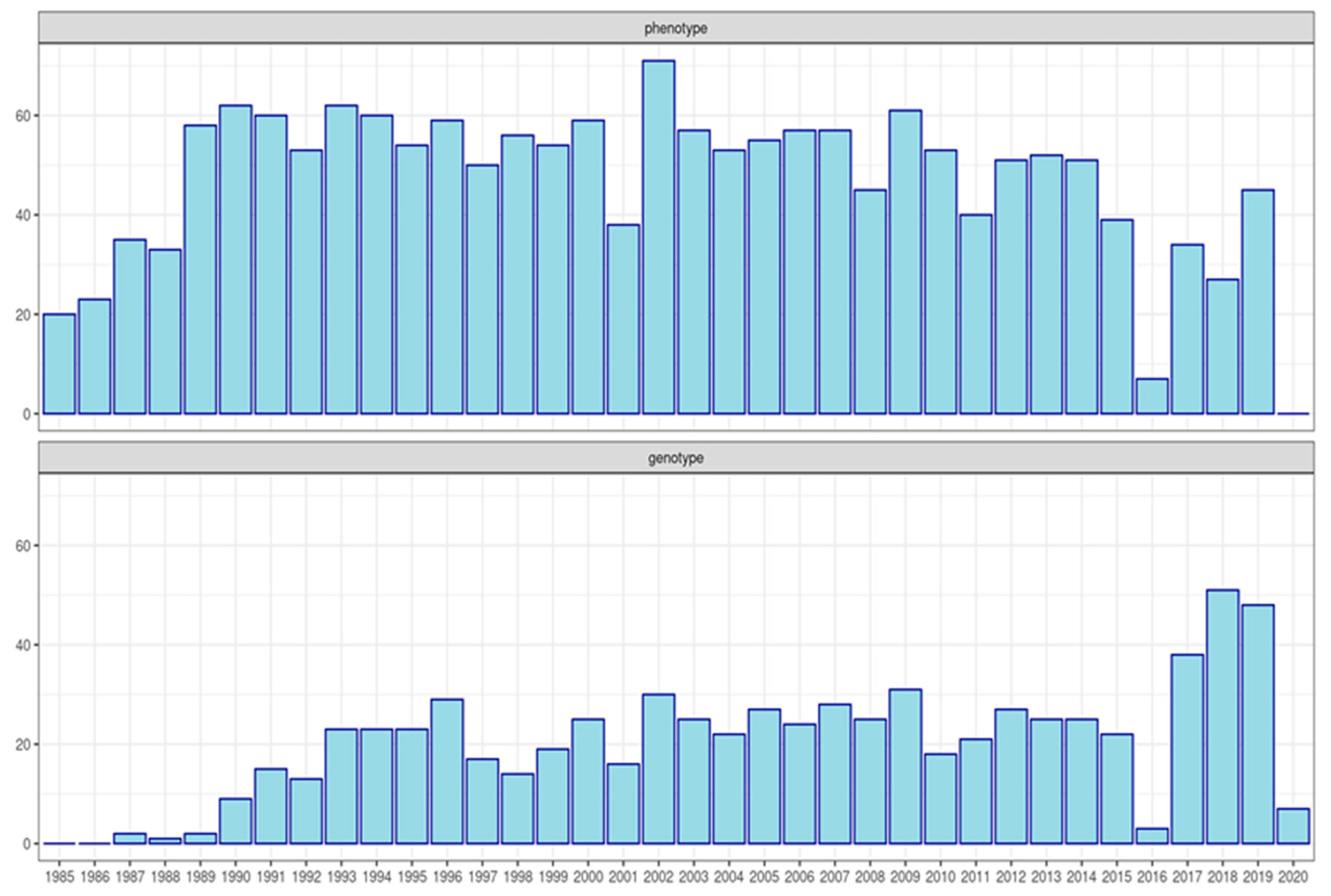
2.1.1. Phenotypic and Pedigree Data
2.1.2. Genotype Data
2.2. Prediction Model
2.2.1. Pedigree Best Linear Unbiased Prediction (PBLUP)
2.2.2. Single-Step Genomic Best Linear Unbiased Prediction (ssGBLUP)
2.2.3. Weighted Single-Step Genomic Best Linear Unbiased Prediction (WssGBLUP)
- Initial parameters are set to .
- GEBV () is obtained using ssGBLUP algorithm.
- Each element of , such as , is then calculated as in [18], where CT is a shrinkage factor determining how much the distribution of SNP effects departs from normality.
- SNP weights are normalized by keeping genetic variance constant among iteration:
- G is then re-built with the new obtained weights as .
- Further iterations are carried out up to convergence using WssGBLUP.
2.2.4. Weighted Strategies
2.3. LR Cross-Validations
3. Results
3.1. Variance Components
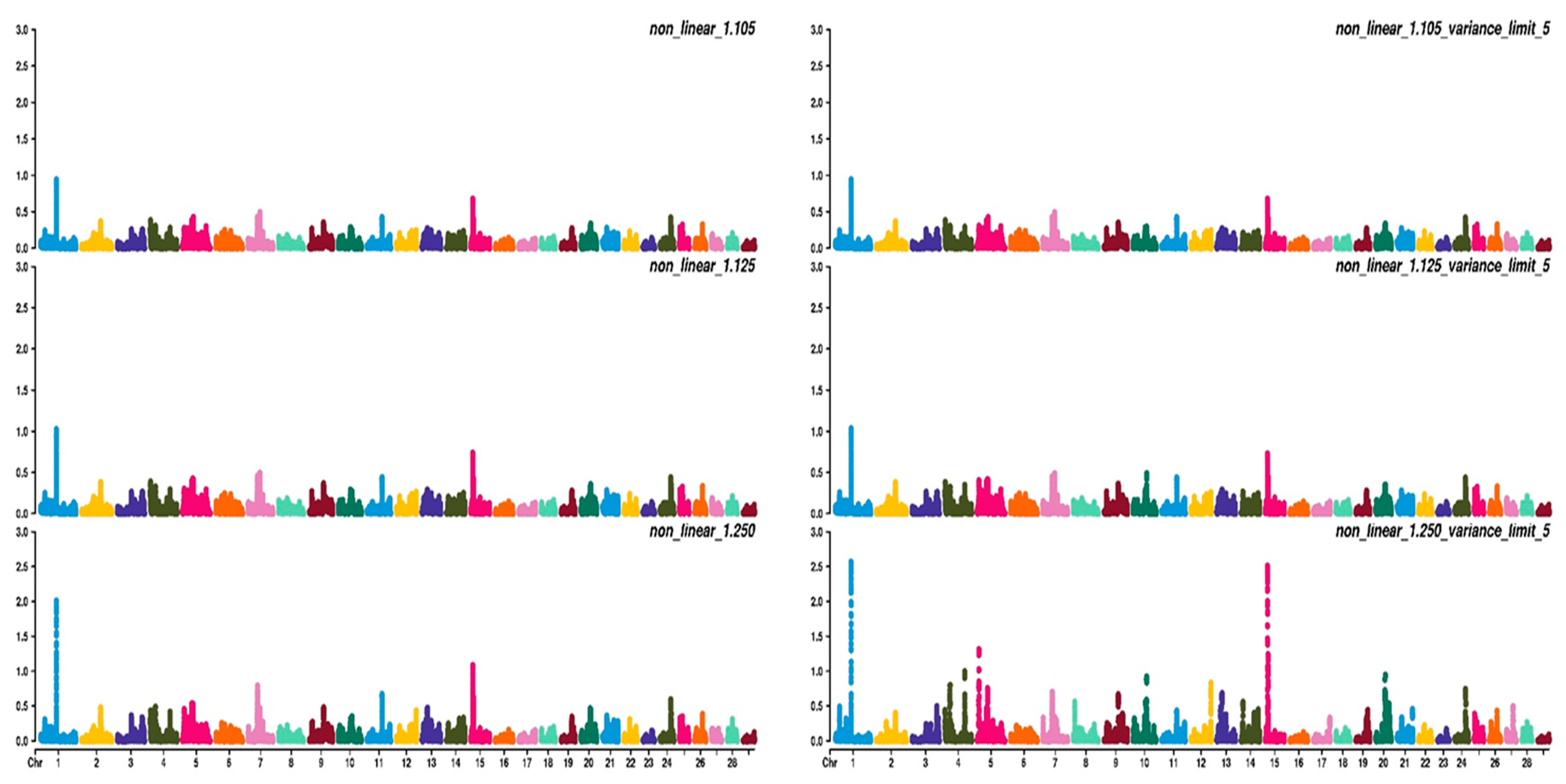
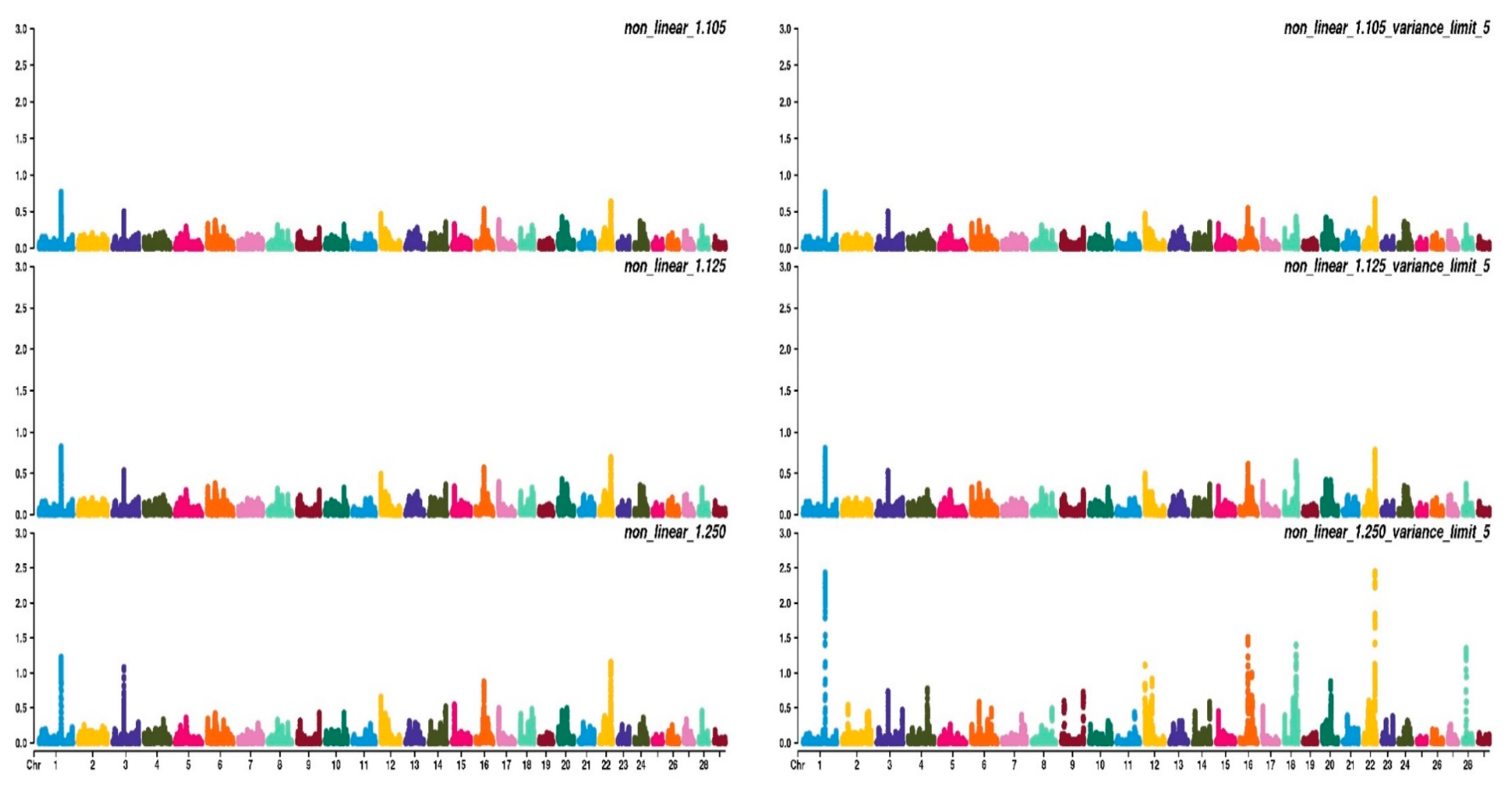
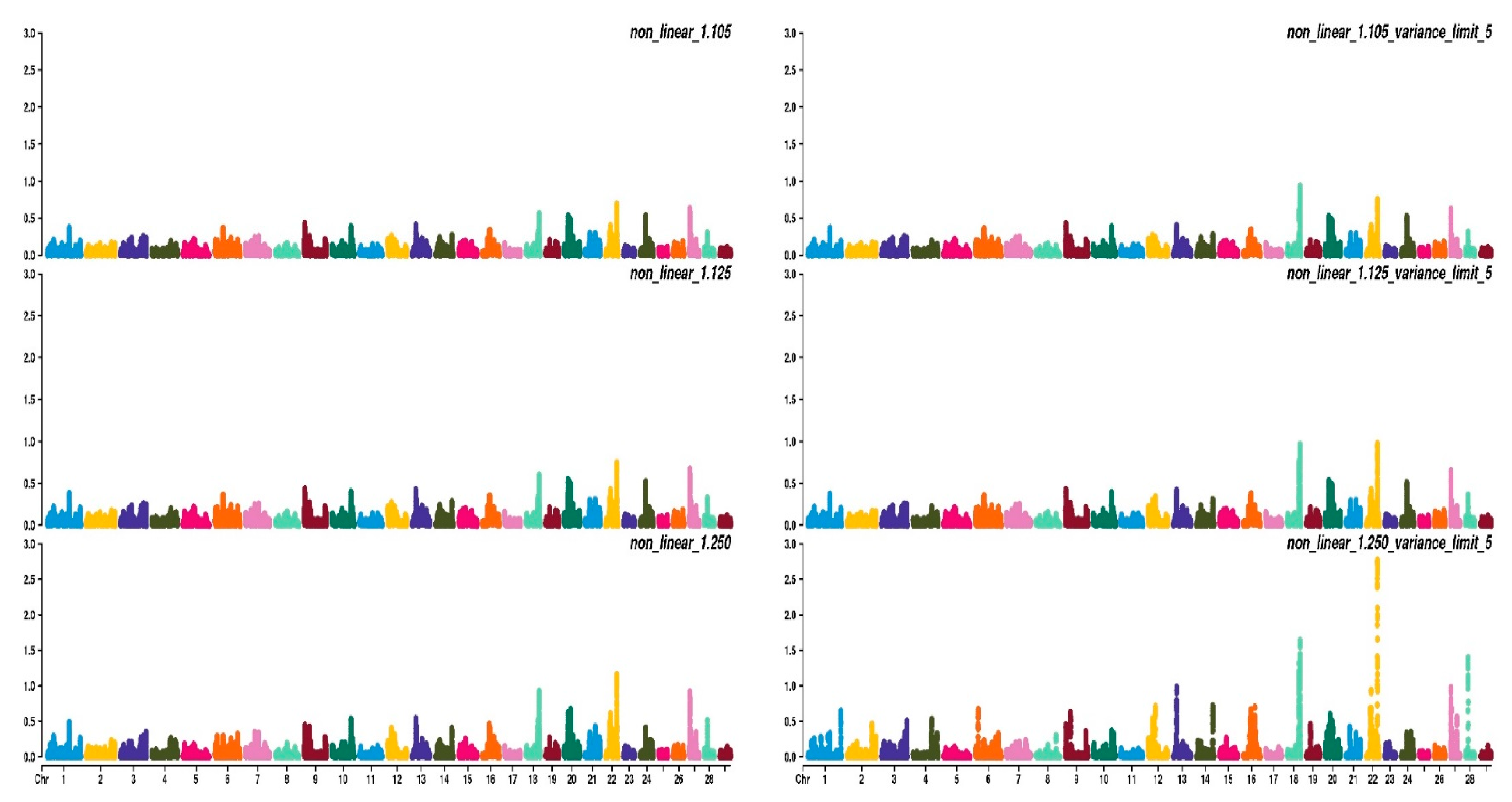
3.2. Weighting Strategies
3.3. Model Comparison
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Acknowledgments
Conflicts of Interest
References
- Schöpke, K.; Swalve, H.H. Review: Opportunities and challenges for small populations of dairy cattle in the era of genomics. Animal 2016, 10, 1050–1060. [Google Scholar] [CrossRef][Green Version]
- Mazza, S.; Guzzo, N.; Sartori, C.; Berry, D.P.; Mantovani, R. Genetic parameters for linear type traits in the Rendena dual-purpose breed. J. Anim. Breed. Genet. 2014, 131, 27–35. [Google Scholar] [CrossRef]
- Sartori, C.; Guzzo, N.; Mazza, S.; Mantovani, R. Genetic correlations among milk yield, morphology, performance test traits and somatic cells in dual-purpose Rendena breed. Animal 2018, 12, 906–914. [Google Scholar] [CrossRef] [PubMed]
- Guzzo, N.; Sartori, C.; Mantovani, R. Analysis of genetic correlations between beef traits in young bulls and primiparous cows belonging to the dual-purpose Rendena breed. Animal 2019, 13, 694–701. [Google Scholar] [CrossRef]
- Zhang, H.; Yin, L.; Wang, M.; Yuan, X.; Liu, X. Factors Affecting the Accuracy of Genomic Selection for Agricultural Economic Traits in Maize, Cattle, and Pig Populations. Front. Genet. 2019, 10, 189. [Google Scholar] [CrossRef] [PubMed]
- Blasco, A.; Toro, M.A. A short critical history of the application of genomics to animal breeding. Livest. Sci. 2014, 166, 4–9. [Google Scholar] [CrossRef]
- Ibanez-Escriche, N.; Simianer, H. Animal breeding in the genomics era. Anim. Front. 2016, 6, 4. [Google Scholar] [CrossRef]
- Van Raden, P.M.; Wiggans, G.R. Derivation, Calculation, and Use of National Animal Model Information. J. Dairy Sci. 1991, 74, 2737–2746. [Google Scholar] [CrossRef]
- VanRaden, P.M.; Van Tassell, C.P.; Wiggans, G.R.; Sonstegard, T.S.; Schnabel, R.D.; Taylor, J.F.; Schenkel, F.S. Invited review: Reliability of genomic predictions for North American Holstein bulls. J. Dairy Sci. 2009, 92, 16–24. [Google Scholar] [CrossRef]
- Masuda, Y.; VanRaden, P.M.; Misztal, I.; Lawlor, T.J. Differing genetic trend estimates from traditional and genomic evaluations of genotyped animals as evidence of preselection. J. Dairy Sci. 2018, 101, 5194–5206. [Google Scholar] [CrossRef] [PubMed]
- Ma, P.; Lund, M.S.; Nielsen, U.S.; Aamand, G.P.; Su, G. Single-step genomic model improved reliability and reduced the bias of genomic predictions in Danish Jersey. J. Dairy Sci. 2015, 98, 9026–9034. [Google Scholar] [CrossRef]
- Aguilar, I.; Misztal, I.; Johnson, D.L.; Legarra, A.; Tsuruta, S.; Lawlor, T.J. Hot topic: A unified approach to utilize phenotypic, full pedigree, and genomic information for genetic evaluation of Holstein final score. J. Dairy Sci. 2010, 93, 743–752. [Google Scholar] [CrossRef]
- Legarra, A.; Aguilar, I.; Misztal, I. A relationship matrix including full pedigree and genomic information. J. Dairy Sci. 2009, 92, 4656–4663. [Google Scholar] [CrossRef]
- Misztal, I.; Lourenco, D.; Legarra, A. Current status of genomic evaluation. J. Anim. Sci. 2020, 98. [Google Scholar] [CrossRef] [PubMed]
- Legarra, A.; Christensen, O.F.; Aguilar, I.; Misztal, I. Single Step, a general approach for genomic selection. Livest. Sci. 2014, 166, 54–65. [Google Scholar] [CrossRef]
- Ricard, A.; Danvy, S.; Legarra, A. Computation of deregressed proofs for genomic selection when own phenotypes exist with an application in French show-jumping horses. J. Anim. Sci. 2013, 91, 1076–1085. [Google Scholar] [CrossRef] [PubMed]
- Misztal, I.; Aggrey, S.E.; Muir, W.M. Experiences with a single-step genome evaluation. Poult. Sci. 2013, 92, 2530–2534. [Google Scholar] [CrossRef] [PubMed]
- VanRaden, P.M. Efficient methods to compute genomic predictions. J. Dairy Sci. 2008, 91, 4414–4423. [Google Scholar] [CrossRef] [PubMed]
- Bedhane, M.; van der Werf, J.; Gondro, C.; Duijvesteijn, N.; Lim, D.; Park, B.; Park, M.N.; Hee, R.S.; Clark, S. Genome-Wide Association Study of Meat Quality Traits in Hanwoo Beef Cattle Using Imputed Whole-Genome Sequence Data. Front. Genet. 2019, 10, 1235. [Google Scholar] [CrossRef]
- Fu, L.; Jiang, Y.; Wang, C.; Mei, M.; Zhou, Z.; Jiang, Y.; Song, H.; Ding, X. A Genome-Wide Association Study on Feed Efficiency Related Traits in Landrace Pigs. Front. Genet. 2020, 11, 692. [Google Scholar] [CrossRef]
- Mehrban, H.; Naserkheil, M.; Lee, D.H.; Cho, C.; Choi, T.; Park, M.; Ibáñez-Escriche, N. Genomic Prediction Using Alternative Strategies of Weighted Single-Step Genomic BLUP for Yearling Weight and Carcass Traits in Hanwoo Beef Cattle. Genes 2021, 12, 266. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Lourenco, D.; Aguilar, I.; Legarra, A.; Misztal, I. Weighting Strategies for Single-Step Genomic BLUP: An Iterative Approach for Accurate Calculation of GEBV and GWAS. Front. Genet. 2016, 7, 151. [Google Scholar] [CrossRef] [PubMed]
- Alvarenga, A.B.; Veroneze, R.; Oliveira, H.R.; Marques, D.B.D.; Lopes, P.S.; Silva, F.F.; Brito, L.F. Comparing Alternative Single-Step GBLUP Approaches and Training Population Designs for Genomic Evaluation of Crossbred Animals. Front. Genet. 2020, 11, 263. [Google Scholar] [CrossRef]
- Purcell, S.; Neale, B.; Todd-Brown, K.; Thomas, L.; Ferreira, M.A.R.; Bender, D.; Maller, J.; Sklar, P.; De Bakker, P.I.W.; Daly, M.J.; et al. PLINK: A tool set for whole-genome association and population-based linkage analyses. Am. J. Hum. Genet. 2007, 81, 559–575. [Google Scholar] [CrossRef] [PubMed]
- Aguilar, I.; Tsuruta, S.; Masuda, Y.; Lourenco, D.A.L.; Legarra, A.; Misztal, I. BLUPF90 suite of programs for animal breeding. In Proceedings of the 11th World Congress on Genetics Applied to Livestock Production, Auckland, New Zealand, 10–15 February 2018; Volume 11, p. 751. [Google Scholar]
- Whalen, A.; Hickey, J.M. AlphaImpute2: Fast and accurate pedigree and population based imputation for hundreds of thousands of individuals in livestock populations. bioRxiv 2020. [Google Scholar] [CrossRef]
- Misztal, I.; Tsuruta, S.; Lourenco, D.; Aguilar, I.; Legarra, A.; Vitezica, Z. Manual for BLUPF90 Family of Programs; University of Georgia: Athens, GA, USA, 2018; Volume 125. [Google Scholar]
- Garcia-Baccino, C.A.; Legarra, A.; Christensen, O.F.; Misztal, I.; Pocrnic, I.; Vitezica, Z.G.; Cantet, R.J.C. Metafounders are related to Fst fixation indices and reduce bias in single-step genomic evaluations. Genet. Sel. Evol. 2017, 49, 34. [Google Scholar] [CrossRef] [PubMed]
- Strandén, I.; Garrick, D.J. Technical note: Derivation of equivalent computing algorithms for genomic predictions and reliabilities of animal merit. J. Dairy Sci. 2009, 92, 2971–2975. [Google Scholar] [CrossRef]
- Fragomeni, B.O.; Lourenco, D.A.L.; Legarra, A.; VanRaden, P.M.; Misztal, I. Alternative SNP weighting for single-step genomic best linear unbiased predictor evaluation of stature in US Holsteins in the presence of selected sequence variants. J. Dairy Sci. 2019, 102, 10012–10019. [Google Scholar] [CrossRef]
- Lopez, B.I.; Lee, S.H.; Shin, D.H.; Oh, J.D.; Chai, H.H.; Park, W.; Park, J.E.; Lim, D. Accuracy of genomic evaluation using imputed high-density genotypes for carcass traits in commercial Hanwoo population. Livest. Sci. 2020, 241, 104256. [Google Scholar] [CrossRef]
- Tiezzi, F.; Maltecca, C. Accounting for trait architecture in genomic predictions of US Holstein cattle using a weighted realized relationship matrix. Genet. Sel. Evol. 2015, 47, 24. [Google Scholar] [CrossRef]
- Legarra, A.; Reverter, A. Semi-parametric estimates of population accuracy and bias of predictions of breeding values and future phenotypes using the LR method 01 Mathematical Sciences 0104 Statistics. Genet. Sel. Evol. 2018, 50, 1–18. [Google Scholar] [CrossRef]
- Bermann, M.; Legarra, A.; Hollifield, M.K.; Masuda, Y.; Lourenco, D.; Misztal, I. Validation of single-step GBLUP genomic predictions from threshold models using the linear regression method: An application in chicken mortality. J. Anim. Breed. Genet. 2021, 138, 4–13. [Google Scholar] [CrossRef] [PubMed]
- Macedo, F.L.; Christensen, O.F.; Astruc, J.M.; Aguilar, I.; Masuda, Y.; Legarra, A. Bias and accuracy of dairy sheep evaluations using BLUP and SSGBLUP with metafounders and unknown parent groups. Genet. Sel. Evol. 2020, 52, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Mancin, E.; Sartori, C.; Guzzo, N.; Tuliozi, B.; Mantovani, R. Selection Response Due to Different Combination of Antagonistic Milk, Beef, and Morphological Traits in the Alpine Grey Cattle Breed. Animals 2021, 11, 1340. [Google Scholar] [CrossRef] [PubMed]
- Sbarra, F.; Mantovani, R.; Quaglia, A.; Bittante, G. Genetics of slaughter precocity, carcass weight, and carcass weight gain in Chianina, Marchigiana, and Romagnola young bulls under protected geographical indication. J. Anim. Sci. 2013, 91, 2596–2604. [Google Scholar] [CrossRef] [PubMed]
- Bonfatti, V.; Albera, A.; Carnier, P. Genetic associations between daily BW gain and live fleshiness of station-tested young bulls and carcass and meat quality traits of commercial intact males in Piemontese cattle. J. Anim. Sci. 2013, 91, 2057–2066. [Google Scholar] [CrossRef] [PubMed]
- Aass, L. Variation in carcass and meat quality traits and their relations to growth in dual purpose cattle. Livest. Prod. Sci. 1996, 46, 1–12. [Google Scholar] [CrossRef]
- De Haas, Y.; Janss, L.L.G.; Kadarmideen, H.N. Genetic and phenotypic parameters for conformation and yield traits in three Swiss dairy cattle breeds. J. Anim. Breed. Genet. 2007, 124, 12–19. [Google Scholar] [CrossRef]
- Jensen, J.; Mao, I.L.; Andersen, B.B.; Madsen, P. Genetic parameters of growth, feed intake, feed conversion and carcass composition of dual-purpose bulls in performance testing. J. Anim. Sci. 1991, 69, 931–939. [Google Scholar] [CrossRef]
- Cesarani, A.; Pocrnic, I.; Macciotta, N.P.P.; Fragomeni, B.O.; Misztal, I.; Lourenco, D.A.L. Bias in heritability estimates from genomic restricted maximum likelihood methods under different genotyping strategies. J. Anim. Breed. Genet. 2019, 136, 40–50. [Google Scholar] [CrossRef]
- Gowane, G.R.; Lee, S.H.; Clark, S.; Moghaddar, N.; Al-Mamun, H.A.; van der Werf, J.H.J. Effect of selection and selective genotyping for creation of reference on bias and accuracy of genomic prediction. J. Anim. Breed. Genet. 2019, 136, 390–407. [Google Scholar] [CrossRef] [PubMed]
- Habier, D.; Fernando, R.L.; Dekkers, J.C.M. The impact of genetic relationship information on genome-assisted breeding values. Genetics 2007, 177, 2389–2397. [Google Scholar] [CrossRef]
- Mehrban, H.; Lee, D.H.; Naserkheil, M.; Moradi, M.H.; Ibáñez-Escriche, N. Comparison of conventional BLUP and single-step genomic BLUP evaluations for yearling weight and carcass traits in Hanwoo beef cattle using single trait and multi-trait models. PLoS ONE 2019, 14, e0223352. [Google Scholar] [CrossRef]
- Onogi, A.; Ogino, A.; Komatsu, T.; Shoji, N.; Simizu, K.; Kurogi, K.; Yasumori, T.; Togashi, K.; Iwata, H. Genomic prediction in Japanese Black cattle: Application of a single-step approach to beef cattle. J. Anim. Sci. 2014, 92, 1931–1938. [Google Scholar] [CrossRef] [PubMed]
- Gordo, D.G.M.; Espigolan, R.; Tonussi, R.L.; Júnior, G.A.F.; Bresolin, T.; Magalhães, A.F.B.; Feitosa, F.L.; Baldi, F.; Carvalheiro, R.; Tonhati, H.; et al. Genetic parameter estimates for carcass traits and visual scores including or not genomic information1. J. Anim. Sci. 2016, 94, 1821–1826. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.; Cheng, H.; Garrick, D.; Golden, B.; Dekkers, J.; Park, K.; Lee, D.; Fernando, R. Comparison of alternative approaches to single-trait genomic prediction using genotyped and non-genotyped Hanwoo beef cattle. Genet. Sel. Evol. 2017, 49, 2. [Google Scholar] [CrossRef]
- Cesarani, A.; Biffani, S.; Garcia, A.; Lourenco, D.; Bertolini, G.; Neglia, G.; Misztal, I.; Macciotta, N.P.P. Genomic investigation of milk production in Italian buffalo. Ital. J. Anim. Sci. 2021, 20, 539–547. [Google Scholar] [CrossRef]
- Lourenco, D.A.L.; Fragomeni, B.O.; Bradford, H.L.; Menezes, I.R.; Ferraz, J.B.S.; Aguilar, I.; Tsuruta, S.; Misztal, I. Implications of SNP weighting on single-step genomic predictions for different reference population sizes. J. Anim. Breed. Genet. 2017, 134, 463–471. [Google Scholar] [CrossRef]
- Mancin, E.; Sosa-Madrid, B.S.; Blasco, A.; Ibáñez-Escriche, N. Genotype imputation to improve the cost-efficiency of genomic selection in rabbits. Animals 2021, 11, 803. [Google Scholar] [CrossRef]
- Pocrnic, I.; Lourenco, D.A.L.; Masuda, Y.; Legarra, A.; Misztal, I. The dimensionality of genomic information and its effect on genomic prediction. Genetics 2016, 203, 573–581. [Google Scholar] [CrossRef]
- Hassani, S.; Saatchi, M.; Fernando, R.L.; Garrick, D.J. Accuracy of prediction of simulated polygenic phenotypes and their underlying quantitative trait loci genotypes using real or imputed whole-genome markers in cattle. Genet. Sel. Evol. 2015, 47, 1–11. [Google Scholar] [CrossRef]
- Habier, D.; Fernando, R.L.; Garrick, D.J. Genomic BLUP decoded: A look into the black box of genomic prediction. Genetics 2013, 194, 597–607. [Google Scholar] [CrossRef]
- Legarra, A.; Reverter, A. Can We Frame and Understand Cross-Validation Results in Animal Breeding? Proc. Assoc. Advmt. Anim. Breed. Genet. 2017, 22, 73–80. [Google Scholar]
- Senczuk, G.; Mastrangelo, S.; Ciani, E.; Ciani, E.L.; Battaglini, F.; Cendron, R.; Ciampolini, P.; Crepaldi, R.; Mantovani, G.; Bongioni, G.; et al. The genetic heritage of Alpine local cattle breeds using genomic SNP data. Genet. Sel. Evol. 2020, 52, 40. [Google Scholar] [CrossRef] [PubMed]
- Mrode, R.; Ojango, J.M.K.; Okeyo, A.M.; Mwacharo, J.M. Genomic selection and use of molecular tools in breeding programs for indigenous and crossbred cattle in developing countries: Current status and future prospects. Front. Genet. 2019, 10. [Google Scholar] [CrossRef]
- Biscarini, F.; Nicolazzi, E.; Alessandra, S.; Boettcher, P.; Gandini, G. Challenges and opportunities in genetic improvement of local livestock breeds. Front. Genet. 2015, 5, 1–16. [Google Scholar] [CrossRef] [PubMed]
- García-Ruiz, A.; Cole, J.B.; Paul, M.; Wiggans, G.R.; Ruiz-lópez, F.J.; Curtis, P. Erratum: Changes in genetic selection differentials and generation intervals in US Holstein dairy cattle as a result of genomic selection. Proc. Natl. Acad. Sci. USA 2016, 113, 4928. [Google Scholar] [CrossRef] [PubMed]

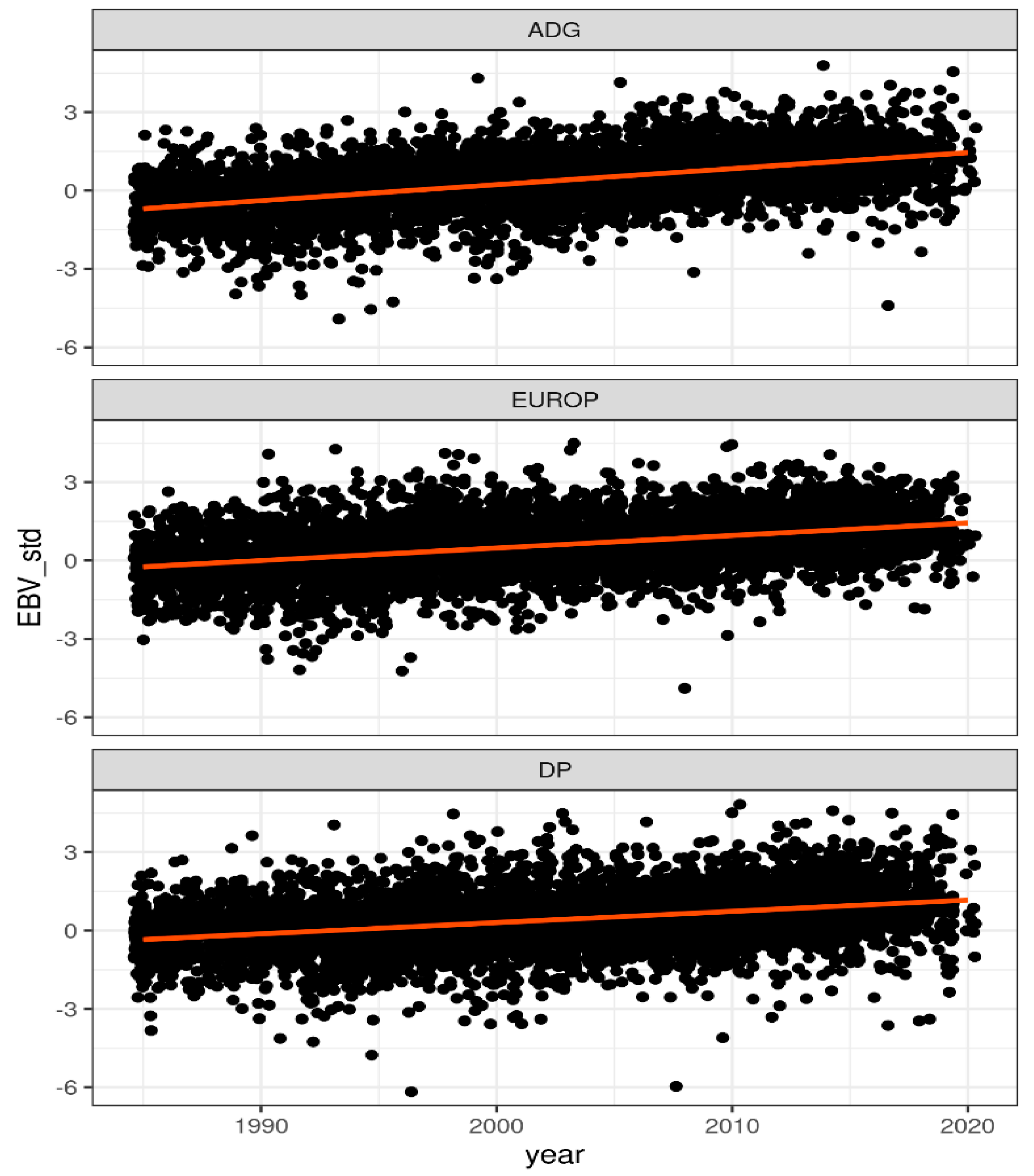
| Taits 1 | Number 2 | Mean | CV % | Min | Max |
|---|---|---|---|---|---|
| ADG (kg/d) | 1691 (690) | 1024.00 | 12.06 | 474.00 | 1562 |
| EUROP (points) | 1691 (690) | 99.05 | 3.84 | 80.00 | 111.10 |
| DP (points) | 1691 (690) | 54.18 | 1.74 | 50.00 | 57.70 |
| ADG | EUROP | DP | |
|---|---|---|---|
| ADG | 0.335 (0.204 ± 0.335) | 0.364 (0.100 ± 0.597) | 0.398 (0.148 ± 0.6315) |
| EUROP | 0.572 (0.660 ± 0.742) | 0.304 (0.174 ± 0.446) | 0.981 (0.962 ± 0.997) |
| DP | 0.613 (0.517 ± 0.702) | 0.792 (0.753 ± 0.836) | 0.392 (0.248 ± 0.541) |
| ADG | EUROP | DP | |
|---|---|---|---|
| ADG | 0.313 (0.223 ± 0.489) | 0.385 (0.153 ± 0.597) | 0.392 (0.160 ± 0.622) |
| EUROP | 0.651 (0.651 ± 0.718) | 0.345 (0.216 ± 0.487) | 0.985 (0.961 ± 0.999) |
| CY | 0.616 (0.530 ± 0.671) | 0.790 (0.753 ± 0.826) | 0.396 (0.250 ± 0.530) |
| Trait | Model | Accuracy | Bias | Disp. | Rel. | Incr_adj |
|---|---|---|---|---|---|---|
| ADG | PBLUP | 0.366 | −0.040 | 1.140 | 0.060 | - |
| ssGBLUP | 0.472 | 0.010 | 1.045 | 0.117 | 45.10% | |
| WssGBLUP_1 | 0.551 | 0.003 | 1.182 | 0.127 | 45.10% | |
| WssGBLUP_2 | 0.693 | 0.020 | 1.562 | 0.206 | 49.21% | |
| EUROP | PBLUP | 0.509 | −0.009 | 0.902 | 0.081 | - |
| ssGBLUP | 0.596 | 0.009 | 1.100 | 0.124 | 39.98% | |
| WssGBLUP_1 | 0.653 | 0.004 | 0.958 | 0.135 | 39.98% | |
| WssGBLUP_2 | 0.749 | 0.014 | 1.165 | 0.192 | 45.17% | |
| DP | PBLUP | 0.464 | −0.021 | 1.114 | 0.114 | - |
| ssGBLUP | 0.528 | 0.021 | 1.056 | 0.158 | 26.70% | |
| WssGBLUP_1 | 0.600 | 0.017 | 1.156 | 0.184 | 27.40% | |
| WssGBLUP_2 | 0.727 | 0.025 | 1.468 | 0.277 | 33.90% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mancin, E.; Tuliozi, B.; Sartori, C.; Guzzo, N.; Mantovani, R. Genomic Prediction in Local Breeds: The Rendena Cattle as a Case Study. Animals 2021, 11, 1815. https://doi.org/10.3390/ani11061815
Mancin E, Tuliozi B, Sartori C, Guzzo N, Mantovani R. Genomic Prediction in Local Breeds: The Rendena Cattle as a Case Study. Animals. 2021; 11(6):1815. https://doi.org/10.3390/ani11061815
Chicago/Turabian StyleMancin, Enrico, Beniamino Tuliozi, Cristina Sartori, Nadia Guzzo, and Roberto Mantovani. 2021. "Genomic Prediction in Local Breeds: The Rendena Cattle as a Case Study" Animals 11, no. 6: 1815. https://doi.org/10.3390/ani11061815
APA StyleMancin, E., Tuliozi, B., Sartori, C., Guzzo, N., & Mantovani, R. (2021). Genomic Prediction in Local Breeds: The Rendena Cattle as a Case Study. Animals, 11(6), 1815. https://doi.org/10.3390/ani11061815







