Evaluation of Inter-Observer Reliability of Animal Welfare Indicators: Which Is the Best Index to Use?
Abstract
Simple Summary
Abstract
1. Introduction
2. Materials and Methods
2.1. Dataset
2.2. Agreement Measures
2.3. Confidence Intervals for Agreement Indexes
2.4. Statistical Analyses
3. Results
3.1. Agreement Measures
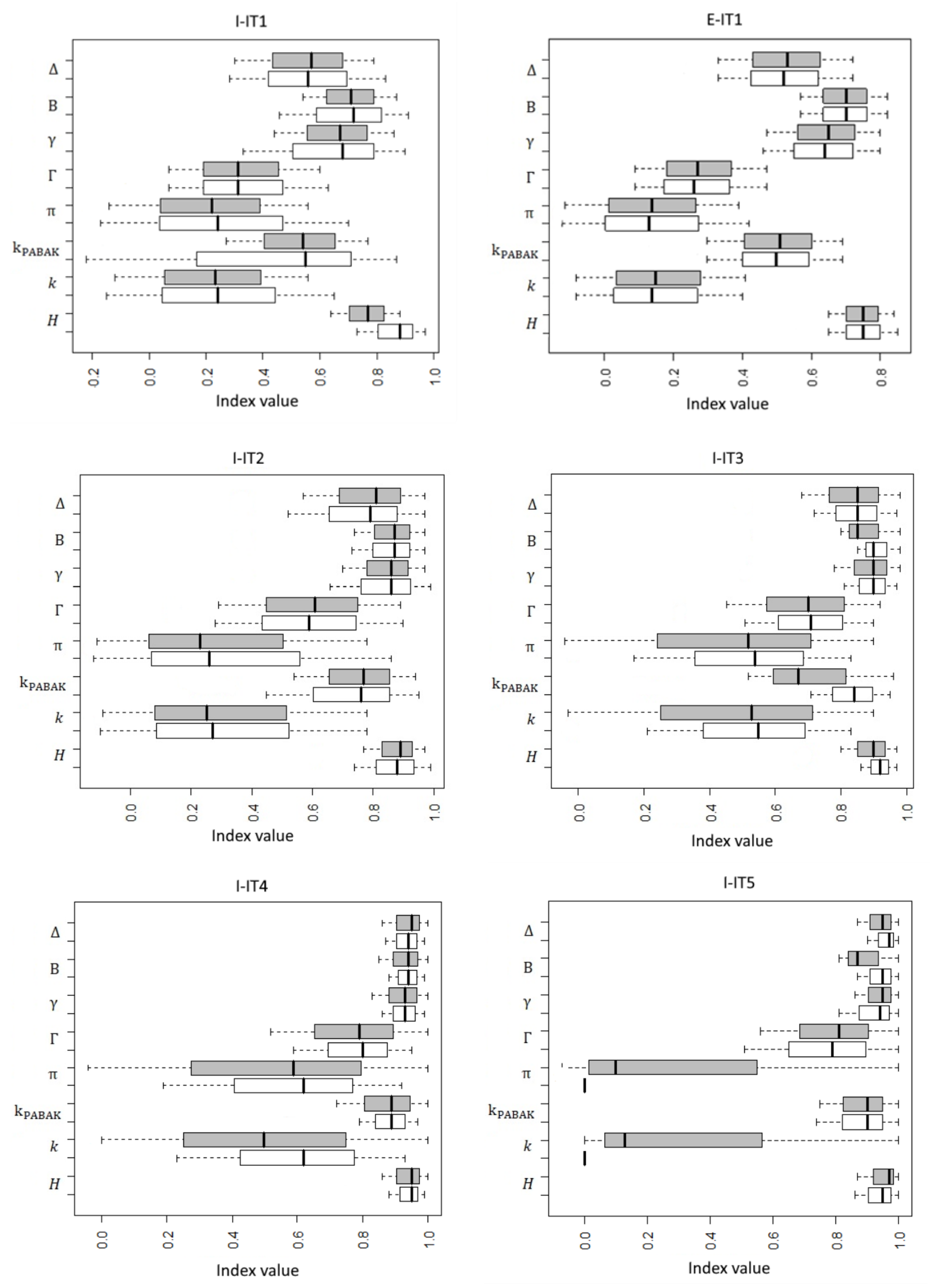
3.2. Confidence Intervals for Agreement Indexes
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1. Index
- is the rate of observed concordance and represents the rate of concordant judgments of two independent observers who analyze the same dataset;
- is the rate of the expected agreement due to chance given by:where:
- M is the number of categories;
- is the proportion of objects assigned to the i-th category.
Appendix A.2. and Indexes
- is the observed hit rate, denoted by ;
- is the proportion of agreement due to chance, denoted by . Hence, the formula can be summarized as:The assumptions for are the following [5,51]:
- (a)
- The N objects categorized are independent;
- (b)
- The categories are independent, mutually exclusive, and exhaustive;
- (c)
- The assigners operate independently.
- is the maximum observed proportion, obtained by adding the minimum values of the individual marginal totals.
Appendix A.3.
- is the concordance rate.
Appendix A.4. Index
- C is the number of concordant judgments;
- NA is the number of judgments of the observer A;
- NB is the number of judgments of the observer B.
Appendix A.5. Index
Appendix A.6. Index
Appendix A.7. Index
Appendix A.8. Index
- is the square of the values of the concordant cells;
- is the total of i-th row;
- is the total of i-th column.
Appendix A.9. Index
Appendix A.10. Index
- is estimated with ;
- is estimated as:with
Appendix B
Appendix B.1. Index
Appendix B.2. , , and Indexes
Appendix B.3. Index
Appendix B.4. Index
Appendix B.5. and Indexes
Appendix B.6. Index
Appendix B.7. Index
References
- Battini, M.; Vieira, A.; Barbieri, S.; Ajuda, I.; Stilwell, G.; Mattiello, S. Invited review: Animal-based indicators for on-farm welfare assessment for dairy goats. J. Dairy Sci. 2014, 97, 6625–6648. [Google Scholar] [CrossRef]
- Meagher, R.K. Observer ratings: Validity and value as a tool for animal welfare research. Appl. Anim. Behav. Sci. 2009, 119, 1–14. [Google Scholar] [CrossRef]
- Kaufman, A.B.; Rosenthal, R. Can you believe my eyes? The importance of interobserver reliability statistics in observations of animal behavior. Anim. Behav. 2009, 78, 1487–1491. [Google Scholar] [CrossRef]
- Krippendorff, K. Reliability in content analysis: Some common misconceptions and recommendations. Hum. Commun. Res. 2004, 30, 411–433. [Google Scholar] [CrossRef]
- Cohen, J. A coefficient of agreement for nominal scales. Educ. Psychol. Meas. 1960, 20, 37–46. [Google Scholar] [CrossRef]
- De Rosa, G.; Grasso, F.; Pacelli, C.; Napolitano, F.; Winckler, C. The welfare of dairy buffalo. Ital. J. Anim. Sci. 2009, 8, 103–116. [Google Scholar] [CrossRef]
- Marasini, D.; Quatto, P.; Ripamonti, E. Assessing the inter-rater agreement for ordinal data through weighted indexes. Stat. Methods Med. Res. 2016, 25, 2611–2633. [Google Scholar] [CrossRef]
- Katzenberger, K.; Rauch, E.; Erhard, M.; Reese, S.; Gauly, M. Inter-rater reliability of welfare outcome assessment by an expert and farmers of South Tyrolean dairy farming. Ital. J. Anim. Sci. 2020, 19, 1079–1090. [Google Scholar] [CrossRef]
- Czycholl, I.; Klingbeil, P.; Krieter, J. Interobserver reliability of the animal welfare indicators welfare assessment protocol for horses. J. Equine Vet. Sci. 2019, 75, 112–121. [Google Scholar] [CrossRef]
- Czycholl, I.; Menke, S.; Straßburg, C.; Krieter, J. Reliability of different behavioral tests for growing pigs on-farm. Appl. Anim. Behav. Sci. 2019, 213, 65–73. [Google Scholar] [CrossRef]
- Pfeifer, M.; Eggemann, L.; Kransmann, J.; Schmitt, A.O.; Hessel, E.F. Inter- and intra-observer reliability of animal welfare indicators for the on-farm self-assessment of fattening pigs. Animal 2019, 13, 1712–1720. [Google Scholar] [CrossRef] [PubMed]
- Vieira, A.; Battini, M.; Can, E.; Mattiello, S.; Stilwell, G. Inter-observer reliability of animal-based welfare indicators included in the Animal Welfare Indicators welfare assessment protocol for dairy goats. Animal 2018, 12, 1942–1949. [Google Scholar] [CrossRef]
- De Rosa, G.; Grasso, F.; Winckler, C.; Bilancione, A.; Pacelli, C.; Masucci, F.; Napolitano, F. Application of the Welfare Quality protocol to dairy buffalo farms: Prevalence and reliability of selected measures. J. Dairy Sci. 2015, 98, 6886–6896. [Google Scholar] [CrossRef] [PubMed]
- Mullan, S.; Edwards, S.A.; Butterworth, A.; Whay, H.R.; Main, D.C.J. Inter-observer reliability testing of pig welfare outcome measures proposed for inclusion within farm assurance schemes. Vet. J. 2011, 190, e100–e109. [Google Scholar] [CrossRef] [PubMed]
- Mattiello, S.; Battini, M.; De Rosa, G.; Napolitano, F.; Dwyer, C. How Can We Assess Positive Welfare in Ruminants? Animals 2019, 9, 758. [Google Scholar] [CrossRef]
- Spigarelli, C.; Zuliani, A.; Battini, M.; Mattiello, S.; Bovolenta, S. Welfare Assessment on Pasture: A Review on Animal-Based Measures for Ruminants. Animals 2020, 10, 609. [Google Scholar] [CrossRef]
- Walsh, P.; Thornton, J.; Asato, J.; Walker, N.; McCoy, G.; Baal, J.; Baal, J.; Mendoza, N.; Banimahd, F. Approaches to describing inter-rater reliability of the overall clinical appearance of febrile infants and toddlers in the emergency department. PeerJ 2014, 2, e651. [Google Scholar] [CrossRef]
- Ato, M.; Lopez, J.J.; Benavente, A. A simulation study of rater agreement measures with 2x2 contingency tables. Psicológica 2011, 32, 385–402. [Google Scholar]
- Scott, W.A. Reliability of content analysis: The case of nominal scale coding. Public Opin. Q. 1955, 19, 321–325. [Google Scholar] [CrossRef]
- Bennett, E.M.; Alpert, R.; Goldstein, A.C. Communications through limited response questioning. Public Opin. Q. 1954, 18, 303–308. [Google Scholar] [CrossRef]
- Gwet, K. Computing inter-rater reliability and its variance in presence of high agreement. Br. J. Math. Stat. Psychol. 2008, 61, 29–48. [Google Scholar] [CrossRef]
- Tanner, M.A.; Young, M.A. Modeling agreement among raters. J. Am. Stat. Assoc. 1985, 80, 175–180. [Google Scholar] [CrossRef]
- Aickin, M. Maximum likelihood estimation of agreement in the constant predictive probability model, and its relation to Cohen’s kappa. Biometrics 1990, 46, 293–302. [Google Scholar] [CrossRef]
- Andrés, A.M.; Marzo, P.F. Delta: A new measure of agreement between two raters. Br. J. Math. Stat. Psychol. 2004, 57, 1–19. [Google Scholar] [CrossRef]
- AWIN (Animal Welfare Indicators). AWIN Welfare Assessment Protocol for Goats. 2015. Available online: https://air.unimi.it/retrieve/handle/2434/269102/384790/AWINProtocolGoats.pdf (accessed on 3 May 2021).
- Battini, M.; Stilwell, G.; Vieira, A.; Barbieri, S.; Canali, E.; Mattiello, S. On-farm welfare assessment protocol for adult dairy goats in intensive production systems. Animals 2015, 5, 934–950. [Google Scholar] [CrossRef] [PubMed]
- Holley, J.W.; Guilford, J.P. A note on the G index of agreement. Educ. Psychol. Meas. 1964, 34, 749–753. [Google Scholar] [CrossRef]
- Quatto, P. Un test di concordanza tra più esaminatori. Statistica 2004, 64, 145–151. [Google Scholar]
- Holsti, O.R. Content Analysis for the Social Sciences and Humanities; Addison-Wesley: Reading, MA, USA, 1969; pp. 1–235. [Google Scholar]
- Krippendorff, K. Estimating the reliability, systematic error and random error of interval data. Educ. Psychol. Meas. 1970, 30, 61–70. [Google Scholar] [CrossRef]
- Hubert, L. Nominal scale response agreement as a generalized correlation. Br. J. Math. Stat. Psychol. 1977, 30, 98–103. [Google Scholar] [CrossRef]
- Janson, S.; Vegelius, J. On the applicability of truncated component analysis based on correlation coefficients for nominal scales. Appl. Psychol. Meas. 1978, 2, 135–145. [Google Scholar] [CrossRef][Green Version]
- Bangdiwala, S.I. A graphical test for observer agreement. In Proceedings of the 45th International Statistical Institute Meeting, Amsterdam, The Netherlands, 12–22 August 1985; Bishop, Y.M.M., Fienberg, S.E., Holland, P.W., Eds.; SpringerLink: Berlin, Germany, 1985; pp. 307–308. [Google Scholar]
- Efron, B. Bootstrap methods: Another look at the jackknife. Ann. Stat. 1979, 7, 1–26. [Google Scholar] [CrossRef]
- Klar, N.; Lipsitz, S.R.; Parzen, M.; Leong, T. An exact bootstrap confidence interval for k in small samples. J. R. Stat. Soc. Ser. D-Stat. 2002, 51, 467–478. [Google Scholar] [CrossRef]
- Kinsella, A. The ‘exact’ bootstrap approach to confidence intervals for the relative difference statistic. J. R. Stat. Soc. Ser. D-Stat. 1987, 36, 345–347, correction, 1988, 37, 97. [Google Scholar] [CrossRef]
- Quatto, P.; Ripamonti, E. Raters: A Modification of Fleiss’ Kappa in Case of Nominal and Ordinal Variables. R Package Version 2.0.1. 2014. Available online: https://CRAN.R-project.org/package=raters (accessed on 5 May 2021).
- Meyer, D.; Zeileis, A.; Hornik, K. The Strucplot Framework: Visualizing Multi-Way contingency Table with vcd. J. Stat. Softw. 2006, 17, 1–48. [Google Scholar] [CrossRef]
- S Original, from StatLib and by Tibshirani, R. R Port by Friedrich Leisch. Bootstrap: Functions for the Book ”An Introduction to the Bootstrap”. R Package Version 2019.6. 2019. Available online: https://CRAN.R-project.org/packages=bootstrap (accessed on 5 May 2021).
- Banerjee, M.; Capozzoli, M.; Mc Sweeney, L.; Sinha, D. Beyond kappa: A review of interrater agreement measures. Can. J. Stat.-Rev. Can. Stat. 1999, 27, 3–23. [Google Scholar] [CrossRef]
- Wang, W. A Content Analysis of Reliability in Advertising Content Analysis Studies. Paper 1375. Master’s Thesis, Department of Communication, East Tennessee State Univ., Johnson City, TN, USA, 2011. Available online: https://dc.etsu.edu/etd/1375 (accessed on 22 March 2021).
- Lombard, M.; Snyder-Duch, J.; Bracken, C.C. Content analysis in mass communication: Assessment and reporting of intercoder reliability. Hum. Commun. Res. 2002, 28, 587–604. [Google Scholar] [CrossRef]
- Kuppens, S.; Holden, G.; Barker, K.; Rosenberg, G. A Kappa-related decision: K, Y, G, or AC1. Soc. Work Res. 2011, 35, 185–189. [Google Scholar] [CrossRef]
- Feinstein, A.R.; Cicchetti, D.V. High agreement but low kappa: I. The problem of two paradoxes. J. Clin. Epidemiol. 1990, 43, 543–549. [Google Scholar] [CrossRef]
- Lantz, C.A.; Nebenzahl, E. Behavior and interpretation of the κ statistics: Resolution of the two paradoxes. J. Clin. Epidemiol. 1996, 49, 431–434. [Google Scholar] [CrossRef]
- Byrt, T.; Bishop, J.; Carli, J.B. Bias, prevalence and kappa. J. Clin. Epidemiol. 1993, 46, 423–429. [Google Scholar] [CrossRef]
- Shankar, V.; Bangdiwala, S.I. Observer agreement paradoxes in 2 × 2 tables: Comparison of agreement measures. BMC Med. Res. Methodol. 2014, 14, 100. [Google Scholar] [CrossRef]
- Landis, J.R.; Koch, G.G. The measurement of observer agreement for categorical data. Biometrics 1977, 33, 159–174. [Google Scholar] [CrossRef]
- Fleiss, J.L. Measuring nominal scale agreement among many raters. Psychol. Bull. 1981, 76, 378–382. [Google Scholar] [CrossRef]
- Cicchetti, D.V.; Feinstein, A.R. High agreement but low kappa: II. Resolving the paradoxes. J. Clin. Epidemiol. 1990, 43, 551–558. [Google Scholar] [CrossRef]
- Brennan, R.L.; Prediger, D.J. Coefficient kappa: Some uses, misuses, and alternatives. Educ. Psychol. Meas. 1981, 41, 687–699. [Google Scholar] [CrossRef]
- Zhao, X. When to Use Scott’s π or Krippendorff’s α, If Ever? Presented at the Annual Conference of Association for Education in Journalism and Mass Communication, St. Louis, MO, USA, 10–13 August 2011; Available online: https://repository.hkbu.edu.hk/cgi/viewcontent.cgi?referer=&httpsredir=1&article=1002&context=coms_conf (accessed on 22 March 2021).
- Gwet, K.L. On Krippendorff’s Alpha Coefficient. Available online: http://www.bwgriffin.com/gsu/courses/edur9131/content/onkrippendorffalpha.pdf (accessed on 22 March 2021).
- Falotico, R.; Quatto, P. On avoiding paradoxes in assessing inter-rater agreement. Ital. J. Appl. Stat. 2010, 22, 151–160. [Google Scholar]
- Friendly, M. Visualizing Categorical Data; SAS Institute: Cary, NC, USA, 2000. [Google Scholar]
- McCray, G. Assessing Inter-Rater Agreement for Nominal Judgement Variables. Presented at the Language Testing Forum, University of Lancaster, Nottingham, UK, 15–17 November 2013; Available online: https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.725.8104&rep=rep1&type=pdf (accessed on 22 March 2021).
- Wongpakaran, N.; Wongpakaran, T.; Wedding, D.; Gwet, K.L. A comparison of Cohen’s Kappa and Gwet’s AC1 when calculating inter-rater reliability coefficients: A study conducted with personality disorder samples. BMC Med. Res. Methodol. 2013, 13, 61. [Google Scholar] [CrossRef]
- Kendall, M.G. Rank Correlation Methods; Hafner Publishing Co.: New York, NY, USA, 1955; pp. 1–196. [Google Scholar]
- Janson, S.; Vegelius, J. The J-index as a measure of nominal scale response agreement. Appl. Psychol. Meas. 1982, 6, 111–121. [Google Scholar] [CrossRef]
- Fleiss, J.L.; Cohen, J.; Everitt, B. Large-sample standard errors of kappa and weighted kappa. Psychol. Bull. 1969, 72, 323–327. [Google Scholar] [CrossRef]
- Everitt, B.S. Moments of the statistics kappa and weighted kappa. Br. J. Math. Stat. Psychol. 1968, 21, 97–103. [Google Scholar] [CrossRef]
- Altman, D.G. Statistics in medical journals: Some recent trends. Stat. Med. 2000, 19, 3275–3289. [Google Scholar] [CrossRef]

| Agreement Index 1 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Farm | 2 | 3 | ||||||||||
| E-IT1 | 75 | 0.15 | 0.16 | 0.23 | 0.51 | 75 | 0.15 | 0.25 | 0.25 | 0.70 | 0.52 | 0.65 |
| I-IT1 | 77 | 0.24 | 0.24 | 0.24 | 0.54 | 77 | 0.24 | 0.28 | 0.30 | 0.71 | 0.54 | 0.68 |
| I-IT2 | 88 | 0.27 | 0.27 | 0.43 | 0.77 | 88 | 0.28 | 0.58 | 0.58 | 0.87 | 0.79 | 0.86 |
| I-IT3 | 92 | 0.55 | 0.55 | 0.55 | 0.84 | 92 | 0.56 | 0.69 | 0.70 | 0.90 | 0.84 | 0.90 |
| I-IT4 | 95 | 0.64 | 0.64 | 1.00 | 0.89 | 95 | 0.64 | 0.79 | 0.79 | 0.94 | 0.95 | 0.94 |
| I-IT5 | 95 | −0.02 | 0.00 | 0.00 | 0.90 | 95 | −0.01 | 0.80 | 0.81 | 0.95 | 0.95 | 0.95 |
| I-IT6 | 97 | 0.78 | 0.78 | 1.00 | 0.93 | 97 | 0.78 | 0.87 | 0.87 | 0.96 | 0.97 | 0.96 |
| I-IT7 | 97 | −0.02 | 0.00 | 0.00 | 0.93 | 97 | 0.00 | 0.87 | 0.87 | 0.97 | 0.97 | 0.96 |
| I-PT1 | 100 | 1.00 | 1.00 | 1.00 | 1.00 | 100 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Giammarino, M.; Mattiello, S.; Battini, M.; Quatto, P.; Battaglini, L.M.; Vieira, A.C.L.; Stilwell, G.; Renna, M. Evaluation of Inter-Observer Reliability of Animal Welfare Indicators: Which Is the Best Index to Use? Animals 2021, 11, 1445. https://doi.org/10.3390/ani11051445
Giammarino M, Mattiello S, Battini M, Quatto P, Battaglini LM, Vieira ACL, Stilwell G, Renna M. Evaluation of Inter-Observer Reliability of Animal Welfare Indicators: Which Is the Best Index to Use? Animals. 2021; 11(5):1445. https://doi.org/10.3390/ani11051445
Chicago/Turabian StyleGiammarino, Mauro, Silvana Mattiello, Monica Battini, Piero Quatto, Luca Maria Battaglini, Ana C. L. Vieira, George Stilwell, and Manuela Renna. 2021. "Evaluation of Inter-Observer Reliability of Animal Welfare Indicators: Which Is the Best Index to Use?" Animals 11, no. 5: 1445. https://doi.org/10.3390/ani11051445
APA StyleGiammarino, M., Mattiello, S., Battini, M., Quatto, P., Battaglini, L. M., Vieira, A. C. L., Stilwell, G., & Renna, M. (2021). Evaluation of Inter-Observer Reliability of Animal Welfare Indicators: Which Is the Best Index to Use? Animals, 11(5), 1445. https://doi.org/10.3390/ani11051445








