Clinical Scores in Veterinary Medicine: What Are the Pitfalls of Score Construction, Reliability, and Validation? A General Methodological Approach Applied in Cattle
Abstract
:Simple Summary
Abstract
1. Introduction
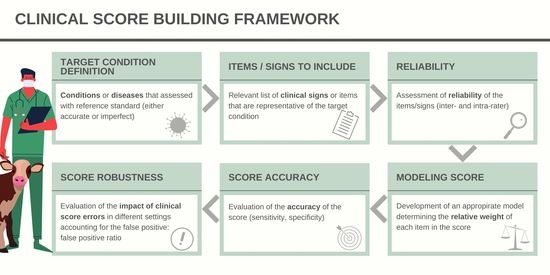
2. Condition That Needs to Be Measured: Notion of Construct
3. How to Measure Items Present in the Score?
3.1. Items Selected and Classification of the Different Possible Categories of Items
3.1.1. Intra and Inter-Rater Reliability
3.1.2. Two Raters Categorical Scale
3.1.3. Multiple Raters
3.1.4. Numeric Items
3.1.5. Benchmarking Reliability Parameters
4. How Can the Best Combination of Items Be Determined for Use in a Score?
4.1. Score Building to Determine the Relative Weight between and within Items That Are Assessed to Measure a Simple Construct
Internal vs. External Validation of the Model
4.2. Measurement of Complex Construct
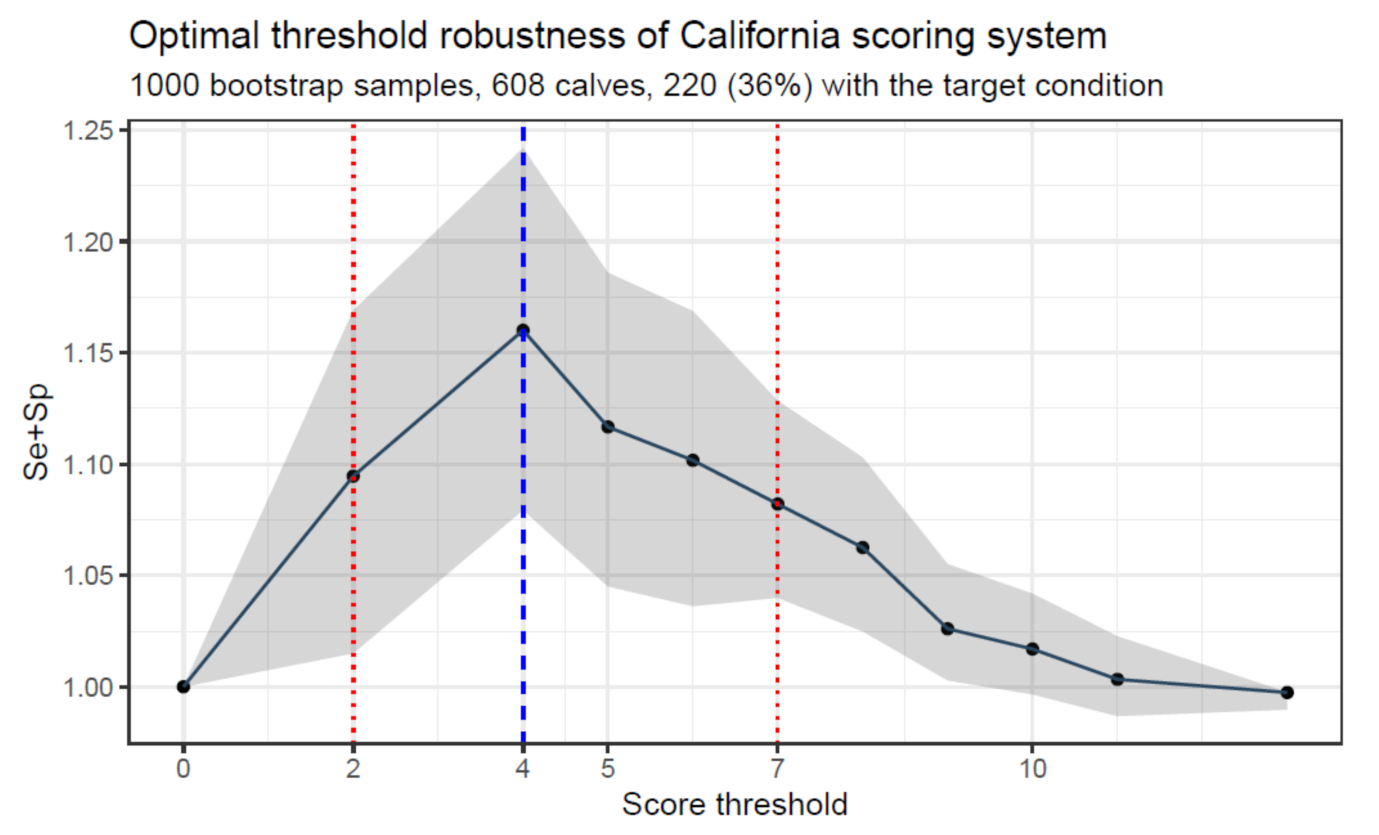
5. Accuracy of the Score
5.1. Case 1: The True Status of the Construct Can Be Determined (Directly or Indirectly)
5.2. Case 2: More Complex Construct
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Carslake, C.; Vázquez-Diosdado, J.A.; Kaler, J. Machine learning algorithms to classify and quantify multiple behaviours in dairy calves using a sensor: Moving beyond classification in precision livestock. Sensors 2021, 21, 88. [Google Scholar] [CrossRef]
- Duthie, C.A.; Bowen, J.M.; Bell, D.J.; Miller, G.A.; Mason, C.; Haskell, M.J. Feeding behaviour and activity as early indicators of disease in pre-weaned dairy calves. Animal 2021, 15, 100150. [Google Scholar] [CrossRef] [PubMed]
- Stachowicz, J.; Umstätter, C. Do we automatically detect health-or general welfare-related issues? A framework. Proc. R. Soc. B 2021, 288, 20210190. [Google Scholar] [CrossRef]
- Knauer, W.A.; Godden, S.M.; Dietrich, A.; James, R.E. The association between daily average feeding behaviors and morbidity in automatically fed group-housed preweaned dairy calves. J. Dairy Sci. 2017, 100, 5642–5652. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Knauer, W.A.; Godden, S.M.; Dietrich, A.; Hawkins, D.M.; James, R.E. Evaluation of applying statistical process control techniques to daily average feeding behaviors to detect disease in automatically fed group-housed preweaned dairy calves. J. Dairy Sci. 2018, 101, 8135–8145. [Google Scholar] [CrossRef] [PubMed]
- Boateng, G.O.; Neilands, T.B.; Frongillo, E.A.; Melgar-Quiñonez, H.R.; Young, S.L. Best practices for developing and validating scales for health, social, and behavioral research: A primer. Front. Public Health 2018, 6, 149. [Google Scholar] [CrossRef] [PubMed]
- McGuirk, S.M. Disease management of dairy calves and heifers. Vet. Clin. N. Am. Food Anim. Pract. 2008, 24, 139–153. [Google Scholar] [CrossRef]
- Love, W.J.; Lehenbauer, T.W.; Kass, P.H.; Van Eenennaam, A.L.; Aly, S.S. Development of a novel clinical scoring system for on-farm diagnosis of bovine respiratory disease in pre-weaned dairy calves. PeerJ 2014, 2, e238. [Google Scholar] [CrossRef] [Green Version]
- Buczinski, S.; Fecteau, G.; Dubuc, J.; Francoz, D. Validation of a clinical scoring system for bovine respiratory disease complex diagnosis in preweaned dairy calves using a Bayesian framework. Prev. Vet. Med. 2018, 156, 102–112. [Google Scholar] [CrossRef]
- Berman, G.; Francoz, D.; Dufour, S.; Buczinski, S. Un Nouvel Outil Diagnostique Pour Détecter les Bronchopneumonies Infectieuses à Traiter Chez les Veaux Lourds! Available online: http://bovin.qc.ca/wp-content/uploads/2021/03/P44-45-46-Outil-bronchopneumonies.pdf (accessed on 1 September 2021).
- Schlageter-Tello, A.; Bokkers, E.A.; Groot Koerkamp, P.W.; Van Hertem, T.; Viazzi, S.; Romanini, C.E.; Halachmi, I.; Bahr, C.; Berckmans, D.; Lokhorst, K. Effect of merging levels of locomotion scores for dairy cows on intra- and interrater reliability and agreement. J. Dairy Sci. 2014, 97, 5533–5542. [Google Scholar] [CrossRef]
- Roche, J.R.; Friggens, N.C.; Kay, J.K.; Fisher, M.W.; Stafford, K.J.; Berry, D.P. Invited review: Body condition score and its association with dairy cow productivity, health, and welfare. J. Dairy Sci. 2009, 92, 5769–5801. [Google Scholar] [CrossRef] [Green Version]
- Tomacheuski, R.M.; Monteiro, B.P.; Evangelista, M.C.; Luna, S.P.L.; Steagall, P.V. Measurement properties of pain scoring instruments in farm animals: A systematic review protocol using the COSMIN checklist. PLoS ONE 2021, 16, e0251435. [Google Scholar] [CrossRef]
- Van Nuffel, A.; Zwertvaegher, I.; Pluym, L.; Van Weyenberg, S.; Thorup, V.; Pastell, M.; Sonck, B.; Saeys, W. Lameness detection in dairy cows: Part 1. How to distinguish between non-lame and lame cows based on differences in locomotion or behavior. Animals 2015, 5, 838–860. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Perryman, L.E.; Kapil, S.J.; Jones, M.L.; Hunt, E.L. Protection of calves against cryptosporidiosis with immune bovine colostrum induced by a Cryptosporidium parvum recombinant protein. Vaccine 1999, 17, 2142–2149. [Google Scholar] [CrossRef]
- De Vet, H.C.; Terwee, C.B.; Mokkink, L.B.; Knol, D.L. Concepts, Theories and Models, and Types of Measurements. In Measurement in Medicine: A practical Guide; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Buczinski, S.; Pardon, B. Bovine respiratory disease diagnosis: What progress has been made in clinical diagnosis? Vet. Clin. N. Am. Food Anim. Pract. 2020, 36, 399–423. [Google Scholar] [CrossRef]
- Heinrichs, A.J.; Heinrichs, B.S.; Jones, C.M.; Erickson, P.S.; Kalscheur, K.F.; Nennich, T.D.; Heins, B.J.; Cardoso, F.C. Short communication: Verifying Holstein heifer heart girth to body weight prediction equations. J. Dairy Sci. 2017, 100, 8451–8454. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Naylor, J.M.; Streeter, R.M.; Torgerson, P. Factors affecting rectal temperature measurement using commonly available digital thermometers. Res. Vet. Sci. 2012, 92, 121–123. [Google Scholar] [CrossRef]
- Buczinski, S.; Buathier, C.; Bélanger, A.M.; Michaux, H.; Tison, N.; Timsit, E. Inter-rater agreement and reliability of thoracic ultrasonographic findings in feedlot calves, with or without naturally occurring bronchopneumonia. J. Vet. Intern. Med. 2018, 32, 1787–1792. [Google Scholar] [CrossRef] [PubMed]
- Maier, G.U.; Rowe, J.D.; Lehenbauer, T.W.; Karle, B.M.; Williams, D.R.; Champagne, J.D.; Aly, S.S. Development of a clinical scoring system for bovine respiratory disease in weaned dairy calves. J. Dairy Sci. 2019, 102, 7329–7344. [Google Scholar] [CrossRef]
- Kottner, J.; Audigé, L.; Brorson, S.; Donner, A.; Gajewski, B.J.; Hróbjartsson, A.; Streiner, D.L. Guidelines for reporting reliability and agreement studies (GRRAS) were proposed. Int. J. Nurs. Stud. 2011, 48, 661–671. [Google Scholar] [CrossRef]
- Gwet, K.L. Handbook of Inter-Rater Reliability: The Definitive Guide to Measuring the Extent of Agreement among Raters, 4th ed.; Advanced Analytics LLC: Piedmont, CA, USA, 2014. [Google Scholar]
- Cohen, J.A. Coefficient of agreement for nominal scales. Educ. Psychol. Meas. 1960, 20, 37–46. [Google Scholar] [CrossRef]
- Hilden, J. Commentary: On NRI, IDI, and “good-looking” statistics with nothing underneath. Epidemiology 2014, 25, 265–267. [Google Scholar] [CrossRef]
- Berman, J.; Francoz, D.; Abdallah, A.; Dufour, S.; Buczinski, S. Evaluation of inter-rater agreement of the clinical signs used to diagnose bovine respiratory disease in individually housed veal calves. J. Dairy Sci 2021, in press. [Google Scholar] [CrossRef] [PubMed]
- Broemeling, L.D. Bayesian Methods for Measures of Agreement, 1st ed.; Chapman and Hall/CRC: Boca Raton, FL, USA, 2020. [Google Scholar]
- Van Oest, R.; Girard, J.M. Weighting Schemes and Incomplete Data: A Generalized Bayesian Framework for Chance-Corrected Interrater Agreement. 2021. Available online: https://psyarxiv.com/s5n4e/ (accessed on 2 September 2021).
- de Vet, H.C.W.; Mokkink, L.B.; Terwee, C.B.; Hoekstra, O.S.; Knol, D.L. Clinicians are right not to like Cohen’s k. Br. Med. J. 2013, 346, f2125. [Google Scholar] [CrossRef] [Green Version]
- Walsh, P.; Thornton, J.; Asato, J.; Walker, N.; McCoy, G.; Baal, J.; Banimahd, F. Approaches to describing inter-rater reliability of the overall clinical appearance of febrile infants and toddlers in the emergency department. PeerJ 2014, 2, e651. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pardon, B.; Buczinski, S.; Deprez, P.R. Accuracy and inter-rater reliability of lung auscultation by bovine practitioners when compared with ultrasonographic findings. Vet. Rec. 2019, 185, 109. [Google Scholar] [CrossRef] [PubMed]
- Zapf, A.; Castell, S.; Morawietz, L.; Karch, A. Measuring inter-rater reliability for nominal data–which coefficients and confidence intervals are appropriate? Med. Res. Methodol. 2016, 16, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Koo, T.K.; Li, M.Y. A Guideline of Selecting and Reporting Intraclass Correlation Coefficients for Reliability Research. J. Chiropr. Med. 2016, 15, 155–163. [Google Scholar] [CrossRef] [Green Version]
- Dohoo, I.R.; Martin, S.W.; Stryhn, H. Veterinary Epidemiologic Research, 2nd ed.; VER. Inc.: Charlottetown, PEI, Canada, 2009. [Google Scholar]
- Collins, G.S.; Reitsma, J.B.; Altman, D.G.; Moons, K.G. Transparent reporting of a multivariable prediction model for individual prognosis or diagnosis (TRIPOD): The TRIPOD statement. Br. J. Surg. 2015, 102, 148–158. [Google Scholar] [CrossRef] [Green Version]
- Schiller, I.; van Smeden, M.; Hadgu, A.; Libman, M.; Reitsma, J.B.; Dendukuri, N. Bias due to composite reference standards in diagnostic accuracy studies. Stat. Med. 2016, 35, 1454–1470. [Google Scholar] [CrossRef]
- Branscum, A.J.; Gardner, I.A.; Johnson, W.O. Estimation of diagnostic-test sensitivity and specificity through Bayesian modeling. Prev. Vet. Med. 2005, 68, 145–163. [Google Scholar] [CrossRef] [PubMed]
- McInturff, P.; Johnson, W.O.; Cowling, D.; Gardner, I.A. Modelling risk when binary outcomes are subject to error. Stat. Med. 2004, 23, 1095–1109. [Google Scholar] [CrossRef] [PubMed]
- Harrell, F.E. Regression Modeling Strategies: With Applications to Linear Models, Logistic and Ordinal Regression, and Survival Analysis, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Steyerberg, E.W. Clinical Prediction Models, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Moons, K.G.; Harrell, F.E.; Steyerberg, E.W. Should scoring rules be based on odds ratios or regression coefficients? J. Clin. Epidemiol. 2002, 55, 1054–1055. [Google Scholar] [CrossRef]
- Pepe, M.S. The Statistical Evaluation of Medical Tests for Classification and Prediction, 1st ed.; Oxford University Press: Oxford, UK, 2003. [Google Scholar]
- Greiner, M. Two-graph receiver operating characteristic (TG-ROC): Update version supports optimisation of cut-off values that minimise overall misclassification costs. J. Immunol. Methods 1996, 191, 93–94. [Google Scholar] [CrossRef]




| Test = 1 for Rater or Test 2 | Test = 0 for Rater or Test 2 | ||
|---|---|---|---|
| Test = 1 for rater or test 1 | n11 = n×r11 | n10 = n×r10 | |
| Test = 0 for rater or test 1 | n01 = n×r01 | n00 = n×r00 | n |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Buczinski, S.; Boccardo, A.; Pravettoni, D. Clinical Scores in Veterinary Medicine: What Are the Pitfalls of Score Construction, Reliability, and Validation? A General Methodological Approach Applied in Cattle. Animals 2021, 11, 3244. https://doi.org/10.3390/ani11113244
Buczinski S, Boccardo A, Pravettoni D. Clinical Scores in Veterinary Medicine: What Are the Pitfalls of Score Construction, Reliability, and Validation? A General Methodological Approach Applied in Cattle. Animals. 2021; 11(11):3244. https://doi.org/10.3390/ani11113244
Chicago/Turabian StyleBuczinski, Sébastien, Antonio Boccardo, and Davide Pravettoni. 2021. "Clinical Scores in Veterinary Medicine: What Are the Pitfalls of Score Construction, Reliability, and Validation? A General Methodological Approach Applied in Cattle" Animals 11, no. 11: 3244. https://doi.org/10.3390/ani11113244
APA StyleBuczinski, S., Boccardo, A., & Pravettoni, D. (2021). Clinical Scores in Veterinary Medicine: What Are the Pitfalls of Score Construction, Reliability, and Validation? A General Methodological Approach Applied in Cattle. Animals, 11(11), 3244. https://doi.org/10.3390/ani11113244