Determination of Body Parts in Holstein Friesian Cows Comparing Neural Networks and k Nearest Neighbour Classification
Simple Summary
Abstract
1. Introduction
2. Materials and Methods
2.1. Recording Unit with Six Kinect Cameras
- U: Top view camera; the upper camera in a pair; oriented upside down (base up)
- N: Top view camera; the bottom camera in a pair; oriented normally (base down)
- S: Side view camera
2.2. Recording Software
2.3. Data Collection and Recorded Cows
2.4. Preparation of a Data Set of Pixel Properties
2.4.1. Balancing the Data Set Using Synthetic Minority Oversampling Technique (SMOTE)
2.5. Applied Machine Learning Methods
2.5.1. k Nearest Neighbours Classification
2.5.2. Neural Networks
2.5.3. Evaluation Metrics
‘One Versus Rest’: Precision, Recall, F1-Score
Overall Metrics: Accuracy and Hamming Loss
Kruskal–Wallis Tests
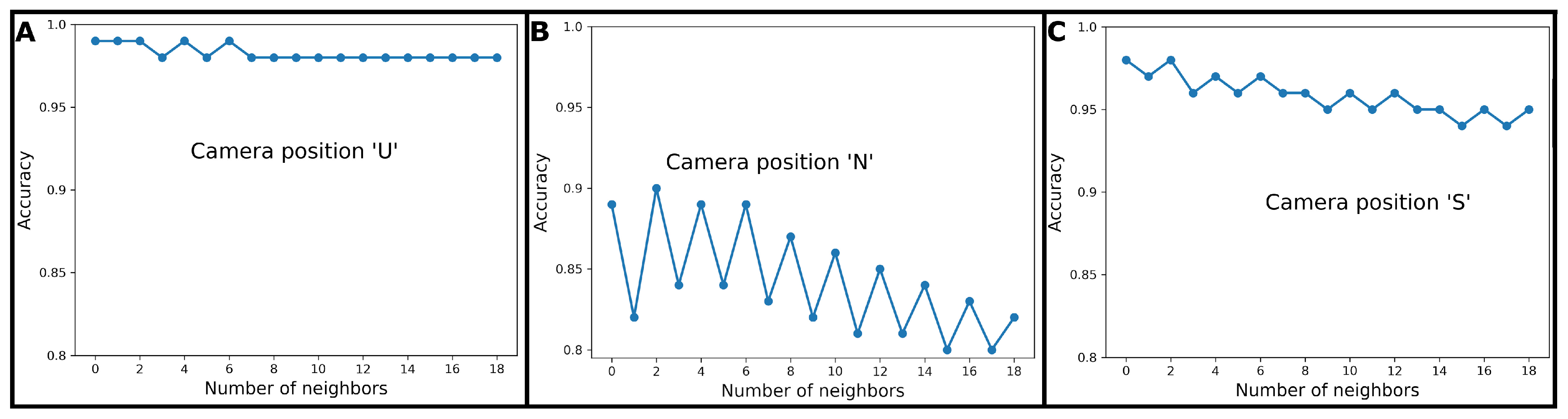
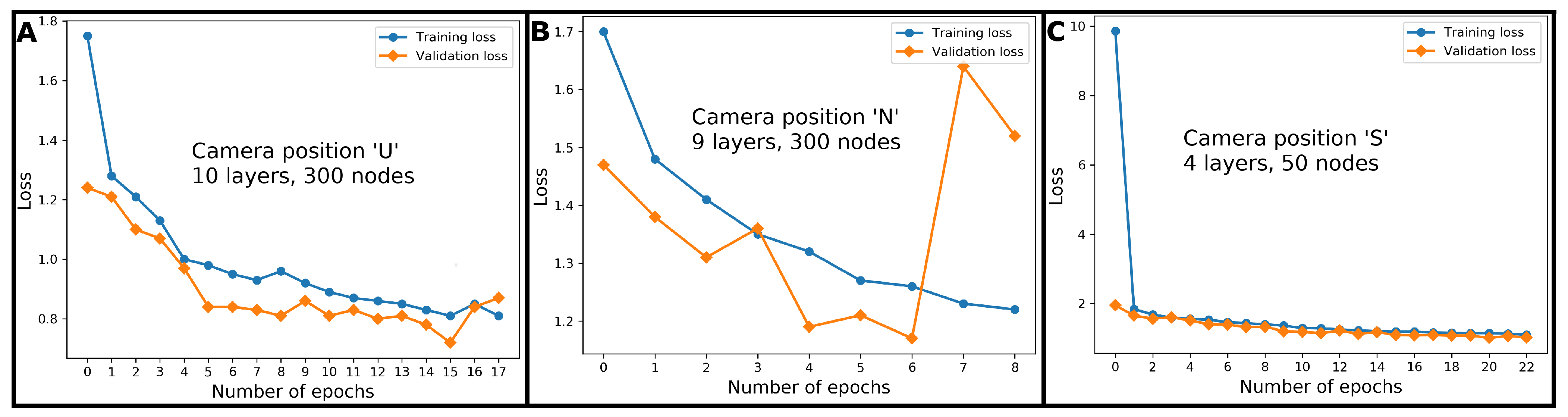
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Berckmans, D. Precision livestock farming (PLF). Comput. Electron. Agric. 2008, 62, 1. [Google Scholar] [CrossRef]
- Neethirajan, S. Recent advances in wearable sensors for animal health management. Sens. Bio-Sens. Res. 2017, 12, 15–29. [Google Scholar] [CrossRef]
- Fournel, S.; Rousseau, A.N.; Laberge, B. Rethinking environment control strategy of confined animal housing systems through precision livestock farming. Biosyst. Eng. 2017, 155, 96–123. [Google Scholar] [CrossRef]
- Van Hertem, T.; Alchanatis, V.; Antler, A.; Maltz, E.; Halachmi, I.; Schlageter-Tello, A.; Lokhorst, C.; Viazzi, S.; Romanini, C.E.B.; Pluk, A.; et al. Comparison of segmentation algorithms for cow contour extraction from natural barn background in side view images. Comput. Electron. Agric. 2013, 91, 65–74. [Google Scholar] [CrossRef]
- Salau, J.; Bauer, U.; Haas, J.H.; Thaller, G.; Harms, J.; Junge, W. Quantification of the effects of fur, fur color, and velocity on Time-Of-Flight technology in dairy production. SpringerPlus 2015, 4. [Google Scholar] [CrossRef]
- Van Nuffel, A.; Zwertvaegher, I.; Van Weyenberg, S.; Pastell, M.; Thorup, V.M.; Bahr, C.; Sonck, B.; Saeys, W. Lameness Detection in Dairy Cows: Part 2. Use of Sensors to Automatically Register Changes in Locomotion or Behavior. Animals 2015, 5, 861–885. [Google Scholar] [CrossRef]
- Viazzi, S.; Bahr, C.; Schlageter-Tello, A.; Van Hertem, T.; Romanini, C.E.B.; Pluk, A.; Halachmi, I.; Lokhorst, C.; Berckmans, D. Analysis of individual classification of lameness using automatic measurement of back posture in dairy cattle. J. Dairy Sci. 2013, 96, 257–266. [Google Scholar] [CrossRef]
- Zhao, K.; Bewley, J.; He, D.; Jin, X. Automatic lameness detection in dairy cattle based on leg swing analysis with an image processing technique. Comput. Electron. Agric. 2018, 148, 226–236. [Google Scholar] [CrossRef]
- Zhao, K.; He, D.; Bewley, J. Detection of Lameness in Dairy Cattle Using Limb Motion Analysis with Automatic Image Processing; Precision Dairy Farming 2016; Wageningen Academic Publishers: Leeuwarden, The Netherlands, 2016; pp. 97–104. [Google Scholar]
- Van Hertem, T.; Viazzi, S.; Steensels, M.; Maltz, E.; Antler, A.; Alchanatis, V.; Schlageter-Tello, A.; Lokhorst, K.; Romanini, C.E.B.; Bahr, C.; et al. Automatic lameness detection based on consecutive 3D-video recordings. Biosyst. Eng. 2014, 119, 108–116. [Google Scholar] [CrossRef]
- Pluk, A.; Bahr, C.; Poursaberi, A.; Maertens, W.; van Nuffel, A.; Berckmans, D. Automatic measurement of touch and release angles of the fetlock joint for lameness detection in dairy cattle using vision techniques. J. Dairy Sci. 2012, 95, 1738–1748. [Google Scholar] [CrossRef]
- Halachmi, I.; Klopcic, M.; Polak, P.; Roberts, D.J.; Bewley, J.M. Automatic assessment of dairy cattle body condition score using thermal imaging. Comput. Electron. Agric. 2013, 99, 35–40. [Google Scholar] [CrossRef]
- Azzaro, G.; Caccamo, M.; Ferguson, J.; Battiato, S.; Farinella, G.; Guarnera, G.; Puglisi, G.; Petriglieri, R.; Licitra, G. Objective estimation of body condition score by modeling cow body shape from digital images. J. Dairy Sci. 2011, 94, 2126–2137. [Google Scholar] [CrossRef] [PubMed]
- Alvarez, R.J.; Arroqui, M.; Mangudo, P.; Toloza, J.; Jatip, D.; Rodriguez, J.M.; Teyseyre, A.; Sanz, C.; Zunino, A.; Machado, C.; et al. Estimating Body Condition Score in Dairy Cows from Depth Images Using Convolutional Neural Networks, Transfer Learning and Model Ensembling Techniques. Agronomy 2019, 9, 90. [Google Scholar] [CrossRef]
- Song, X.; Bokkers, E.; van Mourik, S.; Koerkamp, P.G.; van der Tol, P. Automated body condition scoring of dairy cows using 3-dimensional feature extraction from multiple body regions. J. Dairy Sci. 2019, 102, 4294–4308. [Google Scholar] [CrossRef]
- Imamura, S.; Zin, T.T.; Kobayashi, I.; Horii, Y. Automatic evaluation of Cow’s body-condition-score using 3D camera. In Proceedings of the 2017 IEEE 6th Global Conference on Consumer Electronics (GCCE), Nagoya, Japan, 24–27 October 2017; pp. 1–2. [Google Scholar] [CrossRef]
- Spoliansky, R.; Edan, Y.; Parmet, Y.; Halachmi, I. Development of automatic body condition scoring using a low-cost 3-dimensional Kinect camera. J. Dairy Sci. 2016, 99, 7714–7725. [Google Scholar] [CrossRef]
- Weber, A.; Salau, J.; Haas, J.H.; Junge, W.; Bauer, U.; Harms, J.; Suhr, O.; Schönrock, K.; Rothfuß, H.; Bieletzki, S.; et al. Estimation of backfat thickness using extracted traits from an automatic 3D optical system in lactating Holstein-Friesian cows. Livest. Sci. 2014, 165, 129–137. [Google Scholar] [CrossRef]
- Thomasen, J.R.; Lassen, J.; Nielsen, G.G.B.; Borggard, C.; Stentebjerg, P.R.B.; Hansen, R.H.; Hansen, N.W.; Borchersen, S. Individual cow identification in a commercial herd using 3D camera technology; Technologies-Novel Phenotypes. In Proceedings of the World Congress on Genetics Applied to Livestock Production, Auckland, New Zealand, 11–16 February 2018; p. 613. [Google Scholar]
- Guzhva, O.; Ardö, H.; Herlin, A.; Nilsson, M.; Åström, K.; Bergsten, C. Feasibility study for the implementation of an automatic system for the detection of social interactions in the waiting area of automatic milking stations by using a video surveillance system. Comput. Electron. Agric. 2016, 127, 506–509. [Google Scholar] [CrossRef]
- Tsai, D.M.; Huang, C.Y. A motion and image analysis method for automatic detection of estrus and mating behavior in cattle. Comput. Electron. Agric. 2014, 104, 25–31. [Google Scholar] [CrossRef]
- Salau, J.; Haas, J.H.; Junge, W.; Thaller, G. How does the Behaviour of Dairy Cows during Recording Affect an Image Processing Based Calculation of the Udder Depth? Agric. Sci. 2018, 9. [Google Scholar] [CrossRef]
- Salau, J.; Krieter, J. Analysing the Space-Usage-Pattern of a cow herd using video surveillance and automated motion detection. Biosyst. Eng. 2020, 197, 122–134. [Google Scholar] [CrossRef]
- Salau, J.; Haas, J.H.; Junge, W.; Leisen, M.; Thaller, G. 2.3. Development of a multi-Kinect-system for gait analysis and measuring body characteristics in dairy cows. In Precision Livestock Farming Applications; Wageningen Academic Publishers: Noordwijk, The Netherlands, 2015; Chapter 4; pp. 55–64. [Google Scholar] [CrossRef]
- International Committee for Animal Recording–Conformation Recording Dairy and Beef Cattle. 2015. Available online: https://www.icar.org/wp-content/uploads/2015/08/Conformation-Recording-CR-WG.pdf (accessed on 13 February 2017).
- Deutscher Holstein Verband e.V. Exterieurbeurteilung–Lineare Beschreibung. Available online: https://www.holstein-dhv.de/seiteninhalte/exterieur.html (accessed on 19 October 2016).
- Holstein Association USA, Inc.–Linear Descriptive Traits. 2014. Available online: https://www.holsteinusa.com/pdf/print_material/linear_traits.pdf (accessed on 30 June 2016).
- Salau, J.; Haas, J.H.; Junge, W.; Thaller, G. Automated calculation of udder depth and rear leg angle in Holstein-Friesian cows using a multi-Kinect cow scanning system. Biosyst. Eng. 2017, 160, 154–169. [Google Scholar] [CrossRef]
- PrimeSense Supplies 3-D-Sensing Technology to “Project Natal” for Xbox 360. 2010. Available online: https://news.microsoft.com/2010/03/31/primesense-supplies-3-d-sensing-technology-to-project-natal-for-xbox-360/ (accessed on 2 June 2016).
- Kinect for Windows. 2014. Available online: https://www.microsoft.com/en-us/download/details.aspx?id=44561 (accessed on 2 June 2016).
- Andersen, M.R.; Jensen, T.; Lisouski, P.; Mortensen, A.K.; Hansen, M.K.; Gregersen, T.; Ahrent, P. Kinect Depth Sensor Evaluation for Computer Vision Applications. Tech. Rep. Electron. Comput. Eng. 2012, 1. Available online: https://tidsskrift.dk/ece/article/view/21221 (accessed on 24 September 2020).
- Hansard, M.; Lee, S.; Choi, O.; Horaud, R. Time-of-Flight Cameras–Principles, Methods and Applications; Springer Briefs in Computer Science; Springer: London, UK, 2012. [Google Scholar] [CrossRef]
- Nelson, S.; Haadem, C.; Dtvedt, A.N.; Hessle, A.; Martin, A. Automated activity monitoring and visual observation of estrus in a herd of loose housed Hereford cattle: Diagnostic accuracy and time to ovulation. Theriogenology 2017, 87, 205–211. [Google Scholar] [CrossRef] [PubMed]
- Shotton, J.; Fitzgibbon, A.; Cook, M.; Sharp, T.; Finocchio, M.; Moore, R.; Kipman, A.; Blake, A. Real-Time Human Pose Recognition in Parts from Single Depth Images. In Machine Learning for Computer Vision; Springer: Berlin/Heidelberg, Germany, 2013; pp. 119–135. [Google Scholar] [CrossRef]
- McCulloch, W.S.; Pitts, W. A logical calculus of the ideas immanent in nervous activity. Bull. Math. Biophys. 1943, 5, 115–133. [Google Scholar] [CrossRef]
- Rojas, R. Neural Networks: A Systematic Introduction; Springer: Berlin, Germany, 1996. [Google Scholar] [CrossRef]
- Hashimoto, Y. Applications of artificial neural networks and genetic algorithms to agricultural systems. Comput. Electron. Agric. 1997, 18, 71–72. [Google Scholar] [CrossRef]
- Samborska, I.A.; Alexandrov, V.; Sieczko, L.; Kornatowska, B.; Goltsev, V.; Cetner, M.D.; Kalaji, H.M. Artificial neural networks and their application in biological and agricultural research. Signpost Open Acess J. NanoPhotoBioSci. 2014, 2, 14–30. [Google Scholar]
- Sanzogni, L.; Kerr, D. Milk production estimates using feed forward artificial neural networks. Comput. Electron. Agric. 2001, 32, 21–30. [Google Scholar] [CrossRef]
- Alvarez, J.R.; Arroqui, M.; Mangudo, P.; Toloza, J.; Jatip, D.; Rodríguez, J.M.; Teyseyre, A.; Sanz, C.; Zunino, A.; Machado, C.; et al. Body condition estimation on cows from depth images using Convolutional Neural Networks. Comput. Electron. Agric. 2018, 155, 12–22. [Google Scholar] [CrossRef]
- Peng, Y.; Kondo, N.; Fujiura, T.; Suzuki, T.; Wulandari; Yoshioka, H.; Itoyama, E. Classification of multiple cattle behavior patterns using a recurrent neural network with long short-term memory and inertial measurement units. Comput. Electron. Agric. 2019, 157, 247–253. [Google Scholar] [CrossRef]
- Foldager, L.; Trénel, P.; Munksgaard, L.; Thomsen, P.T. Technical note: Random forests prediction of daily eating time of dairy cows from 3-dimensional accelerometer and radiofrequency identification. J. Dairy Sci. 2020, 103, 6271–6275. [Google Scholar] [CrossRef]
- Ebrahimie, E.; Ebrahimi, F.; Ebrahimi, M.; Tomlinson, S.; Petrovski, K.R. Hierarchical pattern recognition in milking parameters predicts mastitis prevalence. Comput. Electron. Agric. 2018, 147, 6–11. [Google Scholar] [CrossRef]
- Mammadova, N.; Keskin, I. Application of the Support Vector Machine to Predict Subclinical Mastitis in Dairy Cattle. Sci. World J. 2013, 2013, 603897. [Google Scholar] [CrossRef] [PubMed]
- da Rosa Righi, R.; Goldschmidt, G.; Kunst, R.; Deon, C.; da Costa, C.A. Towards combining data prediction and internet of things to manage milk production on dairy cows. Comput. Electron. Agric. 2020, 169, 105156. [Google Scholar] [CrossRef]
- Cover, T.; Hart, P. Nearest neighbor pattern classification. IEEE Trans. Inf. Theory 1967, 13, 21–27. [Google Scholar] [CrossRef]
- Wu, D.; Wu, Q.; Yin, X.; Jiang, B.; Wang, H.; He, D.; Song, H. Lameness detection of dairy cows based on the YOLOv3 deep learning algorithm and a relative step size characteristic vector. Biosyst. Eng. 2020, 189, 150–163. [Google Scholar] [CrossRef]
- Shen, W.; Cheng, F.; Zhang, Y.; Wei, X.; Fu, Q.; Zhang, Y. Automatic recognition of ingestive-related behaviors of dairy cows based on triaxial acceleration. Inf. Process. Agric. 2019. [Google Scholar] [CrossRef]
- Chollet, F.; O’Malley, T.; Tan, Z.; Bileschi, S.; Gibson, A.; Allaire, J.J.; Rahman, F.; Branchaud-Charron, F.; Lee, T.; de Marmiesse, G. Keras. 2015. Available online: https://keras.io (accessed on 13 March 2017).
- Salau, J.; Haas, J.H.; Junge, W.; Thaller, G. A multi-Kinect cow scanning system: Calculating linear traits from manually marked recordings of Holstein-Friesian dairy cows. Biosyst. Eng. 2017, 157, 92–98. [Google Scholar] [CrossRef]
- OpenNI. The SimpleViewer-Example from the OpenNI-Project. Available online: https://github.com/OpenNI/OpenNI2/blob/master/Samples/SimpleViewer.java/src/org/openni/Samples/SimpleViewer/SimpleViewer.java (accessed on 31 July 2013).
- Tsai, R. A versatile camera calibration technique for high-accuracy 3D machine vision metrology using off-the-shelf TV cameras and lenses. IEEE J. Robot. Autom. 1987, 3, 323–344. [Google Scholar] [CrossRef]
- Smisek, J.; Jancosek, M.; Pajdla, T. 3D with Kinect. In Consumer Depth Cameras for Computer Vision: Research Topics and Applications; Fossati, A., Gall, J., Grabner, H., Ren, X., Konolige, K., Eds.; Springer: London, UK, 2013; pp. 3–25. [Google Scholar] [CrossRef]
- Khoshelham, K.; Elberink, S.O. Accuracy and Resolution of Kinect Depth Data for Indoor Mapping Applications. Sensors 2012, 12, 1437–1454. [Google Scholar] [CrossRef]
- Salau, J.; Haas, J.H.; Junge, W.; Thaller, G. Extrinsic calibration of a multi-Kinect camera scanning passage for measuring functional traits in dairy cows. Biosyst. Eng. 2016, 151, 409–424. [Google Scholar] [CrossRef]
- Piccardi, M. Background subtraction techniques: A review. In Proceedings of the 2004 IEEE International Conference on Systems, Man and Cybernetics (IEEE Cat. No.04CH37583), The Hague, The Netherlands, 10–13 October 2004; Volume 4, pp. 3099–3104. [Google Scholar] [CrossRef]
- Salau, J.; Haas, J.H.; Thaller, G.; Leisen, M.; Junge, W. Developing a multi-Kinect-system for monitoring in dairy cows: Object recognition and surface analysis using wavelets. Animal 2016, 10, 1513–1524. [Google Scholar] [CrossRef] [PubMed]
- Kühnel, W. Differentialgeometrie, Kurven-Flächen-Mannigfaltigkeiten, 6th ed.; Springer Spektrum: Heidelberg, Germany, 2013. [Google Scholar] [CrossRef]
- van Rossum, G. Python Tutorial; Technical Report CS-R9526; Centrum voor Wiskunde en Informatica (CWI): Amsterdam, The Netherlands, 1995. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Chawla, N.V.; Bowyer, K.W.; Hall, L.O.; Kegelmeyer, W.P. SMOTE: Synthetic Minority Over-sampling Technique. J. Artif. Intell. Res. 2002, 16, 321–357. [Google Scholar] [CrossRef]
- Lemaître, G.; Nogueira, F.; Aridas, C.K. Imbalanced-learn: A Python Toolbox to Tackle the Curse of Imbalanced Datasets in Machine Learning. J. Mach. Learn. Res. 2017, 18, 1–5. [Google Scholar]
- Abadi, M.; Agarwal, A.; Barham, P.; Brevdo, E.; Chen, Z.; Citro, C.; Corrado, G.S.; Davis, A.; Dean, J.; Devin, M.; et al. TensorFlow: Large-Scale Machine Learning on Heterogeneous Systems. In Proceedings of the 12th USENIX Conference on Operating Systems Design and Implementation, Savannah, GA, USA, 2–4 November 2016; USENIX Association: Washington, DC, USA, 2016. OSDI 16. pp. 265–283. [Google Scholar]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A Simple Way to Prevent Neural Networks from Overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Sasaki, Y. The Truth of the F-Measure. 2007. Available online: https://www.cs.odu.edu/~mukka/cs795sum09dm/Lecturenotes/Day3/F-measure-YS-26Oct07.pdf (accessed on 21 April 2017).
- Hamming, R.W. Error detecting and error correcting codes. Bell Syst. Tech. J. 1950, 29, 147–160. [Google Scholar] [CrossRef]
- Everitt, B.S.; Landau, S.; Leese, M.; Stahl, D. Miscellaneous Clustering Methods. In Cluster Analysis; John Wiley & Sons, Ltd.: London, UK, 2011; Chapter 8; pp. 215–255. [Google Scholar] [CrossRef]
- Duda, R.O.; Hart, P.E.; Stork, D.G. Pattern Classification, 2nd ed.; John Wiley & Sons, Ltd.: London, UK, 2000. [Google Scholar]
- Baldi, P.; Vershynin, R. The capacity of feedforward neural networks. arXiv 2019, arXiv:1901.00434. [Google Scholar] [CrossRef]
- Wang, A.; Zhou, H.; Xu, W.; Chen, X. Deep Neural Network Capacity. arXiv 2017, arXiv:1708.05029. [Google Scholar]
- Stathakis, D. How many hidden layers and nodes? Int. J. Remote Sens. 2009, 30, 2133–2147. [Google Scholar] [CrossRef]
- Wolpert, D.H. The Lack of A Priori Distinctions Between Learning Algorithms. Neural Comput. 1996, 8, 1341–1390. [Google Scholar] [CrossRef]
- Powers, D. Evaluation: From Precision, Recall and F-Factor to ROC, Informedness, Markedness & Correlation. J. Mach. Learn. Technol. 2011, 2, 37–63. [Google Scholar]
- Nir, O.; Parmet, Y.; Werner, D.; Adin, G.; Halachmi, I. 3D Computer-vision system for automatically estimating heifer height and body mass. Advances in the Engineering of Sensor-based Monitoring and Management Systems for Precision Livestock Farming. Biosyst. Eng. 2018, 173, 4–10. [Google Scholar] [CrossRef]
- Le Cozler, Y.; Allain, C.; Caillot, A.; Delouard, J.; Delattre, L.; Luginbuhl, T.; Faverdin, P. High-precision scanning system for complete 3D cow body shape imaging and analysis of morphological traits. Comput. Electron. Agric. 2019, 157, 447–453. [Google Scholar] [CrossRef]
- Le Cozler, Y.; Allain, C.; Xavier, C.; Depuille, L.; Caillot, A.; Delouard, J.; Delattre, L.; Luginbuhl, T.; Faverdin, P. Volume and surface area of Holstein dairy cows calculated from complete 3D shapes acquired using a high-precision scanning system: Interest for body weight estimation. Comput. Electron. Agric. 2019, 165, 104977. [Google Scholar] [CrossRef]
- Banko, M.; Brill, E. Scaling to Very Very Large Corpora for Natural Language Disambiguation. In Proceedings of the 39th Annual Meeting of the Association for Computational Linguistics, Toulouse, France, 6–11 July 2001; pp. 26–33. [Google Scholar] [CrossRef]
- Halevy, A.; Norvig, P.; Pereira, F. The Unreasonable Effectiveness of Data. IEEE Intell. Syst. 2009, 24, 8–12. [Google Scholar] [CrossRef]

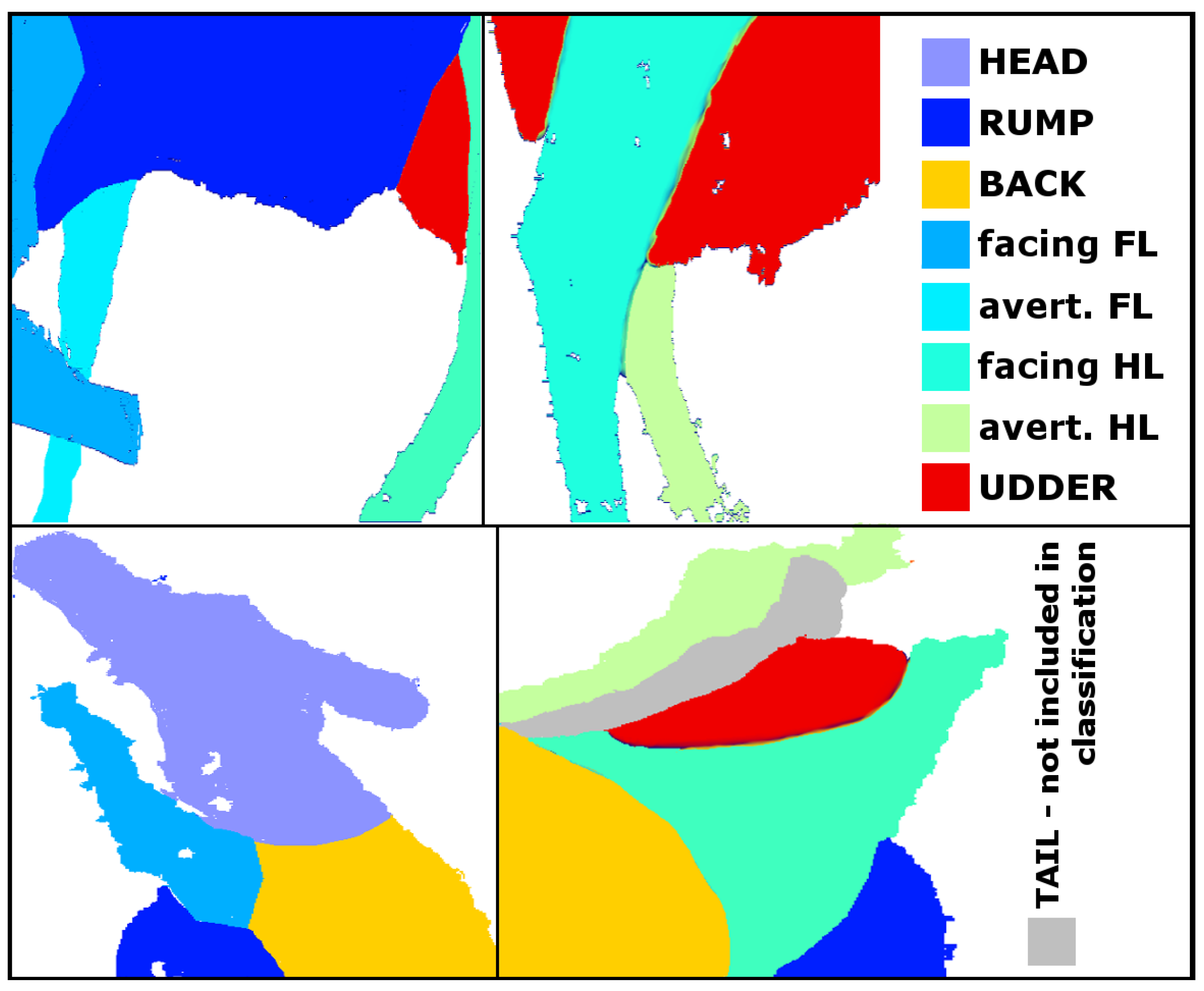
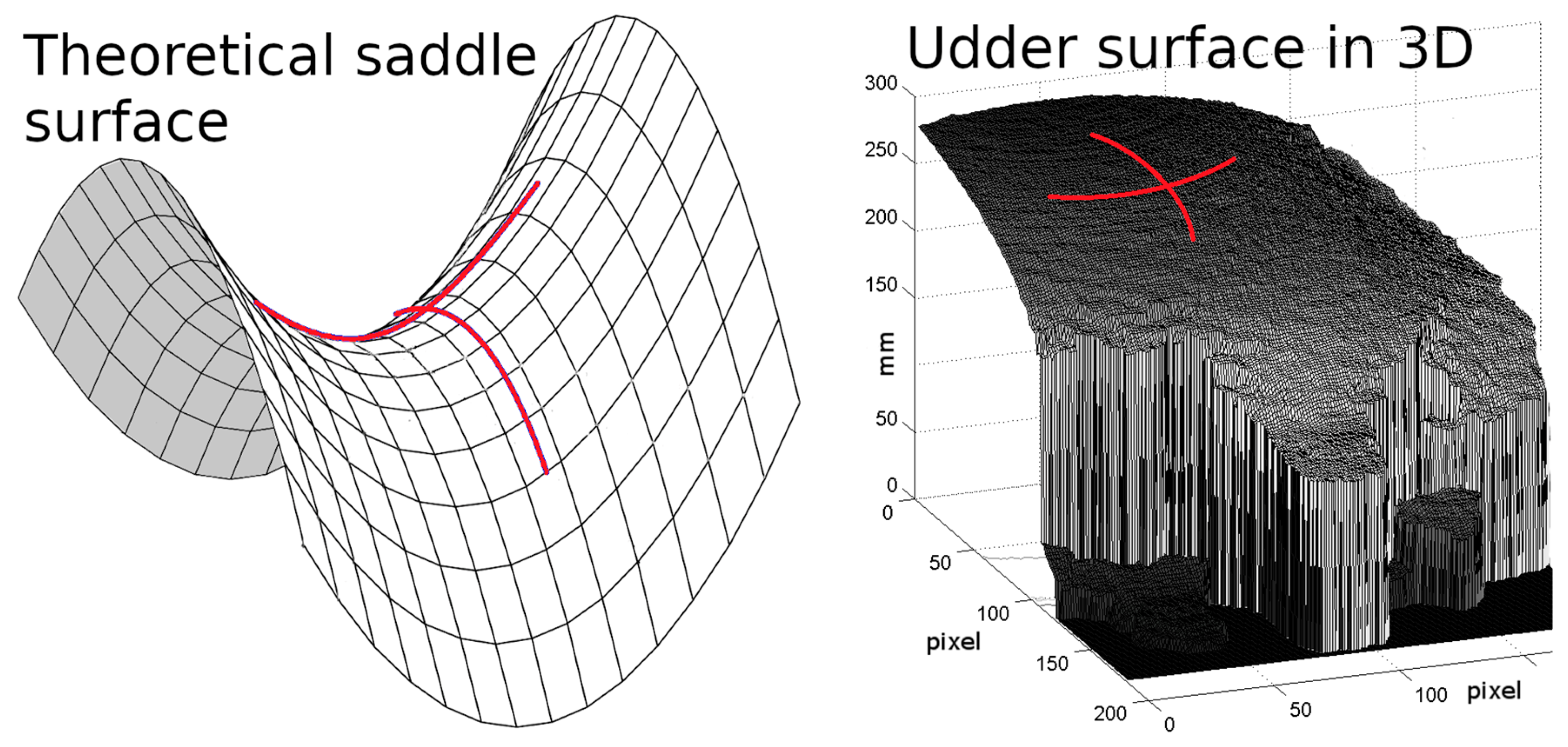
| No | Row | Col | Depth | m_curv | var | He | Ru | Ba | fFL | aFL | fHL | aHL | Ud |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 139 | 113 | 1050 | 0.66 | 5.4990 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 356 | 295 | 672 | 0.50 | 0.1945 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 366 | 46 | 931 | −0.04 | 2.2500 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 3 | 352 | 60 | 746 | 0.36 | 0.6115 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| 4 | 107 | 111 | 644 | 0.50 | 0.1109 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 5 | 110 | 267 | 1140 | 2.00 | 4.4437 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 6 | 326 | 160 | 801 | 1.00 | 0.7779 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 7 | 75 | 301 | 976 | 0.00 | 0.0000 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 8 | 283 | 388 | 1076 | −0.05 | 2.2512 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 9 | 573 | 153 | 936 | 3.00 | 2.4996 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 10 | 460 | 244 | 1050 | 1.50 | 1.7503 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 11 | 544 | 297 | 1001 | 0.55 | 3.2509 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 12 | 235 | 93 | 685 | 0.00 | 0.1109 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| ... | ...... | ... | ... |
| Pixel on body part = True | Pixel on body part = False | |
| Pixel classified to be on body part = True | TP | FP |
| Pixel classified to be on body part = False | FN | TN |
| knn | NN | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Accuracy | U | 0.976 | 0.841 | ||||||||||||||
| N | 0.888 | 0.684 | |||||||||||||||
| S | 0.963 | 0.777 | |||||||||||||||
| Ha.loss | U | 0.007 | 0.045 | ||||||||||||||
| N | 0.027 | 0.079 | |||||||||||||||
| S | 0.009 | 0.056 | |||||||||||||||
| He | Ru | Ba | fFL | aFL | fHL | aHL | Ud | He | Ru | Ba | fFL | aFL | fHL | aHL | Ud | ||
| Precision | U | 0.96 | 0.97 | 0.99 | 0.99 | 1.00 | 0.96 | 1.00 | - | 0.80 | 0.77 | 0.90 | 0.82 | 0.97 | 0.69 | 0.95 | - |
| N | 0.93 | 0.87 | 0.77 | 0.89 | 0.92 | 0.90 | 0.95 | 0.84 | 0.82 | 0.55 | 0.97 | 0.58 | 0.73 | 0.68 | 0.63 | 0.53 | |
| S | 0.95 | 0.96 | 0.97 | 0.96 | 1.00 | 0.96 | 0.98 | 0.96 | 0.67 | 0.78 | 0.78 | 0.75 | 0.94 | 0.68 | 0.81 | 0.74 | |
| Recall | U | 0.96 | 0.97 | 0.98 | 0.99 | 1.00 | 0.97 | 1.00 | - | 0.70 | 0.66 | 0.85 | 0.93 | 0.99 | 0.84 | 0.94 | - |
| N | 0.95 | 0.84 | 0.98 | 0.87 | 0.96 | 0.88 | 0.93 | 0.83 | 0.71 | 0.60 | 1.00 | 0.70 | 0.70 | 0.57 | 0.71 | 0.48 | |
| S | 0.95 | 0.96 | 0.97 | 0.97 | 1.00 | 0.96 | 0.99 | 0.98 | 0.45 | 0.61 | 0.85 | 0.90 | 1.00 | 0.62 | 0.95 | 0.83 | |
| F1-score | U | 0.96 | 0.97 | 0.99 | 0.99 | 1.00 | 0.97 | 1.00 | - | 0.75 | 0.71 | 0.87 | 0.87 | 0.98 | 0.76 | 0.94 | - |
| N | 0.94 | 0.85 | 0.86 | 0.88 | 0.94 | 0.89 | 0.94 | 0.84 | 0.76 | 0.58 | 0.99 | 0.63 | 0.72 | 0.62 | 0.67 | 0.50 | |
| S | 0.95 | 0.96 | 0.97 | 0.97 | 1.00 | 0.96 | 0.98 | 0.97 | 0.54 | 0.69 | 0.81 | 0.82 | 0.97 | 0.65 | 0.88 | 0.78 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Salau, J.; Haas, J.H.; Junge, W.; Thaller, G. Determination of Body Parts in Holstein Friesian Cows Comparing Neural Networks and k Nearest Neighbour Classification. Animals 2021, 11, 50. https://doi.org/10.3390/ani11010050
Salau J, Haas JH, Junge W, Thaller G. Determination of Body Parts in Holstein Friesian Cows Comparing Neural Networks and k Nearest Neighbour Classification. Animals. 2021; 11(1):50. https://doi.org/10.3390/ani11010050
Chicago/Turabian StyleSalau, Jennifer, Jan Henning Haas, Wolfgang Junge, and Georg Thaller. 2021. "Determination of Body Parts in Holstein Friesian Cows Comparing Neural Networks and k Nearest Neighbour Classification" Animals 11, no. 1: 50. https://doi.org/10.3390/ani11010050
APA StyleSalau, J., Haas, J. H., Junge, W., & Thaller, G. (2021). Determination of Body Parts in Holstein Friesian Cows Comparing Neural Networks and k Nearest Neighbour Classification. Animals, 11(1), 50. https://doi.org/10.3390/ani11010050





