Social Experience of Captive Livingstone’s Fruit Bats (Pteropus livingstonii)
Abstract
Simple Summary
Abstract
1. Introduction
2. Materials and Methods
2.1. Ethics
2.2. Study Population
2.3. Behavioural Observations
2.4. Social Network Construction
2.5. Social Network Analysis
2.5.1. Social Complexity and Structure in P. livingstonii
2.5.2. Dominance in P. livingstonii
2.5.3. Social Roles of P. livingstonii
3. Results
3.1. Data Collection Summary
3.2. Social Complexity and Structure
3.2.1. Network Complexity
3.2.2. Relationships between Network Types
3.2.3. Network Assortment
3.3. Social Roles
3.3.1. Dominance Hierarchy Analysis
3.3.2. Class Membership and Social Roles
3.3.3. Temporal Stability of Social Roles
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
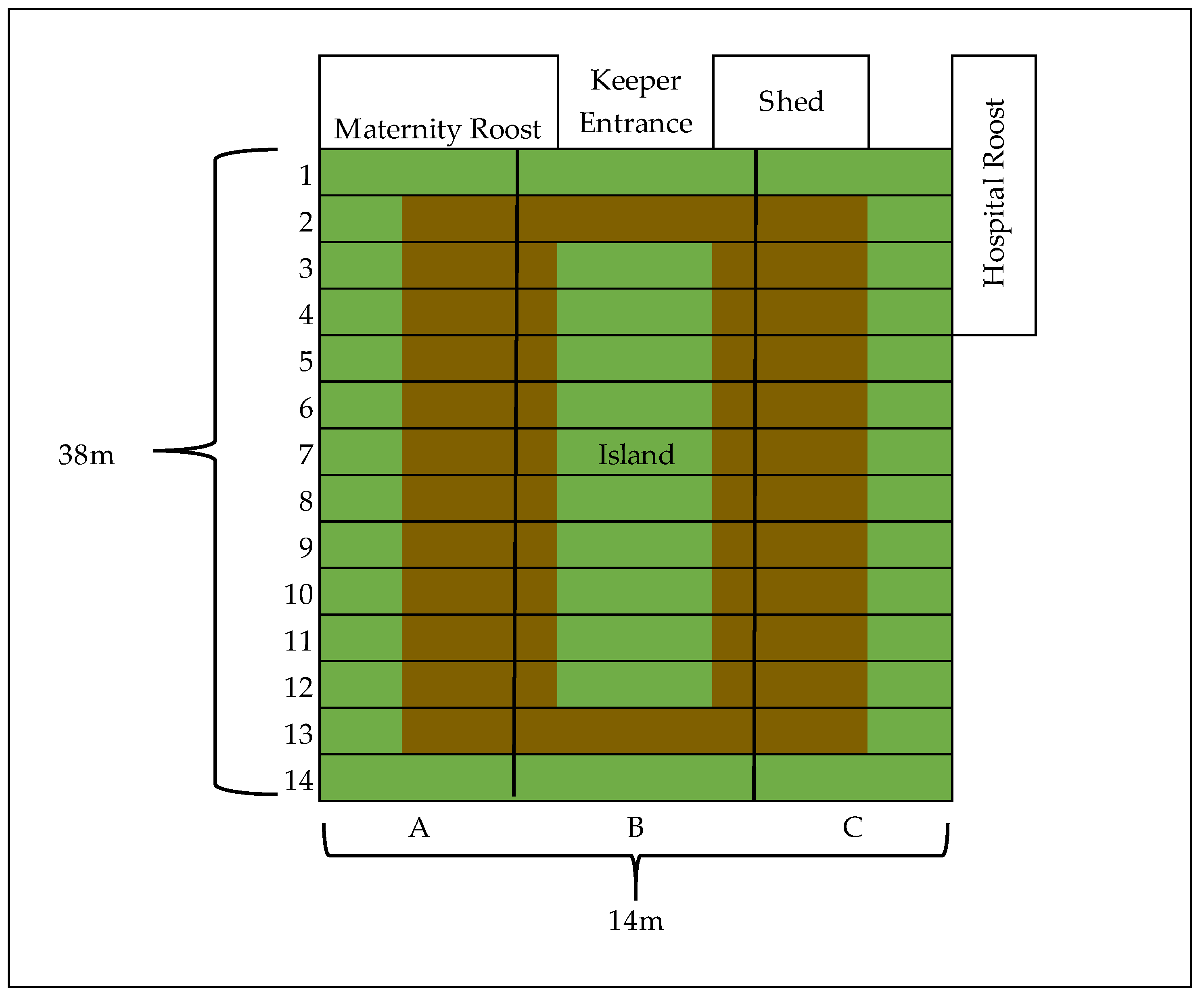
Appendix A
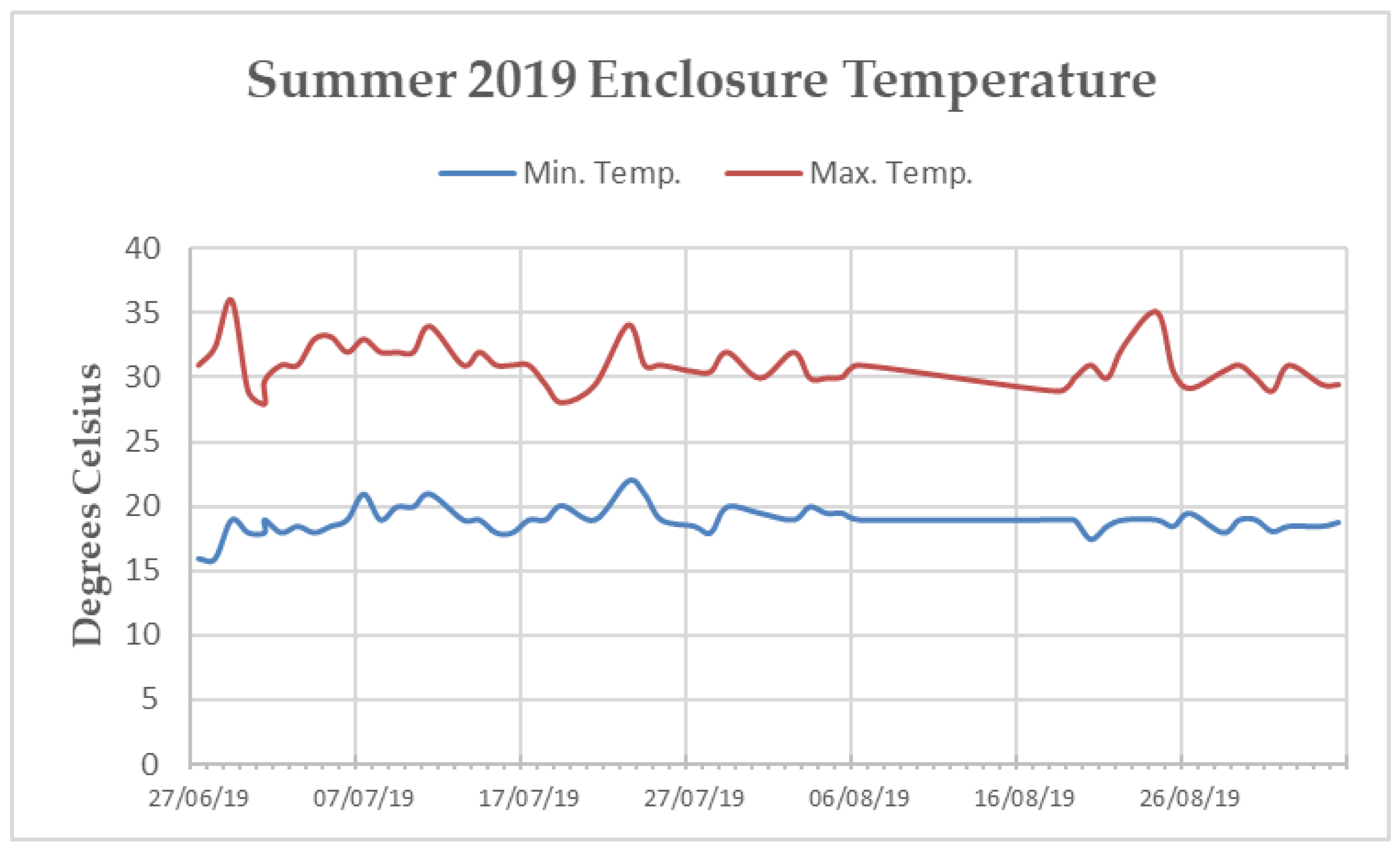
Appendix B
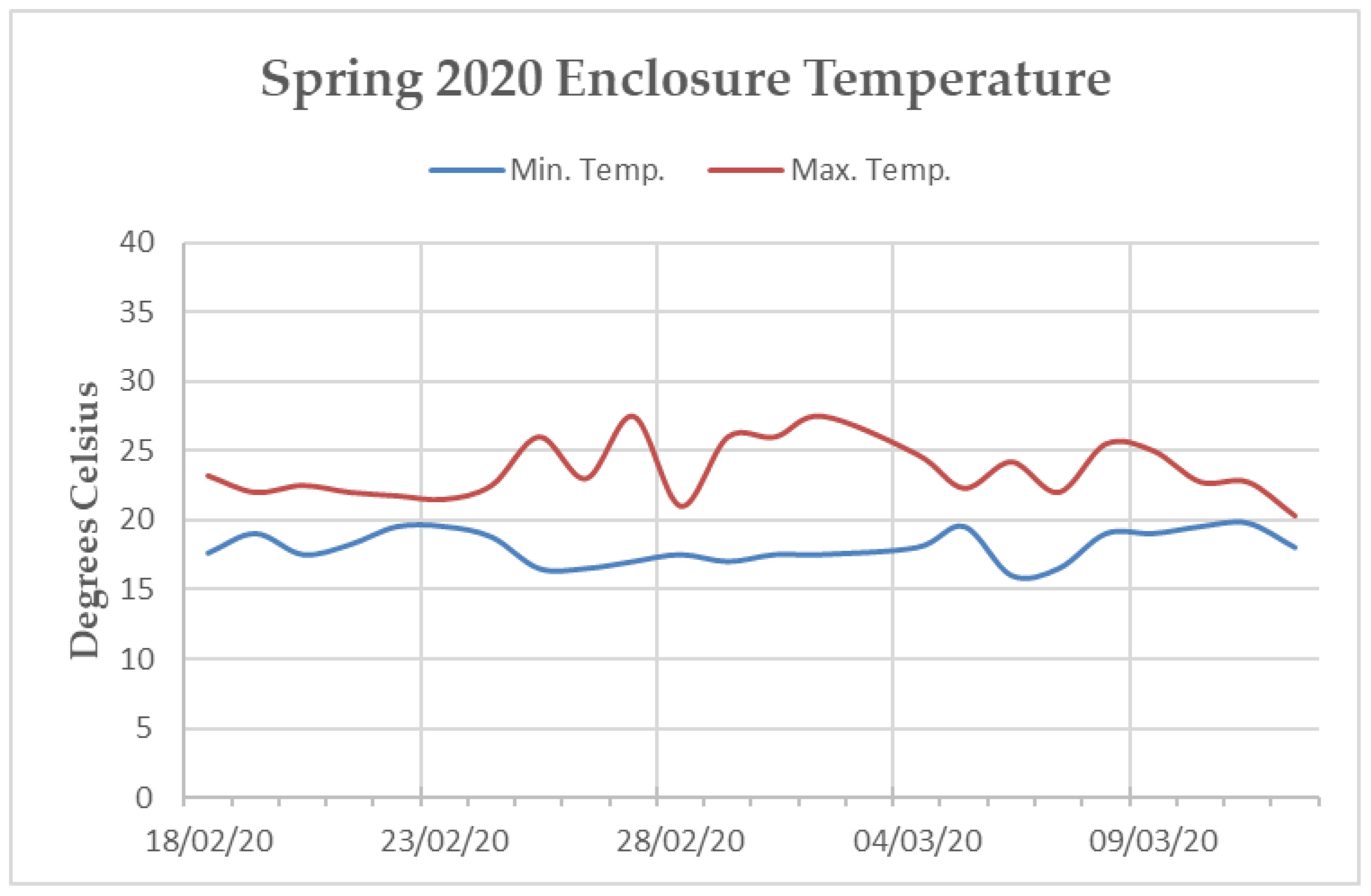
Appendix C
| Ethogram of Dyadic LFB Behaviours | ||
|---|---|---|
| Category | Behaviour | Definition |
| Aggression | open mouth | mouth open and directed at another individual in close proximity |
| food steal | one individual takes food from another with force | |
| lunge | one individual lunges (either whole body or head) toward another | |
| bite | one individual’s mouth makes forceful contact with any part of another (usually the head/neck) during an aggressive encounter | |
| thumb jab | the hook of the thumb is jabbed at another individual during an aggression encounter | |
| wrestle | intense form of aggression involving biting, thumb jabbing, and attempts at connecting blows, one or both bats may lose their grip on the mesh, accompanied by vocalisations | |
| double thumb jab/shove | both thumb hooks make contact with another individual during an aggressive encounter | |
| chase | one individual rapidly pursues another | |
| displace | an individual’s approach along a path causes another individual to leave the area | |
| flight-displaced by | one individual flies away from a location in order to be out of the path of another approaching individual | |
| mesh movement-avoid | one individual moves horizontally along the mesh to get out of the way of or move away from another individual | |
| climb-avoid | one individual moves vertically along mesh or substrate to get out of the way of or move away from another individual | |
| vocal-male cackle | made by males during an aggressive encounter | |
| vocal-call | a two tone sound used predominantly by males in territory defence, directed at an intruder, wings are often spread, frequency of calls varies with dominance level, females can produce a quieter version | |
| vocal-female cackle | made by females to ward off males, much louder than chatter or male cackle | |
| wing spread-social wing flick | one or both wings vigorously flapped toward another individual and then withdrawn | |
| wing spread-shaking | wings shaken repeatedly at another individual or threatening object/hazard, can be both together or alternating or with whole body movements | |
| wing spread-marching | wings move back and forth alternately toward another individual or a threatening object/hazard | |
| wing spread-rotating | whole body and wings moving 45 degrees either side of a threatening subject | |
| wing clap | both wings rapidly drawn together in direction of another individual, making a clapping sound as they meet | |
| wing ruffle | partially folded wings drawn together in direction of another individual, making a ruffling sound as they meet | |
| Affiliation | roost in pair | hanging by hind limb(s), wings wrapped around ventral region or wings of other individual, muzzle usually tucked into chest, eyes closed, no ear movements |
| allogrooming-mutual | two animals simultaneously groom each other with licking, biting, or scratching of similar intensity | |
| allogrooming-nonmutual | one animal within a pair grooms the other by licking, biting, or scratching with no reciprocation | |
| play | prolonged gentle wrestling, holding, mouthing, biting, and genital sniffing and grooming with no vocalisations, may lead to mounting | |
| food share | involves one individual vigorously licking the mouth of another while they chew, the feeding individual usually holds the other behind the head or both individuals hold each other | |
| follow | one individual follows another, not the same as chase as both individuals often stay together once movement has ceased | |
| approach without displacement | one individual approaches another by climbing or flying without displacement | |
| touch nose | two individuals make physical contact with their noses | |
| body/genital sniff | one individual sniffs the body, genitals, or air around another individual | |
| pre-copulation | involves sniffing, genital allogrooming, mutual jabbing and light wrestling | |
| copulatory mount | male with an erect penis mounts a female, male grips female from behind, male restrains females forelimbs with his own and holds the scruff of her neck in his mouth | |
| air sniff | an individual smells the air around another by directing its head and nose | |
| hook | one individual hooks onto or touches another with its thumbs down, more gentle than thumb jab | |
| intervene in aggression | a third individual attempts to break up a bout of wrestling or fighting between two other individuals, this can halt the fight, cause one or both animals to move off, or initiate aggression directed at the third party | |
| lean towards | movement of body only towards another individual when in the hanging position | |
References
- Naug, D. Nutritional stress due to habitat loss may explain recent honeybee colony collapses. Biol. Conserv. 2009, 142, 2369–2372. [Google Scholar] [CrossRef]
- Thomas, P.; Croft, D.P.; Morrell, L.J.; Davis, A.; Faria, J.; Dyer, J.; Piyapong, C.; Ramnarine, I.; Ruxton, G.; Krause, J. Does defection during predator inspection affect social structure in wild shoals of guppies? Anim. Behav. 2008, 75, 43–53. [Google Scholar] [CrossRef]
- Manno, T.G. Social networking in the Columbian ground squirrel, Spermophilus columbianus. Anim. Behav. 2008, 75, 1221–1228. [Google Scholar] [CrossRef]
- Wittemyer, G.; Douglas-Hamilton, I.; Getz, W. The socioecology of elephants: Analysis of the processes creating multitiered social structures. Anim. Behav. 2005, 69, 1357–1371. [Google Scholar] [CrossRef]
- Lusseau, D. The emergent properties of a dolphin social network. Proc. R. Soc. B Biol. Sci. 2003, 270, S186–S188. [Google Scholar] [CrossRef] [PubMed]
- Koyama, N.F. Matrilineal Cohesion and Social Networks in Macaca fuscata. Int. J. Primatol. 2003, 24, 797–811. [Google Scholar] [CrossRef]
- Stanley, C.; Dunbar, R. Consistent social structure and optimal clique size revealed by social network analysis of feral goats, Capra hircus. Anim. Behav. 2013, 85, 771–779. [Google Scholar] [CrossRef]
- Silk, J.B.; Alberts, S.C.; Altmann, J. Patterns of coalition formation by adult female baboons in Amboseli, Kenya. Anim. Behav. 2004, 67, 573–582. [Google Scholar] [CrossRef]
- Sueur, C.; Petit, O.; De Marco, A.; Jacobs, A.; Watanabe, K.; Thierry, B. A comparative network analysis of social style in macaques. Anim. Behav. 2011, 82, 845–852. [Google Scholar] [CrossRef]
- Whitehead, H. Analyzing Animal Societies; University of Chicago Press: Chicago, IL, USA, 2008. [Google Scholar]
- Groenewoud, F.; Frommen, J.G.; Josi, D.; Tanaka, H.; Jungwirth, A.; Taborsky, M. Predation risk drives social complexity in cooperative breeders. Proc. Natl. Acad. Sci. USA 2016, 113, 4104–4109. [Google Scholar] [CrossRef]
- Krause, J.; Croft, D.P.; James, R. Social network theory in the behavioural sciences: Potential applications. Behav. Ecol. Sociobiol. 2007, 62, 15–27. [Google Scholar] [CrossRef] [PubMed]
- Snyder-Mackler, N.; Burger, J.R.; Gaydosh, L.; Belsky, D.W.; Noppert, G.A.; Campos, F.A.; Bartolomucci, A.; Yang, Y.C.; Aiello, A.E.; O’Rand, A.; et al. Social determinants of health and survival in humans and other animals. Science 2020, 368, eaax9553. [Google Scholar] [CrossRef] [PubMed]
- Silk, J.B.; Beehner, J.C.; Bergman, T.J.; Crockford, C.; Engh, A.L.; Moscovice, L.R.; Wittig, R.M.; Seyfarth, R.M.; Cheney, D.L. The benefits of social capital: Close social bonds among female baboons enhance offspring survival. Proc. R. Soc. B Biol. Sci. 2009, 276, 3099–3104. [Google Scholar] [CrossRef] [PubMed]
- Brando, S.; Buchanan-Smith, H.M. The 24/7 approach to promoting optimal welfare for captive wild animals. Behav. Process. 2018, 156, 83–95. [Google Scholar] [CrossRef] [PubMed]
- Wolfensohn, S.E.; Shotton, J.; Bowley, H.; Davies, S.; Thompson, S.; Justice, W.S.M. Assessment of Welfare in Zoo Animals: Towards Optimum Quality of Life. Animals 2018, 8, 110. [Google Scholar] [CrossRef]
- Rose, P.; Croft, D.P. The potential of Social Network Analysis as a tool for the management of zoo animals. Anim. Welf. 2015, 24, 123–138. [Google Scholar] [CrossRef]
- Mickleburgh, S.; Carroll, J.B. The Role of Captive Breeding in the Conservation of Old World Fruit Bats; Springer Science and Business Media LLC: Dordrecht, The Netherlands, 1994; pp. 352–364. [Google Scholar]
- Bell, E.; Price, E.; Balthes, S.; Cordon, M.; Wormell, D. Flight patterns in zoo-housed fruit bats (Pteropus spp.). Zoo Biol. 2019, 38, 248–257. [Google Scholar] [CrossRef]
- Brann, D.W.; Mahesh, V.B. Role of corticosteroids in female reproduction. FASEB J. 1991, 5, 2691–2698. [Google Scholar] [CrossRef]
- Wielebnowski, N. Stress and distress: Evaluating their impact for the well-being of zoo animals. J. Am. Vet. Med. Assoc. 2003, 223, 973–977. [Google Scholar] [CrossRef]
- McFarland, R.; Murphy, D.; Lusseau, D.; Henzi, S.P.; Parker, J.L.; Pollet, T.V.; Barrett, L. The ‘strength of weak ties’ among female baboons: Fitness-related benefits of social bonds. Anim. Behav. 2017, 126, 101–106. [Google Scholar] [CrossRef]
- Johnson, J.S.; Kropczynski, J.N.; Lacki, M.J. Social Network Analysis and the Study of Sociality in Bats. Acta Chiropterologica 2013, 15, 1–17. [Google Scholar] [CrossRef]
- Daniel, B.M.; Green, K.E.; Doulton, H.; Salim, D.M.; Said, I.; Hudson, M.; Dawson, J.S.; Young, R.P.; Houmadi, A. A bat on the brink? A range-wide survey of the Critically Endangered Livingstone’s fruit bat Pteropus livingstonii—CORRIGENDUM. Oryx 2017, 51, 753. [Google Scholar] [CrossRef][Green Version]
- Smith, S.J.; Leslie, D.M. Pteropus livingstonii. Mamm. Species 2006, 792, 1–5. [Google Scholar] [CrossRef]
- Courts, S. An ethogram of captive Livingstone’s fruit bats Pteropus livingstonii in a new enclosure at Jersey Wildlife Preservation Trust. Dodo 1996, 32, 15–37. [Google Scholar]
- Sewall, B.J.; Granek, E.F.; Moutui, M.F.E.; Trewhella, W.J.; Reason, P.F.; Rodríguez-Clark, K.M.; Saïd, I.; Carroll, J.B.; Masefield, W.; Toilibou, N.; et al. Conservation Action Plan for Livingstone’s Flying Fox; 2007; pp. 1–52. Available online: https://sites.temple.edu/bjsewall/files/2016/05/Sewall_et_al_2007_Liv_Cons_Action_Plan_En.pdf (accessed on 1 February 2019).
- Stanley, C.R. (Department of Biological Sciences, Chester, UK). Unpublished work. 2016. [Google Scholar]
- Ruiz-Garcia, L.; Lunadei, L.; Barreiro, P.; Robla, J.I. A Review of Wireless Sensor Technologies and Applications in Agriculture and Food Industry: State of the Art and Current Trends. Sensors 2009, 9, 4728–4750. [Google Scholar] [CrossRef]
- Powell, V.J.; Wehnelt, S.C. A new estimate of the population size of the Critically Endangered Rodrigues fruit bat Pteropus rodricensis. Oryx 2003, 37, 353–357. [Google Scholar] [CrossRef]
- Farine, D.R.; Aplin, L.M.; Sheldon, B.C.; Hoppitt, W.J.E. Interspecific social networks promote information transmission in wild songbirds. Proc. R. Soc. B Biol. Sci. 2015, 282, 20142804. [Google Scholar] [CrossRef]
- Meise, K.; Franks, D.W.; Bro-Jørgensen, J. Using social network analysis of mixed-species groups in African savannah herbivores to assess how community structure responds to environmental change. Philos. Trans. R. Soc. B Biol. Sci. 2019, 374, 20190009. [Google Scholar] [CrossRef]
- Caillaud, D.; Animal Observer; Dian Fossey Gorilla Fund International. 2016. Available online: https://apps.apple.com/us/app/animal-observer/ (accessed on 1 March 2019).
- Altmann, J. Observational Study of Behavior: Sampling Methods. Behaviour 1974, 49, 227–266. [Google Scholar] [CrossRef]
- Stanley, C.; Mettke-Hofmann, C.; Hager, R.; Shultz, S. Social stability in semiferal ponies: Networks show interannual stability alongside seasonal flexibility. Anim. Behav. 2018, 136, 175–184. [Google Scholar] [CrossRef]
- Hoppitt, W.; Farine, D.R. Association indices for quantifying social relationships: How to deal with missing observations of individuals or groups. Anim. Behav. 2018, 136, 227–238. [Google Scholar] [CrossRef]
- Farine, D.R.; Whitehead, H. Constructing, conducting and interpreting animal social network analysis. J. Anim. Ecol. 2015, 84, 1144–1163. [Google Scholar] [CrossRef]
- Csardi, G.; Nepusz, T. The igraph software package for complex network research. InterJournal Complex Syst. 2006, 1695, 1–9. [Google Scholar]
- Borgatti, S. NetDraw: Graph Visualization Software. Harvard: Analystic Technologies. 2002. Available online: https://sites.google.com/site/netdrawsoftware/download (accessed on 1 March 2019).
- Fischer, J.; Farnworth, M.; Sennhenn-Reulen, H.; Hammerschmidt, K. Quantifying social complexity. Anim. Behav. 2017, 130, 57–66. [Google Scholar] [CrossRef]
- Freeberg, T.M.; Dunbar, R.I.M.; Ord, T.J. Social complexity as a proximate and ultimate factor in communicative complexity. Philos. Trans. R. Soc. B Biol. Sci. 2012, 367, 1785–1801. [Google Scholar] [CrossRef]
- McNicholas, S. Model-Based Clustering. J. Classif. 2016, 33, 331–373. [Google Scholar] [CrossRef]
- Biernacki, C.; Celeux, G.; Govaert, G. Assessing a mixture model for clustering with the integrated completed likelihood. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 719–725. [Google Scholar] [CrossRef]
- Weiss, M.N.; Franks, D.W.; Croft, D.P.; Whitehead, H. Measuring the complexity of social associations using mixture models. Behav. Ecol. Sociobiol. 2019, 73, 8. [Google Scholar] [CrossRef]
- Yee, T.W.; Yee, M.T. VGAMdata, Package ‘VGAM’. 2020. Available online: https://cran.r-project.org/web/packages/VGAM/index.html (accessed on 1 May 2020).
- Shannon, C.E.; Weaver, W. The Mathematical Theory of Information; University of Illinois Press: Urbana, IL, USA, 1949; p. 97. [Google Scholar]
- Dekker, D.; Krackhardt, D.; Snijders, T.A.B. Sensitivity of MRQAP Tests to Collinearity and Autocorrelation Conditions. Psychometrika 2007, 72, 563–581. [Google Scholar] [CrossRef] [PubMed]
- Farine, D. Asnipe: Animal Social Network Inference and Permutations for Ecologists (R Package Version 1.1. 3); R Foundation for Statistical Computing: Vienna, Austria, 2017; Available online: https://CRAN.R-project.org/package¼asnipe (accessed on 1 May 2020).
- Croft, D.P.; Krause, J.; Darden, S.; Ramnarine, I.W.; Faria, J.J.; James, R. Behavioural trait assortment in a social network: Patterns and implications. Behav. Ecol. Sociobiol. 2009, 63, 1495–1503. [Google Scholar] [CrossRef]
- Farine, D.R. Measuring phenotypic assortment in animal social networks: Weighted associations are more robust than binary edges. Anim. Behav. 2014, 89, 141–153. [Google Scholar] [CrossRef]
- Croft, D.P.; James, R.; Ward, A.; Botham, M.S.; Mawdsley, D.; Krause, J. Assortative interactions and social networks in fish. Oecologia 2005, 143, 211–219. [Google Scholar] [CrossRef] [PubMed]
- Farine, D. Assortnet 0.12: Calculate the Assortativity Coefficient of Weighted and Binary Networks. 2016. Available online: https://cran.r-project.org/web/packages/assortnet/index.html (accessed on 1 May 2020).
- Butts, C. Social network analysis with sna. J. Stat. Softw. 2008, 24, 1–51. [Google Scholar] [CrossRef]
- Weiss, M.N.; Franks, D.W.; Brent, L.J.N.; Ellis, S.; Silk, M.J.; Croft, D.P. Common datastream permutations of animal social network data are not appropriate for hypothesis testing using regression models. bioRxiv 2020. [Google Scholar] [CrossRef]
- Farine, D.R. A guide to null models for animal social network analysis. Methods Ecol. Evol. 2017, 8, 1309–1320. [Google Scholar] [CrossRef]
- Sih, A.; Hanser, S.F.; McHugh, K.A. Social network theory: New insights and issues for behavioral ecologists. Behav. Ecol. Sociobiol. 2009, 63, 975–988. [Google Scholar] [CrossRef]
- David, H.A. Ranking from unbalanced paired-comparison data. Biometrika 1987, 74, 432–436. [Google Scholar] [CrossRef]
- Sánchez-Tójar, A.; Schroeder, J.; Farine, D.R. A practical guide for inferring reliable dominance hierarchies and estimating their uncertainty. J. Anim. Ecol. 2017, 87, 594–608. [Google Scholar] [CrossRef]
- Neumann, C.; Kulik, L. EloRating: Animal Dominance Hierarchies by Elo-Rating. R Package Version 46. 2020. Available online: https://cran.r-project.org/web/packages/EloRating/EloRating.pdf (accessed on 1 May 2020).
- Richards, S.A.; Whittingham, M.J.; Stephens, P.A. Model selection and model averaging in behavioural ecology: The utility of the IT-AIC framework. Behav. Ecol. Sociobiol. 2010, 65, 77–89. [Google Scholar] [CrossRef]
- Makagon, M.M.; McCowan, B.; Mench, J.A. How can social network analysis contribute to social behavior research in applied ethology? Appl. Anim. Behav. Sci. 2012, 138, 152–161. [Google Scholar] [CrossRef] [PubMed]
- Lusseau, D.; Newman, M.E.J. Identifying the role that animals play in their social networks. Proc. R. Soc. B Biol. Sci. 2004, 271, S477–S481. [Google Scholar] [CrossRef] [PubMed]
- Thierry, B.; Singh, M.; Kaumanns, W. Macaque Societies: A Model for the Study of Social Organization; Cambridge University Press: Cambridge, UK, 2004; Volume 41. [Google Scholar]
- Newman, M.E.J. Analysis of weighted networks. Phys. Rev. E 2004, 70, 056131. [Google Scholar] [CrossRef]
- Bonacich, P. Some unique properties of eigenvector centrality. Soc. Netw. 2007, 29, 555–564. [Google Scholar] [CrossRef]
- Candeloro, L.; Savini, L.; Conte, A. A New Weighted Degree Centrality Measure: The Application in an Animal Disease Epidemic. PLoS ONE 2016, 11, e0165781. [Google Scholar] [CrossRef]
- Wickham, H.; Averick, M.; Bryan, J.; Chang, W.; McGowan, L.D.; François, R.; Grolemund, G.; Hayes, A.; Henry, L.; Hester, J.; et al. Welcome to the Tidyverse. J. Open Source Softw. 2019, 4, 1686. [Google Scholar] [CrossRef]
- Simpson, W. The Quadratic Assignment Procedure (QAP). In Proceedings of the North American Stata Users’ Group Meetings, Boston, MA, USA, 12–13 March 2001. [Google Scholar]
- Chase, I.D.; Tovey, C.A.; Spangler-Martin, D.; Manfredonia, M. Individual differences versus social dynamics in the formation of animal dominance hierarchies. Proc. Natl. Acad. Sci. USA 2002, 99, 5744–5749. [Google Scholar] [CrossRef]
- De Vries, H.; Stevens, J.M.; Vervaecke, H. Measuring and testing the steepness of dominance hierarchies. Anim. Behav. 2006, 71, 585–592. [Google Scholar] [CrossRef]
- Marino, A. Costs and Benefits of Sociality Differ between Female Guanacos Living in Contrasting Ecological Conditions. Ethology 2010, 116, 999–1010. [Google Scholar] [CrossRef]
- Mosser, A.; Packer, C. Group territoriality and the benefits of sociality in the African lion, Panthera leo. Anim. Behav. 2009, 78, 359–370. [Google Scholar] [CrossRef]
- Courts, S. General behaviour and social interactions in a group of Livingstone’s fruit bats Pteropus livingstonii at Jersey Wildlife Preservation Trust. Dodo 1997, 33, 154. [Google Scholar]
- Voigt, C.C. Chapter 16: Sexual Selection in Neotropical Bats in Sexual Selection: Perspectives and Models from the Neotropics; Academic Press: Berlin, Germany; Leibniz Institute for Zoo and Wildlife Research: Berlin, Germany, 2014; pp. 409–432. [Google Scholar]
- Wilkinson, G.S.; Carter, G.; Bohn, K.M.; Caspers, B.; Chaverri, G.; Farine, D.; Günther, L.; Kerth, G.; Knörnschild, M.; Mayer, F.; et al. Kinship, association, and social complexity in bats. Behav. Ecol. Sociobiol. 2019, 73, 7. [Google Scholar] [CrossRef]
- King, A.J.; Cowlishaw, G. All together now: Behavioural synchrony in baboons. Anim. Behav. 2009, 78, 1381–1387. [Google Scholar] [CrossRef]
- Wey, T.W.; Blumstein, D.T. Social cohesion in yellow-bellied marmots is established through age and kin structuring. Anim. Behav. 2010, 79, 1343–1352. [Google Scholar] [CrossRef]
- Michelena, P.; Gautrais, J.; Gérard, J.-F.; Bon, R.; Deneubourg, J.-L. Social cohesion in groups of sheep: Effect of activity level, sex composition and group size. Appl. Anim. Behav. Sci. 2008, 112, 81–93. [Google Scholar] [CrossRef]
- King, A.J.; Cowlishaw, G. Leaders, followers and group decision-making. Commun. Integr. Biol. 2009, 2, 147–150. [Google Scholar] [CrossRef]
- Trewhella, W.J.; Reason, P.F.; Davies, J.G.; Wray, S. Observations on the timing of reproduction in the congeneric Comoro Island fruit bats, Pteropus livingstonii and P. seychellensis comorensis. J. Zool. 1995, 236, 327–331. [Google Scholar] [CrossRef]
- Schapiro, S.J.; Lambeth, S.P. Control, Choice, and Assessments of the Value of Behavioral Management to Nonhuman Primates in Captivity. J. Appl. Anim. Welf. Sci. 2007, 10, 39–47. [Google Scholar] [CrossRef]
- Sih, A.; Spiegel, O.; Godfrey, S.S.; Leu, S.T.; Bull, C.M. Integrating social networks, animal personalities, movement ecology and parasites: A framework with examples from a lizard. Anim. Behav. 2018, 136, 195–205. [Google Scholar] [CrossRef]
- Kulahci, I.G.; Ghazanfar, A.A.; Rubenstein, D.I. Consistent individual variation across interaction networks indicates social personalities in lemurs. Anim. Behav. 2018, 136, 217–226. [Google Scholar] [CrossRef]
- Plaza, M.; Burke, T.; Cox, T.; Carroll, A.F.; Girndt, A.; Halford, G.; Martin, D.A.; Sánchez-Fortún, M.; Sánchez-Tójar, A.; Somerville, J.; et al. Social network node-based metrics can function as proxies for animal personality traits. EcoEvoRxiv 2019. [Google Scholar] [CrossRef]
- Schülke, O.; Bhagavatula, J.; Vigilant, L.; Ostner, J. Social Bonds Enhance Reproductive Success in Male Macaques. Curr. Biol. 2010, 20, 2207–2210. [Google Scholar] [CrossRef] [PubMed]
- Cameron, E.Z.; Setsaas, T.H.; Linklater, W.L. Social bonds between unrelated females increase reproductive success in feral horses. Proc. Natl. Acad. Sci. USA 2009, 106, 13850–13853. [Google Scholar] [CrossRef]
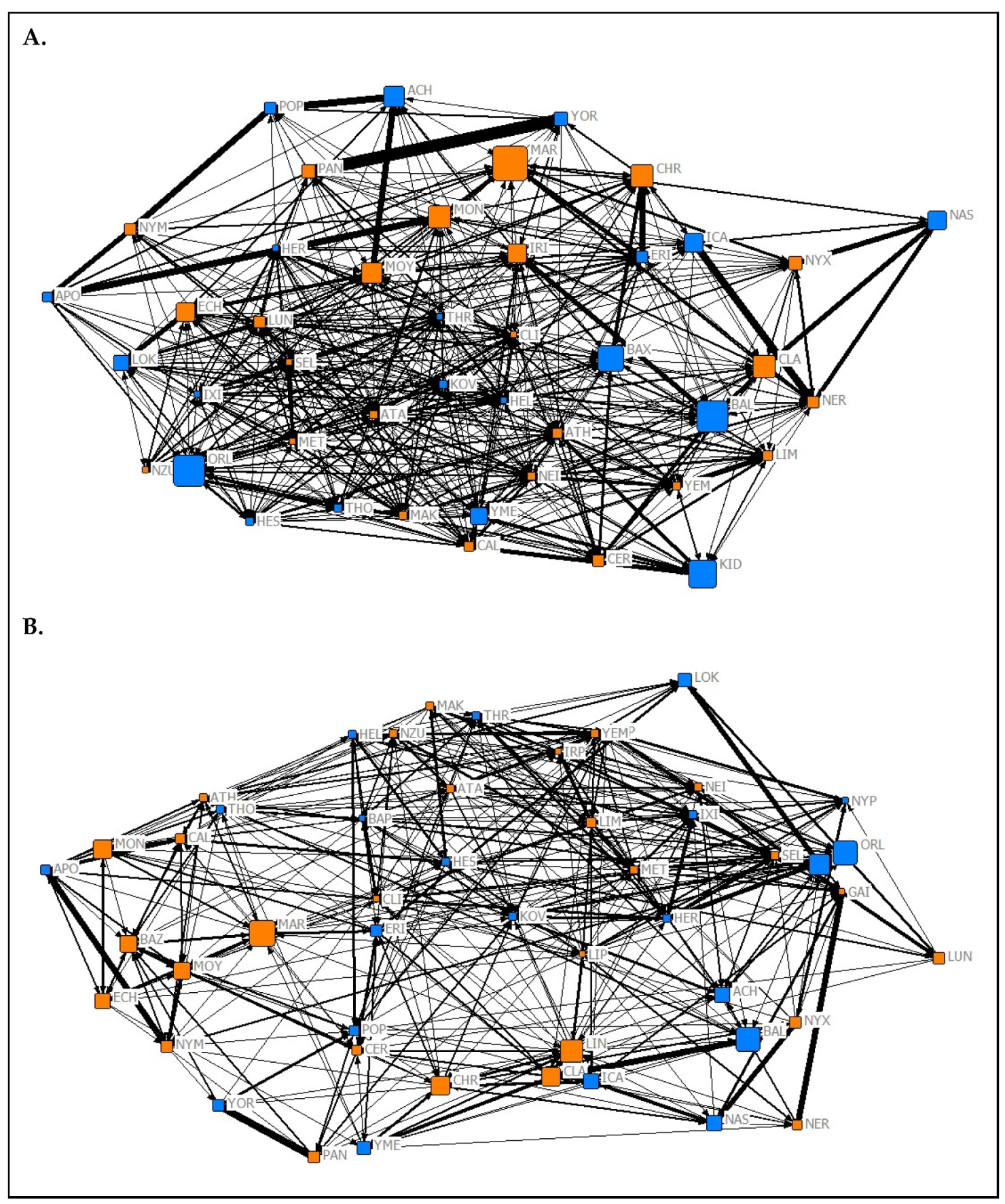
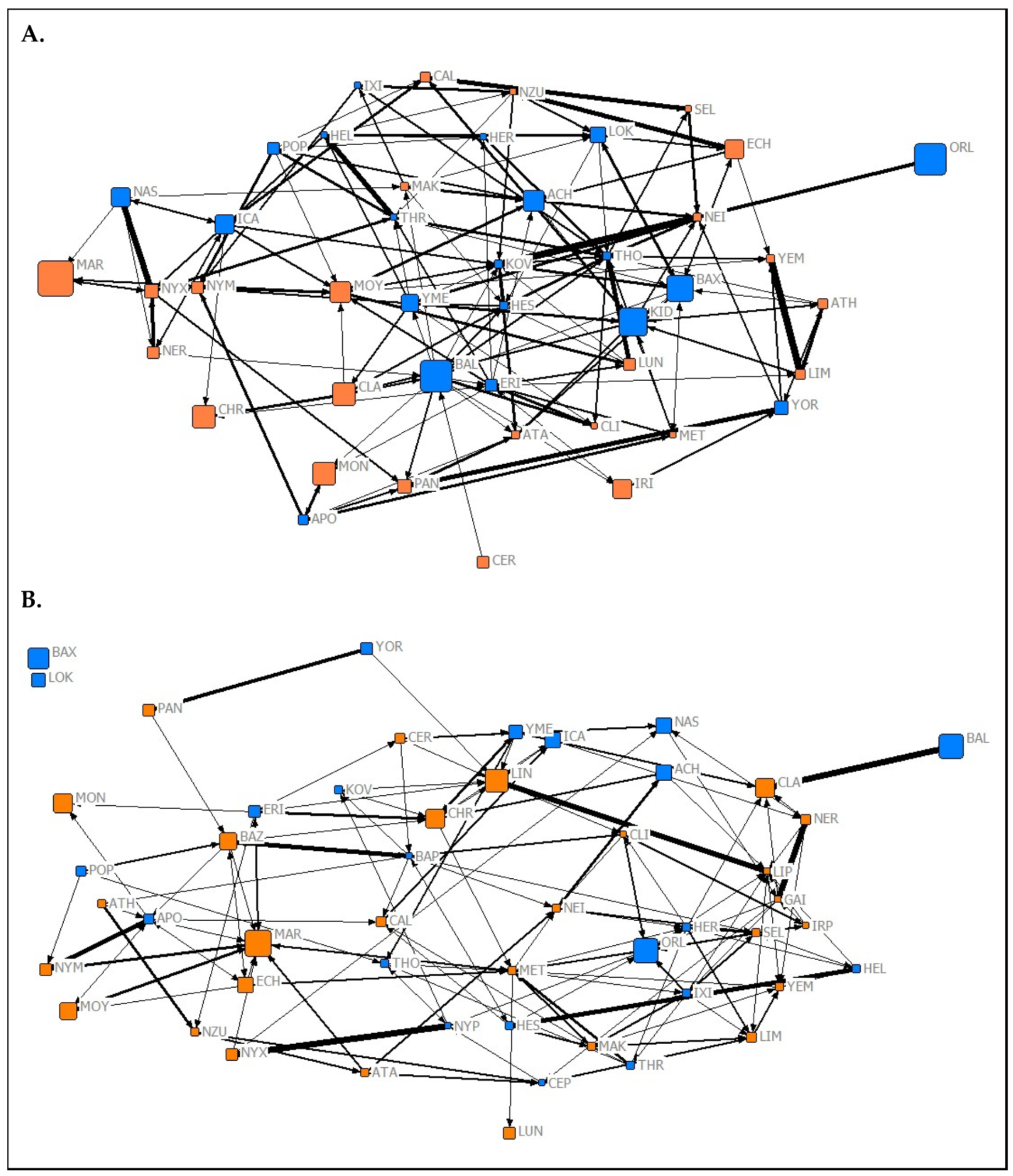
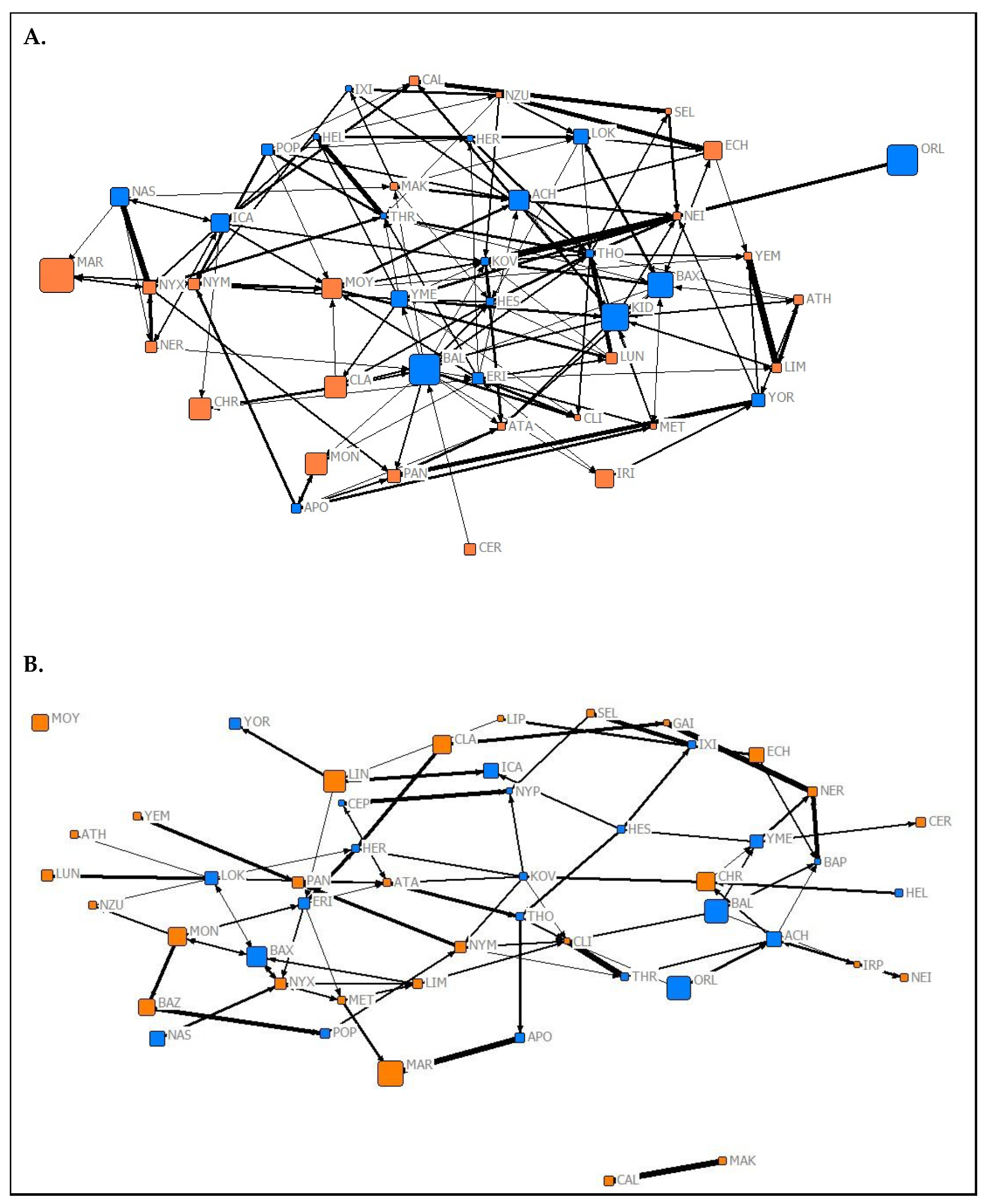
| Network Complexity | |||||
|---|---|---|---|---|---|
| Network Type | Data Collection Period | Types (K) | Mean Strength | Frequency | S Index (H) |
| Association | Summer 2019 | 4 | 0.001 | 0.772 | 1.214 |
| 0.028 | 0.166 | ||||
| 0.082 | 0.042 | ||||
| 0.213 | 0.019 | ||||
| Spring 2020 | 3 | 0.000 | 0.861 | 0.689 | |
| 0.062 | 0.132 | ||||
| 0.369 | 0.008 | ||||
| Affiliation | Summer 2019 | 3 | 0.000 | 0.919 | 0.686 |
| 0.108 | 0.058 | ||||
| 0.341 | 0.023 | ||||
| Spring 2020 | 3 | 0.000 | 0.939 | 0.73 | |
| 0.083 | 0.055 | ||||
| 0.643 | 0.006 | ||||
| Aggression | Summer 2019 | 4 | 0.000 | 0.916 | 0.973 |
| 0.036 | 0.042 | ||||
| 0.206 | 0.03 | ||||
| 0.381 | 0.012 | ||||
| Spring 2020 | 3 | 0.000 | 0.962 | 0.507 | |
| 0.129 | 0.025 | ||||
| 1.000 | 0.013 | ||||
| Network Assortment | ||||
|---|---|---|---|---|
| Network Type | Data Collection Period | Assorted Variable | Effect Size(r) | p-Value |
| Association | Summer 2019 | Dominance | 0.139 | 0.049 |
| Spring 2020 | Age | 0.291 | 0.002 | |
| Affiliation | Summer 2019 | N/A | N/A | N/A |
| Spring 2020 | Dominance | 0.332 | 0.025 | |
| Aggression | Summer 2019 | Age | 0.208 | 0.043 |
| Dominance | 0.343 | 0.002 | ||
| Spring 2020 | Dominance | 0.237 | 0.037 | |
| Node Metrics and Class Membership | ||||||
|---|---|---|---|---|---|---|
| Network Type | Data Collection Period | Node Metric | Factors Included in Best Model | Effect Size | Standard Error | p-Value |
| Association | Summer 2019 | Betweenness Centrality | Dominance | −0.0007 | 0.0003 | 0.52 |
| Spring 2020 | Betweenness Centrality | None | N/A | N/A | N/A | |
| Summer 2019 | Closeness Centrality | None | N/A | N/A | N/A | |
| Spring 2020 | Closeness Centrality | Age | −0.192 | 0.076 | 0.698 | |
| Summer 2019 | Weighted Degree | None | N/A | N/A | N/A | |
| Spring 2020 | Weighted Degree | None | N/A | N/A | N/A | |
| Affiliation | Summer 2019 | Betweenness Centrality | Dominance | −0.003 | 0.0007 | 0.514 |
| Spring 2020 | Betweenness Centrality | None | N/A | N/A | N/A | |
| Summer 2019 | Closeness Centrality | Dominance | −0.023 | 0.009 | 1 | |
| Spring 2020 | Closeness Centrality | Sex | Male = 0.042 | 0.023 | 1 | |
| Age | −0.004 | 0.002 | 1 | |||
| Summer 2019 | Weighted Degree | Sex | Male= −0.249 | 0.125 | 0.968 | |
| Dominance | −0.008 | 0.004 | 0.945 | |||
| Spring 2020 | Weighted Degree | None | N/A | N/A | N/A | |
| Aggression | Summer 2019 | Betweenness Centrality | Sex | Male = 0.057 | 0.024 | 0.5 |
| Dominance | 0.003 | 0.0008 | 0.509 | |||
| Spring 2020 | Betweenness Centrality | Sex | Male = 0.0009 | 0.0004 | 0.498 | |
| Summer 2019 | Closeness Centrality | Dominance | 0.024 | 0.013 | p < 0.05 | |
| Spring 2020 | Closeness Centrality | Sex | Male = 0.028 | 0.017 | p < 0.05 | |
| Summer 2019 | Weighted Degree | Sex | Male = 0.31 | 0.14 | 0.004 | |
| Dominance | −0.025 | 0.005 | 1 | |||
| Spring 2020 | Weighted Degree | Dominance | −0.037 | 0.014 | 0.997 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Welch, M.J.; Smith, T.; Hosie, C.; Wormell, D.; Price, E.; Stanley, C.R. Social Experience of Captive Livingstone’s Fruit Bats (Pteropus livingstonii). Animals 2020, 10, 1321. https://doi.org/10.3390/ani10081321
Welch MJ, Smith T, Hosie C, Wormell D, Price E, Stanley CR. Social Experience of Captive Livingstone’s Fruit Bats (Pteropus livingstonii). Animals. 2020; 10(8):1321. https://doi.org/10.3390/ani10081321
Chicago/Turabian StyleWelch, Morgan J., Tessa Smith, Charlotte Hosie, Dominic Wormell, Eluned Price, and Christina R. Stanley. 2020. "Social Experience of Captive Livingstone’s Fruit Bats (Pteropus livingstonii)" Animals 10, no. 8: 1321. https://doi.org/10.3390/ani10081321
APA StyleWelch, M. J., Smith, T., Hosie, C., Wormell, D., Price, E., & Stanley, C. R. (2020). Social Experience of Captive Livingstone’s Fruit Bats (Pteropus livingstonii). Animals, 10(8), 1321. https://doi.org/10.3390/ani10081321





