Evaluation of the Physical Properties of Bedding Materials for Dairy Cattle Using Fuzzy Clustering Analysis
Simple Summary
Abstract
1. Introduction
2. Materials and Methods
2.1. Physical Properties of the Bedding Materials
2.2. Data Analysis
2.2.1. Principal Components Analysis (PCA)
2.2.2. Fuzzy Clustering Analysis
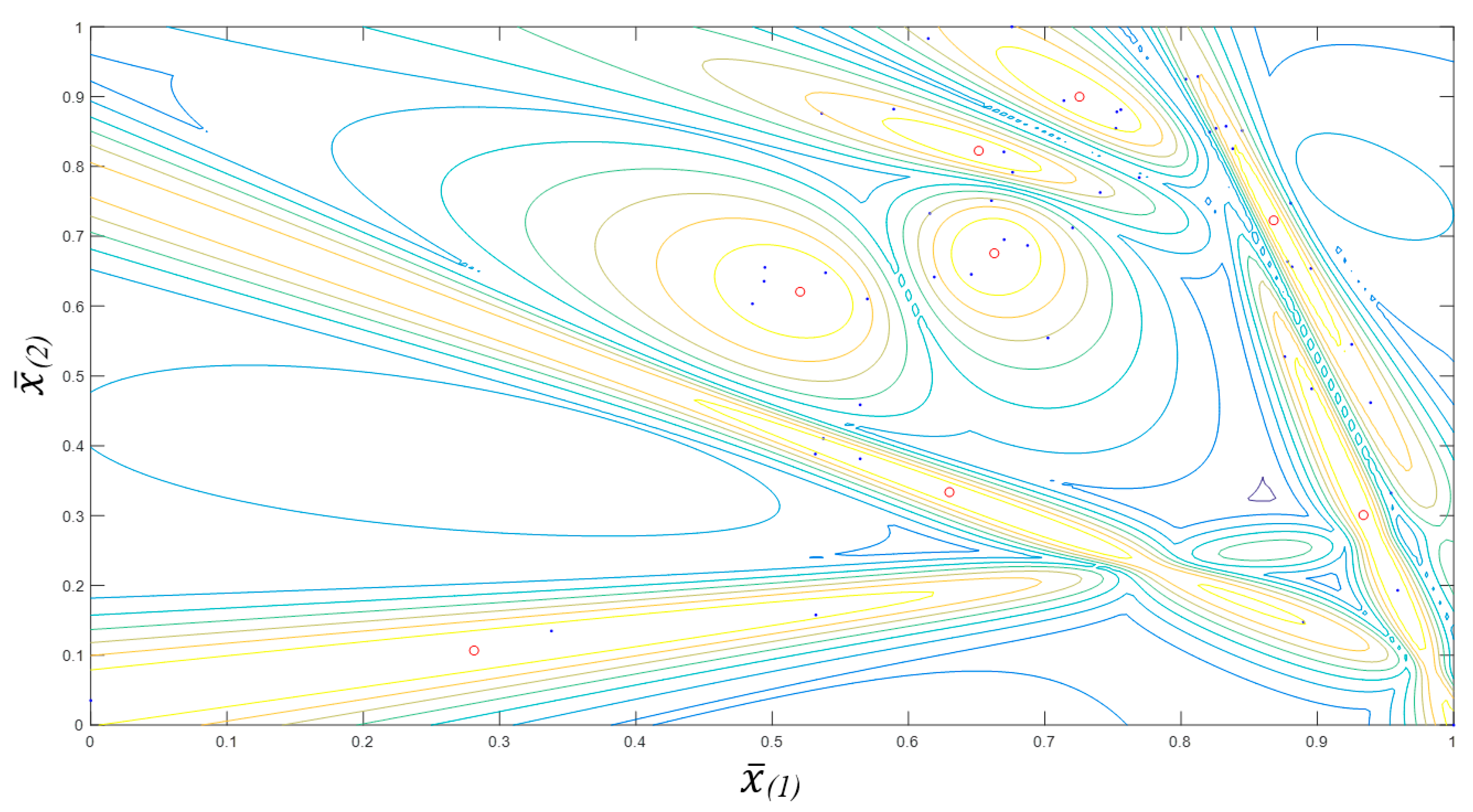
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Jensen, M.B.; Pedersen, L.J.; Munksgaard, L. The effect of reward duration on demand functions for rest in dairy heifers and lying requirements as measured by demand functions. Appl. Anim. Behav. Sci. 2005, 90, 207–217. [Google Scholar] [CrossRef]
- Mitev, J.; Varlyakov, I.; Miteva, T.; Vasilev, N.; Gergovska, J.; Uzunova, K.; Dimova, V. Preferences of freestall housed dairy cows to different bedding materials. İstanb. Üniv. Vet. Fak. Derg. 2012, 38, 135–140. [Google Scholar]
- Cecchin, D.; Campos, A.T.; Pires, M.; Yanagi Junior, T.; Souza, M. Avaliação de diferentes materiais para recobrimento de camas em baias de galpão modelo free-stall. Revis. Bras. Eng. Agríc. Ambient. 2014, 18, 109–115. [Google Scholar] [CrossRef]
- Tucker, C.B.; Weary, D.M.; Fraser, D. Effects of three types of free-stall surfaces on preferences and stall usage by dairy cows. J. Dairy Sci. 2003, 86, 521–529. [Google Scholar] [CrossRef]
- Bewley, J.M.; Boyce, R.E.; Hockin, J.; Munksgaard, L.; Eicher, S.D.; Einstein, M.E.; Schutz, M.M. Influence of milk yield, stage of lactation, and body condition on dairy cattle lying behaviour measured using an automated activity monitoring sensor. J. Dairy Res. 2010, 77, 1–6. [Google Scholar] [CrossRef]
- Husfeldt, A.W.; Endres, M.I. Association between stall surface and some animal welfare measurements in freestall dairy herds using recycled manure solids for bedding. J. Dairy Sci. 2012, 95, 5626–5634. [Google Scholar] [CrossRef]
- Haley, D.B.; De Passille, A.M.; Rushen, J. Assessing cow comfort: Effects of two floor types and two tie stall designs on the behaviour of lactating dairy cows. Appl. Anim. Behav. Sci. 2001, 71, 105–117. [Google Scholar] [CrossRef]
- Wolfe, T.; Vasseur, E.; DeVries, T.J.; Bergeron, R. Effects of alternative deep bedding options on dairy cow preference, lying behavior, cleanliness, and teat end contamination. J. Dairy Sci. 2018, 101, 530–536. [Google Scholar] [CrossRef]
- Fregonesi, J.A.; Veira, D.M.; Von Keyserlingk, M.A.G.; Weary, D.M. Effects of bedding quality on lying behavior of dairy cows. J. Dairy Sci. 2007, 90, 5468–5472. [Google Scholar] [CrossRef]
- Ito, K.; Weary, D.M.; Von Keyserlingk, M.A.G. Lying behavior: Assessing within-and between-herd variation in free-stall-housed dairy cows. J. Dairy Sci. 2009, 92, 4412–4420. [Google Scholar] [CrossRef]
- Lombard, J.E.; Tucker, C.B.; Von Keyserlingk, M.A.G.; Kopral, C.A.; Weary, D.M. Associations between cow hygiene, hock injuries, and free stall usage on US dairy farms. J. Dairy Sci. 2010, 93, 4668–4676. [Google Scholar] [CrossRef] [PubMed]
- Van Gastelen, S.; Westerlaan, B.; Houwers, D.J.; Van Eerdenburg, F.J.C.M. A study on cow comfort and risk for lameness and mastitis in relation to different types of bedding materials. J. Dairy Sci. 2011, 94, 4878–4888. [Google Scholar] [CrossRef] [PubMed]
- Barrientos, A.K.; Chapinal, N.; Weary, D.M.; Galo, E.; Von Keyserlingk, M.A.G. Herd-level risk factors for hock injuries in freestall-housed dairy cows in the northeastern United States and California. J. Dairy Sci. 2013, 96, 3758–3765. [Google Scholar] [CrossRef] [PubMed]
- Endres, M.I.; Barberg, A.E. Behavior of dairy cows in an alternative bedded-pack housing system. J. Dairy Sci. 2007, 90, 4192–4200. [Google Scholar] [CrossRef]
- Galama, P.J. On Farm Development of Bedded Pack Dairy Barns in The Netherlands. Report 707. Wageningen UR Livestock Research. Lelystad, The Netherlands. 2014, p. 35. Available online: https://library.wur.nl/WebQuery/wurpubs/fulltext/296350 (accessed on 21 February 2020).
- Fávero, S.; Portilho, F.V.R.; Oliveira, A.C.R.; Langoni, H.; Pantoja, J.C.F. Factors associated with mastitis epidemiologic indexes, animal hygiene, and bulk milk bacterial concentrations in dairy herds housed on compost bedding. Livest. Sci. 2015, 181, 220–230. [Google Scholar] [CrossRef]
- Leso, L.; Conti, L.; Rossi, G.; Barbari, M. Criteria of design for deconstruction applied to dairy cows housing: A case study in Italy. Agron. Res. 2018, 16, 794–805. [Google Scholar]
- Kheravii, S.K.; Swick, R.A.; Choct, M.; Wu, S.B. Potential of pelleted wheat straw as an alternative bedding material for broilers. Poult. Sci. 2017, 96, 1641–1647. [Google Scholar] [CrossRef]
- Agnew, J.M.; Leonard, J.J. The physical properties of compost. Compos. Sci. Util. 2003, 11, 238–264. [Google Scholar] [CrossRef]
- Lam, P.S.; Sokhansanj, S.; Bi, X.; Lim, C.J.; Naimi, L.J.; Hoque, M.; Mani, S.; Womac, A.R.; Narayan, S.; Ye, X.P. Bulk density of wet and dry wheat straw and switchgrass particles. Appl. Eng. Agric. 2008, 24, 351–358. [Google Scholar] [CrossRef]
- Dunlop, M.W.; McAuley, J.; Blackall, P.J.; Stuetz, R.M. Water activity of poultry litter: Relationship to moisture content during a grow-out. J. Environ. Manag. 2016, 172, 201–206. [Google Scholar] [CrossRef]
- Gosain, A.; Dahiya, S. Performance analysis of various fuzzy clustering algorithms: A review. Procedia Comput. Sci. 2016, 79, 100–111. [Google Scholar] [CrossRef]
- Mota, V.C.; Damasceno, F.A.; Leite, D.F. Fuzzy clustering and fuzzy validity measures for knowledge discovery and decision making in agricultural engineering. Comput. Electron. Agric. 2018, 150, 118–124. [Google Scholar] [CrossRef]
- ASABE Standards. S269.4. Cubes, Pellets and Crumbles—Definitions and Methods for Determining Density, Durability and Moisture Content; ASABE: St. Joseph, MI, USA, 2007. [Google Scholar]
- Dunlop, M.W.; Blackall, P.J.; Stuetz, R.M. Water addition, evaporation and water holding capacity of poultry litter. Sci. Total Environ. 2015, 538, 979–985. [Google Scholar] [CrossRef] [PubMed]
- Standards Australia. Potting Mixes (AS 3743–2003). Australian/New Zealand Standards (Standards Australia/Standards New Zealand, Sydney); Standards Australia: Sydney, Australia, 2003. [Google Scholar]
- White, J.; M astalerz, J. Soil moisture as related to “Container Capacity”. In Proceedings of the American Society for Horticultural Science, Maryland, MA, USA, 15–20 August 1966. [Google Scholar]
- Martínez, P.F.; Burés, S.; Blanca, F.; Yuste, M.P.; Valero, J. Experimental and theoretical air/water ratios of different substrate mixtures at container capacity. Acta Hortic. 1991, 294, 241–248. [Google Scholar] [CrossRef]
- Caron, J.; Nkongolo, V.K.N. Aeration in growing media: Recent developments. In Proceedings of the International Symposium on Growing Media and Hydroponics, Windsor, ON, Canada, 1 January 1997; Volume 481, pp. 545–552. [Google Scholar]
- Jobim, C.C.; Nussio, L.G.; Reis, R.A.; Schmidt, P. Avanços metodológicos na avaliação da qualidade da forragem conservada. Revis. Bras. Zootec. 2007, 36, 101–119. [Google Scholar] [CrossRef]
- Jolliffe, I.T.; Cadima, J. Principal component analysis: A review and recent developments. Philosophical Trans. Royal Soc. A Math. Phys. Eng. Sci. 2016, 374, 1–16. [Google Scholar] [CrossRef]
- Olive, D.J. Principal component analysis. In Robust Multivariate Analysis; Springer: Cham, Switzerland, 2017; pp. 189–217. [Google Scholar]
- Moradi, A.; Razmi, J.; Babazadeh, R.; Sabbaghnia, A. An integrated Principal Component Analysis and multi-objective mathematical programming approach to agile supply chain network design under uncertainty. J. Ind. Manag. Optim. 2019, 15, 855–879. [Google Scholar] [CrossRef]
- Sharma, N.; Saroha, K. A novel dimensionality reduction method for cancer dataset using PCA and feature ranking. In Proceedings of the 2015 International Conference on Advances in Computing, Communications and Informatics (ICACCI), Kochi, India, 10–13 August 2015; pp. 2261–2264. [Google Scholar]
- Jolliffe, I.T. Discarding variables in a principal component analysis. I: Artificial data. J. Royal Stat. Soc. Ser. C Appl. Stat. 1972, 21, 160–173. [Google Scholar] [CrossRef]
- Mackey, L.W. Deflation methods for sparse PCA. In Advances in Neural Information Processing Systems; NeurIPS: Berkeley, CA, USA, 2009; pp. 1017–1024. [Google Scholar]
- Cooley, W.C.; Lohnes, P.R. Multivariate Data Analysis; Wiley: New York, NY, USA, 1971. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing. 2019. Available online: https://www.r-project.org/ (accessed on 12 September 2019).
- Tang, Y.; Hu, X.; Pedrycz, W.; Song, X. Possibilistic fuzzy clustering with high-density viewpoint. Neurocomputing 2019, 329, 407–423. [Google Scholar] [CrossRef]
- Browning, T.R. Applying the design structure matrix to system decomposition and integration problems: A review and new directions. IEEE Trans. Eng. Manag. 2001, 48, 292–306. [Google Scholar] [CrossRef]
- Liu, Y.; Li, W.; Li, Y.C. Network traffic classification using k-means clustering. In Proceedings of the Second International Multi-Symposiums on Computer and Computational Sciences (IMSCCS 2007), Lowa City, IA, USA, 13–15 August 2007; pp. 360–365. [Google Scholar]
- Migdady, H.; Al-Talib, M.M. An enhanced fuzzy K-means clustering with application to missing data imputation. Electron. J. Appl. Stat. Anal. 2018, 11, 674–686. [Google Scholar]
- Gindy, N.N.Z.; Ratchev, T.M.; Case, K. Component grouping for GT applications—A fuzzy clustering approach with validity measure. Int. J. Prod. Res. 1995, 33, 2493–2509. [Google Scholar] [CrossRef]
- Sadri, S.; Burn, D.H. A Fuzzy C-Means approach for regionalization using a bivariate homogeneity and discordancy approach. J. Hydrol. 2011, 401, 231–239. [Google Scholar] [CrossRef]
- Lin, W.; Ren, H.; Ma, Z.; Yang, L. Using fuzzy clustering and weighted cumulative probability distribution techniques for optimal design of phase change material thermal energy storage. J. Clean. Prod. 2019, 233, 1259–1268. [Google Scholar] [CrossRef]
- Wu, K.L. Analysis of parameter selections for fuzzy c-means. Pattern Recognit. 2012, 45, 407–415. [Google Scholar] [CrossRef]
- Sarbu, C.; Zehl, K.; Einax, J.W. Fuzzy divisive hierarchical clustering of soil data using Gustafson-Kessel algorithm. Chemom. Intell. Lab. Syst. 2007, 86, 121–129. [Google Scholar] [CrossRef]
- Gustafson, D.E.; Kessel, W.C. Fuzzy clustering with a fuzzy covariance matrix. In Proceedings of the 1978 IEEE Conference on Decision and Control Including the 17th Symposium on Adaptive Processes, San Digeo, CA, USA, 10–12 January 1979; pp. 761–766. [Google Scholar]
- Seo, J.B.; Kim, D.W. A parallel implementation of the Gustafson-Kessel clustering algorithm with CUDA. IEICE Trans. Inf. Syst. 2012, 95, 1162–1165. [Google Scholar] [CrossRef]
- Babuska, R. Fuzzy Modeling for Control; Springer, (Fuzzy Clustering Algorithms): Dordrecht, The Netherlands, 1998. [Google Scholar]
- Neto, J.C.; Meyer, G.E.; Jones, D.D. Individual leaf extractions from young canopy images using Gustafson-Kessel clustering and a genetic algorithm. Comput. Electron. Agric. 2006, 51, 66–85. [Google Scholar] [CrossRef]
- Abonyi, J. Clustering Toolbox. Available online: https://www.mathworks.com/matlabcentral/fileexchange/7486-clustering-toolbox (accessed on 13 September 2019).
- Bernal, M.P.; Lopez-Real, J.M.; Scott, K.M. Application of natural zeolites for the reduction of ammonia emissions during the composting of organic wastes in a composting simulator. Bioresour. Technol. 1993, 43, 35–39. [Google Scholar] [CrossRef]
- Masiello, C.A.; Dugan, B.; Brewer, C.E.; Spokas, K.A.; Novak, J.M.; Liu, Z.; Sorrenti, G. Biochar effects on soil hydrology. In Biochar for Environmental Management; Routledge: London, UK, 2015; pp. 575–594. [Google Scholar]
- Samadi, S.; van Eerdenburg, F.J.C.M.; Jamshidifard, A.R.; Otten, G.P.; Droppert, M.; Heederik, D.J.J.; Wouters, I.M. The influence of bedding materials on bio-aerosol exposure in dairy barns. J. Expo. Sci. Environ. Epidemiol. 2012, 22, 361–368. [Google Scholar] [CrossRef]
- Breum, N.O.; Nielsen, B.H.; Lyngbye, M.; Midtgard, U. Dustiness of chopped straw as affected by lignosulfonate as a dust suppressant. Ann. Agric. Environ. Med. 1999, 6, 133–140. [Google Scholar] [PubMed]
- Ward, P.L.; Wohlt, J.E.; Zajac, P.K.; Cooper, K.R. Chemical and physical properties of processed newspaper compared to wheat straw and wood shavings as animal bedding. J. Dairy Sci. 2000, 83, 359–367. [Google Scholar] [CrossRef]
- Damasceno, F.A. Compost Bedded Pack Barns System and Computational Simulation of Airflow Through Naturally Ventilated Reduced Model. Ph.D. Thesis, Universidade Federal de Viçosa, Viçosa, Brazil, 15 August 2012. [Google Scholar]
- Proietto, R.L.; Hinckley, L.S.; Fox, L.K.; Andrew, S.M. Evaluation of a clay-based acidic bedding conditioner for dairy cattle bedding. J. Dairy Sci. 2013, 96, 1044–1053. [Google Scholar] [CrossRef] [PubMed]
- Zdanowicz, M.; Shelford, J.A.; Tucker, C.B.; Weary, D.M.; Von Keyserlingk, M.A.G. Bacterial populations on teat ends of dairy cows housed in free stalls and bedded with either sand or sawdust. J. Dairy Sci. 2004, 87, 1694–1701. [Google Scholar] [CrossRef]
- Hogan, J.S.; Smith, K.L.; Hoblet, K.H.; Todhunter, D.A.; Schoenberger, P.S.; Hueston, W.D.; Pritchard, D.E.; Bowman, G.L.; Heider, L.E.; Brockett, B.L.; et al. Bacterial counts in bedding materials used on nine commercial dairies. J. Dairy Sci. 1989, 72, 250–258. [Google Scholar] [CrossRef]
- Ferrero, B.; Fombuena, V.; Fenollar, O.; Boronat, T.; Balart, R. Development of natural fiber-reinforced plastics (NFRP) based on biobased polyethylene and waste fibers from Posidonia oceanica seaweed. Polym. Compos. 2015, 36, 1378–1385. [Google Scholar] [CrossRef]
- Ahn, H.K.; Richard, T.L.; Glanville, T.D. Laboratory determination of compost physical parameters for modelling of airflow characteristics. Waste Manag. 2008, 28, 660–670. [Google Scholar] [CrossRef]
| Bedding Material | Number of Samples | Country of Origin |
|---|---|---|
| Pine tree bark | 1 | Slovenia |
| Barley husk | 2 | Slovenia |
| Barley straw | 2 | Slovenia and the Netherlands |
| Coniferous needle litter | 1 | Italy |
| Dried manure | 1 | Italy |
| Dry sawdust | 5 | Italy and from Slovenia |
| Flax straw | 3 | Slovenia |
| Mix of fresh forest | 1 | Slovenia |
| Fresh sawdust | 3 | Italy and Slovenia |
| Hemp straw | 3 | Slovenia |
| Miscanthus grass | 3 | Italy, the Netherlands, and Slovenia |
| Posidonia oceanica | 1 | Italy |
| Spelt husk | 3 | Slovenia |
| Triticale husk | 2 | Slovenia |
| Triticale straw | 1 | Italy |
| Wheat husk | 2 | Slovenia |
| Wheat straw | 8 | Italy and Slovenia |
| Wood chips | 6 | Italy, the Netherlands, and Slovenia |
| Wood shavings | 3 | Italy and Slovenia |
| Properties | WHC | AFP | GD | CC | TEP | SH | H | BD | APS |
|---|---|---|---|---|---|---|---|---|---|
| WHC | 1.000 | ||||||||
| AFP | −0.106 | 1.000 | |||||||
| GD | −0.329 | −0.763 | 1.000 | ||||||
| CC | 0.258 | −0.961 | 0.665 | 1.000 | |||||
| TEP | 0.304 | 0.738 | −0.731 | −0.524 | 1.000 | ||||
| SH | 0.678 | −0.122 | −0.365 | 0.298 | 0.353 | 1.000 | |||
| H | −0.272 | −0.163 | 0.228 | 0.165 | −0.100 | −0.136 | 1.000 | ||
| BD | −0.444 | −0.662 | 0.900 | 0.590 | −0.605 | −0.290 | 0.542 | 1.000 | |
| APS | −0.095 | 0.552 | −0.365 | −0.501 | 0.481 | −0.259 | −0.083 | −0.369 | 1.000 |
| Principal Components | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| Standard deviation | 129.72 | 72.54 | 28.09 | 17.36 | 8.35 | 5.65 | 3.50 | 0.84 | 0.00 |
| Proportion of variance | 0.72 | 0.23 | 0.03 | 0.01 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| Cumulative proportion | 0.72 | 0.95 | 0.98 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| Number of Clusters | Validation Indexes | ||||
|---|---|---|---|---|---|
| PC | CE | SC | XB | DI | |
| KM | |||||
| 2 | 1 | NA | 1.7471 | 6.6417 | 0.1302 |
| 3 | 1 | NA | 1.1971 | 4.2439 | 0.0667 |
| 4 | 1 | NA | 0.8542 | 3.1541 | 0.616 |
| 5 | 1 | NA | 0.4949 | 2.8345 | 0.1013 |
| 6 | 1 | NA | 0.4743 | 3.9985 | 0.0765 |
| 7 | 1 | NA | 0.4081 | 2.3799 | 5.7206 × 10−4 |
| 8 | 1 | NA | 0.3609 | 3.3177 | 0.0997 |
| FCM | |||||
| 2 | 0.7630 | 0.3776 | 2.4857 | 5.1551 | 0.0485 |
| 3 | 0.6817 | 0.5748 | 1.7016 | 2.0421 | 0.0622 |
| 4 | 0.6487 | 0.6679 | 0.9798 | 3.6290 | 0.0756 |
| 5 | 0.6427 | 0.7259 | 0.7563 | 5.5302 | 0.0048 |
| 6 | 0.6468 | 0.7444 | 0.5745 | 1.9239 | 0.0823 |
| 7 | 0.6327 | 0.7960 | 0.5257 | 1.9913 | 0.1007 |
| 8 | 0.6328 | 0.8264 | 0.5041 | 2.0863 | 0.1016 |
| GK | |||||
| 2 | 0.8098 | 0.3121 | 4.2196 | 11.4240 | 0.0304 |
| 3 | 0.7724 | 0.4279 | 1.3597 | 2.7344 | 0.0682 |
| 4 | 0.7769 | 0.4210 | 0.8025 | 2.8975 | 0.0615 |
| 5 | 0.7369 | 0.5221 | 0.6131 | 1.8799 | 0.0473 |
| 6 | 0.7308 | 0.5424 | 0.6657 | 1.6741 | 0.0339 |
| 7 | 0.7028 | 0.6223 | 0.8663 | 1.9032 | 0.0120 |
| 8 | 0.7270 | 0.5932 | 0.4748 | 1.6092 | 0.0709 |
| Cluster | Material | WHC | AFP | CC | TEP | SH | H | GD | BD | APS |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | Hemp straw (Sample 2) | 1.60 | 91.92 | 7.43 | 99.35 | 66.44 | 10.12 | 37.55 | 46.93 | 365.79 |
| Hemp straw (Sample 3) | 1.23 | 93.71 | 5.63 | 99.34 | 64.53 | 9.49 | 30.93 | 46.12 | 267.91 | |
| Miscanthus grass (Sample 2) | 2.76 | 89.29 | 7.16 | 96.45 | 67.48 | 28.44 | 34.27 | 26.26 | 141.26 | |
| Wheat straw (Sample 1) | 3.00 | 82.74 | 8.03 | 90.77 | 64.22 | 9.16 | 43.63 | 27.08 | 126.94 | |
| Average | 2.15 (±0.86) | 89.41 (±4.80) | 7.06 (±1.02) | 96.48 (±4.04) | 65.67 (±1.56) | 14.30 (±9.44) | 36.60 (±5.41) | 36.60 (±11.47) | 225.47 (±112.97) | |
| 2 | Dry sawdust (Sample 1) | 2.27 | 28.13 | 45.84 | 73.97 | 73.18 | 11.05 | 168.02 | 203.24 | 4.08 |
| Dry sawdust (Sample 5) | 1.98 | 41.74 | 39.49 | 81.23 | 73.96 | 13.32 | 139.00 | 201.28 | 3.41 | |
| Fresh sawdust (Sample 1) | 2.14 | 33.22 | 51.84 | 85.06 | 80.61 | 46.35 | 124.78 | 244.82 | 2.51 | |
| Fresh sawdust (Sample 2) | 2.01 | 33.02 | 46.87 | 79.89 | 75.45 | 41.09 | 152.51 | 227.37 | 1.99 | |
| Wood chips (Sample 1) | 0.94 | 60.59 | 18.28 | 78.87 | 55.29 | 11.34 | 147.71 | 196.16 | 9.24 | |
| Wood chips (Sample 6) | 1.75 | 55.43 | 32.67 | 88.10 | 69.63 | 10.56 | 139.48 | 187.98 | 3.52 | |
| Average | 1.85 (±0.48) | 42.02 (±13.24) | 39.17 (±12.19) | 81.19 (±4.94) | 71.35 (±8.64) | 22.28 (±16.71) | 145.25 (±14.62) | 210.14 (±21.50) | 4.13 (±2.62) | |
| 3 | Dried manure | 4.55 | 46.75 | 32.24 | 78.99 | 83.32 | 14.11 | 64.59 | 71.60 | 11.78 |
| Flax straw (Sample 1) | 3.25 | 67.44 | 24.01 | 91.45 | 81.99 | 7.87 | 52.62 | 74.64 | 8.32 | |
| Fresh sawdust (Sample 3) | 5.39 | 19.79 | 61.85 | 81.64 | 87.26 | 13.34 | 90.35 | 115.68 | 1.91 | |
| Wheat straw (Sample 8) | 4.12 | 63.40 | 24.85 | 88.24 | 81.27 | 8.61 | 57.27 | 60.34 | 7.47 | |
| Wood shavings (Sample 1) | 2.55 | 68.31 | 24.08 | 92.39 | 89.67 | 11.41 | 27.70 | 95.18 | 4.97 | |
| Wood shavings (Sample 3) | 8.80 | 35.04 | 52.94 | 87.99 | 84.09 | 9.34 | 99.91 | 60.85 | 5.34 | |
| Average | 4.78 (±2.21) | 50.12 (±19.83) | 36.66 (±16.59) | 86.78 (±5.37) | 84.6 (±3.24) | 10.78 (±2.58) | 65.41 (±26.32) | 79.72 (±21.70) | 6.63 (±3.37) | |
| 4 | Dry sawdust (Sample 2) | 3.73 | 27.78 | 55.38 | 83.16 | 84.03 | 8.02 | 105.29 | 148.69 | 1.40 |
| Dry sawdust (Sample 3) | 4.52 | 17.10 | 66.02 | 83.11 | 81.46 | 12.20 | 150.48 | 147.31 | 1.50 | |
| Flax straw (Sample 2) | 2.64 | 56.85 | 30.46 | 87.32 | 78.68 | 10.06 | 82.55 | 116.18 | 4.81 | |
| Spelt husks (Sample 1) | 1.94 | 65.91 | 14.06 | 79.97 | 70.08 | 11.38 | 60.02 | 72.42 | 5.36 | |
| Wood chips (Sample 3) | 2.35 | 74.52 | 14.16 | 88.68 | 71.22 | 8.47 | 55.56 | 58.92 | 5.96 | |
| Wood shavings (Sample 2) | 3.32 | 53.48 | 34.47 | 87.95 | 78.46 | 9.52 | 94.69 | 104.51 | 2.63 | |
| Average | 3.08 (±0.96) | 49.27 (±22.30) | 35.76 (±21.30) | 85.03 (±3.46) | 77.32 (±5.56) | 9.94 (±1.63) | 91.43 (±34.76) | 108.01 (±37.30) | 3.61 (±2.02) | |
| 5 | Barley husk (Sample 1) | 1.59 | 68.98 | 18.96 | 87.94 | 69.08 | 10.47 | 84.84 | 119.89 | 3.74 |
| Barley husk (Sample 2) | 1.65 | 58.64 | 25.01 | 83.65 | 67.87 | 8.80 | 118.36 | 153.40 | 3.42 | |
| Coniferous needle litter | 0.78 | 79.91 | 9.56 | 89.47 | 53.49 | 12.27 | 82.98 | 123.01 | 9.02 | |
| Hemp straw (Sample 1) | 2.16 | 53.21 | 26.51 | 79.72 | 75.41 | 10.89 | 86.36 | 123.94 | 4.96 | |
| Miscanthus grass (Sample 1) | 2.35 | 45.49 | 32.28 | 77.77 | 73.55 | 7.85 | 115.92 | 137.24 | 4.58 | |
| Miscanthus grass (Sample 3) | 1.82 | 58.06 | 20.24 | 78.30 | 67.15 | 9.52 | 98.91 | 108.30 | 6.63 | |
| Spelt husks (Sample 2) | 1.69 | 67.40 | 14.38 | 81.77 | 65.38 | 11.54 | 76.15 | 82.99 | 4.83 | |
| Spelt husks (Sample 3) | 1.33 | 57.75 | 18.39 | 76.14 | 65.09 | 11.62 | 98.67 | 135.32 | 3.63 | |
| Average | 1.67 (±0.49) | 61.18 (±10.61) | 20.67 (±7.16) | 81.84 (±4.85) | 67.13 (±6.63) | 10.37 (±1.53) | 95.27 (±15.53) | 123.01 (±21.07) | 5.1 (±1.89) | |
| 6 | Barley straw (Sample 1) | 5.31 | 81.84 | 8.95 | 90.80 | 78.93 | 8.64 | 23.99 | 16.42 | 172.89 |
| Barley straw (Sample 2) | 3.02 | 85.67 | 9.74 | 95.41 | 79.11 | 9.84 | 25.67 | 32.60 | 98.04 | |
| Flax straw (Sample 3) | 1.44 | 83.25 | 3.53 | 86.78 | 68.00 | 10.32 | 16.53 | 23.83 | 231.73 | |
| Posidonia oceanica | 7.32 | 71.49 | 22.62 | 94.11 | 84.53 | 13.16 | 41.47 | 30.90 | 13.06 | |
| Triticale husk (Sample 1) | 2.82 | 86.78 | 7.66 | 94.44 | 79.98 | 10.94 | 19.15 | 27.37 | 10.69 | |
| Triticale husk (Sample 2) | 3.03 | 84.02 | 9.10 | 93.12 | 79.32 | 10.19 | 23.69 | 30.39 | 7.08 | |
| Triticale straw (Sample 1) | 2.90 | 89.85 | 5.63 | 95.49 | 77.05 | 10.02 | 16.76 | 19.60 | 56.55 | |
| Wheat husk (Sample 1) | 3.11 | 83.49 | 11.14 | 94.63 | 79.68 | 8.43 | 28.53 | 35.96 | 8.79 | |
| Wheat husk (Sample 2) | 2.80 | 81.83 | 10.60 | 92.44 | 78.80 | 9.70 | 28.54 | 36.91 | 7.42 | |
| Wheat straw (Sample 3) | 3.10 | 83.71 | 9.19 | 92.90 | 78.60 | 8.71 | 24.88 | 29.87 | 104.02 | |
| Wheat straw (Sample 4) | 4.83 | 72.66 | 21.35 | 94.01 | 90.30 | 11.12 | 22.70 | 44.71 | 16.58 | |
| Wheat straw (Sample 5) | 3.00 | 86.42 | 6.59 | 93.01 | 77.11 | 9.22 | 19.50 | 21.97 | 103.28 | |
| Wheat straw (Sample 6) | 4.07 | 81.60 | 12.48 | 94.08 | 80.75 | 10.93 | 29.58 | 29.88 | 32.02 | |
| Wheat straw (Sample 7) | 3.53 | 85.56 | 9.88 | 95.44 | 81.06 | 8.52 | 22.91 | 28.24 | 205.81 | |
| Average | 3.59 (±1.43) | 82.73 (±5.05) | 10.61 (±5.34) | 93.33 (±2.29) | 79.52 (±4.74) | 9.98 (±1.30) | 24.56 (±6.39) | 29.19 (±7.35) | 76.28 (±78.71) | |
| 7 | Wheat straw (Sample 2) | 1.64 | 80.98 | 3.23 | 84.21 | 29.29 | 9.99 | 77.94 | 19.72 | 214.90 |
| Wood chips (Sample 2) | 0.83 | 59.71 | 18.30 | 78.01 | 53.30 | 17.95 | 160.34 | 222.27 | 11.94 | |
| Wood chips (Sample 4) | 1.02 | 55.18 | 20.29 | 75.46 | 53.65 | 8.85 | 175.79 | 200.27 | 22.09 | |
| Wood chips (Sample 5) | 0.83 | 62.65 | 16.76 | 79.41 | 52.79 | 19.77 | 149.67 | 204.43 | 24.95 | |
| Average | 1.08 (±0.39) | 64.63 (±11.33) | 14.64 (±7.74) | 79.27 (±3.68) | 47.26 (±11.98) | 14.14 (±5.52) | 140.94 (±43.34) | 161.67 (±95.12) | 68.47 (±97.78) | |
| 8 | Pine tree bark | 0.61 | 65.75 | 17.73 | 83.48 | 60.09 | 57.75 | 130.59 | 285.43 | 69.78 |
| Dry sawdust (Sample 4) | 1.27 | 5.93 | 67.90 | 73.83 | 61.91 | 8.02 | 418.54 | 532.93 | 2.89 | |
| Mix of fresh forest | 0.70 | 56.27 | 31.70 | 87.98 | 67.40 | 63.81 | 153.10 | 453.10 | 7.93 | |
| Average | 0.86 (±0.36) | 42.65 (±32.15) | 39.11 (±25.89) | 81.76 (±7.23) | 63.13 (±3.81) | 43.19 (±30.61) | 234.07 (±160.15) | 423.82 (±126.32) | 26.87 (±37.25) |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ferreira Ponciano Ferraz, P.; Araújo e Silva Ferraz, G.; Leso, L.; Klopčič, M.; Rossi, G.; Barbari, M. Evaluation of the Physical Properties of Bedding Materials for Dairy Cattle Using Fuzzy Clustering Analysis. Animals 2020, 10, 351. https://doi.org/10.3390/ani10020351
Ferreira Ponciano Ferraz P, Araújo e Silva Ferraz G, Leso L, Klopčič M, Rossi G, Barbari M. Evaluation of the Physical Properties of Bedding Materials for Dairy Cattle Using Fuzzy Clustering Analysis. Animals. 2020; 10(2):351. https://doi.org/10.3390/ani10020351
Chicago/Turabian StyleFerreira Ponciano Ferraz, Patrícia, Gabriel Araújo e Silva Ferraz, Lorenzo Leso, Marija Klopčič, Giuseppe Rossi, and Matteo Barbari. 2020. "Evaluation of the Physical Properties of Bedding Materials for Dairy Cattle Using Fuzzy Clustering Analysis" Animals 10, no. 2: 351. https://doi.org/10.3390/ani10020351
APA StyleFerreira Ponciano Ferraz, P., Araújo e Silva Ferraz, G., Leso, L., Klopčič, M., Rossi, G., & Barbari, M. (2020). Evaluation of the Physical Properties of Bedding Materials for Dairy Cattle Using Fuzzy Clustering Analysis. Animals, 10(2), 351. https://doi.org/10.3390/ani10020351









