Modelling Sand Fly Lutzomyia longipalpis Attraction to Host Odour: Synthetic Sex-Aggregation Pheromone Dominates the Response
Abstract
1. Introduction
2. Materials and Methods
3. Results
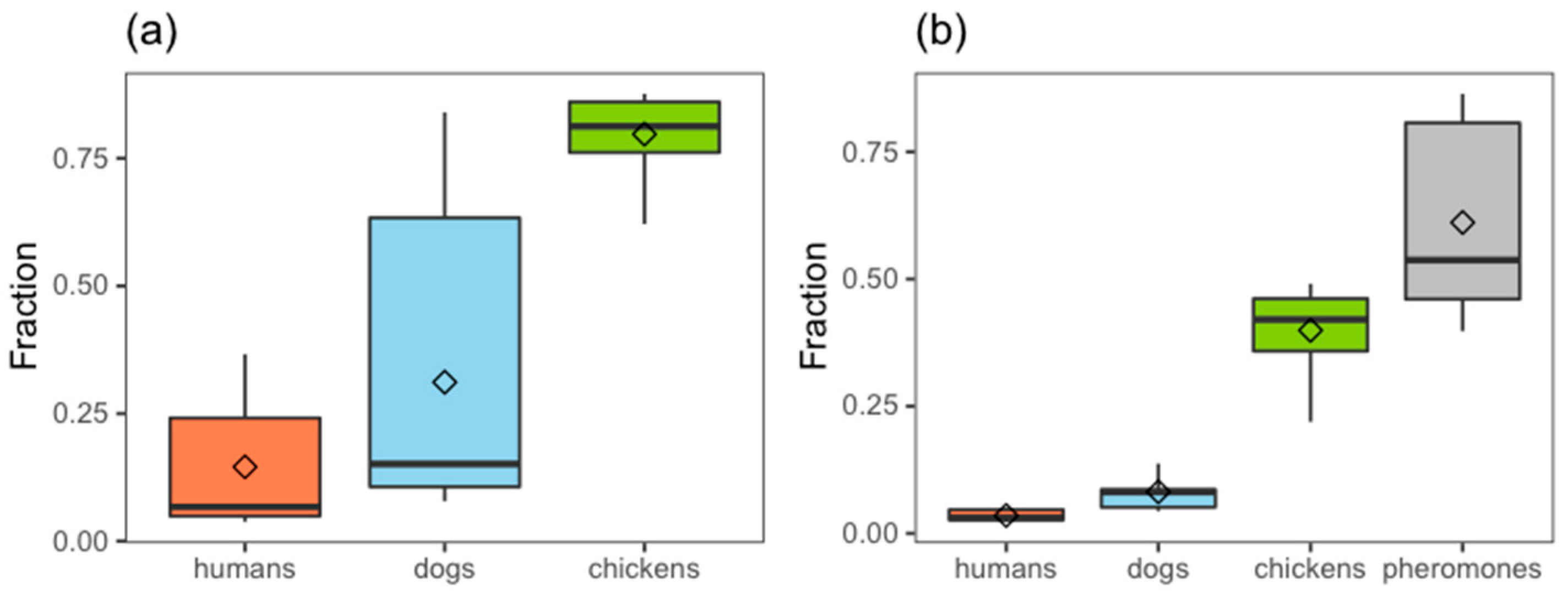
3.1. Parametrisation of Attraction Profiles
3.2. Effect of the Synthetic Pheromone on Lu. longipalpis Host Preference
4. Discussion
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B
References
- Wilson, A.L.; Courtenay, O.; Kelly-Hope, L.A.; Scott, T.W.; Takken, W.; Torr, S.J.; Lindsay, S.W. The importance of vector control for the control and elimination of vector-borne diseases. PLoS Neglected Trop. Dis. 2020, 14, e0007831. [Google Scholar] [CrossRef]
- Carrasco, D.; Lefèvre, T.; Moiroux, N.; Pennetier, C.; Chandre, F.; Cohuet, A. Behavioural adaptations of mosquito vectors to insecticide control. Curr. Opin. Insect Sci. 2019, 34, 48–54. [Google Scholar] [CrossRef]
- Killeen, G.F.; Chitnis, N. Potential causes and consequences of behavioural resilience and resistance in malaria vector populations: A mathematical modelling analysis. Malar. J. 2014, 13, 97. [Google Scholar] [CrossRef]
- Kreppel, K.S.; Viana, M.; Main, B.J.; Johnson, P.C.D.; Govella, N.J.; Lee, Y.; Maliti, D.; Meza, F.C.; Lanzaro, G.C.; Ferguson, H.M. Emergence of behavioural avoidance strategies of malaria vectors in areas of high LLIN coverage in Tanzania. Sci. Rep. 2020, 10, 14527. [Google Scholar] [CrossRef]
- Shani, A. Chemical communication agents (pheromones) in integrated pest management. Drug Dev. Res. 2000, 50, 400–405. [Google Scholar] [CrossRef]
- Cook, S.M.; Khan, Z.R.; Pickett, J.A. The Use of Push-Pull Strategies in Integrated Pest Management. Annu. Rev. Entomol. 2007, 52, 375–400. [Google Scholar] [CrossRef] [PubMed]
- Mansour, R.; Belzunces, L.P.; Suma, P.; Zappalà, L.; Mazzeo, G.; Grissa-Lebdi, K.; Russo, A.; Biondi, A. Vine and citrus mealybug pest control based on synthetic chemicals. A review. Agron. Sustain. Dev. 2018, 38, 37. [Google Scholar] [CrossRef]
- Logan, J.G.; Birkett, M.A. Semiochemicals for biting fly control: Their identification and exploitation. Pest Manag. Sci. 2007, 63, 647–657. [Google Scholar] [CrossRef] [PubMed]
- Alvar, J.; Vélez, I.D.; Bern, C.; Herrero, M.; Desjeux, P.; Cano, J.; Jannin, J.; den Boer, M.; WHO Leishmaniasis Control Team. Leishmaniasis Worldwide and Global Estimates of Its Incidence. PLoS ONE 2012, 7, e35671. [Google Scholar] [CrossRef]
- Bray, D.P.; Hamilton, J.G.C. Host Odor Synergizes Attraction of Virgin Female Lutzomyia longipalpis (Diptera: Psychodidae). J. Med. Entomol. 2007, 44, 779–787. [Google Scholar] [CrossRef][Green Version]
- Quinnell, R.J.; Courtenay, O. Transmission, reservoir hosts and control of zoonotic visceral leishmaniasis. Parasitology 2009, 136, 1915–1934. [Google Scholar] [CrossRef] [PubMed]
- Dye, C.; Davies, C.R.; Lainson, R. Communication among phlebotomine sandflies: A field study of domesticated Lutzomyia longipalpis populations in Amazonian Brazil. Anim. Behav. 1991, 42, 183–192. [Google Scholar] [CrossRef]
- Morrison, A.C.; Ferro, C.; Morales, A.; Tesh, R.B.; Wilson, M.L. Dispersal of the Sand Fly Lutzomyia longipalpis (Diptera: Psychodidae) at an Endemic Focus of Visceral Leishmaniasis in Colombia. J. Med. Entomol. 1993, 30, 427–435. [Google Scholar] [CrossRef] [PubMed]
- Galvis-Ovallos, F.; Casanova, C.; Bergamaschi, D.P.; Galati, E.A.B. A field study of the survival and dispersal pattern of Lutzomyia longipalpis in an endemic area of visceral leishmaniasis in Brazil. PLoS Negl. Trop. Dis. 2018, 12, e0006333. [Google Scholar] [CrossRef]
- Kelly, D.W.; Dye, C. Pheromones, kairomones and the aggregation dynamics of the sandflyLutzomyia longipalpis. Anim. Behav. 1997, 53, 721–731. [Google Scholar] [CrossRef]
- Alexander, B.; De Carvalho, R.L.; McCallum, H.; Pereira, M.H. Role of the Domestic Chicken (Gallus gallus)in the Epidemiology of Urban Visceral Leishmaniasis in Brazil. Emerg. Infect. Dis. 2002, 8, 1480–1485. [Google Scholar] [CrossRef]
- Saul, A. Zooprophylaxis or zoopotentiation: The outcome of introducing animals on vector transmission is highly dependent on the mosquito mortality while searching. Malar. J. 2003, 2, 32. [Google Scholar] [CrossRef]
- Bern, C.; Courtenay, O.; Alvar, J. Of Cattle, Sand Flies and Men: A Systematic Review of Risk Factor Analyses for South Asian Visceral Leishmaniasis and Implications for Elimination. PLoS Negl. Trop. Dis. 2010, 4, e599. [Google Scholar] [CrossRef]
- Bray, D.P.; Bandi, K.K.; Brazil, R.P.; Oliveira, A.G.; Hamilton, J.G.C. Synthetic Sex Pheromone Attracts the Leishmaniasis Vector Lutzomyia longipalpis (Diptera: Psychodidae) to Traps in the Field. J. Med. Entomol. 2009, 46, 428–434. [Google Scholar] [CrossRef]
- Bray, D.P.; Alves, G.B.; Dorval, M.E.; Brazil, R.P.; Hamilton, J.G. Synthetic sex pheromone attracts the leishmaniasis vector Lutzomyia longipalpis to experimental chicken sheds treated with insecticide. Parasit. Vectors 2010, 3, 16. [Google Scholar] [CrossRef][Green Version]
- Bray, D.P.; Carter, V.; Alves, G.B.; Brazil, R.P.; Bandi, K.K.; Hamilton, J.G.C. Synthetic Sex Pheromone in a Long-Lasting Lure Attracts the Visceral Leishmaniasis Vector, Lutzomyia longipalpis, for up to 12 Weeks in Brazil. PLoS Negl. Trop. Dis. 2014, 8, e2723. [Google Scholar] [CrossRef]
- Bell, M.J.; Sedda, L.; Gonzalez, M.A.; De Souza, C.F.; Dilger, E.; Brazil, R.P.; Courtenay, O.; Hamilton, J.G.C. Attraction of Lutzomyia longipalpis to synthetic sex-aggregation pheromone: Effect of release rate and proximity of adjacent pheromone sources. PLoS Negl. Trop. Dis. 2018, 12, e0007007. [Google Scholar] [CrossRef]
- González, M.A.; Bell, M.; Souza, C.F.; Maciel-De-Freitas, R.; Brazil, R.P.; Courtenay, O.; Hamilton, J.G.C. Synthetic sex-aggregation pheromone of Lutzomyia longipalpis, the South American sand fly vector of Leishmania infantum, attracts males and females over long-distance. PLoS Negl. Trop. Dis. 2020, 14, e0008798. [Google Scholar] [CrossRef]
- Courtenay, O.; Dilger, E.; Calvo-Bado, L.A.; Kravar-Garde, L.; Carter, V.; Bell, M.J.; Alves, G.B.; Goncalves, R.; Makhdoomi, M.M.; González, M.A.; et al. Sand fly synthetic sex-aggregation pheromone co-located with insecticide reduces the incidence of infection in the canine reservoir of visceral leishmaniasis: A stratified cluster randomised trial. PLoS Negl. Trop. Dis. 2019, 13, e0007767. [Google Scholar] [CrossRef]
- Gonçalves, R.; de Souza, C.F.; Rontani, R.B.; Pereira, A.; Farnes, K.B.; Gorsich, E.E.; Silva, R.A.; Brazil, R.P.; Hamilton, J.G.C.; Courtenay, O. Community deployment of a synthetic pheromone of the sand fly Lutzomyia longipalpis co-located with insecticide reduces vector abundance in treated and neighbouring untreated houses: Implications for control of Leishmania infantum. PLoS Negl. Trop. Dis. 2021, 15, e0009080. [Google Scholar] [CrossRef] [PubMed]
- Kelly, D.W. Why are some people bitten more than others? Trends Parasitol. 2001, 17, 578–581. [Google Scholar] [CrossRef]
- Zahid, M.H.; Kribs, C.M. Impact of dogs with deltamethrin-impregnated collars on prevalence of visceral leishmaniasis. Infect. Dis. Model. 2020, 5, 235–247. [Google Scholar] [CrossRef]
- Smith, T.; Killeen, G.F.; Maire, N.; Dietz, K.; Molineaux, L.; Vounatsou, P.; Tanner, M. Relationship between the entomologic inoculation rate and the force of infection for plasmodium falciparum malaria. Am. J. Trop. Med. Hyg. 2006, 75, 11–18. [Google Scholar] [CrossRef]
- Buckingham-Jeffery, E.; Hill, E.M.; Datta, S.; Dilger, E.; Courtenay, O. Spatio-temporal modelling of Leishmania infantum infection among domestic dogs: A simulation study and sensitivity analysis applied to rural Brazil. Parasit. Vectors 2019, 12, 215. [Google Scholar] [CrossRef] [PubMed]
- Dilger, E. The Effects of Host-Vector Relationships and Density Dependence on the Epidemiology of Visceral Leishmaniasis. Ph.D Thesis, University of Warwick, Coventry, UK, 2013. Available online: http://webcat.warwick.ac.uk/record=b2704268~S1 (accessed on 27 February 2021).
- Roberts, G.O.; Rosenthal, J.S. Examples of Adaptive MCMC. J. Comput. Graph. Stat. 2009, 18, 349–367. [Google Scholar] [CrossRef]
- Agrela, I.; Sanchez, E.; Gomez, B.; Feliciangeli, M.D. Feeding Behavior of Lutzomyia pseudolongipalpis (Diptera: Psychodidae), a Putative Vector of Visceral Leishmaniasis in Venezuela. J. Med. Entomol. 2002, 39, 440–445. [Google Scholar] [CrossRef] [PubMed]
- Quinnell, R.J.; Dye, C. An experimental study of the peridomestic distribution of Lutzomyia longipalpis (Diptera: Psychodidae). Bull. Entomol. Res. 1994, 84, 379–382. [Google Scholar] [CrossRef]
- Okumu, F.O.; Govella, N.J.; Moore, S.J.; Chitnis, N.; Killeen, G.F. Potential Benefits, Limitations and Target Product-Profiles of Odor-Baited Mosquito Traps for Malaria Control in Africa. PLoS ONE 2010, 5, e11573. [Google Scholar] [CrossRef] [PubMed]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Retkute, R.; Dilger, E.; Hamilton, J.G.C.; Keeling, M.J.; Courtenay, O. Modelling Sand Fly Lutzomyia longipalpis Attraction to Host Odour: Synthetic Sex-Aggregation Pheromone Dominates the Response. Microorganisms 2021, 9, 602. https://doi.org/10.3390/microorganisms9030602
Retkute R, Dilger E, Hamilton JGC, Keeling MJ, Courtenay O. Modelling Sand Fly Lutzomyia longipalpis Attraction to Host Odour: Synthetic Sex-Aggregation Pheromone Dominates the Response. Microorganisms. 2021; 9(3):602. https://doi.org/10.3390/microorganisms9030602
Chicago/Turabian StyleRetkute, Renata, Erin Dilger, James G. C. Hamilton, Matt J. Keeling, and Orin Courtenay. 2021. "Modelling Sand Fly Lutzomyia longipalpis Attraction to Host Odour: Synthetic Sex-Aggregation Pheromone Dominates the Response" Microorganisms 9, no. 3: 602. https://doi.org/10.3390/microorganisms9030602
APA StyleRetkute, R., Dilger, E., Hamilton, J. G. C., Keeling, M. J., & Courtenay, O. (2021). Modelling Sand Fly Lutzomyia longipalpis Attraction to Host Odour: Synthetic Sex-Aggregation Pheromone Dominates the Response. Microorganisms, 9(3), 602. https://doi.org/10.3390/microorganisms9030602





