Multi-Level Model to Predict Antibody Response to Influenza Vaccine Using Gene Expression Interaction Network Feature Selection
Abstract
1. Introduction
2. Materials and Methods
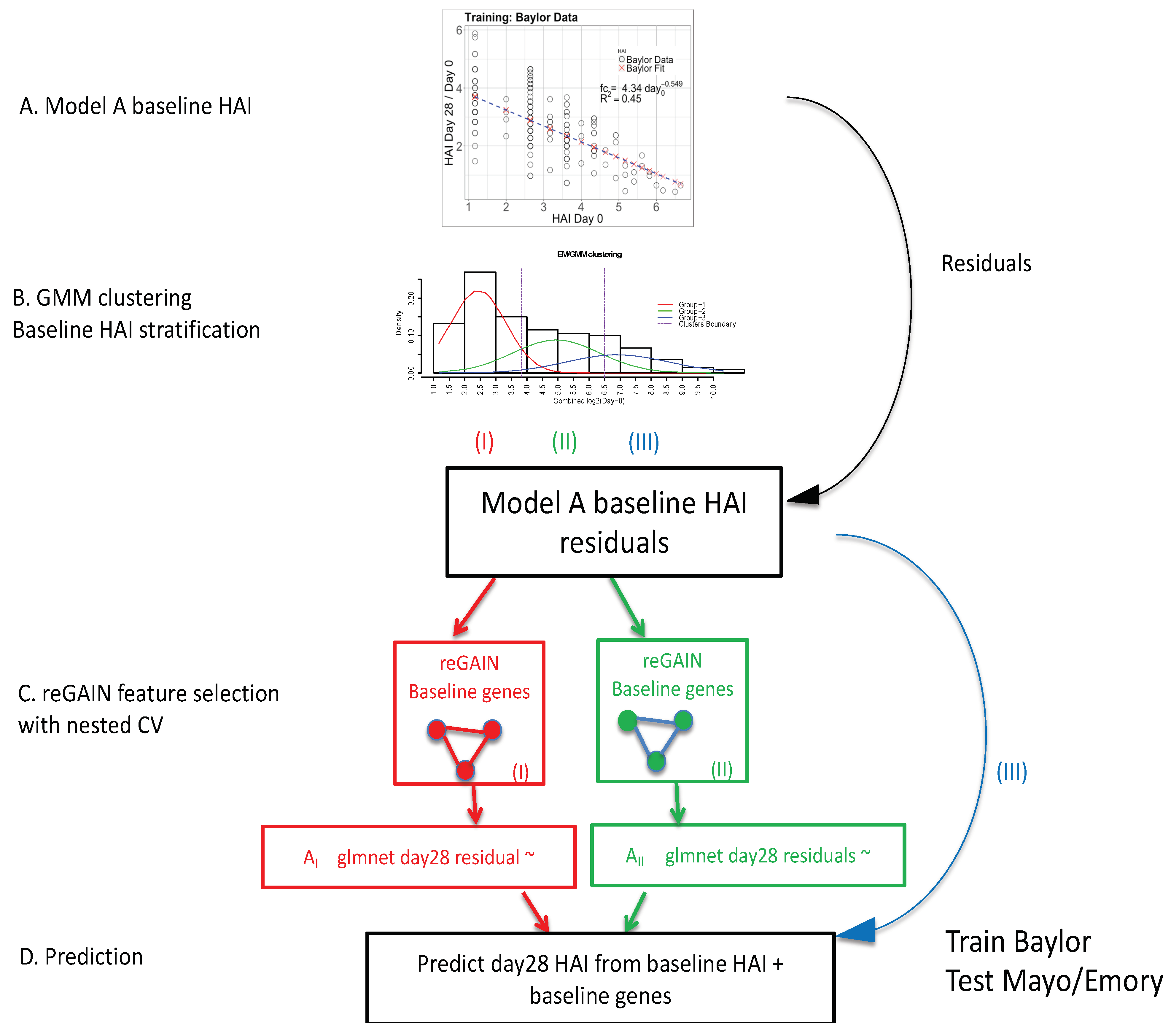
2.1. Overall Approach
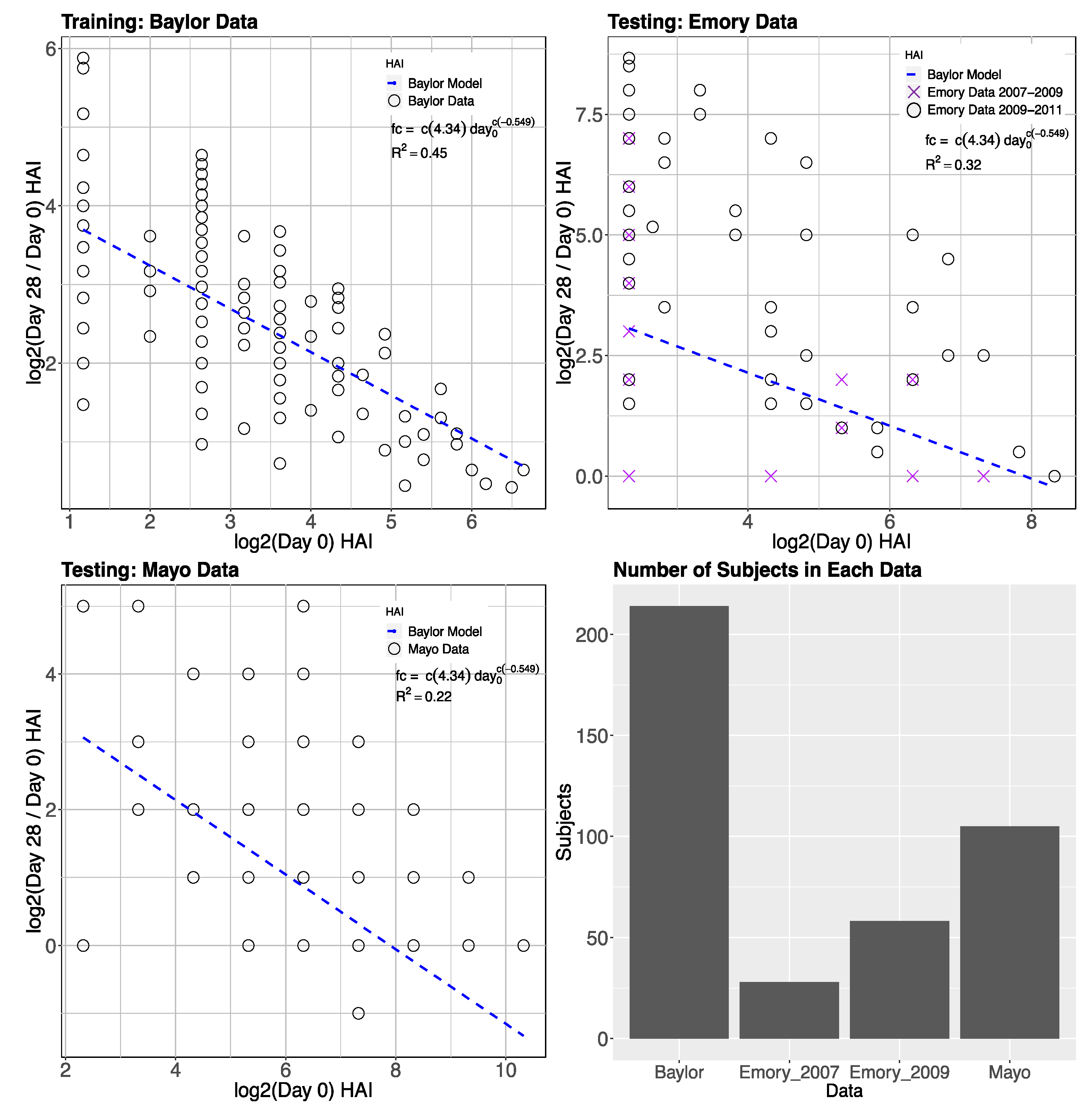
2.1.1. Inverse Power of Baseline HAI to Model Post-Vaccine HAI Fold Change
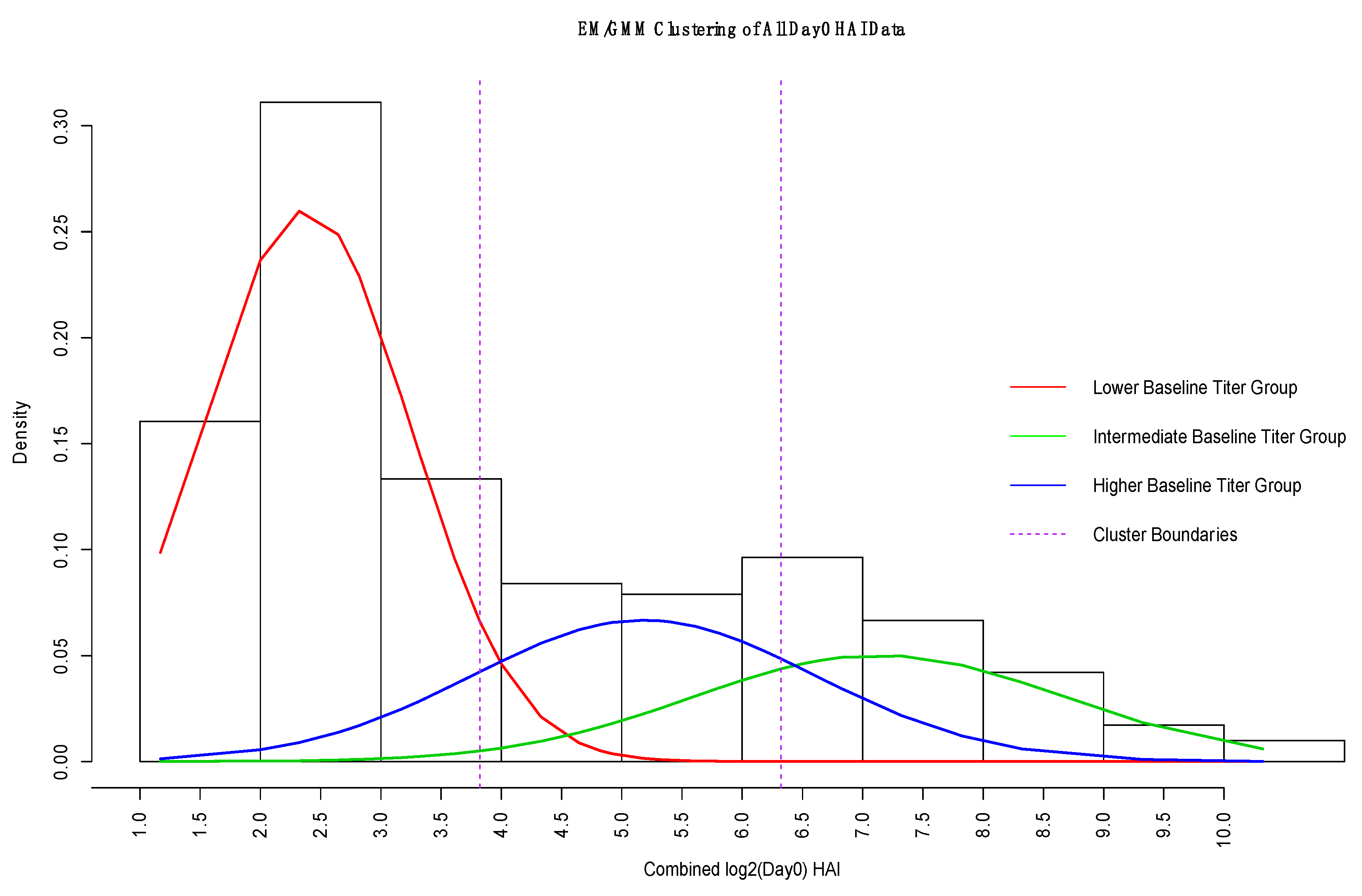
2.1.2. Expectation Maximization/Gaussian Mixture Model
2.1.3. reGAIN Gene−Gene Interaction Based Feature Selection of Baseline Gene Expression
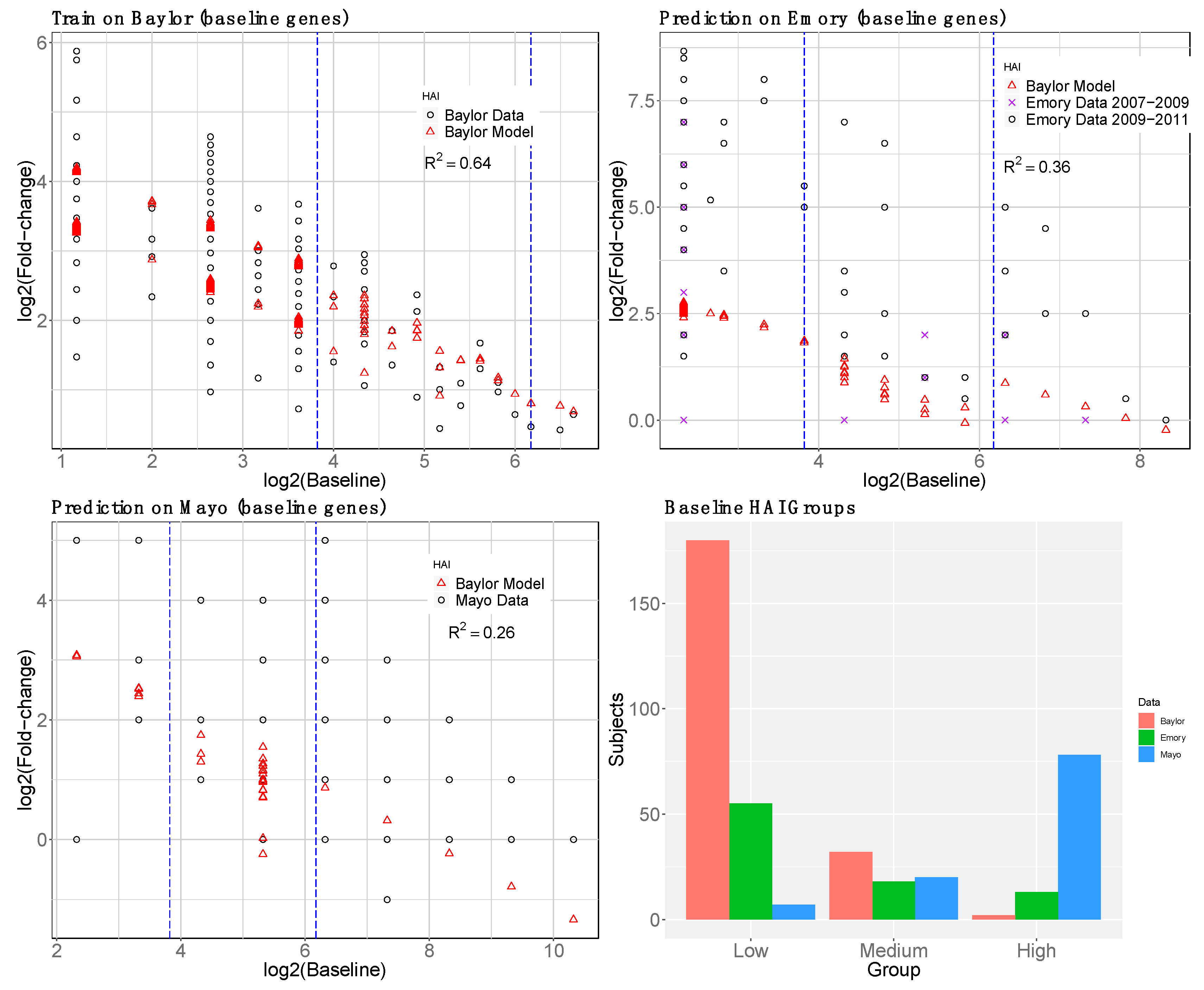
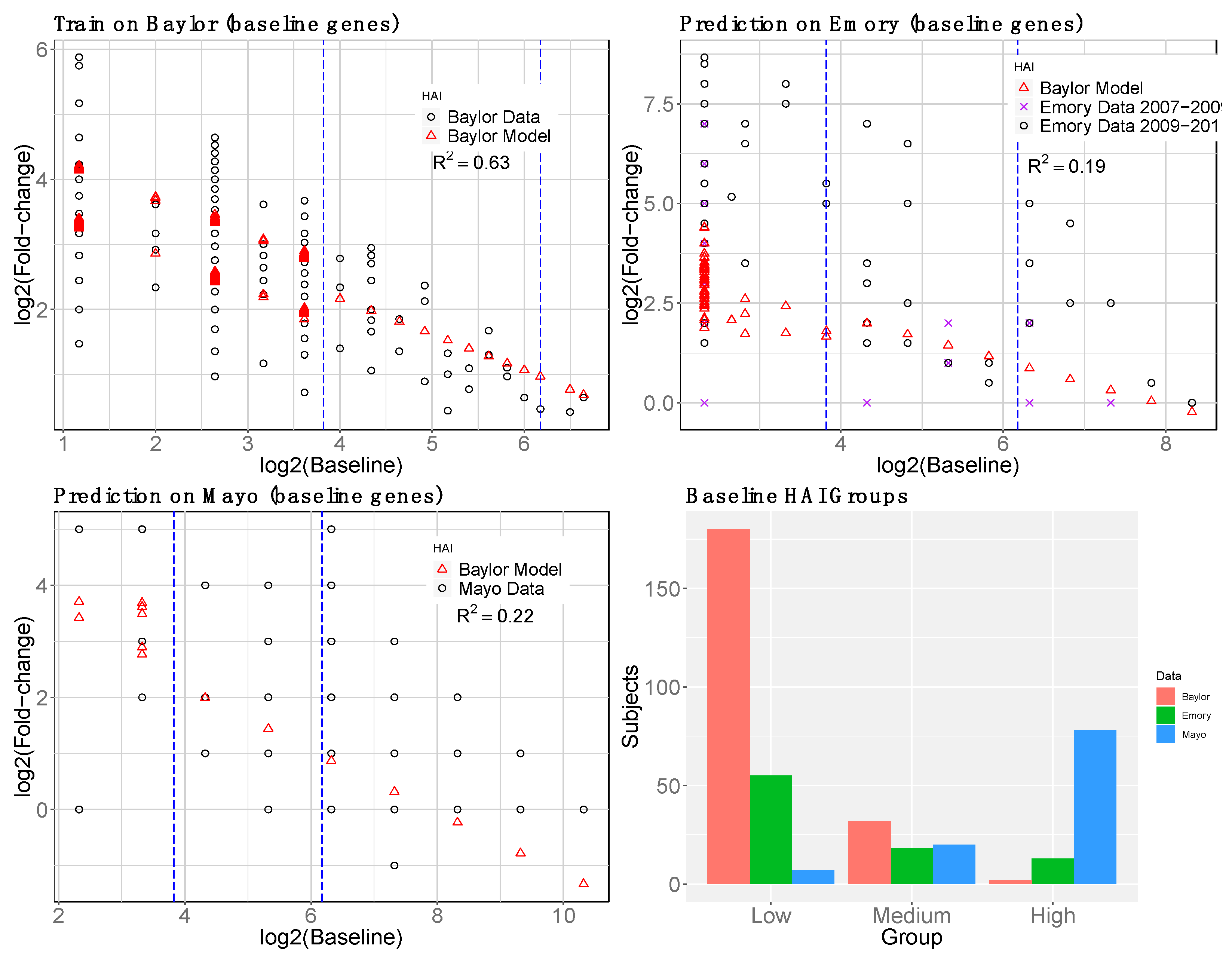
2.1.4. Baseline Gene Expression Machine Learning Model to Improve Baseline HAI Model
3. Results
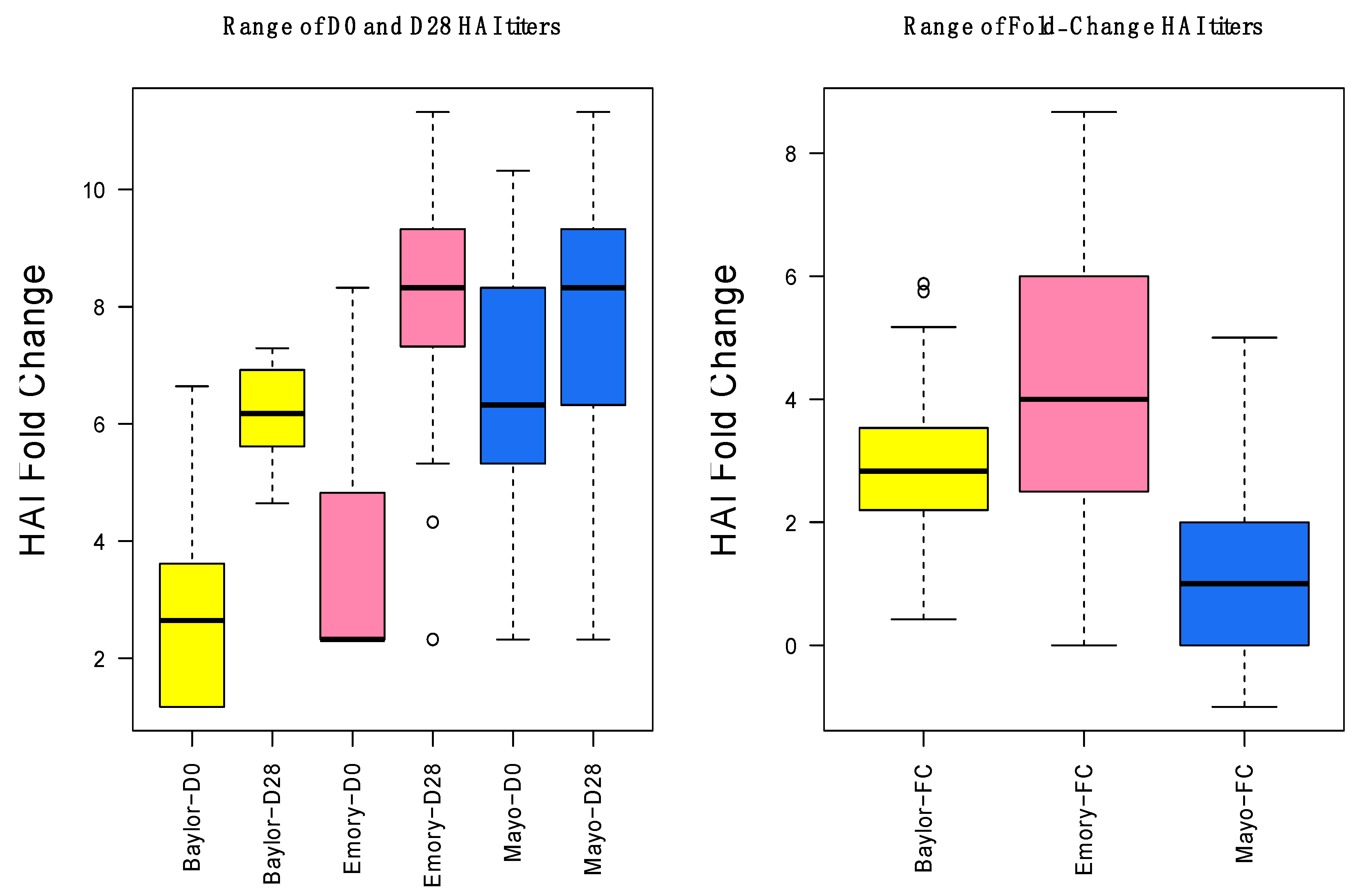
3.1. Gene Expression and HAI Training and Testing Data
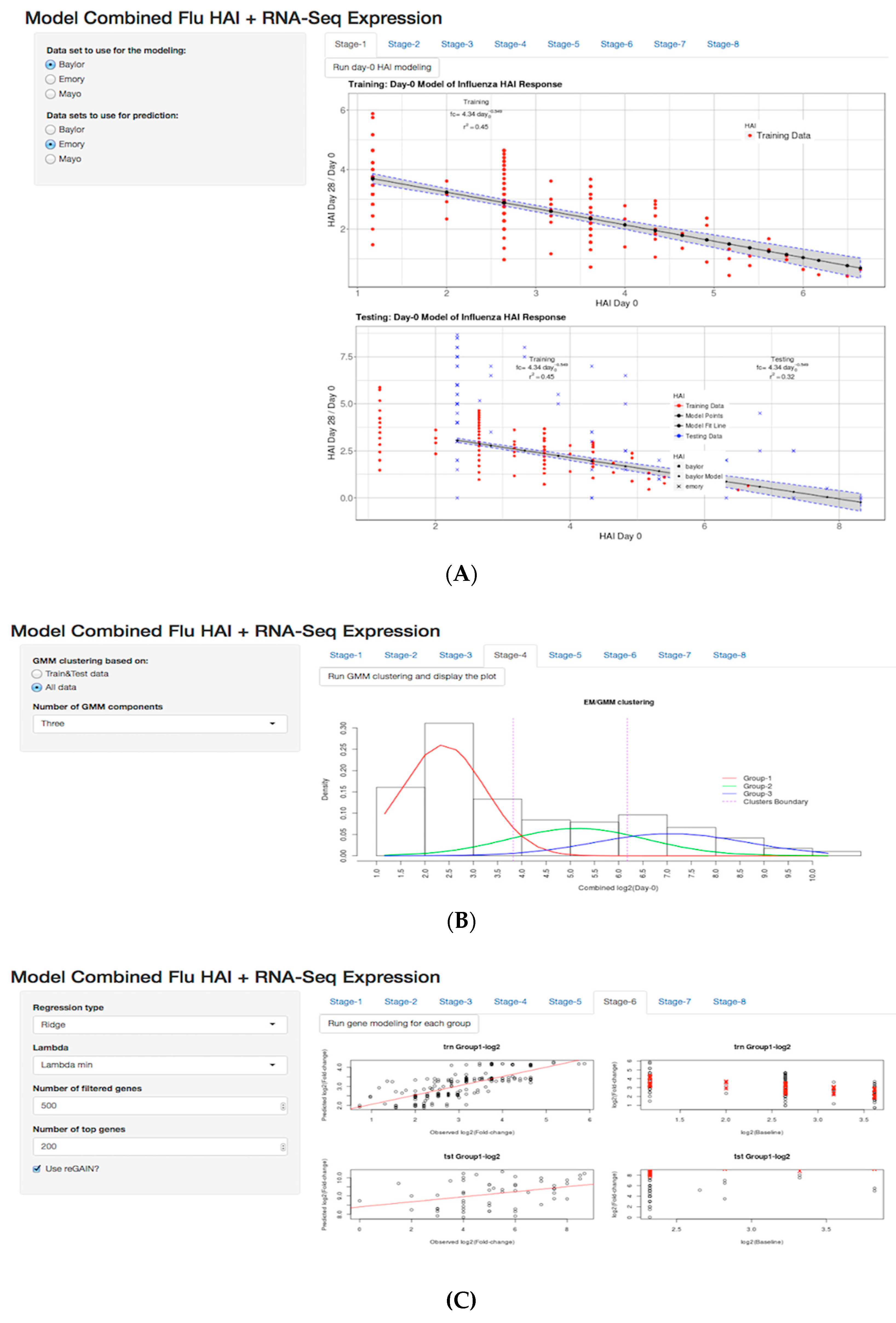
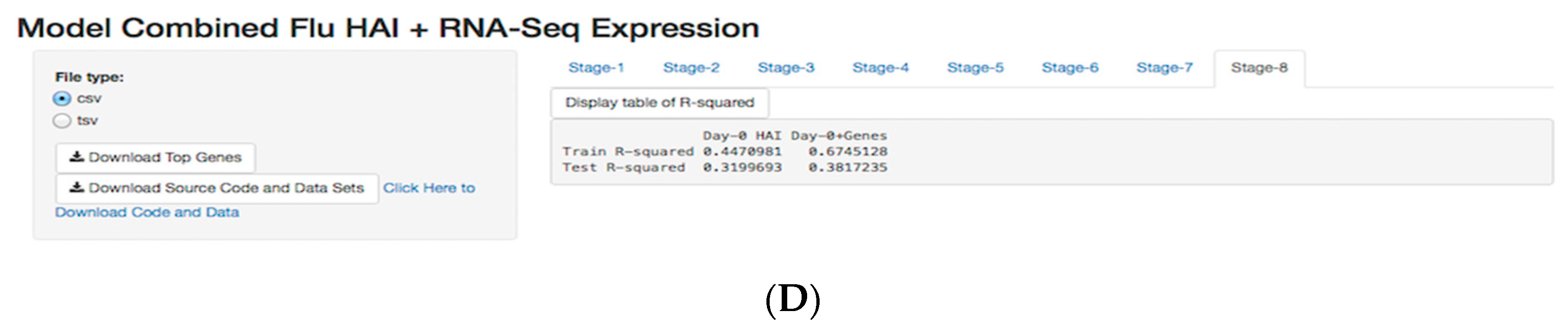
3.2. Day-0 HAI Model of Post-Vaccination HAI Fold Change
3.3. GMM for Day-0 Clustering
3.4. reGAIN for Constructing the Interaction Network
3.5. Shiny Application
4. Discussion
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Tan, Y.; Tamayo, P.; Nakaya, H.; Pulendran, B.; Mesirov, J.P.; Haining, W.N. Gene signatures related to B-cell proliferation predict influenza vaccine-induced antibody response. Eur. J. Immunol. 2014, 44, 285–295. [Google Scholar] [CrossRef] [PubMed]
- Beyer, W.E.P.; Palalche, A.M.; Sprenger, M.J.W.; Hendriksen, E.; Tukker, J.J.; Van der Water, G.L.; Masurel, N.; Osterhaus, A.D.M.E. Effects of repeated annual influenza vaccination on vaccine sero-response in young and elderly adults. Vaccine 1996, 14, 1331–1339. [Google Scholar] [CrossRef]
- Keitel, W.A.; Cate, T.R.; Couch, R.B.; Huggins, L.L.; Hess, K.R. Efficacy of repeated annual immunization with inactivated influenza virus vaccines over a five year period. Vaccine 1997, 15, 1114–1122. [Google Scholar] [CrossRef]
- Bucasas, K.L.; Franco, F.M.; Shaw, A.C.; Bray, M.S.; Wells, M.J.; Nino, D.; Arden, N.; Quarles, M.J.; Coucj, M.J.; Belmont, W.J. Early patterns of gene expression correlate with the humoral immune response to influenza vaccination in humans. J. Infect. Dis. 2011, 203, 921–929. [Google Scholar] [CrossRef] [PubMed]
- Sasaki, S.; He, X.S.; Holmes, H.T.; Dekker, L.C.; Kemble, G.W.; Arvin, M.A.; Greenberg, H.B. Influence of prior influenza vaccination on antibody and B-cell responses. PLoS ONE 2008, 3, e2975. [Google Scholar] [CrossRef] [PubMed]
- Furman, D.; Jojic, V.; Kidd, B.; Shen-Orr, S.; Prince, J.; Jarrell, J.; Tse, T.; Huang, H.; Lund, P.; Maecker, T.H.; et al. Apoptosis and other immune biomarkers predict influenza vaccine responsiveness. Mol. Syst. Biol. 2014, 9, 659. [Google Scholar] [CrossRef] [PubMed]
- Tsang, J.S.; Shwartzberg, P.L.; Kotliarov, Y.; Biancotto, A.; Xie, Z.; Germain, R.N.; Wang, E.; Olnes, M.J.; Narayanan, M.; Golding, H.; et al. Global analyses of human immune variation reveal baseline predictors of postvaccination responses. Cell 2014, 157, 499–513. [Google Scholar] [CrossRef]
- HIPC-CHI Signatures Project Team; HIPC-I Consortium. Multicohort analysis reveals baseline transcriptional predictors of influenza vaccination responses. Sci. Immunol. 2017, 2, eaal4656. [Google Scholar] [CrossRef]
- Harrell, E.F.; Frank, E. Regression Modeling Strategies: With Applications to Linear Models, Logistic Regression, and Survival Analysis; Springer: New York, NY, USA, 2001. [Google Scholar]
- Milliken, G.A.; Johnson, D.E. Analysis of Messy Data; Lifetime Learning Publications: Belmon, CA, USA, 1984. [Google Scholar]
- Tarca, A.L.; Lauria, M.; Unger, M.; Bilal, E.; Boue, S.; Dey, K.K.; Hoeng, J.; Koeppl, H.; Martin, F.; Meyer, P.; et al. Strengths and limitations of microarray-based phenotype prediction: Lessons learned from the improver diagnostic signature challenge. Bioinformatics 2013, 29, 2892–2899. [Google Scholar] [CrossRef]
- Lareau, C.A.; White, B.C.; Oberg, A.L.; McKinney, B.A. Differential co-expression network centrality and machine learning feature selection for identifying susceptibility hubs in networks with scale-free structure. BioData Min. 2015, 8, 5. [Google Scholar] [CrossRef]
- Le, T.T.; Savitz, J.; Suzuku, H.; Misaki, M.; Teauge, K.; White, B.C.; Marino, J.H.; Wiley, G.; Gaffeny, P.M.; Drevets, W.C.; et al. Identification and replication of RNA-Seq gene network modules associated with depression severity. Transl. Psychiatry 2018, 8, 180. [Google Scholar] [CrossRef]
- Varma, S.; Simon, R. Bias in error estimation when using cross-validation for model selection. BMC Bioinformatics 2006, 7, 91. [Google Scholar] [CrossRef]
- Arlot, S.; Celisse, A. A survey of cross-validation procedures for model selection. Stat. Surv. 2010, 4, 40–79. [Google Scholar] [CrossRef]
- Parvandeh, S.; McKinney, B.A. EpistasisRank and EpistasisKatz: Interaction network centrality methods that integrate prior knowledge networks. Bioinformatics 2018. [Google Scholar] [CrossRef]
- Feng, J.; Gulati, V.; Zhang, X.; Keitel, W.A.; Thompson, D.M.; James, A.J.; Thompson, L.F.; Air, G.M. Antibody quantity versus quality after influenza vaccination. Vaccine 2009, 27, 6358–6362. [Google Scholar] [CrossRef]
- Benaglia, T.; Chauveau, D.; Hunter, D.R.; Young, D. Mixtools: An R package for analyzing finite mixture models. J. Stat. Softw. 2009, 32, 1–29. [Google Scholar] [CrossRef]
- Davis, N.A.; Crowe, J.E.; Pajewski, N.M.; McKinney, B.A. Surfing a genetic association interaction network to identify modulators of antibody response to smallpox vaccine. Genes Immun. 2010, 11, 630–636. [Google Scholar] [CrossRef]
- McKinney, B.A.; Crowe, J.E.; Guo, J.; Tian, D. Capturing the spectrum of interaction effects in genetic association studies by simulated evaporative cooling network analysie. PLoS Genet. 2009, 5, e1000432. [Google Scholar] [CrossRef]
- Davis, N.A.; Lareav, C.A.; White, B.C.; Pandey, A.; Wiley, G.; Montgomery, C.G.; Gaffney, P.M.; McKinney, B.A. Encore: Genetic association interaction network centrality pipeline and application to SLE exome data. Genet. Epidemiol. 2013, 37, 614–621. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Jerome, J.H.; Friedman, H. The Elements of Statistical Learning: Data Mining, Inference, and Prediction; Springer: New York, NY, USA, 2009. [Google Scholar]
- Dwork, C.; Feldman, V.; Hardt, M.; Pitassi, T.; Reingold, O.; Roth, A. The reusable holdout: Preserving validity in adaptive data analysis. Science 2015, 349, 636–638. [Google Scholar] [CrossRef]
- Le, T.T.; Simmons, W.K.; Misaki, M.; Bodurka, J.; White, B.C.; Savitz, J.; McKinney, B.A. Differential privacy-based evaporative cooling feature selection and classification with relief-F and random forests. Bioinformatics 2017, 33, 2906–2913. [Google Scholar] [CrossRef] [PubMed]
- Nakaya, H.I.; Wrammert, J.; Lee, K.E.; Racioppi, L.; Marie-Kunze, S.; Hainig, W.N.; Means, R.A.; Kasturi, S.P.; Khan, N.; Li, G.M.; et al. Systems biology of vaccination for seasonal influenza in humans. Nat. Immunol. 2011, 12, 786–795. [Google Scholar] [CrossRef] [PubMed]
- Nakaya, H.I.; Hagan, T.; Duraisingham, S.S.; Lee, E.K.; Kwissa, M.; Rouphael, N.; Frasca, D.; Gersten, M.; Mehta, A.K.; Gaujoux, R.; et al. Systems analysis of immunity to influenza vaccination across multiple years and in diverse populations reveals shared molecular signatures. Immunity 2015, 43, 1186–1198. [Google Scholar] [CrossRef] [PubMed]
- Bolstad, B.M.; Irizarry, R.A.; Astrand, M.; Speed, T.P. A comparison of normalization methods for high density oligonucleotide array data based on variance and bias. Bioinformatics 2003, 19, 185–193. [Google Scholar] [CrossRef] [PubMed]
- McKinney, B.A.; White, B.C.; Grill, D.E.; Li, P.W.; Kennedy, R.B.; Poland, G.A.; Oberg, A.L. ReliefSeq: A gene-wise adaptive-K nearest-neighbor feature selection tool for finding gene-gene interactions and main effects in mRNA-Seq gene expression data. PLoS One 2013, 8, e81527. [Google Scholar] [CrossRef]
- Subramanian, A.; Tamayo, P.; Mootha, V.K.; Mukhejee, S.; Ebert, B.L.; Gillette, M.A.; Paulovich, A.; Pomeroy, S.L.; Golub, T.R.; Lander, E.S.; et al. Gene set enrichment analysis: a knowledge-based approach for interpreting genome-wide expression profiles. Proc. Natl. Acad. Sci. USA 2005, 102, 15545–15550. [Google Scholar] [CrossRef]
- Pilkinton, M.A.; Nicholas, K.J.; Warren, C.M.; Smith, R.M.; Yoder, S.M.; Talbot, H.K.; Kalams, S.A. Greater activation of peripheral T follicular helper cells following high dose influenza vaccine in older adults forecasts seroconversion. Vaccine 2017, 35, 329–336. [Google Scholar] [CrossRef] [PubMed]
- Sasaki, S.; Sullivan, M.; Naravez, C.F.; Holmes, T.H.; Furman, D.; Zheng, N.Y.; Nishtala, M.; Wrammert, J.; Smith, K.; James, J.A.; et al. Limited efficacy of inactivated influenza vaccine in elderly individuals is associated with decreased production of vaccine-specific antibodies. J. Clin. Invest. 2011, 121, 3109–3119. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.H.; Talbot, H.K.; Mishina, M.; Zhu, Y.; Chen, J.; Cao, W.; Reber, A.J.; Griffin, M.R.; Shay, D.K.; Spencer, S.M.; et al. High-dose influenza vaccine favors acute plasmablast responses rather than long-term cellular responses. Vaccine 2014, 34, 4594–4601. [Google Scholar] [CrossRef]
| GEO Acc# | Location | Male:Female | Age | HAI at Day 0 and 28 | Gene Expression Array Data | ||||
|---|---|---|---|---|---|---|---|---|---|
| Day 0 | Day 1 | Day 3 | Day 7 | Day 14 | |||||
| GSE48018 | Baylor Male | 111:0 | 19–41 | 111 | 111 | 110 | 101 | x | 109 |
| GSE48023 | Baylor Female | 0:107 | 19–41 | 107 | 107 | 107 | 105 | x | 98 |
| SDY67 | Mayo | 57:92 | 50–74 | 149 | 105 | x | 105 | x | 105 |
| GSE29619 | Emory 2007–2009 | 27:38 | 22–40 | 63 | 63 | x | 63 | 63 | x |
| GSE74817 | Emory 2009–2011 | 35:51 | 21–85 | 80 | 58 | 58 | 58 | 58 | 58 |
| Gene Set Name | Description | Overlap Genes | p-Value | FDR |
|---|---|---|---|---|
| Immune system | Genes involved in immune system | 25 | 5.6 × 10−13 | 3.78 × 10−10 |
| Adaptive immune system | Genes involved in adaptive immune system | 15 | 1.81 × 10−8 | 6.1 × 10−5 |
| Class I MHC mediated antigen processing presentation | Genes involved class I MHC mediated antigen processing and presentation | 10 | 1.79 × 10−7 | 4.02 × 10−5 |
| Antigen processing ubiquitination proteasome degradation | Genes involved in antigen processing: ubiquitination and proteasome degradation | 9 | 4.38 × 10−7 | 7.39 × 10−5 |
| Metabolism of RNA | Genes involved in metabolism of RNA | 10 | 2.14 × 10−6 | 2.89 × 10−4 |
| Generic transcription pathway | Genes involved in generic transcription pathway | 10 | 3.8 × 10−6 | 4.27 × 10−4 |
| Signaling by the B cell receptor BCR | Genes involved in signaling by the B cell receptor (BCR) | 6 | 2.01 × 10−5 | 1.94 × 10−3 |
| Mitotic G1_G1/S phases | Genes involved in mitotic G1-G1/S phases | 6 | 3.23 × 10−5 | 2.34 × 10−3 |
| Innate immune system | Genes involved in innate immune system | 8 | 3.37 × 10−5 | 2.34 × 10−3 |
| Regulation of mRNA stability by proteins that bind AU rich elements | Genes in involved in regulation of mRNA stability by proteins that bind AU-rich elements | 5 | 3.47 × 10−5 | 2.34 × 10−3 |
| Immune System | Adaptive Immune System | Class I MHC Mediated Antigen Processing Presentation | Antigen Processing Ubiquitination Proteasome Degradation | Metabolism of RNA | Generic Transcription Pathway | Signaling by the B Cell Receptor BCR |
|---|---|---|---|---|---|---|
| BCL2 | CD36 | CD36 | DET1 | CNOT10 | MAML2 | ORAI1 |
| CASP1 | CRTAM | DET1 | HUWE1 | DDX20 | MED31 | PIK3R1 |
| CD36 | CTSF | HUWE1 | LRSAM1 | EXOSC2 | RBL1 | PSMA4 |
| CRTAM | DET1 | LRSAM1 | PJA1 | EXOSC4 | RORA | PSMC5 |
| CTSF | HUWE1 | PJA1 | PSMA4 | PSMA4 | ZNF160 | PSMF1 |
| DET1 | LRSAM1 | PSMA4 | PSMC5 | PSMC5 | ZNF180 | SOS1 |
| FLNB | ORAI1 | PSMC5 | PSMF1 | PSMF1 | ZNF197 | |
| HUWE1 | PIK3R1 | PSMF1 | RNF4 | RBM8A | ZNF430 | |
| IL6R | PJA1 | RNF4 | UBOX5 | RPLP1 | ZNF517 | |
| LRSAM1 | PSMA4 | UBOX5 | SNRPD3 | ZNF589 | ||
| MAP2K7 | PSMC5 | |||||
| MAPK1 | PSMF1 | |||||
| MAPK13 | RNF4 | |||||
| NLRP3 | SOS1 | |||||
| ORAI1 | UBOX5 | |||||
| PIK3R1 | ||||||
| PJA1 | ||||||
| PSMA4 | ||||||
| PSMC5 | ||||||
| PSMF1 | ||||||
| RNF4 | ||||||
| RPS6KA3 | ||||||
| SOS1 | ||||||
| TLR1 | ||||||
| UBOX5 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Parvandeh, S.; Poland, G.A.; Kennedy, R.B.; McKinney, B.A. Multi-Level Model to Predict Antibody Response to Influenza Vaccine Using Gene Expression Interaction Network Feature Selection. Microorganisms 2019, 7, 79. https://doi.org/10.3390/microorganisms7030079
Parvandeh S, Poland GA, Kennedy RB, McKinney BA. Multi-Level Model to Predict Antibody Response to Influenza Vaccine Using Gene Expression Interaction Network Feature Selection. Microorganisms. 2019; 7(3):79. https://doi.org/10.3390/microorganisms7030079
Chicago/Turabian StyleParvandeh, Saeid, Greg A. Poland, Richard B. Kennedy, and Brett A. McKinney. 2019. "Multi-Level Model to Predict Antibody Response to Influenza Vaccine Using Gene Expression Interaction Network Feature Selection" Microorganisms 7, no. 3: 79. https://doi.org/10.3390/microorganisms7030079
APA StyleParvandeh, S., Poland, G. A., Kennedy, R. B., & McKinney, B. A. (2019). Multi-Level Model to Predict Antibody Response to Influenza Vaccine Using Gene Expression Interaction Network Feature Selection. Microorganisms, 7(3), 79. https://doi.org/10.3390/microorganisms7030079





