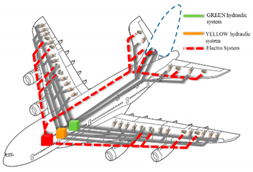
Abstract
The aircraft hydraulic system is very important for the actuation system and its failure has led to a number of catastrophic accidents in the past few years. The reasons for hydraulic loss can be leakage, blockage, and structural damage. Fortunately, the development of more electric aircraft (MEA) provides a new means of solving this difficult problem. This paper designs an active fault tolerant control (AFTC) method for MEA suffering from total hydraulic loss and actuation system failure. Two different kinds of scenarios are considered: leakage/blockage and vertical tail damage. With the application of the dissimilar redundant actuation system (DRAS) in MEA, a switching mechanism can be used to change the hydraulic actuation (HA) system into an electro-hydrostatic actuation (EHA) system when the whole hydraulic system fails. Taking account of the gap between HA and EHA, a degraded model is built. As for vertical tail damage, engine differential thrust control is adopted to help regain lateral-directional stability. The engine thrust dynamics are modeled and the mapping relationship between engine differential thrust and rudder deflection is formulated. Moreover, model reference control (MRC) and linear quadratic regulator (LQR) are used to design the AFTC method. Comparative simulation with the NASA generic transportation model (GTM) is carried out to prove the proposed strategy.
1. Introduction
Safety and reliability are increasingly important requirements in modern transportation systems, especially for civil aircrafts. Normally, fault tolerance can be realized by software and hardware redundancy as well as different control strategies. With abundant redundancies in modern civil aircraft, fault-tolerant control strategies have been widely developed [1], which are important to ensure the aircraft’s recovery from severe failure and improve its reliability.
However, this is not enough. Loss of control (LoC) is still is major contributor to aircraft accidents [2]. For example, the Japan Airlines Flight JL123 crash [3], caused by the vertical tail breaking down, was a result of its hydraulic system. When the hydraulic system fails, accidents are unavoidable for aircrafts. One more example is when a DHL cargo airplane (A300) was hit by a missile when flying over Baghdad in 2003. The missile damaged the outer half of the trailing edge flaps on the left wing and all hydraulic lines [4].
Therefore, the failure of the whole hydraulic system is dangerous to traditional hydraulic-driving aircraft. As a result, more electric aircraft (MEA) has been developed to address this problem by combining the power of the hydraulic system and electric system, which is called a dissimilar redundant actuation system (DRAS)—for example, the A380 with dual hydraulic/electric (2H/2E) type [5,6]. Research [7,8,9] on the DRAS shows that it can much improve an aircraft’s chances of recovering from some severe failures. Furthermore, the MEA is useful for optimizing the performance and cost of the flight [10], which contribute to the development of the MEA. Thus, it is necessary to conduct research into MEA fault-tolerant control strategies.
In the case of active fault-tolerant control (AFTC), which is the focus of our study, related research works are found mainly in dynamics-oriented studies and control strategy-oriented research. Gautam H. Shah used the wind tunnel to investigate the aerodynamic effects of damage to the primary aircraft control surfaces [11]. Crider et al. analyzed the mathematical model of aircraft without vertical tail [12]. Wang J et al. introduced a damage degree coefficient to parameterize the damaged aircraft dynamic model [13]. As for control strategies, many AFTC approaches to combating actuator failure and structural damage can be found, such as linear parameter varying (LPV) [14,15], multi-model (MM) [16], adaptive control [17,18,19,20,21,22], model following [23,24], neural networks [25,26,27], and model predictive control (MPC) [28], etc. Researchers such as Hitachi and Liu [29], James M et al. [30], and Lu [31] propose a method that uses engine differential thrust control to provide the yaw moment for vertical tail loss. In addition, monitoring techniques, failure identification, and health management for electro-hydraulic actuators are well discussed in [32,33,34,35]. Nevertheless, the literature fails to consider that for the traditional hydraulic driving aircraft, structural damage is always accompanied by total hydraulic loss, leading to the malfunction of all actuators. Total hydraulic loss has not been considered as a reason for actuator failure or as a result of structural damage. Thus far, techniques for designing AFTC have not yet been suggested in relation to the MEA.
Therefore, designing an AFTC strategy for MEA is necessary. Due to the whole elevators being equipped with DRAS, the elevators can provide the necessary pitch moment to ensure longitudinal dynamics control when the hydraulic system fails. Then, lateral-directional motion control should be considered, which is related to more control surfaces as well as engines.
In this paper, the lateral dynamic modeling of the damaged aircraft and its AFTC strategy are investigated. Firstly, the problem of total hydraulic loss is considered in two representative scenarios: with and without structural damage to the lateral-directional control surfaces. Due to the advantage of MEA, the DRAS integrated by the hydraulic actuation (HA) system and electro-hydrostatic actuation (EHA) system is utilized to combat total hydraulic loss. Moreover, engine differential thrust control is adopted while the vertical tail is damaged. Two different kinds of damaged aircraft model are built. Then, the AFTC strategy based on model reference control (MRC) and linear quadratic regulator (LQR) is proposed. Combined with other control methods, MRC is widely used on different fault-tolerant systems for its simplicity and practicality. Here, we combine MRC with the LQR method and apply them to the NASA generic transportation model (GTM). The simulation proved the performance of the designed AFTC strategy when the hydraulic system fails.
2. Preliminaries and Dynamic Modeling
2.1. Dissimilar Redundant Actuation System
Hydraulic failure can be caused by leakage, blockage, and structural damage, which are dangerous for an aircraft. When the MEA suffers from this, the longitudinal control of the aircraft can be ensured when failure happens, because the elevators of the more electric aircraft are all adopted by DRAS based on the hydraulic actuator and electro-hydrostatic actuator (HA/EHA). Hence, when the hydraulic system fails, the control of lateral behavior will be seriously affected. This paper focuses on a lateral AFTC strategy design for aircraft. The detailed layout of DRAS can be found in my previous work [36,37].
2.2. Nominal and Damaged Aircraft Modeling
The lateral model of the aircraft, which is described by the linearized state-space equation, can be expressed as [38]:
The corresponding matrices are
However, the nominal model cannot express the real control surfaces due to simplification. Therefore, an MEA model with independent control of all actuators is necessary. More details about the nominal and the damaged model can be found in our previous work [36,37].
There are two severe scenarios in which the aircraft experiences total hydraulic loss:
- Scenario I: without structural damage towards lateral-directional surfaces;
- Scenario II: with structural damage towards lateral-directional surfaces.
The aircraft model in scenario I (without structural damage) is built with hydraulic leakage or blockage, which causes total hydraulic loss yet has a negligible influence on the lateral-directional aerodynamic parameters. In scenario II (with structural damage), the aircraft model is built with completely vertical tail loss. These two scenarios have been responsible for many flight accidents and caused huge fatalities. Therefore, it is appropriate to validate and assess the proposed AFTC strategy towards these representative scenarios.
2.2.1. Scenario I: Aircraft Model under Hydraulic Leakage/Blockage
Assuming that the change in lateral-directional parameters can be neglected under such horizontal stabilizer damage, the point focuses on the influence of the THL. Therefore, as shown in Table 1, the outboard aileron and the upper rudder are unavailable. The state space equation of the damaged aircraft model is expressed as follows:

Table 1.
Scenario I damage effects towards the MEA aircraft.
The state variable vector and the output remain the same and , while
The control input vector becomes , which are the input of inboard aileron, spoilers and lower rudder, which are all driven by the EHA system.
2.2.2. Scenario II: Aircraft Model under Completely Vertical Tail Loss
In the case of modeling a damaged aircraft without vertical tail, since the whole aerodynamic structure will be changed, the relative lateral-directional stability variables and parameters need to be reconsidered and recalculated. The effects on the aircraft are summarized in Table 2.

Table 2.
Scenario II damage effects towards the aircraft.
The lateral derivatives that related with the vertical tail are given as:
where , and are the derivatives of side force, yaw moment and roll moment, respectively, related to . is the vertical tail volume ratio, is the vertical tail area, is the aircraft wing area, is the distance from the vertical stabilizer aerodynamic center to the aircraft gravity center and is the wing span. Because of the completely vertical tail loss, the vertical tail volume, area, weight and efficiency factors all become zero, which means . Since the vertical stabilizer works for the directional stability, then and .
Therefore, engine differential thrust control is proposed to take the place of the rudder deflection, serving as an alternate control input to regain directional stability. Then, the lateral-directional state space equation of the damaged aircraft can be expressed as:
2.3. Engine Thrust Dynamics
Firstly, it is assumed that the aircraft model has four engines. Considering the complexity of the engine system, the differential thrust input is generated by the two outside engines, which can provide the yaw moment more efficiently because of the longer moment arm. Then, the inside engine thrust is kept the same to maintain the required flying thrust, as shown in Figure 1. The equation is as follows:
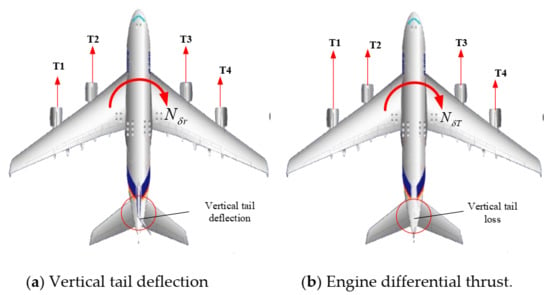
Figure 1.
Diagram of vertical tail deflection and engine differential thrust.
As a matter of fact, the aircraft engine is a highly complex system and shows a lot of nonlinearities. In order to integrate the aircraft engine thrust into control input, a typical engine system can be simplified and expressed as a time-delay second-order system:
where is the damping ratio, is the bandwidth frequency; is the thrust command and is the engine time delay constant.
The time constant of the engine response can be defined as and the damping ratio sets to 1 (), which means a critical damped engine system. Therefore, the engine dynamics can be expressed as:
In this paper, the corresponding parameters are based on a JT9D engine. Under the flight condition of Mach 0.8 and 30,000 feet, the engine time constant is 1.6 s and the time delay is 0.6 s. Besides this, the trimmed thrust at this condition is 2789 lbf. The engine increasing and decreasing thrust response is shown in Figure 2. Meanwhile, in the system equipped with the Fast engine response (FastER) system proposed in [30], the time constant and time delay can be reduced by up to 75%.
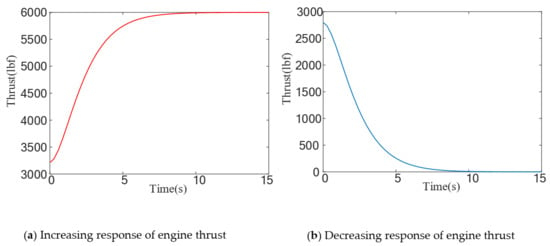
Figure 2.
The engine response under the flight condition of Mach 0.8 and 30,000 feet.
2.4. EHA Performance Analysis
The EHA system, which is a novel technology applied to the MEA, aims at replacing the centralized HA system by a self-contained and localized direct-driving system. EHA plays an important role in today’s modern flight control systems, contributing to reduced leakage, more convenient maintenance and lower overall weight [10].
Based on such advantages, EHA may offer higher survivability in severe conditions such as THL. However, it should be highlighted that the EHA system suffers from lower bandwidth and reduced stiffness compared with the HA system.
Therefore, a performance-degraded model which is described by a second-order delay system should be proposed to express the performance gap between HA and EHA [8].
where is the input of the HA system and is the input of the EHA system.
3. Active Fault-Tolerant Control Strategy
3.1. The Overall Structure
The structure of the designed AFTC method is shown in Figure 3. The baseline controller operates under normal conditions, which are described in a previous work [36,37], and the control is realized by the HA system. When total hydraulic loss occurs, the controller will switch to reconfigurable control law, which is described in [36,37]. Meanwhile, the actuator will switch to the EHA system and launch the engine differential thrust control system, which will operate depending on the situation.
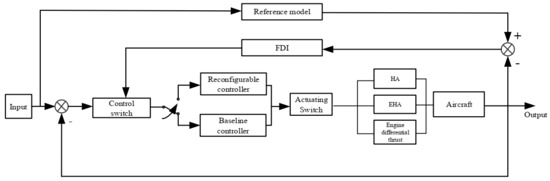
Figure 3.
Structure of active fault-tolerant control strategy.
3.2. The Relationship between Engine Differential Thrust and Rudder Deflection
When the vertical stabilizer is completely damaged, the directional control is assumed to be immediately conducted by the engine differential thrust. Therefore, the rudder input should be mapped onto the engine differential thrust input, as shown in Figure 4.
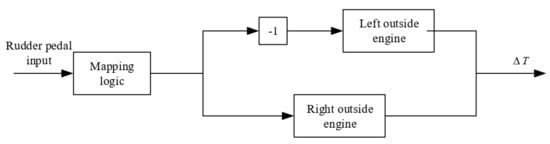
Figure 4.
Conversion from rudder input to differential thrust.
By analyzing the yaw moment generated by rudder deflection and by differential thrust, the relationship between them can be obtained as follows: .
Therefore, the mapping relationship between the rudder input and the differential thrust can be formulated as:
where the right-side of the equation is the mapping factor.
4. Simulation Study and Results Analysis
4.1. Pre-Simulation and State Space Parameters
The AFTC strategy is implemented on the NASA GTM model, and the flight condition and the aircraft parameters are shown in Table 3.

Table 3.
Stability and control derivatives of nominal GTM aircraft.
Thus, we can obtain the detailed state space matrices in normal conditions:
The control input in normal conditions is .
While the aircraft suffers THL from complete loss of the vertical stabilizer, the weight and some related inertia data will change. Such values related to this scenario can be calculated [31] and are shown in Table 4.

Table 4.
Related data for the damaged aircraft.
Thus, the detailed state space matrices for the damages scenario I are:
Considering the configuration of DRAS, the actuation system switches to the EHA system, so the control input is .
The detailed state space matrices for the damages scenario II are
and the control input is .
4.2. Lateral-Directional Simulation through Turning Coordination
In this set of simulations, an attitude control of turning coordination is simulated. In order to maintain the altitude, the attack angle should be adjusted to meet the equilibrium of the gravity and the lift in the vertical direction. Since this can be realized by the full functionally electro-hydrostatic driven elevators after the hydraulic loss, this analysis is not presented here in the interest of space.
Here, the roll command is set as a step signal for 15 degrees and the aircraft is set to turn positive 20 degrees from the present heading direction. The simulation results for normal conditions, damage scenario I and damage scenario II are presented in Figure 5, Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10.
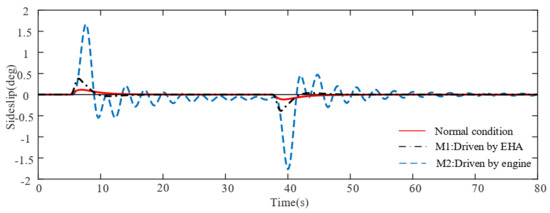
Figure 5.
Sideslip angle response for damage scenario I.
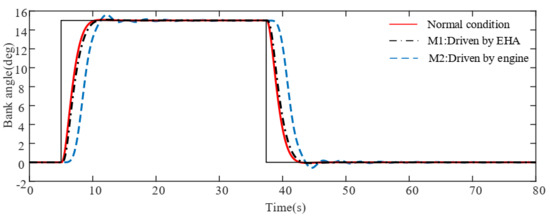
Figure 6.
Bank angle response for damage scenario I.
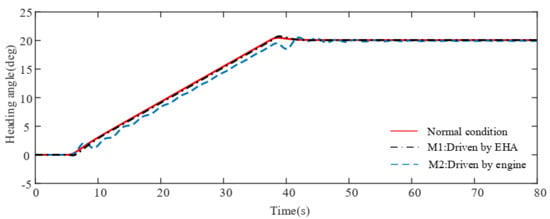
Figure 7.
Heading angle response for damage scenario I.
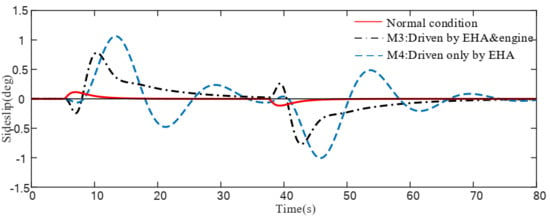
Figure 8.
Sideslip angle response for damage scenario II.
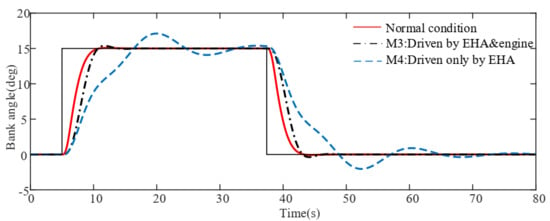
Figure 9.
Bank angle response for damage scenario II.
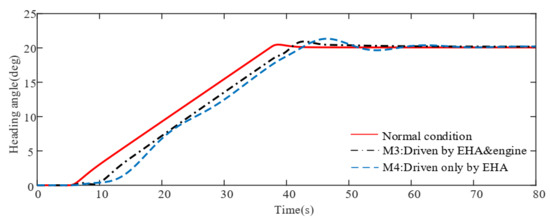
Figure 10.
Heading angle response for damage scenario II.
4.2.1. Damage Scenario I
In normal conditions, we use the baseline control law to track the command. For scenario I, we choose two kinds of control strategies to illustrate the improvement of the proposed control strategy and effectiveness of the proposed configuration:
M1: the proposed AFTC strategy by MRC composed with LQR regulator for scenario I using EHA system;
M2: in comparison, we use the control strategy proposed in [30] for the damaged aircraft driven by engine under total hydraulic loss.
Figure 5, Figure 6 and Figure 7 give the compared responses with sideslip angle, bank angle and heading angle in normal, driven-by-EHA and driven-by-engine conditions for damage scenario I. We give a step signal of 15 degrees at 5 s and give a turning signal of positive 20 degrees. Comparing the simulation results, we can see that the aircraft with THL can be properly controlled by switching the actuation system to the EHA system using the proposed AFTC law. The system performance is very close to normal conditions, with a slightly bigger sideslip and slightly longer raising time. This result demonstrates that there is no necessity of using the engine system in this damage scenario. In Figure 5, we present another simulation result for the traditional aircraft under THL, which is conducted only by engine thrust differential control. It shows a large oscillation in sideslip motion which in turn produces rolling oscillation through the dihedral effect . While it can roughly achieve the flight requirement, it sacrifices the flight quality and requires high proficiency of the crew in a real situation. Such results show the effectiveness of the proposed control law applied on MEA towards scenario I.
4.2.2. Damage Scenario II
In scenario II, we also choose two kinds of control strategies to illustrate the effectiveness of using engine differential thrust:
M3: the AFTC strategy combining the EHA and engine differential thrust system for the damaged aircraft is used in scenario II;
M4: in comparison, the damaged aircraft is driven only by the EHA system in scenario II.
As can be seen from Figure 8, Figure 9 and Figure 10, we still give a step signal of 15 degrees at 5 s and give a turning signal of positive 20 degrees. For the aircraft in scenario II, M3 changes the rudder input into the engine differential thrust input and the system performance is better than the system controlled by M4. With the utilization of differential thrust, the sideslip converges more quickly and the fluctuation amplitude is limited in degrees, which is smaller than degrees when driven only by EHA. Moreover, the bank angle tracks the command well, which has a small overshoot other than oscillation. When driven only by EHA, due to the loss of vertical tail, the damaged aircraft lost its directional stability and its Dutch-roll mode became unstable [31]. Therefore, the sideslip and bank angle are oscillating and struggle to follow the command and the yaw response is seriously delayed for more than 5 s.
This simulation result validates the effectiveness of the proposed AFTC control strategy for scenario II when adding engine differential thrust as the input.
4.3. Lateral-Directional Simulation Analysis of Recovery Ability
Under severe conditions, it is very important for the aircraft to be able to recover from the undesired attitude. Therefore, in this subsection, we discuss the response performance of the damaged aircraft’s recovery ability. Here, we set the perturbation with a bank angle of 5 degrees and sideslip of 5 degrees, and the commands are both set to zero.
4.3.1. Damage Scenario I
As we can see from Figure 11, it is obvious that M1 performs much better than M2. Compared with normal conditions, M1 has a similar performance to normal conditions, while M2 has a very oscillating response, with the sideslip and bank angle amplitude both up to −5 degrees and converging very slowly. This simulation result shows that the proposed control strategy for scenario I has a higher ability to recover from the undesired attitude.
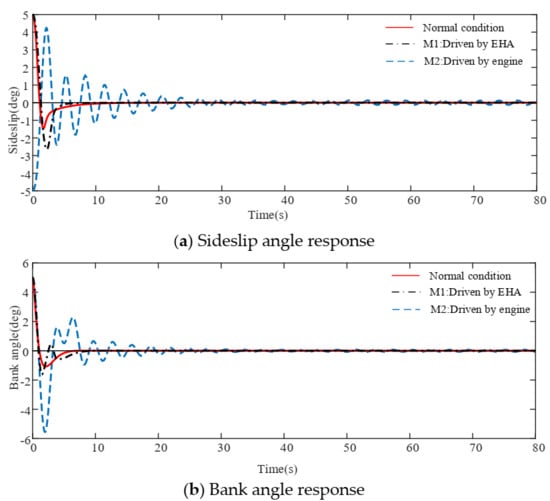
Figure 11.
Recovery performance of damaged aircraft in scenario I under perturbation.
4.3.2. Damage Scenario II
Figure 12 gives the compared dynamic responses with M3 and M4. Comparing M3 and M4, we can find that the performance of M3 is close to normal conditions, while M4 can hardly achieve the required performance as the sideslip converges very slowly and the bank angle diverges at first and the amplitude is up to degrees.
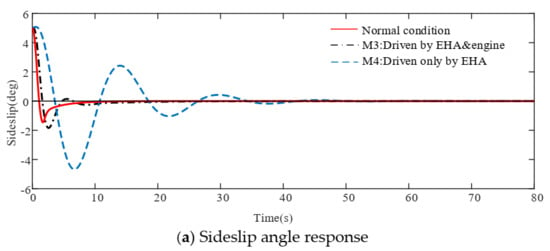
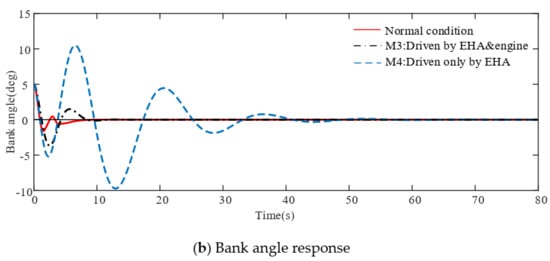
Figure 12.
Recovery performance of damaged aircraft in scenario II under perturbation.
Overall, the proposed AFTC strategy shows its ability to recover the attitude under total hydraulic loss and guarantee the stability of the lateral-directional control system.
4.4. Simulation with Uncertainties, Wind Turbulence and Measurement Noise
This set of simulations analyzes the performance of a damaged aircraft under wind turbulence and measurement noise. Considering the fault detection error, 5% mismatch in coefficients of tangential force and side force and 5% uncertainty in coefficients of roll moment and yaw moment are considered in the vertical tail loss case. The Dryden wind model is used to generate the wind turbulence velocities by filtering white noise. Filter designs representing the effect towards and are as follows:
where , and are the wind scale lengths and , and are the standard deviations for different altitudes and atmospheric conditions. Moreover, measurement noises for sideslip and bank angle are considered with the magnitude rad of white noise.
Figure 13, Figure 14, Figure 15, Figure 16, Figure 17 and Figure 18 show the response of the different configurations of the damaged aircraft in scenario I and II, respectively, under wind gust and uncertainties. When a moderate wind gust is considered in the damaged aircraft simulation, as shown in Figure 13, Figure 14, Figure 15, Figure 16, Figure 17 and Figure 18, the responses in scenario I of M2 are oscillating very strongly, where the amplitude of sideslip oscillation reaches up to degrees and the amplitude of bank angle oscillation reaches up to degrees. Such performance deterioration risks the safety of the aircraft. Compared to this, the M1 shows better performance which is very close to normal conditions. Responses in scenario II show an undesired tracking performance of bank angle by M4, while M3 demonstrates its ability to maintain acceptable performance in damaged scenarios.
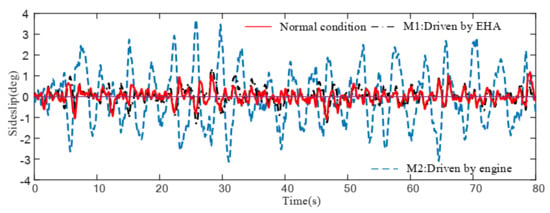
Figure 13.
Sideslip angle response for damage scenario I under uncertainties and turbulences.
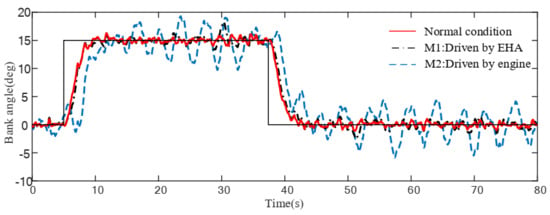
Figure 14.
Bank angle response for damage scenario I under uncertainties and turbulences.
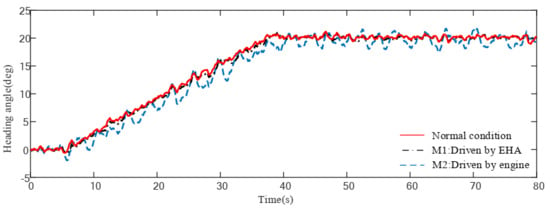
Figure 15.
Heading angle response for damage scenario I under uncertainties and turbulences.
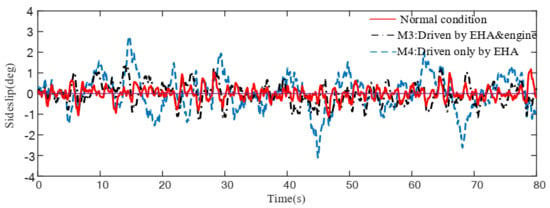
Figure 16.
Sideslip angle response for damage scenario II under uncertainties and turbulences.
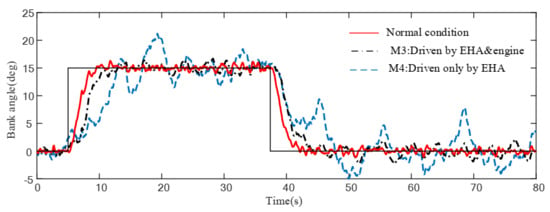
Figure 17.
Bank angle response for damage scenario II under uncertainties and turbulences.
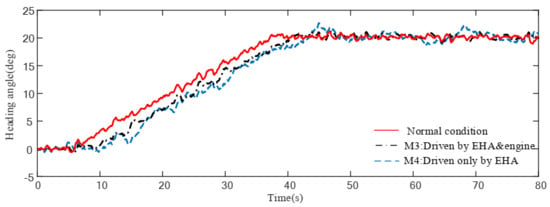
Figure 18.
Heading angle response for damage scenario II under uncertainties and turbulences.
5. Conclusions
Throughout this paper, nominal and damaged lateral-directional MEA models were built, and an AFTC strategy based on the MRC algorithm combined with LQR regulator was proposed for two scenarios of MEA suffering from total hydraulic loss. The damaged aircraft models in two scenarios were developed in this paper and the damaged aircraft tracking and mimicking the behavior of the normal aircraft based on the proposed control law and different aircraft configuration was assessed. The MEA’s DRAS is fully used, and it shows its great capability to deal with extreme situations such as total hydraulic loss. The utilization of differential thrust towards completely vertical tail damage not only helps to stabilize the directional behavior but also provides the momentum to compensate for the effects caused by vertical tail loss. Comparative results applied to the NASA GTM demonstrated that the proposed AFTC strategy can achieve better performance on the MEA.
Author Contributions
X.S. and X.W. designed the active fault-tolerant control strategy. X.S. and Z.Z. (Zhihan Zhou) performed the simulations. Z.Z. (Zhiyuan Zhou) and Z.Z. (Zhihan Zhou) wrote the paper. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Open Fund of Key Laboratory of Civil Aircraft Airworthiness Technology (Grant No. SH20190709-2) and the National Natural Science Foundation of China (Grant No. 51675019).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zhang, Y.; Jiang, J. Bibliographical review on reconfigurable fault-tolerant control systems. Annu. Rev. Control. 2008, 32, 229–252. [Google Scholar] [CrossRef]
- Boeing Commercial Airplanes. Statistical summary of commercial jet airplane accidents, worldwide operations, 1959–2018. Aviat. Saf. 2019, 9, 1–25. [Google Scholar]
- Edwards, C.; Lombaerts, T.; Smaili, H. Fault Tolerant Flight Control; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Hughes, D.; Dornheim, M. DHL/EAT crew lands A300 with no hydraulics after being hit by missile. Aviat. Week Space Technol. 2003, 8, 42. [Google Scholar]
- Van, D.; Bossche, D. The A380 flight control electrohydrostatic actuators, achievements and lessons learnt. In Proceedings of the 25th International Congress of the Aeronautical Sciences, Hamburg, Germany, 3–8 September 2006; pp. 1–8. [Google Scholar]
- Goupil, P. AIRBUS state of the art and practices on FDI and FTC in flight control system. Control Eng. Pract. 2011, 19, 524–539. [Google Scholar] [CrossRef]
- Fu, Y.; Yao, P. Design and working mode analysis of dissimilar redundant actuator system. J. Beijing Univ. Aeronaut. Astronaut. 2012, 38, 432–437. [Google Scholar]
- Shi, C.; Wang, X.; Wang, S.; Wang, J.; Tomovic, M.M. Adaptive decoupling synchronous control of dissimilar redundant actuation system for large civil aircraft. Aerosp. Sci. Technol. 2015, 47, 114–124. [Google Scholar] [CrossRef]
- Rongjie, K.; Zongxia, J.; Shaoping, W.; Lisha, C. Design and Simulation of Electro-hydrostatic Actuator with a Built-in Power Regulator. Chin. J. Aeronaut. 2009, 22, 700–706. [Google Scholar] [CrossRef]
- Naayagi, R. A review of more electric aircraft technology. In Proceedings of the International Conference on Energy Efficient Technologies for Sustainability, Miami, FL, USA, 10–12 April 2013; pp. 750–753. [Google Scholar]
- Shah, G. Aerodynamic Effects and Modeling of Damage to Transport Aircraft. In Proceedings of the AIAA Atmospheric Flight Mechanics Conference and Exhibit, Keystone, CO, USA, 21–24 August 2008; p. 6203. [Google Scholar]
- Crider, L. Control of Commercial Aircraft with Vertical Tail Loss. In Proceedings of the AIAA 4th Aviation Technology, Integration and Operations (ATIO) Forum, Chicago, IL, USA, 20–22 September 2004. [Google Scholar]
- Wang, J.; Wang, S.; Wang, X.; Shi, C.; Tomovic, M. Active fault tolerant control for vertical tail damaged aircraft with dissimilar redundant actuation system. Chin. J. Aeronaut. 2016, 29, 1313–1325. [Google Scholar] [CrossRef]
- Chen, L.; Alwi, H.; Edwards, C. Development and Application of an LPV Fault Tolerant Integral Sliding Mode Control Allocation Scheme for the RECONFIGURE Benchmark Model. IFAC Pap. 2015, 48, 994–999. [Google Scholar] [CrossRef]
- Marcos, A.; Balas, G. Development of Linear-Parameter-Varying Models for Aircraft. J. Guid. Control Dyn. 2004, 27, 218–228. [Google Scholar] [CrossRef]
- Zhang, Y.; Jiang, J. Integrated active fault-tolerant control using IMM approach. IEEE Trans. Aerosp. Electron. Syst. 2001, 37, 1221–1235. [Google Scholar] [CrossRef]
- Ye, D.; Yang, G.-H. Adaptive Fault-Tolerant Tracking Control against Actuator Faults with Application to Flight Control. IEEE Trans. Control Syst. Technol. 2006, 14, 1088–1096. [Google Scholar] [CrossRef]
- Bošković, J.D.; Mehra, R.K. Intelligent Adaptive Control of a Tailless Advanced Fighter Aircraft under Wing Damage. J. Guid. Control Dyn. 2000, 23, 876–884. [Google Scholar] [CrossRef]
- Kim, K.-S.; Lee, K.-J.; Kim, Y. Reconfigurable Flight Control System Design Using Direct Adaptive Method. J. Guid. Control Dyn. 2003, 26, 543–550. [Google Scholar] [CrossRef]
- Sun, D.; Choe, R.; Xargay, E.; Hovakimyan, N. An L1 Adaptive Backup Flight Control Law for Transport Aircraft with Vertical-Tail Damage. AIAA Guid. Navig. Control Conf. 2016, 0633. [Google Scholar] [CrossRef]
- Lombaerts, T.; Looye, G.; Chu, Q.; Mulder, J. Design and simulation of fault tolerant flight control based on a physical approach. Aerosp. Sci. Technol. 2012, 23, 151–171. [Google Scholar] [CrossRef]
- Rong, H.; Sundararajan, N.; Saratchandran, P.; Huang, G.B. Adaptive fuzzy fault-tolerant controller for aircraft autolanding under failures. IEEE Trans. Aerosp. Electron. Syst. 2007, 43, 1586–1603. [Google Scholar] [CrossRef]
- Wang, X.; Wang, S.; Yang, Z.; Zhang, C. Active fault-tolerant control strategy of large civil aircraft under elevator failures. Chin. J. Aeronaut. 2015, 28, 1658–1666. [Google Scholar] [CrossRef][Green Version]
- Liu, Y.; Tao, G.; Joshi, S. Modeling and Model Reference Adaptive Control of Aircraft with Asymmetric Damage. J. Guid. Control Dyn. 2009, 33, 1500–1517. [Google Scholar] [CrossRef]
- Pashilkar, A.; Sundararajan, N.; Saratchandran, P. A fault-tolerant neural aided controller for aircraft auto-landing. Aerosp. Sci. Technol. 2006, 10, 49–61. [Google Scholar] [CrossRef]
- Mora-Camino, F.; Zhong, L. Neural Networks Based Aircraft Fault Tolerant Control. In Proceedings of the AIAA Aviation Technology, Integration and Operations, Indianapolis, IN, USA, 17–19 September 2013; p. 5683. [Google Scholar]
- Napolitano, M.R.; An, Y.; Seanor, B.A. A fault tolerant flight control system for sensor and actuator failures using neural networks. Aircr. Des. 2000, 3, 103–128. [Google Scholar] [CrossRef]
- Bavili, R.; Khosrowjerdi, M.; Vatankhah, R. Active Fault Tolerant Controller Design using Model Predictive Control. Control Eng. Appl. Inform. 2015, 17, 68–76. [Google Scholar]
- Hitachi, Y. Damage-tolerant Control System Design for Propulsion-Controlled Aircraft. Master’s Dissertation, University of Toronto, Toronto, ON, Canada, 2009. [Google Scholar]
- Urnes, J.; Nielsen, Z. Use of Propulsion Commands to Control Directional Stability of a Damaged Transport Aircraft. In Proceedings of the AIAA Infotech Aerospace Conference, Atlanta, GA, USA, 20–22 April 2010. [Google Scholar]
- Lu, L.K.; Turkoglu, K. H ∞ Loop-Shaping Robust Differential Thrust Control Methodology for Lateral/Directional Stability of an Aircraft with a Damaged Vertical Stabilizer. In Proceedings of the AIAA Guidance, Navigation, and Control Conference 2016, San Diego, CA, USA, 4–8 January 2016. [Google Scholar]
- Borello, L.; Villero, G.; Vedova, M.D.L.D. New asymmetry monitoring techniques: Effects on attitude control. Aerosp. Sci. Technol. 2009, 13, 475–487. [Google Scholar] [CrossRef]
- Borello, L.; Villero, G.; Vedova, M.D.D. Flap failure and aircraft controllability: Developments in asymmetry monitoring techniques. J. Mech. Sci. Technol. 2014, 28, 4593–4603. [Google Scholar] [CrossRef]
- De Martin, A.; Autin, S.N.; Socheleau, J.; Dellacasa, A.; Vachtsevanos, G. Feasibility study of a PHM system for electro-hydraulic servoactuators for primary flight controls. In Proceedings of the Annual Conference of the Prognostics and Health Management Society, PHM Society, Philadelphia, PA, USA, 24–27 September 2018. [Google Scholar]
- Gentile, R.; Bruno, D.; Jacazio, G.; Sorli, M.; Marino, F. Electro-hydraulic servoactuators failure identification: Health features extraction through a high-fidelity physical model. Int. J. Mech. Control 2020, 21, 91–100. [Google Scholar]
- Zhou, Z.; Wang, S.; Wang, X. Fault tolerant control strategy based on actuation switch mechanism for more-electric aircraft with vertical tail damage. In Proceedings of the 2017 IEEE International Conference on Mechatronics and Automation, IEEE, Kagawa, Japan, 6–9 August 2017. [Google Scholar]
- Zhou, Z.; Wang, S.; Wang, X.; Wang, J. LQR-MRC Active Fault Tolerant Control for More-Electric Aircraft without Hydraulic Power. In Proceedings of the 2016 IEEE Chinese Guidance, Navigation and Control Conferences (IEEE), Nanjing, China, 12–14 August 2016. [Google Scholar]
- Etkin, B.; Teichmann, T. Dynamics of Flight: Stability and Control; Wiley: New York, NY, USA, 1996; Volume 3. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).