Inter-Particle Effects with a Large Population in Acoustofluidics
Abstract
1. Introduction
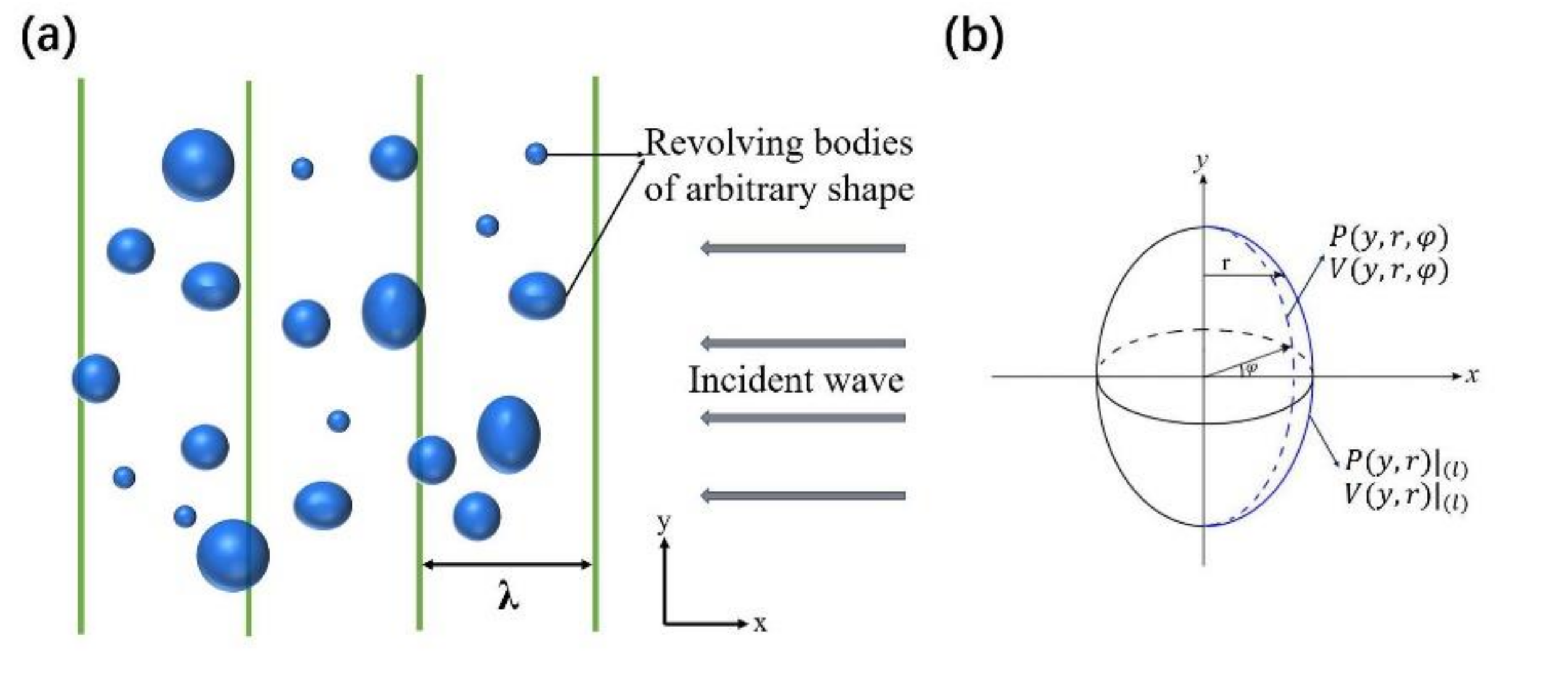
2. Hybrid Algorithm for Massive Particle Interactions
2.1. ARF Acting on Massive Cylindrically Symmetrical Targets
2.2. Force in the y-Direction
2.3. Force in the x-Direction
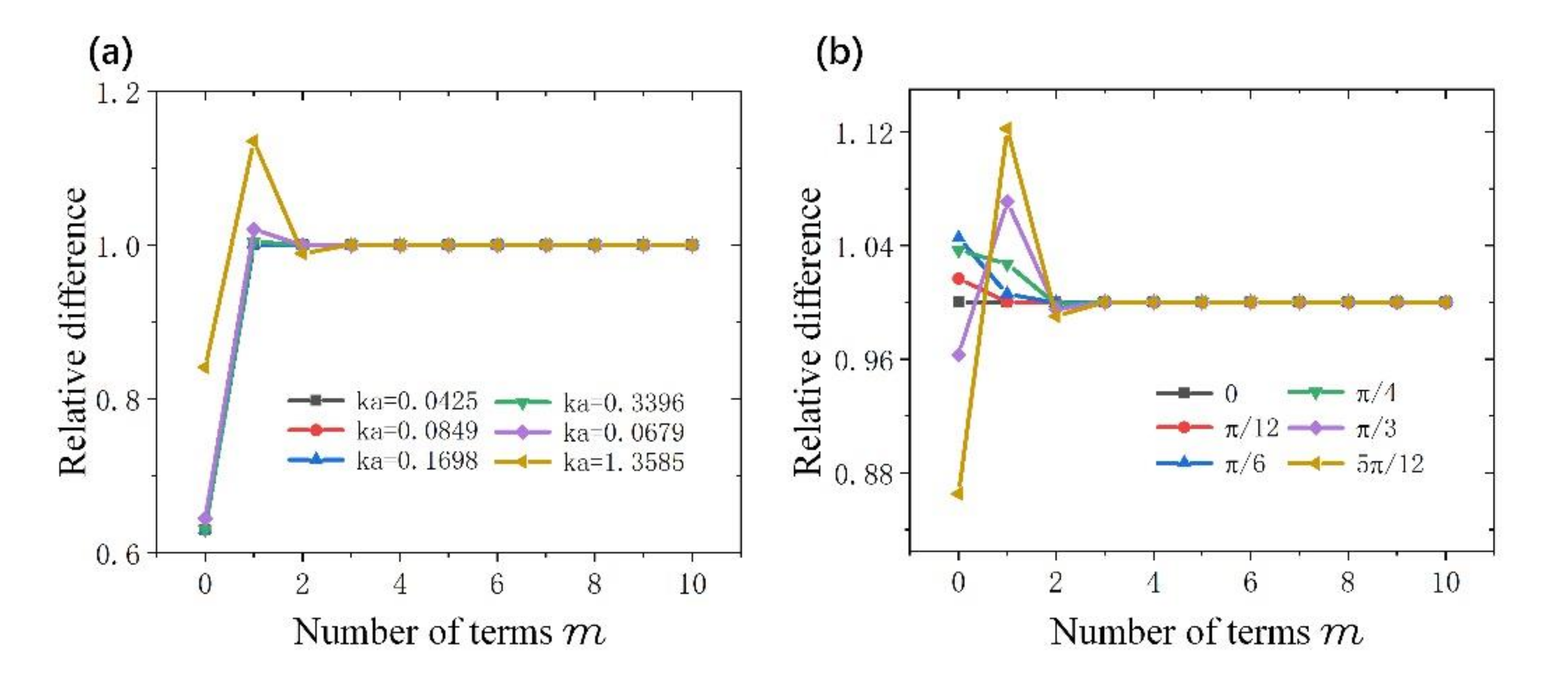
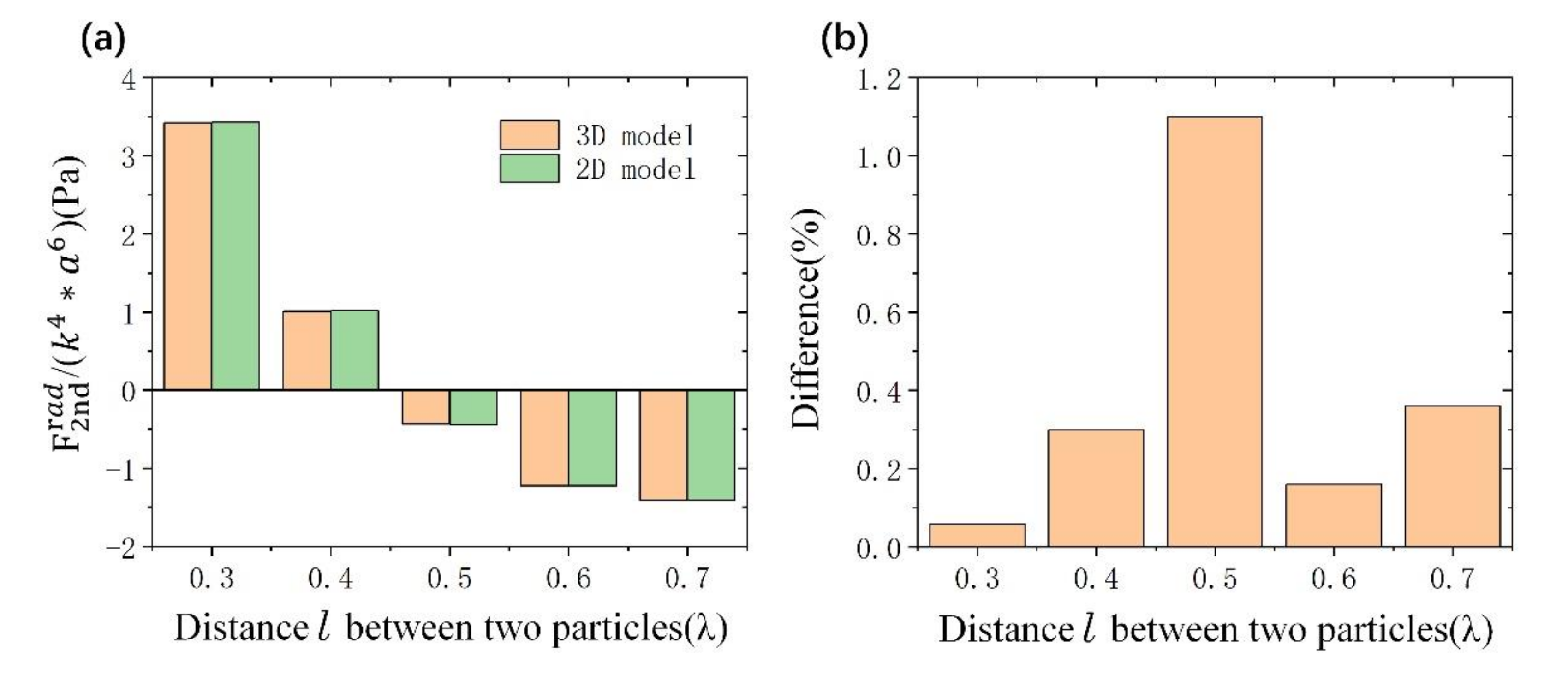
3. Method Validation
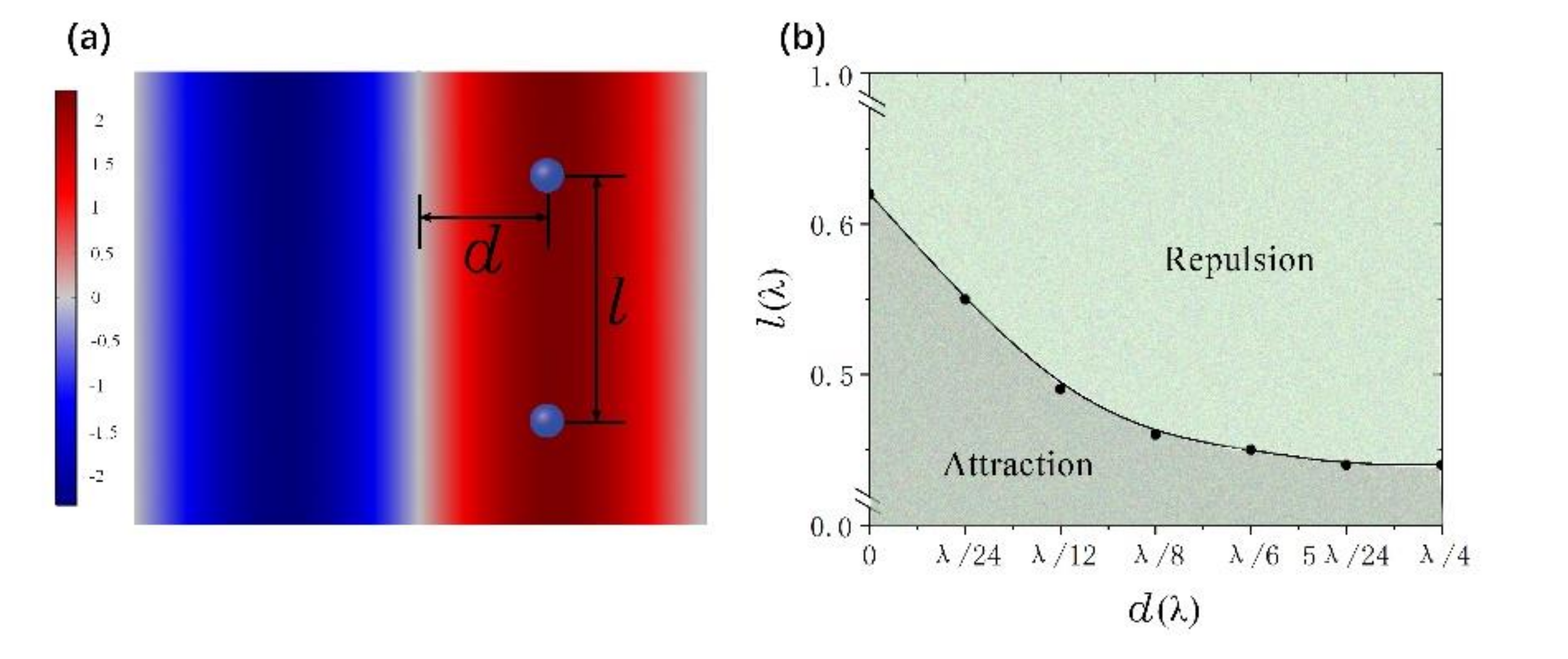
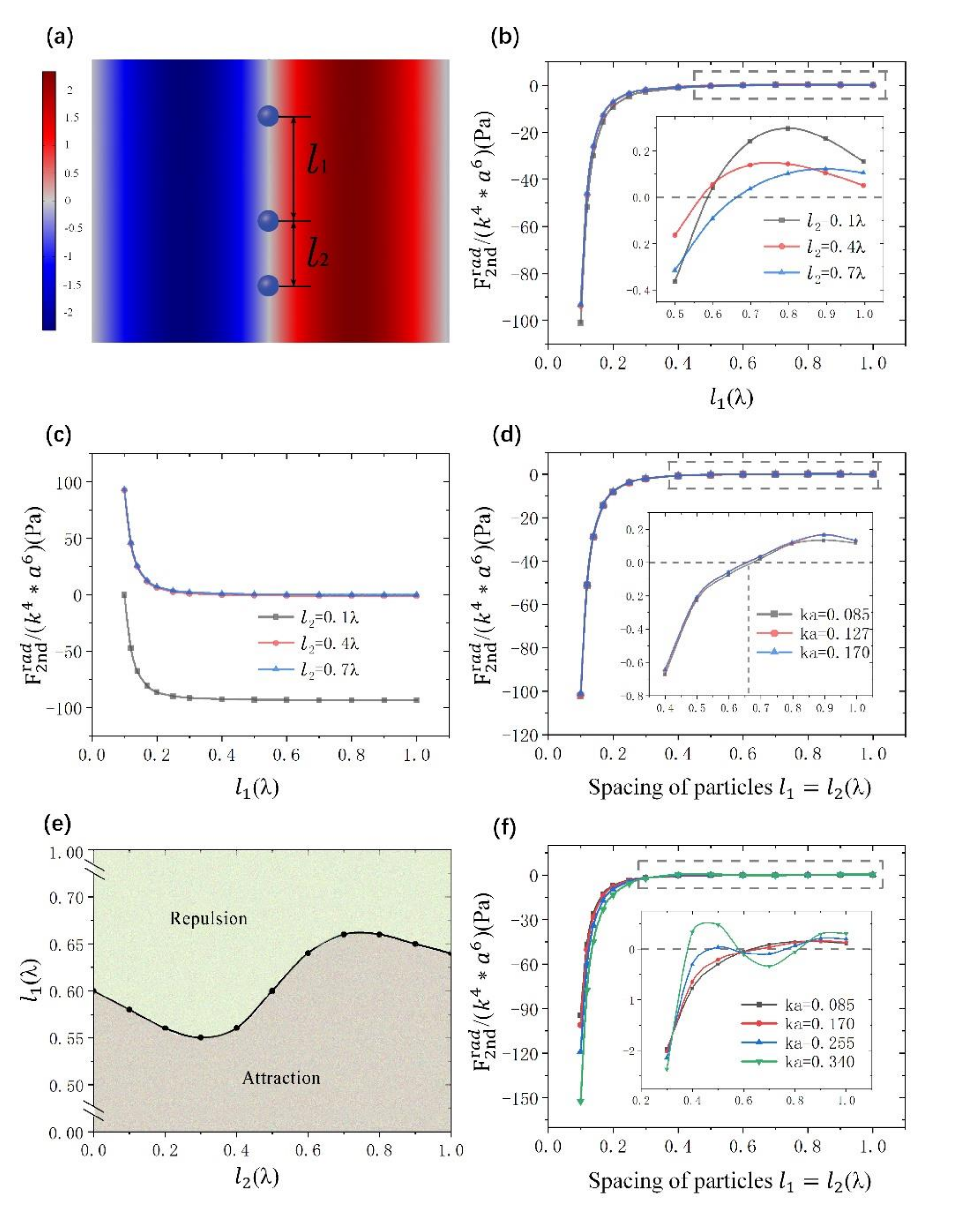
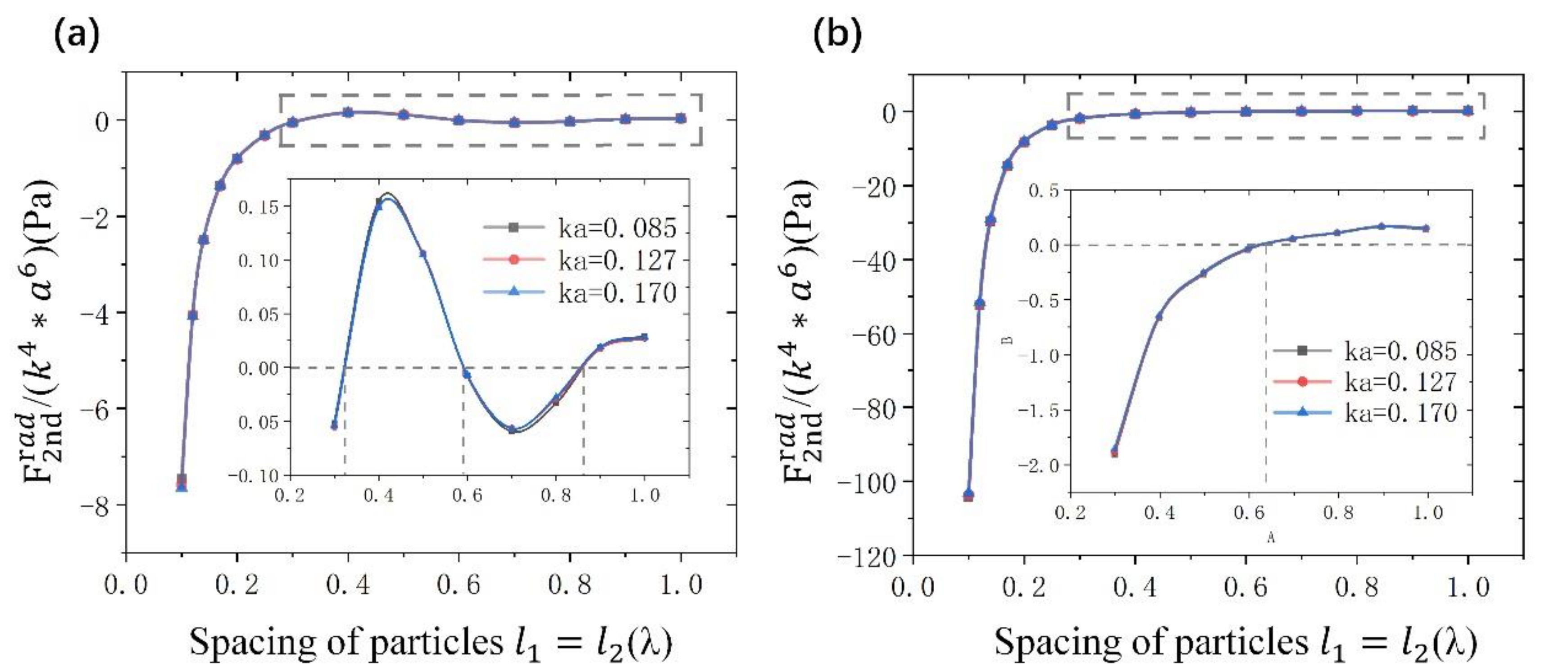
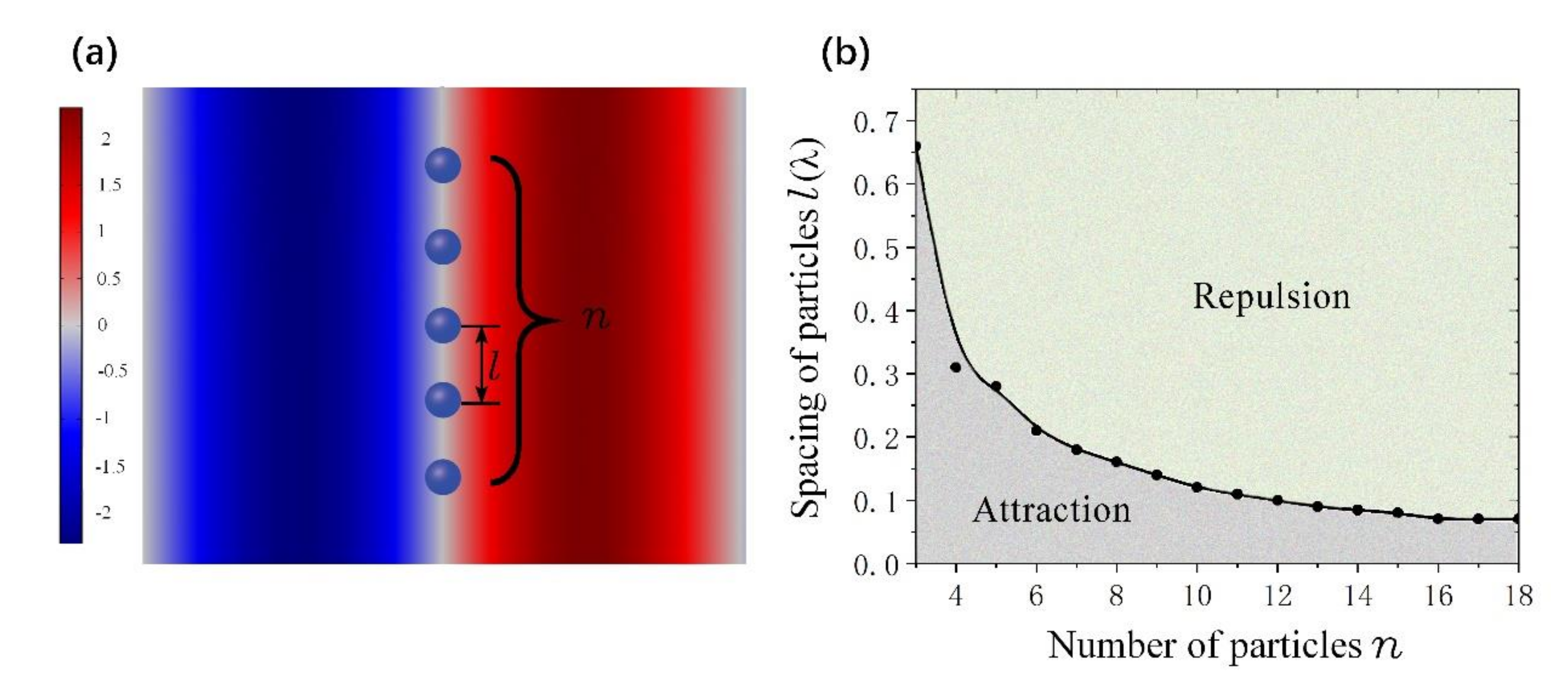
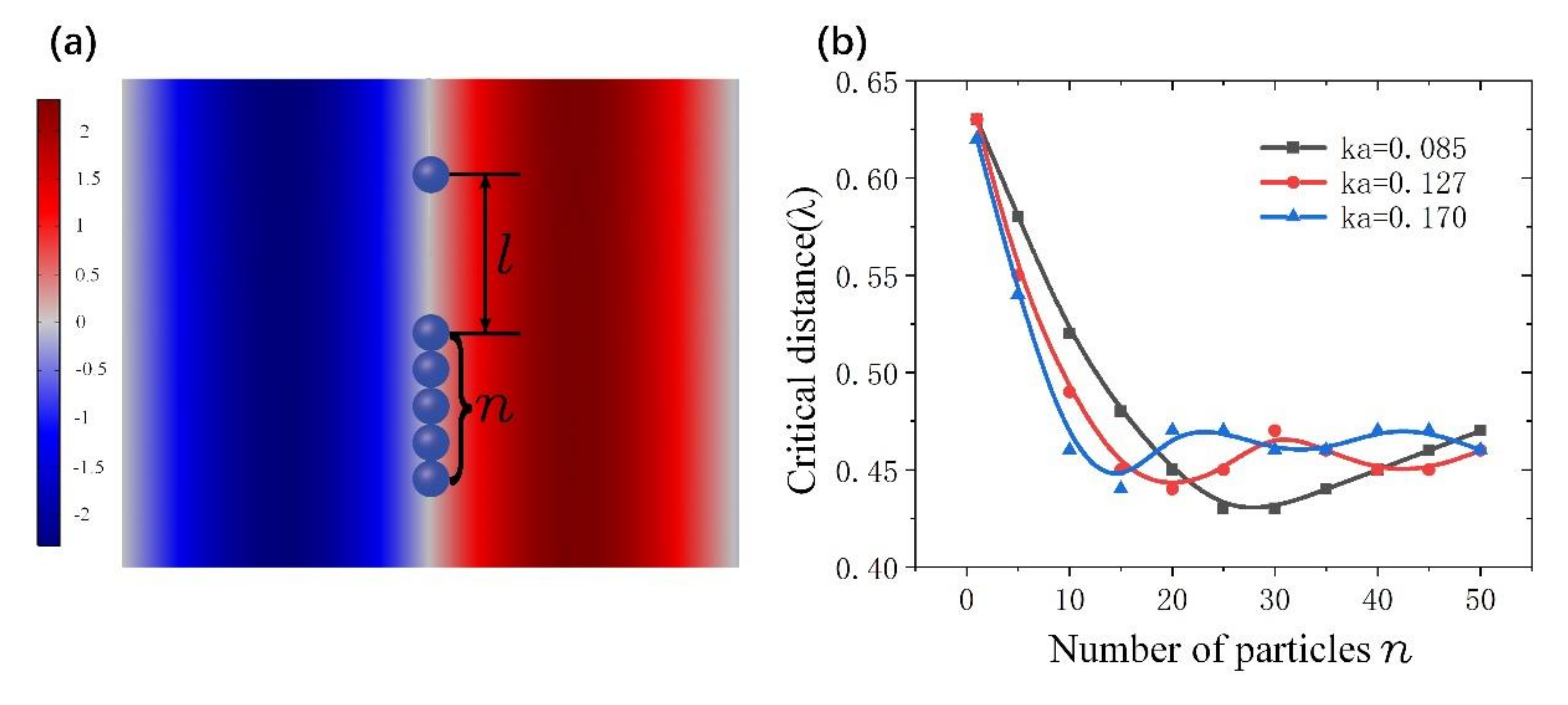
4. Acoustic Interactions Between Massive Particles
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Delsing, P.; Cleland, A.; Schuetz, M.; Knörzer, J.; Giedke, G.; Cirac, J.; Srinivasan, K.; Wu, M.; Coimbatore Balram, K.; Bäuerle, C.; et al. The 2019 surface acoustic waves roadmap. J. Phys. D Appl. Phys. 2019, 52, 353001. [Google Scholar] [CrossRef]
- Destgeer, G.; Sung, H.J. Recent advances in microfluidic actuation and micro-object manipulation via surface acoustic waves. Lab Chip 2015, 15, 2722–2738. [Google Scholar] [CrossRef] [PubMed]
- Ozcelik, A.; Rufo, J.; Guo, F.; Gu, Y.; Li, P.; Lata, J.; Huang, T.J. Acoustic tweezers for the life sciences. Nat. Methods 2018, 15, 1021–1028. [Google Scholar] [CrossRef]
- Winkler, A.; Brünig, R.; Faust, C.; Weser, R.; Schmidt, H. Towards efficient surface acoustic wave (SAW)-based microfluidic actuators. Sens. Actuators A Phys. 2016, 247, 259–268. [Google Scholar] [CrossRef]
- Meng, L.; Cai, F.; Li, F.; Zhou, W.; Niu, L.; Zheng, H. Acoustic tweezers. J. Phys. D Appl. Phys. 2019, 52, 273001. [Google Scholar] [CrossRef]
- Connacher, W.; Zhang, N.; Huang, A.; Mei, J.; Zhang, S.; Gopesh, T.; Friend, J. Micro/nano acoustofluidics: Materials, phenomena, design, devices, and applications. Lab Chip 2018, 18, 1952–1996. [Google Scholar] [CrossRef] [PubMed]
- Marx, V. Biophysics: Using sound to move cells. Nat. Methods 2015, 12, 41–44. [Google Scholar] [CrossRef]
- Ding, X.; Peng, Z.; Lin, S.-C.; Geri, M.; Li, S.; Li, P.; Chen, Y.; Dao, M.; Suresh, S.; Huang, T. Cell separation using tilted-angle standing surface acoustic waves. Proc. Natl. Acad. Sci. USA 2014, 111, 12992–12997. [Google Scholar] [CrossRef]
- Ding, X.; Lin, S.-C.; Kiraly, B.; Yue, H.; Li, S.; Chiang, I.K.; Shi, J.; Benkovic, S.; Huang, T. On-chip manipulation of single microparticles, cells, and organisms using surface acoustic waves. Proc. Natl. Acad. Sci. USA 2012, 109, 11105–11109. [Google Scholar] [CrossRef]
- Wang, K.; Zhou, W.; Lin, Z.; Cai, F.; Li, F.; Wu, J.; Meng, L.; Niu, L.; Zheng, H. Sorting of tumour cells in a microfluidic device by multi-stage surface acoustic waves. Sens. Actuators B Chem. 2018, 258, 1174–1183. [Google Scholar] [CrossRef]
- Li, L.; Jia, K.; Wu, E.; Zhu, Y.; Yang, K. Design of acoustofluidic device for localized trapping. Biomicrofluidics 2020, 14, 034107. [Google Scholar] [CrossRef] [PubMed]
- Li, S.; Ma, F.; Bachman, H.; Cameron, C.E.; Zeng, X.; Huang, T.J. Acoustofluidic bacteria separation. J. Micromech. Microeng. 2017, 27, 015031. [Google Scholar] [CrossRef] [PubMed]
- Joshi, S.G.; Zaitsev, B.D.; Kuznetsova, I.E. Miniature high efficiency transducers for use in ultrasonic flow meters. J. Appl. Phys. 2009, 105, 034501. [Google Scholar] [CrossRef]
- Yeo, L.Y.; Friend, J.R. Surface Acoustic Wave Microfluidics. Annu. Rev. Fluid Mech 2014, 46, 379–406. [Google Scholar] [CrossRef]
- Satya, K.; Martin, W.; Birgitta, J.; Gaio, P.; Dmitry, G. Investigation of polymer-shelled microbubble motions in acoustophoresis. Ultrasonics 2016, 70, 275–283. [Google Scholar]
- Chen, Y.; Nawaz, A.A.; Zhao, Y.; Huang, P.-H.; McCoy, J.P.; Levine, S.J.; Wang, L.; Huang, T.J. Standing surface acoustic wave (SSAW)-based microfluidic cytometer. Lab Chip 2014, 14, 916–923. [Google Scholar] [CrossRef]
- Gao, L.; Shields, C.W.; Johnson, L.M.; Graves, S.W.; Yellen, B.B.; Lopez, G.P. Two-dimensional spatial manipulation of microparticles in continuous flows in acoustofluidic systems. Biomicrofluidics 2015, 9, 014105. [Google Scholar] [CrossRef]
- Jia, K.; Yang, K.; Mei, D. Quantitative trap and long range transportation of micro-particles by using phase controllable acoustic wave. J. Appl. Phys. 2012, 112, 054908. [Google Scholar] [CrossRef]
- Yoon, C.; Kang, B.; Lee, C.; Kim, H.H.; Shung, K. Multi-particle trapping and manipulation by a high-frequency array transducer. Appl. Phys. Lett. 2014, 105, 214103. [Google Scholar] [CrossRef]
- King, L.V. On the Acoustic Radiation Pressure on Spheres. Proc. R. Soc. A Math. Phys. Eng. Sci. 1934, 147, 212–240. [Google Scholar]
- Hasegawa, T.; Yosioka, K. Acoustic-Radiation Force on a Solid Elastic Sphere. J. Acoust. Soc. Am. 1969, 46, 1139–1143. [Google Scholar] [CrossRef]
- Doinikov, A.A. Acoustic Radiation Pressure on a Rigid Sphere in a Viscous Fluid. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1994, 447, 447–466. [Google Scholar]
- Doinikov, A.A. Acoustic radiation pressure on a compressible sphere in a viscous fluid. J. Fluid Mech. 1994, 267, 1–21. [Google Scholar] [CrossRef]
- Settnes, M.; Bruus, H. Forces acting on a small particle in an acoustical field in a viscous fluid. Phys. Rev. E 2012, 85, 016327. [Google Scholar] [CrossRef] [PubMed]
- Haydock, D. Lattice Boltzmann simulations of the time-averaged forces on a cylinder in a sound field. J. Phys. A 2005, 38, 3265–3277. [Google Scholar] [CrossRef]
- Wang, J.; Dual, J. Numerical simulations for the time-averaged acoustic forces acting on rigid cylinders in ideal and viscous fluids. J. Phys. A Math. Theor. 2009, 42, 285502. [Google Scholar] [CrossRef]
- Cai, F.; Meng, L.; Jiang, C.; Pan, Y.; Zheng, H. Computation of the acoustic radiation force using the finite-difference time-domain method. J. Acoust. Soc. Am. 2010, 128, 1617–1622. [Google Scholar] [CrossRef]
- Glynne-Jones, P.; Mishra, P.P.; Boltryk, R.J.; Hill, M. Efficient finite element modeling of radiation forces on elastic particles of arbitrary size and geometry. J. Acoust. Soc. Am. 2013, 133, 1885–1893. [Google Scholar] [CrossRef]
- Baasch, T.; Dual, J. Acoustofluidic particle dynamics: Beyond the Rayleigh limit. J. Acoust. Soc. Am. 2018, 143, 509–519. [Google Scholar] [CrossRef]
- Mitri, F.G. Acoustic radiation force on a cylindrical particle near a planar rigid boundary. J. Phys. Commun. 2018, 2, 045019. [Google Scholar] [CrossRef]
- Mitri, F.G. Acoustic radiation force on oblate and prolate spheroids in Bessel beams. Wave Motion 2015, 57, 231–238. [Google Scholar] [CrossRef]
- Mitri, F.G. Acoustic radiation force and spin torque on a viscoelastic cylinder in a quasi-Gaussian cylindrically-focused beam with arbitrary incidence in a non-viscous fluid. Wave Motion 2016, 66, 31–44. [Google Scholar] [CrossRef]
- Leão-Neto, J.P.; Lopes, J.H.; Silva, G.T. Core-Shell Particles that are Unresponsive to Acoustic Radiation Force. Phys. Rev. Appl. 2016, 6, 024025. [Google Scholar] [CrossRef]
- Jerome, T.S.; Ilinskii, Y.A.; Zabolotskaya, E.A.; Hamilton, M.F. Born approximation of acoustic radiation force and torque on soft objects of arbitrary shape. J. Acoust. Soc. Am. 2019, 145, 36–44. [Google Scholar] [CrossRef]
- Shirgaonkar, I.Z.; Lanthier, S.; Kamen, A. Acoustic cell filter: A proven cell retention technology for perfusion of animal cell cultures. Biotechnol. Adv. 2004, 22, 433–444. [Google Scholar] [CrossRef]
- Mohapatra, A.; Sepehrirahnama, S.; Lim, K. Experimental measurement of interparticle acoustic radiation force in the Rayleigh limit. Phys. Rev. E 2016, 93, 023307. [Google Scholar] [CrossRef]
- Hoque, S.Z.; Sen, A.K. Interparticle acoustic radiation force between a pair of spherical particles in a liquid exposed to a standing bulk acoustic wave. Phys. Fluids 2020, 32, 072004. [Google Scholar] [CrossRef]
- Mettin, R.; Akhatov, I.S.; Parlitz, U.; Ohl, C.; Lauterborn, W. Bjerknes forces between small cavitation bubbles in a strong acoustic field. Phys. Rev. E 1997, 56, 2924–2931. [Google Scholar] [CrossRef]
- Crum, L. Bjerknes Forces on Bubbles in a Stationary Sound Field. J. Acoust. Soc. Am. 1975, 57, 1363–1370. [Google Scholar] [CrossRef]
- Crum, L.A.; Eller, A.I. The Motion of Bubbles in a Stationary Sound Field. J. Acoust. Soc. Am. 1969, 48, 181–189. [Google Scholar] [CrossRef]
- Embleton, T. Mutual Interaction between Two Spheres in a Plane Sound Field. J. Acoust. Soc. Am. 1962, 34, 1714–1720. [Google Scholar] [CrossRef]
- Zhuk, A.P. Hydrodynamic interaction of two spherical particles due to sound waves propagating perpendicularly to the center line. Sov. Appl. Mech. 1985, 21, 307–312. [Google Scholar] [CrossRef]
- Zhuk, A.P. Hydrodynamic interaction of two spherical particles from sound waves. Int. Appl. Mech. 1984, 20, 875–880. [Google Scholar] [CrossRef]
- Doinikov, A.A. Bjerknes forces between two bubbles in a viscous fluid. J. Acoust. Soc. Am. 1999, 106, 3305–3312. [Google Scholar] [CrossRef]
- Doinikov, A.A. Acoustic radiation interparticle forces in a compressible fluid. J. Fluid Mech. 2001, 444, 1–21. [Google Scholar] [CrossRef]
- Doinikov, A.A.; Zavtrak, S.T. Radiation forces between two bubbles in a compressible liquid. J. Acoust. Soc. Am. 1997, 102, 1424–1431. [Google Scholar] [CrossRef]
- Doinikov, A.A.; Zavtrak, S.T. On the mutual interaction of two gas bubbles in a sound field. Phys. Fluids 1995, 7, 1923–1930. [Google Scholar] [CrossRef]
- Doinikov, A.A. Mutual interaction between a bubble and a drop in a sound field. J. Acoust. Soc. Am. 1996, 99, 3373–3379. [Google Scholar] [CrossRef]
- Doinikov, A.A.; Zavtrak, S.T. Interaction force between a bubble and a solid particle in a sound field. Ultrasonics 1996, 34, 807–815. [Google Scholar] [CrossRef]
- Zheng, X.; Apfel, R.E. Acoustic interaction forces between two fluid spheres in an acoustic field. J. Acoust. Soc. Am. 1993, 97, 2218–2226. [Google Scholar] [CrossRef]
- Silva, G.; Bruus, H. Acoustic interaction forces between small particles in an ideal fluid. Phys. Rev. E 2014, 90, 063007. [Google Scholar] [CrossRef]
- Wu, J.H.; Liu, A.Q.; Chen, H.; Chen, T.N. Multiple scattering of a spherical acoustic wave from fluid spheres. J. Sound Vib. 2006, 290, 17–33. [Google Scholar] [CrossRef]
- Sepehrirahnama, S. Numerical study of interparticle radiation force acting on rigid spheres in a standing wave. J. Acoust. Soc. Am. 2015, 137, 2614–2622. [Google Scholar] [CrossRef]
- Feng, K.; Wang, C.; Mo, R.; Hu, J.; Li, S. Interaction between particles and bubbles driven by ultrasound: Acoustic radiation force on an elastic particle immersed in the ideal fluid near a bubble. Ultrason. Sonochemistry 2020, 67, 105166. [Google Scholar] [CrossRef]
- Simon, G.; Andrade, M.; Desmulliez, M.; Riehle, M.; Bernassau, A. Numerical Determination of the Secondary Acoustic Radiation Force on a Small Sphere in a Plane Standing Wave Field. Micromachines 2019, 10, 431. [Google Scholar] [CrossRef]
- Jia, K.; Li, L.; Wang, Y.; Yang, K.; Chen, J. Interplays between elastic particles in an ultrasonic standing wave. Appl. Phys. Express 2020, 13, 027005. [Google Scholar] [CrossRef]
- Watson, G.N. A Treatise on the Theory of Bessel Functions; Cambridge University Press: London, UK, 1922. [Google Scholar]
| Name | Value |
|---|---|
| fluid density | 998 kg/m3 |
| fluid speed of sound | 1480 m/s |
| particle density | 2000 kg/m3 |
| particle speed of sound | 6559 m/s |
| frequency | 1 MHz |
| ka | Analytical | 3D FEM | 2D FEM | Difference (3D/2D) | Difference (Analytical/2D) |
|---|---|---|---|---|---|
| 0.0425 | 7.550 | 7.525 | 7.541 | 0.21% | 0.12% |
| 0.0849 | 7.550 | 7.503 | 7.515 | 0.13% | 0.47% |
| 0.170 | 7.550 | 7.408 | 7.412 | 0.054% | 1.9% |
| 0.340 | 7.550 | 7.013 | 7.016 | 0.043% | 7.6% |
| Φ | 0 | π/9 | 2π/9 | π/3 | 4π/9 | |
|---|---|---|---|---|---|---|
| 3D | 5.480 | 5.503 | 5.558 | 5.618 | 5.660 | |
| 2D | 5.480 | 5.503 | 5.558 | 5.620 | 5.660 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jia, K.; Wang, Y.; Li, L.; Chen, J.; Yang, K. Inter-Particle Effects with a Large Population in Acoustofluidics. Actuators 2020, 9, 101. https://doi.org/10.3390/act9040101
Jia K, Wang Y, Li L, Chen J, Yang K. Inter-Particle Effects with a Large Population in Acoustofluidics. Actuators. 2020; 9(4):101. https://doi.org/10.3390/act9040101
Chicago/Turabian StyleJia, Kun, Yulong Wang, Liqiang Li, Jian Chen, and Keji Yang. 2020. "Inter-Particle Effects with a Large Population in Acoustofluidics" Actuators 9, no. 4: 101. https://doi.org/10.3390/act9040101
APA StyleJia, K., Wang, Y., Li, L., Chen, J., & Yang, K. (2020). Inter-Particle Effects with a Large Population in Acoustofluidics. Actuators, 9(4), 101. https://doi.org/10.3390/act9040101




