Active Mass Damper for Reducing Wind and Earthquake Vibrations of a Long-Period Bridge
Abstract
1. Introduction
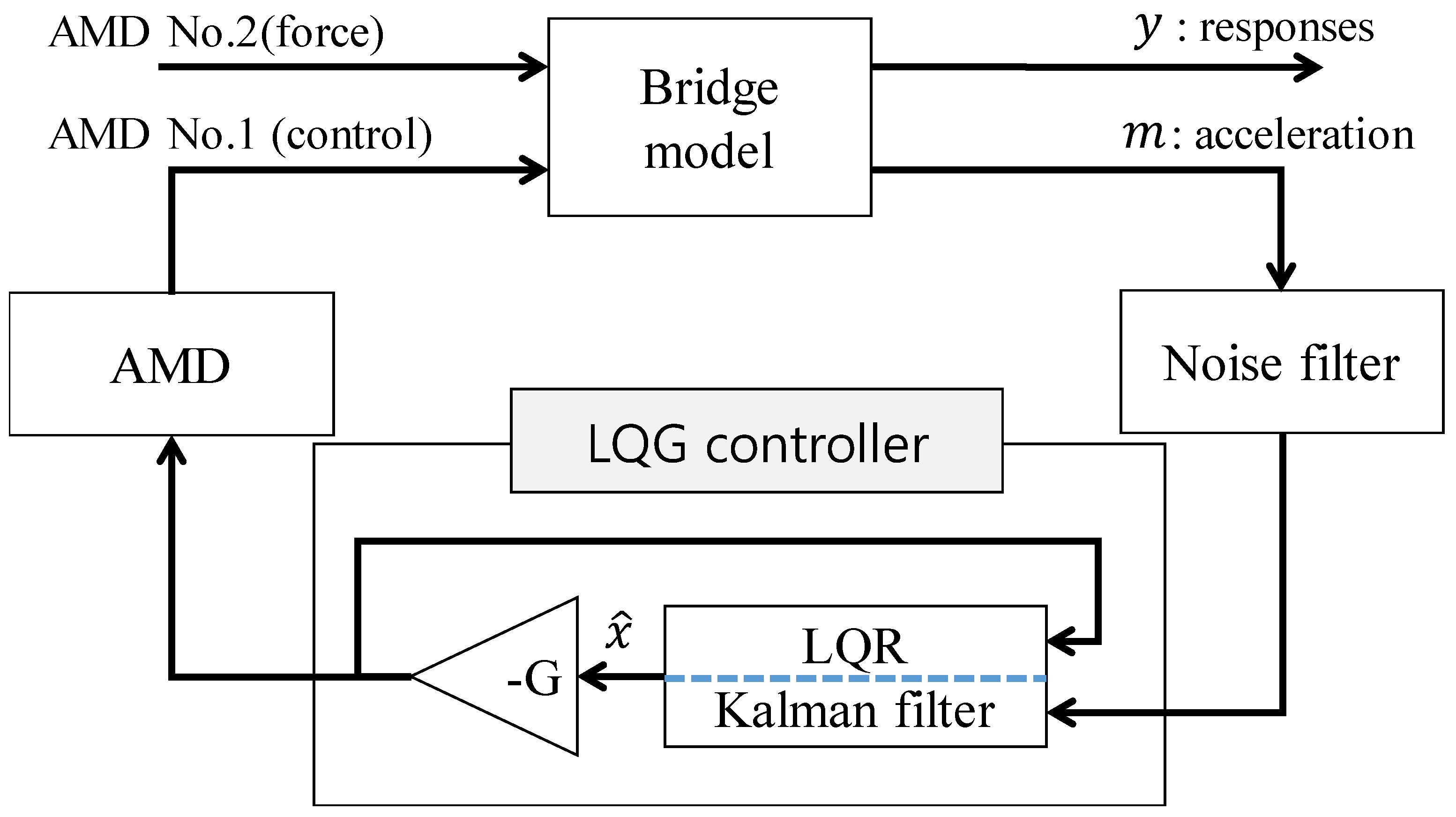
2. LQG Control Algorithm
2.1. LQR Controller
2.2. Kalman Filter
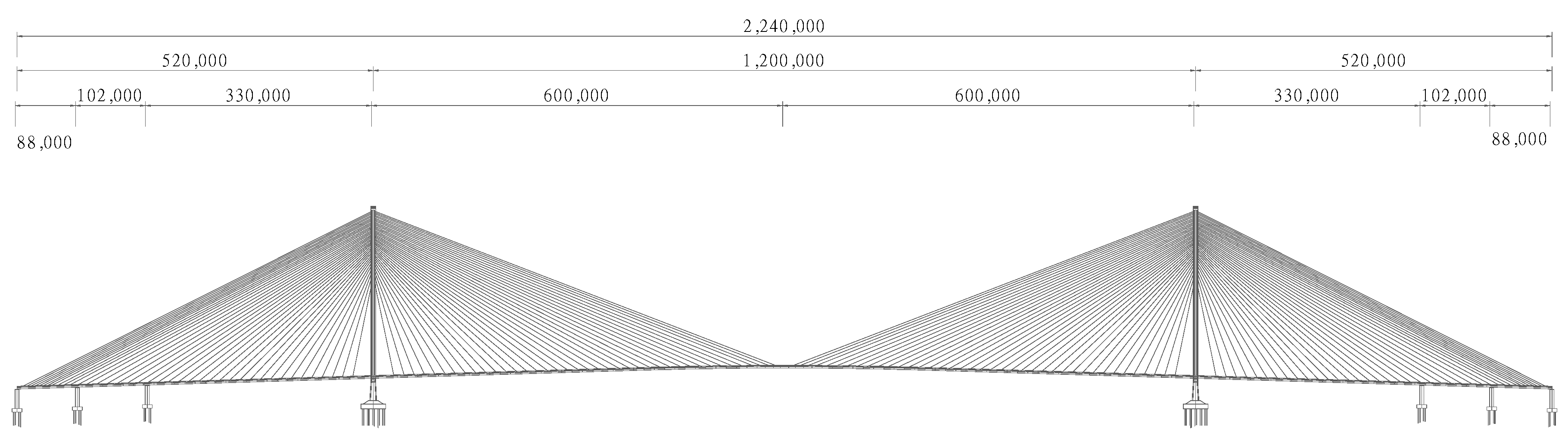
3. Target Bridge and Scaled-Down Experimental Model
3.1. Cable-Stayed Bridge Model
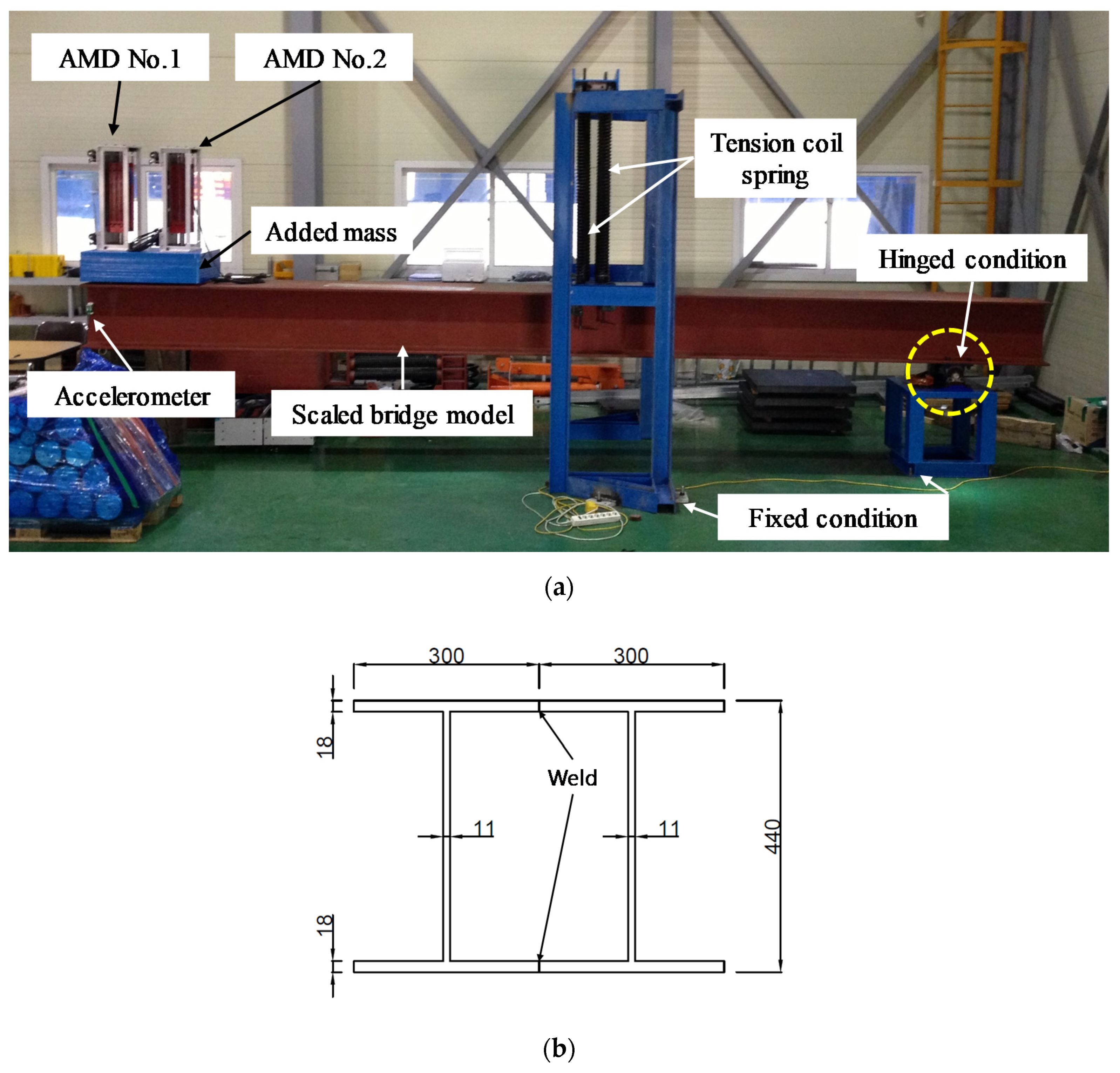
3.2. Scaled-Down Experimental Model
3.3. AMD Design and Fabrication
4. Verification of the Control Performance
4.1. Definition of the Equation of Motion for the Entire System
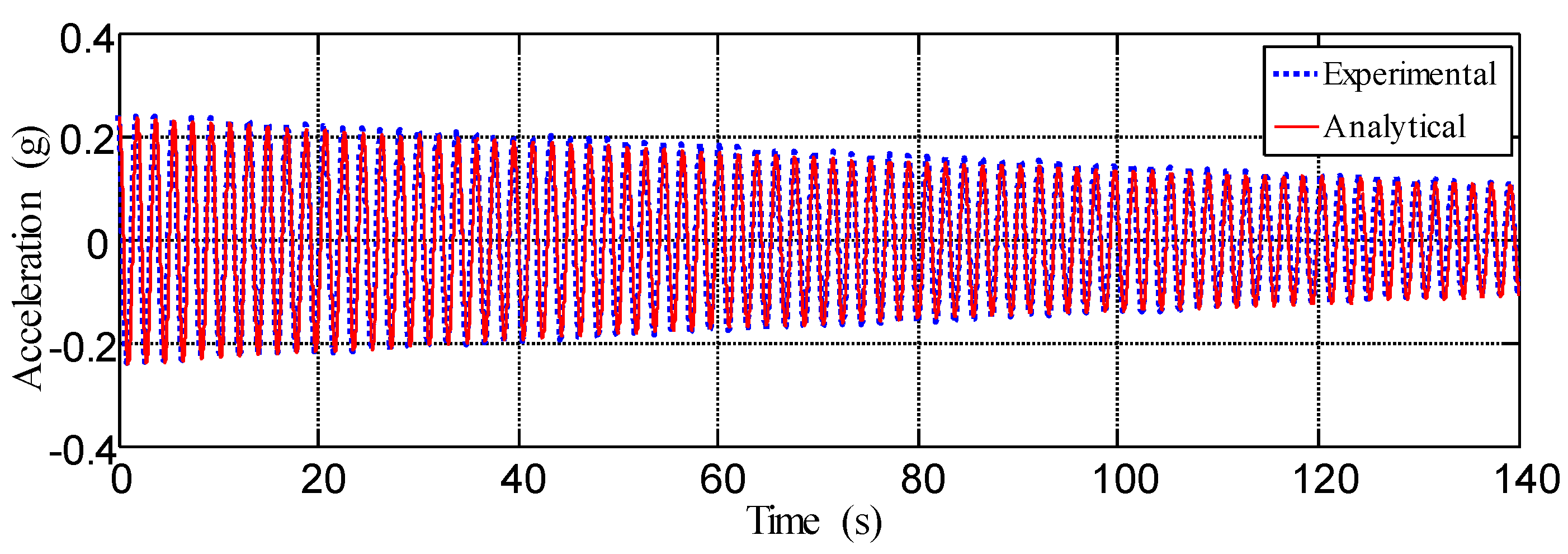
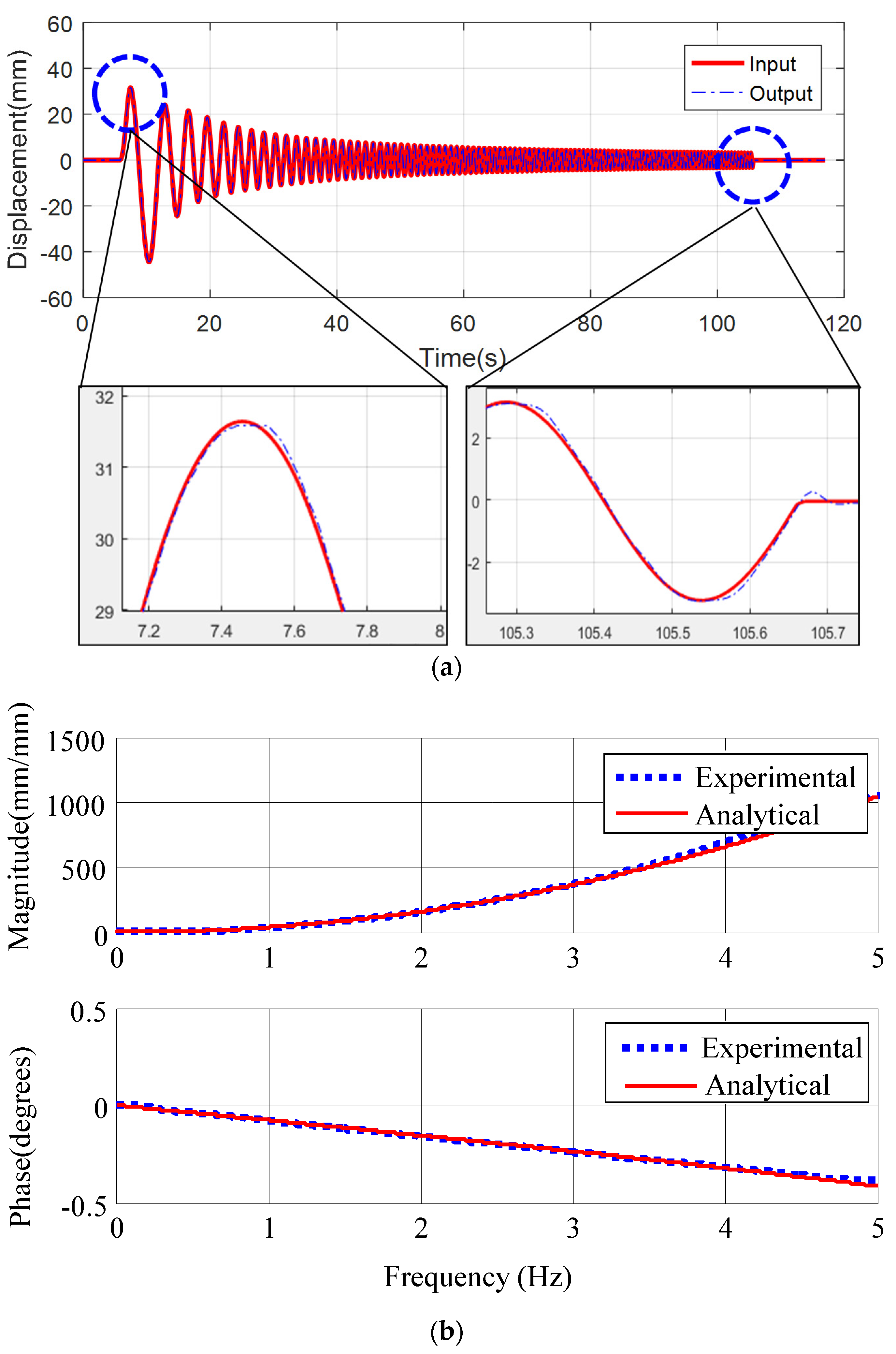
4.2. System Identification
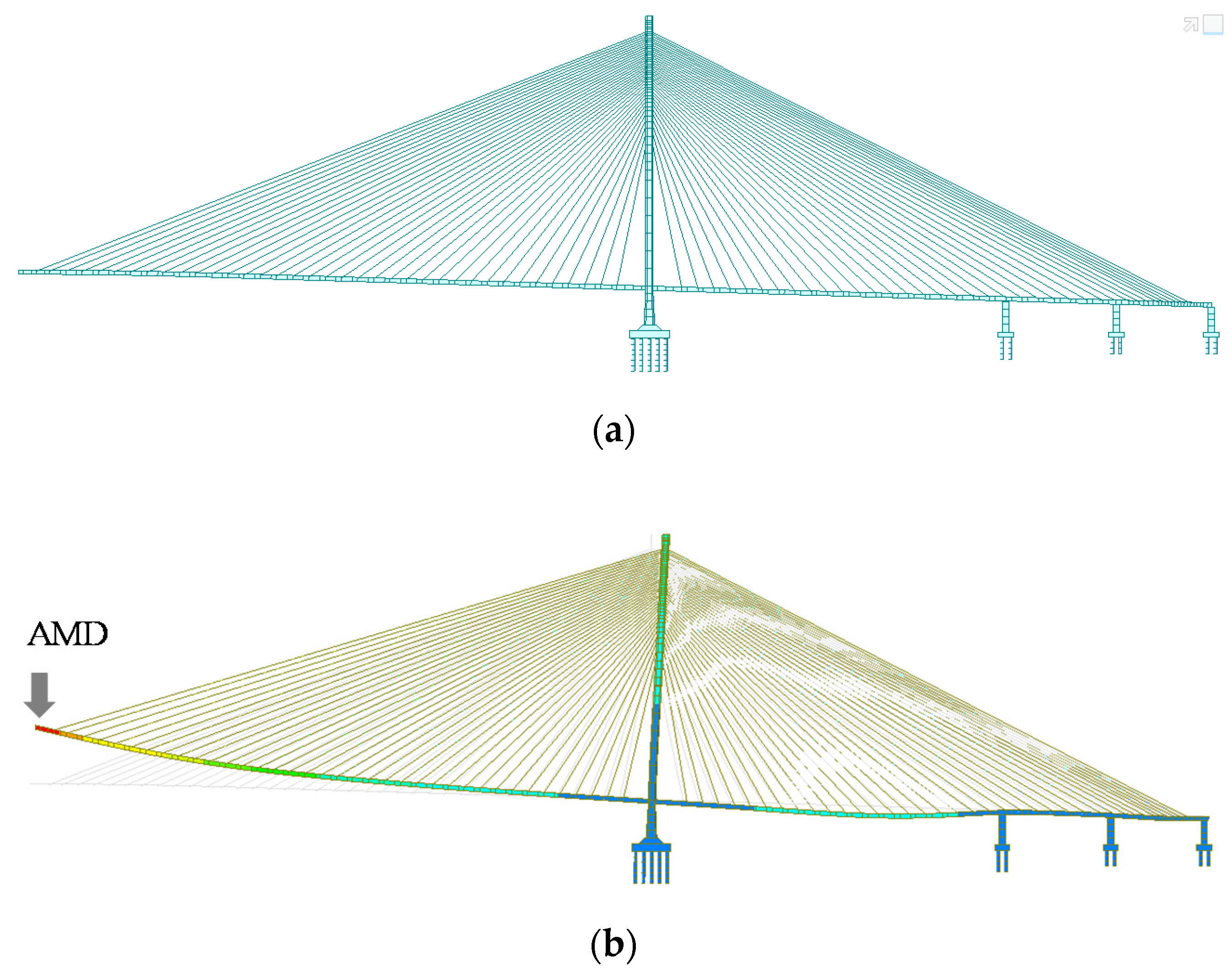
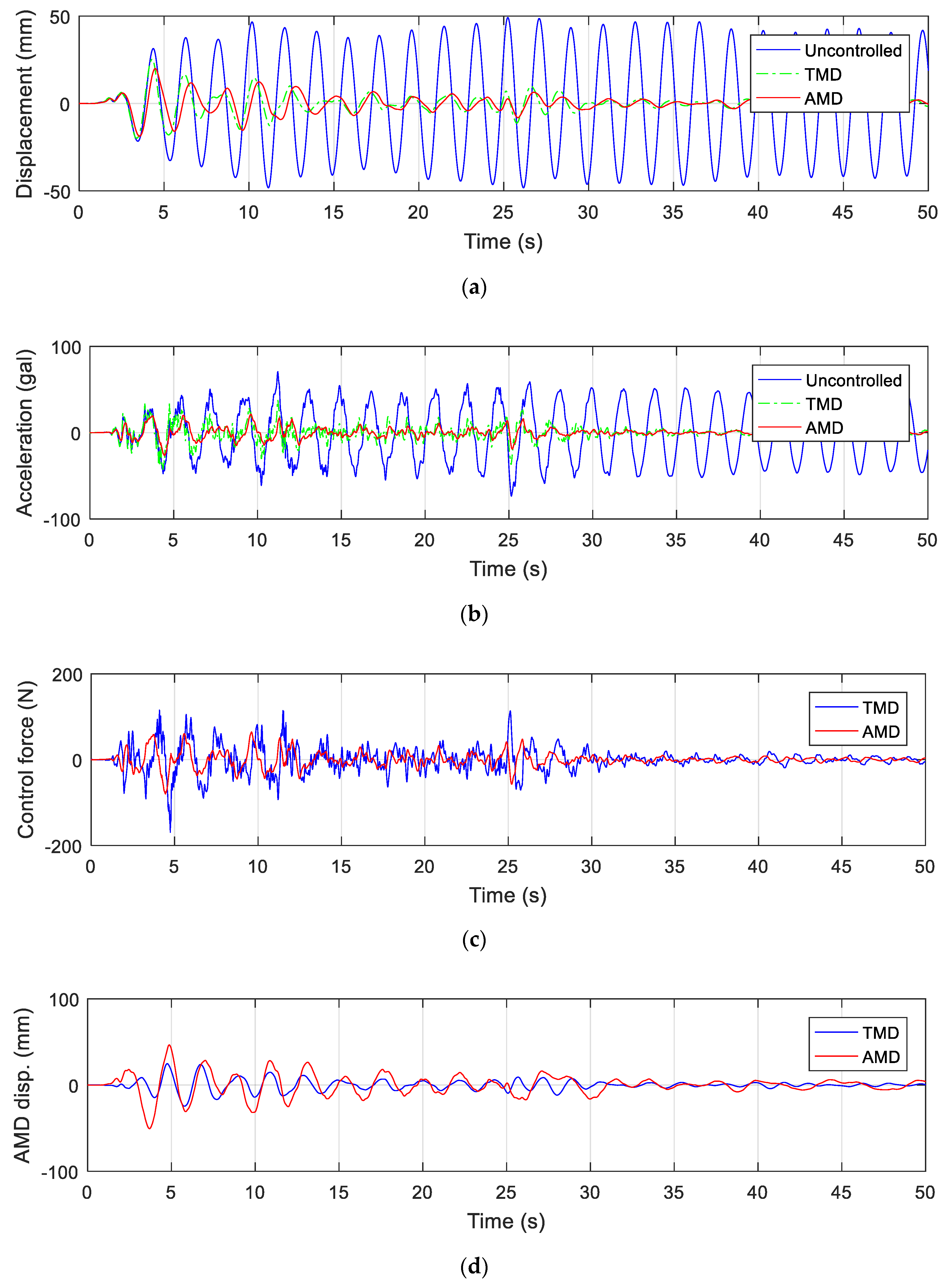
4.3. Verification of the AMD Design and Control Performance
5. Conclusions
- The basic theory of LQG control, which combines an LQR and Kalman filter, was used to control the AMD.
- A scaled-down bridge model and AMD were fabricated, and the analytical responses of the bridge model and AMD agreed with the experimental results.
- When the bridge model was subjected to free vibration and a harmonic load, the proposed AMD rapidly reduced the vibration and significantly increased the damping ratio of the bridge from 0.17% to 9.2%.
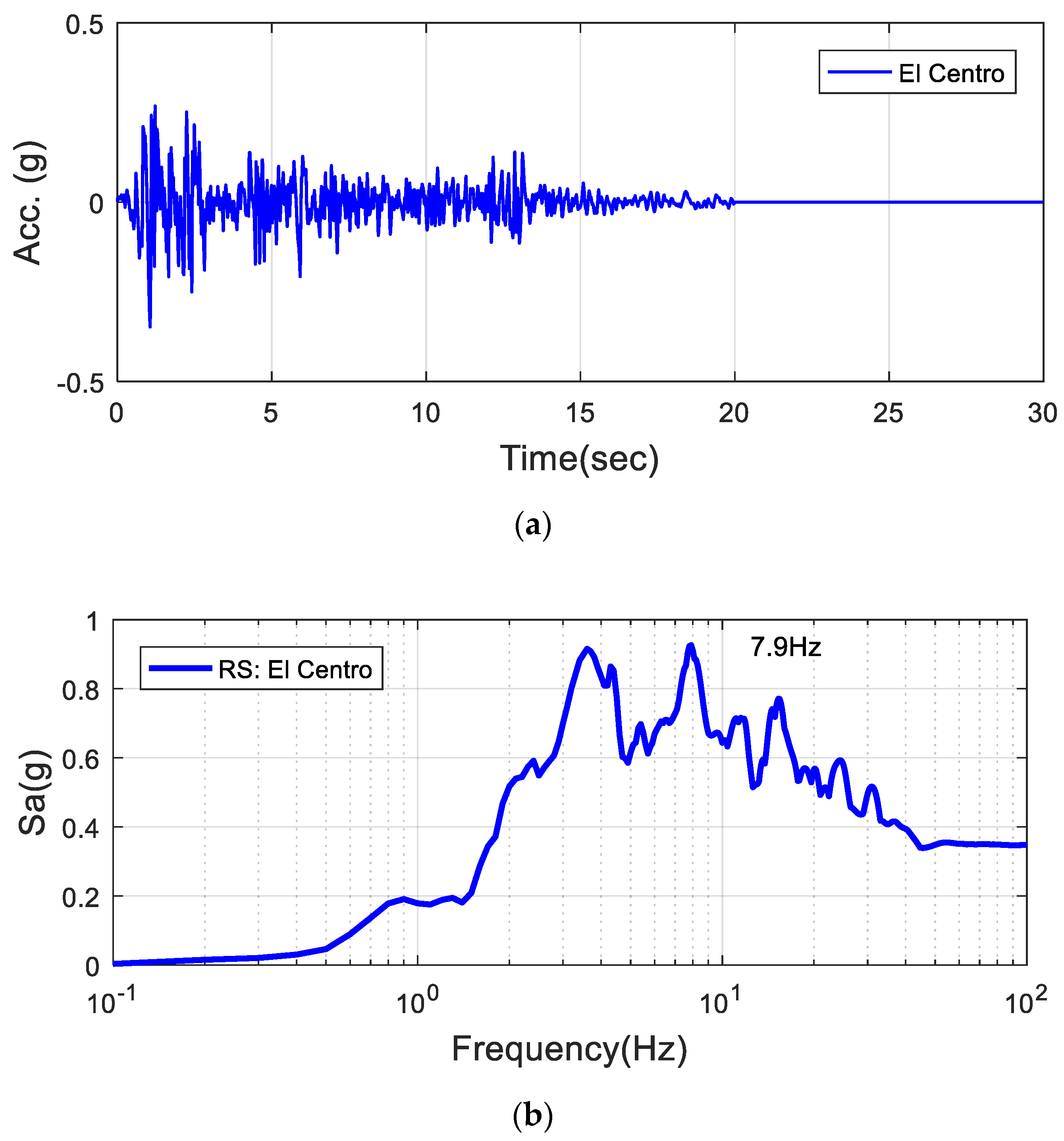
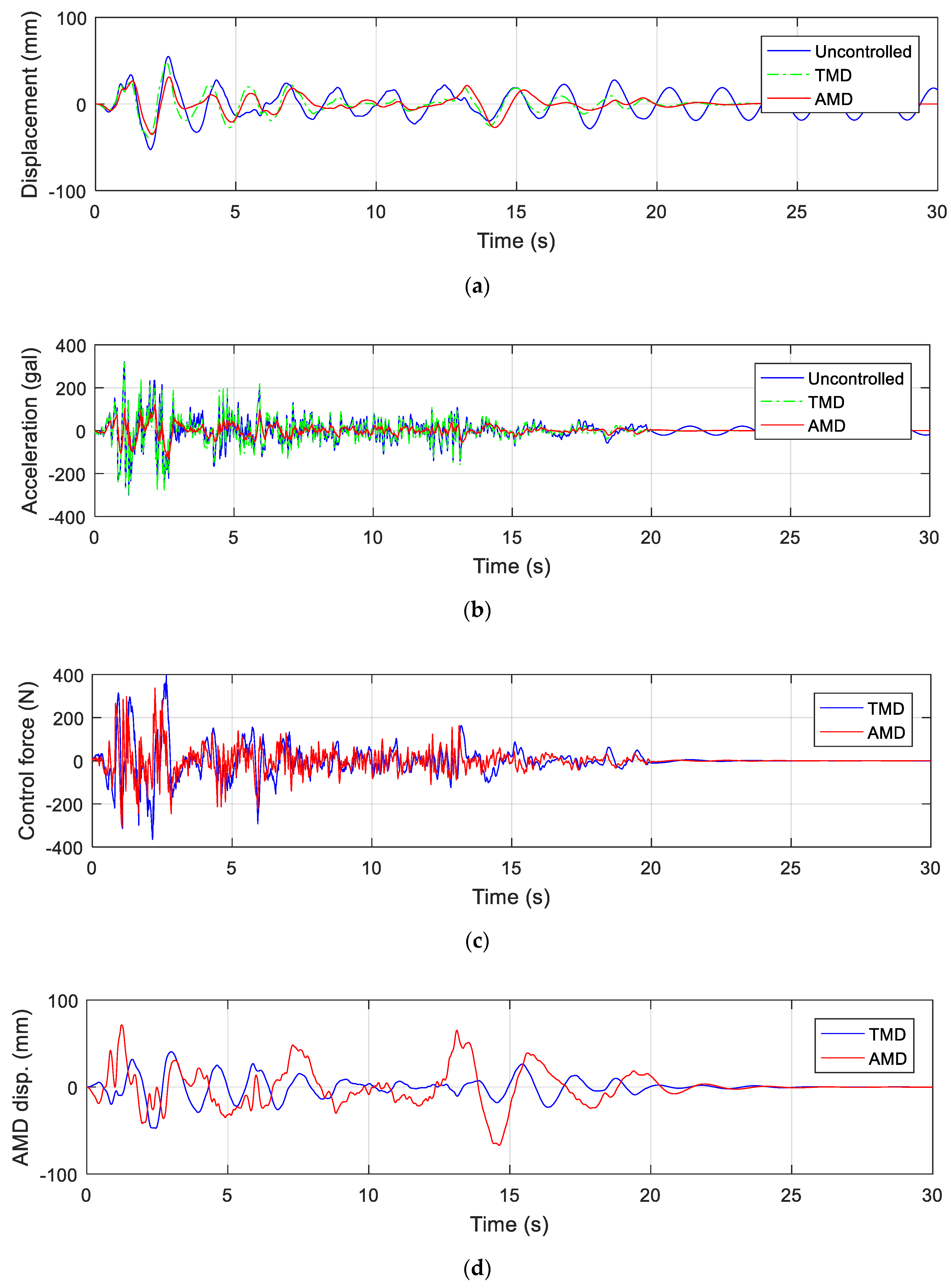
- Numerical analysis showed that the proposed AMD reduced the acceleration of the bridge model by about 60% during the El Centro earthquake and the Imperial valley-02 earthquake;
- Moreover, in the case of the TMD, the vibration control performance was shown only for a special earthquake; however, the proposed AMD showed excellent vibration control performance for both earthquakes.
Funding
Acknowledgments
Conflicts of Interest
References
- Haque, M.N.; Katsuchi, H.; Yamada, H.; Nishio, M. Investigation of edge fairing shaping effects on aerodynamic response of long-span bridge deck by unsteady RANS. Arch. Civ. Mech. Eng. 2016, 16, 888–900. [Google Scholar] [CrossRef]
- Omenzetter, P.; Wilde, K.; Fujino, Y. Suppression of wind-induced instabilities of a long span bridge by a passive deck-flaps control system: Part I: Formulation. J. Wind Eng. Ind. Aerodyn. 2000, 87, 61–79. [Google Scholar] [CrossRef]
- Den Hartog, J.P. Mechanical Vibrations, 4th ed.; McGraw-Hill: New York, NY, USA, 1956. [Google Scholar]
- Chang, S.; Sun, W.; Cho, S.G.; Kim, D. Vibration control of nuclear power plant piping system using Stockbridge damper under earthquakes. Sci. Technol. Nucl. Install. 2016, 2016, 5014093. [Google Scholar] [CrossRef]
- Rahman, M.S.; Chang, S.; Kim, D. Multiple wall dampers for multi-mode vibration control of building structures under earthquake excitation. Struct. Eng. Mech. 2017, 63, 537–549. [Google Scholar]
- Cho, S.G.; Chang, S.; Sung, D. Application of tuned mass damper to mitigation of the seismic responses of electrical equipment in nuclear power plants. Energies 2020, 13, 427. [Google Scholar] [CrossRef]
- Meng, F.; Wan, J.; Xia, Y.; Ma, Y.; Yu, J. A multi-degree of freedom tuned mass damper design for vibration mitigation of a suspension bridge. Appl. Sci. 2020, 10, 457. [Google Scholar] [CrossRef]
- Gu, M.; Xiang, H.F.; Chen, A.R. A practical method of passive TMD for suppressing wind-induced vertical buffeting of long-span cable-stayed bridges and its application. J. Wind Eng. Ind. Aerodyn. 1994, 51, 203–213. [Google Scholar] [CrossRef]
- Xing, C.; Wang, H.; Li, A.; Xu, Y. Study on wind-induced vibration control of a long-span cable-stayed bridge using TMD-type counterweight. J. Bridge Eng. 2014, 19, 141–148. [Google Scholar] [CrossRef]
- Domaneschi, M.; Martinelli, L.; Po, E. Control of wind buffeting vibrations in a suspension bridge by TMD: Hybridization and robustness issues. Comput. Struct. 2015, 155, 3–17. [Google Scholar] [CrossRef]
- Wang, W.; Wang, X.; Hua, X.; Song, G.; Chen, Z. Vibration control of vortex-induced vibrations of a bridge deck by a singleside pounding tuned mass damper. Eng. Struct. 2018, 173, 61–75. [Google Scholar] [CrossRef]
- Pourzeynali, S.; Bahar, A.; Pourzeynali, S. Vertical vibration control of suspension bridges subjected to earthquake by semi-active MR dampers. Sci. Iran. 2017, 24, 439–451. [Google Scholar] [CrossRef][Green Version]
- Fiebig, W. Reduction of vibrations of pedestrian bridges using tuned mass dampers (TMD). Arch. Acoust. 2010, 34, 165–174. [Google Scholar] [CrossRef][Green Version]
- Debnath, N.; Duttab, A.; Deb, S.K. Multi-modal passive-vibration control of bridges under general loading-condition. Procedia Eng. 2016, 144, 264–273. [Google Scholar] [CrossRef]
- Yin, X.; Song, G.; Liu, Y. Vibration suppression of wind/traffic/bridge coupled system using multiple pounding tuned mass dampers. Sensors 2019, 19, 1133. [Google Scholar] [CrossRef] [PubMed]
- Chen, Z.; Fang, H.; Han, Z.; Sun, S. Influence of bridge-based designed TMD on running trains. J. Vib. Control 2019, 25, 182–193. [Google Scholar] [CrossRef]
- Nugroho, W.O.; Widarda, D.R.; Dwyana, O.H. Analysis study the used of tuned mass damper (TMD) on an existing train bridge due to high speed train with moving mass load approach. MATEC Web Conf. 2019, 258, 05005. [Google Scholar] [CrossRef][Green Version]
- El Ouni, M.H.; Kahla, N.B.; Preumont, A. Numerical and experimental dynamic analysis and control of a cable stayed bridge under parametric excitation. Eng. Struct. 2012, 45, 244–256. [Google Scholar] [CrossRef]
- El Ouni, M.H.; Kahla, N.B. Numerical study of the active tendon control of a cable-stayed bridge in a construction phase. Shock. Vib. 2014, 2014, 937541. [Google Scholar] [CrossRef]
- Crusells-Girona, M.; Aparicio, A.C. Active control implementation in cable-stayed bridges for quasi-static loading patterns. Eng. Struct. 2016, 118, 394–406. [Google Scholar] [CrossRef]
- Soneji, B.B.; Jangid, R.S. Seismic control of cable-stayed bridge using semi-active hybrid system. Bridge Struct. 2006, 2, 45–60. [Google Scholar] [CrossRef]
- Ok, S.Y.; Kim, D.S.; Park, K.S.; Koh, H.M. Semi-active fuzzy control of cable-stayed bridges using magneto-rheological dampers. Eng. Struct. 2007, 29, 776–788. [Google Scholar] [CrossRef]
- Soto, M.G.; Adeli, H. Semi-active vibration control of smart isolated highway bridge structures using replicator dynamics. Eng. Struct. 2019, 186, 536–552. [Google Scholar] [CrossRef]
- Soares, R.W.; Barroso, L.R.; Al-Fahdawi, O.A.S. Response attenuation of cable-stayed bridge subjected to central US earthquakes using neuro-fuzzy and simple adaptive control. Eng. Struct. 2000, 203, 109874. [Google Scholar] [CrossRef]
- Scheller, J.; Starossek, U. A Versatile Active Mass Damper for Structural Vibration Control. In Proceedings of the 8th International Conference on Structural Dynamics, Leuven, Belgium, 4–6 July 2011. [Google Scholar]
- Zhang, Y.; Lia, L.; Zhang, X. Switch control of twin rotor damper for bridge vibration mitigation under different excitations. Procedia Eng. 2017, 199, 1707–1712. [Google Scholar] [CrossRef]
- Goorts, K.; Ashasi-Sorkhabi, A.; Narasimhan, S. Deployable active mass dampers for vibration mitigation in lightweight bridges. J. Struct. Eng. 2017, 143, 04017159. [Google Scholar] [CrossRef]
- Setio, H.D.; Gunawan, A.S. Numerical study of active mass damper application on cable-stayed bridge structure using artificial neural network algorithm. Int. J. Civ. Environ. Eng. 2017, 17, 1–17. [Google Scholar]
- Lu, L.T.; Chiang, W.L.; Tang, J.P. LQG/LTR control methodology in active structural control. J. Eng. Mech. 1998, 124, 446–454. [Google Scholar] [CrossRef]
- Lee, M.H. Active vibration control of smart structural system using a novel control approach. J. Vibroeng. 2013, 15, 845–855. [Google Scholar]
- Koszewnik, A. The Active Vibration Control of the Plate Structure by Using LQG Controller and Piezo-Stripes. In Proceedings of the 2017 22nd International Conference on Methods and Models in Automation and Robotics (MMAR), Międzyzdroje, Poland, 28–31 August 2017; pp. 797–802. [Google Scholar]
- Rosoł, M.; Martynowicz, P. Implementation of the LQG controller for a wind turbine tower-nacelle model with an mr tuned vibration absorber. J. Theor. App. Mech. 2016, 54, 1109–1123. [Google Scholar] [CrossRef]
- Islam, M.; Jahra, F.; Hiscock, S. Data analysis methodologies for hydrodynamic experiments in waves. J. Nav. Archit. Mar. Eng. 2016, 13, 1–15. [Google Scholar] [CrossRef][Green Version]
- Preumont, A. Twelve Lectures on Structural Dynamics; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Lindgren, E.R. The generalized energy method for the formulation of the equations of motion in classical mechanics. Phys. Scr. 2002, 66, 114–124. [Google Scholar] [CrossRef]
- Ljung, L. MATLAB System Identification Toolbox User’s Guide; MathWorks: Natick, MA, USA, 2014. [Google Scholar]







| Item | Value |
|---|---|
| Stroke (mm) | ±550 |
| Max control force (N) | 3600 |
| Frequency range (Hz) | 0.1 to 0.3 |
| Mass (kg) | 14,000 |
| Power (kw) | 11 |
| Item | Prototype | Scaled Model |
|---|---|---|
| Mass (ton) | 1526 | 1.509 |
| Frequency (Hz) | 0.170 | 0.542 |
| Item | Value |
|---|---|
| Moving mass (kg) | 50 |
| Stroke (mm) | ±70 |
| Force (N) | 38.8 |
| El Centro | Imperial Valley-02 | ||||
|---|---|---|---|---|---|
| Displacement (mm) | Acceleration (gal) | Displacement (mm) | Acceleration (gal) | ||
| AMD | Uncontrolled | 54.9 | 320.5 | 49.1 | 73.5 |
| Controlled | 35.1 | 132.0 | 19.9 | 26.7 | |
| Decreasing rate | 36.1% | 58.8% | 59.4% | 63.7% | |
| TMD | Uncontrolled | 54.9 | 320.5 | 49.1 | 73.5 |
| Controlled | 48.4 | 318.3 | 21.1 | 35.6 | |
| Decreasing rate | 11.8% | 0.7% | 57.1% | 51.6 | |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chang, S. Active Mass Damper for Reducing Wind and Earthquake Vibrations of a Long-Period Bridge. Actuators 2020, 9, 66. https://doi.org/10.3390/act9030066
Chang S. Active Mass Damper for Reducing Wind and Earthquake Vibrations of a Long-Period Bridge. Actuators. 2020; 9(3):66. https://doi.org/10.3390/act9030066
Chicago/Turabian StyleChang, Seongkyu. 2020. "Active Mass Damper for Reducing Wind and Earthquake Vibrations of a Long-Period Bridge" Actuators 9, no. 3: 66. https://doi.org/10.3390/act9030066
APA StyleChang, S. (2020). Active Mass Damper for Reducing Wind and Earthquake Vibrations of a Long-Period Bridge. Actuators, 9(3), 66. https://doi.org/10.3390/act9030066





