Improved Decoupling Control for a Powershift Automatic Mechanical Transmission Employing a Model-Based PID Parameter Autotuning Method

Abstract

Automatic mechanical transmission (AMT) with a gearshift assistant mechanism is a novel transmission architect concept aiming to improve the torque interruption and driveline jerk of AMT. During the shifting process, the shifting performance deteriorates as the varying road gradient and the friction coefficient worsen the coupling effect between the motor torque and the clutch friction torque. This paper focuses on improving the controller’s robustness of AMT with a gearshift assistant mechanism against the perturbed parameters during the stage of torque gap filling. In this paper, a detailed powertrain simulation model was presented. Based on a decoupling controller and a disturbance compensator, proportional-integral-differential (PID) controllers are applied to enhance the robustness and the decoupling effect. The PID parameters are automatically tuned by employing the Nelder-Mead method. In the tuning process, a cost function was established to demonstrate the outputs’ reference tracking performance, and the PID parameters are tuned by minimizing the cost function. Finally, the tuned parameters are stored in PID maps to make them adjustable online. Simulation results show that with the perturbed parameters well estimated, the upshift process was successful and the torque filling effect was also acceptable. The proposed transmission is a promising structure for industry applications.

1. Introduction

With the continuous implementation of energy-saving and emission reduction policies, hybrid electric vehicles and pure electric vehicles are gradually replacing traditional internal combustion engine (ICE) vehicles. Automatic mechanical transmission (AMT) based novel structures have drawn rising attention from hybrid and electric vehicle manufacturers [1,2]. An AMT equipped with a shift assist mechanism can enhance the shift quality and the fuel consumption of the traditional AMT by properly coordinating the friction clutch and the motor connected to the output shaft [3]. The auxiliary shifting mechanism added to AMT changed the shifting process in a way that is different compared to the traditional ones, and its performance still needs to be further validated.

The vehicle usually operates under elaborate and varying conditions. Waving roads are a common driving condition, especially in mountainous regions [4]. The main disadvantage of the traditional AMT is the torque interruption [5]. The increase of the road grade is always accompanied by surging resistant torque, which deteriorates the transmission’s shifting performance.

Over the last decade, researchers throughout the world have attempted to improve the transmission shift performance and fuel saving. The approaches are generally classified into two different types [6]: (a) increasing the gear step number in current transmission layouts, such as 9-speed automatic transmission (AT) and 10-speed AT and (b) inventing or developing novel transmission architecture, such as the dual-clutch transmission (DCT) or AMT with a torque gap filler (TGF). The TGF indicates the device or the mechanism planted on the AMT architecture that provides additional power routes in the shifting process. Various TGFs have been proposed, such as planting an epicyclic mechanism transmitting the engine torque to the AMT secondary shaft [7] and utilizing a flywheel to store the engine power for torque compensation as demonstrated in [8]. Replacing the synchronizer of the fifth gear by a friction clutch, namely assistant clutch (ACL), allows the engine torque to be transmitted through the secondary shaft to the output shaft [9]. However, the application of the foregoing TGFs are normally restricted by conditions such as allowable thermal loads or the torque gap filling performance.

AMT integrated with an electric motor, or a hybridized AMT (HAMT), is a new alternative for torque gap filling [10]. The new architecture preserves the advantage of high efficiency, high torque capacity, and simple structure of AMT, and it also improves riding comfort. Nevertheless, in the shifting process of MT and AMT, the clutch is required to be entirely disengaged to minimize the friction load on synchronizers, which aims to boost the engagement and disengagement of gears. While the electric motor works to fill the torque gap, the gear engagement demands higher friction torque from synchronizers, which will cause extra abrasive wear on them.

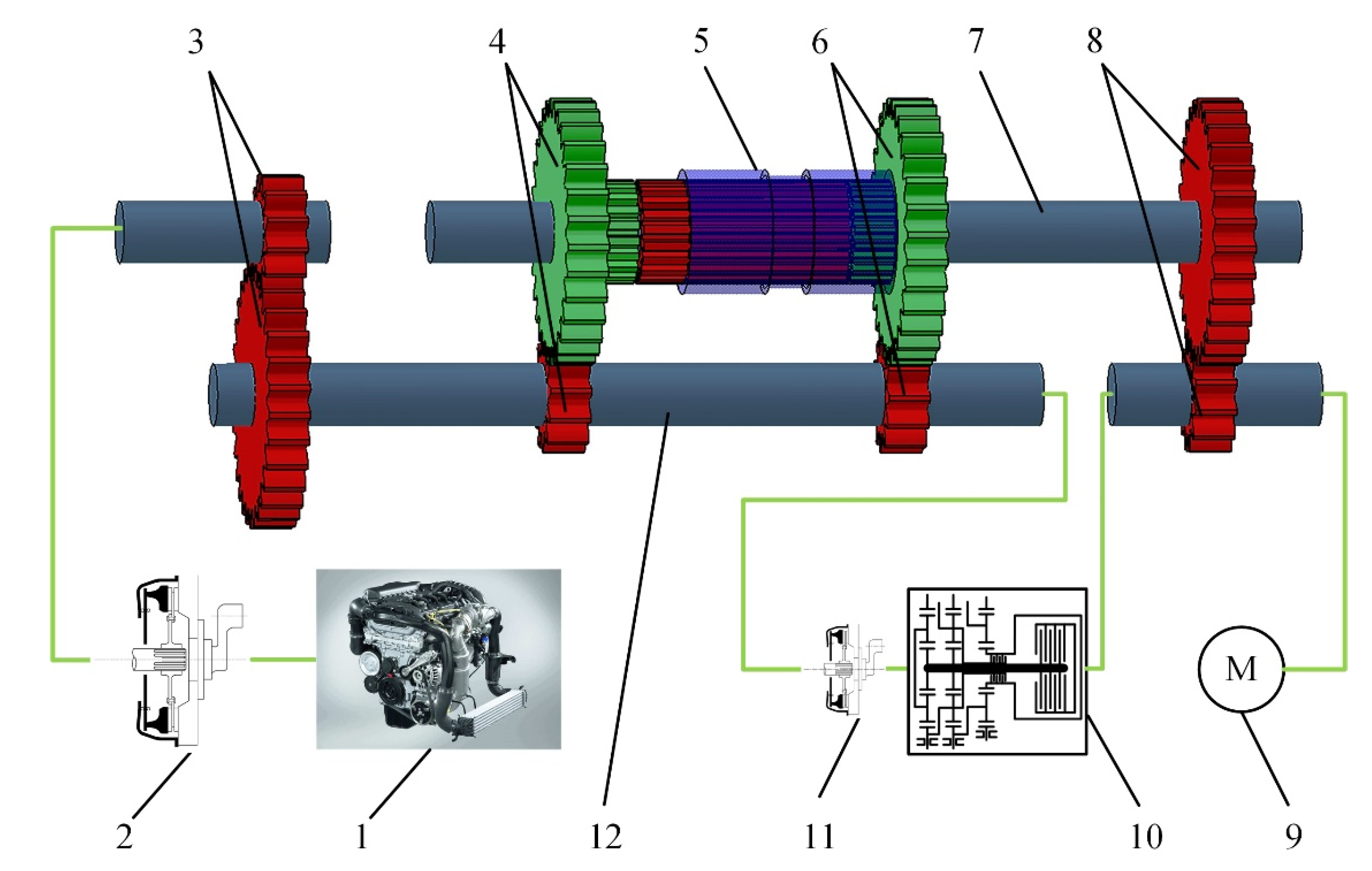
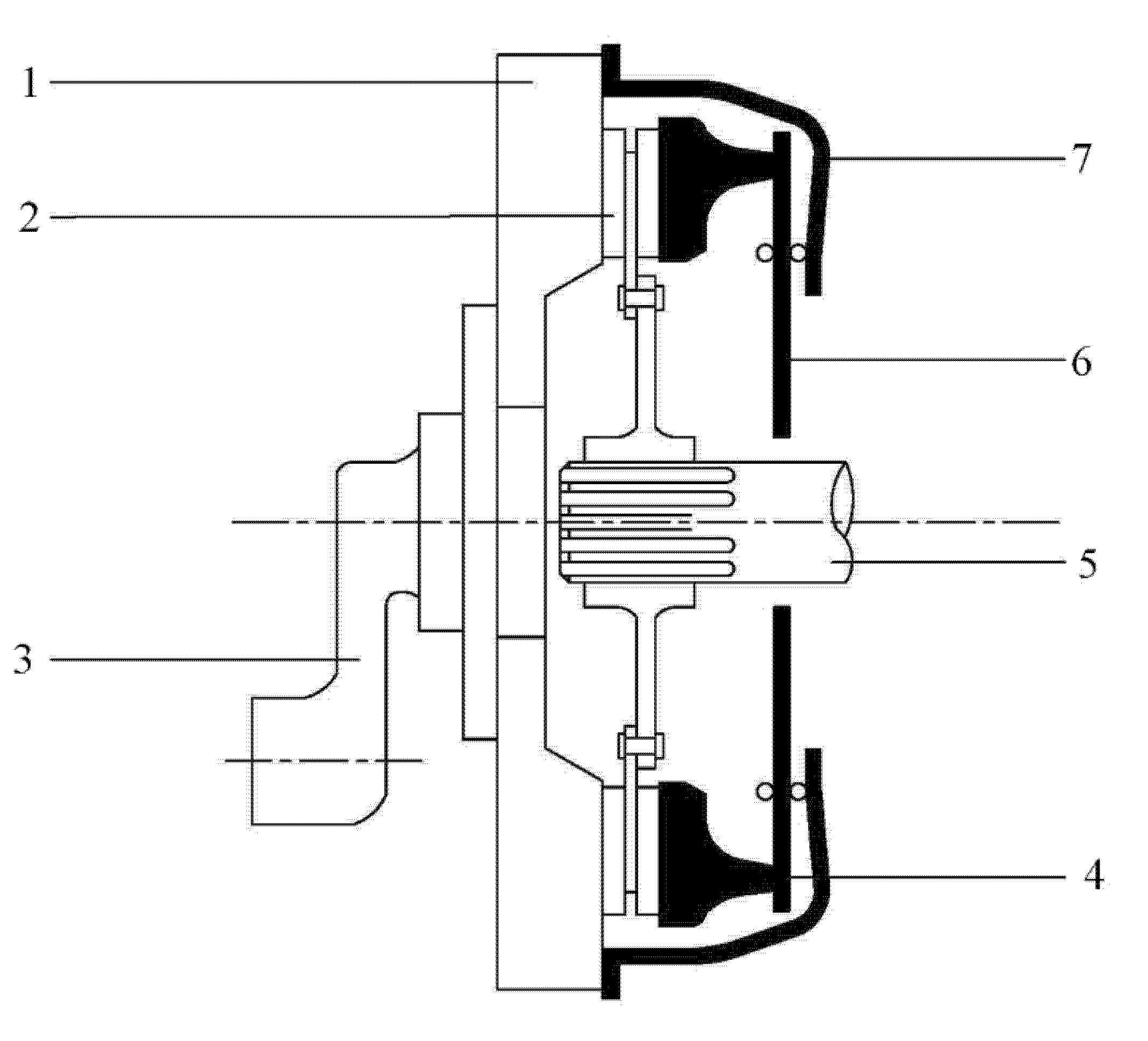
The gearshift assist mechanism is designed as an auxiliary shifting device concept for traditional AMT to fix the above issues. In the shifting process, the torque of an electric motor will be utilized to compensate for the torque interruption, which alleviates the surging resistant torque. Simultaneously, a synchronizing clutch will be engaged to synchronize the preshift gear and the transmission output shaft. The synchronizing clutch is a substitute for the synchronizers and the clutch of AMT in the shifting process (as shown in Figure 1). Yet, the structure of the gearshift assistant mechanism inevitably leads to mutual coupling between the motor torque and the clutch friction torque. In addition, the friction coefficient of the relatively rubbing dry clutch pads varies depending on the working speed, temperature, and surface worn condition. The uncertainty of the friction torque also degenerates the torque filling performance. In general, the key to a steady auxiliary shifting performance hinges on the proper dynamic coordination of the motor torque and the clutch friction torque with respect to the perturbations of the road grade and of the friction coefficient.

However, only by applying the feedforward decoupling controller and the disturbance compensation controller cannot guarantee that the friction torque and the motor torque would have an ideal target tracking performance against the parameter perturbations. Proportional-integral-differential (PID) controllers are widely utilized in the industry, owing to their simplicity and satisfactory efficiency. With the development of the computer, the massive tuning work could be automatically done by proper programming. Applying PID controllers for feedback adjustment can effectively improve the robustness of the target tracking performance of the system outputs, and the key to the implementation of the PID controllers in the transmission is their tuning of the parameters.

In the upshifting process of AMT with a gearshift assistant mechanism, the vehicle is powered by both the friction torque and the motor torque, and the shifting performance is evaluated by the reference tracking performance of the clutch speed differences and the output acceleration. In other words, AMT with a gearshift assistant mechanism is considered as a two-input and two-output (TITO) system, and the self-tuning method of PID parameters for the foregoing TITO system is an essential point for the controller’s implementations [11]. Unlike the single-input/single-output (SISO) system, the TITO system is more sophisticated to be properly controlled. Generally, the TITO system cannot be directly decomposed into two SISO systems, especially when complex coupling relationships exist between variables [12]. Therefore, some methods that are suitable for the online tuning for the SISO system are not applicable for the TITO situation, such as the self-tuning methods employed fuzzy control principles [13], neural network algorithms [14], genetic algorithms [15,16], etc.

Generally, for a multi-input and multi-output (MIMO) system, three major control schemes have been proposed: decentralized (multiloop) control, decoupled control, and centralized control [17]. The decentralized type has been widely applied in the industrial process and is also the control scheme applied in this paper.

The online tuning processes usually require the system to be identified firstly as a mathematical model such as the first-order plus dead-time (FOPDT) model [18]. Such methods do not consider the full knowledge of the process as a must. Yet, since the information on the system dynamic behavior is limited, in many cases the satisfied tuning or closed-loop response is hardly obtained. Extensive research has been done for multiloop decentralized PID controller tuning, which can be roughly classified into the following categories: detuning methods, sequential tuning, independent design, relay-feedback autotuning, and optimization methods. However, very few of the foregoing methods have been implemented in the industry [19].

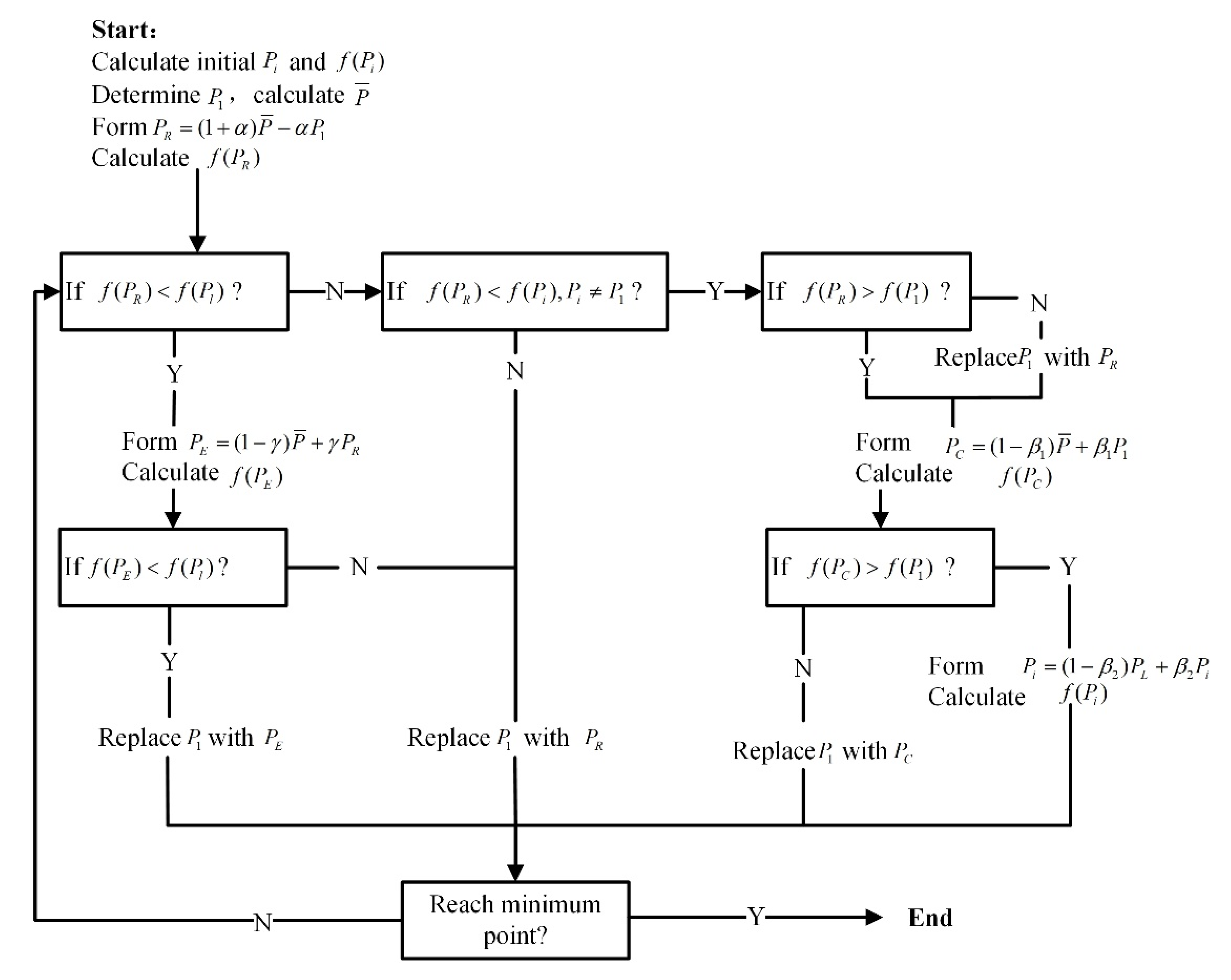
As the purpose of applying the PID controller is to improve the robustness of the outputs’ reference tracking performance, the Nelder-Mead method is thus considered a suitable alternative. The Nelder-Mead method is a subtle optimizing algorithm for optimum tracking [20]. The algorithm employs a geometric construct called a simplex to minimize the cost function. However, the Nelder-Mead method requires a large amount of calculation, which makes the algorithm incapable of being directly applied in the vehicle control unit, let alone when the driving condition varies. Storing the tuned parameters in PID maps is a commonly used method for reference tracking feedback control. The PID maps that store the calibrated PID parameters of different working conditions could be easily implemented in the transmission control unit. Moreover, the PID map is an effective method to avoid integration drift. With the perturbed parameters well estimated, the exports of the maps will be able to improve the robustness of the output reference tracking performance.

The proposed tuning method is a simplified alternative optimization method similar to the time-domain optimal-tuning PID control concept proposed for SISO system in [21], which has been considered a reliable, optimal solution to solve industrial problems, but several extensions and advantages could be observed:

• The proposed tuning method is concise and applicable in both SISO and TITO systems.
• The tuned PID parameters stored in the maps are proven by simulations or experimental tests to have satisfying system responses, which makes the performance prediction part negligible.
• It requires little knowledge of the system identification and other complicated, theoretical control laws or algorithms from engineers.

The objective of this paper is to improve the controller’s robustness performance of the AMT with the gearshift assistant mechanism concept against the variation of the road gradient and the friction coefficients. The perturbed parameters are modeled in the numerical models. Based on a decoupling controller and a disturbance compensator, online adjustable PID maps are applied to cope with the perturbed parameters. In the tuning process, the cost function taking the PID parameters as independent variables is established, and the minimum value of the cost function is calculated by using the Nelder-Mead method. The PID parameters are then automatically tuned when the minimum value is reached. Weighting coefficients are inserted into the cost function; by changing the weighting coefficients, the system performance varies as well. The designed controller is tested on a whole powertrain simulation model; the results show that the controllers are robust to the perturbed parameters, which makes the gearshift assistant mechanism a promising mechanism for torque gap filling.

2. Principle Architecture and Working Theory of the Gearshift Assistant Mechanism Concept

As shown in Figure 1, the gearshift assistant mechanism consists of an electric motor, an epicyclic mechanism, and a synchronizing clutch. The motor directly transmits power to the output shaft through a pair of gears, namely the complementary gear. Meanwhile, the power of the motor will also be transmitted to the secondary shaft of the gearbox through the epicyclic mechanism and the synchronizing clutch. The synchronizing clutch connects the output shaft of the gearbox to the secondary shaft. The epicyclic mechanism transmits the speed and torque of the output shaft to the driven clutch plate (i.e., the clutch plate on the output shaft side) of the synchronizing clutch at a certain gear ratio. After the synchronizing clutch starts to engage, the secondary shaft in the AMT gearbox is affected by the clutch friction torque to change the speed, and the speed of the preshift gear will be changed by the toque transmitted through the complementary gear pair. When the gear-to-gear ratio of the preshift gears is equal to that of the epicyclic mechanism gear ratio, the preshift gears will be synchronized with the output shaft due to the engagement of the synchronizing clutch, and the engine speed will be simultaneously synchronized with the vehicle speed.

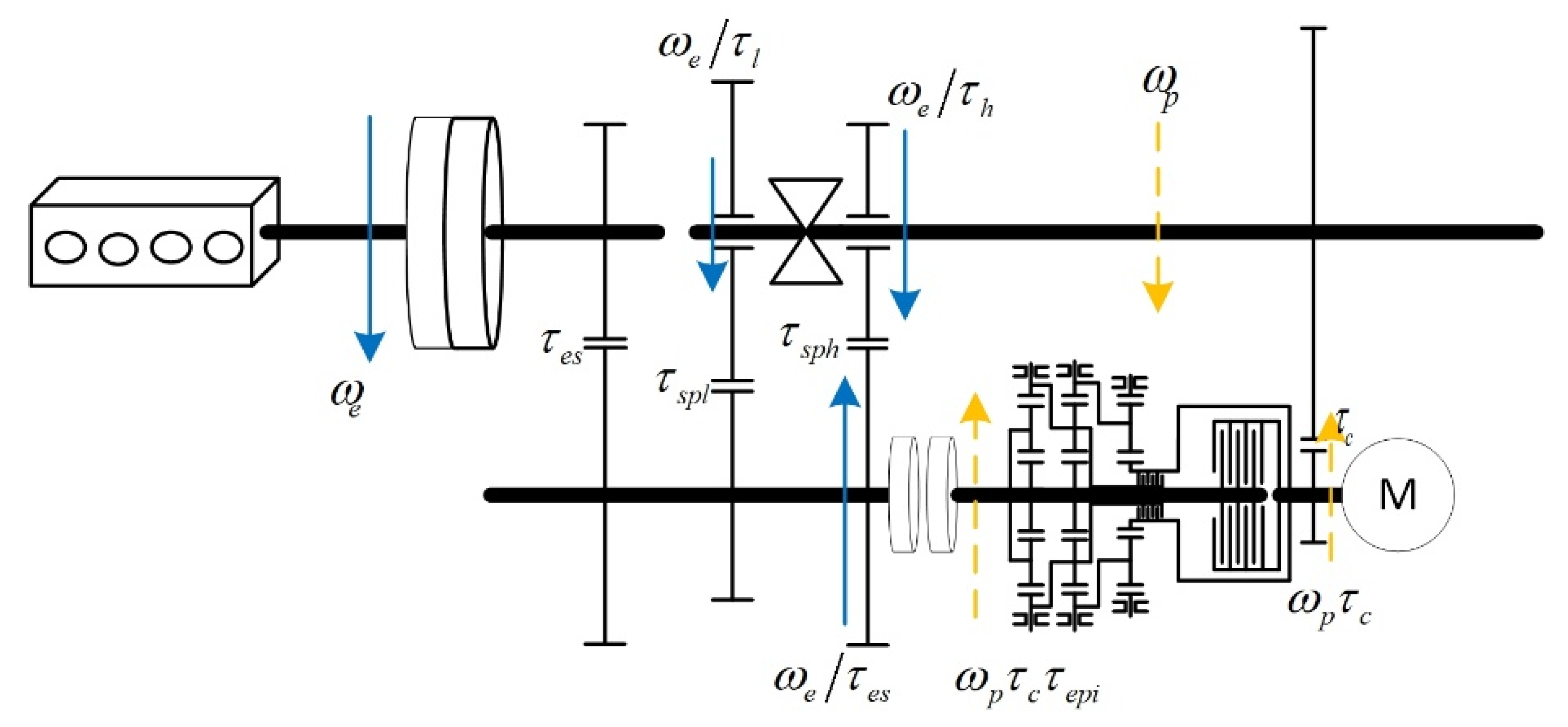
As shown in Figure 2, the kinematics of AMT with the gearshift assistant mechanism could be described by two angular velocities, ${\omega }_e$ and ${\omega }_{\mathrm{p}}$, as:

$$\{\begin{array}{c}{\omega }_{scle}={\omega }_e/{\tau }_{es}\\ {\omega }_l={\omega }_e/{\tau }_l={\omega }_{scle}/{\tau }_{spl}\\ {\omega }_h={\omega }_e/{\tau }_h={\omega }_{scle}/{\tau }_{sph}\\ {\omega }_{sclp}={\omega }_p{\tau }_c{\tau }_{epi}\\ {\omega }_m={\omega }_m{\tau }_c\end{array}$$

(1)

where ${\tau }_{\mathrm{epi}}$ is the angular velocity of the engine side clutch plate, ${\omega }_{\mathrm{sclp}}$ is the angular velocity of the engine side clutch plate, ${\omega }_{\mathrm{l}}$ is the angular velocity of the lower gear step idling gear on the output shaft, ${\omega }_{\mathrm{h}}$ is the angular velocity of the higher gear step idling gear on the output shaft, ${\omega }_{\mathrm{p}}$ is the gearbox output shaft angular velocity, ${\omega }_{\mathrm{m}}$ is the angular velocity of the electric motor, ${\tau }_{\mathrm{l}}$ is the gear ratio of the lower gear step, ${\tau }_{\mathrm{spl}}$ is the gear ratio of the lower gear pair, ${\tau }_{\mathrm{h}}$ is the gear ratio of the higher gear step, ${\tau }_{\mathrm{sph}}$ is the gear ratio of the higher gear pair, ${\tau }_{\mathrm{epi}}$ is the epicyclic mechanism gear ratio, ${\tau }_{\mathrm{es}}$ is the engine output shaft to secondary shaft gear ratio, and ${\tau }_{\mathrm{c}}$ is the torque complementary gear pair gear ratio.

Taking the upshifting process as an example, the epicyclic mechanism and the complementary gear pair are designed as:

$${\tau }_c{\tau }_{epi}={\tau }_{sph}=\tau$$

(2)

The target is to synchronize the output shaft angular velocity ${\omega }_p$ and the preshift gear angular velocity ${\omega }_h$, which must satisfy the following equation:

$${\omega }_h-{\omega }_p={\omega }_{scle}/{\tau }_{sph}-{\omega }_{sclp}/{\tau }_c{\tau }_{epi}=({\omega }_{scle}-{\omega }_{sclp})/\tau =0.$$

(3)

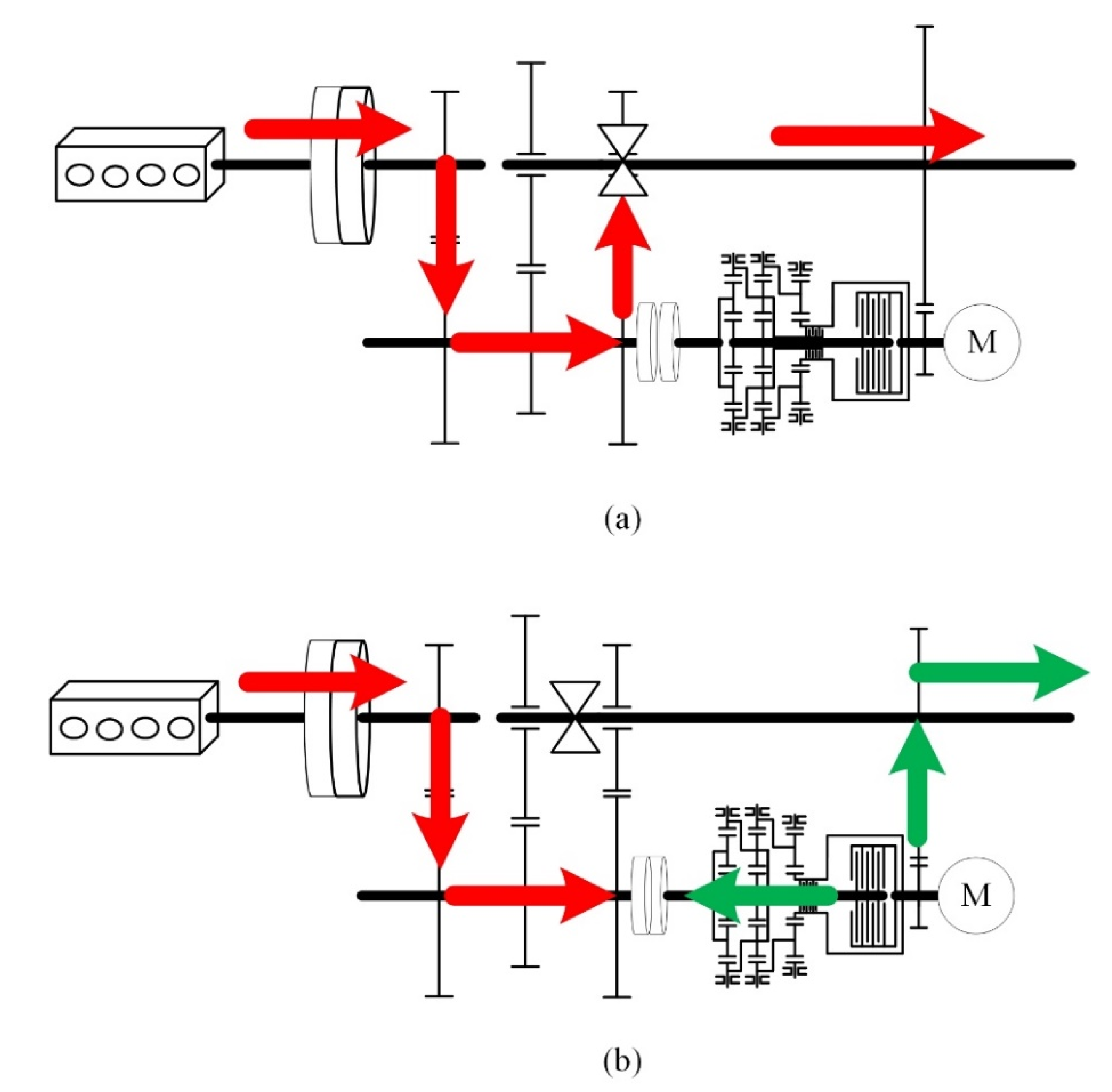
The above equation shows the kinematic theory of shifting with the proposed mechanism. As shown in Figure 3a, the transmission operates in the same manner as traditional AMT in fixed gear steps. In comparison, the gearshift assistant mechanism idles along with the output shaft, which brings extra power loss according to the inertia effect.

Figure 3b shows the shifting process of AMT with the gearshift assistant mechanism. The engine torque is interrupted, and the power source of the output shaft is substituted by the motor torque. When the torque gap is being filled, the engagement of the synchronizing clutch is interfered by the motor torque and the engine torque.

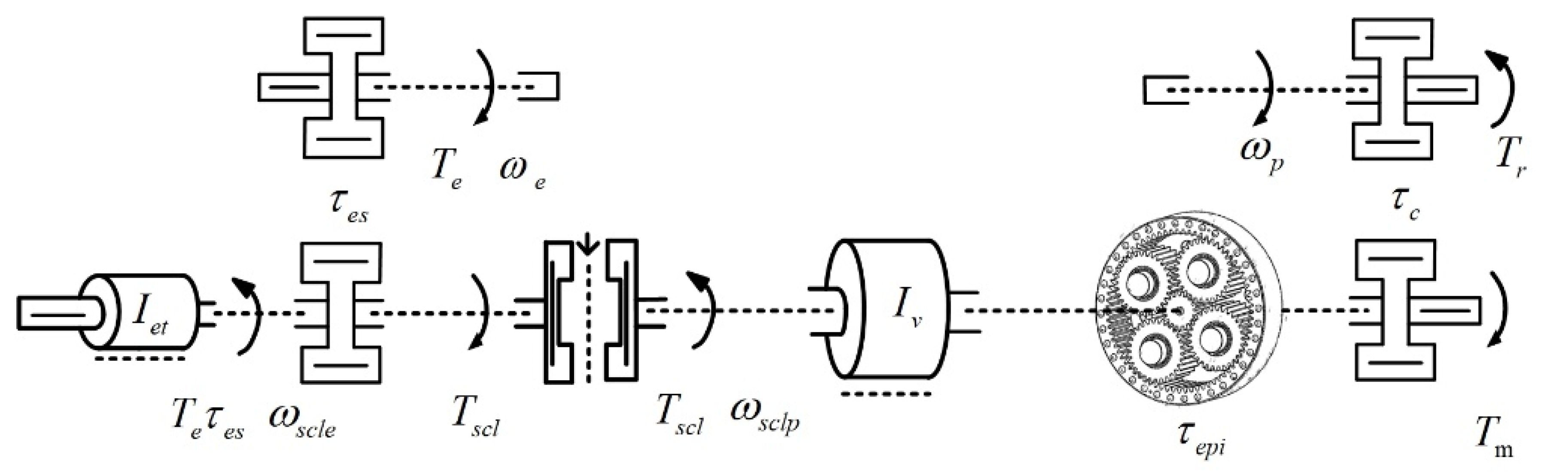
In the shifting process, as shown in Figure 4, the AMT with a gearshift assistant mechanism has two degrees of freedoms: the angular velocity of the engine side clutch pad ${\omega }_{scle}$ and that of the output shaft side clutch pad ${\omega }_{sclp}$. The dynamics of the clutch pads could be described as follows:

$$I_{et}{\dot{\omega }}_{scle}=T_e{\tau }_{es}-\frac{C_{et}{\omega }_e}{{\tau }_{es}}-T_{scl}sign({\omega }_{scle}-{\omega }_{sclp}),$$

(4)

$$I_v{\dot{\omega }}_{sclp}=\frac{T_m}{{\tau }_{epi}}+T_{scl}sign({\omega }_{scle}-{\omega }_{sclp})-C_v{\omega }_p{\tau }_{epi}{\tau }_c-\frac{T_r}{{\tau }_{epi}{\tau }_c}$$

(5)

where $T_e$ is the engine torque; $T_{scl}$ is the friction torque on the synchronous clutch; $T_m$ is the motor torque; $T_r$ is the vehicle driving resistance torque; $I_{et}$ is the equivalent rotational inertia of the engine, main clutch, and secondary shafts; $I_v$ is the equivalent rotational inertia of the remaining transmission; $c_{et}$ is the equivalent damping coefficient of the engine, main clutch, and secondary shafts; and $c_v$ is the equivalent damping coefficient of the remaining transmission. The function sign outputs 1 when the value in parentheses is positive, otherwise −1.

From the dynamic equations, it could be observed that the change of the engine side clutch pad’s angular velocity ${\dot{\omega }}_{scle}$ is decided by $T_e$ and $T_{scl}$, while the change of the output shaft side clutch pad’s angular velocity mainly hinges on $T_m$, $T_r$, and $T_{scl}$.

The friction torque will be produced once the clutch pads start to engage. In association with Equation (3), the synchronization will be able to be accomplished by properly coordinating the engine torque, the friction torque, and the motor torque.

If the gear ratios of the epicyclic mechanism satisfy Equation (2), the engagement of the synchronizing clutch, which takes the clutch torque capacity to be sufficient, will ensure the synchronization of the preshift gear and the output shaft. It is worth noting that the engine torque is set to be zero in the shifting process to minimize the size of the gearshift assistant mechanism since such a setting requires a lower torque capacity from the mechanism. Consequently, the proposed mechanism, especially the synchronizing clutch, will only have to overcome the equivalent moment of inertia and other resistant torques of the engine and its connected parts to accomplish the foregoing process.

The shifting process after the AMT is equipped with the gearshift assistant mechanism can be summarized as follows: (a) The epicyclic mechanism output gear ratio is required for shifting; (b) the synchronizer is disconnected, and the gearbox is in neutral; (c) The motor starts to work and provides the torque, while the synchronous clutch starts to engage simultaneously; (d) the synchronizer locks the target gear, and the gearbox outputs the target gear ratio; (e) the engine restores power, and the synchronizing clutch is disengaged.

3. Materials and Methods

3.1. Powertrain Simulation Model with Perturbed Parameters

In this paper, the performance evaluation index of the gearshift assistant mechanism during the shifting process is expressed by the angular velocity difference between the master and the driven clutch plates $\Delta {\omega }_{scl}$ and the angular acceleration of the output shaft ${\dot{\omega }}_p$.

Making $\Delta {\omega }_{scl}={\omega }_{scle}-{\omega }_{sclp}$ derives the following:

$$\Delta {\dot{\omega }}_{scl}=c_1{T}_e-(c_2-c_4){\omega }_{sc{l}_e}-c_3{T}_{scl}-c_4\Delta {\omega }_{scl}-\frac{T_m}{I_v{\tau }_{epi}}+\frac{T_r}{I_v{\tau }_{epi}{\tau }_c},$$

(6)

$${\dot{\omega }}_p=\frac{T_m{\tau }_c}{I_v}+c_5{T}_{scl}-c_6{\omega }_p-\frac{T_r}{I_v},$$

(7)

with

$$c_1=\frac{{\tau }_{es}}{(I_{et})}{c}_2=\frac{c_{et}{\tau }_{es}^2}{I_{et}},c_3=\left(\frac{1}{I_{et}}+\frac{1}{I_v}\right)sign(\Delta {\omega }_{scl}),c_4=\frac{c_v{\tau }_{epi}{\tau }_c}{I_v},c_5=\frac{sign(\Delta {\omega }_{scl}){\tau }_{epi}{\tau }_c}{I_v},c_6=\frac{c_v{\tau }_{epi}^2{\tau }_c^2}{I_v}.$$

(8)

Equations (6) and (7) describe the dynamic characteristic of $\Delta {\omega }_{scl}$ and ${\dot{\omega }}_p$. The structure of a single-plate dry friction clutch is shown in Figure 5. When the clutch pads are relatively rubbing, the torque delivered by the synchronizing clutch $T_{\mathrm{scl}}$ is usually estimated by the pinching force $F_{\mathrm{n}}$ applied on the clutch disc:

$$T_{\mathrm{sc}}{}_{\mathrm{l}}=F_{\mathrm{n}}\mu (\Delta {\omega }_{\mathrm{scl}}{)\mathrm{R}}_{\mathrm{scl}},$$

(9)

where $F_{\mathrm{n}}$ is the pinching force, $\mu$ is the dynamic friction coefficient of the synchronizing clutch, and $R_{\mathrm{scl}}$ is the effective radius.

The friction coefficient $\mu$ varies according to the working temperature, the rubbing speed, and the roughness of the clutch surface, etc. To simplify the friction torque model, $\mu$ is defined as a function of $\Delta {\omega }_{scl}$; the relationship is presented in Figure 6.

The resistant torque consists of three parts: the drag resistance of the road inclination, the running resistance, and the air resistance produced by the tire.

$$T_r=\frac{mg\sin \theta R_w+T_w}{{\tau }_{df}}+\frac{C_A{R}_w^3}{{\tau }_{df}^3}{\omega }_p^2,$$

(10)

where m is the mass of the vehicle; g is the acceleration of gravity; $\theta$ is the inclination of the road; $T_w$ and $R_{\mathrm{w}}$ are the rolling resistance torque and tire radius, respectively; $C_A$ is the air resistance calculation constant; and ${\tau }_{df}$ is the differential transmission ratio.

3.2. Nominal Model

We define the amount of disturbance in Equation (6) and the amount of disturbance in Equation (7):

$${\Gamma }_{scl}=c_1{T}_e-(c_2-c_4){\omega }_{sc{l}_e}+\frac{T_r}{I_v{\tau }_{epi}{\tau }_c},$$

(11)

$${\Gamma }_m=-\frac{T_r}{I_v},$$

(12)

Defining $\Delta {\omega }_{scl}$ and ${\dot{\omega }}_p$ as the system output $\mathit{Y}$ and ${\dot{T}}_{scl}$, ${\dot{T}}_m$ as the system input $\mathit{U}$, the nominal model of the system without disturbance can be deduced:

$$\mathit{Y}{=\mathrm{G}}_0\mathit{U},$$

(13)

$$\left[\begin{array}{c}\Delta {\omega }_{scl}\\ {\dot{\omega }}_p\end{array}\right]=\left[\begin{array}{cc}-\frac{c_3}{s(s+c_4)}& \frac{1}{{\tau }_{epi}s(s+c_4)}\\ \frac{c_5\mu (\Delta {\omega }_{\mathrm{scl}}{)\mathrm{R}}_{\mathrm{scl}}}{s(s+c_6)}& \frac{{\tau }_c}{s(s+c_6)I_v}\end{array}\right]\left[\begin{array}{c}{\dot{F}}_n\\ {\dot{T}}_m\end{array}\right],$$

(14)

The nominal model for the disturbance to the system output is as follows:

$$\mathit{Y}=E_0\mathit{\Gamma },$$

(15)

$$\left[\begin{array}{c}\Delta {\omega }_{scl}\\ {\dot{\omega }}_p\end{array}\right]=\left[\begin{array}{cc}\frac{1}{(s+c_4)}& 0\\ 0& \frac{1}{(s+c_6)}\end{array}\right]\left[\begin{array}{c}{\Gamma }_{scl}\\ {\Gamma }_m\end{array}\right]$$

(16)

3.3. Controller Design

The main purpose of implementing the gearshift assistant mechanism for traditional AMT is to improve the shift performance from the following aspects: (a) to speed up the shifting process and (b) to compensate for torque interruption. The shift time is indicated by the $\Delta {\omega }_{scl}$ decrease while tracking the target value, and the power interruption compensation is indicated by the change that is in ${\dot{\omega }}_p$. The above two parameters are the output that the system can measure or estimate in the system transfer function matrix.

As shown in Figure 7, the designed control system employs both a decoupling controller and a disturbance compensator as the feedforward controller and online adjustable PID maps as the feedback controller. The controllers will be introduced in the following sections.

3.3.1. Decoupling Controller Q and Disturbance Compensator $K_{cd}$

As shown in Figure 7, the system consists of a decoupling controller Q [22], a disturbance compensator, and two PID controllers. As a feedforward controller, Q decouples the output reference trajectories of the two systems to reduce the coupling effect between the system inputs:

$$Q=G_0^{-1}\left[\begin{array}{cc}{T}_{11}(s)& 0\\ 0& T_{22}(s)\end{array}\right]$$

(17)

In the diagonal matrix, the determination of $T_{11}(s)$, $T_{22}(s)$ needs to consider whether all the elements in Q satisfy the limitations of being a transfer function.

The disturbance compensator [23] offsets the system interference for the system:

$${\mathit{K}}_{cd}=-G_0^{-1}\mathit{E}(s)$$

(18)

Detailed decoupling controller Q design and anti-interference controller $K_{cd}$ design are referred to in [3].

3.3.2. PID Feedback Controller

In this paper, the PID controller is the key point used to improve the robustness of the tracking performance of the two output quantities of the system, and the appropriate PID control parameters decide the controller performance. An objective function that reflects the output target tracking ability is established. The function takes PID control parameters as independent variables; once the minimum value is reached, the self-tuning of PID control parameters will be completed as well.

The error signal between the two output signals of the system and the two reference tracks can be expressed as:

$$e={[e_{scl},e_m]}^{\mathrm{T}},$$

(19)

where $e_{scl}$ is the error between the output parameter, $\Delta {\dot{\omega }}_{scl}$ and the reference value, and $e_m$ is the error between ${\dot{\omega }}_p$ and the reference value.

Among the system inputs, the part provided by the PID controller can be expressed as

$$u_{fb}{=\mathrm{k}}_{p}e+{\mathrm{k}}_i\int edt+{\mathrm{k}}_d\frac{de}{dt},$$

(20)

with

$${\mathrm{k}}_p=\left[k_{pscl},k_{pm}\right],{\mathrm{k}}_i=\left[k_{iscl},k_{im}\right],{\mathrm{k}}_d=\left[k_{dscl},k_{dm}\right],$$

(21)

where $k_{pscl},k_{iscl},k_{dscl},k_{pm},k_{im},k_{dm}$ are the parameters of the proportional link, integral link, and the differential link, which control the corresponding errors in two PID controllers, respectively. The control block diagram and the description of the PID controller show that this simulation system requires two sets of PID controllers for two system outputs to track their reference trajectories.

3.4. PID Parameter Tuning

3.4.1. Establishment of the Objective Function

The form of the objective function to evaluate the target tracking ability of the two output quantities is expressed as:

$$V(k_{pscl},k_{iscl},k_{dscl},k_{pm},k_{im},k_{dm})=w_{scl}{\Vert {\mathrm{e}}_{scl}\Vert }_1+w_m{\Vert {\mathrm{e}}_m\Vert }_1$$

(22)

The value of the function takes the 6 parameters of the PID controller as independent variables. Here, ${\mathrm{e}}_{scl}$, ${\mathrm{e}}_m$ represents the time series data of $e_{scl}$ and $e_m$ during the simulation; $w_{scl}$ and $w_m$ are the weighting coefficients. Once one of the weighting coefficients is adjusted higher, the corresponding output target tracking ability will be improved, and vice versa.

3.4.2. Principle and Application of the Nelder-Mead Tuning Method

The Nelder-Mead method calculates the minimum value of the objective function by iteration. When it is applied to the function with N independent variables, N + 1 points are required to be initially defined; taking Equation (22) as an example, 7 initial points are required. The coordinates of these initial points, namely the initial PID control parameters, either can be directly selected near the target point by empirical judgment to reduce the corresponding number of iterations or can be selected randomly. In some cases, randomly selected initial points can be used to more accurately determine the function range space.

Through the calculation, the function value $f(P_i)$ of each initial point $P_i$ can be attained, and at the same time we define the point with the smallest function value as $P_L$ as well as the maximum value point $P_1$ and the second maximum point $P_2$ according to the function value, and we calculate the average of other function value points $\overline{P}$ besides the maximum function value $P_1$. As demonstrated in Figure 8, the simple algorithm will complete the following steps in each iteration process: (a) reflection, (b) shrinkage; (c) extension; (d) shrinking in one direction; and (e) shrinking around the minimum point.

In the reflection step, $P_1$ is reflected through $\overline{P}$ with the following equation, and a reflected point $P_R$ will be derived as:

$$P_R=(1+\alpha )\overline{P}-\alpha P_1,$$

(23)

where $\alpha$ is defined as the reflection factor. $P_R$ will replace $P_1$ if $f(P_L)<f(P_R)<f(P_1)$.

In the extension step, if $f(P_R)<f(P_L)$, the simplex increases along the centroid direction, attempting to form an extended point $P_E$, which is better than $P_L$. The extended point is defined as:

$$P_E=(1-\gamma )\overline{P}+\gamma P_R,$$

(24)

where $\gamma$ is defined as the extended factor. If $f(P_E)<f(P_L)$, $P_E$ will replace $P_L$.

In shrinking in one direction, if $f(P_R)>f(P_2)$, the simplex shrinks along the centroid direction, attempting to form a shrinking point $P_c$, which is better than $P_2$. The shrinking point is defined as:

$$P_c=(1-{\beta }_1)\overline{P}+{\beta }_1{P}_0$$

(25)

where ${\beta }_1$ is defined as the shrinking factor and $P_0$ indicates the point with lower function values between $P_R$ and $P_1$. If $f(P_c)<f(P_0)$, $P_c$ will replace $P_1$.

In shrinking around the minimum point, if $f(P_c)>f(P_0)$, the condition for shrinking in one direction does not suffice, and the entire simplex will shrink around the minimum point. The shrinking points are defined as:

$$P_i=(1-{\beta }_2)P_L+{\beta }_2{P}_i$$

(26)

where ${\beta }_2$ is the full shrinking factor, and $P_i$ indicates all points except $P_L$.

Generally, the replacement of $P_1$ indicates the end of the current iteration, and then the termination standard will be checked. If the tolerance fails to meet the standard, the next iteration begins. If the standard is met, the optimization is done [17,24].

The standard of iteration termination is to compare the standard deviation $\sigma$ with a given termination threshold Thres. When $\sigma$ decreases below Thres, iteration terminates. The calculation method of $\sigma$ is as follows:

$$\sigma =\sqrt{\left\{{\displaystyle \sum (f(p_i)-\overline{f(p_i)}}{)}^2/(N+1)\right\}}.$$

(27)

According to the above principle, we iteratively solve the objective equation in Equation (22), and we obtain the PID parameter value that corresponds to the minimum point of the cost function.

Figure 9 shows the tuned PID parameters with respect to the road gradient $\theta$ and friction coefficient $\mu$, which will be applied in the simulation model. It is worth noting that the tuning method is based on the model, and hence the accuracy of the feedback control depends on the accuracy of the model.

4. Results and Discussion

The vehicle upshift model is built on the MATLAB/Simulink simulation platform according to the detailed analysis of the AMT with the gearshift assistant mechanism in [3]. For the parameters used in the simulation process, please refer to

Table 1. Basic parameters and design requirements of AMT with a gearshift assistant mechanism.

Parameter	Value	Unit	Parameter	Value	Unit
${\tau }_{epi}$	1.0503	-	m	1500	kg
${\tau }_{es}$	1.5	-	$T_w$	40	Nm
${\tau }_c$	10	-	$C_A$	0.84	-
${\tau }_{df}$	2	-	$R_w^{}$	0.2	m
$I_{et}$	0.285	s	$\alpha$	1	-
$I_v$	5.08	kg ${\mathrm{m}}^2$	$\gamma$	2	-
$c_{et}$	0.36	kg ${\mathrm{m}}^2$	${\beta }_1$	0.5	-
$c_v$	0.08	kg ${\mathrm{m}}^2$	${\beta }_2$	0.5	-

. During the upshift process from 1st gear to 2nd gear, the engine throttle opening stays at 70%. When the engine speed exceeds 800 rpm, the gearbox upshifts.

4.1. Results Analysis of the Parameter Tuning Process

Seven initial points of the cost function are randomly given and stored in the 7 × 6 matrix A:

$$\mathbf{A}=\left[\begin{array}{cccccc}20& 1& 1& 1& 1& 1\\ 1& 20& 1& 1& 1& 1\\ 1& 1& 20& 1& 1& 1\\ 1& 1& 1& 20& 1& 1\\ 1& 20& 1& 1& 20& 1\\ 1& 1& 1& 1& 20& 1\\ 1& 1& 1& 1& 1& 20\end{array}\right]$$

(28)

Among them, the seven rows of A represent the PID parameters of seven different initial points from top to bottom, and the six columns represent $\left[k_{pscl},k_{iscl},k_{dscl},k_{pm},k_{im},k_{dm}\right]$ from left to right, respectively.

As shown in Figure 10, when Thres = 0.001, the calculation finishes at 99 iterations, and the minimum value obtained by the simulation results is about 80.3; when Thres is reduced to 0.0001, the calculation finishes at 377 iterations, and the result is about 57.02. If Thres is set to 0, the simulation will continue, but after 1022 iterations, the result is about 56.79, and the simulation has not finished yet. Therefore, it can be inferred that if the Thres selected is too large, the simulation result is likely to fall into the local minimum; if Thres is selected too small, as the number of iterations continues to increase (taking the standard shown in Figure 4 as more than 300 iterations), the convergence rate of the function value does not change significantly.

As shown in Figure 11 and Figure 12, after changing the weight coefficients $w_{scl}$ and $w_m$, the cost function value $V(x)$ changes accordingly. In the current model, increasing $w_m$ will increase the value of the function because the two variables ${\mathrm{e}}_{scl}$ and ${\mathrm{e}}_m$ are calculated in scalar form, and the latter is numerically larger than the former. The minimum values obtained by convergence in Figure 11 and Figure 12 have increased in different degrees compared to that in Figure 10, and so does the number of iterations.

In order to explore the effect of different initial points on the simulation results, seven random initial points were defined into the 7 × 6 matrix B:

$$\mathbf{B}=\left[\begin{array}{cccccc}20& 1& 1& 1& -1& 1\\ -1& 20& 1& 1& -1& 1\\ -1& 1& 20& 1& -1& 1\\ -1& 1& 1& 20& -1& 1\\ -1& 20& 1& 1& -20& 1\\ -1& 1& 1& 1& -20& 1\\ -1& 1& 1& 1& -1& 20\end{array}\right]$$

(29)

The meaning of matrix B is consistent with the meaning of matrix A in Formula (13).

As shown in Figure 13, the simulation was aborted at 349 iterations and the function value converged to about 60.58. Compared with Figure 10, after 99 iterations, the function value of each initial point in Figure 13 is about 89, and the iteration is not terminated; the function value of each initial point in Figure 10 converges to 80.3 and satisfies Thres = 0.001. When the function value of each initial point in Figure 13 meets Thres = 0.001, the convergence result is close to the minimum value of 57.02, which is the minimum function value in Figure 10 when its initial points iterated to meet Thres = 0.0001. It can be deduced from this that the selection of the initial value points will affect the number of iterations and the accuracy of the result; when the function value change has a greater impact on the system output performance, the value of Thres should be reduced to obtain a more accurate result. The PID parameters obtained by iteration are shown in

Table 2. PID parameters derived by autotuning.

	${\mathit{k}}_{\mathit{p}\mathit{s}\mathit{c}\mathit{l}}$	${\mathit{k}}_{\mathit{i}\mathit{s}\mathit{c}\mathit{l}}$	${\mathit{k}}_{\mathit{d}\mathit{s}\mathit{c}\mathit{l}}$	${\mathit{k}}_{\mathit{p}\mathit{m}}$	${\mathit{k}}_{\mathit{i}\mathit{m}}$	${\mathit{k}}_{\mathit{d}\mathit{m}}$
Initial point from A, weighting coefficient a, Thres = 0.001	−10,624.6	−5978.5	2623.8	−44.4	7761.5	4573.8
Initial point from A, weighting coefficient a, Thres = 0.0001	−19,502.3	−20,572.8	9055.5	164.3	−7078.3	21,558.3
Initial point from A, weighting coefficient b, Thres = 0.001	−4804.2	2942.1	2738.7	131.3	−5296.9	3227.1
Initial point from A, weighting coefficient c, Thres = 0.001	−4330.3	−15,761.7	1328.2	117.9	−4679.3	8118.7
Initial point from B, weighting coefficient a, Thres = 0.001	−43,360.5	−5296.4	−10,274.5	191.3	−5244.0	−34,772.4

.

4.2. Simulation Analysis of the Upshifting Process

In our analysis, the following definitions were made: $w_{scl}=0.96,w_m=0.04$ as weight coefficient a; $w_{scl}=0.5,w_m=0.5$ as weight coefficient b; $w_{scl}=0.04,w_m=0.96$ as weight coefficient c; y1, y5, y4 as the situation with initial points from A, with Thres = 0.001 and weighting parameters chosen as a, b, c, respectively; y2, y6 as the situation with initial points from A, with weighting parameters chosen as a and the Thres set to 0.0001 and 0, respectively; y3 as the situation with initial points from B, with weighting parameters chosen as a and Thres = 0.01. As shown in Figure 14, at 3.56 s, the gearbox starts to shift, and the criterion of finishing the gearshift is that $\Delta {\omega }_{scl}$ satisfies the angular speed interval [−y, y]. The greater the value of y, the criterion for the completion of the shift will be easier to meet, which will shorten the shift time consequently; otherwise, the shift time will be longer. However, if the value of y is too large, the torsional vibration of the drive train will be unacceptable. If the value of y is too small, the clutch plates will be excessively worn. Although the calculation result can converge to a smaller function value when Thres = 0.0001 compared to the situation when Thres = 0.001, and although the former’s target tracking ability is shown to be better, the improvement is not significant: When Thres < 0.0001, although the function value decreases, the inclination is flat, and the target tracking ability can be consistent with that when Thres = 0.0001. To reduce the amount of calculation, Thres can be directly set as 0.0001 in this case.

As shown in Figure 14, when Thres is unchanged and the weight coefficient $w_{scl}$ is reduced to 0.5, the target tracking ability will be decreased, and as it decreases below 0.5, the target tracking ability will also decrease, but the trend is flat. In the case of applying the same weight coefficients to the initial points taken from matrix B, although more iterations are required to meet the same Thres condition, the results obtain a lower function value and better target tracking ability.

As shown in Figure 15, the relationship between the target tracking ability of the output shaft angular acceleration ${\dot{\omega }}_p$ and Thres is similar to that of $\Delta {\omega }_{scl}$, but when Thres = 0.001, the fluctuation is large, which will deteriorate the riding comfort of the vehicle. Combining with Figure 14, when Thres = 0.0001, the algorithm can get better target tracking ability of two outputs through 377 iterations at the same time.

As shown in Figure 15, when the other conditions remain unchanged, increasing the weight coefficient of the error norm of output ${\dot{\omega }}_p$ up to 0.5 will significantly improve the target tracking ability. However, when the weight coefficient is greater than 0.5, the performance will not be significantly improved. By changing the initial points, the value of the cost function obtained from matrix B is lower, and the improvement of the target tracking ability can be more obvious than in Figure 15.

4.3. Simulation Analysis of the Shifting Process in Different Grade

The shifting process on assent demands high power density from the electric motor for the torque gap. The surging toque interferes with the synchronization of the clutch pads. As shown in Figure 15, higher weighting parameters or lower termination thresholds are essential for preventing the output torque from overshooting. Hence, the weighting parameters are selected as $w_{scl}=0.5,w_m=0.5$.

Figure 16, Figure 17 and Figure 18 show the shifting performance of AMT with the gearshift assistant mechanism in different road grades. It is shown that with the perturbing parameters and the interferences well estimated, the upshift of the proposed transmission can still be successful, and the torque filling effect is also acceptable.

5. Conclusions

In aiming to improve drivability and alleviate the deteriorated coupling effect between the clutch and motor torque caused by road gradient variation and friction coefficient fluctuation in the AMT with the gearshift assistant mechanism, PID feedback controllers are employed in this paper in association with a decoupling controller and a disturbance compensator. The PID controller parameters are tuned based on the powertrain mathematical model by minimizing the cost function in relation to the outputs’ tracking errors with the Nelder-Mead method. By storing the tuned parameters in relation to different friction coefficients and road grades in the PID maps, the PID controllers become adjustable online and easy to be planted in the transmission control unit.

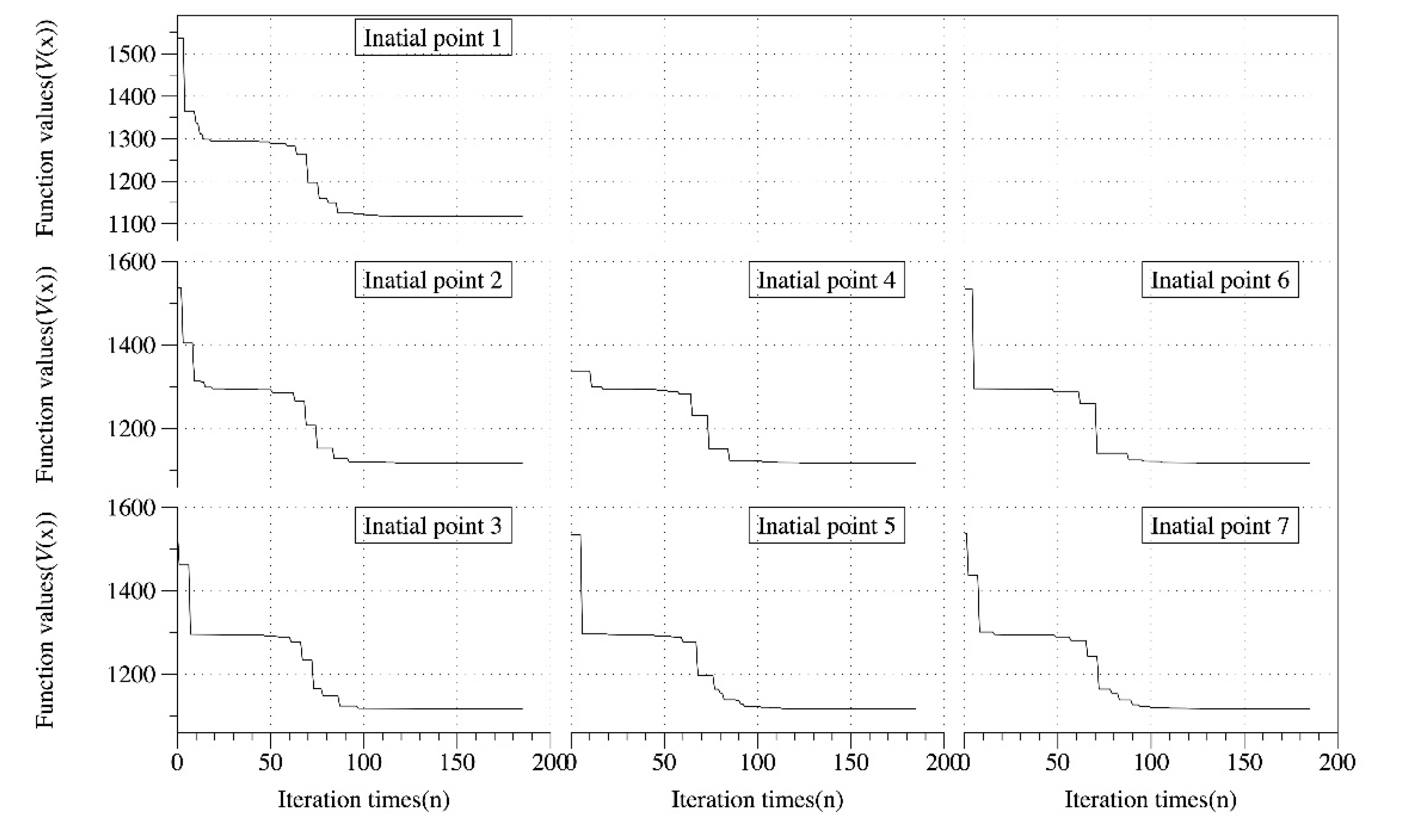
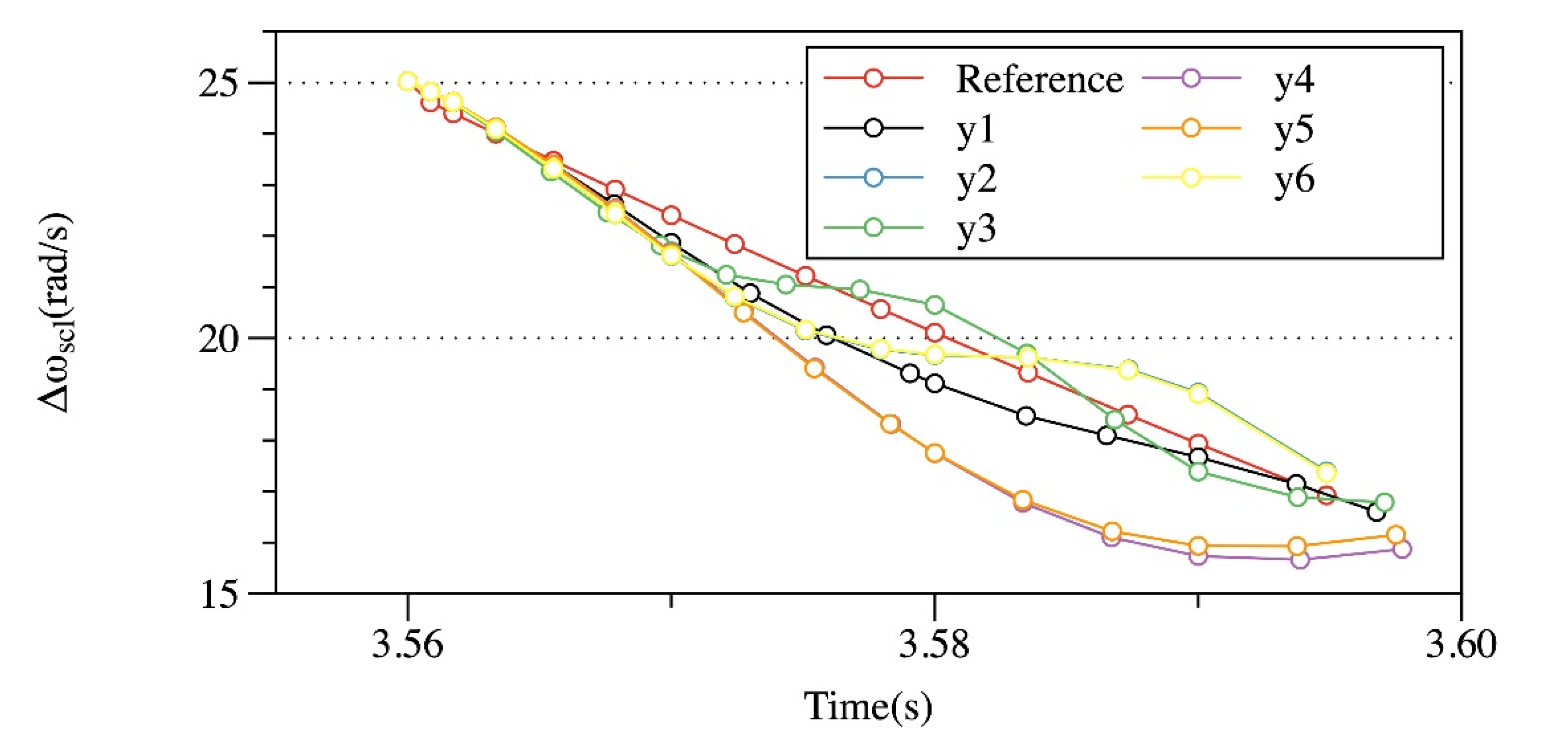
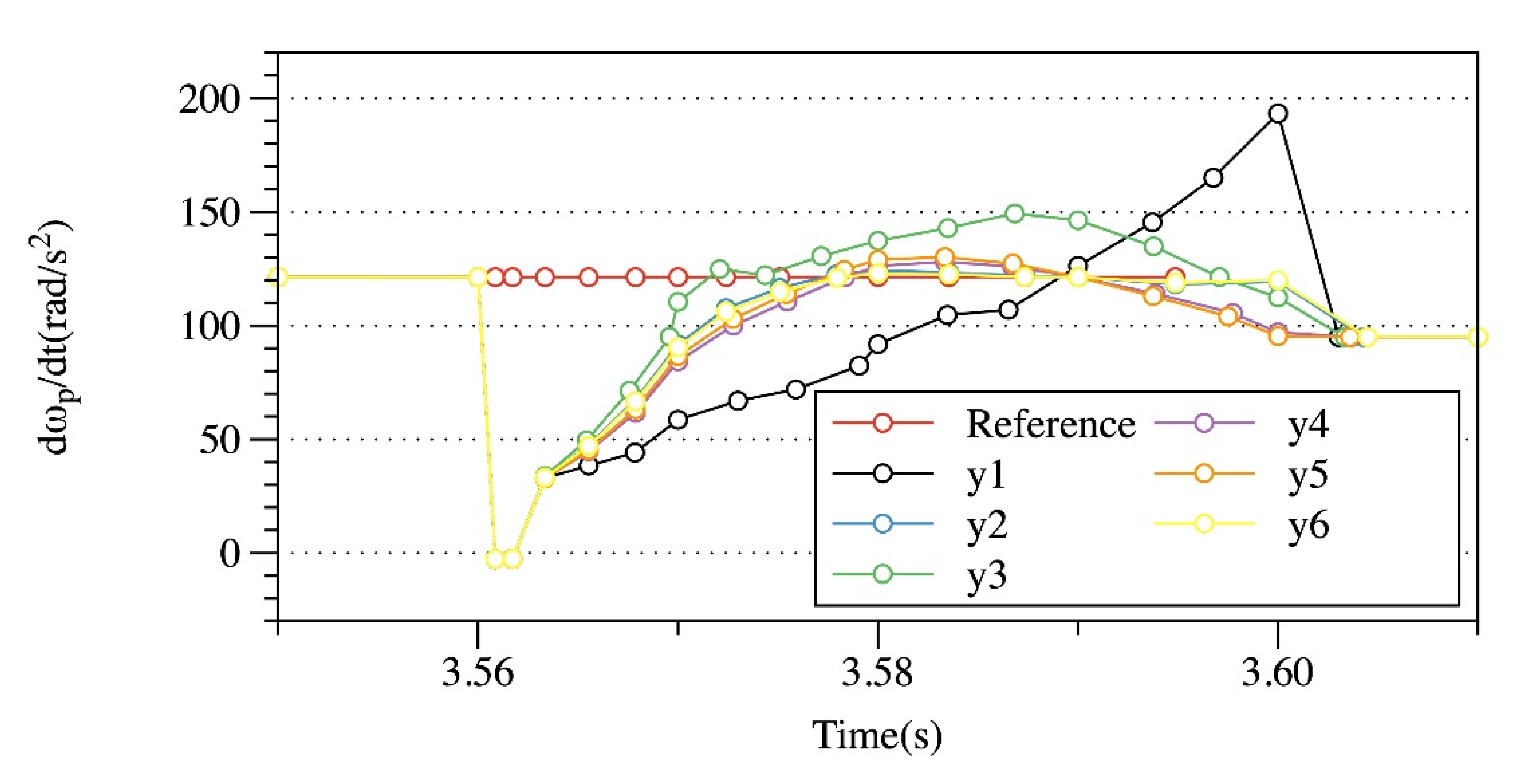
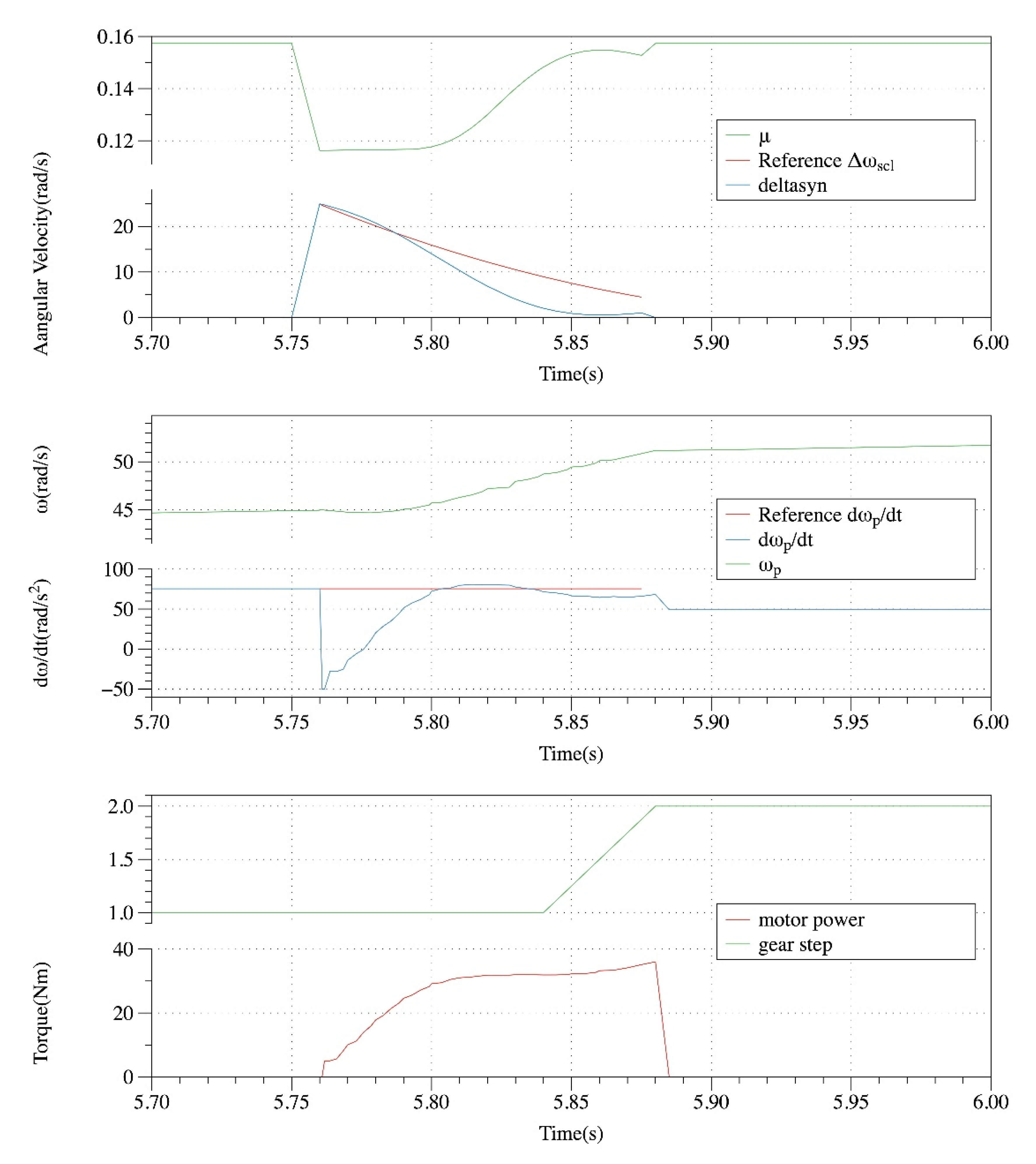
Simulations have been carried out to analyze the PID parameter tuning process, the shifting performance, and the improvement of the robustness. Simulation results show that the outputs’ reference tracking ability improves as the cost function values decrease, and it deteriorates as the corresponding weighting parameters decrease, which proves the effectiveness of the cost function. In association with the analysis on the upshift performance, it could be observed that with the same initial points, namely the same termination threshold, the output’s reference tracking ability varies obviously with the weighting parameters changed within specific ranges. With the same initial points, namely the same weighting parameters, decreasing the terminating threshold in a limited range significantly improves the outputs’ tracking ability; with the same weighting parameters and the same termination threshold, the closer the initial points are to the optimal points, the fewer iteration times will be required to obtain similar tracking ability. With the assumption that the perturbed parameters were well estimated, the simulation results show that the proposed controllers enhance the outputs’ tracking ability against the varying friction coefficient and the road grade.

The AMT with a gearshift assistant mechanism has great potential to become a fast, uninterrupted powershift transmission. Future works will concentrate on the following aspects: (a) optimization of the gear selector, since the traditional synchronizers have been replaced by the synchronizing clutch; (b) optimization of the shifting logics and operating modes to minimize the energy consumption in different driving cycles; (c) developing proper controllers to achieve a seamless power source switch between the engine and the electric motor; and (d) carrying out experimental validation on the proposed conceptual mechanism.