Presentation, Modeling and Experiments of an Electrostatic Actuator Based Catom for Programmable Matter
Abstract
1. Introduction
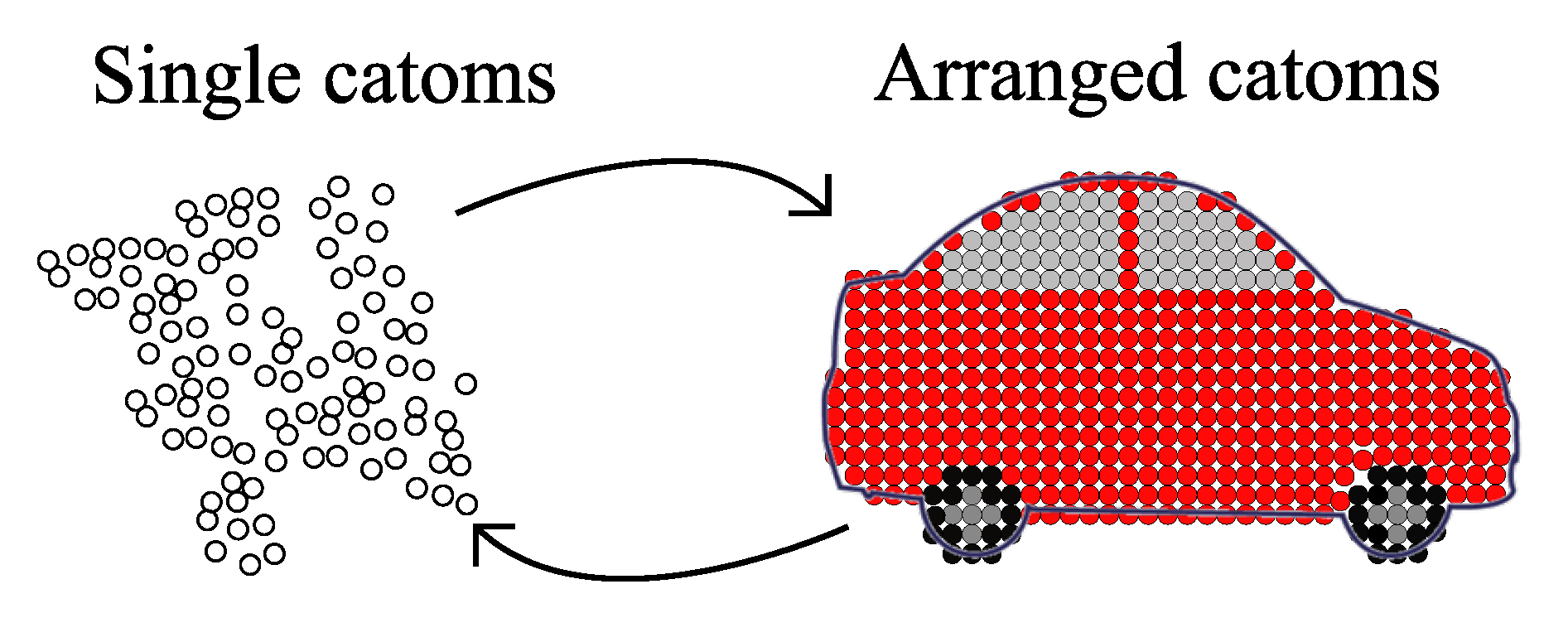
1.1. Programmable Matter
1.2. State of the Art
1.3. Comparison of Different Actuation Technologies
- force generated by a module (Latching force),
- energy required for latching (Energy),
- miniaturization possibility (Miniaturization),
- ease of integration of the actuation on a module (Integration),
- and possibility to use the same latching actuation for relative movement (Movement).
1.4. Contributions
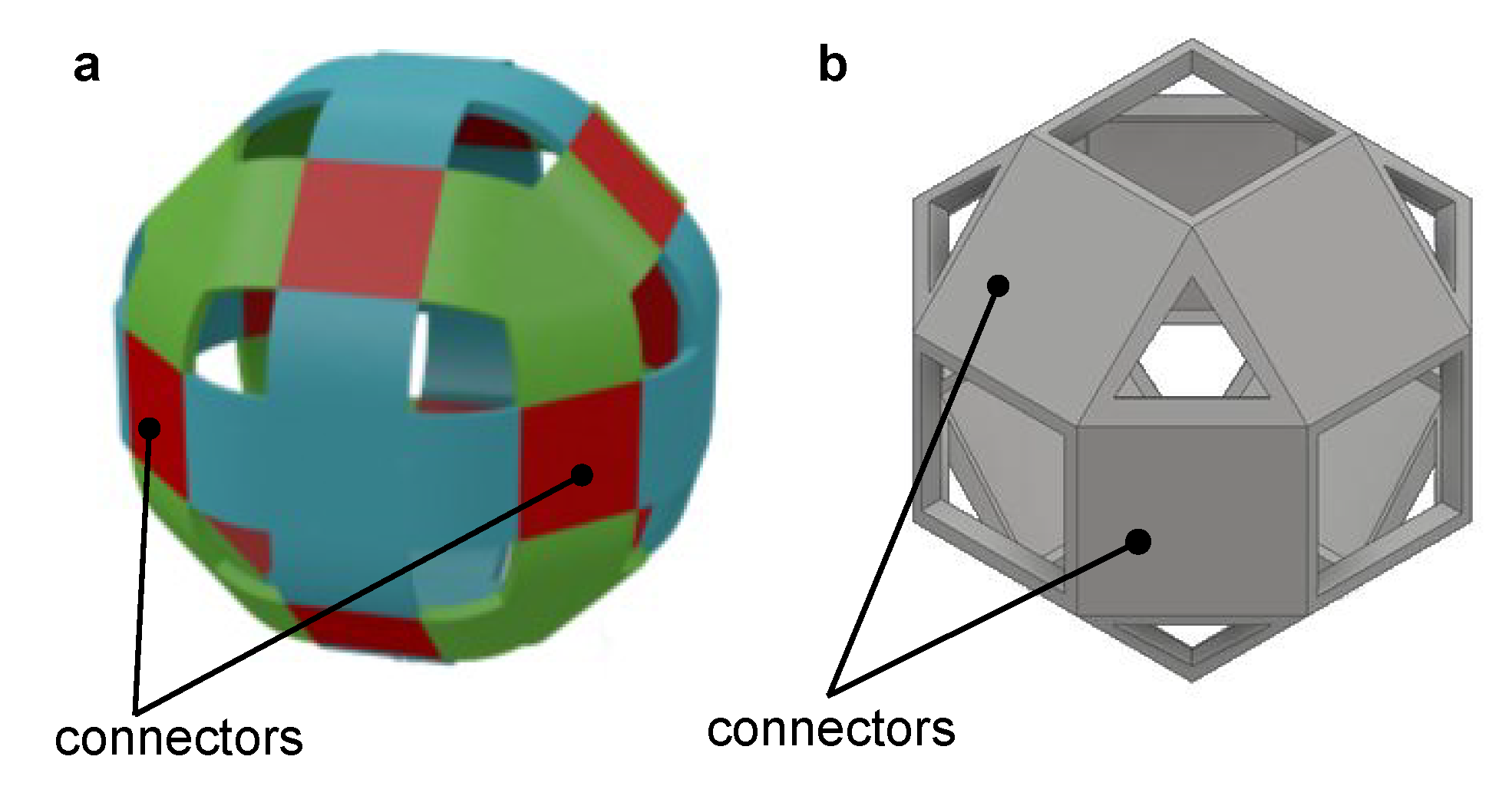
- connection between several catoms with minimization of void space between them in order to regularly fill a 3D space,
- large contact and electrodes surfaces between two catoms in order to maximize the efficiency of electrostatic actuation,
- centimeter scale for the catom size and ease of miniaturization,
- mass fabrication possibility.
2. Catom’s Shape and Modeling of the Actuation
2.1. Quasi-Spherical Catom as a Module
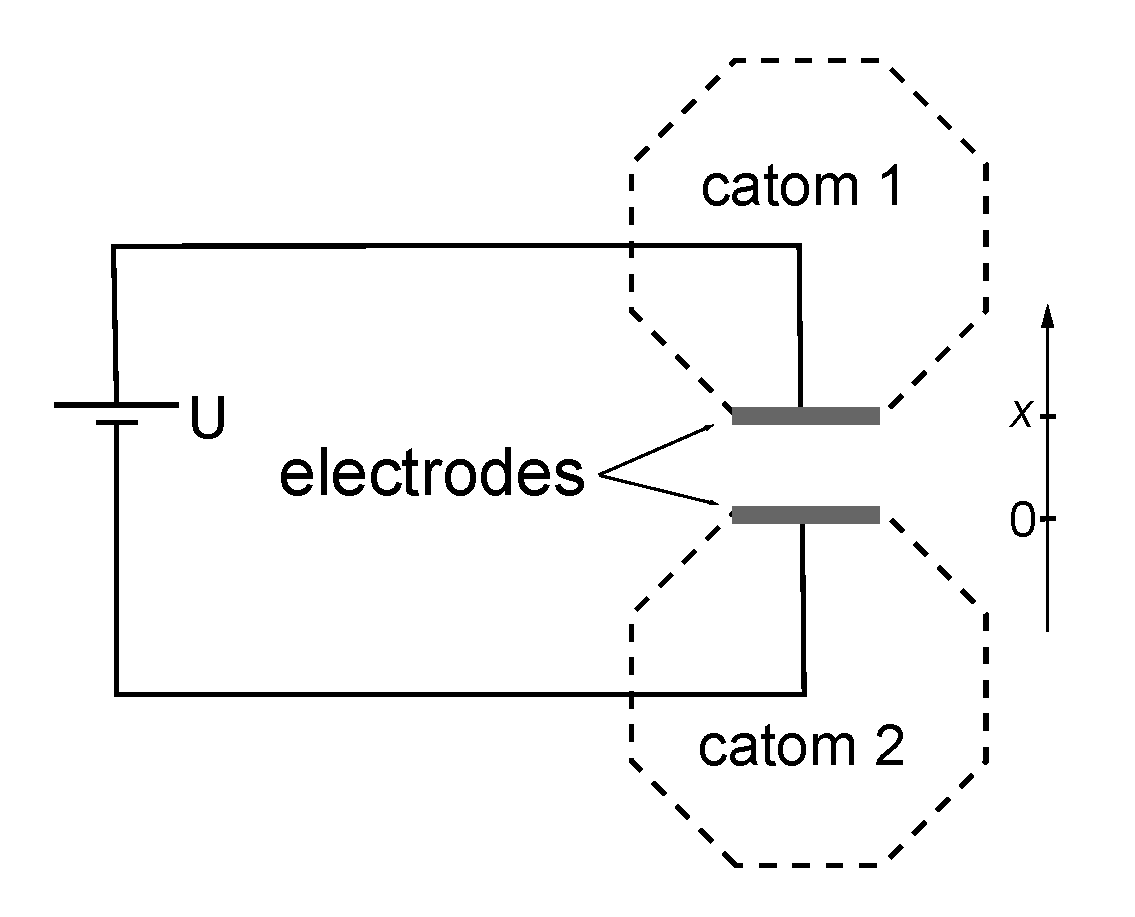
2.2. Principle of Electrostatic Latching
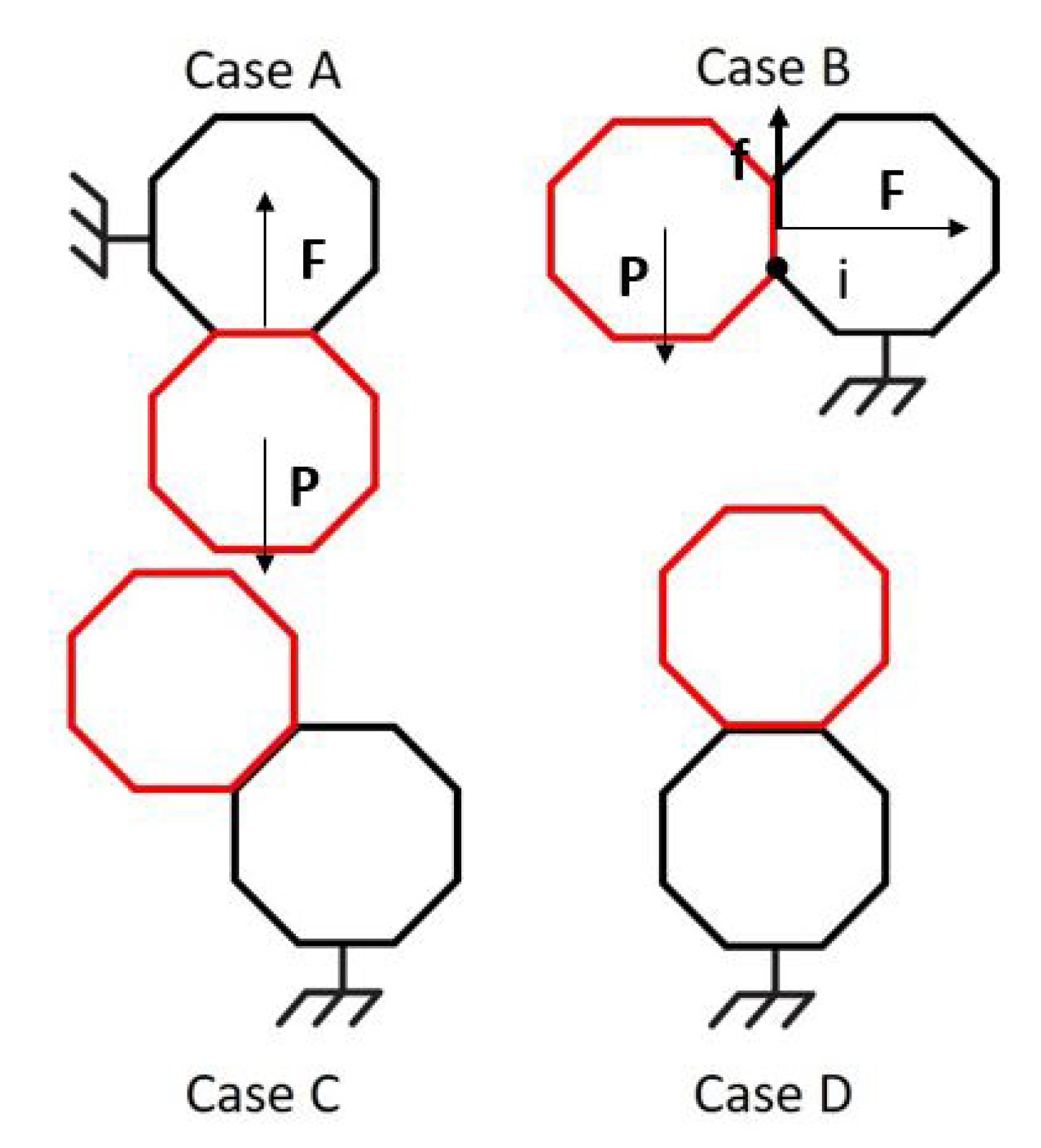
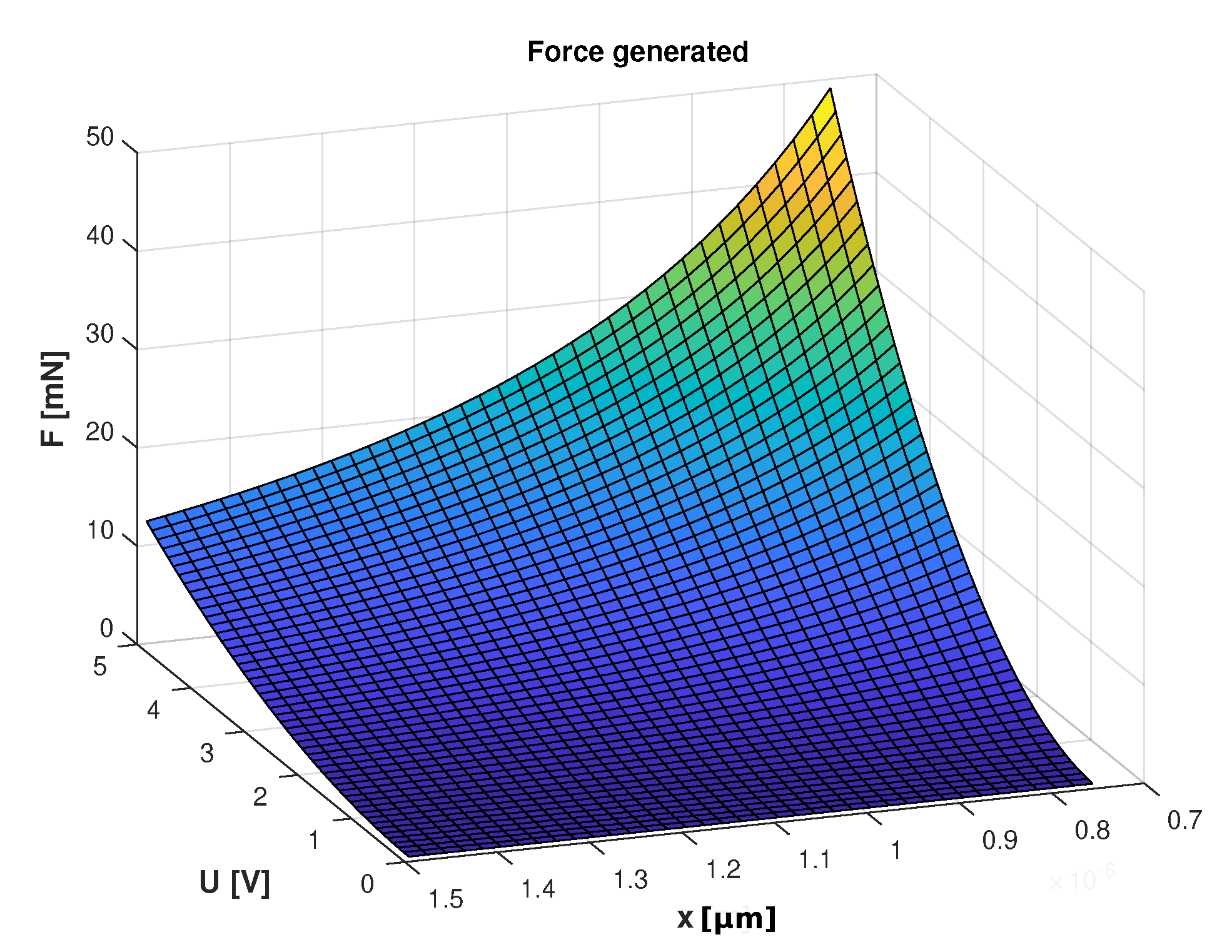
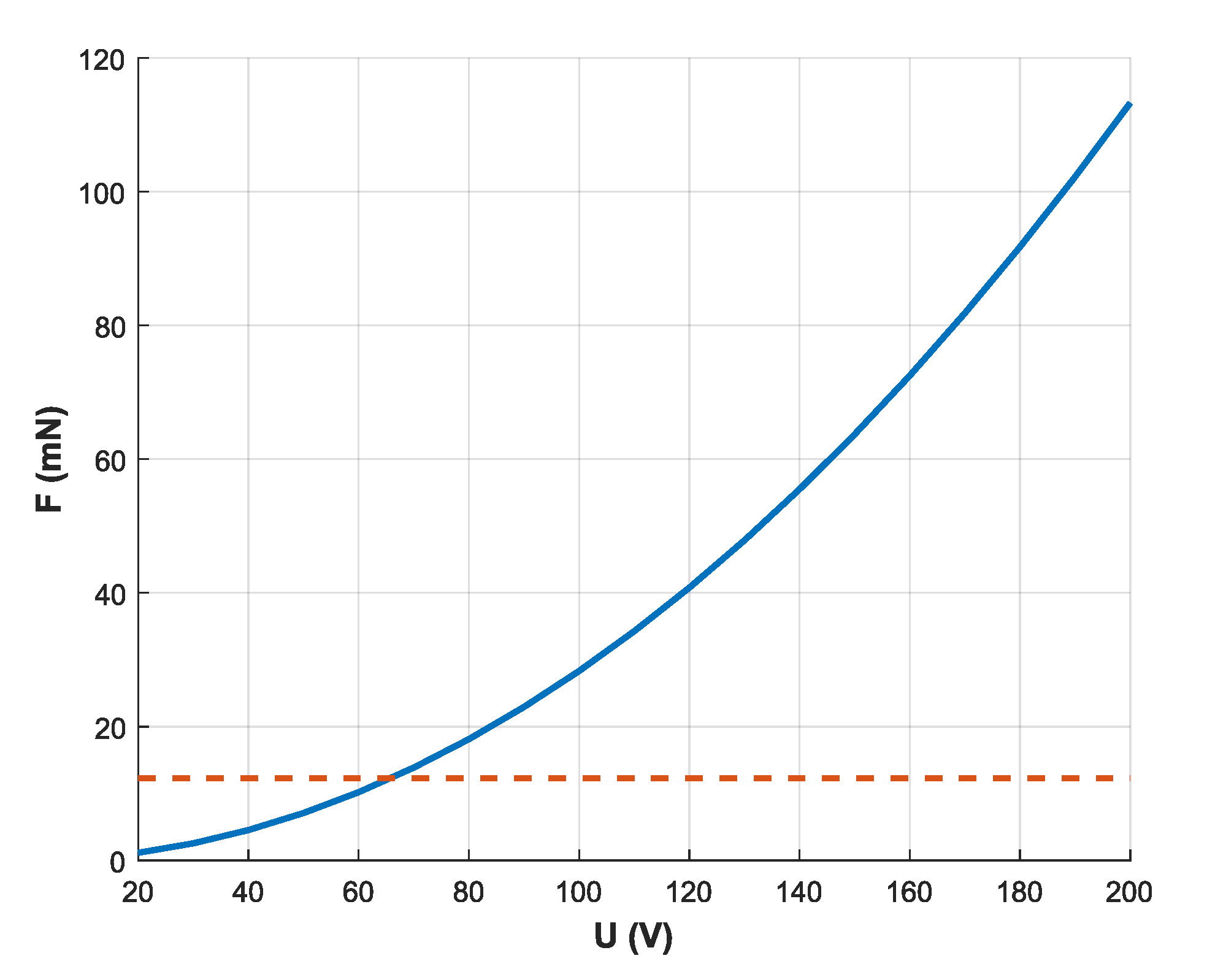
2.3. Simulations
3. Fabrication of the Catoms
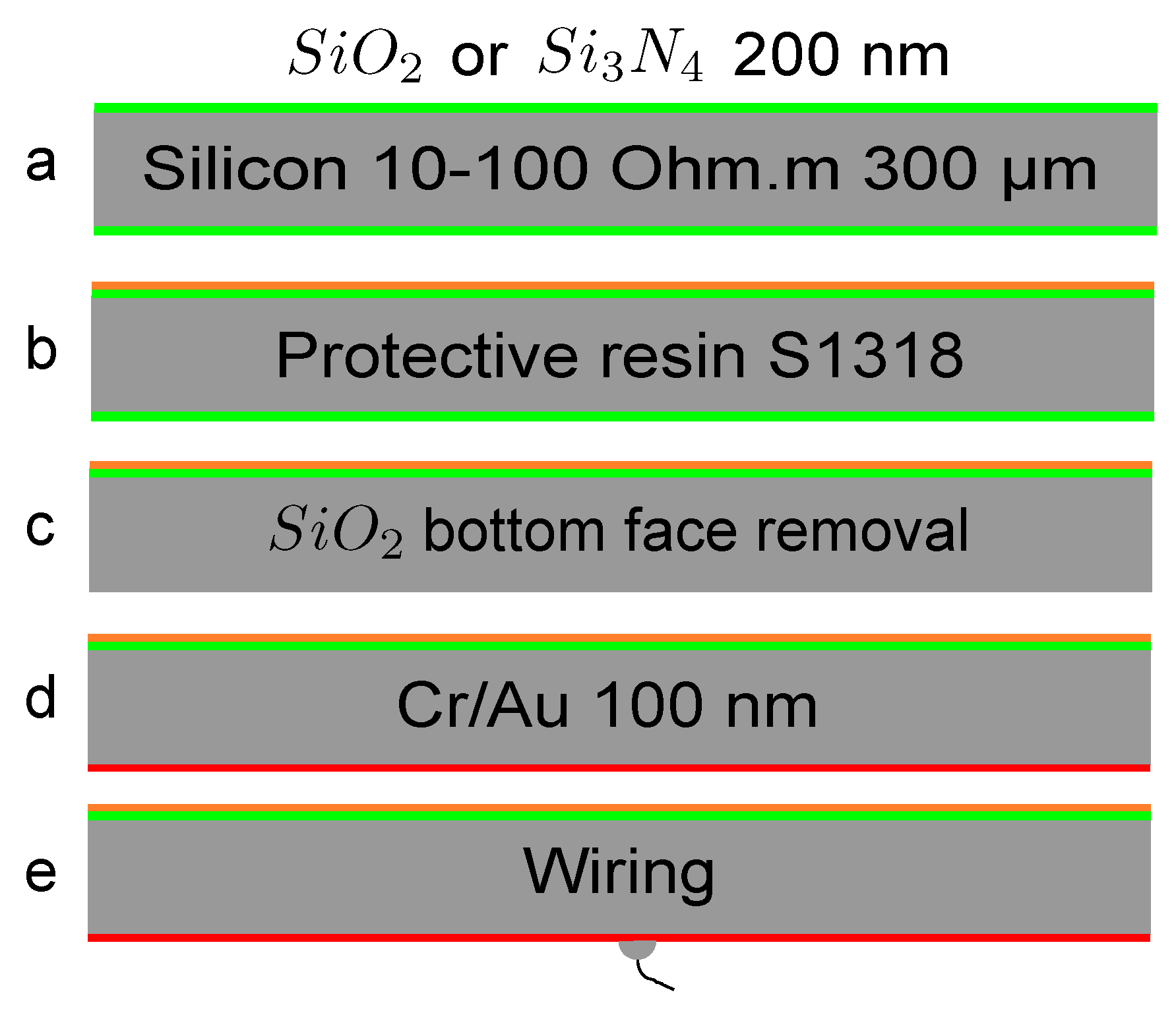
3.1. Realization of the Catom Structure
3.2. Clean Room Process
4. Experimental Validation
4.1. Presentation of the Experimental Benchmark
- -
- a tensile test machine equipped with a load cell having a force capability up to 2 N with a resolution of 3 mN. The top part of the machine is the moving part which produces a tensile force. The bottom part is fixed and connected to a load cell which acts as the sensor.
- -
- two catoms fixed on the jaws of the tensile machine. One catom is fixed on the top of the machine while the second is fixed on the bottom of the machine.
- -
- a generator that can provide a voltage up to 200 V allowing to supply the electrodes of the catoms.
- -
- and a computer and acquisition system used to acquire signals from the tensile machine, to visualize and to record data, and to analyze them.
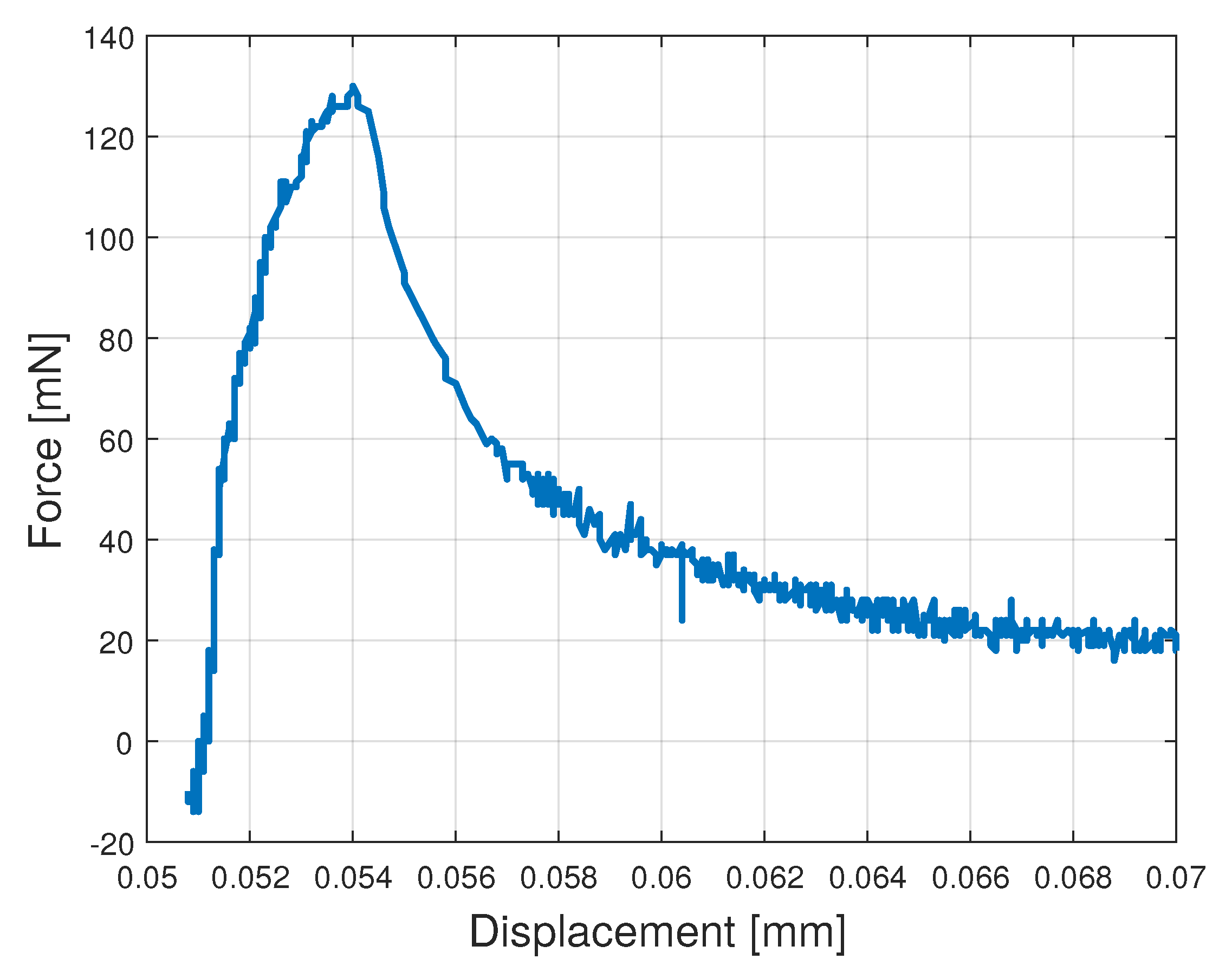
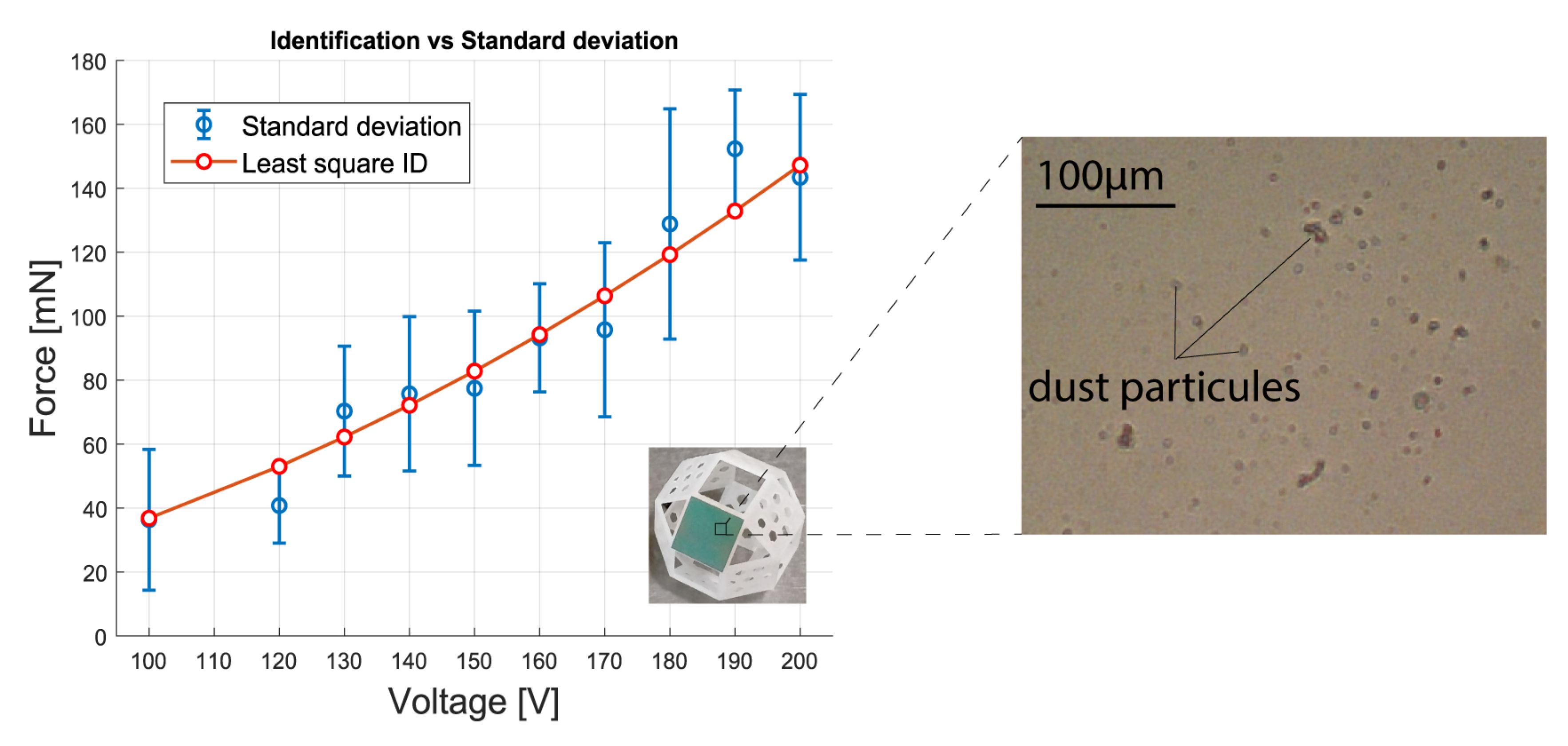
4.2. Tests and Results
- 1-
- The first catom is clamped to the bottom jaw of the tensile machine.
- 2-
- The second catom is placed on top of the first one.
- 3-
- The two catoms are powered to latch them together.
- 4-
- The second catom is clamped to the top jaw of the tensile machine while latching to the first catom.
- 5-
- The tensile test begins by moving up the top jaw of the tensile machine with a constant speed of 1 μm/s.
4.3. Discussions
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Toffoli, T.; Margolus, N. Programmable matter: Concepts and realization. Phys. D 1991, 47, 263–272. [Google Scholar] [CrossRef]
- Yim, M.; White, P.; Park, M.; Sastra, J. Modular Self-Reconfigurable Robots. In Encyclopedia of Complexity and Systems Science; Springer: New York, NY, USA, 2009; pp. 5618–5631. [Google Scholar]
- Fukuda, T.; Ueyama, T.; Kawauchi, Y.; Arai, F. Concept of cellular robotic system (CEBOT) and basic strategies for its realization. Comput. Electr. Eng. 1992, 18, 11–39. [Google Scholar] [CrossRef]
- Satoshi, M.; Eiichi, Y.; Kohji, T.; Kurokawa, H.; Kammimura, A.; Kokaji, S. Hardware Design of Modular Robotic System; IEEE IROS: Piscataway, NJ, USA, 2000. [Google Scholar]
- Romanishin, J.W.; Gilpin, K.; Rus, D. M-Blocks: Momentum-Driven Magnetic Modular Robots. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Tokyo, Japan, 3–7 November 2013; pp. 4288–4295. [Google Scholar]
- Available online: http://www.cs.cmu.edu/~claytronics/hardware/helium.html (accessed on 3 June 2020).
- Garcia, R.F.M.; Hiller, J.D.; Lipson, H. A Vacuum-Based Bonding Mechanism for Modular Robotics; IEEE ICRA Workshop: Piscataway, NJ, USA, 2010. [Google Scholar]
- Kotay, K.; Rus, D.; Vona, M.; McGray, C. The Self-Reconfiguring Robotic Molecule; IEEE: Piscataway, NJ, USA, 1998. [Google Scholar]
- Murata, S.; Kurokawa, H.; Yoshida, E.; Tomita, K.; Kokaji, S. A 3-D Self-Reconfigurable Structure; IEEE ICRA: Leuven, Belgium, 1998; pp. 432–439. [Google Scholar]
- Jorgensen, M.W.; Ostergaard, E.H.; Lund, H.H. Modular ATRON: Modules for a Self-Reconfigurable Robot; IEEE IROS: Piscataway, NJ, USA, 2004; Volume 2, pp. 2068–2073. [Google Scholar]
- Chirikjian, G. Kinematics of a Metamorphic Robotic System; IEEE ICRA: Leuven, Belgium, 1994; pp. 449–455. [Google Scholar]
- Will, P.; Castano, A.; Shen, W. Robot modularity for self-reconfiguration. Proc. SPIE 1999, 3839, 236–245. [Google Scholar] [CrossRef]
- Belisle, R.; Yu, C.; Nagpal, R. Mechanical design and locomotion of modular-expanding robots. In Proceedings of the IEEE 2010 International Conference on Roboticsand Automation Workshop, Modular Robotics: State of the Art, New York, NY, USA, 3 May 2010; pp. 17–23. [Google Scholar]
- Karagozler, M.E. Design, Fabrication and Characterization of an Autonomous, Sub-Millimeter Scale Modular Robot. Ph.D. Thesis, CMU, Pittsburgh, PA, USA, 2012. [Google Scholar]
- Gilpin, K.; Knaian, A.; Rus, D. Robot Pebbles: One Centimeter Modules for Programmable Matter through Selfdisassembly; IEEE ICRA: Leuven, Belgium, 2010; pp. 2485–2492. [Google Scholar]
- Piranda, B.; Laurent, G.; Bourgeois, J.; Clévy, C.; Mobes, S.; Le Fort-Piat, N. A new concept of planar self-reconfigurable modular robot for conveying microparts. Mechatronics 2016, 23, 906–915. [Google Scholar] [CrossRef]
- Ostergaard, E.H.; Kassow, K.; Beck, R.; Lund, H.H. Design of the ATRON lattice-based self-reconfigurable robot. Auton. Robot. 2006, 21, 165–183. [Google Scholar] [CrossRef]
- Pengwang, T.E.; Rabenorosoa, K.; Rakotondrabe, M.; Andreff, N. Scanning micromirror platform based on MEMStechnology for medical applications. Micromachines 2016, 7, 24. [Google Scholar] [CrossRef] [PubMed]
- Available online: https://projects.femto-st.fr/programmable-matter/teams (accessed on 3 June 2020).
- Piranda, B.; Bourgeois, J. Designing a quasi-spherical module for a huge modular robot to create programmable matter. Auton. Robot. 2018, 42, 1619–1633. [Google Scholar] [CrossRef]
- Available online: http://eesemi.com/sio2si3n4.htm (accessed on 3 June 2020).



| Labels | Force | Energy | Miniaturization | Integration | Movement |
|---|---|---|---|---|---|
| Mech | 2 | 3 | 3 | 2 | 1 |
| P mag | 2 | 1 | 4 | 3 | 4 |
| E mag | 5 | 4 | 2 | 4 | 2 |
| Elec | 4 * | 2 | 1 | 1 | 3 |
| Pn | 1 | 5 | 5 | 5 | 5 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Catry, R.; Mohand-Ousaid, A.; Rakotondrabe, M.; Lutz, P. Presentation, Modeling and Experiments of an Electrostatic Actuator Based Catom for Programmable Matter. Actuators 2020, 9, 43. https://doi.org/10.3390/act9020043
Catry R, Mohand-Ousaid A, Rakotondrabe M, Lutz P. Presentation, Modeling and Experiments of an Electrostatic Actuator Based Catom for Programmable Matter. Actuators. 2020; 9(2):43. https://doi.org/10.3390/act9020043
Chicago/Turabian StyleCatry, Romain, Abdenbi Mohand-Ousaid, Micky Rakotondrabe, and Philippe Lutz. 2020. "Presentation, Modeling and Experiments of an Electrostatic Actuator Based Catom for Programmable Matter" Actuators 9, no. 2: 43. https://doi.org/10.3390/act9020043
APA StyleCatry, R., Mohand-Ousaid, A., Rakotondrabe, M., & Lutz, P. (2020). Presentation, Modeling and Experiments of an Electrostatic Actuator Based Catom for Programmable Matter. Actuators, 9(2), 43. https://doi.org/10.3390/act9020043






