Research on an Electromagnetic Actuator for Vibration Suppression and Energy Regeneration
Abstract
1. Introduction
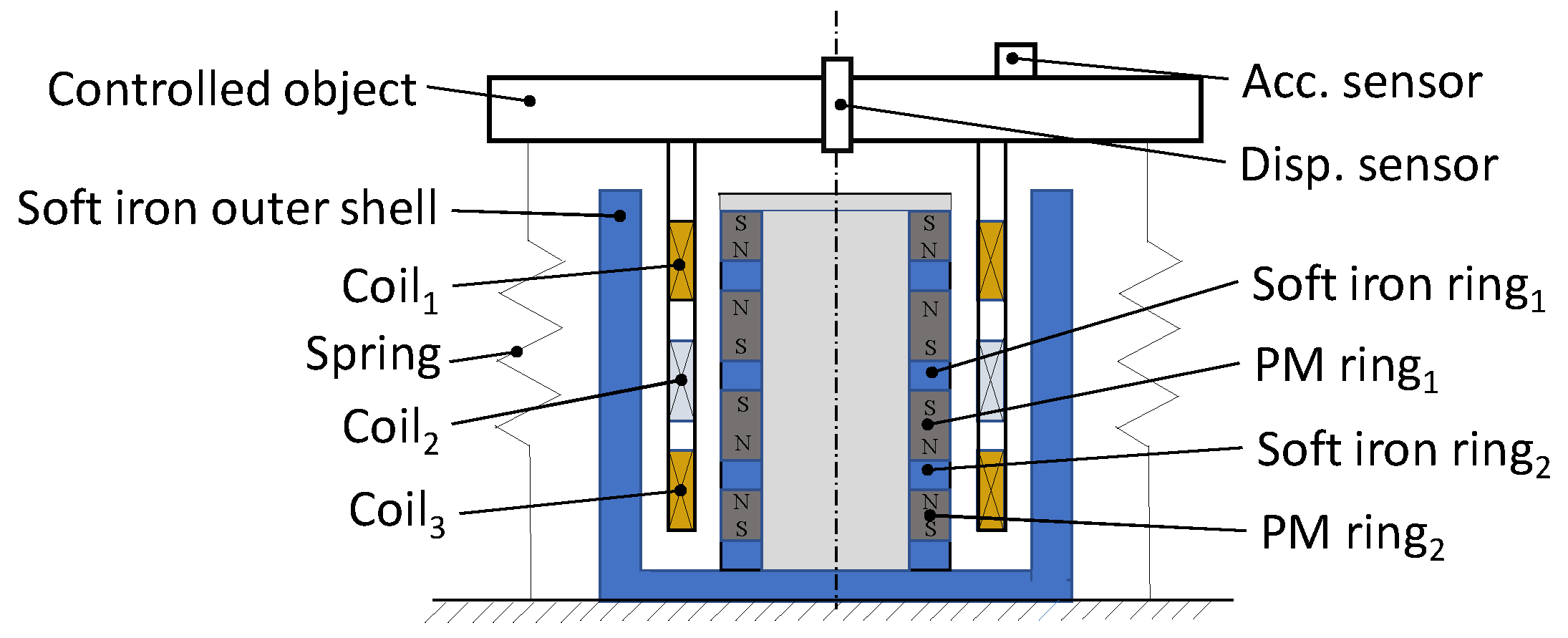
2. Structure and Working Functions
2.1. Structure
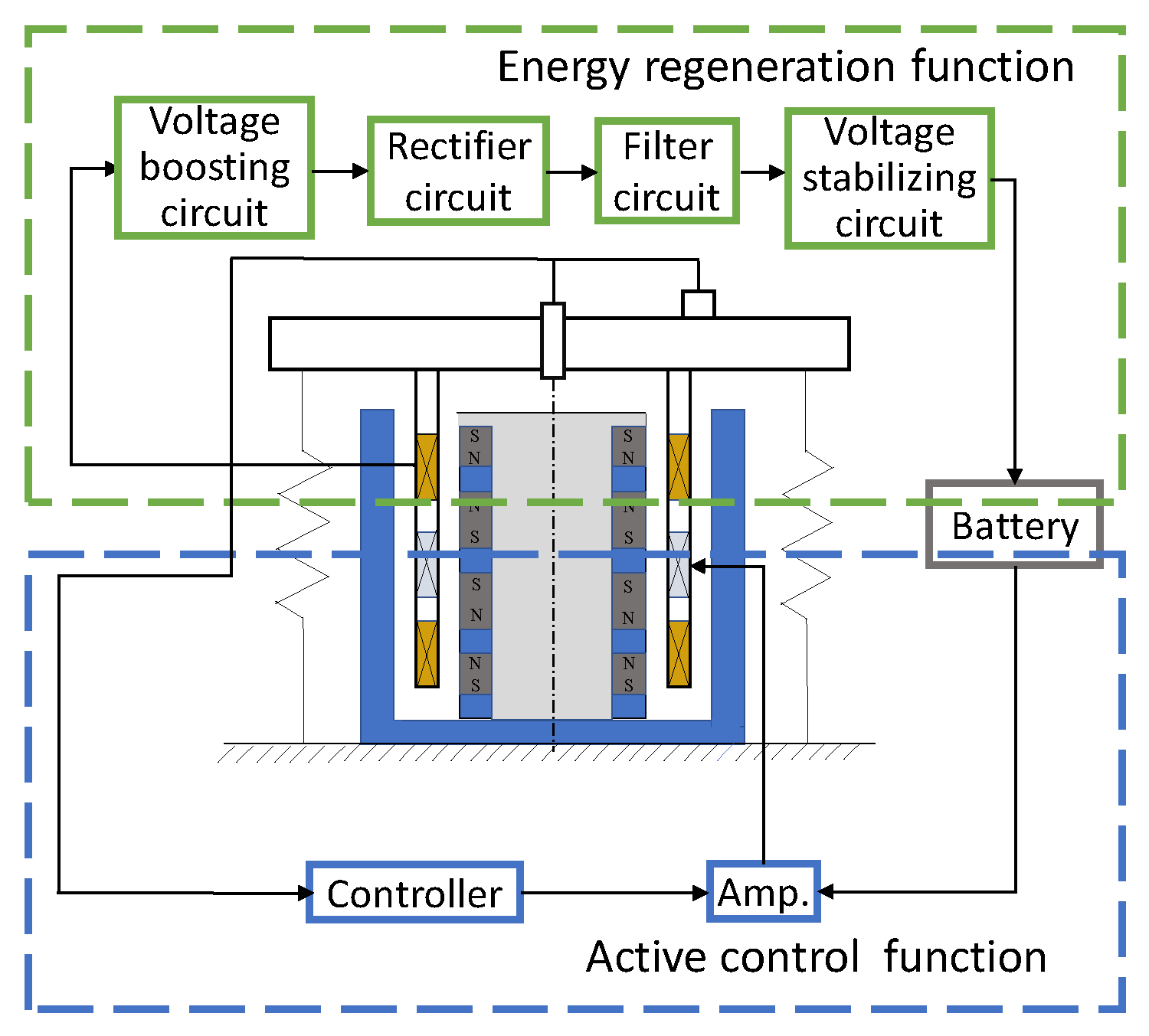
2.2. Working Functions
3. Design and Fabrication of the Electromagnetic Actuator
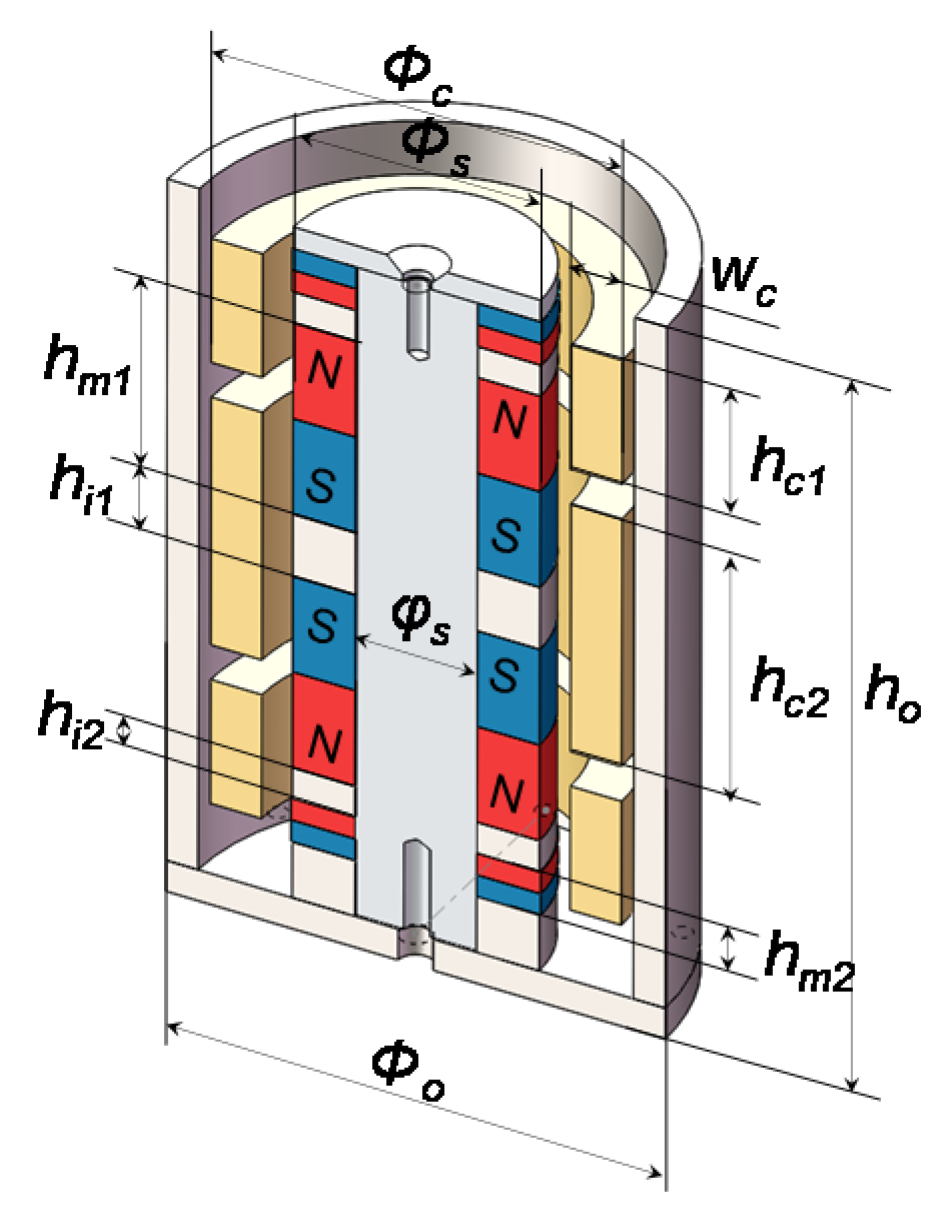
3.1. Design of the Electromagnetic Actuator
3.2. Fabrication of the Prototype
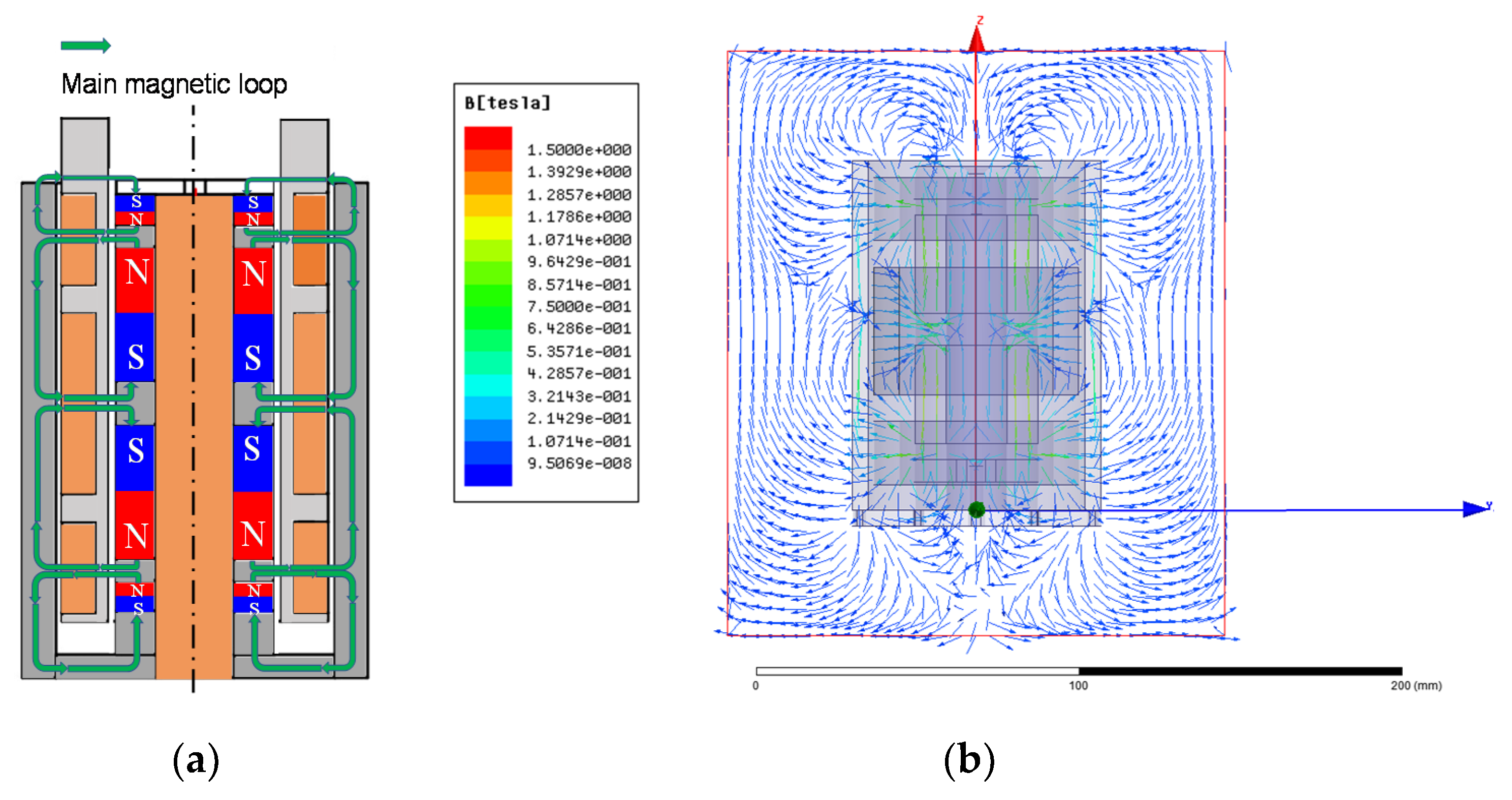
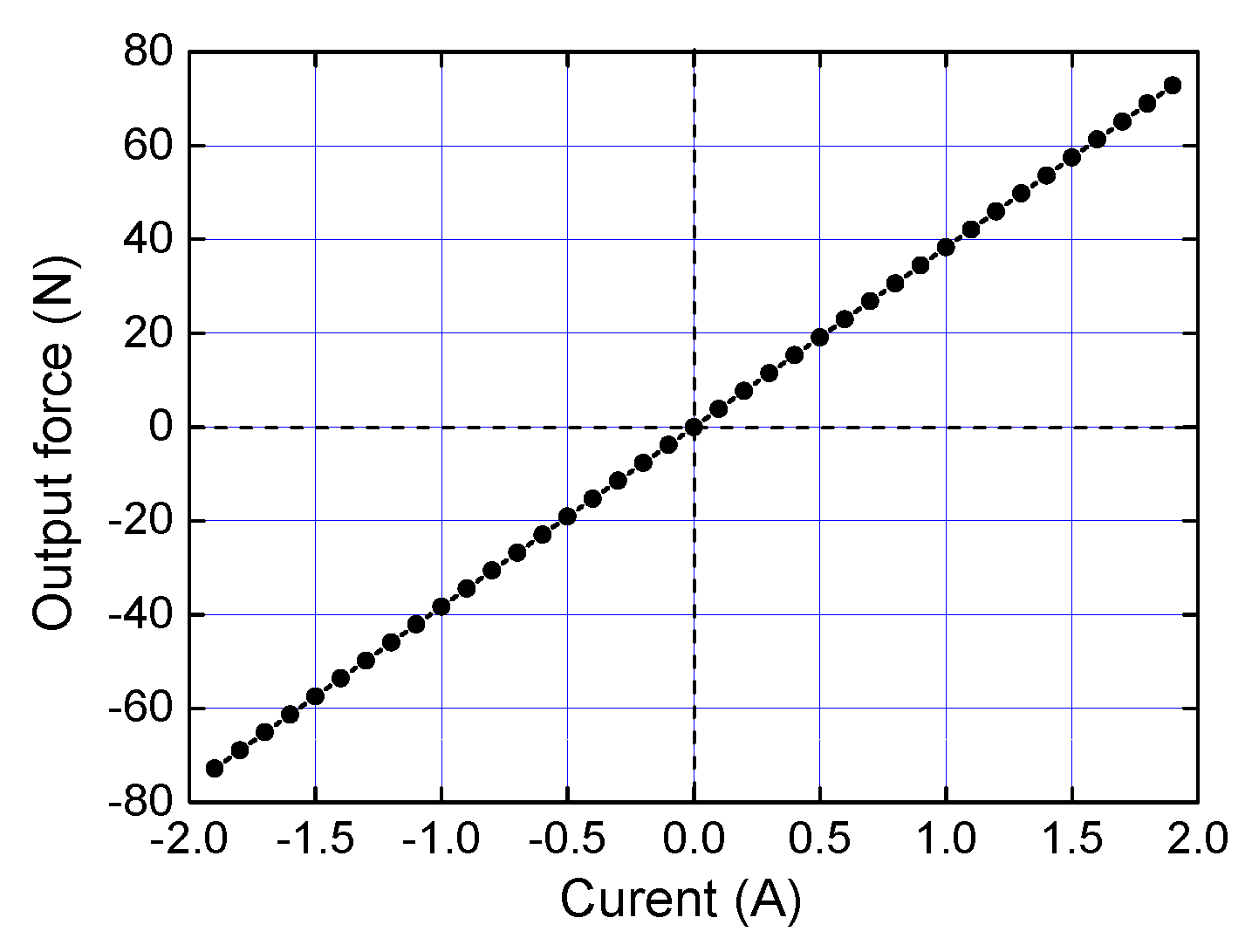
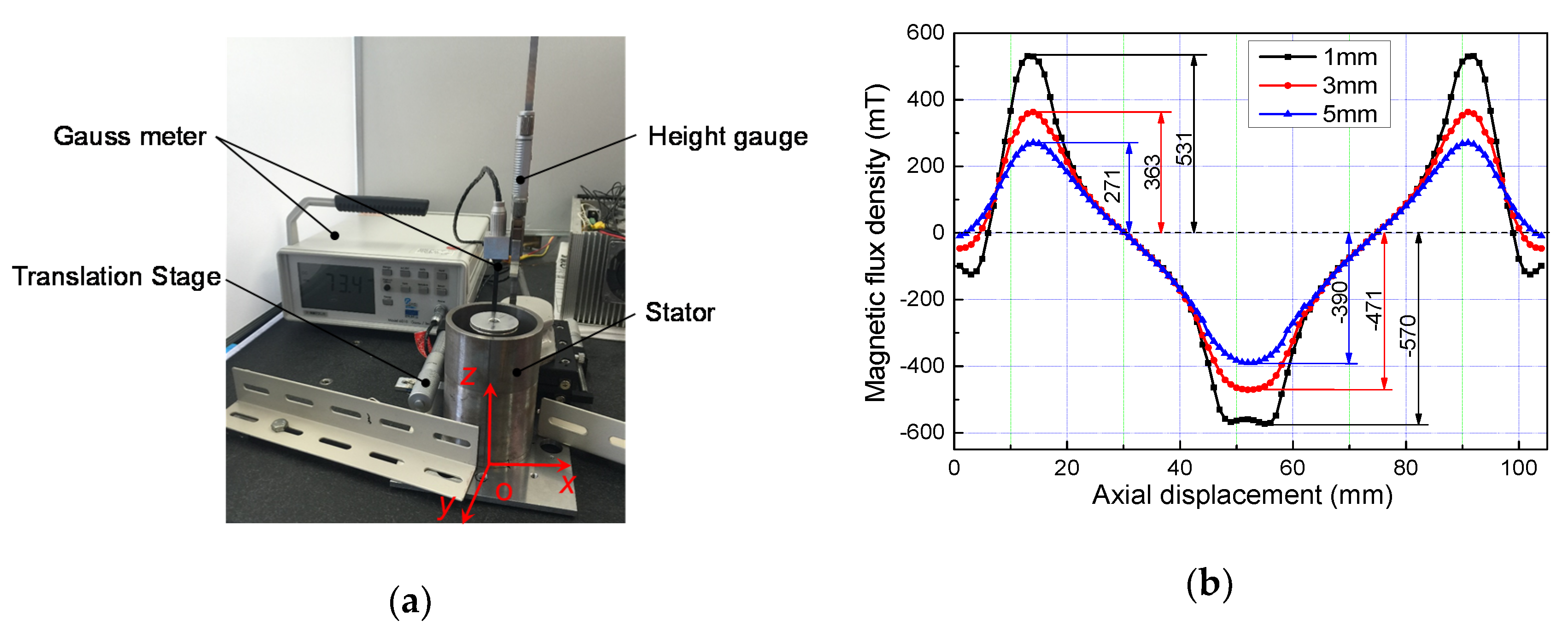
3.3. Characteristics of the Electromagnetic Actuator
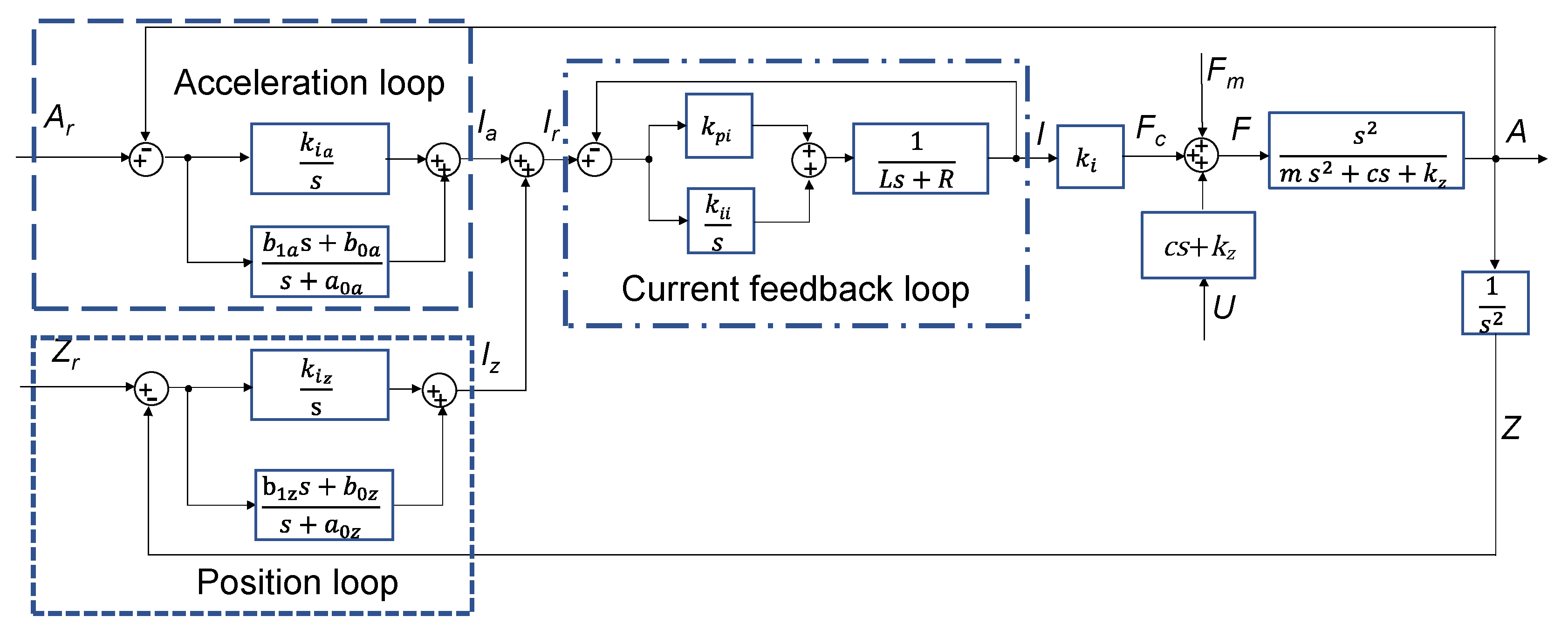
4. Control System
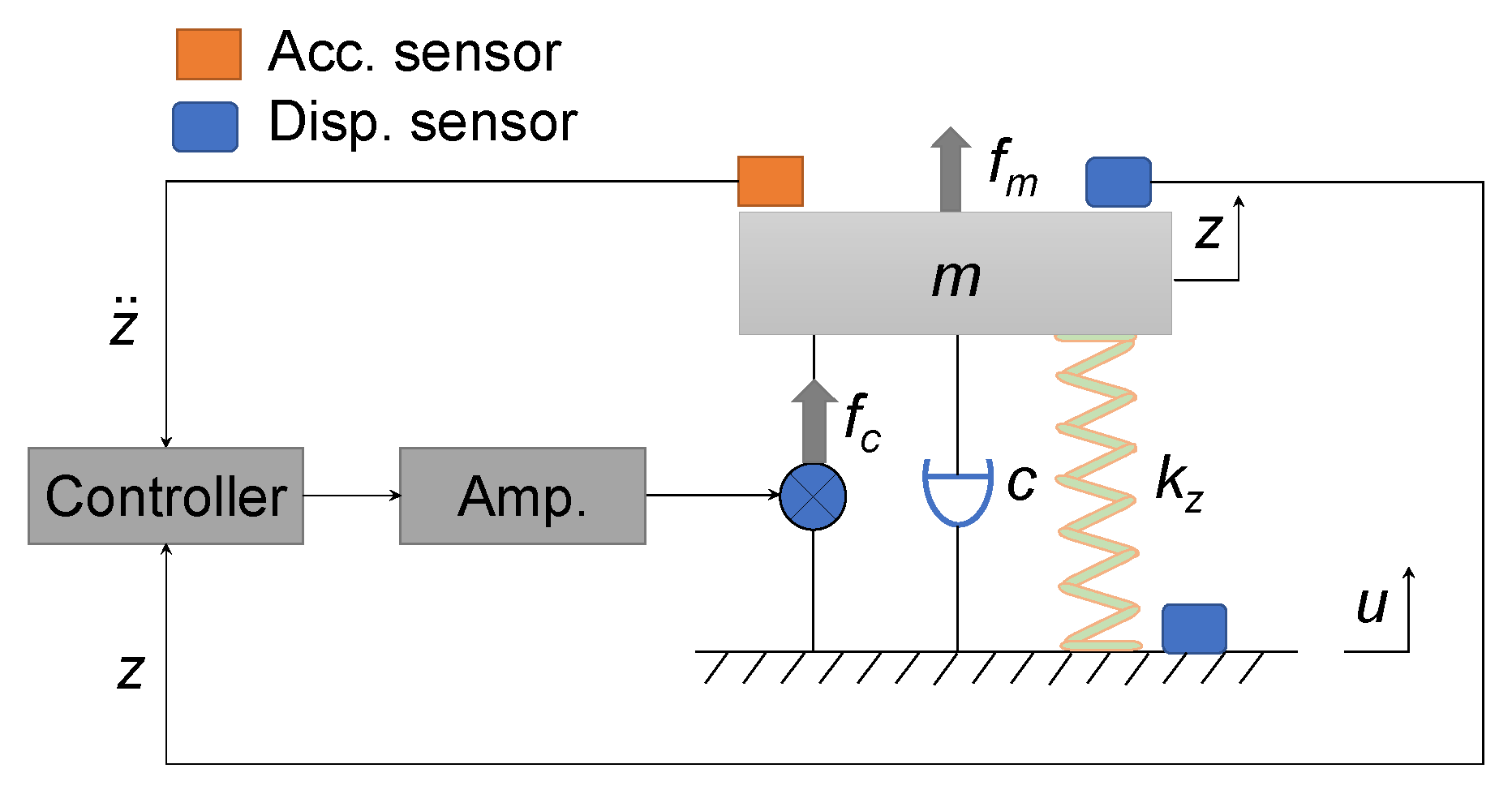
4.1. Dynamics Model
4.2. Controller Design
5. Experimental Results
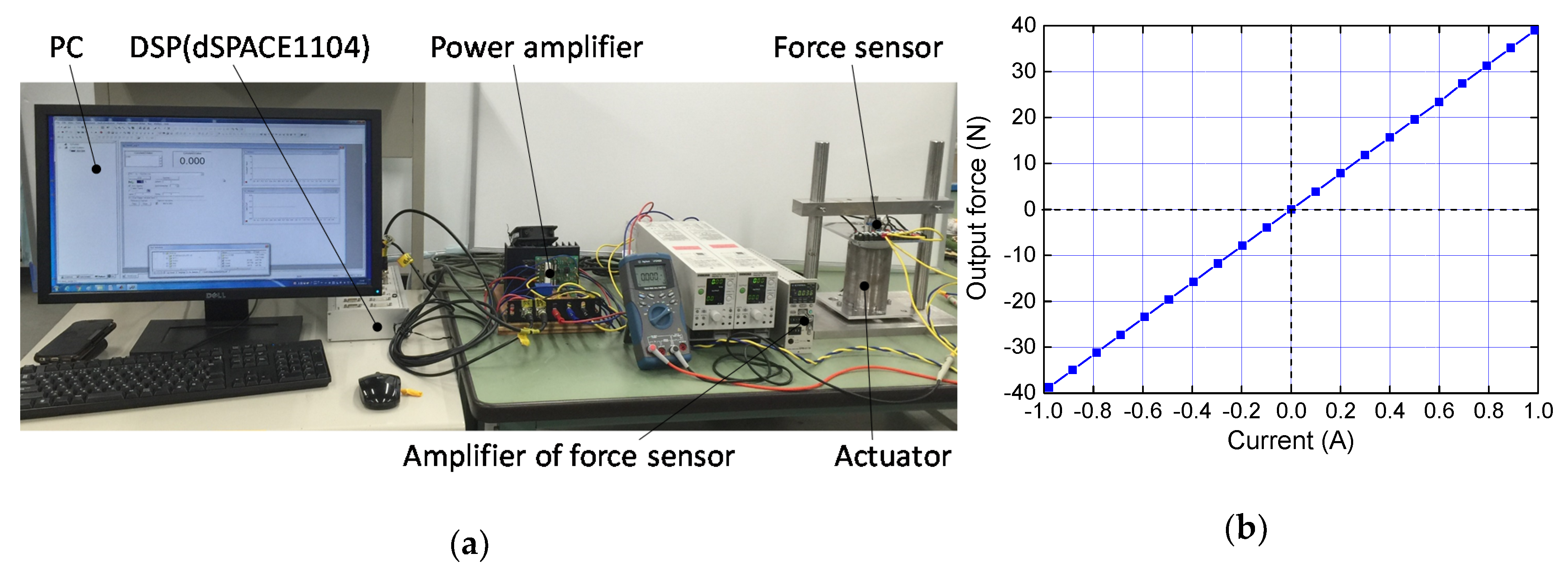
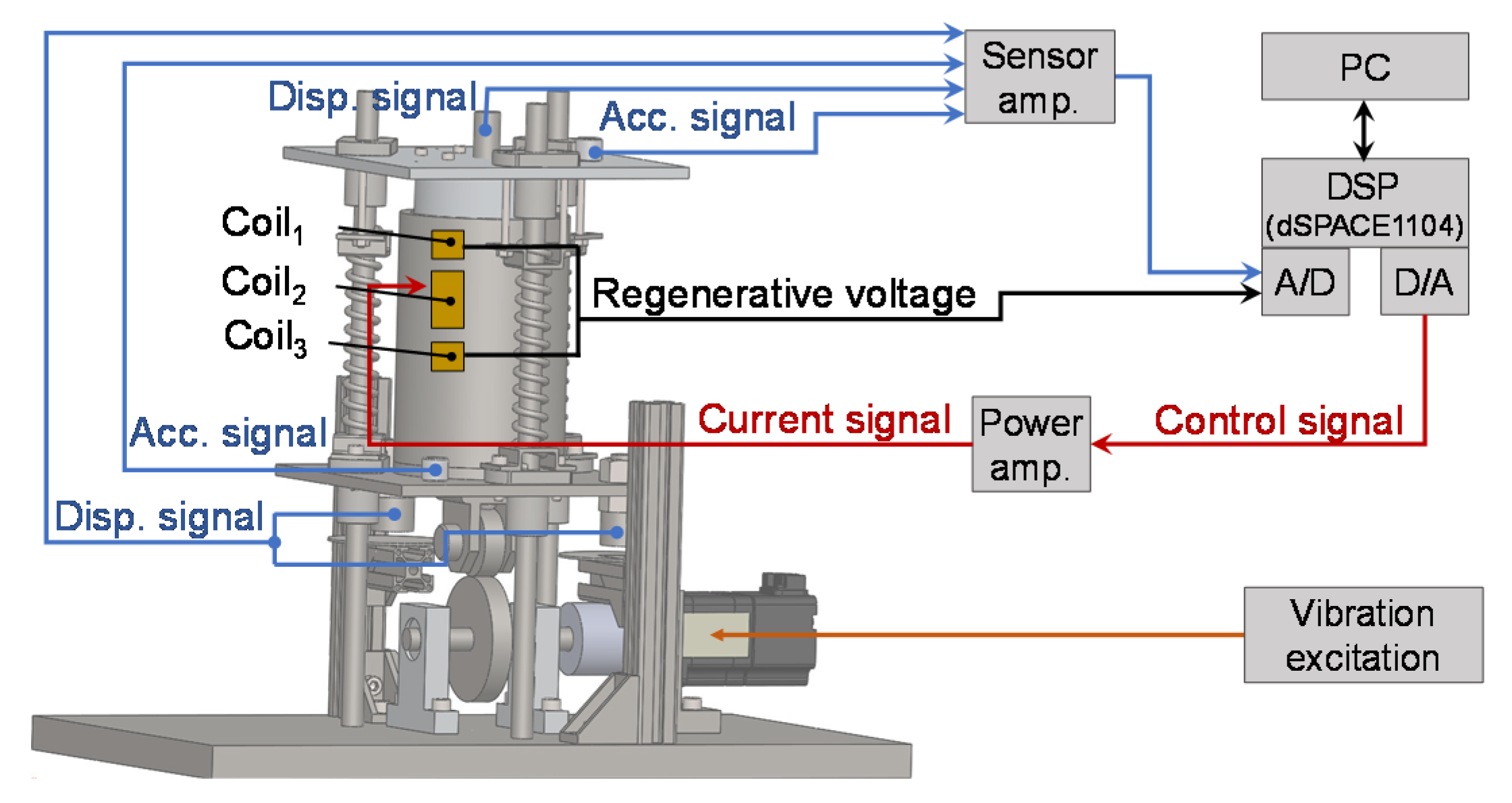
5.1. Experimental Control System
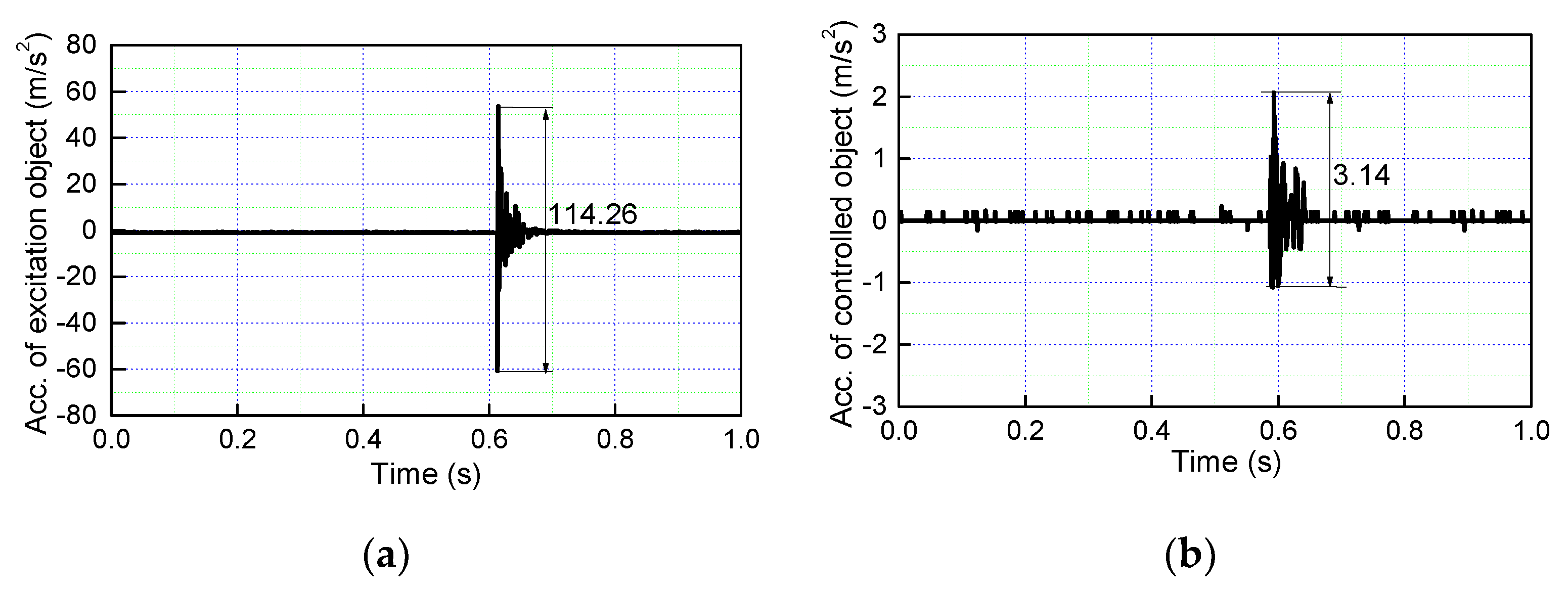
5.2. Impulse Excitation Response
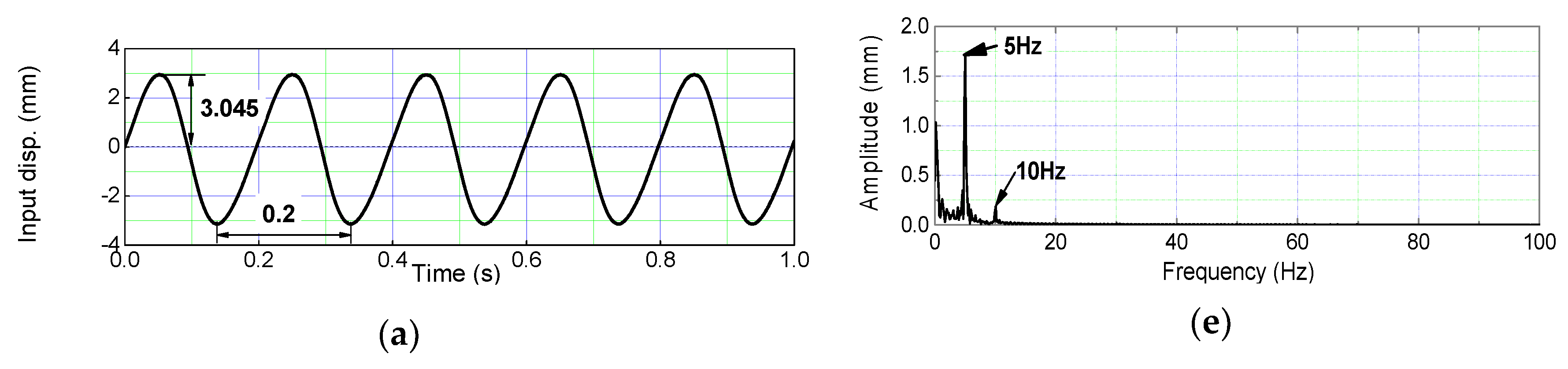
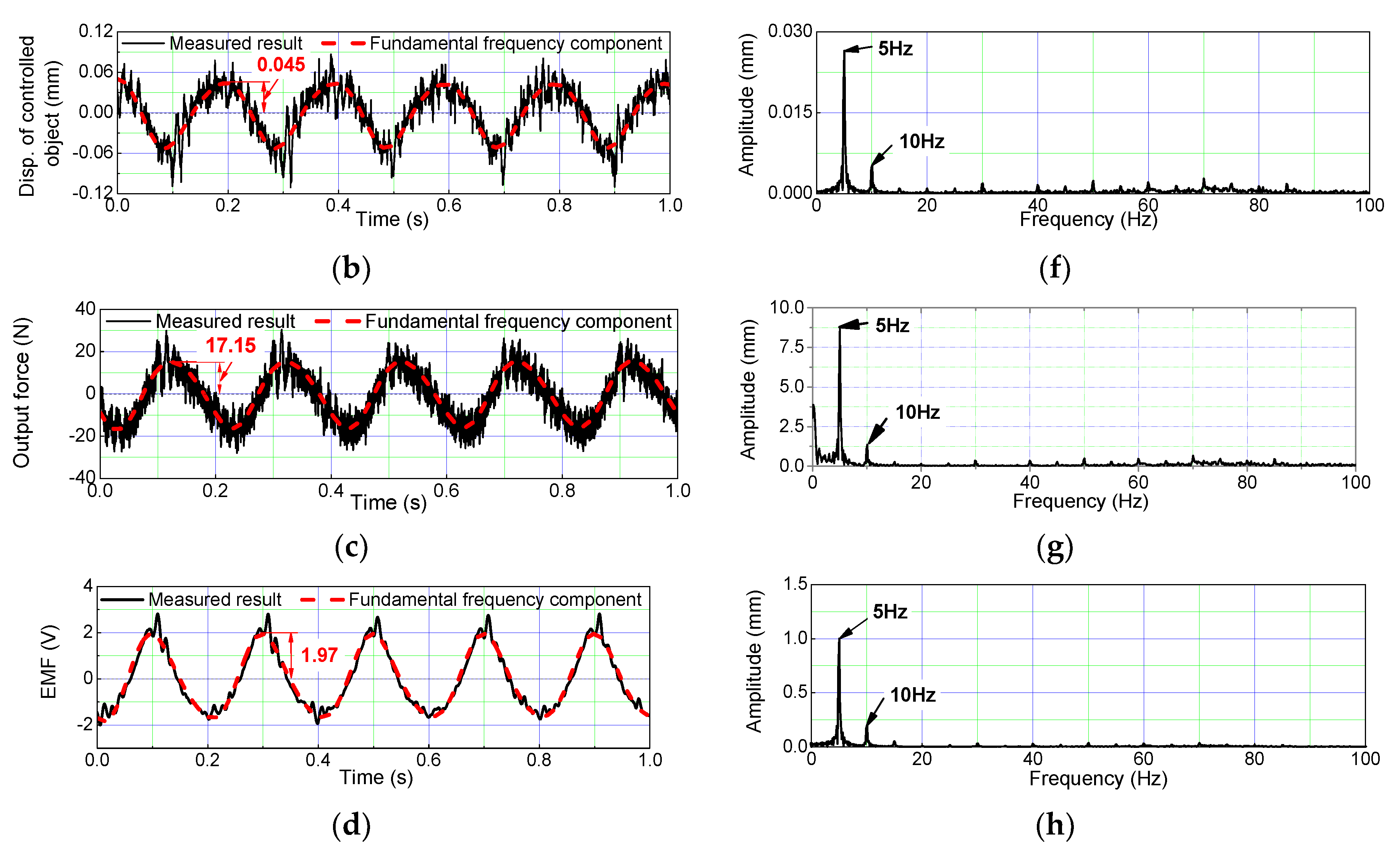
5.3. Sinusoidal Excitation Response
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hoque, M.E.; Mizuno, T.; Ishino, Y.; Takasaki, M. A three-axis vibration isolation system using modified zero-power controller with parallel mechanism technique. Mechatronics 2011, 6, 1055–1062. [Google Scholar] [CrossRef]
- Fu, J.; Li, P.; Liao, G.; Lai, J.; Yu, M. Development and dynamic characterization of a mixed mode magnetorheological elastomer isolator. IEEE T. Magn. 2017, 53, 13–17. [Google Scholar] [CrossRef]
- Beltran-Carbajal, F.; Valderrabano-Gonzalez, A.; Favela-Contreras, A.; Hernandez-Avila, J.L.; Lopez-Garcia, I.; Tapia-Olvera, R. An active vehicle suspension control approach with electromagnetic and hydraulic actuators. Actuators 2019, 8, 35. [Google Scholar] [CrossRef]
- Pomorski Linessio, R.; Sousa, K.D.M.; Silva, T.D.; Bavastri, C.A.; Antunes, P.F.D.C.; Silva, J.C.C.D. Induction motors vibration monitoring using a viaxial optical fiber accelerometer. IEEE Sens. J. 2016, 16, 8075–8082. [Google Scholar] [CrossRef]
- Liu, H.; Cui, S.; Liu, Y.; Ren, Y.; Sun, Y. Design and Vibration Suppression Control of a Modular Elastic Joint. Sensors 2018, 18, 1869. [Google Scholar] [CrossRef]
- Braz César, M.; Coelho, J.P.; Gonçalves, J. Semi-active vibration control of a non-collocated civil structure using evolutionary-based BELBIC. Actuators 2019, 8, 43. [Google Scholar] [CrossRef]
- Chen, A.; He, G. Wind-induced vibration analysis and remote monitoring test of wind turbine power tower. Adv. Mater. Res. 2013, 639–640, 293–296. [Google Scholar] [CrossRef]
- Zhang, B.; Li, Y. Nonlinear vibration of rotating pre-deformed blade with thermal gradient. Nonlinear Dyn. 2016, 86, 459–478. [Google Scholar] [CrossRef]
- Xu, Z.; Xu, F.; Chen, X. Vibration suppression on a platform by using vibration isolation and mitigation devices. Nonlinear Dyn. 2016, 83, 1341–1353. [Google Scholar] [CrossRef]
- Le, T.D.; Ahn, K.K. Experimental investigation of a vibration isolation system using negative stiffness structure. Int. J. Mech. Sci. 2013, 70, 99–112. [Google Scholar] [CrossRef]
- Wu, Q.; Cui, N.; Zhao, S.; Zhang, H.; Liu, B. Modeling and control of a six degrees of freedom maglev vibration isolation system. Sensors 2019, 19, 3608. [Google Scholar] [CrossRef] [PubMed]
- Moradi, H.; Vossoughi, G.; Behzad, M.; Movahhedy, R.M. Vibration absorber design to suppress regenerative chatter in nonlinear milling process: Application for machining of cantilever plates. Appl. Math. Model. 2015, 39, 600–620. [Google Scholar] [CrossRef]
- Rosbi, S.; Ryu, T.; Nakae, T.; Matsuzaki, K.; Sueoka, A.; Takikawa, Y.; Ooi, Y. Evaluation of dynamic absorber to suppress subharmonic nonlinear vibration in car powertrain. Mech. Eng. J. 2015, 2, 14–00528. [Google Scholar] [CrossRef][Green Version]
- Stelzer, G.J.; Schulz, M.J.; Kim, J.; Allemang, R.J. A magnetorheological semi-active isolator to reduce noise and vibration transmissibility in automobiles. J. Intell. Mater. Syst. Struct. 2003, 14, 743–765. [Google Scholar] [CrossRef]
- Yang, J.; Xiong, Y.P.; Xing, J.T. Vibration power flow and force transmission behaviour of a nonlinear isolator mounted on a nonlinear base. Int. J. Mech. Sci. 2016, 115–116, 238–252. [Google Scholar] [CrossRef]
- Wang, X.; Zhou, J.; Xu, D.; Ouyang, H.; Duan, Y. Force transmissibility of a two-stage vibration isolation system with quasi-zero stiffness. Nonlinear Dyn. 2017, 87, 633–646. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, C.; Gao, R.X.; Yan, R.; Chen, X.; Wang, S. A novel hybrid error criterion-based active control method for on-line milling vibration suppression with piezoelectric actuators and sensors. Sensors 2016, 16, 68. [Google Scholar] [CrossRef]
- Lou, J.; Wei, Y.; Li, G.; Yang, Y.; Xie, F. Optimal trajectory planning and linear velocity feedback control of a flexible piezoelectric manipulator for vibration suppression. Shock Vib. 2015, 2015, 952708. [Google Scholar] [CrossRef]
- Zhou, D.; Yu, P.; Wang, L.; Li, J. An adaptive vibration control method to suppress the vibration of the maglev train caused by track irregularities. J. Sound Vib. 2017, 408, 331–350. [Google Scholar] [CrossRef]
- Kotake, S.; Yagi, K.; Takigami, T. Application of sampled-data control by using vibration manipulation function to suppress residual vibration of travelling crane. Mech. Eng. J. 2015, 2, 15–00033. [Google Scholar] [CrossRef][Green Version]
- Shao, X.; Naghdy, F.; Du, H. Reliable fuzzy H∞ control for active suspension of in-wheel motor driven electric vehicles with dynamic damping. Mech. Syst. Signal Process. 2017, 87, 365–383. [Google Scholar] [CrossRef]
- Ze, Q.; Liang, D.; Kou, P.; Yu, Y. Improvement of power generation performance in a doubly salient permanent magnet generator with a capacitive energy recovery converter. IET Electr. Power Appl. 2017, 11, 108–120. [Google Scholar]
- Warner, H.; Simon, D.; Richter, H. Design optimization and control of a crank-slider actuator for a lower-limb prosthesis with energy regeneration. In Proceedings of the 2013 IEEE 13th International Conference on Rehabilitation Robotics (ICORR), Banff, AB, Canada, 12–15 July 2016; pp. 1–6. [Google Scholar]
- Manna, B.P.; Sims, N.D. Energy harvesting from the nonlinear oscillations of magnetic levitation. J. Sound Vib. 2009, 319, 515–530. [Google Scholar] [CrossRef]
- Elvin, N.G.; Elvin, A.A. An experimentally validated electromagnetic energy harvester. J. Sound Vib. 2011, 330, 2314–2324. [Google Scholar] [CrossRef]
- Glynne-Jones, P.; Tudor, M.J.; Beeby, S.P.; White, N.M. An electromagnetic, vibration-powered generator for intelligent sensor systems. Sens. Actuators A 2004, 110, 344–349. [Google Scholar] [CrossRef]
- Xu, G.; Xu, K.; Zheng, C.; Zhang, X.; Zahid, T. Fully electrified regenerative braking control for deep energy recovery and safety maintaining of electric vehicles. IEEE Trans. Veh. Technol. 2016, 65, 1186–1198. [Google Scholar] [CrossRef]
- Zhang, X.; Göhlich, D.; Li, J. Energy-Efficient Toque Allocation Design of Traction and Regenerative Braking for Distributed Drive Electric Vehicles. IEEE Trans. Veh. Technol. 2018, 67, 285–295. [Google Scholar] [CrossRef]
- Yan, S.; Sun, W. Self-powered suspension criterion and energy regeneration implementation scheme of motor-driven active suspension. Mech. Syst. Signal Process. 2017, 94, 297–311. [Google Scholar] [CrossRef]
- Khaligh, A.; Zeng, P.; Zheng, C. Kinetic energy harvesting using piezoelectric and electromagnetic technologies—State of the art. IEEE Trans. Ind. Electron. 2010, 57, 850–860. [Google Scholar] [CrossRef]
- Maravandi, A.; Mehrdad, M. Regenerative shock absorber using a two-leg motion conversion mechanism. IEEE ASME Trans. Mech. 2015, 20, 2853–2861. [Google Scholar] [CrossRef]
- Liu, Y.; Xu, L.; Zuo, L. Design, modeling, lab, and field tests of a mechanical-motion-rectifier-based energy harvester using a ball-screw mechanism. IEEE ASME Trans. Mech. 2017, 22, 1933–1943. [Google Scholar] [CrossRef]
- Jiang, L.; Zhang, W.; Ma, G.J.; Wu, C.W. Shape optimization of energy storage flywheel rotor. Struct. Multidiscip. Optim. 2017, 55, 739–750. [Google Scholar] [CrossRef]
- Asadi, E.; Ribeiro, R.; Khamesee, M.B.; Khajepour, A. Analysis, prototyping, and experimental characterization of an adaptive hybrid electromagnetic damper for automotive suspension systems. IEEE Trans. Veh. Technol. 2017, 66, 3703–3713. [Google Scholar] [CrossRef]
- Buren, T.; Troster, G. Design and optimization of a linear vibration-driven electromagnetic micro-power generator. Sens. Actuators A 2007, 135, 765–775. [Google Scholar] [CrossRef]
- Arroyo, E.; Badel, A.; Formosa, F. Energy harvesting from ambient vibrations: Electromagnetic device and synchronous extraction circuit. J. Intell. Mater. Syst. Struct. 2013, 24, 2023–2035. [Google Scholar] [CrossRef]
- Tang, X.; Lin, T.; Zuo, L. Design and optimization of a tubular linear electromagnetic vibration energy harvester. IEEE ASME Trans. Mechatron. 2014, 19, 615–622. [Google Scholar] [CrossRef]
- Sapiński, B. Energy-harvesting linear MR damper: Prototyping and testing. Smart Mater. Struct. 2014, 23, 035021. [Google Scholar] [CrossRef]
- Gljuš’ci’c, P.; Zelenika, S.; Blaževi´c, D.; Kamenar, E. Kinetic energy harvesting for wearable medical sensors. Sensors 2019, 19, 4922. [Google Scholar] [CrossRef]
- Liu, H.; Tay, J.; Quan, C.; Kobayashi, T.; Lee, C. Piezoelectric MEMS energy harvester for low-frequency vibrations with wideband operation range and steadily increased output power. J. Microelectromec. Syst. 2011, 20, 1131–1142. [Google Scholar] [CrossRef]
- Liu, H.; Cong, C.; Cao, C.; Zhao, Q. Analysis of the key factors affecting the capability and optimization for magnetostrictive iron-gallium alloy ambient vibration harvesters. Sensors 2020, 20, 401. [Google Scholar] [CrossRef]


| Level | Height of Coil2 (mm) A | Thickness of Coil2 (mm) B | Height of Soft Iron Ring1 (mm) C |
|---|---|---|---|
| 1 | 30 | 5 | 8 |
| 2 | 35 | 6 | 10 |
| 3 | 40 | 8 | 12 |
| Number | Height of Coil2 (mm) | Thickness of Coil2 (mm) | Height of Soft Iron Ring1 (mm) | Output Force (N) |
|---|---|---|---|---|
| 1 | A1 | B1 | C1 | 43.45 |
| 2 | A1 | B2 | C2 | 50.40 |
| 3 | A1 | B3 | C3 | 66.14 |
| 4 | A2 | B1 | C2 | 45.80 |
| 5 | A2 | B2 | C3 | 54.15 |
| 6 | A2 | B3 | C1 | 67.57 |
| 7 | A3 | B1 | C3 | 47.68 |
| 8 | A3 | B2 | C1 | 56.30 |
| 9 | A3 | B3 | C2 | 72.78 |
| Value Name | Height of Coil2 (mm) | Thickness of Coil2 (mm) | Height of Soft Iron Ring1 (mm) |
|---|---|---|---|
| Kj1 | 159.99 | 136.93 | 167.32 |
| Kj2 | 167.52 | 160.85 | 168.98 |
| Kj3 | 176.76 | 206.49 | 167.97 |
| Kjp1 | 55.33 | 45.64 | 55.77 |
| Kjp2 | 55.84 | 53.62 | 56.33 |
| Kjp3 | 58.92 | 68.83 | 55.99 |
| Rj | 5.59 | 23.19 | 0.55 |
| Primary and secondary order | B > A > C | ||
| Optimal levels | A3 | B3 | C2 |
| Optimal combination | A3B3C2 | ||
| Symbol | Description | Value (mm) |
|---|---|---|
| Φc | Coils outer diameter | 64.2 |
| Φo | Outer diameter of soft iron outer shell | 78 |
| Φs | PM rings outer diameter, soft iron rings outer diameter | 39 |
| φs | PM rings inner diameter | 19 |
| ho | Stator height | 115 |
| hm1 | PM ring1 height | 30.9 |
| hm2 | PM ring2 height | 7 |
| hi1 | Height of soft iron ring1 | 10 |
| hi2 | Height of soft iron ring2 | 5 |
| hc1 | Coil1 and coil3 height | 20 |
| hc2 | Coil2 height | 40 |
| wc | Coils thickness | 8 |
| Symbol | Value |
|---|---|
| m | 1.37 (kg) |
| kz | 4.2 (kN/m) |
| L | 21.98 (mH) |
| R2 | 21 (Ω) |
| c | 5.0 (N/(m/s)) |
| ki | 39.49 (N/A) |
| Symbol | Value |
|---|---|
| a0a | 10.5 |
| b1a | 1.3 × 10−3 |
| b0a | 3.0 |
| kia | 0 |
| Symbol | Value |
|---|---|
| a0z | 1.13 × 103 |
| b1z | 1.46 × 104 |
| b0z | 1.74 × 106 |
| kiz | 80 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, W.; Li, Q.; Xu, F.; Zhang, X.; Jin, J.; Jin, J.; Sun, F. Research on an Electromagnetic Actuator for Vibration Suppression and Energy Regeneration. Actuators 2020, 9, 42. https://doi.org/10.3390/act9020042
Wei W, Li Q, Xu F, Zhang X, Jin J, Jin J, Sun F. Research on an Electromagnetic Actuator for Vibration Suppression and Energy Regeneration. Actuators. 2020; 9(2):42. https://doi.org/10.3390/act9020042
Chicago/Turabian StyleWei, Wei, Qiang Li, Fangchao Xu, Xiaoyou Zhang, Junjie Jin, Jiaqi Jin, and Feng Sun. 2020. "Research on an Electromagnetic Actuator for Vibration Suppression and Energy Regeneration" Actuators 9, no. 2: 42. https://doi.org/10.3390/act9020042
APA StyleWei, W., Li, Q., Xu, F., Zhang, X., Jin, J., Jin, J., & Sun, F. (2020). Research on an Electromagnetic Actuator for Vibration Suppression and Energy Regeneration. Actuators, 9(2), 42. https://doi.org/10.3390/act9020042





