Multi-Fidelity Design Optimisation of a Solenoid-Driven Linear Compressor
Abstract
:1. Introduction
2. Compressor Design
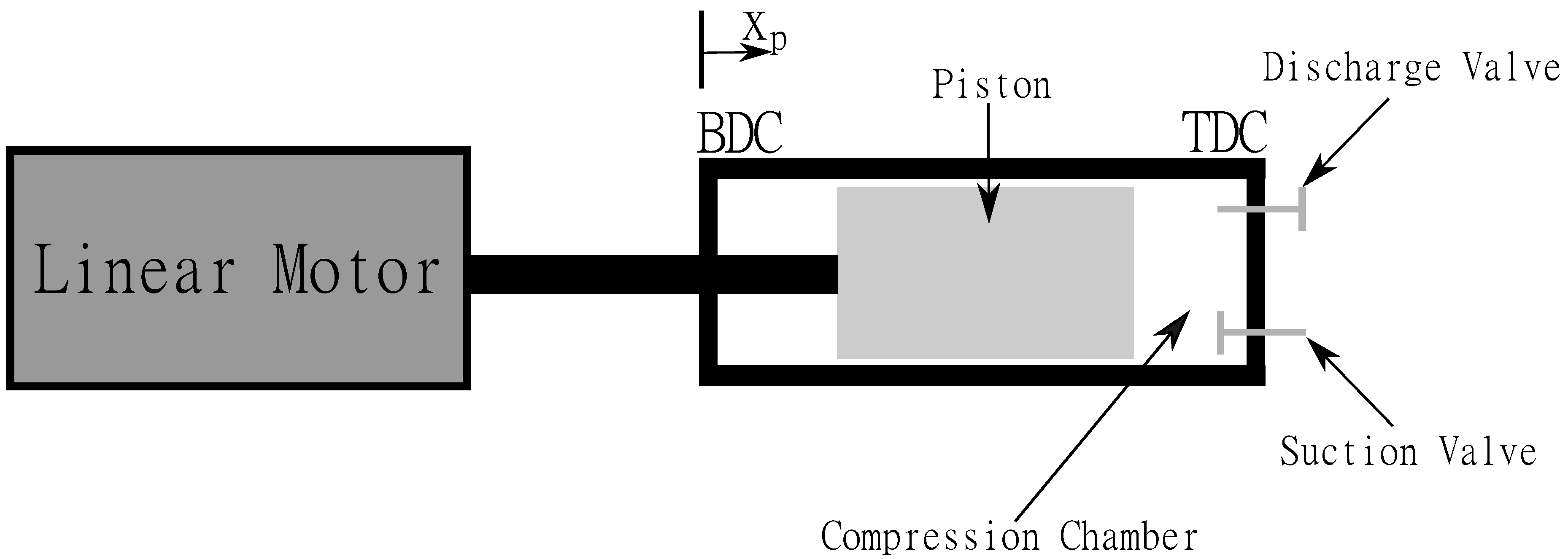
2.1. Reciprocating Compressor Kit RCK-1 Configuration
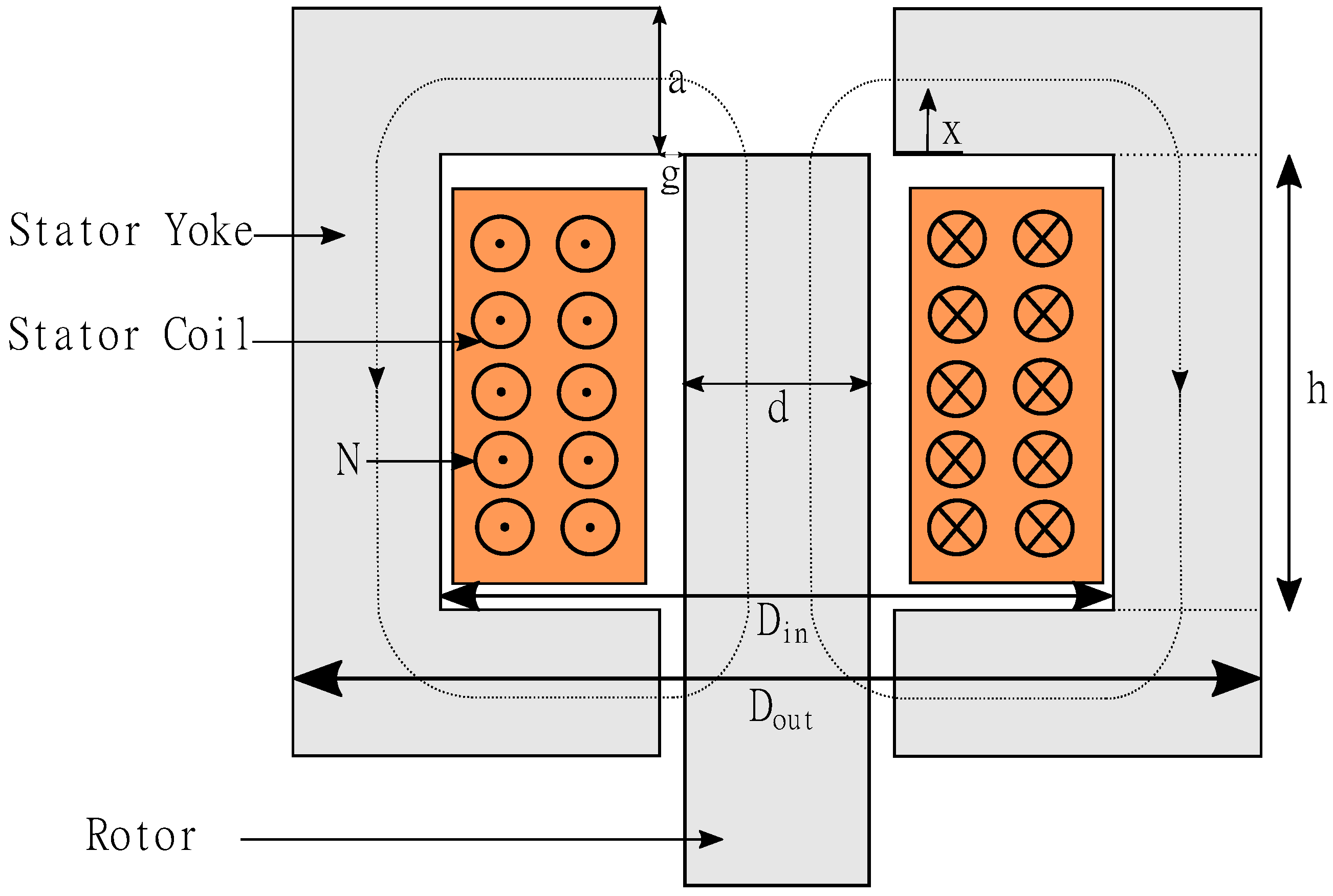
2.2. Electromagnetic Design
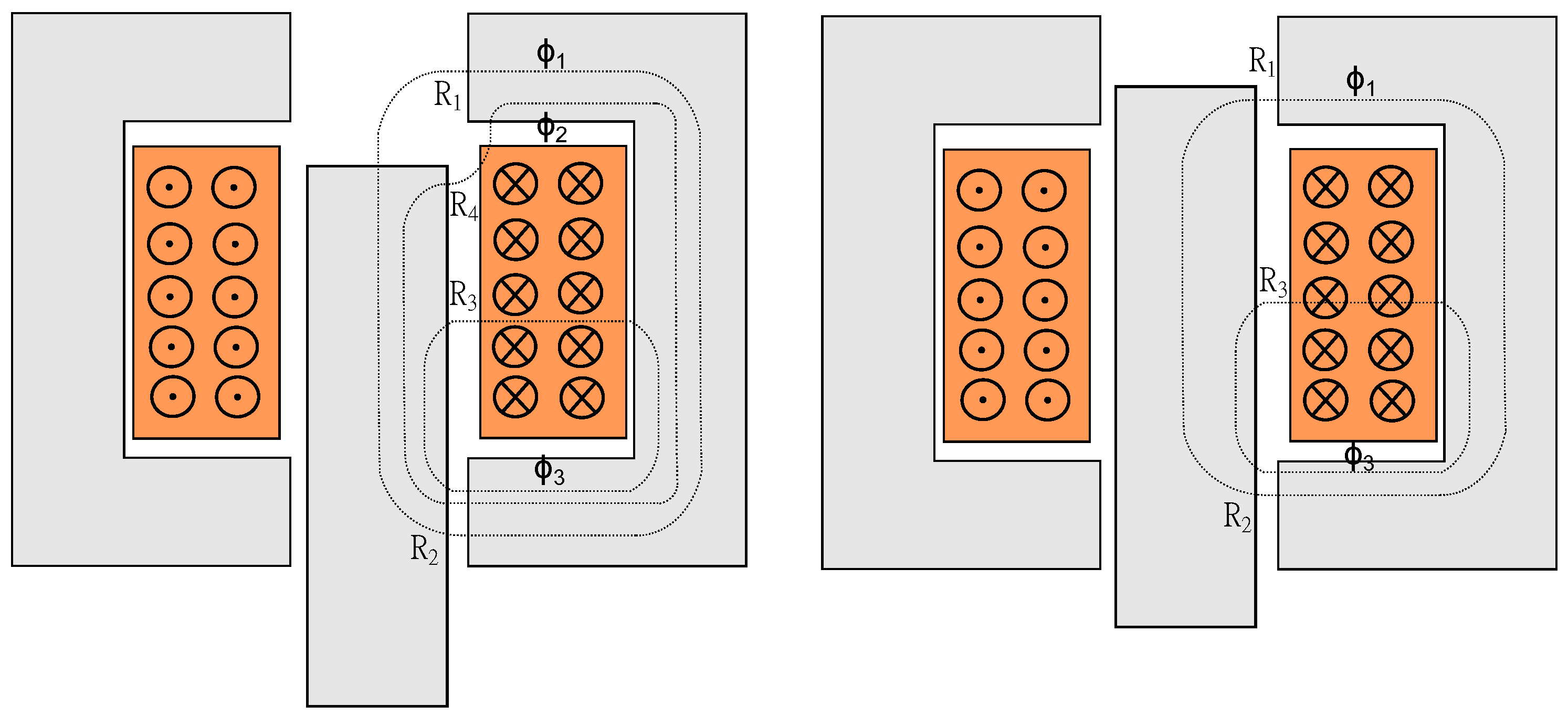
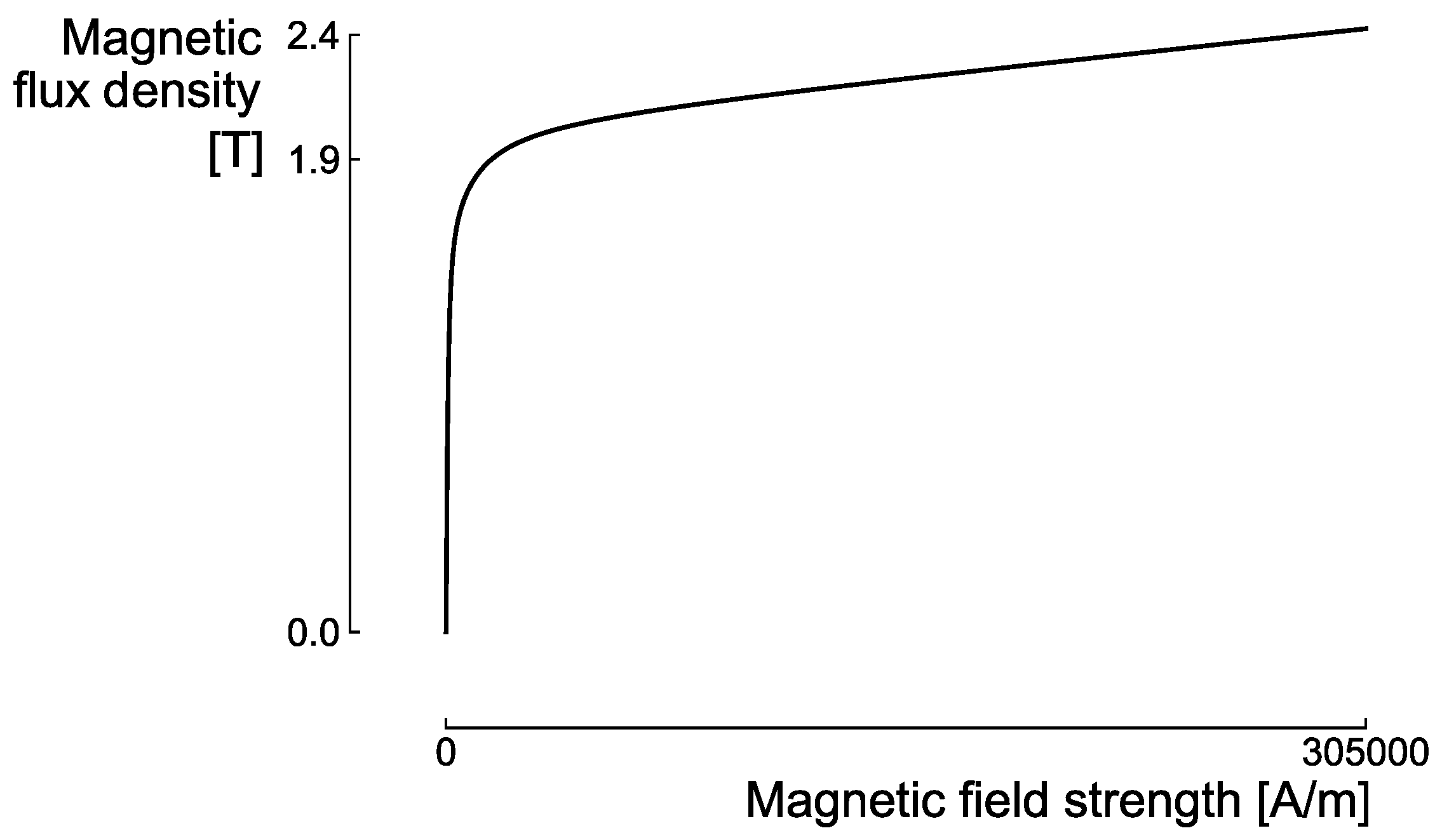
2.2.1. Analytical Model
- the left configuration corresponds to and illustrates three main flux paths and ;
- the right configuration corresponds to and simplifies to two main flux paths and .
2.2.2. Finite Element Method
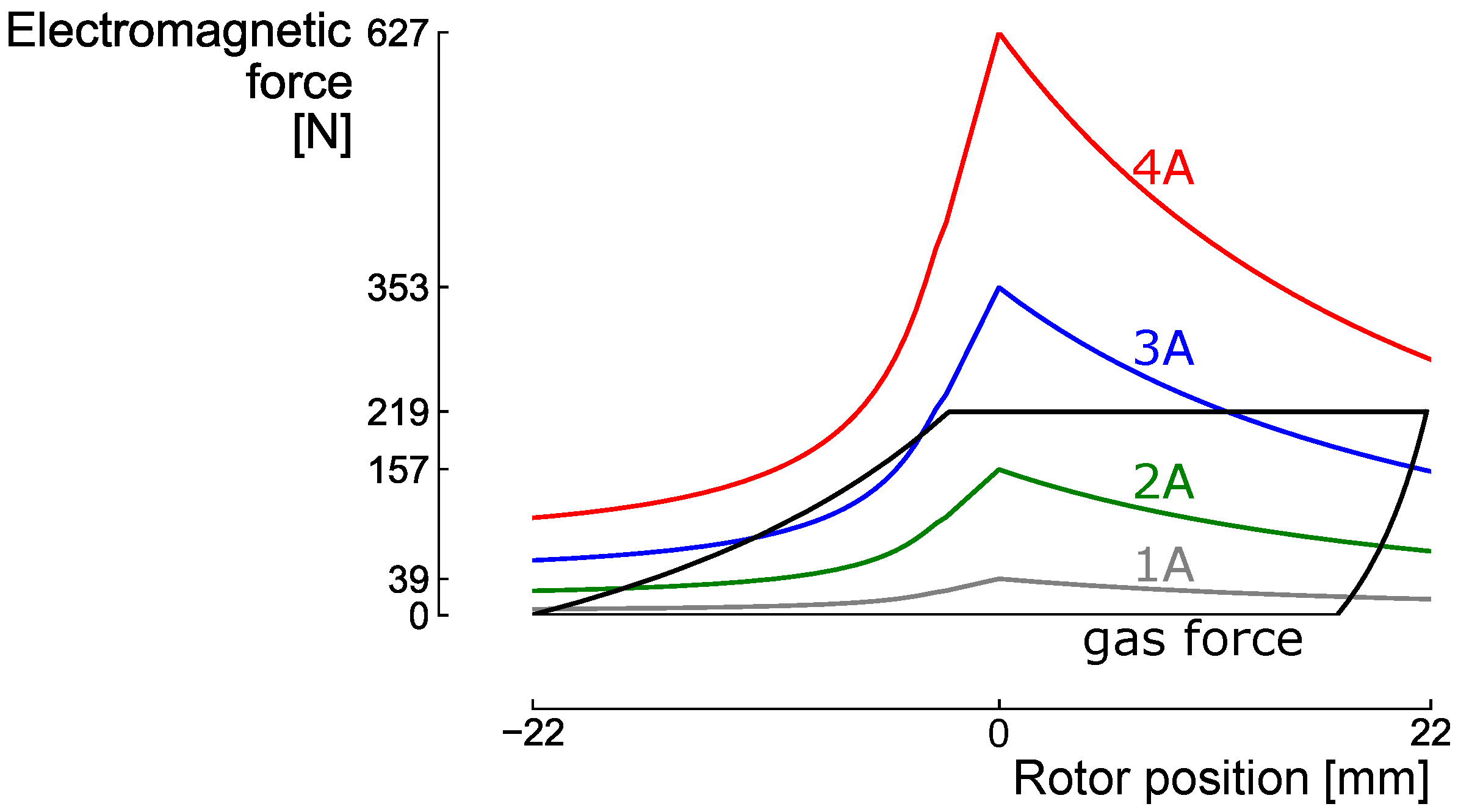
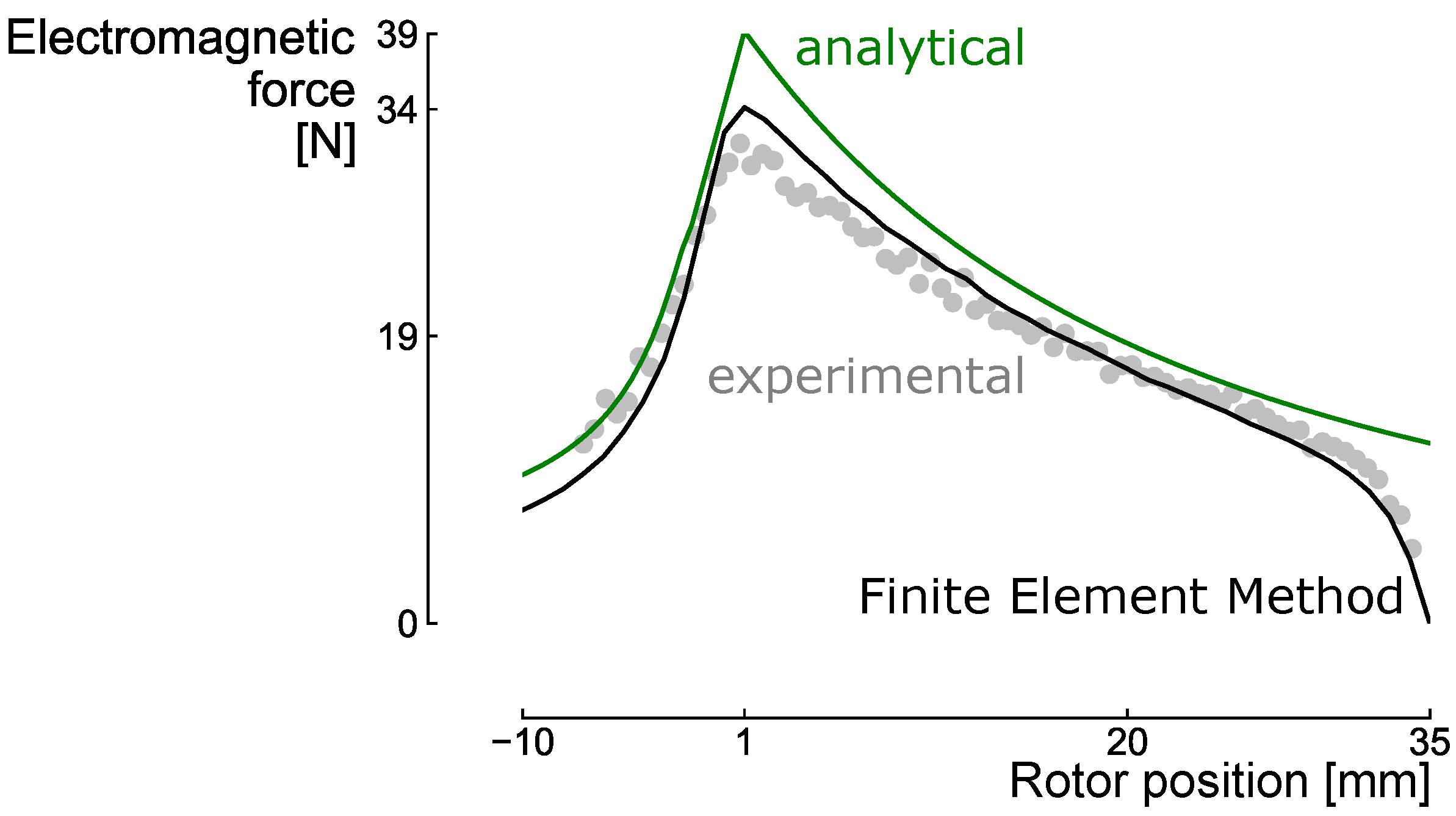
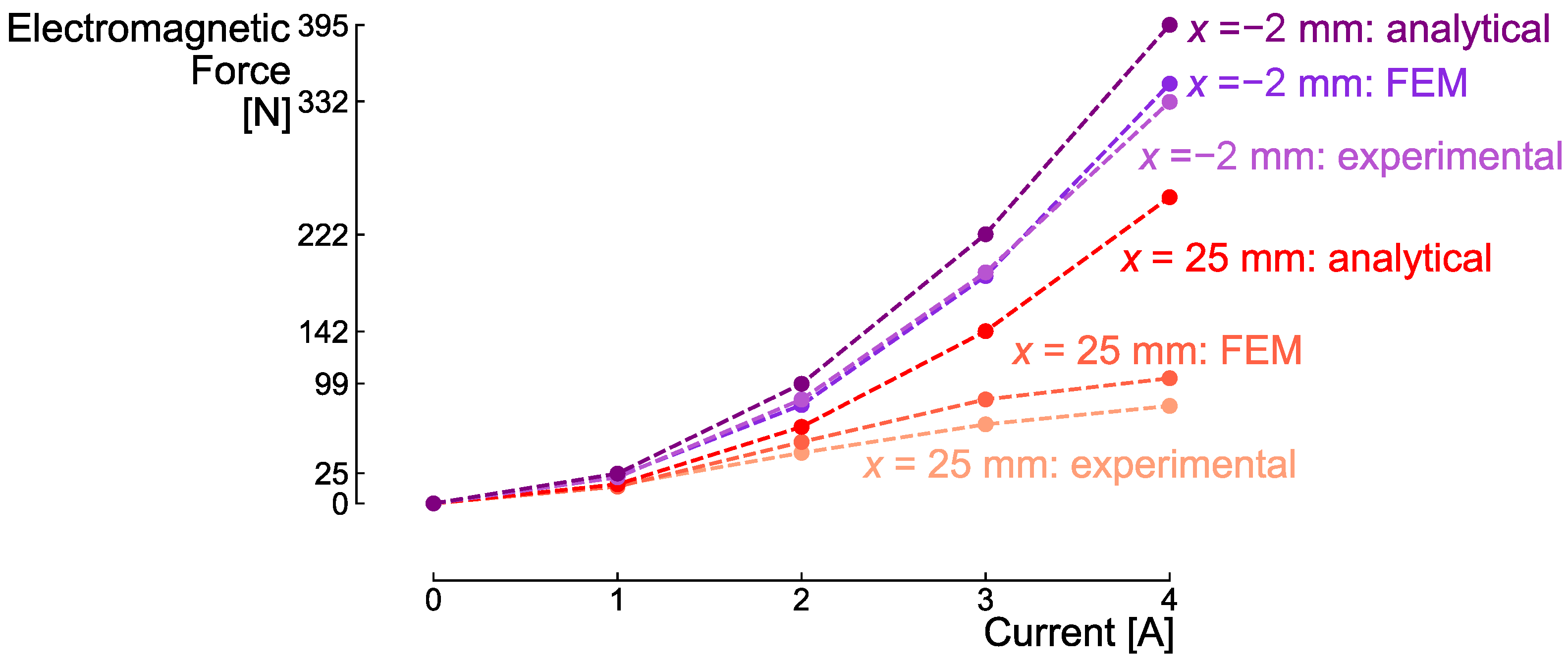
2.2.3. Model Validation
3. Design Optimisation
3.1. Design Parameters
3.2. Constraints
3.3. Objective Functions
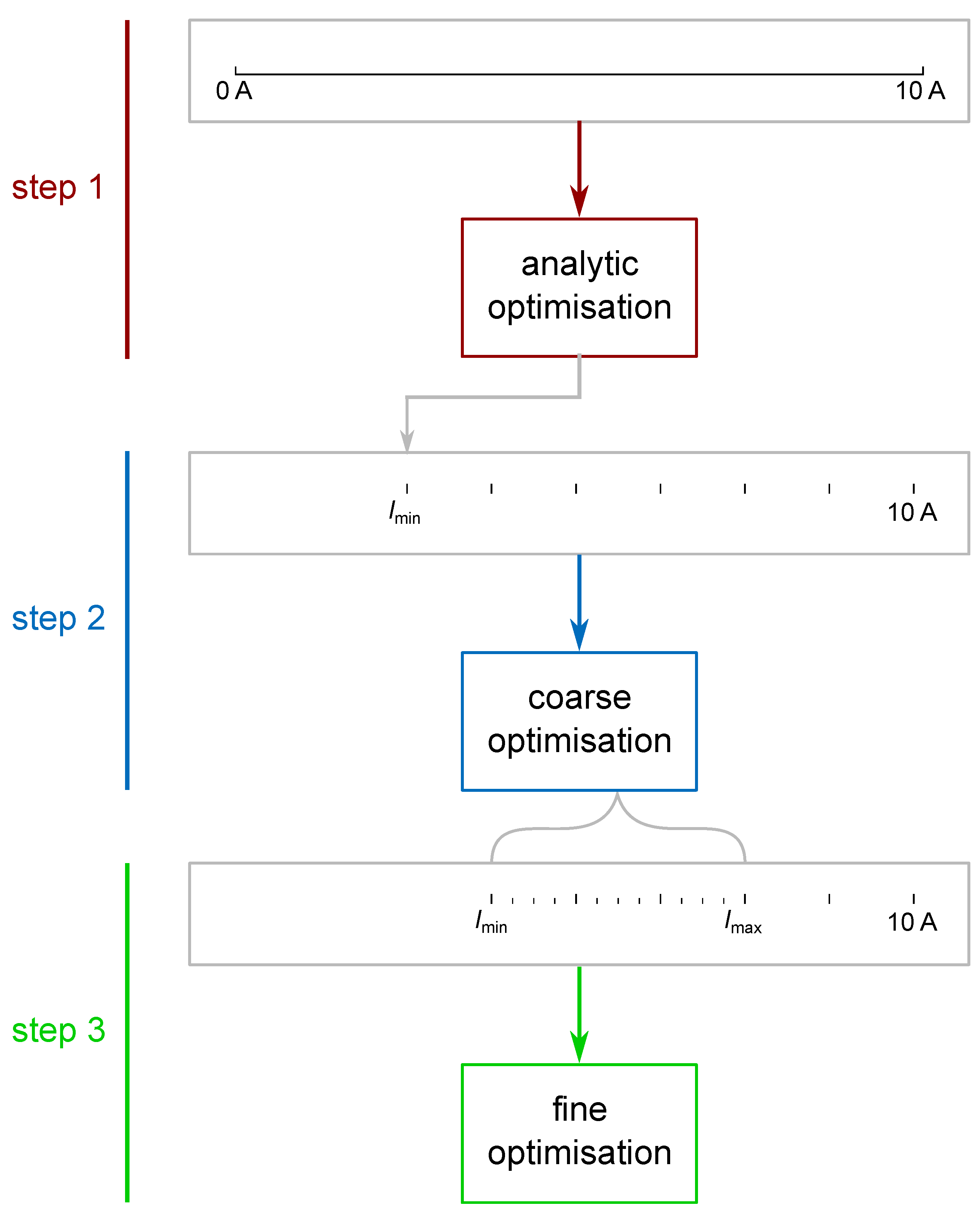
3.4. Multi-Fidelity Optimisation Approach
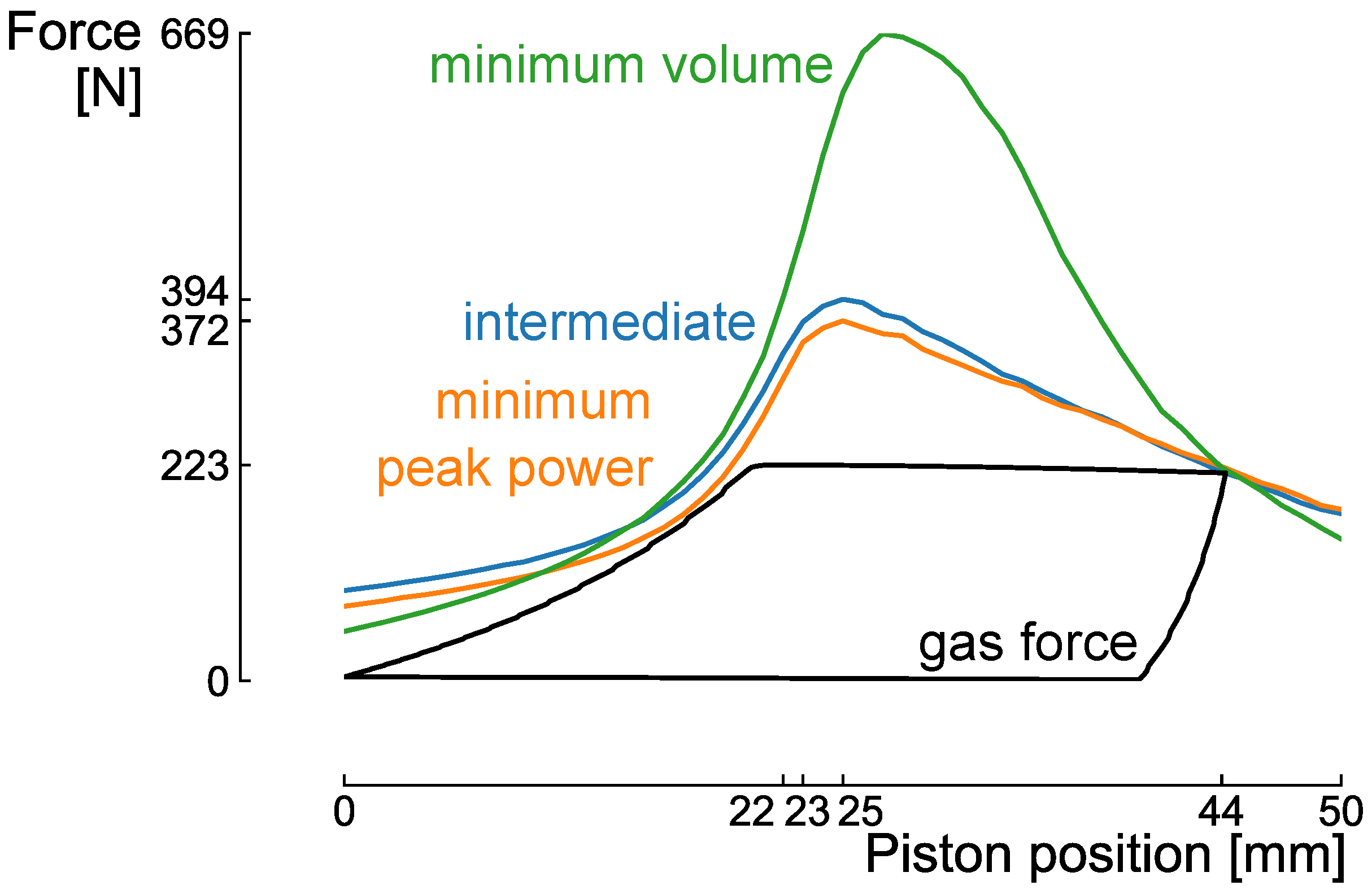
4. Results
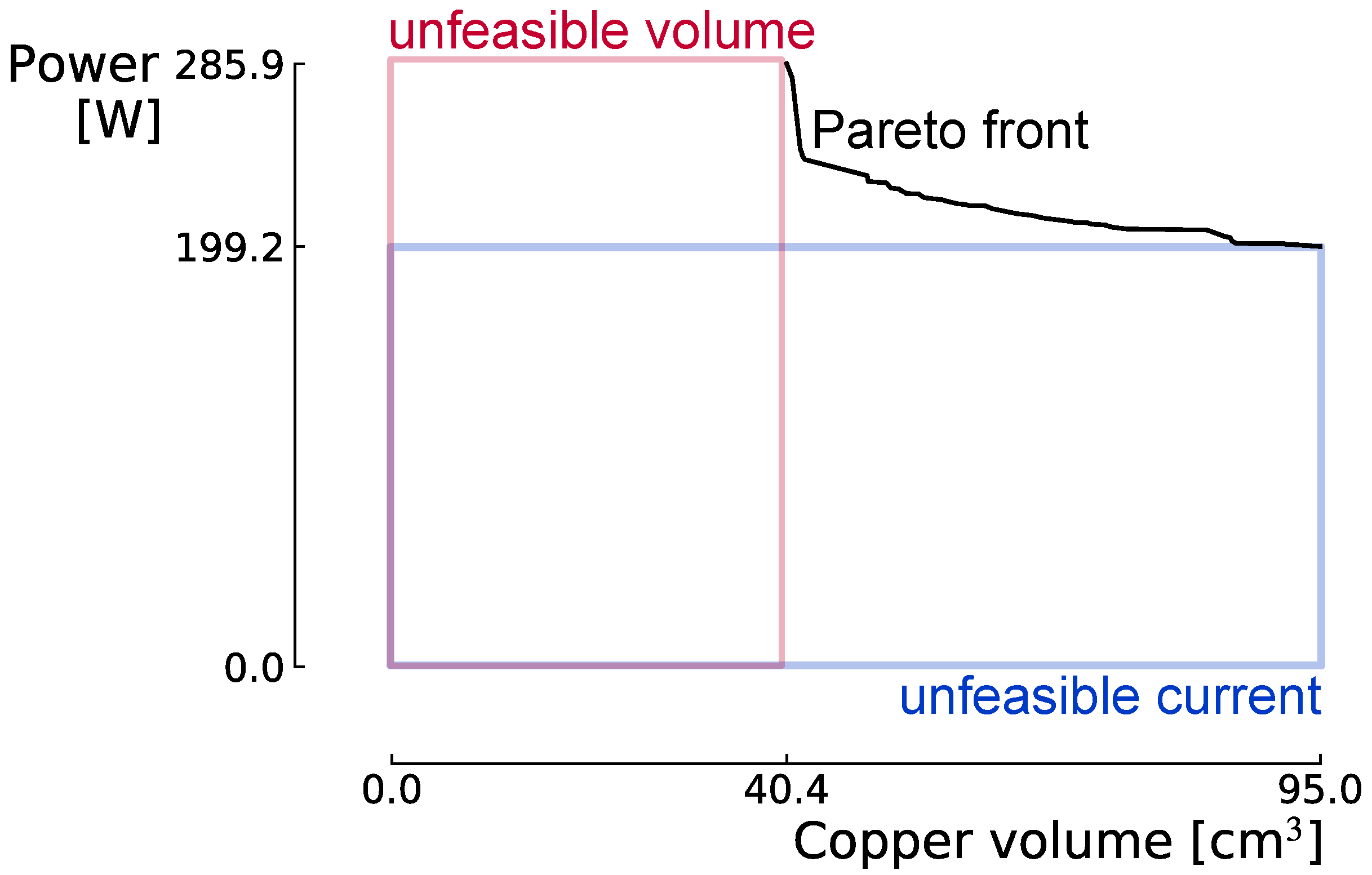
4.1. First Step: Optimisation of Analytical Model
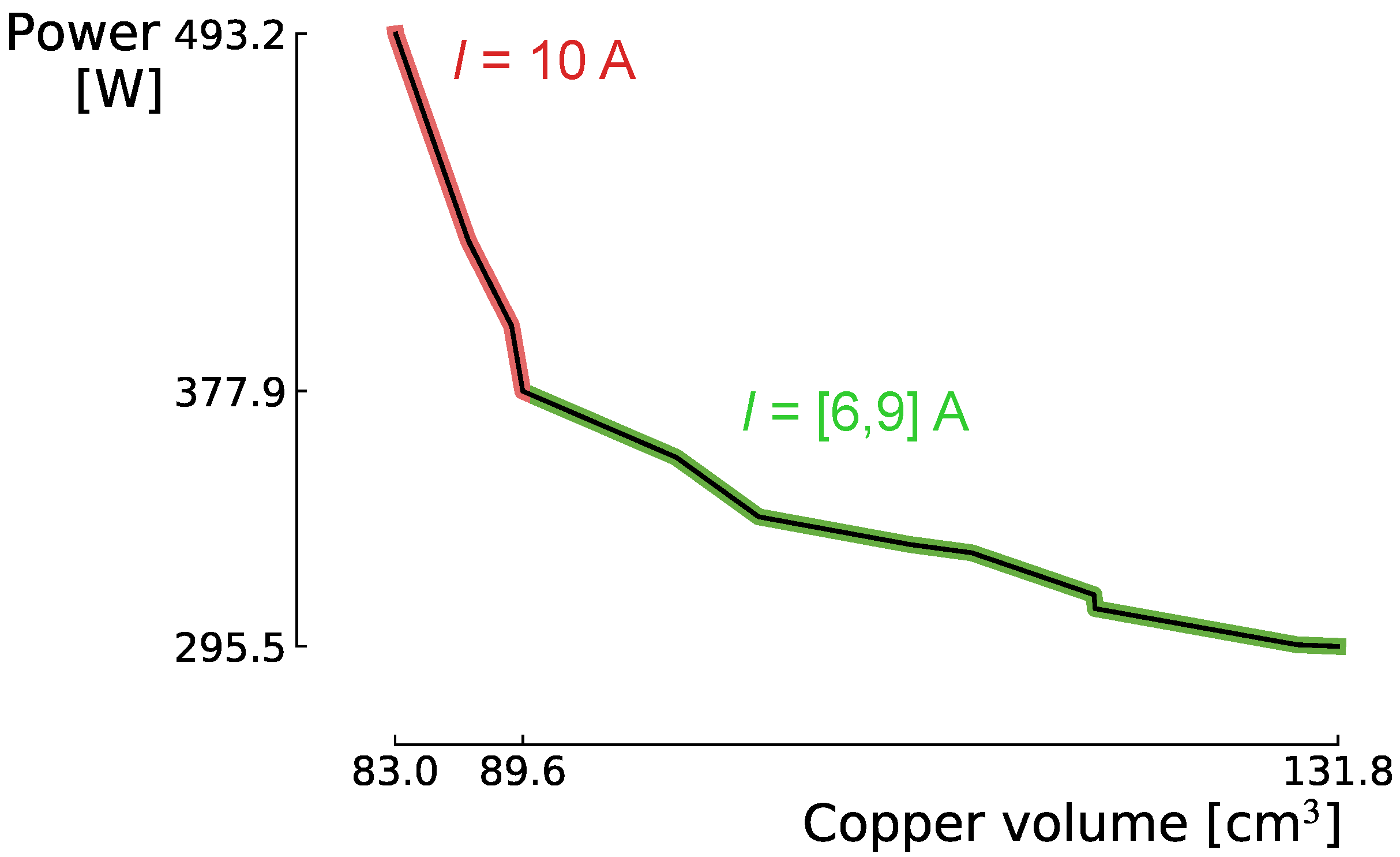
4.2. Second Step: Coarse Optimisation
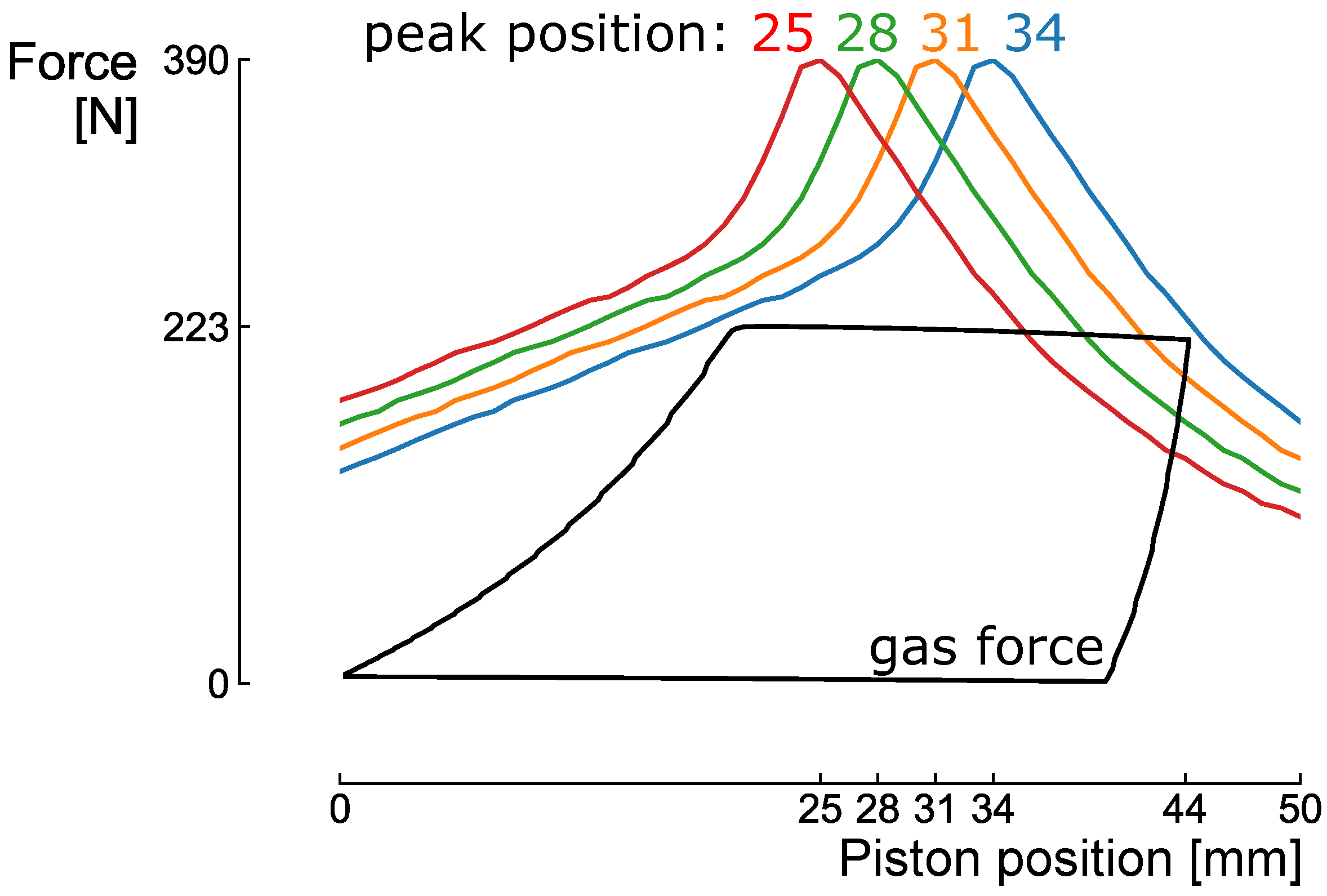
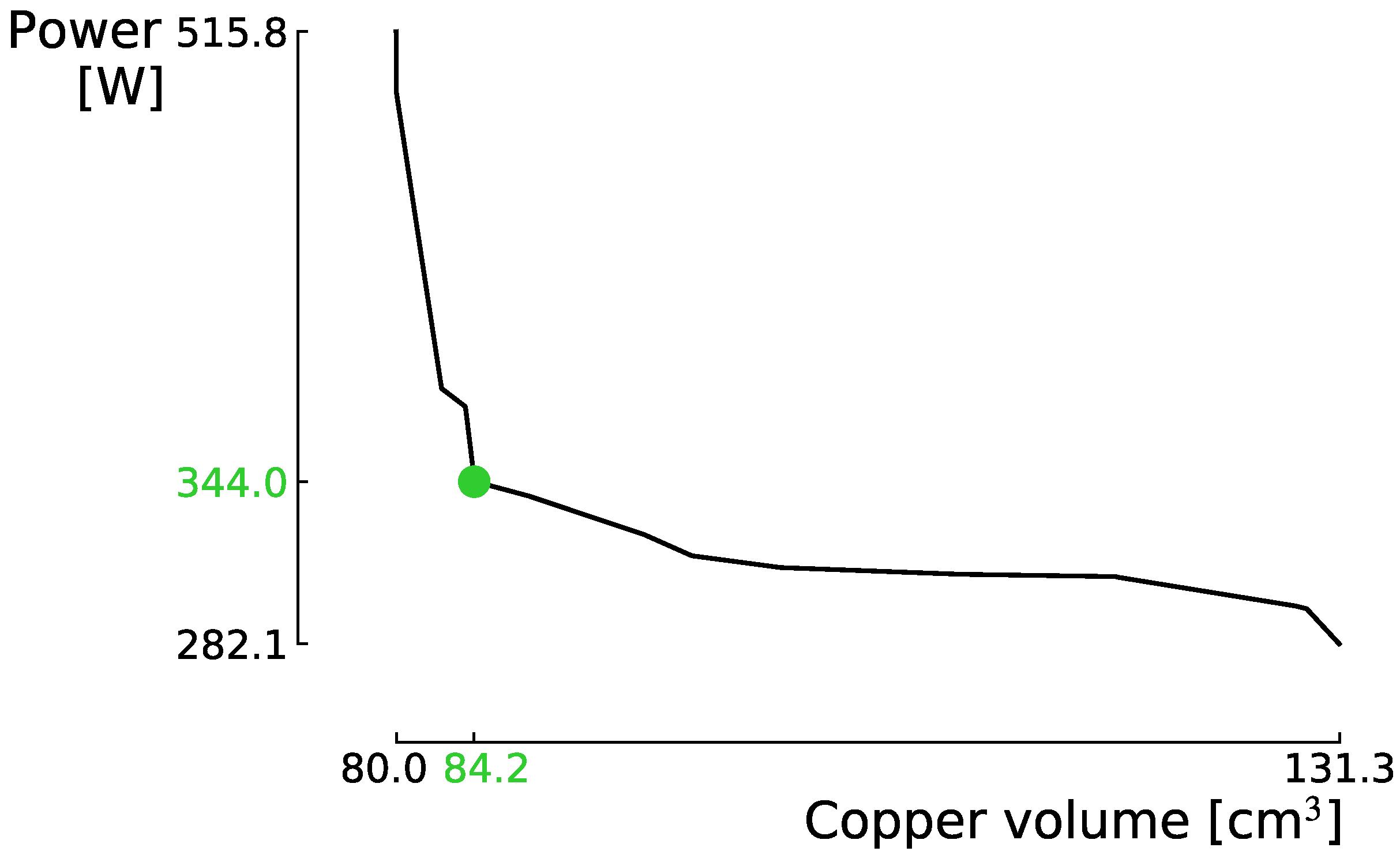
4.3. Third Step: Fine Optimisation
4.4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hawken, P. Drawdown: The Most Comprehensive Plan Ever Proposed to Reverse Global Warming; Penguin Books: New York, NY, USA, 2017. [Google Scholar]
- Liang, K.; Stone, R.; Hancock, W.; Dadd, M.; Bailey, P. Comparison between a Crank-drive Reciprocating Compressor and a Novel Oil-free Linear Compressor. Int. J. Refrig. 2014, 45, 25–34. [Google Scholar] [CrossRef]
- Bradshaw, C.; Groll, E.; Garimella, S. Linear compressors for electronics cooling: Energy recovery and the useful benefits. In Proceedings of the International Compressor Engineering Conference, West Lafayette, IN, USA, 16–19 July 2012. [Google Scholar]
- Ku, B.; Park, J.; Hwang, Y.; Lee, J. Performance evaluation of the energy efficiency of crank-driven compressor and linear compressor for a household refrigerator. In Proceedings of the International Compressor Engineering Conference, West Lafayette, IN, USA, 12–15 July 2010. [Google Scholar]
- Bailey, P.; Dadd, M.; Stone, C. An oil-free linear compressor for use with compact heat exchangers. In Proceedings of the International Conference on Compressors and their Systems 2009, London, UK, 7–9 September 2009; pp. 259–268. [Google Scholar]
- Kim, J.K.; Roh, C.G.; Kim, H.; Jeong, J.H. An experimental and numerical study on an inherent capacity modulated linear compressor for home refrigerators. Int. J. Refrig. 2011, 34, 1415–1423. [Google Scholar] [CrossRef]
- Won Sung, J.; Park, J.C.; Kim, G.S.; Won, C.Y.; Choi, S. Sensorless stroke control for linear compressors. Int. J. Appl. Electromagn. Mech. 2005, 24, 604219. [Google Scholar]
- Yang, S.B. Output Control Apparatus for Linear Compressor and Method of the Same. U.S. Patent US6176683B1, 6 April 1999. [Google Scholar]
- Hahn, G.W.; Kusumba, S.; Mcintyre, M.L.; Latham, J.W. Method for Operating a Linear Compressor. U.S. Patent US20180187674, 13 February 2018. [Google Scholar]
- Oh, K.T.; Kim, J.W. Apparatus for Controlling Linear Compressor and Method Thereof. U.S. Patent US6289680B1, 4 November 1999. [Google Scholar]
- Latham, J.; McIntyre, M.L.; Mohebbi, M. Sensorless Resonance Tracking and Stroke Control of a Linear Vapor Compressor Via Nonlinear Observers. IEEE Trans. Ind. Electron. 2018, 65, 3720–3729. [Google Scholar] [CrossRef]
- Chun, T.W.; Ann, J.R.; Yoo, J.Y.; Lee, C.W. Analysis and control for linear compressor system driven by PWM inverter. In Proceedings of the 30th Annual Conference of IEEE Industrial Electronics Society, Busan, Korea, 2–6 November 2004; pp. 263–267. [Google Scholar]
- Otaibi, Z.A. Spring-Less Buried Magnet Linear-Resonant Motor. U.S. Patent US9350221B2, 15 April 2011. [Google Scholar]
- Otaibi, Z.A. Spring-less permanent magnet linear-resonant motor for compressor applications. In Proceedings of the IEEE International Conference on Power and Energy (PECon), Kota Kinabalu, Malaysia, 2–5 December 2012. [Google Scholar]
- Poltschak, F.; Ebetshuber, P. Design of Integrated Magnetic Springs for Linear Oscillatory Actuators. IEEE Trans. Ind. Appl. 2018, 54, 2185–2192. [Google Scholar] [CrossRef]
- Jiang, H.; Liang, K.; Li, Z. Characteristics of a novel moving magnet linear motor for linear compressor. Mech. Syst. Signal Process. 2019, 121, 828–840. [Google Scholar] [CrossRef]
- Redlich, R.; Unger, R.; der Walt, N. Linear compressors: Motor configuration, modulation and systems. In Proceedings of the International Compressor Engineering Conference, West Lafayette, IN, USA, 23–26 July 1996. [Google Scholar]
- Cadman, R.V.; Cohen, R. Electrodynamic Oscillating Compressors: Part 1—Design Based on Linearized Loads. J. Basic Eng. 1969, 91, 656–663. [Google Scholar] [CrossRef]
- Cadman, R.V.; Cohen, R. Electrodynamic Oscillating Compressors: Part 2—Evaluation of Specific Designs for Gas Loads. J. Basic Eng. 1969, 91, 664–670. [Google Scholar] [CrossRef]
- Dainez, P.; Oliveira, J.; Nied, A.; Santos Matos Cavalca, M. A linear resonant compressor model based on a new linearization method of the gas pressure force. Int. J. Refrig. 2014, 48, 201–209. [Google Scholar] [CrossRef]
- Jonge, A.D. Analysis and optimisation of a linear motor for the compressor of cryogenic refrigeration. Adv. Cryog. Eng. 1981, 27, 631–640. [Google Scholar]
- Pollak, E.; Soedel, W.; Cohen, R.; Friedlaender, F. On the resonance and operational behavior of an oscillating electrodynamic compressor. J. Sound Vib. 1979, 67, 121–133. [Google Scholar] [CrossRef]
- Chen, N.; Tang, Y.J.; Wu, Y.N.; Chen, X.; Xu, L. Study on static and dynamic characteristics of moving magnet linear compressors. Cryogenics 2007, 47, 457–467. [Google Scholar] [CrossRef]
- Sung, B.; Lee, E.; Lee, J. A design method of solenoid actuator using empirical design coefficients and optimisation technique. In Proceedings of the 2007 IEEE International Electric Machines Drives Conference, Antalya, Turkey, 3–5 May 2007; pp. 279–284. [Google Scholar]
- Bijanzad, A.; Hassan, A.; Lazoglu, I. Analysis of solenoid based linear compressor for household refrigerator. Int. J. Refrig. 2017, 74, 116–128. [Google Scholar] [CrossRef]
- Tsai, N.C.; Chiang, C.W. Design and analysis of magnetically-drive actuator applied for linear compressor. Mechatronics 2010, 20, 596–603. [Google Scholar] [CrossRef]
- Wu, J.; Huang, Y.; Song, Y.; Wu, D. Integrated design of a novel force tracking electro-hydraulic actuator. Mechatronics 2019, 62, 102247. [Google Scholar] [CrossRef]
- De Paepe, W.; Coppitters, D.; Abraham, S.; Tsirikoglou, P.; Ghorbaniasl, G.; Contino, F. Robust Operational Optimization of a Typical micro Gas Turbine. Energy Procedia 2019, 158, 5795–5803. [Google Scholar] [CrossRef]
- Coppitters, D.; De Paepe, W.; Contino, F. Surrogate-assisted robust design optimisation and global sensitivity analysis of a directly coupled photovoltaic-electrolyzer system under techno-economic uncertainty. Appl. Energy 2019, 248, 310–320. [Google Scholar] [CrossRef]
- Verleysen, K.; Coppitters, D.; Parente, A.; De Paepe, W.; Contino, F. How can power-to-ammonia be robust? Optimization of an ammonia synthesis plant powered by a wind turbine considering operational uncertainties. Fuel 2020, 266, 117049. [Google Scholar] [CrossRef]
- Rao, J.S.; Tiwari, R. Design optimisation of double-acting hybrid magnetic thrust bearings with control integration using multi-objective evolutionary algorithms. Mechatronics 2009, 19, 945–964. [Google Scholar] [CrossRef]
- Lee, S.; Yi, H.; Han, K.; Kim, J.H. Genetic algorithm-based design optimisation of electromagnetic valve actuators in combustion engines. Energies 2015, 8, 13222–13230. [Google Scholar] [CrossRef]
- Leati, E.; Poltschak, F.; Scheidl, R. An electromagnetically actuated high frequency oscillation pump. Mechatronics 2017, 47, 233–245. [Google Scholar] [CrossRef]
- Ciarella, A.; Tsotskas, C.; Hahn, M.; Werter, N.; De Breuker, R.; Beaverstock, C.; Friswell, M.I.; Yang, Y.; Özgen, S.; Antoniadis, A.; et al. A Multi-Fidelity, Multi-Disciplinary Analysis and Optimization Framework for the Design of Morphing UAV Wing. In Proceedings of the 16th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference, Dallas, TX, USA, 22–26 June 2015; p. 2326. [Google Scholar]
- Reitenbach, S.; Schnoes, M.; Becker, R.G.; Otten, T. Optimization of compressor variable geometry settings using multi-fidelity simulation. In Proceedings of the ASME Turbo Expo 2015: Turbine Technical Conference and Exposition, Montreal, QC, Canada, 15–19 June 2015. [Google Scholar]
- Wang, J.; Howe, D.; Lin, Z. Design Optimization of Short-Stroke Single-Phase Tubular Permanent-Magnet Motor for Refrigeration Applications. IEEE Trans. Ind. Electron. 2010, 57, 327–334. [Google Scholar] [CrossRef]
- Zhi, L.; Yan, L.; Yuan, Z. Parameters Optimization of Linear Compressor for Refrigerator. Appl. Mech. Mater. 2013, 331, 84–87. [Google Scholar]
- Rane, M.V.; Uphade, D.B. Novel Long Stroke Reciprocating Compressor for Energy Efficient Jaggery Making. In Proceedings of the IOP Conference Series: Materials Science and Engineering, London, UK, 11–13 September 2017; Volume 232, p. 012004. [Google Scholar]
- Gomis-Bellmunt, O.; Galceran-Arellano, S.; Sudrià-Andreu, A.; Montesinos-Miracle, D.; Campanile, L.F. Linear electromagnetic actuator modeling for optimisation of mechatronic and adaptronic systems. Mechatronics 2007, 17, 153–163. [Google Scholar] [CrossRef]
- Bently Nevada. RCK-1 Reciprocating Compressor Simulation Kit, Technical Report. 2015.
- Arnold, K.; Stewart, M. Chapter 11—Reciprocating Compressors **Reviewed for the 1999 edition by Lonnie W. Shelton of Paragon Engineering Services, Inc. In Surface Production Operations: Design of Gas-Handling Systems and Facilities, 2nd ed.; Arnold, K., Stewart, M., Eds.; Gulf Professional Publishing: Woburn, MA, USA, 1999; pp. 286–326. [Google Scholar]
- Ribas, F.; Deschamps, C.; Fagotti, F.; Morriesen, A.; Dutra, T. Thermal Analysis of Reciprocating Compressors—A Critical Review. In Proceedings of the International Compressor Engineering Conference, West Lafayette, IN, USA, 17–20 July 2006. [Google Scholar]
- Choi, B.J.; Jang, C.Y.; Cho, M.S.; Park, S.H.; Kim, H.; Shin, J.M.; Jeon, Y.H.; Roh, C.G. Linear Compressor. U.S. Patent US20090047154A1, 30 August 2004. [Google Scholar]
- Fitzgerald, A.E.; Charles Kingsley, J.; Umans, S.D. Electric Machinery; McGraw-Hill Higher Education: New York, NY, USA, 2003. [Google Scholar]
- Roters, H.C. Electromagnetic Devices; John Wiley and Sons: New York, NY, USA, 1941. [Google Scholar]
- Querfurth, W. Coil Winding: A Description of Coil Winding Procedures, Winding Machines and Associated Equipment; G. Stevens Mfg. Company: Peoria, IL, USA, 1954. [Google Scholar]
- Giorgetti, S.; Coppitters, D.; Contino, F.; Paepe, W.D.; Bricteux, L.; Aversano, G.; Parente, A. Surrogate-Assisted Modeling and Robust Optimization of a Micro Gas Turbine Plant With Carbon Capture. J. Eng. Gas Turbines Power 2020, 142, 011010. [Google Scholar] [CrossRef]
- Tsirikoglou, P.; Abraham, S.; Contino, F.; Bağci, Ö.; Vierendeels, J.; Ghorbaniasl, G. Comparison of metaheuristics algorithms on robust design optimisation of a plain-fin-tube heat exchanger. In Proceedings of the 18th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference, Denver, CO, USA, 5 June 2017; p. 3827. [Google Scholar]
- Sharma, N.; Anupama, K. On the use of NSGA-II for multi-objective resource allocation in MIMO-OFDMA systems. Wirel. Netw. 2011, 17, 1191–1201. [Google Scholar] [CrossRef]



| Specifications Reciprocating Compressor Kit | |
|---|---|
| Stroke s (mm) | 44.2 |
| Length connecting rod l (mm) | 127 |
| Outlet pressure (bar) | 2.07 |
| Inlet pressure (bar) | 0.85 |
| Compression ratio | 7.9:1 |
| Diameter piston (mm) | 50.8 |
| Clearance volume (cc) | 13.04 |
| Nominal speed n (rpm) | 100 |
| Piston mass (kg) | 0.505 |
| Volumetric efficiency (%) | 90 |
| Specifications Electromagnetic Prototype | |
|---|---|
| Tooth length a (mm) | 35 |
| Diameter plunger d (mm) | 65 |
| Airgap g (mm) | 1.5 |
| Inner diameter yoke (mm) | 100 |
| Outer diameter yoke (mm) | 120 |
| Distance between 2 teeth h (mm) | 50 |
| Number of windings N (turns) | 780 |
| Input current i (A) | 1 |
| Specifications Electromagnetic Prototype | |
|---|---|
| Number of windings N (turns) | [300–1000] |
| Tooth length a (mm) | [22.1–100] |
| Outer diameter yoke (mm) | [100–200] |
| Inner diameter yoke (mm) | [60–85]% of |
| Diameter plunger d (mm) | [65–95]% of |
| Airgap g (mm) | [2–10]% of d |
| Minimum Volume | Intermediate | Minimum Peak Power | |
|---|---|---|---|
| volume copper (cm) | 80.0 | 84.2 | 131.3 |
| peak power (W) | 515.8 | 344.0 | 282.1 |
| current I (A) | 10.0 | 8.0 | 5.5 |
| voltage V (V) | 51.6 | 43.0 | 51.3 |
| number of windings N | 375 | 363 | 509 |
| tooth length a (mm) | 76.3 | 76.3 | 76.3 |
| outer diameter (mm) | 134.4 | 133.4 | 147.9 |
| inner diameter (mm) | 98.4 | 97.6 | 108.5 |
| plunger diameter d (mm) | 66.4 | 81.7 | 90.7 |
| air gap thickness g (mm) | 1.9 | 2.4 | 2.6 |
| peak position (mm) | 25 | 23 | 22 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Beckers, J.; Coppitters, D.; De Paepe, W.; Contino, F.; Van Mierlo, J.; Verrelst, B. Multi-Fidelity Design Optimisation of a Solenoid-Driven Linear Compressor. Actuators 2020, 9, 38. https://doi.org/10.3390/act9020038
Beckers J, Coppitters D, De Paepe W, Contino F, Van Mierlo J, Verrelst B. Multi-Fidelity Design Optimisation of a Solenoid-Driven Linear Compressor. Actuators. 2020; 9(2):38. https://doi.org/10.3390/act9020038
Chicago/Turabian StyleBeckers, Jarl, Diederik Coppitters, Ward De Paepe, Francesco Contino, Joeri Van Mierlo, and Björn Verrelst. 2020. "Multi-Fidelity Design Optimisation of a Solenoid-Driven Linear Compressor" Actuators 9, no. 2: 38. https://doi.org/10.3390/act9020038
APA StyleBeckers, J., Coppitters, D., De Paepe, W., Contino, F., Van Mierlo, J., & Verrelst, B. (2020). Multi-Fidelity Design Optimisation of a Solenoid-Driven Linear Compressor. Actuators, 9(2), 38. https://doi.org/10.3390/act9020038







