Electromechanical Vibration Characteristics of Porous Bimorph and Unimorph Doubly Curved Panels
Abstract
1. Introduction
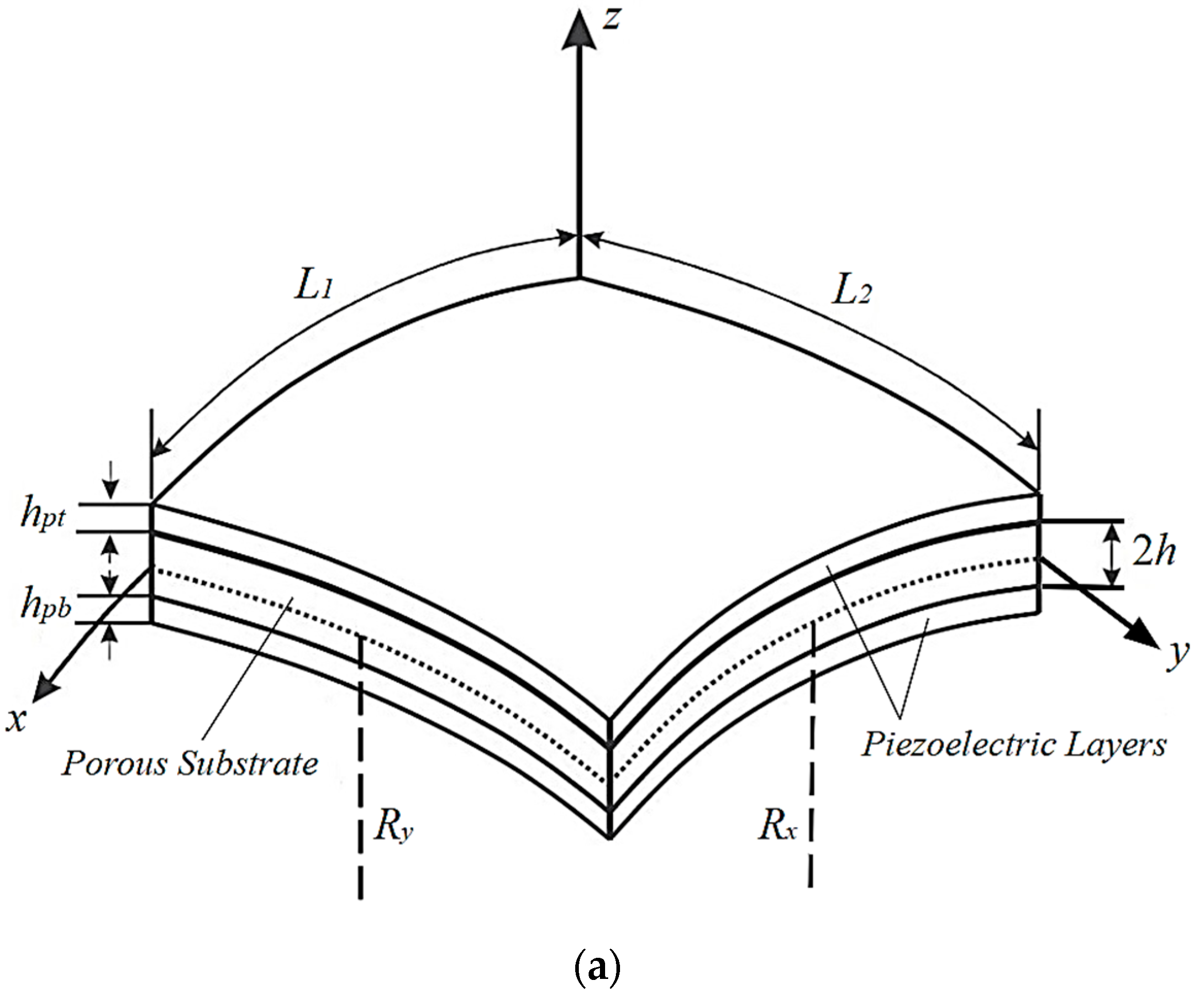
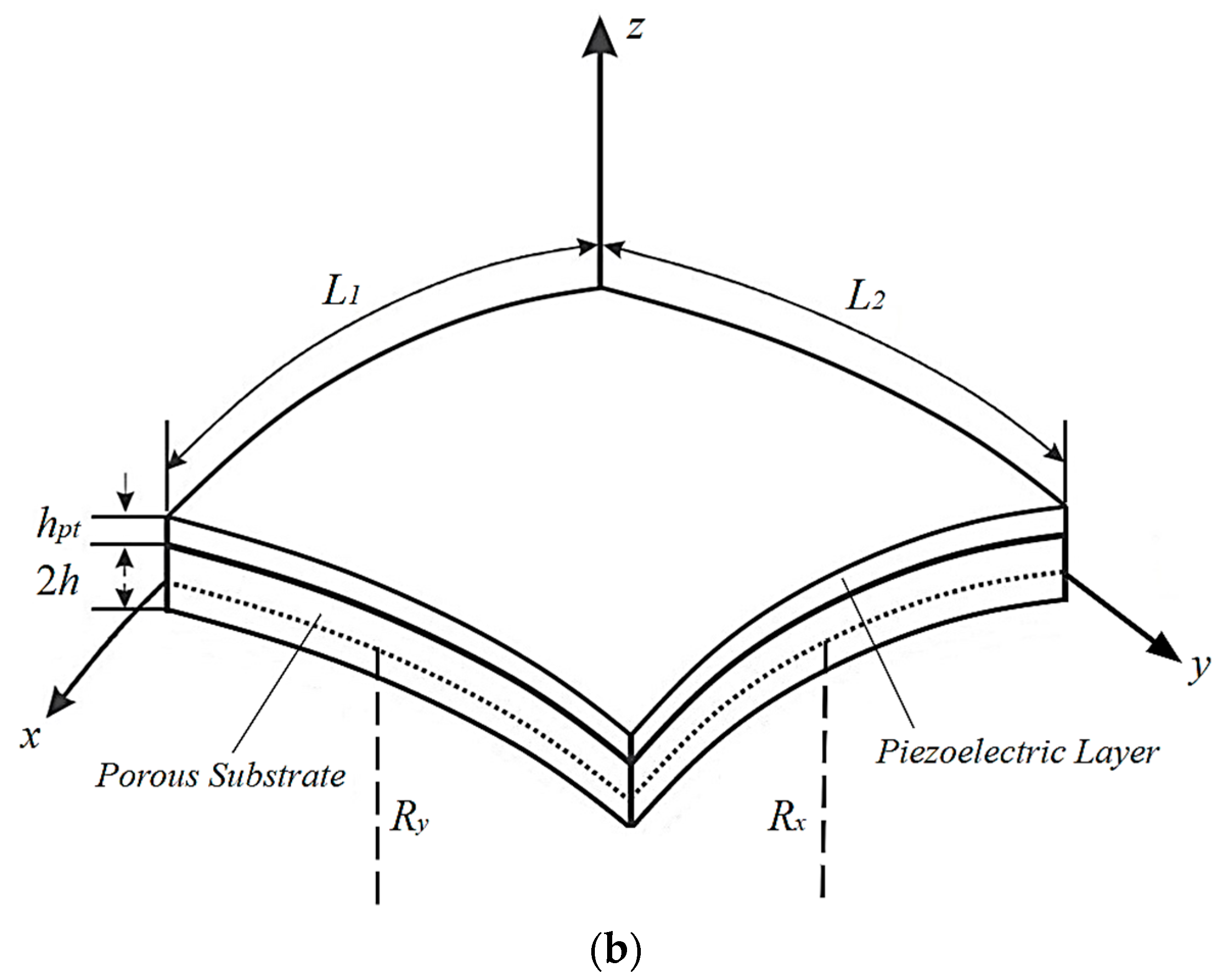
2. System Modelling
2.1. Kinematic Assumptions
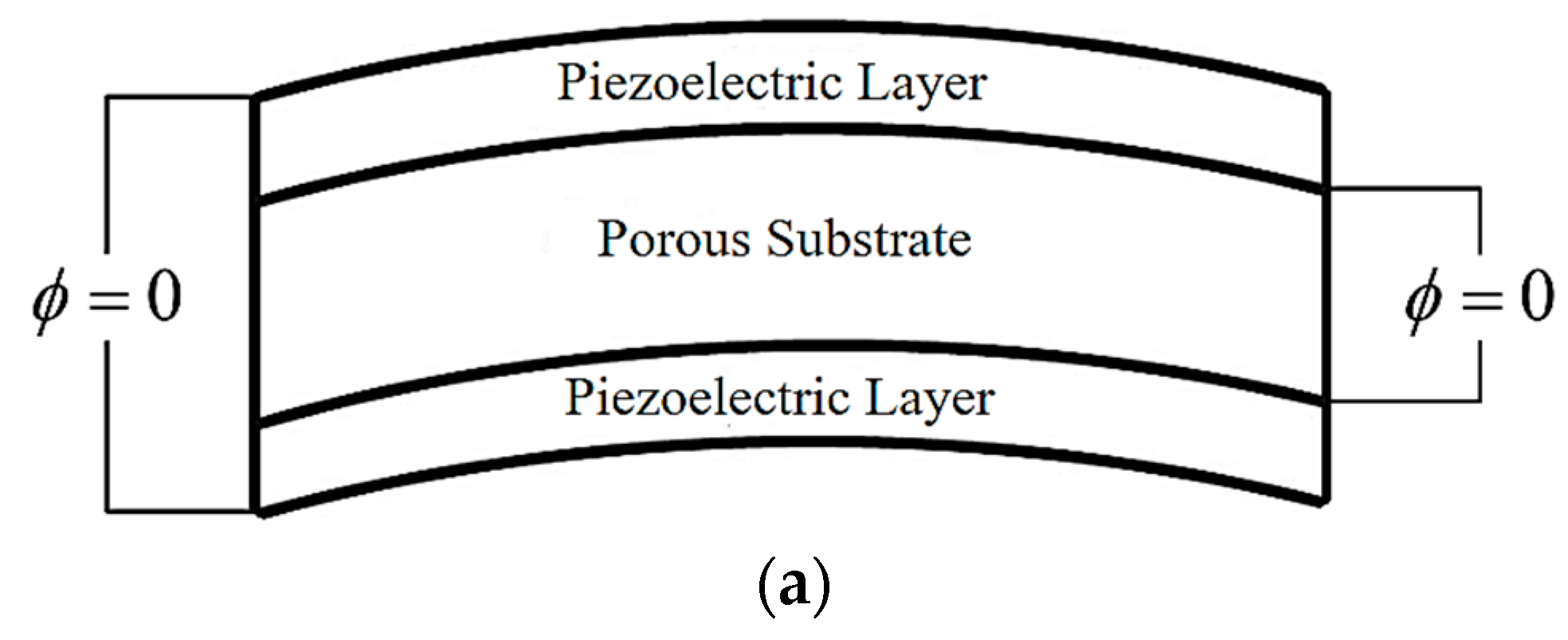
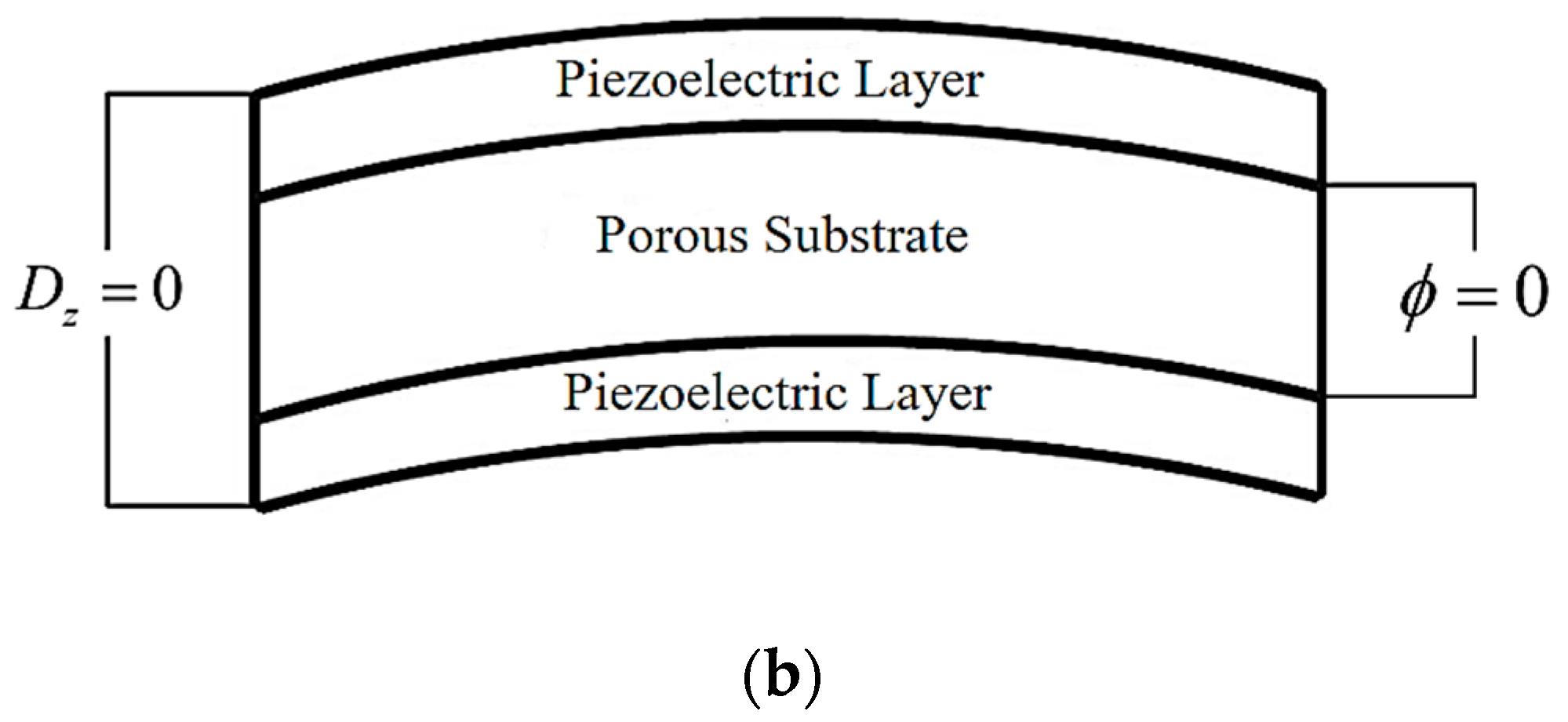
2.2. Constitutive Equations and Electric Potential
2.3. Electromechanically Coupled Equations of Motion
2.4. Solution Procedure
3. Numerical Results and Discussion
3.1. Verification Studies
3.2. New Results and Discussion
4. Conclusions
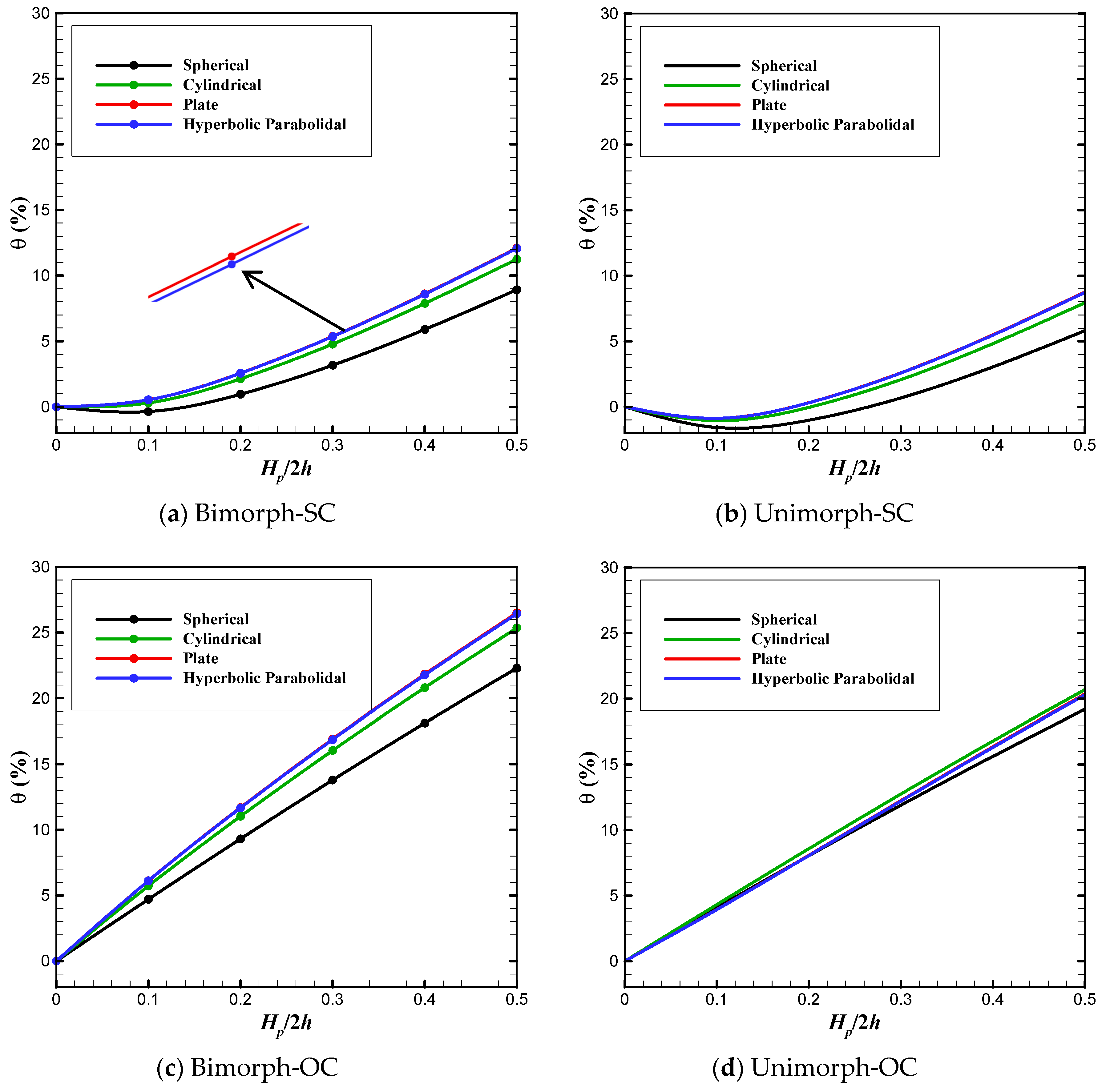
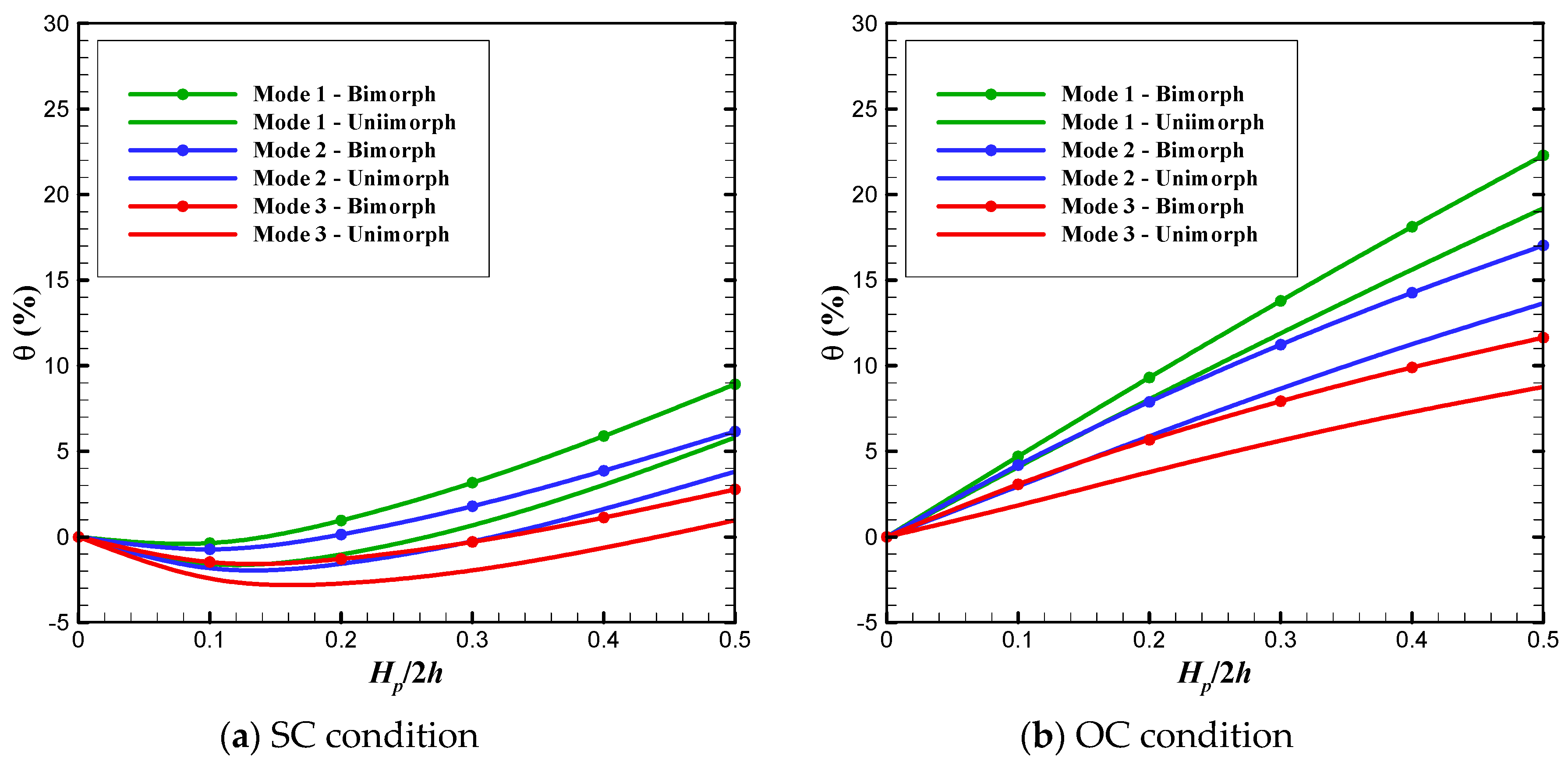
- it is necessary to consider the electrical effects for the smart panels under OC conditions unlike the SC one;
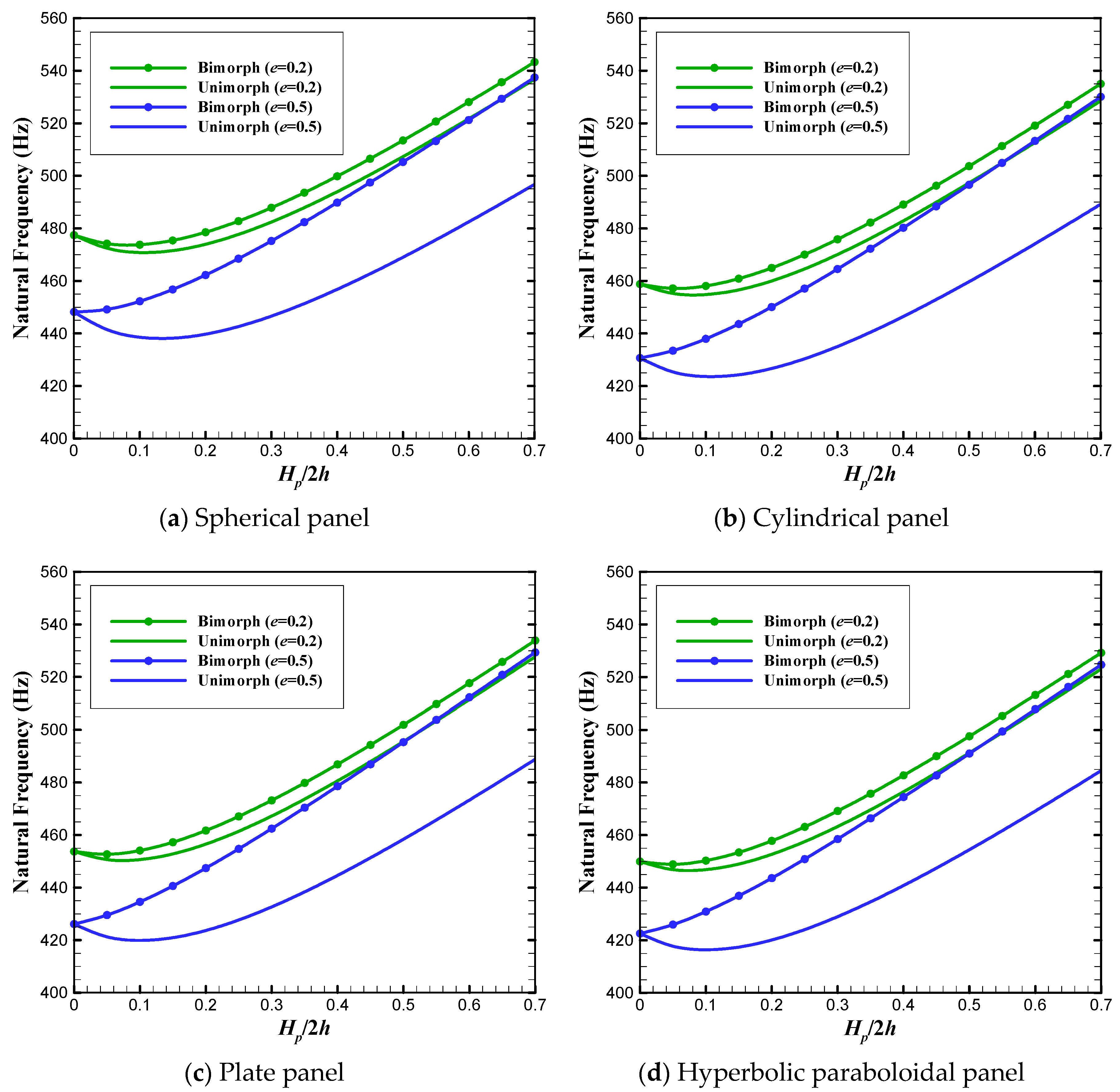
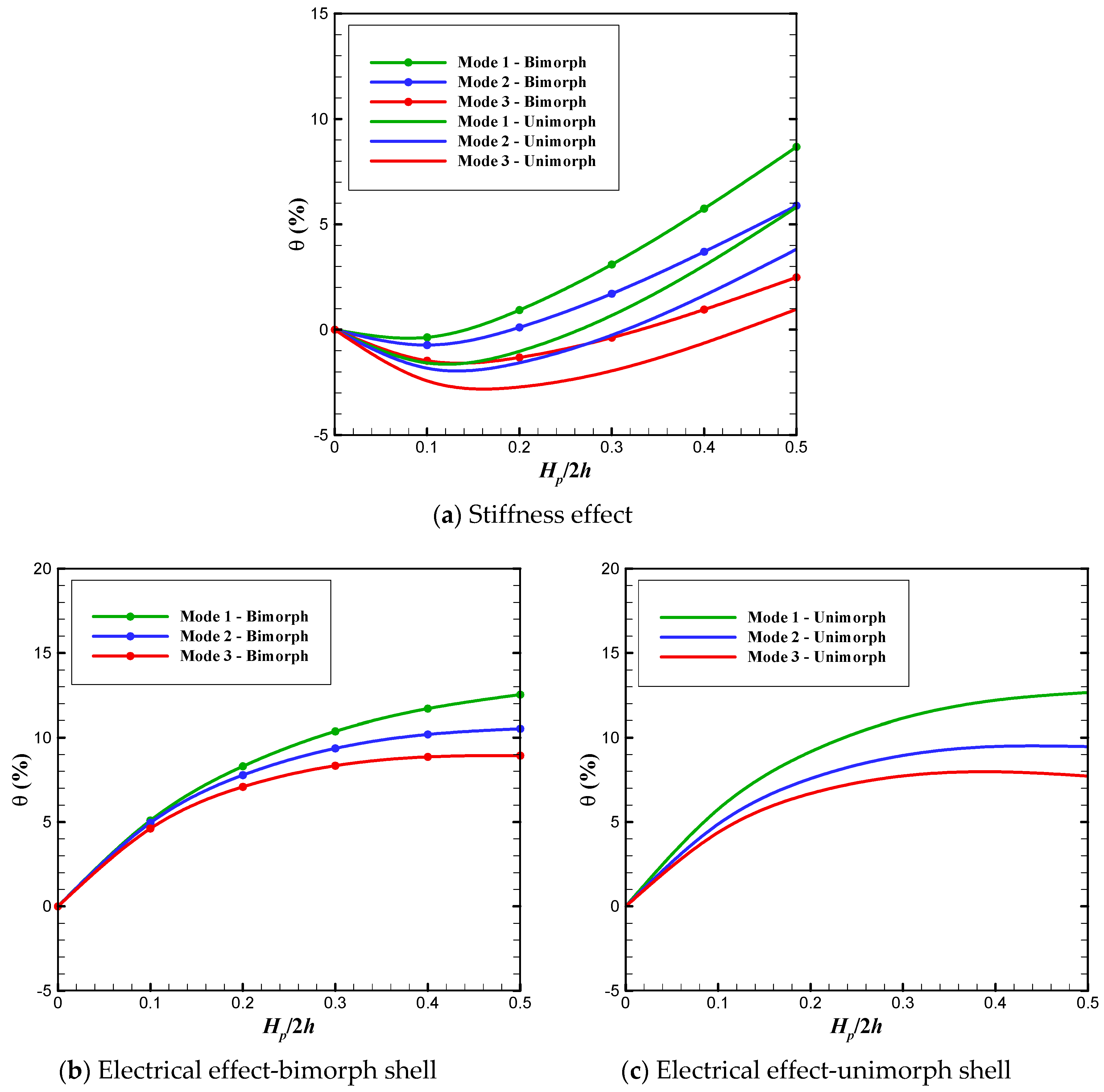
- bimorph structures usually exhibit higher frequencies compared to the unimorph ones;
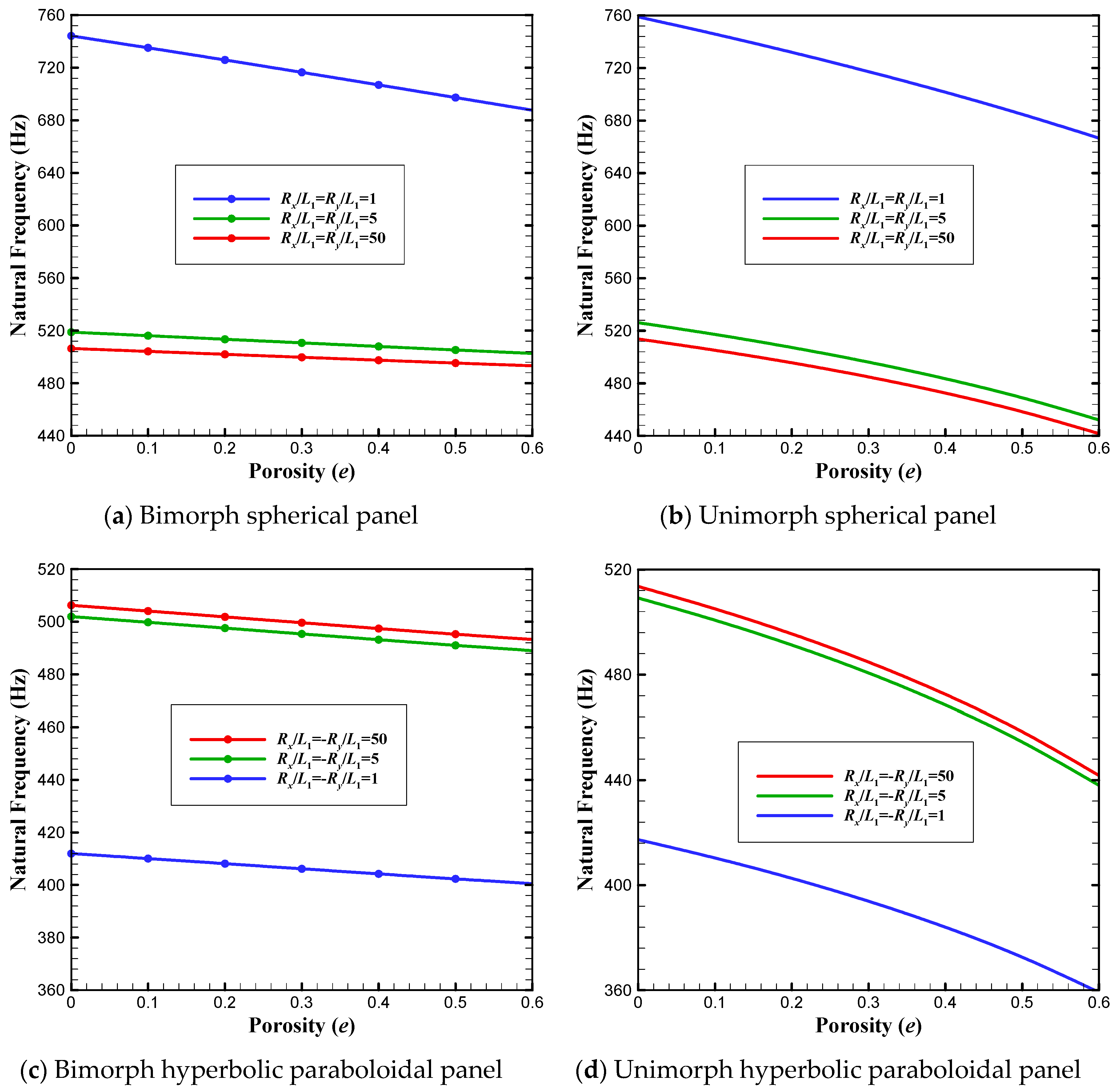
- increasing the porosity parameter reduces the natural frequencies, having a greater effect on the frequencies of unimorphs compared to those of bimorph panels;
- by increasing the curvature, the resonant frequencies of spherical and cylindrical shells remarkably decline, while ascending trend is seen for hyperbolic paraboloidal panels;
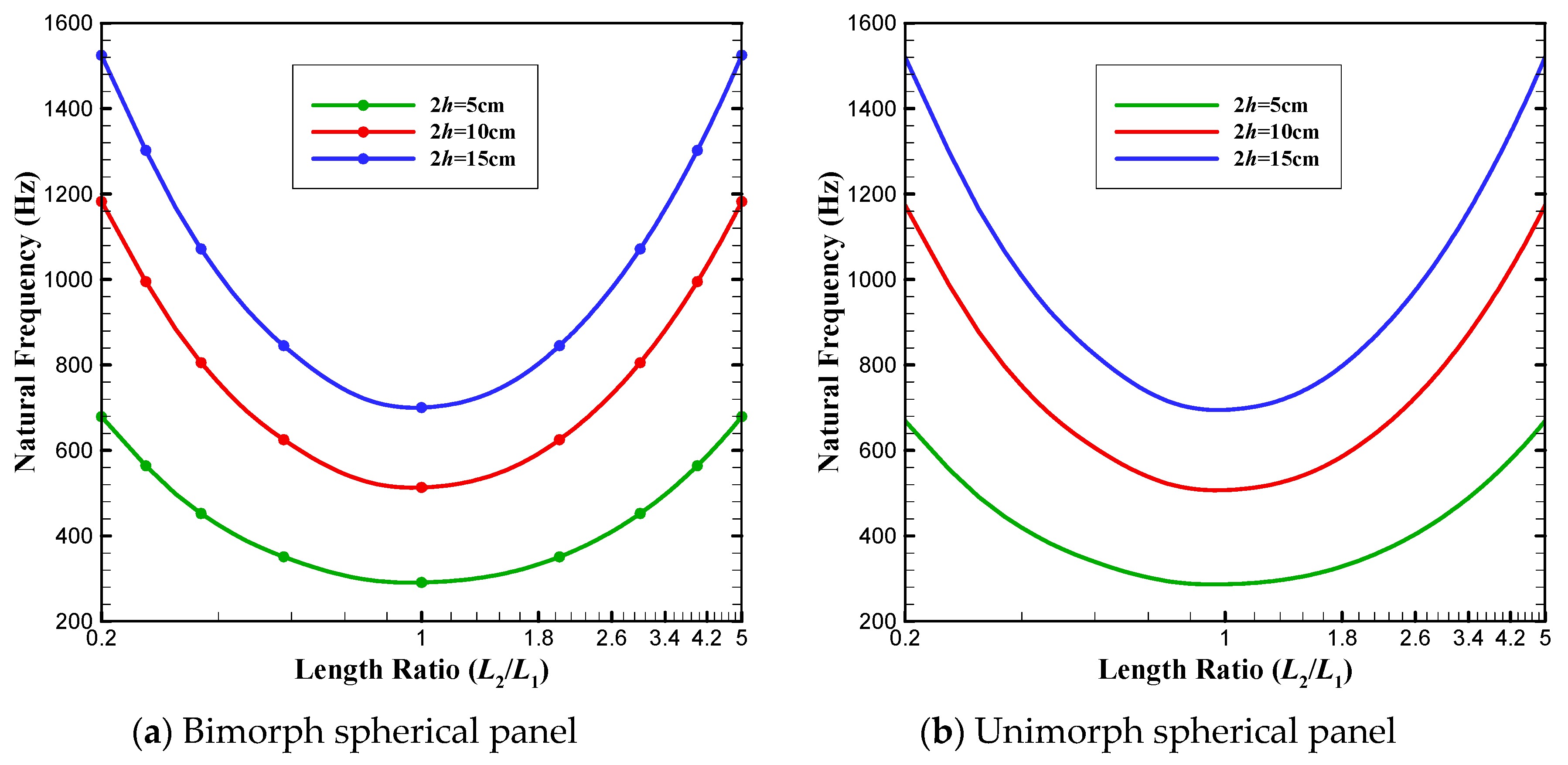
- keeping the volume constant, spherical shells exhibit the highest frequencies followed by cylindrical, plate, and hyperbolic paraboloidal panels, in descending order of frequency;
- keeping the surface area L1 L2 constant, the lowest value of natural frequency is achieved when L2/L1 = 1, irrespective of the value of curvature.
- frequencies of higher vibration modes are more influenced by the variation of porosity and thickness ratio, compared to the fundamental frequency.
Author Contributions
Funding
Conflicts of Interest
Appendix A
References
- Warren, W.E.; Kraynik, A.M. The linear elastic properties of open-cell foams. J. Appl. Mech. 1988, 55, 341–346. [Google Scholar] [CrossRef]
- Gibson, L.J. Mechanical behavior of metallic foams. Ann. Rev. Mater. Sci. 2000, 30, 191–227. [Google Scholar] [CrossRef]
- Avalle, M.; Belingardi, G.; Montanini, R. Characterization of polymeric structural foams under compressive impact loading by means of energy-absorption diagram. Int. J. Impact Eng. 2001, 25, 455–472. [Google Scholar] [CrossRef]
- Banhart, J. Manufacture, characterisation and application of cellular metals and metal foams. Prog. Mater. Sci. 2001, 46, 559–632. [Google Scholar] [CrossRef]
- Rabiei, A.; Vendra, L.J. A comparison of composite metal foam’s properties and other comparable metal foams. Mater. Lett. 2009, 63, 533–536. [Google Scholar] [CrossRef]
- Smith, B.H.; Szyniszewski, S.; Hajjar, J.F.; Schafer, B.W.; Arwade, S.R. Steel foam for structures: A review of applications, manufacturing and material properties. J. Constr. Steel. Res. 2012, 71, 1–10. [Google Scholar] [CrossRef]
- Chen, D.; Yang, J.; Kitipornchai, S. Elastic buckling and static bending of shear deformable functionally graded porous beam. Compos. Struct. 2015, 133, 54–61. [Google Scholar] [CrossRef]
- Brusa, E.; Carabelli, S.; Carraro, F.; Tonoli, A. Electromechanical tuning of self-sensing piezoelectric transducers. J. Intell. Mater. Syst. Struct. 1998, 9, 198–209. [Google Scholar] [CrossRef]
- Zhang, S.Q.; Schmidt, R. Static and dynamic FE analysis of piezoelectric integrated thin-walled composite structures with large rotations. Compos. Struct. 2014, 112, 345–357. [Google Scholar] [CrossRef]
- Zhang, S.Q.; Li, Y.X.; Schmidt, R. Modeling and simulation of macro-fiber composite layered smart structures. Compos. Struct. 2015, 126, 89–100. [Google Scholar] [CrossRef]
- Zhang, S.Q.; Li, Y.X.; Schmidt, R. Active shape and vibration control for piezoelectric bonded composite structures using various geometric nonlinearities. Compos. Struct. 2015, 122, 239–249. [Google Scholar] [CrossRef]
- Abbasi, A.; Khadem, S.E.; Bab, S. Vibration control of a continuous rotating shaft employing high-static low-dynamic stiffness isolators. J. Vib. Control. 2018, 24, 760–783. [Google Scholar] [CrossRef]
- Brusa, E.; Sari, M.M. Modeling of the electromechanical coupling between crack propagation and piezoelectric behavior in active layers of smart devices. Mech. Adv. Mater. Struct. 2018, 25, 115–123. [Google Scholar] [CrossRef]
- Zhang, S.Q.; Zhao, G.Z.; Rao, M.N.; Schmidt, R.; Yu, Y.J. A review on modeling techniques of piezoelectric integrated plates and shells. J. Intell. Mater. Syst. Struct. 2019, 30, 1133–1147. [Google Scholar] [CrossRef]
- Benasciutti, D.; Moro, L.; Zelenika, S.; Brusa, E. Vibration energy scavenging via piezoelectric bimorphs of optimized shapes. Microsyst. Technol. 2010, 16, 657–668. [Google Scholar] [CrossRef]
- Erturk, A.; Inman, D.J. Piezoelectric energy harvesting; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Brusa, E. Optimisation of a hybrid energy scavenger with piezoelectric/magnetic coupling for sensor-bearing units. In Advanced Materials Research; Trans Tech Publications Ltd: Stafa-Zurich, Switzerland, 2013; pp. 41–56. [Google Scholar]
- Kang, M.-G.; Jung, W.-S.; Kang, C.-Y.; Yoon, S.-J. Recent progress on PZT based piezoelectric energy harvesting technologies. Actuators 2016, 5, 5. [Google Scholar] [CrossRef]
- Brusa, E. Design of a kinematic vibration energy harvester for a smart bearing with piezoelectric/magnetic coupling. Mech. Adv. Mater. Struc. 2018, 1–9. [Google Scholar] [CrossRef]
- Yang, Z.; Zhou, S.; Zu, J.; Inman, D. High-performance piezoelectric energy harvesters and their applications. Joule 2018, 2, 642–697. [Google Scholar] [CrossRef]
- Płaczek, M. Applications of Composite Piezoelectric Transducers in Innovative Mechatronic Systems. In Proceedings of the International Conference Mechatronics, Gippsland, Australia, 14–17 February 2017; pp. 326–336. [Google Scholar]
- Al-Wahab, M.A.; Kasper, R.; Kostadinov, K.; Chakarov, D.; Tiankov, T. Structured piezo-ceramic mechatronic handling devices for micro and nano manipulations. In Proceedings of the 2008 5th International Symposium on Mechatronics and Its Applications, Amman, Jordan, 27–29 May 2008; pp. 1–6. [Google Scholar]
- Alaluf, D.; Bastaits, R.; Wang, K.; Horodinca, M.; Martic, G.; Mokrani, B.; Preumont, A. Unimorph mirror for adaptive optics in space telescopes. Appl. Opt. 2018, 57, 3629–3638. [Google Scholar] [CrossRef]
- Preumont, A. Mechatronics: Dynamics of electromechanical and piezoelectric systems; Springer: Berlin, Germany, 2006; Volume 136, pp. 61–157. [Google Scholar]
- Preumont, A.; Alaluf, D.; Wang, K.; Rodrigues, G. Adaptive Thin Shell Reflectors for Future Space Telescopes. In Proceedings of the European Conference on Spacecraft Structures Materials and Environmental Testing (ECSSMET 2016), Toulouse, France, 27–30 September 2016. [Google Scholar]
- Preumont, A.; Voltan, M.; Sangiovanni, A.; Bastaits, R.; Mokrani, B.; Alaluf, D. An investigation of the active damping of suspension bridges. Mathematics and Mechanics of Complex Systems 2016, 3, 385–406. [Google Scholar] [CrossRef]
- Viguié, R.; Verhelst, D.; Preumont, A.; Mokrani, B.; Bastaits, R. Piezoelectric damper system for an axial turbomachine rotor. U.S. Patent 10,125,794, 13 November 2018. [Google Scholar]
- Kessler, S.S. Piezoelectric-based in-situ damage detection of composite materials for structural health monitoring systems. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2002. [Google Scholar]
- Thanagasundram, S.; Schlindwein, F.S. Comparison of integrated micro-electrical-mechanical system and piezoelectric accelerometers for machine condition monitoring. Proc. Inst. Mech. Eng. Pt. C J. Mechan. Eng. Sci. 2006, 220, 1135–1146. [Google Scholar] [CrossRef]
- Magnucki, K.; Malinowski, M.; Kasprzak, J. Bending and buckling of a rectangular porous plate. Steel Compos. Struct. 2006, 6, 319–333. [Google Scholar] [CrossRef]
- Jasion, P.; Magnucka-Blandzi, E.; Szyc, W.; Magnucki, K. Global and local buckling of sandwich circular and beam-rectangular plates with metal foam core. Thin Wall. Struct. 2012, 61, 154–161. [Google Scholar] [CrossRef]
- Chen, D.; Yang, J.; Kitipornchai, S. Free and forced vibrations of shear deformable functionally graded porous beams. Int. J. Mech. Sci. 2016, 108, 14–22. [Google Scholar] [CrossRef]
- Chen, D.; Kitipornchai, S.; Yang, J. Nonlinear free vibration of shear deformable sandwich beam with a functionally graded porous core. Thin Wall. Struct. 2016, 107, 39–48. [Google Scholar] [CrossRef]
- Chen, D.; Yang, J.; Kitipornchai, S. Buckling and bending analyses of a novel functionally graded porous plate using Chebyshev-Ritz method. Arch. Civ. Mech. Eng. 2019, 19, 157–170. [Google Scholar] [CrossRef]
- Rezaei, A.S.; Saidi, A.R. On the effect of coupled solid-fluid deformation on natural frequencies of fluid saturated porous plates. Eur. J. Mech. A Solids 2017, 63, 99–109. [Google Scholar] [CrossRef]
- Rezaei, A.S.; Saidi, A.R.; Abrishamdari, M.; Pour Mohammadi, M.H. Natural frequencies of functionally graded plates with porosities via a simple four variable plate theory: An analytical approach. Thin Wall. Struct. 2017, 120, 366–377. [Google Scholar] [CrossRef]
- Rezaei, A.S.; Saidi, A.R. Buckling response of moderately thick fluid-infiltrated porous annular sector plates. Acta Mech. 2017, 228, 3929–3945. [Google Scholar] [CrossRef]
- Rezaei, A.S.; Saidi, A.R. An analytical study on the free vibration of moderately thick fluid-infiltrated porous annular sector plates. J. Vib. Control 2018, 24, 4130–4144. [Google Scholar] [CrossRef]
- Rezaei, A.S.; Saidi, A.R. Application of Carrera Unified Formulation to study the effect of porosity on natural frequencies of thick porous–cellular plates. Compos. B. Eng. 2018, 91, 361–370. [Google Scholar] [CrossRef]
- Kamranfard, M.R.; Saidi, A.R.; Naderi, A. Analytical solution for vibration and buckling of annular sectorial porous plates under in-plane uniform compressive loading. Proc. Inst. Mech. Eng. Pt. C J. Mechan. Eng. Sci. 2018, 232, 2211–2228. [Google Scholar] [CrossRef]
- Wang, Y.Q.; Zu, J.W. Vibration behaviors of functionally graded rectangular plates with porosities and moving in thermal environment. Aerosp. Sci. Technol. 2017, 69, 550–562. [Google Scholar] [CrossRef]
- Wang, Y.Q.; Yang, Z. Nonlinear vibrations of moving functionally graded plates containing porosities and contacting with liquid: Internal resonance. Nonlinear Dyn. 2017, 90, 1461–1480. [Google Scholar] [CrossRef]
- Xue, Y.; Jin, G.; Ma, X.; Chen, H.; Ye, T.; Chen, M.; Zhang, Y. Free vibration analysis of porous plates with porosity distributions in the thickness and in-plane directions using isogeometric approach. Int. J. Mech. Sci. 2019, 152, 346–362. [Google Scholar] [CrossRef]
- Thang, P.T.; Nguyen-Thoi, T.; Lee, D.; Kang, J.; Lee, J. Elastic buckling and free vibration analyses of porous-cellular plates with uniform and non-uniform porosity distributions. Aerosp. Sci. Technol. 2018, 79, 278–287. [Google Scholar] [CrossRef]
- Qin, Q.; Zheng, X.; Zhang, J.; Yuan, C.; Wang, T. Dynamic response of square sandwich plates with a metal foam core subjected to low-velocity impact. Int. J. Impact Eng. 2018, 111, 222–235. [Google Scholar] [CrossRef]
- Wang, Y.; Wu, D. Free vibration of functionally graded porous cylindrical shell using a sinusoidal shear deformation theory. Aerosp. Sci. Technol. 2017, 66, 83–91. [Google Scholar] [CrossRef]
- Ghadiri, M.; SafarPour, H. Free vibration analysis of size-dependent functionally graded porous cylindrical microshells in thermal environment. J. Therm. Stress. 2017, 40, 55–71. [Google Scholar] [CrossRef]
- Belica, T.; Magnucki, K. Stability of a porous-cellular cylindrical shell subjected to combined loads. J. Theor. Appl. Mech. 2013, 51, 927–936. [Google Scholar]
- Ghasemi, A.R.; Meskini, M. Free vibration analysis of porous laminated rotating circular cylindrical shells. J. Vib. Control 2019, 25, 2494–2508. [Google Scholar] [CrossRef]
- Jabbari, M.; Joubaneh, E.F.; Khorshidvand, A.R.; Eslami, M.R. Buckling analysis of porous circular plate with piezoelectric actuator layers under uniform radial compression. Int. J. Mech. Sci. 2013, 70, 50–56. [Google Scholar] [CrossRef]
- Jabbari, M.; Joubaneh, E.F.; Mojahedin, A. Thermal buckling analysis of porous circular plate with piezoelectric actuators based on first order shear deformation theory. Int. J. Mech. Sci. 2014, 83, 57–64. [Google Scholar] [CrossRef]
- Khorshidvand, A.R.; Joubaneh, E.F.; Jabbari, M.; Eslami, M.R. Buckling analysis of a porous circular plate with piezoelectric sensor–actuator layers under uniform radial compression. Acta Mech. 2014, 225, 179–193. [Google Scholar] [CrossRef]
- Mojahedin, A.; Joubaneh, E.F.; Jabbari, M. Thermal and mechanical stability of a circular porous plate with piezoelectric actuators. Acta Mech. 2014, 225, 3437–3452. [Google Scholar] [CrossRef]
- Farzaneh Joubaneh, E.; Mojahedin, A.; Khorshidvand, A.R.; Jabbari, M. Thermal buckling analysis of porous circular plate with piezoelectric sensor-actuator layers under uniform thermal load. J. Sandwich Struct. Mater. 2015, 17, 3–25. [Google Scholar] [CrossRef]
- Arshid, E.; Khorshidvand, A.R. Free vibration analysis of saturated porous FG circular plates integrated with piezoelectric actuators via differential quadrature method. Thin Wall. Struct. 2018, 125, 220–233. [Google Scholar] [CrossRef]
- Zhang, X.; Sun, C.T. Analysis of a sandwich plate containing a piezoelectric core. Smart Mater. Struct. 1999, 8, 31. [Google Scholar] [CrossRef]
- Wang, Q.; Quek, S.T.; Sun, C.T.; Liu, X. Analysis of piezoelectric coupled circular plate. Smart Mater. Struct. 2001, 10, 229. [Google Scholar] [CrossRef]
- Wang, Q.; Quek, S. A model for the analysis of beams with embedded piezoelectric layers. J. Intell. Mater. Syst. Struct. 2002, 13, 61–70. [Google Scholar] [CrossRef]
- Sayyaadi, H.; Rahnama, F.; Farsangi, M.A.A. Energy harvesting via shallow cylindrical and spherical piezoelectric panels using higher order shear deformation theory. Compos. Struct. 2016, 147, 155–167. [Google Scholar] [CrossRef]
- Sayyaadi, H.; Farsangi, M.A.A. An analytical solution for dynamic behavior of thick doubly curved functionally graded smart panels. Compos. Struct. 2014, 107, 88–102. [Google Scholar] [CrossRef]
- Rouzegar, J.; Abad, F. Free vibration analysis of FG plate with piezoelectric layers using four-variable refined plate theory. Thin Wall. Struct. 2015, 89, 76–83. [Google Scholar] [CrossRef]
- Malakooti, M.H.; Sodano, H.A. Piezoelectric energy harvesting through shear mode operation. Smart Mater. Struct 2015, 24, 055005. [Google Scholar] [CrossRef]
- Jin, J.; Batra, R.C. Effect of electromechanical coupling on static deformations and natural frequencies. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2005, 52, 1079–1093. [Google Scholar] [PubMed]
- Farsangi, M.A.A.; Saidi, A.R.; Batra, R.C. Analytical solution for free vibrations of moderately thick hybrid piezoelectric laminated plates. J. Sound Vib. 2013, 332, 5981–5998. [Google Scholar] [CrossRef]
- Askari, M.; Saidi, A.R.; Rezaei, A.S. An investigation over the effect of piezoelectricity and porosity distribution on natural frequencies of porous smart plates. J. Sandwich Struct. Mater. 2018, 1099636218791092. [Google Scholar] [CrossRef]
- Askari, M.; Saidi, A.R.; Rezaei, A.S. On natural frequencies of Levy-type thick porous-cellular plates surrounded by piezoelectric layers. Compos. Struct. 2017, 179, 340–354. [Google Scholar] [CrossRef]
- Rezaei, A.S.; Saidi, A.R. Exact solution for free vibration of thick rectangular plates made of porous materials. Compos. Struct. 2015, 134, 1051–1060. [Google Scholar] [CrossRef]
- Reddy, J.N. Mechanics of laminated composite plates and shells: Theory and analysis; CRC press: Boca raton, FL, USA, 2003. [Google Scholar]
- He, X.Q.; Ng, T.Y.; Sivashanker, S.; Liew, K.M. Active control of FGM plates with integrated piezoelectric sensors and actuators. Int. J. Solids Struct. 2001, 38, 1641–1655. [Google Scholar] [CrossRef]


| EBC | L1/Rx | Hp/2h | Ref. [60] | Present |
|---|---|---|---|---|
| SC | 0.0 | 0.1 | 839.368 | 838.273 |
| 0.2 | 801.794 | 799.360 | ||
| 0.1 | 0.1 | 853.147 | 852.075 | |
| 0.2 | 813.413 | 811.024 | ||
| OC | 0.0 | 0.1 | 856.455 | 854.844 |
| 0.2 | 833.781 | 829.958 | ||
| 0.1 | 0.1 | 870.057 | 868.476 | |
| 0.2 | 845.108 | 841.347 |
| Mode (m,n) | Ref. [69] | Ref. [64] | Ref. [61] | Present |
|---|---|---|---|---|
| 1st (1,1) | 144.25 | 145.35 | 145.35 | 144.49 |
| 2nd (1,2) | 359.00 | 363.05 | 363.06 | 360.89 |
| 3rd (2,1) | 359.00 | 363.05 | 363.06 | 360.89 |
| 4th (2,2) | 564.10 | 580.35 | 580.37 | 576.90 |
| 5th (1,3) | 717.80 | 725.00 | 725.03 | 720.70 |
| 6th (3,1) | 717.80 | 725.00 | 725.03 | 720.70 |
| 7th (2,3) | 908.25 | 941.64 | 941.69 | 936.06 |
| 8th (3,2) | 908.25 | 941.64 | 941.69 | 936.06 |
| 9th (1,4) | 1223.14 | 1229.88 | 1229.96 | 1222.61 |
| 10th (4,1) | 1223.14 | 1229.88 | 1229.96 | 1222.61 |
| Geometry | Hp/2h | Bimorph | Unimorph | ||
|---|---|---|---|---|---|
| Ref. [59] | Present | Ref. [59] | Present | ||
| Spherical | 0.5 | 2652 | 2653 | 2654 | 2654 |
| 1.0 | 2405 | 2408 | 2411 | 2411 | |
| 2.0 | 2211 | 2215 | 2217 | 2217 | |
| Cylindrical | 0.5 | 1526 | 1527 | 1531 | 1531 |
| 1.0 | 1383 | 1387 | 1393 | 1393 | |
| 2.0 | 1273 | 1280 | 1285 | 1285 | |
| Plate | 0.5 | 873 | 875 | 887 | 887 |
| 1.0 | 791 | 797 | 813 | 813 | |
| 2.0 | 730 | 743 | 755 | 755 | |
| EBC | e | Spherical (Ry/L1 = Rx/L1) | Cylindrical (Ry/L1 = ∞) | Plate (Ry/L1 = Rx/L1 = ∞) | Hyperbolic Paraboloidal (Ry/L1 = -Rx/L1) |
|---|---|---|---|---|---|
| Bimorph | |||||
| SC | 0.0 | 280.488 | 253.228 | 244.123 | 242.135 |
| 0.1 | 277.570 | 251.004 | 242.163 | 240.189 | |
| 0.2 | 274.537 | 248.677 | 240.104 | 238.147 | |
| 0.3 | 271.374 | 246.232 | 237.931 | 235.992 | |
| 0.4 | 268.070 | 243.653 | 235.627 | 233.706 | |
| 0.5 | 264.614 | 240.924 | 233.173 | 231.271 | |
| OC | 0.0 | 299.762 | 273.571 | 264.980 | 262.815 |
| 0.1 | 297.286 | 271.846 | 263.589 | 261.434 | |
| 0.2 | 294.738 | 270.074 | 262.168 | 260.023 | |
| 0.3 | 292.116 | 268.254 | 260.720 | 258.586 | |
| 0.4 | 289.423 | 266.391 | 259.252 | 257.129 | |
| 0.5 | 286.673 | 264.500 | 257.784 | 255.672 | |
| Unimorph | |||||
| SC | 0.0 | 281.395 | 254.198 | 245.202 | 243.203 |
| 0.1 | 276.825 | 250.150 | 241.350 | 239.382 | |
| 0.2 | 271.804 | 245.632 | 237.019 | 235.086 | |
| 0.3 | 266.223 | 240.522 | 232.082 | 230.189 | |
| 0.4 | 259.937 | 234.655 | 226.365 | 224.520 | |
| 0.5 | 252.739 | 227.794 | 219.620 | 217.829 | |
| OC | 0.0 | 308.683 | 278.646 | 265.389 | 263.218 |
| 0.1 | 303.993 | 274.389 | 261.260 | 259.123 | |
| 0.2 | 298.796 | 269.602 | 256.590 | 254.491 | |
| 0.3 | 292.975 | 264.155 | 251.242 | 249.186 | |
| 0.4 | 286.368 | 257.868 | 245.028 | 243.023 | |
| 0.5 | 278.758 | 250.492 | 237.683 | 235.739 | |
| Geometry of the Smart Panel | Rx/L1 = 1 | Rx/L1 = 2 | Rx/L1 = 5 | Rx/L1 = 10 |
|---|---|---|---|---|
| 2h/L1 = 0.1, Hp/2h = 0.05 | ||||
| Spherical (Ry/L1 = Rx/L1) | 817.439 | 572.816 | 474.190 | 458.105 |
| Cylindrical (Ry/L1 = ∞) | 549.656 | 480.008 | 457.156 | 453.776 |
| Plate (Ry/L1 = Rx/L1 = ∞) | 452.686 | 452.686 | 452.686 | 452.686 |
| Hyperbolic Paraboloidal (Ry/L1 = -Rx/L1) | 369.247 | 429.736 | 448.902 | 451.736 |
| 2h/L1 = 0.1, Hp/2h = 0.1 | ||||
| Spherical (Ry/L1 = Rx/L1) | 794.466 | 564.937 | 473.786 | 459.051 |
| Cylindrical (Ry/L1 = ∞) | 541.781 | 478.626 | 458.098 | 455.074 |
| Plate (Ry/L1 = Rx/L1 = ∞) | 454.102 | 454.102 | 454.102 | 454.102 |
| Hyperbolic Paraboloidal (Ry/L1 = -Rx/L1) | 370.360 | 431.054 | 450.301 | 453.147 |
| 2h/L1 = 0.15, Hp/2h = 0.05 | ||||
| Spherical (Ry/L1 = Rx/L1) | 911.460 | 727.852 | 662.487 | 652.559 |
| Cylindrical (Ry/L1 = ∞) | 694.283 | 661.115 | 651.139 | 649.757 |
| Plate (Ry/L1 = Rx/L1 = ∞) | 649.386 | 649.386 | 649.386 | 649.386 |
| Hyperbolic Paraboloidal (Ry/L1 = -Rx/L1) | 526.775 | 615.218 | 643.723 | 647.963 |
| 2h/L1 = 0.15, Hp/2h = 0.1 | ||||
| Spherical (Ry/L1 = Rx/L1) | 889.776 | 720.098 | 660.438 | 651.429 |
| Cylindrical (Ry/L1 = ∞) | 686.543 | 658.381 | 650.006 | 648.858 |
| Plate (Ry/L1 = Rx/L1 = ∞) | 648.562 | 648.562 | 648.562 | 648.562 |
| Hyperbolic Paraboloidal (Ry/L1 = -Rx/L1) | 525.963 | 614.352 | 642.888 | 647.136 |
| Geometry of the Smart Panel | Rx/L1 = 1 | Rx/L1 = 2 | Rx/L1 = 5 | Rx/L1 = 10 |
|---|---|---|---|---|
| 2h/L1 = 0.1, Hp/2h = 0.05 | ||||
| Spherical (Ry/L1 = Rx/L1) | 819.827 | 572.226 | 472.471 | 456.188 |
| Cylindrical (Ry/L1 = ∞) | 548.928 | 478.424 | 455.241 | 451.794 |
| Plate (Ry/L1 = Rx/L1 = ∞) | 450.657 | 450.657 | 450.657 | 450.657 |
| Hyperbolic Paraboloidal (Ry/L1 = -Rx/L1) | 367.585 | 427.808 | 446.890 | 449.711 |
| 2h/L1 = 0.1, Hp/2h = 0.1 | ||||
| Spherical (Ry/L1 = Rx/L1) | 798.410 | 563.822 | 470.813 | 455.765 |
| Cylindrical (Ry/L1 = ∞) | 540.425 | 475.869 | 454.816 | 451.688 |
| Plate (Ry/L1 = Rx/L1 = ∞) | 450.646 | 450.646 | 450.646 | 450.646 |
| Hyperbolic Paraboloidal (Ry/L1 = -Rx/L1) | 367.510 | 427.764 | 446.872 | 449.698 |
| 2h/L1 = 0.15, Hp/2h = 0.05 | ||||
| Spherical (Ry/L1 = Rx/L1) | 914.868 | 727.352 | 660.50 | 650.254 |
| Cylindrical (Ry/L1 = ∞) | 693.449 | 659.300 | 648.835 | 647.317 |
| Plate (Ry/L1 = Rx/L1 = ∞) | 646.825 | 646.825 | 646.825 | 646.825 |
| Hyperbolic Paraboloidal (Ry/L1 = -Rx/L1) | 524.677 | 612.786 | 641.183 | 645.407 |
| 2h/L1 = 0.15, Hp/2h = 0.1 | ||||
| Spherical (Ry/L1 = Rx/L1) | 895.375 | 719.168 | 657.105 | 647.585 |
| Cylindrical (Ry/L1 = ∞) | 685.017 | 655.306 | 646.164 | 644.804 |
| Plate (Ry/L1 = Rx/L1 = ∞) | 644.319 | 644.319 | 644.319 | 644.319 |
| Hyperbolic Paraboloidal (Ry/L1 = -Rx/L1) | 522.440 | 610.305 | 638.677 | 642.901 |
| Hp/2h | Bimorph | Unimorph | ||||
|---|---|---|---|---|---|---|
| (eij = 0 1) | SC (Ω(%) 2) | OC (Ω(%) 2) | (eij = 0 1) | SC (Ω(%) 2) | OC (Ω(%) 2) | |
| Spherical (Ry/L1 = Rx/L1) | ||||||
| 0.0 | 468.898 | 468.898 (0.00) | 468.898 (0.00) | 468.898 | 468.898 (0.00) | 468.898 (0.00) |
| 0.1 | 467.185 | 467.205 (0.00) | 490.957 (5.09) | 461.490 | 461.490 (0.00) | 488.044 (5.75) |
| 0.2 | 473.266 | 473.395 (0.03) | 512.563 (8.30) | 464.088 | 464.088 (0.00) | 506.619 (9.16) |
| 0.3 | 483.409 | 483.762 (0.07) | 533.559 (10.4) | 472.066 | 472.066 (0.00) | 524.660 (11.1) |
| 0.4 | 495.832 | 496.527 (0.14) | 553.864 (11.7) | 483.163 | 483.163 (0.00) | 542.115 (12.2) |
| Cylindrical (Ry/L1 = ∞) | ||||||
| 0.0 | 450.644 | 450.644 (0.00) | 450.644 (0.00) | 450.644 | 450.644 (0.00) | 450.644 (0.00) |
| 0.1 | 451.961 | 451.982 (0.00) | 476.423 (5.41) | 445.870 | 445.870 (0.00) | 470.093 (5.43) |
| 0.2 | 460.132 | 460.265 (0.03) | 500.343 (8.74) | 450.444 | 450.444 (0.00) | 489.287 (8.62) |
| 0.3 | 471.819 | 472.182 (0.08) | 522.934 (10.8) | 459.984 | 459.984 (0.00) | 508.060 (10.5) |
| 0.4 | 485.438 | 486.150 (0.15) | 544.411 (12.1) | 472.363 | 472.363 (0.00) | 526.285 (11.4) |
| Plate (Ry/L1 = Rx/L1 = ∞) | ||||||
| 0.0 | 445.780 | 445.780 (0.00) | 445.780 (0.00) | 445.780 | 445.780 (0.00) | 445.780 (0.00) |
| 0.1 | 448.158 | 448.180 (0.00) | 473.069 (5.56) | 441.867 | 441.867 (0.00) | 463.333 (4.86) |
| 0.2 | 457.080 | 457.215 (0.03) | 497.912 (8.93) | 447.164 | 447.164 (0.00) | 481.775 (7.74) |
| 0.3 | 469.339 | 469.707 (0.08) | 521.138 (11.0) | 457.328 | 457.328 (0.00) | 500.345 (9.41) |
| 0.4 | 483.415 | 484.136 (0.15) | 543.091 (12.3) | 470.262 | 470.262 (0.00) | 518.664 (10.3) |
| Hyperbolic Paraboloidal (Ry/L1 = -Rx/L1) | ||||||
| 0.0 | 442.057 | 442.057 (0.00) | 442.057 (0.00) | 442.057 | 442.057 (0.00) | 442.057 (0.00) |
| 0.1 | 444.406 | 444.427 (0.00) | 469.070 (5.55) | 438.167 | 438.167 (0.00) | 459.427 (4.85) |
| 0.2 | 453.234 | 453.368 (0.03) | 493.662 (8.92) | 443.398 | 443.398 (0.00) | 477.665 (7.73) |
| 0.3 | 465.365 | 465.730 (0.08) | 516.631 (11.0) | 453.449 | 453.449 (0.00) | 496.020 (9.93) |
| 0.4 | 479.293 | 480.006 (0.15) | 538.329 (12.3) | 466.240 | 466.240 (0.00) | 514.118 (10.3) |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Askari, M.; Brusa, E.; Delprete, C. Electromechanical Vibration Characteristics of Porous Bimorph and Unimorph Doubly Curved Panels. Actuators 2020, 9, 7. https://doi.org/10.3390/act9010007
Askari M, Brusa E, Delprete C. Electromechanical Vibration Characteristics of Porous Bimorph and Unimorph Doubly Curved Panels. Actuators. 2020; 9(1):7. https://doi.org/10.3390/act9010007
Chicago/Turabian StyleAskari, Mahmoud, Eugenio Brusa, and Cristiana Delprete. 2020. "Electromechanical Vibration Characteristics of Porous Bimorph and Unimorph Doubly Curved Panels" Actuators 9, no. 1: 7. https://doi.org/10.3390/act9010007
APA StyleAskari, M., Brusa, E., & Delprete, C. (2020). Electromechanical Vibration Characteristics of Porous Bimorph and Unimorph Doubly Curved Panels. Actuators, 9(1), 7. https://doi.org/10.3390/act9010007







