Characteristics and Analysis of an Eddy Current Shock Absorber Damper Using Finite Element Analysis †
Abstract
1. Introduction
2. Materials and Methods
2.1. Construction and Materials
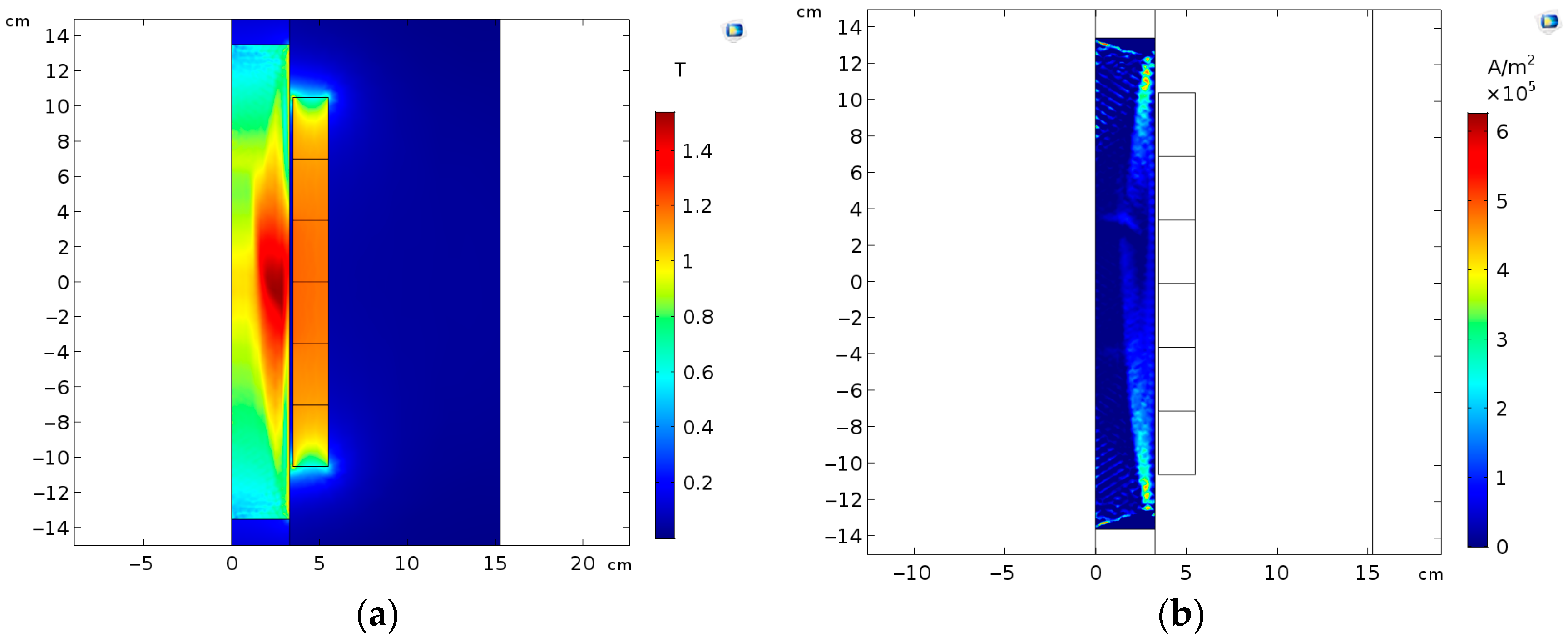
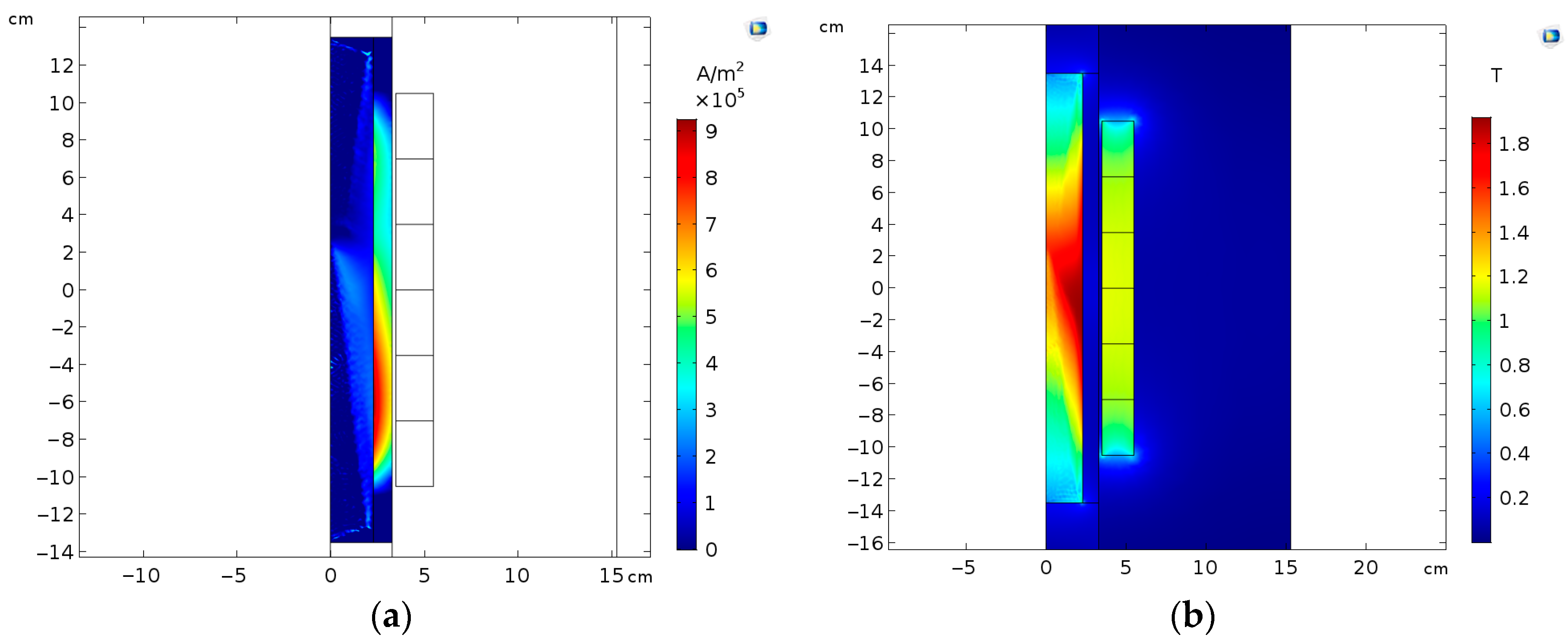
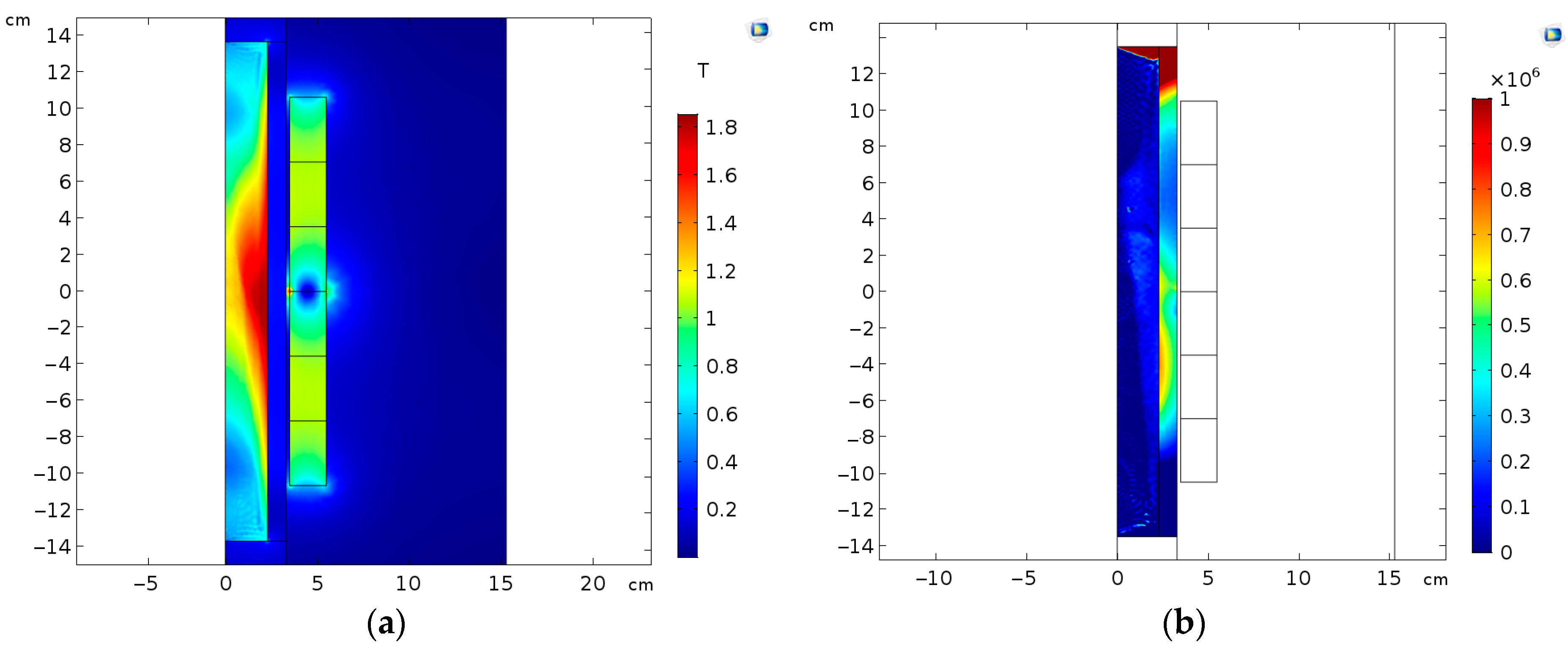
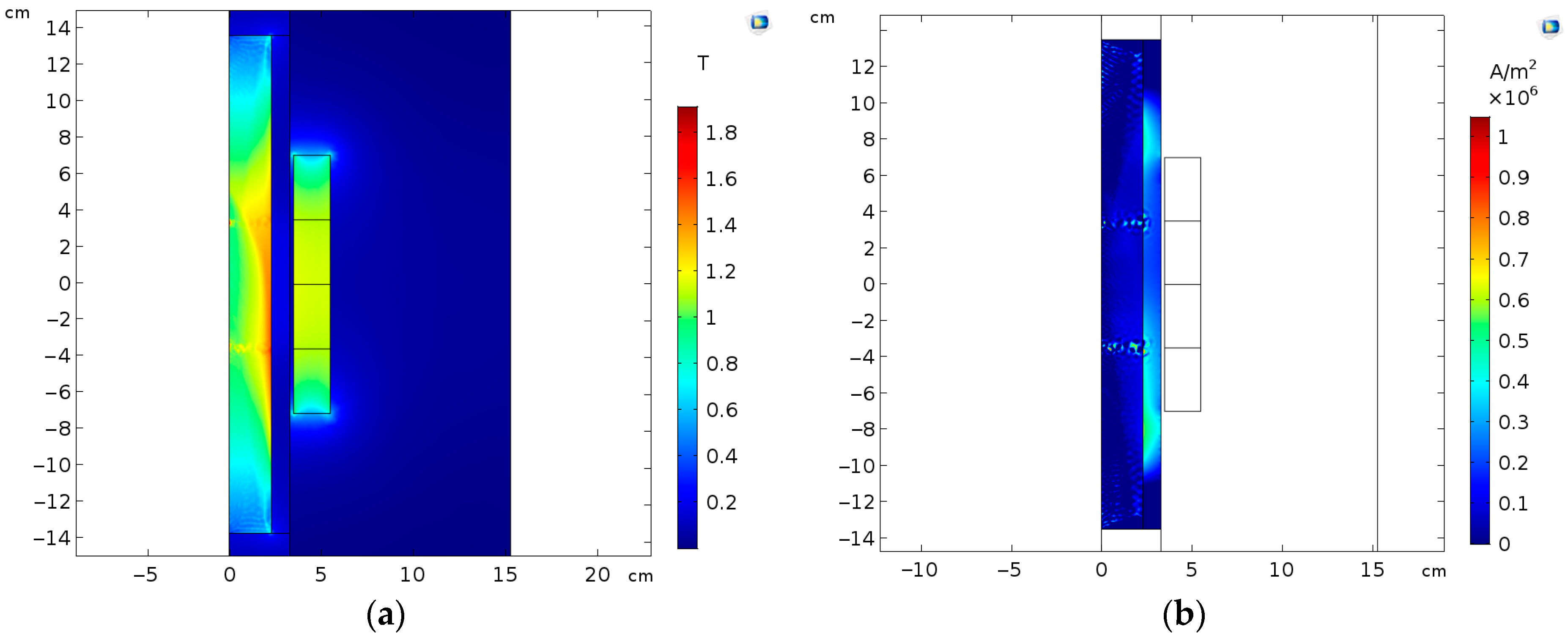
2.2. Electromagnetic Simulation of ECD
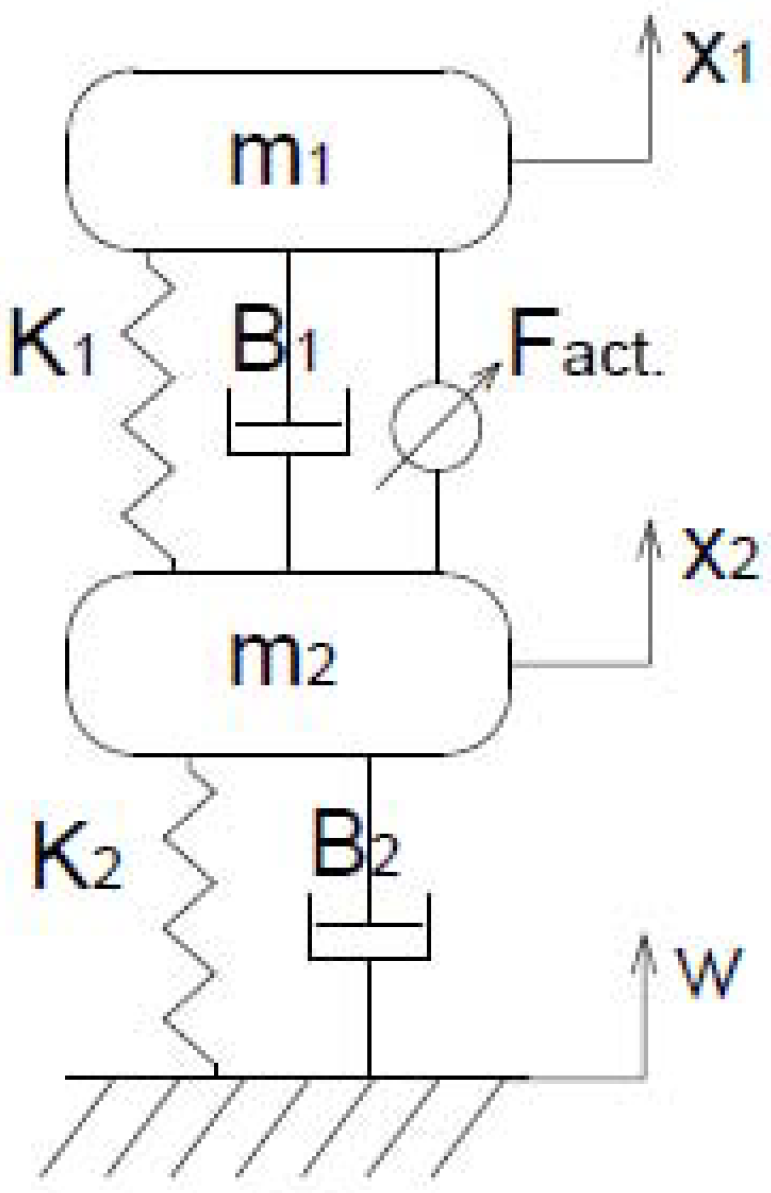
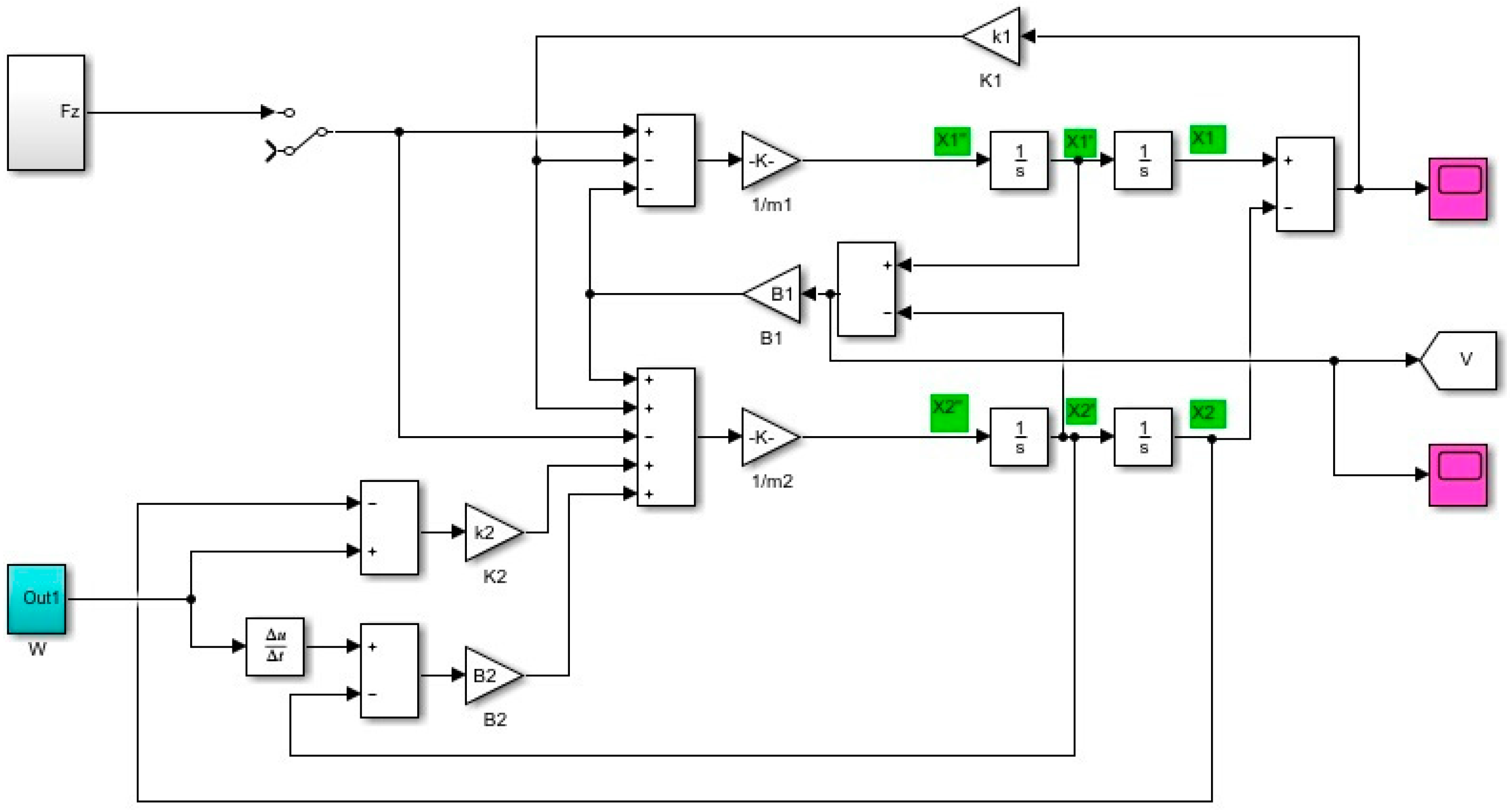
2.3. Quarter-Car Model
3. Results
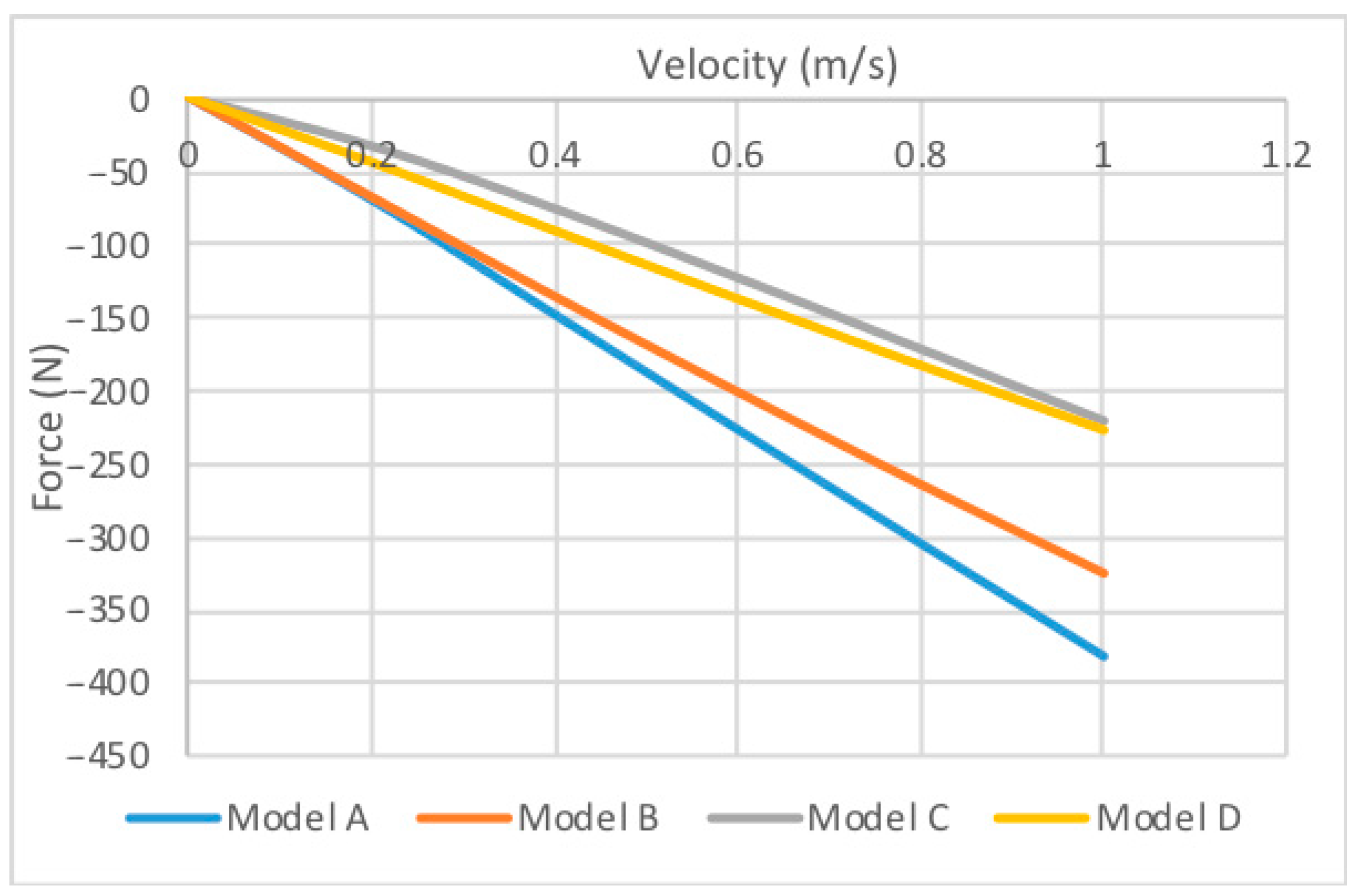
3.1. Force Calculations from the FEM Model
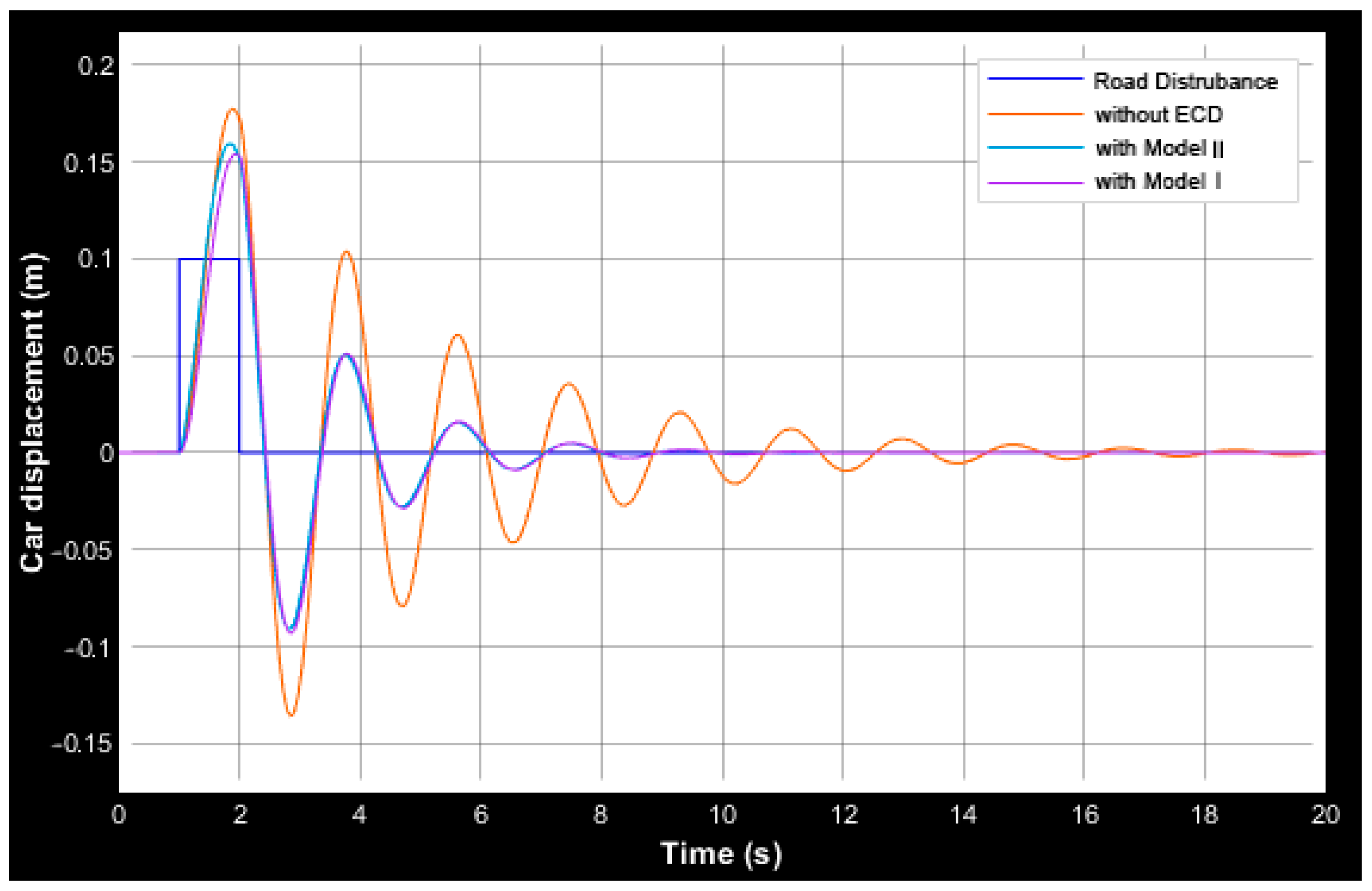
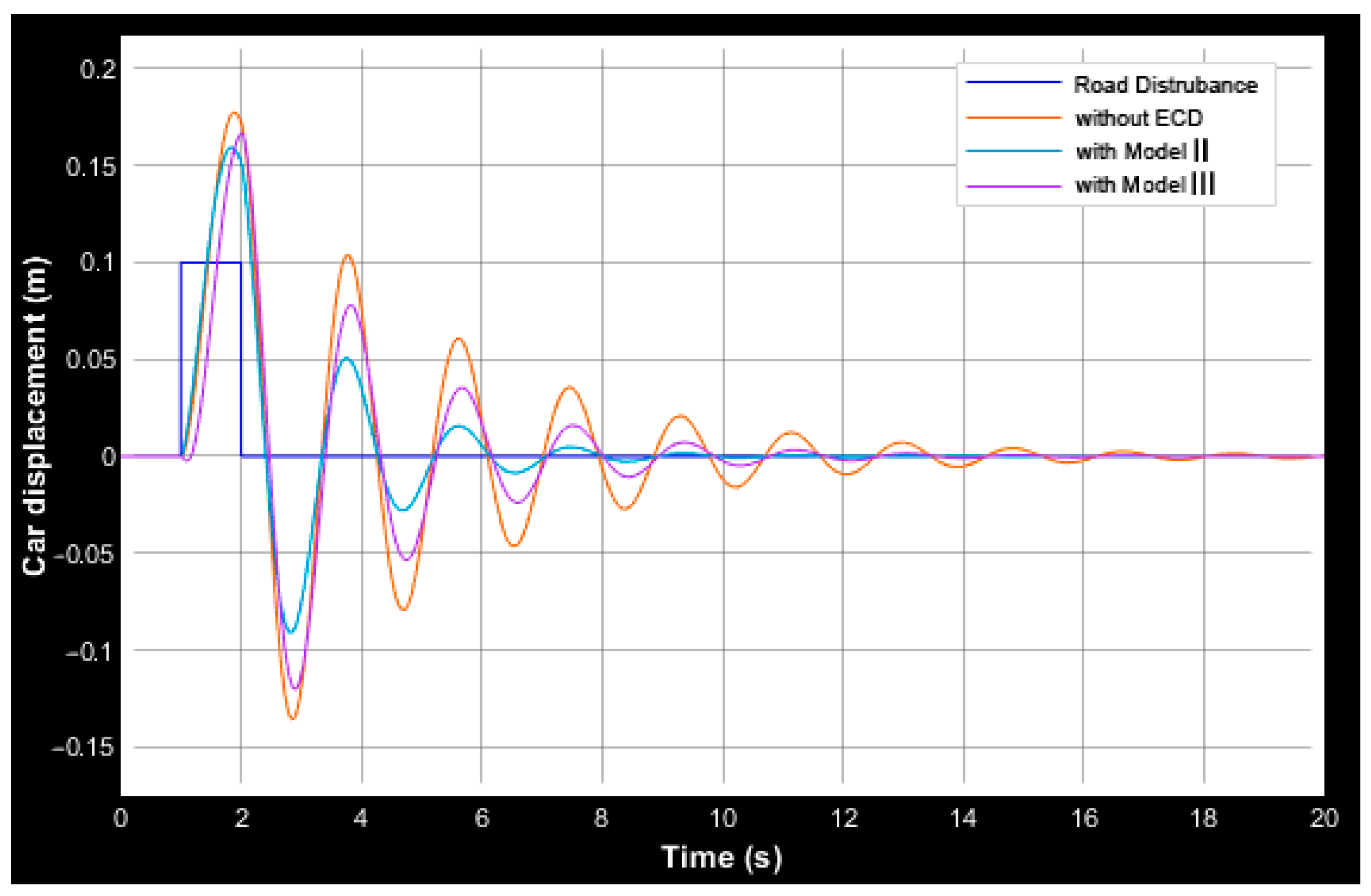
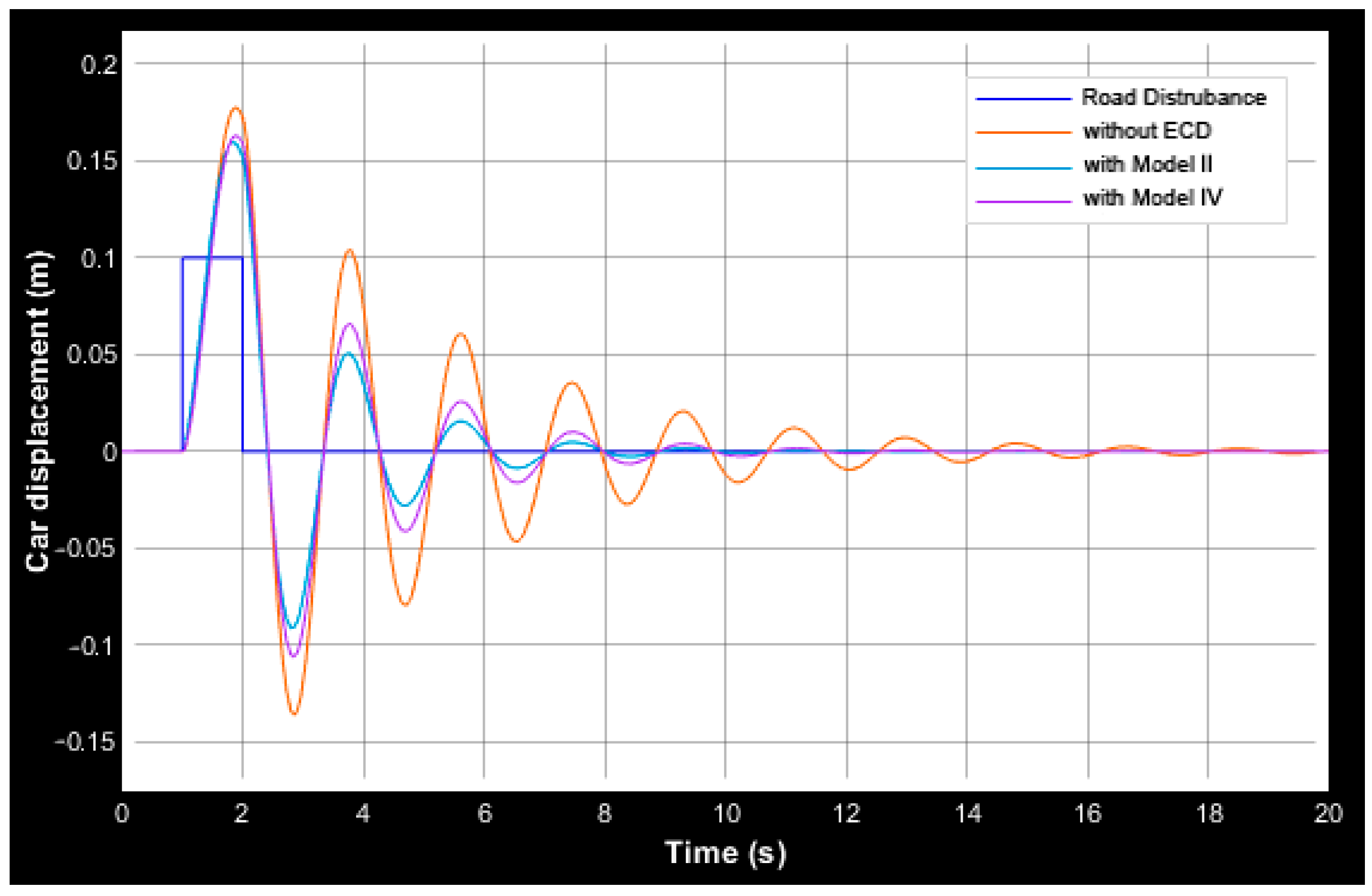
3.2. Quarter-Car Model Response
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Wiederick, H.D.; Gauthier, N.; Campbell, D.A.; Rochon, P. Magnetic braking: Simple theory and experiment. Am. J. Phys. 1987, 55, 500–503. [Google Scholar] [CrossRef]
- Ma, D.-M.; Shiau, J.-K. The design of eddy-current magnet brakes. Trans. Can. Soc. Mech. Eng. 2011, 35. [Google Scholar] [CrossRef]
- Adly, A.A.; Abd-El-Hafiz, S.K. Speed Range Based Optimization of Non-linear Electromagnetic Braking Systems. IEEE Trans. Magn. 2007, 43, 2606–2608. [Google Scholar] [CrossRef]
- Saxena, A.; Patel, R.K. Vibration control of cantilever beam using Eddy Current Damper. Int. J. Eng. Sci. Innov. Technol. (IJESIT) 2013, 2. [Google Scholar]
- Bae, J.; Hwang, J.; Kwag, D.; Park, J.; Inman, D.J. Vibration Suppression of a Large Beam Structure Using Tuned Mass Damper and Eddy Current Damping. Shock Vib. 2014, 2014, 893914. [Google Scholar] [CrossRef]
- Singh, R.; Sharma, M.; Singh, V.P. An Experimental Study of Vibration Control of Cantilever Beam Using Eddy Current Damper. Int. J. Appl. Eng. Res. 2012, 7. [Google Scholar]
- Graves, K.E.; Tonicich, D.; Iovenitti, P.G. Theoretical comparison of motional and transformer EMF device damping efficiency. J. Sound Vib. 2012, 233, 441–453. [Google Scholar] [CrossRef]
- Tonoli, A. Dynamic characteristics of eddy current dampers and couplers. J. Sound Vib. 2007, 301, 576–591. [Google Scholar] [CrossRef]
- Sodano, H.A.; Bae, J.-S.; Inman, D.J.; Belvin, W.K. Improved Concept and Model of Eddy Current Damper. J. Vib. Acoust. 2005, 128, 294–302. [Google Scholar] [CrossRef]
- Ebrahimi, B.; Khamesee, M.B.; Golnaraghi, M.F. Design and modeling of a magnetic shock absorber based on eddy current damping effect. J. Sound Vib. 2008, 315, 875–889. [Google Scholar] [CrossRef]
- Bae, J.-S.; Hwang, J.-H.; Park, J.-S.; Kwag, D.-G. Modeling and experiments on eddy current damping caused by a permanent magnet in a conductive tube. J. Mech. Sci. Technol. 2009, 23, 3024–3035. [Google Scholar] [CrossRef]
- Ebrahimi, B.; Khamesee, M.B.; Golnaraghi, F. Eddy current damper feasibility in automobile suspension: Modeling, simulation and testing. Smart Mater. Struct. 2009, 18. [Google Scholar] [CrossRef]
- Kim, S.-W.; Jung, H.-K.; Hahn, S.-Y. Experimental Study for Dynamic Characteristics of Eddy Current Shock Absorber. J. Korean Soc. Aeronaut. Space Sci. 2007, 35, 1089–1094. [Google Scholar]
- Guo, L.; Guo, N.; Wang, S.; Qiu, J.; Zhu, J.G.; Guo, Y.; Wang, Y. Performance of hybrid electromagnetic damper for vehicle suspension. Int. J. Innov. Eng. Res. Technol. 2015, 2. [Google Scholar]
- Adly, A.A.; Abd-El-Hafiz, S.K. Active electromagnetic suspension system design using hybrid neural-swarm optimization. Int. J. Appl. Electromagn. Mech. 2013, 43, 85–91. [Google Scholar] [CrossRef]
- Adly, A.A.; Adly, M.A. Utilizing Electromechanical Energy Harvesting in Vehicle Suspension Vibration Damping. In Proceedings of the 23rd IEEE International Conference on Electronics, Circuits and Systems (ICECS), Monte Carlo, Monaco, 11–14 December 2016; pp. 672–675. [Google Scholar]
- Abdullah, A.A.; Abdo, T.M.; Huzayyin, A.A.; Adly, A.A. Performance Analysis of Eddy Current Shock Absorber Damper Using Finite Element Analysis. In Proceedings of the 19th International Middle-East Power Systems Conference (MEPCON 2017), Cairo, Egypt, 19–21 December 2017. [Google Scholar]
- Paulides, J.J.H.; Encica, L.; Lomonova, E.A.; Vandenput, A.J.A. Design Considerations for a Semi-Active Electromagnetic Suspension System. IEEE Trans. Magn. 2006, 42, 3446–3448. [Google Scholar] [CrossRef]
- Gysen, B.L.J.; Paulides, J.J.H.; Lomonova, E.A. Active Electromagnetic Suspension System for Improved Vehicle Dynamics. IEEE Trans. Veh. Technol. 2010, 59, 1156–1163. [Google Scholar] [CrossRef]
- Grant, A.M. Analysis of Automotive Damper Data and Design of a Portable Measurement System. Ph.D. Thesis, The Ohio State University, Department of Mechanical Engineering, Center for Automotive Research, Columbus, OH, USA, 2005. [Google Scholar]
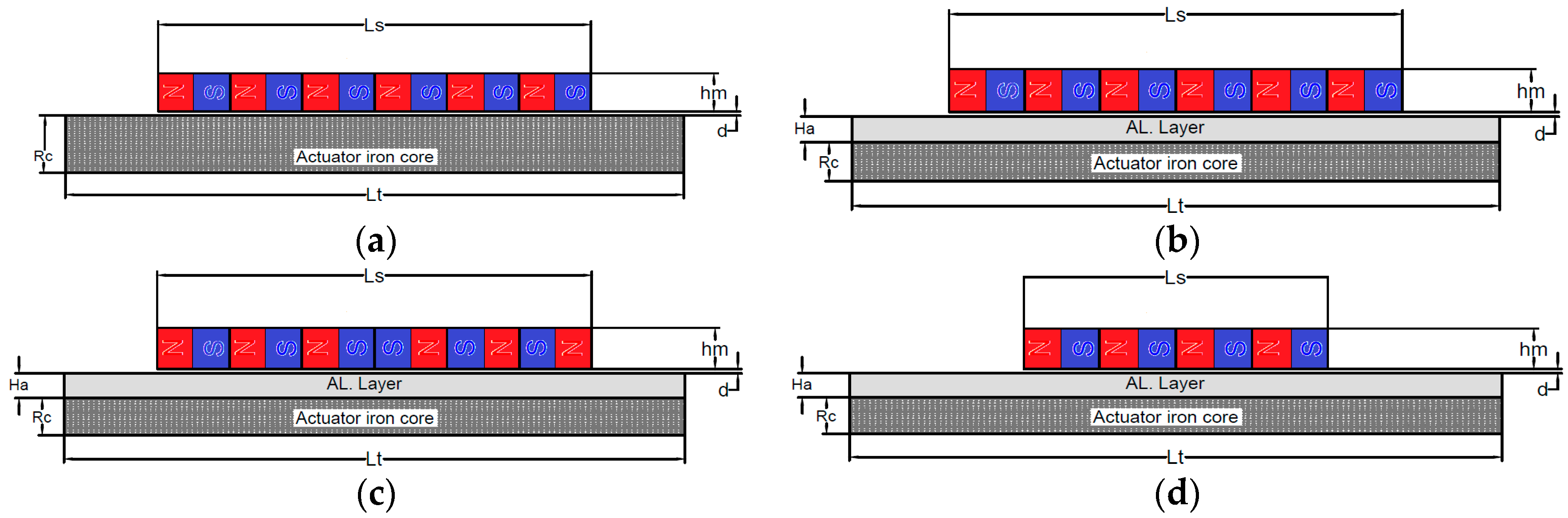
| Parameter | Model I | Model II | Model III | Model IV |
|---|---|---|---|---|
| Stator length (Ls) | 21 cm | 21 cm | 21 cm | 10.5 cm |
| Translator length (Lt) | 30 cm | 30 cm | 30 cm | 30 cm |
| Stator iron thickness (hi) | 2 cm | 2 cm | 2 cm | 2 cm |
| Magnets thickness (hm) | 2 cm | 2 cm | 2 cm | 2 cm |
| Al. layer thickness (Ha) | - | 1 cm | 1 cm | 1 cm |
| Iron core radius (Rc) | 1.9 cm | 1.8 cm | 1.8 cm | 1.8 cm |
| Air gap length (d) | 0.2 cm | 0.2 cm | 0.2 cm | 0.2 cm |
| Parameter | Value |
|---|---|
| Sprung mass () | 466 kg |
| Un-sprung mass () | 50 kg |
| Spring stiffness (K1) | 5700 |
| Tire stiffness (K2) | 135,000 |
| Suspension damping coefficient (B1) | 290 |
| Tire damping coefficient (B2) | 1400 |
| Hydraulic Damper | Model I | Model II | |
|---|---|---|---|
| Performance relative to volume | Good | Excellent | Excellent |
| Weight | High (about 10 kg) | Low (6.7 kg) | Fair (9.1 kg) |
| Manufacturing cost | Fair | Low | High |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abdo, T.M.; Huzayyin, A.A.; Abdallah, A.A.; Adly, A.A. Characteristics and Analysis of an Eddy Current Shock Absorber Damper Using Finite Element Analysis. Actuators 2019, 8, 77. https://doi.org/10.3390/act8040077
Abdo TM, Huzayyin AA, Abdallah AA, Adly AA. Characteristics and Analysis of an Eddy Current Shock Absorber Damper Using Finite Element Analysis. Actuators. 2019; 8(4):77. https://doi.org/10.3390/act8040077
Chicago/Turabian StyleAbdo, Tamer M., Ahmed A. Huzayyin, Ahmed A. Abdallah, and Amr A. Adly. 2019. "Characteristics and Analysis of an Eddy Current Shock Absorber Damper Using Finite Element Analysis" Actuators 8, no. 4: 77. https://doi.org/10.3390/act8040077
APA StyleAbdo, T. M., Huzayyin, A. A., Abdallah, A. A., & Adly, A. A. (2019). Characteristics and Analysis of an Eddy Current Shock Absorber Damper Using Finite Element Analysis. Actuators, 8(4), 77. https://doi.org/10.3390/act8040077





