Statistical Modeling of Photo-Bending Actuation of Hybrid Silicones Mixed with Azobenzene Powder
Abstract
1. Introduction
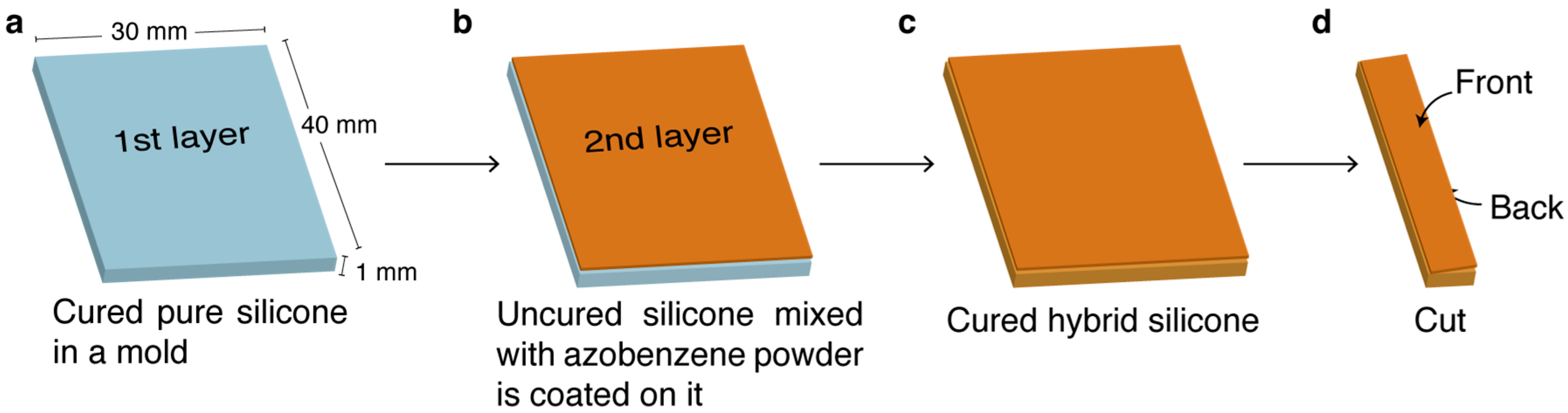
2. Materials and Methods
3. Results & Discussions
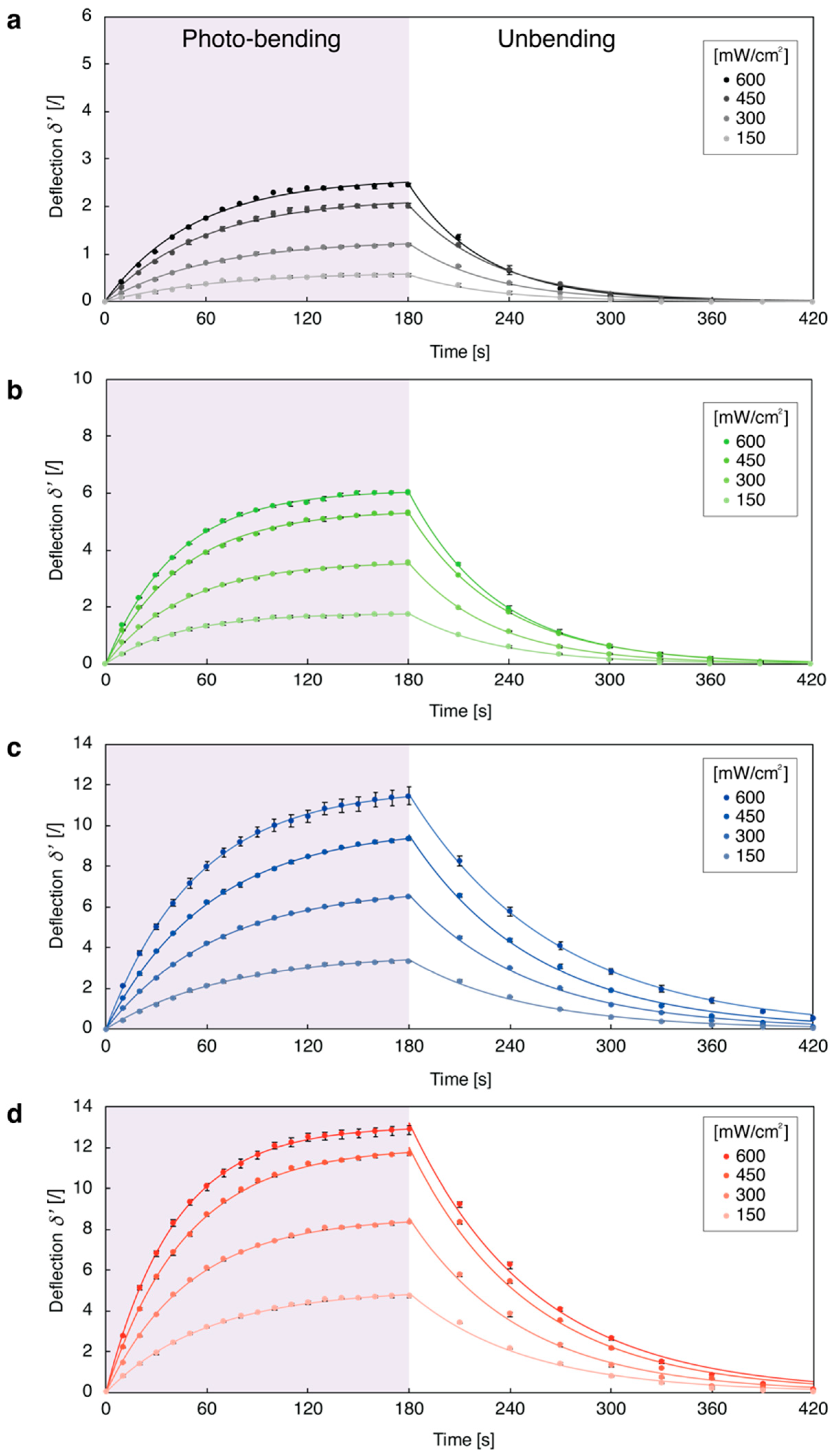
3.1. Photo-Actuation Behavior
3.2. Bending Evaluation
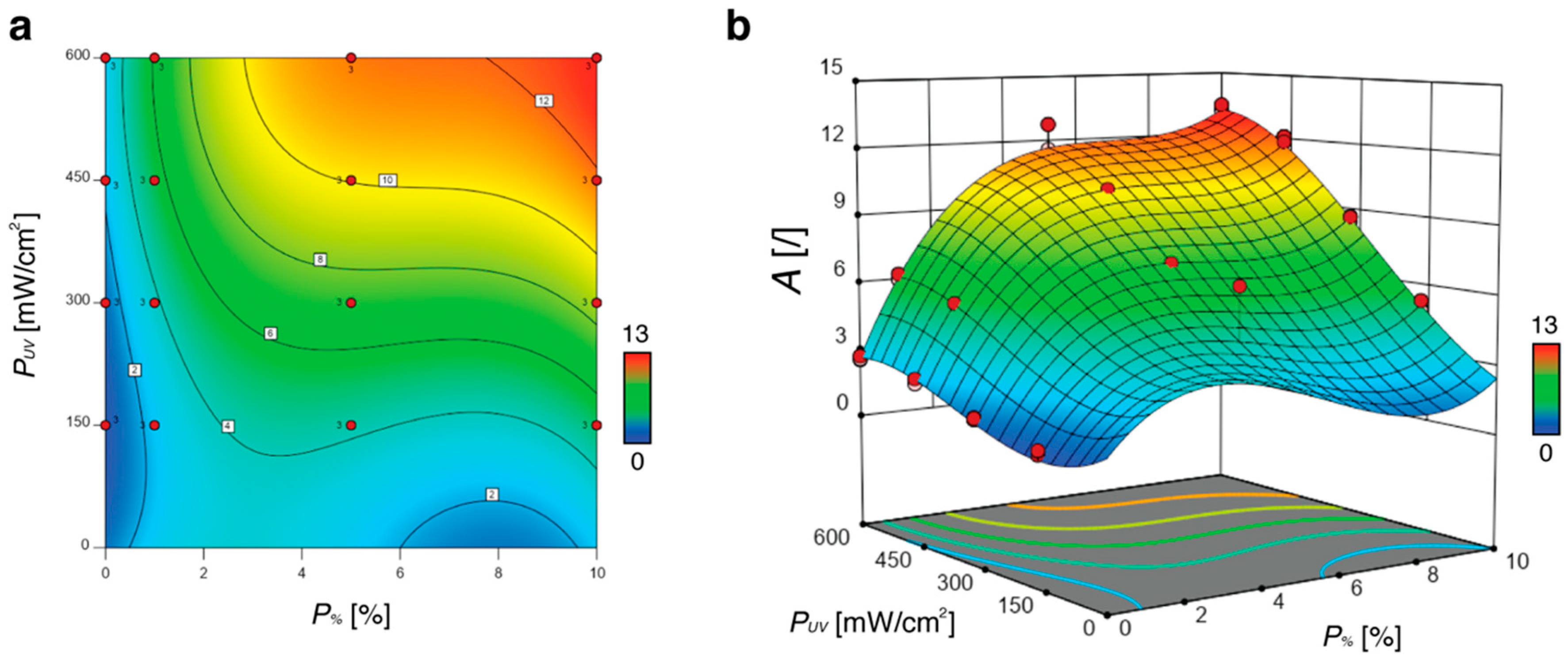
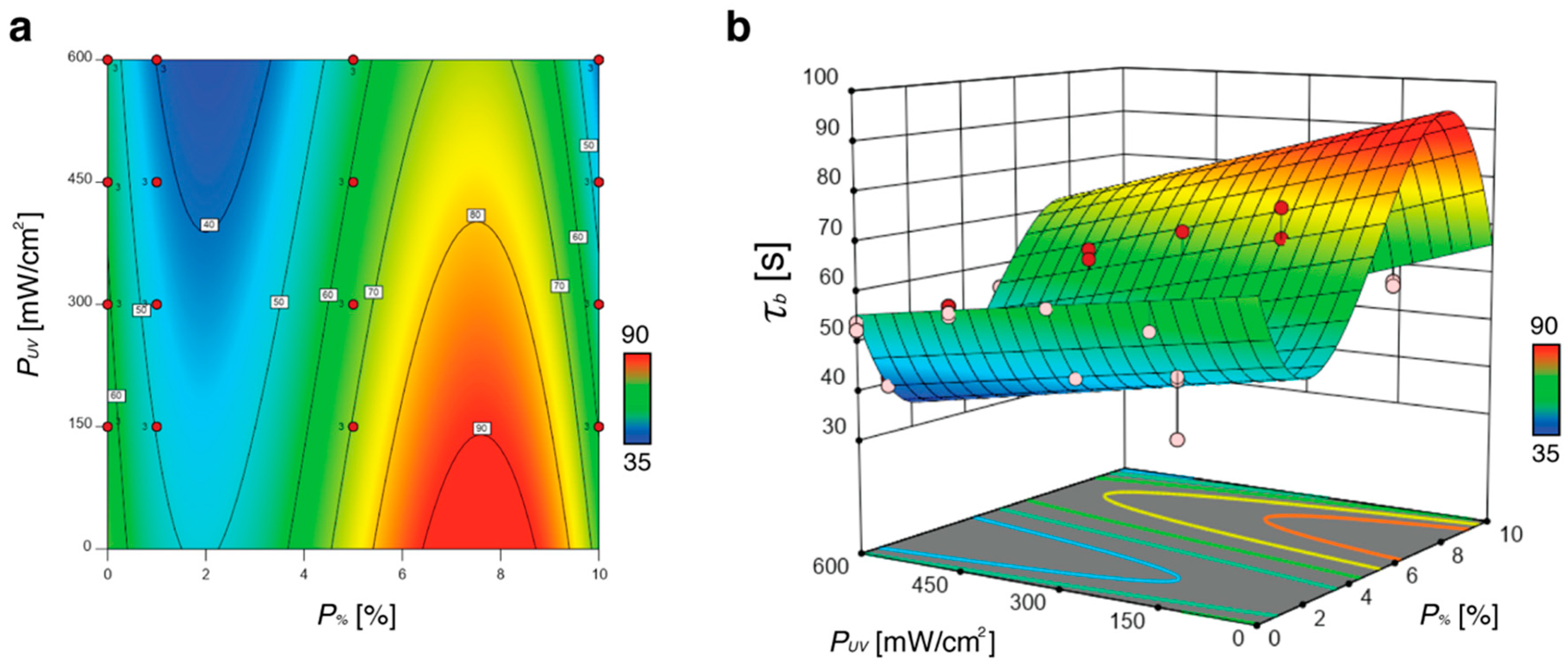
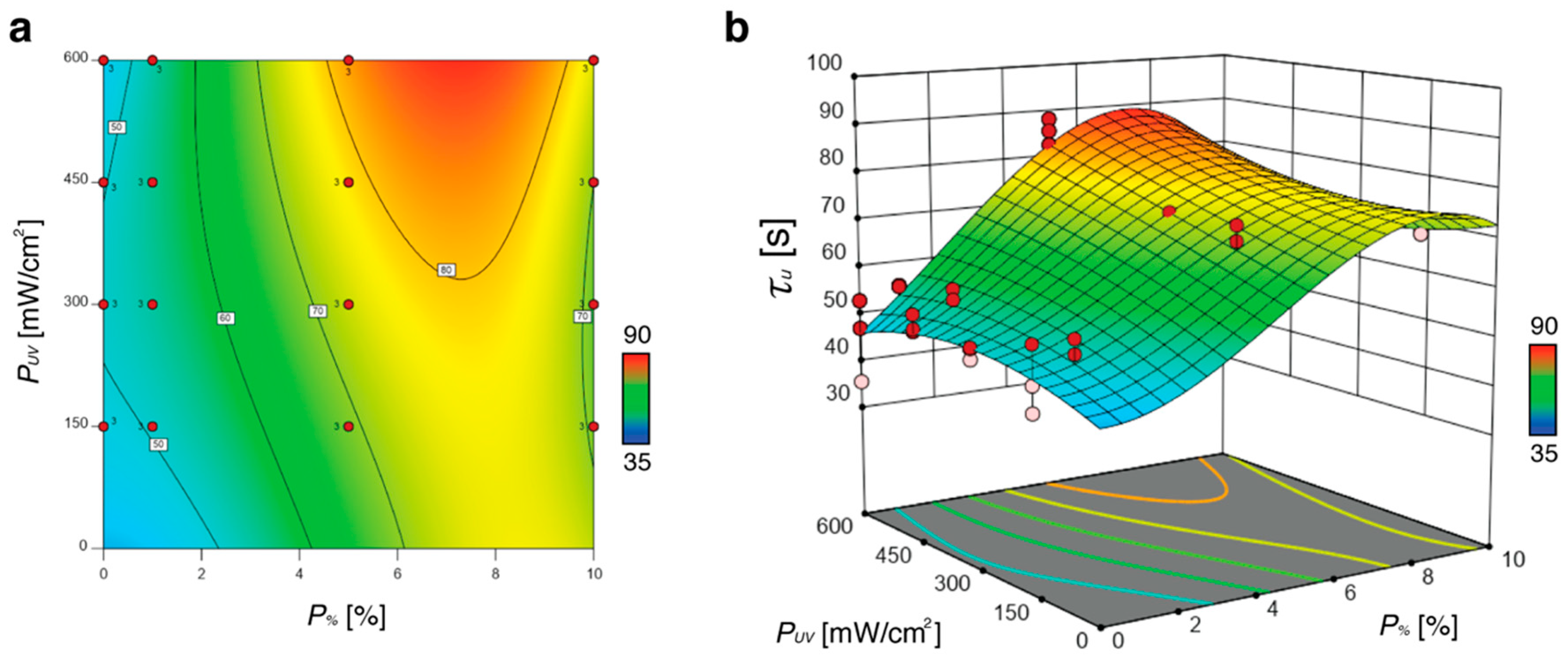
3.3. Model Construction
3.3.1. Model Construction for Photo-Bending
3.3.2. Model Construction for Unbending
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Capek, K.R.U. R (Rossum’s Universal Robots); Penguin Books: New York, NY, USA, 2004. [Google Scholar]
- Rus, D.; Tolley, M.T. Design, fabrication and control of soft robots. Nature 2015, 521, 467–475. [Google Scholar] [CrossRef] [PubMed]
- Laschi, C.; Mazzolai, B.; Cianchetti, M. Soft robotics: Technologies and systems pushing the boundaries of robot abilities. Sci. Robot. 2016, 1, eaah3690. [Google Scholar] [CrossRef]
- Cianchetti, M.; Laschi, C.; Menciassi, A.; Dario, P. Biomedical applications of soft robotics. Nat. Rev. Mater. 2018, 3, 143–153. [Google Scholar] [CrossRef]
- Yang, G.Z.; Fischer, P.; Nelson, B. New materials for next-generation robots. Sci. Robot. 2017, 2, eaap9294. [Google Scholar] [CrossRef]
- Banerjee, H.; Suhail, M.; Ren, H. Hydrogel actuators and sensors for biomedical soft robots: Brief overview with impending challenges. Biomimetics 2018, 3, 15. [Google Scholar] [CrossRef] [PubMed]
- Montero De Espinosa, L.; Meesorn, W.; Moatsou, D.; Weder, C. Bioinspired polymer systems with stimuli-responsive mechanical properties. Chem. Rev. 2017, 117, 12851–12892. [Google Scholar] [CrossRef] [PubMed]
- Lv, J.A.; Liu, Y.; Wei, J.; Chen, E.; Qin, L.; Yu, Y. Photocontrol of fluid slugs in liquid crystal polymer microactuators. Nature 2016, 537, 179–184. [Google Scholar] [CrossRef] [PubMed]
- Iwaso, K.; Takashima, Y.; Harada, A. Fast response dry-type artificial molecular muscles with [c2] daisy chains. Nat. Chem. 2016, 8, 625–632. [Google Scholar] [CrossRef]
- Wani, O.M.; Zeng, H.; Priimagi, A. A light-driven artificial flytrap. Nat. Commun. 2017, 8, 15546. [Google Scholar] [CrossRef]
- Lahikainen, M.; Zeng, H.; Priimagi, A. Reconfigurable photoactuator through synergistic use of photochemical and photothermal effects. Nat. Commun. 2018, 9, 4148. [Google Scholar] [CrossRef]
- Kobatake, S.; Takami, S.; Muto, H.; Ishikawa, T.; Irie, M. Rapid and reversible shape changes of molecular crystals on photoirradiation. Nature 2007, 446, 778–781. [Google Scholar] [CrossRef] [PubMed]
- Koshima, H.; Ojima, N.; Uchimoto, H. Mechanical motion of azobenzene crystals upon photoirradiation. J. Am. Chem. Soc. 2009, 131, 6890–6891. [Google Scholar] [CrossRef] [PubMed]
- Taniguchi, T.; Fujisawa, J.; Shiro, M.; Koshima, H.; Asahi, T. Mechanical motion of chiral azobenzene crystals with twisting upon photoirradiation. Chem. Eur. J. 2016, 22, 7950–7958. [Google Scholar] [CrossRef] [PubMed]
- Naumov, P.; Chizhik, S.; Panda, M.K.; Nath, N.K.; Boldyreva, E. Mechanically responsive molecular crystals. Chem. Rev. 2015, 115, 12440–12490. [Google Scholar] [CrossRef] [PubMed]
- Taniguchi, T.; Asahi, T.; Koshima, H. Photomechanical azobenzene crystals. Crystals 2019, 9, 437. [Google Scholar] [CrossRef]
- Lan, T.; Chen, W. Hybrid nanoscale organic molecular crystals assembly as a photon-controlled actuator. Angew. Chem. Int. Ed. 2013, 52, 6496–6500. [Google Scholar] [CrossRef] [PubMed]
- Chandra Sahoo, S.; Nath, N.K.; Zhang, L.; Semreen, M.H.; Al-Tel, T.H.; Naumov, P. Actuation based on thermo/photosalient effect: A biogenic smart hybrid driven by light and heat. RSC Adv. 2014, 4, 7640–7647. [Google Scholar] [CrossRef]
- Yu, Q.; Yang, X.; Chen, Y.; Yu, K.; Gao, J.; Liu, Z.; Cheng, P.; Zhang, Z.; Aguila, B.; Ma, S. Fabrication of light-triggered soft artificial muscles via a mixed-matrix membrane strategy. Angew. Chem. Int. Ed. 2018, 57, 10192–10196. [Google Scholar] [CrossRef] [PubMed]
- Shi, Y.X.; Zhang, W.H.; Abrahams, B.F.; Braunstein, P.; Lang, J.P. Fabrication of photoactuators: Macroscopic photomechanical responses of metal–organic frameworks to irradiation by UV light. Angew. Chem. Int. Ed. 2019, 58, 9453–9458. [Google Scholar] [CrossRef]
- Koshima, H.; Matsudomi, M.; Uemura, Y.; Kimura, F.; Kimura, T. Light-driven bending of polymer films in which salicylidenephenylethylamine crystals are aligned magnetically. Chem. Lett. 2013, 42, 1517–1519. [Google Scholar] [CrossRef]
- Zhang, X.; Yu, Z.; Wang, C.; Zarrouk, D.; Seo, J.W.T.; Cheng, J.C.; Buchan, A.D.; Takei, K.; Zhao, Y.; Ager, J.W.; et al. Photoactuators and motors based on carbon nanotubes with selective chirality distributions. Nat. Commun. 2014, 5, 2983. [Google Scholar] [CrossRef] [PubMed]
- Nakata, K.; Sakai, M.; Ochiai, T.; Murakami, T.; Fujishima, A. Bending motion of a polyacrylamide/graphite fiber driven by a wide range of light from UV to NIR. Mater. Lett. 2012, 74, 68–70. [Google Scholar] [CrossRef]
- Deng, J.; Li, J.; Chen, P.; Fang, X.; Sun, X.; Jiang, Y.; Weng, W.; Wang, B.; Peng, H. Tunable photothermal actuators based on a pre-programmed aligned nanostructure. J. Am. Chem. Soc. 2016, 138, 225–230. [Google Scholar] [CrossRef] [PubMed]
- Lee, E.; Kim, D.; Kim, H.; Yoon, J. Photothermally driven fast responding photo-actuators fabricated with comb-type hydrogels and magnetite nanoparticles. Sci. Rep. 2015, 5, 15124. [Google Scholar] [CrossRef] [PubMed]
- Ahir, S.V.; Terentjev, E.M. Photomechanical actuation in polymer-nanotube composites. Nat. Mater. 2005, 4, 491–495. [Google Scholar] [CrossRef] [PubMed]
- Hu, Y.; Li, Z.; Lan, T.; Chen, W. Photoactuators for direct optical-to-mechanical energy conversion: From nanocomponent assembly to macroscopic deformation. Adv. Mater. 2016, 28, 10548–10556. [Google Scholar] [CrossRef] [PubMed]
- Niu, D.; Jiang, W.; Liu, H.; Zhao, T.; Lei, B.; Li, Y.; Yin, L.; Shi, Y.; Chen, B.; Lu, B. Reversible bending behaviors of photomechanical soft actuators based on graphene nanocomposites. Sci. Rep. 2016, 6, 27366. [Google Scholar] [CrossRef] [PubMed]
- Van Oosten, C.L.; Harris, K.D.; Bastiaansen, C.W.M.; Broer, D.J. Glassy photomechanical liquid-crystal network actuators for microscale devices. Eur. Phys. J. E 2007, 23, 329–336. [Google Scholar] [CrossRef] [PubMed]
- Cheng, L.; Torres, Y.; Min Lee, K.; McClung, A.J.; Baur, J.; White, T.J.; Oates, W.S. Photomechanical bending mechanics of polydomain azobenzene liquid crystal polymer network films. J. Appl. Phys. 2012, 112, 013513. [Google Scholar] [CrossRef]
- Nath, N.K.; Pejov, L.; Nichols, S.M.; Hu, C.; Saleh, N.I.; Kahr, B.; Naumov, P. Model for photoinduced bending of slender molecular crystals. J. Am. Chem. Soc. 2014, 136, 2757–2766. [Google Scholar] [CrossRef]
- Zhou, B.; Bernhardt, E.; Bhuyan, A.; Ghorbanishiadeh, Z.; Rasmussen, N.; Lanska, J.; Kuzyk, M.G. Theoretical and experimental studies of photomechanical materials. J. Opt. Soc. Am. B 2019, 36, 1492–1517. [Google Scholar] [CrossRef]
- Koshima, H.; Ojima, N. Photomechanical bending of 4-aminoazobenzene crystals. Dyes Pigment. 2012, 92, 798–801. [Google Scholar] [CrossRef]

| x1 | x2 | x1x2 | x12 | x22 | x12x2 | x1x22 | x13 | x23 | x12x22 | x13x2 | x1x23 | x14 | x24 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Linear | Y | Y | - | - | - | - | - | - | - | - | - | - | - | - |
| 2FI | Y | Y | Y | - | - | - | - | - | - | - | - | - | - | - |
| Quadratic | Y | Y | Y | Y | Y | Y | Y | - | - | - | - | - | - | - |
| Cubic | Y | Y | Y | Y | Y | Y | Y | Y | Y | - | - | - | - | - |
| Quartic | Y | Y | Y | Y | Y | Y | Y | Y | Y | Y | Y | Y | Y | Y |
| 0 wt% | 1 wt% | 5 wt% | 10 wt% | |
|---|---|---|---|---|
| Length from irradiated center to the tip/mm | 20.0 | 18.9 | 18.0 | 16.5 |
| Width/mm | 4.9 | 4.5 | 4.9 | 5.5 |
| Thickness/mm | 1.4 | 1.5 | 1.7 | 1.5 |
| Light (mW/cm2) | The Value of A | |||||||
|---|---|---|---|---|---|---|---|---|
| 0 wt% | 1 wt% | 5 wt% | 10 wt% | 0 wt% | 1 wt% | 5 wt% | 10 wt% | |
| 150 | 0.57 | 1.78 | 3.41 | 4.88 | 66.7 | 43.6 | 70.7 | 60.1 |
| 300 | 1.23 | 3.57 | 6.61 | 8.56 | 61.6 | 46.9 | 65.8 | 49.8 |
| 450 | 2.04 | 5.32 | 9.54 | 12.0 | 58.0 | 45.6 | 62.1 | 47.0 |
| 600 | 2.48 | 6.07 | 11.5 | 13.2 | 52.9 | 41.8 | 53.6 | 40.2 |
| Light (mW/cm2) | The Value of A | |||||||
|---|---|---|---|---|---|---|---|---|
| 0 wt% | 1 wt% | 5 wt% | 10 wt% | 0 wt% | 1 wt% | 5 wt% | 10 wt% | |
| 150 | 0.62 | 1.78 | 3.69 | 5.05 | 48.7 | 52.5 | 70.9 | 69.0 |
| 300 | 1.28 | 3.59 | 6.97 | 8.60 | 49.9 | 50.9 | 72.4 | 67.6 |
| 450 | 2.18 | 6.97 | 9.91 | 12.0 | 51.4 | 55.5 | 74.7 | 71.2 |
| 600 | 2.60 | 8.60 | 11.8 | 13.1 | 44.7 | 52.8 | 85.7 | 74.4 |
| Source | Sequential p-Value | Lack of Fit p-Value | Adjusted R2 | Predicted R2 |
|---|---|---|---|---|
| Linear | 7.49 × 10−19 | 4.86 × 10−15 | 0.837 | 0.820 |
| 2FI | 1.42 × 10−4 | 4.62 × 10−13 | 0.880 | 0.864 |
| Quadratic | 1.09 × 10−12 | 4.66 × 10−5 | 0.966 | 0.960 |
| Cubic | 2.18 × 10−6 | 0.228 | 0.983 | 0.977 |
| Quartic | 0.0871 | 0.619 | 0.985 | 0.977 |
| Source | Sum of Squares | df | Mean Square | F-Value | p-Value |
|---|---|---|---|---|---|
| Model | 739. 9 | 9 | 82.2 | 311.4 | 9.14 × 10−33 |
| P% | 0.69 | 1 | 0.69 | 2.6 | 0.113 |
| PUV | 60.6 | 1 | 60.6 | 229.4 | 1.09 × 10−17 |
| P%PUV | 22.7 | 1 | 22.7 | 86.1 | 2.62 × 10−11 |
| P%2 | 35.6 | 1 | 35.6 | 134.8 | 4.60 × 10−14 |
| PUV2 | 0.026 | 1 | 0.026 | 0.099 | 0.755 |
| P%2PUV | 5.4 | 1 | 5.4 | 20.4 | 5.98 × 10−5 |
| P%PUV2 | 1.5 | 1 | 1.5 | 5.6 | 0.0229 |
| P%3 | 4.5 | 1 | 4.5 | 17.0 | 1.93 × 10−4 |
| PUV3 | 1.3 | 1 | 1.3 | 4.8 | 0.0345 |
| Residual | 10.0 | 38 | 0.26 | - | - |
| Lack of Fit | 2.1 | 6 | 0.36 | 1.45 | 0.228 |
| Pure Error | 7.9 | 32 | 0.25 | - | - |
| Corrected Total | 749.9 | 47 | - | - | - |
| Source | Sequential p-Value | Lack of Fit p-Value | Adjusted R2 | Predicted R2 |
|---|---|---|---|---|
| Linear | 0.00140 | 3.84 × 10−10 | 0.220 | 0.156 |
| 2FI | 0.202 | 3.75 × 10−10 | 0.232 | 0.157 |
| Quadratic | 0.0253 | 1.51 × 10−9 | 0.324 | 0.225 |
| Cubic | 1.76 × 10−11 | 0.107 | 0.824 | 0.761 |
| Quartic | 0.0186 | 0.837 | 0.856 | 0.785 |
| Source | Sum of Squares | df | Mean Square | F-Value | p-Value |
|---|---|---|---|---|---|
| Model | 4075.7 | 9 | 452.9 | 25.5 | 1.77 × 10−13 |
| P% | 1988.5 | 1 | 1988.5 | 112.1 | 6.84 × 10−13 |
| PUV | 79.1 | 1 | 79.1 | 4.5 | 0.0413 |
| P% PUV | 116.7 | 1 | 116.7 | 6.6 | 0.0144 |
| P%2 | 508.5 | 1 | 508.5 | 28.7 | 4.38 × 10−6 |
| PUV2 | 9.8 | 1 | 9.76 | 0.55 | 0.463 |
| P%2PUV | 0.24 | 1 | 0.24 | 0.01 | 0.907 |
| P%PUV2 | 18.4 | 1 | 18.4 | 1.0 | 0.315 |
| P%3 | 2158.7 | 1 | 2158.7 | 121.7 | 2.09 × 10−13 |
| PUV3 | 16.1 | 1 | 16.1 | 0.9 | 0.346 |
| Residual | 674.2 | 38 | 17.7 | - | - |
| Lack of Fit | 178.7 | 6 | 29. 8 | 1.92 | 0.107 |
| Pure Error | 495.5 | 32 | 15.5 | - | - |
| Corrected Total | 4749.9 | 47 | - | - | - |
| Source | Sequential p-Value | Lack of Fit p-Value | Adjusted R2 | Predicted R2 |
|---|---|---|---|---|
| Linear | 2.26 × 10−9 | 1.85 × 10−10 | 0.569 | 0.531 |
| 2FI | 0.277 | 1.54 × 10−10 | 0.571 | 0.528 |
| Quadratic | 5.88 × 10−12 | 0.00260 | 0.869 | 0.844 |
| Cubic | 3.64 × 10−4 | 0.263 | 0.915 | 0.888 |
| Quartic | 0.144 | 0.493 | 0.921 | 0.884 |
| Source | Sum of Squares | df | Mean Square | F-Value | p-Value |
|---|---|---|---|---|---|
| Model | 6718.9 | 9 | 746.5 | 57.05 | 2.53 × 10−19 |
| P% | 311.3 | 1 | 311.3 | 23.79 | 1.95 × 10−5 |
| PUV | 159.7 | 1 | 159.7 | 12.21 | 0.00123 |
| P% PUV | 0.010 | 1 | 0.010 | 0.0 | 0.978 |
| P%2 | 1313.2 | 1 | 1313.2 | 100.34 | 3.26 × 10−12 |
| PUV2 | 27.3 | 1 | 27.3 | 2.08 | 0.157 |
| P%2PUV | 168.3 | 1 | 168.3 | 12.86 | 9.44 × 10−4 |
| P% PUV2 | 64.0 | 1 | 64.0 | 4.89 | 0.0331 |
| P%3 | 101.8 | 1 | 101.8 | 7.78 | 0.00823 |
| PUV3 | 14.8 | 1 | 14.8 | 1.13 | 0.294 |
| Residual | 497.3 | 38 | 13.1 | - | - |
| Lack of Fit | 100.7 | 6 | 16.8 | 1.35 | 0.263 |
| Pure Error | 396.6 | 32 | 12.4 | - | - |
| Corrected Total | 7216.2 | 47 | - | - | - |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Taniguchi, T.; Blanc, L.; Asahi, T.; Koshima, H.; Lambert, P. Statistical Modeling of Photo-Bending Actuation of Hybrid Silicones Mixed with Azobenzene Powder. Actuators 2019, 8, 68. https://doi.org/10.3390/act8040068
Taniguchi T, Blanc L, Asahi T, Koshima H, Lambert P. Statistical Modeling of Photo-Bending Actuation of Hybrid Silicones Mixed with Azobenzene Powder. Actuators. 2019; 8(4):68. https://doi.org/10.3390/act8040068
Chicago/Turabian StyleTaniguchi, Takuya, Loïc Blanc, Toru Asahi, Hideko Koshima, and Pierre Lambert. 2019. "Statistical Modeling of Photo-Bending Actuation of Hybrid Silicones Mixed with Azobenzene Powder" Actuators 8, no. 4: 68. https://doi.org/10.3390/act8040068
APA StyleTaniguchi, T., Blanc, L., Asahi, T., Koshima, H., & Lambert, P. (2019). Statistical Modeling of Photo-Bending Actuation of Hybrid Silicones Mixed with Azobenzene Powder. Actuators, 8(4), 68. https://doi.org/10.3390/act8040068





