1. Introduction
Some gas turbine components work in an extreme environment of high temperatures. This has an impact on the maintenance cycle, and performance of the turbine [
1,
2,
3].
In the Summer, a Gas Turbine Power Plant can decrease its capacity of energy production by 24% when the temperature increases to 50 °C [
3,
4].
To define a gas turbine maintenance schedule [
3], we must consider what kind of problem it has, what possible solutions are available, and what the owners want. For example, we may detect a rising problem with vibration due to imbalance with a turbine blade. The substitution of the whole engine, substitution of only the damaged parts or adjustments in those parts or operating modes, may all be possible solutions for that given situation, and the owners must decide what course to take.
The chosen fuel for gas turbine operation [
4] and the environment in which it works has influence on its performance, and consequently in the maintenance and life cycle [
5]. This study intends to define the state of a gas turbine considering the vibration and temperature selected sensors facing the different environment in which the data is collected. Thirty samples were taken from the gas turbine sensors with different environment temperatures, and 18 anomalies were studied in a certain time interval.
2. Reliability and Condition Based Maintenance
The reliability knowledge allows knowing the probability of a system failure in a certain time interval, conducing to an action in time to correct an anomalous situation if it is needed.
Many techniques may be applied, for example, Failure Mode Effect and Criticality Analysis (FMECA) can be used to identify equipment hiatus and take some preventive measures to eliminate potential failures [
6].
A failure means that the functioning of a component or system is finished or its state is degraded, and the operating parameters are unsatisfactory. In addition, probably low level of operability, high reparation cost or risk to safety, both material and personal, will exist.
Some statistical techniques are available and can be developed to support failure and reliability analysis, such as Pareto Analysis, Weibull Probability Density Function, calculation of Mean Time Between Failure (MTBF) and Laplace Test.
These statistical methods support and allow the strongest diagnosis and assumptions contributing to an accurate diagnosis [
7].
Before we start a condition monitoring study, we must confirm that the chosen point of measures and the selected parameters are the ones that will represent the equipment state.
2.1. Pareto Analysis
The Pareto analysis applied as a tool to a strategic management can support the definition of an organization or system “strengths and weakness” [
8]. When applied on equipment condition, monitoring can give the organization the opportunity to define the strategies to correct the causes of anomalies, so the preventive or corrections occurs when an opportunity in an operational cycle is given, maximizing the availability time.
The Pareto analysis may be used when a reliability study begins. This methodology can group the failures according to the causes, so in this case, the number of failures is usually more than the causes. This analysis allows to focus on the study and prevention of the failures that occurs most often, saving economic resources [
9]. The collected data are represented graphically by columns, which represents the systems that failed, causes are in the horizontal axis and the number of causes are in the vertical axis.
Despite the importance of Pareto Analysis to determine the maintenance priorities and what leads to the cause of failure, it does not allow to determine exactly what is influencing the downtime, for that we use other statistics techniques [
10].
2.2. Weibull Probability Density Function
The failure distribution is the probability of a system failure in function of time [
11]. The Weibull distribution is a viable model to equipment and systems reliability study and life-testing [
12].
The Weibull Probability Density Function is usually used in failure analysis and it can be adapted to various studies. In this study we will use the equation:
where
t is the time interval,
µ is the mean,
β,
δ (
δ = 1/
λ) are the form factor, and
λ is the proportionality factor. Furthermore, in
F(
t) = 1 −
R(
t) the reliability
R is the complement of the distribution
F(
t), the system failure function [
13].
So, in the Weibull distribution a failure of a component from an equipment or system can be treated as a failure of the equipment or system, and the probability of equipment “survival” depends “on the probability of not having died” [
14], in the present case if the equipment is not damaged.
2.3. Statistics of a Reparable System
A reparable system is a system that if a failure occurs it operationally can be restored under certain condition, considering components repair or substitution [
15].
The availability of a reparable system is a function of the Loading Time (LT) and Down Time (DT). For a system with a stable failure rate, the availability is [
16]:
where
LT is the time in which the equipment is operating, and the
DT the time when the equipment is down in a sequence of an anomaly/reparation.
For the systems which the failure rate is stable we calculate the MTBF using (3):
where
T is the total functioning time for the system, and
nf is the number of failures.
Laplace Test
The Laplace test is a simple test of the failure data collected from a component or equipment which allows to determine the failure tendency [
11].
Considering a time limited test:
nf is the number of components that fail, T is the interval of the test, τi the system age for a failure of i order, considering H0 with stable failure rate, H1 with non-stable failure rate, and α = 0.05.
In a Homogeneous Poisson Process, if
the
H0 is rejected [
10].
For the systems with increasing failure rate, generally we propose improvements on the maintenance management and re-evaluate the equipment state.
2.4. Vibration Measure
Vibration is a good state indicator of rotating equipment, because vibration in a good state has one frequency signature and with a bad performance has another [
17].
To measure and analyze vibration we can use Spectrum Frequency or Root Mean Square (RMS). RMS vibration level is essential because it usually represents the machine’s overall state and, in a later situation, frequency analysis can be performed to effectively diagnose the anomaly [
18,
19].
In this article because of the transducer characteristics we will use the RMS.
RMS values allow the detection of abnormal vibration in most cases, this vibration can be given by:
It should be noted that in the measurement and analysis of vibrations, the frequency is essential because repeatability is the ability of a given measuring equipment, under the same conditions, to provide similar values of a characteristic, in order to obtain a reliable result that can serve as a basis for detection and diagnosis in online condition monitoring.
The vibration analysis will be used in complement to others. Once a detection is made, the severity of the value obtained and, if possible, the affected components must be determined. Patterns are then detected and comparisons must be made with previous readings of the same machine and similar ones [
20].
Because we are not analyzing vibration frequency, we analyze the tendency measuring the RMS values. Vibration limits must be defined for the control. In addition, in this analysis, the actions to be performed should be considered as soon as a trend is detected and when they must be taken to determine the time available for the operation of the equipment [
20].
3. Inspection and Maintenance Plan
Although the gas turbine has a defined preventive maintenance plan, we will develop a methodology to control the engine functioning and act when an anomaly, a product of various conjugated parameters and factors, demonstrates to us that necessity.
The data should be collected continuously throughout and periodically in the gas turbine life-cycle, because some vibration registers can indicate various failures type, the sample must be in a value capable of characterizing the equipment performance, and the values should always be carefully analyzed and if it is possible compared to other collected parameters [
21].
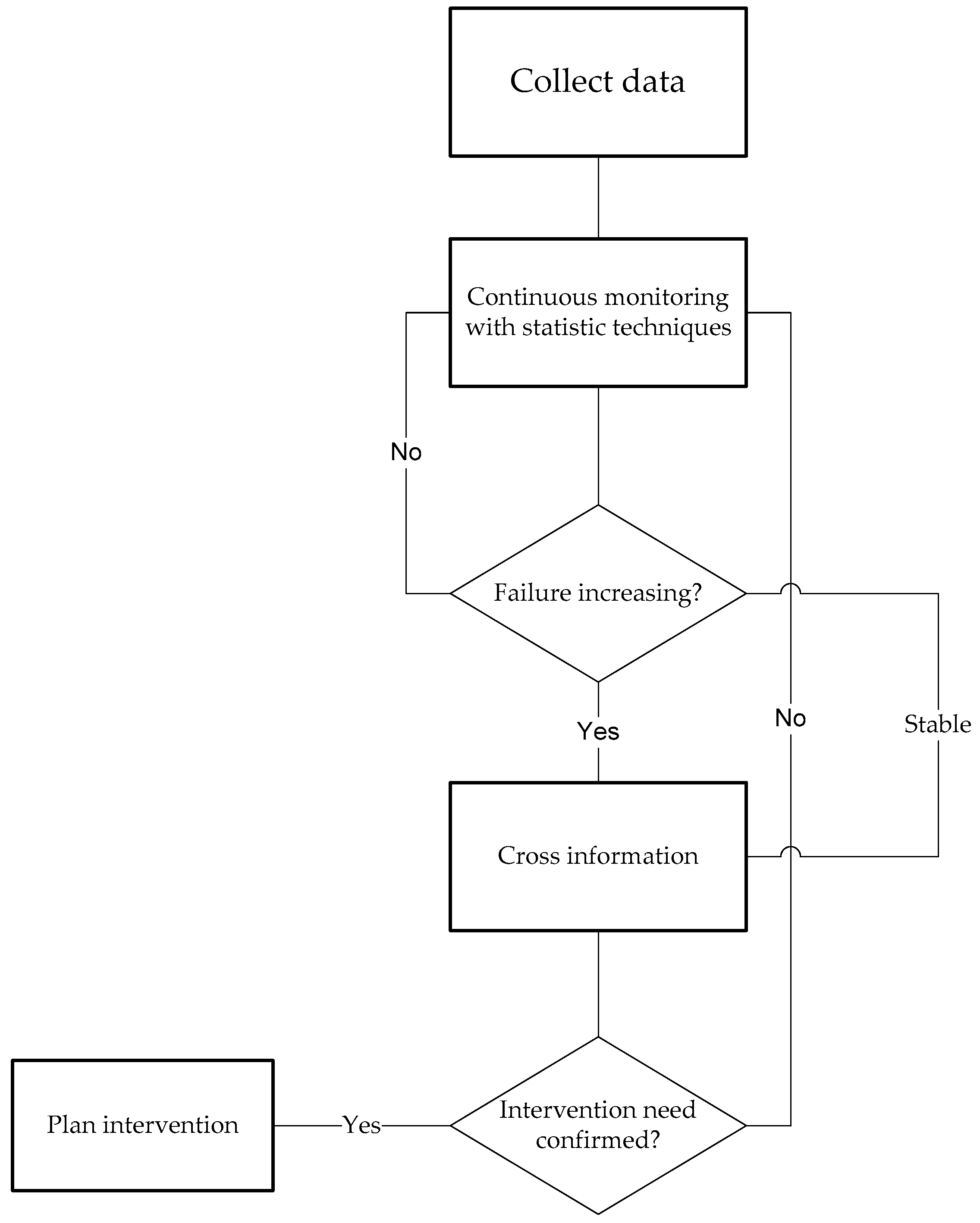
Therefore, the methodology we proposed next is as follows,
Figure 1:
Proceed to online condition monitoring by continuous collection of the data;
Collect data from vibration and temperature sensors;
Collected registered failures of gas turbine;
Analyze the distribution of vibration and temperature in time.
Apply Pareto analysis;
Calculate the reliability of the gas turbine;
Apply the Laplace Test;
Calculate the MTBF;
Calculate the Availability;
Evaluate the results:
If the failure rate is increasing: evaluate with the sensors’ parameters to decide the intervention or substitution;
If the failure rate is decreasing: maintain the observation;
If the rate failure is stable: check if the obtained parameters are admissible, if not, decide when the intervention or substitution takes place.
4. Results
The gas turbine LM2500 under study is a maritime aero derivate gas turbine installed in a ship, and has the characteristics in
Table 1:
The considered sensors for this study are list in
Table 2:
This LM2500 gas turbine usually uses marine gasoil for its functioning, and for initiate running, it uses high-pressure compressed air.
To understand the Gas Turbine Vibrations results we must mention that this turbine is divided into two parts, the Gas Generator and the Power Turbine. The Gas Generator is divided into three parts: Compressor, Combustion Chamber and the High Pressure Turbine. The connection from the Gas Generator to the Power Turbine are thermodynamics. So, the Gas Generator has one shaft and the Power Turbine another, and there is no physical connection to transmit the motion between both, only the temperature and gas mixture expansion from the combustion are transmitted to the Power Turbine allowing it to rotate. However, the connections of the gas generator to the power turbine are made by the cover and accessories, which allows the turbine to be a whole.
The failures in gas turbine can occur in various components, but the hot parts are especially sensitive, because many gas turbine failures are in the section with hot components (e.g., blades, combustion chamber) [
22].
The time event registering is crucial for gas turbine condition monitoring [
23].
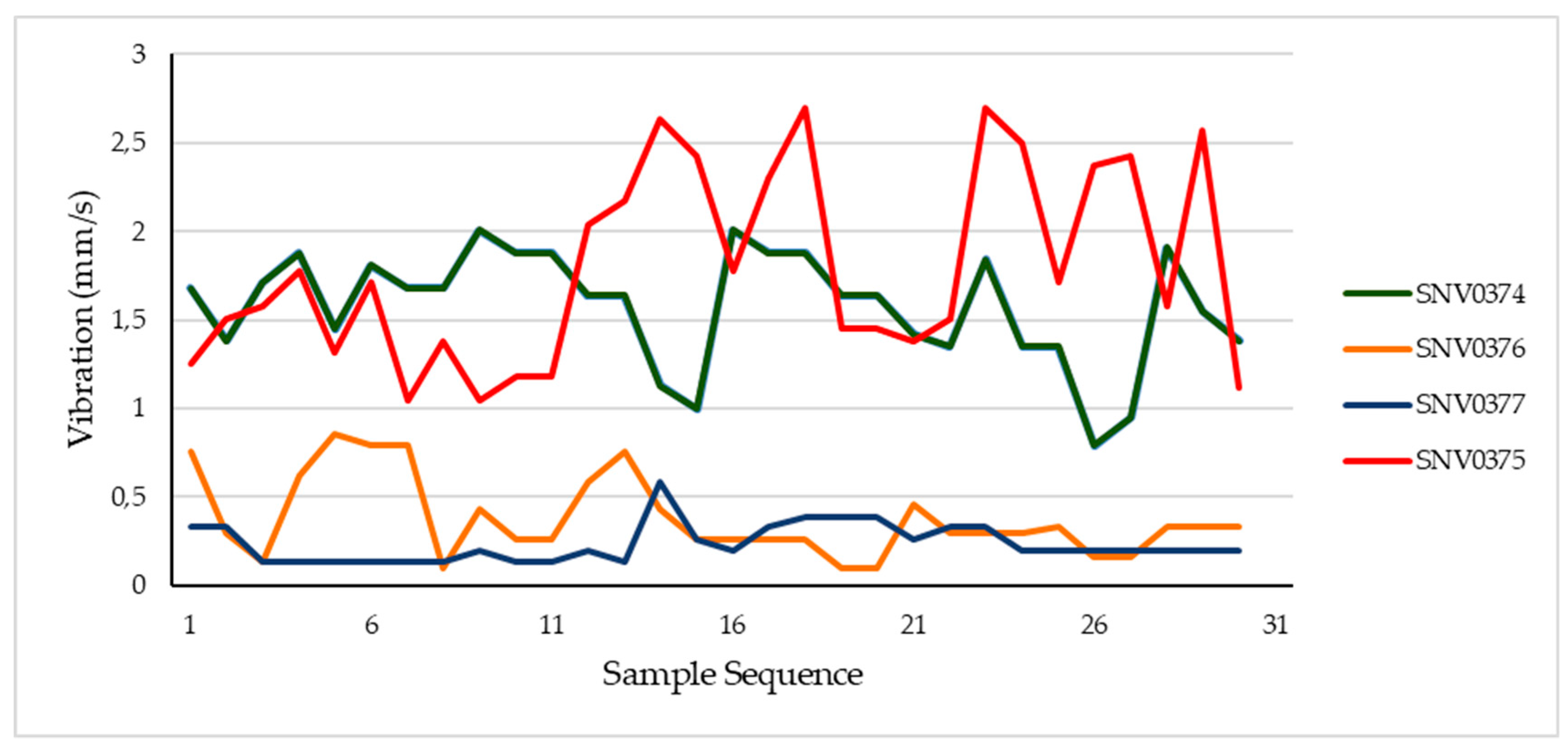
The collected vibration and oil temperatures were collected at the same conditions, considering the gas generator rotating at 7450 rpm and the power turbine at 1590 rpm. The data were collected considering the ship navigating, and collected with a 30 min of interval. The results of gas turbine data vibration sensors (accelerometers) collection are in
Figure 2 and scavenges temperatures in Figure 4. Since the installed accelerometers only measure in one direction, which is not specified in the user manual, to complement the vibration behaviour usually vibrations are measured in the three axis (Vertical, horizontal and axial) [
24]. The vibration values are in millimeters per second (mm/s) and are Root Mean Square Values. The gas generators’ self-vibrations are the vibrations from the gas generator, and the induced vibrations are the vibrations of the power turbine induced in the gas generator. The power turbine self-vibrations are the vibrations with origin in the power turbine, and the induced are the vibrations of the gas generator induced on the power turbine.
The SNV sensors represent vibrations and the SOT represent scavenge temperatures.
We can see that for the same moment the vibration on SNV0374 and SNV0375 that represents the self and induced vibration on the compressor are higher than for the turbine. The SNV0376 and SNV0377 have lower values relative to compressor sensors.
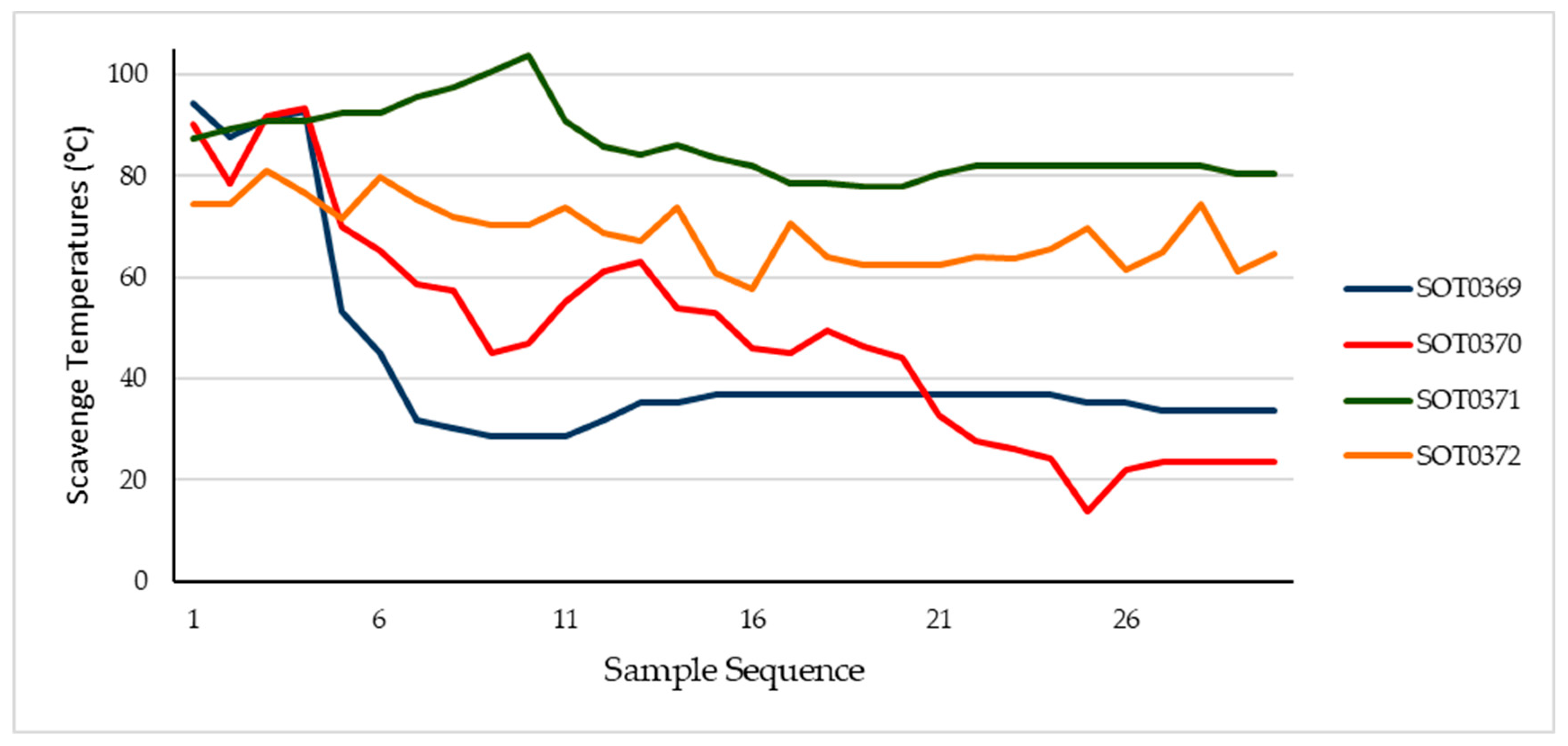
In
Figure 3 we can see the temperature descending along the observations, probably the engine decreases its velocity, so the temperature decreases, but the operators did not register the change in power. This can be one of the problems in data accuracy analysis: analyzing values which do not correspond to the power levels registered.
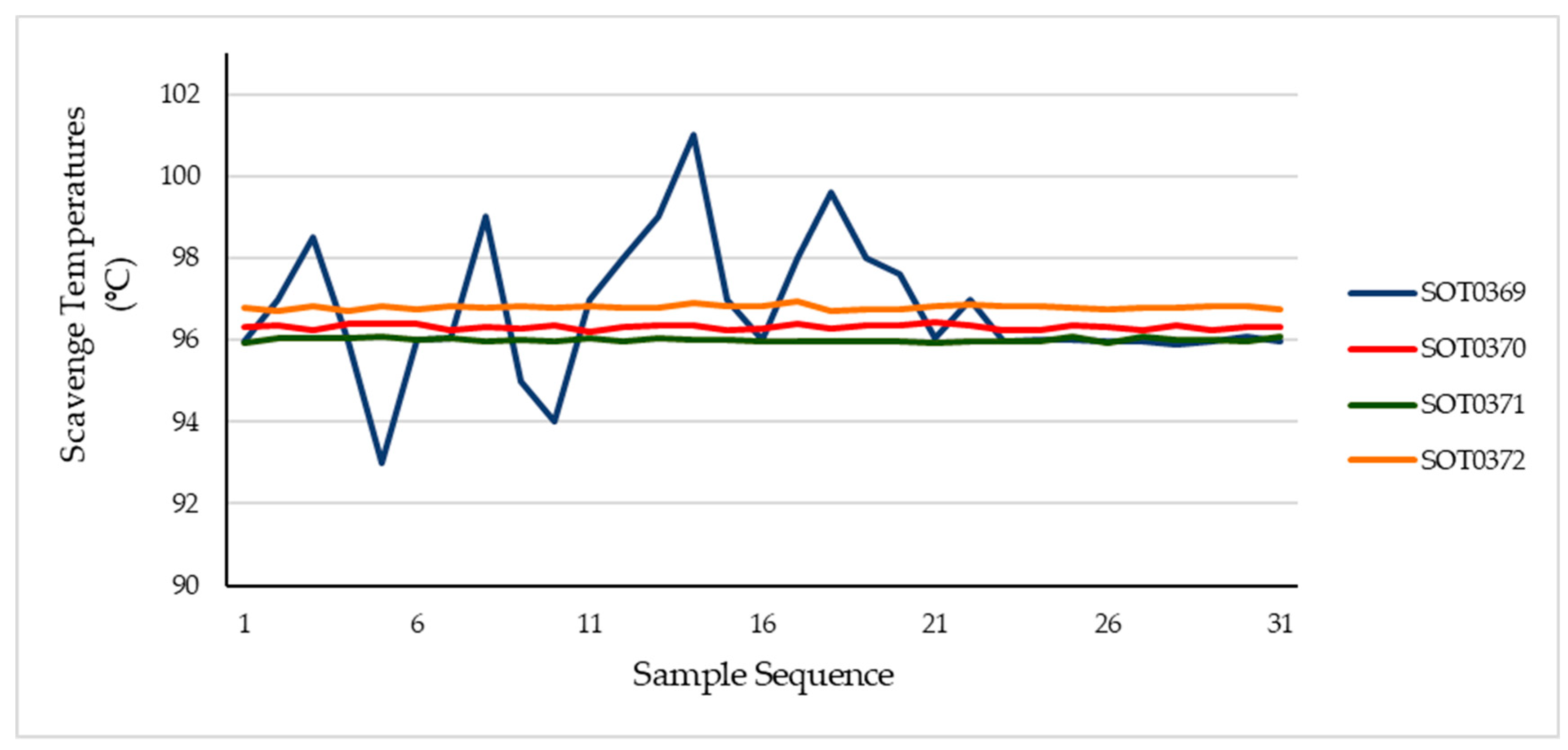
Then, if we considered the environment temperature increasing, we may have all the temperatures higher, so we simulate a 16 °C increase in the temperature inlet on the gas turbine compressor, which we obtained in
Figure 4.
Apparently, the scavenge temperatures had stabilized at higher temperatures, the result for the sensor SOT0369 is to demonstrate the result of sensor malfunction, the procedure is to substitute the anomalous sensor and the results stabilize, in this case since observation [
22].
For the environment high temperature levels there is no evidence or alarm, in short time, of vibration increasing, so the vibration graphical data for higher seawater temperature is not present in this article. A common reason for this lack of evidence is when the gas turbine power is reduced because of the high exhaust gas temperature, consequently no other parameter gets higher or close to the limit. However, there is a certainty by other literature that the gas turbine performance decreases when the temperature environment increases to high levels like 50° [
1,
25].
The results show that the conjugation of various variables with statistical treatment can be more accurate to define a maintenance plan for the gas turbine.
The degradation of the gas turbine depends on the environment conditions and in which “power plant” or system it is applied.
This turbine shows high vibration on the compressor. It is known that it was not close to the limit because the gas turbine power was limited. This revealed the need for balance on this system (rotor). This was a real situation, and the Gas Turbine had an intervention maintenance, a mechanical balance on the compressor rotor blades conducted by a specialist of this gas turbine.
4.1. Pareto Analysis
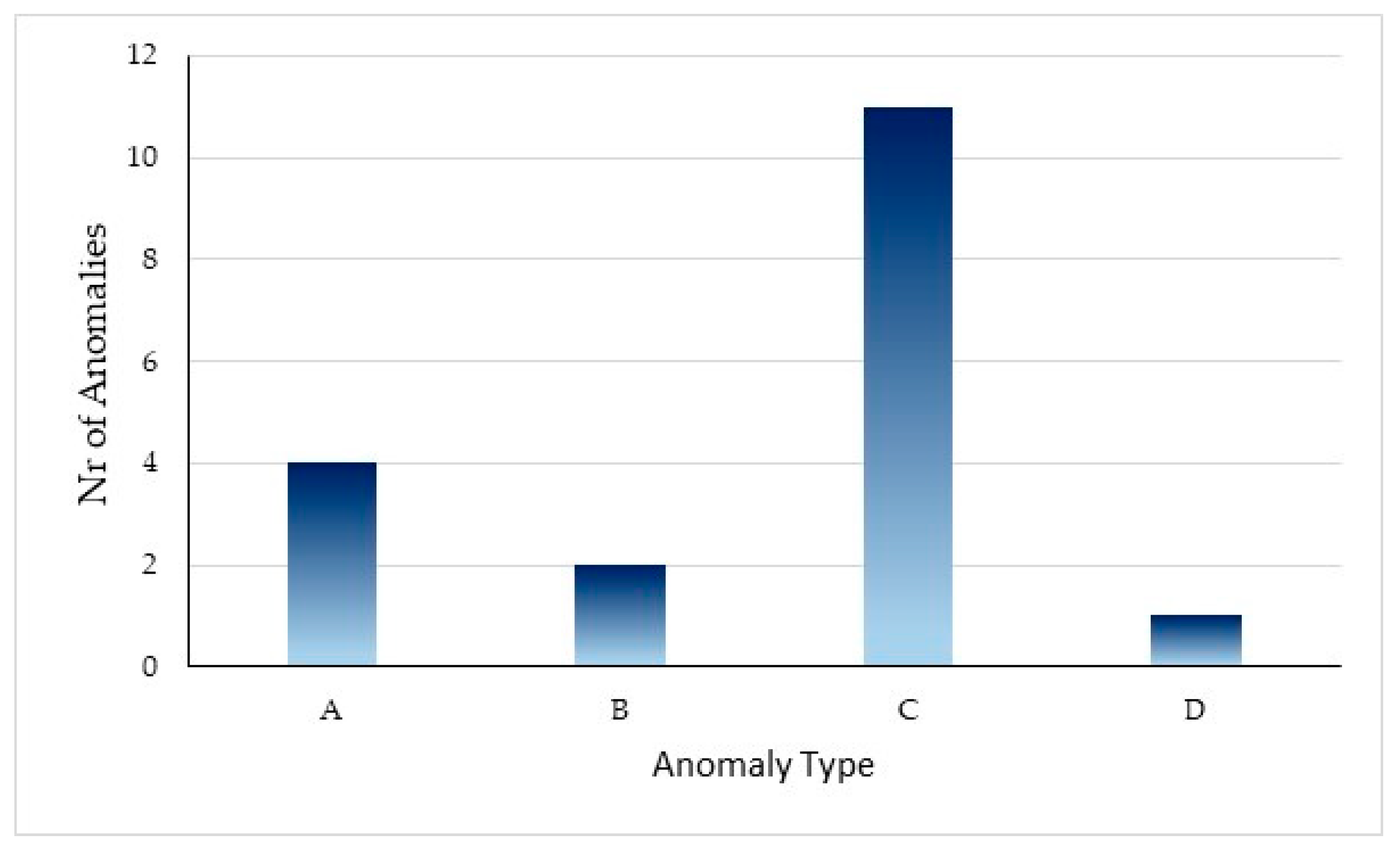
For the actual study, we group four types of gas turbine failures.
In the evaluation of the system, 18 failures occurred. The failure registration contemplated a 365 day period; we subdivided the failures into four types: compressed air system (A), fuel system (B), vibrations (C), and various components failures (D),
Figure 5.
The compressed air system had four failures, the fuel system two failures; 11 vibrations alarms were registered and one registered failure of other components. The vibration alarms were the highest type of occurrences,
Figure 5. It should be noted that some of the vibration alarms registration can be sensor malfunctions, or some specific and punctual registration related with the platform and environment conditions.
4.2. Gas Turbine Reliability―Laplace Test and MTBF
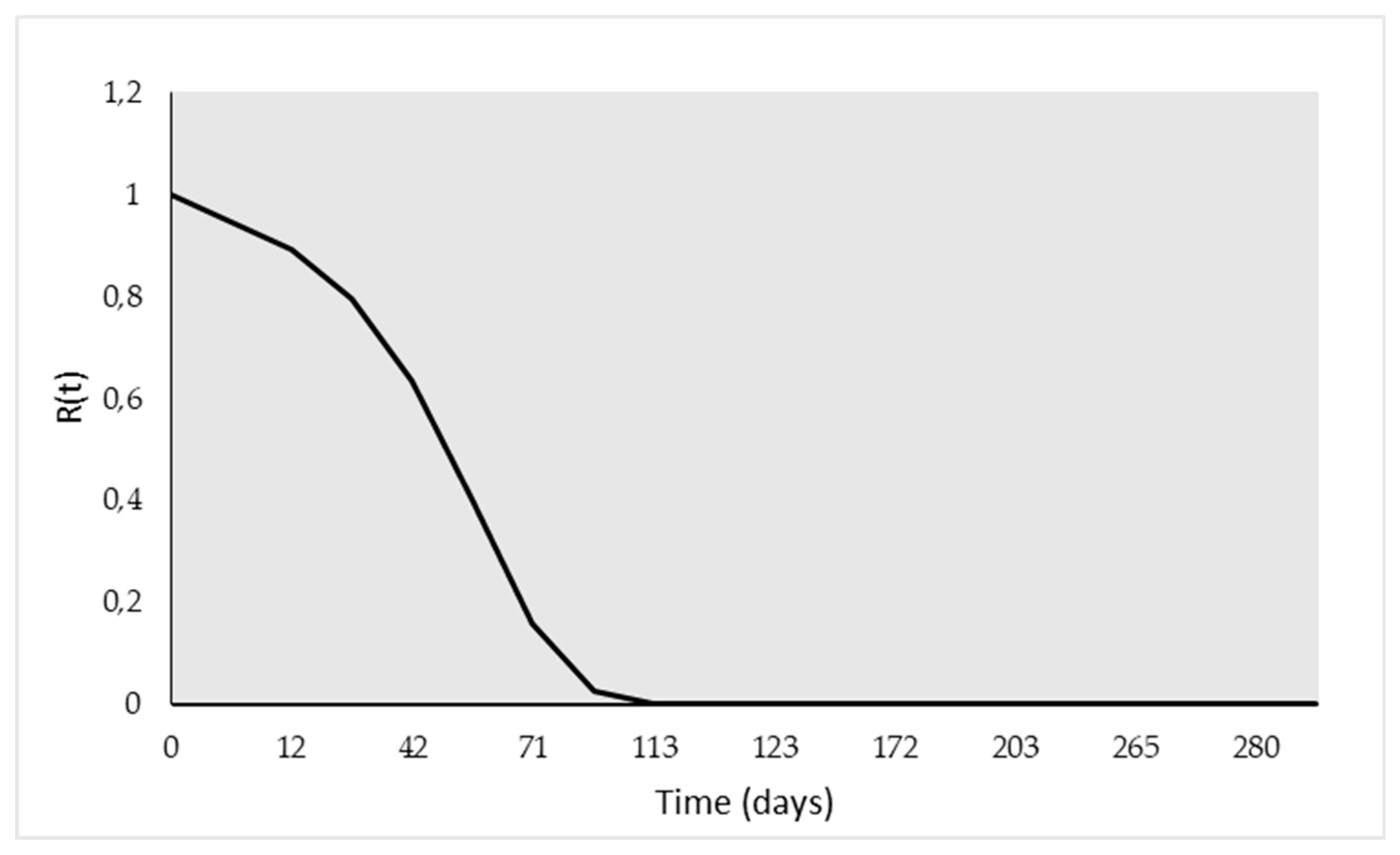
The reliability function of the gas turbine not considering the repairs between failures and considering a study of 365 days is represented by
Figure 6. The study begins in day zero, not mathematical considering what happened before. The Weibull distribution is a reasonable fit for the equipment under study.
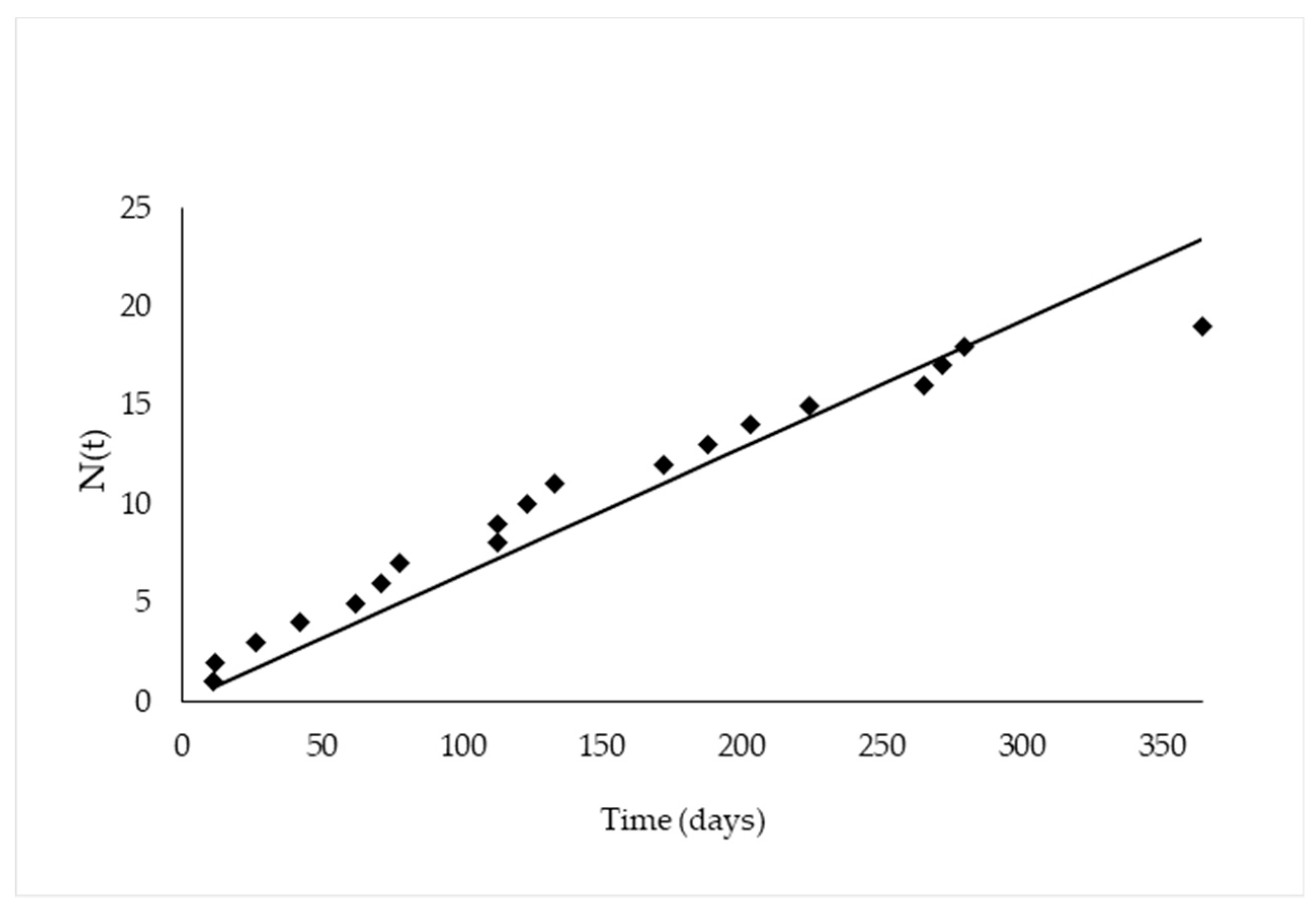
The time failure distribution is accordingly
Figure 7, where
N(
t) is the total number of failures from the 0 to 365 day).
Along one year, the gas turbine registered 18 anomalies. We applied the Laplace Test to define the gas turbine reliability, and calculate the MTBR.
For the Laplace test we use nf = 18, for a 365 days of data collection, a ∑τi = 2753, and a Z0 = −1.1900717 so the failure rate is constant for a confidence interval with α = 5%, .
With the Z0 result, the H0 is not rejected for a 5% significance level, and so, because the system has a constant failure rate, it is a Poisson Homogenous Process.
Studying the failures distribution, we obtain an MTBR of 20.28. In all the registered failures, none were catastrophic. We also calculate the availability A (Equation (2)), considering a year of study and a down time of 24 days, and we obtained a 93%, which is a high and acceptable value.
Currently in the organization, the proposed methodology is not applied, but it is believed that with limited financial resources it will be possible to implement it.
5. Discussion
Integrating the statistical analysis, the Laplace test showed a constant failure rate, comparing with the obtained parameters data, vibration and scavenge temperatures, it was not possible to define a direct relation between them. Although the known anomaly on the compressor registered by the vibrations, its values are not increasing, they are steady. The values oscillation on a certain interval at the constant power input can perhaps be explained by the influence of other equipment’s, platform where it is installed and the variation of the environment (considering sea and wind state). We must understand that this is an aero-derivate gas turbine which is installed in a ship with others propulsion systems and equipment to sustain a ship operation on sea for several days. The sea has great influence on the equipment functioning; sometimes, the propellers come to the surface because of the waves, and this fact changes shortly the propulsion systems parameters, including power.
The MTBF results are reasonable considering that none catastrophic anomaly occurred.
The Pareto Analysis showed us which systems or components of the gas turbine more frequently fail, so this one should be monitored more often.
The availability allowed us to know the percentage of time in which the gas turbine was functioning.
In future work the temperature in the power turbine of the gas turbine system should be analyzed together with the scavenge temperature. For this study we could not connect the gas turbine state with the temperature results.
Given the collected and simulated data it was possible, in scavenge temperature sensor, to connect the environment temperature with the results. Higher temperatures of environment lead to higher temperature in gas turbine parameters. The comparison between the specifications of the used marine gasoil and other combustibles on the gas turbine performance was not considered.
For the obtained results, and because recording data is not defined in the actual maintenance system, we propose to:
Daily collect and register data for the various power levels registered on the gas turbine, considering compressor and turbine vibration signature and temperature of the scavenge and temperature from the existing temperature sensors of the gas turbine;
Implement a statistical software system associated with others in order to treat the collected data (considering Pareto Analysis, Laplace test, reliability function, availability calculus and MTBR);
Study and monitor online similar gas turbines from other ships with the same methods.
6. Conclusions
The Pareto analysis is important to initiate the reliability study, allowing to group the anomalies, highlighting the incidence on subsystems. With this technique, we can decide which gas turbine systems or components should be more frequently monitored.
We can calculate the gas turbine reliability with a continuous monitoring and anomalies historic registry and by applying the Laplace Test. The Laplace Test allowed us to determine that the gas turbine has a steady rate failure.
The calculation of the MTBF shows on which time interval the failures occurs, and allied to Laplace Test supported us in predicting when a failure happens, but we still not know the availability. So, the availability was calculated and showed a high percentage which contributes to a high availability of the ship where the gas turbine is installed. The time failure distribution shows that the failures mostly occurred near the normal.
Various statistical techniques may be applied simultaneously to allow a mechanical system monitoring with more information certainty.
Statistical control may be essential for equipment performance monitoring and condition maintenance, mostly when ships operate in areas where adverse environment conditions exist and the equipment performance decreases.