Piezoelectric Energy Harvesting with an Ultrasonic Vibration Source
Abstract
:1. Introduction
2. Structure of the Energy Harvester
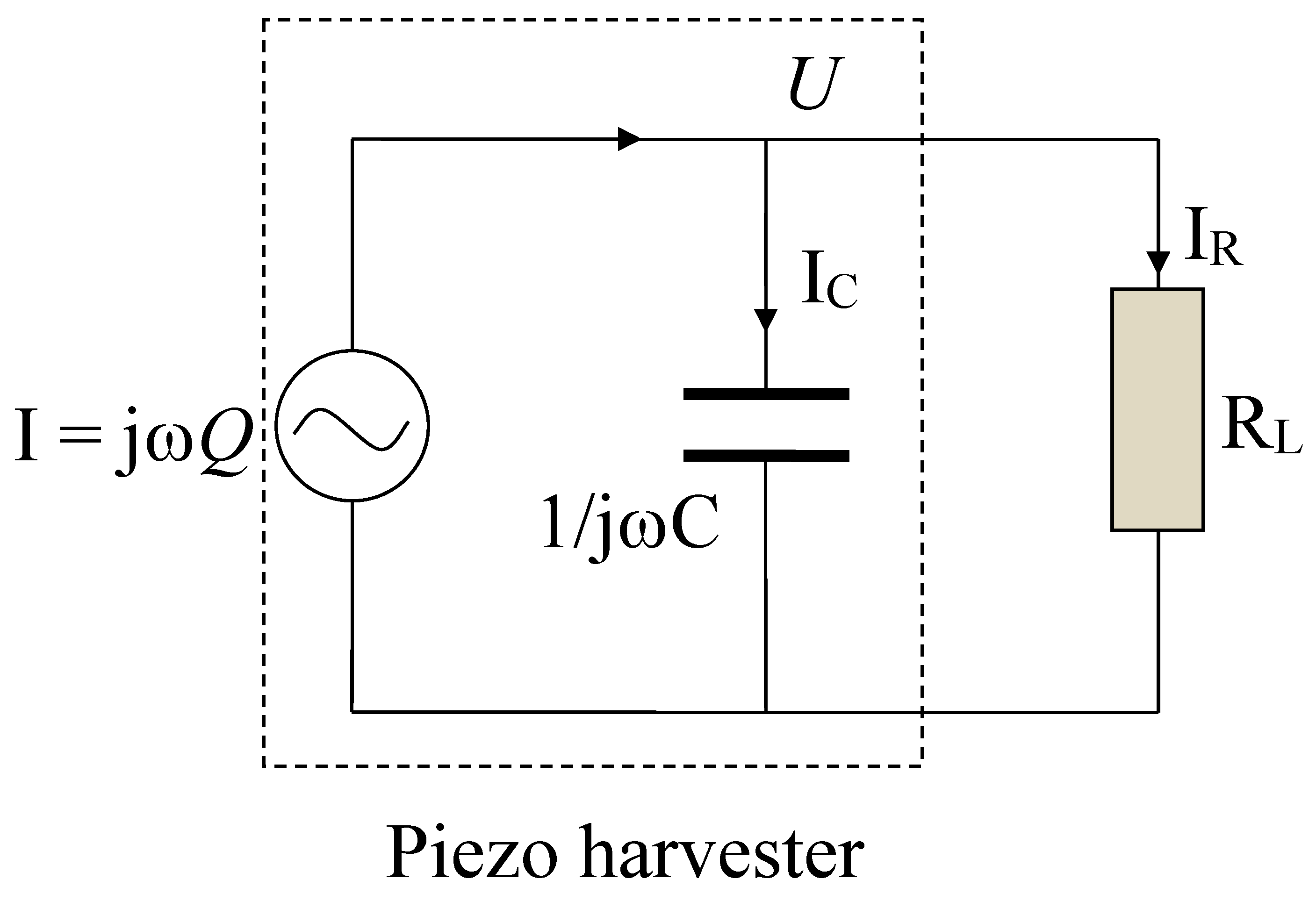
3. Theory
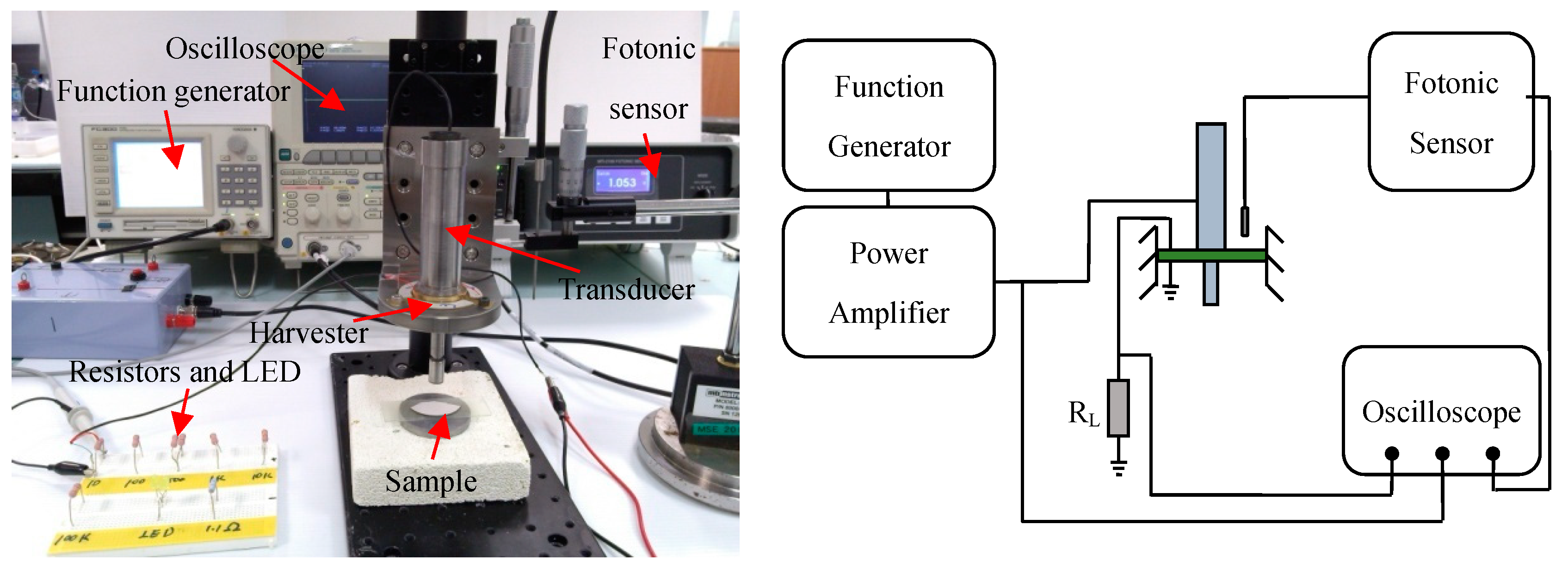
4. Experimental Section
5. Results and Discussion
5.1. Displacement and Open Circuit Voltage
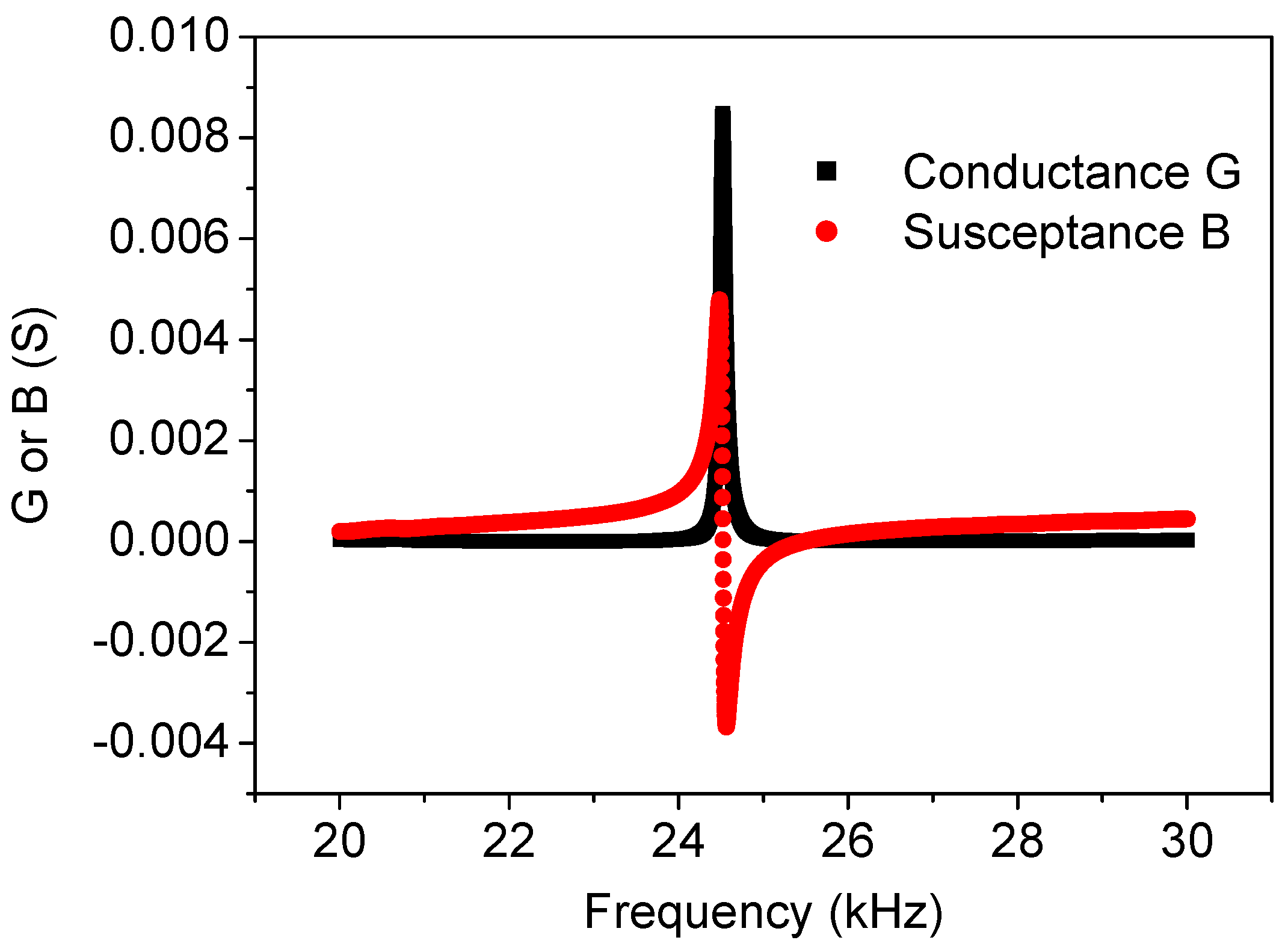
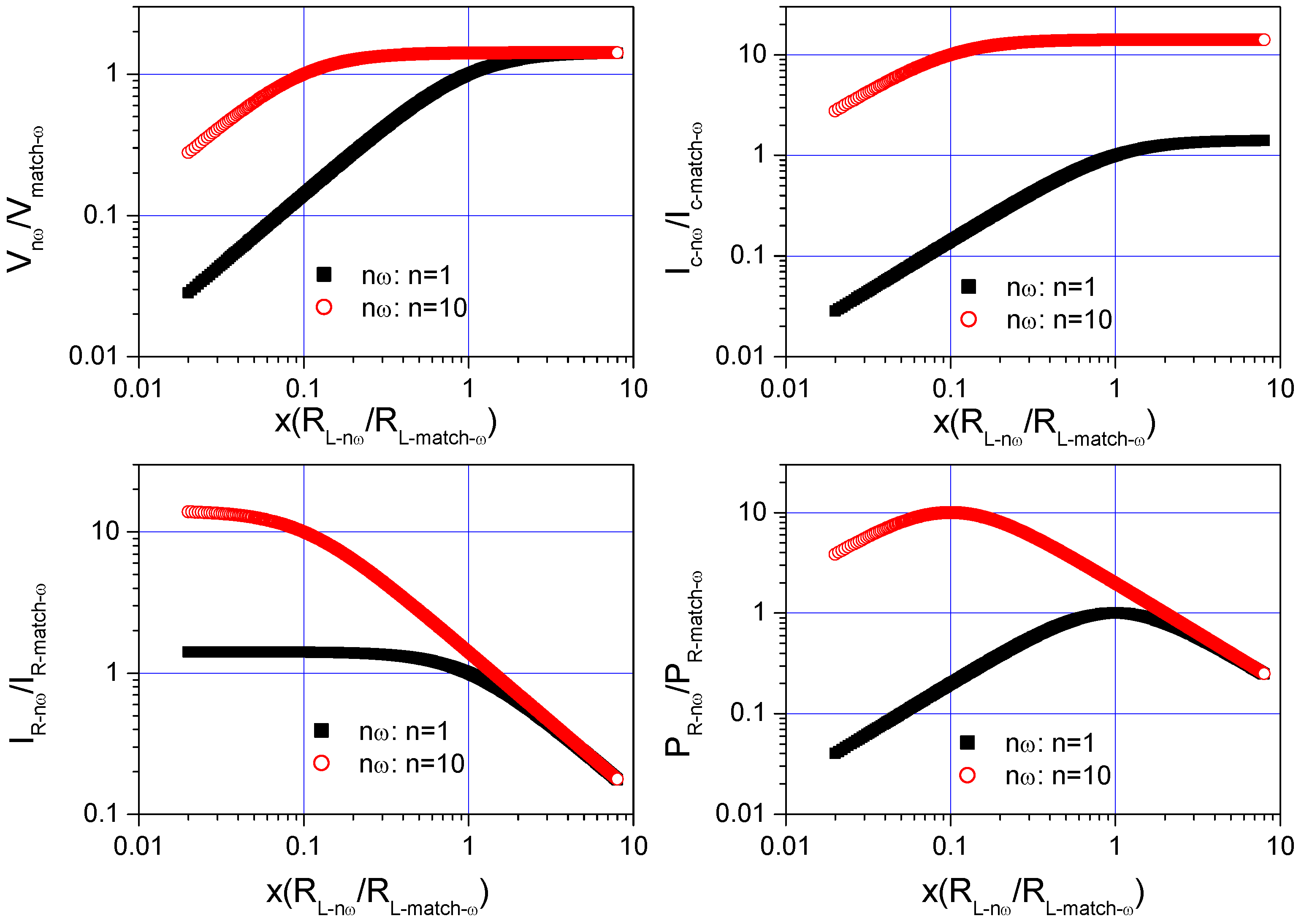
5.2. Current, Power, and Impedance Matching
5.3. Testing under Cutting Conditions
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Bogue, R. Energy harvesting and wireless sensors: A review of recent developments. Sens. Rev. 2009, 29, 194–199. [Google Scholar] [CrossRef]
- Khaligh, A.; Zeng, P.; Zheng, C. Kinetic energy harvesting using piezoelectric and electromagnetic technologies—State of the art. IEEE Trans. Ind. Electron. 2010, 57, 850–860. [Google Scholar] [CrossRef]
- Chalasani, S.; Conrad, J.M. A survey of energy harvesting sources for embedded systems. In Proceedings of the SoutheastCon, Huntsville, AL, USA, 3–6 April 2008. [Google Scholar]
- Saadon, S.; Sidek, O. A review of vibration-based MEMS piezoelectric energy harvesters. Energy Convers. Manag. 2011, 52, 500–504. [Google Scholar] [CrossRef]
- Harb, A. Energy harvesting: State-of-the-art. Renew. Energy 2011, 36, 2641–2654. [Google Scholar] [CrossRef]
- Ibrahim, S.W.; Ali, W.G. Power enhancement for piezoelectric energy harvester. In Proceedings of the World Congress on Engineering, London, UK, 4–6 July 2012. [Google Scholar]
- Priya, S. Modeling of electric energy harvesting using piezoelectric windmill. Appl. Phys. Lett. 2005, 87, 184101. [Google Scholar] [CrossRef]
- Sodano, H.A.; Park, G.; Inman, D.J. Estimation of electric charge output for piezoelectric energy harvesting. Strain 2004, 40, 49–58. [Google Scholar] [CrossRef]
- Rocha, J.G.; Goncalves, L.M.; Rocha, P.F.; Silva, M.P.; Lanceros-Mendez, S. Energy Harvesting from Piezoelectric Materials Fully Integrated in Footwear. IEEE Trans. Ind. Electron. 2010, 57, 813–819. [Google Scholar] [CrossRef]
- Kim, H.W.; Priya, S.; Uchino, K.; Newnham, R.E. Piezoelectric energy harvesting under high pre-stressed cyclic vibrations. J. Electroceram. 2005, 15, 27–34. [Google Scholar] [CrossRef]
- Donohoe, M.; Jornet, J.M.; Balasubramaniam, S. Nanodeive arrays for peripheral nerve fascicle activation using ultrasound energy-harvesting. IEEE Trans. Nanotechnol. 2017, 16, 919–930. [Google Scholar] [CrossRef]
- Mazzilli, F.; Thoppay, P.E.; Praplan, V.; Dehollain, C. Ultrasound energy harvesting system for deep implanted-mideical-devices (IMDs). In Proceedings of the IEEE International Symposium on Circuits and Systems, Seoul, Korea, 20–23 May 2012. [Google Scholar]
- Kim, H.W.; Batra, A.; Priya, S.; Uchino, K.; Markley, D.; Hofmann, R.E. Energy harvesting using a piezoelectric ‘Cymbal’ transducer in dynamic environment. Jpn. J. Appl. Phys. 2004, 43, 6178–6183. [Google Scholar] [CrossRef]
- Zhu, D.B.; Beeby, S.; Tudor, J.; White, N.; Harris, N. Improving output power of piezoelectric energy harvesters using multilayer structures. Procedia Eng. 2011, 25, 199–202. [Google Scholar] [CrossRef]
- Kamel, T.M.; Elfrink, R.; Renaud, M.; Hohlfeld, D.; Goedbloed, M.; de Nooijer, C.; Jambunathan, M.; van Schaijk, R. Modeling and characterization of MEMS-based piezoelectric harvesting devices. J. Micromech. Microeng. 2010, 20, 105023. [Google Scholar] [CrossRef]
- Guan, M.J.; Liao, W.H. On the efficiencies of piezoelectric energy harvesting circuits towards storage device voltages. Smart Mater. Struct. 2007, 16, 498–505. [Google Scholar] [CrossRef]
- Ottman, G.K.; Hofmann, H.F.; Bhatt, A.C.; Lesieutre, G.A. Adaptive piezoelectric energy harvesting circuit for wireless remote power supply. IEEE Trans. Power Electron. 2002, 17, 669–676. [Google Scholar] [CrossRef]
- Umeda, M.; Nakamura, K.; Ueha, S. Analysis of the transformation of mechanical impact energy to electric energy using piezoelectric vibrator. Jpn. J. Appl. Phys. 1996, 35, 3267–3273. [Google Scholar] [CrossRef]
- Abramovich, H.; Harash, E.; Milgrom, C.; Amit, U. Power Harvesting from Apparatus, System and Method. U.S. Patent US20090195226A1, 6 August 2009. [Google Scholar]
- Li, T.; Chen, Y.H.; Ma, J. Frequency dependence of piezoelectric vibration velocity. Sens. Actuators 2007, 138, 404–410. [Google Scholar] [CrossRef]
- Li, T.; Ma, J.; Low, A.F. Horn-type piezoelectric ultrasonic transducer: Modelling and applications. In Advances in Piezoelectric Transducers; Ebrahimi, F., Ed.; InTech: Rijeka, Croatia, 2011; ISBN 978-953-307-931-8. [Google Scholar]
- Law, H.H.; Rossiter, P.L.; Simon, G.P.; Koss, L.L. Characterization of mechanical vibration damping by piezoelectric materials. J. Sound Vib. 1996, 197, 489–513. [Google Scholar] [CrossRef]
- Sodano, H.A.; Inman, D.J. Comparison of piezoelectric energy harvesting devices for researching batteries. J. Intell. Mater. Syst. Struct. 2005, 16, 799–807. [Google Scholar] [CrossRef]
- Li, T.; Wang, Y.; Lee, P.S. Power Transducer and Piezoelectric Pump; Lambert Academic Publishing: Saarbrücken, Germany, 2012. [Google Scholar]

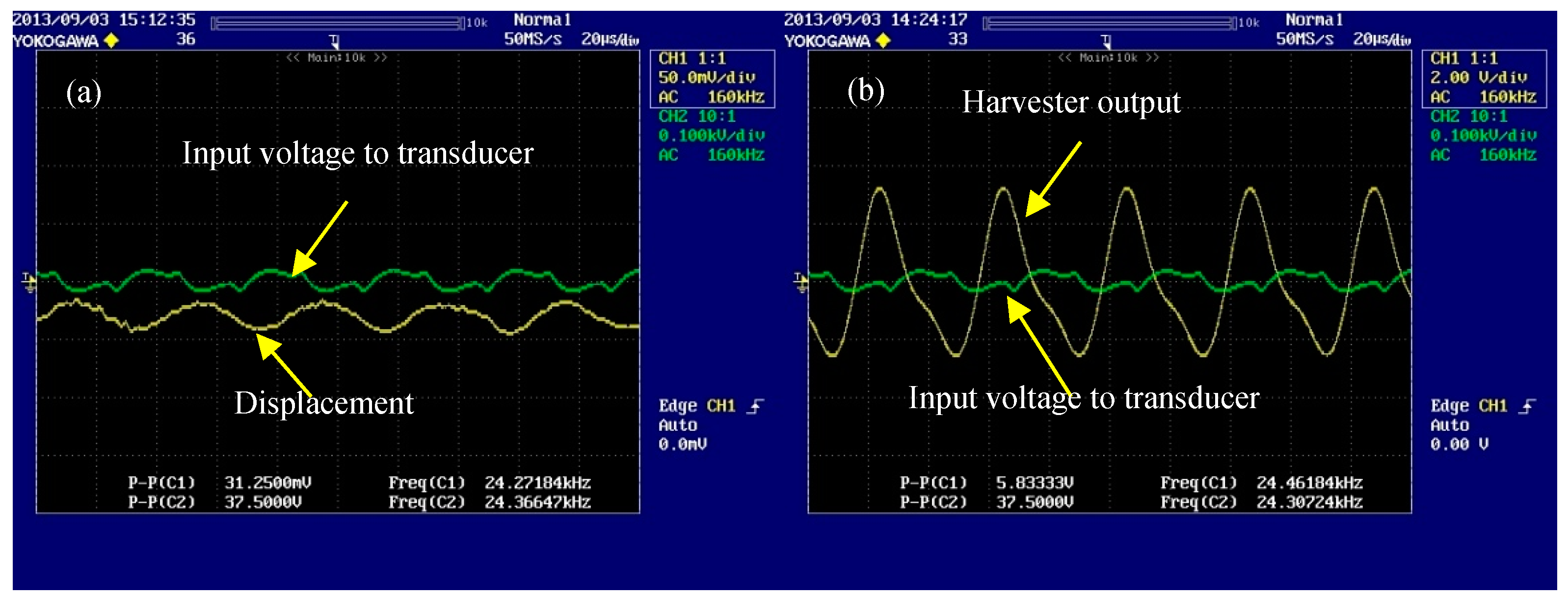
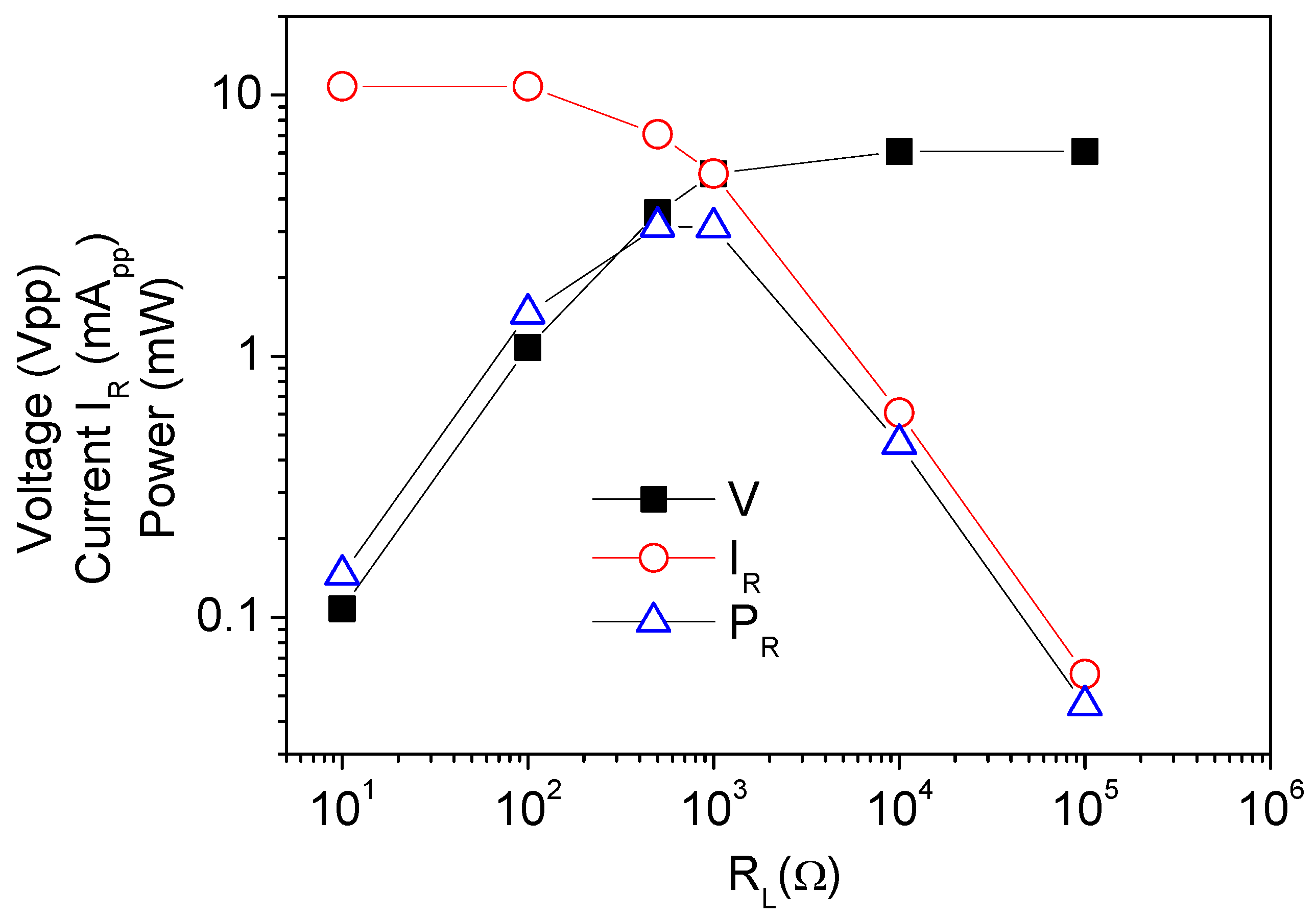
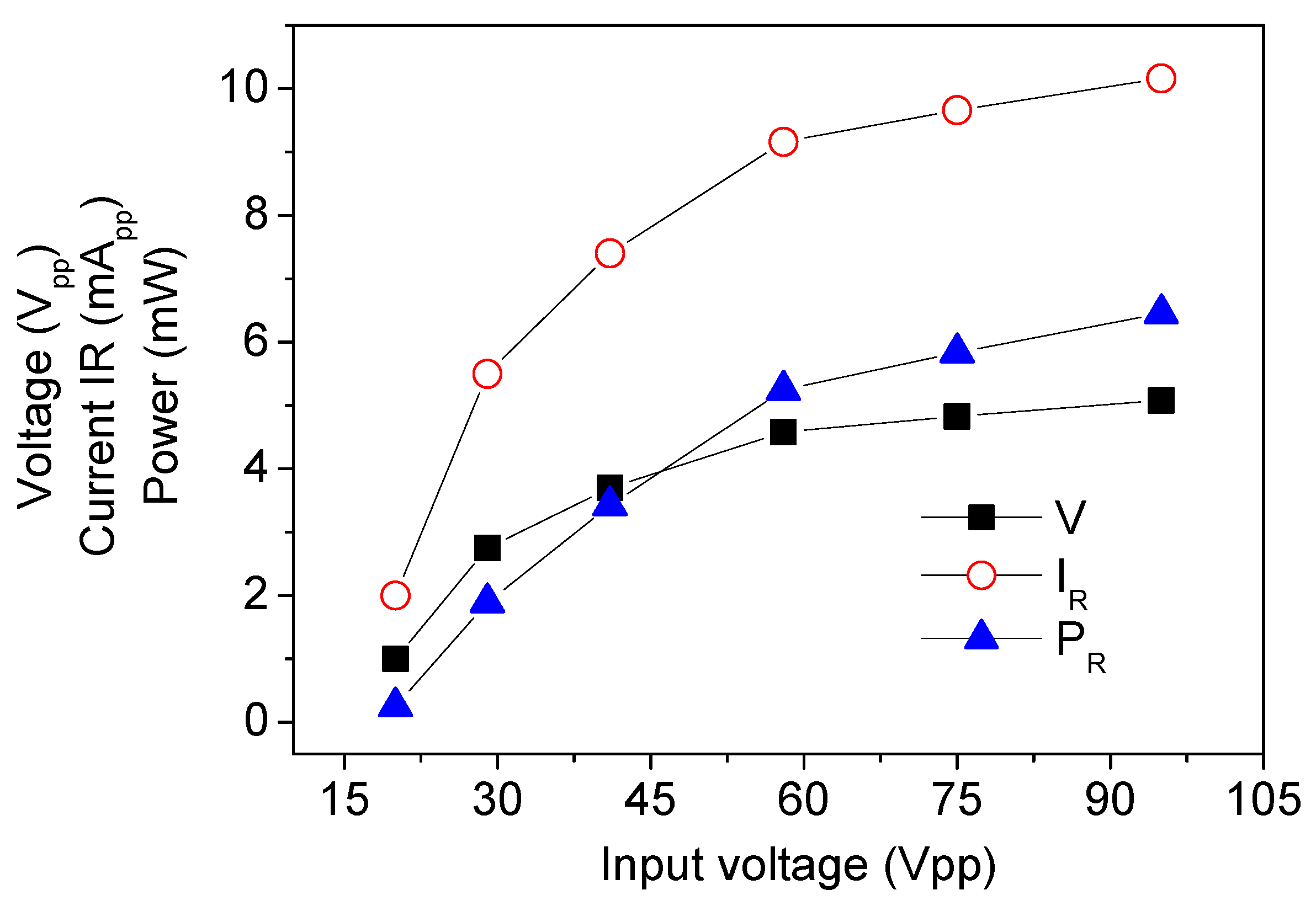
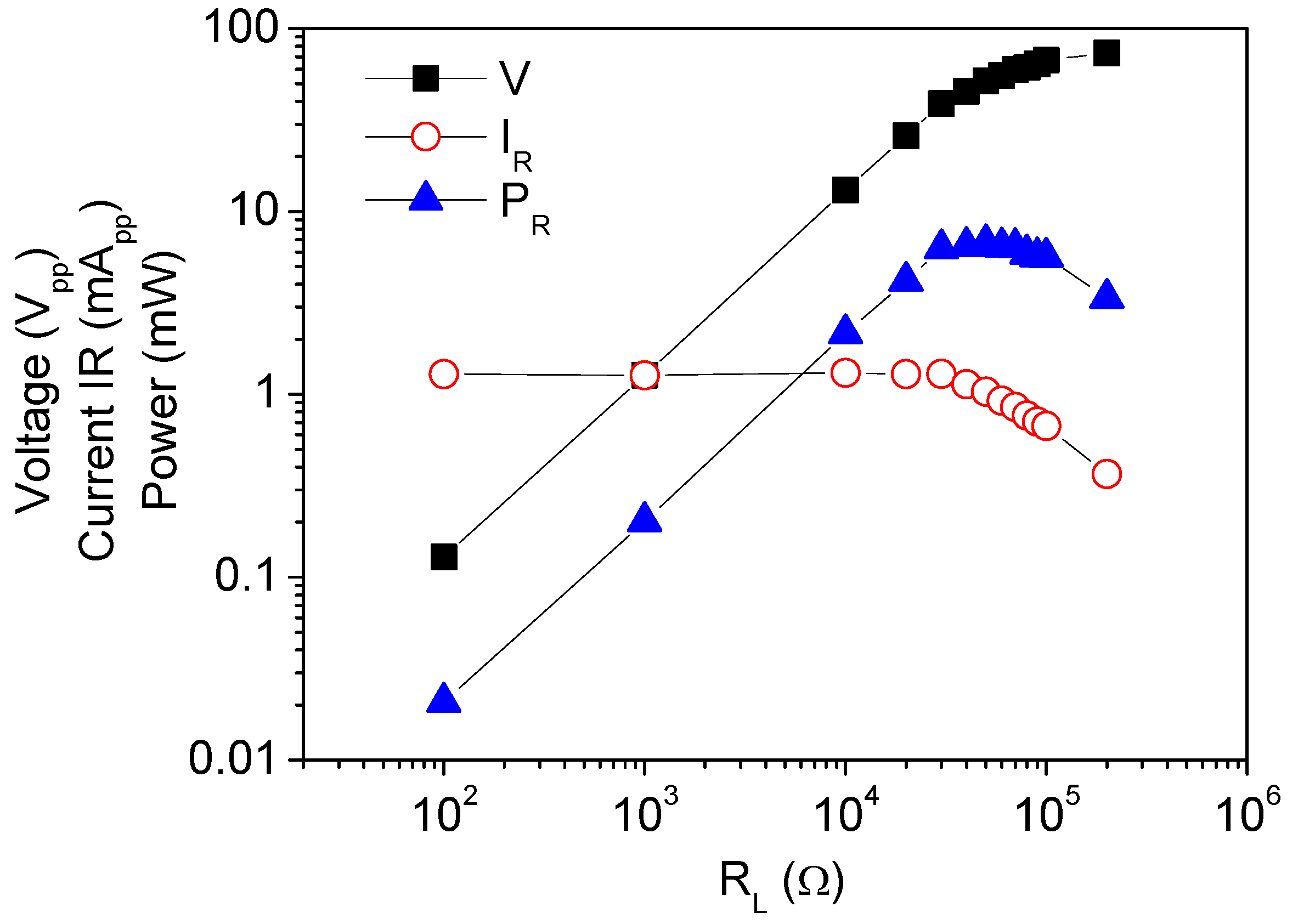
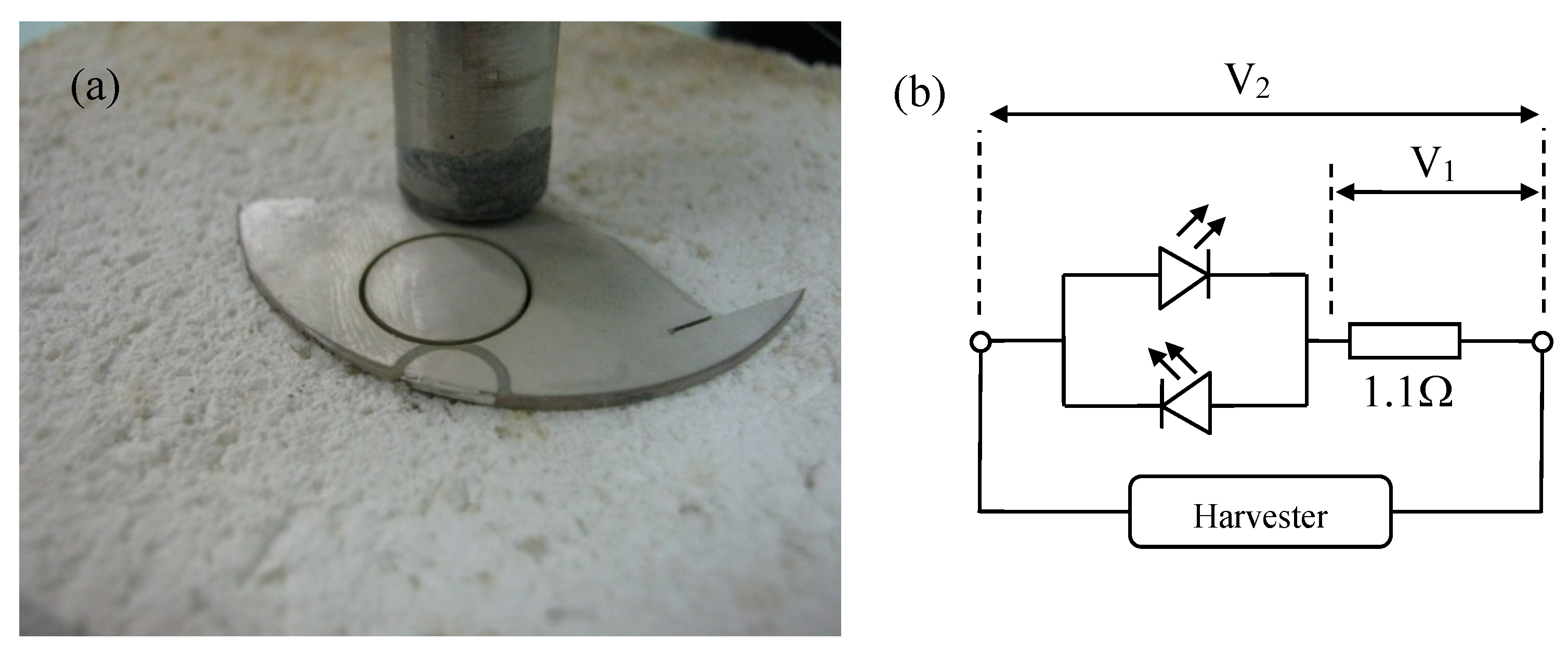
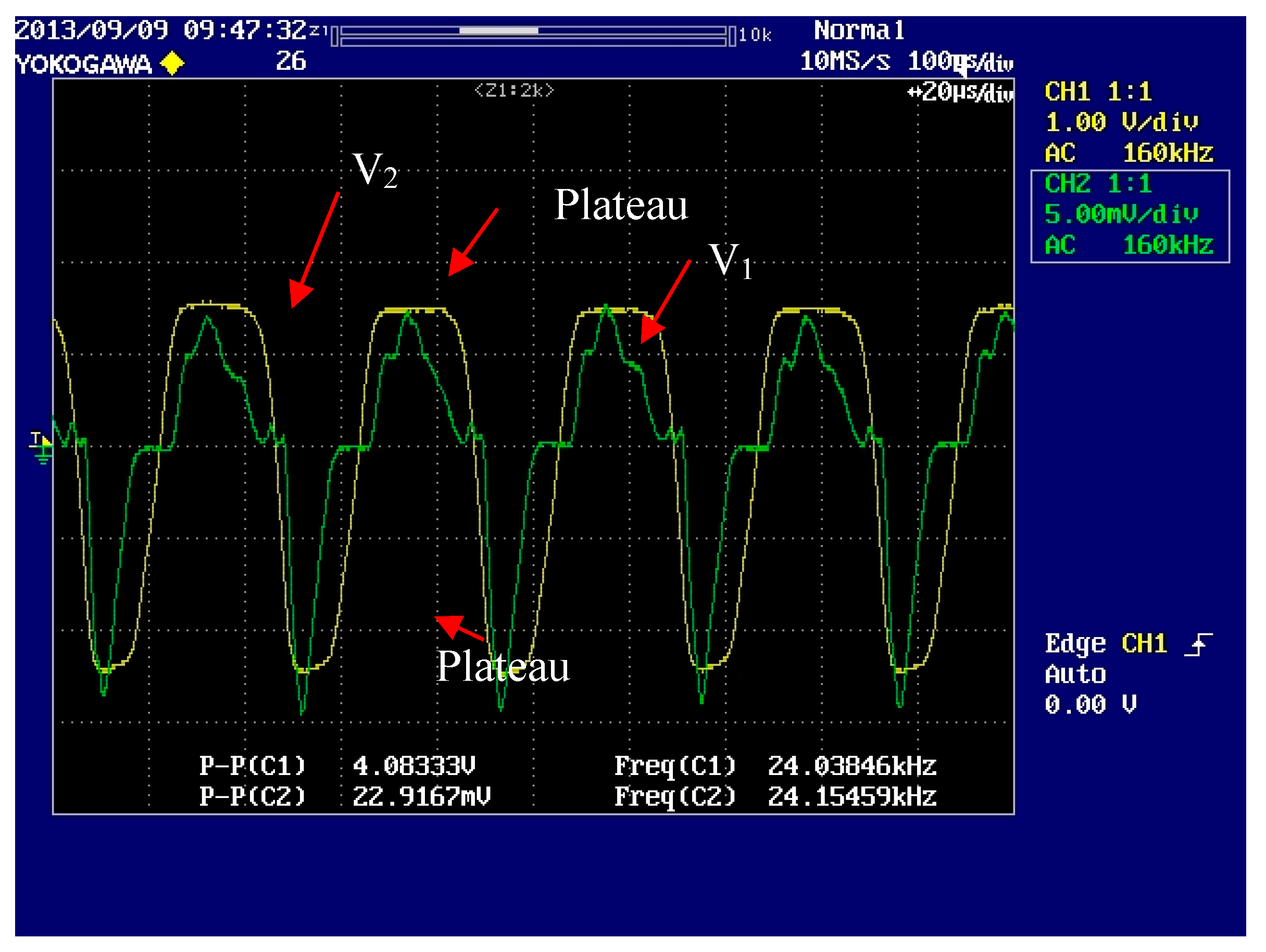
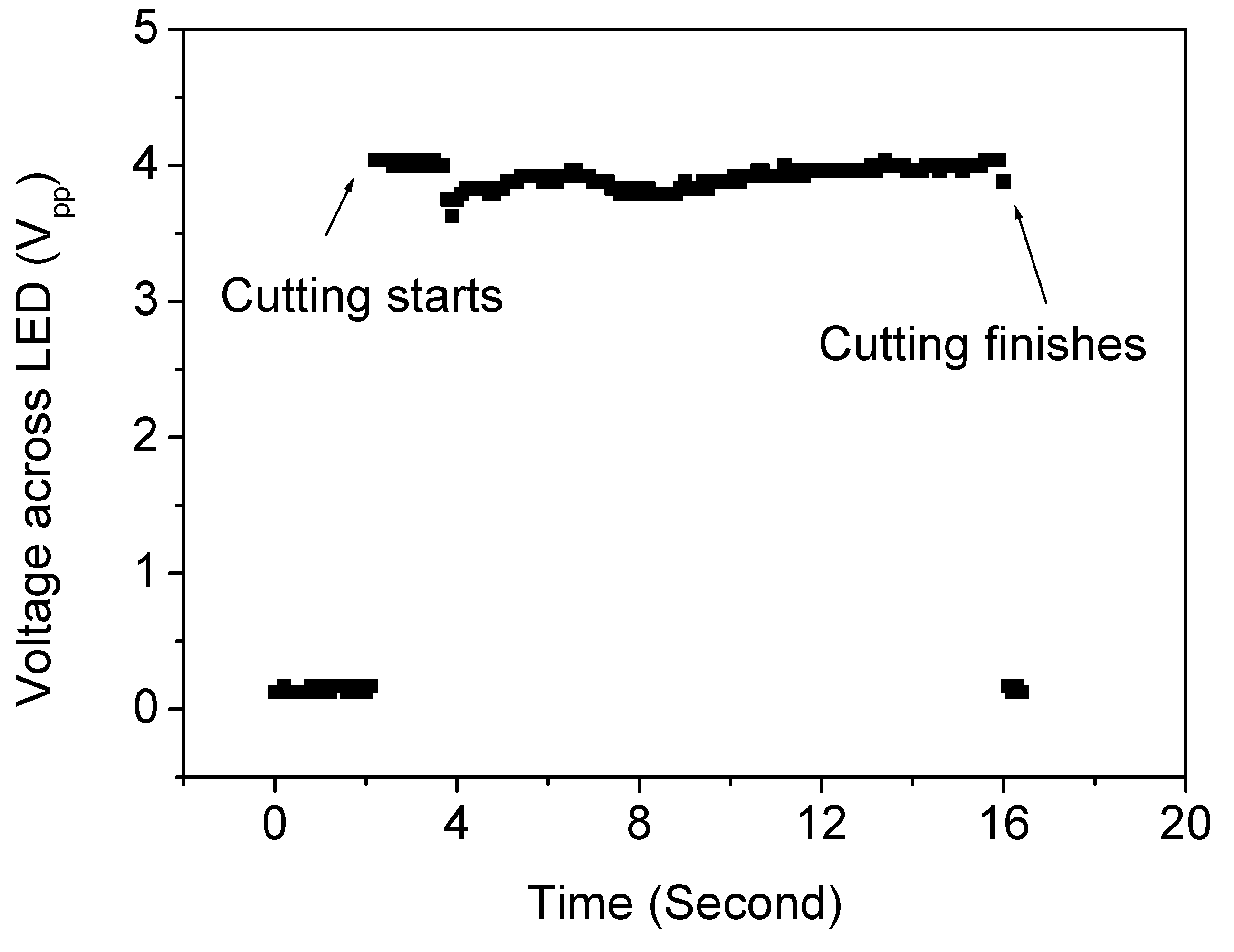
| Harvester | Excitation Level | Maximum Output Voltage (Vpp) | Maximum Output Current (mApp) | Maximum Output Power (mW) | Experimental Impedance Matching Resistance (Ω) |
|---|---|---|---|---|---|
| 24.4 kHz | 37.5 Vpp; 0.73 μmpp | 5.8 | 10 | 3.13 | 500 |
| 95 Vpp; 500 Ω load | 5.08 | 10.1 | 6.45 | ||
| 66 Hz | 115 μmpp | 70 | 1.3 | 6.68 | 50 k |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, T.; Lee, P.S. Piezoelectric Energy Harvesting with an Ultrasonic Vibration Source. Actuators 2019, 8, 8. https://doi.org/10.3390/act8010008
Li T, Lee PS. Piezoelectric Energy Harvesting with an Ultrasonic Vibration Source. Actuators. 2019; 8(1):8. https://doi.org/10.3390/act8010008
Chicago/Turabian StyleLi, Tao, and Pooi See Lee. 2019. "Piezoelectric Energy Harvesting with an Ultrasonic Vibration Source" Actuators 8, no. 1: 8. https://doi.org/10.3390/act8010008






