1. Introduction
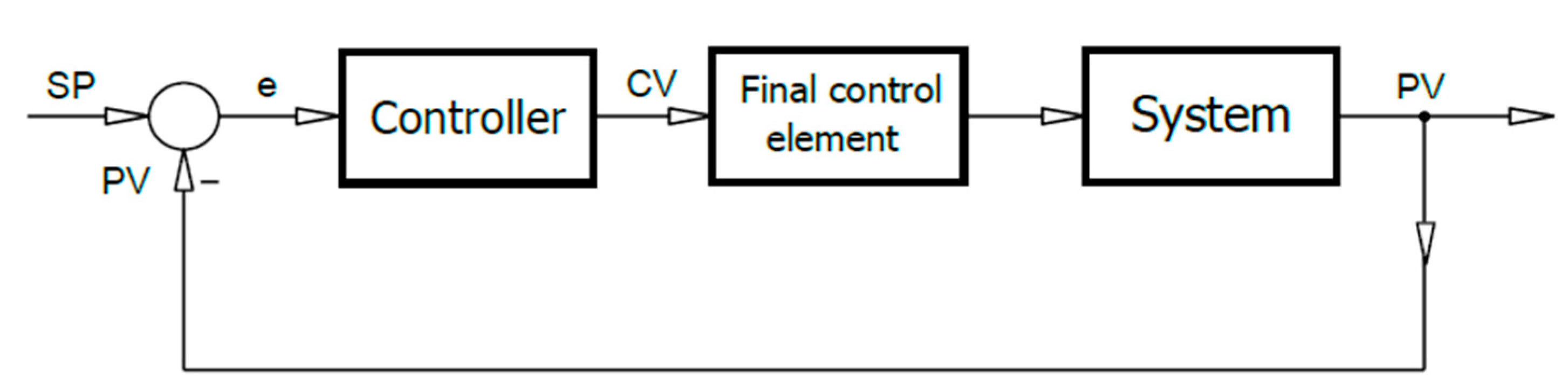
In the structures of the closed loop industrial automation systems, we can generally distinguish: Controlled systems, controllers, measuring instrumentation, and final control elements [
1,
2,
3]. The general structure of a single-loop control system is depicted in
Figure 1. The final control elements are physical units directly affecting the streams of energy and materials. In the structure of a control system, they simply play the role of adapters between controllers and controlled systems.
In fact, the final control elements are acting as energy or power transformers that convert the low-energy or informative control value (CV) into a high-energy driving output. Clearly, due to the principle of energy conservation, the final control elements require an additional auxiliary power supply source.
The main interest of this paper is focused on the certain class of final control elements in which the compressed air is used as an auxiliary energy supply source. These elements are commonly used in automatic control systems in the following industries: Power, chemical, petrochemical, pharmaceutical, and food.
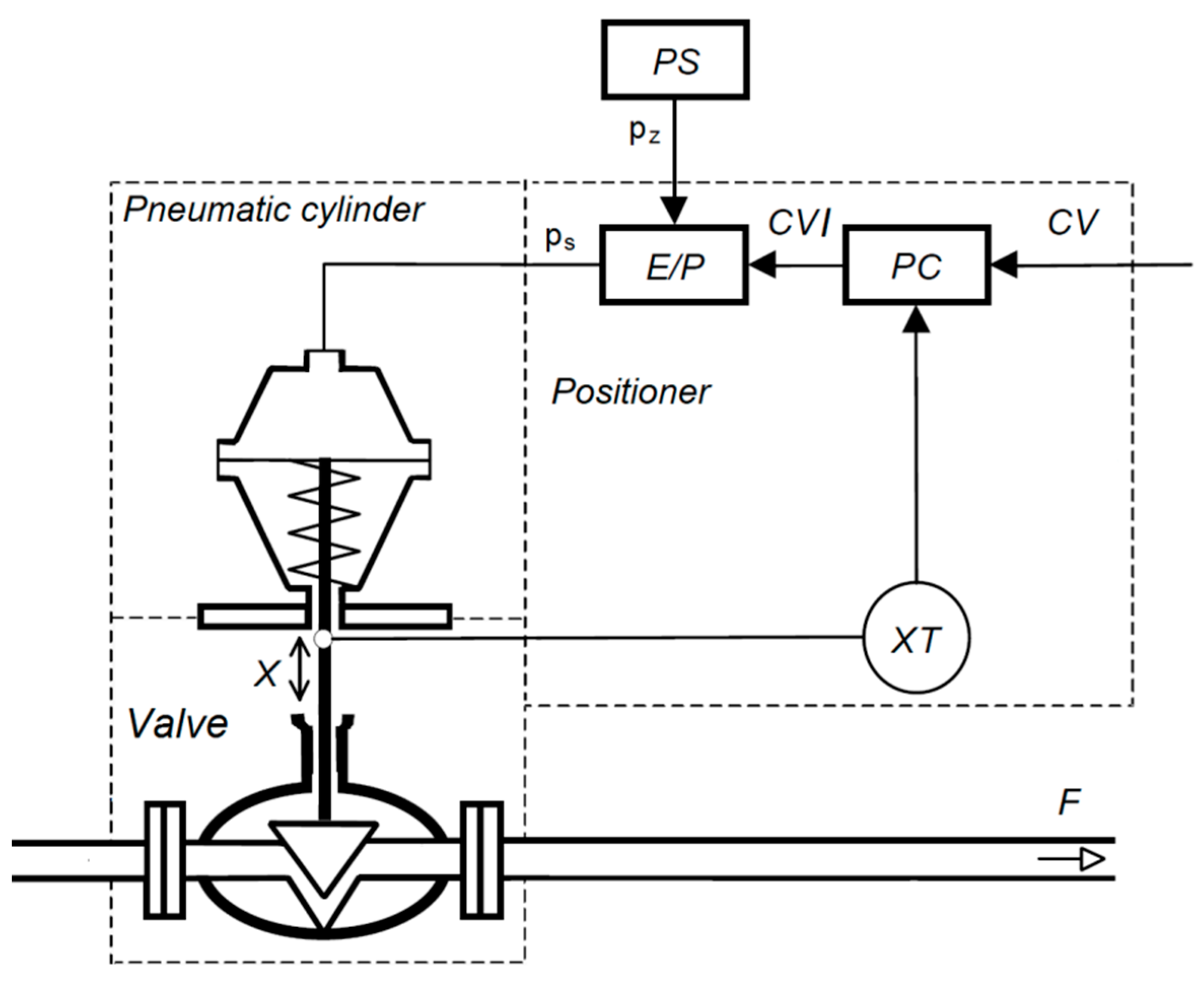
A typical electro-pneumatic final control element consists of a pneumatic actuator with linear or rotational movement of its stem, a positioner, and a control valve (
Figure 2). By adjusting the position of the valve plug attached to the end of the actuator’s stem towards the valve seat, it is possible to control the flow rate of a medium passing through the valve.
The primary goal of the positioner is to follow-up the CV. In order to do it, the positioner has to control the pressure of the pneumatic actuator in such a way that the position of the valve plug will depend exclusively on CV and will suppress the influence of the disturbances such as: Changes of operating temperature, supply pressure fluctuations, changes in the static and dynamic load of the actuator’s stem, friction, and the evolution of friction forces.
The final static and dynamic properties of the actuator are shaped by the positioner. In fact, the positioner is a specialized, autonomous control system of the stem position. The simplified block diagram of the final control element is shown in
Figure 3.
When applied, one requires, from the final control element, a repetitive non-hysteresis static characteristics, aperiodic step response, and minimal control time. In principle, realization of these requirements becomes realistic only due to the use of a positioner.
It should be noted that the final control elements are exposed to adverse environmental conditions such as thermal shocks, a wide range of operating temperatures, vibrations, humidity, dusty pollutants, corrosive working environment, and electromagnetic interference. Therefore, the final control elements are classified as belonging to the group of elements of automation systems subjected to the most frequent failures. It is estimated [
7] that the probability of the failure of actuator may be even at least one order higher than for sensors.
The faulty final control element can lead to a deterioration of the quality of the final product, and can even lead to the process shutdown. All these factors influence the safety of the process and humans involved, as well as worsen the economic indices of the process. For this reason, the assurance of the most trouble-free operation of such devices becomes more important. In this context, the issues of fault prediction and diagnostics, as well as ways of prevention actions and fault tolerant control become particularly pertinent [
8]. Most frequently, the electro-pneumatic transducer is subject to fail in the case of electro-pneumatic final control elements. This component fails due to poor quality of supply air, friction wear of its mechanical components, and material fatigue of its moving parts.
In this paper, a practical and economic approach to prolongation of the final control element lifetime is proposed. It is based on the appropriate shaping and tuning of the positioner controller in such a manner that it results in the limitation of the amplitude and of the number of cycles on its output. This directly influences the wear and fatigue of moving elements of the electro-pneumatic transducer. This type of approach, due to the conclusions drawn from the Wöhler’s fatigue curve [
9], has significant impact on mean-time-between-failures (MTBF), and therefore, reduces wear and increases functional safety of the controlled process.
The essence of the proposed approach is to change the structure and parameters of the positioner controller (PC) in order to minimize its effort, but not at the expense of worsening the control quality factors of the controlled system in which such an element is used.
The structures of positioner controllers of temporary final control elements are programmable as a rule. In order to achieve sufficiently short sampling time, the implementation of the controller algorithm should be time effective. This is not a trivial task when taking into account strong limitations of truly disposed computational power. Therefore, the structure of the controller should not be too complex. This paper tries to answer how to choose the controller’s structure from the limited set of arbitrary chosen low complexity potential positioner’s controllers in order to keep the desired control quality factors by minimal effort of the controller.
The results of research of the proposed approach were obtained in the Matlab-Simulink simulation environment with the use of the final control element model [
10], which is recognized in the process fault detection and isolation (FDI) society. This is, to some extent, enhances trustworthiness of presented results.
2. The Controller Effort
The term controller effort is not novel, however, may be, undeserved discussed relatively very rare. Moreover, the term controller effort does not have any unambiguously established definition. Some papers refer to this term, however, leaves it undefined [
11,
12]. In these papers, controller effort is understood as controller output. In turn, in Reference [
13], the control effort is defined as the instantaneous value of the controller output. In Reference [
14], the term actuator effort is defined quite differently, as connected with a physical value of a force. This rather complies with the generalized term of effort known from the bond graph theory. In the papers from References [
15,
16], the control effort is defined as an integral part of the power of a control signal. Therefore, this definition can alternatively be interpreted in terms of energy of the control signal. Alternately, Beshi et al. in [
17] verbally defined the control effort as root-mean-square value of the control signal increments. This definition may be interpreted as penalizing averaged changes of the energy of the control signal velocity when applied to the optimization problem. The control effort index defined in Reference [
18] reflects the control energy usage normalized by the energy of the raw reference signal. In fact, the introduced index characterizes the output-input signal energy effectiveness of the controller. However, from the practical point of view, this definition is less important, because the instantaneous consumption of energy in real systems is rather a function of control signal.
For the sake of this paper we introduce a slightly different definition of the controller effort together with some associated terms referring to the variability of the control signal. These outcomes from a heuristic rule connect the lifetime of the mechanical component with the number of working cycles. Further, the definitions will be given for the continuous and discrete time domain systems. Definitions in a discrete time domain are useful for real implementations in a digital environment.
Definition 1. Define the normalized variability of the controller output as:where: —nominal range of controller output. Definition 2. Define the controller’s mean time effort over time interval as an average normalized variability of the controller output.where:. By changing integration limits in Equation (2), we can define cumulative time effort: Definition 3. Define the controller’s cumulative effort as an averaged over time normalized variability of the controller output. In the discrete time domain, the normalized variability can be expressed as:
where:
—
k-th sample of the controller output
. By analogy to Equation (2), the mean time effort in the discrete time domain can be expressed as the averaged sum of the variability of control signal over the number of
samples:
where:
—sampling frequency of controller output
;
—time interval.
Remark. The introduction of sampling frequency in Equation (5) avoids deflating/inflating effects of the mean time effort for different sampling frequencies.
Finally, by analogy to Equation (3), the cumulative effort in the discrete time domain can be expressed as the averaged sum of the variability of control signal over the
samples:
where:
—time horizon.
In practice, in automation systems, the control value is usually normalized. In this case: and therefore respective Formulas (1)–(6) appropriately simplify it.
If we further assume that the movable elements of the electro-pneumatic transducer of positioner approximately reproduce the trajectory of the control signal, then the reduction of the controller’s effort leads to a diminishing of the average amplitude and the totalized travel of its moving elements. As a result, it is expected to reduce the intensity of the wear of its mechanical components and thus extends MTBF.
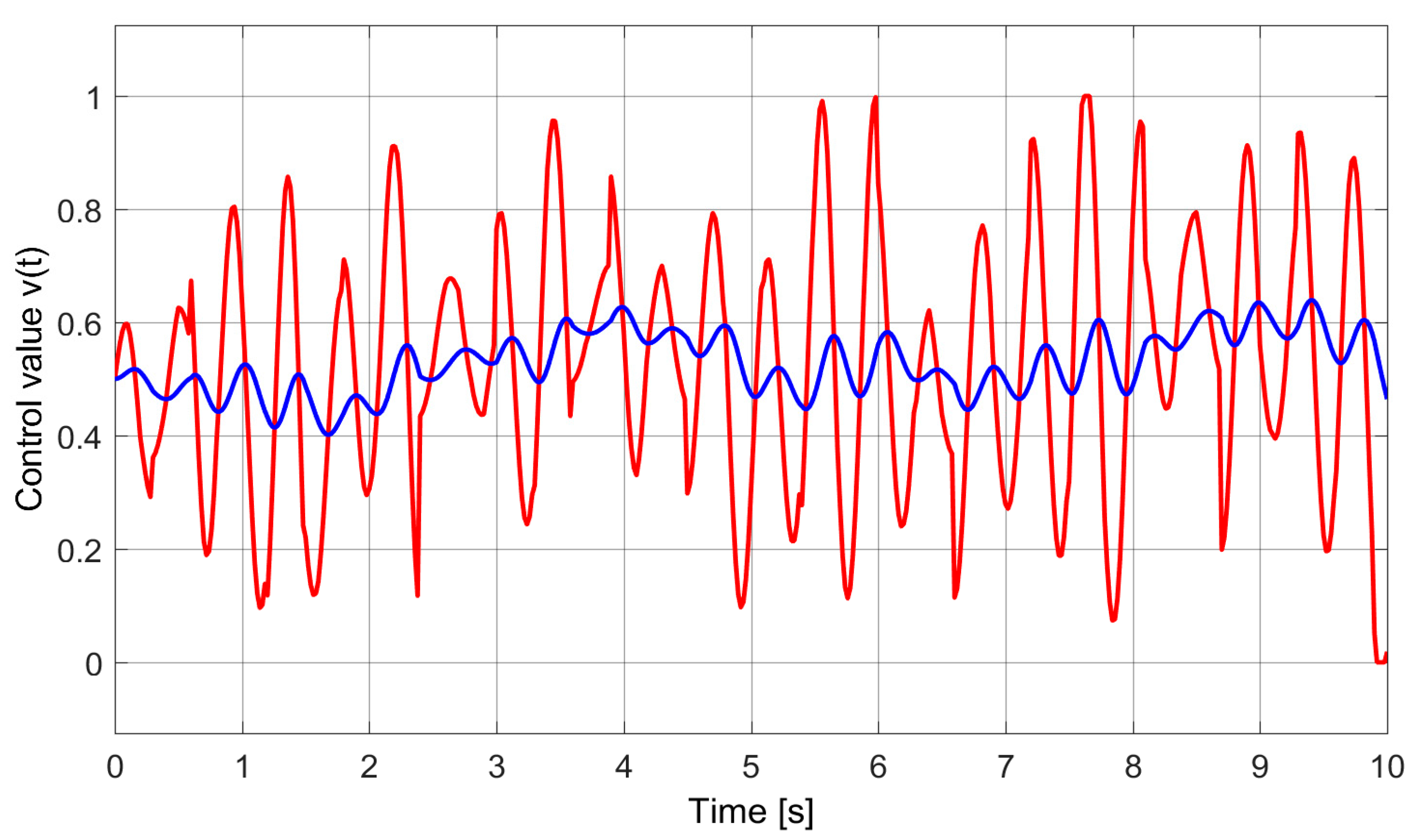
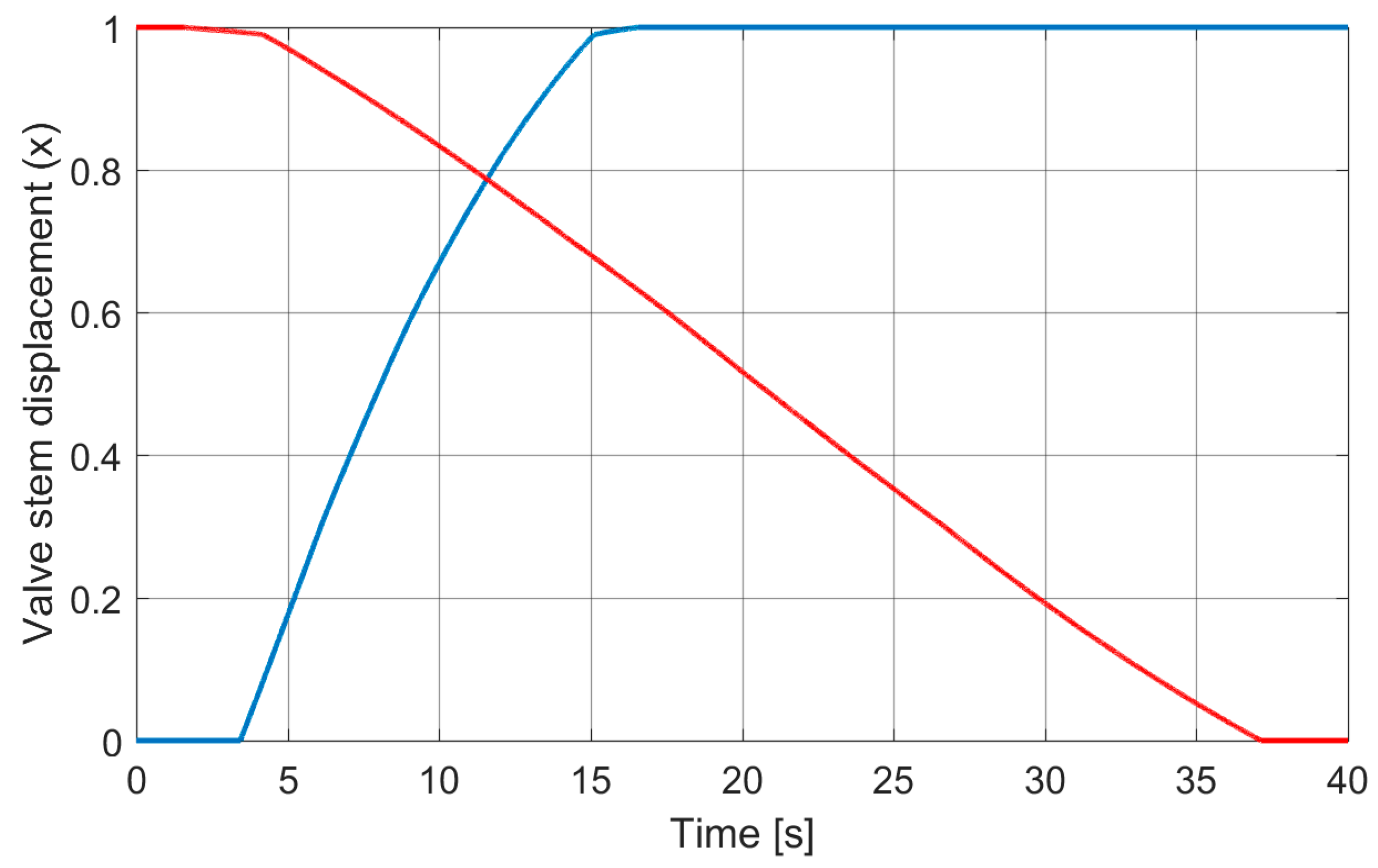
Figure 4 presents an example of two control strategies for the electro-pneumatic transducer: An aggressive—marked with a red line and a conservative marked by the dark blue line. The appropriate cumulative effort values for both strategies in the time horizon of
= 10 s differ significantly, and respectively, are equal to: 0.32 and 0.029. In this case, the eleven-fold reduction in the controller’s effort allows the increase of the permissible number of work cycles due to the significant decrease of their amplitude.
3. Research Environment
The implementation of experimental investigations in a real life scenario is usually costly and time consuming. For this reason, the choice of the structure, parameters, and tests of the proposed control strategy was carried out in a simulation. For this purpose, a complex, phenomenological model of an electro-pneumatic final control element was used. This model was prepared and validated especially for the assessment model based fault detection and isolation approaches [
20].
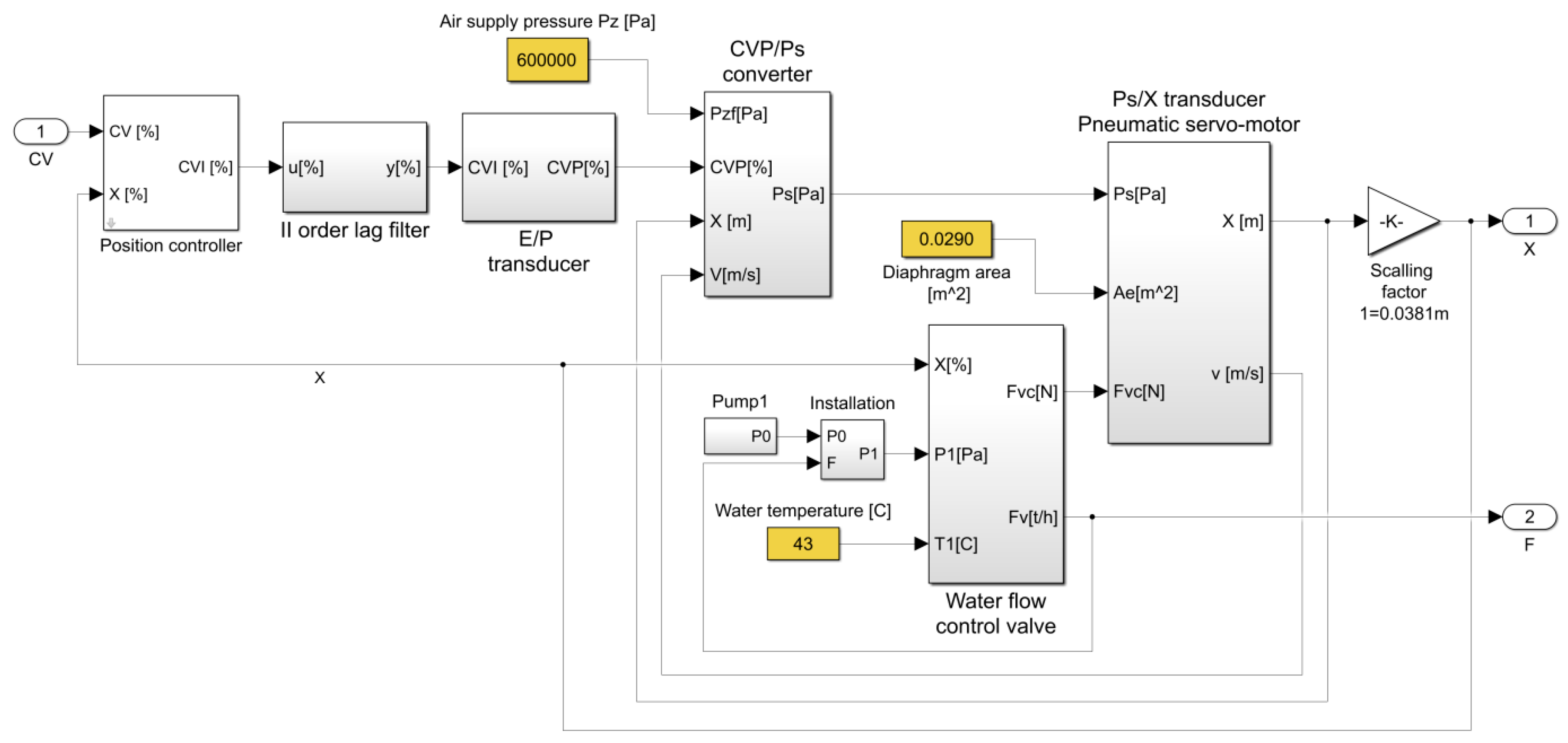
The choice of this model was motivated by its availability [
10] and the recognition in the international community of process safety diagnostics. Simulation tests were performed by means of the liquid level control system in which the final control element from Reference [
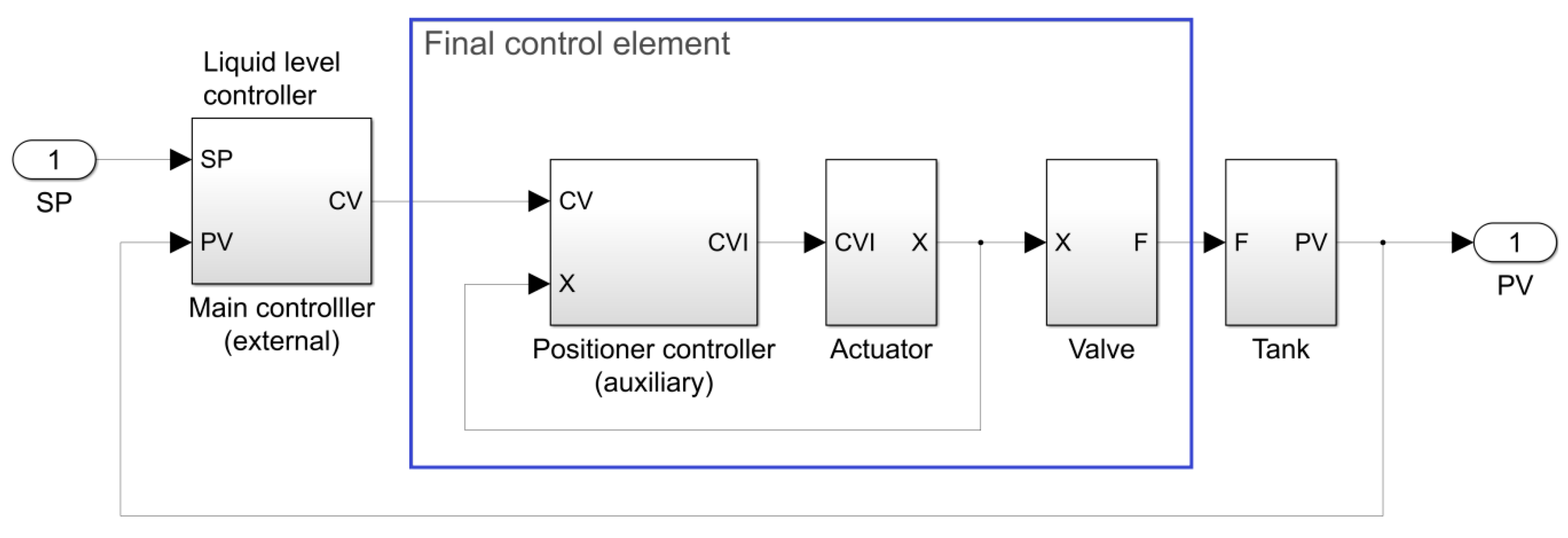
10] was applied. A simplified block diagram of the simulated control system is shown in
Figure 5.
The constant set-point liquid level control system was taken from the DABlib library [
6] in order to provide the near realistic and traceable conditions. Some comments regarding the adopted model referred to in Reference [
6], as a Simple Process Example IV, are given below.
The liquid is stored in a cylindrically shaped tank having constant cross-sectional area
A = 20 m
2. The liquid level is measured by means of level sensor. Level signal is fed back to the main proportional-integral controller (
which governs the final control element. The liquid is free discharged from the tank. The liquid outflow is modeled by the equation:
where
—flow contraction coefficient;
= 1kg/dm
3—specific gravity of the liquid;
= 9.81 m/s
2—gravitational constant; and
—liquid level in [m].
The liquid level is described by the following equation:
where
—liquid inflow into tank.
The inflow liquid is supplied from a positive displacement pump. The static pressure generated by the pump forcing liquid is equal to 3.5 MPa. The pressure drop in the supply pipeline is simulated by a constant hydraulic resistance equal to 1 kPa/m3/s. The final control element is intended for controlling liquid inflow to the tank.
A simplified block diagram of the simulated final control element is depicted in the
Figure 6. The detailed model of the final control element is available if we look under the mask of the block ACT from the DABlib Simulink library [
10]. The usage of the model is described in the document Using Damadics Actuator Benchmark Library (DABLib) available from the same site.
The second order lag filter visible in
Figure 6, and following the positioner controller, represents dynamics of the electro-pneumatic transducer E/P. This filter is not a part of the positioner controller.
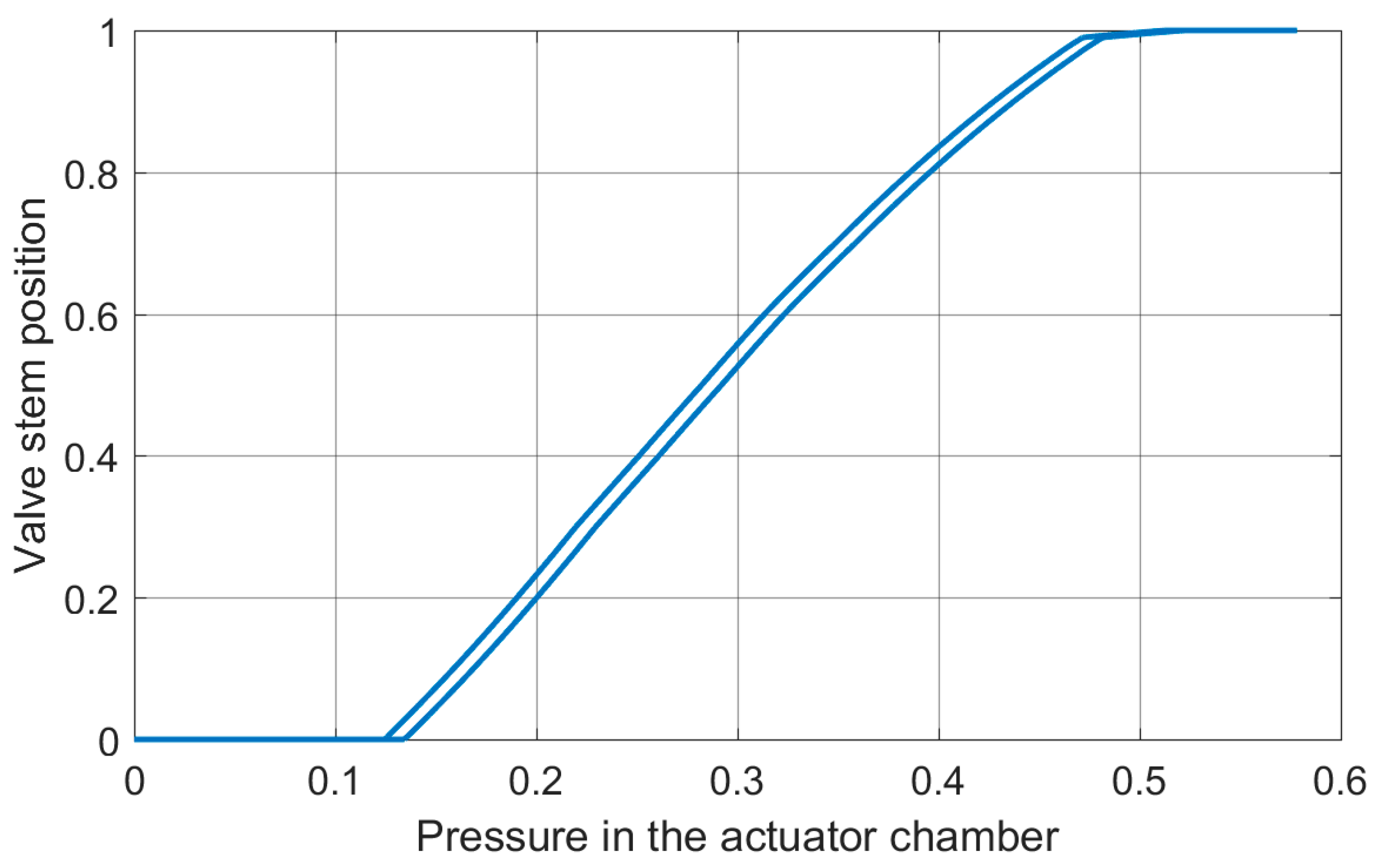
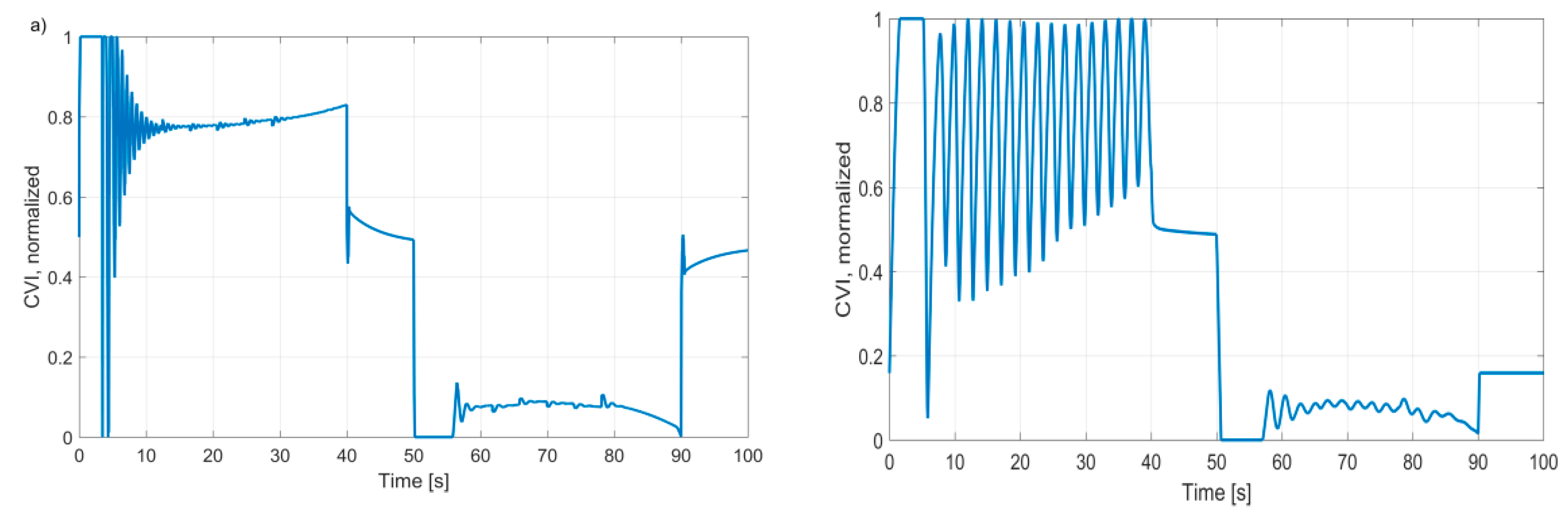
Applied final control element exhibits non-linearity, ambiguity, and asymmetry of the static and dynamic characteristics (
Figure 7 and
Figure 8).
It should be noted that the directionality of dynamic characteristics is a major challenge for the internal positioner’s controller and has a significant impact on the variability of the controller’s effort.
5. Positioner Controller
Without any doubt, the structure and parameters of internal controller of positioner influences control quality factors as well as control effort. This paper presents briefly the results of an experimental selection of the structure and parameters of the internal controller of the positioner applied in the control system shown in
Figure 5.
As noted in Reference [
21], choosing the controller for a given control problem is not a trivial task. Cit. “This choice is often made heuristically by the design engineer.” This problem is exhaustively exemplified in [
22]. This paper tries to answer how to choose the structure of positioner controller from a certain limited set in order to maintain desired plant control quality factors and simultaneously minimizing controller effort.
5.1. Methodology
The limited set of four arbitrary chosen controller structures were examined: proportional (P), proportional-derivative (PD), fuzzy PD (FPD) and neural network (NN). The set of chosen controllers is not exhaustive but sufficient enough for exemplification of the issue of control effort. Integral action of controllers was not considered here because of the system stability problem and therefore necessity in assuring sufficient gain and phase margins.
Firstly, the necessary and sufficient conditions regarding comparability of achieved results are formulated.
the all controllers should be applied successively in the same control system. This allows a meeting of the necessary condition of comparability.
the settings of all investigated controllers should be optimized by means of the same cost function. This satisfies the sufficient condition of comparability.
The chosen ad hoc cost function (11) reflects the weighted linear combination of desirable properties of the positioner, i.e., some trade-off between tracking error and controller effort.
where
—is the weight of the controller effort. The weight
= 30 was finally chosen for experiments.
Here, the question appears why do not construct the cost function in such a manner that it will allow for minimizing of the positioner controller effort instead of minimizing its tracking error? While this expectedly leads to solution where the optimal effort would be close to zero and therefore does not have practical sense.
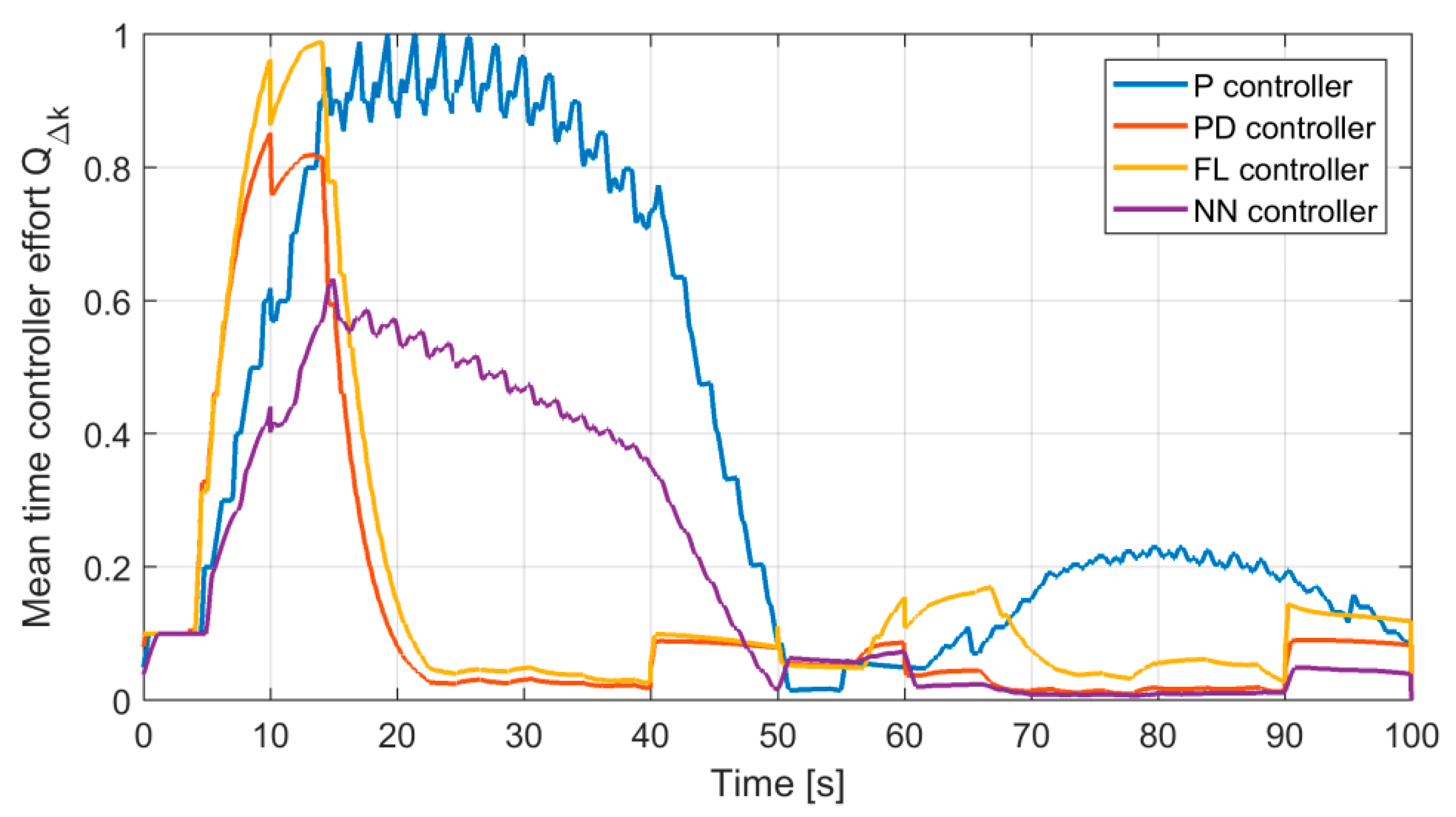
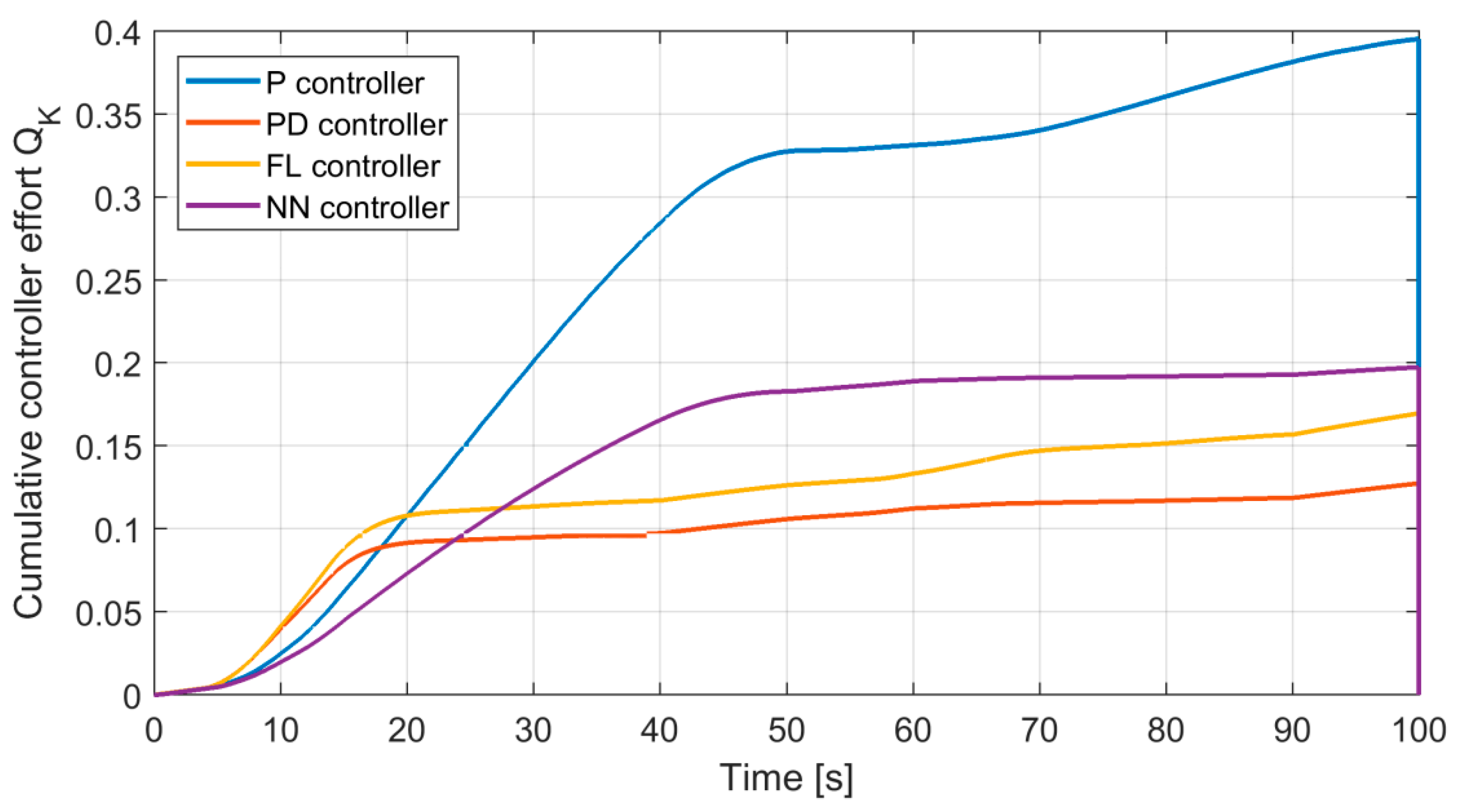
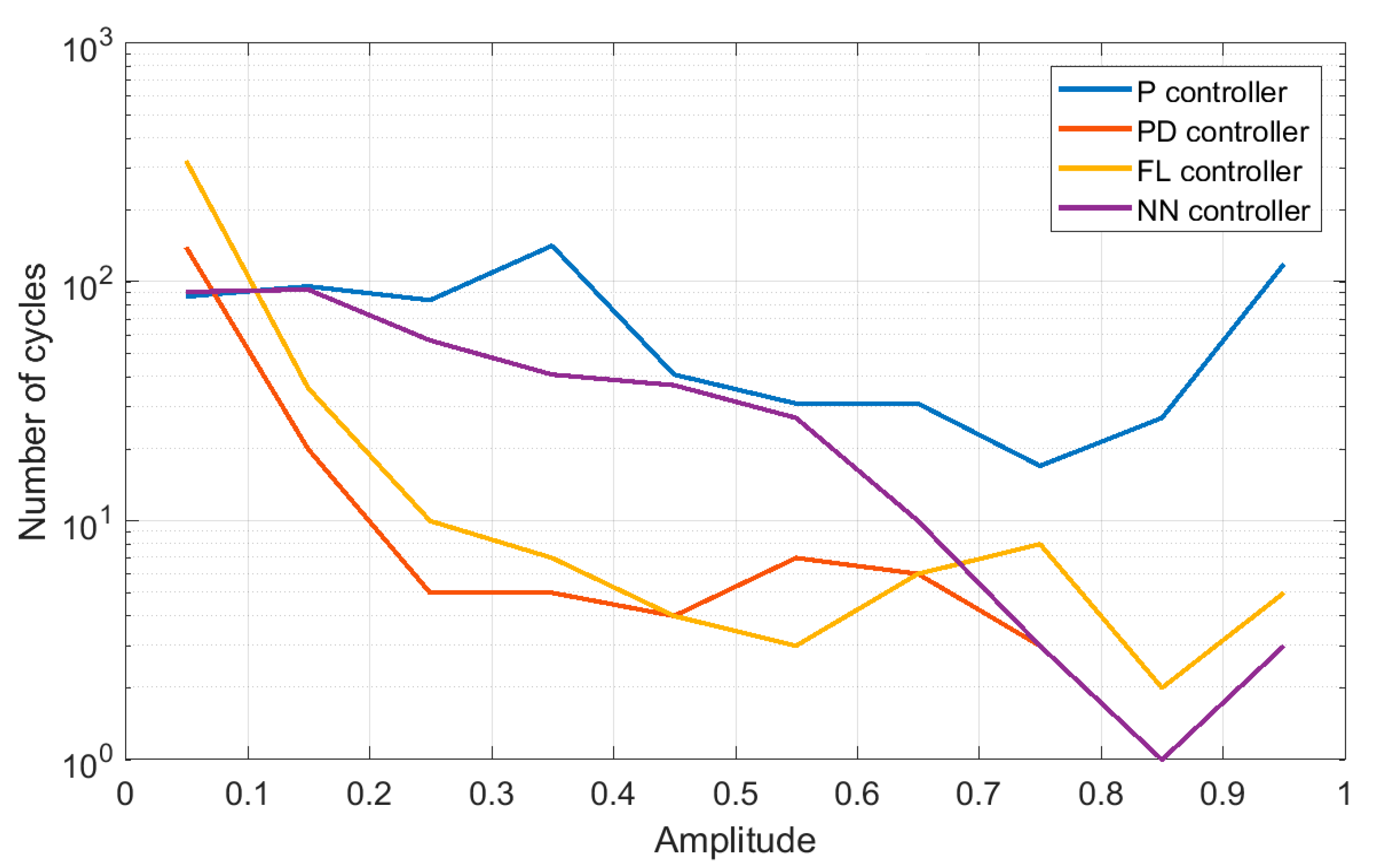
Next, for all investigated controller structures there were calculated values of all quality factors presented in
Section 4. Obtained results are shown in Table 3.
5.2. Proportional and Proportionl-Derivative Controller
The settings of classic linear proportional (P) and proportional-derivative (PD) controllers are shown in
Table 1.
Despite the high proportional gain, the final control element behaves stable. High proportional gain allows for obtaining low tracking errors and fast responses to disturbances. Thus, the resulting equivalent stiffness of the final control element is beneficially high.
5.3. Fuzzy PD Controller
The development of fuzzy nonlinear controllers became a mile-stone for the applied fuzzy logic theory. Early fuzzy controller solutions can be found in References [
23,
24]. A proportional-derivative fuzzy controller with error and error derivative inputs was presented in [
25]. Its simple structure allows for easier optimization and reduction of the required computational power. Therefore, this type of controller is extensively exploited in research reported in this paper. The development of the new optimization approaches for fuzzy controllers [
24,
26] allows for improvement of the quality of fuzzy controllers. Interesting evidence of the equivalence of the classic PID and Mamdani fuzzy controllers can be found in Reference [
27]. Over the years, new and better structures of fuzzy controllers were developed [
28,
29,
30], but their implementation in a positioner controller could be too burdensome.
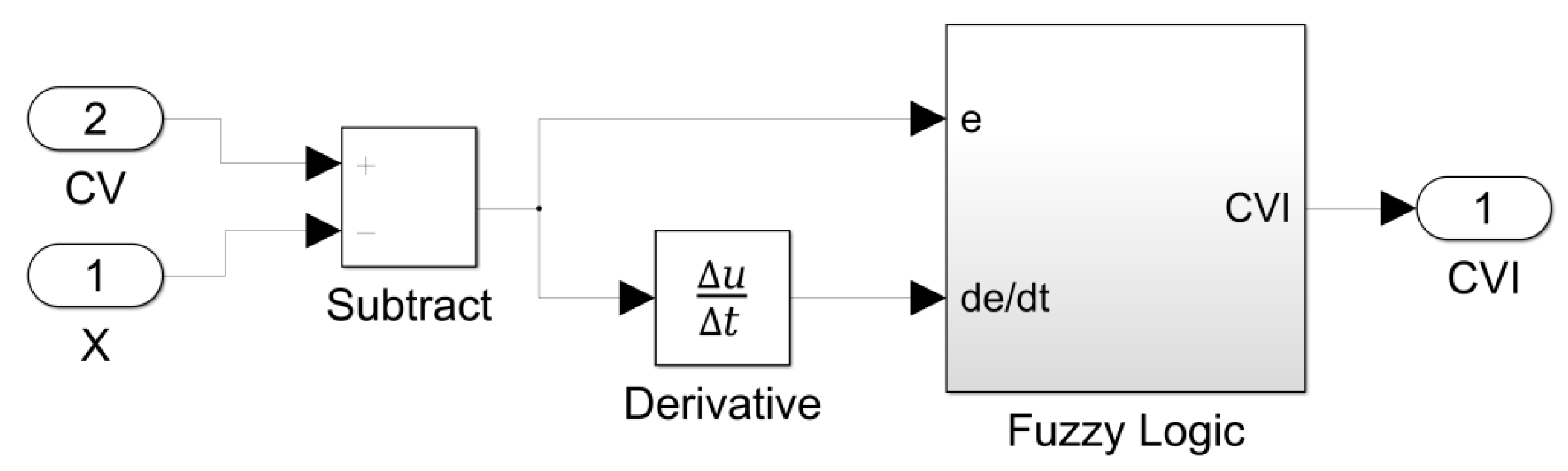
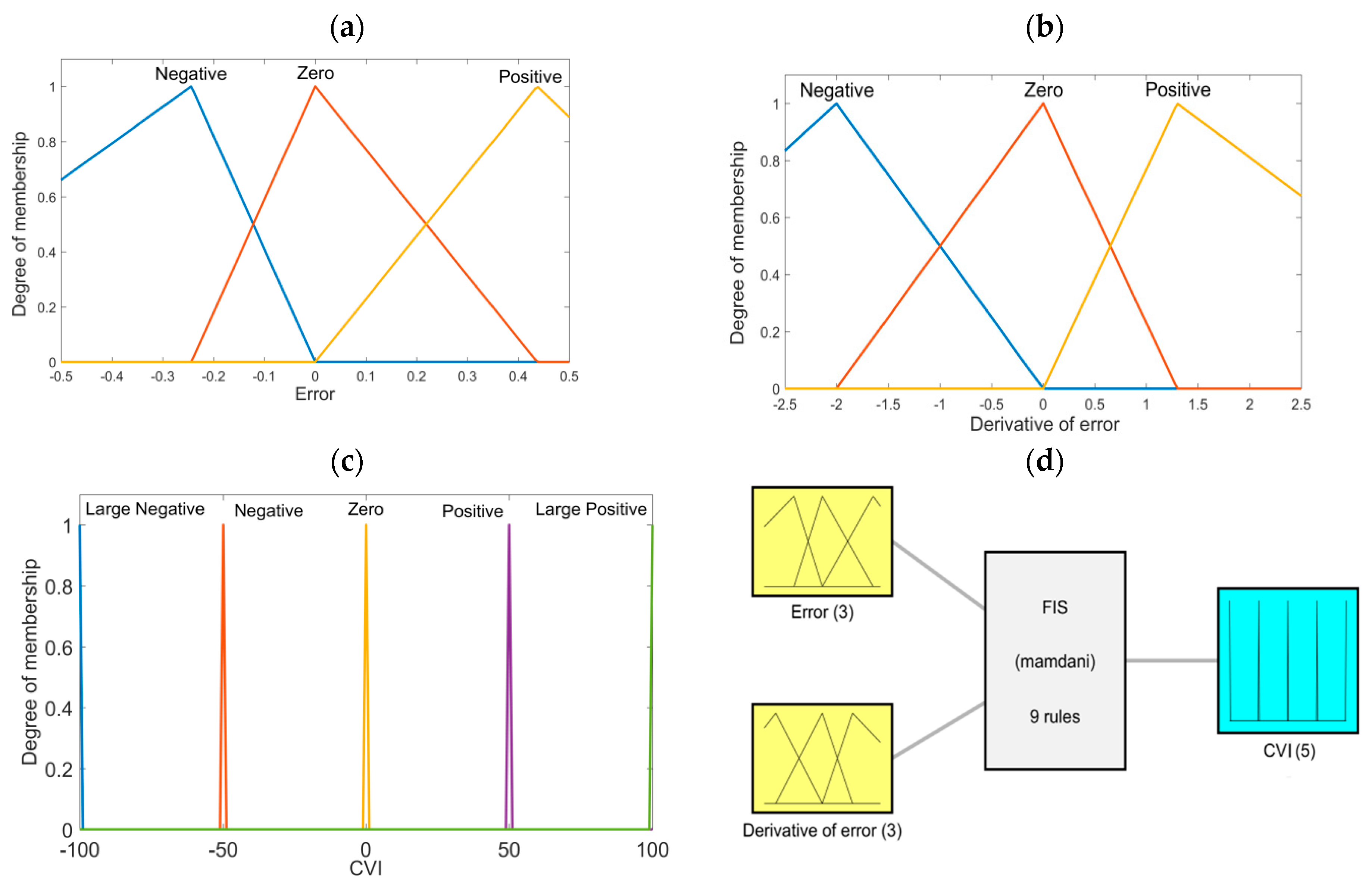
The structure of the fuzzy PD controller used in this research is depicted in
Figure 9. The fuzzy controller has two inputs (control error and derivative of the control error) and one control value output. The three linguistic values (membership functions) were associated with each input. The shapes of input membership functions are depicted, respectively, in
Figure 10a,b. Further, the five singleton membership functions visible in
Figure 10c were associated with the controller output. This allows for using fast center of gravity defuzzification algorithm of the aggregated fuzzy conclusion generated by the nine rules shown in
Table 2.
The fuzzy reasoning is based on standard skeleton base rule depicted in
Table 2. It counts together nine rules. The classic Mamdani’s fuzzy inference machine is applied for fuzzy reasoning.
5.4. Neural Network Controller
The neural controller developed and exploited in this research exhibits properties similar to proportional-derivative action. The developed controller is based on the structures presented in References [
31,
32,
33,
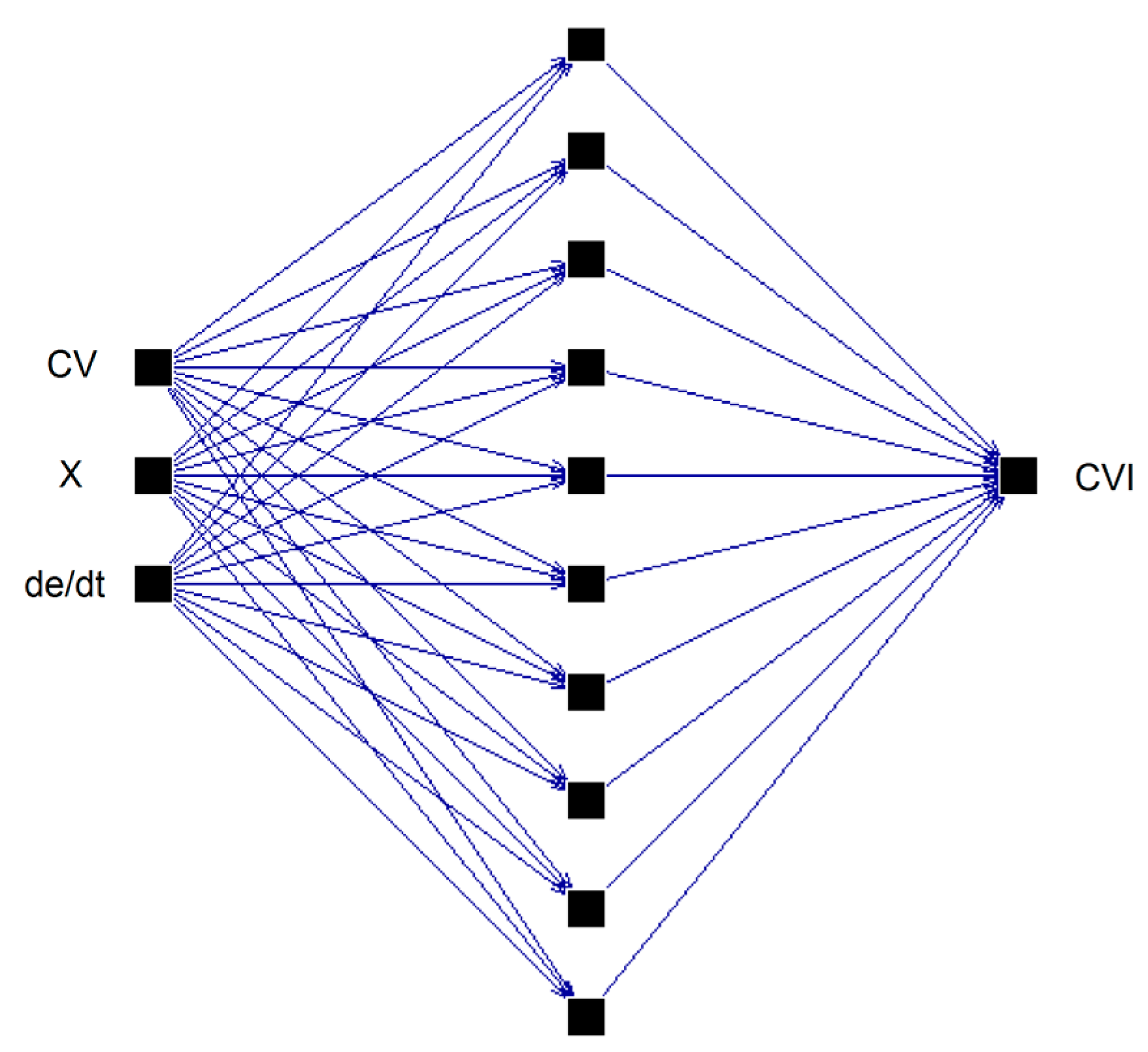
34], realizing a control action similar to PD. The use of three inputs, where one of them is the derivative of the control error, removes the problem of necessity of implementation of memory block within the network structure. However, the neural network controller, contrary to PID or fuzzy, is not a standard solution for the final control elements.
As a rule, the available computational power of real positioners is strongly limited. Therefore, the simple, unidirectional straightforward neural network structure was chosen in order to speed up the processing time. Moreover, the use of a unidirectional network facilitates the optimization of weights. The two-layer neural network structure with a hidden layer counting 10 neurons was designed. A sigmoid activation function is applied for each neuron. The network was trained by means of the back-propagation algorithm. The structure of applied neural network is presented in
Figure 11.
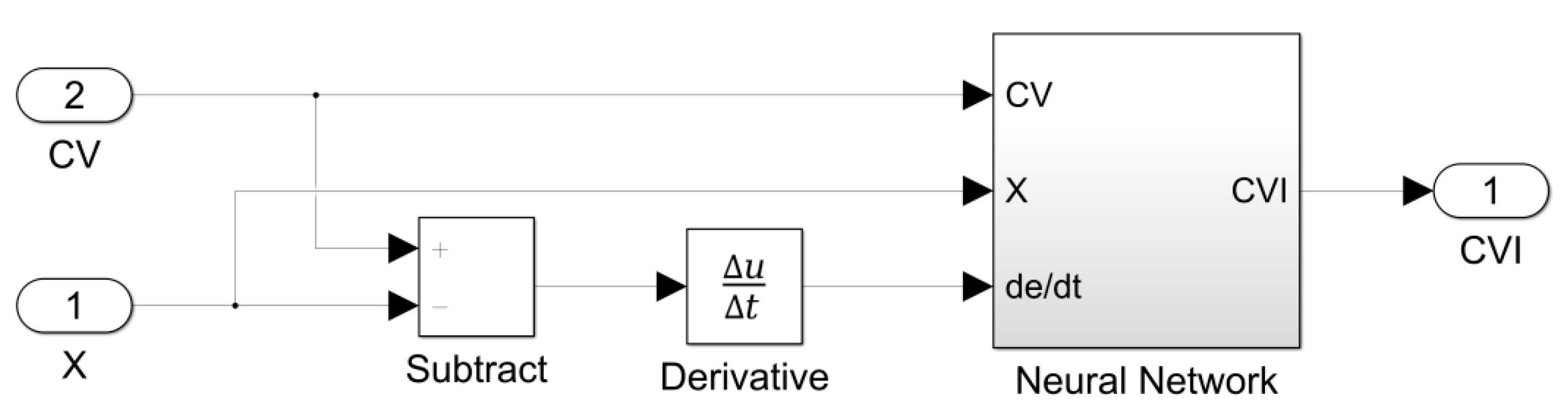
The block diagram of the Simulink model of neural network controller is depicted in
Figure 12.
6. The Choice of Simulation Tests
Let us briefly discuss operational conditions of the investigated final control element in order to choose the set of its components liable to accelerated wear. This would be assumed as justifying to some extent the rational choice of the primary set of performed simulation tests. Let us firstly define the list of harsh working conditions of the final control element:
chemically aggressive and corrosive environment,
leakages of the controlled aggressive media,
high operating temperature,
environmental pollution,
control loop oscillations,
mechanical impacts,
vibrations.
The two exemplary snap shots approaching real operational conditions of the final control elements are presented in
Figure 13.
The corrosion, mechanical impacts as well as dusty environment influences friction force in control valve packing. The friction may be assumed as the root cause of the hysteresis loop visible in
Figure 7. This hysteresis may significantly expand or shrink during the exploitation period. The positioner of the final control element should compensate for the effects of changes of the hysteresis of the pneumatic actuator. Therefore, it is justified to investigate the influence of the bi-directional changes of the friction of the controller effort.
Moreover, the chemically aggressive environment is not inactive in regard to the actuator’s spring. The spring is surrounded by an ambient atmosphere in the single acting actuators. Even tiny shrinkage of the diameter of the spring’s wire caused by a corrosion seriously influences the spring’s elasticity. The reason is that spring elasticity depends on the fourth power of the wire diameter. This justifies the experiments were the actuator’s spring elasticity drops down. On the other hand, there is imaginable a replacement of the worn spring by a new one. This also justifies the experiments where the spring elasticity could be greater than nominal.
The tests of internal positioner controller were carried out for:
nominal values of friction and actuator’s spring elasticity;
friction varying within the range [−50%, +50%];
actuator’s spring elasticity varying within the range [−50%, +50%].
In order to minimize the simulation time, the tests were performed only for the extreme values of the above-mentioned influencing quantities.
8. Summary
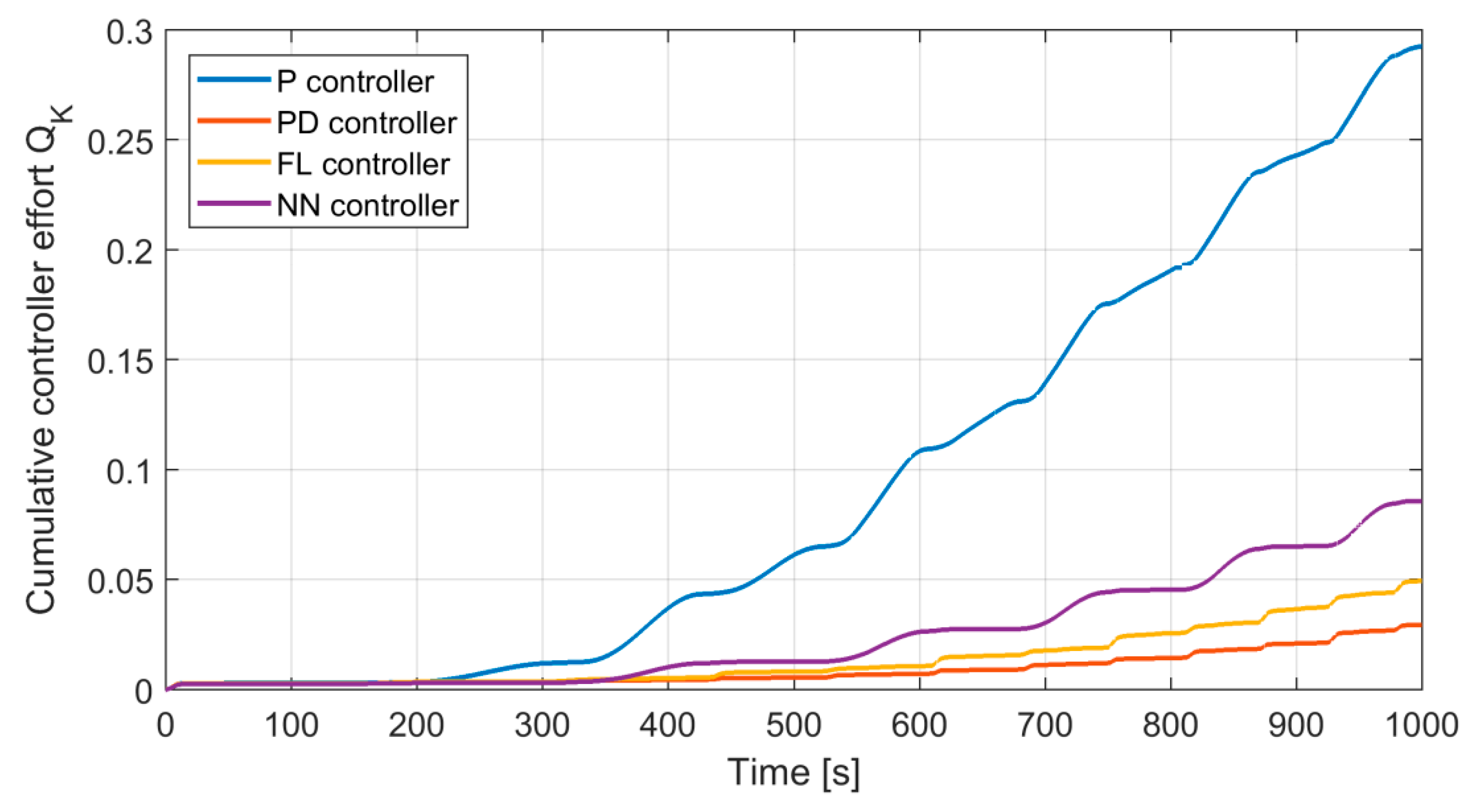
The three practical measures of the control quality have been proposed in this paper, namely: Variability, mean time, and the cumulative effort. These measures can be applied for the design of a cost function, which allows for optimization of positioner controller settings with respect to the controller effort. Minimization of the controller effort would be beneficial because the lower effort the lower wear of moving parts of positioner is, the lower the energy (compressed air) consumption.
On the example of a fairly typical liquid level control system, it was shown (
Table 3) that the replacement of positioner controller from classic P algorithm to PD or fuzzy PD allows more than a three-fold reduction of effort, while simultaneously obtaining much better values of other quality control factors. It is worth mentioning that frequently the P controller is preferred in positioners. This comes from considerations regarding the cascade system where the external controller performs integral action and internal controller proportional action. As follows from the results of investigations presented in this paper, it does not promise either longer lifetime nor better control quality.
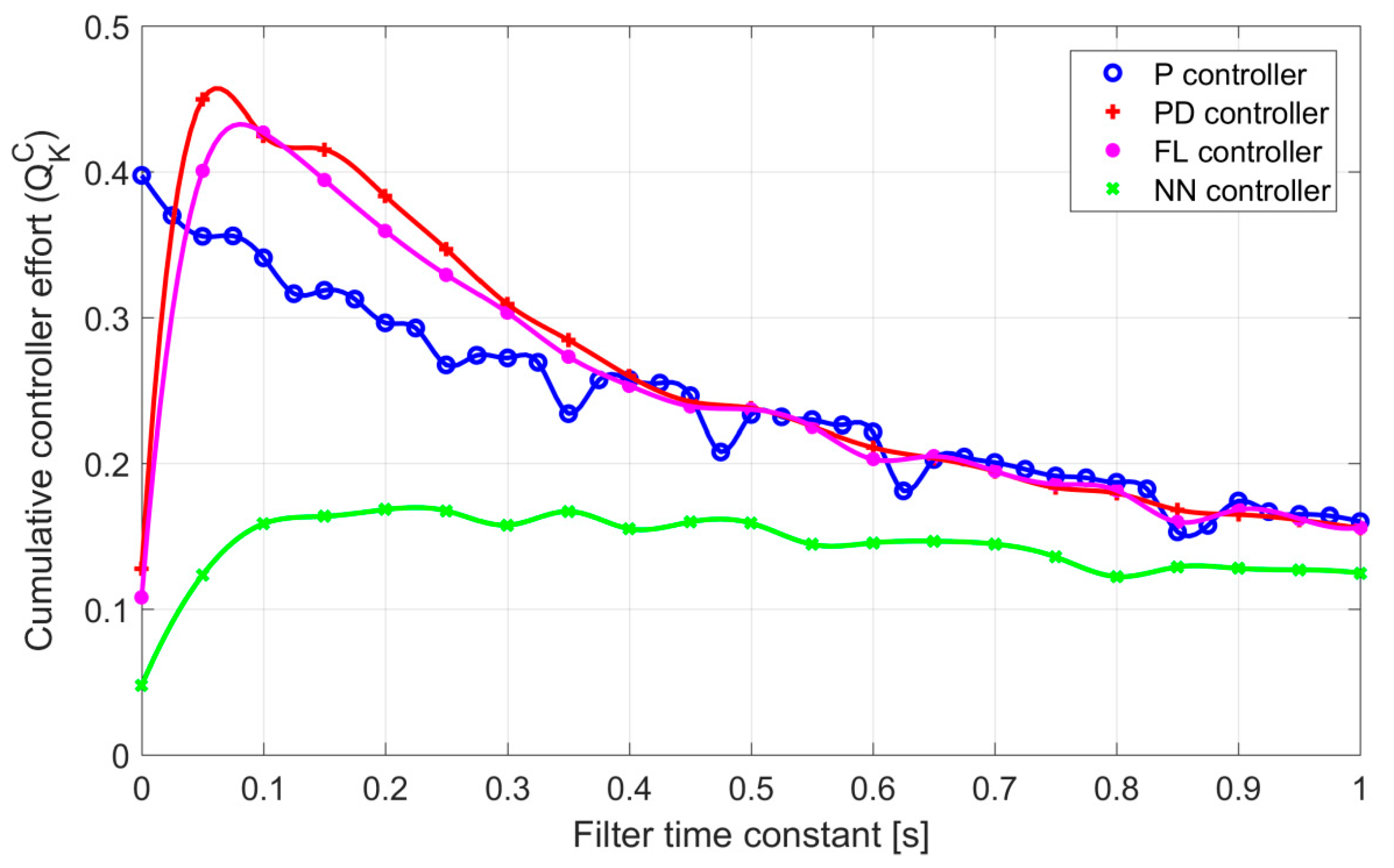
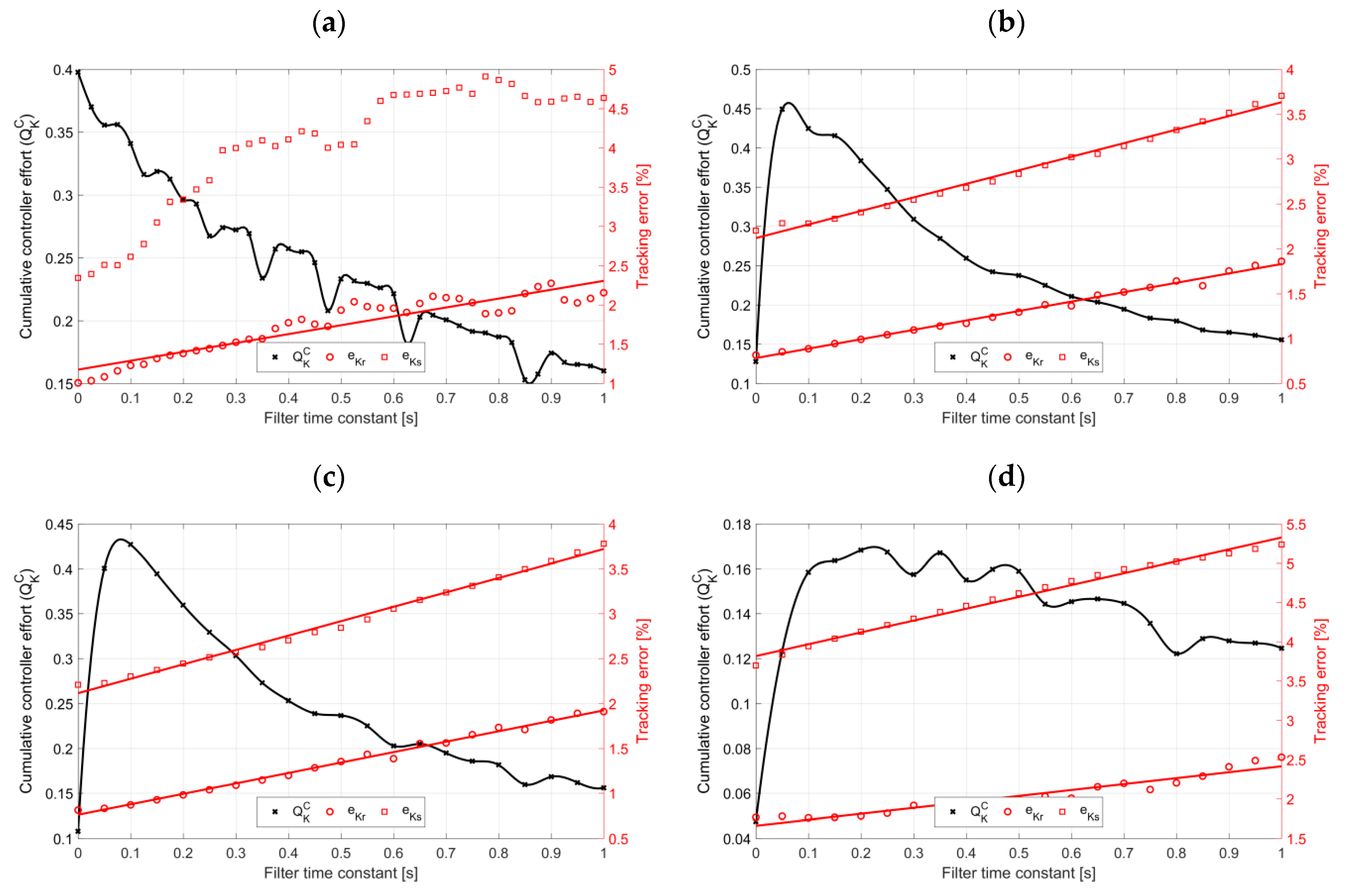
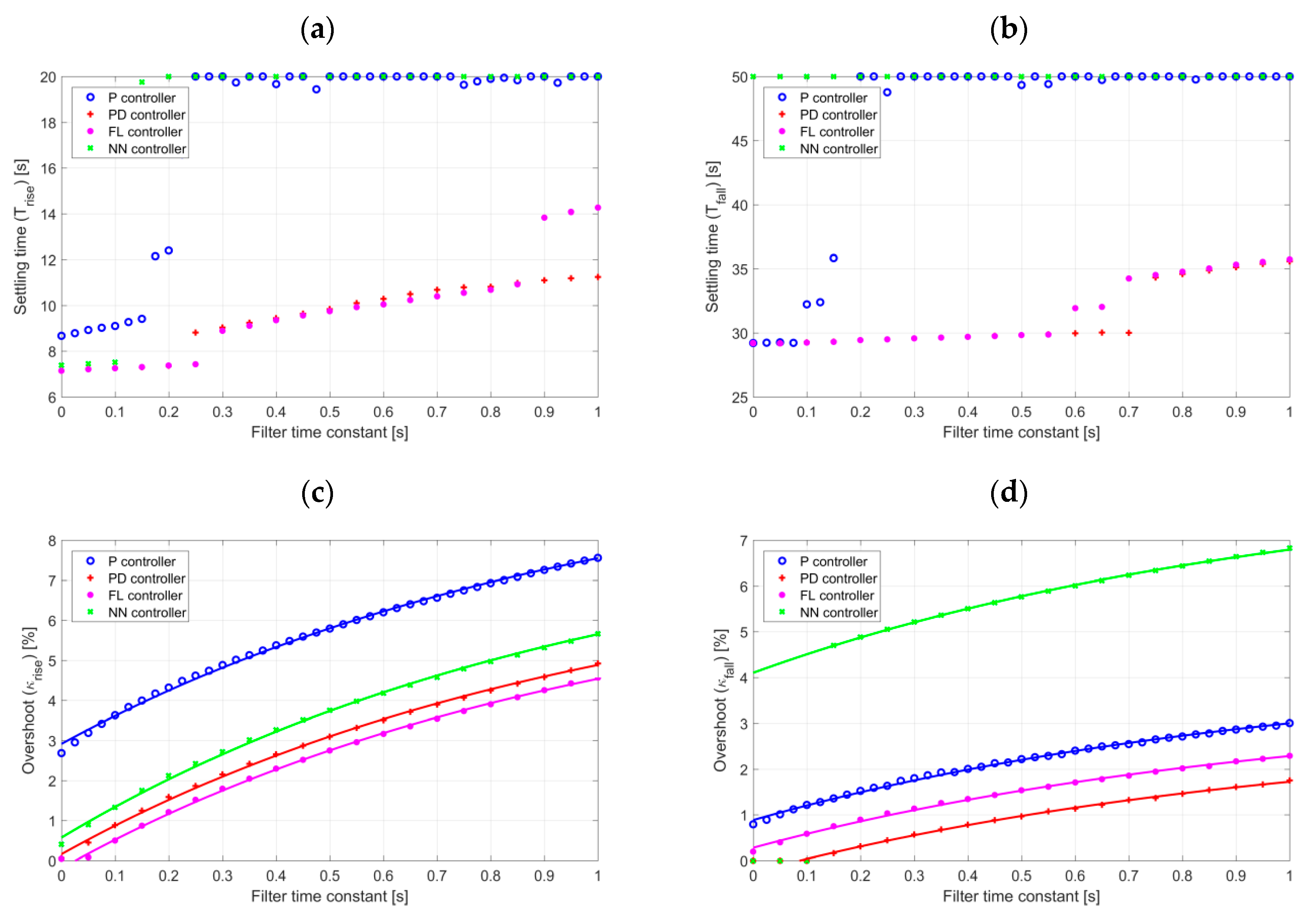
As shown in the paper, the diminishing of the control effort by means of low pass filter of the control output is possible, however, may significantly worsen tracking properties of the control system. This applies to settling times and overshoots as well. Therefore, the use of low pass filter of the control signal should be considered as problematic.
The simulation tests demonstrate that by the proper selection of the structure and parameters of the internal controller of the final control element, one can achieve two seemingly contradictory outcomes. On the one hand, better quality control, while on the other, simultaneous reduction of the controller effort. Obviously, the experimental verification of simulation findings is necessary. This is foreseen for the near future.