Finite Element Model of Vibration Control for an Exponential Functionally Graded Timoshenko Beam with Distributed Piezoelectric Sensor/Actuator
Abstract
:1. Introduction
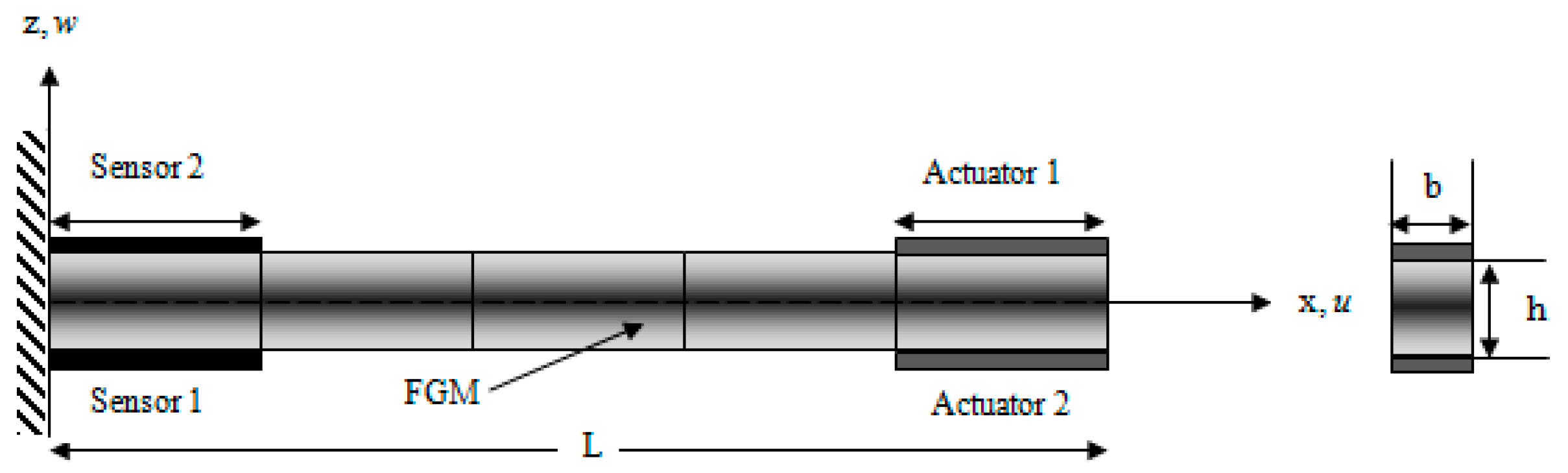
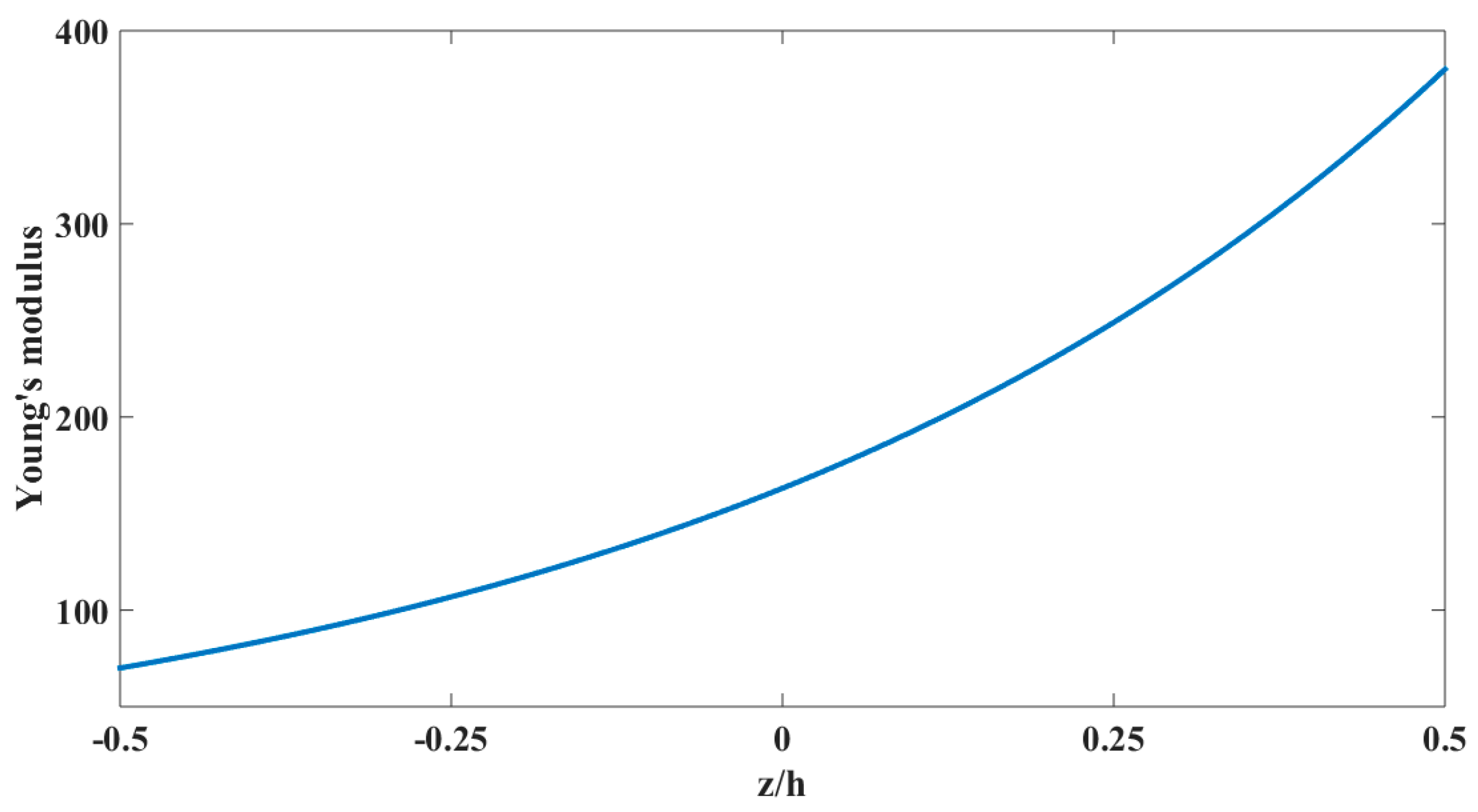
2. Mathematical Modeling
3. Finite Element Formulation
4. Sensor/Actuator Equations
5. Dynamic Equation and State Space Model
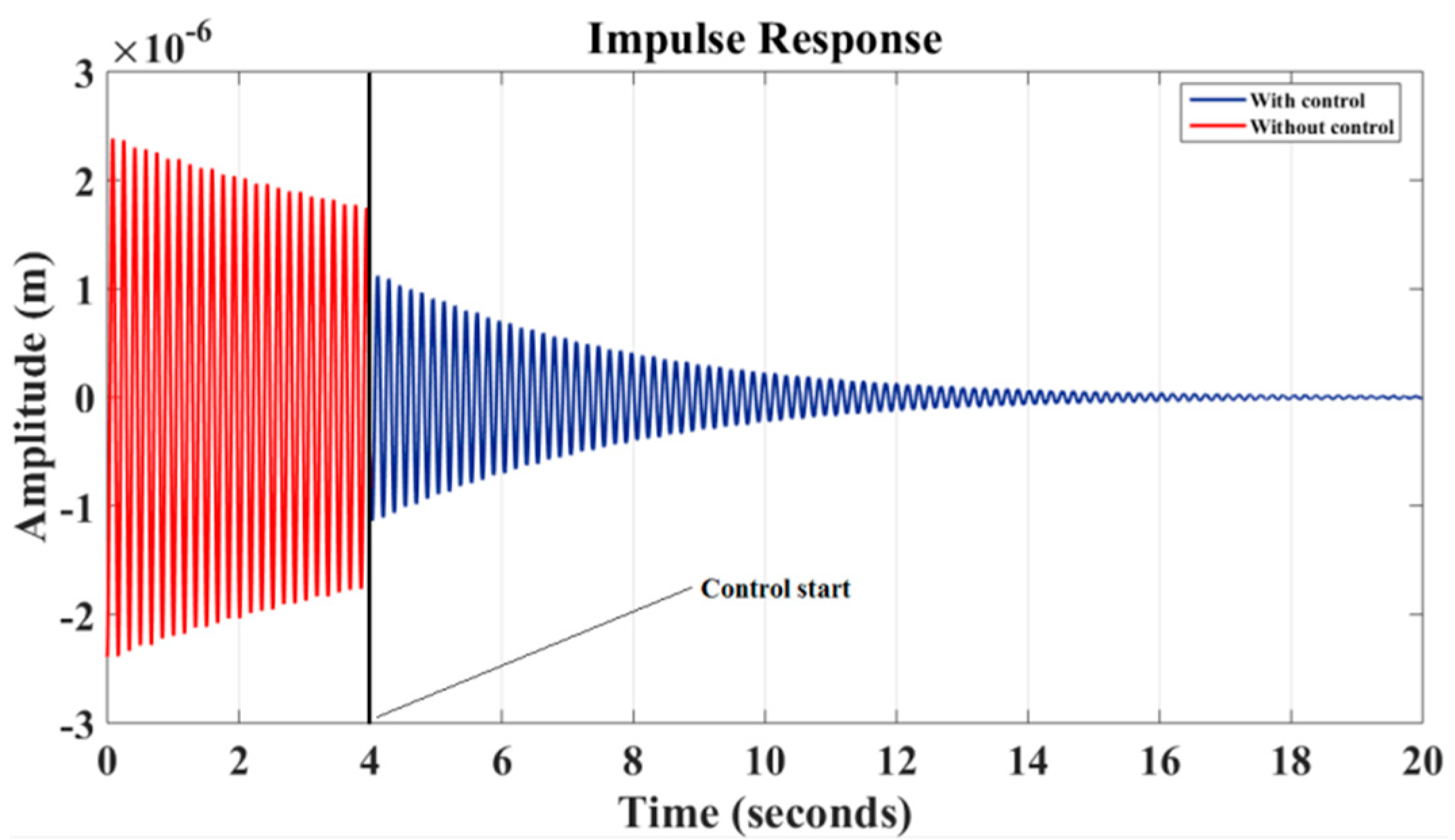
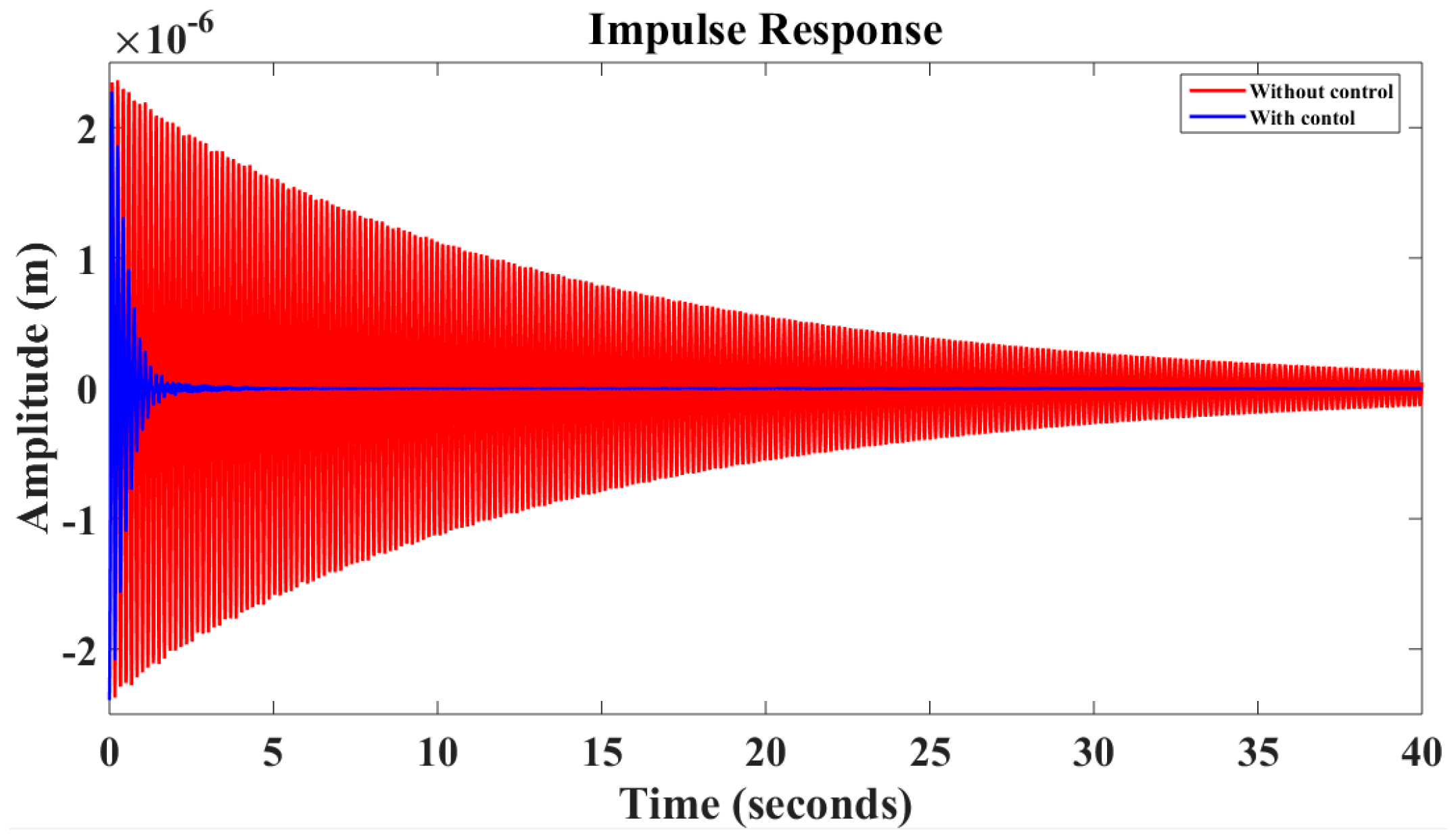
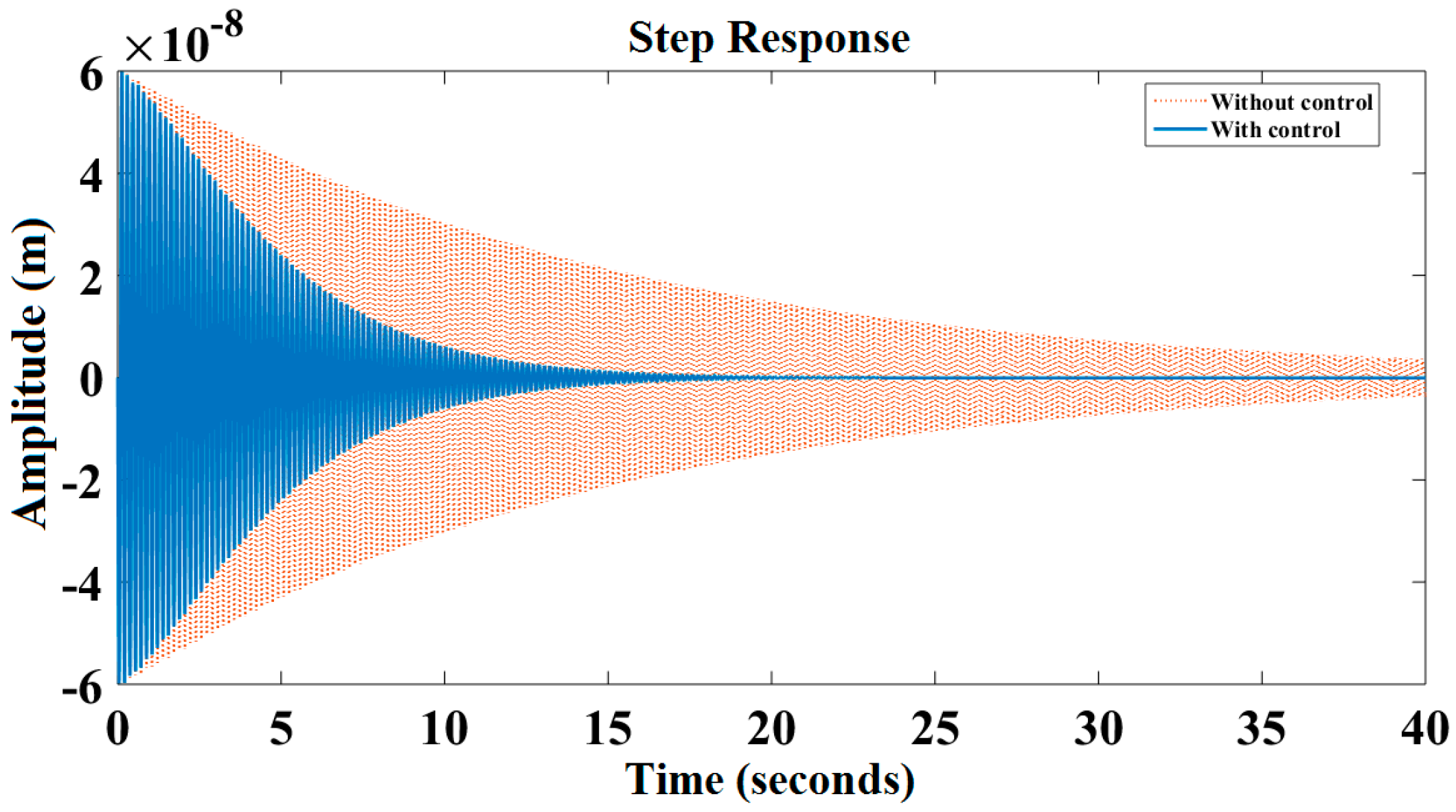
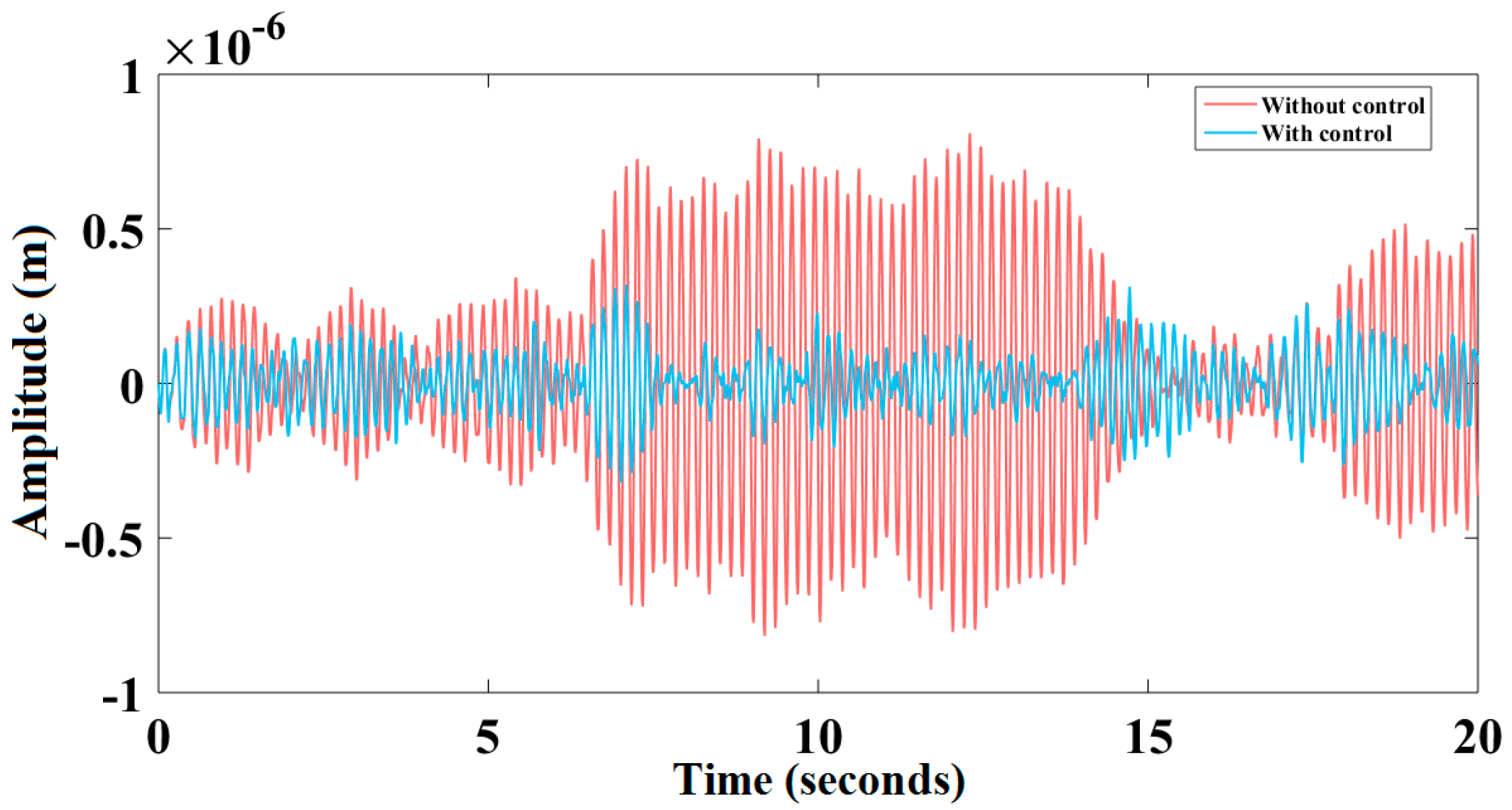
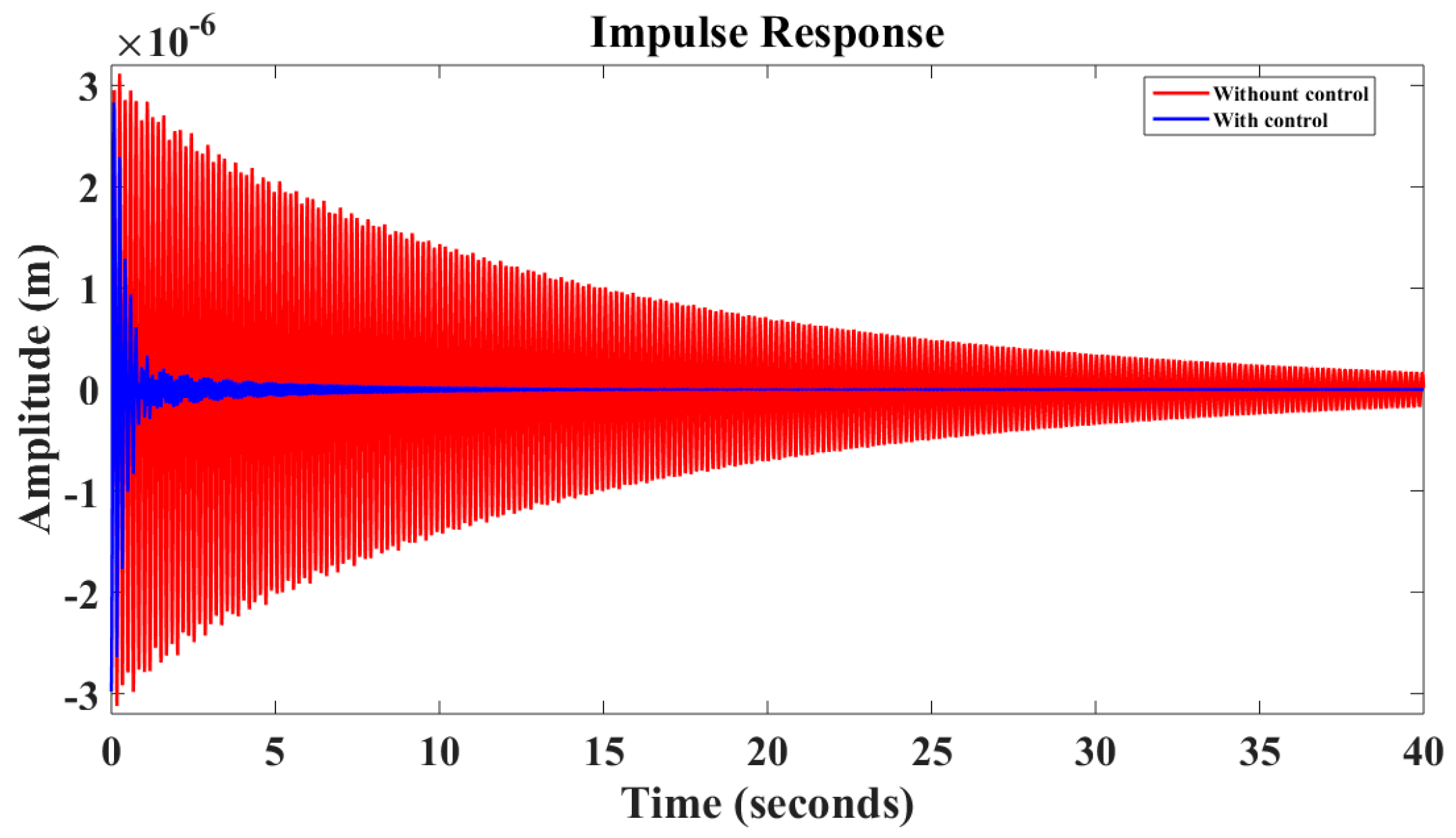
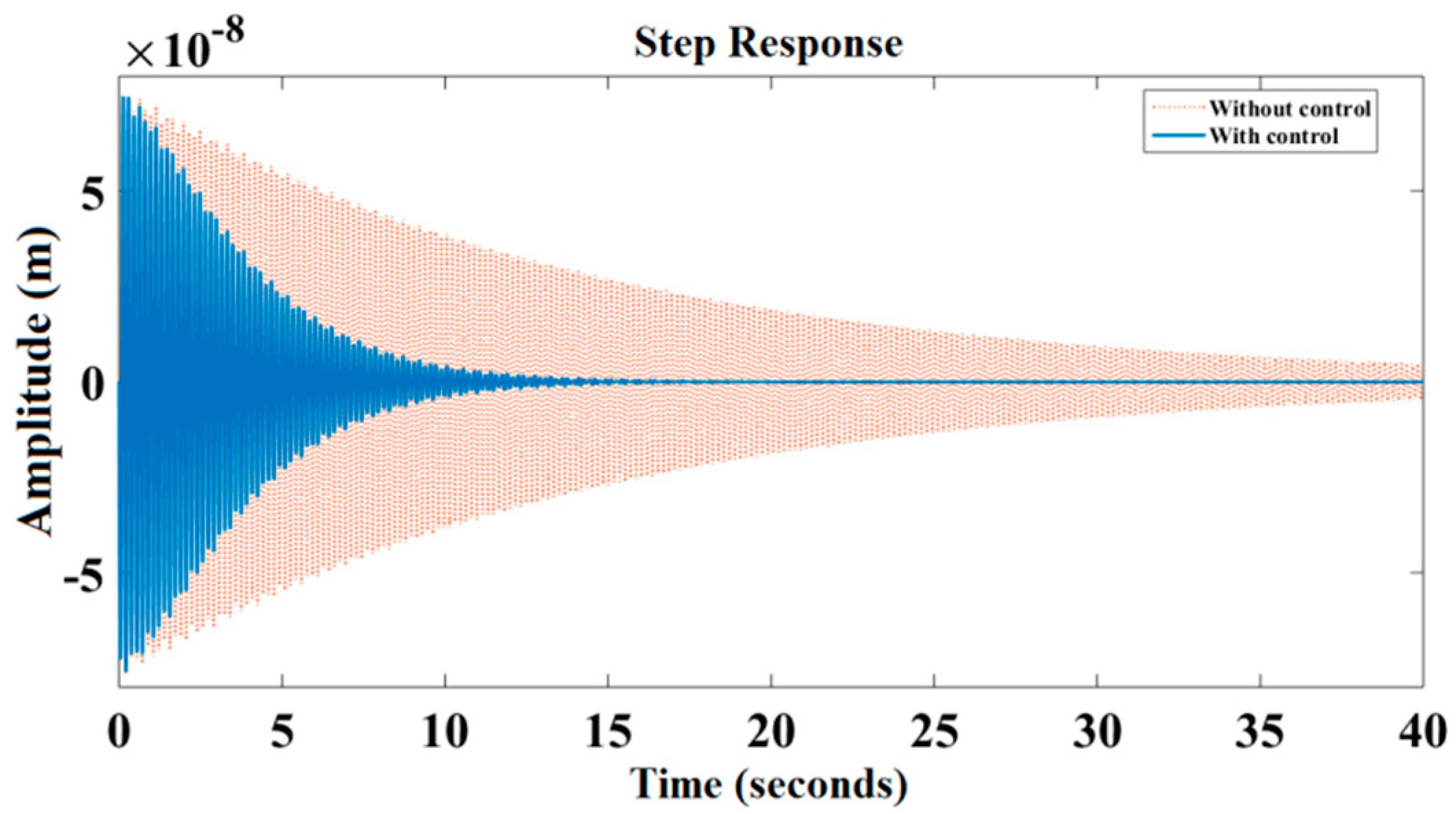
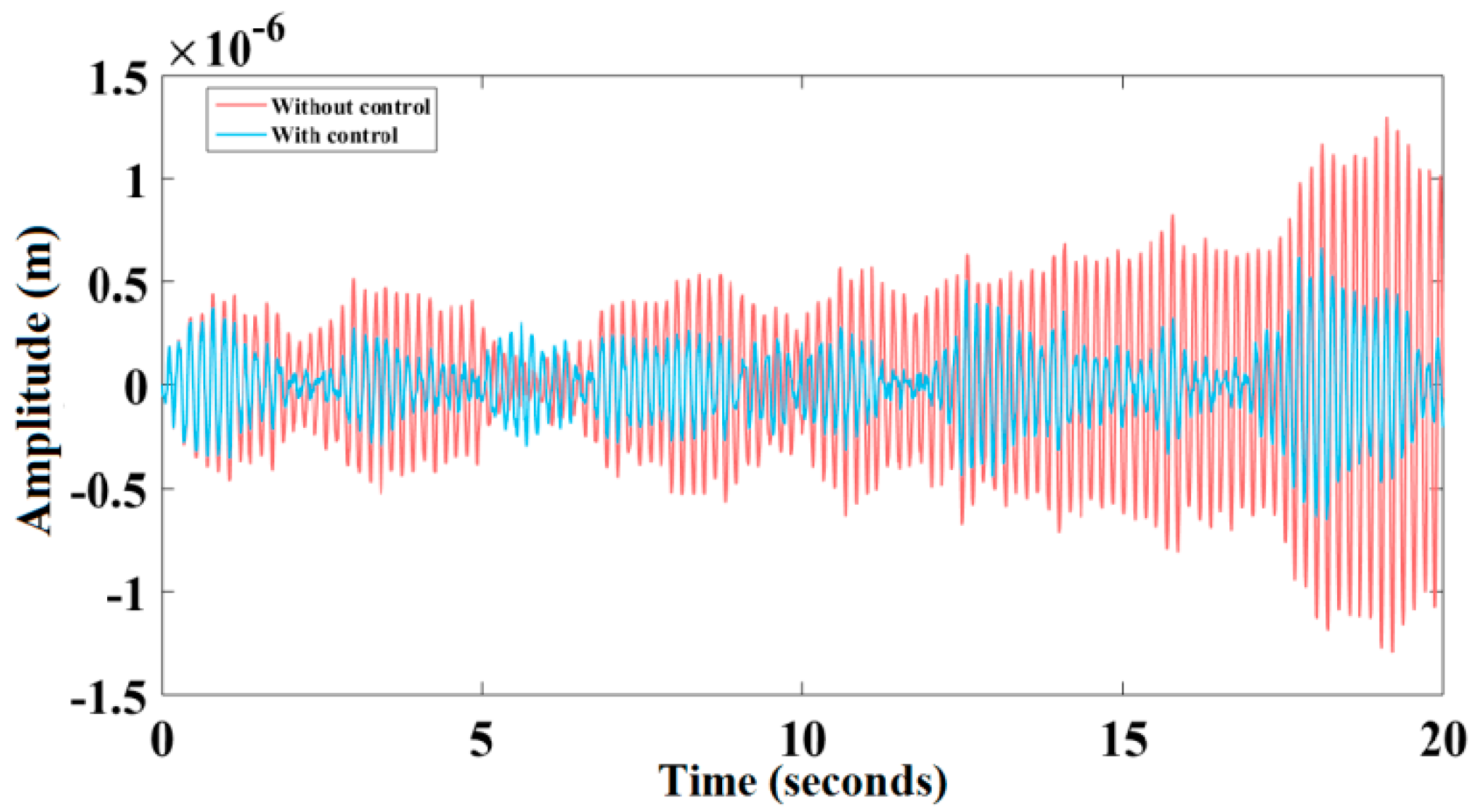
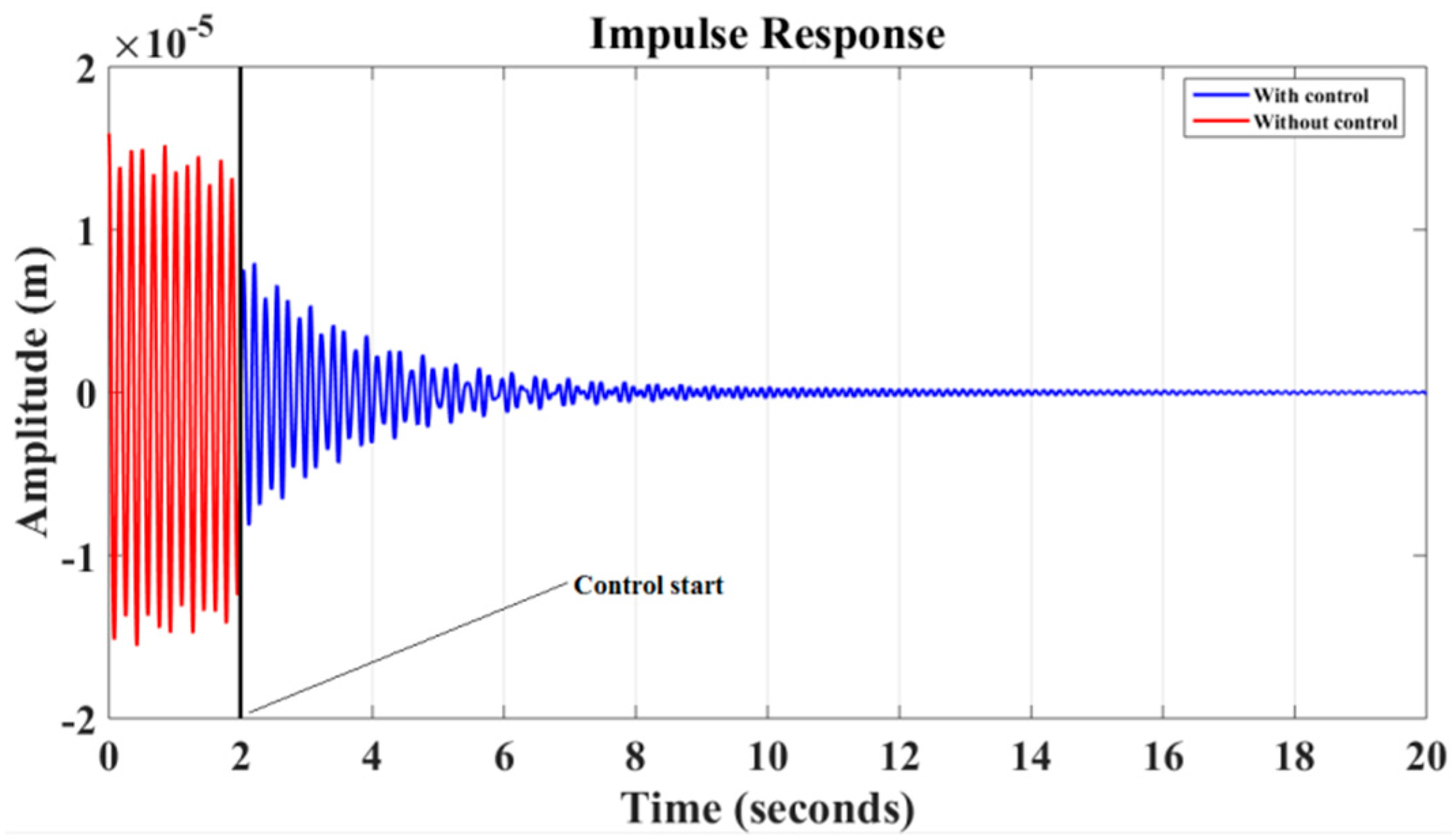
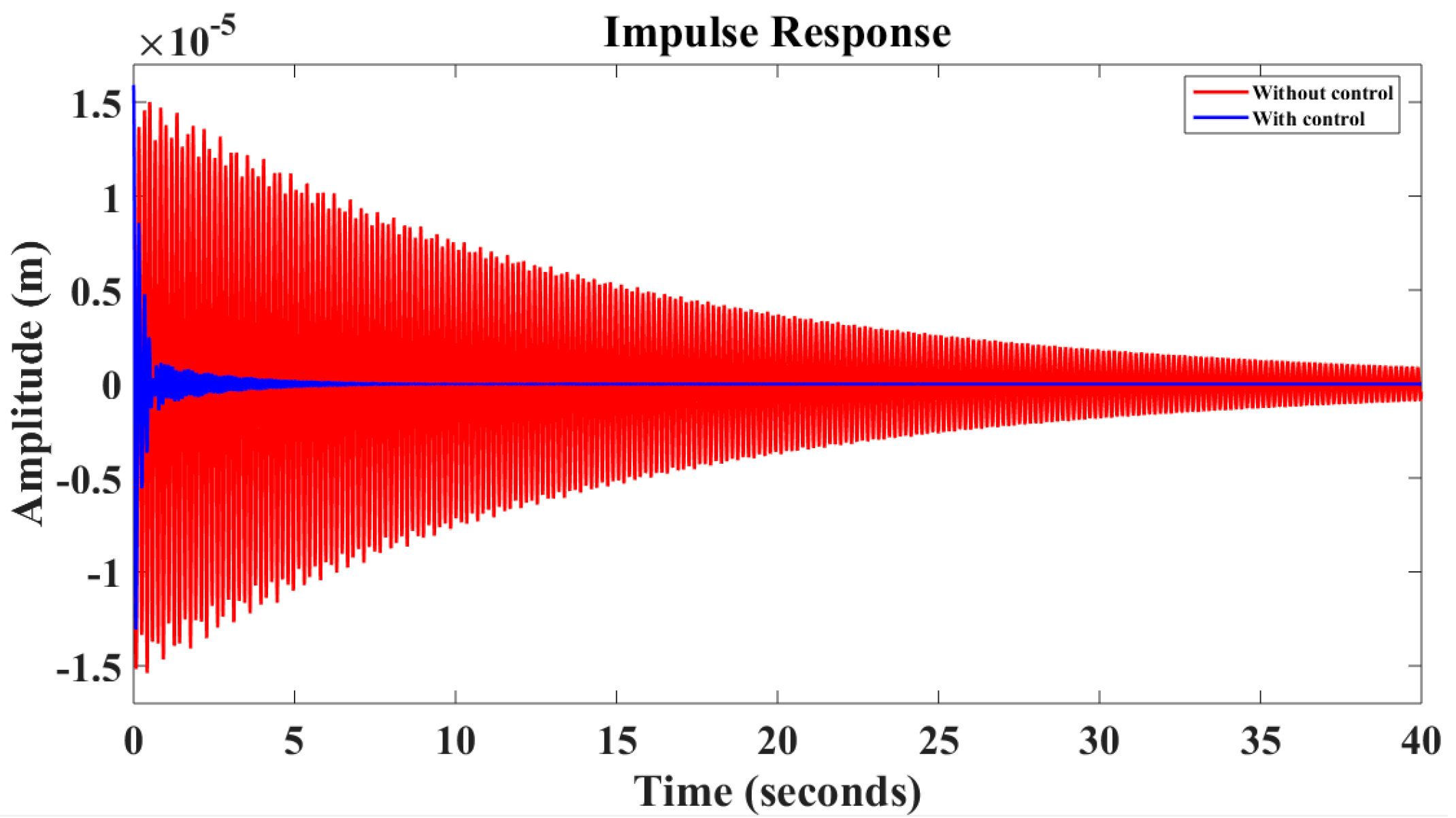
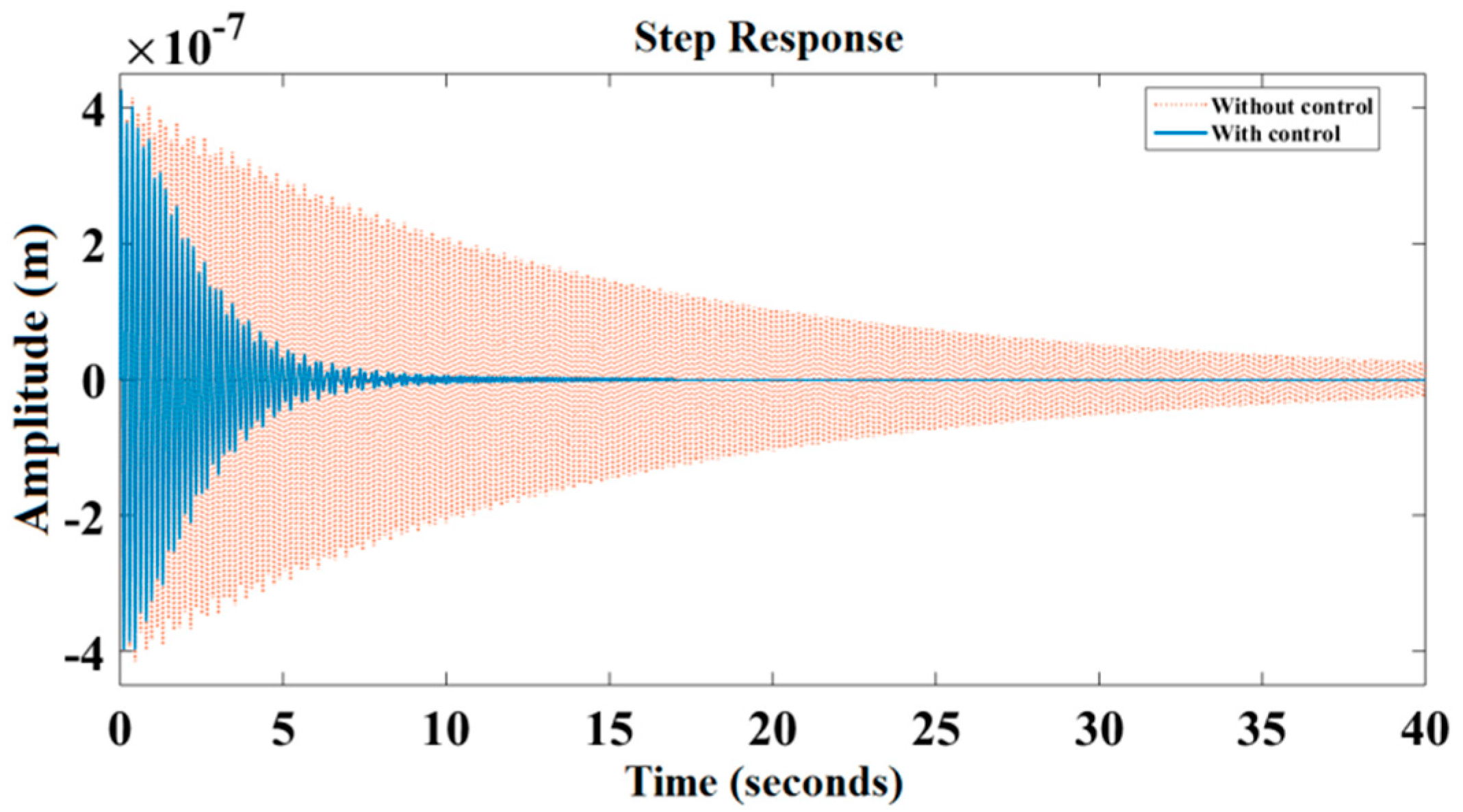
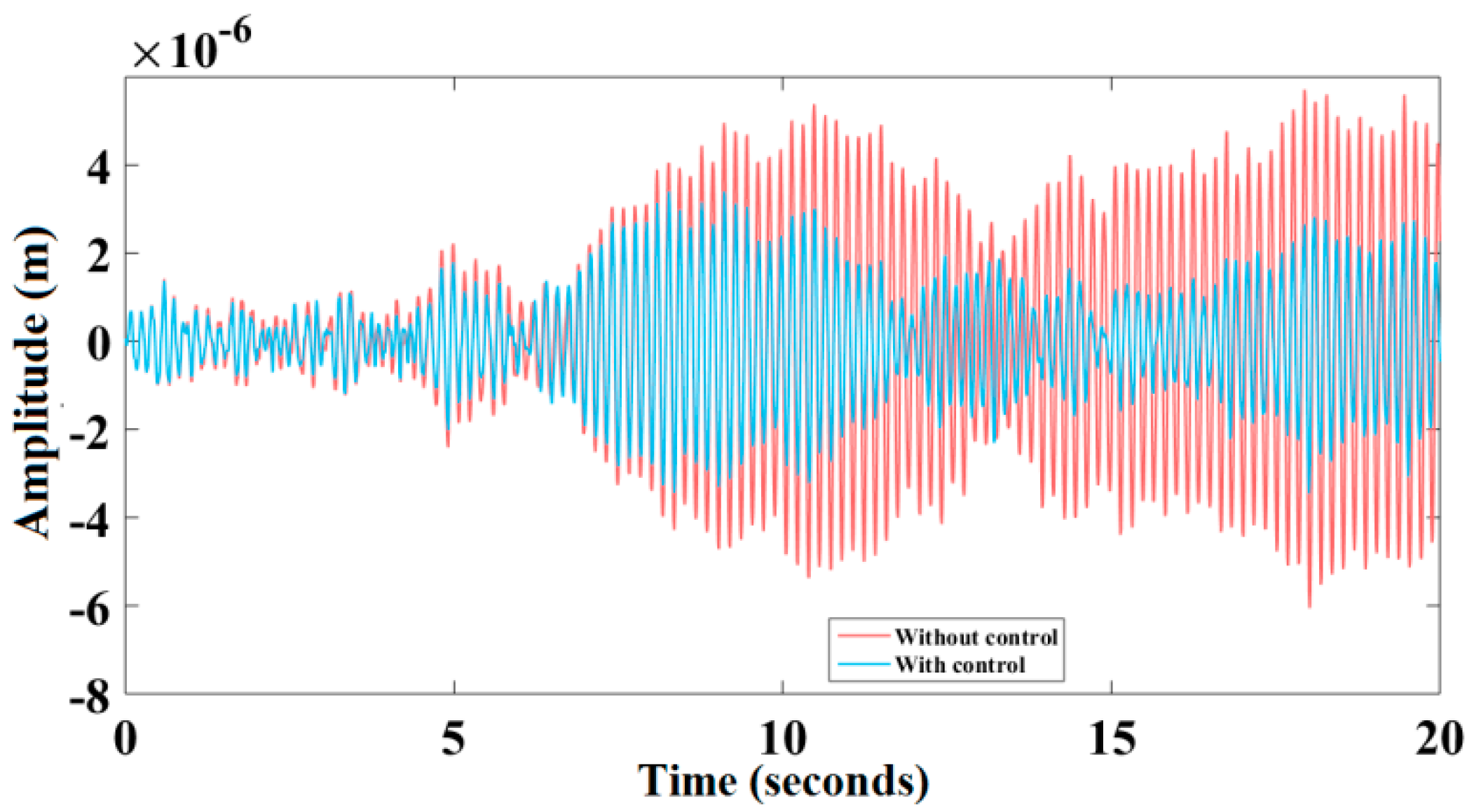
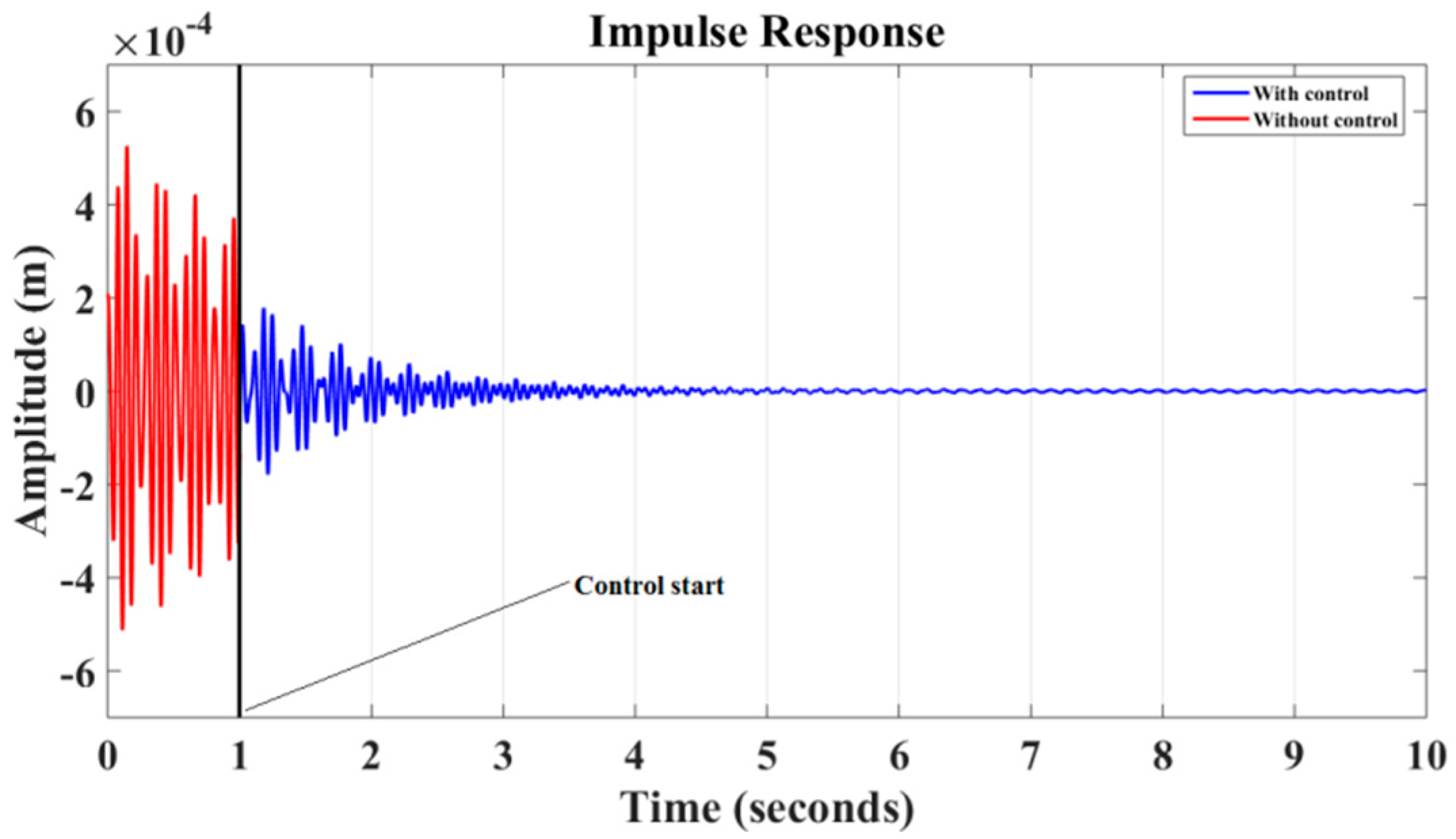
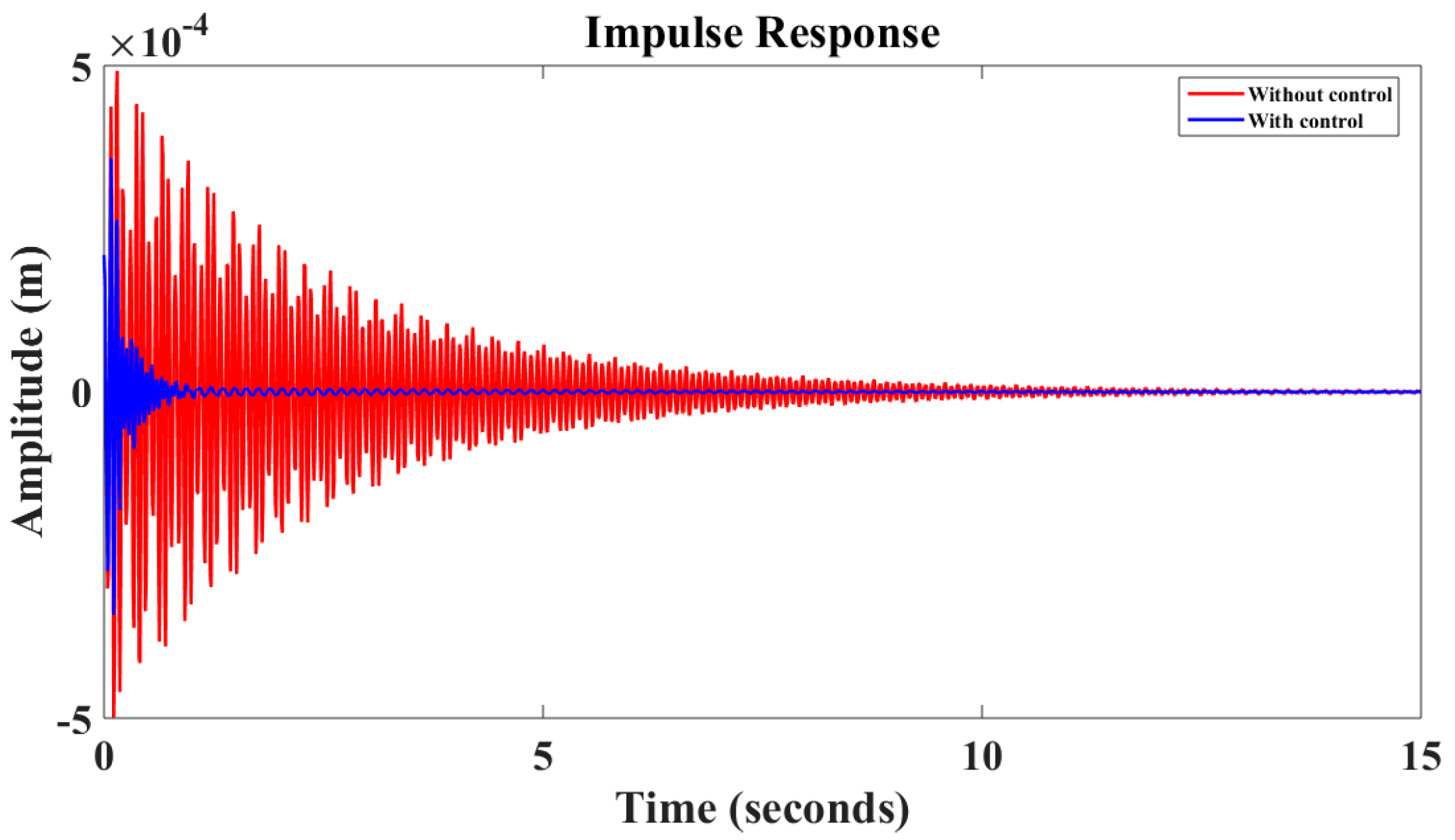
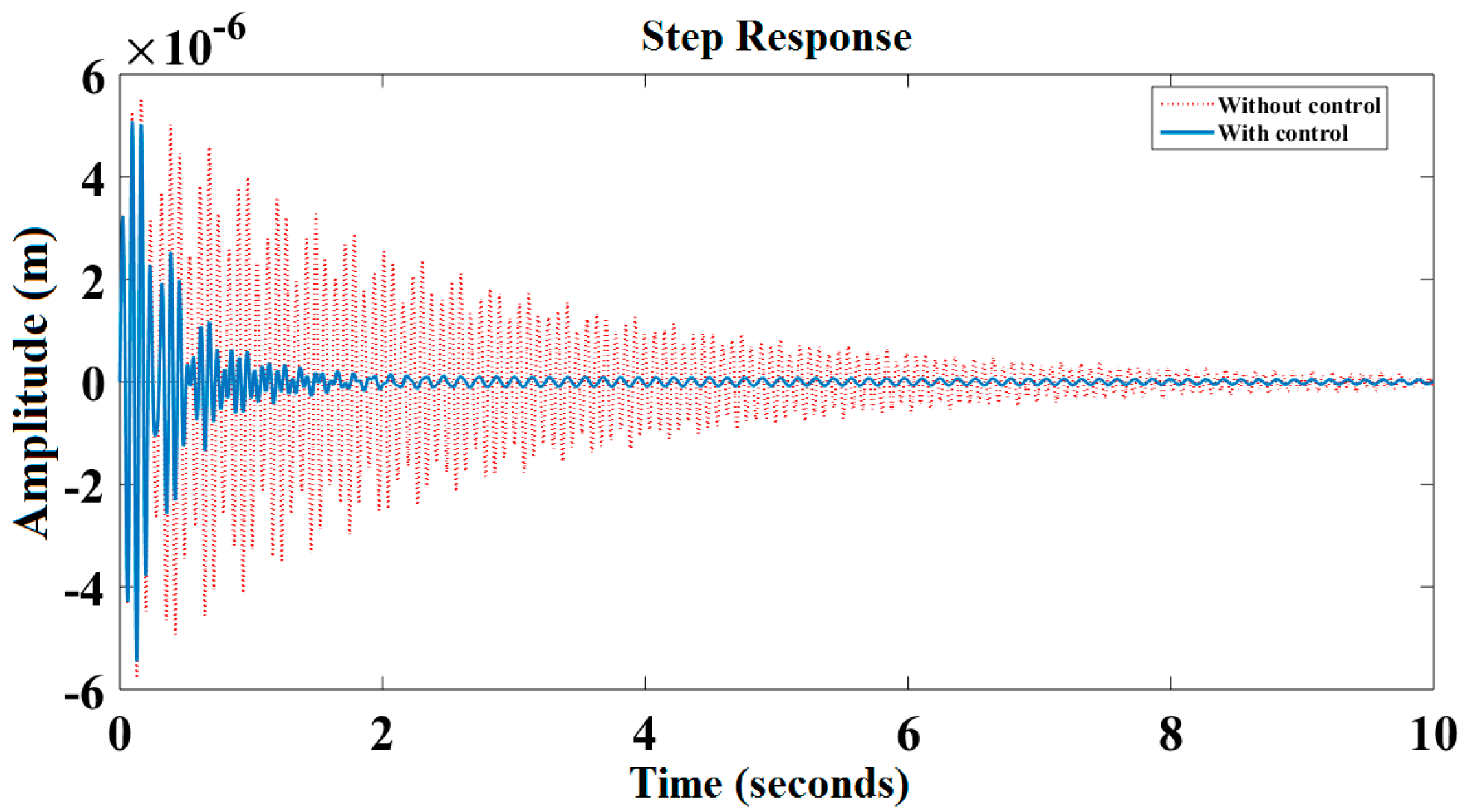
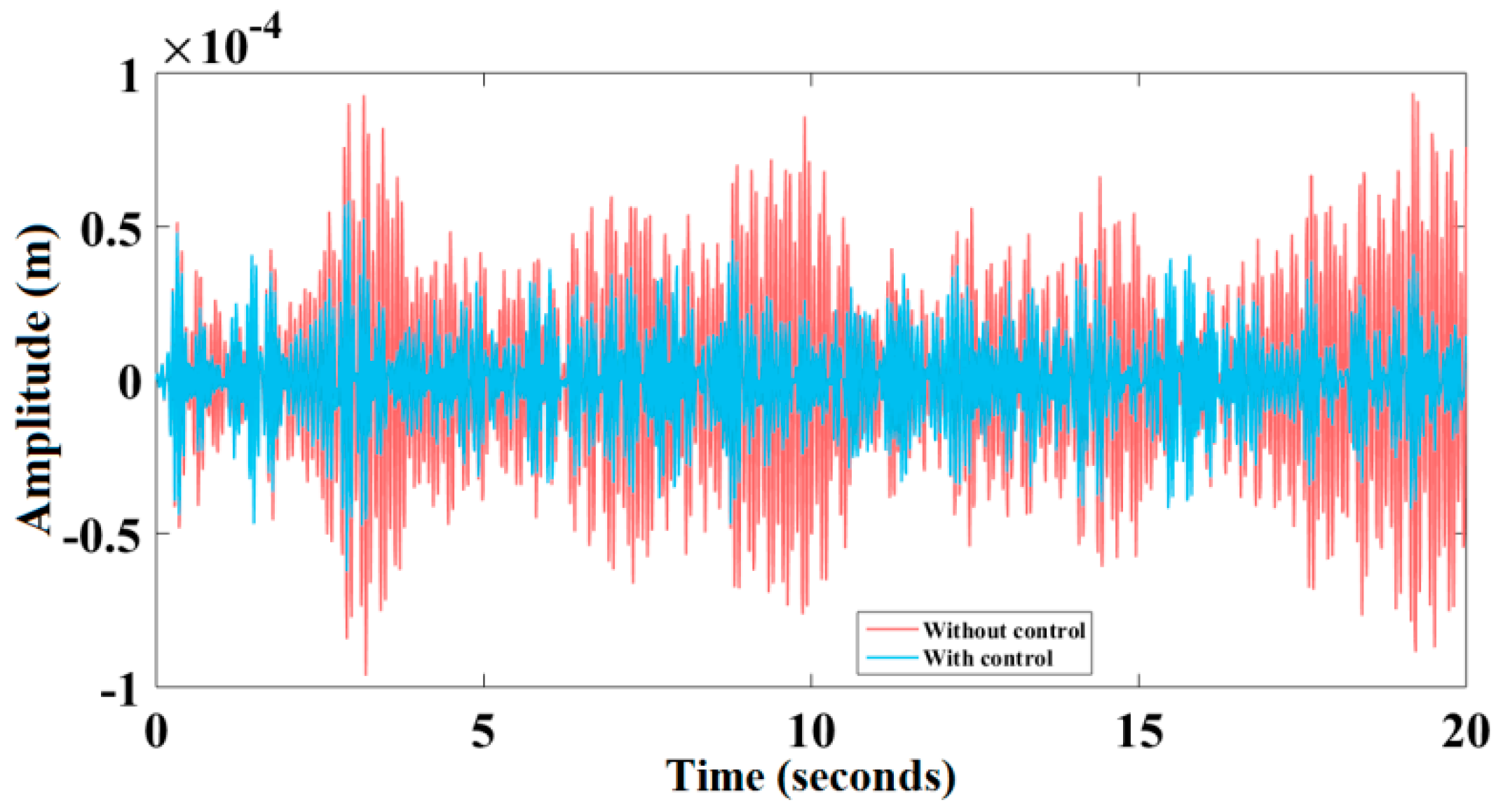
6. Results and Discussion
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Koizumi, M. FGM activities in Japan. Compos. Part B Eng. 1997, 28, 1–4. [Google Scholar] [CrossRef]
- Bharti, I.; Gupta, N.; Gupta, K.M. Novel Applications of Functionally Graded Nano, Optoelectronic and Thermoelectric Materials. Int. J. Mater. Mech. Manuf. 2013, 1, 221–224. [Google Scholar] [CrossRef]
- Miyamoto, Y. Functionally Graded Materials: Design, Processing and Applications; Springer Science Business Media: New York, NY, USA, 1999. [Google Scholar]
- Bao, G.; Cai, H. Delamination cracking in functionally graded coating/metal substrate systems. Acta Mater. 1997, 45, 1055–1066. [Google Scholar] [CrossRef]
- Yongsheng, L.; Xiaoting, H.; Sijie, S.; Xue, L.; Zhixin, Y.; Junyi, S. A Multi-Parameter Perturbation Solution for Functionally Graded Piezoelectric Cantilever Beams under Combined Loads. Materials 2018, 11, 1222. [Google Scholar]
- Tanigawa, Y. Some basic thermo-elastic problems for non homogeneous structural materials. Appl. Mech. Rev. 1995, 48, 287–300. [Google Scholar] [CrossRef]
- Suresh, S.; Mortensen, A. Fundamentals of Functionally Graded Materials; IOM Communications Ltd.: London, UK, 1998. [Google Scholar]
- Beards, C.E. Structural Vibration: Analysis and Damping, 1st ed.; Arnold: London, UK, 1996. [Google Scholar]
- Sanbi, M. Contribution à l’étude de quelques structures mécatroniques: Dynamique, contrôle actif et propagation d’ondes. Ph.D. Thesis, Docteur de l’université de Moulay Ismail, UFR Sciences de l’Ingénieur, Meknes, Morocco, 2010. [Google Scholar]
- Sanbi, M.; Saadani, R.; Sbai, K.; Rahmoune, M. Thermoelastic and pyroelectric couplings effects on dynamics and active control of smart piezolaminated beam modeled by finite element method. Smart Mater. Res. 2014. [Google Scholar] [CrossRef]
- Bendine, K.; Boukhoulda, F.B.; Nouari, M. Active vibration control of functionally graded beams with piezoelectric layers based on higher order shear deformation theory. Earthq. Eng. Vib. 2016, 15, 611–620. [Google Scholar] [CrossRef]
- El Harti, K.; Sanbi, M.; Rahmoune, M.; Saadani, R.; Agounoun, R. Active vibration control of sandwich FGM beam with piezoelectric sensor/actuator. Int. J. Appl. Eng. Res. 2017, 12, 9338–9345. [Google Scholar]
- Panda, R.K.; Nayak, B.; Kumar, S.S. Active vibration control of smart functionally graded beams. In Proceedings of the 12th International Conference on Vibration Problems, ICOVP 2015, Guwahati, India, 14–17 December 2015. [Google Scholar]
- Elshafei, M.A.; Alraiess, F. Modeling and analysis of smart piezoelectric beams using simple higher order shear deformation theory. Smart Mater. Struct. 2013, 22, 035006. [Google Scholar] [CrossRef]
- Ferdek, U.; Kozie, M.S. Simulation of application of FGM piezoelectric actuators for active reduction of beam vibrations. Acta Phys. Polonica A 2013, 123, 1044–1047. [Google Scholar] [CrossRef]
- Bodaghi, M.; Damanpack, A.R.; Aghdam, M.M. Non-linear active control of FG beams in thermal environments subjected to blast loads with integrated FGP sensor/actuator layers. Compos. Struct. 2012, 94, 3612–3623. [Google Scholar] [CrossRef]
- Allahverdizadeh, A.; Mahjoob, M.J.; Eshraghi, I. On the vibration behavior of functionally graded electrorheological sandwich beams. Int. J. Mech. Sci. 2013, 70, 130–139. [Google Scholar] [CrossRef]
- Gharib, A.; Salehi, M.; Fazeli, S. Deflection control of functionally graded material beams with bonded piezoelectric sensors and actuators. Mater. Sci. Eng. A 2008, 498, 110–114. [Google Scholar] [CrossRef]
- Ebrahimi, F.; Hashemi, M. Vibration analysis of non-uniform imperfect functionally graded beams with porosities in thermal environment. J. Mech. 2017. [Google Scholar] [CrossRef]
- Narayanana, S.; Balamurugan, V. Finite element modeling of piezolaminated smart structures for active vibration control with distributed sensors and actuators. J. Sound Vib. 2003, 262, 529–562. [Google Scholar] [CrossRef]
- Kargarnovin, M.H.; Najafizadeh, M.M.; Viliani, N.S. Vibration control of a functionally graded material plate patched with piezoelectric actuators and sensors under a constant electric charge. Smart Mater. Struct. 2007, 16, 1252. [Google Scholar] [CrossRef]
- Priyanka, A.J.; Kamal, M.B. Free and forced vibration control of piezoelectric FGM plate subjected to electro-mechanical loading. Smart Mater. Struct. 2013, 22, 065021. [Google Scholar]
- Rahmoune, M.; Bouachrine, A.; Hamdi-Alaoui, M.A. Dynamics and shape control of vibrating composite plate containing piezoelectric laminas: design of an intelligent structural antifouling system. Ferroelectrics 2004, 304, 55–59. [Google Scholar] [CrossRef]
- Zhu, Y.; Zheng, X.; Li, L. Evaluation of shear piezoelectric coefficient d15 of piezoelectric ceramics by using piezoelectric cantilever beam in dynamic resonance. Ferroelectrics 2017, 520, 202–211. [Google Scholar] [CrossRef]
- Abramovich, H.; Lishvits, A. Free vibrations of non-symmetric cross-ply laminated composite beams. J. Sound Vib. 1994, 179, 597–612. [Google Scholar] [CrossRef]
- Badel, A. Récupération d’énergie et contrôle vibratoire par éléments piézoélectriques suivant une approche non linéaire. Ph.D. Thesis, Docteur de l’université de Savoie, Ecole Doctorale de l’Université, Chambéry, France, 2008. [Google Scholar]
- Ducarne, J. Modélisation et optimisation de dispositifs non-linéaire d’amortissement de structures par systèmes piézoélectriques commutés. Ph.D. Thesis, Docteur de l’université de Paris, LMSSC Cnam, Paris, France, 2009. [Google Scholar]
- Delale, F.; Erdogan, F. The crack problem for a non homogeneous plane ASME. J. Appl. Mech. 1983, 50, 609–614. [Google Scholar] [CrossRef]
- Friedman, Z.; Kosmataka, J.B. An improved two-node Timoshenko beam finite element. Comput. Struct. 1993, 47, 473–481. [Google Scholar] [CrossRef]
- Eisenberger, M.; Abramovich, H. Shape control of non-symmetric piezolaminated composite beams. Comput. Struct. 1977, 38, 565–571. [Google Scholar] [CrossRef]
- Cowper, G.R. The shear coefficient in Timoshenko’s beam theory. ASME J. App. Mech. 1966, 33, 335–340. [Google Scholar] [CrossRef]
- Tessler, A.; Dong, S.B. On a hierarchy of conforming Timoshenko beam elementys. Comput. Struct. 1981, 14, 335–344. [Google Scholar] [CrossRef]
- Gaudenzi, P. Exact higher order solutions for a simple adaptive structures. Int. J. Solids Struct. 1998, 35, 3595–3610. [Google Scholar] [CrossRef]
- Robbins, D.H.; Reddy, J.N. Analysis of a piezo-electrically actuate beams using a layer-wise displacement theory. Comput. Struct. 1991, 41, 265–279. [Google Scholar] [CrossRef]
- Murthy, M.V.V.S.; Roy-Mahapatra, D.; Badrinarayana, K. A refined higher order finite element for asymmetric composite beams. Compos. Struct. 2005, 67, 27–35. [Google Scholar] [CrossRef]
- Xang, Z.; Chen, S.H.; Wanzhi, H. The static shape control for intelligent structures. Finite Elem. Anal. Des. 1997, 26, 303–314. [Google Scholar]
- Aldraihem, O.J.; Wetherhold, T.; Singh, T. Distributed control of laminated beams: Timoshenko vs. Euler Bernouilli theory. J. Intell. Mater. Syst. Struct. 1997, 8, 149–157. [Google Scholar] [CrossRef]
- Anjanappa, M.; Bi, J. Magnetostrictive mini actuators for smart structures applications. Int. J. Smart Mater. Struct. 1994, 3, 383–390. [Google Scholar] [CrossRef]
- Debard, Y. Méthode des éléments finis: Poutre soumise à un effort normal; Mans: Le Mans, France, 2011. [Google Scholar]
- Boyere, E. Modélisation de l’amortissement en dynamique. Clé: R5.05.04: 2011. Available online: https://www.code-aster.org/V2/doc/v10/fr/man_r/r5/r5.05.04.pdf (accessed on 7 September 2018).
- Lou, J.; Liao, J.; Wei, Y.; Yang, Y.; Li, G. Experimental Identification and Vibration Control of a Piezoelectric Flexible Manipulator Using Optimal Multi-Poles Placement Control. Appl. Sci. 2017, 7, 309. [Google Scholar] [CrossRef]

| Physical Properties | FG Material | Material (PZT) Sensor/Actuator |
|---|---|---|
| Length (m) | ||
| Width (m) | ||
| Thickness (m) | ||
| Density (Kg/m3) | ||
| Young’s Modulus (G Pa) | ||
| Poisson’s ratio | ||
| PZT Strain constants (m/V) | ||
| PZT Stress constant (Vm/N) |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
El Harti, K.; Rahmoune, M.; Sanbi, M.; Saadani, R.; Bentaleb, M.; Rahmoune, M. Finite Element Model of Vibration Control for an Exponential Functionally Graded Timoshenko Beam with Distributed Piezoelectric Sensor/Actuator. Actuators 2019, 8, 19. https://doi.org/10.3390/act8010019
El Harti K, Rahmoune M, Sanbi M, Saadani R, Bentaleb M, Rahmoune M. Finite Element Model of Vibration Control for an Exponential Functionally Graded Timoshenko Beam with Distributed Piezoelectric Sensor/Actuator. Actuators. 2019; 8(1):19. https://doi.org/10.3390/act8010019
Chicago/Turabian StyleEl Harti, Khalid, Mohammed Rahmoune, Mustapha Sanbi, Rachid Saadani, Mouhcine Bentaleb, and Miloud Rahmoune. 2019. "Finite Element Model of Vibration Control for an Exponential Functionally Graded Timoshenko Beam with Distributed Piezoelectric Sensor/Actuator" Actuators 8, no. 1: 19. https://doi.org/10.3390/act8010019
APA StyleEl Harti, K., Rahmoune, M., Sanbi, M., Saadani, R., Bentaleb, M., & Rahmoune, M. (2019). Finite Element Model of Vibration Control for an Exponential Functionally Graded Timoshenko Beam with Distributed Piezoelectric Sensor/Actuator. Actuators, 8(1), 19. https://doi.org/10.3390/act8010019




