1. Introduction
Liver cancer is the second leading cause of cancer-related death worldwide [
1]. Surgical resection is the preferred, and most effective, treatment approach for primary and metastatic liver malignancies. Despite the large number of patients affected by these diseases, current treatment options are less than ideal, as 80–90% of patients are not good candidates for surgery [
2], 50% of patients with solid tumors have full resistance to chemotherapy [
2], and liver tissue is more sensitive to external radiation than the tumor itself [
3].
Selective internal radiation therapy (SIRT) is an emerging treatment for liver cancer during which the blood vessels supplying tumors are embolized with radioactive microspheres. These microspheres contain the radioactive isotope yttrium-90 (
90Y) which delivers high-energy, low-penetrating radiation that destroys tumor tissue while limiting adverse effects to surrounding healthy liver tissue [
4]. Currently, SIRT uses a single-lumen microcatheter (1.0 mm diameter) and a manually operated syringe to deliver the
90Y microspheres into the hepatic artery. Recent studies have documented significant increases in patient survival (29.4 months with SIRT and systemic chemotherapy vs. 12.8 months with chemotherapy alone [
5]). Despite the documented advantages of SIRT, the inability to directly target tumor sites has limited its widespread adoption. The tortuous and patient-variable arterial anatomy limits the direct targeting of tumors, causing damage to healthy liver tissue and other organs via ischemia or radiation [
6].
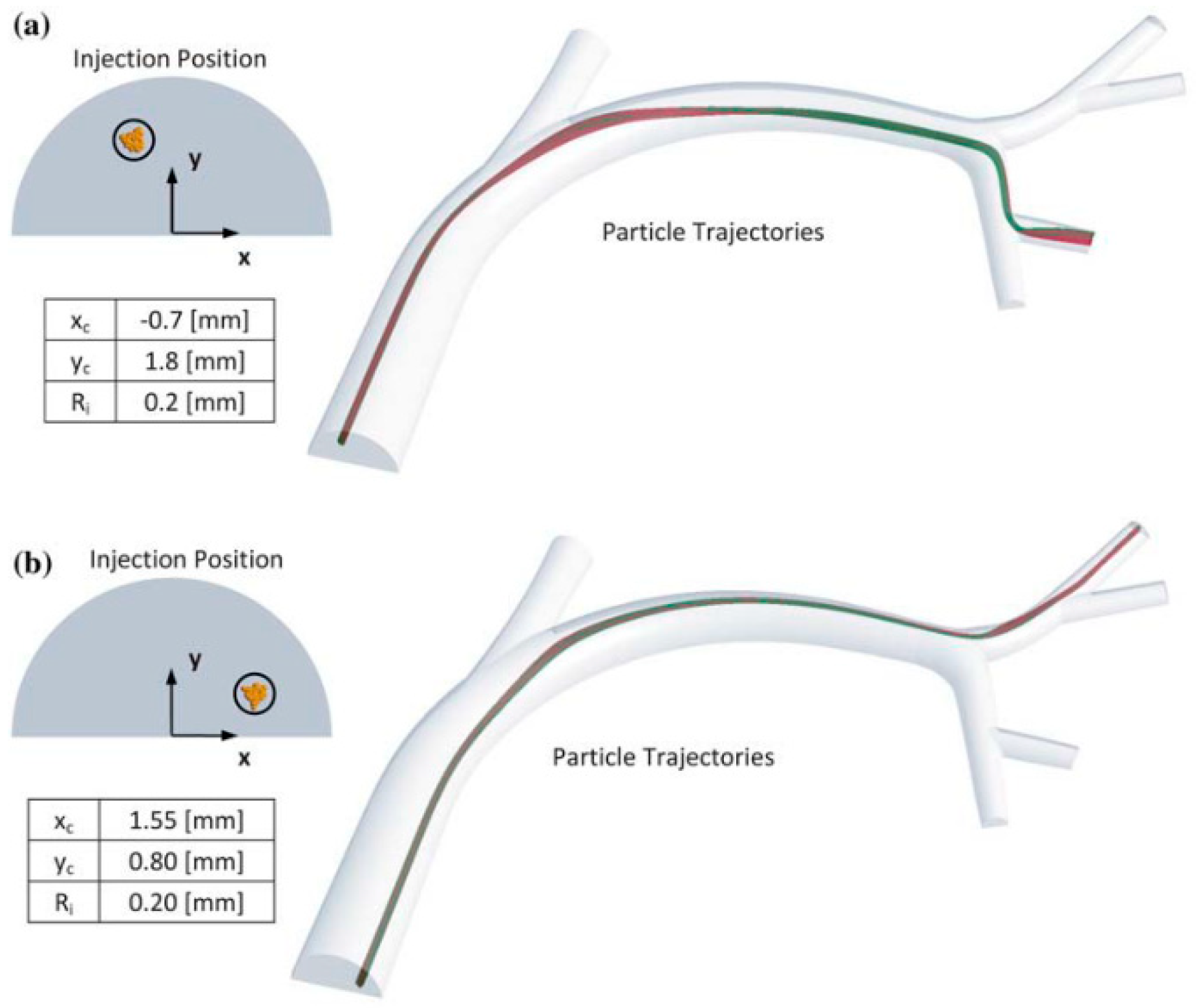
Computational fluid dynamic (CFD) simulations have shown that precise tumor targeting can be achieved by controlling the catheter tip location within the cross-section of the common hepatic artery (CHA) (mean diameter 6.3 ± 0.9 mm) [
7], as shown in
Figure 1. This finding has been validated experimentally by Richards et al. [
6], who concluded that the development of an actuated microcatheter is necessary for direct tumor targeting to be realized. Therefore, to position a microcatheter anywhere within the cross section of the CHA, a miniature actuator needs to be developed that can produce a stroke of at least 7 mm with minimal disruption to the blood flow around the catheter.
Because shape memory alloys (SMAs) exhibit high energy densities, they are attractive options for microscale actuation [
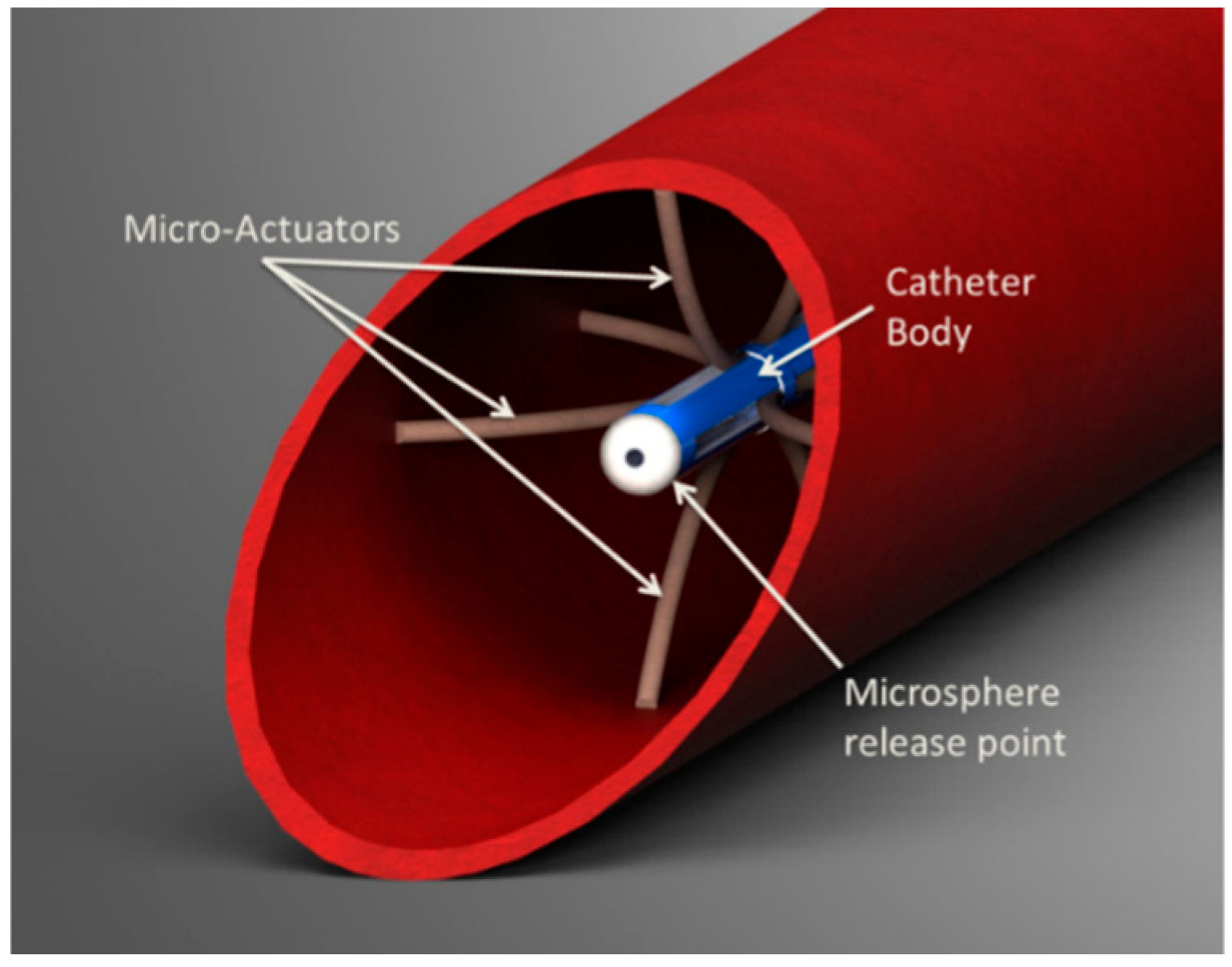
8]. One actuator option consists of shape-set SMA tendons embedded within an elastic structure to generate large bending moments. The elastic structure of this “flexural actuator” produces a stress-induced martensitic phase transformation in the SMA, which can be recovered by Joule heating. While flexural actuators can also be designed by offsetting the SMA from the neutral axis, this offset increases the diameter of the actuator, making it less suitable for size-critical applications. One proposed active catheter concept, shown in
Figure 2, uses eight shape-set flexural actuators arranged radially. With this configuration, the microcatheter’s release point within the cross section of the CHA could be precisely regulated while keeping the catheter parallel with the surrounding blood flow.
In this paper, we build on our previous research [
9] to present a design optimization strategy for shape-set flexural actuators based on the homogenized energy framework [
10,
11]. Previous research on flexural actuators has focused on modeling and understanding the influences of flexible beam composition. Lagoudas, et al. successfully modeled a flexible rod with a single embedded off-neutral axis SMA fiber [
12]. Wang, et al. presented numerical simulations and an experimental validation of a similar actuator composed of a flexible inner cylindrical beam, a SMA tendon, and an outer elastic cylindrical beam [
12]. These designs, however, are difficult to miniaturize because the offset SMA increases the diameter of the actuator and introduces complexity into the manufacturing process.
Baz, et al. modeled shape-set SMA strips embedded on the neutral plane in a fiberglass beam [
13]. The model showed good correlation with experimental data, proving that shape-setting SMA is a viable way to control the shape of a flexural actuator. However, the model did not take into account stress non-linearities across the cross-section of the SMA. Ryu, et al. [
14] investigated the relationship between composite beam stiffness and bending performance.
The remainder of this paper is organized as follows. The flexural actuator system model is presented first. Next, the experimental setup is presented. The SMA model parameters are then estimated using a single-objective genetic algorithm. A multi-objective genetic algorithm is utilized to optimize actuator design parameters. Finally, modeled and experimental data are compared.
2. System Model
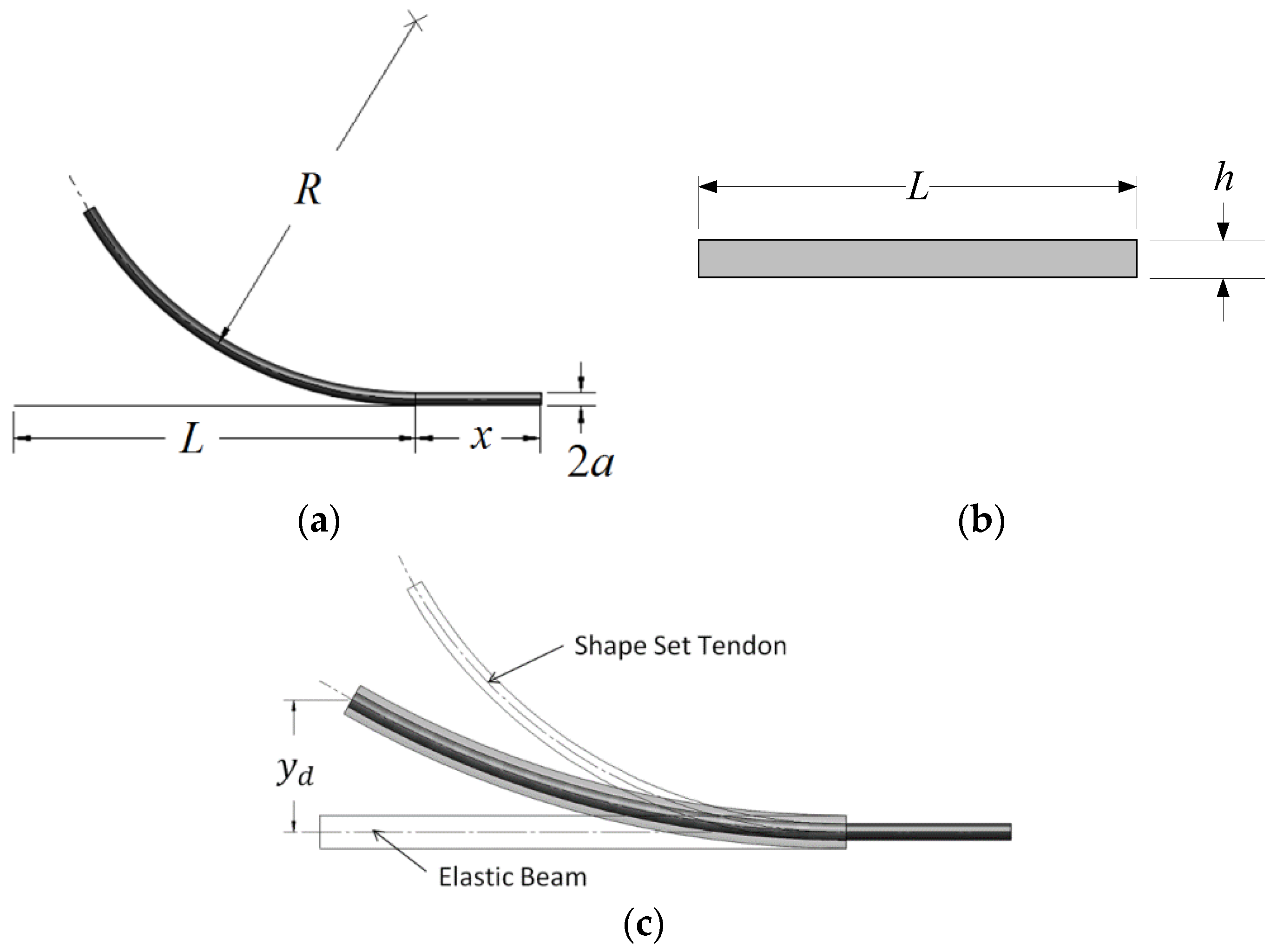
Each flexural actuator design consists of two components: a curved SMA tendon embedded within a straight elastic sleeve. The SMA tendon (diameter
a, straight length
L, and connection length
x as in
Figure 3a) is shape-set (or thermally trained) to a particular curvature
κ0, where
and
R is the radius of the curvature, shown in
Figure 3a. The SMA tendon is embedded within a rectangular elastic sleeve (height
h, width
w, and length
L, as in
Figure 3b) which produces a strain-induced phase transition to detwinned martensite, resulting in a reduced deactivated equilibrium curvature
κd (
Figure 3c). As the tendon is heated to temperatures above the austenitic finish temperature
Af, the material undergoes a phase transformation to austenite and recovers some of this strain, establishing a larger activated equilibrium curvature
κa, such that
κd <
κa <
κ0.
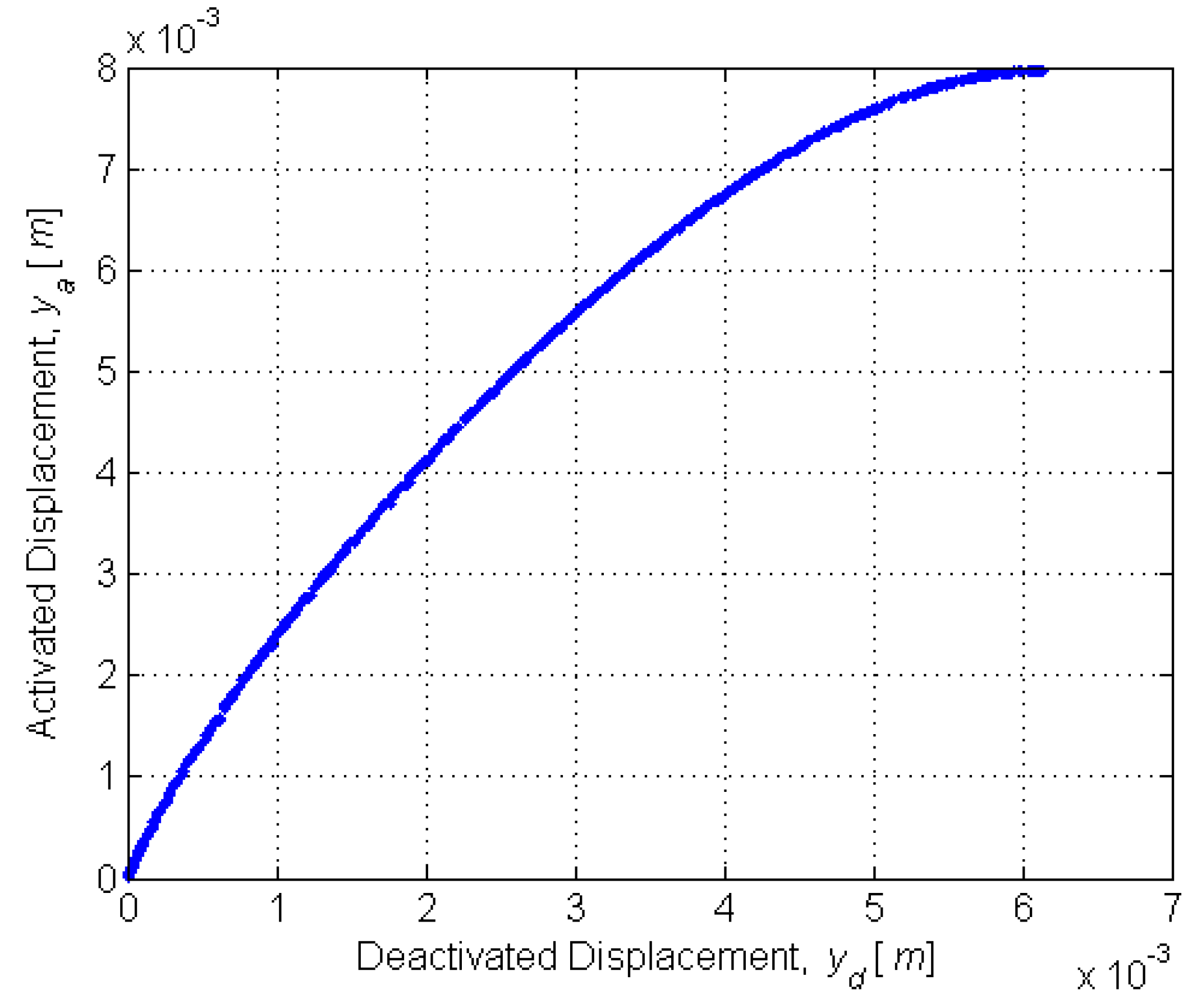
To accurately model the deactivated and activated displacements, the equilibrium curvature must be found for each SMA state. Curvature is related to tip displacement by
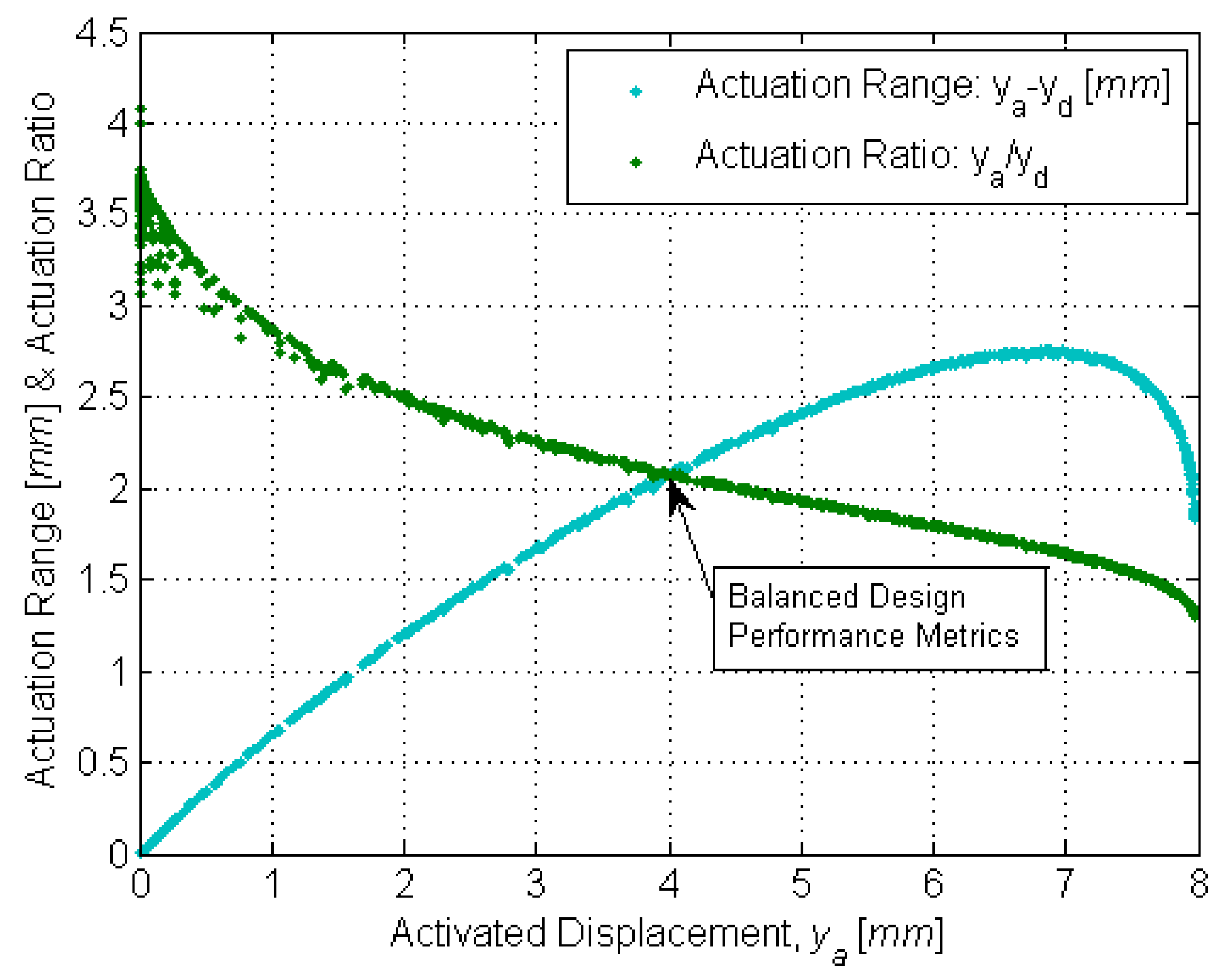
To enable precise catheter navigation and positioning, the deactivated displacement
yd must be minimized while the activated displacement
ya must be maximized (
Figure 4).
2.1. Homogenized Energy Model of SMA Flexural Actuators
The homogenized energy model (HEM) is used to describe the nonlinear hysteretic relationships between stress, strain, and temperature [
10]. The HEM is a macroscopic model that incorporates material inhomogeneities and interaction effects. In [
10], the macroscopic strain is modeled as a function of applied stress. Here, we invert the relationship to obtain the macroscopic stress
where the local stress
depends on the SMA phase fractions: austenite
xA, martensite plus
xM+, and martensite minus
xM-. The relative stress
σR and interaction stress
σI are assumed to be manifestations of underlying densities that affect the equilibrium phase fractions. In Equation (4),
EA is the austenitic elastic modulus,
EM is the martensitic elastic modulus, and
εT is the maximum recoverable strain.
2.2. Equilibrium Equations
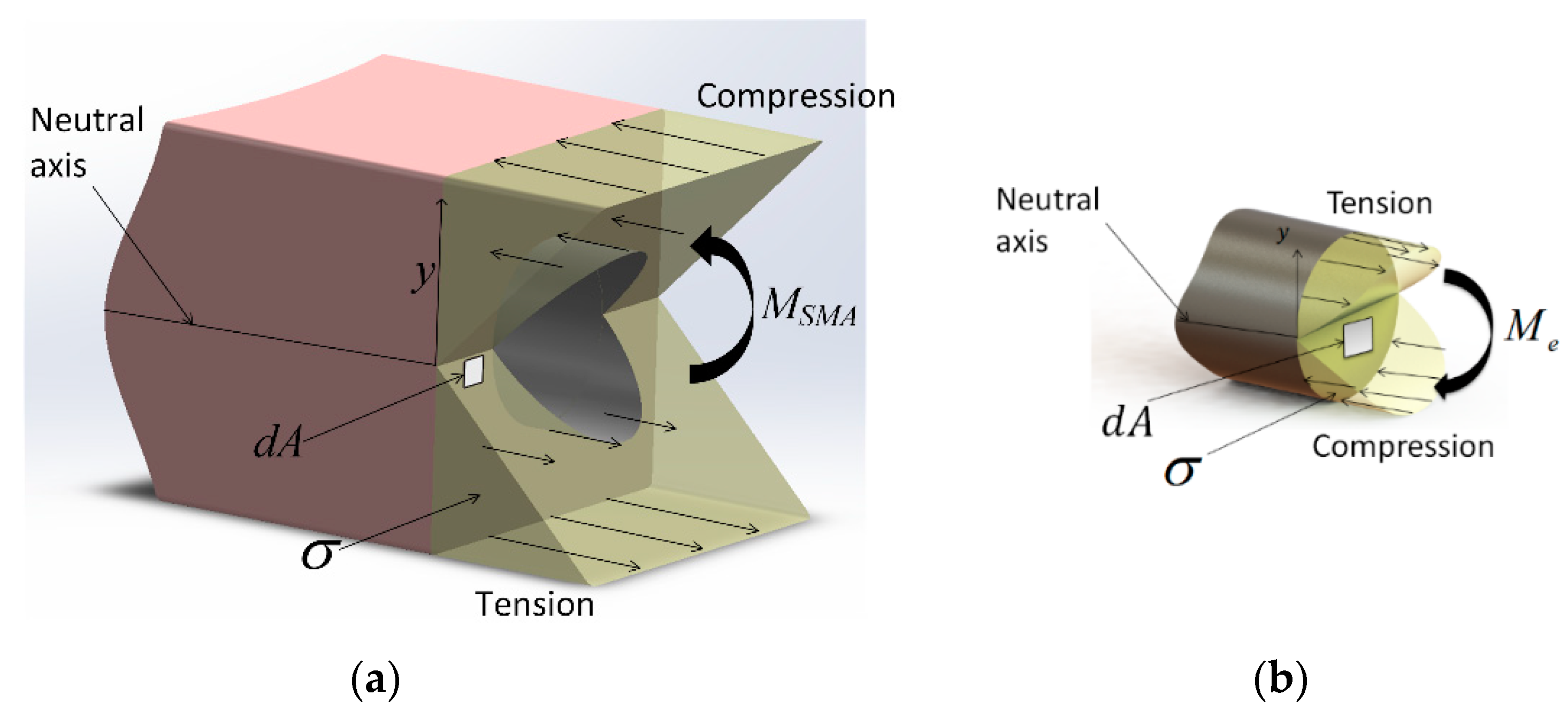
At equilibrium, the composite actuator’s internal forces and moments must sum to zero. Neglecting gravity and external forces, the actuator’s equilibrium position is solely determined by the moment balance between the SMA tendon and the elastic sleeve (
Figure 5a). The elastic moment is given by
where
E is the sleeve’s elastic (Young’s) modulus,
I is its area moment of inertia, and
κ is its curvature. The SMA moment is given by
where
dA is the differential area of the tendon cross-section, as shown in
Figure 5b. Note that the stress depends non-linearly on strain
ε and temperature
T.
We assume that strain varies linearly over the cross-sectional area according to
Therefore, at the initial (shape-set) curvature
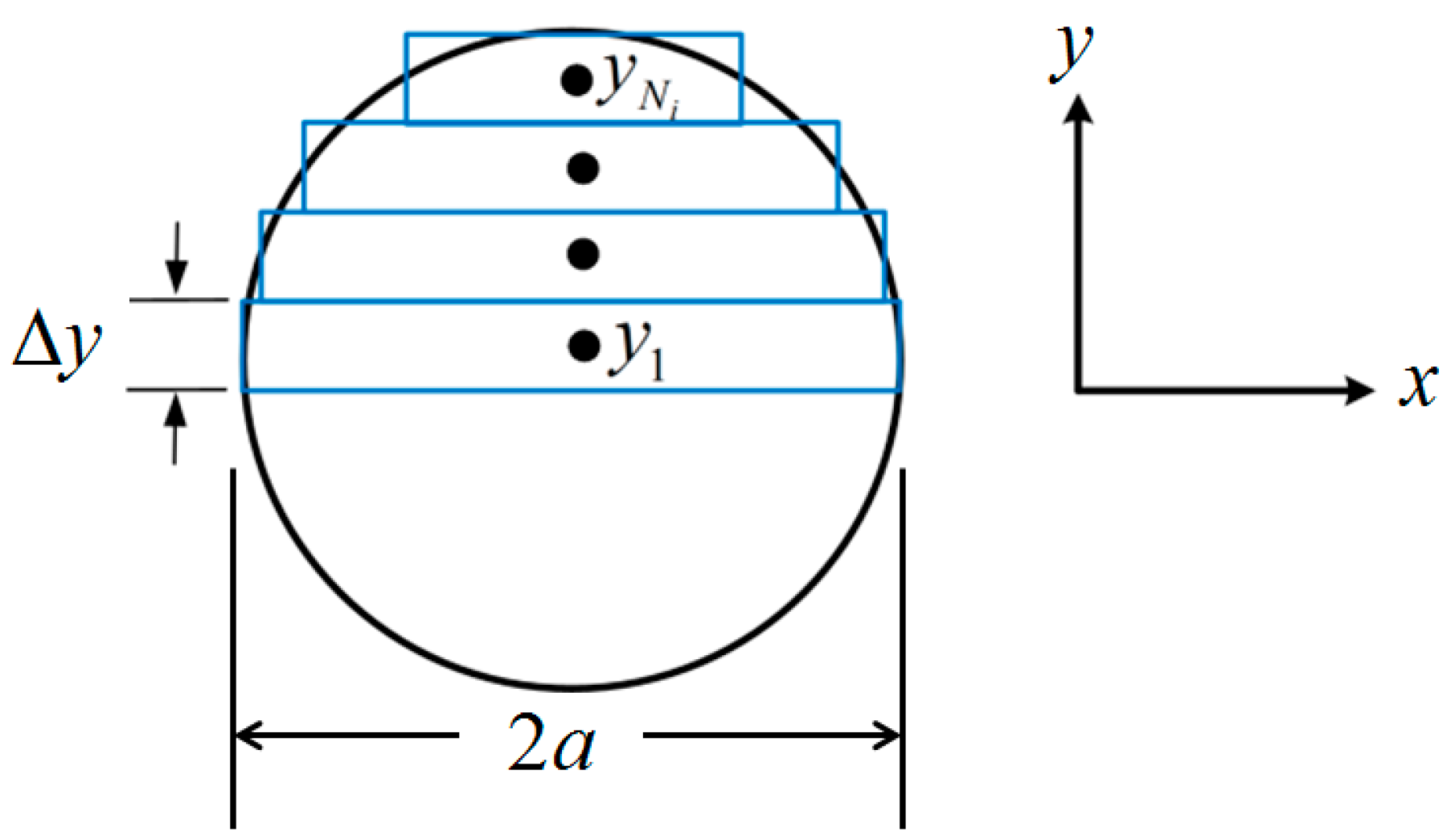
κ0, the SMA has zero strain over its cross-sectional area.The moment integral (6) is discretized using rectangular elements [
15], as shown in
Figure 6. Assuming the stress distribution is symmetric about the neutral axis, this discretization yields
where
a is the SMA tendon radius,
yi is the midpoint of the
rectangle, and
is the width of the rectangle.
The equilibrium deactivated curvature minimizes
where
T∞ is the ambient temperature. Equation (9) can be solved using a variety of nonlinear optimization algorithms; here, we employ the golden section search method [
16]. After finding the deactivated curvature (and associated equilibrium phase fractions), the equilibrium activated curvature minimizes
where
Tss is the SMA’s activated steady-state temperature.
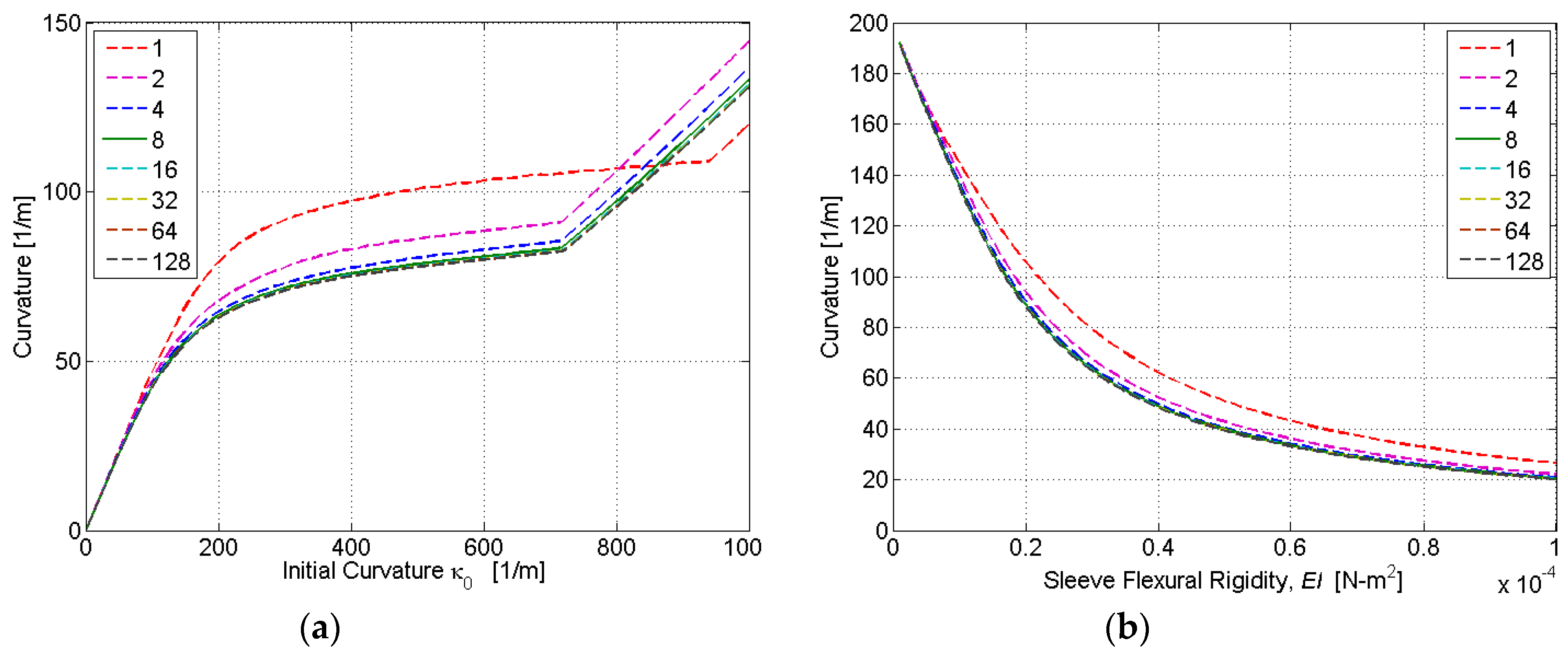
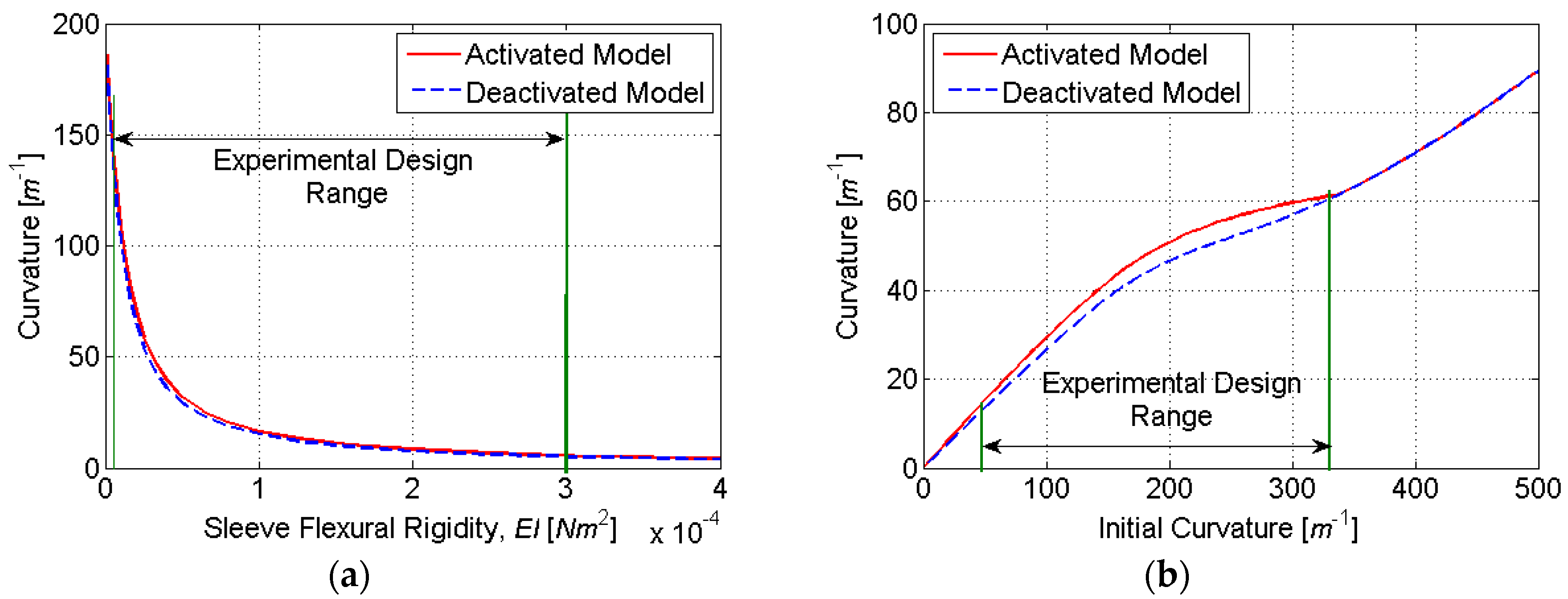
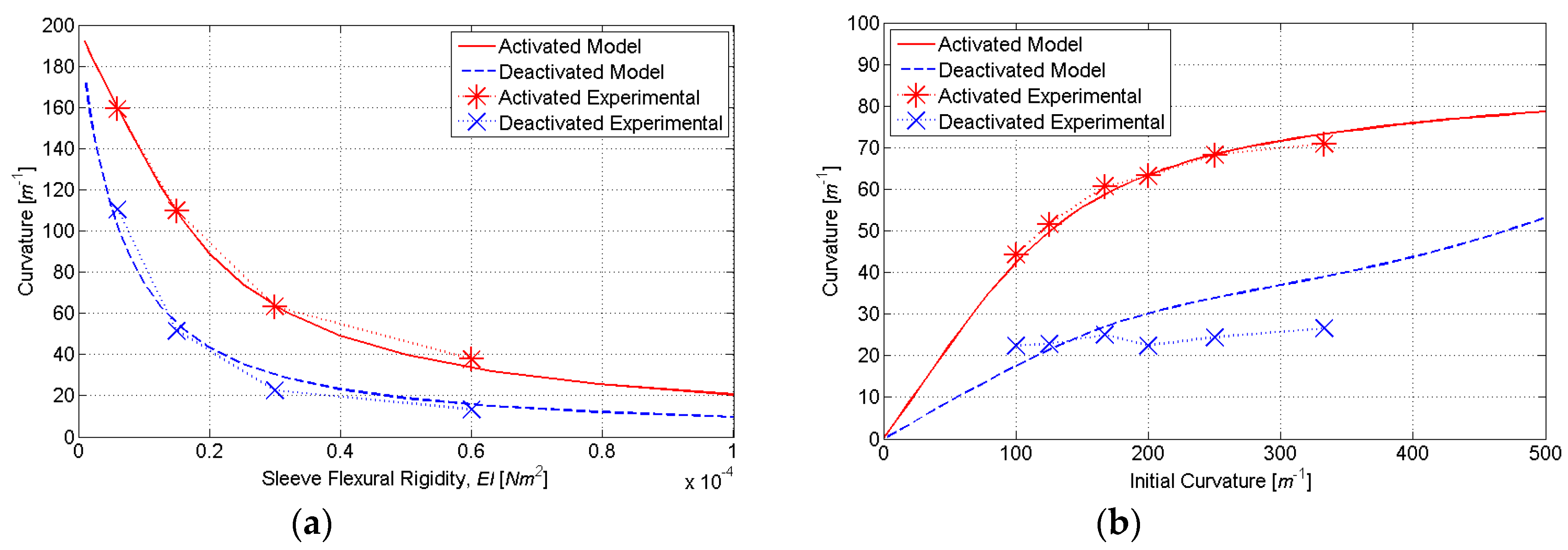
To determine the ideal number of discretization layers, simulations were conducted for a varying initial curvature
κ0 and sleeve flexural rigidity
EI. The nonlinear relationship between the initial and final curvature in
Figure 7 is due to the nonlinear stress–strain characteristics of SMA, which are included in our HEM model. At very low initial strains, the SMA is in its austenite phase, and the stress–strain relationship is relatively linear. This characteristic is evident in
Figure 7a for initial curvatures up to approximately 100 m
−1. At larger strains, the austenite to martensite transformation causes a plateauing of the stress–strain relationship. This characteristic is evident in
Figure 7a for initial curvatures between approximately 100 and 700 m
−1. When the phase transformation is complete (to fully detwinned martensite), a linear stress–strain relationship resumes. This characteristic is evident in
Figure 7a for initial curvatures above approximately 700 m
−1. As shown in
Figure 7, the accuracy of computed actuator curvature improves with the number of discretization layers (
N). However, because computational time is directly proportional to
N, there exists a tradeoff between model accuracy and computational time. Based on the simulation results,
N = 8 was found to adequately balance this tradeoff, as it produced curvature estimates within 2% of the full-order model (
N = 128) with only 6.25% of the computational burden.
3. Experimental Setup
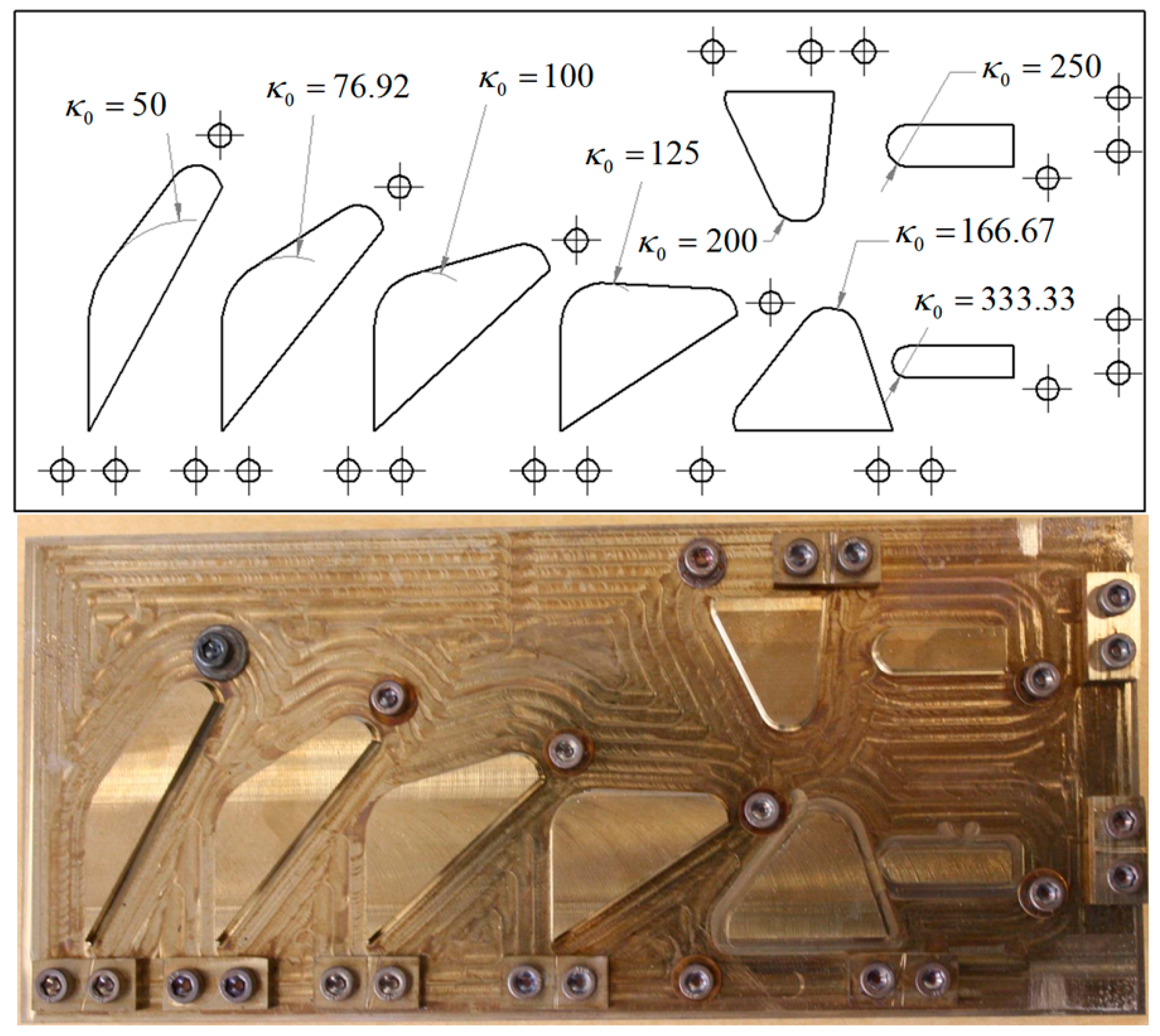
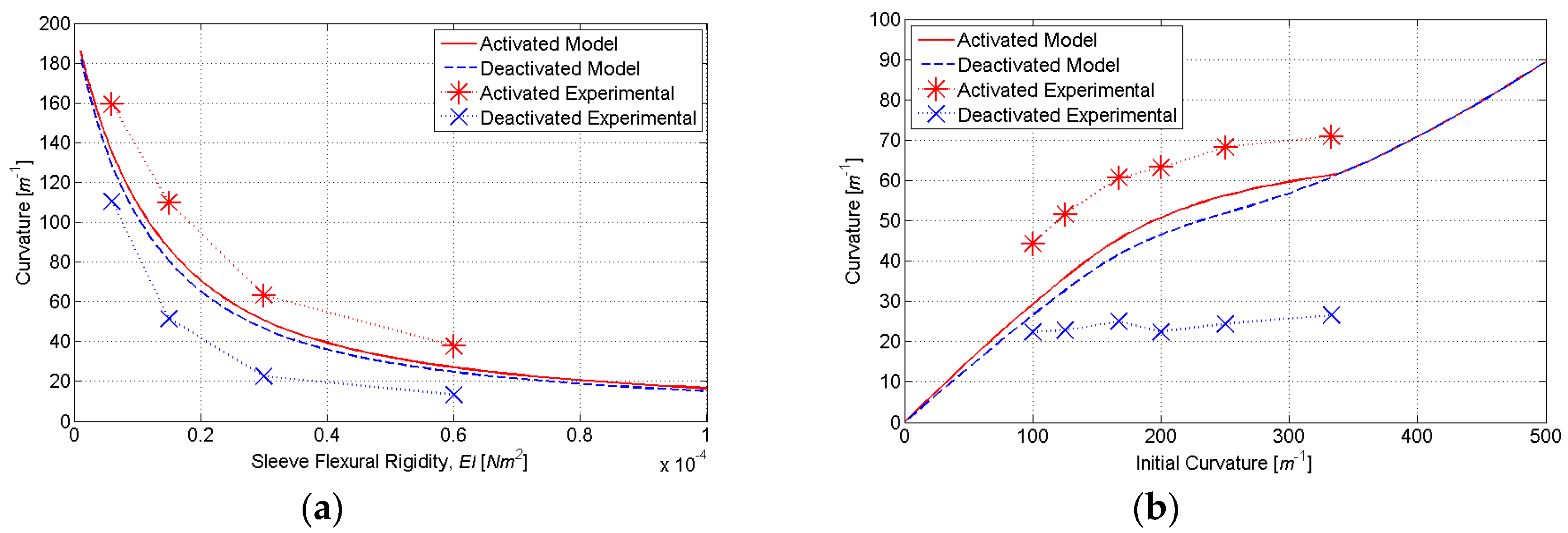
To constrain the SMA tendons during the shape setting process, a custom fixture (
Figure 8) was designed and fabricated from a 304 stainless steel plate (0.305 m × 0.102 m × 0.013 m). This fixture features eight precisely machined curvature profiles ranging from 50 to 333 (m
−1), with bolts and washers used to secure the SMA tendon during shape setting (
Figure 9). This range of initial curvatures was determined from simulations to provide the largest difference in the activated and deactivated curvature (
Figure 10b). To standardize the electrical resistance of each 0.31 mm diameter SMA tendon (Dynalloy, Inc., Irvine, CA, USA), each curvature profile was machined to provide the same arc length and straight length. Constant tendon tension was maintained by suspending a 400 g mass vertically from each SMA tendon during the fixture tightening process.
To shape-set the SMA tendons, a computer-controlled furnace (Thermolyne 1500) was preheated to 500 °C, and the loaded fixture was placed inside for 20 min [
17]. Immediately following heating, the fixture was quenched in room-temperature water. After cooling, each SMA tendon was removed from the fixture, resulting in stress-induced deformations. To experimentally quantify each tendon’s initial curvature
κ0, a programmable power supply (Agilent E3615A) was used to activate the specimen (maintaining 1.4 amps of DC current for 5.0 s, resulting in thermally-induced austenitic phase transformation). The curvature of the actuated specimen was measured by comparison to a printed scale.
To fabricate elastic sleeves with specific flexural rigidities (
EI) in the bending plane, molds were designed with rectangular cross-sections (
Figure 11). By specifying the cross-sectional height to be three times the width, the sleeve is 27 times more compliant in the bending plane than out-of-plane; the effects of self-weight are thus minimized during experimental testing. The range of flexural rigidities (6 × 10
−6 to 3 × 10
−4 Nm
2) was determined from simulations to provide the largest change in activated and deactivated curvature (
Figure 10). The molds were fabricated using rapid prototyping in ABS
plus material (Dimension Elite, Stratasys, Eden Prairie, MN, USA). Nylon monofilament (0.31 mm diameter) was tensioned along the neutral axis of each rectangular mold to provide space for SMA tendon insertion. Each mold was cast with polydimethylsiloxane (PDMS, Dow Corning SYLGARD 184) and allowed to cure for two days.
Each actuator was assembled by inserting a shape-set SMA tendon into a molded elastic sleeve. The experimental set up consisted of a cantilevered actuator connected to a programmable power supply (E3615A, Agilent Technologies) by 36 AWG magnet wire. Actuation was achieved by passing 1.4 A of DC current through the SMA tendon for 30 s. The actuator was then deactivated for one minute, cooling via heat transfer to the ambient air. High-resolution photographs (Canon DS126191 EOS Rebel 10.1MP) were taken immediately before and after each actuation cycle. Digital images were acquired and stored for subsequent evaluation of κa and κd. The process of activating, deactivating and image acquisition was automated using a custom LabView program (National Instruments, Austin, TX, USA).
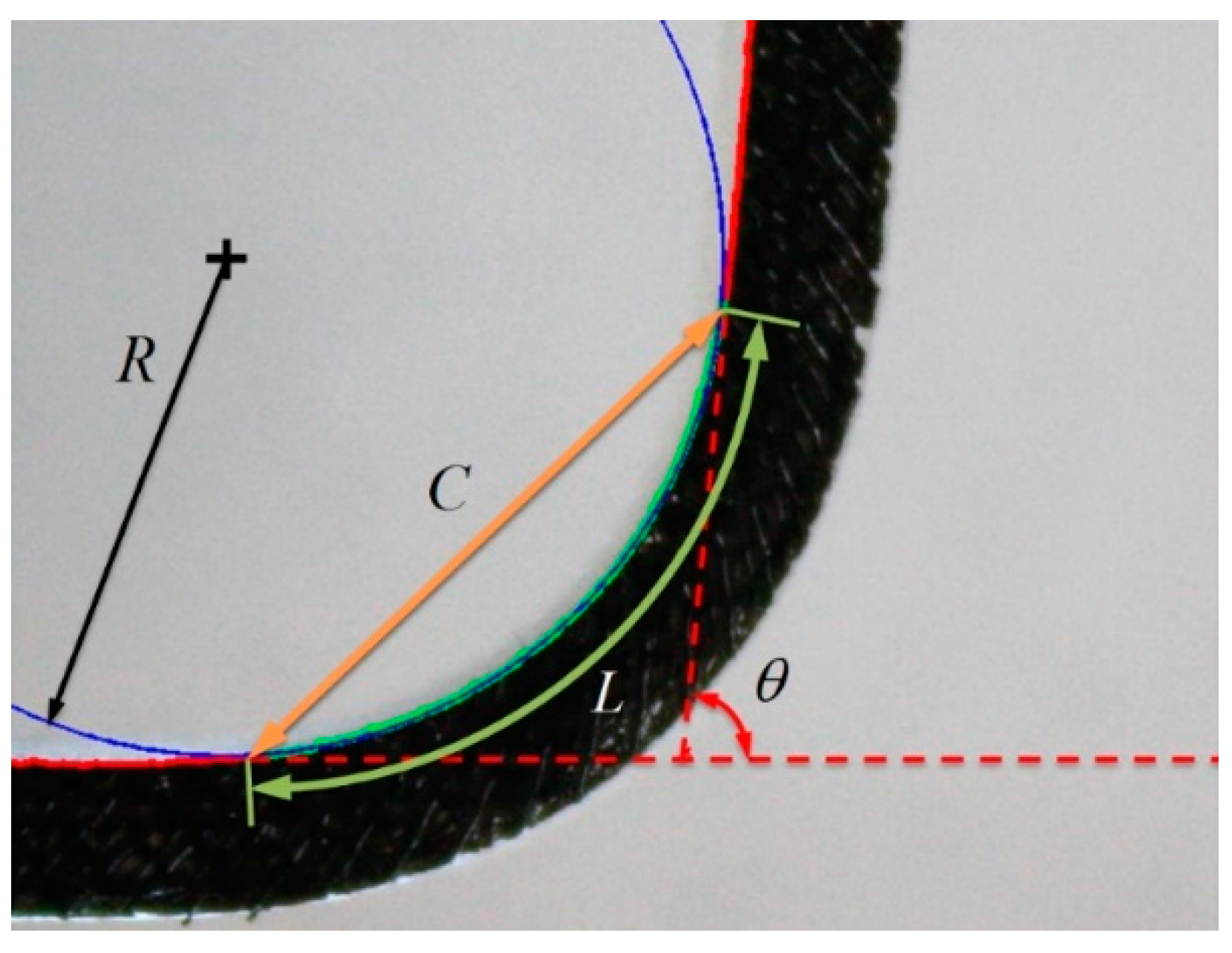
To compute
κa and
κd, an image processing code was developed using MATLAB’s Image Processing toolbox (Mathworks, Inc., Natick, MA, USA). The code applied golden-section optimization to find the bending radius
R (
Figure 12) that minimizes the difference between predicted (
Lpred) and actual bending length (
Lact) according to
where
C is the corresponding chord length and
θ is the included angle between the linear sections of the sleeve (
Figure 12). To evaluate the curvature along the actuator’s neutral axis, half of the known width of the elastic sleeve was added to the computed inner radius (
R). This computation was repeated for 110 consecutive actuations, averaging the last 10 cycles to eliminate variance and drift associated with low cycle fatigue [
18].
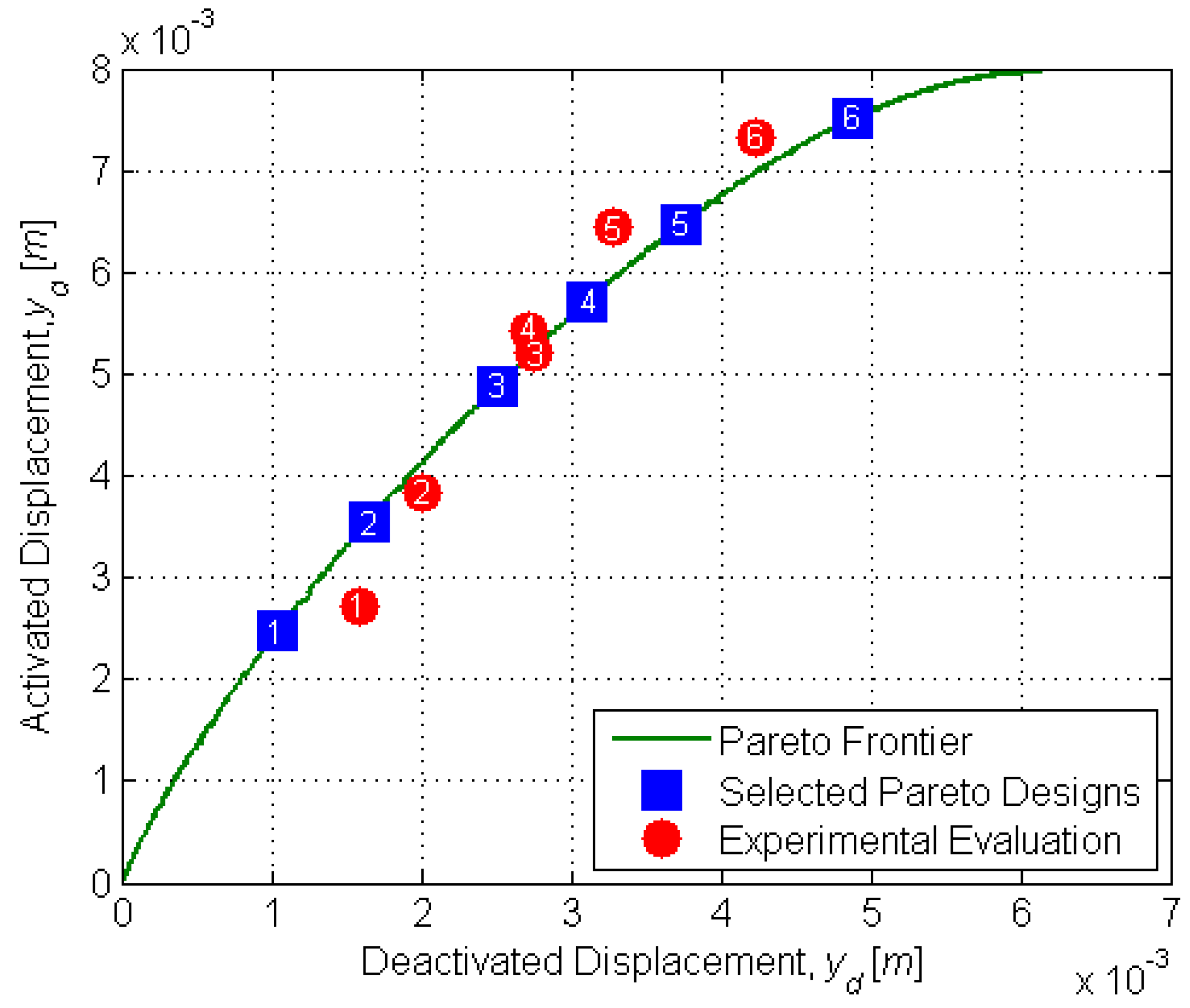
Design optimization was conducted using multi-objective genetic algorithm (MOGA) techniques. Genetic algorithms (GAs) are optimization methods based on the principles of natural selection. These algorithms minimize (or maximize) one or more objective functions and are reliable and efficient in optimizing non-linear, multi-modal and complex systems. An excellent overview of GAs can be found in [
19,
20].