Survey on Recent Designs of Compliant Micro-/Nano-Positioning Stages
Abstract
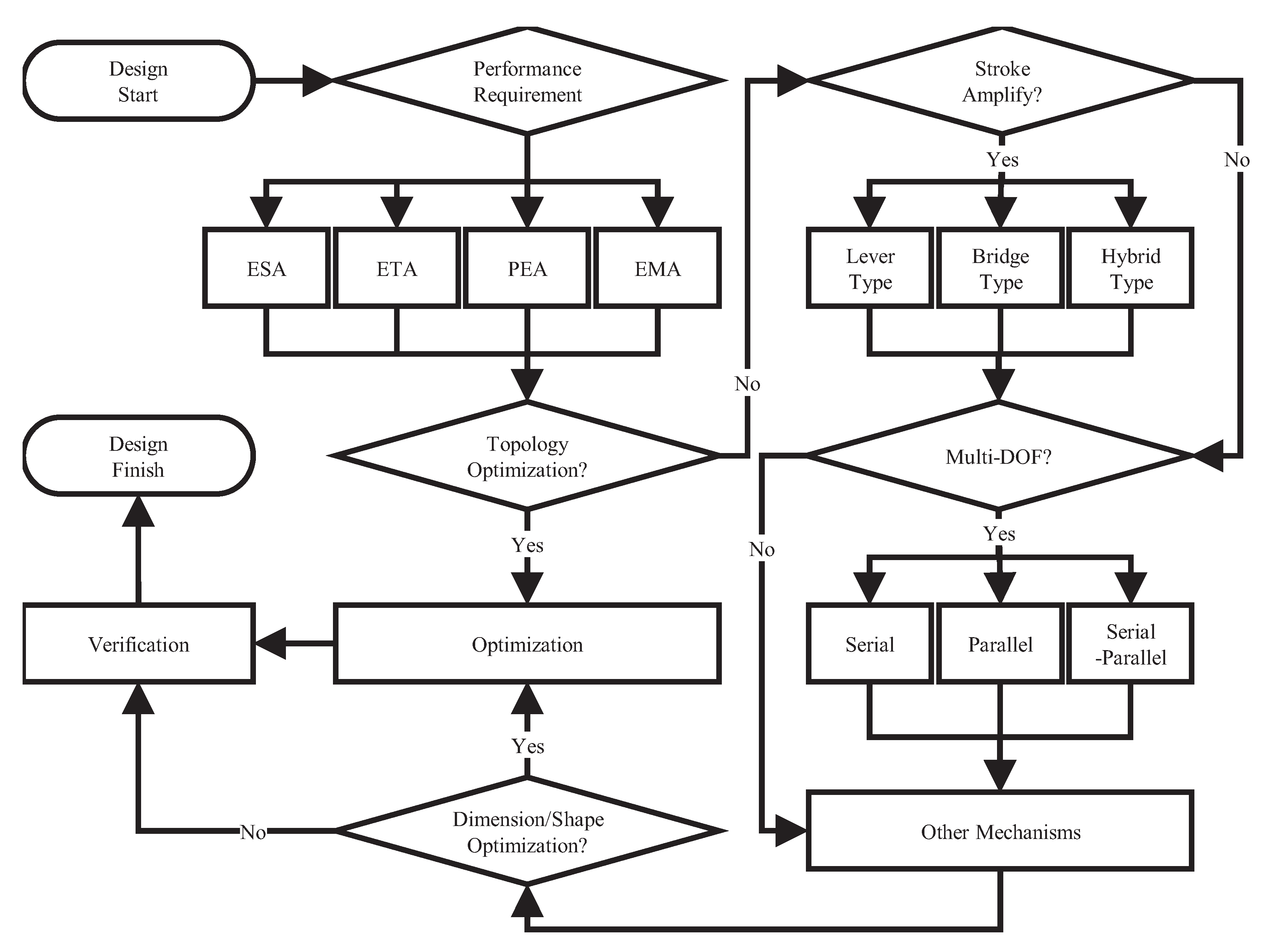
1. Introduction
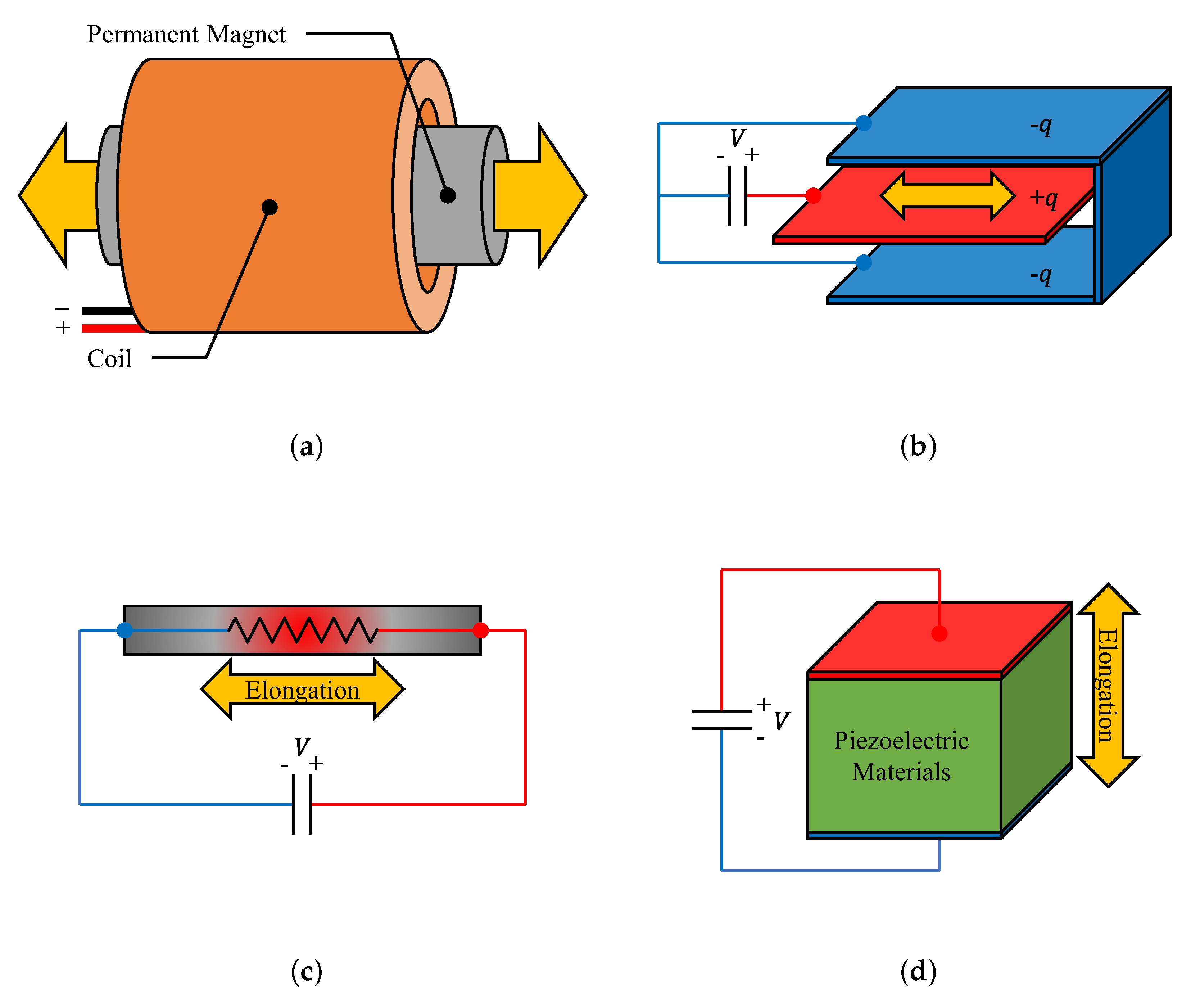
2. Actuators
2.1. Electromagnetic Actuator
2.2. Electrostatic Actuator
2.3. Electrothermal Actuator
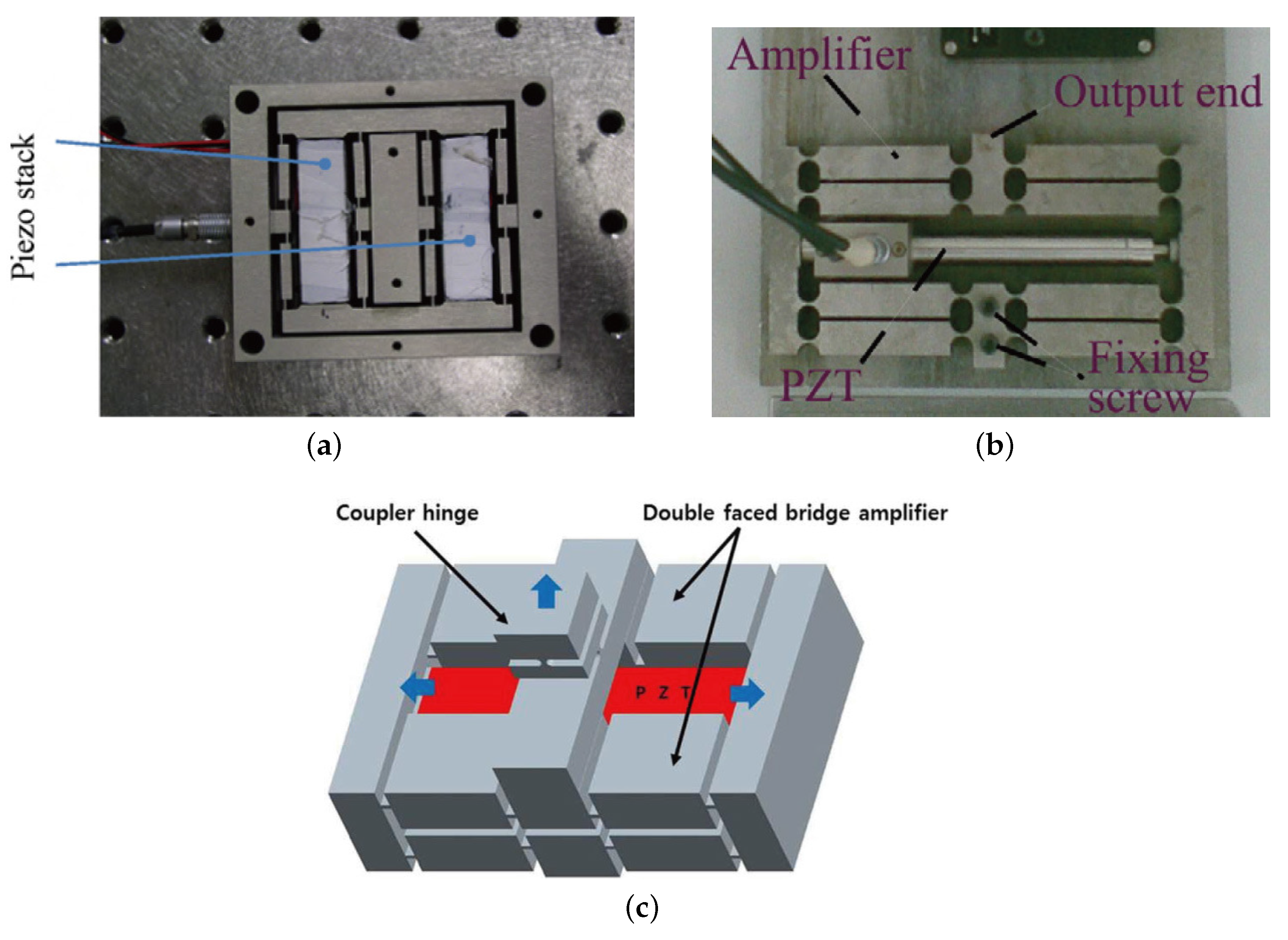
2.4. Piezoelectric Actuator
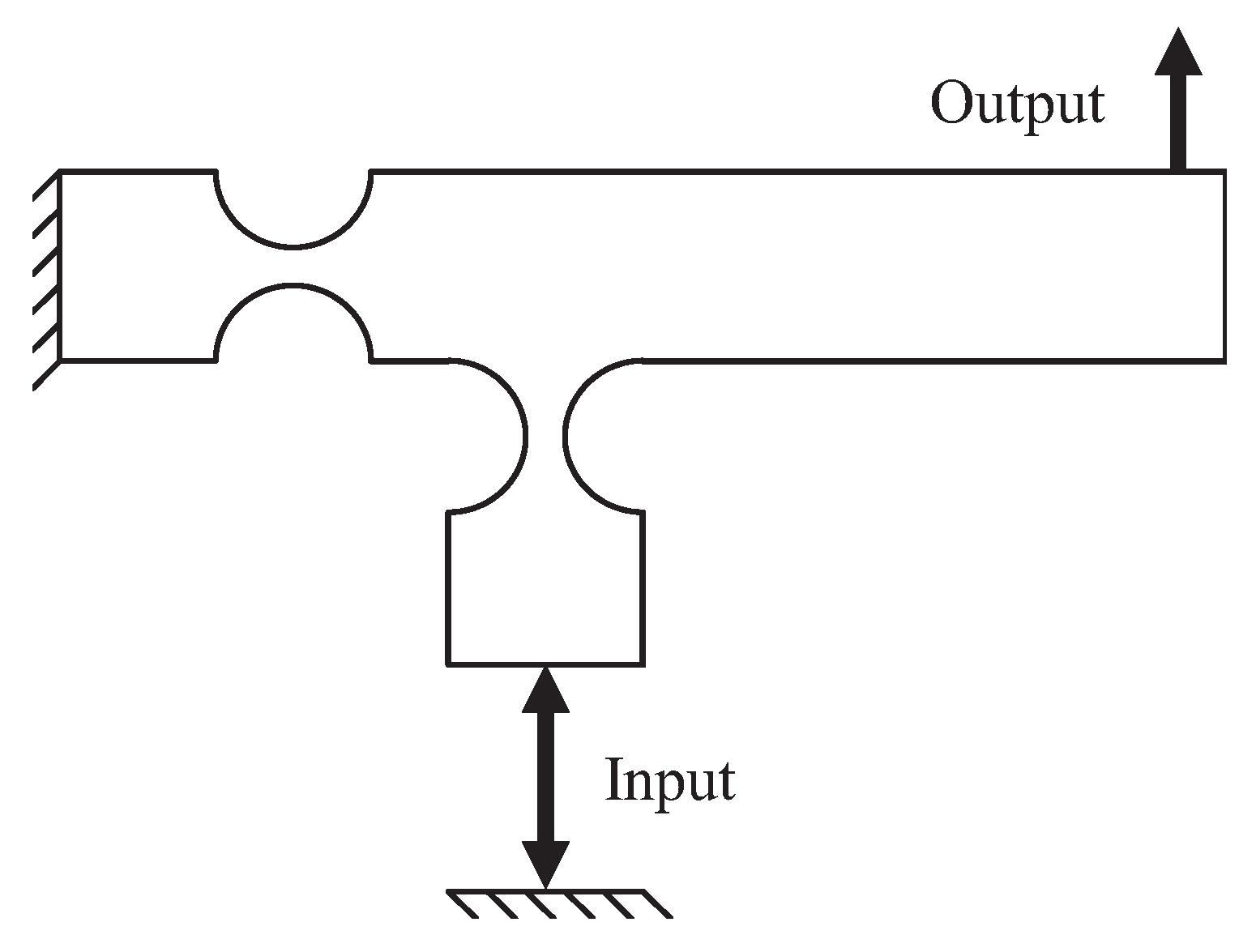
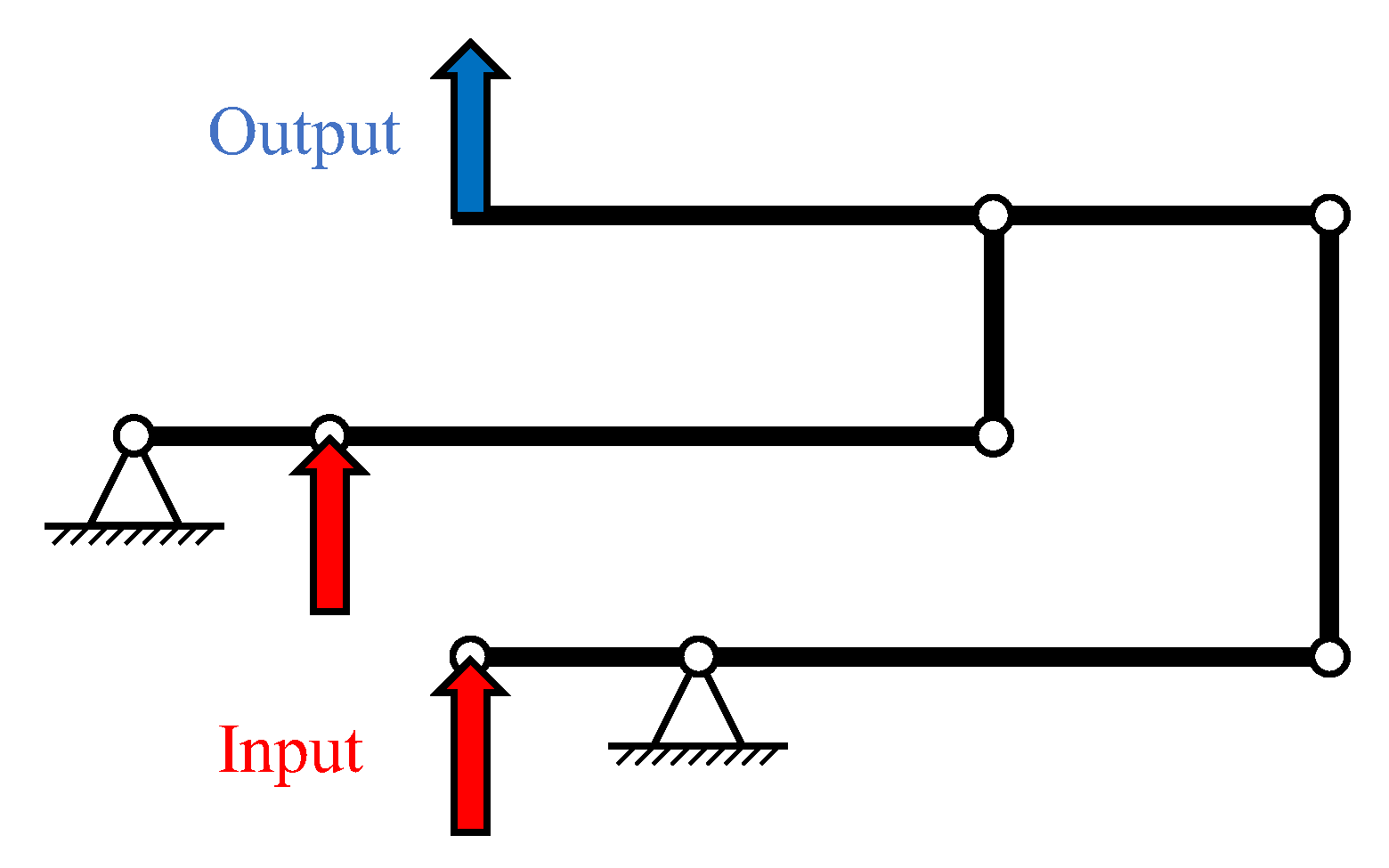
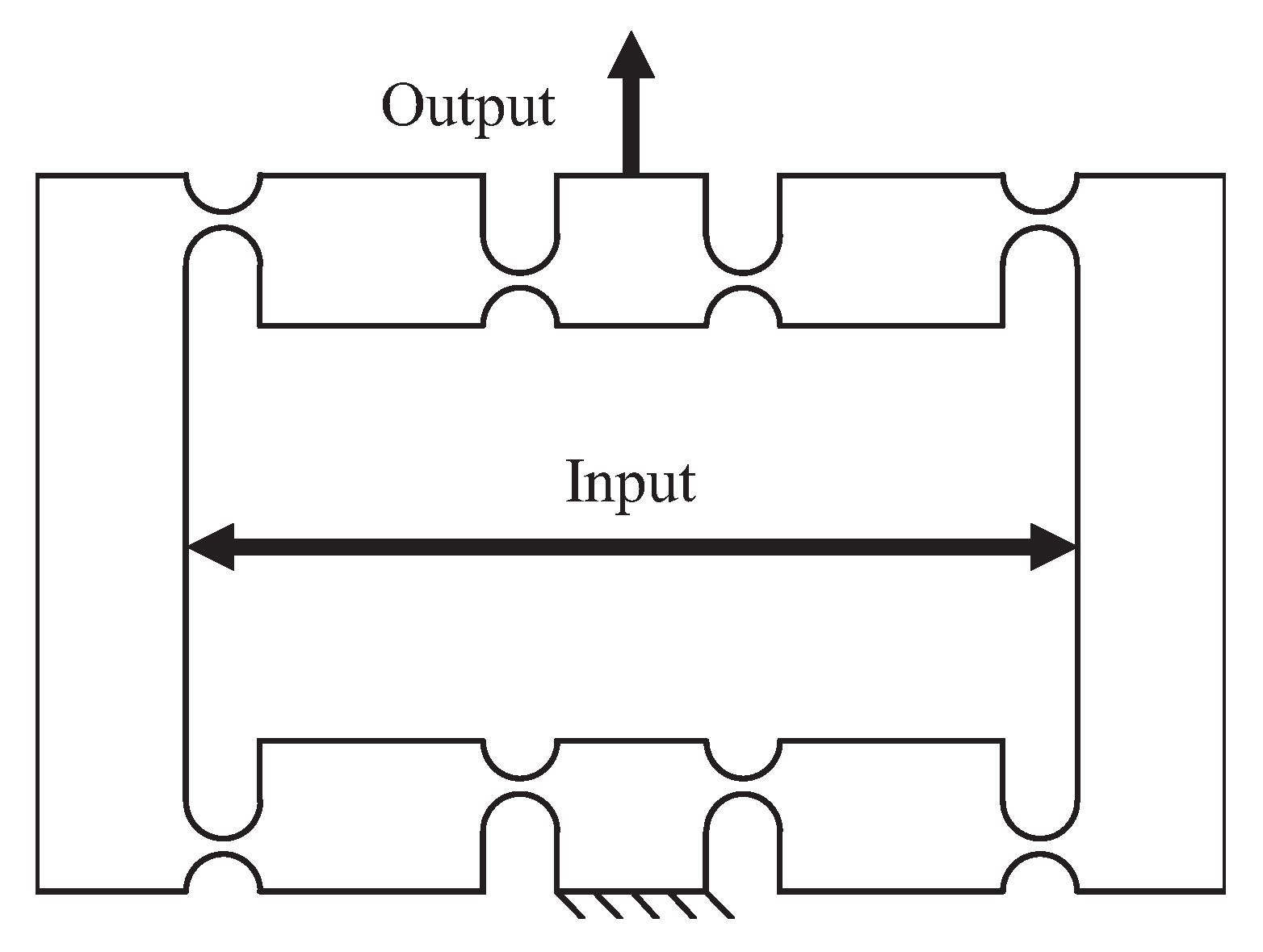
3. Stroke Amplifiers
3.1. Lever-Type Amplifier
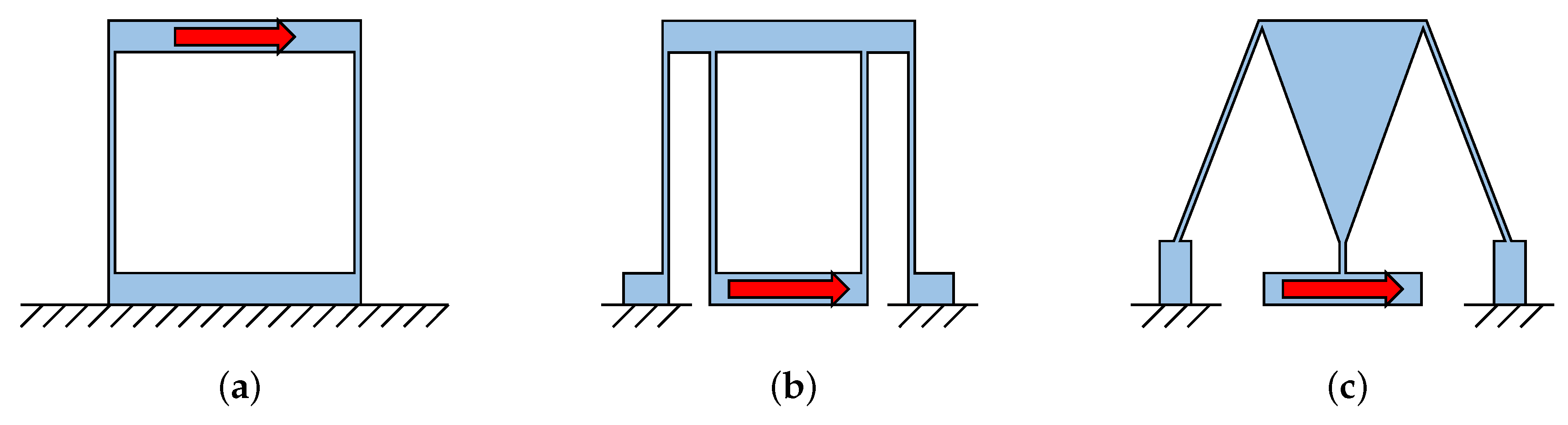
3.2. Bridge-Type Amplifier
3.3. Hybrid-Type Amplifier
4. Design of a Multi-DOF Stage
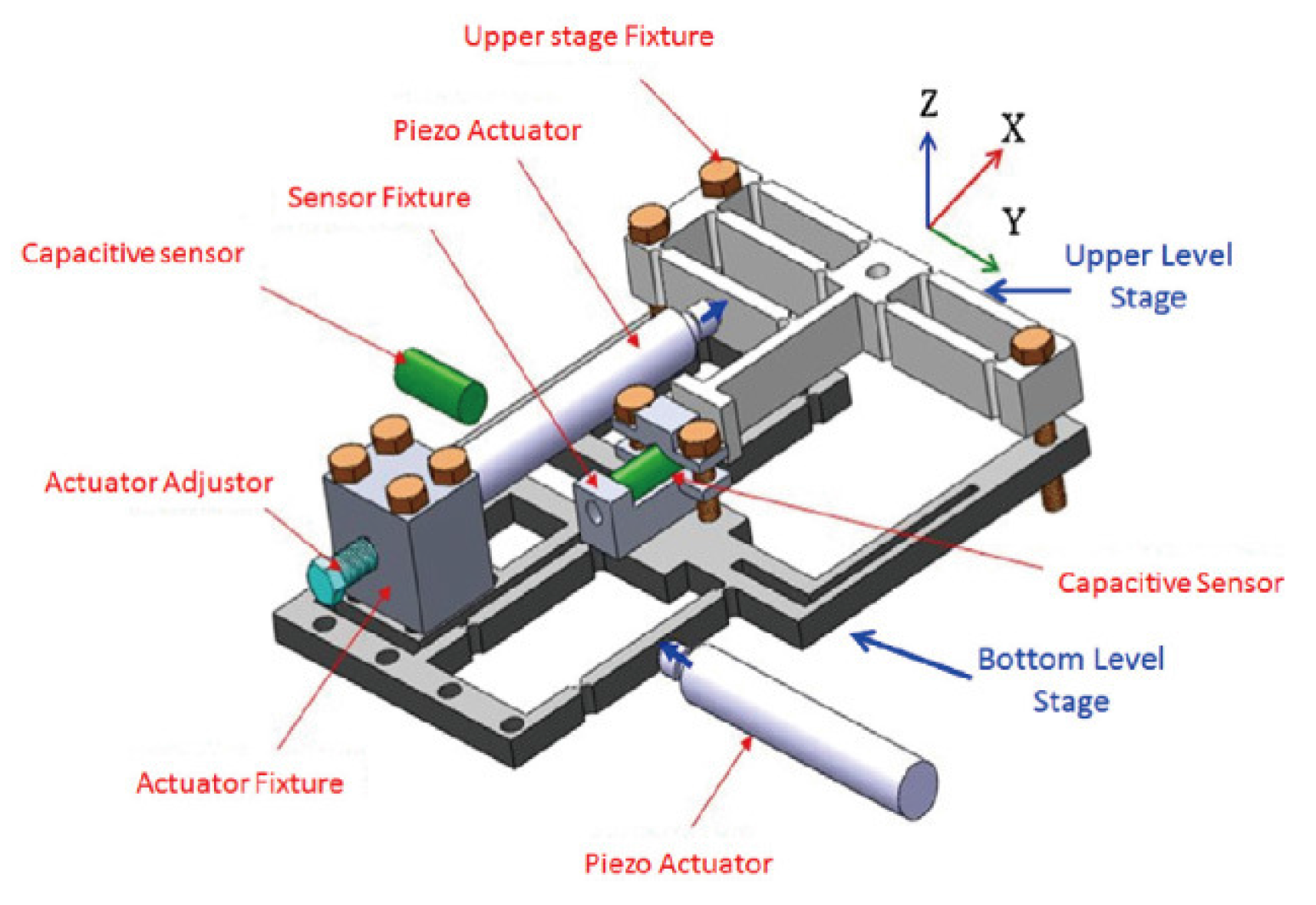
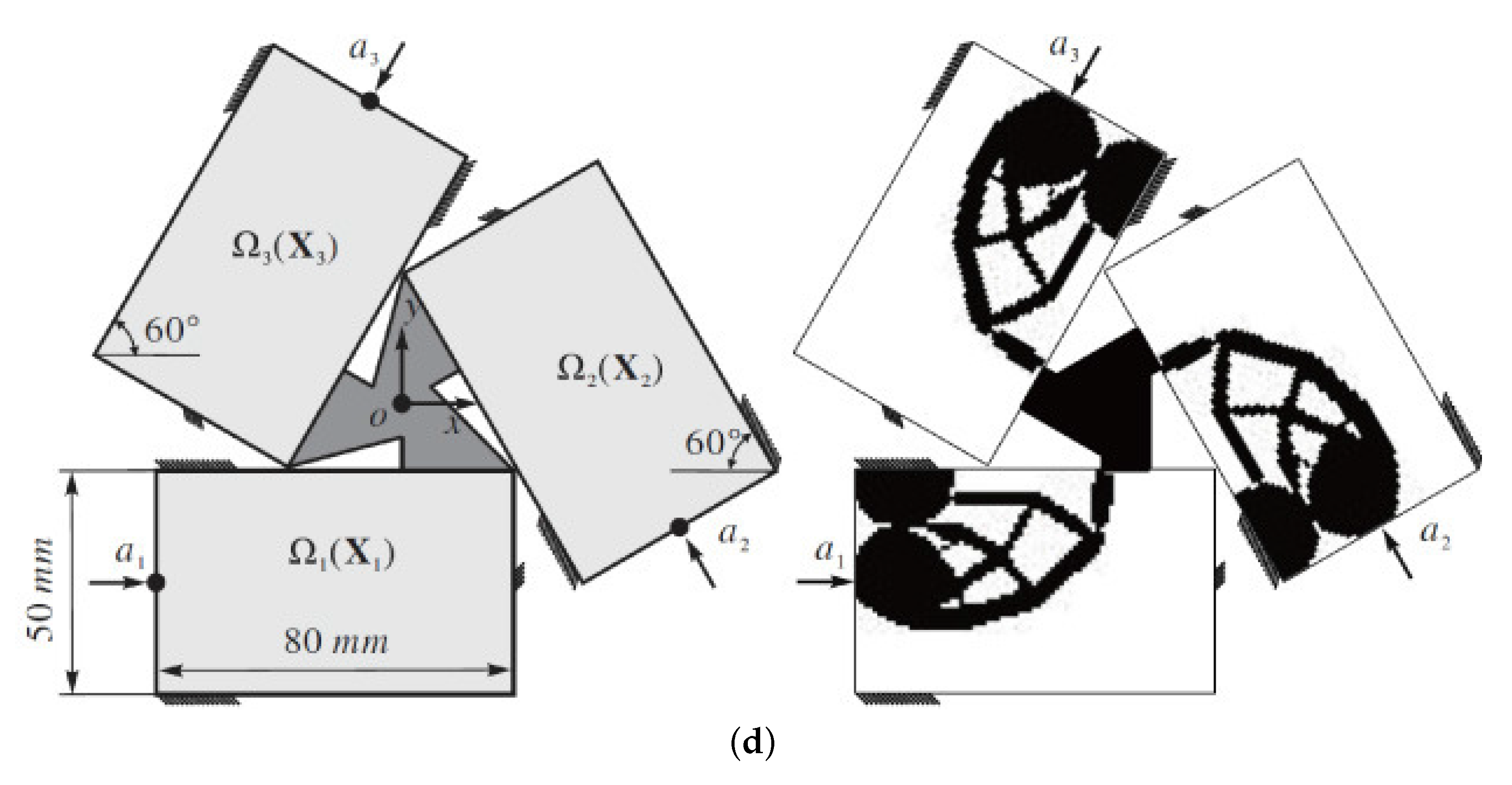
4.1. Serial Scheme Design
4.2. Parallel Scheme Design
4.3. Serial-Parallel Scheme Design
5. Optimization Methods
5.1. Dimension and Shape Optimization
5.1.1. Non-Heuristic Algorithms
5.1.2. Heuristic Algorithm
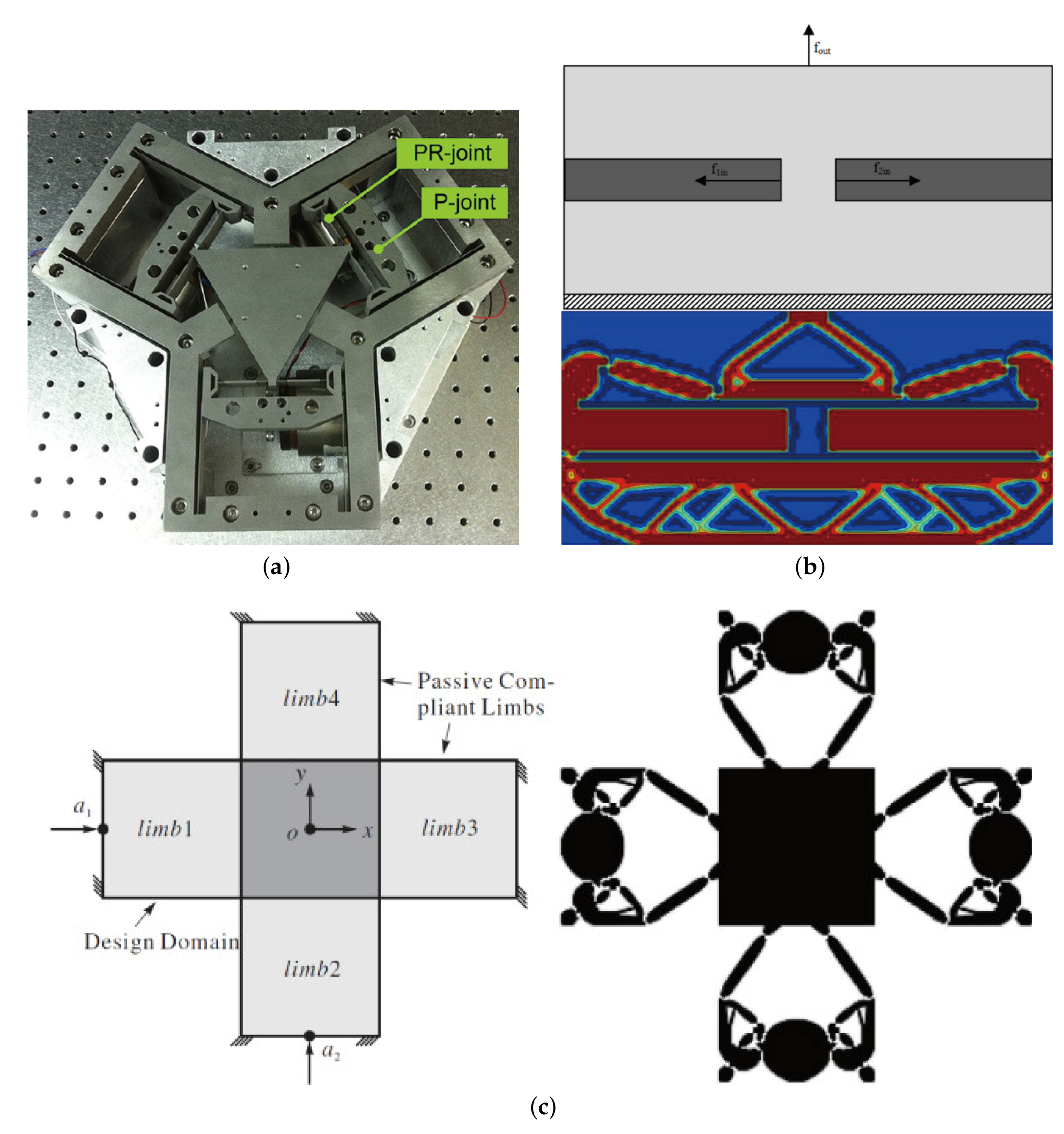
5.2. Topology Optimization
6. Further Discussion
7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Preston, D.J.; Anders, A.; Barabadi, B.; Tio, E.; Zhu, Y.; Dai, D.A.; Wang, E.N. Electrowetting-on-dielectric actuation of a vertical translation and angular manipulation stage. Appl. Phys. Lett. 2016, 109, 244102. [Google Scholar] [CrossRef]
- Warnat, S.; King, H.; Wasay, A.; Sameoto, D.; Hubbard, T. Direct integration of MEMS, dielectric pumping and cell manipulation with reversibly bonded gecko adhesive microfluidics. J. Micromech. Microeng. 2016, 26, 097001. [Google Scholar] [CrossRef]
- Belfiore, N.P.; Verotti, M.; Crescenzi, R.; Balucani, M. Design, optimization and construction of MEMS-based micro grippers for cell manipulation. In Proceedings of the 2013 International Conference on System Science and Engineering (ICSSE), Budapest, Hungary, 4–6 July 2013; pp. 105–110. [Google Scholar]
- Jain, R.K.; Majumder, S.; Ghosh, B.; Saha, S. Design and manufacturing of mobile micro manipulation system with a compliant piezoelectric actuator based micro gripper. J. Manuf. Syst. 2015, 35, 76–91. [Google Scholar] [CrossRef]
- Cecil, J.; Vasquez, D.; Powell, D. A review of gripping and manipulation techniques for micro-assembly applications. Int. J. Prod. Res. 2005, 43, 819–828. [Google Scholar] [CrossRef]
- Ouyang, P.R.; Tjiptoprodjo, R.C.; Zhang, W.J.; Yang, G.S. Micro-motion devices technology: The state of arts review. Int. J. Adv. Manuf. Technol. 2007, 38, 463–478. [Google Scholar] [CrossRef]
- Howell, L.L. Compliant Mechanisms. In 21st Century Kinematics; Springer: London, UK, 2013; pp. 189–216. [Google Scholar]
- Lobontiu, N. Compliant Mechanisms; CRC Press: Boca Raton, FL, USA, 2002. [Google Scholar]
- Xu, Q. Design and Implementation of Large-Range Compliant Micropositioning Systems; John Wiley & Sons Singapore Pte. Ltd.: Singapore, 2016. [Google Scholar]
- Ryu, J.W.; Gweon, D.G. Error analysis of a flexure hinge mechanism induced by machining imperfection. Precis. Eng. 1997, 21, 83–89. [Google Scholar] [CrossRef]
- Verotti, M.; Dochshanov, A.; Belfiore, N.P. A Comprehensive Survey on Microgrippers Design: Mechanical Structure. J. Mech. Des. 2017, 139, 060801. [Google Scholar] [CrossRef]
- Dochshanov, A.; Verotti, M.; Belfiore, N.P. A Comprehensive Survey on Microgrippers Design: Operational Strategy. J. Mech. Des. 2017, 139, 070801. [Google Scholar] [CrossRef]
- Xu, Q. Design and Development of a Compact Flexure-Based XY Precision Positioning System with Centimeter Range. IEEE Trans. Ind. Electron. 2014, 61, 893–903. [Google Scholar] [CrossRef]
- Mekid, S.; Bashmal, S.; Ouakad, H.M. Nanoscale Manipulators: Review of Conceptual Designs Through Recent Patents. Recent Pat. Nanotechnol. 2016, 10, 44–58. [Google Scholar] [CrossRef] [PubMed]
- Nikoobin, A.; Niaki, M.H. Deriving and analyzing the effective parameters in microgrippers performance. Sci. Iran. 2012, 19, 1554–1563. [Google Scholar] [CrossRef]
- Hao, G.; Li, H.; He, X.; Kong, X. Conceptual design of compliant translational joints for high-precision applications. Front. Mech. Eng. 2014, 9, 331–343. [Google Scholar] [CrossRef]
- Hao, G.; Kong, X. A structure design method for compliant parallel manipulators with actuation isolation. Mech. Sci. 2016, 7, 247–253. [Google Scholar] [CrossRef]
- Hubbard, N.B.; Culpepper, M.L.; Howell, L.L. Actuators for Micropositioners and Nanopositioners. Appl. Mech. Rev. 2006, 59, 324. [Google Scholar] [CrossRef]
- Bell, D.J.; Lu, T.J.; Fleck, N.A.; Spearing, S.M. MEMS actuators and sensors: Observations on their performance and selection for purpose. J. Micromech. Microeng. 2005, 15, S153–S164. [Google Scholar] [CrossRef]
- Ghosh, A.; Corves, B. Introduction to Micromechanisms and Microactuators; Springer: New Delhi, India, 2015. [Google Scholar]
- Zhang, Z.; Liu, B.; Wang, P.; Yan, P. Design of an additive manufactured XY compliant manipulator with spatial redundant constraints. In Proceedings of the 2016 35th Chinese Control Conference (CCC), Chengdu, China, 27–29 July 2016; pp. 9149–9154. [Google Scholar]
- Wang, N.; Liang, X.; Zhang, X. Design and Analysis of a Novel XY Micro-positioning Stage Used Corrugated Flexure Beams. In Intelligent Robotics and Applications; Zhang, X., Liu, H., Chen, Z., Wang, N., Eds.; Springer International Publishing: Cham, Switzerland, 2014; pp. 586–595. [Google Scholar]
- Kim, D.H.; Kim, B.; Kang, H. Development of a piezoelectric polymer-based sensorized microgripper for microassembly and micromanipulation. Microsyst. Technol. 2004, 10, 275–280. [Google Scholar] [CrossRef]
- Kim, D.H.; Lee, M.G.; Kim, B.; Sun, Y. A superelastic alloy microgripper with embedded electromagnetic actuators and piezoelectric force sensors: A numerical and experimental study. Smart Mater. Struct. 2005, 14, 1265–1272. [Google Scholar] [CrossRef]
- Jia, Y.; Xu, Q. MEMS Microgripper Actuators and Sensors: The State-of-the-Art Survey. Recent Pat. Mech. Eng. 2013, 6, 132–142. [Google Scholar] [CrossRef]
- Madou, M.J. Fundamentals of Microfabrication: The Science of Miniaturization, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2002. [Google Scholar]
- Li, L.; Chew, Z. Microactuators: Design and technology. In Smart Sensors and Mems; Elsevier: Amsterdam, The Netherlands, 2014; pp. 305–348. [Google Scholar]
- Piriyanont, B.; Moheimani, S.O.R. MEMS Rotary Microgripper With Integrated Electrothermal Force Sensor. J. Microelectromech. Syst. 2014, 23, 1249–1251. [Google Scholar] [CrossRef]
- Yeh, J.A.; Chen, C.N.; Lui, Y.S. Large rotation actuated by in-plane rotary comb-drives with serpentine spring suspension. J. Micromech. Microeng. 2004, 15, 201–206. [Google Scholar] [CrossRef]
- Belfiore, N.P.; Broggiato, G.B.; Verotti, M.; Balucani, M.; Crescenzi, R.; Bagolini, A.; Bellutti, P.; Boscardin, M. Simulation and construction of a MEMS CSFH based microgripper. Int. J. Mech. Control 2015, 16, 21–30. [Google Scholar]
- Chang, H.; Zhao, H.; Ye, F.; Yuan, G.; Xie, J.; Kraft, M.; Yuan, W. A rotary comb-actuated microgripper with a large displacement range. Microsyst. Technol. 2013, 20, 119–126. [Google Scholar] [CrossRef]
- Cecchi, R.; Verotti, M.; Capata, R.; Dochshanov, A.; Broggiato, G.; Crescenzi, R.; Balucani, M.; Natali, S.; Razzano, G.; Lucchese, F.; et al. Development of Micro-Grippers for Tissue and Cell Manipulation with Direct Morphological Comparison. Micromachines 2015, 6, 1710–1728. [Google Scholar] [CrossRef]
- Piriyanont, B.; Fowler, A.G.; Moheimani, S.O.R. Force-Controlled MEMS Rotary Microgripper. J. Microelectromech. Syst. 2015, 24, 1164–1172. [Google Scholar] [CrossRef]
- Yeh, J.; Jiang, S.S.; Lee, C. MOEMS variable optical attenuators using rotary comb drive actuators. IEEE Photonics Technol. Lett. 2006, 18, 1170–1172. [Google Scholar] [CrossRef]
- Mita, M.; Arai, M.; Tensaka, S.; Kobayashi, D.; Fujita, H. A micromachined impact microactuator driven by electrostatic force. J. Microelectromech. Syst. 2003, 12, 37–41. [Google Scholar] [CrossRef]
- Maroufi, M.; Moheimani, S.O.R. Design, fabrication and characterization of a high-bandwidth 2DOF MEMS nanopositioner. In Proceedings of the 2013 IEEE/ASME International Conference on Advanced Intelligent Mechatronics, Wollongong, Australia, 9–12 July 2013; pp. 335–340. [Google Scholar]
- Zhang, W.M.; Meng, G.; Chen, D. Stability, Nonlinearity and Reliability of Electrostatically Actuated MEMS Devices. Sensors 2007, 7, 760–796. [Google Scholar] [CrossRef]
- Bazaz, S.A.; Khan, F.; Shakoor, R.I. Design, simulation and testing of electrostatic SOI MUMPs based microgripper integrated with capacitive contact sensor. Sens. Actuators A Phys. 2011, 167, 44–53. [Google Scholar] [CrossRef]
- Wierzbicki, R.; Adda, C.; Hotzendorfer, H. Electrostatic Silicon Microgripper with Low Voltage of Actuation. In Proceedings of the 2007 International Symposium on Micro-NanoMechatronics and Human Science, Nagoya, Japan, 11–14 November 2007; pp. 344–349. [Google Scholar]
- Nakic, C.; Bieker, J.; Lammle, D.; Winterstein, T.; Schlaak, H.F.; Schaumann, G.; Abel, T. Development of an electrothermal micro positioning platform for laser targets with two degrees of freedom. In Proceedings of the 2016 International Conference on Manipulation, Automation and Robotics at Small Scales (MARSS), Paris, France, 18–22 July 2016; pp. 1–5. [Google Scholar]
- Fu, Y.; Luo, J.; Flewitt, A.; Milne, W. Smart microgrippers for bioMEMS applications. In MEMS for Biomedical Applications; Elsevier: Amsterdam, The Netherlands, 2012; pp. 291–336. [Google Scholar]
- Nikoobin, A.; Niaki, M.H. Describing the effective parameters in grippers, and designing the novel micro-nano gripper. In Proceedings of the 2nd International Conference on Control, Instrumentation and Automation, Shiraz, Iran, 27–29 December 2011; pp. 957–963. [Google Scholar]
- Tsai, Y.C.; Lei, S.H.; Sudin, H. Design and analysis of planar compliant microgripper based on kinematic approach. J. Micromech. Microeng. 2004, 15, 143–156. [Google Scholar] [CrossRef]
- Demaghsi, H.; Mirzajani, H.; Ghavifekr, H.B. Design and simulation of a novel metallic microgripper using vibration to release nano objects actively. Microsyst. Technol. 2013, 20, 65–72. [Google Scholar] [CrossRef]
- Varona, J.; Saenz, E.; Fiscal-Woodhouse, S.; Hamoui, A.A. Design and fabrication of a novel microgripper based on electrostatic actuation. In Proceedings of the 2009 52nd IEEE International Midwest Symposium on Circuits and Systems, Cancun, Mexico, 2–5 August 2009; pp. 827–832. [Google Scholar]
- Maluf, N. An Introduction to Microelectromechanical Systems Engineering. Meas. Sci. Technol. 2002, 13, 229. [Google Scholar] [CrossRef]
- Engelen, J.B. Optimization of Comb-Drive Actuators. Ph.D. Thesis, University of Twente, Enschede, The Netherlands, 2011. [Google Scholar]
- Rakotondrabe, M.; Ivan, I.A. Development and Force/Position Control of a New Hybrid Thermo-Piezoelectric MicroGripper Dedicated to Micromanipulation Tasks. IEEE Trans. Autom. Sci. Eng. 2011, 8, 824–834. [Google Scholar] [CrossRef]
- Habineza, D.; Rakotondrabe, M.; Gorrec, Y.L. Bouc–Wen Modeling and Feedforward Control of Multivariable Hysteresis in Piezoelectric Systems: Application to a 3-DoF Piezotube Scanner. IEEE Trans. Control Syst. Technol. 2015, 23, 1797–1806. [Google Scholar] [CrossRef]
- Gu, G.Y.; Li, C.X.; Zhu, L.M.; Su, C.Y. Modeling and Identification of Piezoelectric-Actuated Stages Cascading Hysteresis Nonlinearity With Linear Dynamics. IEEE/ASME Trans. Mechatron. 2016, 21, 1792–1797. [Google Scholar] [CrossRef]
- Yang, M.J.; Li, C.X.; Gu, G.Y.; Zhu, L.M. Modeling and compensating the dynamic hysteresis of piezoelectric actuators via a modified rate-dependent Prandtl–Ishlinskii model. Smart Mater. Struct. 2015, 24, 125006-1–125006-12. [Google Scholar] [CrossRef]
- Xu, Q. Identification and Compensation of Piezoelectric Hysteresis Without Modeling Hysteresis Inverse. IEEE Trans. Ind. Electron. 2013, 60, 3927–3937. [Google Scholar] [CrossRef]
- Xu, Q.; Li, Y. Model Predictive Discrete-Time Sliding Mode Control of a Nanopositioning Piezostage Without Modeling Hysteresis. IEEE Trans. Control Syst. Technol. 2012, 20, 983–994. [Google Scholar] [CrossRef]
- Xu, Q.; Li, Y. Analytical modeling, optimization and testing of a compound bridge-type compliant displacement amplifier. Mech. Mach. Theory 2011, 46, 183–200. [Google Scholar] [CrossRef]
- Zhu, X.; Wen, Z.; Liu, P. A Piezo-Driven Compliant Nanopositioning Stage with Large Stroke for Micro/Nano Manipulation. MATEC Web Conf. 2016, 77, 01040. [Google Scholar] [CrossRef]
- Lobontiu, N.; Garcia, E. Analytical model of displacement amplification and stiffness optimization for a class of flexure-based compliant mechanisms. Comput. Struct. 2003, 81, 2797–2810. [Google Scholar] [CrossRef]
- Gan, J.; Zhang, X.; Li, H.; Wu, H. Full closed-loop controls of micro/nano positioning system with nonlinear hysteresis using micro-vision system. Sens. Actuators A Phys. 2017, 257, 125–133. [Google Scholar] [CrossRef]
- Bhagat, U.; Shirinzadeh, B.; Clark, L.; Chea, P.; Qin, Y.; Tian, Y.; Zhang, D. Design and analysis of a novel flexure-based 3-DOF mechanism. Mech. Mach. Theory 2014, 74, 173–187. [Google Scholar] [CrossRef]
- Li, Y.; Xu, Q. Design and Optimization of an XYZ Parallel Micromanipulator with Flexure Hinges. J. Intell. Robot. Syst. 2008, 55, 377–402. [Google Scholar] [CrossRef]
- Dao, T.P.; Huang, S.C. Optimization of a two degrees of freedom compliant mechanism using Taguchi method-based grey relational analysis. Microsyst. Technol. 2017, 23, 4815–4830. [Google Scholar] [CrossRef]
- Qu, J.; Chen, W.; Zhang, J.; Chen, W. A piezo-driven 2-DOF compliant micropositioning stage with remote center of motion. Sens. Actuators A Phys. 2016, 239, 114–126. [Google Scholar] [CrossRef]
- Ren, G.; Zhang, Q.; Li, C.; Zhang, X. Research on a 3-DOF Compliant Precision Positioning Stage Based on Piezoelectric Actuators. In Intelligent Robotics and Applications; Huang, Y., Wu, H., Liu, H., Yin, Z., Eds.; Springer International Publishing: Cham, Switzerland, 2017; pp. 346–358. [Google Scholar]
- Gao, J.; Zeng, Z.; Tang, H.; Chen, X.; Qiu, Q.; He, S.; He, Y.; Yang, Z. Design and assessment of a piezo-actuated 3-DOF flexible nanopositioner with large stroke. In Proceedings of the 2016 IEEE International Conference on Manipulation, Manufacturing and Measurement on the Nanoscale (3M-NANO), Chongqing, China, 18–22 July 2016; pp. 19–24. [Google Scholar]
- Choi, K.B.; Lee, J.J.; Hata, S. A piezo-driven compliant stage with double mechanical amplification mechanisms arranged in parallel. Sens. Actuators A Phys. 2010, 161, 173–181. [Google Scholar] [CrossRef]
- Kim, J.J.; Choi, Y.M.; Ahn, D.; Hwang, B.; Gweon, D.G.; Jeong, J. A millimeter-range flexure-based nano-positioning stage using a self-guided displacement amplification mechanism. Mech. Mach. Theory 2012, 50, 109–120. [Google Scholar] [CrossRef]
- Lee, H.J.; Kim, H.C.; Kim, H.Y.; Gweon, D.G. Optimal design and experiment of a three-axis out-of-plane nano positioning stage using a new compact bridge-type displacement amplifier. Rev. Sci. Instrum. 2013, 84, 115103. [Google Scholar] [CrossRef] [PubMed]
- Zhu, Z.; Zhou, X.; Liu, Z.; Wang, R.; Zhu, L. Development of a piezoelectrically actuated two-degree-of-freedom fast tool servo with decoupled motions for micro-/nanomachining. Precis. Eng. 2014, 38, 809–820. [Google Scholar] [CrossRef]
- Zhang, X.; Xu, Q. Mechanism design of a compact XYZ parallel flexure stage. In Proceedings of the 2015 IEEE International Conference on Information and Automation, Lijiang, China, 8–10 August 2015; pp. 953–957. [Google Scholar]
- Zhang, X.; Xu, Q. Design of a new flexure-based XYZ parallel nanopositioning stage. In Proceedings of the 2015 IEEE International Conference on Robotics and Biomimetics (ROBIO), Zhuhai, China, 6–9 December 2015; pp. 1962–1966. [Google Scholar]
- Li, T.; Du, Y.; Jiang, Y.; Zhang, J. Empirical Compliance Equations for Constant Rectangular Cross Section Flexure Hinges and Their Applications. Math. Probl. Eng. 2016, 2016, 1–11. [Google Scholar] [CrossRef]
- Dong, W.; Chen, F.; Yang, M.; Du, Z.; Tang, J.; Zhang, D. Development of a highly efficient bridge-type mechanism based on negative stiffness. Smart Mater. Struct. 2017, 26, 095053. [Google Scholar] [CrossRef]
- Chen, F.; Du, Z.; Yang, M.; Gao, F.; Dong, W.; Zhang, D. Design and analysis of a three-dimensional bridge-type mechanism based on the stiffness distribution. Precis. Eng. 2018, 51, 48–58. [Google Scholar] [CrossRef]
- Yao, Q.; Dong, J.; Ferreira, P. Design, analysis, fabrication and testing of a parallel-kinematic micropositioning XY stage. Int. J. Mach. Tools Manuf. 2007, 47, 946–961. [Google Scholar] [CrossRef]
- Clark, L.; Shirinzadeh, B.; Zhong, Y.; Tian, Y.; Zhang, D. Design and analysis of a compact flexure-based precision pure rotation stage without actuator redundancy. Mech. Mach. Theory 2016, 105, 129–144. [Google Scholar] [CrossRef]
- Chu, C.L.; Chen, H.C.; Sie, M.H. Development of a XYθz 3-DOF nanopositioning stage with linear displacement amplification device. MATEC Web Conf. 2017, 123, 00006. [Google Scholar] [CrossRef]
- Zhang, X.; Xu, Q. Design and modeling of a novel 3-PSS flexure nanopositioning stage. In Proceedings of the 2017 IEEE International Conference on Advanced Intelligent Mechatronics (AIM), Munich, Germany, 3–7 July 2017; pp. 1322–1327. [Google Scholar]
- Xu, Q. Design and Development of a Flexure-Based Dual-Stage Nanopositioning System With Minimum Interference Behavior. IEEE Trans. Autom. Sci. Eng. 2012, 9, 554–563. [Google Scholar] [CrossRef]
- Xue, G.; Toda, M.; Ono, T. Comb-drive XYZ-microstage based on assembling technology for low temperature measurement systems. In Proceedings of the 2015 International Conference on Electronic Packaging and iMAPS All Asia Conference (ICEP-IAAC), Kyoto, Japan, 14–17 April 2015; pp. 83–88. [Google Scholar]
- Lee, J.W.; Li, Y.C.; Chen, K.S.; Liu, Y.H. Design and control of a cascaded piezoelectric actuated two-degrees-of-freedom positioning compliant stage. Precis. Eng. 2016, 45, 374–386. [Google Scholar] [CrossRef]
- Liu, X.; Huang, W.; Wang, Y. A novel 2D piezo-nanopositioning stage based on triangle amplifier mechanism. In Proceedings of the 2016 Symposium on Piezoelectricity, Acoustic Waves, and Device Applications (SPAWDA), Xi’an, China, 21–24 October 2016; pp. 314–318. [Google Scholar]
- Pinskier, J.; Shirinzadeh, B.; Clark, L.; Qin, Y.; Fatikow, S. Design, development and analysis of a haptic-enabled modular flexure-based manipulator. Mechatronics 2016, 40, 156–166. [Google Scholar] [CrossRef]
- Liu, X.J.; Wang, J. Parallel Kinematics; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Wan, S.; Zhang, Y.; Xu, Q. Design and development of a new large-stroke XY compliant micropositioning stage. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2016, 231, 3263–3276. [Google Scholar] [CrossRef]
- Hao, G.; He, X. Designing a monolithic tip-tilt-piston flexure manipulator. Arch. Civ. Mech. Eng. 2017, 17, 871–879. [Google Scholar] [CrossRef]
- Awtar, S.; Slocum, A.H. Constraint-Based Design of Parallel Kinematic XY Flexure Mechanisms. J. Mech. Des. 2007, 129, 816–830. [Google Scholar] [CrossRef]
- Awtar, S.; Parmar, G. Design of a Large Range XY Nanopositioning System. J. Mech. Robot. 2013, 5, 021008. [Google Scholar] [CrossRef]
- Xu, Q. New Flexure Parallel-Kinematic Micropositioning System with Large Workspace. IEEE Trans. Robot. 2012, 28, 478–491. [Google Scholar] [CrossRef]
- Lai, L.J.; Gu, G.Y.; Zhu, L.M. Design and control of a decoupled two degree of freedom translational parallel micro-positioning stage. Rev. Sci. Instrum. 2012, 83, 045105-1–045105-17. [Google Scholar] [CrossRef] [PubMed]
- Olfatnia, M.; Cui, L.; Chopra, P.; Awtar, S. Large range dual-axis micro-stage driven by electrostatic comb-drive actuators. J. Micromech. Microeng. 2013, 23, 105008-1–105008-11. [Google Scholar] [CrossRef]
- Qin, Y.; Shirinzadeh, B.; Tian, Y.; Zhang, D. Design issues in a decoupled XY stage: Static and dynamics modeling, hysteresis compensation, and tracking control. Sens. Actuators A Phys. 2013, 194, 95–105. [Google Scholar] [CrossRef]
- Xu, Q. A modular two-axis compliant parallel micropositioning stage with long travel range. In Proceedings of the 2013 IEEE International Conference on Information and Automation (ICIA), Yinchuan, China, 26–28 August 2013; pp. 898–903. [Google Scholar]
- Tian, Y.; Liu, C.; Liu, X.; Wang, F.; Li, X.; Qin, Y.; Zhang, D.; Shirinzadeh, B. Design, modelling and characterization of a 2-DOF precision positioning platform. Trans. Inst. Meas. Control 2014, 37, 396–405. [Google Scholar] [CrossRef]
- Huang, S.C.; Dao, T.P. Design and computational optimization of a flexure-based XY positioning platform using FEA-based response surface methodology. Int. J. Precis. Eng. Manuf. 2016, 17, 1035–1048. [Google Scholar] [CrossRef]
- Pang, J.; Liu, P.; Yan, P.; Zhang, Z. Modeling and experimental testing of a composite bridge type amplifier based nano-positioner. In Proceedings of the 2016 IEEE International Conference on Manipulation, Manufacturing and Measurement on the Nanoscale (3M-NANO), IEEE, Chongqing, China, 18–22 July 2016; pp. 25–30. [Google Scholar]
- Wan, S.; Xu, Q. Design and analysis of a new compliant XY micropositioning stage based on Roberts mechanism. Mech. Mach. Theory 2016, 95, 125–139. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, Y.; Xu, Q. Design and control of a novel piezo-driven XY parallel nanopositioning stage. Microsyst. Technol. 2016, 23, 1067–1080. [Google Scholar] [CrossRef]
- Guo, Z.; Tian, Y.; Liu, C.; Wang, F.; Liu, X.; Shirinzadeh, B.; Zhang, D. Design and control methodology of a 3-DOF flexure-based mechanism for micro-/nano-positioning. Robot. Comput.-Integr. Manuf. 2015, 32, 93–105. [Google Scholar] [CrossRef]
- Cai, K.; Tian, Y.; Wang, F.; Zhang, D.; Shirinzadeh, B. Development of a piezo-driven 3-DOF stage with T-shape flexible hinge mechanism. Robot. Comput.-Integr. Manuf. 2016, 37, 125–138. [Google Scholar] [CrossRef]
- Wang, R.; Zhang, X. A planar 3-DOF nanopositioning platform with large magnification. Precis. Eng. 2016, 46, 221–231. [Google Scholar] [CrossRef]
- Li, Y.; Xu, Q. A Totally Decoupled Piezo-Driven XYZ Flexure Parallel Micropositioning Stage for Micro/Nanomanipulation. IEEE Trans. Autom. Sci. Eng. 2011, 8, 265–279. [Google Scholar] [CrossRef]
- Zhang, X.; Xu, Q. Design of a new decoupled compliant XYZ parallel-kinematic nanopositioning stage. In Proceedings of the TENCON 2015—2015 IEEE Region 10 Conference, Macao, China, 1–4 November 2015; pp. 1–4. [Google Scholar]
- Zhang, X.; Xu, Q.; Macau, P. Design and Analysis of a New XYZ Parallel Flexure Stage. In Proceedings of the 14th IFToMM World Congress, Taibei, Taiwan, 25–30 October 2015; pp. 706–710. [Google Scholar]
- Merlet, J.P. Parallel Robots; Springer Science & Business Media: New York, NY, USA, 2006; Volume 128. [Google Scholar]
- Huang, Z.; Kong, L.; Fang, Y.F. Theory on Parallel Robotics and Control; Machinery Industry: Beijing, China, 1997; pp. 293–302. [Google Scholar]
- Law, M.; Ihlenfeldt, S.; Wabner, M.; Altintas, Y.; Neugebauer, R. Position-dependent dynamics and stability of serial-parallel kinematic machines. CIRP Ann. 2013, 62, 375–378. [Google Scholar] [CrossRef]
- Oba, Y.; Yamada, Y.; Igarashi, K.; Katsura, S.; Kakinuma, Y. Replication of skilled polishing technique with serial–parallel mechanism polishing machine. Precis. Eng. 2016, 45, 292–300. [Google Scholar] [CrossRef]
- Tang, C.; Zhang, M.; Cao, G. Design and testing of a novel flexure-based 3-degree-of-freedom elliptical micro-/nano-positioning motion stage. Adv. Mech. Eng. 2017, 9, 168781401772524. [Google Scholar] [CrossRef]
- Cai, K.; Tian, Y.; Wang, F.; Zhang, D.; Liu, X.; Shirinzadeh, B. Design and control of a 6-degree-of-freedom precision positioning system. Robot. Comput.-Integr. Manuf. 2017, 44, 77–96. [Google Scholar] [CrossRef]
- Lobontiu, N. Compliance-based matrix method for modeling the quasi-static response of planar serial flexure-hinge mechanisms. Precis. Eng. 2014, 38, 639–650. [Google Scholar] [CrossRef]
- Koseki, Y.; Tanikawa, T.; Koyachi, N.; Arai, T. Kinematic analysis of a translational 3-DOF micro-parallel mechanism using the matrix method. Adv. Robot. 2002, 16, 251–264. [Google Scholar] [CrossRef]
- Pham, H.H.; Chen, I.M. Stiffness modeling of flexure parallel mechanism. Precis. Eng. 2005, 29, 467–478. [Google Scholar] [CrossRef]
- Venkiteswaran, V.K.; Su, H.J. Pseudo-Rigid-Body Models of Initially-Curved and Straight Beams for Designing Compliant Mechanisms. In Proceedings of the Volume 5A: 41st Mechanisms and Robotics Conference, Cleveland, OH, USA, 6–9 August 2017. [Google Scholar]
- Li, N.; Su, H.J.; Zhang, X.P. Accuracy Assessment of Pseudo-Rigid-Body Model for Dynamic Analysis of Compliant Mechanisms. J. Mech. Robot. 2017, 9, 054503. [Google Scholar] [CrossRef]
- Verotti, M. Analysis of the center of rotation in primitive flexures: Uniform cantilever beams with constant curvature. Mech. Mach. Theory 2016, 97, 29–50. [Google Scholar] [CrossRef]
- Verotti, M. Effect of initial curvature in uniform flexures on position accuracy. Mech. Mach. Theory 2018, 119, 106–118. [Google Scholar] [CrossRef]
- Belfiore, N.P.; Balucani, M.; Crescenzi, R.; Verotti, M. Performance Analysis of Compliant MEMS Parallel Robots Through Pseudo-Rigid-Body Model Synthesis. In Proceedings of the ASME 2012 11th Biennial Conference on Engineering Systems Design and Analysis, Nantes, France, 2–4 July 2012; pp. 329–334. [Google Scholar]
- Jiang, Y.; Li, T.; Wang, L. Design, Development, and Application of a Compact Flexure-Based Decoupler With High Motion Transmission Efficiency and Excellent Input Decoupling Performance. IEEE/ASME Trans. Mechatron. 2017, 22, 1071–1081. [Google Scholar] [CrossRef]
- Xu, Q.; Li, Y. Optimal design and fabrication of a piezoactuated flexure XYZ parallel micropositioning stage. In Proceedings of the 2010 IEEE/RSJ International Conference on Intelligent Robots and Systems, Taiwan, 18–22 October 2010; pp. 3682–3687. [Google Scholar]
- Li, Y.; Xu, Q. Design and Analysis of a Totally Decoupled Flexure-Based XY Parallel Micromanipulator. IEEE Trans. Robot. 2009, 25, 645–657. [Google Scholar]
- Li, Y.; Xu, Q. A Novel Piezoactuated XY Stage With Parallel, Decoupled, and Stacked Flexure Structure for Micro-/Nanopositioning. IEEE Trans. Ind. Electron. 2011, 58, 3601–3615. [Google Scholar] [CrossRef]
- Lin, S.; Jia, Y.; Lei, I.P.; Xu, Q. Design and optimization of a long-stroke compliant micropositioning stage driven by voice coil motor. In Proceedings of the 2012 12th International Conference on Control Automation Robotics & Vision (ICARCV). IEEE, Guangzhou, China, 5–7 December 2012; pp. 1716–1721. [Google Scholar]
- Liu, Y.; Wu, K.; Xu, D.; Xu, Q. Design of a microscope auto-focusing device based on multi-stage leaf spring. In Proceedings of the 2014 IEEE International Conference on Information and Automation (ICIA), Hailar, China, 28–30 July 2014; pp. 1–6. [Google Scholar]
- Sigmund, O. On the Design of Compliant Mechanisms Using Topology Optimization. Mech. Struct. Mach. 1997, 25, 493–524. [Google Scholar] [CrossRef]
- Jonsmann, J.; Sigmund, O.; Bouwstra, S. Compliant thermal microactuators. Sens. Actuators A Phys. 1999, 76, 463–469. [Google Scholar] [CrossRef]
- Lee, E.; Gea, H.C. A strain based topology optimization method for compliant mechanism design. Struct. Multidiscip. Optim. 2013, 49, 199–207. [Google Scholar] [CrossRef]
- Gaynor, A.T.; Meisel, N.A.; Williams, C.B.; Guest, J.K. Multiple-Material Topology Optimization of Compliant Mechanisms Created Via PolyJet Three-Dimensional Printing. J. Manuf. Sci. Eng. 2014, 136, 061015-1–061015-10. [Google Scholar] [CrossRef]
- Huang, X.; Li, Y.; Zhou, S.; Xie, Y. Topology optimization of compliant mechanisms with desired structural stiffness. Eng. Struct. 2014, 79, 13–21. [Google Scholar] [CrossRef]
- Wang, Y.; Luo, Z.; Zhang, X.; Kang, Z. Topological design of compliant smart structures with embedded movable actuators. Smart Mater. Struct. 2014, 23, 045024-1–045024-15. [Google Scholar] [CrossRef]
- Leon, D.M.D.; Alexandersen, J.; Fonseca, J.S.O.; Sigmund, O. Stress-constrained topology optimization for compliant mechanism design. Struct. Multidiscip. Optim. 2015, 52, 929–943. [Google Scholar] [CrossRef]
- Yoo, K.S.; Han, S.Y. Topology optimum design of compliant mechanisms using modified ant colony optimization. J. Mech. Sci. Technol. 2015, 29, 3321–3327. [Google Scholar] [CrossRef]
- Lum, G.Z.; Teo, T.J.; Yang, G.; Yeo, S.H.; Sitti, M. Integrating mechanism synthesis and topological optimization technique for stiffness-oriented design of a three degrees-of-freedom flexure-based parallel mechanism. Precis. Eng. 2015, 39, 125–133. [Google Scholar] [CrossRef]
- Bharanidaran, R.; Srikanth, S.A. A new method for designing a compliant mechanism based displacement amplifier. IOP Conf. Ser. Mater. Sci. Eng. 2016, 149, 012129-1–012129-7. [Google Scholar] [CrossRef]
- Jin, M.; Zhang, X. A new topology optimization method for planar compliant parallel mechanisms. Mech. Mach. Theory 2016, 95, 42–58. [Google Scholar] [CrossRef]
- Xu, Q. Design of a Large-Stroke Bistable Mechanism for the Application in Constant-Force Micropositioning Stage. J. Mech. Robot. 2016, 9, 011006-1–011006-7. [Google Scholar] [CrossRef]
- Wang, P.; Xu, Q. Design of a flexure-based constant-force XY precision positioning stage. Mech. Mach. Theory 2017, 108, 1–13. [Google Scholar] [CrossRef]
- Xu, Q. Micromachines for Biological Micromanipulation; Springer: New York, NY, USA, 2018. [Google Scholar]
- Bikas, H.; Stavropoulos, P.; Chryssolouris, G. Additive manufacturing methods and modelling approaches: A critical review. Int. J. Adv. Manuf. Technol. 2015, 83, 389–405. [Google Scholar] [CrossRef]


| Year | Ref. | Planar Size (mm) | Actuator | Workspace (m) | Resolution (nm) | Frequency (Hz) | Decoupler | Coupling Error (%) |
|---|---|---|---|---|---|---|---|---|
| 2007 | [85] | 300 × 300 | PEA | 5 × 5 × 10 | - | - | CPF | 1 |
| 2010 | [86] | 385 × 385 | EMA | 10 × 10 × 10 | 4 | 18 | CPF | - |
| 2012 | [87] | 214 × 214 | EMA | 10.5 × 10.5 × 10 | - | 23 | CPF | 1.6 |
| 2012 | [88] | - | PEA | 41 × 41 | 3 | 340 | CPF | 0.5 |
| 2013 | [89] | 2.6 × 2.6 | ESA | 225 × 225 | - | 400 | PF | 3 |
| 2013 | [90] | 230 × 230 | PEA | 8 × 8 | - | 665.4 | PF | 2 |
| 2013 | [91] | 120 × 120 | EMA | 11.77 × 11.62 × 10 | 200 | 30 | CPF | 0.55 |
| 2014 | [92] | - | PEA | 8 × 8 | - | 231 | PF | 0.6 |
| 2016 | [93] | 130.9 × 130.9 | PEA | 125 × 125 | - | 740 | PF | 0.5 |
| 2016 | [94] | - | PEA | 100.9 × 100.2 | - | - | PF | 0.4 |
| 2016 | [95] | 244 × 244 | EMA | 14 × 14 × 10 | - | 20 | RM | 1.7 |
| 2016 | [96] | 61 × 61 | PEA | 127 × 127 | 20 | 200 | PF | 4.7 |
| Year | Ref. | Planar Size (mm) | Actuator | Workspace (m, mrad) | Resolution (nm, rad) | Frequency (Hz) | |
|---|---|---|---|---|---|---|---|
| Translation | Rotation | ||||||
| 2014 | [58] | 142 × 110 | PEA | {39.03 × 24.96, -} | - | 1291.4 | 2089.4 |
| 2015 | [97] | 170 × 170 | PEA | {12.74 × 12.22, 16.67} | - | 1050 | 790 |
| 2016 | [98] | - | PEA | {6.9 × 8.5, 0.29} | {50, 1.25} | 629.3 | 522.5 |
| 2016 | [99] | - | PEA | {283.13 × 284.78, 8.73} | {5.7, 1} | 243.09 | 405.52 |
| 2017 | [57] | 162.7 × 141.7 | PEA | {147.84 × 137.96, 3.75} | - | 199.7 | - |
| 2017 | [75] | 200 × 200 | PEA | {36.5 × 32, 1.24} | - | 349.8 | - |
| Year | Ref. | Prototype | Size (mm) | Actuator | Workspace (m/axis) | Resolution (nm) | Frequency (Hz) | Decoupler | Coupling Error (%) |
|---|---|---|---|---|---|---|---|---|---|
| 2011 | [100] | Yes | - | PEA | 165 | 180 | - | CPF | 3.6 |
| 2015 | [101] | No | - | EMA | - | - | 60.6 | RM | 1 |
| 2015 | [102] | No | - | PEA | 22.32 | - | 106.3 | CPF | 0.5 |
| 2015 | [68] | No | - | PEA | 153 | - | - | CPF | 0.73 |
| 2015 | [69] | No | 68.5 × 68.5 × 68.5 | PEA | 120 | - | 226 | PF | 0.75 |
| 2016 | [63] | No | - | PEA | - | - | 274 | PF | - |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Z.; Xu, Q. Survey on Recent Designs of Compliant Micro-/Nano-Positioning Stages. Actuators 2018, 7, 5. https://doi.org/10.3390/act7010005
Wu Z, Xu Q. Survey on Recent Designs of Compliant Micro-/Nano-Positioning Stages. Actuators. 2018; 7(1):5. https://doi.org/10.3390/act7010005
Chicago/Turabian StyleWu, Zeyi, and Qingsong Xu. 2018. "Survey on Recent Designs of Compliant Micro-/Nano-Positioning Stages" Actuators 7, no. 1: 5. https://doi.org/10.3390/act7010005
APA StyleWu, Z., & Xu, Q. (2018). Survey on Recent Designs of Compliant Micro-/Nano-Positioning Stages. Actuators, 7(1), 5. https://doi.org/10.3390/act7010005






