Next Article in Journal
Optimization Design of Electromagnetic Actuator Applied as Fast Tool Servo
Next Article in Special Issue
Efficient Structure-Based Models for the McKibben Contraction Pneumatic Muscle Actuator: The Full Description of the Behaviour of the Contraction PMA
Previous Article in Journal
Flexible Medical Devices: Review of Controllable Stiffness Solutions
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Actuators
Volume 6
Issue 3
10.3390/act6030024
actuators-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Review

Recent Progress on BaTiO3-Based Piezoelectric Ceramics for Actuator Applications

by
Jinghui Gao
1,*,
Dezhen Xue
1,
Wenfeng Liu
1,
Chao Zhou
1 and
Xiaobing Ren
1,2,*
1
State Key Laboratory of Electrical Insulation and Power Equipment and Multi-Disciplinary Materials Research Center, Frontier Institute of Science and Technology, Xi’an Jiaotong University, Xi’an 710049, China
2
Ferroic Physics Group, National Institute for Materials Science, Tsukuba 305-0047, Ibaraki, Japan
*
Authors to whom correspondence should be addressed.
Actuators 2017, 6(3), 24; https://doi.org/10.3390/act6030024
Submission received: 15 June 2017 / Revised: 14 July 2017 / Accepted: 23 July 2017 / Published: 31 July 2017
(This article belongs to the Special Issue Electrochemical and Electromechanical Actuators)
Browse Figures
Versions Notes

Abstract

:
Due to issues with Pb toxicity, there is an urgent need for high performance Pb-free alternatives to Pb-based piezoelectric ceramics. Although pure BaTiO3 material exhibits fairly low piezoelectric coefficients, further designing of such a material system greatly enhances the piezoelectric response by means of domain engineering, defects engineering, as well as phase boundary engineering. Especially after the discovery of a Ba(Zr0.2Ti0.8)O3–x(Ba0.7Ca0.3)TiO3 system with extraordinarily high piezoelectric properties (d33 > 600 pC/N), BaTiO3-based piezoelectric ceramics are considered as one of the promising Pb-free substitutes. In the present contribution, we summarize the idea of designing high property BaTiO3 piezoceramic through domain engineering, defect-doping, as well as morphotropic phase boundary (MPB). In spite of its drawback of low Curie temperature, BaTiO3-based piezoelectric materials can be considered as an excellent model system for exploring the physics of highly piezoelectric materials. The relevant material design strategy in BaTiO3-based materials can provide guidelines for the next generation of Pb-free materials with even better piezoelectric properties that can be anticipated in the near future.

1. Introduction

Actuators are devices that can convert input energy into mechanical energy [1]. Among the varieties of actuators with different input energy (including electromagnetic, electrostatic, and thermal energies [2,3,4] etc.), piezoelectric actuators feature high strain output, high response speed, and high displacement control accuracy. As a result of those advantages, piezoelectric actuators have found wide applications ranging from high-tech equipment such as scanning tunnel microscopy (STM) and atomic force microscopy (AFM), to our daily life devices such as digital cameras and cellular phone terminals [5]. Most piezoelectric actuators rely on a material with fairly large electromechanical response, known as the piezoelectric material. When applying an electric field in a certain direction, the piezoelectric material can generate a series of strain components satisfying various specific application requirements for actuators. The degree of electromechanical response for piezoelectric material, which determines the strain level with respect to external electric field, plays a crucial role on the performance of actuators.
For more than 70 years, PZT (PbZr1 − xTixO3) piezoelectric ceramics have been the workhorse of piezoelectric actuator technology [6]. Later in the 1990s, relaxor type piezoelectric single crystal materials, such as PMN–PT (Pb(Mg1/3Nb2/3)O3–xPbTiO3) and PZN–PT(Pb(Zn1/3Nb2/3)O3–xPbTiO3) were discovered [6,7,8,9,10,11]. All these Pb-based piezoelectric materials dominate the actuator applications of piezoelectric materials due to their high longitudinal electromechanical coupling ( k 33 ) and large longitudinal piezoelectric coefficient ( d 33 ). Table 1 lists the properties of these Pb-based materials [6,7,12,13,14,15]. The Pb-containing piezoelectrics have been further modified into a number of materials, and the corresponding products have been well commercialized and found mature applications.
However, the family of Pb-based materials is now facing the challenge for its environmental compatibility, since it contains the toxic heavy-metal element Pb. And, there exists potential danger during the manufacture, use, and disposal of these materials. In particular, recent global restrictions are demanding the elimination of Pb from all consumer items, which makes it an urgent need to develop a Pb-free substitute that can have piezoelectric properties resembling the Pb-containing materials [16,17,18,19,20,21,22,23]. Although the majority of existing Pb-free materials have inferior piezoelectric properties compared with Pb-based ones [24,25,26,27], the solid-state physicians and material scientists have never given up on developing environmental-friendly piezoelectrics, and the publication number for Pb-free piezoelectric materials keeps growing in recent decades (Figure 1).
Up to now, the widely investigated Pb-free piezoelectric materials have focused on, but are not limited to KNN ((K1/2Na1/2)NbO3)-based, BNT ((Bi1/2Na1/2)TiO3) or BKT ((Bi1/2K1/2)TiO3)-based, and BaTiO3-based ferroelectric material systems, which show large piezoelectric response [17,18,19,20,21,22,23,24,25,26,27]. Among these potential substitutions for PZT, the class of BaTiO3-based piezoelectric material is easy to process with better electromechanical properties. Despite its drawback of fairly low Curie temperature of approximately 100 °C, the recent discoveries of large electromechanical activities in BaTiO3-based material (shown in Table 1) make it a model system for understanding the underlying physics of Pb-free piezoelectrics, and thus it can provide a tutorial for the design of Pb-free piezoelectric material systems [14]. Due to these reasons, the number of research papers on the piezoelectric response in BaTiO3–based material has been increasing year by year (Figure 1).
This contribution will give an overview of BaTiO3-based piezoelectric materials with high piezoelectric properties and will be arranged as follows. Section 2 introduces the piezoelectric response in an undoped BaTiO3 material system and its domain engineering. Section 3 reviews the enhanced electromechanical effect induced by doping point defects. And, we will focus on the large piezoelectric effect caused by introducing phase boundary or interferroelectric transitions in Section 4. The applications and prospective thoughts will be given in Section 5.

2. Undoped BaTiO3

2.1. BaTiO3 Ceramics and Single Crystal

The BaTiO3 was discovered during World War II as a high capacitance material and was the first discovered ferroelectric compound with a perovskite structure. Later on, the electrostriction effect for the unpoled polycrystalline ceramics of BaTiO3 as well as the piezoelectricity for the electrically poled samples was found, leading to many applications earlier than the Pb-containing material, PZT.
Table 2 shows the basic piezoelectric coefficients for undoped BaTiO3 single crystal and the polycrystalline ceramic [28]. It can be seen that these parameters are fairly low compared with PZT ceramics. For example, the piezoelectric coefficient d33 can only reach the value of 191 pC/N for a BaTiO3 ceramic and 85.6 pC/N for a single crystal specimen, which are only 3–5 fold that of PZT materials [29]. Moreover, the Curie temperature for a BaTiO3 system Tc~130 °C is much lower compared with PZT and the relevant Pb-containing piezoelectric material systems. Owing to these disadvantages, although being earlier discovered, the BaTiO3 has not been found the satisfactory application on the associated piezoelectric devices such as actuators. Therefore, further treatments are necessary to enhance the piezoelectric properties for such a material system.

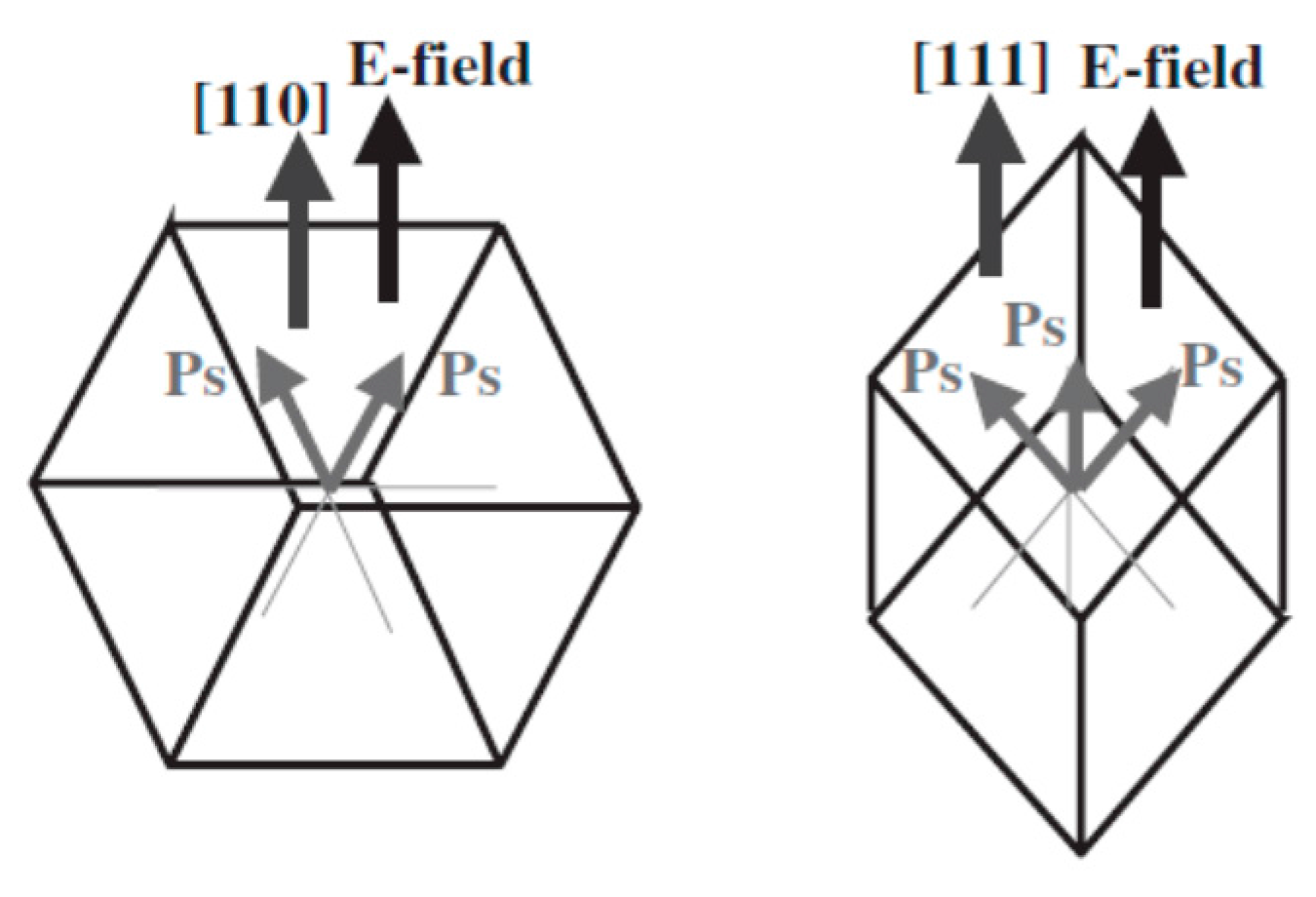
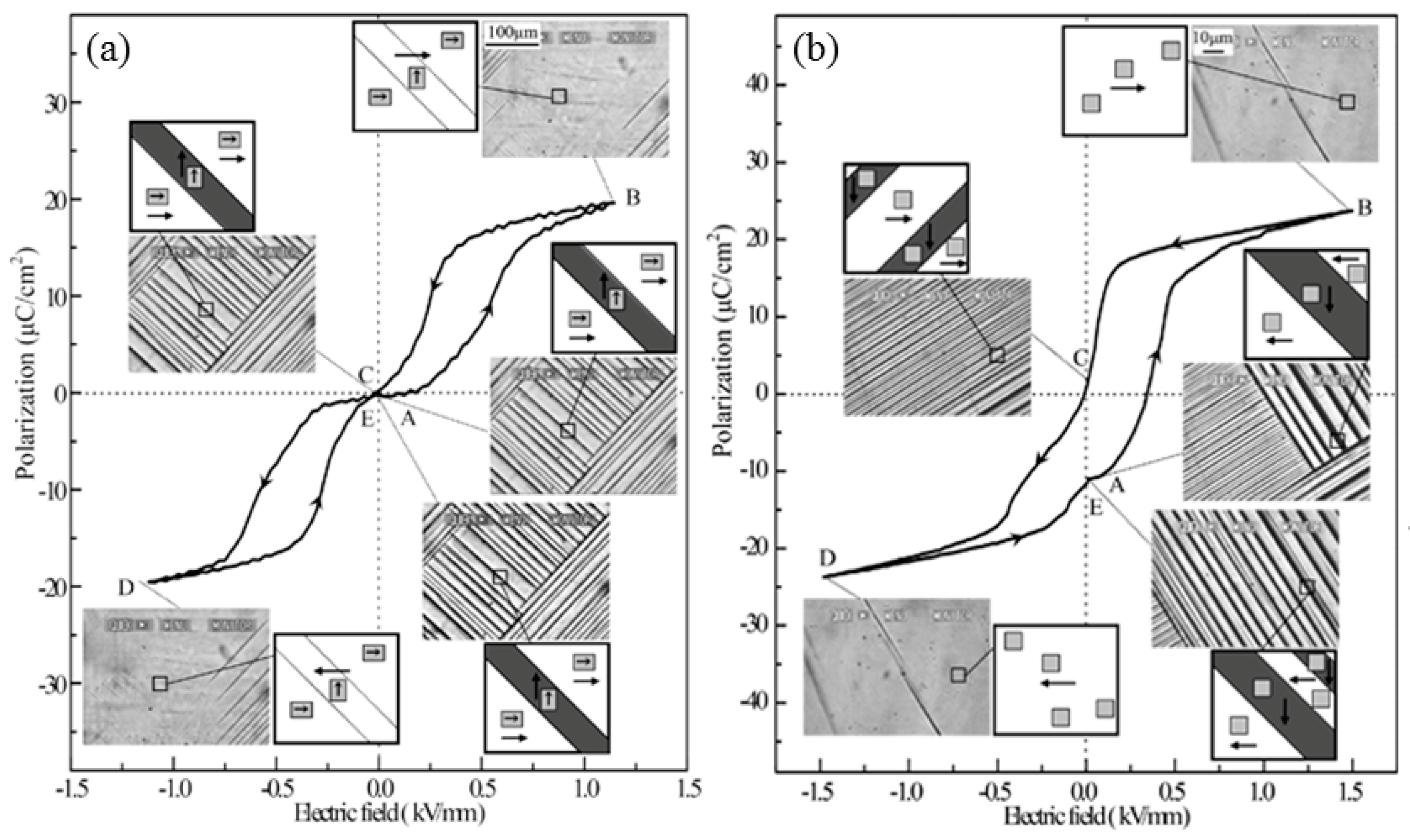
2.2. Domain-Engineered BaTiO3

Since the piezoelectric effect is fairly low for a BaTiO3 single crystal poled along the polar axis, a so-called domain wall engineering technique has been employed, making use of the piezoelectric anisotropy of single crystals [30,31,32]. It has been performed by poling the single crystal with the electric field along the direction which has an intersection angle with respect to the crystallographic polar axis. For example, Figure 2 shows the schematic model of the engineered domain configurations for the tetragonal 4 mm ferroelectric crystals [33]. If the poling electric field is along the [110] direction, it will generate two equally-preferred ferroelectric domains with spontaneous polarizations (PS) along [100] and [010], respectively. In the case of [111] poled crystal, [100], [010], and [001] are three favorable PS alignments for ferroelectric domains. Complex domain configuration has been formed, which enables enlarged piezoelectric response of the domain-engineered crystal.
The intrinsic piezoelectric anisotropy can be considered as one of the reasons for the enhanced piezoelectric response in a BaTiO3 single crystal [32]. It should be noted that the piezoelectric coefficients (e.g., d33) usually show orientation-dependent phenomenon related with their Gibbs free energy, considering the crystal symmetry. For example, Figure 3 shows the change of piezoelectric coefficient d33* with respect to the orientation in a tetragonal phase crystal [30]. It can be seen that the maximum d33 value has not been achieved along the polar axis which is <001> for tetragonal crystal symmetry. Instead, the d33 along the [111] direction shows a larger value compared with that of <001> directions, which is mainly due to the piezoelectric anisotropy in the crystal.
On the other hand, the extrinsic contribution also plays a crucial role in further enhancing the piezoelectric response for BaTiO3 single crystals. Wada et al. reported that high piezoelectric effect can be obtained by reducing the size of ferroelectric domains with a domain-engineered configuration [34]. As shown in Figure 4, as the domain size decrease from 40 μm to 5.5 μm according to their polling conditions, the piezoelectric coefficient d31 increases from 97.8 pC/N to 230 pC/N, which suggests that enhanced piezoelectric response can be achieved in a fine engineered-domain configuration [34]. Moreover, a strong piezoelectric response can be obtained by forming even smaller domains, i.e., nanodomains in BaTiO3 ceramic, suggested by Takahashi et al. and Karaki et al. Wada et al. even reported d33 value of 788 pC/N in a template-grain-grown BaTiO3 ceramic which might have partial contribution from orientation effects [35,36,37]. Such a size-dependent phenomenon might be due to the enlarged charged domain wall density in an engineered-domain configuration [38]. On the other hand, the 90° domain wall contribution has also been considered as the reason for enhanced piezoelectric in nanodomain tetragonal BaTiO3 single crystals [39].

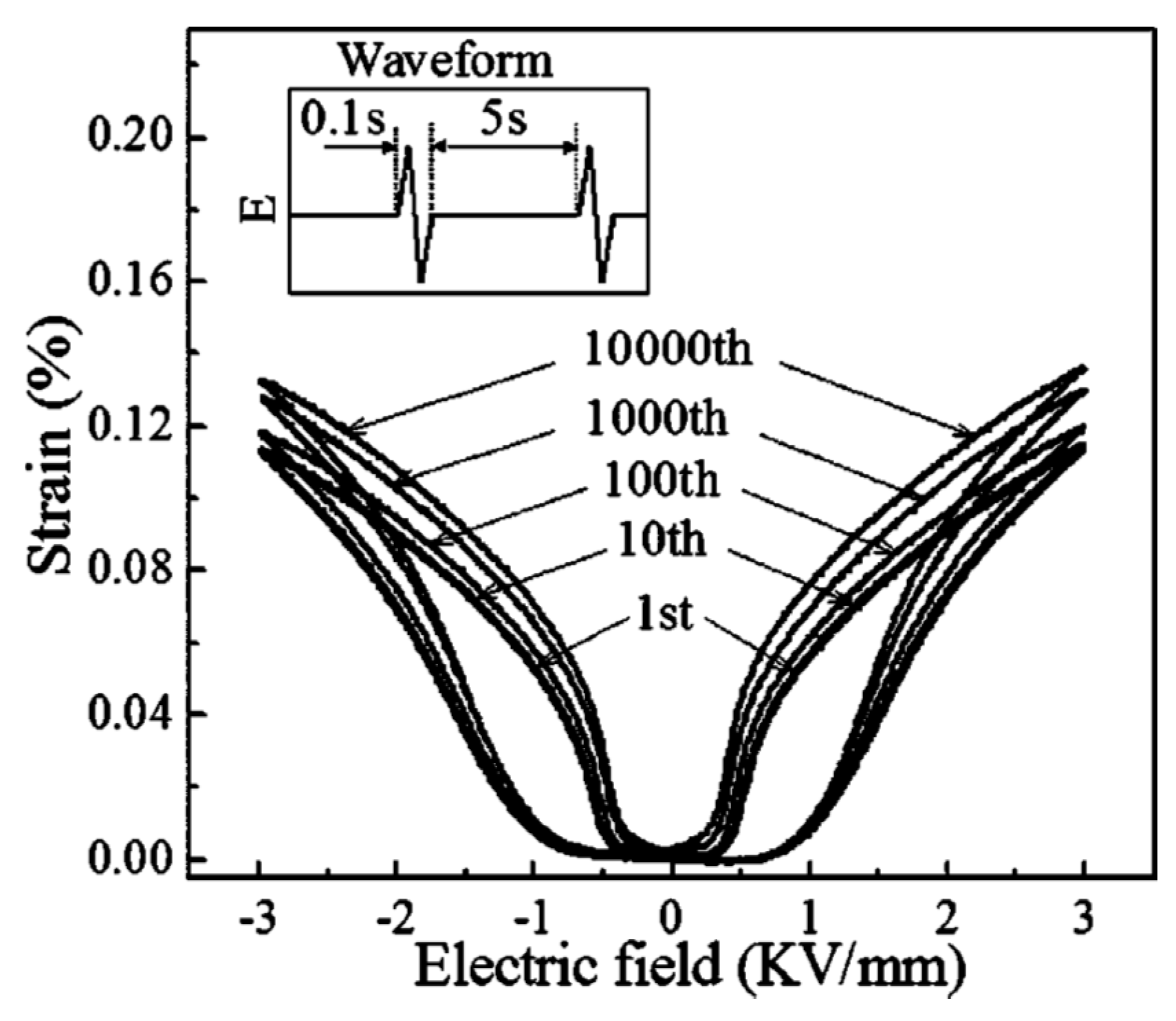
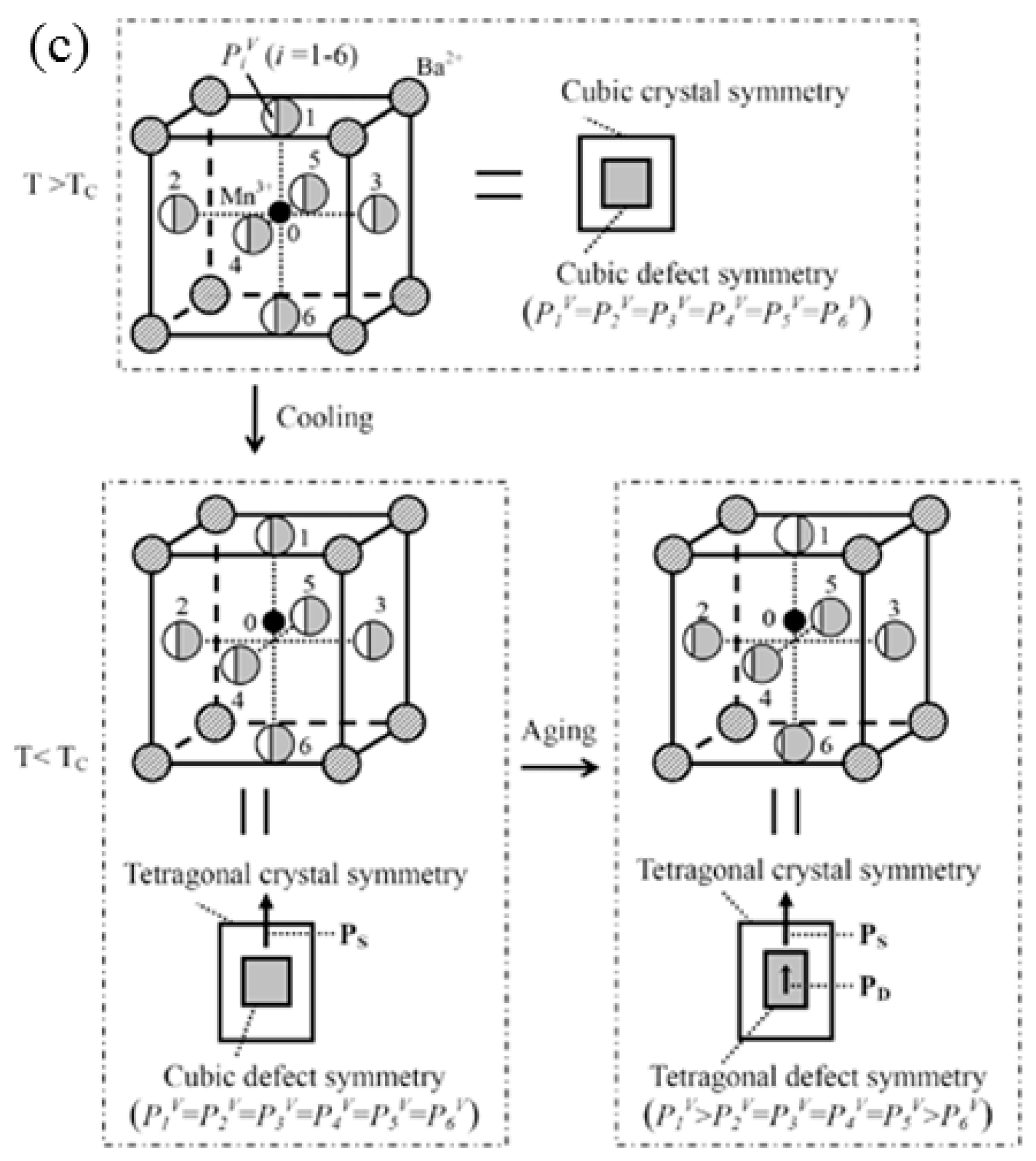
3. Large Non-Linear Electrostrain in Aging Point-Defect-Doped BaTiO3

The non-180° domain switching is always accompanied with a large electrostrain due to the exchange of non-equal crystallographic axes. The level of strain due to such a process can reach one or two orders of magnitude larger than the linear strain of poled piezoelectric materials. However, on removal of the electric field, it cannot return to the original unpoled domain configuration, leading to a remnant polarization when the electric field is zero. Hence, it makes the domain switching a one-time or irrecoverable effect that restricts the application of non-180° domain switching for actuator applications. In 2004, our group reported a giant recoverable electrostrain in a ferroelectric-aged BaTiO3 single crystal doped by acceptor ions [40]. And, the strain level can reach up to 0.75% at a low field of 200 V/mm, which largely exceeds the strain of soft PZT ceramics and PZN–PT single crystals under the same electric field conditions. The similar effect was later reported in the aged acceptor-doped BaTiO3-based ceramic (BaSr0.05TiO3–0.01Mn) with a large recoverable nonlinear strain of about 0.12–0.15% at a field of 3 kV/mm, which is higher than that of conventional hard PZT piezoelectric ceramics (as shown in Figure 5) [41]. It should be noted that the electric fatigue study shows that the electrostrain has a good recoverability even after 10,000 cycles at 3 kV/mm electric field as shown in Figure 6.
In order to understand the large recoverable electrostrain in such a material system, in-situ optical microscopic observation has been conducted for BaTiO3 single crystals upon electric field loading [42]. The mesoscopic evidence suggests that using in-situ domain observation shows that the aged Mn-doped BaTiO3 single crystal exhibits a remarkable reversible domain switching during electric field cycling. The giant recoverable electrostrain effect switching a maximum strain of 0.4% has also been observed simultaneously.
The ferroelectric aging effect is quite difficult to understand by the classical ferroelectric theories. It is now generally considered that ferroelectric aging effect originates from the migration of oxygen vacancies inside the materials with time. There are several models to understand the exotic ferroelectric aging effect, including the grain boundary effect, domain wall effect, and the volume effect. (1) The grain boundary effect refers to the oxygen migration into the secondary phase in the grain boundary to form the space charge layer, driven by the depolarization field, and stabilizes the ferroelectric domains [43,44]. (2) The domain wall effect involves the oxygen vacancy migration to the domain walls and pinning of the domain walls electrically or elastically [45,46]. (3) The volume effect refers to the reorientation of point defects with respect to the PS direction with the whole volume, and thus stabilizes the ferroelectric domain states [47,48,49,50,51,52,53]. Among them, the volume effect can explain all ferroelectric aging effects in different systems, and is thus the intrinsic effect for ferroelectric aging.
Based on the volume effect explanation for ferroelectric aging, a more detailed microscopic model has been proposed to consider the interaction between the spontaneous polarization (PS) and the defect dipolar polarization (PD) [40]. The idea of such a principle is that the distribution of oxygen vacancies around the acceptor dopant shows statistic symmetry, known as “defect symmetry”, which has the tendency to conform to the crystal symmetry after aging. As shown in Figure 7, the cubic crystal symmetry has the cubic defect symmetry with symmetric distribution of oxygen vacancies around the acceptor dopants. However, on cooling the sample below TC, the ferroelectric transition will occur, but such a diffusionless transition does not allow the defect symmetry to change abruptly. During aging, the oxygen vacancies will migrate into a non-symmetric defect configuration, which is suitable for the tetragonal crystal symmetry and causes gradual stabilization with time. The above-mentioned degradation of small-signal properties and change of large-signal properties can be explained by such a principle. Besides, a recent study shows that the stabilization effect can be manifested as the Curie temperature gradually increases with aging time [54].

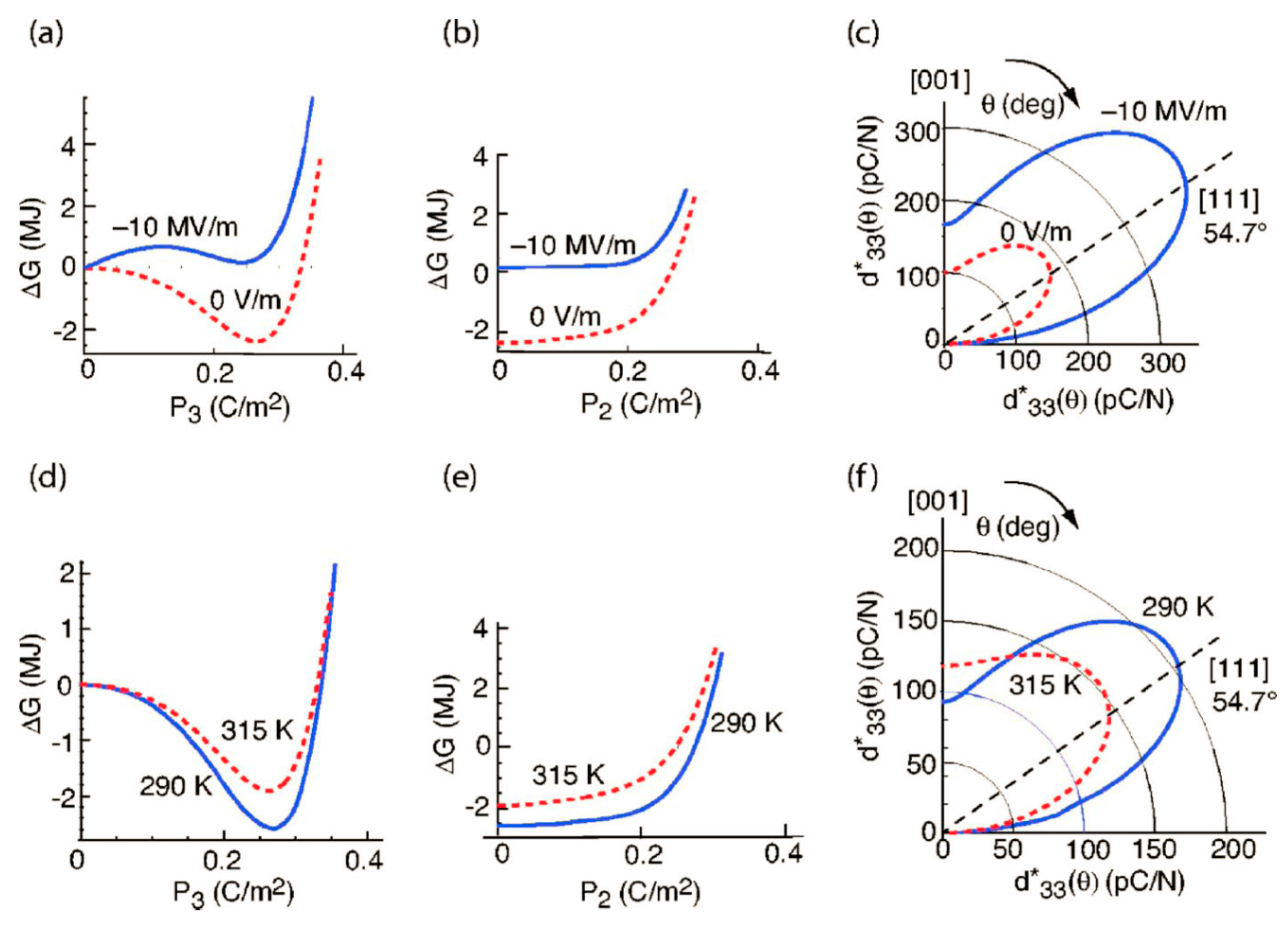
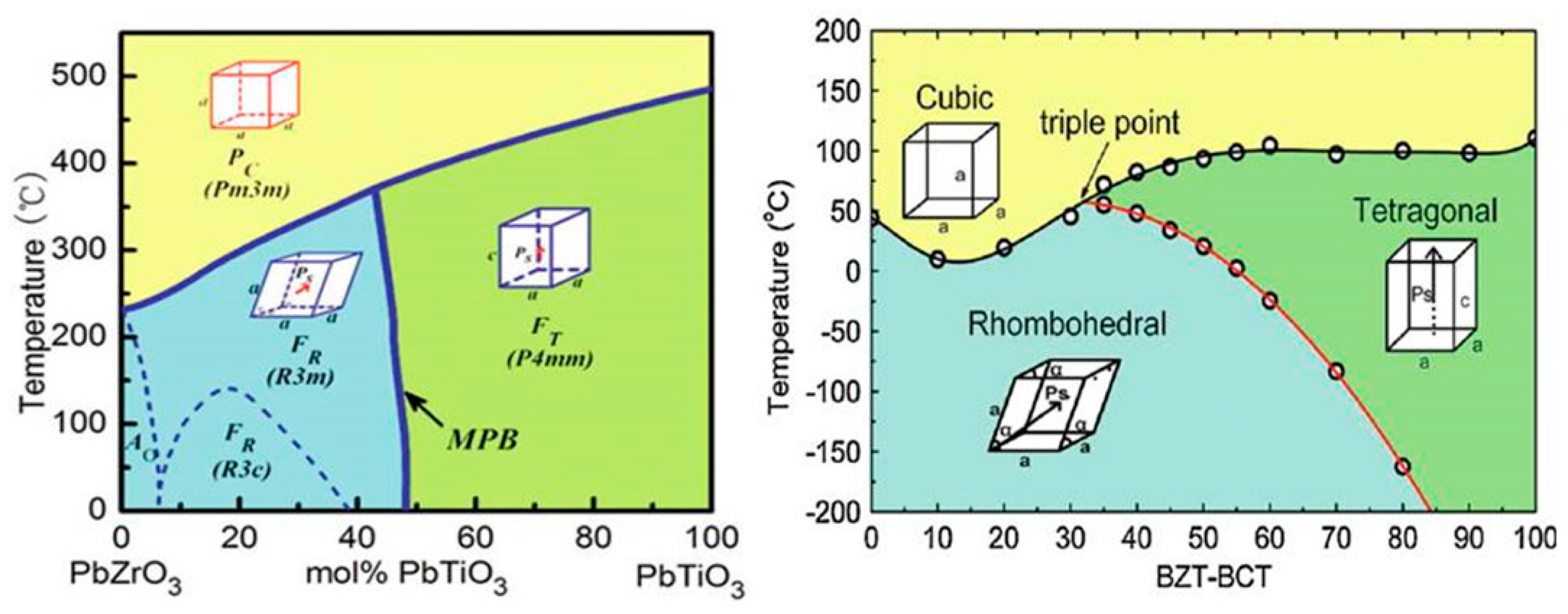
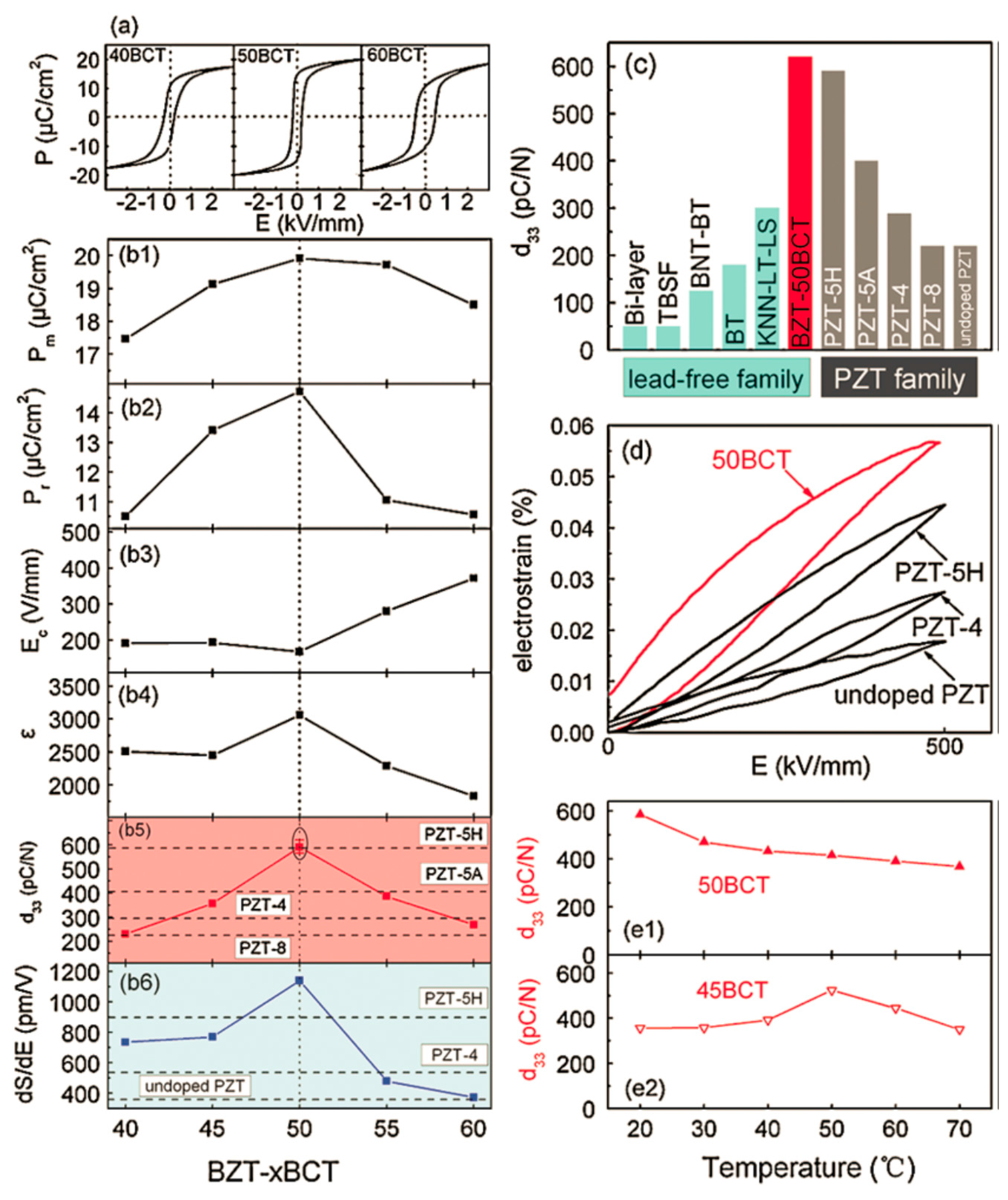
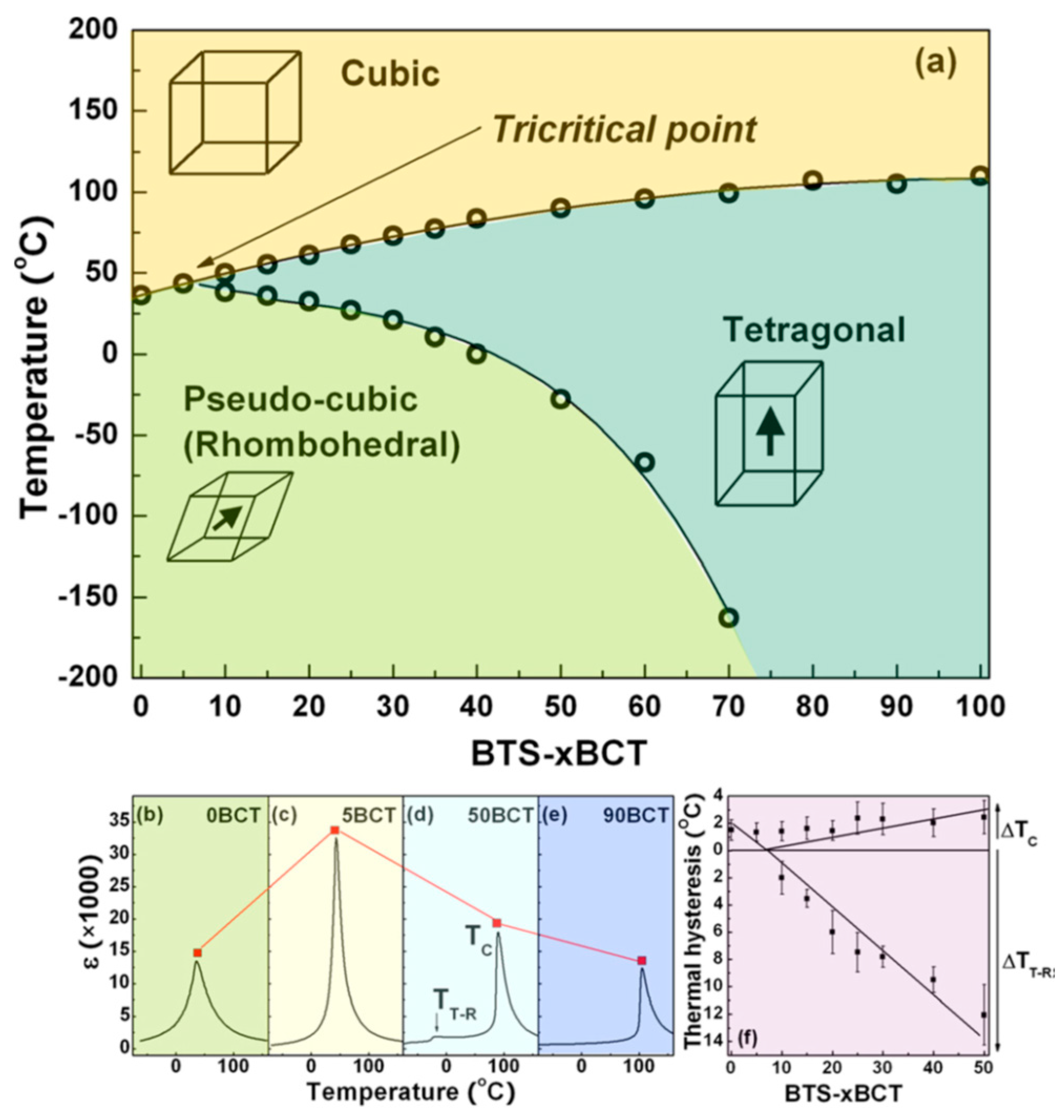
4. Large Piezoelectric Response Caused by Morphotropic Phase Boundary in BaTiO3

4.1. Ba(Zr0.2Ti0.8)O3–(Ba0.7Ca0.3)TiO3

The common approach to achieving high piezoelectricity is to place the composition of the material in the proximity of a phase transition regime between two ferroelectric phases. Such a composition-induced phase transition region in the pseudo-binary composition-temperature phase diagram has been known as the “morphotropic phase boundary (MPB)”. Figure 8 shows the typical phase diagram of PZT [55,56], which is characterized by a vertical MPB separating a ferroelectric rhombohedral (R) phase and a ferroelectric (T) tetragonal phase. At the MPB, there are strong polarization instabilities and vanishing polarization anisotropy, which facilitate ease of polarization rotation by external stress or electric field. It thus results in a high piezoelectricity and permittivity. It should be noted that although MPB and the relevant mechanisms for high piezoelectricity have mainly been discussed for Pb-based systems, it seems to be applicable to Pb-free systems as well.
In our previous work, we proposed a design strategy that combines two Pb-free end compositions to establish a pseudo-binary system with MPB. We selected a certain composition that undergoes only cubic (C) to tetragonal (T) phase transition at the T-end and a certain composition with only cubic (C) to rhombohedral (R) phase transition at the R-end. Then the combination of the selected T-end and R-end will result in a pseudo-binary phase diagram, possessing a MPB separating R and T phases. The first system we designed was the (1 − x)Ba(Zr0.2Ti0.8)O3–x(Ba0.7Ca0.3)TiO3 ((1 − x)BZT–xBCT) [14], where x is the molar percent of BCT, as shown in Figure 8. The Ca2+ concentration was set to be 30 at.% to ensure the pure C-T phase transition, and the Zr4+ concentration was fixed to be 20 at.% to let the pure C-R phase transition occur. The resulting pseudo-binary phase diagram of BZT–BCT is thus characterized by a MPB separating ferroelectric R (BZT side) and T (BCT side) phases. It should be noted that this material system was abbreviated as BZCT or BCZT in some literatures. However, it should be pointed out that it is physically clearer to use BZT–BCT to demonstrate the morphotropic phase boundary origin for such a material system. Such a physical idea has also been adopted in the designing of KNN–based, lead-free piezoelectric materials, and a promisingly large piezoelectric response has been achieved on the phase boundary of some material systems [18,22,57,58].
The terminology “morphotropic phase boundary (MPB)” has been employed for BZT–BCT piezoelectric ceramics. Admittedly, for most of the BaTiO3-based systems such a boundary is named “polymorphic phase boundary (PPB)”, because it is not vertical to the composition axis and thus dependent on temperature. The reason why MPB is still used for BZT–BCT hereafter is to illustrate its similarity with PZT in the phase diagram.
The piezoelectric response and the associated physical properties have been largely enhanced on MPB composition at room temperature, i.e., 0.5BZT–0.5BCT. As shown in Figure 9c, the composition-dependence of the piezoelectric coefficient exhibits a peak with a maximum d33 value of 620 pC/N for 0.5BZT–0.5BCT. Such a d33 level is superior than most of the Pb-free piezoelectric ceramics, and is even comparable with commercialized high-end PZT ceramics [13]. The strain for a 0.5BZT–0.5BCT ceramic can reach 0.05% in an electric field of 500 kV/mm [14], which is even larger than PZT–5H at the same electric field condition. Moreover, Bowman’s group and other groups even reported a larger strain level at a near-MPB composition [59,60,61], which makes BZT–BCT ceramic a promising material for actuator application [62,63,64,65]. Besides piezoelectric coefficients, other parameters, such as maximum polarization, remnant polarization, dielectric permittivity etc. are also enhanced on the MPB composition 0.5BZT–0.5BCT. The detailed physical parameters for the optimal composition of 0.5BZT–0.5BCT are shown in Table 3 [66]. It should be emphasized that the values of the listed parameters are largely determined by the material processing conditions and poling conditions for BZT–BCT ceramics [58,64,65], and the appropriate condition should be selected in order to achieve best properties for the piezoceramic.

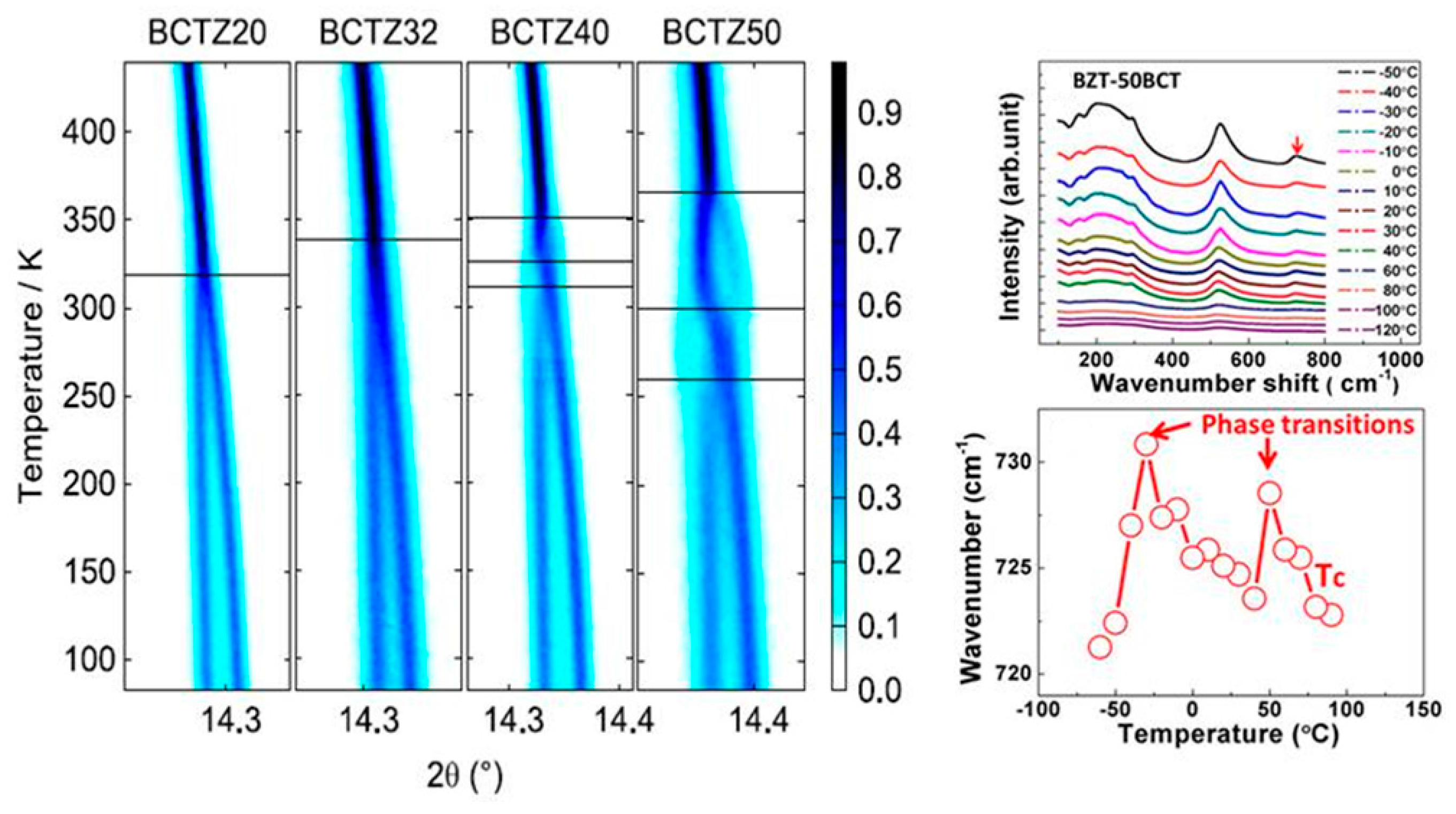
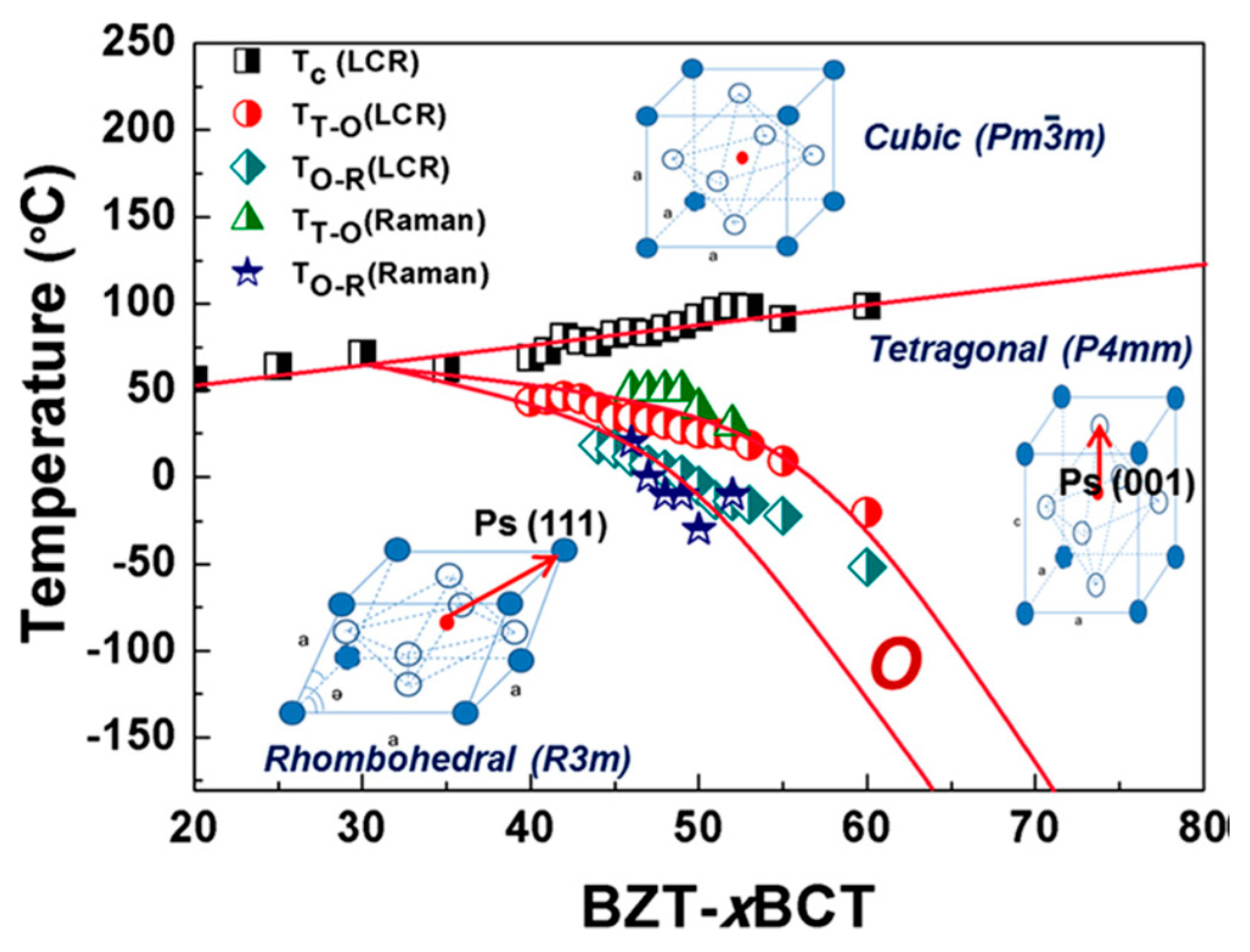
4.2. Crystal Structure

The original idea for the material design for BZT–BCT system was to mix two binaries with tetragonal and rhombohedral symmetries, respectively. Therefore it is natural to expect that on MPB the crystal structure is a combination of tetragonal and rhombohedral. The lab X-ray diffraction studies on 0.5BZT–0.5BCT suggests that the result can be interpreted as a coexisting of tetragonal and rhombohedral crystal symmetries [14,67]. Haugen et al. further employed the high-resolution XRD to study the crystal structure of 0.5BZT–0.5BCT followed by Rietveld analysis. The measured data can be fitted by using the T-R coexisting model [68]. We also used the convergent beam electron diffraction method to prove that diffraction symmetry satisfies the tetragonal and rhombohedral model [69,70].
In contrast, Keeble et al. pointed out that there exists an intermediate phase interleafing the tetragonal and rhombohedral models by investigating the temperature-evolution of high-resolution XRD reflections, and the result is shown in Figure 10 [71]. It can be seen that the measured temperature window can be divided into 4 regions for 0.5BZT–0.5BCT, which is the indication that there exists another phase besides the already-known C, T, and R phases. The Rietveld analysis further suggests an orthorhombic crystal symmetry for such an intermediate phase. And similar conclusions have been drawn from the temperature-dependence of elastic anomalies as well as the Rama spectrum [72,73]. The phase diagram has been modified accordingly as shown in Figure 11. It should be noticed that even if the orthorhombic phase interleafs the T and R phases, it appears in a very narrow temperature and composition region, which blurs the measurements results.

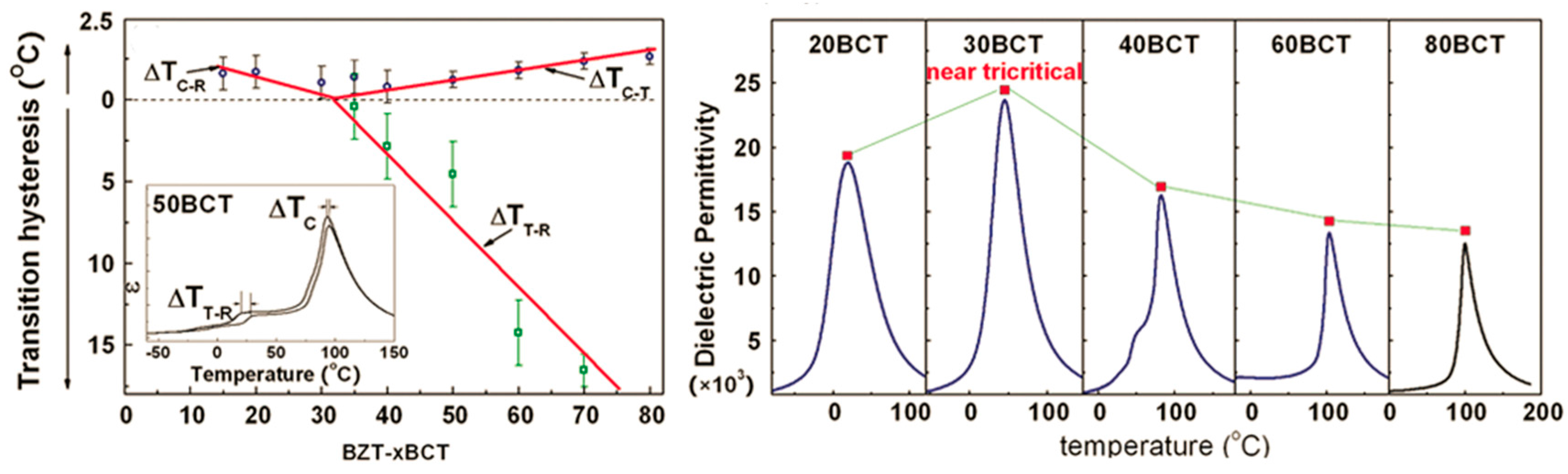
4.3. Tricritical Phenomenon

It should be noted that an important feature of this phase diagram (Figure 11) is the existence of a C-R-T triple point or a C-T-O-R quadruple point in the phase diagram located at x of 32% and at TC of 57 °C. Now, the phase transition behavior for such a point remains controversial, and a central issue is whether or not the multi-phase-coexisting point is a thermodynamic tricritical point, and whether the high piezoelectricity at MPB is affected by the tricritical phenomenon. Liu and Ren proposed that large the piezoelectric response for BZT–BCT is associated with the starting point of MPB, i.e., the C-T-R triple point, which shows a tricritical behavior with the crossover between first order and second order transition (as shown in Figure 12) [14]. On the other hand, it has also been proposed that there is no need for the coincidence between the tricritical point and the triple point, and Acosta et al. pointed out that the maximum coefficient d33 value (best piezoelectric property) does not occur at the triple point [74,75,76]. This indicates the irrelevance between the tricritical point and the high piezoelectric response. It should be noted that the reason for such a dispute stems from the challenge in accurate determination of the position of the triple point and the tricritical point. Further investigations are required in order to solve the discrepancy [77,78,79,80].

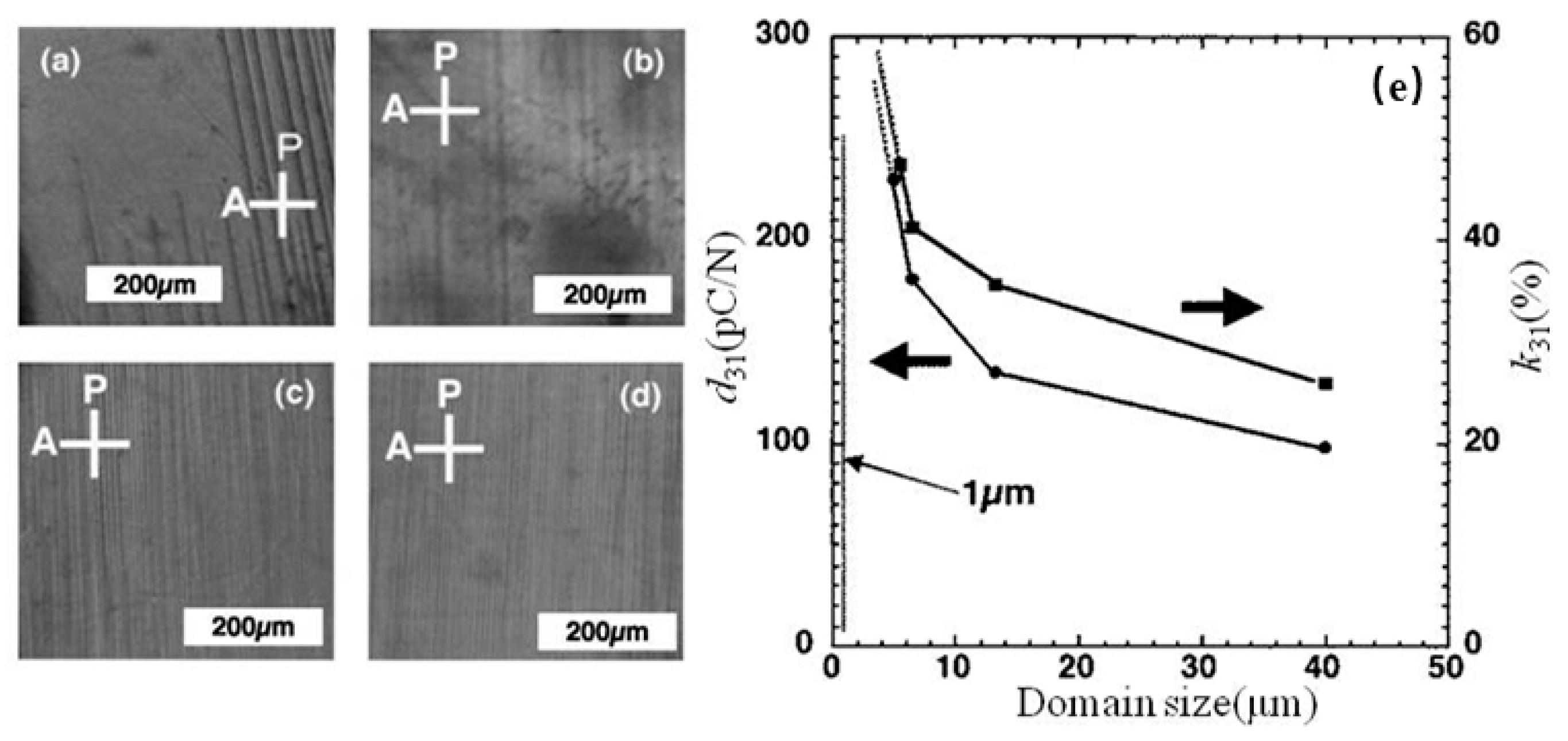
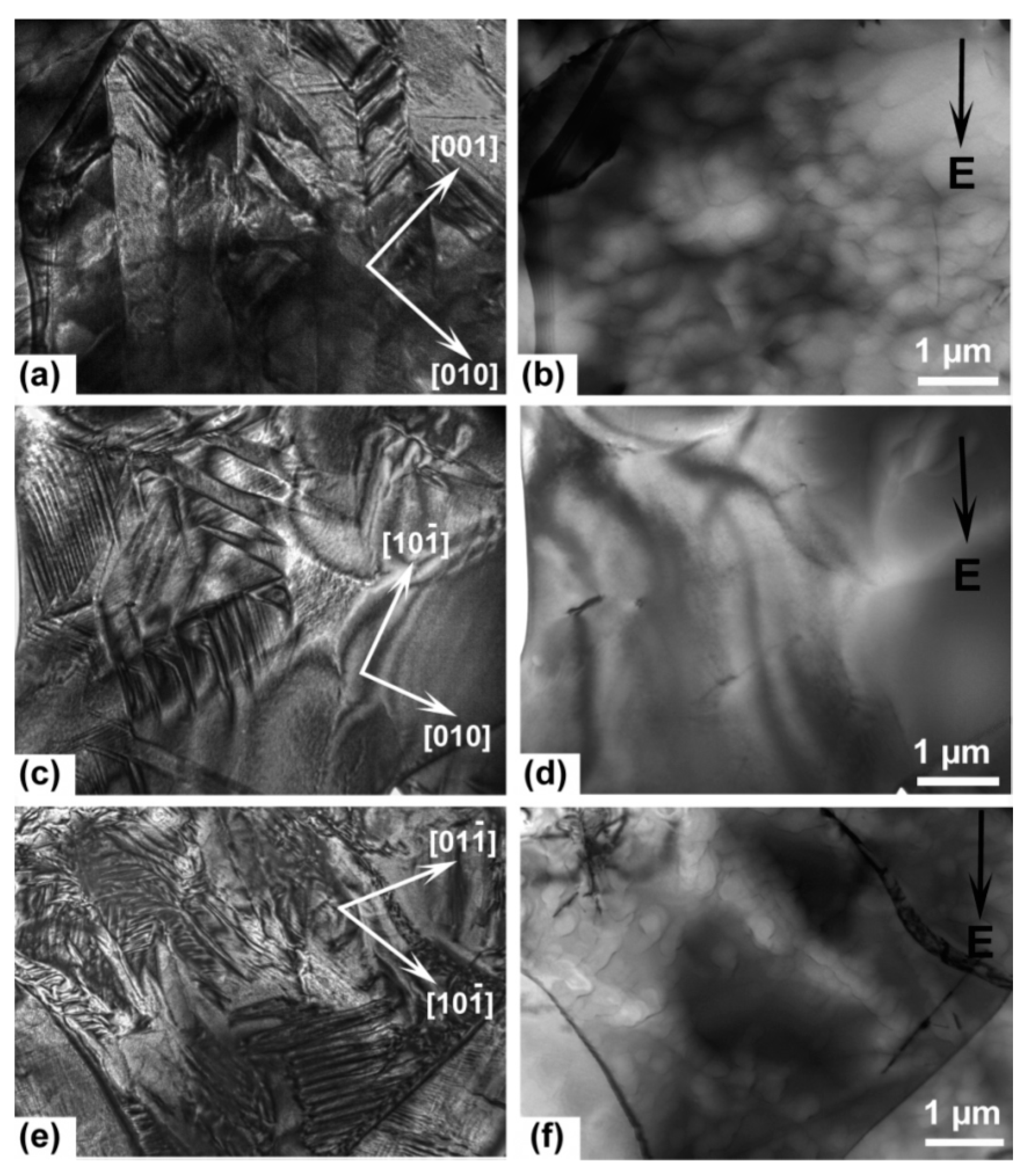
4.4. Microstructure of Ferroelectric Domains

It is well-known that the ferroelectric domain configuration as well as its domain dynamics play very important roles on the piezoelectric response. There are intensive studies on the microstructure for the Pb-containing piezoelectric materials. For example, for PZT, PMN–PT, and PZT–PT, the ferroelectric domain structures manifest themselves as the nano-sized domains inside a domain hierarchy. The domain dynamics or domain wall motion, on the other hand, has invoked great interest for Pb-containing piezoelectric materials. Hence, the microstructure study of Pb-free piezoelectric materials is also crucial for understanding the mechanism underneath the piezoelectric response and further utilization of the materials.
For domain structure observation, transmission electron microscopy (TEM) was used. Bright field (BF) TEM images in Figure 13 show the microstructure evolution with composition at room temperature [69]. The 40 BCT specimen shows a zigzag domain pattern, which is a typical characteristic for rhombohedral phase (Figure 13a). The 40 BCT specimen, on the other hand, shows a lamellar domain structure with 90° domain walls, which is a typical tetragonal microstructure (Figure 13c). The above two microstructures are plain structures that can be observed in ordinary ferroelectrics. However, at 50 BCT in the MPB regime, the sample exhibits as a totally different microstructure: fine domains with an average domain size of 20 nm are embedded in the frame of micron-scale domains forming a kind of “domain hierarchy”. The study of microstructure evolution with composition uncovers a micron-nano-micron microdomain-nanodomain-microdomain nature in domain structure across MPB. The miniaturized domain structure corresponds to the MPB state with the highest d33. A similar domain pattern has also been observed in KNN-based, lead-free piezoelectric materials [81,82]. Guo et al. further reported the observation of nanodomain structure changing to a single-domain state in a BaTiO3-based polycrystalline ceramic at intermediate poling electric fields with in situ TEM as shown in Figure 14 [83,84]. This has been taken as the evidence for the existence of orthorhombic symmetry. Moreover, by using the same method, Zakhozheva et al. reported that the domain configuration after electric field loading can reappear, which raises interest to study the domain switching or domain wall motion for the BZT–BCT material system [85].
The domain wall displacement for BZT–BCT studies can be divided into two categories. One is the long-range domain wall displacement under a large electric field, which leads to large strain that can be utilized for actuators. Tutuncu et al. pointed out that the domain switching process accompanied with domain wall displacement contributes the majority of the effect under a large electric field, and it thus can be considered as the main effect for the large strain of BZT–BCT for actuator applications [86]. On the other hand, the piezoelectric effect at the subswitching condition is determined by Rayleigh relation under a small electric field [87]. The result shows that the intrinsic piezoelectric response exhibits a peak close to the composition-induced R–MPB and MPB–T phase transitions, but the value is much less than total d33 value. In contrast, the extrinsic piezoelectric response, in particular the one corresponding with reversible domain wall motion, has been greatly enhanced close to MPB. Therefore, it is concluded that the extrinsic piezoelectric activity is the major contributor to the high piezoelectricity in BZT–BCT ceramics under subswitching conditions.

4.5. General Systems

BZT–BCT has been proved to be a promising Pb-free piezoelectric system with a large electromechanical response. Later, following the same strategy as BZT–BCT, we have developed Ba(Sn0.12Ti0.88)O3–x(Ba0.7Ca0.3)TiO3 (BTS–BCT) and Ba(Hf0.2Ti0.8)O3–x(Ba0.7Ca0.3)TiO3 (BHT–BCT), and large piezoelectric activity has also be reported in a BaTiO3–BaSnO3 (BT–BS) [15,88].
The phase diagram of the Ba(Sn0.12Ti0.88)O3–x(Ba0.7Ca0.3)O3 (BTS–xBCT) material system is shown in Figure 15. It is characterized by its phase boundary starting from the triple point of a paraelectric cubic phase, ferroelectric rhombohedral, and tetragonal phases. The room temperature MPB composition BTS–30BCT exhibits a high piezoelectric coefficient d33 = 530 pC/N. It can thus be considered as a promising high-performance Pb-free piezoceramic. Another high-property, triple-point type Pb-free material system, Ba(Ti0.8Hf0.2)O3–(Ba0.7Ca0.3)TiO3 was also designed according to a similar idea. The system shows anomalies of both small field (dielectric and piezoelectric) and large field (P-E hysteresis) properties at the MPB, and especially the d33 coefficient can reach 550 pC/N at room temperature, which further verifies the generality for such a design idea.
Further large piezoelectric properties with d33 of 697 pC/N have been found in BaTiO3–xBaSnO3 Pb-free ferroelectric system (Figure 16) [89]. By re-examining the Sn-doped BaTiO3, we found it also exhibits a T-O phase boundary. Its quasi-quadruple point, which is a point where four phases (C-T-O-R) nearly coexist together in the temperature-composition phase diagram, the piezoelectric as well as dielectric coefficient values reach their optimal values. Therefore, it is highly possible that the multi-phase coexisting point (i.e., quadruple point or triple point) is of great significance for the piezoelectric response of ferroelectric system, which might provide a guideline for developing Pb-free piezoelectric materials with large electrometrical responses.

5. Applications and Outline

The BaTiO3-based materials, such as BZT–BCT piezoceramic, exhibit superior piezoelectricity compared with other Pb-free systems, which is comparable with soft PZT. It thus brings about strong hope for Pb-free materials that can eventually be substituted for PZT in the future. Admittedly, we have to point out that BaTiO3-based material systems have the drawback of low Curie temperature (Tc < 130 °C), which restricts their application, especially due to their temperature stability performance. However, such a system can still be considered as an excellent model for exploring the physics of highly piezoelectric materials (a teacher for highly piezoelectric Pb-free materials). Even better Pb-free piezoelectric systems can be anticipated based on the new insights obtained from BZT–BCT.
Here, we would like to give an example of the application of BZT–BCT piezoceramic as the transducer of medical ultrasound imaging systems. As shown above, the 0.5BZT–0.5BCT ceramics have a high dielectric constant of 2800 and superior piezoelectric performance d33 of 600 pC/N. Although there are not real applications of such materials in actuators, it has been shown that the 0.5BZT–0.5BCT ceramic is a promising lead-free piezoelectric material for high-frequency transducer applications. Yan et al. has used the 0.5BZT–0.5BCT ceramics to fabricate a high-frequency (~30 MHz) needle-type ultrasonic transducer for intravascular imaging application [90]. Such a lead-free transducer was found to exhibit a −6 dB bandwidth of 53% with an insertion loss of 18.7 dB. As shown in Figure 17, an in vitro intravascular ultrasound (IVUS) image of a human cadaver coronary artery was obtained by such a lead-free transducer with adequate resolution and contrast to differentiate the vessel wall and fibrous plaque. Various studies have also shown potential applications of such BaTiO3-based lead-free ceramics, ranging from energy harvesting to energy storage, which can provide guidelines for the next generation of Pb-free materials with even better piezoelectric properties, for example in high TC KNN based piezoceramics [18,91,92].

6. Summary

BaTiO3-based piezoelectric ceramics are interesting Pb-free materials for actuator applications as they exhibit high strain under fairly low electric fields. The piezoelectric properties have been greatly enhanced via domain engineering, defect engineering, and phase boundary engineering processes. After the report of the BZT–BCT piezoelectric ceramic systems, the research interest in this family of materials for electromechanical applications has increased. Although the low Tc of such a system may hinder its application due to issues of its temperature stability, the BaTiO3-based piezoelectrics can still be considered as a model system for Pb-free piezoelectric material design.

Acknowledgments

We thank Yongbin Liu, Yan Wang and Zhixin He for helpful discussion. The authors gratefully acknowledge the support of National Basic Research Program of China (Grant No. 2012CB619401), the National Natural Science Foundation of China (Grant Nos. 51571156, 51321003, 51302209, 51431007, and 51320105014), and Program for Changing Scholars and Innovative Research Team in University (IRT13034). J.G acknowledges the Fundamental Research Funds for the Central Universities and State Key Laboratory of Electrical Insulation and Power Equipment (EIPE16311) for financial support.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Uchino, K. Ferroelectric Devices; Marcel Dekker: New York, NY, USA, 2000. [Google Scholar]
  2. Malek, C.K.; Saile, V. Applications of LIGA technology to precision manufacturing of high-aspect-ratio micro-components and -systems: A review. Microelectron. J. 2004, 35, 131–143. [Google Scholar] [CrossRef]
  3. Fennimore, A.M.; Yuzvinsky, T.D.; Han, W.Q.; Fuhrer, M.S.; Cumings, J.; Zettl, A. Rotational actuators based on carbon nanotubes. Nature 2003, 424, 408–410. [Google Scholar] [CrossRef] [PubMed]
  4. Tadaki, T.; Otsuka, K.; Shimizu, K. Shape memory alloys. Annu. Rev. Mater. Sci. 1988, 18, 25–45. [Google Scholar] [CrossRef]
  5. Setter, N.; Damjanovic, D.; Eng, L.; Fox, G.; Gevorgian, S.; Hong, S.; Kingon, A.; Kohlstedt, H.; Park, N.Y.; Stephenson, G.B.; et al. Ferroelectric thin films: Review of materials, properties, and applications. J. Appl. Phys. 2006, 100, 051606. [Google Scholar] [CrossRef]
  6. Haertling, G.H. Ferroelectric ceramics: History and technology. J. Am. Ceram. Soc. 1999, 82, 797–818. [Google Scholar] [CrossRef]
  7. Park, S.-E.; Shrout, T.R. Ultrahigh strain and piezoelectric behavior in relaxor based ferroelectric single crystals. J. Appl. Phys. 1997, 82, 1804–1811. [Google Scholar] [CrossRef]
  8. Zhang, S.; Li, F. High performance ferroelectric relaxor-PbTiO3 single crystals: Status and perspective. J. Appl. Phys. 2012, 111, 031301. [Google Scholar] [CrossRef]
  9. Zhang, S.; Li, F.; Jiang, X.; Kim, J.; Luo, J.; Geng, X. Advantages and challenges of relaxor-PbTiO3 ferroelectric crystals for electroacoustic transducers—A review. Prog. Mater. Sci. 2015, 68, 1–66. [Google Scholar] [CrossRef] [PubMed]
  10. Li, F.; Jin, L.; Xu, Z.; Zhang, S. Electrostrictive effect in ferroelectrics: An alternative approach to improve piezoelectricity. Appl. Phys. Rev. 2014, 1, 011103. [Google Scholar] [CrossRef]
  11. Li, F.; Zhang, S.; Yang, T.; Xu, Z.; Zhang, N.; Liu, G.; Wang, J.; Wang, J.; Cheng, Z.; Ye, Z.-G.; et al. The origin of ultrahigh piezoelectricity in relaxor-ferroelectric solid solution crystals. Nat. Commun. 2016, 7, 13807. [Google Scholar] [CrossRef] [PubMed]
  12. Zhang, Q.M.; Zhang, J. Electromechanical properties of lead zirconate titanate piezoceramics under the influence of mechanical stresses. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 1999, 46, 1518–1526. [Google Scholar] [CrossRef] [PubMed]
  13. Shrout, T.R.; Park, S.E.E.; Lopath, P.D.; Meyer, J.R.J.; Ritter, T.A.; Shung, K.K. Innovations in piezoelectric materials for ultrasound transducers. Proc. SPIE 1998, 3341, 174–183. [Google Scholar]
  14. Liu, W.; Ren, X. Large piezoelectric effect in Pb-free ceramics. Phys. Rev. Lett. 2009, 103, 257602. [Google Scholar] [CrossRef] [PubMed]
  15. Xue, D.; Zhou, Y.; Bao, H.; Gao, J.; Zhou, C.; Ren, X. Large piezoelectric effect in Pb-free Ba(Ti,Sn)O3–x(Ba,Ca)TiO3 ceramics. Appl. Phys. Lett. 2011, 99, 122901. [Google Scholar] [CrossRef]
  16. Directive 2002/95/EC: Restriction of the Use of Certain Hazardous Substances in Electrical and Electronic Equipment (RoHS). Available online: https://ec.europa.eu/growth/single-market/european-standards/harmonised-standards/restriction-of-hazardous-substances_en (accessed on 23 July 2017).
  17. Wu, J.; Xiao, D.; Zhu, J. Potassium–sodium niobate lead-free piezoelectric materials: Past, present, and future of phase boundaries. Chem. Rev. 2015, 115, 2559–2595. [Google Scholar] [CrossRef] [PubMed]
  18. Zheng, T.; Yuan, Y.; Lv, X.; Li, Q.; Men, T.; Zhao, C.; Xiao, D.; Wu, J.; Wang, K.; Li, J.-F. The structural origin of enhanced piezoelectric performance and stability in lead free ceramics. Energy Environ. Sci. 2017, 10, 528–537. [Google Scholar] [CrossRef]
  19. Wang, K.; Yao, F.Z.; Jo, W.; Gobeljic, D.; Shvartsman, V.V.; Lupascu, D.C.; Li, J.F.; Rödel, J. Temperature-insensitive (K,Na)NbO3-based lead-free piezoactuator ceramics. Adv. Funct. Mater. 2013, 23, 4079–4086. [Google Scholar] [CrossRef]
  20. Zhang, S.; Xia, R.; Shrout, T.R.; Zang, G.; Wang, J. Piezoelectric properties in perovskite 0.948(K0.5Na0.5)NbO3–0.052LiSbO3 lead-free ceramics. J. Appl. Phys. 2006, 100, 104108. [Google Scholar] [CrossRef]
  21. Zhang, S.; Xia, R.; Shrout, T.R.; Zang, G.; Wang, J. Characterization of lead free (K0.5Na0.5)NbO3–LiSbO3 piezoceramic. Solid State Commun. 2007, 141, 675–679. [Google Scholar] [CrossRef]
  22. Wang, X.; Wu, J.; Xiao, D.; Zhu, J.; Cheng, X.; Zheng, T.; Zhang, B.; Lou, X.; Wang, X. Giant piezoelectricity in potassium–sodium niobate lead-free ceramics. J. Am. Chem. Soc. 2014, 136, 2905–2910. [Google Scholar] [CrossRef] [PubMed]
  23. Zhang, H.; Xu, P.; Patterson, E.; Zang, J.; Jiang, S.; Rödel, J. Preparation and enhanced electrical properties of grain-oriented (Bi1/2Na1/2)TiO3-based lead-free incipient piezoceramics. J. Eur. Ceram. Soc. 2015, 35, 2501–2512. [Google Scholar] [CrossRef]
  24. Shrout, T.R.; Zhang, S.J. Lead-free piezoelectric ceramics: Alternatives for PZT? J. Electroceram. 2007, 19, 113–126. [Google Scholar] [CrossRef]
  25. Rödel, J.; Jo, W.; Seifert, K.T.P.; Anton, E.M.; Granzow, T.; Damjanovic, D. Perspective on the development of lead-free piezoceramics. J. Am. Ceram. Soc. 2009, 92, 1153–1177. [Google Scholar] [CrossRef]
  26. Takenaka, T.; Nagata, H. Current status and prospects of lead-free piezoelectric ceramics. J. Eur. Ceram. Soc. 2005, 25, 2693–2700. [Google Scholar] [CrossRef]
  27. Li, J.-F.; Wang, K.; Zhu, F.-Y.; Cheng, L.-Q.; Yao, F.-Z. (K,Na)NbO3-based lead-free piezoceramics: Fundamental aspects, processing technologies, and remaining challenges. J. Am. Ceram. Soc. 2013, 96, 3677–3696. [Google Scholar] [CrossRef]
  28. Berlincourt, D.; Jaffe, H. Elastic and piezoelectric coefficients of single-crystal barium titanate. Phys. Rev. 1958, 111, 143–148. [Google Scholar] [CrossRef]
  29. Takenaka, T.; Nagata, H.; Hiruma, Y.; Yoshii, Y.; Matumoto, K. Lead-free piezoelectric ceramics based on perovskite structures. J. Electroceram. 2007, 19, 259–265. [Google Scholar] [CrossRef]
  30. Budimir, M.; Damjanovic, D.; Setter, N. Piezoelectric response and free-energy instability in the perovskite crystals BaTiO3, PbTiO3, and Pb(Zr,Ti)O3. Phys. Rev. B 2006, 73, 174106. [Google Scholar] [CrossRef]
  31. Budimir, M.; Damjanovic, D.; Setter, N. Enhancement of the piezoelectric response of tetragonal perovskite single crystals by uniaxial stress applied along the polar axis: A free-energy approach. Phys. Rev. B 2005, 72, 064107. [Google Scholar] [CrossRef]
  32. Damjanovic, D. Contributions to the piezoelectric effect in ferroelectric single crystals and ceramics. J. Am. Ceram. Soc. 2005, 88, 2663–2676. [Google Scholar] [CrossRef]
  33. Wada, S.; Kakemoto, H.; Tsurumi, T. Enhanced piezoeletric properties of piezoelectric single crystals by domain engineering. Mater. Trans. 2004, 45, 178–187. [Google Scholar] [CrossRef]
  34. Wada, S.; Yako, K.; Kakemoto, H.; Tsurumi, T.; Kiguchi, T. Enhanced piezoelectric properties of barium titanate single crystals with different engineered-domain sizes. J. Appl. Phys. 2005, 98, 014109. [Google Scholar] [CrossRef]
  35. Takahashi, H.; Numamoto, Y.; Tani, J.; Tsurekawa, S. Piezoelectric properties of BaTiO3 ceramics with high performance fabricated by microwave sintering. Jpn. J. Appl. Phys. 2006, 45, 7405–7408. [Google Scholar] [CrossRef]
  36. Karaki, T.; Yan, K.; Miyamoto, T.; Adachi, M. Lead-free piezoelectric ceramics with large dielectric and piezoelectric constants manufactured from BaTiO3 nano-powder. Jpn. J. Appl. Phys. 2007, 46, L97–L98. [Google Scholar]
  37. Satoshi, W.; Kotaro, T.; Tomomitsu, M.; Hirofumi, K.; Takaaki, T.; Toshio, K. Preparation of [110] grain oriented barium titanate ceramics by templated grain growth method and their piezoelectric properties. Jpn. J. Appl. Phys. 2007, 46, 7039. [Google Scholar]
  38. Yin, J.; Cao, W. Domain configurations in domain engineered 0.955Pb(Zn1/3Nb2/3)O3–0.045PbTiO3 single crystals. J. Appl. Phys. 2000, 87, 7438–7441. [Google Scholar] [CrossRef]
  39. Shen, Z.-Y.; Li, J.-F. Enhancement of piezoelectric constant d33 in BaTiO3 ceramics due to nano-domain structure. J. Ceram. Soc. Jpn. 2010, 118, 940–943. [Google Scholar] [CrossRef]
  40. Ren, X. Large electric-field-induced strain in ferroelectric crystals by point-defect-mediated reversible domain switching. Nat. Mater. 2004, 3, 91–94. [Google Scholar] [CrossRef] [PubMed]
  41. Zhang, L.X.; Chen, W.; Ren, X. Large recoverable electrostrain in Mn-doped (Ba,Sr)TiO3 ceramics. Appl. Phys. Lett. 2004, 85, 5658–5660. [Google Scholar] [CrossRef]
  42. Zhang, L.X.; Ren, X. In situ observation of reversible domain switching in aged Mn-doped BaTiO3 single crystals. Phys. Rev. B 2005, 71, 174108. [Google Scholar] [CrossRef]
  43. Kiyoshi, O.; Hiroshi, M. Space charge effects on ferroelectric ceramic particle surfaces. Jpn. J. Appl. Phys. 1992, 31, 3113. [Google Scholar]
  44. Carl, K.; Hardtl, K.H. Electrical after-effects in Pb(Ti,Zr)O3 ceramics. Ferroelectrics 1977, 17, 473–486. [Google Scholar] [CrossRef]
  45. Postnikov, V.S.; Pavlov, V.S.; Turkov, S.K. Internal friction in ferroelectrics due to interaction of domain boundaries and point defects. J. Phys. Chem. Solids 1970, 31, 1785–1791. [Google Scholar] [CrossRef]
  46. Yang, T.J.; Gopalan, V.; Swart, P.J.; Mohideen, U. Direct observation of pinning and bowing of a single ferroelectric domain wall. Phys. Rev. Lett. 1999, 82, 4106–4109. [Google Scholar] [CrossRef]
  47. Lambeck, P.V.; Jonker, G.H. The nature of domain stabilization in ferroelectric perovskites. J. Phys. Chem. Solids 1986, 47, 453–461. [Google Scholar] [CrossRef]
  48. Robels, U.; Arlt, G. Domain wall clamping in ferroelectrics by orientation of defects. J. Appl. Phys. 1993, 73, 3454–3460. [Google Scholar] [CrossRef]
  49. Lambeck, P.V.; Jonker, G.H. Ferroelectric domain stabilization in BaTiO3 by bulk ordering of defects. Ferroelectrics 1978, 22, 729–731. [Google Scholar] [CrossRef]
  50. Zhang, L.; Ren, X. Aging behavior in single-domain Mn-doped BaTiO3 crystals: Implication for a unified microscopic explanation of ferroelectric aging. Phys. Rev. B 2006, 73, 094121. [Google Scholar] [CrossRef]
  51. Gao, J.; Xue, D.; Zhang, L.; Wang, Y.; Bao, H.; Zhou, C.; Liu, W.; Chen, W.; Ren, X. Aging-induced domain memory in acceptor-doped perovskite ferroelectrics associated with ferroelectric-ferroelectric transition cycle. EPL 2011, 96, 37001. [Google Scholar] [CrossRef]
  52. Gao, J.; Xue, D.; Bao, H.; Zhang, L.; Zhou, C.; Liu, W.; Chen, W.; Ren, X. Aging-induced two-step ferroelectric-to-paraelectric transition in acceptor-doped ferroelectrics. Appl. Phys. Lett. 2010, 96, 082906. [Google Scholar] [CrossRef]
  53. Gao, J.; Xue, D.; Bao, H.; Zhang, L.; Zhou, C.; Liu, W.; Chen, W.; Ren, X. Two-step ferroelectric to paraelectric transition caused by peak aging. Ferroelectrics 2010, 401, 24–29. [Google Scholar] [CrossRef]
  54. Sun, D.; Ren, X.; Otsuka, K. Stabilization effect in ferroelectric materials during aging in ferroelectric state. Appl. Phys. Lett. 2005, 87, 142903. [Google Scholar] [CrossRef]
  55. Jaffe, B.; Roth, R.S.; Marzullo, S. Properties of piezoelectric ceramics in the solid-solution series lead titanate-lead zirconate-lead oxide-tin oxide and lead titanate-lead hafnate. J. Res. Natl. Bur. Stand. 1955, 55, 239–254. [Google Scholar] [CrossRef]
  56. Jaffe, B.; Roth, R.S.; Marzullo, S. Piezoelectric properties of lead zirconate-lead titanate solid-solution ceramics. J. Appl. Phys. 1954, 25, 809–810. [Google Scholar] [CrossRef]
  57. Wu, B.; Wu, H.; Wu, J.; Xiao, D.; Zhu, J.; Stephen, J.P. Giant piezoelectricity and high Curie temperature in nanostructured alkali niobate lead-free piezoceramics through phase coexistence. J. Am. Chem. Soc. 2016, 138, 15459–15464. [Google Scholar] [CrossRef] [PubMed]
  58. Wu, J.; Xiao, D.; Wu, W.; Chen, Q.; Zhu, J.; Yang, Z.; Wang, J. Role of room-temperature phase transition in the electrical properties of (Ba,Ca)(Ti,Zr)O3 ceramics. Scr. Mater. 2011, 65, 771–774. [Google Scholar] [CrossRef]
  59. Li, B.; Blendell, J.E.; Bowman, K.J. Temperature-dependent poling behavior of lead-free BZT–BCT piezoelectrics. J. Am. Ceram. Soc. 2011, 94, 3192–3194. [Google Scholar] [CrossRef]
  60. Ehmke, M.C.; Glaum, J.; Hoffman, M.; Blendell, J.E.; Bowman, K.J. The effect of electric poling on the performance of lead-free (1 − x)Ba(Zr0.2Ti0.8)O3–x(Ba0.7Ca0.3)TiO3 piezoceramics. J. Am. Ceram. Soc. 2013, 96, 3805–3811. [Google Scholar] [CrossRef]
  61. Li, B.; Ehmke, M.C.; Blendell, J.E.; Bowman, K.J. Optimizing electrical poling for tetragonal, lead-free BZT–BCT piezoceramic alloys. J. Eur. Ceram. Soc. 2013, 33, 3037–3044. [Google Scholar] [CrossRef]
  62. Jin, L.; Huo, R.; Guo, R.; Li, F.; Wang, D.; Tian, Y.; Hu, Q.; Wei, X.; He, Z.; Yan, Y.; et al. Diffuse phase transitions and giant electrostrictive coefficients in lead-free Fe3+-doped 0.5Ba(Zr0.2Ti0.8)O3–0.5(Ba0.7Ca0.3)TiO3 ferroelectric ceramics. ACS Appl. Mater. Interfaces 2016, 8, 31109–31119. [Google Scholar] [CrossRef] [PubMed]
  63. Li, F.; Jin, L.; Guo, R. High electrostrictive coefficient Q33 in lead-free Ba(Zr0.2Ti0.8)O3–x(Ba0.7Ca0.3)TiO3 piezoelectric ceramics. Appl. Phys. Lett. 2014, 105, 232903. [Google Scholar] [CrossRef]
  64. Wu, J.; Xiao, D.; Wu, W.; Chen, Q.; Zhu, J.; Yang, Z.; Wang, J. Composition and poling condition-induced electrical behavior of (Ba0.85Ca0.15)(Ti1 − xZrx)O3 lead-free piezoelectric ceramics. J. Eur. Ceram. Soc. 2012, 32, 891–898. [Google Scholar] [CrossRef]
  65. Wu, J.; Xiao, D.; Wu, B.; Wu, W.; Zhu, J.; Yang, Z.; Wang, J. Sintering temperature-induced electrical properties of (Ba0.90Ca0.10)(Ti0.85Zr0.15)O3 lead-free ceramics. Mater. Res. Bull. 2012, 47, 1281–1284. [Google Scholar] [CrossRef]
  66. Xue, D.; Zhou, Y.; Bao, H.; Zhou, C.; Gao, J.; Ren, X. Elastic, piezoelectric, and dielectric properties of Ba(Zr0.2Ti0.8)O3–50(Ba0.7Ca0.3)TiO3 Pb-free ceramic at the morphotropic phase boundary. J. Appl. Phys. 2011, 109, 054110. [Google Scholar] [CrossRef]
  67. Ehmke, M.C.; Ehrlich, S.N.; Blendell, J.E.; Bowman, K.J. Phase coexistence and ferroelastic texture in high strain (1 − x)Ba(Zr0.2Ti0.8)O3–x(Ba0.7Ca0.3)TiO3 piezoceramics. J. Appl. Phys. 2012, 111, 124110. [Google Scholar] [CrossRef]
  68. Haugen, A.B.; Forrester, J.S.; Damjanovic, D.; Li, B.; Bowman, K.J.; Jones, J.L. Structure and phase transitions in 0.5(Ba0.7Ca0.3TiO3)–0.5(BaZr0.2Ti0.8O3) from −100 °C to 150 °C. J. Appl. Phys. 2013, 113, 014103. [Google Scholar] [CrossRef]
  69. Gao, J.; Xue, D.; Wang, Y.; Wang, D.; Zhang, L.; Wu, H.; Guo, S.; Bao, H.; Zhou, C.; Liu, W.; et al. Microstructure basis for strong piezoelectricity in Pb-free Ba(Zr0.2Ti0.8)O3–(Ba0.7Ca0.3)TiO3 ceramics. Appl. Phys. Lett. 2011, 99, 092901. [Google Scholar] [CrossRef]
  70. Gao, J.; Zhang, L.; Xue, D.; Kimoto, T.; Song, M.; Zhong, L.; Ren, X. Symmetry determination on Pb-free piezoceramic 0.5Ba(Zr0.2Ti0.8)O3–0.5(Ba0.7Ca0.3)TiO3 using convergent beam electron diffraction method. J. Appl. Phys. 2014, 115, 054108. [Google Scholar] [CrossRef]
  71. Keeble, D.S.; Benabdallah, F.; Thomas, P.A.; Maglione, M.; Kreisel, J. Revised structural phase diagram of (Ba0.7Ca0.3TiO3)–(BaZr0.2Ti0.8O3). Appl. Phys. Lett. 2013, 102, 092903. [Google Scholar] [CrossRef]
  72. Zhang, L.; Zhang, M.; Wang, L.; Zhou, C.; Zhang, Z.; Yao, Y.; Zhang, L.; Xue, D.; Lou, X.; Ren, X. Phase transitions and the piezoelectricity around morphotropic phase boundary in Ba(Zr0.2Ti0.8)O3–x(Ba0.7Ca0.3)TiO3 lead-free solid solution. Appl. Phys. Lett. 2014, 105, 162908. [Google Scholar] [CrossRef]
  73. Damjanovic, D.; Biancoli, A.; Batooli, L.; Vahabzadeh, A.; Trodahl, J. Elastic, dielectric, and piezoelectric anomalies and Raman spectroscopy of 0.5Ba(Ti0.8Zr0.2)O3–0.5(Ba0.7Ca0.3)TiO3. Appl. Phys. Lett. 2012, 100, 192907. [Google Scholar] [CrossRef]
  74. Acosta, M.; Novak, N.; Rossetti, G.A., Jr.; Rödel, J. Mechanisms of electromechanical response in (1 − x)Ba(Zr0.2Ti0.8)O3–x(Ba0.7Ca0.3)TiO3 ceramics. Appl. Phys. Lett. 2015, 107, 142906. [Google Scholar] [CrossRef]
  75. Acosta, M.; Novak, N.; Jo, W.; Rödel, J. Relationship between electromechanical properties and phase diagram in the Ba(Zr0.2Ti0.8)O3–x(Ba0.7Ca0.3)TiO3 lead-free piezoceramic. Acta Mater. 2014, 80, 48–55. [Google Scholar] [CrossRef]
  76. Acosta, M.; Khakpash, N.; Someya, T.; Novak, N.; Jo, W.; Nagata, H.; Rossetti, G.A.; Rödel, J. Origin of the large piezoelectric activity in (1 − x)Ba(Zr0.2Ti0.8)O3–x(Ba0.7Ca0.3)TiO3 ceramics. Phys. Rev. B 2015, 91, 104108. [Google Scholar] [CrossRef]
  77. Gao, J.; Ye, D.; Xinghao, H.; Xiaoqin, K.; Lisheng, Z.; Shengtao, L.; Lixue, Z.; Yu, W.; Dong, W.; Yan, W.; et al. Phase transition behaviours near the triple point for Pb-free (1 − x)Ba(Zr0.2Ti0.8)O3–x(Ba0.7Ca0.3)TiO3 piezoceramics. EPL 2016, 115, 37001. [Google Scholar] [CrossRef]
  78. Gao, J.; Wang, Y.; Liu, Y.; Hu, X.; Ke, X.; Zhong, L.; He, Y.; Ren, X. Enhancing dielectric permittivity for energy-storage devices through tricritical phenomenon. Sci. Rep. 2017, 7, 40916. [Google Scholar] [CrossRef] [PubMed]
  79. Gao, J.H.; Hu, X.H.; Wang, Y.; Liu, Y.B.; Zhang, L.X.; Ke, X.Q.; Zhong, L.S.; Zhao, H.; Ren, X.B. Understanding the mechanism of large dielectric response in Pb-free (1 − x)Ba(Zr0.2Ti0.8)O3–x(Ba0.7Ca0.3)TiO3 ferroelectric ceramics. Acta Mater. 2017, 125, 177–186. [Google Scholar] [CrossRef]
  80. Gao, J.; Liu, Y.; Wang, Y.; Hu, X.; Yan, W.; Ke, X.; Zhong, L.; He, Y.; Ren, X. Designing high dielectric permittivity material in barium titanate. J. Phys. Chem. C 2017, 121, 13106–13113. [Google Scholar] [CrossRef]
  81. Gao, J.; Ren, S.; Zhang, L.; Hao, Y.; Fang, M.; Zhang, M.; Dai, Y.; Hu, X.; Wang, D.; Zhong, L.; et al. Phase transition sequence in Pb-free 0.96(K0.5Na0.5)0.95Li0.05Nb0.93Sb0.07O3–0.04BaZrO3 ceramic with large piezoelectric response. Appl. Phys. Lett. 2015, 107, 032902. [Google Scholar] [CrossRef]
  82. Gao, J.; Hao, Y.; Ren, S.; Takayoshi, K.; Fang, M.; Li, H.; Wang, Y.; Zhong, L.; Li, S.; Ren, X. Large piezoelectricity in Pb-free 0.96(K0.5Na0.5)0.95Li0.05Nb0.93Sb0.07O3–0.04BaZrO3 ceramic: A perspective from microstructure. Appl. Phys. Lett. 2015, 117, 084106. [Google Scholar] [CrossRef]
  83. Guo, H.; Voas, B.K.; Zhang, S.; Zhou, C.; Ren, X.; Beckman, S.P.; Tan, X. Polarization alignment, phase transition, and piezoelectricity development in polycrystalline 0.5Ba(Zr0.2Ti0.8)O3–0.5(Ba0.7Ca0.3)TiO3. Phys. Rev. B 2014, 90, 014103. [Google Scholar] [CrossRef]
  84. Guo, H.; Zhou, C.; Ren, X.; Tan, X. Unique single-domain state in a polycrystalline ferroelectric ceramic. Phys. Rev. B 2014, 89, 100104. [Google Scholar] [CrossRef]
  85. Zakhozheva, M.; Schmitt, L.A.; Acosta, M.; Jo, W.; Rödel, J.; Kleebe, H.-J. In situ electric field induced domain evolution in Ba(Zr0.2Ti0.8)O3–0.3(Ba0.7Ca0.3)TiO3 ferroelectrics. Appl. Phys. Lett. 2014, 105, 112904. [Google Scholar] [CrossRef]
  86. Tutuncu, G.; Li, B.; Bowman, K.; Jones, J.L. Domain wall motion and electromechanical strain in lead-free piezoelectrics: Insight from the model system (1 − x)Ba(Zr0.2Ti0.8)O3–x(Ba0.7Ca0.3)TiO3 using in situ high-energy X-ray diffraction during application of electric fields. J. Appl. Phys. 2014, 115, 144104. [Google Scholar] [CrossRef]
  87. Gao, J.; Hu, X.; Zhang, L.; Li, F.; Zhang, L.; Wang, Y.; Hao, Y.; Zhong, L.; Ren, X. Major contributor to the large piezoelectric response in (1 − x)Ba(Zr0.2Ti0.8)O3–x(Ba0.7Ca0.3)TiO3 ceramics: Domain wall motion. Appl. Phys. Lett. 2014, 104, 252909. [Google Scholar] [CrossRef]
  88. Zhou, C.; Liu, W.; Xue, D.; Ren, X.; Bao, H.; Gao, J.; Zhang, L. Triple-point-type morphotropic phase boundary based large piezoelectric Pb-free material—Ba(Ti0.8Hf0.2)O3–(Ba0.7Ca0.3)TiO3. Appl. Phys. Lett. 2012, 100, 222910. [Google Scholar] [CrossRef]
  89. Yao, Y.; Zhou, C.; Lv, D.; Wang, D.; Wu, H.; Yang, Y.; Ren, X. Large piezoelectricity and dielectric permittivity in BaTiO3–xBaSnO3 system: The role of phase coexisting. EPL 2012, 98, 27008. [Google Scholar] [CrossRef]
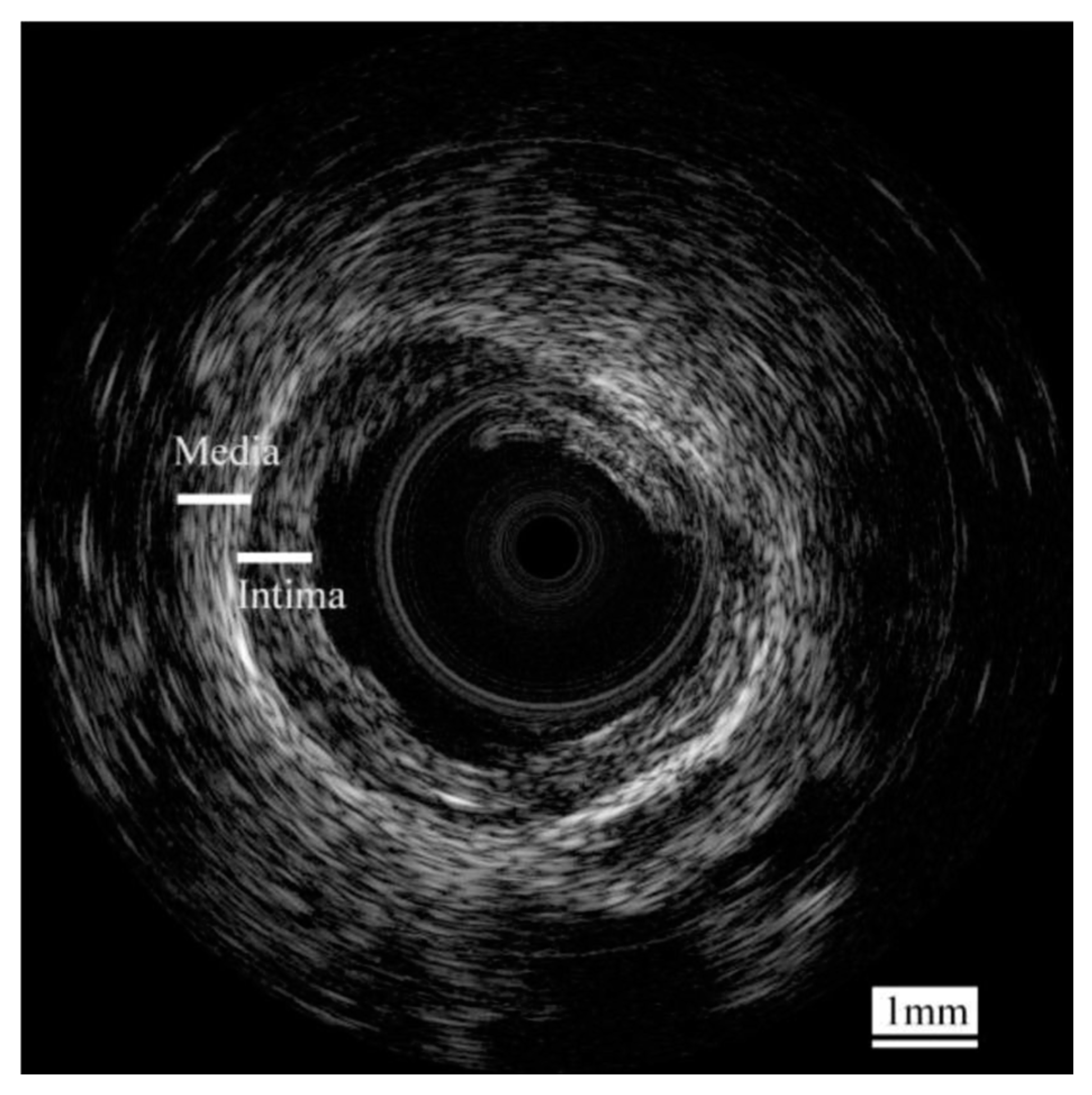
  90. Yan, X.; Lam, K.H.; Li, X.; Chen, R.; Ren, W.; Ren, X.; Zhou, Q.; Shung, K.K. Correspondence: Lead-free intravascular ultrasound transducer using 0.5BZT–0.5BCT ceramics. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2013, 60, 1272–1276. [Google Scholar] [CrossRef] [PubMed]
  91. Xu, K.; Li, J.; Lv, X.; Wu, J.; Zhang, X.; Xiao, D.; Zhu, J. Superior piezoelectric properties in potassium-sodium niobate lead-free ceramics. Adv. Mater. 2016, 28, 8519–8523. [Google Scholar] [CrossRef] [PubMed]
  92. Gao, J.; Liu, Y.; Wang, Y.; Wang, D.; Zhong, L.; Ren, X. High temperature-stability of (Pb0.9La0.1)(Zr0.65Ti0.35)O3 ceramic for energy-storage applications at finite electric field strength. Scr. Mater. 2017, 137, 114–118. [Google Scholar] [CrossRef]
Actuators 06 00024 g001 550
Figure 1. The publication number relates with Pb-free and BaTiO3-based piezoelectrics.
Figure 1. The publication number relates with Pb-free and BaTiO3-based piezoelectrics.
Actuators 06 00024 g001
Actuators 06 00024 g002 550
Figure 2. Schematic model of the engineered domain configurations for the tetragonal 4mm ferroelectric crystals (Ps: spontaneous polar vector along the <001>c directions) [33].
Figure 2. Schematic model of the engineered domain configurations for the tetragonal 4mm ferroelectric crystals (Ps: spontaneous polar vector along the <001>c directions) [33].
Actuators 06 00024 g002
Actuators 06 00024 g003 550
Figure 3. (a–c) The role of an electric bias field (E3 = 0, −10 MV/m) at T = 298 K on anisotropic free energy flattening and piezoelectric enhancement. (d–f) The change of anisotropic free energy and piezoelectric coefficient around the tetragonal-orthorhombic phase transition temperature in BaTiO3 (which is adapted with permission from [30]. Copyrighted by the American Physical Society).
Figure 3. (a–c) The role of an electric bias field (E3 = 0, −10 MV/m) at T = 298 K on anisotropic free energy flattening and piezoelectric enhancement. (d–f) The change of anisotropic free energy and piezoelectric coefficient around the tetragonal-orthorhombic phase transition temperature in BaTiO3 (which is adapted with permission from [30]. Copyrighted by the American Physical Society).
Actuators 06 00024 g003
Actuators 06 00024 g004 550
Figure 4. (a–d) Domain configurations of 31 resonators with different domain sizes ranging from 5.5 µm to 40 µm. (e) Domain size dependence of d31 and k31 for <111>c-poled BaTiO3 single crystals [34].
Figure 4. (a–d) Domain configurations of 31 resonators with different domain sizes ranging from 5.5 µm to 40 µm. (e) Domain size dependence of d31 and k31 for <111>c-poled BaTiO3 single crystals [34].
Actuators 06 00024 g004
Actuators 06 00024 g005 550
Figure 5. The non-linear electrostrain in aged point-defect-doped BaTiO3 single crystal (left) and ceramics (right) [40,41].
Figure 5. The non-linear electrostrain in aged point-defect-doped BaTiO3 single crystal (left) and ceramics (right) [40,41].
Actuators 06 00024 g005
Actuators 06 00024 g006 550
Figure 6. Electric-fatigue in Mn-doped BaTiO3 ceramic [41].
Figure 6. Electric-fatigue in Mn-doped BaTiO3 ceramic [41].
Actuators 06 00024 g006
Actuators 06 00024 g007a 550Actuators 06 00024 g007b 550
Figure 7. (a) Direct evidence for reversible domain-switching process and its relation to a double hysteresis loop in aged Mn-BaTiO3 single-crystal sample. (b) Its comparison to an unaged specimen. (c) Based on the observation, the mechanism is given regarding defect symmetry and related crystal symmetry in a perovskite BaTiO3 structure doped with Mn3+ ions at Ti4+ sites [42].
Figure 7. (a) Direct evidence for reversible domain-switching process and its relation to a double hysteresis loop in aged Mn-BaTiO3 single-crystal sample. (b) Its comparison to an unaged specimen. (c) Based on the observation, the mechanism is given regarding defect symmetry and related crystal symmetry in a perovskite BaTiO3 structure doped with Mn3+ ions at Ti4+ sites [42].
Actuators 06 00024 g007aActuators 06 00024 g007b
Actuators 06 00024 g008 550
Figure 8. The comparison of phase diagram for PbZr1 − xTixO3 (left) and Ba(Zr0.2Ti0.8)O3–(Ba0.7Ca0.3)TiO3 (right) [14].
Figure 8. The comparison of phase diagram for PbZr1 − xTixO3 (left) and Ba(Zr0.2Ti0.8)O3–(Ba0.7Ca0.3)TiO3 (right) [14].
Actuators 06 00024 g008
Actuators 06 00024 g009 550
Figure 9. The composition dependence of the piezoelectric, dielectric, and ferroelectric properties for BZT–BCT piezoelectric system [14]. (a) P-E hysteresis loop. (b1–b6) Maximum polarization, remnant polarization, coercive field, dielectric permittivity, d31, dS/dE. (c,d) The comparison for the piezoelectric parameters between BZT–BCT and other systems. (e1,e2) The temperature stability for BZT–BCT.
Figure 9. The composition dependence of the piezoelectric, dielectric, and ferroelectric properties for BZT–BCT piezoelectric system [14]. (a) P-E hysteresis loop. (b1–b6) Maximum polarization, remnant polarization, coercive field, dielectric permittivity, d31, dS/dE. (c,d) The comparison for the piezoelectric parameters between BZT–BCT and other systems. (e1,e2) The temperature stability for BZT–BCT.
Actuators 06 00024 g009
Actuators 06 00024 g010 550
Figure 10. The high-resolution X-ray diffraction (XRD) (left) and Raman spectrum for BZT–BCT piezoceramics (right) [71,72].
Figure 10. The high-resolution X-ray diffraction (XRD) (left) and Raman spectrum for BZT–BCT piezoceramics (right) [71,72].
Actuators 06 00024 g010
Actuators 06 00024 g011 550
Figure 11. New phase diagram for BZT–BCT based on the crystal structure studies [72].
Figure 11. New phase diagram for BZT–BCT based on the crystal structure studies [72].
Actuators 06 00024 g011
Actuators 06 00024 g012 550
Figure 12. Thermal hysteresis studies (left) and permittivity maximum measurement (right) indicates a tricritical point for the triple point of BZT–BCT [14].
Figure 12. Thermal hysteresis studies (left) and permittivity maximum measurement (right) indicates a tricritical point for the triple point of BZT–BCT [14].
Actuators 06 00024 g012
Actuators 06 00024 g013 550
Figure 13. Transmission electron microscopy (TEM) images of different compositions of (1 − x)BZT–xBCT. (a) x = 0.4; (b) x = 0.5; (c) x = 0.6; (a1,b1,b2,c1) the convergent beam electron diffraction pattern obtained from one grain [69].
Figure 13. Transmission electron microscopy (TEM) images of different compositions of (1 − x)BZT–xBCT. (a) x = 0.4; (b) x = 0.5; (c) x = 0.6; (a1,b1,b2,c1) the convergent beam electron diffraction pattern obtained from one grain [69].
Actuators 06 00024 g013
Actuators 06 00024 g014 550
Figure 14. In situ TEM observations of a series of grains in the same specimen of the 0.5Ba(Zr0.2Ti0.8)O3–0.5(Ba0.7Ca0.3)TiO3 ceramic. (a,c,e) show the virgin state of domain patterns; (b,d,f) bright-field micrographs are compared with different electric field conditions [83].
Figure 14. In situ TEM observations of a series of grains in the same specimen of the 0.5Ba(Zr0.2Ti0.8)O3–0.5(Ba0.7Ca0.3)TiO3 ceramic. (a,c,e) show the virgin state of domain patterns; (b,d,f) bright-field micrographs are compared with different electric field conditions [83].
Actuators 06 00024 g014
Actuators 06 00024 g015 550
Figure 15. (a) Phase diagram for the BST–BCT material system. (b–e) Dielectric permttivity for 0BCT, 5BCT, 90BCT. (f) Change of thermal hysteresis with composition [15].
Figure 15. (a) Phase diagram for the BST–BCT material system. (b–e) Dielectric permttivity for 0BCT, 5BCT, 90BCT. (f) Change of thermal hysteresis with composition [15].
Actuators 06 00024 g015
Actuators 06 00024 g016 550
Figure 16. Contour map of the d33 coefficient in temperature-composition dimensions of BT–BS piezoelectric materials [89].
Figure 16. Contour map of the d33 coefficient in temperature-composition dimensions of BT–BS piezoelectric materials [89].
Actuators 06 00024 g016
Actuators 06 00024 g017 550
Figure 17. An intravascular ultrasound image acquired from a 0.5BZT–0.5BCT transducer [90].
Figure 17. An intravascular ultrasound image acquired from a 0.5BZT–0.5BCT transducer [90].
Actuators 06 00024 g017
Table
Table 1. Piezoelectric properties of Pb-based systems and BaTiO3 based systems.
Table 1. Piezoelectric properties of Pb-based systems and BaTiO3 based systems.
MaterialsPoly/Single Crystald33 (pC/N)k33Reference
PZT–5A (soft)Polycrystalline3740.71[6]
PZT–8 (hard)Polycrystalline2250.64[12]
PMN–70PTSingle crystal1500>0.9[7]
92%PZN–8%PTSingle crystal2200>0.9[13]
0.5BZT–0.5BCTPolycrystalline6200.65[14]
0.7BTS–0.3BCTPolycrystalline5300.57[15]
Table
Table 2. Piezoelectric coefficients for BaTiO3 single crystal and ceramic.
Table 2. Piezoelectric coefficients for BaTiO3 single crystal and ceramic.
CrystalCeramic
d15392270
d31−34.5−79
d3385.6191
g1515.218.8
g31−23.0−4.7
g3357.511.4
k310.3150.208
k330.5600.494
k150.5700.466
ε11T/ε029201436
ε33T/ε01681680
ε11S/ε019701123
ε33S/ε01091256
S11E8.058.55
S33E15.78.93
S12E−2.35−2.61
S13E−5.242.85
S44E18.423.3
S668.8422.3
S11D7.258.18
S33D10.86.76
S12D−3.15−2.98
S13D−3.26−1.95
S44D12.418.3
Note: Data from [28].
Table
Table 3. The piezoelectric coefficients for 0.5BZT–0.5BCT [66].
Table 3. The piezoelectric coefficients for 0.5BZT–0.5BCT [66].
Piezoelectric Coefficients
dij (10−12 N/C) eij (C/m2) gij (10−3 Vm/N) hij (108 V/m)
Materiald33d31d15 e33e31e15 g33g31g15 h33h31h15
BZT–50BCT546−231453 22.4−5.712.1 15.3−6.531.0 8.6−2.18.3
BaTiO3191−79270 11.6−4.418.6 11.4−4.718.8 9.2−3.516.6
PZT5A374−171584 15.8−5.412.3 24.9−11.438.0 21.4−7.315.0
Dielectric Constants Electromechanical Coupling Factors
ε i j (ε0) β i j (10−4/ε0)
ε 33 T a ε 11 T a ε 33 S a ε 11 S a β 33 T β 11 T β 33 S β 11 S k33k31k15ktkp
BZT-50BCT4050273229301652 2.473.663.416.05 0.650.310.480.420.53
BaTiO31898162214191269 5.36.27.07.9 0.490.210.48…0.35
PZT5A17001730830916 5.95.812.010.9 0.700.340.680.490.60
a Directly measured properties.

Share and Cite

MDPI and ACS Style

Gao, J.; Xue, D.; Liu, W.; Zhou, C.; Ren, X. Recent Progress on BaTiO3-Based Piezoelectric Ceramics for Actuator Applications. Actuators 2017, 6, 24. https://doi.org/10.3390/act6030024

AMA Style

Gao J, Xue D, Liu W, Zhou C, Ren X. Recent Progress on BaTiO3-Based Piezoelectric Ceramics for Actuator Applications. Actuators. 2017; 6(3):24. https://doi.org/10.3390/act6030024

Chicago/Turabian Style

Gao, Jinghui, Dezhen Xue, Wenfeng Liu, Chao Zhou, and Xiaobing Ren. 2017. "Recent Progress on BaTiO3-Based Piezoelectric Ceramics for Actuator Applications" Actuators 6, no. 3: 24. https://doi.org/10.3390/act6030024

APA Style

Gao, J., Xue, D., Liu, W., Zhou, C., & Ren, X. (2017). Recent Progress on BaTiO3-Based Piezoelectric Ceramics for Actuator Applications. Actuators, 6(3), 24. https://doi.org/10.3390/act6030024

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop