Flexible Medical Devices: Review of Controllable Stiffness Solutions
Abstract
:1. Introduction
2. Basic Principles and State of the Art
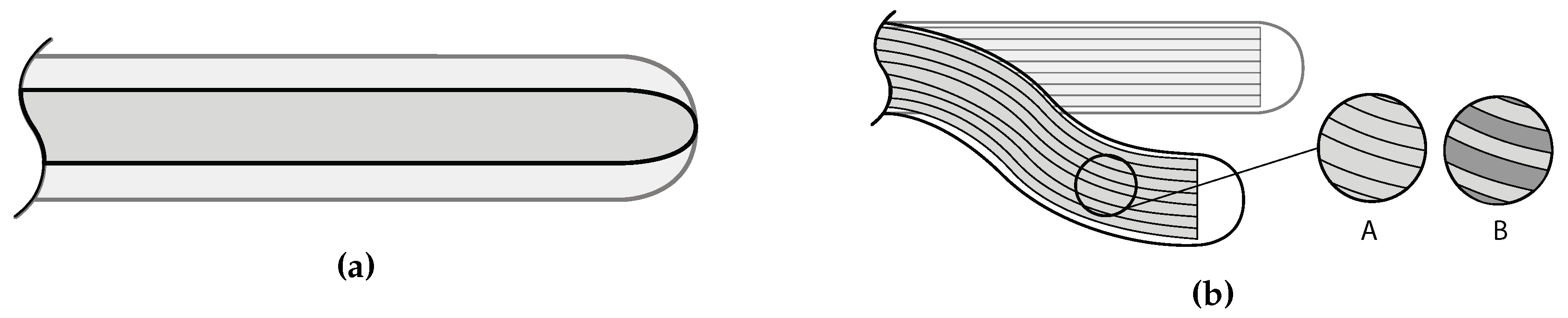
2.1. Geometrical Properties
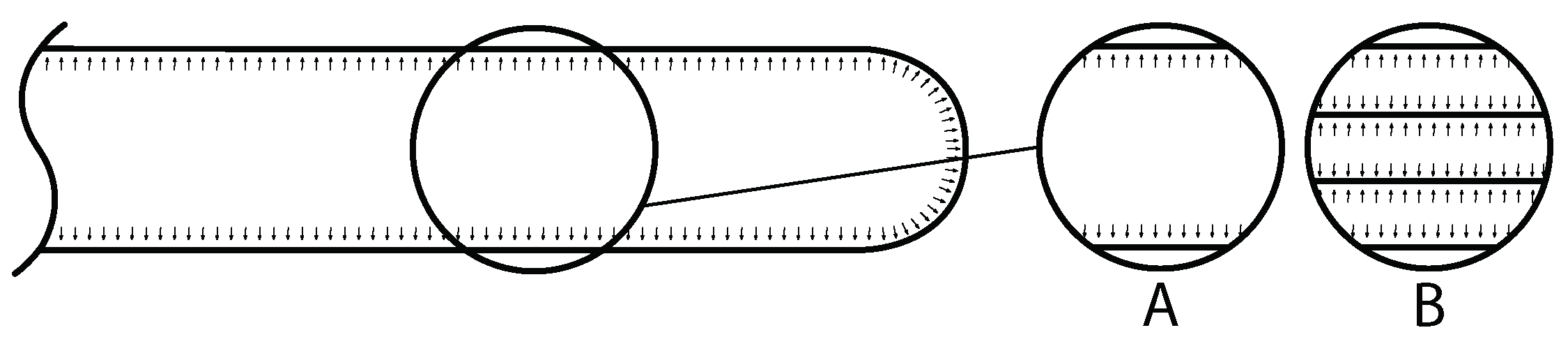
2.1.1. Cross-Section Shaping
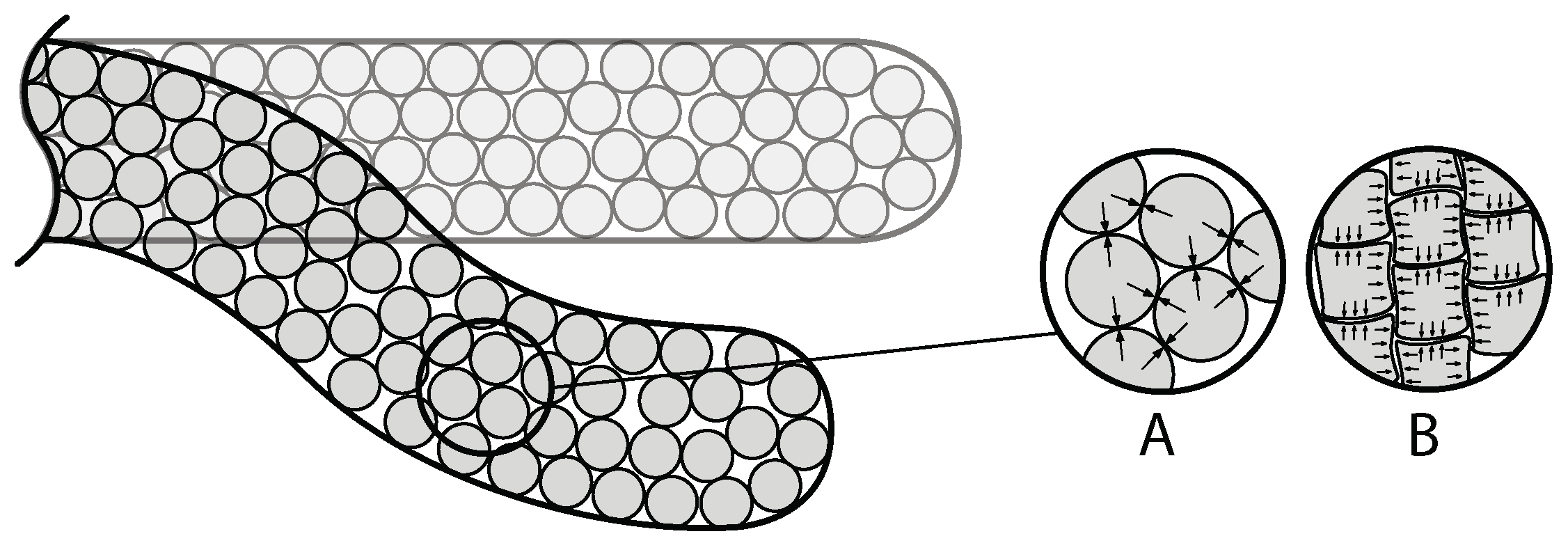
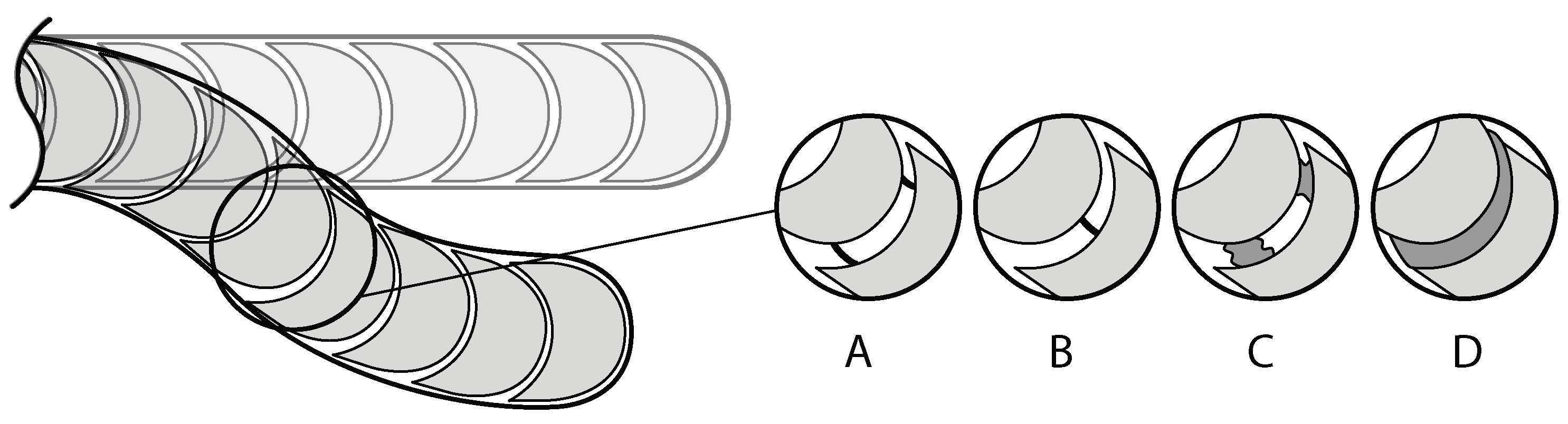
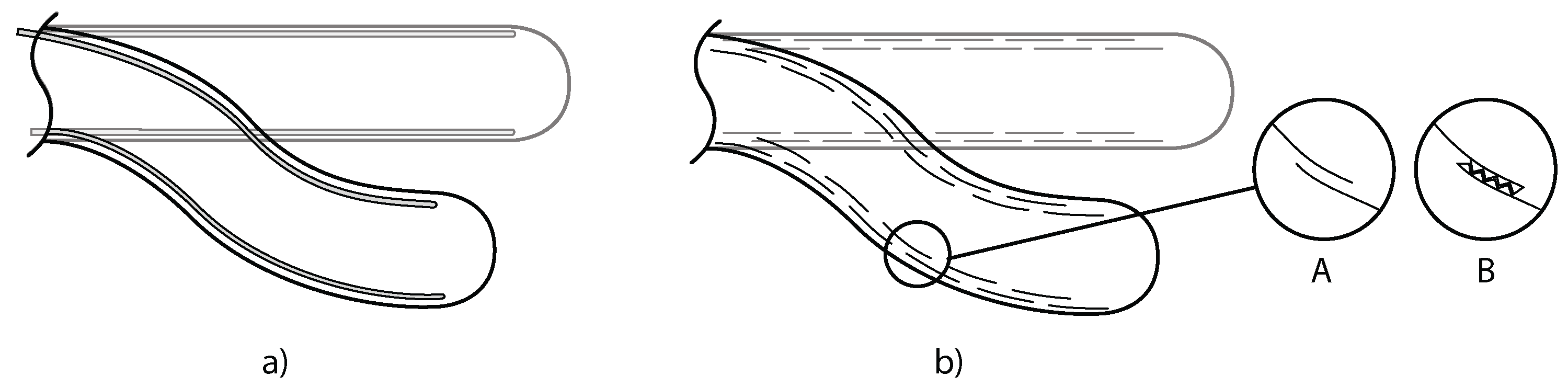
2.1.2. Structural Interactions
2.2. Elastic Properties
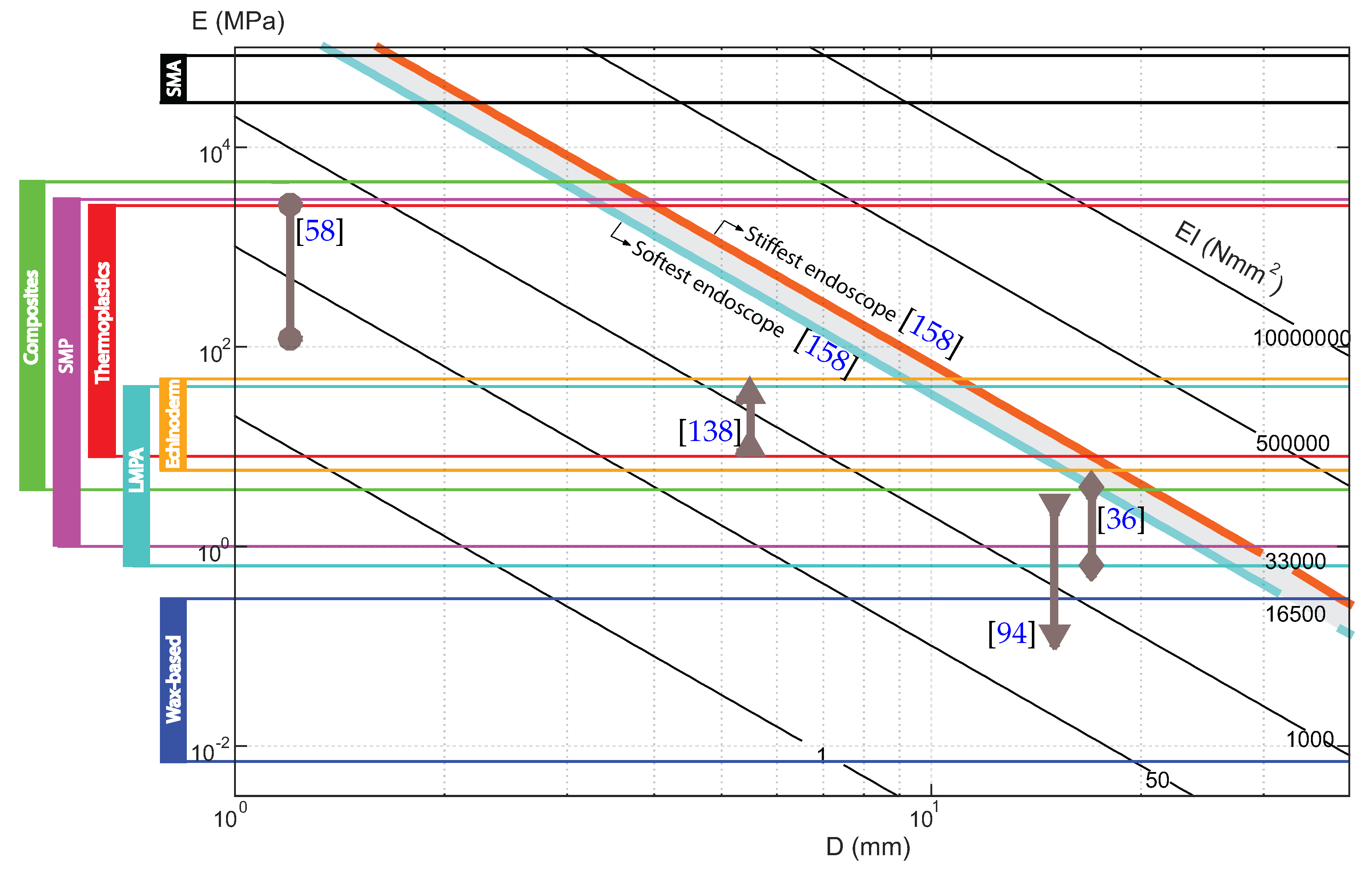
2.2.1. Material
- Wax: Foam-like structures covered with wax are rigid at ambient temperature and flexible at higher temperature [43]. When these structures are heated up, the wax changes phase, and the structure has the flexibility of the inner structure (e.g., foam). The advantages of this solution are the availability, the low cost and the ease of manufacturing of the elements while performing well.
- Solder: A worm-like robot demonstrates the use of polymeric elements connected by solder-joints for controllable stiffness performances [44]. A crawling robot with “solder-activated joints” uses joints with the phase-change as the locking mechanism [45]. The first phase-change joints (made with hot glue sticks) have been studied by Boston Dynamics. The global stiffness of the device can be adjusted by controlling the temperature of each element and joint. The elements contain thermorheological fluids, while the joints are made of solder-alloy mixture (60Sn-40Pb and Chip Quik) to lock or unlock the structure [44].
- Low melting point material: A solution based on Low Melting Point Alloy (LMPA) is presented in [32]. Joule losses are used in a circuit made of Galinstan in the liquid phase at ambient temperature (being therefore a soft heater). A thin layer of Field’s metal is heated by the latter circuit to change its phase and therefore its mechanical properties. A solution based on Cerrolow 117, an LMPA, integrated in a PDMS shell uses Joule heating by voltage difference applied on the LMPA for phase transition and stiffness change [34]. Joule heating of Cerrolow 117 embedded in dielectric elastomer is also used for a variable stiffness gripper [35]. An overtube for endoscopic applications based on LMPA is described in [36], using hot water to activate the change in stiffness. Numerous low melting point polymers are available with various transition temperatures [13,38]. The performances of such solutions will depend on the design, which could be optimized for obtaining very high performances [39].
2.2.2. Structural Interactions
2.2.3. Hybrid
2.3. Actuator-Like Solutions
2.3.1. Fluid-Based Solutions
2.3.2. Mechanical Solutions
2.3.3. Muscles
3. Flexible Medical Instruments Requirements
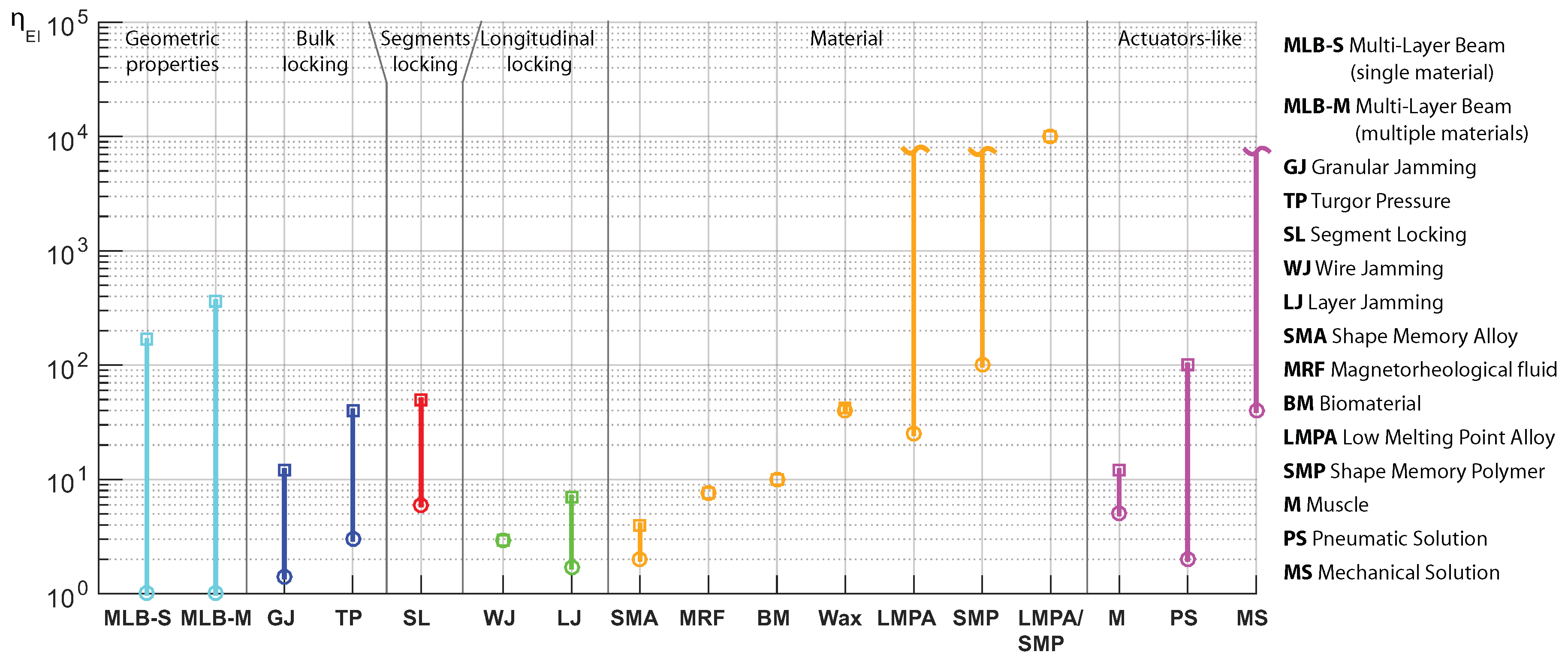
4. Specific Characterization
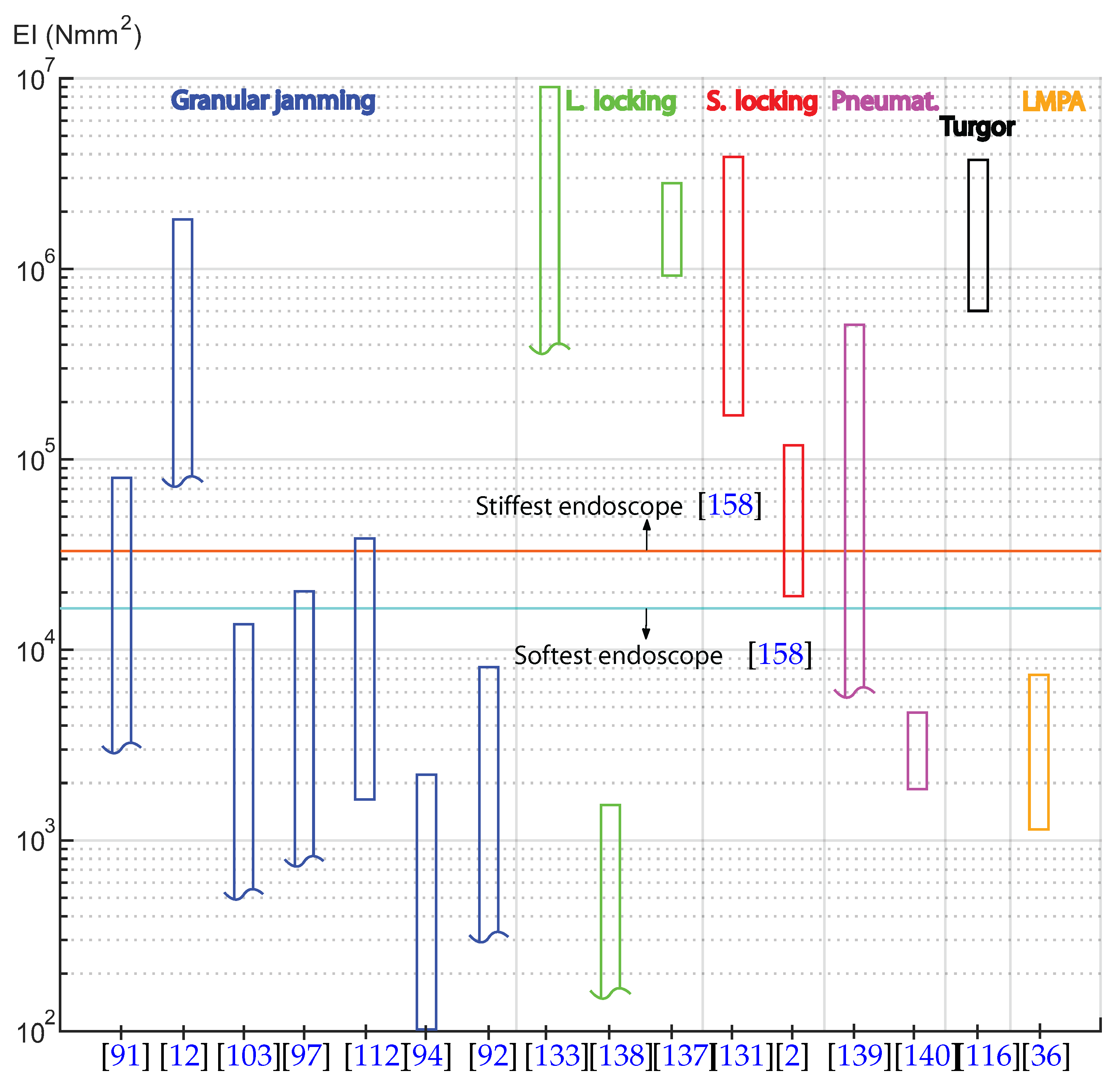
4.1. Flexural Stiffness
4.2. Ultimate Force
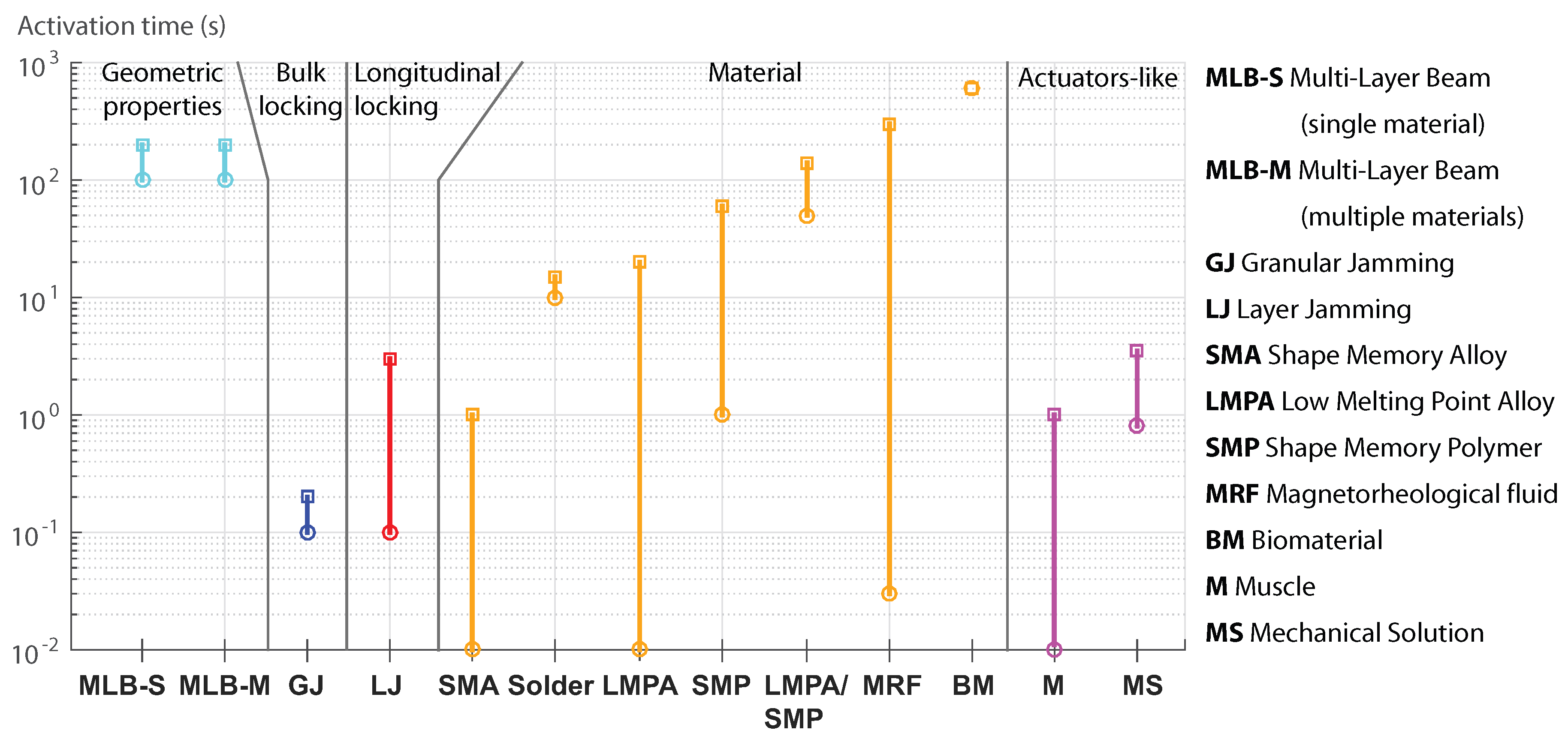
4.3. Activation Time
4.4. Scalability
4.5. Medical Requirements
5. Applications
5.1. Medical Devices
5.2. Patented Medical Applications
5.3. Aerospace Engineering
5.4. Soft Robotics
5.5. Biomimetics
5.6. Other Applications
6. Perspectives and Conclusions
Acknowledgments
Conflicts of Interest
Appendix A. Flexural Stiffness of Endoscopes
| # | Ref | Type | Brand | Type | Testing Method | Remarks | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (Avg) | (Min) | (Max) | (Avg Range) | |||||||||
| mm | cm | N cm | N cm | N cm | N cm | |||||||
| 1 | [158] | c | Pentax | EC-3800TL (1) | 165 | 164.19 | 216.13 | 190.16 | b | no stiffener | ||
| 2 | c | Pentax | EC-3800TL (1) | 215 | b | with stiffener | ||||||
| 3 | c | Pentax | EC-3800TL (2) | 170 | 173.23 | 250.00 | 211.61 | b | no stiffener | |||
| 4 | c | Pentax | EC-3800TL (2) | 250 | 227.42 | 330.65 | 279.03 | b | with stiffener | |||
| 5 | c | Olympus | CF-100TI | 185 | 182.00 | 225.00 | 203.50 | b | no stiffener | |||
| 6 | c | Olympus | CF-100TI | 200 | 210.00 | 259.27 | 234.64 | b | with stiffener | |||
| 7 | c | Olympus | CF-P20L | 200 | 180.00 | 220.00 | 200.00 | b | no stiffener | |||
| 8 | c | Olympus | CF-100L (1) | 210.00 | 220.00 | 215.00 | b | |||||
| 9 | c | Olympus | CF-100L (2) | 180.00 | 225.00 | 202.50 | b | |||||
| 10 | [5] | c | Olympus | XCF-SH230L | 12.9 | 168 | 70.33 | 264.65 | 167.49 | 3pb | VS flexible | |
| 11 | c | Olympus | XCF-SH230L | 12.9 | 168 | 93.53 | 316.12 | 204.83 | 3pb | VS rigid | ||
| 12 | c | Olympus | CF200HL | 13.3 | 165 | 70.33 | 421.26 | 245.79 | 3pb | |||
| 13 | c | Olympus | PCF230 | 11.3 | 130 | 59.45 | 237.09 | 148.27 | 3pb | Pediatric | ||
| 14 | [204] | c | Olympus | PCF240l | 11.2 | 117.46 | 201,00 | 159.23 | fbb | |||
| 15 | c | Olympus | CF20HL | 13.3 | 210.97 | 522.69 | 366.83 | fbb | ||||
| 16 | c | Olympus | CF-240AL | 12 | 103.74 | 425.44 | 264.59 | fbb | VS flexible | |||
| 17 | c | Olympus | CF-240AL | 12 | 164.84 | 609.98 | 387.41 | fbb | VS stiff | |||
| 18 | [4] | c | Olympus | CF140S | 13.3 | 260.00 | 400.00 | 330.00 | 3pb | at 24 C | ||
| 19 | c | Olympus | CF140S | 13.3 | 225.00 | 375.00 | 300.00 | 3pb | at 37 C | |||
| 20 | [201] | cf | Olympus | single-channel | 71.46 | 118.69 | 95.07 | fbb | ||||
| 21 | cf | Olympus | two-channels | 82.36 | 155.02 | 118.69 | fbb | |||||
| 22 | cf | ACM | two-channels | 249.49 | 283.40 | 266.44 | fbb | |||||
| 23 | c | ACM | single-channel | 71.46 | 405.72 | 238.59 | fbb | |||||
| 24 | gf | Olympus | single-channel | 81.14 | 164.71 | 122.93 | fbb | |||||
| 25 | [203] | c | Olympus | CF-Q160L | 274.50 | 655.96 | 465.23 | 3pb | ||||
| 26 | [205] | c | 900 | fbb | at 20 C | |||||||
| 27 | c | 540 | fbb | at 40 C |
References
- Degani, A.; Choset, H.; Wolf, A.; Ota, T.; Zenati, M.A. Percutaneous intrapericardial interventions using a highly articulated robotic probe. In Proceedings of the First IEEE/RAS-EMBS International Conference on Biomedical Robotics and Biomechatronics, Pisa, Italy, 20–22 February 2006; pp. 7–12. [Google Scholar]
- Kim, Y.J.; Cheng, S.; Kim, S.; Iagnemma, K. A stiffness-adjustable hyperredundant manipulator using a variable neutral-line mechanism for minimally invasive surgery. IEEE Trans. Robot. 2014, 30, 382–395. [Google Scholar] [CrossRef]
- Loeve, A.; Breedveld, P.; Dankelman, J. Scopes too flexible... and too stiff. IEEE Pulse 2010, 1, 26–41. [Google Scholar] [CrossRef] [PubMed]
- Hellier, D.; Albermani, F.; Evans, B.; De Visser, H.; Adam, C.; Passenger, J. Flexural and torsional rigidity of colonoscopes at room and body temperatures. Proc. Inst. Mech. Eng. Part H J. Eng. Med. 2011, 225, 389–399. [Google Scholar] [CrossRef]
- Brooker, J.; Saunders, B.; Shah, S.; Williams, C. A new variable stiffness colonoscope makes colonoscopy easier: A randomised controlled trial. Gut 2000, 46, 801–805. [Google Scholar] [CrossRef] [PubMed]
- Park, S.; Cha, K.; Park, J. Development of biomedical microrobot for intravascular therapy. Int. J. Adv. Robot. Syst. 2010, 7, 1. [Google Scholar] [CrossRef]
- Kinoshita, I.; Katoh, O.; Nariyama, J.; Otsuji, S.; Tateyama, H.; Kobayashi, T.; Shibata, N.; Ishihara, T.; Ohsawa, N. Coronary angioplasty of chronic total occlusions with bridging collateral vessels: Immediate and follow-up outcome from a large single-center experience. J. Am. Coll. Cardiol. 1995, 26, 409–415. [Google Scholar] [CrossRef]
- Haga, Y.; Mineta, T.; Makishi, W.; Matsunaga, T.; Esashi, M. Active bending catheter and endoscope using shape memory alloy actuators. In Shape Memory Alloys; Cismasiu, C., Ed.; InTech: Rijeka, Croatia, 2010; pp. 107–126. ISBN 978-953-307-106-0. [Google Scholar]
- Qaiser, Z.; Kang, L.; Johnson, S. Design of a bioinspired tunable stiffness robotic foot. Mech. Mach. Theory 2017, 110, 1–15. [Google Scholar] [CrossRef]
- Liu, Y.; Matsuhisa, H.; Utsuno, H. Semi-active vibration isolation system with variable stiffness and damping control. J. Sound Vib. 2008, 313, 16–28. [Google Scholar] [CrossRef]
- Fan, X.; Zhu, L.; Wang, K.; Wang, B.; Wu, Y.; Xie, W.; Huang, C.; Chan, B.P.; Du, Y. Stiffness-Controlled Thermoresponsive Hydrogels for Cell Harvesting with Sustained Mechanical Memory. Adv. Healthc. Mater. 2017, 6. [Google Scholar] [CrossRef] [PubMed]
- Cheng, N.G.; Lobovsky, M.B.; Keating, S.J.; Setapen, A.M.; Gero, K.I.; Hosoi, A.E.; Iagnemma, K.D. Design and analysis of a robust, low-cost, highly articulated manipulator enabled by jamming of granular media. In Proceedings of the 2012 IEEE International Conference on Robotics and Automation (ICRA), Saint Paul, MN, USA, 14–18 May 2012; pp. 4328–4333. [Google Scholar]
- McEvoy, M.A.; Correll, N. Thermoplastic variable stiffness composites with embedded, networked sensing, actuation, and control. J. Compos. Mater. 2015, 49, 1799–1808. [Google Scholar] [CrossRef]
- Manti, M.; Cacucciolo, V.; Cianchetti, M. Stiffening in soft robotics: A review of the state of the art. IEEE Robot. Autom. Mag. 2016, 23, 93–106. [Google Scholar] [CrossRef]
- Kuder, I.K.; Arrieta, A.F.; Raither, W.E.; Ermanni, P. Variable stiffness material and structural concepts for morphing applications. Prog. Aerosp. Sci. 2013, 63, 33–55. [Google Scholar] [CrossRef]
- Gere, J.M.; Goodno, B.J. Mechanics of Materials, 7th ed.; Cengage Learning: Boston, MA, USA, 2009. [Google Scholar]
- Hayes, G.J.; Liu, Y.; Genzer, J.; Lazzi, G.; Dickey, M.D. Self-folding origami microstrip antennas. IEEE Trans. Antennas Propag. 2014, 62, 5416–5419. [Google Scholar] [CrossRef]
- Henry, C.; McKnight, G. Cellular variable stiffness materials for ultra-large reversible deformations in reconfigurable structures. Proc. SPIE 2006, 6170, 617023. [Google Scholar]
- Krishnan, G.; Bishop-Moser, J.; Kim, C.; Kota, S. Kinematics of a generalized class of pneumatic artificial muscles. J. Mech. Robot. 2015, 7, 041014. [Google Scholar] [CrossRef]
- Kawamura, S.; Yamamoto, T.; Ishida, D.; Ogata, T.; Nakayama, Y.; Tabata, O.; Sugiyama, S. Development of passive elements with variable mechanical impedance for wearable robots. In Proceedings of the IEEE International Conference on Robotics and Automation, Washington, DC, USA, 11–15 May 2002; pp. 248–253. [Google Scholar]
- Tabata, O.; Konishi, S.; Cusin, P.; Ito, Y.; Kawai, F.; Hirai, S.; Kawamura, S. Micro fabricated tunable bending stiffness devices. Sens. Actuators A Phys. 2001, 89, 119–123. [Google Scholar] [CrossRef]
- Henke, M.; Gerlach, G. On a high-potential variable-stiffness device. Microsyst. Technol. 2014, 20, 599–606. [Google Scholar] [CrossRef]
- Henke, M.; Gerlach, G. A multi-layered variable stiffness device based on smart form closure actuators. J. Intell. Mater. Syst. Struct. 2016, 27, 375–383. [Google Scholar] [CrossRef]
- Ou, J.; Yao, L.; Tauber, D.; Steimle, J.; Niiyama, R.; Ishii, H. JamSheets: Thin interfaces with tunable stiffness enabled by layer jamming. In Proceedings of the 8th International Conference on Tangible, Embedded and Embodied Interaction, Munich, Germany, 16–19 February 2014; pp. 65–72. [Google Scholar]
- Veneman, J.; Manterola, I.; Bureau, M.; Jung, J.H. Varstiff, An Innovative Variable Stiffness Material, Applied in a Wheelchair Positioning Device. Available online: https://www.ige.tu-berlin.de/fileadmin/fg176/IGE_Printreihe/TAR_2015/Session_order/Postersession_Event_6_paper_Veneman_Jan_.pdf (accessed on 3 July 2017).
- Gandhi, F.; Kang, S.G. Beams with controllable flexural stiffness. Smart Mater. Struct. 2007, 16, 1179. [Google Scholar] [CrossRef]
- Mcknight, G.; Doty, R.; Keefe, A.; Herrera, G.; Henry, C. Segmented reinforcement variable stiffness materials for reconfigurable surfaces. J. Intell. Mater. Syst. Struct. 2010, 21, 1783–1793. [Google Scholar] [CrossRef]
- Bergamini, A. Electrostatic Modification of the Bending Stiffness of Adaptive Structures. Ph.D. Thesis, ETH Zurich, Zurich, Switzerland, 2009. [Google Scholar]
- Murray, G.; Gandhi, F.; Kang, S.G. Flexural stiffness control of multilayered beams. AIAA J. 2009, 47, 757–766. [Google Scholar] [CrossRef]
- Murray, G.; Gandhi, F. Multi-layered controllable stiffness beams for morphing: Energy, actuation force, and material strain considerations. Smart Mater. Struct. 2010, 19, 045002. [Google Scholar] [CrossRef]
- Natterer, J.; Weinand, Y. Modeling of multi-layer beam with interlayer slips. In Proceedings of the 10th World Conference on Timber Engineering (WCTE), Miyazaki, Japan, 2–5 June 2008. [Google Scholar]
- Shan, W.; Lu, T.; Majidi, C. Soft-matter composites with electrically tunable elastic rigidity. Smart Mater. Struct. 2013, 22, 085005. [Google Scholar] [CrossRef]
- Shan, W.; Lu, T.; Wang, Z.; Majidi, C. Thermal analysis and design of a multi-layered rigidity tunable composite. Int. J. Heat Mass Transf. 2013, 66, 271–278. [Google Scholar] [CrossRef]
- Schubert, B.E.; Floreano, D. Variable stiffness material based on rigid low-melting-point-alloy microstructures embedded in soft poly(dimethylsiloxane) (PDMS). Rsc Adv. 2013, 3, 24671–24679. [Google Scholar] [CrossRef]
- Shintake, J.; Schubert, B.; Rosset, S.; Shea, H.; Floreano, D. Variable stiffness actuator for soft robotics using dielectric elastomer and low-melting-point alloy. In Proceedings of the 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Hamburg, Germany, 28 September–2 October 2015; pp. 1097–1102. [Google Scholar]
- Zhao, R.; Yao, Y.; Luo, Y. Development of a Variable Stiffness Over Tube Based on Low-Melting-Point-Alloy for Endoscopic Surgery. J. Med. Dev. 2016, 10, 021002. [Google Scholar] [CrossRef]
- Zheng, L.; Yoshida, S.; Morimoto, Y.; Onoe, H.; Takeuchi, S. Pneumatic balloon actuator with tunable bending points. In Proceedings of the 2015 28th IEEE International Conference on Micro Electro Mechanical Systems (MEMS), Estoril, Portugal, 18–22 January 2015; pp. 18–21. [Google Scholar]
- Loeve, A.J.; Bosma, J.H.; Breedveld, P.; Dodou, D.; Dankelman, J. Polymer rigidity control for endoscopic shaft-guide “Plastolock”—A feasibility study. J. Med. Dev. 2010, 4, 045001. [Google Scholar] [CrossRef]
- Balasubramanian, A.; Standish, M.; Bettinger, C.J. Microfluidic thermally activated materials for rapid control of macroscopic compliance. Adv. Funct. Mater. 2014, 24, 4860–4866. [Google Scholar] [CrossRef]
- McEvoy, M.; Correll, N. Shape change through programmable stiffness. In Experimental Robotics; Springer: Hamburg, Germany, 2016; pp. 893–907. [Google Scholar]
- Shan, W.; Diller, S.; Tutcuoglu, A.; Majidi, C. Rigidity-tuning conductive elastomer. Smart Mater. Struct. 2015, 24, 065001. [Google Scholar] [CrossRef]
- Cheng, N.G. Design and Analysis of Active Fluid-and-Cellular Solid Composites for Controllable Stiffness Robotic Elements. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2009. [Google Scholar]
- Cheng, N.G.; Gopinath, A.; Wang, L.; Iagnemma, K.; Hosoi, A.E. Thermally Tunable, Self-Healing Composites for Soft Robotic Applications. Macromol. Mater. Eng. 2014, 299, 1279–1284. [Google Scholar] [CrossRef]
- Cheng, N.; Ishigami, G.; Hawthorne, S.; Chen, H.; Hansen, M.; Telleria, M.; Playter, R.; Iagnemma, K. Design and analysis of a soft mobile robot composed of multiple thermally activated joints driven by a single actuator. In Proceedings of the 2010 IEEE International Conference on Robotics and Automation (ICRA), Anchorage, AK, USA, 3–7 May 2010; pp. 5207–5212. [Google Scholar]
- Telleria, M.J.; Hansen, M.; Campbell, D.; Servi, A.; Culpepper, M.L. Modeling and implementation of solder-activated joints for single-actuator, centimeter-scale robotic mechanisms. In Proceedings of the 2010 IEEE International Conference on Robotics and Automation (ICRA), Anchorage, AK, USA, 3–7 May 2010; pp. 1681–1686. [Google Scholar]
- Hodgson, D.E.; Ming, W.; Biermann, R.J. Shape memory alloys. ASM Int. Met. Handb. Tenth Ed. 1990, 2, 897–902. [Google Scholar]
- Liu, C.; Qin, H.; Mather, P. Review of progress in shape-memory polymers. J. Mater. Chem. 2007, 17, 1543–1558. [Google Scholar] [CrossRef]
- Swensen, J.P.; Dollar, A.M. Optimization of parallel spring antagonists for Nitinol shape memory alloy actuators. In Proceedings of the 2014 IEEE International Conference on Robotics and Automation (ICRA), Hong Kong, China, 31 May–7 June 2014; pp. 6345–6349. [Google Scholar]
- Kianzad, S.; Amini, A.; Karkouti, S.O. Force control of laparoscopy grasper using antagonistic shape memory alloy. In Proceedings of the 2011 1st Middle East Conference on Biomedical Engineering (MECBME), Sharjah, United Arab Emirates, 21–24 February 2011; pp. 335–338. [Google Scholar]
- Ikuta, K.; Tsukamoto, M.; Hirose, S. Shape memory alloy servo actuator system with electric resistance feedback and application for active endoscope. In Proceedings of the 1988 IEEE International Conference on Robotics and Automation, Philadelphia, PA, USA, 24–29 April 1988; pp. 427–430. [Google Scholar]
- Ho, M.; Desai, J.P. Characterization of SMA actuator for applications in robotic neurosurgery. In Proceedings of the Annual International Conference of the Engineering in Medicine and Biology Society, Minneapolis, MN, USA, 3–6 September 2009; pp. 6856–6859. [Google Scholar]
- Haga, Y.; Mizushima, M.; Matsunaga, T.; Totsu, K.; Esashi, M. Active bending ileus tube using shape memory alloy for treatment of intestinal obstruction. In Proceedings of the 3rd IEEE/EMBS Special Topic Conference on Microtechnology in Medicine and Biology, Oahu, HI, USA, 12–15 May 2005; pp. 249–252. [Google Scholar]
- Arora, A.; Ambe, Y.; Kim, T.H.; Ariizumi, R.; Matsuno, F. Development of a maneuverable flexible manipulator for minimally invasive surgery with varied stiffness. Artifi. Life Robot. 2014, 19, 340–346. [Google Scholar] [CrossRef]
- SMP Technologies Inc. Intelligent Material Able to Adjust Itself Accordingly to Ensure the Highest Llevel of Comfort & Affinity with Human Body; Technical Report; SMP Technologies Inc.: Scotts Valley, CA, USA, 2014. [Google Scholar]
- Ratna, D.; Karger-Kocsis, J. Recent advances in shape memory polymers and composites: A review. J. Mater. Sci. 2008, 43, 254–269. [Google Scholar] [CrossRef]
- Lendlein, A.; Langer, R. Biodegradable, elastic shape-memory polymers for potential biomedical applications. Science 2002, 296, 1673–1676. [Google Scholar] [CrossRef] [PubMed]
- Meng, Q.; Hu, J. A review of shape memory polymer composites and blends. Compos. Part A Appl. Sci. Manuf. 2009, 40, 1661–1672. [Google Scholar] [CrossRef]
- Chenal, T.P.; Case, J.C.; Paik, J.; Kramer, R.K. Variable stiffness fabrics with embedded shape memory materials for wearable applications. In Proceedings of the 2014 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS 2014), Chicago, IL, USA, 14–18 September 2014; pp. 2827–2831. [Google Scholar]
- Chen, Y.; Sun, J.; Liu, Y.; Leng, J. Variable stiffness property study on shape memory polymer composite tube. Smart Mater. Struct. 2012, 21, 094021. [Google Scholar] [CrossRef]
- Amano, Y.; Hidema, R.; Gong, J.; Furukawa, H. Creation of Shape-memory Gels with Inter-crosslinking Network Structure. Chem. Lett. 2012, 41, 1029–1031. [Google Scholar] [CrossRef]
- Yamano, M.; Akiba, N.; Gong, J.; Furukawa, H. Experiments of a two-arm robot using shape memory gel. In Proceedings of the 2012 IEEE/SICE International Symposium on System Integration (SII), Fukuoka, Japan, 16–18 December 2012; pp. 236–241. [Google Scholar]
- Yamano, M.; Goto, D.; Ujiie, K.; Akiba, N.; Gong, J.; Furukawa, H.; Tadakuma, R. Experiments of a variable stiffness robot using shape memory gel. In Proceedings of the 2013 IEEE/SICE International Symposium on System Integration (SII), Kobe, Japan, 15–17 December 2013; pp. 647–652. [Google Scholar]
- Yokoo, T.; Hidema, R.; Furukawa, H. Smart lenses developed with high-strength and shape memory gels. E-J. Surf. Sci. Nanotechnol. 2012, 10, 243–247. [Google Scholar] [CrossRef]
- Harada, S.; Hidema, R.; Gong, J.; Furukawa, H. Intelligent Button Developed Using Smart Soft and Wet Materials. Chem. Lett. 2012, 41, 1047–1049. [Google Scholar] [CrossRef]
- Jolly, M.R.; Bender, J.W.; Carlson, J.D. Properties and applications of commercial magnetorheological fluids. J. Intell. Mater. Syst. Struct. 1999, 10, 5–13. [Google Scholar] [CrossRef]
- Sadeghi, A.; Beccai, L.; Mazzolai, B. Innovative soft robots based on electro-rheological fluids. In Proceedings of the 2012 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vilamoura, Portugal, 7–12 October 2012; pp. 4237–4242. [Google Scholar]
- Park, G.; Bement, M.T.; Hartman, D.A.; Smith, R.E.; Farrar, C.R. The use of active materials for machining processes: A review. Int. J. Mach. Tools Manuf. 2007, 47, 2189–2206. [Google Scholar] [CrossRef]
- Yalcintas, M.; Dai, H. Magnetorheological and electrorheological materials in adaptive structures and their performance comparison. Smart Mater. Struct. 1999, 8, 560. [Google Scholar] [CrossRef]
- Majidi, C.; Wood, R.J. Tunable elastic stiffness with microconfined magnetorheological domains at low magnetic field. Appl. Phys. Lett. 2010, 97, 164104. [Google Scholar] [CrossRef]
- Pettersson, A.; Davis, S.; Gray, J.; Dodd, T.; Ohlsson, T. Design of a magnetorheological robot gripper for handling of delicate food products with varying shapes. J. Food Eng. 2010, 98, 332–338. [Google Scholar] [CrossRef]
- Ma, H.; Chen, B.; Qin, L.; Liao, W.H. Design and testing of a regenerative magnetorheological actuator for assistive knee braces. Smart Mater. Struct. 2017, 26, 035013. [Google Scholar] [CrossRef]
- Furusho, J.; Kikuchi, T.; Tokuda, M.; Kakehashi, T.; Ikeda, K.; Morimoto, S.; Hashimoto, Y.; Tomiyama, H.; Nakagawa, A.; Akazawa, Y. Development of shear type compact MR brake for the intelligent ankle-foot orthosis and its control; research and development in NEDO for practical application of human support robot. In Proceedings of the IEEE 10th International Conference on Rehabilitation Robotics, Noordwijk, The Netherlands, 13–15 June 2007; pp. 89–94. [Google Scholar]
- Wen, W.; Huang, X.; Yang, S.; Lu, K.; Sheng, P. The giant electrorheological effect in suspensions of nanoparticles. Nat. Mater. 2003, 2, 727–730. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Liao, W.H. Development and testing of a magnetorheological actuator for an assistive knee brace. In Proceedings of the the 15th International Symposium on Smart Structures and Materials & Nondestructive Evaluation and Health Monitoring, San Diego, CA, USA, 9 March 2008. [Google Scholar]
- Chen, J.; Liao, W.H. Design and testing of assistive knee brace with magnetorheological actuator. In Proceedings of the IEEE International Conference on Robotics and Biomimetics, Bangkok, Thailand, 22–25 February 2009; pp. 512–517. [Google Scholar]
- Chen, J.; Liao, W. Design, testing and control of a magnetorheological actuator for assistive knee braces. Smart Mater. Struct. 2010, 19, 035029. [Google Scholar] [CrossRef]
- Chen, J.; Liao, W.H. Design and control of a magnetorheological actuator for leg exoskeleton. In Proceedings of the IEEE International Conference on Robotics and Biomimetics, Sanya, China, 15–18 December 2007; pp. 1388–1393. [Google Scholar]
- Carlson, J.D.; Matthis, W.; Toscano, J.R. Smart prosthetics based on magnetorheological fluids. In Proceedings of the SPIE’s 8th Annual International Symposium on Smart Structures and Materials, Newport Beach, CA, USA, 4 March 2001; pp. 308–316. [Google Scholar]
- Ahmadkhanlou, F.; Zite, J.L.; Washington, G.N. A magnetorheological fluid-based controllable active knee brace. In Proceedings of the 14th International Symposium on Smart Structures and Materials & Nondestructive Evaluation and Health Monitoring, San Diego, CA, USA, 18 March 2007. [Google Scholar]
- Herr, H.; Wilkenfeld, A. User-adaptive control of a magnetorheological prosthetic knee. Ind. Robot Int. J. 2003, 30, 42–55. [Google Scholar] [CrossRef]
- Trotter, J.; Tipper, J.; Lyons-Levy, G.; Chino, K.; Heuer, A.; Liu, Z.; Mrksich, M.; Hodneland, C.; Dillmore, W.S.; Koob, T.; et al. Towards a fibrous composite with dynamically controlled stiffness: Lessons from echinoderms. Biochem. Soc. Trans. 2000, 357–362. [Google Scholar] [CrossRef]
- Shanmuganathan, K.; Capadona, J.R.; Rowan, S.J.; Weder, C. Biomimetic mechanically adaptive nanocomposites. Prog. Polym. Sci. 2010, 35, 212–222. [Google Scholar] [CrossRef]
- Shanmuganathan, K.; Capadona, J.R.; Rowan, S.J.; Weder, C. Bio-inspired mechanically-adaptive nanocomposites derived from cotton cellulose whiskers. J. Mater. Chem. 2010, 20, 180–186. [Google Scholar] [CrossRef]
- Capadona, J.R.; Shanmuganathan, K.; Tyler, D.J.; Rowan, S.J.; Weder, C. Stimuli-responsive polymer nanocomposites inspired by the SEA cucumber dermis. Science 2008, 319, 1370–1374. [Google Scholar] [CrossRef] [PubMed]
- Brown, E.; Rodenberg, N.; Amend, J.; Mozeika, A.; Steltz, E.; Zakin, M.R.; Lipson, H.; Jaeger, H.M. Universal robotic gripper based on the jamming of granular material. Proc. Natl. Acad. Sci. USA 2010, 107, 18809–18814. [Google Scholar] [CrossRef]
- Amend, J.R.; Brown, E.; Rodenberg, N.; Jaeger, H.M.; Lipson, H. A positive pressure universal gripper based on the jamming of granular material. IEEE Trans. Robot. 2012, 28, 341–350. [Google Scholar] [CrossRef]
- Amend, J.; Cheng, N.; Fakhouri, S.; Culley, B. Soft Robotics Commercialization: Jamming Grippers from Research to Product. Soft Robot. 2016, 3, 213–222. [Google Scholar] [CrossRef] [PubMed]
- Jaeger, H.M. Celebrating soft matter’s 10th anniversary: Toward jamming by design. Soft Matter 2015, 11, 12–27. [Google Scholar] [CrossRef] [PubMed]
- Cheng, N.G. Design and Analysis of Jammable Granular Systems. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2013. [Google Scholar]
- Cheng, N.; Amend, J.; Farrell, T.; Latour, D.; Martinez, C.; Johansson, J.; McNicoll, A.; Wartenberg, M.; Naseef, S.; Hanson, W.; et al. Prosthetic jamming terminal device: A case study of untethered soft robotics. Soft Robot. 2016, 3, 205–212. [Google Scholar] [CrossRef] [PubMed]
- Loeve, A.J.; van de Ven, O.S.; Vogel, J.G.; Breedveld, P.; Dankelman, J. Vacuum packed particles as flexible endoscope guides with controllable rigidity. Granul. Matter 2010, 12, 543–554. [Google Scholar] [CrossRef]
- Jiang, A.; Xynogalas, G.; Dasgupta, P.; Althoefer, K.; Nanayakkara, T. Design of a variable stiffness flexible manipulator with composite granular jamming and membrane coupling. Proceediongs of the 2012 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vilamoura, Portugal, 7–12 October 2012; pp. 2922–2927. [Google Scholar]
- Jiang, A.; Althoefer, K.; Dasgupta, P.; Nanayakkara, T. The Core Snake, the variable stiffness laparoscopic camera. In Proceedings of the Hamlyn Symposium on Medical Robotics, London, UK, 22–25 June 2013. [Google Scholar]
- Jiang, A.; Ranzani, T.; Gerboni, G.; Lekstutyte, L.; Althoefer, K.; Dasgupta, P.; Nanayakkara, T. Robotic granular jamming: Does the membrane matter? Soft Robot. 2014, 1, 192–201. [Google Scholar] [CrossRef]
- Jiang, A.; Adejokun, S.; Faragasso, A.; Althoefer, K.; Nanayakkara, T.; Dasgupta, P. The granular jamming integrated actuator. In Proceedings of the 2014 International Conference on Advanced Robotics and Intelligent Systems (ARIS), Taipei, Taiwan, 6–8 June 2014; pp. 12–17. [Google Scholar]
- Yanagida, T.; Adachi, K.; Nakamura, T. Development of endoscopic device to veer out a latex tube with jamming by granular materials. In Proceedings of the 2013 IEEE International Conference on Robotics and Biomimetics (ROBIO), Shenzhen, China, 12–14 December 2013; pp. 1474–1479. [Google Scholar]
- Yanagida, T.; Kamagata, T.; Nakamura, T. Development of an Endoscopic Support Device Using Veering-out Tube with Stiffening Capability by Granular Jamming. Trans. Soc. Instrum. Control Eng. 2015, 51, 290–296. [Google Scholar] [CrossRef]
- Mitsuda, T.; Kuge, S.; Wakabayashi, M.; Kawamura, S. Haptic displays implemented by controllable passive elements. In Proceedings of the IEEE International Conference on Robotics and Automation, Washington, DC, USA, 11–15 May 2002; Volume 4, pp. 4223–4228. [Google Scholar]
- Huijben, F.; van Herwijnen, F.; Lindner, G. Vacuumatic pre-stressed flexible architectural structures. In Proceedings of the III International Conference on Textile Composites and Inflatable Structures, Barcelona, Spain, 17–19 September 2007; pp. 197–200. [Google Scholar]
- Huijben, F.; Van Herwijnen, F. Vacuumatics; Shaping space by “freezing” the geometry of structures. In Proceedings of the Tectonics Making Meaning Conference, Eindhoven, The Netherlands, 10–12 December 2007. [Google Scholar]
- Huijben, F.; Herwijnen, F.V.; Nijsse, R. VACUUMATICS; Systematic Flexural Rigidity Analysis. In Proceedings of the International Association for Shell and Spatial Structures (IASS) Symposium, Shanghai, China, 8–12 November 2010; pp. 8–12. [Google Scholar]
- Athanassiadis, A.G.; Miskin, M.Z.; Kaplan, P.; Rodenberg, N.; Lee, S.H.; Merritt, J.; Brown, E.; Amend, J.; Lipson, H.; Jaeger, H.M. Particle shape effects on the stress response of granular packings. Soft Matter 2014, 10, 48–59. [Google Scholar] [CrossRef] [PubMed]
- Cianchetti, M.; Ranzani, T.; Gerboni, G.; De Falco, I.; Laschi, C.; Menciassi, A. STIFF-FLOP surgical manipulator: Mechanical design and experimental characterization of the single module. In Proceedings of the 2013 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Tokyo, Japan, 3–7 November 2013; pp. 3576–3581. [Google Scholar]
- Cianchetti, M.; Ranzani, T.; Gerboni, G.; Nanayakkara, T.; Althoefer, K.; Dasgupta, P.; Menciassi, A. Soft robotics technologies to address shortcomings in today’s minimally invasive surgery: The STIFF-FLOP approach. Soft Robot. 2014, 1, 122–131. [Google Scholar] [CrossRef]
- De Falco, I.; Cianchetti, M.; Menciassi, A. A soft and controllable stiffness manipulator for minimally invasive surgery: Preliminary characterization of the modular design. In Proceedings of the 36th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Chicago, IL, USA, 26–30 August 2014. [Google Scholar]
- De Falco, I.; Cianchetti, M.; Menciassi, A. STIFF-FLOP surgical manipulator: Design and preliminary motion evaluation. In Proceedings of the 4th WorkShop on Computer/Robot Assisted Surgery (CRAS), Genoa, Italy, 14–16 October 2014; pp. 131–134. [Google Scholar]
- Follmer, S.; Leithinger, D.; Olwal, A.; Cheng, N.; Ishii, H. Jamming user interfaces: Programmable particle stiffness and sensing for malleable and shape-changing devices. In Proceedings of the 25th Annual ACM Symposium on User Interface Software and Technology, Cambridge, MA, USA, 7–10 October 2012; pp. 519–528. [Google Scholar]
- Letts, R.; Hobson, D. The vacuum splint: An aid in emergency splinting of fractures. Can. Med. Assoc. J. 1973, 109, 599. [Google Scholar] [PubMed]
- Mustaza, S.M.; Mahdi, D.; Saaj, C.; Albukhanajer, W.A.; Lekakou, C.; Elsayed, Y.; Fras, J. Tuneable Stiffness Design of Soft Continuum Manipulator. In Proceedings of the International Conference on Intelligent Robotics and Applications, Portsmouth, UK, 24–27 August 2015; pp. 152–163. [Google Scholar]
- Tachi, T.; Masubuchi, M.; Iwamoto, M. Rigid Origami Structures with Vacuumatics: Geometric Considerations. In Proceedings of the IASS-APCS 2012, Seoul, Korea, 21–24 May 2012. [Google Scholar]
- Wall, V.; Deimel, R.; Brock, O. Selective stiffening of soft actuators based on jamming. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; pp. 252–257. [Google Scholar]
- Wei, Y.; Chen, Y.; Ren, T.; Chen, Q.; Yan, C.; Yang, Y.; Li, Y. A Novel, Variable Stiffness Robotic Gripper Based on Integrated Soft Actuating and Particle Jamming. Soft Robot. 2016, 3, 134–143. [Google Scholar] [CrossRef]
- Nilsson, S.B.; Hertz, C.H.; Falk, S. On the Relation between Turgor Pressure and Tissue Rigidity. II. Theoretical Calculations on Model Systems. Physiol. Plant. 1958, 11, 818–837. [Google Scholar]
- Falk, S.; Hertz, C.H.; Virgin, H.I. On the Relation between Turgor Pressure and Tissue Rigidity. I. Experiments on Resonance Frequency and Tissue Rigidity. Physiol. Plant. 1958, 11, 802–817. [Google Scholar]
- Georget, D.; Smith, A.; Waldron, K. Modelling of carrot tissue as a fluid-filled foam. J. Materi. Sci. 2003, 38, 1933–1938. [Google Scholar] [CrossRef]
- Faisal, T.R.; Abad, E.M.K.; Hristozov, N.; Pasini, D. The impact of tissue morphology, cross-section and turgor pressure on the mechanical properties of the leaf petiole in plants. J. Bionic Eng. 2010, 7, S11–S23. [Google Scholar] [CrossRef]
- Lin, T.T.; Pitt, R. Rheology of apple and potato tissue as affected by cell turgor pressure. J. Texture Stud. 1986, 17, 291–313. [Google Scholar] [CrossRef]
- Karunasena, H.; Gu, Y.; Brown, R.; Senadeera, W. Numerical Investigation of Case Hardening of Plant Tissue During Drying and Its Influence on the Cellular-Level Shrinkage. Dry. Technol. 2015, 33, 713–734. [Google Scholar] [CrossRef]
- Pasini, D. On the biological shape of the Polygonaceae Rheum Petiole. Int. J. Des. Nat. Ecodynamics 2008, 3, 39–64. [Google Scholar] [PubMed]
- Caringella, M.A.; Bergman, B.A.; Stanfield, R.C.; Ewers, M.M.; Bobich, E.G.; Ewers, F.W. Effects of phyllotaxy on biomechanical properties of stems of Cercis occidentalis (Fabaceae). Am. J. Bot. 2014, 101, 206–210. [Google Scholar] [CrossRef] [PubMed]
- Tadrist, L.; Darbois-Texier, B. Are leaves optimally designed for self-support? An investigation on giant monocots. J. Theor. Biol. 2016, 396, 125–131. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Chang, J.H.; Greenlee, A.S.; Cheung, K.C.; Slocum, A.H.; Gupta, R. Multi-turn, tension-stiffening catheter navigation system. In Proceedings of the 2010 IEEE International Conference on Robotics and Automation (ICRA), Anchorage, AK, USA, 3–7 May 2010; pp. 5570–5575. [Google Scholar]
- Degani, A.; Choset, H.; Wolf, A.; Zenati, M.A. Highly articulated robotic probe for minimally invasive surgery. In Proceedings of the 2006 IEEE International Conference on Robotics and Automation, Orlando, FL, USA, 15–19 May 2006; pp. 4167–4172. [Google Scholar]
- Sturges, R.H., Jr.; Laowattana, S. A flexible, tendon-controlled device for endoscopy. Int. J. Robot. Res. 1993, 12, 121–131. [Google Scholar] [CrossRef]
- Ota, T.; Degani, A.; Schwartzman, D.; Zubiate, B.; McGarvey, J.; Choset, H.; Zenati, M.A. A highly articulated robotic surgical system for minimally invasive surgery. Ann. Thorac. Surg. 2009, 87, 1253–1256. [Google Scholar] [CrossRef] [PubMed]
- Jung, J.; Penning, R.S.; Ferrier, N.J.; Zinn, M.R. A modeling approach for continuum robotic manipulators: Effects of nonlinear internal device friction. In Proceedings of the 2011 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), San Francisco, CA, USA, 25–30 September 2011; pp. 5139–5146. [Google Scholar]
- Raju, G.S.; Rex, D.K.; Kozarek, R.A.; Ahmed, I.; Brining, D.; Pasricha, P.J. A novel shape-locking guide for prevention of sigmoid looping during colonoscopy. Gastrointest. Endosc. 2004, 59, 416–419. [Google Scholar] [CrossRef]
- Rex, D.K.; Khashab, M.; Raju, G.S.; Pasricha, J.; Kozarek, R. Insertability and safety of a shape-locking device for colonoscopy. Am. J. Gastroenterol. 2005, 100, 817–820. [Google Scholar] [CrossRef] [PubMed]
- Swanstrom, L.L.; Kozarek, R.; Pasricha, P.J.; Gross, S.; Birkett, D.; Park, P.O.; Saadat, V.; Ewers, R.; Swain, P. Development of a new access device for transgastric surgery. J. Gastrointest. Surg. 2005, 9, 1129–1137. [Google Scholar] [CrossRef] [PubMed]
- Chalhoub, M.S.; Kelly, J.M. Effect of bulk compressibility on the stiffness of cylindrical base isolation bearings. Int. J. Solids Struct. 1990, 26, 743–760. [Google Scholar] [CrossRef]
- Huh, T.M.; Park, Y.J.; Cho, K.J. Design and analysis of a stiffness adjustable structure using an endoskeleton. Int. J. Precis. Eng. Manuf. 2012, 13, 1255–1258. [Google Scholar] [CrossRef]
- Kim, Y.J.; Cheng, S.; Kim, S.; Iagnemma, K. Design of a tubular snake-like manipulator with stiffening capability by layer jamming. In Proceedings of the 2012 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vilamoura, Portugal, 7–12 October 2012; pp. 4251–4256. [Google Scholar]
- Kim, Y.J.; Cheng, S.; Kim, S.; Iagnemma, K. A novel layer jamming mechanism with tunable stiffness capability for minimally invasive surgery. IEEE Trans. Robot. 2013, 29, 1031–1042. [Google Scholar] [CrossRef]
- Zuo, S.; Iijima, K.; Tokumiya, T.; Masamune, K. Variable stiffness outer sheath with “Dragon skin” structure and negative pneumatic shape-locking mechanism. Int. J. Comput. Assist. Radiol. Surg. 2014, 9, 857–865. [Google Scholar] [CrossRef] [PubMed]
- Yagi, A.; Matsumiya, K.; Dohi, T. Slider Linkage Lock Mechanism using Air Pressure for Rigid-Flexible Outer Sheath for Endoscopic Surgery. In Proceedings of the 1st Asian Symposium on Computer Aided Surgery—Robotic and Image guided Surgery, National Institute of Advanced Industrial Science and Technology, Tokyo, Japan, 28 April 2005; pp. 194–197. [Google Scholar]
- Yagi, A.; Matsumiya, K.; Masamune, K.; Liao, H.; Dohi, T. Rigid-flexible outer sheath model using shape lock mechanism by air pressure and wire driven curving mechanism. In Proceedings of the World Congress on Medical Physics and Biomedical Engineering 2006, Seoul, Korea, 27 August–1 September 2006; pp. 3108–3111. [Google Scholar]
- Moses, M.S.; Kutzer, M.D.; Ma, H.; Armand, M. A continuum manipulator made of interlocking fibers. In Proceedings of the 2013 IEEE International Conference on Robotics and Automation (ICRA), Karlsruhe, Germany, 6–10 May 2013; pp. 4008–4015. [Google Scholar]
- Loeve, A.J.; Plettenburg, D.H.; Breedveld, P.; Dankelman, J. Endoscope Shaft-Rigidity Control Mechanism: “FORGUIDE”. IEEE Trans. Biomed. Eng. 2012, 59, 542–551. [Google Scholar] [CrossRef] [PubMed]
- Stilli, A.; Wurdemann, H.A.; Althoefer, K. A novel concept for safe, stiffness-controllable robot links. Soft Robot. 2017, 4, 16–22. [Google Scholar] [CrossRef]
- Shiva, A.; Stilli, A.; Noh, Y.; Faragasso, A.; De Falco, I.; Gerboni, G.; Cianchetti, M.; Menciassi, A.; Althoefer, K.; Wurdemann, H.A. Tendon-based stiffening for a pneumatically actuated soft manipulator. IEEE Robot. Autom. Lett. 2016, 1, 632–637. [Google Scholar] [CrossRef]
- Wurdemann, H.A.; Stilli, A.; Althoefer, K. Lecture notes in computer science: An antagonistic actuation technique for simultaneous stiffness and position control. In Proceedings of the International Conference on Intelligent Robotics and Applications, Portsmouth, UK, 24–27 August 2015; pp. 164–174. [Google Scholar]
- Scarborough, S.E.; Cadogan, D.P. Applications of inflatable rigidizable structures. In Proceedings of the International SAMPE Symposium and Exhibition, Frederica, DE, USA, 30 April–4 May 2006. [Google Scholar]
- Philen, M. Force tracking control of fluidic flexible matrix composite variable stiffness structures. J. Intell. Mater. Syst. Struct. 2011, 22, 31–43. [Google Scholar] [CrossRef]
- Shan, Y.; Philen, M.; Lotfi, A.; Li, S.; Bakis, C.E.; Rahn, C.D.; Wang, K.W. Variable stiffness structures utilizing fluidic flexible matrix composites. J. Intell. Mater. Syst. Struct. 2009, 20, 443–456. [Google Scholar] [CrossRef]
- Philen, M.; Shan, Y.; Prakash, P.; Wang, K.; Rahn, C.; Zydney, A.; Bakis, C. Fibrillar network adaptive structure with ion-transport actuation. J. Intell. Mater. Syst. Struct. 2007, 18, 323–334. [Google Scholar] [CrossRef]
- Jafari, A.; Tsagarakis, N.G.; Caldwell, D.G. AwAS-II: A new actuator with adjustable stiffness based on the novel principle of adaptable pivot point and variable lever ratio. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation (ICRA), Shanghai, China, 9–13 May 2011; pp. 4638–4643. [Google Scholar]
- Jafari, A.; Tsagarakis, N.G.; Caldwell, D.G. A novel intrinsically energy efficient actuator with adjustable stiffness (AwAS). IEEE/ASME Trans. Mechatron. 2013, 18, 355–365. [Google Scholar] [CrossRef]
- Tagliamonte, N.L.; Sergi, F.; Carpino, G.; Accoto, D.; Guglielmelli, E. Design of a variable impedance differential actuator for wearable robotics applications. In Proceedings of the 2010 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Taipei, Taiwan, 18–22 October 2010; pp. 2639–2644. [Google Scholar]
- Aukes, D.; Kim, S.; Garcia, P.; Edsinger, A.; Cutkosky, M.R. Selectively compliant underactuated hand for mobile manipulation. In Proceedings of the 2012 IEEE International Conference on Robotics and Automation (ICRA), Saint Paul, MN, USA, 14–18 May 2012; pp. 2824–2829. [Google Scholar]
- Nakabayashi, M.; Kobayashi, R.; Kobayashi, S.; Morikawa, H. Bioinspired propulsion mechanism using a fin with a dynamic variable-effective-length spring. J. Biomech. Sci. Eng. 2009, 4, 82–93. [Google Scholar] [CrossRef]
- Hunter, I.W.; Lafontaine, S. A comparison of muscle with artificial actuators. In Proceedings of the IEEE 5th Technical Digest Solid-State Sensor and Actuator Workshop, Hilton Head Island, SC, USA, 22–25 June 1992; pp. 178–185. [Google Scholar]
- Jung, D.; Blangé, T.; De Graaf, H.; Treijtel, B. Elastic properties of relaxed, activated, and rigor muscle fibers measured with microsecond resolution. Biophys. J. 1988, 54, 897–908. [Google Scholar] [CrossRef]
- Paetsch, C.; Trimmer, B.; Dorfmann, A. A constitutive model for active-passive transition of muscle fibers. Int. J. Non-Linear Mech. 2012, 47, 377–387. [Google Scholar] [CrossRef]
- Shoa, T.; Munce, N.R.; Yang, V.; Madden, J.D. Conducting polymer actuator driven catheter: Overview and applications. Proc. SPIE 2009, 7287, 72871J. [Google Scholar]
- McEvoy, M.A.; Correll, N. Materials that couple sensing, actuation, computation, and communication. Science 2015, 347, 1261689. [Google Scholar] [CrossRef] [PubMed]
- Breedveld, P.; Sheltes, J.; Blom, E.M.; Verheij, J.E. A new, easily miniaturized steerable endoscope. IEEE Eng. Med. Biol. Mag. 2005, 24, 40–47. [Google Scholar] [CrossRef] [PubMed]
- Catherine, J.; Rotinat-Libersa, C.; Micaelli, A. Comparative review of endoscopic devices articulations technologies developed for minimally invasive medical procedures. Appl. Bionics Biomech. 2011, 8, 151–171. [Google Scholar] [CrossRef]
- Wehrmeyer, J.; Barthel, J.; Roth, J.; Saifuddin, T. Colonoscope flexural rigidity measurement. Med. Biol. Eng. Comput. 1998, 36, 475–479. [Google Scholar] [CrossRef] [PubMed]
- Trejos, A.L.; Jayaraman, S.; Patel, R.V.; Naish, M.D.; Schlachta, C.M. Force sensing in natural orifice transluminal endoscopic surgery. Surg. Endosc. 2011, 25, 186–192. [Google Scholar] [CrossRef] [PubMed]
- Varadarajulu, S.; Banerjee, S.; Barth, B.A.; Desilets, D.J.; Kaul, V.; Kethu, S.R.; Pedrosa, M.C.; Pfau, P.R.; Tokar, J.L.; Wang, A.; et al. GI endoscopes. Gastrointest. Endosc. 2011, 74, 1–6. [Google Scholar] [CrossRef] [PubMed]
- Haga, Y.; Mineta, T.; Esashi, M. Multi-functional active catheter. Sens. Update 2000, 8, 147–186. [Google Scholar] [CrossRef]
- Okamura, A.M.; Simone, C.; O’leary, M.D. Force modeling for needle insertion into soft tissue. IEEE Trans. Biomed. Eng. 2004, 51, 1707–1716. [Google Scholar] [CrossRef] [PubMed]
- Yarmolenko, P.S.; Moon, E.J.; Landon, C.; Manzoor, A.; Hochman, D.W.; Viglianti, B.L.; Dewhirst, M.W. Thresholds for thermal damage to normal tissues: An update. Int. J. Hyperth. 2011, 27, 320–343. [Google Scholar] [CrossRef] [PubMed]
- Henke, M.; Gerlach, G. On the development of planar actuators for variable stiffness devices. Proc. SPIE 2013, 8687, 868727. [Google Scholar]
- Islam, A.; Hansen, H.N.; Tang, P.T.; Sun, J. Process chains for the manufacturing of molded interconnect devices. Int. J. Adv. Manuf. Technol. 2009, 42, 831–841. [Google Scholar] [CrossRef]
- Cheng, W.B.; Moser, M.A.; Kanagaratnam, S.; Zhang, W.J. Overview of upcoming advances in colonoscopy. Dig. Endosc. 2012, 24, 1–6. [Google Scholar] [CrossRef] [PubMed]
- Loeb, J.; Plantif, B.E. System of Protection by Modeling. US Patent 4,045,830, 6 September 1977. [Google Scholar]
- Coppard, B.M.; Lohman, H. Introduction to Splinting; Elsevier Health Sciences: Amsterdam, The Netherlands, 2008. [Google Scholar]
- Fukuda, T.; Guo, S.; Kosuge, K.; Arai, F.; Negoro, M.; Nakabayashi, K. Micro active catheter system with multi degrees of freedom. In Proceedings of the 1994 IEEE International Conference on Robotics and Automation, San Diego, CA, USA, 8–13 May 1994; pp. 2290–2295. [Google Scholar]
- Wache, H.; Tartakowska, D.; Hentrich, A.; Wagner, M. Development of a polymer stent with shape memory effect as a drug delivery system. J. Mater. Sci. Mater. Med. 2003, 14, 109–112. [Google Scholar]
- Metcalfe, A.; Desfaits, A.C.; Salazkin, I.; Yahia, L.; Sokolowski, W.M.; Raymond, J. Cold hibernated elastic memory foams for endovascular interventions. Biomaterials 2003, 24, 491–497. [Google Scholar] [CrossRef]
- Faddis, M.N.; Blume, W.; Finney, J.; Hall, A.; Rauch, J.; Sell, J.; Bae, K.T.; Talcott, M.; Lindsay, B. Novel, magnetically guided catheter for endocardial mapping and radiofrequency catheter ablation. Circulation 2002, 106, 2980–2985. [Google Scholar] [CrossRef] [PubMed]
- Schiemann, M.; Killmann, R.; Kleen, M.; Abolmaali, N.; Finney, J.; Vogl, T.J. Vascular Guide Wire Navigation with a Magnetic Guidance System: Experimental Results in a Phantom 1. Radiology 2004, 232, 475–481. [Google Scholar] [CrossRef] [PubMed]
- Naito, H.; Akazawa, Y.; Tagaya, K.; Matsumoto, T.; Tanaka, M. An ankle-foot orthosis with a variable-resistance ankle joint using a magnetorheological-fluid rotary damper. J. Biomech. Sci. Eng. 2009, 4, 182–191. [Google Scholar] [CrossRef]
- Campanaro, L.; Goldstone, N.; Shepherd, C. Rigidized Evacuated Structure. US Patent 3,258,883, 5 July 1966. [Google Scholar]
- Zinner, N.R.; Sterling, A.M. Penile Prosthesis and Method. US Patent 5,069,201, 30 September 1991. [Google Scholar]
- Bauerfeind, P.; Bauerfeind, H. Tubular Inserting Device with Variable Rigidity. US Patent 5,337,733, 16 August 1994. [Google Scholar]
- Bureau, M.; Jung, J.H.; Keller, T. Fitting Element with Controlled Stiffness. US Patent Application 13/520,102 2009, 14 June 2012. [Google Scholar]
- Bureau, M.; Keller, T.; Veneman, J.F.; MARTIN, C.V. Element with Variable Stiffness Controlled by Negative Pressure. US Patent Application 14/369,766, 24 December 2015. [Google Scholar]
- Masters, B.P.; Van Schoor, M.C. Variable Stiffness Shaft. US Patent 6,361,451, 26 March 2002. [Google Scholar]
- Brenneman, R.; Ewers, R.; Saadat, V.; Chen, E. Apparatus and Methods for Guiding an Endoscope via a Rigidizable Wire Guide. US Patent Application 10/757,980 2004, 23 September 2004. [Google Scholar]
- Rudloff, D.A. Penile Implant. US Patent 4,664,100, 28 May 1987. [Google Scholar]
- Olson, G. Medical Devices with Variable Stiffness. US Patent 8,376,960, 19 Fabruary 2013. [Google Scholar]
- Eidenschink, T.E. Variable Manipulative Strength Catheter. US Patent 7,291,127, 6 November 2007. [Google Scholar]
- Smith, K.W.; Palmer, M.A.; Deville, D.D.; McBrayer, S.M.; Kline, K.R. Catheter with Controllable Stiffness and Method for Operating a Selective Stiffening Catheter. US Patent 7,559,916, 14 July 2009. [Google Scholar]
- Sokolowski, W. Cold Hibernated Elastic Memory Self-Deployable and Rigidizable Structure and Method Therefor. US Patent 6,702,976, 9 March 2004. [Google Scholar]
- Larson, L. Thermoplastic Splint or Cast. US Patent 3,809,600, 10 December 1974. [Google Scholar]
- Patel, J.I. Endoscope Having Variable Flexibility. US Patent 4,815,450, 28 March 1989. [Google Scholar]
- Griffin, S. Selectively Flexible Catheter and Method of Use. US Patent 7,828, 790 November 2010. [Google Scholar]
- Thill, C.; Etches, J.; Bond, I.; Potter, K.; Weaver, P. Morphing skins. Aeronaut. J. 2008, 112, 117–139. [Google Scholar] [CrossRef]
- Weisshaar, T.A. Morphing aircraft systems: Historical perspectives and future challenges. J. Aircr. 2013, 50, 337–353. [Google Scholar] [CrossRef]
- Laschi, C.; Cianchetti, M. Soft robotics: New perspectives for robot bodyware and control. Front. Bioeng. Biotechnol. 2014, 2, 3. [Google Scholar] [CrossRef] [PubMed]
- Park, Y.J.; Jeong, U.; Lee, J.; Kim, H.Y.; Cho, K.J. The effect of compliant joint and caudal fin in thrust generation for robotic fish. In Proceedings of the 2010 3rd IEEE RAS and EMBS International Conference on Biomedical Robotics and Biomechatronics (BioRob), Tokyo, Japan, 26–29 September 2010; pp. 528–533. [Google Scholar]
- Park, Y.J.; Jeong, U.; Lee, J.; Kwon, S.R.; Kim, H.Y.; Cho, K.J. Kinematic condition for maximizing the thrust of a robotic fish using a compliant caudal fin. IEEE Trans. Robot. 2012, 28, 1216–1227. [Google Scholar] [CrossRef]
- Park, Y.J.; Cho, K.J. Design and manufacturing a bio-inspired variable stiffness mechanism in a robotic dolphin. In Proceedings of the International Conference on Intelligent Robotics and Applications, Seoul, Korea, 25–28 September 2013; pp. 302–309. [Google Scholar]
- Chu, W.S.; Lee, K.T.; Song, S.H.; Han, M.W.; Lee, J.Y.; Kim, H.S.; Kim, M.S.; Park, Y.J.; Cho, K.J.; Ahn, S.H. Review of biomimetic underwater robots using smart actuators. Int. J. Precis. Eng. Manuf. 2012, 13, 1281–1292. [Google Scholar] [CrossRef]
- Park, Y.J.; Lee, J.G.; Jeon, S.; Ahn, H.; Koh, J.; Ryu, J.; Cho, M.; Cho, K.J. Dual-stiffness structures with reconfiguring mechanism: Design and investigation. J. Intell. Mater. Syst. Struct. 2016, 27, 995–1010. [Google Scholar] [CrossRef]
- Wang, L.; Melnik, R.V. Nonlinear dynamics of shape memory alloy oscillators in tuning structural vibration frequencies. Mechatronics 2012, 22, 1085–1096. [Google Scholar] [CrossRef]
- Giataganas, P.; Evangeliou, N.; Koveos, Y.; Kelasidi, E.; Tzes, A. Design and experimental evaluation of an innovative SMA-based tendon-driven redundant endoscopic robotic surgical tool. In Proceedings of the 19th Mediterranean Conference on Control & Automation (MED), Corfu, Greece, 20–23 June 2011; pp. 1071–1075. [Google Scholar]
- Majidi, C. Soft robotics: A perspective—Current trends and prospects for the future. Soft Robot. 2014, 1, 5–11. [Google Scholar] [CrossRef]
- Nemirovskii, M.; Kuz’min, A. Investigation of the flexural and torsional rigidity of flexible elements of endoscopes. Biomed. Eng. 1984, 18, 214–217. [Google Scholar] [CrossRef]
- Delaplace, A.; Gatuingt, F.; Ragueneau, F. Aide-Mémoire de Mécanique des Structures: Résistance des Matériaux; Dunod: Paris, France, 2008. (In French) [Google Scholar]
- Cheng, W. Development of a Kinetic Model for Loop-Free Colonoscopy Technology. Ph.D. Thesis, University of Saskatchewan, Saskatoon, SK, Canada, 2014. [Google Scholar]
- Bell, G.; Burn, K. Measurement of the stiffness of endoscopes—A plea for commonality. Gut 2001, 49. [Google Scholar] [CrossRef] [PubMed]
- Dogramadzi, S.; Bell, G.; Bicker, R.; Burn, K. A novel system to rapidly analyse the flexural rigidity of endoscopes used in colonoscopy and flexible sigmoidoscopy. Int. J. Cond. Monit. Diagn. Eng. Manag. 2003, 6, 24–32. [Google Scholar]
- Dogramadzi, S.; Burn, K.; Bicker, R.; Bell, G. The effect of temperature on the flexural rigidity of various commercially available colonoscopes and gastroscopes. Gut 2002, 50, A41. [Google Scholar]
- Sullivan, M.J. Variable stiffening device for colonoscopy. Gastrointest. Endosc. 1990, 36, 642–643. [Google Scholar] [CrossRef]
| Classification | Acronyms | References | |||
|---|---|---|---|---|---|
| Geometrical Properties | Cross-Section Shaping | CS | [17,18,19] | ||
| Structural Interactions | Multi-Layer Beam | Single material | MLB-S | [20,21,22,23,24,25] | |
| Multiple materials | MLB-M | [26,27,28,29,30,31] | |||
| Elastic Properties | Material | Phase Transition | Low Melting Point Alloy | LMPA | [32,33,34,35,36,37] |
| Low Melting Point Polymer | LMPP | [13,38,39,40,41] | |||
| Wax | [42,43] | ||||
| Solder | [44,45] | ||||
| Glass Transition | Shape Memory Alloy | SMA | [46,47,48,49,50,51,52,53] | ||
| Shape Memory Polymer | SMP | [38,47,54,55,56] | |||
| Shape Memory Composite | SMC | [57,58,59,60] | |||
| Shape Memory Gel | SMG | [61,62,63,64] | |||
| Rheological Fluids | Magnetorheological | MRF | [14,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80] | ||
| Electrorheological | ERF | [14,65,66,67,68] | |||
| Biomaterials | BM | [39,81,82,83,84] | |||
| Structural Interactions | Bulk Locking | Granular Jamming | GJ | [12,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112] | |
| Turgor Pressure | TP | [113,114,115,116,117,118,119,120,121] | |||
| Segments Locking | Central Wire | CW | [122,123,124] | ||
| Multiple Wires | MW | [1,2,123,125,126,127,128,129] | |||
| Bellows Connections | BC | [66] | |||
| Soft Layer | SL | [130,131] | |||
| Longitudinal Locking | Layer Jamming | LJ | [111,132,133,134,135,136] | ||
| Wire Jamming | WJ | [137,138] | |||
| Actuator-Like Solution | Fluid-based | Pneumatic Solution | PS | [19,139,140,141,142] | |
| Fluidic Flexible Matrix Composite | FFMC | [143,144,145] | |||
| Mechanical Solution | MS | [146,147,148,149,150] | |||
| Muscles | M | [151,152,153] | |||
| Stiffness | Stiffness | Ultimate | Activation Time | External | Device |
|---|---|---|---|---|---|
| (Rigid State) | (Flexible State) | Force | Diameter | Temperature | |
| ≥330 | ≤165 | ≥16 N | as small as possible | ≤15 mm | ≤41 C |
| [158] | [158] | [159] | [160] | [161] |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Blanc, L.; Delchambre, A.; Lambert, P. Flexible Medical Devices: Review of Controllable Stiffness Solutions. Actuators 2017, 6, 23. https://doi.org/10.3390/act6030023
Blanc L, Delchambre A, Lambert P. Flexible Medical Devices: Review of Controllable Stiffness Solutions. Actuators. 2017; 6(3):23. https://doi.org/10.3390/act6030023
Chicago/Turabian StyleBlanc, Loïc, Alain Delchambre, and Pierre Lambert. 2017. "Flexible Medical Devices: Review of Controllable Stiffness Solutions" Actuators 6, no. 3: 23. https://doi.org/10.3390/act6030023
APA StyleBlanc, L., Delchambre, A., & Lambert, P. (2017). Flexible Medical Devices: Review of Controllable Stiffness Solutions. Actuators, 6(3), 23. https://doi.org/10.3390/act6030023





