Parameters Identification for a Composite Piezoelectric Actuator Dynamics

Abstract

This work presents an approach for identifying the model of a composite piezoelectric (PZT) bimorph actuator dynamics, with the objective of creating a robust model that can be used under various operating conditions. This actuator exhibits nonlinear behavior that can be described using backlash and hysteresis. A linear dynamic model with a damping matrix that incorporates the Bouc–Wen hysteresis model and the backlash operators is developed. This work proposes identifying the actuator’s model parameters using the hybrid master-slave genetic algorithm neural network (HGANN). In this algorithm, the neural network exploits the ability of the genetic algorithm to search globally to optimize its structure, weights, biases and transfer functions to perform time series analysis efficiently. A total of nine datasets (cases) representing three different voltage amplitudes excited at three different frequencies are used to train and validate the model. Four cases are considered for training the NN architecture, connection weights, bias weights and learning rules. The remaining five cases are used to validate the model, which produced results that closely match the experimental ones. The analysis shows that damping parameters are inversely proportional to the excitation frequency. This indicates that the suggested hysteresis model is too general for the PZT model in this work. It also suggests that backlash appears only when dynamic forces become dominant.

1. Introduction

Recent advances in the area of piezoelectric (PZT) actuators have resulted in their use in many applications. These actuators are relatively low cost, noninvasive in nature and simple to install. A recent development is the composite PZT actuators, which use interdigitated electrodes for poling and subsequent actuation of an internal layer of machined piezoceramic fibers. A thorough discussion of their characteristics can be found in [1]. Composite PZT actuators have been used in the aviation industry for controlling various types of aircraft structural members, such as wings [2,3] and fins [4,5,6].

In [7], they showed that the maximum deflection and axial stresses in the bimorph actuators were highly dependent on the linearity of the models involved. Some researchers developed control algorithms based on linear models [8,9]. Their experimental results indicated that the response of the actuator experienced saturation and asymmetry, which were the results of hysteresis and backlash. Due to the added complexity associated with modeling hysteresis and backlash in PZT actuators, several researchers [8,9,10] used different optimization techniques to model these nonlinear effects. Recently, a compensation strategy for the asymmetric hysteresis that used two models, connected in series, for symmetric and asymmetric hysteresis, was proposed [11]. The work in [12] introduced a simple fuzzy system to model hysteresis in PZT actuators using the inverse of the model, which can be analytically computed. Another work [13] proposed numerical simulations of the mechanical behavior of a macro-fiber composite (MFC) actuator shunted by a negative capacitance electronic circuit. They showed that the elastic parameters of the piezoelectric material can be influenced if a negative capacitance circuit is connected in parallel to the piezoelectric plate. The authors of [14] introduced a model to characterize an MFC piezoelectric bimorph actuator that included a generalized Maxwell slip operator and a creep operator. A finite element model to describe unimorph MFC actuators used in micro wing models was proposed [3]. In [15], an approximate Galerkin method was used to describe the relation between the displacement of the MFC actuator’s free end and the amplitude and frequency of the applied voltage. A finite element method to model an MFC actuator for applications that involve flat or curved attachments was proposed [16]. Recently, an optimization criteria that can be used for optimal placement of piezoelectric actuators on laminated structures was introduced [17].

A typical neural network has a fixed architecture and rigid search algorithms that depend on the number of hidden layers. These issues render typical neural networks computationally intensive; the search may also be trapped in local minima, which prevents it from performing a generalized search in a very large space. Several researchers recommended combining genetic algorithms (GA) with neural networks (NN) to create evolutionary artificial neural networks, which can overcome the typical limitations of using one of the two methods alone. The suggested synergy between the two approaches does not only allow the GA to optimize the NN’s weights and biases; it can optimize the architecture of the NN, as well. In this context, the GA dedicates part of each individual to code the architecture of the NN (e.g., the number of hidden layers) and iteratively optimizes it.

For example, the work in [18] classified the combination of GA and NN into supportive and collaborative. In supportive combinations, one of these two algorithms was used first to pre-process data and to select a few features to be used in the other one. However, the two algorithms were used simultaneously in the collaborative combinations. Some researchers combined NN learning with GA paradigms to study how learning can improve genetic search [19,20]. Other researchers [21,22,23,24] used GA to train feed-forward NNs. The work in [25] considered combining neural networks with two genetic algorithms, the Baldwin effect and the Lamarckian strategy, to study how learning improved the genetic backpropagation search. Another work [26] addressed the ability of GA in minimizing the resources used for NN coding. They compared two different genotype encodings that emphasized the compromise between search space size with fitness landscape and the identification of the associated genetic operators.

A control procedure that used Bayesian NN and GA to solve complex problems while using a hybrid Monte Carlo method to train the Bayesian networks was proposed [27]. Another work presented a two-stage approach to improve the performance of the feed-forward neural network [28]. The first stage of this algorithm deployed a GA search for the best initial weights and biases, while the second stage included a Newton method to train the network.

The objective of this work is to identify the parameters for the composite piezoelectric bimorph actuator dynamics that is used in a smart fin design. Similar to earlier researchers, initial observations show that the behavior of this actuator is nonlinear; it was decided to add backlash and hysteresis operators to a linear model to describe its behavior accurately. Finding an optimal set of these parameters of such a model is computationally expensive. In addition, some parameters have extended influence (i.e., backlash operators also influence the shape of the hysteresis curve). This work uses a hybrid master-slave genetic algorithm neural network (HGANN) approach [29] to construct a network that can predict these parameters. A classical back-propagation (BP) network suffers from some inherited deficiencies. For instance, it takes a longer time to converge [30], and it may converge to local minima, especially in complex systems [31]. The convergence results are not always guaranteed due to the monotonic nature of the process [32]. The final results may be biased towards smaller weights [33]. The BP algorithm is sensitive to the initial parameter’s values [34]. The literature suggested that using GA for neural network training can overcome most, if not all, problems associated with BP [35,36]. Thus, this work trains the network using GA that is integrated within a feed-forward NN. The proposed HGANN algorithm allows the GA to simultaneously train and optimize the network’s topology, transfer functions, weights and biases. The global nature of the GA search provides the network with better convergence rates and robust results than the traditional BP, as it searches the entire space domain for optimal solutions. In addition, mutation improves the GA’s ability to make significant progression towards an optimal solution, thus saving time and effort without degenerating its converging confidence.

The organization of this work is as follows. The following section describes the prototype of the actuator and its application in a PZT-actuated smart fin. Then, the dynamic model that incorporates hysteresis and asymmetrical backlash is presented. The next section presents the use of a HGANN to identify the parameters for the model. Then, a comparison between the proposed model and experimental data is included to assess the efficiency of the proposed model. The final section presents the conclusions of this work.

2. Prototype of the PZT Bimorph Actuator

A piezoelectric macro-fiber composite (MFC) actuator is considered in this work. The PZT bimorph actuator is fabricated by bonding two MFCs [37], as shown in Figure 1. Table 1 summarizes the properties of the actuator. One MFC is activated in tension by applying positive voltage (along the fiber axis); while the other MFC is activated in compression by applying negative voltage (against the fiber axis). The tensile and compressive strains induce a distributed couple that causes the actuator to bend. The actuator can bend in the reverse direction by changing the polarity of the input voltages.

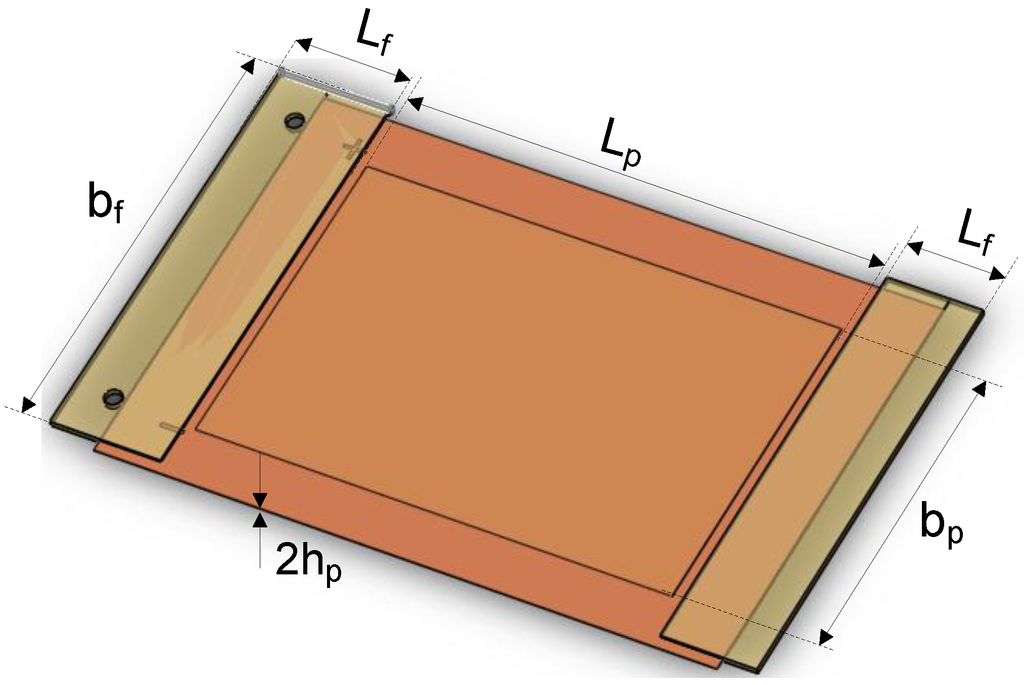
Figure 1. Geometry of a piezoelectric (PZT) bimorph actuator.

Figure 1. Geometry of a piezoelectric (PZT) bimorph actuator.

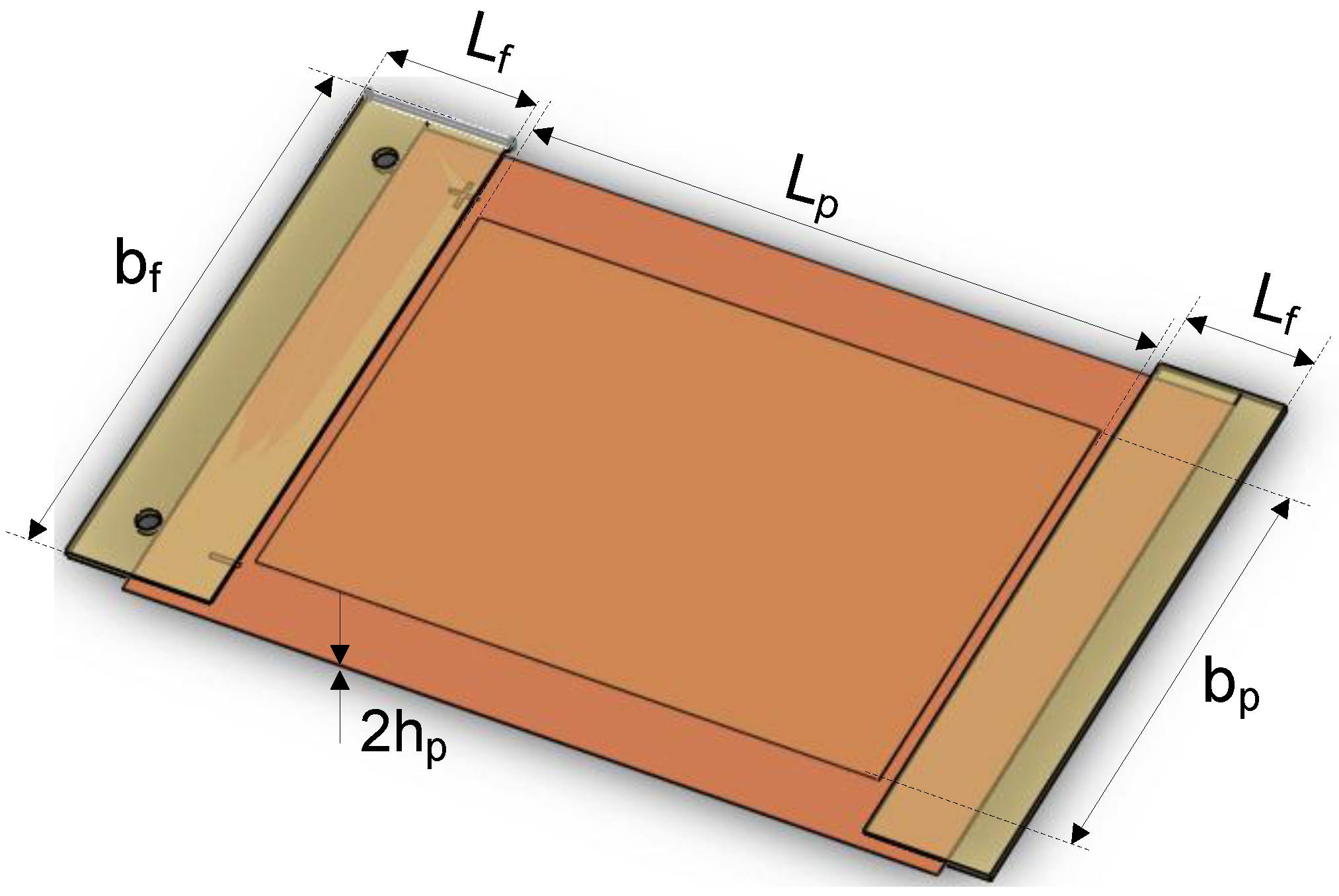
Table 1. Characteristics of the PZT bimorph actuator. MFC, macro-fiber composite.

Variable	Fiberglass	MFC
Length (mm)	Lf = 17	Lp = 85 (active length)
Width (mm)	bf = 75	bp = 56
Height (mm)	hf = 0.5	hp = 0.3
PZT strain constant d33 (m/V)	N/A	d33 = 4.275 × 10−10
Electrode spacing es (mm)	N/A	es = 0.5

Table 1. Characteristics of the PZT bimorph actuator. MFC, macro-fiber composite.

Variable	Fiberglass	MFC
Length (mm)	Lf = 17	Lp = 85 (active length)
Width (mm)	bf = 75	bp = 56
Height (mm)	hf = 0.5	hp = 0.3
PZT strain constant d33 (m/V)	N/A	d33 = 4.275 × 10−10
Electrode spacing es (mm)	N/A	es = 0.5

3. PZT Bimorph-Actuated Smart Fin

To assess the effectiveness of the PZT bimorph actuator, it is incorporated into a smart fin design, which can be used to either steer or stabilize an aerial vehicle. The fin has a rigid hollow shell that rotates around an axle, which is fixed to the body of the vehicle. The actuator is completely enclosed within the fin, as shown in Figure 2. The bending of the PZT actuator is used to control the orientation of the fin. One end of the actuator is rigidly connected to the axle of the fin. The other end passes through a slot in a hinge that is placed at the tip of the fin. This arrangement allows the actuator to slide freely within the slot without binding when activated. A through-shaft incremental encoder is used to measure the rotation angle of the smart fin.

Figure 2. PZT bimorph-actuated smart fin prototype. (a) Rear view (without the shell); (b) top view; (c) side view (without the shell); (d) assembled fin prototype.

Figure 2. PZT bimorph-actuated smart fin prototype. (a) Rear view (without the shell); (b) top view; (c) side view (without the shell); (d) assembled fin prototype.

4. Modeling

Observations of the experimental results show that the PZT actuator experiences hysteresis and asymmetric backlash. The model is composed of three components: a linear dynamic model, a hysteresis model and backlash model. Several approaches have been proposed for modeling PZT actuators. While some researchers have modeled a piezoelectric actuator as a separate cascaded model, this approach may not fully highlight the effect of the internal state variable on the hysteresis. A cascaded model represents the hysteresis as a second stage that is described with variables, which are independent of the input. Therefore, a cascade model may not necessarily describe the inherent nonlinearities of the system. In such case, it can be perceived that hysteresis is a discrete phenomenon, rather than a characteristic of the system. On the other hand, the proposed model uses an additional state variable that depends on the internal state of the input to describe the hysteresis.

A linear model based on the finite element approach is used to describe the dynamics of the actuator. The beam is divided into n elements, and the displacement of any point on the arm is described in terms of nodal displacements. The resulting equations of motion become,

$$M\ddot{q}+C\dot{q}+Kq=F\left(u\left(t\right)\right)$$

(1)

$$q_R={\left[\begin{array}{cc}\begin{array}{cc}{w}_2& {\varnothing }_2\end{array}& \begin{array}{ccc}\begin{array}{cc}\dots & \dots \end{array}& w_{n+1}& {\varnothing }_{n+1}\end{array}\end{array}\right]}^T$$

(2)

where M is the mass matrix, K is the stiffness matrix, u is the excitation signal and w_i and ${\varnothing }_{\text{i}}$ are the nodal displacement and slope of node i, respectively. C is the damping matrix that is expressed in the following form [38]:

$$C=\mu M+\delta \text{K}$$

(3)

where μ and δ are the mass and stiffness matrices coefficients, respectively. A detailed description of the modeling steps is outlined in [8].

To develop a more accurate model, the hysteresis nonlinearity of the PZT actuator is considered using the Bouc–Wen model, where the hysteretic relationship between an additional state variable z and excitation u is defined using the following equation [39]:

$$\dot{z}=\alpha \dot{u}-\beta \left|\dot{u}\right|z-\gamma \dot{u}\left|z\right|$$

(4)

where α, β and γ are the parameters that determine the magnitude and shape of the hysteresis loop. The state variable z is incorporated into Equation (1) as follows,

$$M\ddot{q}+C\dot{q}+Kq=F\left(u\left(t\right)\right)-e^{\text{*}T}z$$

(5)

where e^*T is a unit vector whose (2n−1)-th element is one and the remaining elements are zeros (where n is the number of elements).

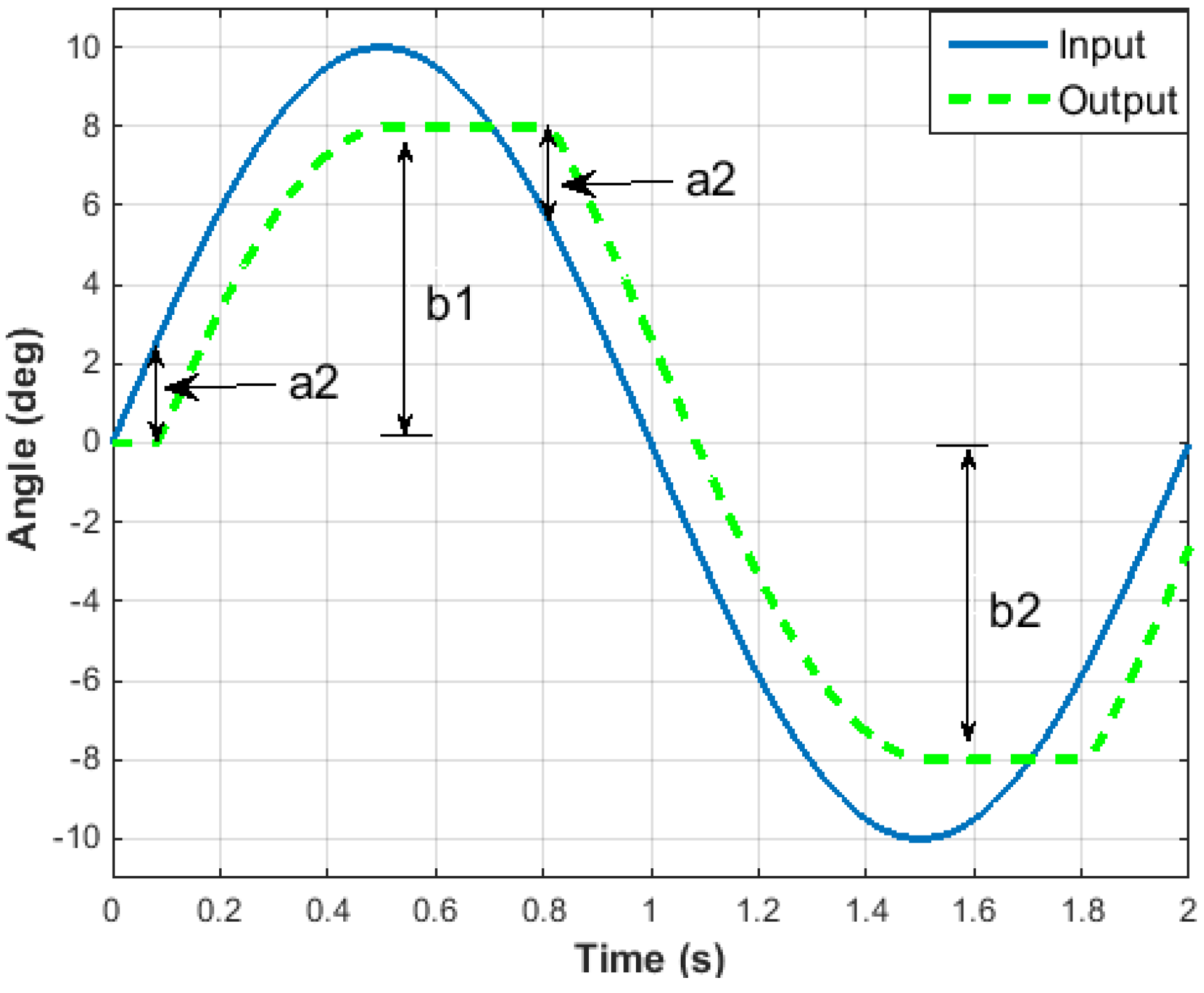
It is observed that the system experiences asymmetric backlash, which is modeled by the superposition of backlash operators with threshold and weight values [40]. This work considers a backlash model that is composed of four operators; two threshold operators (a₁ and a₂) and two saturation operators (b₁ and b₂), as shown in Figure 3. A detailed explanation on incorporating these parameters in the final model is presented in Appendix A.

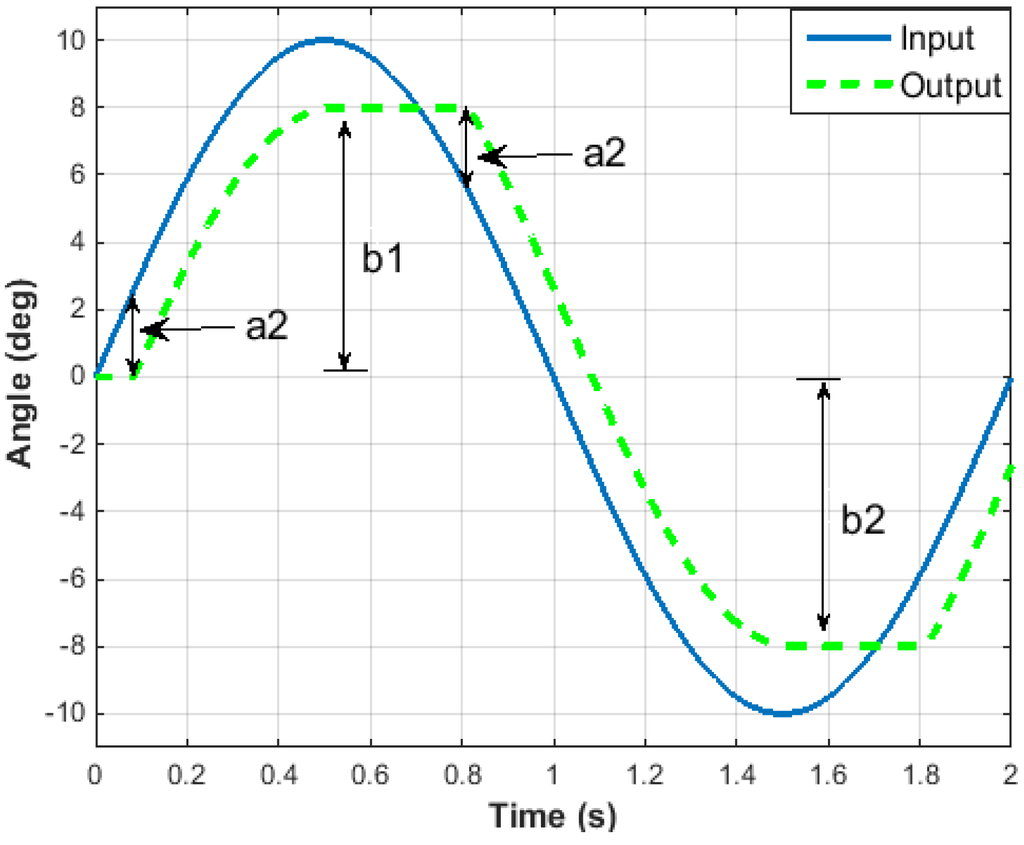
Figure 3. Interaction between the two threshold and the two saturation operators.

Figure 3. Interaction between the two threshold and the two saturation operators.

Identification of the Damping, Hysteresis and Backlash Parameters

Experimental testing showed that saturation parameters (b₁ and b₂) are linear functions of the exciting signal’s voltage and frequency. Appendix B lists the values of these saturation parameters. The remaining seven parameters (μ, δ, α, β, γ, a₁ and a₂) are determined using the HGANN optimization technique introduced in the following section. The major features of this algorithm are presented in Appendix C.

The proposed NN consists of three layers: an input layer that has two nodes for the amplitude and the frequency of the input voltage, an adaptive hidden layer that can have a varying number of nodes between two and nine and an output layer that has seven nodes for the backlash, hysteresis and damping parameters (μ, δ, α, β, γ, a₁ and a₂). Each NN neuron has a bounded transfer function (TF) [41]; these TFs are outlined in Appendix C. The overall characteristics of each member of the GA population are coded and compacted within the chromosome in a segmental style using binary representation. The NN uses a subset of four datasets to optimize the parameters of damping, hysteresis and backlash. The remaining experimental datasets are used after the training to validate the effectiveness of the NN. The algorithm is shown in Figure 4. Table 2 shows the GA parameters used in this algorithm. The full range of the optimization parameters can be achieved by scaling the TFs of the output layer using the gain values of Table 3.

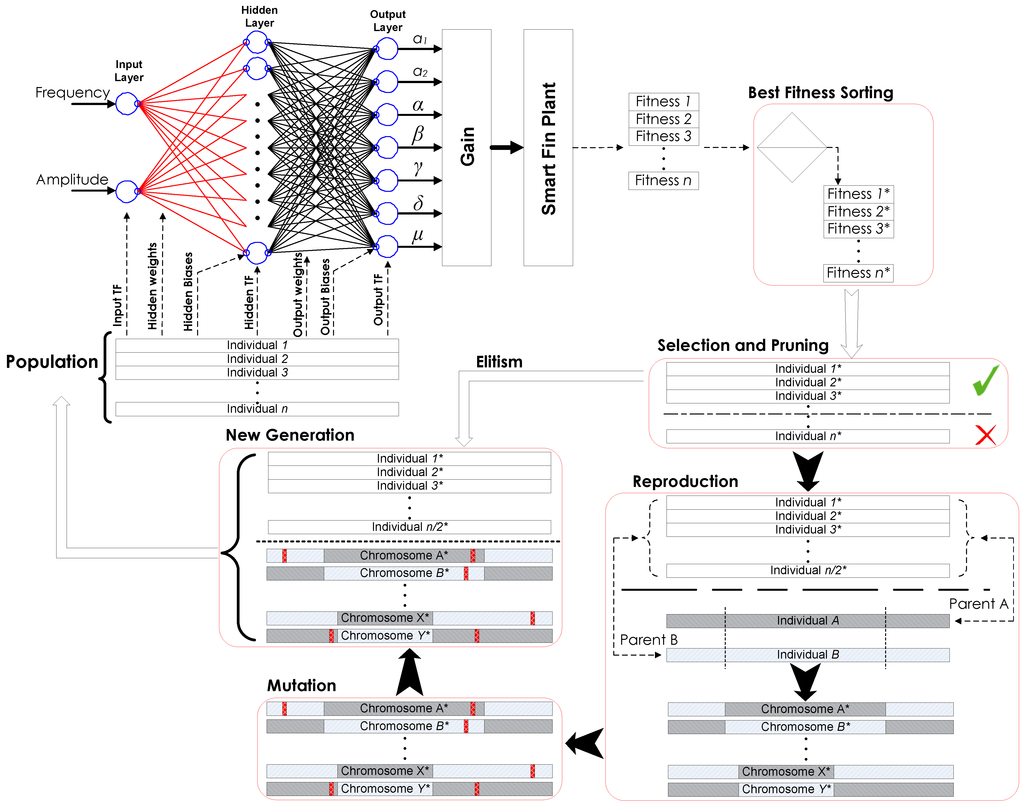
Figure 4. Schematic of the hybrid master-slave genetic algorithm neural network (HGANN) algorithm.

Figure 4. Schematic of the hybrid master-slave genetic algorithm neural network (HGANN) algorithm.

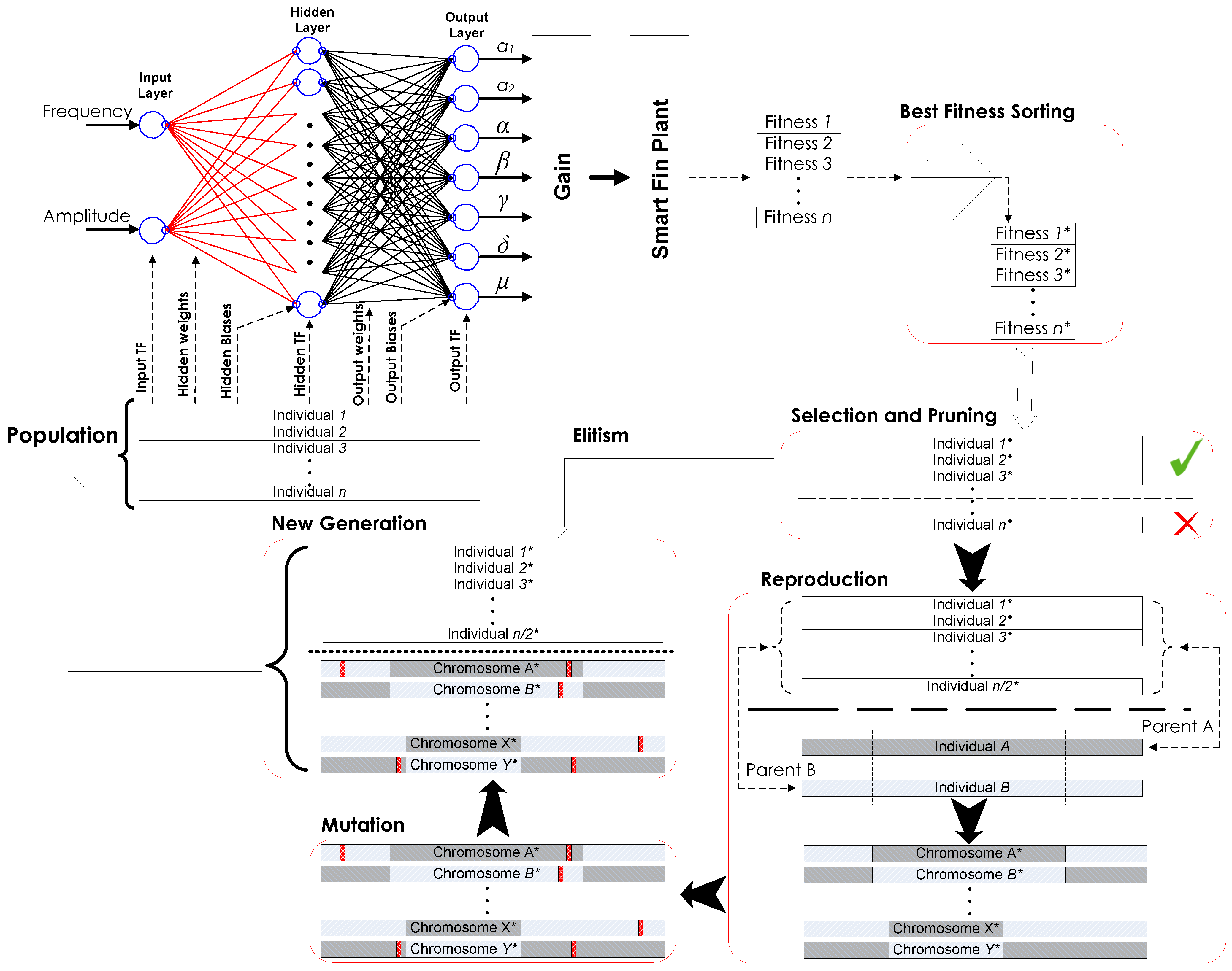
Table 2. GA parameters.

Parameter	Value
Encoding technique	Binary
Number of bits	3 for discrete, 14 for continuous
Population	400
Elitism	50%
Crossover technique	2-points
Mutation rate	0.01
Generation	1000

Table 2. GA parameters.

Parameter	Value
Encoding technique	Binary
Number of bits	3 for discrete, 14 for continuous
Population	400
Elitism	50%
Crossover technique	2-points
Mutation rate	0.01
Generation	1000

Table 3. Parameter ranges for the NN outputs.

	Parameter	Parameter Range
		Lower Limit	Upper Limit	Gain
Damping	μ	0	1	1
	δ	0	300	300
Hysteresis	α	−0.1	0	−0.1
	β	−0.1	0	−0.1
	γ	−0.1	0	−0.1
Backlash	a1	0	2	2
	a2	0	2	2

Table 3. Parameter ranges for the NN outputs.

	Parameter	Parameter Range
		Lower Limit	Upper Limit	Gain
Damping	μ	0	1	1
	δ	0	300	300
Hysteresis	α	−0.1	0	−0.1
	β	−0.1	0	−0.1
	γ	−0.1	0	−0.1
Backlash	a1	0	2	2
	a2	0	2	2

Fourteen bits are used to code the connection weights between different neurons with a resolution of 1.2 × 10⁻³. Similar values are used for the bias weights. These values are based on a preliminary evaluation of the system. Table 4 shows the NN parameters and their bounds for this problem.

Table 4. NN parameters.

Parameter	Number of Nodes	Lower Limit	Upper Limit	Binary Coding	Resolution
Input nodes	2	N/A	N/A	N/A	N/A
Output nodes	7	N/A	N/A	N/A	N/A
Hidden nodes	Adaptive	2	9	3 bits	1
Learning rules	Adaptive	1	8	3 bits	1
Connection weights	NA	−10	10	14 bits	1.2 × 10−3

Table 4. NN parameters.

Parameter	Number of Nodes	Lower Limit	Upper Limit	Binary Coding	Resolution
Input nodes	2	N/A	N/A	N/A	N/A
Output nodes	7	N/A	N/A	N/A	N/A
Hidden nodes	Adaptive	2	9	3 bits	1
Learning rules	Adaptive	1	8	3 bits	1
Connection weights	NA	−10	10	14 bits	1.2 × 10−3

A subset of the experimental data is dedicated to train the NN. All datasets are sampled at 100 Hz. Choosing the left diagonal of Table 5 will only represent data where amplitude and frequency are directly proportional to each other (i.e., Cases 1, 5 and 9), which worsens the performance of other off diagonal cases. After careful consideration, Cases 1, 5, 6 and 7 were selected to include all amplitudes and excitation frequencies. In addition, Cases 1 and 7 have two different amplitudes that are excited at the same frequency; while Cases 5 and 6 are both 500-V sinusoidal signals excited at different frequencies. The remaining cases are used for validation purposes and to test the effectiveness of the NN in identifying new datasets.

Table 5. Experimental datasets.

	Frequency	0.25 Hz	0.5 Hz	1.0 Hz
Voltage
375 V		Case 1	Case 2	Case 3
500 V		Case 4	Case 5	Case 6
750 V		Case 7	Case 8	Case 9

Table 5. Experimental datasets.

	Frequency	0.25 Hz	0.5 Hz	1.0 Hz
Voltage
375 V		Case 1	Case 2	Case 3
500 V		Case 4	Case 5	Case 6
750 V		Case 7	Case 8	Case 9

The objective of the proposed parameter identification method is to minimize the cost function, which is the sum of the performance index for the training cases.

$$CF={\displaystyle \sum }P{I}_C={\displaystyle \sum }{\left({\displaystyle \sum }_{i=1}^n{\left({\beta }_{\exp \left(i\right)}-{\beta }_{mod}\left(i\right)\right)}^2\right)}_C\hspace{1em}\hspace{1em}C=1,5,6,7$$

(6)

where CF is the sum of squared errors, PI is the performance index for each case, n is the total number of data samples, β_exp(i) is the measured fin angle at the i-th sample and β_mod(i) is the fin angle produced by the dynamic model at the same i-th sample.

5. Results

Figure 5 shows the progression of the cost function during a typical run of the HGANN. The results indicate that the solution is stable by 750 generations, with three nodes in the hidden layer and a final fitness value of 10.53. Table 6 shows the parameters that the NN estimated for the four different training cases. The final connection weights, biases and learning rules obtained for this NN are listed in Appendix D.

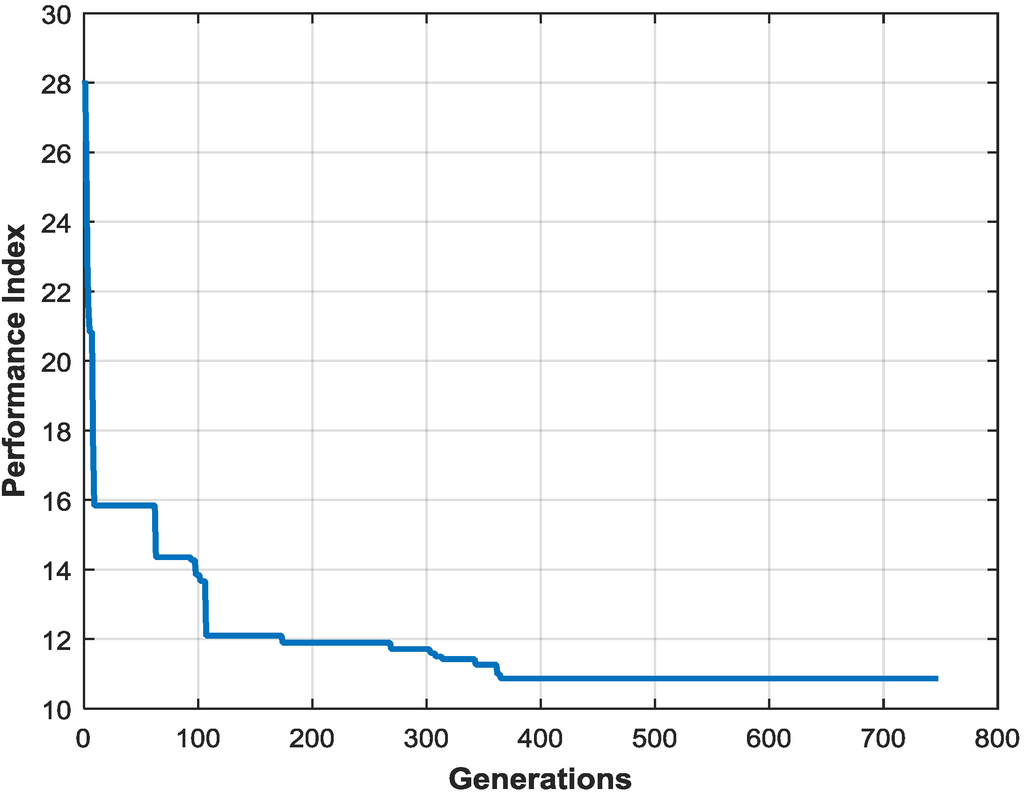
Figure 5. Progression of the solution.

Figure 5. Progression of the solution.

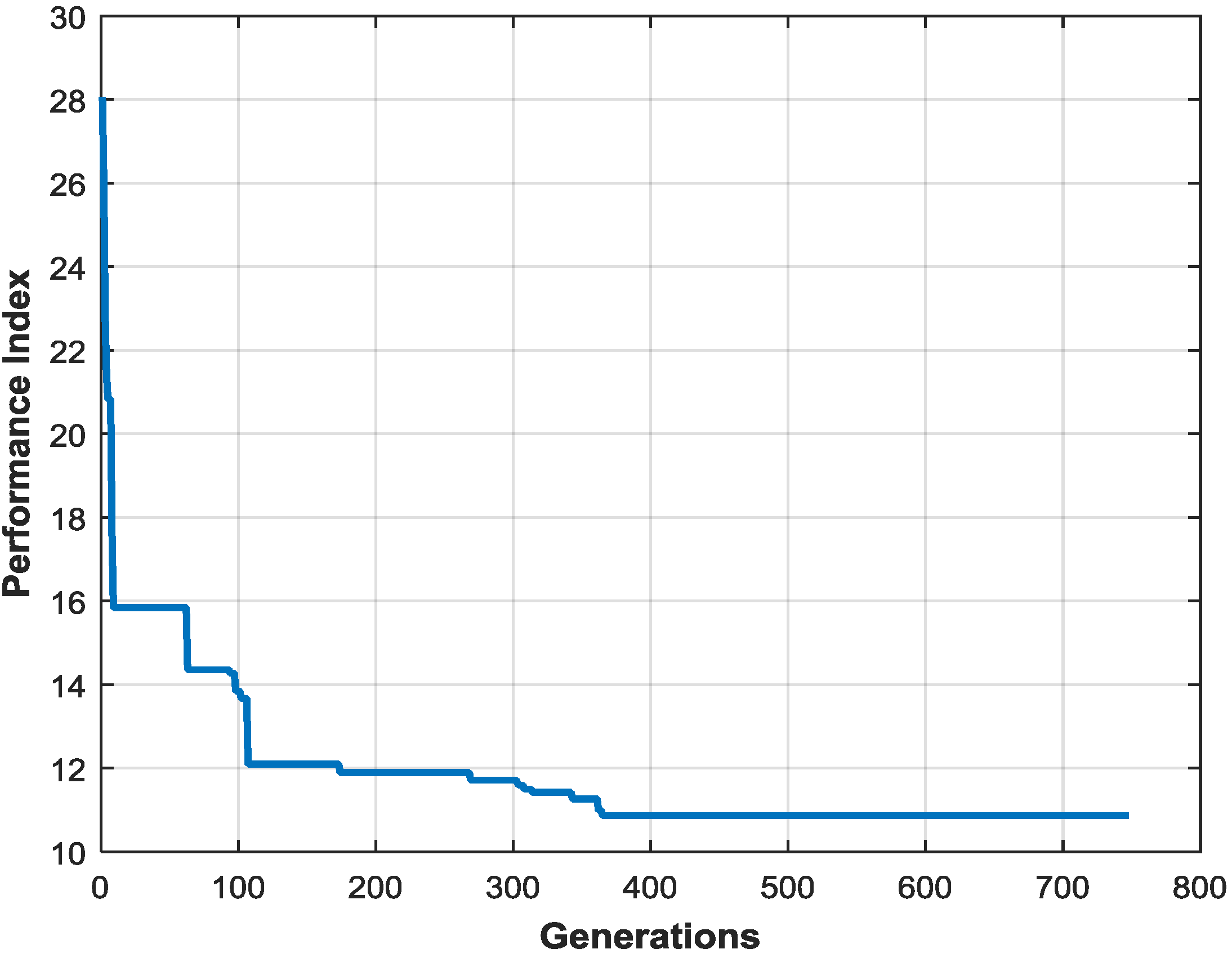
Table 6. Results for parameter estimation for the training cases using HGANN.

		Case 1	Case 5	Case 6	Case 7
Damping	δ	0.312	0.093	0	0.128
	μ	98.650	94.666	75.626	109.210
Hysteresis	α	0	0	0	0
	β	−7.49 × 10−2	−7.88 × 10−2	−8.06 × 10−2	−8.23 × 10−2
	γ	−6.51 × 10−2	−7.20 × 10−2	−7.84 × 10−2	−5.30 × 10−2
Backlash	a1	0	0	0	0.281
	a2	0	0	0	0.294

Table 6. Results for parameter estimation for the training cases using HGANN.

		Case 1	Case 5	Case 6	Case 7
Damping	δ	0.312	0.093	0	0.128
	μ	98.650	94.666	75.626	109.210
Hysteresis	α	0	0	0	0
	β	−7.49 × 10−2	−7.88 × 10−2	−8.06 × 10−2	−8.23 × 10−2
	γ	−6.51 × 10−2	−7.20 × 10−2	−7.84 × 10−2	−5.30 × 10−2
Backlash	a1	0	0	0	0.281
	a2	0	0	0	0.294

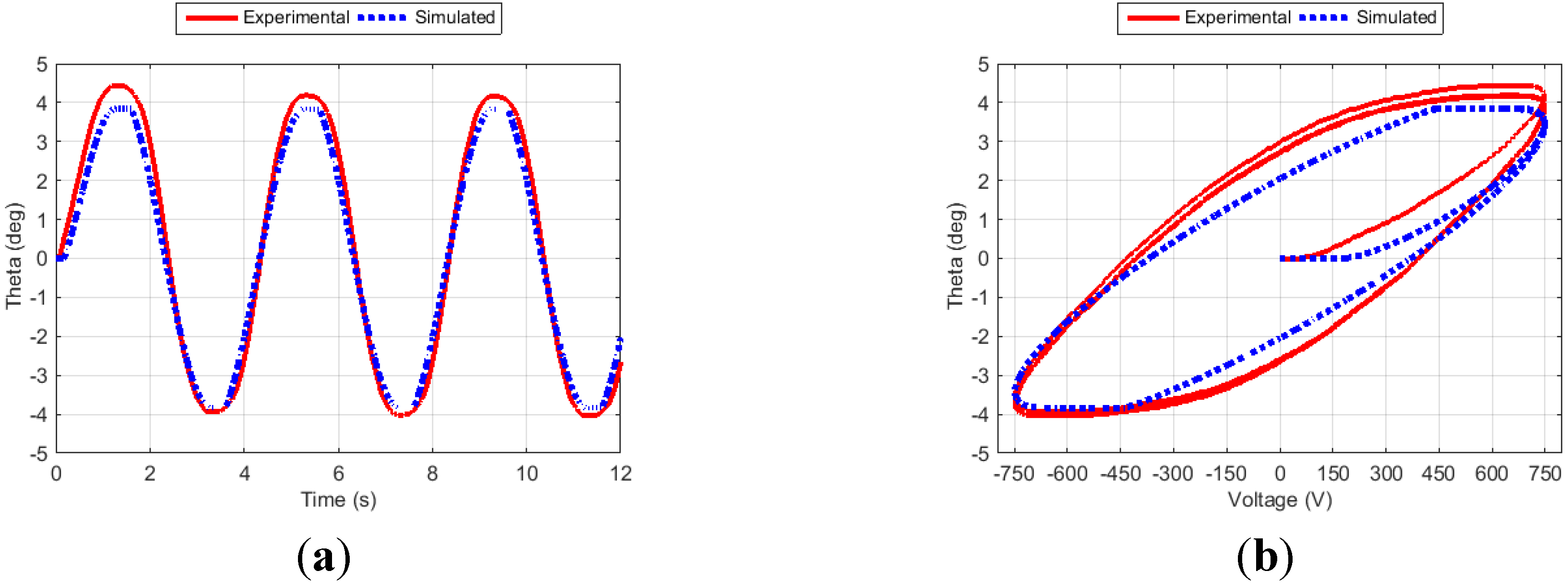
Table 6 shows that training produces different results for the damping, hysteresis and backlash parameters for each case. For example, the results show that the proposed hysteresis model is too general for this system, as α turns out to be zero at all cases. The values of β and γ do not vary significantly for the four training cases. On the other side, the values of the damping coefficients, δ and μ, differ for each case. The results also show that the backlash operators are only active in Case 7.

Figure 6, Figure 7, Figure 8 and Figure 9 show the fin angle responses and the corresponding hysteresis curves for the four training cases. For each case, the fin was excited for three cycles. Studying these results indicates that the proposed approach generates outputs that closely follow the experimental results, especially after the transient phase. It is also noticed that the simulation results closely match the experimental ones in both the time and the hysteresis domains.

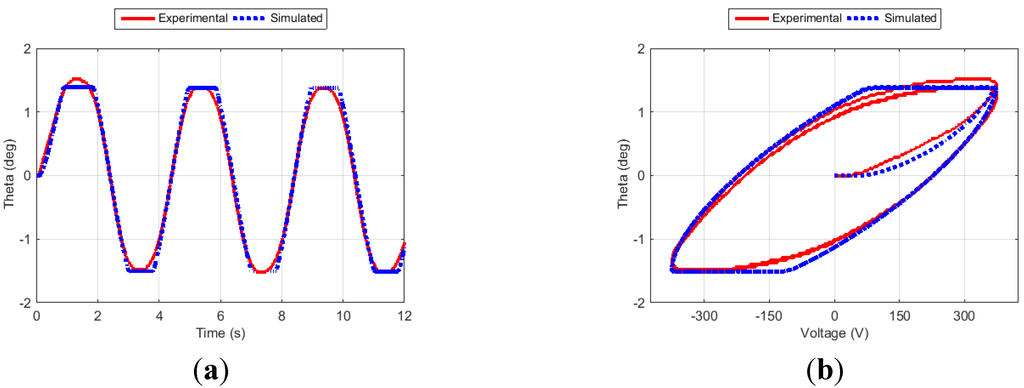
Figure 6. Fin angle (a) and hysteresis curve (b) for Case 1.

Figure 6. Fin angle (a) and hysteresis curve (b) for Case 1.

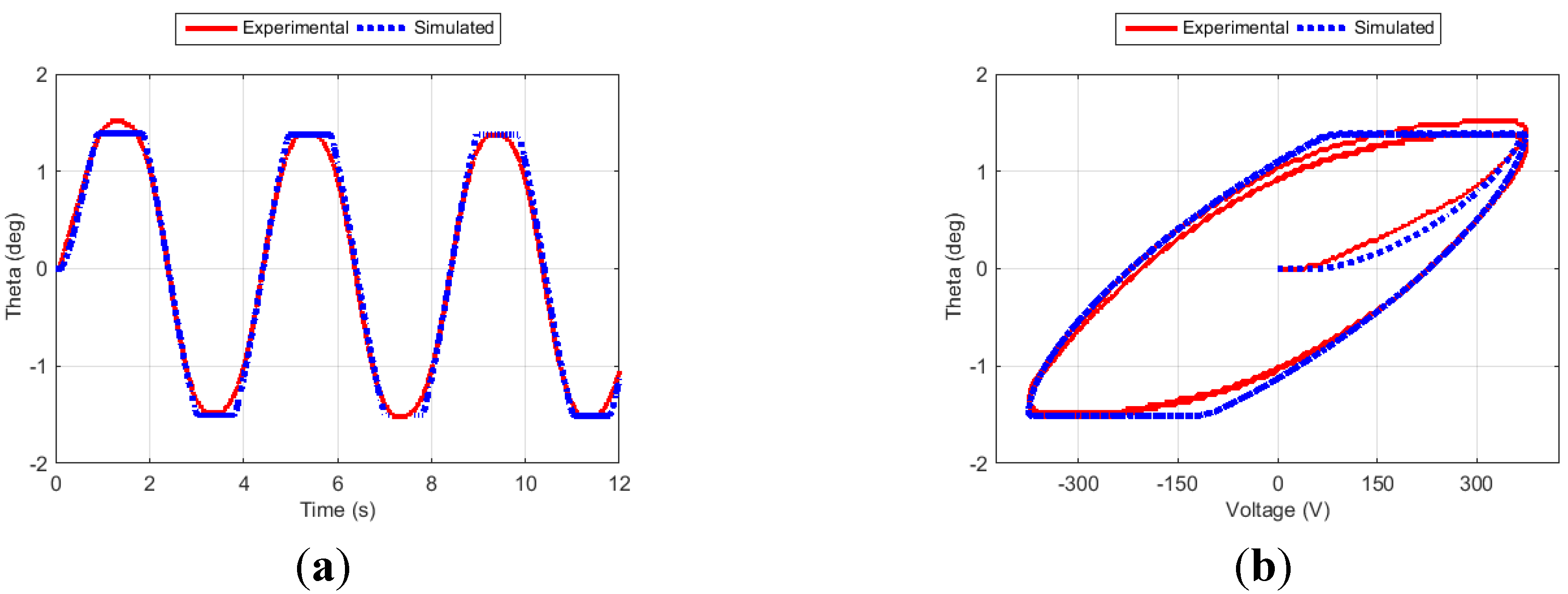
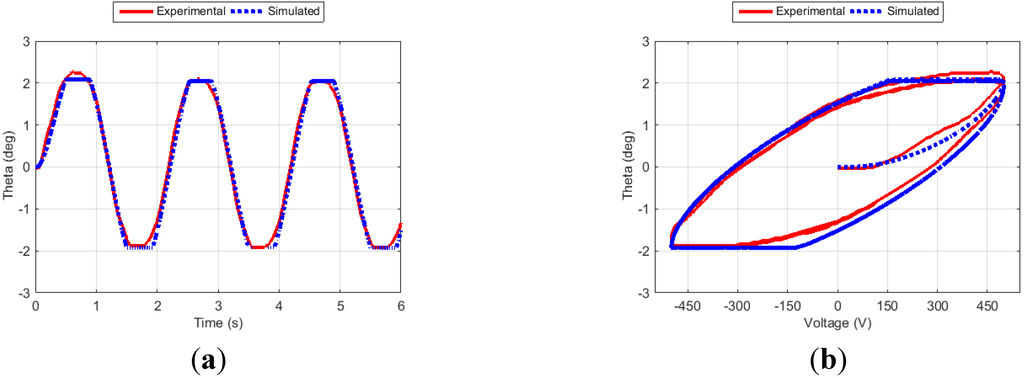
Figure 7. Fin angle (a) and hysteresis curve (b) for Case 5.

Figure 7. Fin angle (a) and hysteresis curve (b) for Case 5.

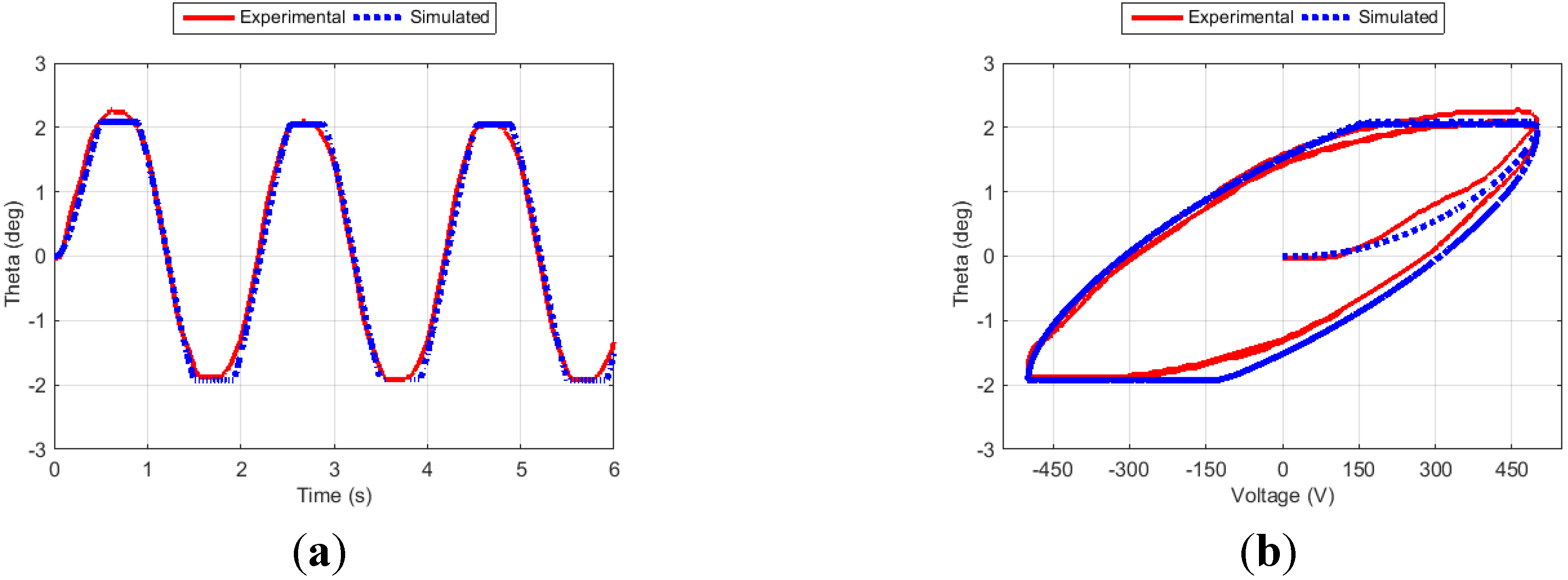
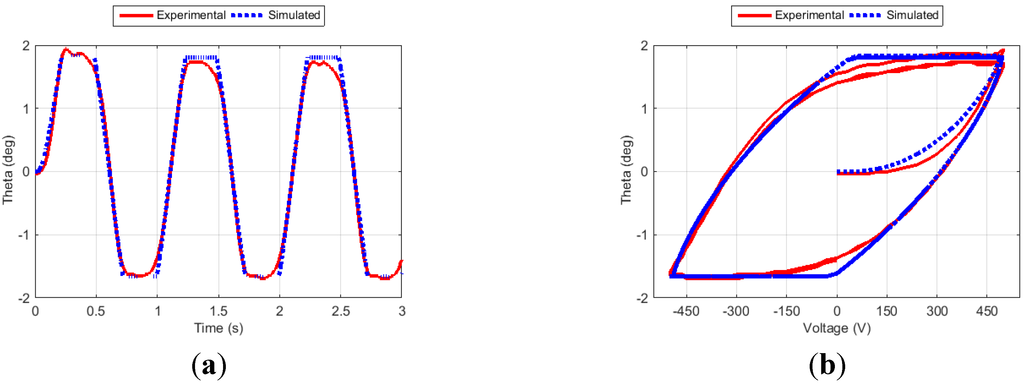
Figure 8. Fin angle (a) and hysteresis curve (b) for Case 6.

Figure 8. Fin angle (a) and hysteresis curve (b) for Case 6.

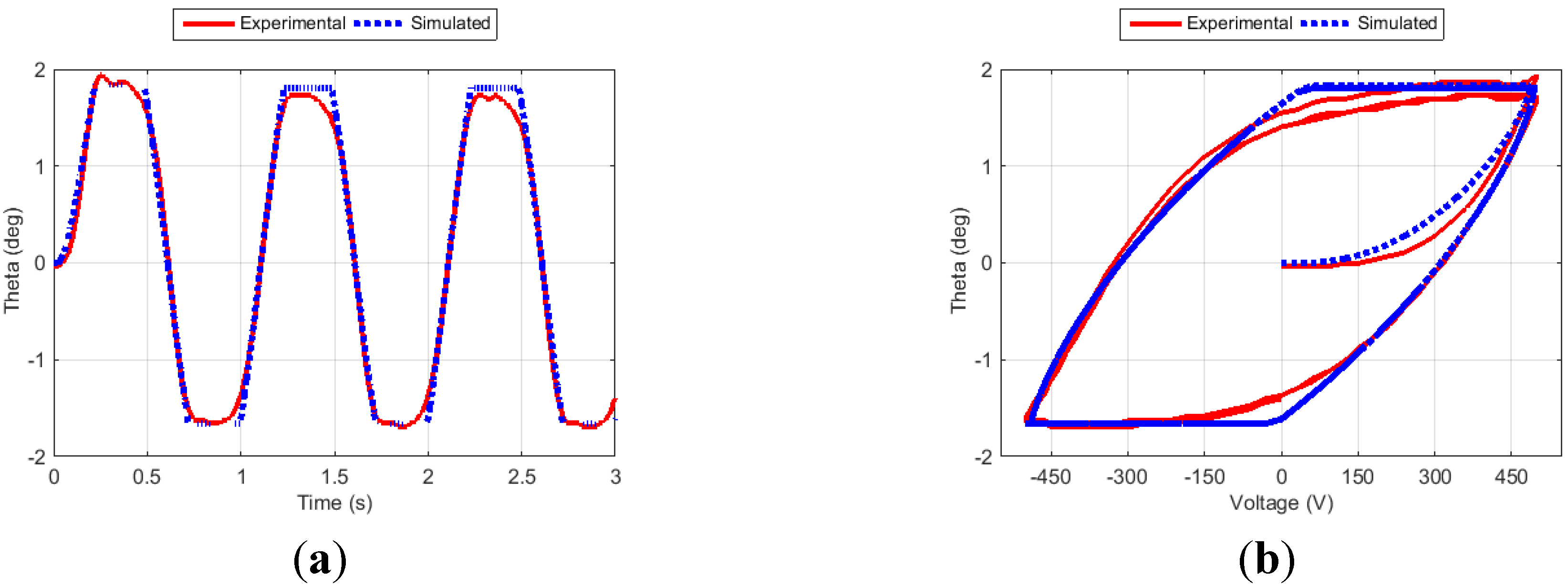
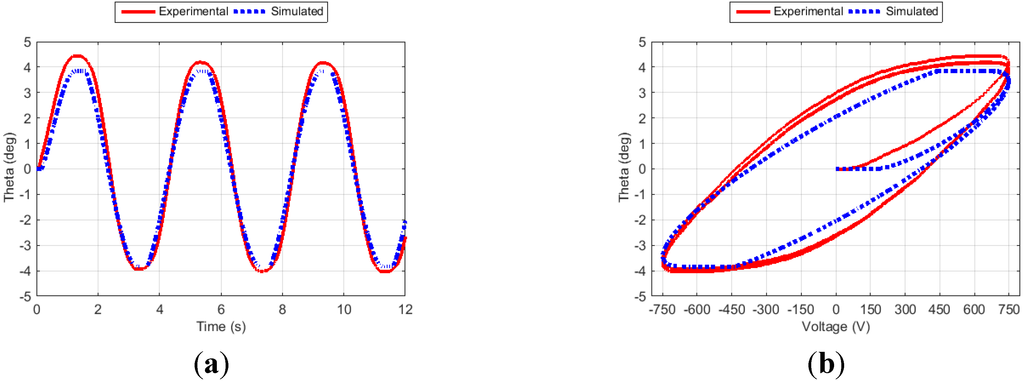
Figure 9. Fin angle (a) and hysteresis curve (b) for Case 7.

Figure 9. Fin angle (a) and hysteresis curve (b) for Case 7.

6. Model Validation

In this phase, the NN uses the connection weights, biases, architecture and learning rules that are obtained in the training phase (Appendix D) to estimate the parameters of the five other cases (2, 3, 4, 8 and 9). The resulting parameters are presented in Table 7. The same form of performance index (defined in Equation (6)) is also used to evaluate all of these cases. The performance index results for all cases after 750 generations are listed in Table 8. Comparing the experimental and simulated results of the validation cases, Figure 10, Figure 11, Figure 12, Figure 13 and Figure 14 indicate that the proposed model is validated, as it was able to produce results that closely match the experimental responses of the fin during the three cycles.

Table 7. Results for parameter estimation for the validation cases.

		Case 2	Case 3	Case 4	Case 8	Case 9
Damping	δ	0.124	0	0.219	0.029	0
	μ	93.534	72.812	104.47	97.144	81.792
Hysteresis	α	0	0	0	0	0
	β	−7.61 × 10−2	−7.92 × 10−2	−7.75 × 10−2	−8.34 × 10−2	−8.32 × 10−2
	γ	−8.00 × 10−2	−8.44 × 10−2	−6.55 × 10−2	−5.59 × 10−2	−6.57 × 10−2
Backlash	a1	0	0	0.041	0.149	0
	a2	0	0	0	0.344	0.255

Table 7. Results for parameter estimation for the validation cases.

		Case 2	Case 3	Case 4	Case 8	Case 9
Damping	δ	0.124	0	0.219	0.029	0
	μ	93.534	72.812	104.47	97.144	81.792
Hysteresis	α	0	0	0	0	0
	β	−7.61 × 10−2	−7.92 × 10−2	−7.75 × 10−2	−8.34 × 10−2	−8.32 × 10−2
	γ	−8.00 × 10−2	−8.44 × 10−2	−6.55 × 10−2	−5.59 × 10−2	−6.57 × 10−2
Backlash	a1	0	0	0.041	0.149	0
	a2	0	0	0	0.344	0.255

Table 8. Performance index for different input voltages.

	Excitation Frequency (Hz)
Amplitude↓	0.25	0.50	1.00
375 V	1.42	2.08	2.38
500 V	2.49	1.96	1.51
750 V	5.64	3.23	6.78

Table 8. Performance index for different input voltages.

	Excitation Frequency (Hz)
Amplitude↓	0.25	0.50	1.00
375 V	1.42	2.08	2.38
500 V	2.49	1.96	1.51
750 V	5.64	3.23	6.78

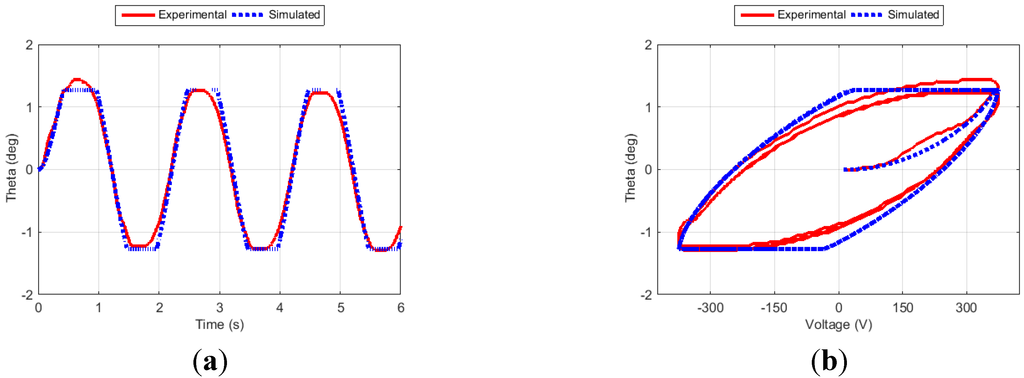
Figure 10. Fin angle (a) and hysteresis curve (b) for Case 2.

Figure 10. Fin angle (a) and hysteresis curve (b) for Case 2.

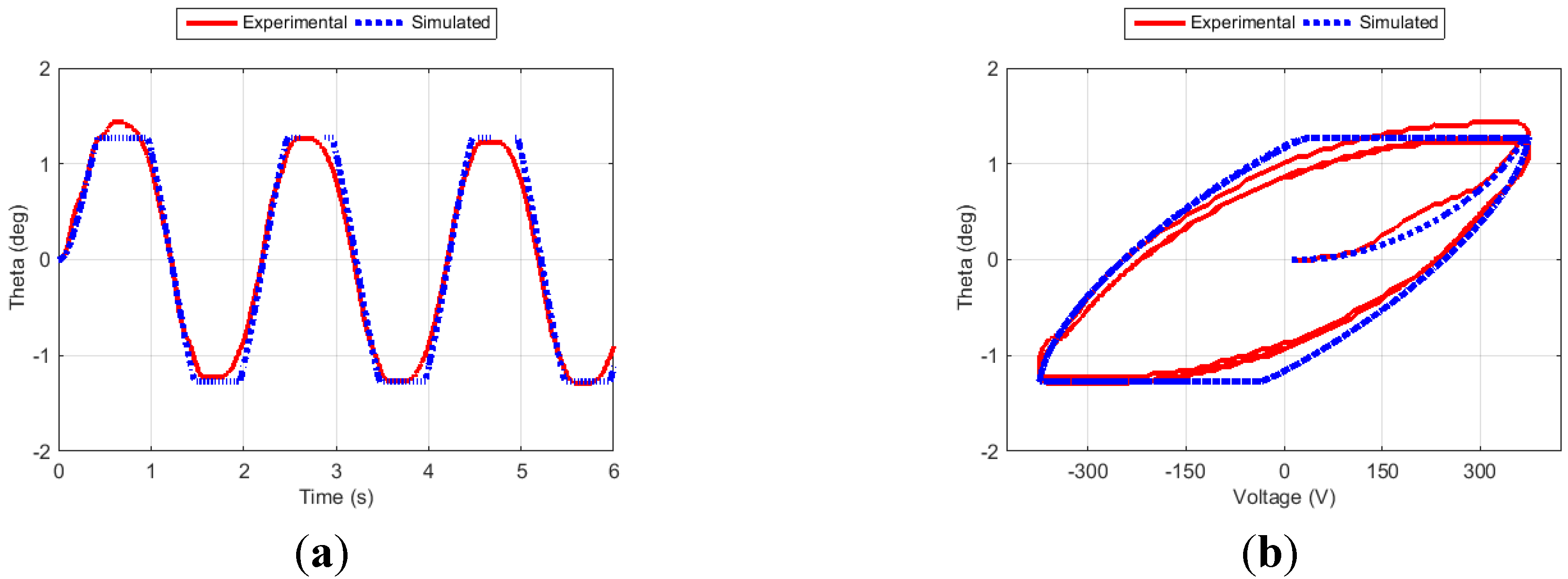
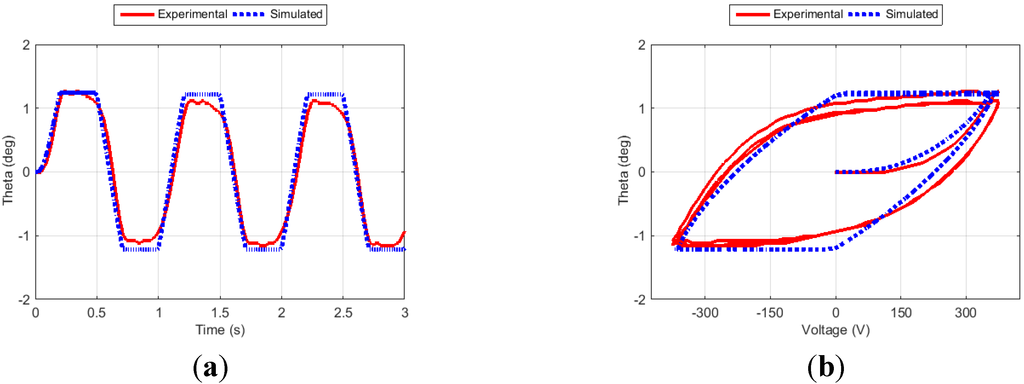
Figure 11. Fin angle (a) and hysteresis curve (b) for Case 3.

Figure 11. Fin angle (a) and hysteresis curve (b) for Case 3.

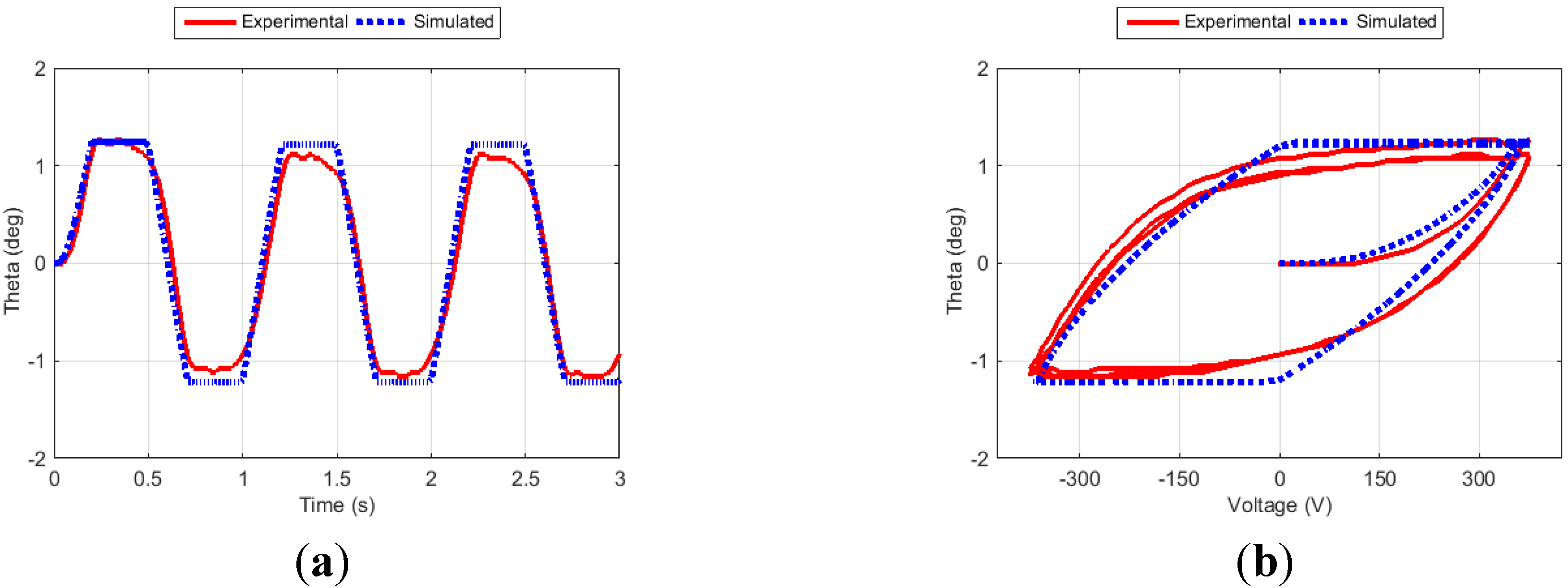
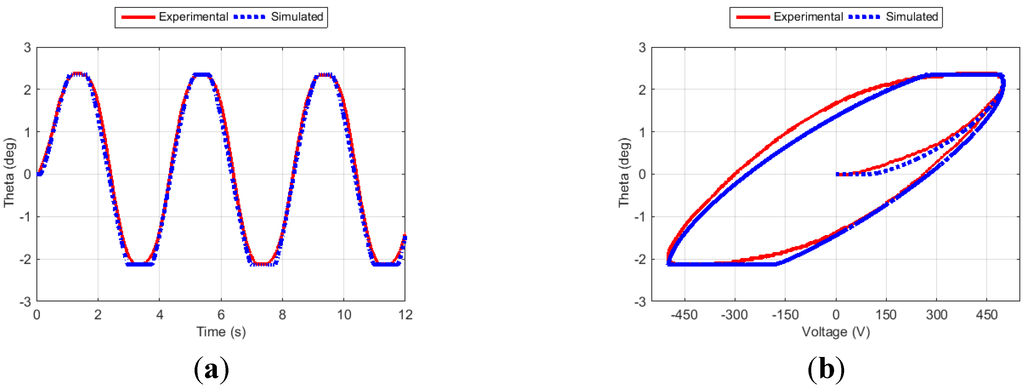
Figure 12. Fin angle (a) and hysteresis curve (b) for Case 4.

Figure 12. Fin angle (a) and hysteresis curve (b) for Case 4.

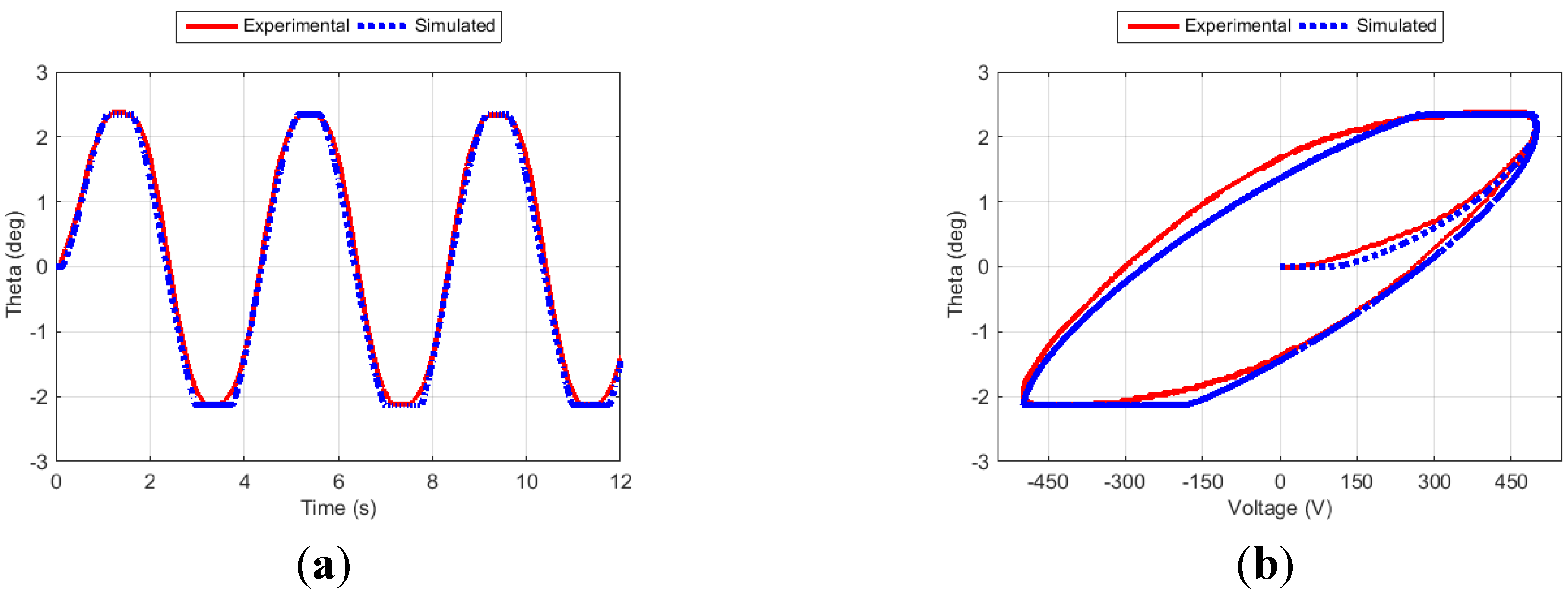
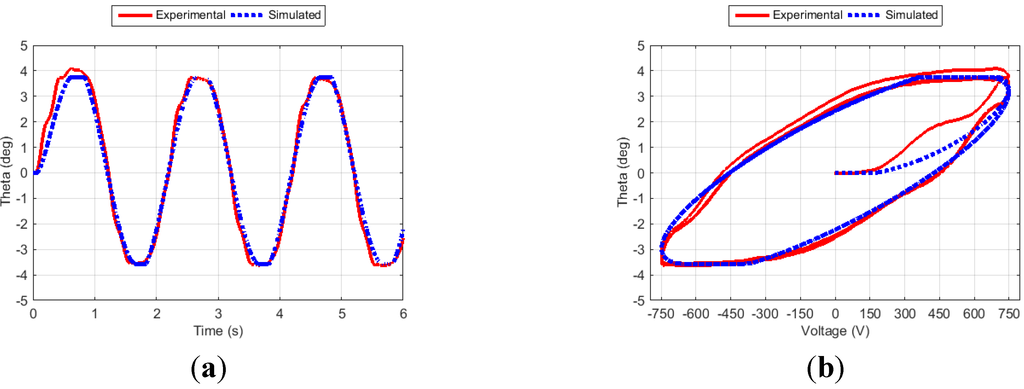
Figure 13. Fin angle (a) and hysteresis curve (b) for Case 8.

Figure 13. Fin angle (a) and hysteresis curve (b) for Case 8.

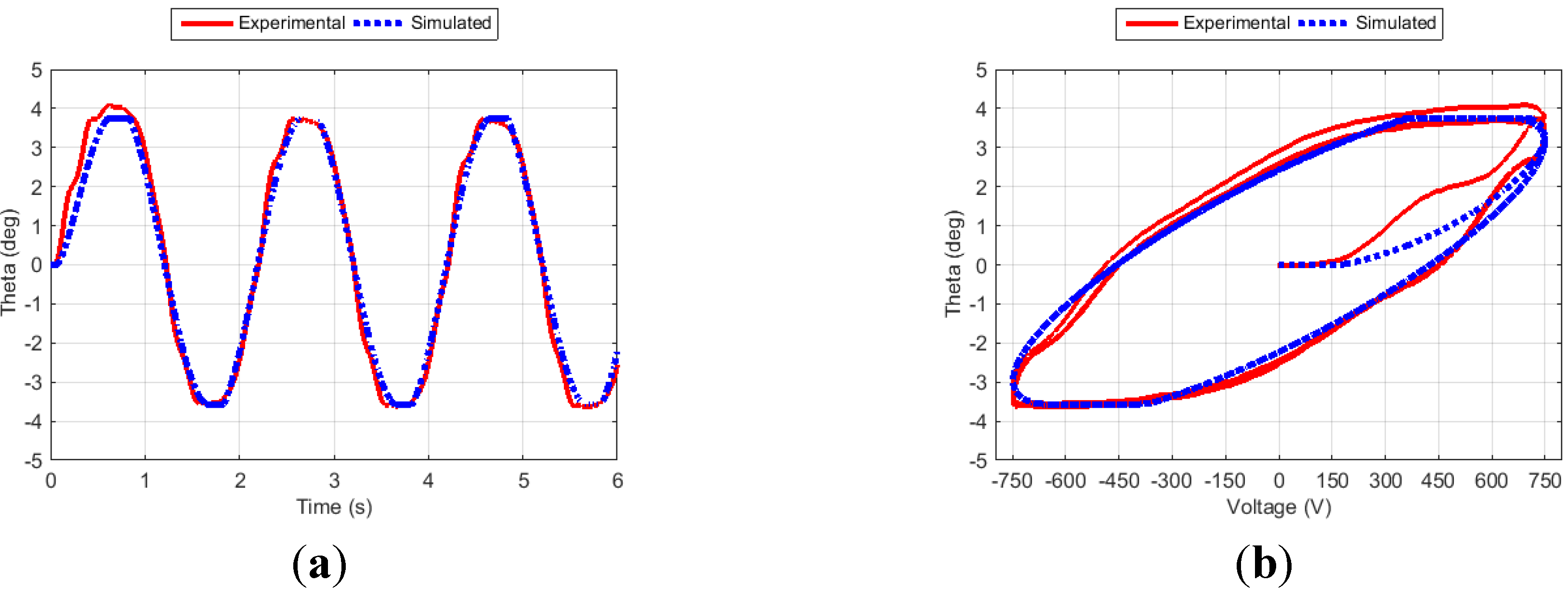
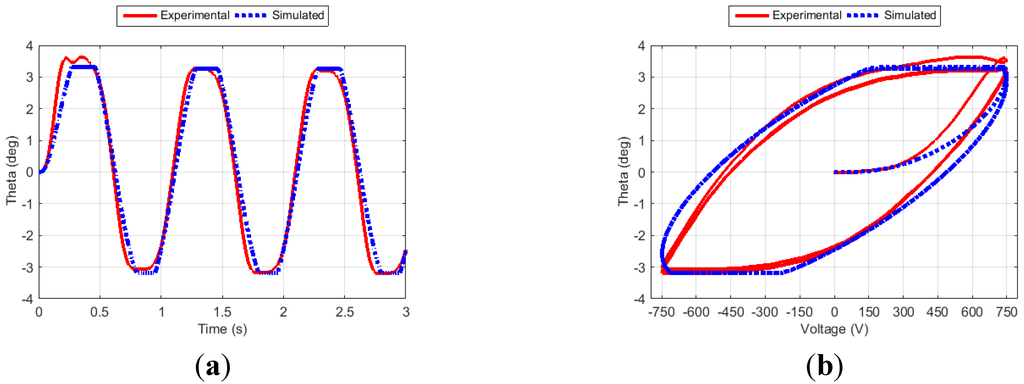
Figure 14. Fin angle (a) and hysteresis curve (b) for Case 9.

Figure 14. Fin angle (a) and hysteresis curve (b) for Case 9.

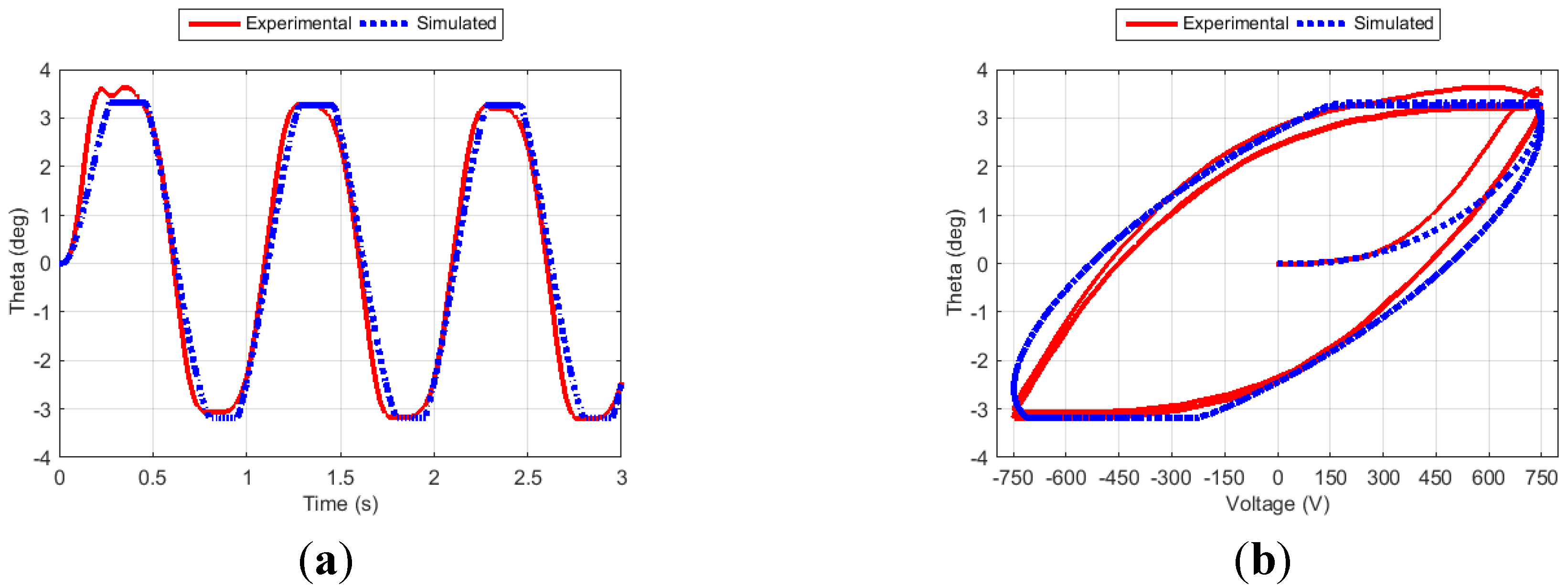
Table 9 and Table 10 list the variations of the damping parameters (δ and μ) in the nine cases, respectively. The results show that the stiffness matrix coefficient, δ, is inversely proportional to voltage amplitude and excitation frequency. It also becomes idle in the cases with 1 Hz (highest tested frequency). The results also suggest that the mass matrix coefficient μ is proportional to both voltage amplitude and excitation frequency (negative coefficient of linearity). This relation is outlined in the following equation:

$$\mu =0.020V-36.525f+102.361$$

(7)

The results of regression analysis (Table 11) show that linear representation of Equation (7) is statistically significant.

Table 9. Variation of the stiffness matrix coefficient δ.

	Excitation Frequency (Hz)
Amplitude↓	0.25	0.50	1.00
375 V	0.312	0.124	0
500 V	0.219	0.093	0
750 V	0.128	0.029	0

Table 9. Variation of the stiffness matrix coefficient δ.

	Excitation Frequency (Hz)
Amplitude↓	0.25	0.50	1.00
375 V	0.312	0.124	0
500 V	0.219	0.093	0
750 V	0.128	0.029	0

Table 10. Variation of the mass matrix coefficient μ.

	Excitation Frequency (Hz)
Amplitude↓	0.25	0.50	1.00
375 V	98.650	93.534	72.812
500 V	104.47	94.666	75.626
750 V	109.210	97.144	81.792

Table 10. Variation of the mass matrix coefficient μ.

	Excitation Frequency (Hz)
Amplitude↓	0.25	0.50	1.00
375 V	98.650	93.534	72.812
500 V	104.47	94.666	75.626
750 V	109.210	97.144	81.792

Table 11. Regression analysis for the damping parameter μ.

V (volts)	f (Hz)	Yintercept	Coefficient of Determination R2
0.0020 p = 0.001	−36.525 p < 0.001	102.361 p < 0.001	0.988

p is a measure of the significance of the relation.

Table 11. Regression analysis for the damping parameter μ.

V (volts)	f (Hz)	Yintercept	Coefficient of Determination R2
0.0020 p = 0.001	−36.525 p < 0.001	102.361 p < 0.001	0.988

p is a measure of the significance of the relation.

The results of Table 6 and Table 7 show that the proposed hysteresis model is independent of α. Thus, this analysis suggests reducing the hysteresis model of Equation (4) to:

$$\dot{z}=-\beta \left|\dot{u}\right|z-\gamma \dot{u}\left|z\right|$$

(8)

The reduced hysteresis model indicates that the rate of the input u alone does not affect the hysteresis curve. Instead, it is mainly influenced by the coupled effect of the rate of change of the input and the state variable z. The values of the two remaining parameters, β and γ, are almost unchanged for the nine cases considered in this study.

The variation of the backlash parameters can be better explained by considering Table 12, which shows that the backlash threshold operator (a₁) is only active at the lower left corner part of the grid (cases with high voltage and low frequency). On the other hand, Table 13 shows the second threshold operator (a₂) is only active when voltage is at the highest amplitude. Consequently, the backlash thresholds of the PZT actuator are activated at cases of higher voltage amplitude, i.e., when the dynamic forces become dominant.

Table 12. Variation of the backlash threshold parameter a₁.

	Excitation Frequency (Hz)
Amplitude↓	0.25	0.50	1.00
375 V	0	0	0
500 V	0.041	0	0
750 V	0.281	0.149	0

Table 12. Variation of the backlash threshold parameter a₁.

	Excitation Frequency (Hz)
Amplitude↓	0.25	0.50	1.00
375 V	0	0	0
500 V	0.041	0	0
750 V	0.281	0.149	0

Table 13. Variation of the backlash threshold parameter a₂.

	Excitation Frequency (Hz)
Amplitude↓	0.25	0.50	1.00
375 V	0	0	0
500 V	0	0	0
750 V	0.294	0.344	0.255

Table 13. Variation of the backlash threshold parameter a₂.

	Excitation Frequency (Hz)
Amplitude↓	0.25	0.50	1.00
375 V	0	0	0
500 V	0	0	0
750 V	0.294	0.344	0.255

7. Conclusions

This work presents an approach for the identification of a composite piezoelectric (PZT) bimorph actuator. As an example for application, the actuator is incorporated within a smart fin prototype. The novelty of the work lies in proposing an approach to use a hybrid neural network to model the behavior of a PZT actuator that does not only mimic a specific behavior, but is also able to predict the behavior under different voltage and excitation frequency. The performance of the actuator is considered for nine test cases that represent three voltage amplitudes (375, 500 and 750 V) excited at three different frequencies (0.25, 0.50 and 1.0 Hz).

Similar to earlier research in this area, it is observed that the actuator experiences hysteresis and backlash. The system is modeled using a linear dynamic model. A damping matrix, the Bouc–Wen hysteresis model and backlash operators are also included in the model. Full identification of the actuator model is needed to predict the performance of the actuator and to utilize it in control schemes.

While it is easy to estimate the values of the saturation operators of the backlash model based on experimental results, it may not be intuitive to determine the correct values of the threshold parameters of the model. A hybrid neural network genetic algorithm (HGANN) is used for identification of the remaining parameters of the model. HGANN allows genetic algorithm to simultaneously tune the weights and learning rules of the neural network representing the model and to adjust the structure of its hidden layer, such that the cost function can be minimized. In this work, four sinusoidal inputs of mixed amplitudes and frequencies are used to train the NN’s biases, weights and learning rules. The other five cases are left for validating the performance of the NN and its robustness to input variations. Comparing the experimental and simulation results of the training cases indicates that the neural network obtained from the training is robust enough to handle multiple operating conditions. Additionally, the robustness of the resulting neural network is verified by its satisfactory performance when applied to each of the remaining five cases.

It may be insightful to study the values of the model parameters in the nine cases to understand the nature of the proposed model. For example, the two damping parameters show that the coefficient of the stiffness matrix, δ, is inversely proportional to the voltage amplitude and excitation frequency. The effect of the stiffness matrix disappears completely in the highest frequency cases (1-Hz cases). On the other hand, the results show that the coefficient of the mass matrix, μ, is proportional to the voltage amplitude and inversely proportional to the excitation frequency. The results also indicate that the hysteresis model is too general for the composite piezoelectric bimorph actuator model, since the rate of change of the input signal ($\dot{u}$) does not influence the hysteresis curve. The remaining two parameters (β and γ) are reasonably consistent for all nine cases, which show the limited sensitivity of the proposed hysteresis model to changes in exciting voltage and frequency. It is observed that the two backlash threshold operators are only active in the cases of high voltage amplitude. The results suggest that backlash appears only when dynamic forces become dominant.