Energetic and Peak Power Advantages of Series Elastic Actuators in an Actuated Prosthetic Leg for Walking and Running
Abstract
:1. Introduction
2. Methods
2.1. Model Input Data
| Number of Subj. | Age (years) | Body Height (m) | Body Mass (kg) | Speeds (m/s) | Leg Length (m) | |
|---|---|---|---|---|---|---|
| Exp. I | 21 | 25.4 ± 2.7 | 1.73 ± 0.09 | 70.9 ± 11.7 | 0.52, 1.04, 1.55, 2.07, 2.59 | 0.96 ± 0.08 |
| Exp. II | 7 | 23.7 ± 1.1 | 1.80 ± 0.10 | 77.5 ± 8.8 | 3.0, 4.0 | 1.02 ± 0.07 |
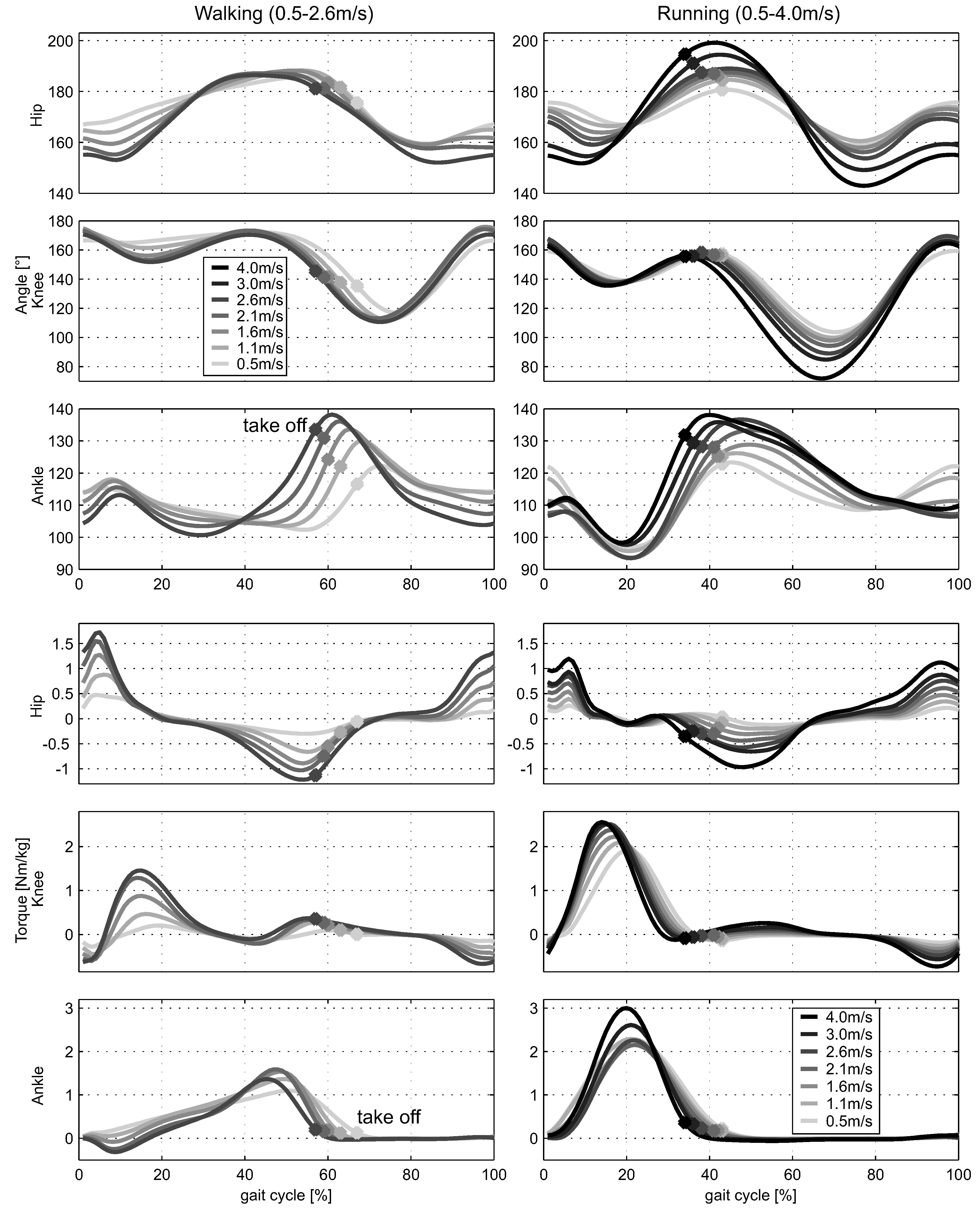
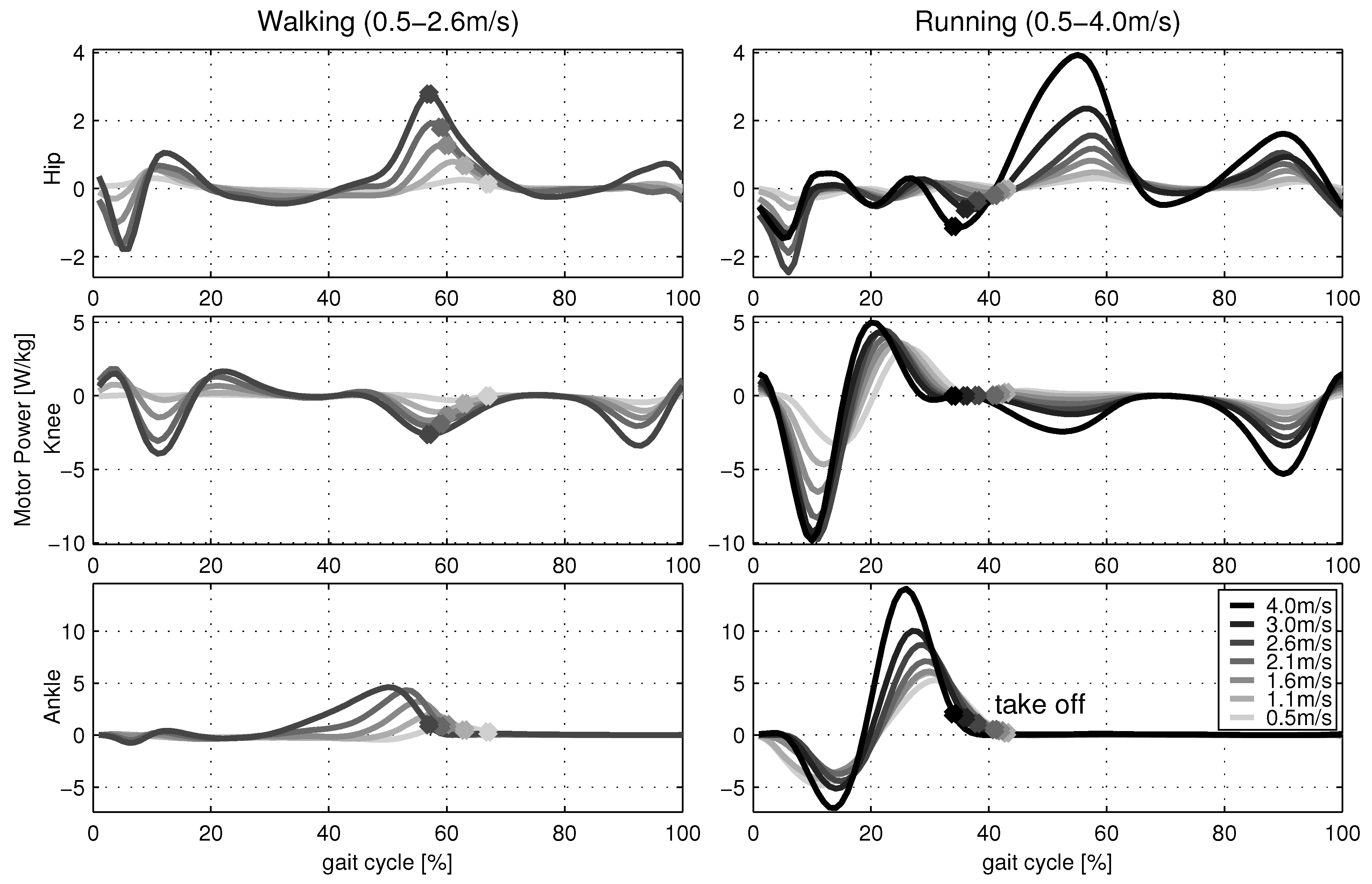
2.2. Power and Energy Calculation
2.3. Finding the Optimal Stiffness
3. Results
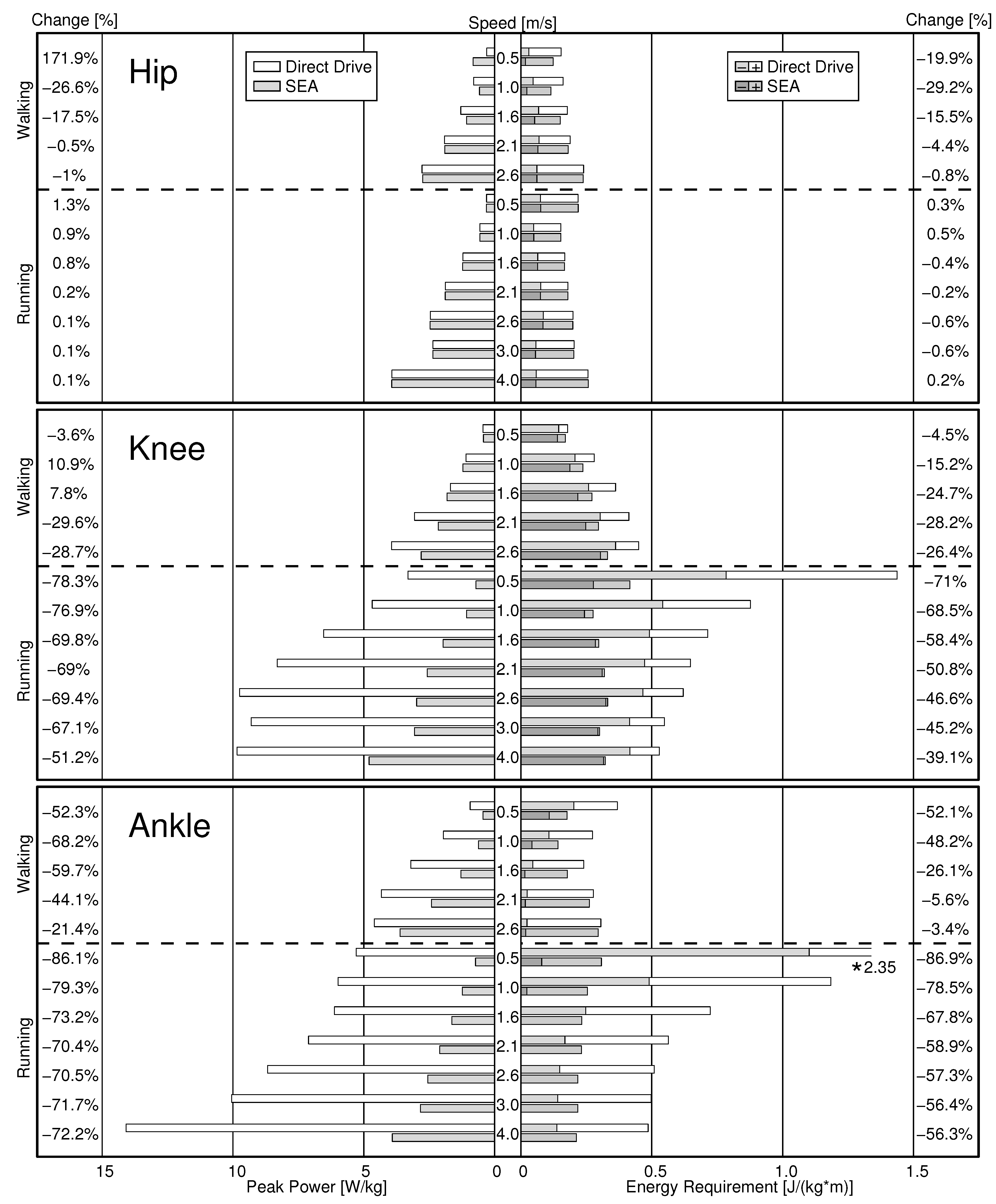
3.1. Peak Power and Energy Requirements at the Joint Level
3.1.1. Hip
3.1.2. Knee
3.1.3. Ankle
3.2. Positive Sagittal Leg Work
3.2.1. Direct Drive
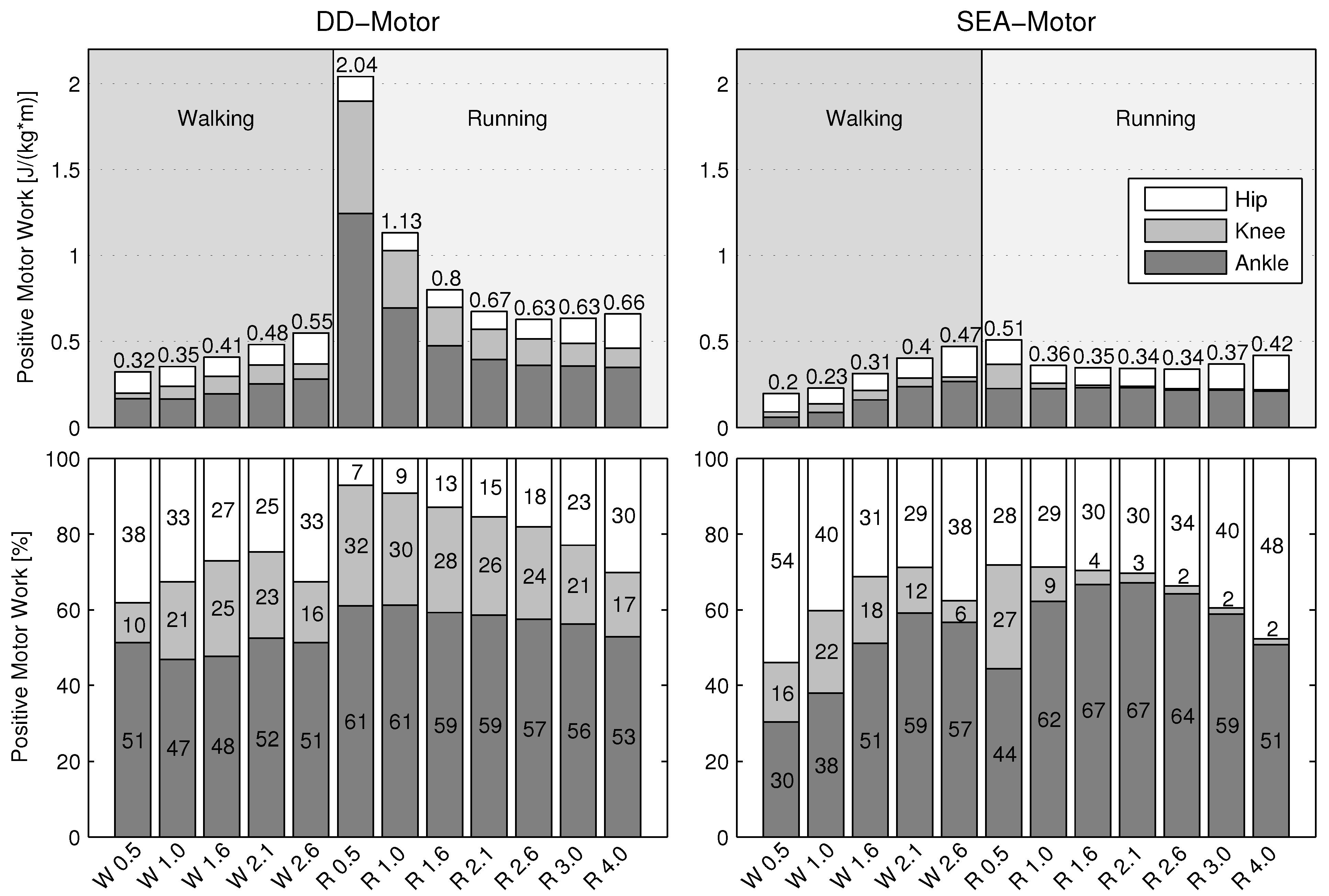
3.2.2. Series Elastic Actuator
3.3. Stiffness
| Gait Speed (m/s) | Walking | Running | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.5 | 1.0 | 1.6 | 2.1 | 2.6 | 0.5 | 1.0 | 1.6 | 2.1 | 2.6 | 3.0 | 4.0 | ||
| Hip | 0.0712 | 0.1817 | 0.4238 | 0.9821 | rigid | rigid | rigid | rigid | rigid | rigid | rigid | rigid | |
| Knee | 0.1848 | 0.0873 | 0.1058 | 0.1215 | 0.1274 | 0.137 | 0.1223 | 0.1159 | 0.1234 | 0.1292 | 0.141 | 0.1508 | |
| Ankle | 0.1136 | 0.0857 | 0.1208 | 0.1822 | 0.2536 | 0.0887 | 0.0929 | 0.0937 | 0.0941 | 0.0946 | 0.1152 | 0.1239 | |
4. Discussion
4.1. Reason for the SEA Benefits
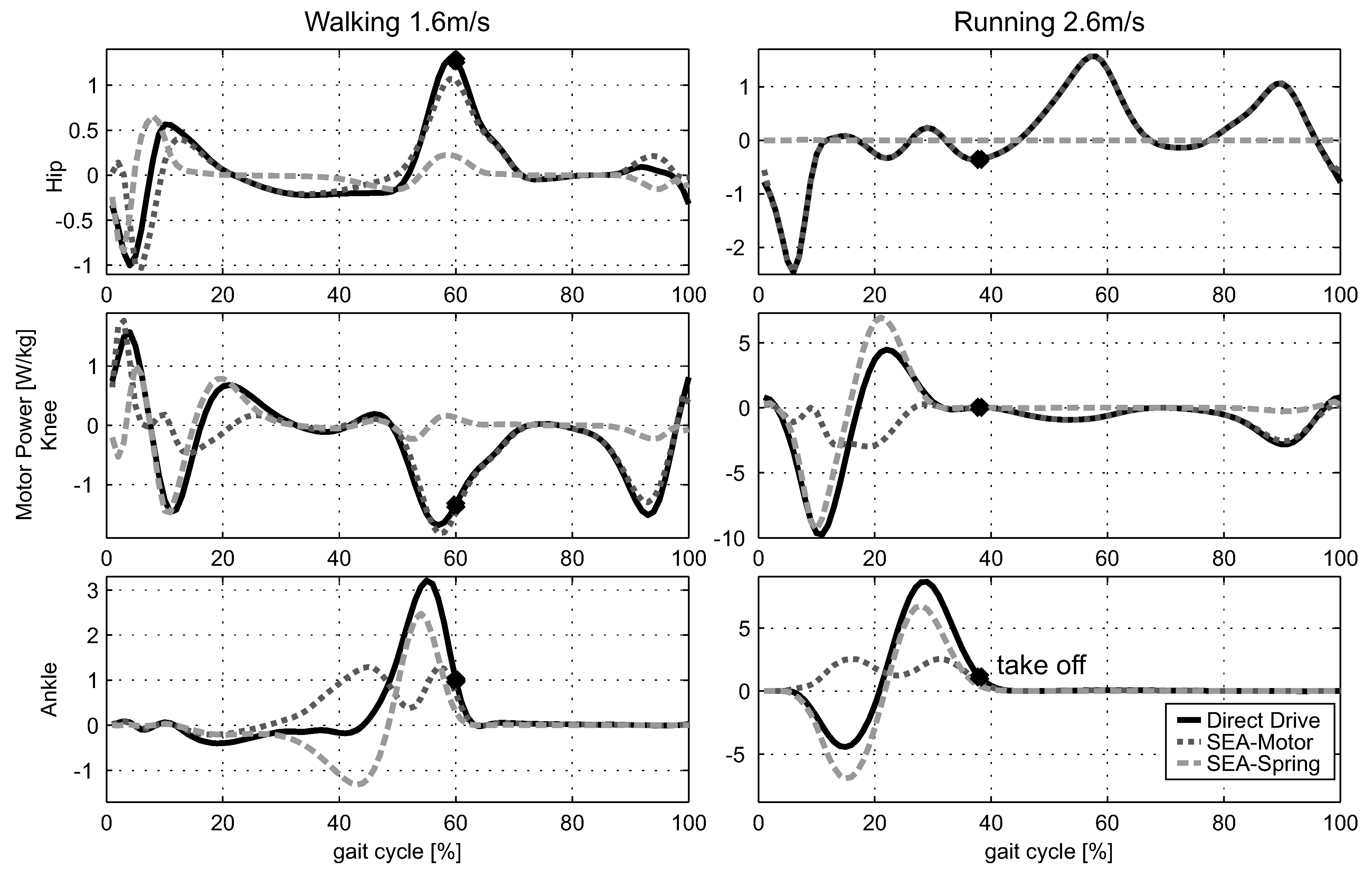
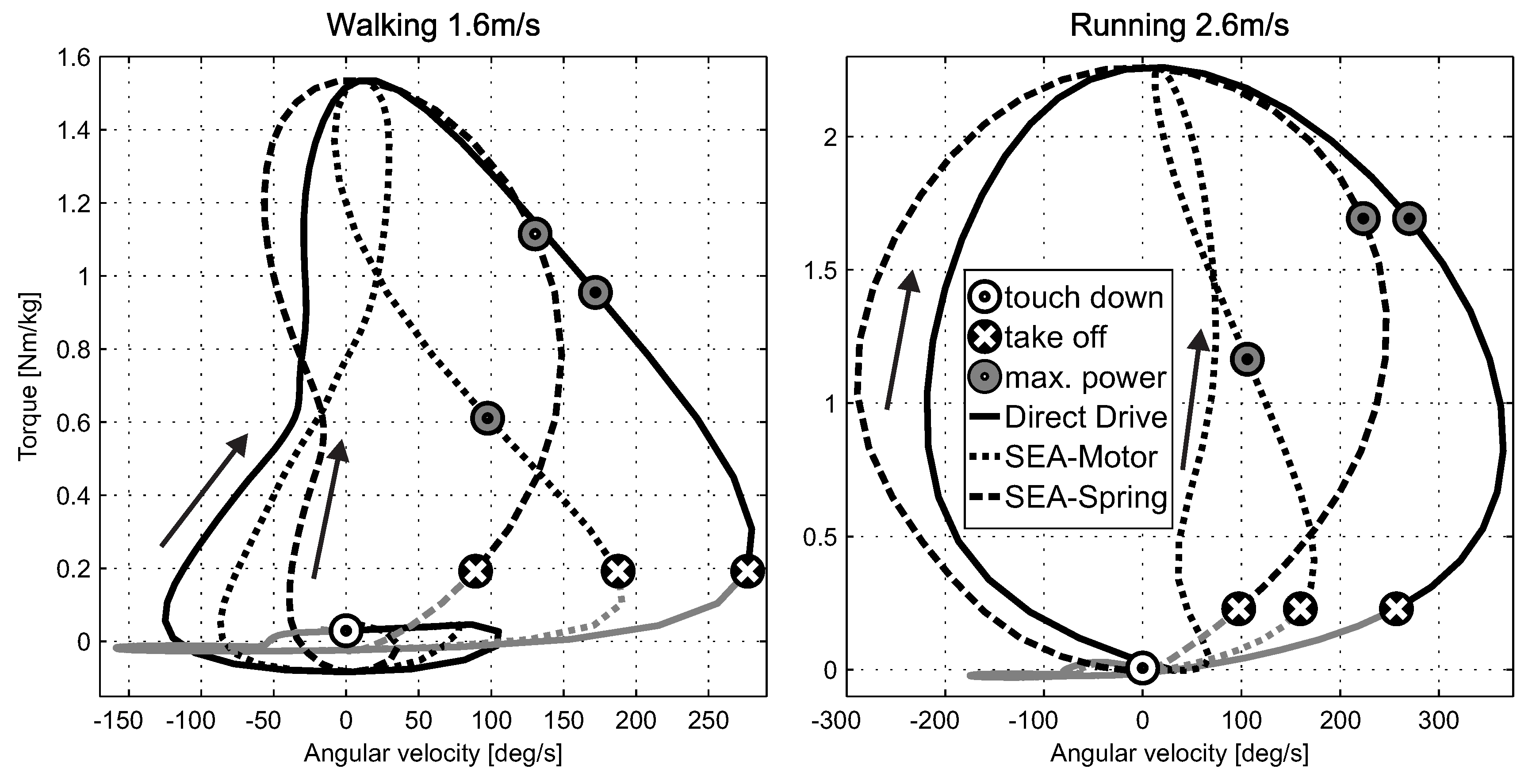
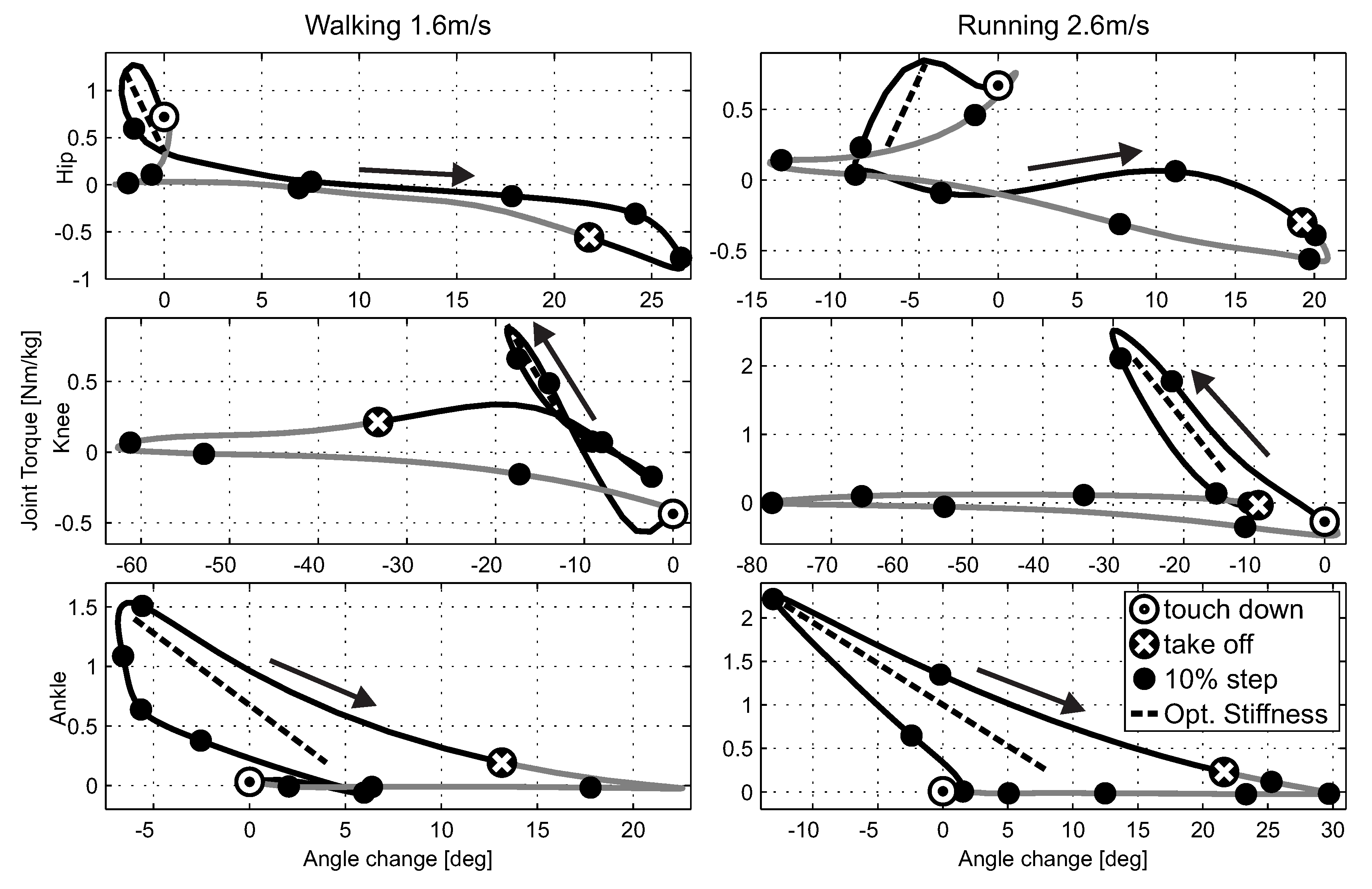
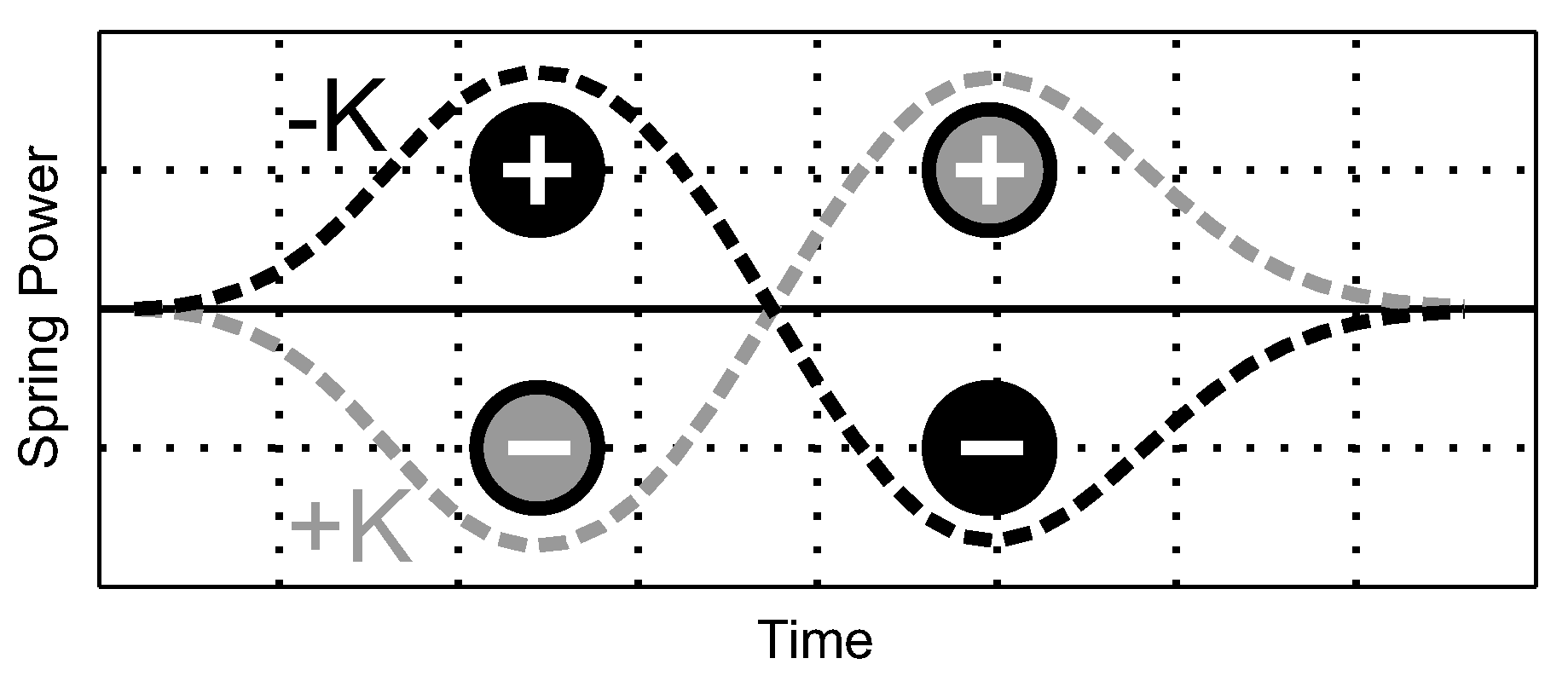
4.2. Positive Leg Work
4.3. Sensitivity of Results
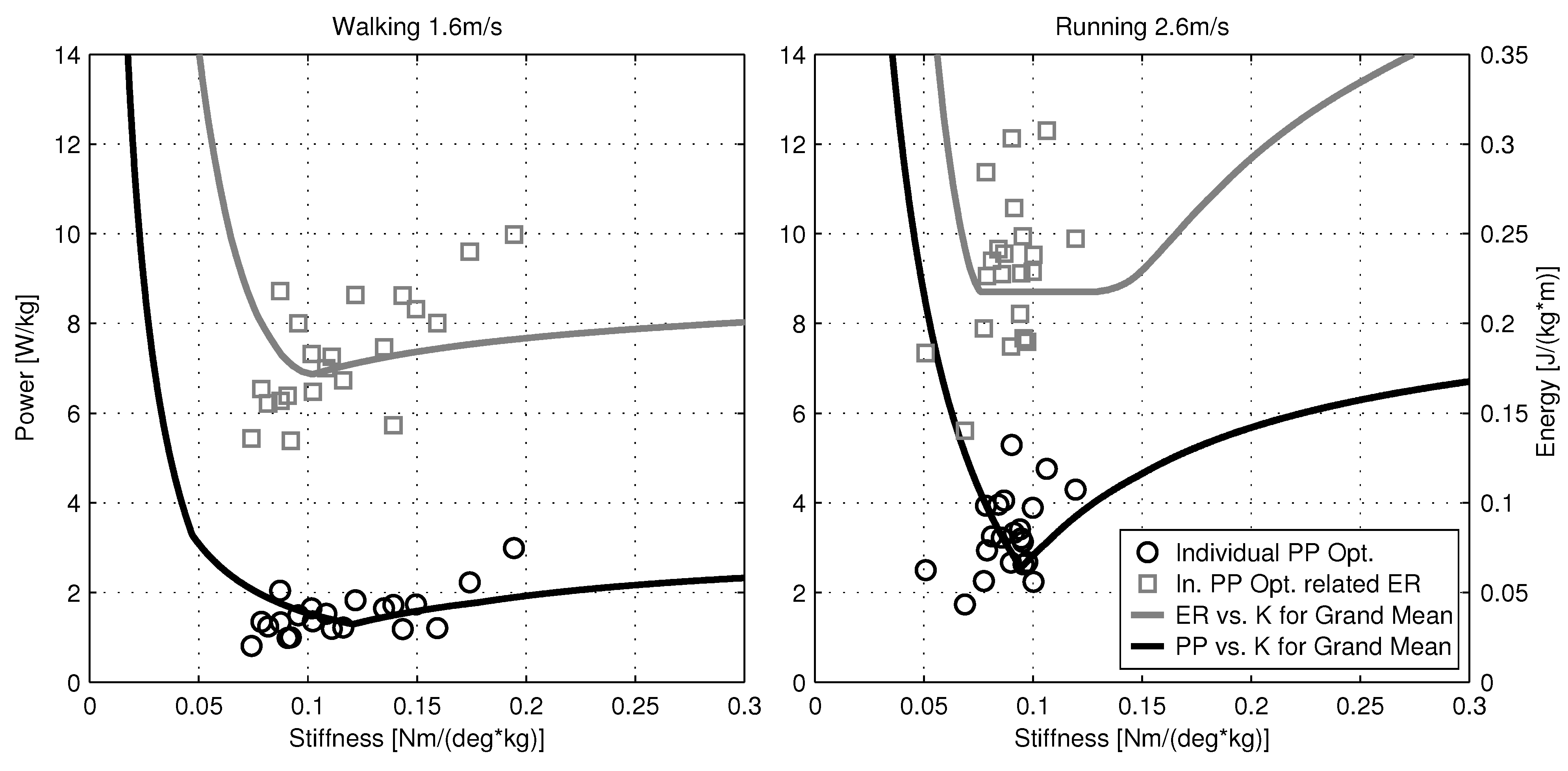
4.4. Methodological Considerations
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Ottobock. Available online: http://www.ottobock.com (accessed on 1 August 2013).
- Ossur. Available online: http://www.ossur.com (accessed on 1 August 2013).
- Mathijssen, G.; Cherelle, P.; Lefeber, D.; Vanderborght, B. Concept of a series-parallel elastic actuator for a powered transtibial prosthesis. Actuators 2013, 2, 59–73. [Google Scholar] [CrossRef]
- Hitt, J.; Sugar, T.; Holgate, M.; Bellman, R. An active foot-ankle prosthesis with biomechanical energy regeneration. J. Med. Devices 2010. [Google Scholar] [CrossRef]
- Zhu, J.; Wang, Q.; Wang, L. PANTOE 1: Biomechanical design of powered ankle-foot prosthesis with compliant joints and segmented foot. In Proceedings of the IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM), Montreal, ON, Canada, 6–9 July 2010; pp. 31–36.
- Sup, F.; Varol, H.; Mitchell, J.; Withrow, T.; Goldfarb, M. Self-contained powered knee and ankle prosthesis: Initial evaluation on a transfemoral amputee. IEEE Int. Conf. Rehabil. Robot. 2009, 2009, 638–644. [Google Scholar] [PubMed]
- Suzuki, R.; Sawada, T.; Kobayashi, N.; Hofer, E. Control method for powered ankle prosthesis via internal model control design. In Proceedings of the International Conference on Mechatronics and Automation (ICMA), Beijing, China, 7–10 August 2011; pp. 237–242.
- Herr, H.; Grabowski, A. Bionic ankle–foot prosthesis normalizes walking gait for persons with leg amputation. Proc. R. Soc. B: Biol. Sci. 2012, 279, 457–464. [Google Scholar] [CrossRef] [PubMed]
- Ferris, A.E.; Aldridge, J.M.; Rábago, C.A.; Wilken, J.M. Evaluation of a powered ankle-foot prosthetic system during walking. Arch. Phys. Med. Rehabil. 2012, 93, 1911–1918. [Google Scholar] [CrossRef] [PubMed]
- Cherelle, P.; Matthys, A.; Grosu, V.; Vanderborght, B.; Lefeber, D. The amp-foot 2.0: Mimicking intact ankle behavior with a powered transtibial prosthesis. In Proceedings of the 2012 4th IEEE RAS & EMBS International Conference on Biomedical Robotics and Biomechatronics (BioRob), Rome, Italy, 24–27 June 2012; pp. 544–549.
- Pratt, G.; Williamson, M. Series elastic actuators. In Proceedings of 1995 IEEE/RSJ International Conference on Intelligent Robots and Systems 95. Human Robot Interaction and Cooperative Robots, Pittsburgh, PA, USA, 5–9 August 1995.
- Hollander, K.; Sugar, T. Design of the robotic tendon. In Proceedings of the Design of Medical Devices Conference (DMD), Minneapolis, MN, USA, 13–14 April 2005.
- Grimmer, M.; Seyfarth, A. Stiffness adjustment of a Series Elastic Actuator in an ankle-foot prosthesis for walking and running: The trade-off between energy and peak power optimization. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Shanghai, China, 9–13 May 2011; pp. 1439–1444.
- Grimmer, M.; Seyfarth, A. Stiffness adjustment of a series elastic actuator in a knee prosthesis for walking and running: The trade-off between energy and peak power optimization. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), San Francisco, CA, USA, 25–30 September 2011; pp. 1811–1816.
- Wang, S.; van Dijk, W.; van der Kooij, H. Spring uses in exoskeleton actuation design. In Proceedings of the IEEE International Conference on Rehabilitation Robotics (ICORR), Zurich, Switzerland, 29 June–1 July 2011; pp. 1–6.
- Segal, A.; Orendurff, M.; Klute, G.; McDowell, M.; Pecoraro, J.; Shofer, J.; Czerniecki, J. Kinematic and kinetic comparisons of transfemoral amputee gait using C-Leg and Mauch SNS prosthetic knees. J. Rehabil. Res. Dev. 2006, 43, 857–870. [Google Scholar] [CrossRef] [PubMed]
- Johansson, J.; Sherrill, D.; Riley, P.; Bonato, P.; Herr, H. A clinical comparison of variable-damping and mechanically passive prosthetic knee devices. Am. J. Phys. Med. Rehabil. 2005, 84, 563–575. [Google Scholar] [CrossRef] [PubMed]
- Donelan, J.; Li, Q.; Naing, V.; Hoffer, J.; Weber, D.; Kuo, A. Biomechanical energy harvesting: Generating electricity during walking with minimal user effort. Science 2008, 319, 807–810. [Google Scholar] [CrossRef] [PubMed]
- Lipfert, S. Kinematic and Dynamic Similarities between Walking and Running; Verlag Dr. Kovac: Hamburg, Germany, 2010; ISBN 978-3-8300-5030-8. [Google Scholar]
- Günther, M.; Sholukha, V.; Keßler, D.; Wank, V.; Blickhan, R. Dealing with skin motion and wobbling masses in inverse dynamics. J. Mech. Med. Biol. 2003, 3, 309–335. [Google Scholar] [CrossRef]
- Dal, U.; Erdogan, T.; Resitoglu, B.; Beydagi, H. Determination of preferred walking speed on treadmill may lead to high oxygen cost on treadmill walking. Gait Posture 2010, 31, 366–369. [Google Scholar] [CrossRef] [PubMed]
- Grimmer, M.; Eslamy, M.; Gliech, S.; Seyfarth, A. A comparison of parallel-and series elastic elements in an actuator for mimicking human ankle joint in walking and running. In Proceedings of the 2012 IEEE International Conference on Robotics and Automation (ICRA), Saint Paul, MN, 14–18 May 2012; pp. 2463–2470.
- Farris, D.; Sawicki, G. The mechanics and energetics of human walking and running: A joint level perspective. J. R. Soc. Interface 2012, 9, 110–118. [Google Scholar] [CrossRef] [PubMed]
- Van Den Bogert, A. Exotendons for assistance of human locomotion. Biomed. Eng. Online 2003, 2. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sasaki, K.; Neptune, R.; Kautz, S. The relationships between muscle, external, internal and joint mechanical work during normal walking. J. Exp. Biol. 2009, 212, 738–744. [Google Scholar] [CrossRef] [PubMed]
- Hreljac, A.; Parker, D.; Quintana, R.; Abdala, E.; Patterson, K.; Sison, M. Energetics and perceived exertion of low speed running and high speed walking. Facta Univ. Ser.: Phys. Educ. Sport 2002, 1, 27–35. [Google Scholar]
- Sasaki, K.; Neptune, R. Muscle mechanical work and elastic energy utilization during walking and running near the preferred gait transition speed. Gait Posture 2006, 23, 383–390. [Google Scholar] [CrossRef] [PubMed]
- Au, S.K.; Herr, H.; Weber, J.; Martinez-Villalpando, E.C. Powered ankle-foot prosthesis for the improvement of amputee ambulation. Conf. Proc. IEEE Eng. Med. Biol. Soc. 2007, 2007, 3020–3026. [Google Scholar] [PubMed]
- Sup, F.; Varol, H.A.; Mitchell, J.; Withrow, T.; Goldfarb, M. Design and control of an active electrical knee and ankle prosthesis. In Proceedings of the 2nd IEEE RAS & EMBS International Conference on Biomedical Robotics and Biomechatronics, Scottsdale, AZ, USA, 19–22 October 2008; pp. 523–528.
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Grimmer, M.; Eslamy, M.; Seyfarth, A. Energetic and Peak Power Advantages of Series Elastic Actuators in an Actuated Prosthetic Leg for Walking and Running. Actuators 2014, 3, 1-19. https://doi.org/10.3390/act3010001
Grimmer M, Eslamy M, Seyfarth A. Energetic and Peak Power Advantages of Series Elastic Actuators in an Actuated Prosthetic Leg for Walking and Running. Actuators. 2014; 3(1):1-19. https://doi.org/10.3390/act3010001
Chicago/Turabian StyleGrimmer, Martin, Mahdy Eslamy, and André Seyfarth. 2014. "Energetic and Peak Power Advantages of Series Elastic Actuators in an Actuated Prosthetic Leg for Walking and Running" Actuators 3, no. 1: 1-19. https://doi.org/10.3390/act3010001
APA StyleGrimmer, M., Eslamy, M., & Seyfarth, A. (2014). Energetic and Peak Power Advantages of Series Elastic Actuators in an Actuated Prosthetic Leg for Walking and Running. Actuators, 3(1), 1-19. https://doi.org/10.3390/act3010001




