Vibration Reduction and Stability Investigation of Van Der Pol–Mathieu–Duffing Oscillator via the Nonlinear Saturation Controller
Abstract
1. Introduction
2. Governing Equations and Approximate Solutions
3. Perturbation Analysis
- (i)
- Primary resonance: or .
- (ii)
- Internal resonance: .
- (iii)
- Simultaneous resonance: Internal and primary resonance.
4. The Periodic Solution
4.1. The Frequency–Response Equations (FREs)
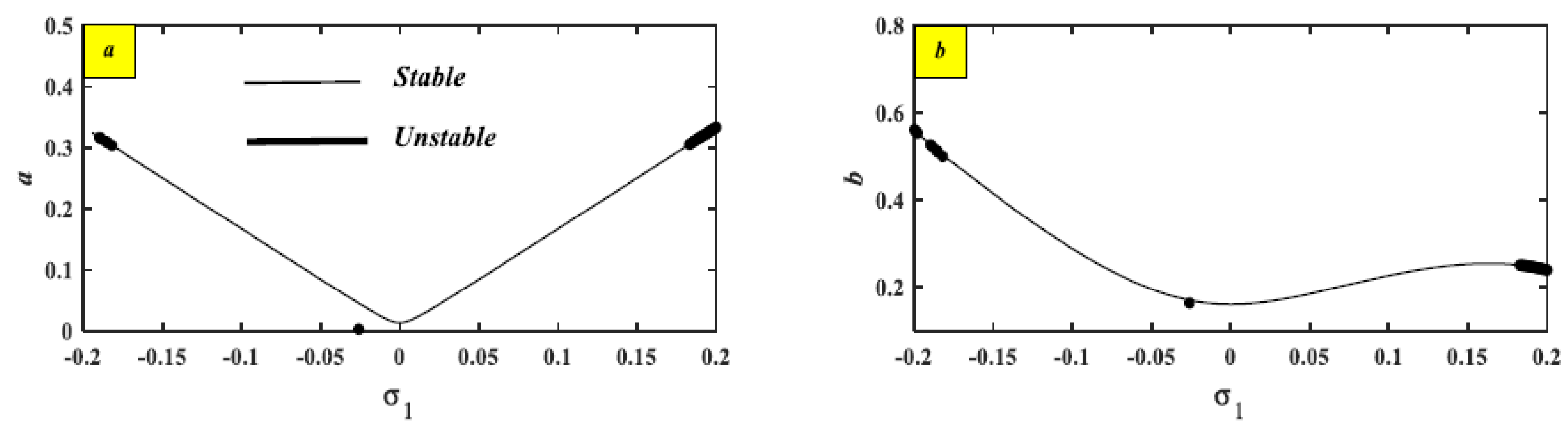
4.2. Stability Analysis at the Fixed Point
5. Findings and Discussion
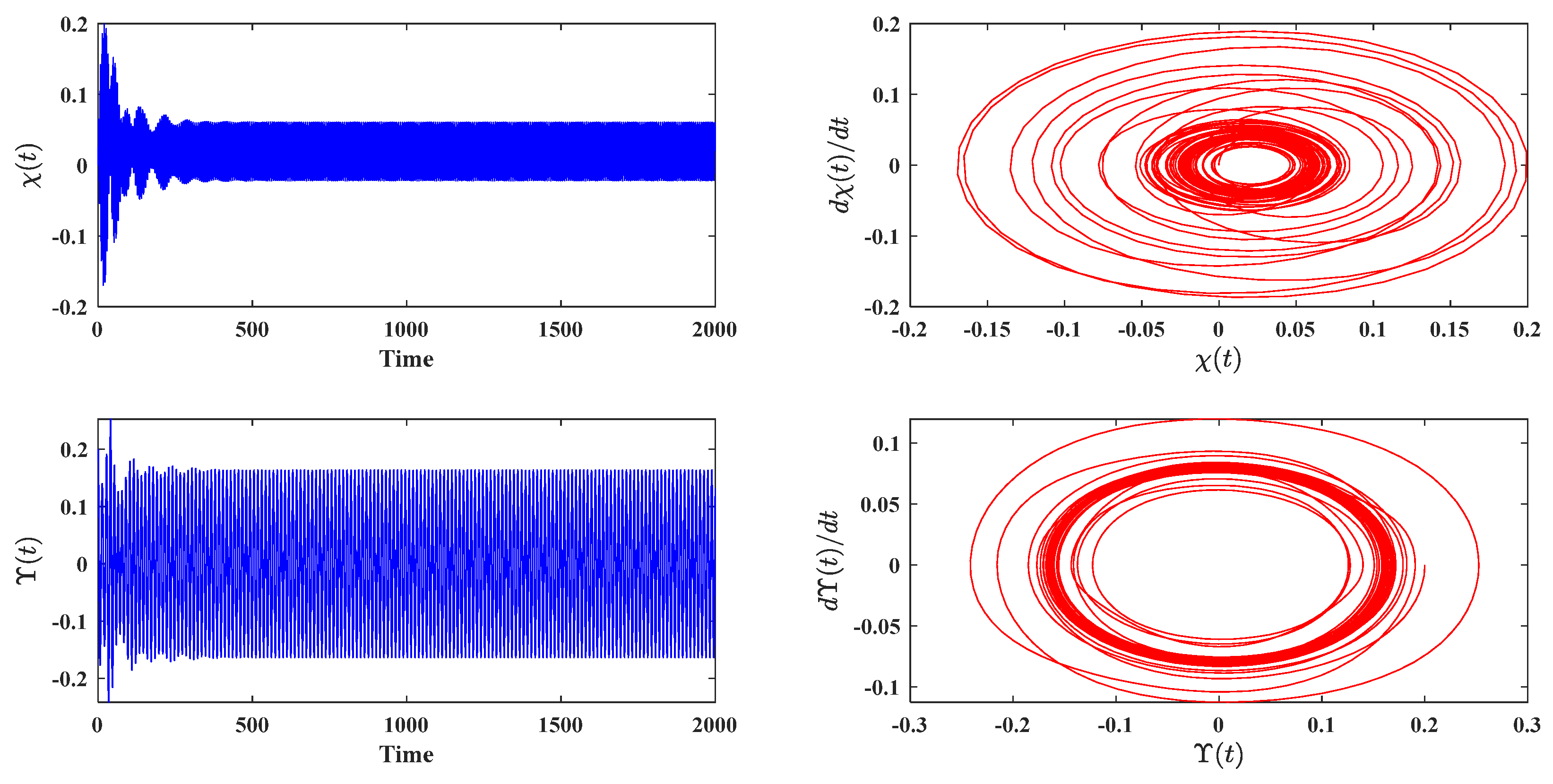
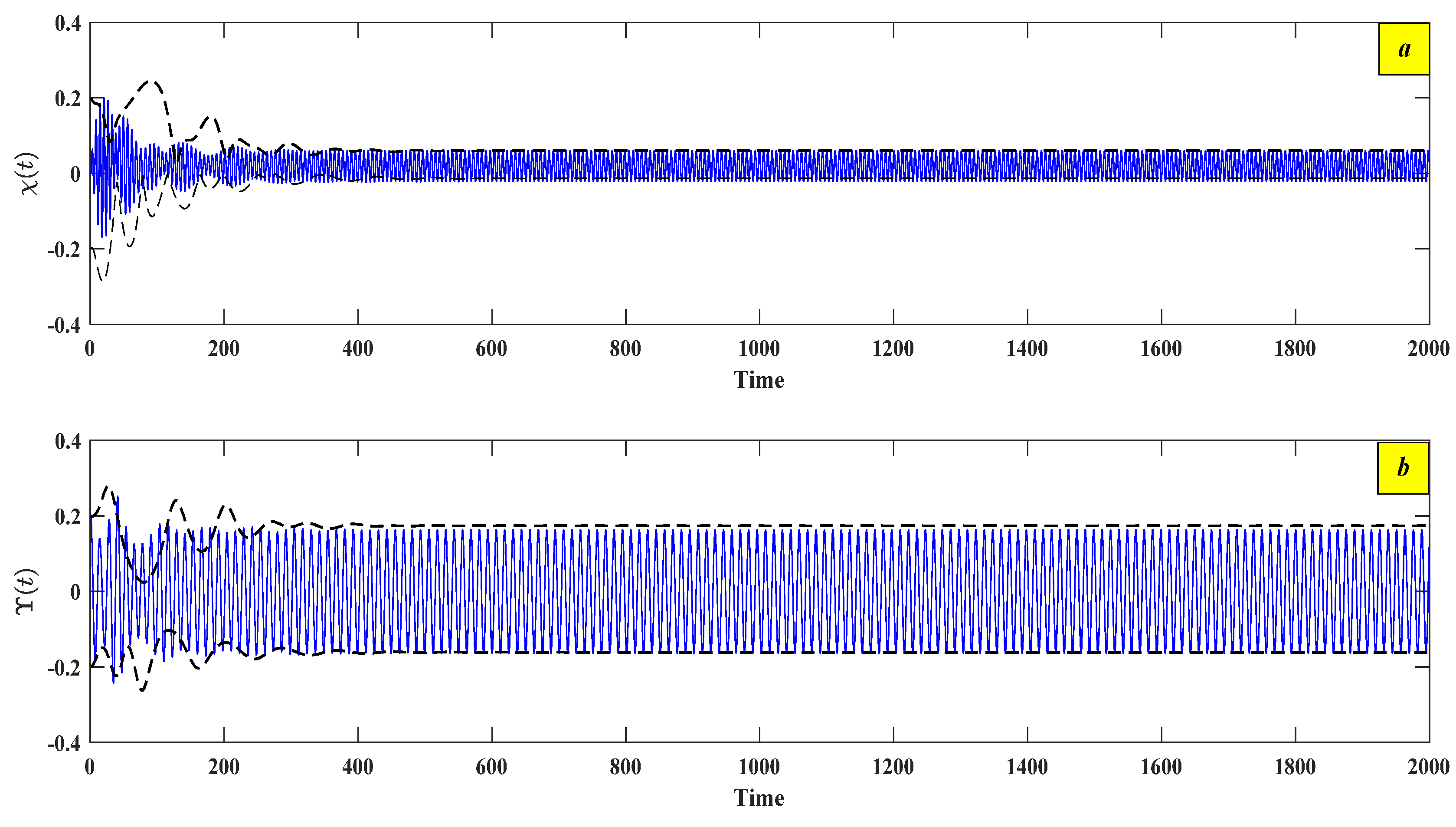
5.1. Numerical Solution with Time History
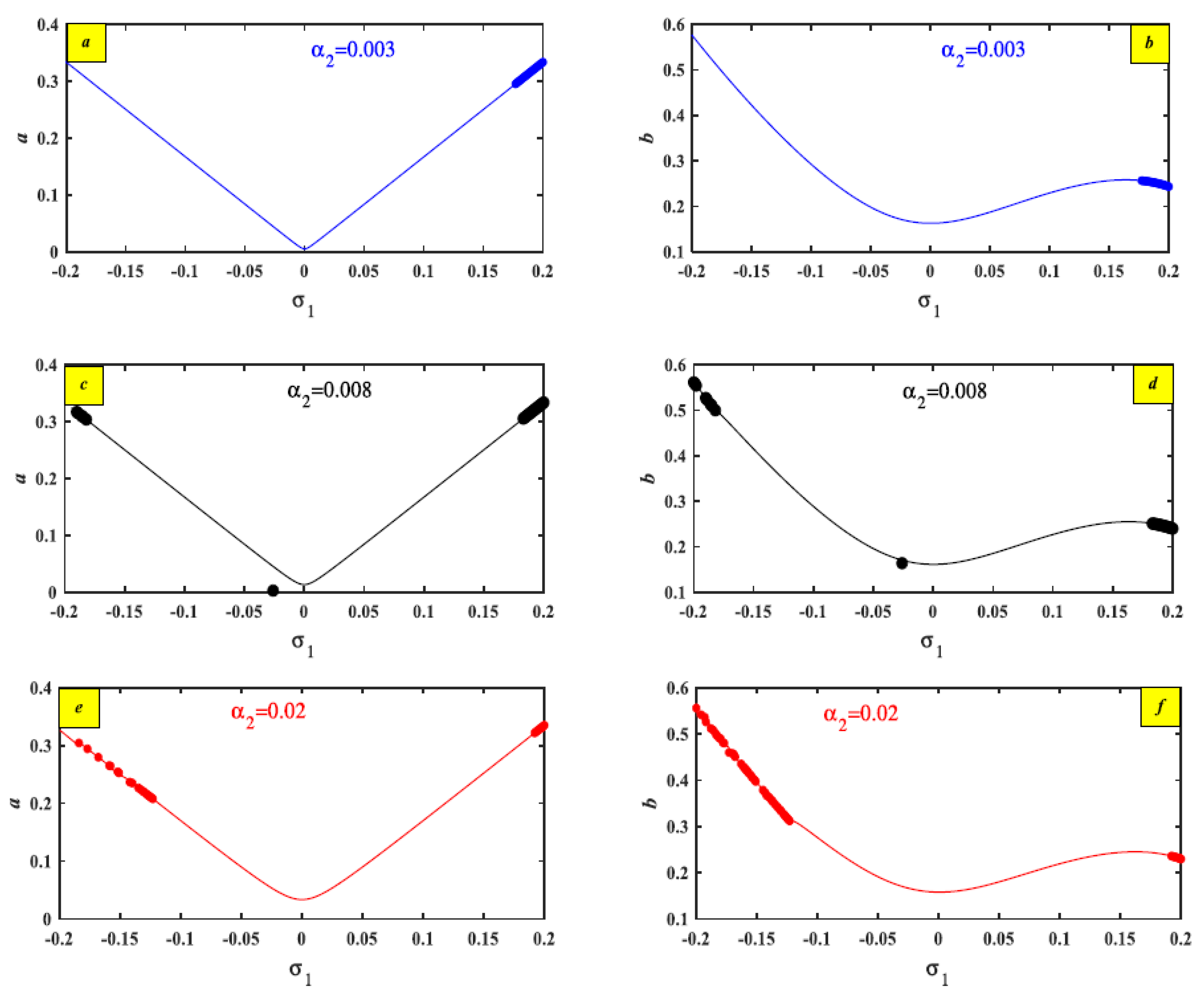
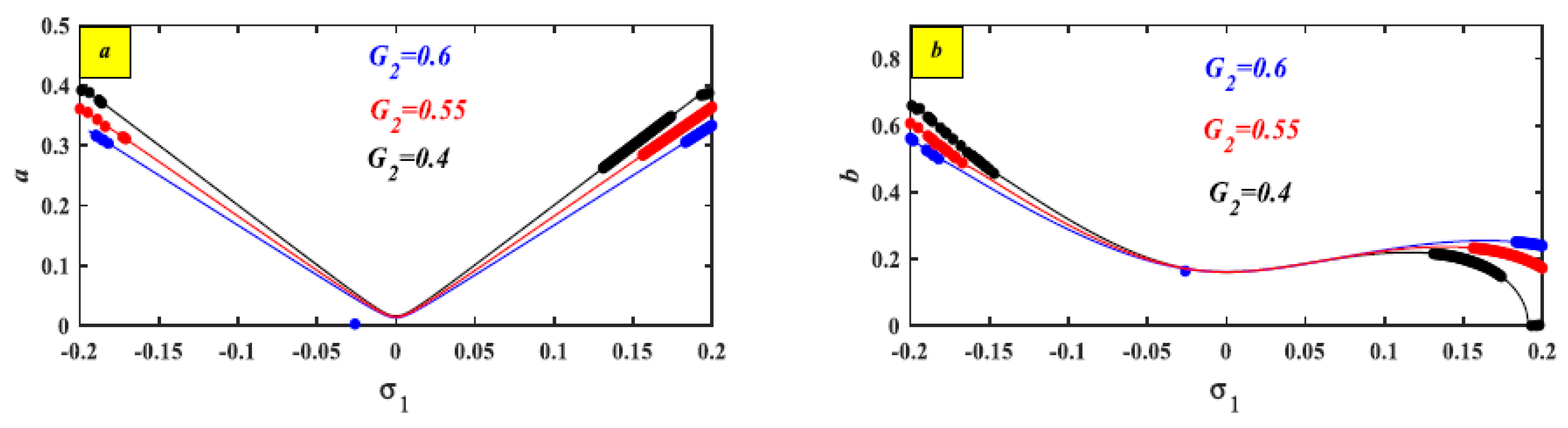
5.2. The Effects of Various Parameters
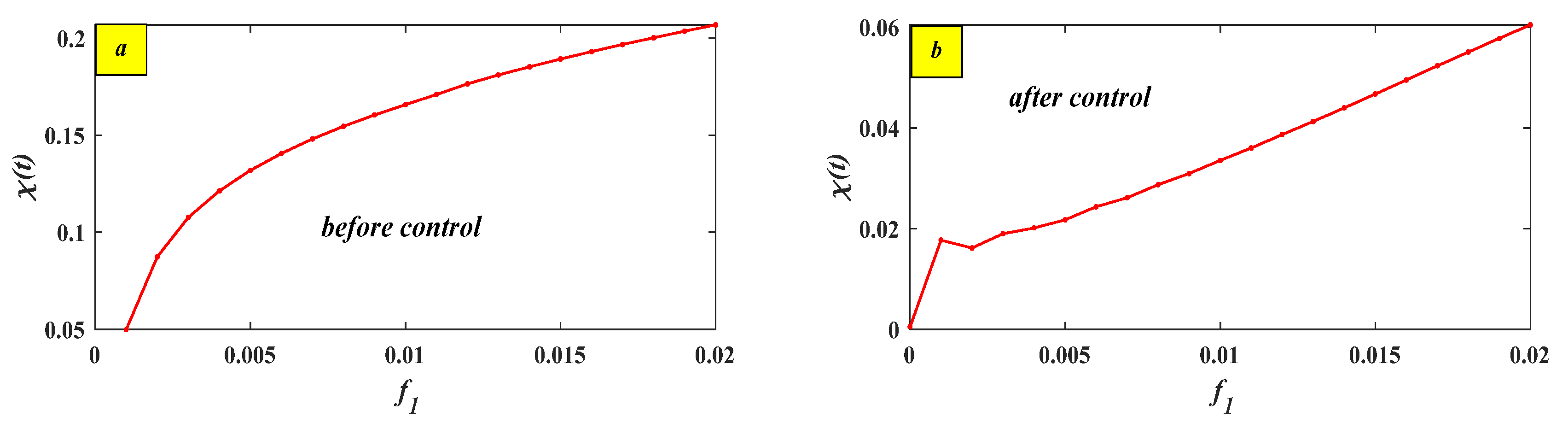
5.3. Effectiveness of External Excitations
5.4. Important Compassion Results on the System
6. Conclusions
- (1)
- Using the NSC technique is the way to drastically reduce the vibration amplitudes of the system.
- (2)
- The unstable region decreased by increasing the excitation external force amplitude in both the system and NSC amplitudes.
- (3)
- The values of the natural frequency increase the steady-state amplitudes of the controller and main system. Furthermore, by raising the damping coefficient values and , the unstable zone grew.
- (4)
- The system’s amplitude fell in the unstable region while the values of the control signal gain increased in the steady state.
- (5)
- The steady scenario for the controller increased, but the unstable region for the system decreased by developing the values of the control feedback signal .
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| The Abbreviations | The Meaning |
| DOF | Degrees of freedom. |
| MSPT | Multiple-scale perturbation. |
| RK-4 | The fourth-order Runge–Kutta method. |
| NSC | Nonlinear saturation controller. |
| VMDO | Van der Pol–Mathieu–Duffing oscillator |
| DE | Differential equation |
| AS | Approximate solution |
| NS | Numerical solution |
| RMSE | Root mean square error |
Appendix A
References
- Xu, J.; Chung, K. Effects of time delayed position feedback on a van der Pol–Duffing oscillator. Phys. D Nonlinear Phenom. 2003, 180, 17–39. [Google Scholar] [CrossRef]
- El-Ganaini, W.A.; Saeed, N.A.; Eissa, M. Positive position feedback (PPF) controller for suppression of nonlinear system vibration. Nonlinear Dyn. 2013, 72, 517–537. [Google Scholar] [CrossRef]
- Wen, S.; Shen, Y.; Li, X.; Yang, S. Dynamical analysis of Mathieu equation with two kinds of van der Pol fractional-order terms. Int. J. Non-Linear Mech. 2016, 84, 130–138. [Google Scholar] [CrossRef]
- Roy, S.; Das, D.; Banerjee, D. Vibrational resonance in a bistable van der Pol-Mathieu–Duffing oscillator. Int. J. Non-Linear Mech. 2021, 135, 103771. [Google Scholar] [CrossRef]
- Ren, Y.; Ma, W. Dynamic Analysis and PD Control in a 12-Pole Active Magnetic Bearing System. Mathematics 2024, 12, 2331. [Google Scholar] [CrossRef]
- Hamed, Y.S.; Alotaibi, H.; El-Zahar, E.R. Nonlinear vibrations analysis and dynamic responses of a vertical conveyor system controlled by a proportional derivative controller. IEEE Access 2020, 8, 119082–119093. [Google Scholar] [CrossRef]
- Jamshidi, R.; Collette, C. Optimal negative derivative feedback controller design for collocated systems based on H2 and H∞ method. Mech. Syst. Signal Process. 2022, 181, 109497. [Google Scholar] [CrossRef]
- Jun, L.; Hongxing, H.; Rongying, S. Saturation-based active absorber for a non-linear plant to a principal external excitation. Mech. Syst. Signal Process. 2007, 21, 1489–1498. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, J.; Zhu, S.; Zhao, H. Bifurcation and chaos detection of a fractional Duffing-van der Pol oscillator with two periodic excitations and distributed time delay. Chaos 2023, 33, 083153. [Google Scholar] [CrossRef]
- Fahsi, A.; Belhaq, M.; Lakrad, F. Suppression of hysteresis in a forced van der Pol-Duffing oscillator. Commun. Nonlinear Sci. Numer. Simul. 2008, 14, 1609–1616. [Google Scholar] [CrossRef]
- Yaman, M. Direct and parametric excitation of a nonlinear cantilever beam of varying orientation with time-delay state feedback. J. Sound Vib. 2009, 324, 892–902. [Google Scholar] [CrossRef]
- Alhazza, K.A.; Majeed, M.A. Free vibrations control of a cantilever beam using combined time delay feedback. J. Vib. Control 2012, 18, 609–621. [Google Scholar] [CrossRef]
- Cai, G.P.; Yang, S.X. A discrete optimal control method for a flexible cantilever beam with time delay. J. Vib. Control 2006, 12, 509–526. [Google Scholar] [CrossRef]
- Mirafzal, S.H.; Khorasani, A.M.; Ghasemi, A.H. Optimizing time delay feedback for active vibration control of a cantilever beam using a genetic algorithm. J. Vib. Control 2016, 22, 4047–4061. [Google Scholar] [CrossRef]
- Kashchenko, S. Van der Pol equation with a large feedback delay. Mathematics 2023, 11, 1301. [Google Scholar] [CrossRef]
- Temnaya, O.S.; Safin, A.R.; Kravchenko, O.V.; Nikitov, S.A. Influence of nonlinearity on an exceptional point in a system of coupled duffing oscillators. J. Commun. Technol. Electron. 2023, 68, 979–982. [Google Scholar] [CrossRef]
- Kandil, A.; Hamed, Y.S.; Abualnaja, K.M.; Awrejcewicz, J.; Bednarek, M. 1/3 order subharmonic resonance control of a mass damper-spring model via cubic-position negative-velocity feedback. Symmetry 2022, 14, 685. [Google Scholar] [CrossRef]
- Ramini, A.H.; Hajjaj, A.Z.; Younis, M.I. Tunable resonators for nonlinear modal interactions. Sci. Rep. 2016, 6, 34717. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Li, X.; Hua, H. Active nonlinear saturation-based control for suppressing the free vibration of a self-excited plant. Commun. Nonlinear Sci. Numer. Simulation 2010, 15, 1071–1079. [Google Scholar] [CrossRef]
- Warminski, J.; Bochenski, M.; Jarzyna, W.; Filipek, P.; Augustyniak, M. Active suppression of nonlinear composite beam vibrations by selected control algorithms. Commun. Nonlinear Sci. Numer. Simul. 2011, 16, 2237–2248. [Google Scholar] [CrossRef]
- Nayfeh, A.H.; Chin, C.M.; Pratt, J. Perturbation methods in nonlinear dynamics applications to machining dynamics. J. Manuf. Sci. Eng. 1997, 119, 485–493. [Google Scholar] [CrossRef]
- Mickens, R.E. Oscillations in Planar Dynamic Systems; World Scientific: Singapore, 1996; Volume 37. [Google Scholar] [CrossRef]
- Moatimid, G.M. Stability Analysis of a Parametric Duffing Oscillator. J. Eng. Mech. 2020, 146, 05020001. [Google Scholar] [CrossRef]
- Barron, M.A. Stability of a ring of coupled van der Pol oscillators with non-uniform distribution of the coupling parameter. J. Appl. Res. Technol. 2016, 14, 62–66. [Google Scholar] [CrossRef]
- Orlov, V.; Chichurin, A. The influence of the perturbation of the initial data on the analytic approximate solution of the Van der Pol equation in the complex domain. Symmetry 2023, 15, 1200. [Google Scholar] [CrossRef]
- Kakou, P.; Gupta, S.K.; Barry, O. A nonlinear analysis of a Duffing oscillator with a nonlinear electromagnetic vibration absorber-inerter for concurrent vibration mitigation and energy harvesting. Nonlinear Dyn. 2024, 112, 5847–5862. [Google Scholar] [CrossRef]
- Bauomy, H.S.; EL-Sayed, A.T. Mixed controller (IRC+NSC) involved in the harmonic vibration response cantilever beam model. Meas. Control 2020, 53, 1954–1967. [Google Scholar] [CrossRef]
- Bauomy, H.S.; EL-Sayed, A.T. Act of nonlinear proportional derivative controller for MFC laminated shell. Phys. Scr. 2020, 95, 095210. [Google Scholar] [CrossRef]
- Bauomy, H.S.; EL-Sayed, A.T. A new six-degrees of freedom model designed for a composite plate through PPF controllers. Appl. Math. Model. 2020, 88, 604–630. [Google Scholar] [CrossRef]
- Bauomy, H.S. New controller (NPDCVF) outcome of FG cylindrical shell structure. Alex. Eng. J. 2022, 61, 1779–1801. [Google Scholar] [CrossRef]
- Binatari, N.; van Horssen, W.T.; Verstraten, P.; Adi-Kusumo, F.; Aryati, L. On the multiple time-scales perturbation method for differential-delay equations. Nonlinear Dyn. 2024, 112, 8431–8451. [Google Scholar] [CrossRef]
- Kevorkian, J.; Cole, J.D. The Method of Multiple Scales for Ordinary Differential Equations. In Multiple Scale and Singular Perturbation Methods. Applied Mathematical Sciences; Springer: New York, NY, USA, 1996; Volume 114. [Google Scholar] [CrossRef]
- Nayfeh, A.H. Perturbation Methods; Wiley: New York, NY, USA, 2000. [Google Scholar] [CrossRef]
- Dukkipati, R.V. Solving Vibration Analysis Problems Using MATLAB; New Age International Pvt Ltd. Publishers: New Delhi, India, 2007. [Google Scholar]
- Alluhydan, K.; Amer, Y.A.; EL-Sayed, A.T.; Agwa, M.M. Stability and Control of Car Dynamics with a Quarter Model via a Novel Simple Harmonic Hump under External Force. Mathematics 2024, 12, 3046. [Google Scholar] [CrossRef]
- Amer, T.S.; Bahnasy, T.A.; Abosheiaha, H.F.; Elameer, A.S.; Almahalawy, A. The stability analysis of a dynamical system equipped with a piezoelectric energy harvester device near resonance. J. Low Freq. Noise Vib. Act. Control 2025, 44, 382–410. [Google Scholar] [CrossRef]
- Arena, A.; Lepidi, M. Nonlinear wave propagation in a two-dimensional lattice model of textile metamaterials. Nonlinear Dyn. 2025, 1–22. [Google Scholar] [CrossRef]
- Razzaq, M.A.; Rocha, R.T.; Tian, Y.; Towfighian, S.; Masri, S.F.; Younis, M.I. Nonparametric identification of a MEMS resonator actuated by levitation forces. Int. J. Non-Linear Mech. 2024, 160, 104633. [Google Scholar] [CrossRef]
- Erturk, V.S.; Rath, B.; Al-Khader, T.M.; Alshaikh, N.; Mallick, P.; Asad, J. Two-dimensional coupled asymmetric van der Pol oscillator. Eur. J. Pure Appl. Math. 2024, 17, 1254–1264. [Google Scholar] [CrossRef]
- Abohamer, M.K.; Amer, T.S.; Galal, A.A.; Darweesh, M.A.; Arab, A.; Bahnasy, T.A. On chaotic behavior, stability analysis, and vibration control of the van der Pol–Mathieu–Duffing oscillator under parametric force and resonance. J. Low Freq. Noise Vib. Act. Control 2025, 1–17. [Google Scholar] [CrossRef]
- Cui, W.; Zhao, L.; Ge, Y.; Xu, K. A generalized van der Pol nonlinear model of vortex-induced vibrations of bridge decks with multistability. Nonlinear Dyn. 2024, 112, 259–272. [Google Scholar] [CrossRef]
- Elnady, A.O.; Newir, A.; Ibrahim, M.A. Novel approach for solving higher-order differential equations with applications to the Van der Pol and Van der Pol–Duffing equations. Beni-Suef Univ. J. Basic Appl. Sci. 2024, 13, 29. [Google Scholar] [CrossRef]
- Herişanu, N.; Marinca, V. An iteration procedure with application to Van der Pol oscillator. Int. J. Nonlinear Sci. Numer. Simul. 2009, 10, 353–362. [Google Scholar] [CrossRef]
- Ali, A.H.; Amir, M.; Rahman, J.U.; Raza, A.; Arif, G.E. Design of Morlet Wavelet Neural Networks for Solving the Nonlinear Van der Pol–Mathieu–Duffing Oscillator Model. Computers 2025, 14, 14. [Google Scholar] [CrossRef]
- Zhao, F.; Ma, X.; Cao, S. Periodic bursting oscillations in a hybrid Rayleigh–Van der Pol–Duffing oscillator. Nonlinear Dyn. 2023, 111, 2263–2279. [Google Scholar] [CrossRef]








| Symbol | Description | Value 1 (Basic) | Value 2 | Value 3 | Figures |
|---|---|---|---|---|---|
| Excitation force | 0.02 | 0.017 | 0.06 | Figure 5 | |
| Damping coefficient of the system | 0.04 | 0.008 | 0.08 | Figure 6 | |
| Damping coefficient | 0.008 | 0.02 | 0.003 | Figure 7 | |
| Control gain | 1.5 | 0.64 | 2.6 | Figure 8 | |
| Feedback control gain | 0.6 | 0.55 | 0.4 | Figure 9 | |
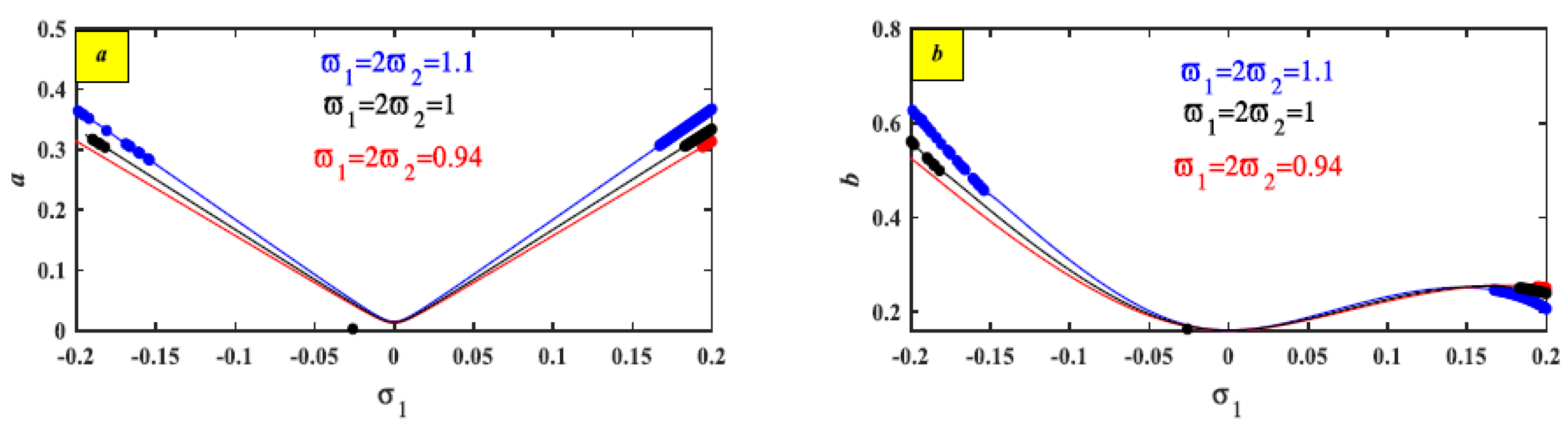
| Nature frequency | 1 | 1.1 | 0.94 | Figure 10 | |
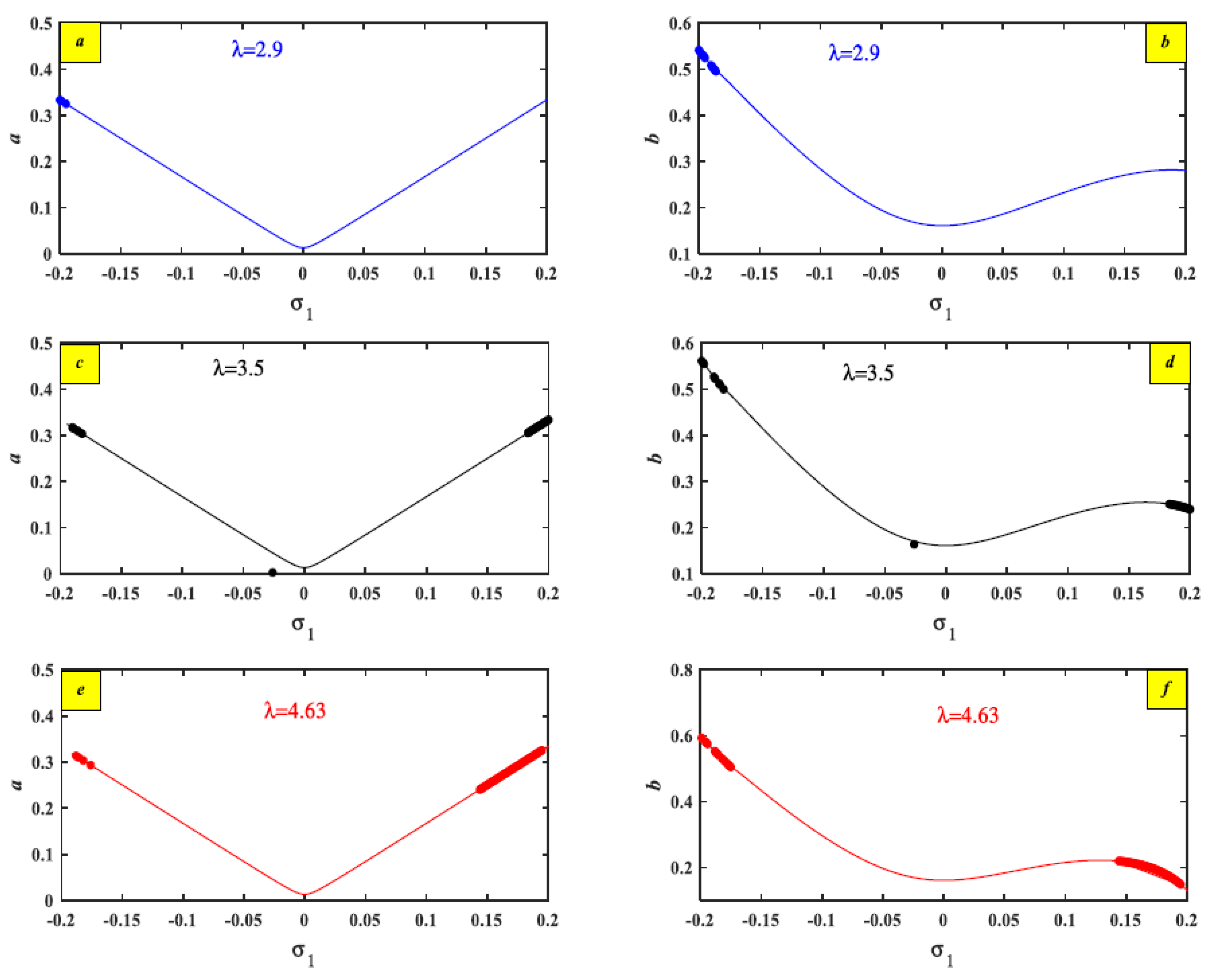
| Nonlinear term | 3.5 | 2.9 | 4.63 | Figure 11 | |
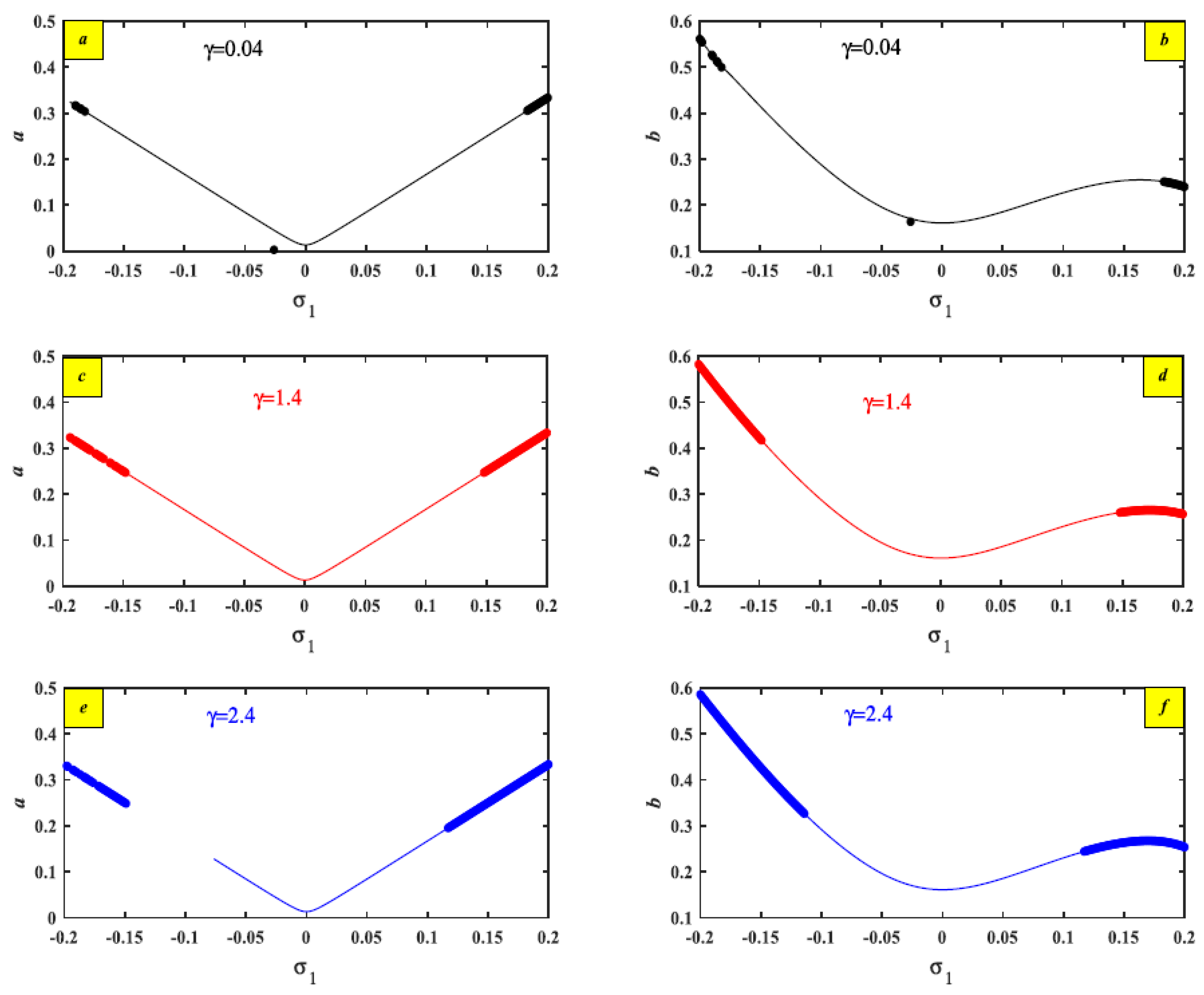
| Nonlinear term | 0.04 | 1.4 | 2.4 | Figure 12 | |
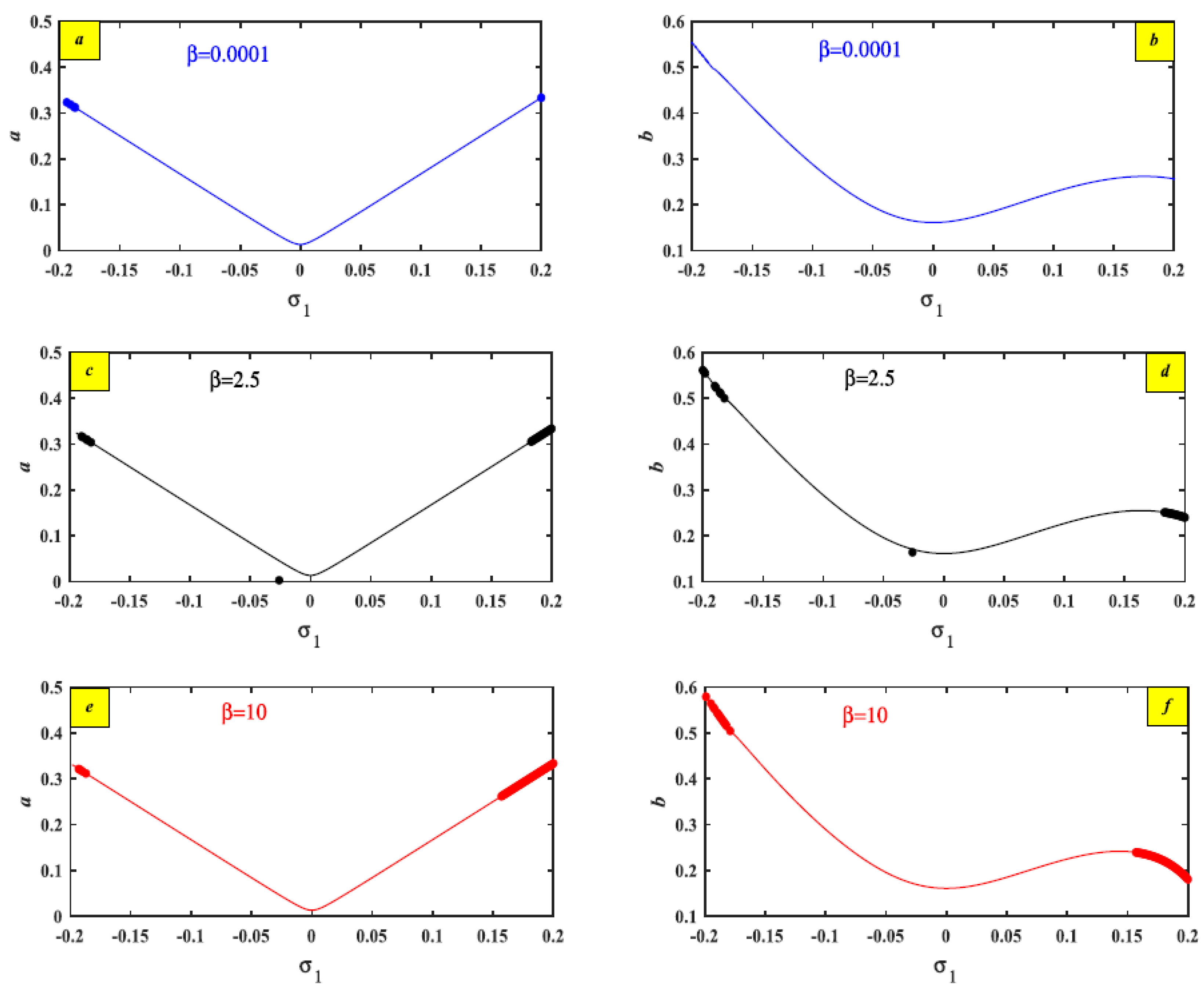
| Nonlinear term | 2.5 | 0.0001 | 10 | Figure 13 | |
| Detuning parameter | 0 | 0.05 | −0.03 | Figure 14 |
| With NSC Control | Without Control | |||||
|---|---|---|---|---|---|---|
| T | AS | NS | AS | NS | ||
| 800 | 0.0546 | 0.04895 | 0.0057 | 0.1472 | 0.1481 | 0.0009 |
| 850 | 0.0163 | 0.02103 | 0.0047 | 0.1217 | 0.1481 | 0.0264 |
| 900 | 0.0711 | 0.07972 | 0.0086 | 0.1891 | 0.1763 | 0.0128 |
| 950 | 0.065 | 0.06736 | 0.0024 | 0.1262 | 0.1279 | 0.0017 |
| 1000 | 0.0552 | 0.05149 | 0.0037 | 0.1560 | 0.1498 | 0.0062 |
| 1050 | 0.0575 | 0.06017 | 0.0027 | 0.1866 | 0.1873 | 0.0007 |
| 1100 | 0.0594 | 0.05239 | 0.0070 | 0.2043 | 0.2317 | 0.0274 |
| 1150 | 0.0568 | 0.05812 | 0.0013 | 0.2058 | 0.2113 | 0.0055 |
| 1200 | 0.0505 | 0.06102 | 0.0105 | 0.1928 | 0.1897 | 0.0031 |
| 1250 | 0.0417 | 0.05016 | 0.0085 | 0.1664 | 0.1672 | 0.0008 |
| 1300 | 0.0318 | 0.03214 | 0.0003 | 0.1287 | 0.1297 | 0.0010 |
| 1350 | 0.0218 | 0.02316 | 0.0014 | 0.1822 | 0.1831 | 0.0009 |
| 1400 | 0.0111 | 0.01213 | 0.0010 | 0.2301 | 0.2325 | 0.0024 |
| 1450 | 0.0086 | 0.01003 | 0.0014 | 0.2241 | 0.2226 | 0.0015 |
| 1500 | 0.0061 | 0.00832 | 0.0022 | 0.1769 | 0.1783 | 0.0014 |
| RMSE = 0.0052 | RMSE = 0.0107 | |||||
| No. | Comparison Items | The Current Study | The Examined Work in [15] | The Investigated Work in [40] |
|---|---|---|---|---|
| 1 | DOF | 1 DOF | 1 DOF | 1 DOF |
| 2 | AS | AS are acquired using MSPT | The nonlocal dynamics procedure with a large delay | The AS are obtained by MSPT |
| 3 | Resonance case | Simultaneous primary and internal | Not investigated | Subharmonic |
| 4 | NS | NS are obtained from RK-4 | The numerical simulation is not achieved | The NS are achieved |
| 5 | Stability area | The stability and instability areas are investigated according to the amplitude’s resonance curves | Amplitude’s resonance curves are not presented | The stability boundaries are drawn |
| 6 | Parameters’ effect | The parameters affecting amplitudes are plotted | Not mapped out | |
| 7 | Feedback control | NSC control is used | Does not exist | Displacement–velocity feedback controller is used |
| 8 | Diagram of the time history of a solution and phase plan | The time history and phase plan are drawn for all cases with and without control | Not presented | Not graphed |
| 9 | Controller effectiveness | The controller’s effectiveness is investigated | Does not exist | Not investigated |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
EL-Sayed, A.T.; Hussein, R.K.; Amer, Y.A.; Mahmoud, S.S.; Abu Alrub, S.; Bahnasy, T.A. Vibration Reduction and Stability Investigation of Van Der Pol–Mathieu–Duffing Oscillator via the Nonlinear Saturation Controller. Actuators 2025, 14, 427. https://doi.org/10.3390/act14090427
EL-Sayed AT, Hussein RK, Amer YA, Mahmoud SS, Abu Alrub S, Bahnasy TA. Vibration Reduction and Stability Investigation of Van Der Pol–Mathieu–Duffing Oscillator via the Nonlinear Saturation Controller. Actuators. 2025; 14(9):427. https://doi.org/10.3390/act14090427
Chicago/Turabian StyleEL-Sayed, Ashraf Taha, Rageh K. Hussein, Yasser A. Amer, Sara S. Mahmoud, Sharif Abu Alrub, and Taher A. Bahnasy. 2025. "Vibration Reduction and Stability Investigation of Van Der Pol–Mathieu–Duffing Oscillator via the Nonlinear Saturation Controller" Actuators 14, no. 9: 427. https://doi.org/10.3390/act14090427
APA StyleEL-Sayed, A. T., Hussein, R. K., Amer, Y. A., Mahmoud, S. S., Abu Alrub, S., & Bahnasy, T. A. (2025). Vibration Reduction and Stability Investigation of Van Der Pol–Mathieu–Duffing Oscillator via the Nonlinear Saturation Controller. Actuators, 14(9), 427. https://doi.org/10.3390/act14090427








