Nonlinearity Characterization of Flexible Hinge Piezoelectric Stages Under Dynamic Preload via a Force-Dependent Prandtl–Ishlinskii Model with a Force-Analyzed Finite Element Method
Abstract
1. Introduction
2. The FPI-FFEM Method for Nonlinearity Characterization
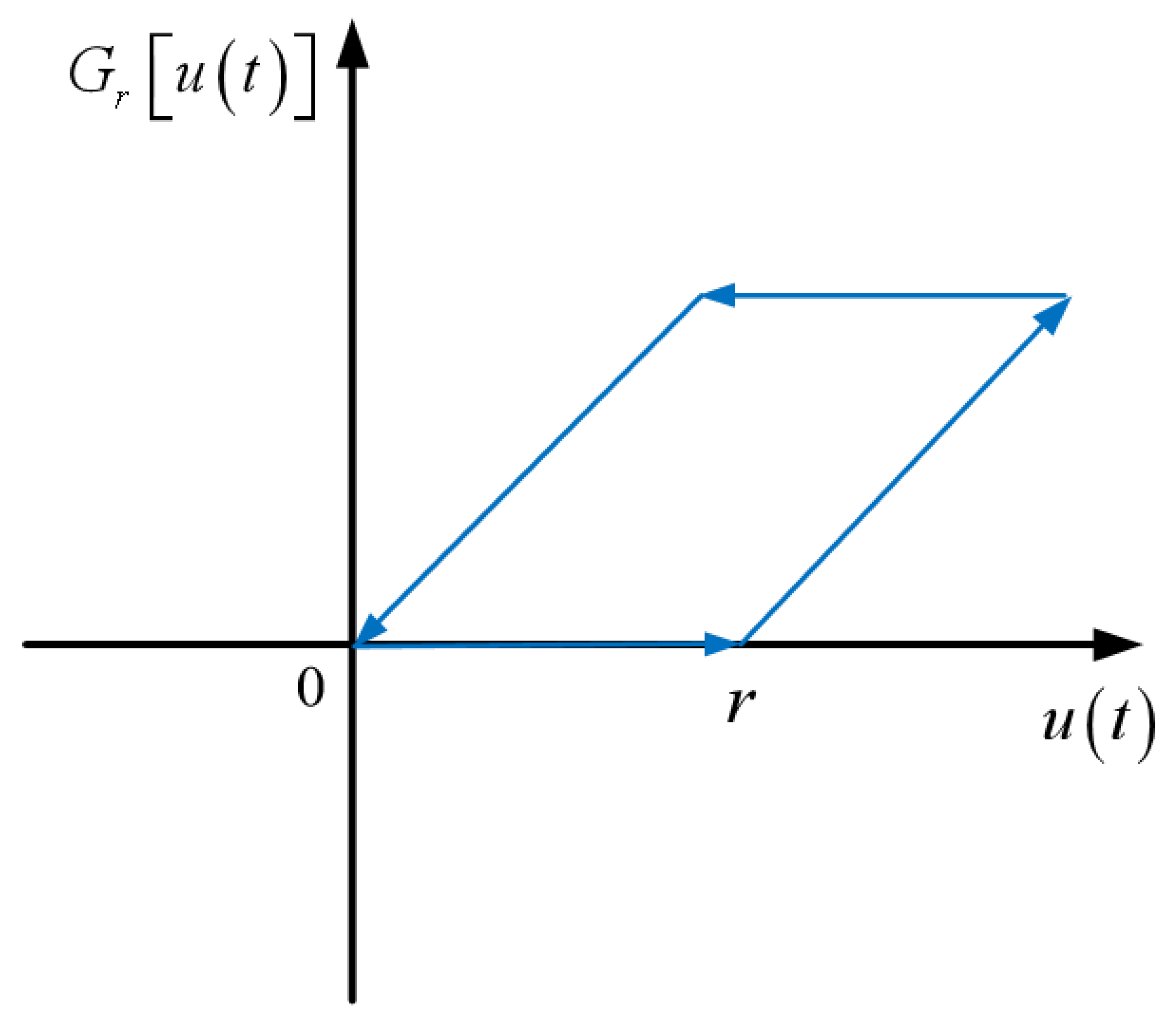
2.1. The Classical Prandtl–Ishlinskii Model
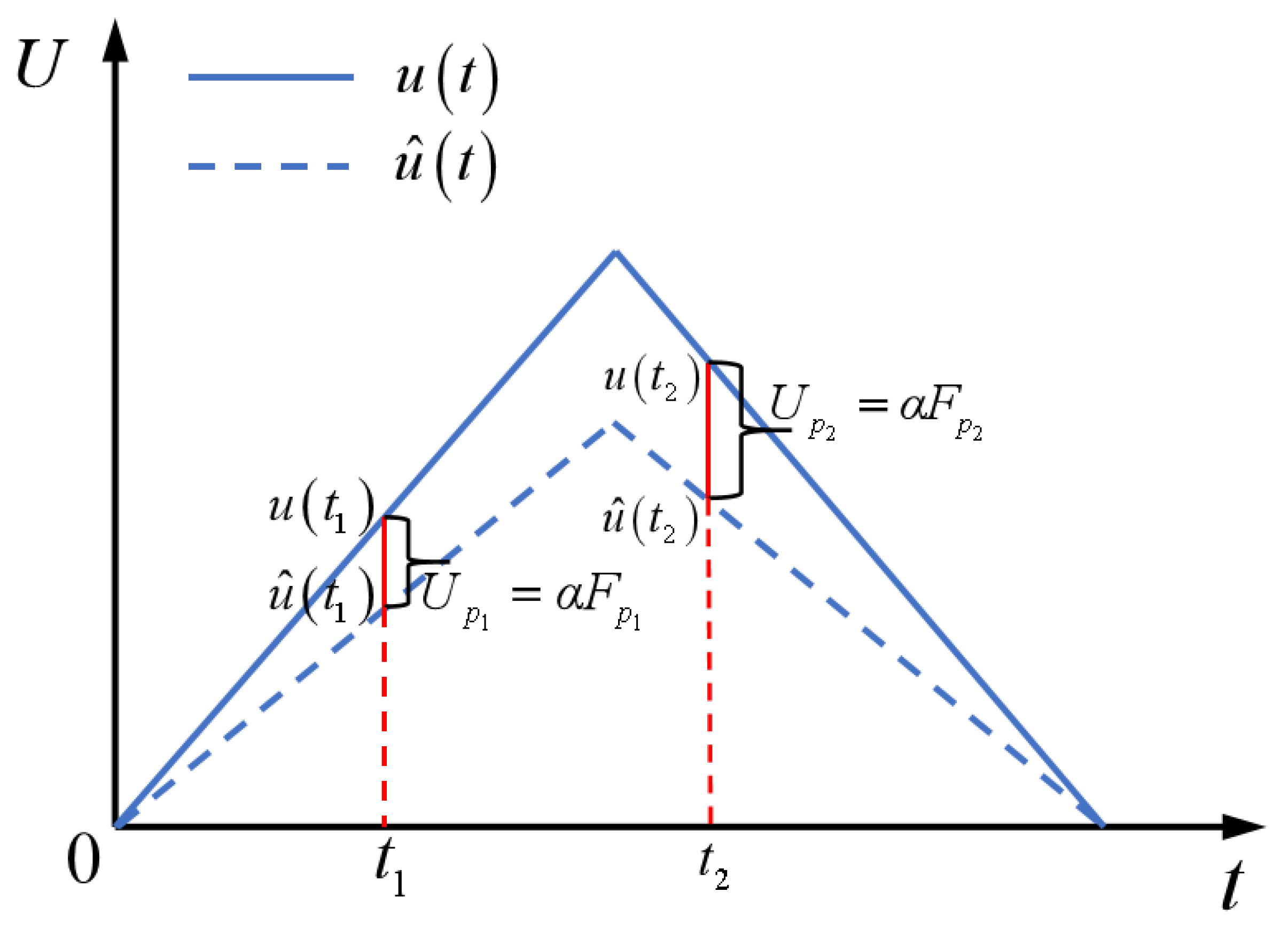
2.2. Formulation of the Force Prandtl–Ishlinskii (FPI) Model
2.3. Integration with the Force-Analyzed Finite Element Method (FFEM)
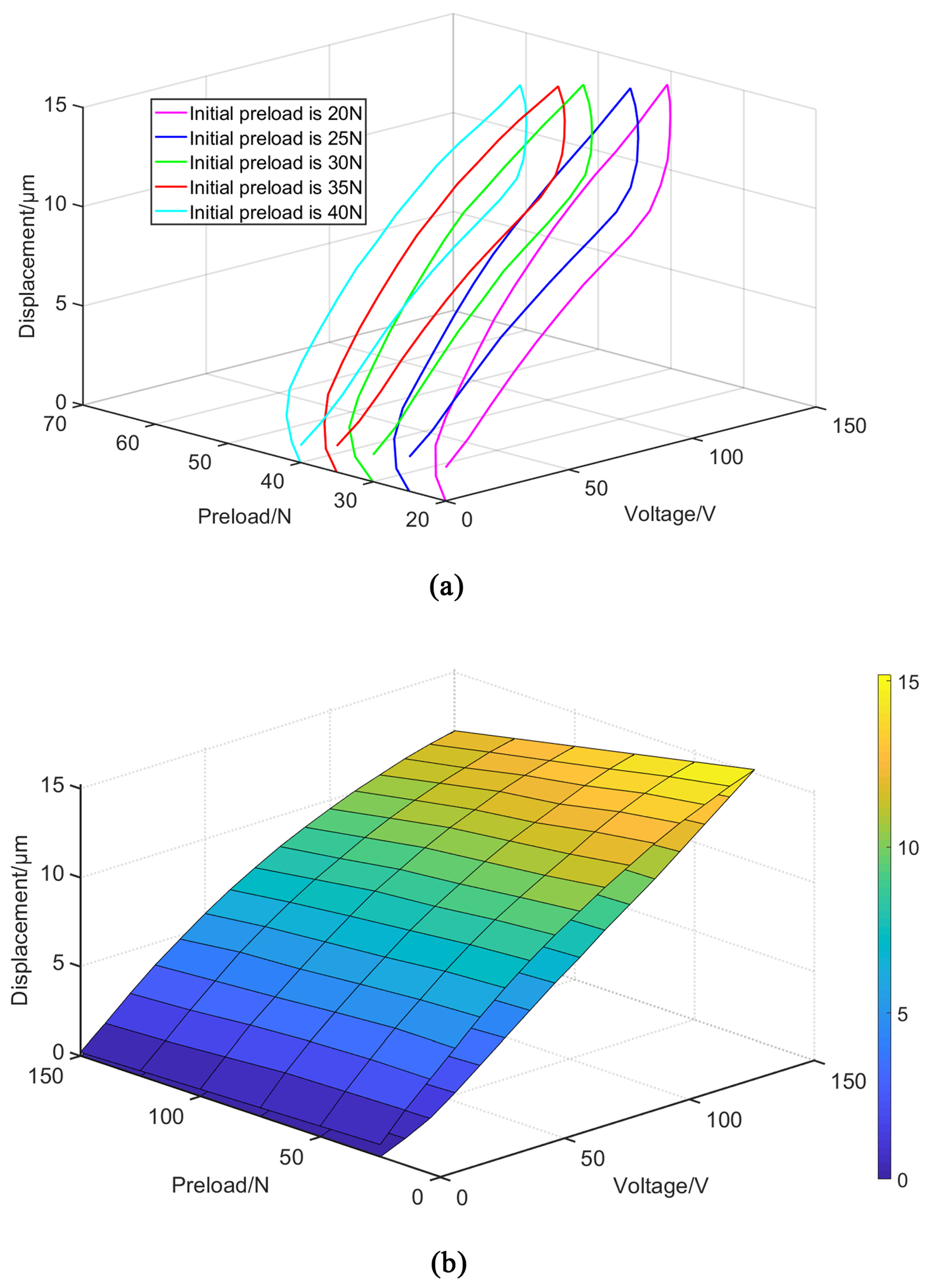
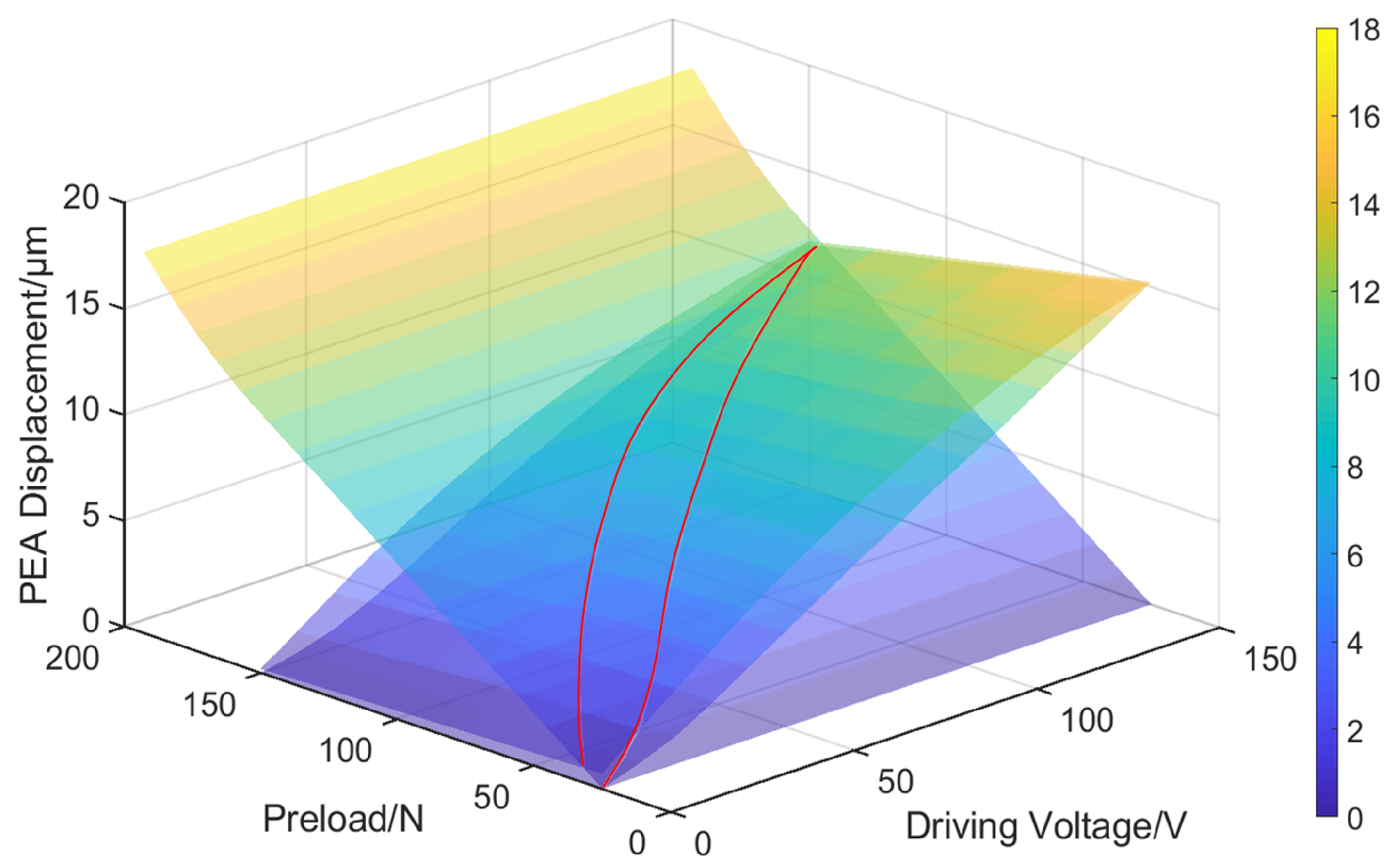
- Quantification of Dynamic Preload: The principal function of the FFEM is to quantify with high precision the preload force exerted on the PEA as a function of its displacement. A digital twin of the FHPS is created, wherein the PEA’s expansion is simulated by applying a series of prescribed, incremental displacements to its interfacing surfaces with the flexible hinge. For each displacement increment, a static structural analysis is performed to compute the consequent reaction force. This systematic process generates a high-fidelity dataset that defines the functional relationship , thereby mapping the PEA’s stroke to the corresponding preload it experiences. This simulated data provides the indispensable force input for calculating the effective voltage within the FPI model.
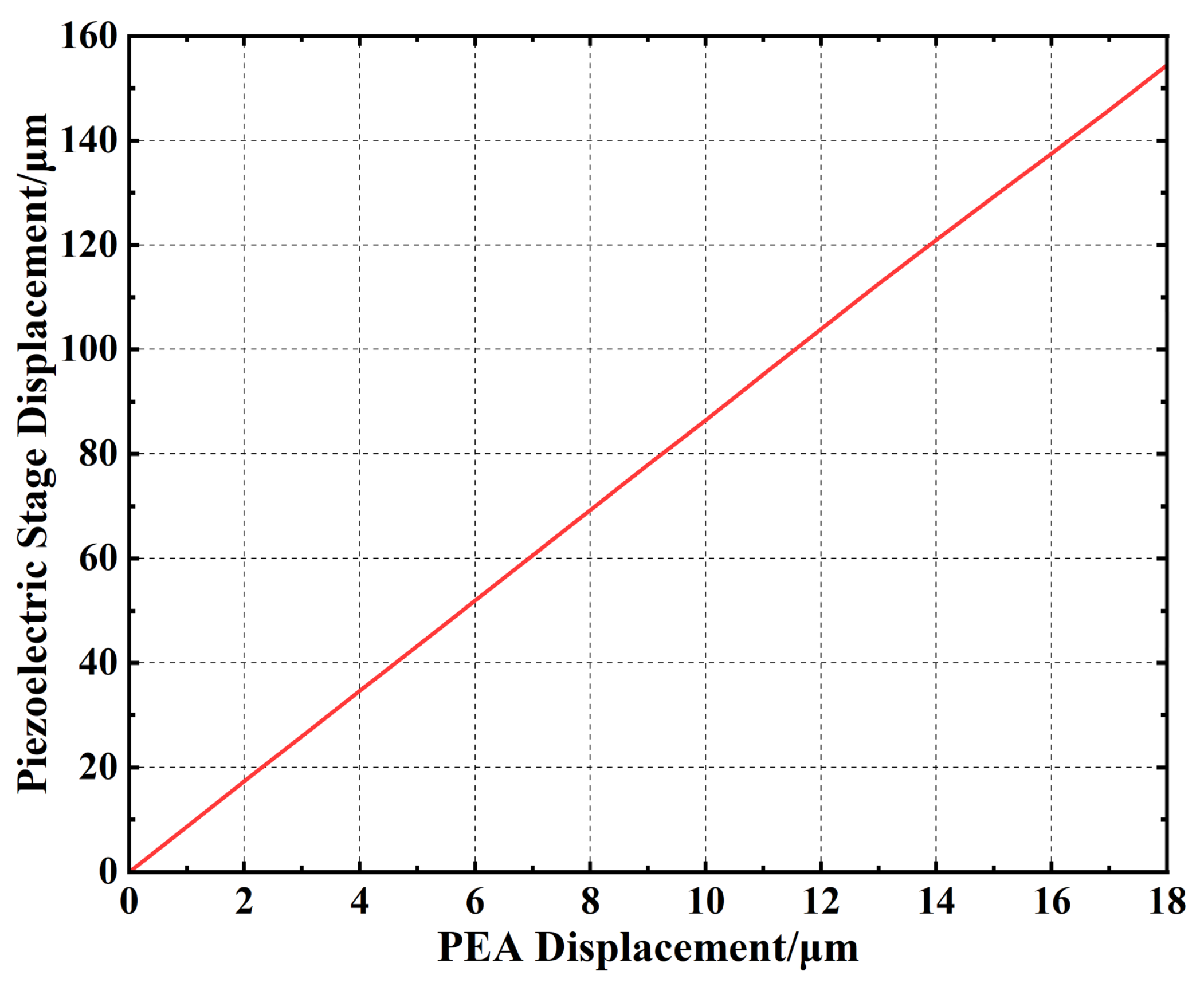
- Kinematic Characterization of the System: Concurrently, the FFEM simulation provides a rigorous characterization of the stage’s kinematics. For the identical set of prescribed PEA displacements, the simulation computes the resultant output displacement of the positioning platform. This establishes the system’s amplification ratio, , capturing nonlinearities that are often intractable to determine analytically through simplified geometric models.
3. Experiment and Discussion
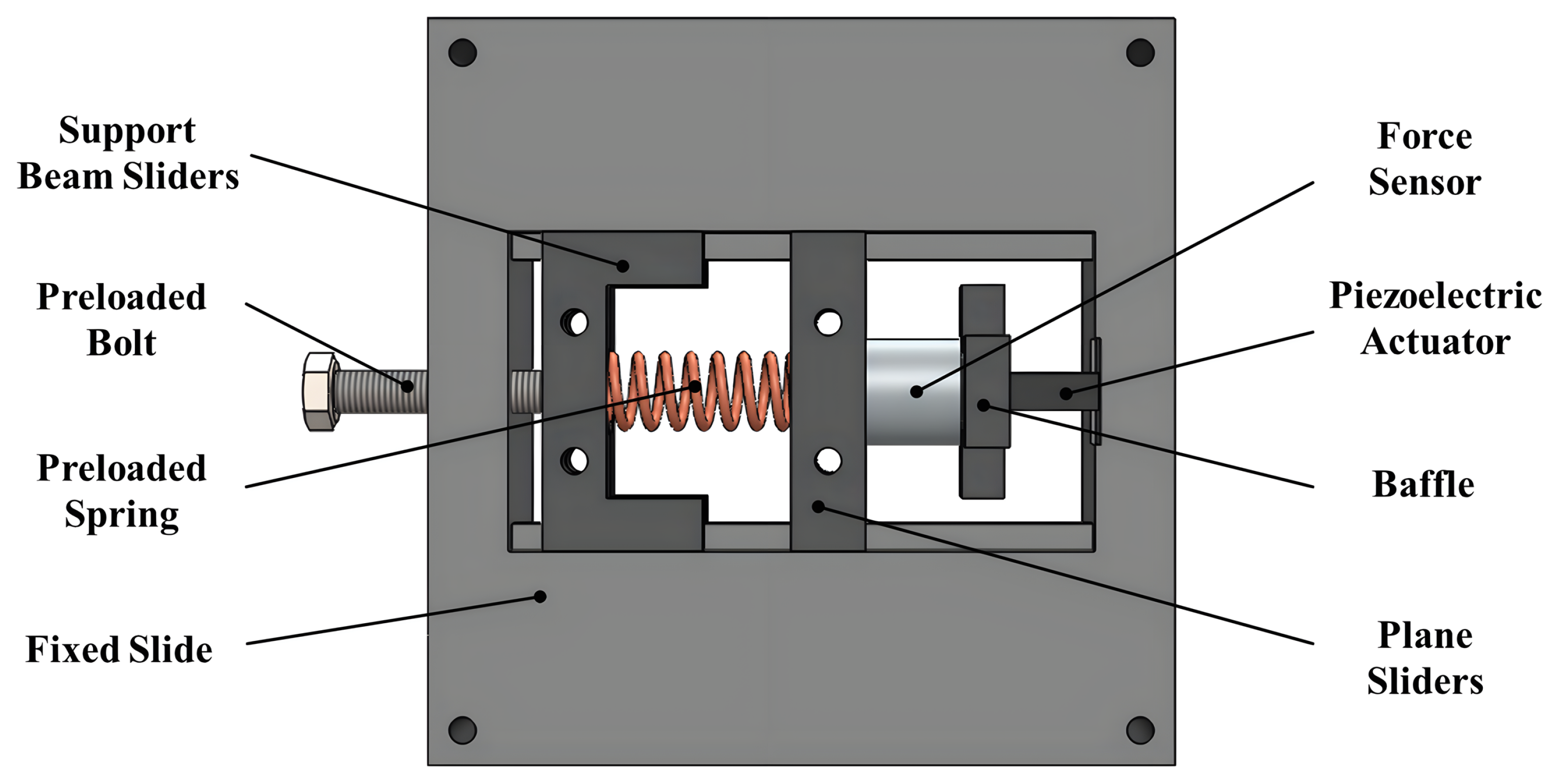
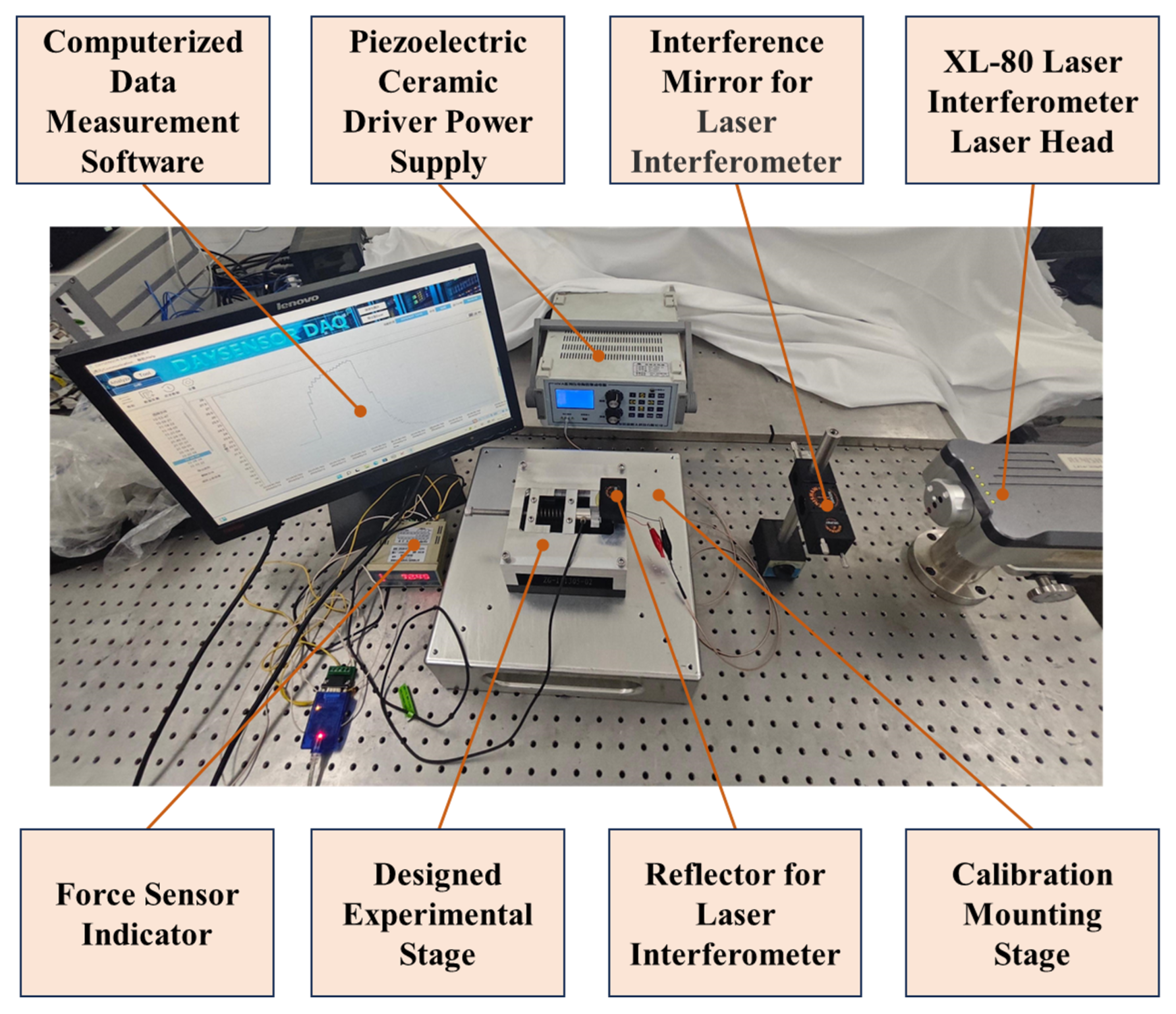
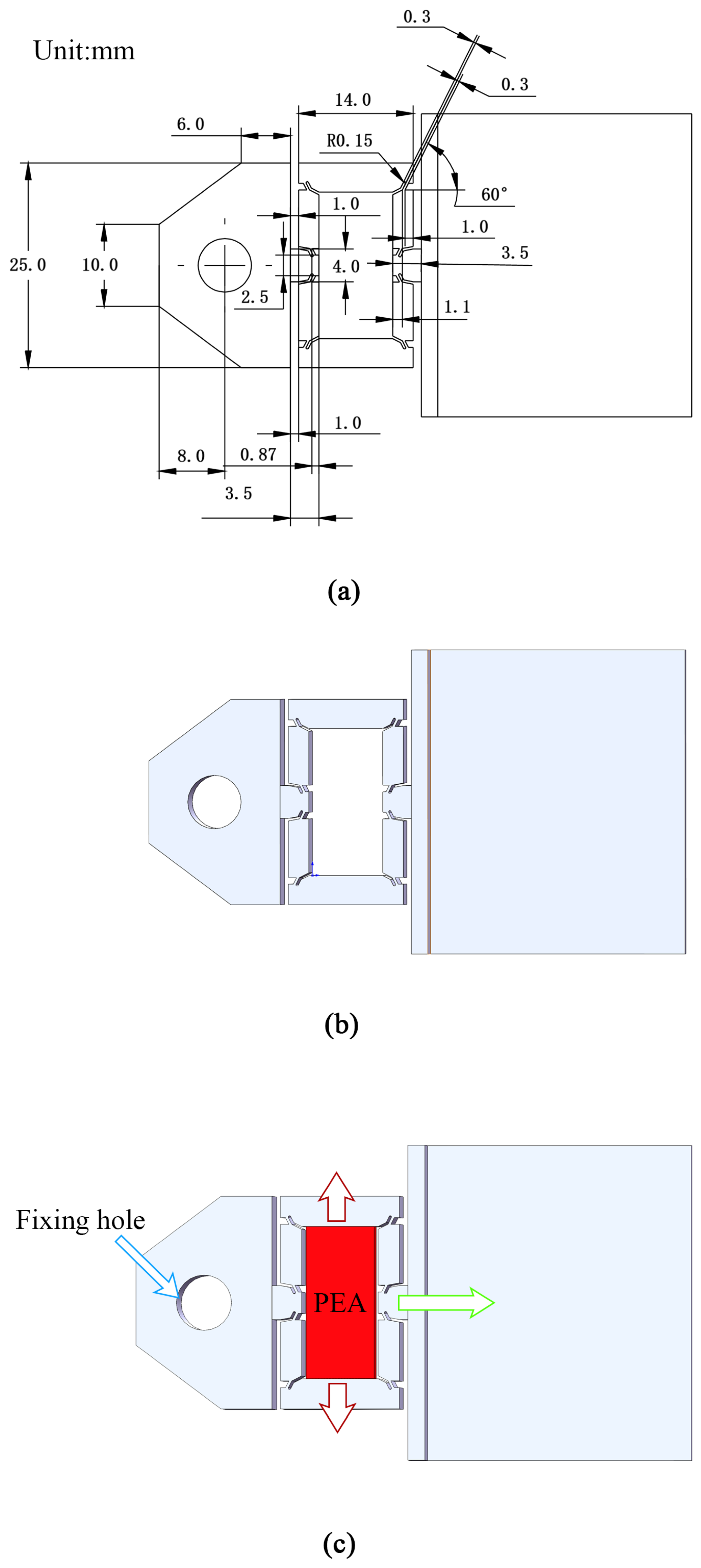
3.1. Design of the Measurable Preload Experimental Setup
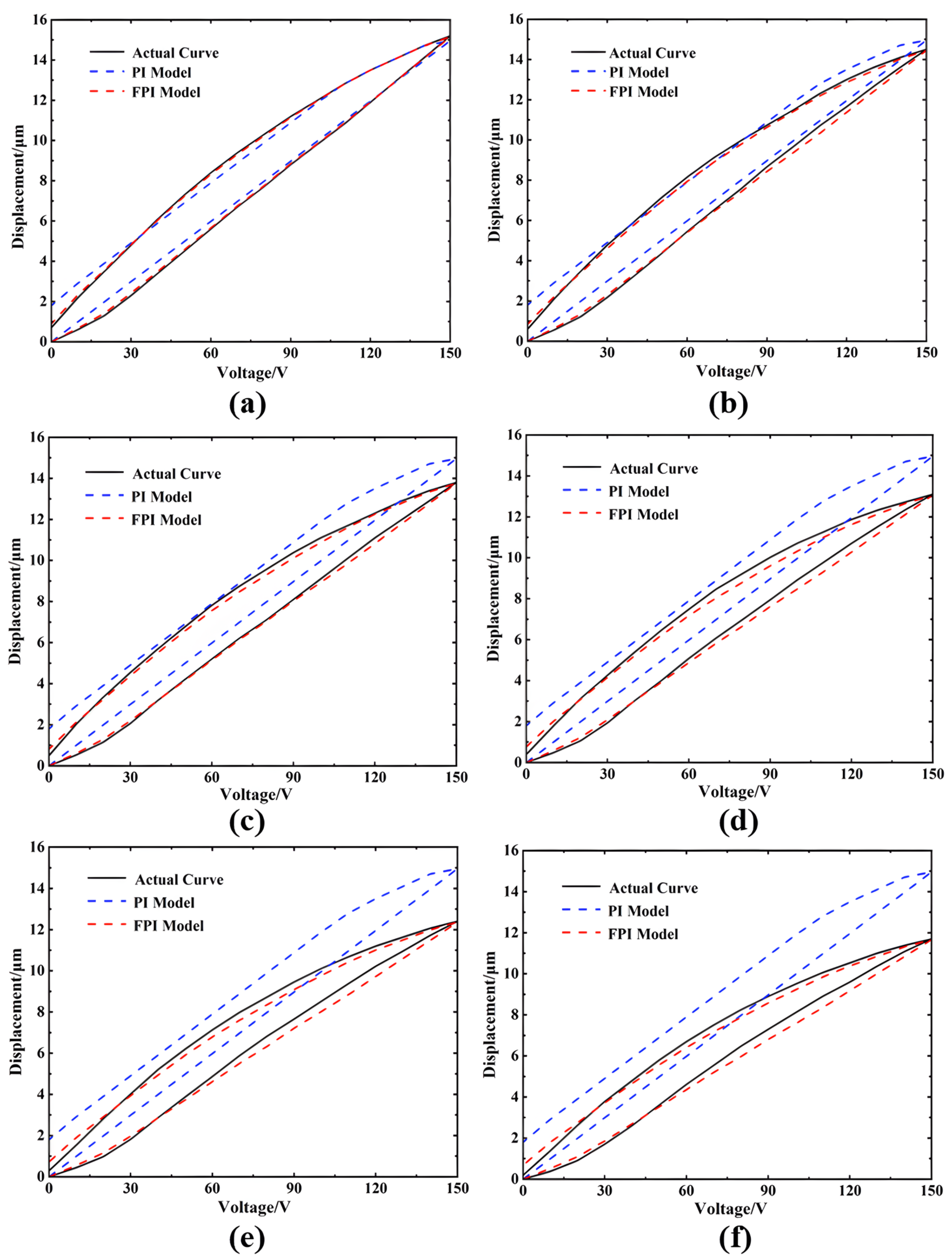
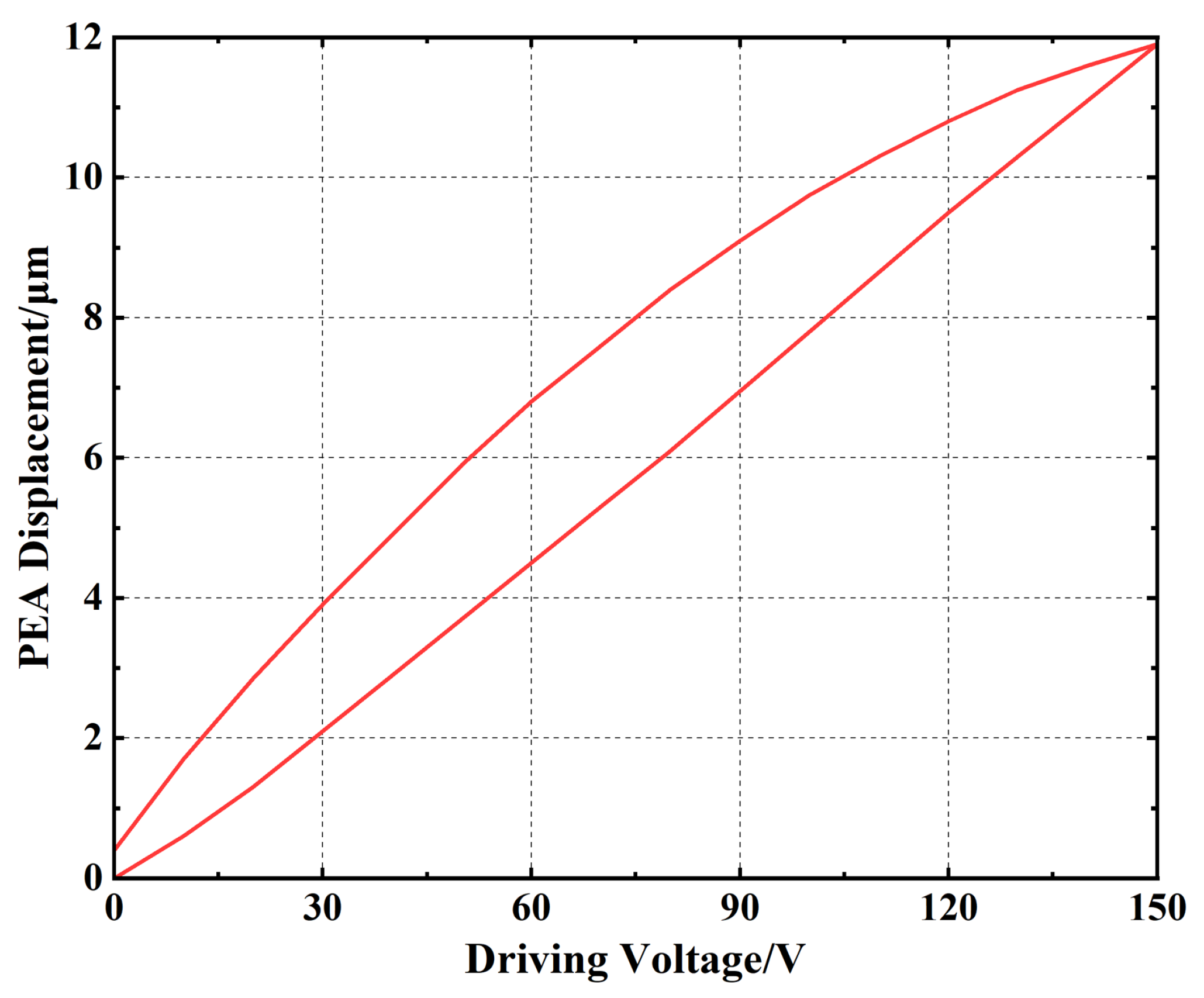
3.2. Validation of the FPI Model
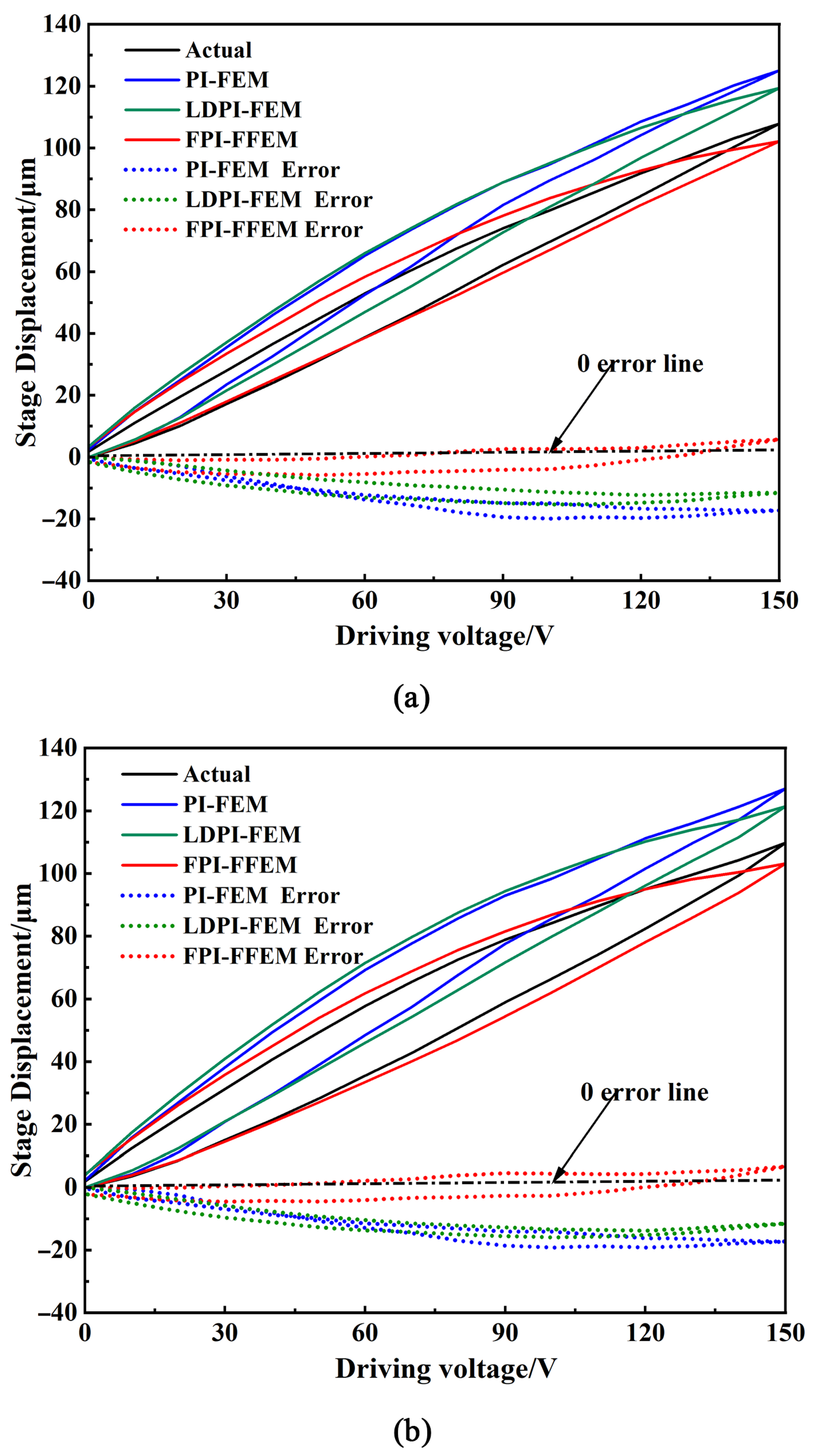
3.3. Verification of the FPI-FFEM Nonlinearity Characterization Method
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Li, L.; Li, C.; Gu, G.; Zhu, L. Modified Repetitive Control Based Cross-Coupling Compensation Approach for the Piezoelectric Tube Scanner of Atomic Force Microscopes. IEEE/ASME Trans. Mechatronics 2019, 24, 666–676. [Google Scholar] [CrossRef]
- Meng, Y.; Li, L.; Wang, X.; Zhang, X.; Zhu, L. Data-driven based cross-coupling compensation method for the piezoelectric tube scanner of atomic force microscopes. Measurement 2023, 219, 113260. [Google Scholar] [CrossRef]
- Zheng, Z.; Zhao, Y.; Wang, G. Research on Piezoelectric Driving Microminiature Three-Legged Crawling Robot. J. Bionic Eng. 2023, 20, 1481–1492. [Google Scholar] [CrossRef]
- Wang, N.; Zhang, Z.; Zhang, X.; Liang, X. Performance comparison and analysis of three two-degree-of-freedom compliant precision positioning platforms. J. Mech. Eng. 2018, 54, 102–109. [Google Scholar] [CrossRef]
- Li, L.; Yao, J.; Guo, F.; Wang, Y.; Wang, L. Hybrid flexible hinge configuration design and flexibility modeling. J. Mech. Eng. 2022, 58, 78–91. [Google Scholar]
- Xie, X.; Cui, Y.; Yu, Y.; Chen, P. Modeling and identification of nonlinear hysteresis behavior of piezoelectric actuators using a computationally efficient phenomenological model and modified cuckoo search algorithm. Smart Mater. Struct. 2023, 32, 15013. [Google Scholar] [CrossRef]
- Mohammad, J.; Mohammad, S.; Tan, X. The Prandtl–Ishlinskii Hysteresis Model: Fundamentals of the Model and Its Inverse Compensator. IEEE Control Syst. Mag. 2023, 43, 66–84. [Google Scholar]
- Arockiarajan, A.; Delibas, B.; Menzel, A.; Seemann, W. Studies on rate-dependent switching effects of piezoelectric materials using a finite element model. Comput. Mater. Sci. 2006, 37, 306–317. [Google Scholar] [CrossRef]
- Dong, R.; Tan, Y.; Chen, H.; Xie, Y. A neural networks based model for rate-dependent hysteresis for piezoceramic actuators. Sens. Actuators A Phys. 2008, 143, 370–376. [Google Scholar] [CrossRef]
- Wang, W.; Wang, J.; Wang, R.; Chen, Z.; Han, F.; Lu, K.; Wang, C.; Xu, Z.; Ju, B. Modeling and Compensation of Dynamic Hysteresis with Force-Voltage Coupling for Piezoelectric Actuators. Micromachines 2021, 12, 1366. [Google Scholar] [CrossRef] [PubMed]
- Feng, Y.; Hu, Z.; Liang, M. Modelling of piezoelectric actuating systems subjected to variable loads and frequencies and applications to prescribed performance control. Int. J. Control 2023, 96, 2356–2373. [Google Scholar] [CrossRef]
- Cai, K.; Tian, Y.; Wang, F.; Zhang, D.; Shirinzadeh, B. Development of a piezo-driven 3-DOF stage with T-shape flexible hinge mechanism. Robot. Comput.-Integr. Manuf. 2016, 37, 125–138. [Google Scholar] [CrossRef]
- Yuan, L.; Wang, L.; Qi, R.; Zhao, Z.; Jin, J.; Zhao, C. A novel hollow-type XY piezoelectric positioning platform. Int. J. Mech. Sci. 2023, 255, 108496. [Google Scholar] [CrossRef]
- Yang, Z.; Li, X.; Tang, J.; Huang, H.; Zhao, H.; Cheng, Y.; Liu, S.; Li, C.; Xiong, M. A Bionic Stick–Slip Piezo-Driven Positioning Platform Designed by Imitating the Structure and Movement of the Crab. J. Bionic Eng. 2023, 20, 2590–2600. [Google Scholar] [CrossRef]
- Mishr, M.; Samantaray, A.; Chakraborty, G. Fractional-order Bouc-wen hysteresis model for pneumatically actuated continuum manipulator. Mech. Mach. Theory 2022, 173, 104841. [Google Scholar] [CrossRef]
- Fang, J.; Wang, J.; Li, C.; Zhong, W.; Long, Z. A Compound Control Based on the Piezo-Actuated Stage with Bouc–Wen Model. Micromachines 2019, 10, 861. [Google Scholar] [CrossRef]
- Zhang, M.; Cui, X.; Xiu, Q.; Zhuang, J.; Yang, X. Dynamic Modeling and Controlling of Piezoelectric Actuator Using a Modified Preisach Operator Based Hammerstein Model. Int. J. Precis. Eng. Manuf. 2023, 24, 537–546. [Google Scholar] [CrossRef]
- Lin, W.; Wing, H. Classical Preisach Model Based on Polynomial Approximation and Applied to Micro-Piezoelectric Actuators. Symmetry 2022, 14, 1008. [Google Scholar] [CrossRef]
- Zhang, C.; Zhou, M.; Nie, L.; Zhang, X.; Su, C.Y. Prandtl–Ishlinskii model based event-triggered prescribed control: Design and application to piezoelectric-driven micropositioning stage. Mech. Syst. Signal Process. 2023, 200, 110562. [Google Scholar] [CrossRef]
- Zhang, C.; Yu, Y.; Zhou, M.; Zhang, X. Event-triggered adaptive trajectory tracking control for hysteretic nonlinear systems with fixed-time performance. IEEE Trans. Syst. Man Cybern. Syst. 2024, 54, 5327–5338. [Google Scholar] [CrossRef]
- Feng, Y.; Li, Z.; Rakheja, S.; Jiang, H. A modified Prandtl-Ishlinskii hysteresis modeling method with load-dependent delay for characterizing magnetostrictive actuated systems. Mech. Sci. 2018, 9, 177–188. [Google Scholar] [CrossRef]





| Input: | |
|---|---|
| 1. Experimental PEA Dataset (Voltage–Force–Displacement). | |
| 2. Geometric and material properties of the FHPS. | |
| 3. Target driving voltage cycle, . | |
| Output: | |
| The predicted nonlinear hysteresis curve of the FHPS, . | |
| Part I: Model Calibration | |
| Step 1 | Calibrate FPI Model Parameters: |
| Using the experimental Voltage–Force–Displacement dataset, perform a system identification procedure on the FPI model. This optimization process simultaneously determines the classical PI parameters (weighting coefficients and thresholds ) and the crucial force–voltage coupling coefficient, . | |
| Output: A calibrated FPI model defined by the identified parameter set , which describes the PEA’s intrinsic electromechanical behavior. | |
| Part II: FFEM System Characterization | |
| Step 2 | Develop FEM Model: |
| Construct a high-fidelity 3D FEM model of the FHPS based on its geometry and material properties. | |
| Output: A virtual stage that accurately reflects the system’s mechanics. | |
| Step 3 | Characterize System Dynamics via FFEM: |
| For a range of prescribed PEA displacements, , applied to the model’s interface: | |
| a. Compute the reaction force, , via static structural analysis. | |
| b. Measure the corresponding FHPS output displacement, . | |
| Output: Two key mappings: the dynamic preload map and the kinematic amplification map . | |
| Part III: Prediction and Integration | |
| Step 4 | Predict System Response: |
| For each time step in the target voltage cycle : | |
| a. Solve for PEA Displacement: Find the PEA displacement that satisfies the coupled FPI equation, using the identified coefficient from Step 1: | |
| b. Predict Stage Output: Use the kinematic map to find the final output:
| |
| Step 5 | Construct Hysteresis Curve: |
| Repeat Step 4 for the entire voltage cycle. Assemble all calculated points to construct the complete predicted nonlinear characteristic curve of the FHPS. | |
| Output: The final predicted hysteresis curve for experimental comparison. | |
| Core Feature | PI-FEM | FPI-FFEM |
|---|---|---|
| Considers Displacement Relationship | ✓ | ✓ |
| Considers Changing Preload | × | ✓ |
| PEA to FHPS’s Deformation Analysis | ✓ | ✓ |
| PEA’s Force–Displacement Coupling Analysis | × | ✓ |
| PI | FPI | |||
|---|---|---|---|---|
| 1 | 0 | |||
| 2 | 10 | |||
| 3 | 20 | |||
| 4 | 30 | |||
| 5 | 40 | |||
| 6 | 50 | |||
| 7 | 60 | |||
| 8 | 70 | |||
| 9 | 80 | |||
| 10 | 90 | |||
| Method | MAE Under 5 Hz (μm) | MAE Under 15 Hz (μm) |
|---|---|---|
| PI-FEM | 12.343 | 11.792 |
| LDPI-FEM | 9.772 | 10.765 |
| FPI-FFEM | 2.882 | 2.949 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; An, D.; Qin, Z.; Wang, C.; Liu, Y.; Yang, Y. Nonlinearity Characterization of Flexible Hinge Piezoelectric Stages Under Dynamic Preload via a Force-Dependent Prandtl–Ishlinskii Model with a Force-Analyzed Finite Element Method. Actuators 2025, 14, 411. https://doi.org/10.3390/act14080411
Wang X, An D, Qin Z, Wang C, Liu Y, Yang Y. Nonlinearity Characterization of Flexible Hinge Piezoelectric Stages Under Dynamic Preload via a Force-Dependent Prandtl–Ishlinskii Model with a Force-Analyzed Finite Element Method. Actuators. 2025; 14(8):411. https://doi.org/10.3390/act14080411
Chicago/Turabian StyleWang, Xuchen, Dong An, Zicheng Qin, Chuan Wang, Yuping Liu, and Yixiao Yang. 2025. "Nonlinearity Characterization of Flexible Hinge Piezoelectric Stages Under Dynamic Preload via a Force-Dependent Prandtl–Ishlinskii Model with a Force-Analyzed Finite Element Method" Actuators 14, no. 8: 411. https://doi.org/10.3390/act14080411
APA StyleWang, X., An, D., Qin, Z., Wang, C., Liu, Y., & Yang, Y. (2025). Nonlinearity Characterization of Flexible Hinge Piezoelectric Stages Under Dynamic Preload via a Force-Dependent Prandtl–Ishlinskii Model with a Force-Analyzed Finite Element Method. Actuators, 14(8), 411. https://doi.org/10.3390/act14080411







