Abstract
This study focuses on optimizing track and grouser structural parameters to enhance UATV drawbar pull, particularly under soft soil conditions. A numerical soil thrust model for single-track shoes was developed based on track–soil interaction mechanics, revealing distinct mechanistic roles: track structural parameters (length/width) govern pressure–sinkage relationships at the track base, while grouser structural parameters (height, spacing, V-shaped angle) dominate shear stress–displacement dynamics on grouser shear planes. A novel DEM-MBD coupling simulation framework was established through soil parameter calibration and multi-body dynamics modeling, demonstrating that soil thrust increases with grouser height and V-shaped angle, but decreases with spacing, with grouser height exhibiting the highest sensitivity. A soil bin test validated the numerical model’s accuracy and the coupling method’s efficacy. Parametric optimization via the Whale Optimization Algorithm (WOA) achieved a 55.86% increase in drawbar pull, 40.38% reduction in ground contact pressure and 57.33% improvement in maximum gradability. These advancements substantially improve the tractive performance of UATVs in soft beach terrains. The proposed methodology provides a systematic framework for amphibious vehicle design, integrating numerical modeling, high-fidelity simulation, and experimental validation.
1. Introduction
Large-scale equipment operating on islands requires substantial fuel supply, which is transported through pipelines. The UATV can directly tow pipelines from offshore supply vessels to designated terrestrial locations. The UATV sequentially traverses marine zones, water–sediment mixed terrains, and beach areas, achieving fully automated operation with enhanced safety and efficiency. The vehicle’s configuration is illustrated in Figure 1. The vehicle is equipped with four segmented tracks, each independently driven by an electric motor. The tractive performance on beach is a critical metric for evaluating the UATV’s capabilities. This performance depends not only on the engine’s output power and transmission efficiency but also on the soil thrust generated through the soil–track interaction. In track design, structural parameters such as track length, width, grouser height, spacing, and V-shaped angle significantly influence soil thrust, making rational structural design of the track system essential. Current research predominantly focuses on stress analysis, wear failure mechanisms, and material optimization of track components, while research on systematic optimization of these parameters remains scarce. However, such optimization holds substantial theoretical and practical value for improving the tractive performance of tracked vehicles on soft soil.
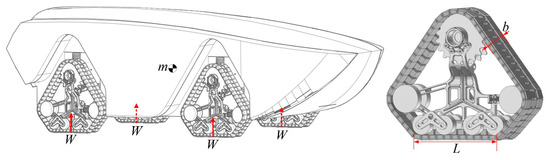
Figure 1.
Model of UATV.
Tracked vehicle performance depends heavily on available driving force, which directly influences acceleration and obstacle negotiation. However, the effective utilization of the driving force not only depends on the soil–track interaction mechanism, but is also closely linked to the grouser–track structural parameters [1,2]. In 1913, R. Bernstein of Germany proposed the foundational expression relating track sinkage depth to ground contact pressure [3]. This theory was subsequently refined by scholars including E.W.E. Micklethwait [4], M.G. Bekker [5], and Z. Janosi [6,7], culminating in the establishment of the traction characteristics theoretical model for tracked vehicles by A.R. Reece and J.Y. Wong [8,9,10], which remains widely adopted in terramechanics research. These scholars also conducted seminal investigations into the grouser effect. Reece established an additional traction force model based on static equilibrium during soil failure [11]. Bekker developed a complementary model utilizing Boussinesq’s stress distribution theory to quantify grouser-induced traction enhancement [12]. J.Y. Wong further advanced this field by deriving horizontal forces acting on grousers through passive earth pressure theory [13]. As evidenced by these models, grouser height exhibits significant influence on drawbar pull. Furthermore, structural parameters including grouser shape, herringbone angle, and spacing collectively modulate the bulldozing effect and shear stress distribution [14]. In 2004, Liu Zhensheng investigated the performance of grousers in desert soil conditions based on soil mechanics theory, systematically analyzing the tractive performance of tracks in dry sand environments [15]. In 2008, South Korean researchers W.Y. Park et al. employed mathematical models to elucidate the relationship between tracked vehicle design parameters and soil properties, demonstrating that ground contact pressure exhibits a curvilinear distribution and predicting tractive performance variations on soft soil [16]. In 2010, Wu Hongyun conducted a comprehensive study on the adhesion behavior of track shoes and grousers in soft cohesive substrates for deep-sea mining vehicles. He developed a mathematical model for adhesion forces and evaluated structural influences on adhesion performance [17].
Early-stage research relied primarily on empirical formulas, numerical solutions, and scale model tests to investigate soil–track interactions. Recent computational advances have shifted the paradigm toward simulation-based methodologies. The Finite Element Method (FEM) enables analysis of stress distribution and plastic deformation in deformable soils under track loading, providing theoretical foundations for optimizing track shoe structural parameters and characterizing soil–track traction mechanisms. Researchers J.P. Hambleton and A. Drescher at the University of Minnesota conducted pioneering studies using 2D/3D FEM simulations to quantify the effects of soil parameters, dilation angle, and wheel geometry on the pressure–sinkage relationship of rigid cylindrical wheels [18,19]. Yang Congbin further developed a soil FEM model integrating elastic theory and the Mohr–Coulomb Criterion, validating an adhesion force model between track shoes and terrain through Abaqus simulations [20]. However, FEM exhibits inherent limitations in simulating dynamic processes such as soil particle collisions, sliding, and frictional interactions. Its applicability diminishes when modeling large soil deformations under mechanical loading or scenarios where soil cannot be treated as a continuum [21]. These constraints are effectively addressed by the Discrete Element Method (DEM), a numerical approach that discretizes the domain into independently moving particles governed by inter-particle contact mechanics. DEM excels in simulating grouser–soil interaction dynamics, particularly in capturing granular flow patterns and localized shear failure mechanisms. In 2021, Shaikh et al. experimentally and via DEM simulations demonstrated that grouser height significantly influences tractive performance, with its efficacy varying across soil moisture conditions [22,23]. Concurrently, Li Yong et al. investigated the impact of track shoe structural parameters on the tractive performance of underwater tracked bulldozers, explicitly accounting for hydrodynamic effects in submerged environments [24]. In 2023, South Korean researchers J.T. Kim et al. employed DEM to analyze grouser shape ratios in coastal beach terrains, identifying optimal geometric proportions for maximizing traction [25]. In 2024, Xie Dongbo established a dynamics model of tracked locomotion systems interacting with straw-mixed soils using DEM-MBD (Multi-Body Dynamics) coupling simulations, validating the interaction mechanisms between tracks and fibrous soil matrices [26]. The DEM-MBD coupling model integrates the advantages of discrete granular analysis and multi-body dynamics, serving as a robust numerical tool for simulating complex system interactions and dynamic behaviors. This methodology provides an efficient simulation framework for investigating how grouser structural parameters modulates drawbar pull while substantially reducing the prohibitive costs associated with full-scale field testing.
In 2021, through RSM optimization, Jun Fu et al. determined the optimal structural parameter combination for grouser shoes, achieving a 12.84% reduction in adhesion force and a 4.63% decrease in adhered soil mass. This provides both a theoretical foundation and an engineering paradigm for anti-adhesion design of tracked vehicles in Northeastern China’s black soil regions [27]. Dingbang Wei et al., in 2025 [28], quantified the influence patterns of tracked vehicle parameters on deep-sea sediment mechanical properties through orthogonal experiments. They established the first multi-parameter integrated nonlinear prediction model and a tractive performance evaluation framework for mining vehicles. Utilizing the NSGA-II multi-objective optimization algorithm to optimize tracked structure parameters, drawbar pull was increased by 29.1%, while subsidence depth was reduced by 12.8% [28]. Both studies established the influence relationships between track structural parameters and objective functions through experimental approaches. Although structural parameter optimization was achieved via optimization algorithms, they lack in-depth research on underlying mechanisms.
A critical synthesis of prior research reveals three primary limitations: First, the existing studies predominantly focus on soil–track interaction mechanisms under varying conditions and soil types, while systematic investigations into the influence of track and grouser structural parameters on tractive performance, along with their parametric optimization, remain notably scarce. Second, regarding simulation methodologies, early research primarily relied on the FEM; however, this approach fails to accurately simulate granular-scale interactions between soil particles or dynamic soil–track interface behaviors. Recent advancements have seen a paradigm shift, with an increasing number of scholars adopting the DEM, thereby offering a novel methodological framework for this study. Second, FEM exhibits inherent limitations in accurately simulating granular-scale interactions between soil particles and dynamic soil–track interface behaviors. Recent research trends reflect a significant paradigm shift, with the DEM increasingly adopted by scholars. This adoption provides a novel framework for the methodology explored in this study. Third, early-stage research heavily relied on experimental validation to establish empirical relationships. Although this approach ensures high precision, it is inefficient due to prolonged experimental cycles and is significantly affected by soil spatial variability.
To address the three aforementioned research gaps, this study focuses on optimizing the structural parameters of tracks and grousers for UATV. A numerical model for predicting soil thrust is established for track shoes based on terramechanics theory. DEM-MBD coupling simulations are employed to investigate the effects of track and grouser structural parameters on soil thrust, and to concurrently validate the numerical model. The accuracy of the numerical model and the efficacy of the coupling simulation methodology are further verified through a soil bin test on track shoes, yielding a validated mathematical optimization framework. Finally, single-track drawbar pull is selected as the optimization objective to iteratively refine structural parameters. The research methodology is systematically outlined in Figure 2.
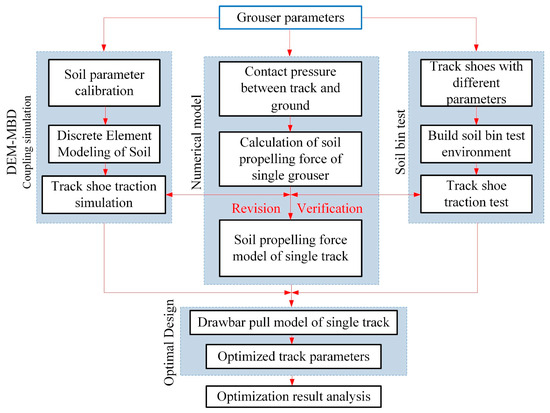
Figure 2.
Research methodology.
2. Numerical Model and Analysis
Track length and width primarily determine the distribution and magnitude of ground contact pressure. Grousers generate shear forces through soil–track interaction, propelling the vehicle forward, with their height, shape, and spacing being critical factors influencing tractive performance. Therefore, establishing a numerical model for the interaction between tracks/grousers and soil based on terramechanics theory holds significant importance for structural parameter analysis and optimization.
2.1. Single-Grouser Soil Thrust Numerical Model
Grouser geometries are primarily categorized into three types: straight-line, V-shaped, and W-shaped. The straight-line grouser fails to form enclosed spaces during operation, resulting in limited efficacy in enhancing soil compaction and drawbar pull, alongside inferior lateral slip resistance. In contrast, V-shaped and W-shaped grousers generate enclosed soil-trapping zones through their geometric profiles, thereby enhancing soil compaction and drawbar pull via compressive and shear interactions. In this study, the vehicle employs a narrow-track configuration. Given dimensional constraints that preclude the application of W-shaped grousers, the V-shaped design is selected. As illustrated in Figure 3, the left panel depicts the actual grouser morphology, while the right panel shows its theoretical simplified model, where denotes the oblique rib width and represents the V-shaped angle.
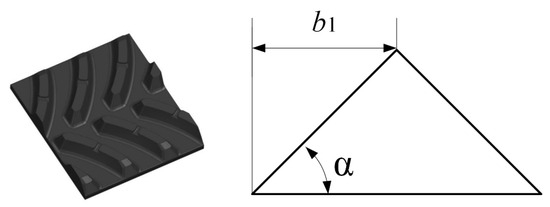
Figure 3.
Grouser diagram.
The V-shaped track can be conceptualized as two straight-line tracks joined symmetrically. We first conduct a mechanical analysis of the straight-line configuration. As illustrated in Figure 4, the sandy soil thrust generated by a single grouser comprises five distinct components: shear force at the track shoe base , shear force at the grouser base , shear forces on track shoe sides , shear forces on grouser sides , and the soil reaction force induced by grouser bulldozing action .
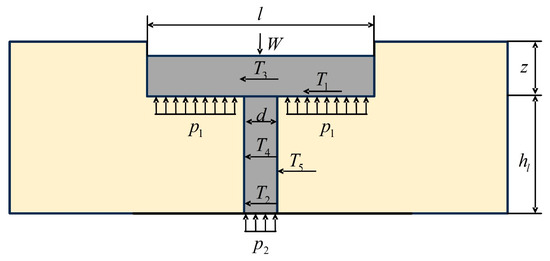
Figure 4.
Diagram of grouser–soil interaction forces.
The calculation can be performed using the normal stress–sinkage relationship proposed by Bekker for static soil deformation conditions:
where is the cohesive modulus of the soil, is the frictional modulus of the soil, is the track width, is the soil subsidence index, and represents the sinkage.
The shear stress in soil is calculated as follows:
where is the soil cohesion, is the soil’s internal friction, is the shear modulus of the soil, is the normal pressure on the shear surface, and is the shear deformation of the soil.
The slip ratio is calculated as follows:
where is the actual UATV speed, is the track linear speed, is the rotational speed of the track’s active wheel, and is the track’s active wheel radius.
At each point along the length of the track grounding surface, the shear deformation of the soil can be expressed as follows:
Let denote the distance from a given point on the track contact patch to the leading edge of the contact patch, then:
and can be determined via stress integration:
During tracked vehicle motion, grousers and track shoes induce relative displacement with surrounding soils. The forces exerted by the track on the soil can be modeled as strip loads acting on a semi-infinite elastic medium. By treating the soil as an elastic continuum, the internal stress distribution can be calculated using Boussinesq’s stress theory. The stress distribution diagram is illustrated in Figure 5.
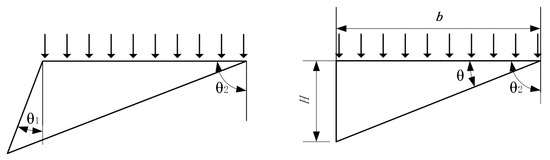
Figure 5.
Stress distribution under strip loads.
According to elasticity theory, the stress components at any point within a semi-infinite elastic medium are expressed as follows:
where is angles between an arbitrary point at depth and the load application plate under strip load influence.
When , the stress at any point within the semi-infinite elastic medium is expressed as follows:
From , and can be expressed as follows:
where is ground contact pressure, while is the load borne by single track shoe.
Taking the straight-line grouser configuration as an example, as the track shoe advances forward, the sandy soil undergoes displacement due to grouser-induced compression. Based on Rankine’s earth pressure theory, the soil in this region is assumed to be in a Rankine passive earth pressure state. The soil is subjected to a uniformly distributed load from the track shoe base. The vertical stress acting on a soil element at depth is calculated by directly superimposing onto the vertical principal stress of the soil element, as illustrated in Figure 6.
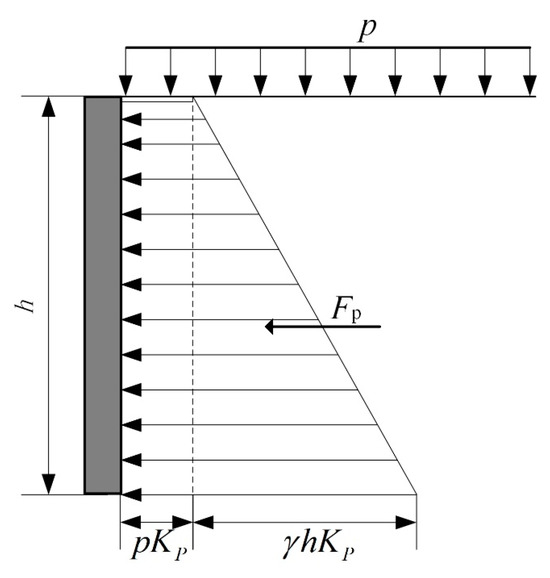
Figure 6.
Rankine passive earth pressure model.
The passive earth pressure intensity at depth is given by the following:
where is passive earth pressure, is passive earth pressure coefficient, , is internal friction angle of soil, is the soil bulk density, and is depth of soil.
From the preceding equation, the earth pressure acting on the grouser exhibits a trapezoidal distribution along depth . Consequently, the horizontal thrust exerted on a straight-line grouser is calculated as follows:
For oblique grouser segments, the horizontal thrust component is as follows:
Total horizontal thrust acting on the grouser is as follows:
The soil thrust force for a single grouser can be calculated as follows:
2.2. Single Track Soil Thrust Numerical Model
The single-track soil thrust model is developed to analyze the influence mechanisms of track and grouser structural parameters on soil thrust under the operating condition of traversing level, straight sandy loam with constant moisture. To ensure consistency among controlled variables during numerical calculation, coupled simulation, and soil bin testing, the model is simplified with the following necessary assumptions. Key assumptions include the following: the track-wheel assembly’s center position remains stationary during motion, with no lateral slippage; only center-of-gravity position and motion resistance are considered in determining the contact forces between track shoes and terrain.
Building upon Bekker’s theory, the ground contact pressure formula is derived as follows:
where is vertical load on the track, is track shoe length, and is track shoe width.
For UATV, the grouser thickness is negligible. Thus, the shear forces at the grouser base are equivalently lumped to the track shoe base.
The total soil thrust along the entire track base is calculated as follows:
Conducted under 5% moisture content sandy loam conditions, Lei Xueyuan’s traction tests on track shoes with grouser heights ranging from 0 to 100 mm demonstrated that soil thrust increases by 4.93% per additional grouser [29]. Since the grouser height range in this study is 0–75 mm with identical sandy loam moisture, the total soil thrust on all grouser shear planes of a single track can therefore be derived by applying the following correction coefficient:
Based on the single track shoe formula derived earlier, the soil shear forces acting on flanks of the entire track can be derived as follows:
Total soil thrust for a single track is then expressed as follows:
2.3. Numerical Analysis
Analysis of the derived soil thrust formula for single track reveals that the soil thrust at the grouser base and track shoe base (F1) is primarily influenced by track length (L) and width (b), with negligible contributions from grouser structural parameters. In contrast, the soil thrust on grouser shear planes (F2) depends on track structural parameters (L, b) and grouser structural parameters (h, l, α), while thrust at track and grouser flanks (F3) is dominated by grouser height (h) and track width (b). Track structural parameters (L, b) govern the magnitudes of F1, F2, and F3, whereas grouser structural parameters (h, l, α) exclusively affect F2 and F3.
By substituting sandy soil and track structural parameters into the soil thrust formula, the influence of track structural parameters (L, b) on F1, F2, F3, and H is analyzed in Figure 7. As can be seen from Figure 7a, F1 and H increase with track length (L), while F2 decreases, and F3 remains unaffected. As can be seen from Figure 7b, F1, F2, and H increase with track width (b), whereas F3 decreases. Track structural parameters (L, b) exhibit a more pronounced impact on F1. The effects of grouser structural parameters (h, l, α) on F2 and F3 are shown in Figure 8. As can be seen from Figure 8a, both F2 and F3 increase with grouser height (h), with F2 showing significant enhancement. As can be seen from Figure 8b, F2 decreases with grouser spacing (l), while F3 remains unaffected. As can be seen from Figure 8c, F2 increases with V-shaped angle (α), whereas F3 shows no dependency.
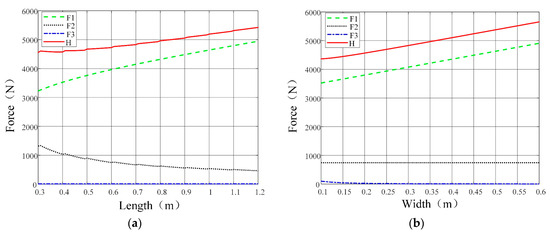
Figure 7.
Impact of track structural parameters on soil thrust: (a) soil thrust vs. length; (b) soil thrust vs. width.
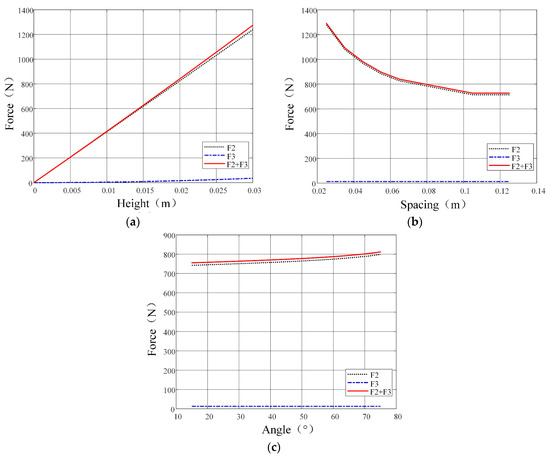
Figure 8.
Impact of grouser structural parameters on soil thrust: (a) soil thrust vs. height; (b) soil thrust vs. spacing; (c) soil thrust vs. angle.
In summary, track structural parameters primarily determine soil thrust at grouser bases and track shoe bases through their deterministic influence on pressure–sinkage relationships, while grouser parameters dictate shear plane thrust via modulation of shear stress-displacement behavior, with grouser height demonstrating the most pronounced effect. Rational design of track structural parameters and grouser structural parameters can effectively enhance soil thrust, thereby improving vehicle tractive performance.
3. Coupling Simulation Model and Analysis
3.1. Soil Parameter Calibration
The simulation methodology demonstrates advantages in computational efficiency and explicit parameter relationships. However, the accuracy of soil physical parameters and tracked vehicle operational parameters is directly dependent on soil parameter calibration. Particularly when employing the DEM for sand soil bin simulation modeling, it is imperative to strictly adhere to the physical-mechanical properties of authentic sandy soil.
This study calibrated the contact parameters between sand soil particles and those between the sand soil and the track through a series of simulation experiments. A sand soil bin simulation environment closely approximating the mechanical properties of actual road surfaces was established, thereby enhancing the fidelity of the simulation methodology.
Firstly, the contact parameters were constrained within a narrow range through angle of repose tests and corresponding simulations. Subsequently, triaxial compression tests with confining pressures set at 100 kPa, 200 kPa, and 300 kPa were conducted alongside corresponding simulations. The parameters derived from the angle of repose tests were implemented in the simulations, and the resulting stress–strain curves were systematically compared with experimental triaxial compression data, as shown in Figure 9. This methodology enabled the acquisition of high-precision sand soil contact parameters. Furthermore, sliding plate tests and corresponding simulations were performed to obtain accurate contact parameters between the sand soil and track, with the finalized parameters summarized in Table 1.
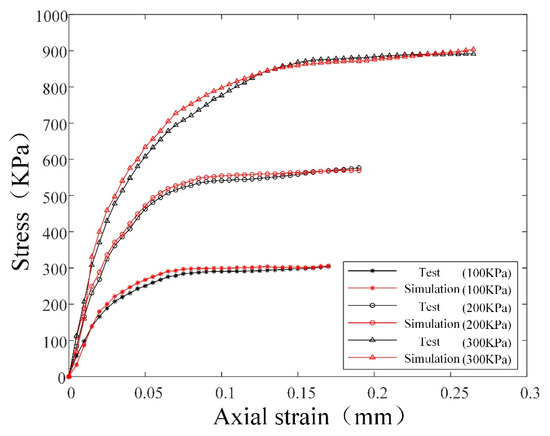
Figure 9.
Triaxial compression calibration stress–strain curve.

Table 1.
Sand soil calibration parameters.
3.2. Track Shoe Coupling Simulation Model
Based on the calibrated sand soil parameters, a sand soil bin was established in the discrete element software EDEM 2020. The sand soil was modeled using spherical particles, with interparticle interactions governed by the Hertz–Mindlin (no slip) contact model, which explicitly excludes cohesive forces between particles. Particle packing generated the soil bin model, measuring 2.5 m (length) × 1 m (width) × 0.2 m (height), as illustrated in Figure 10a.
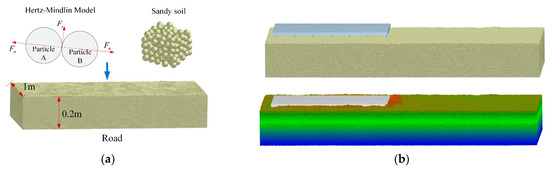
Figure 10.
Track shoe coupling simulation model: (a) discrete meta-model of sandy soil; (b) DEM-MBD coupling simulation model.
Within the multi-body dynamics software RecurDyn V9R2, track shoe models with varying structural parameters were developed, with motion constraints and actuation mechanisms implemented. Intermediate files were subsequently generated and imported into software EDEM. Upon activating the coupling interface to execute the simulation, real-time data exchange and synchronized computation were achieved. The coupling simulation model is illustrated in Figure 10b.
Figure 11a presents the velocity contour map of sand soil particles during 1 s of tracked vehicle operation. During the track shoe movement, substantial particle motion is induced by grouser compaction and track shear effects. Particles ahead of the grouser exhibit significantly higher velocities compared to other regions, with velocity magnitudes decaying as the distance from the grouser increases. Beneath the track shoe, particle velocities progressively diminish with increasing soil depth, reaching zero at the bottom layer of the soil bin. This observation suggests the soil bin depth is sufficient for the intended boundary condition simulation. Figure 11b displays the force contour map of sand soil particles under identical operational conditions. Particles ahead of the grouser experience significantly greater forces compared to those along the track flanks, with force magnitudes intensifying to proximity to the grouser. This phenomenon originates from the soil thrust generated by the grouser exceeding that produced along the track flanks, which aligns conclusively with numerical analysis predictions. In summary, the kinematic behavior of sand soil under simulated conditions demonstrates strong congruence with empirical observations, thereby validating the reliability of the DEM-MBD coupling simulation methodology.
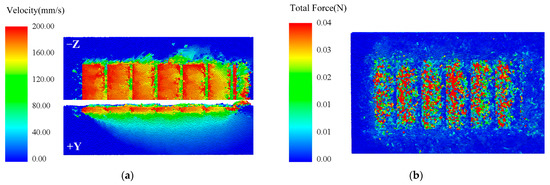
Figure 11.
Sand soil particle contour map: (a) sand soil particle velocity contour map; (b) sand soil particle force contour map.
3.3. Simulation Analysis
To investigate the influence patterns of track shoe soil thrust with respect to vertical load, grouser height, grouser spacing, and V-shaped angle configuration, four sets of simulation experiments were established. Experimental parameters were configured as follows: vertical loads of 5000 N, 7500 N, and 10,000 N; grouser height variations of ±5 mm relative to the 15 mm baseline; grouser spacing variations of ±25 mm relative to the 75 mm baseline; and V-shaped angle variations of ±15° relative to the 45° baseline. The complete experimental parameter matrix is detailed in Table 2.

Table 2.
Simulation experimental parameters.
Linxuan Zhou investigated the relationship between track adhesion and track shear speed, revealing that adhesion increases with rising shear speed, while both the increment value of adhesion and the enhancement efficiency gradually decrease with increasing shear speed. The adhesion enhancement is particularly notable when the speed increases from 0.1 m/s to 0.3 m/s, with increments exceeding 10% across this range; the increment at 0.2 m/s reaches 23.3% [30]. Given that the improvement in soil thrust generated by a single track shoe is relatively small, and simulations under the fixed track shear speed condition of 0.2 m/s exhibit a pronounced adhesion increase, this speed is more suitable for comparative data analysis. Furthermore, constrained by the computational speed and memory limitations of the discrete element software, the simulated sandy loam particles are larger than their real-world counterparts. Higher track shear speeds would cause a large number of sandy loam particles to be thrown backward by the grouser, impeding the investigation into the interaction mechanism between structural parameters and the soil. Consequently, this study was conducted at a fixed track shear speed of 0.2 m/s.
Comparative analyses between simulation and numerical results were conducted for each experimental group, as graphically presented in Figure 12, Figure 13, Figure 14 and Figure 15. Subplots (a) in Figure 12, Figure 13, Figure 14 and Figure 15 present the simulated temporal evolution of track shoe soil thrust. During the 0 s to 0.6 s phase, a transient force equilibrium between the track shoe and sand soil occurs under self-weight and inertial effects, during which no forward velocity is applied to the track shoe. The 0.6 s to 0.7 s interval exhibits velocity acceleration from 0 m/s to 0.2 m/s. From 0.7 s to 1.4 s, kinematic interaction between the track shoe and sand soil induces dynamic fluctuations in soil thrust. Beyond 1.4 s, the soil thrust demonstrates progressive convergence toward steady-state values. Subplots (b) in Figure 12, Figure 13, Figure 14 and Figure 15 display the numerical results of track shoe soil thrust (solid lines) alongside simulation outputs (diamond markers) under varying conditions. As shown in Figure 12, soil thrust exhibits a positive correlation with vertical load magnitude. The simulation results demonstrate strong agreement with the numerical model, thereby validating the efficacy of DEM. Figure 13 reveals that grouser height exerts a pronounced influence on soil thrust, with thrust values increasing with grouser height. Conversely, Figure 14 indicates a marginal inverse relationship between grouser spacing and soil thrust. Figure 15 illustrates that soil thrust moderately escalates with increasing V-shaped angles.
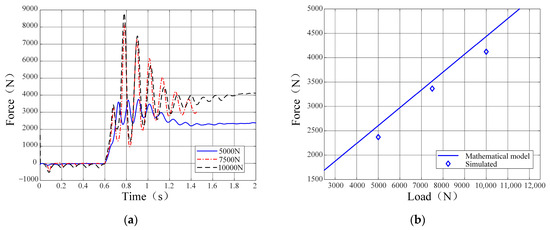
Figure 12.
Relationship between soil thrust and vertical load: (a) soil thrust vs. time; (b) soil thrust vs. load.
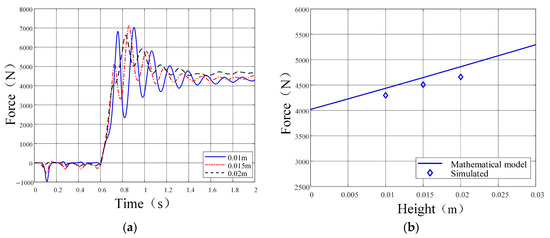
Figure 13.
Relationship between soil thrust and grouser height: (a) soil thrust vs. time; (b) soil thrust vs. height.
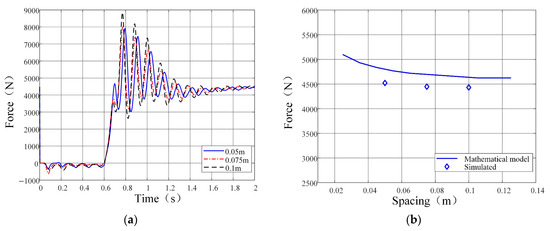
Figure 14.
Relationship between soil thrust and grouser spacing: (a) soil thrust vs. time; (b) soil thrust vs. spacing.
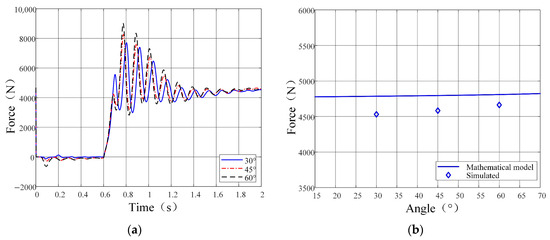
Figure 15.
Relationship between soil thrust and V-shaped angle: (a) soil thrust vs. time; (b) soil thrust vs. angle.
In summary, the accuracy and efficacy of the numerical methodology were validated through DEM-MBD coupling simulations. The analysis revealed that soil thrust exhibits a positive correlation with grouser height, demonstrates an inverse relationship with grouser spacing, and moderately escalates with increasing V-shaped angles. Furthermore, grouser height emerges as the dominant influencing factor.
4. Experimental Validation
The soil bin test method demonstrates superior control over environmental conditions, offering advantages including reduced temporal and economic costs, shortened testing cycles, and high measurement accuracy. As illustrated in Figure 16, the testing apparatus comprises a horizontal rail, vertical rail, counterweight system, tension meter, data acquisition unit, and the soil bin. The tested track shoe is mounted at the base of the vertical rail, where the counterweight mechanism applies vertical loads. Horizontal tensile forces are continuously monitored and recorded via the tension meter’s real-time measurement capabilities.
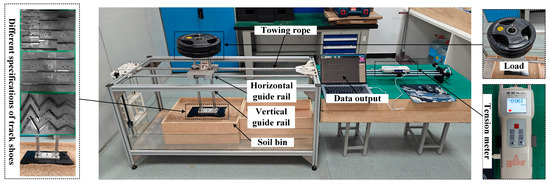
Figure 16.
Soil bin test configuration.
Track shoes with different specifications were tested, and results are summarized in Table 3.

Table 3.
Experimental parameters and results.
Comparative analyses among experimental measurements (circular markers), simulation outputs (diamond markers), and numerical results (solid lines) are graphically presented in Figure 17. Subplots a–c depict the effects of grouser height, spacing, and V-shaped angle on soil thrust, respectively. As evidenced by the figures, soil thrust demonstrates a pronounced positive correlation with increasing grouser height, and its influence is significant. Conversely, an inverse relationship is observed between soil thrust and grouser spacing, though its impact is marginal. Similarly, while soil thrust exhibits a moderate escalation with larger V-shaped angles, the impact of this parameter is also marginal. The maximum error between simulation results and the numerical results was 4.73%, with a mean error (ME) of 4.05% and root mean square error (RMSE) of 11.14 N. For experimental results versus the numerical results, the maximum error reached 5.16%, the ME was 4.43%, and the RMSE measured 12.21 N. This conclusively validates both the predictive accuracy of the numerical computational model and the efficacy of the coupling simulation methodology.
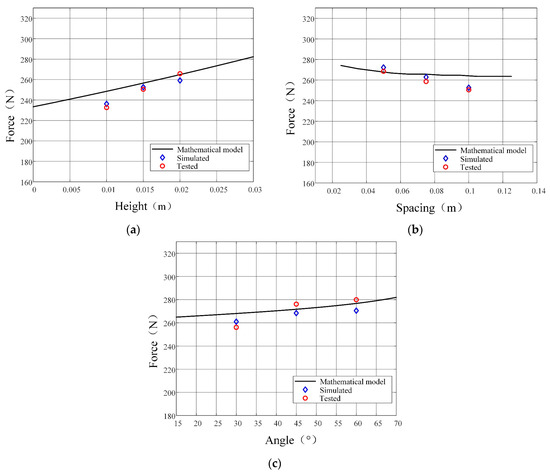
Figure 17.
Soil bin test results: (a) soil thrust vs. height; (b) soil thrust vs. spacing; (c) soil thrust vs. angle.
Figure 18 displays the track imprint patterns generated by the tracked vehicle’s movement on sandy soil. Observations indicate that regular sediment accumulation forms ahead of the grousers due to shear interaction between the grousers and sand soil. Shallower sand soil accumulation along the track flanks demonstrates that soil thrust on the grouser shear plane exceeds that on both the grouser sides and track edges, consistent with numerical model analysis. The consistency between coupling simulation results (velocity and force contour maps) and soil bin test observations validates the effectiveness of the coupling simulation methodology.

Figure 18.
Track shoe travel trace on soil bin.
5. Structural Parameter Optimization Design
Variations in coastal beach terrains and vehicle acceleration/deceleration dynamics cause vertical load redistribution across four tracks [31]. With the vertical loads of single tracks as inputs, the drawbar pull for each track can be calculated. Superimposing the drawbar pull from all tracks yields the total vehicular drawbar pull. Optimization of single-track structural parameters constitutes a critical factor in enhancing whole-vehicle drawbar pull, representing an indispensable foundational step for hierarchical optimization within complex systems. Consequently, this research focuses on optimizing the structural parameters of single tracks.
Using single-track drawbar pull as the objective function and incorporating constraints including vehicle power consumption and operational parameters, the WOA was employed to optimize structural parameters encompassing track length, width, grouser height, spacing, and V-shaped angle.
Enhancing the tractive performance of a single track cannot be solely pursued through maximizing soil thrust, as variations in thrust inherently alter track resistance dynamics. Therefore, drawbar pull optimization must account for four primary resistance components: bulldozing resistance, compaction resistance, rolling resistance, and grade resistance.
The leading edge of the track shoe generates bulldozing resistance by pushing sand soil to form an elevated frontal wave, which is mathematically expressed as follows:
where and are bearing capacity factors under local shear failure, , , and .
The compaction resistance generated by track-induced soil densification is formulated as follows:
The drawbar pull of a single track, serving as the objective function, is defined by the following:
where is the rolling resistance coefficient and has a value of 0.15.
The power consumption during track operation must not exceed the maximum power output of a single track, while the soil thrust on the grouser shear plane is derived from the Rankine passive earth pressure theory. The optimization constraints are as follows:
As the UATV retracts its track system during aquatic locomotion to minimize hydrodynamic resistance, the structural parameters of the track are constrained by the vehicle’s overall architecture. The design variables encompass track length, width, grouser height, spacing, and V-shaped angle, with initial values and parametric bounds specified in Table 4.

Table 4.
Initial values and ranges of design variables.
The WOA, a novel swarm intelligence optimization algorithm inspired by the foraging behaviors of whales, achieves optimal solutions through theoretical models encompassing search, encirclement, and hunting mechanisms. This algorithm exhibits significant advantages for engineering optimization problems, demonstrating high optimization accuracy and rapid convergence, while requiring no complex parameter tuning [32,33,34,35,36]. For the optimization of structural parameters in this study, the WOA was compared with nine other widely-used optimization algorithms: ACO, SMA, RIME, DBO, RFO, GWO, PSO, GA, and SSA. As illustrated in Figure 19, the results demonstrate that for this specific optimization problem, WOA demonstrates superior convergence characteristics and optimization accuracy compared to the other algorithms. Additionally, the convergence curves after 50 independent trials of the WOA are illustrated in Figure 20, where the red dashed line represents the mean curve and the remaining curves depict the convergence trajectories of each independent trial. The mean fitness value was calculated as 3937.32809 N, with a standard deviation of 0.90624 N, indicating that WOA exhibits high stability and robustness in optimizing the structural parameters of tracks and grousers.
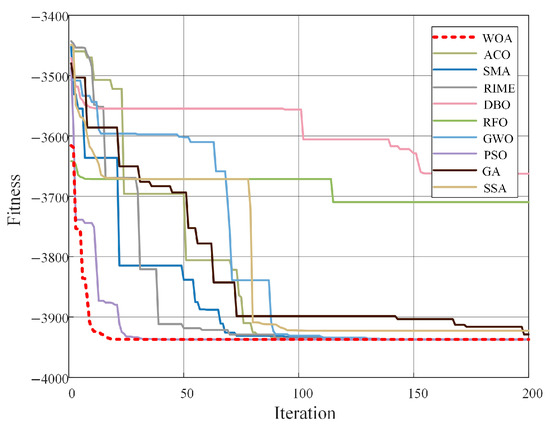
Figure 19.
Iterative curves of different algorithms.
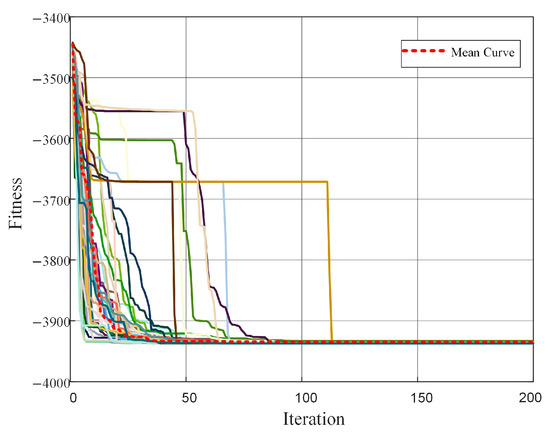
Figure 20.
WOA convergence curves.
Through iterative computation of this algorithm combined with unmanned tracked vehicle design qualification standards, an optimal track parameter configuration was derived to maximize single-track drawbar pull. The optimization outcomes are detailed in Table 5. Taking into account the optimization results and the vehicle structure, a portion of the front face of the original front wheelhouse was removed. The optimized vehicle structure is shown in Figure 21.

Table 5.
Optimization results.
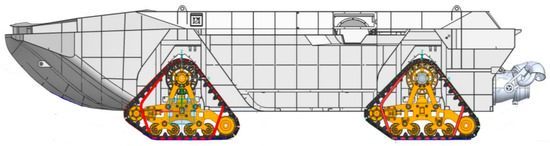
Figure 21.
Chassis structure comparison: pre- vs. post-optimization.
The structural parameters of the track and grouser are critical for track durability and manufacturing. Improper designs may lead to premature track failure and failure to meet production requirements. Yuan Shihao investigated the effects of grouser height and spacing on track wear through DEM-MBD coupled simulation, revealing that the number of baseplate bond fractures and the total wear depth of track shoes increase with higher grouser height but decrease with larger grouser spacing [37]. Rubber tracks are primarily produced via mold vulcanization processes, which offer low manufacturing complexity and adaptability to various track dimensions. Composite rubber tracks—comprising rubber, steel, and composite materials—exhibit superior wear resistance compared to pure rubber tracks while maintaining lower weight than steel tracks [38,39]. In this study, the optimized design with reduced grouser height and increased spacing enhances wear resistance and mitigates bond fracture susceptibility, concurrently lowering manufacturing difficulty.
The driving performance comparison between the original and optimized tracks under straight-line motion is shown in Figure 22. Key metrics include a reduction of 40.38% in ground contact pressure, a 55.86% increase in drawbar pull, an 18.76% drawbar pull improvement from grouser optimization, and a 57.33% enhancement in maximum gradability. The optimized track configuration ensures sufficient tractive performance and climbing capability, while reduced ground pressure mitigates sinkage risks, enabling adaptability to complex terrains.
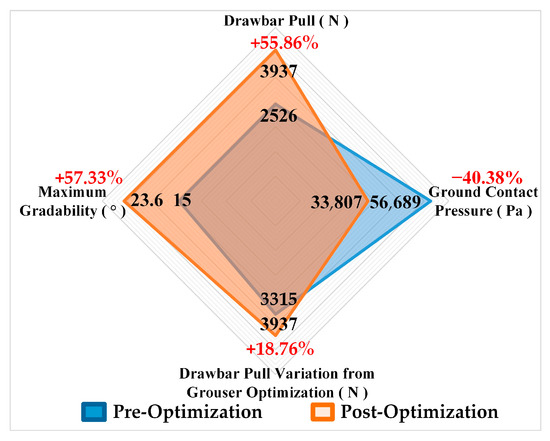
Figure 22.
Driving performance metrics comparison: pre- vs. post-optimization.
6. Conclusions
This study systematically investigated the influence of track and grouser structural parameters on the tractive performance of UATVs using integrated approaches encompassing numerical modeling, DEM-MBD coupling simulations, and soil bin testing. A mathematical optimization model was established and successfully applied to refine the structural parameters of the track system and grousers. Key findings are summarized as follows:
1. Soil Thrust Mechanism Elucidated: A numerical soil thrust model for single-track shoes was developed based on terramechanics theory. This model revealed distinct mechanisms through which structural parameters govern soil thrust in three critical zones: (i) the grouser base and track base, where track parameters (length, width) modulate pressure–sinkage relationships; (ii) the grouser shear plane, where grouser parameters (height, spacing, V-shaped angle) predominantly dictate shear stress-displacement behavior; and (iii) the track/grouser flanks. Significant mechanical coupling effects across these domains were demonstrated.
2. DEM-MBD Simulation Insights: A validated DEM-MBD coupling simulation method was employed to analyze grouser–soil interaction mechanisms. Simulation results indicate that soil thrust increases substantially with grouser height and V-shaped angle but is negatively correlated with grouser spacing. Among these parameters, grouser height exhibits the most significant influence on soil thrust generation.
3. Experimental Validation: Soil bin testing provided robust experimental validation for the numerical model and confirmed the efficacy of the DEM-MBD coupling simulation methodology. These tests offer valuable novel insights for investigating complex terrain interaction mechanisms.
4. Optimized Performance Gains: The optimization design process significantly enhanced the structural parameters. The optimized track configuration yields remarkable improvements: a 40.38% reduction in ground contact pressure, a 55.86% increase in drawbar pull, and a 57.33% enhancement in maximum gradability. These improvements dramatically elevate the UATV’s tractive performance on beach terrains.
In summary, this study not only provides novel experimental and simulation methodologies for investigating the tractive performance of tracked vehicles but also holds significant engineering applicability for optimizing track and grouser structural parameters to enhance vehicular tractive performance.
7. Future Prospects
This study has conducted substantial work on the optimization of single-track structural parameters, yet two limitations remain: First, the soil thrust model assumes no lateral slippage and a stationary track-wheel center, investigating only the influence mechanism between track/grouser structural parameters and soil thrust under straight-line level-ground conditions. It neglects the effects of vehicle dynamics factors and inter-track coupling effects. Second, constrained by laboratory conditions, experimental validation was confined to scaled-down soil bin tests, failing to fully account for scale effects and boundary effects.
Subsequent research efforts will be concentrated on two primary aspects: first, integrating rutting effects and vehicle dynamics factors to optimize structural parameters of front/rear axle tracks; second, conducting full-scale tractive performance tests to validate improvements in vehicle mobility after track optimization.
Author Contributions
Y.C. wrote the manuscript and developed the dynamic model and the DEM model; X.X. assisted with the structural parameter optimization design; W.W. was in charge of the numerical calculations; X.G. assisted with the simulation in Recurdyn; C.Y. assisted with the soil bin test. All authors have read and agreed to the published version of the manuscript.
Funding
This study was supported in part by the National Natural Science Foundation of China under grants 52205485, 52202485 and 52201387.
Data Availability Statement
The datasets presented in this article are not readily available because the data are part of an ongoing study. Requests to access the datasets should be directed to the corresponding author.
Acknowledgments
We thank Yuanjiang Tang for assisting with the simulations in EDEM. All authors have approved the submission, and no conflicts of interest exist.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Wang, L.; Chen, X.; Wang, L.; Li, Z.; Yang, W. Mechanical properties and soil failure process of interface between grouser of tracked mining vehicle and deep-sea sediment. Ocean Eng. 2023, 285, 115336. [Google Scholar] [CrossRef]
- Li, J.; Sun, S.; Sun, C.; Liu, C.; Tang, W.; Wang, H. Analysis of Effect of Grouser Height on Tractive Performance of Tracked Vehicle under Different Moisture Contents in Paddy Soil. Agriculture 2022, 12, 1581. [Google Scholar] [CrossRef]
- Bernstein, R. Problems of the Experimental Mechanics of Motor Ploughs. Der Mot. 1913, 16, 199–206. [Google Scholar]
- Micklethwait, E.W.E. Soil Mechanics in Relation to Fighting Vehicles; Military College of Science: Swindon, UK, 1994. [Google Scholar]
- Bekker, M.G. Theory of Land Locomotion; The University of Michigan Press: Ann Arbor, MI, USA, 1956. [Google Scholar]
- Janosi, Z.; Hanamoto, B. Analytical determination of drawbar pull as a function of slip for tracked vehicles in deformable soils. In Proceedings of the 1st International Conference on Terrain-Vehicle System, Turin, Italy, 1 January 1961. [Google Scholar]
- Janosi, Z.; Hanamoto, B. Analysis and Presentation of Soil-vehicle Mechanics Data. Terramechanics 1965, 2, 69–79. [Google Scholar] [CrossRef]
- Reece, A.R. Principles of Soil-vehicle mechanics. Terramechanics 1965, 180, 45–67. [Google Scholar] [CrossRef]
- Wong, J.Y.; Reece, A.R. Prediction of Rigid Wheel Performance Based on the Analysis of Soil-wheel Stresses: Part I: Performance of Driven Rigid Wheels. Terramechanics 1967, 4, 81–98. [Google Scholar] [CrossRef]
- Wong, J.Y.; Reece, A.R. Prediction of Rigid Wheel Performance Based on the Analysis of Soil-wheel Stresses: Part II. Performance of Towed Rigid Wheels. Terramechanics 1967, 4, 7–25. [Google Scholar] [CrossRef]
- Kejian, Z. Vehicle-Terrain Mechanics; National Defense Industry Press: Beijing, China, 2002; Volume 323. [Google Scholar]
- Gregory, B.M. Introduction to Terrain-Vehicle System; University of Michigan Press: Charleston, SC, USA, 1969. [Google Scholar]
- Wong, J.Y. Theory of Ground Vehicles; John Wiley & Sons, Inc.: Montreal, QC, Canada, 2001. [Google Scholar]
- Jiangang, W. Effect of grouser shape on tangential traction force of crawler tractors. Laiyang Agric. Coll. 1990, 4, 314–318. [Google Scholar]
- Zhensheng, L.; Jiangsheng, K.; Jumei, L. Analysis of track adhesion capability in dry sandy soil areas. Agric. Mech. Res. 2004, 3, 250–252. [Google Scholar]
- Park, W.Y.; Chang, Y.C.; Lee, S.S.; Hong, J.H.; Park, J.G.; Lee, K.S. Prediction of the tractive performance of a flexible tracked vehicle. Terramechanics 2008, 45, 13–23. [Google Scholar] [CrossRef]
- Chen, Y.; Xu, X.; Wang, W.; Gao, X.; Yang, C. Effect of adhesive substrate between track shoes and grousers on adhesion performance of mining collectors. Trans. Chin. Soc. Agric. Eng. 2010, 10, 140–145. [Google Scholar]
- Hambleton, J.P.; Drescher, A. Modeling wheel-induced rutting in soils: Indentation. Terramechanics 2008, 45, 201–211. [Google Scholar] [CrossRef]
- Hambleton, J.P.; Drescher, A. Modeling wheel-induced rutting in soils: Rolling. Terramechanics 2009, 46, 35–47. [Google Scholar] [CrossRef]
- Yang, C. Research on the Adhesion Property of High-Speed Track on Soft Ground and Optimization of Track Shoe; Beijing Institute of Technology: Beijing, China, 2015. (In Chinese) [Google Scholar]
- Yang, P.; Zang, M.; Zeng, H. DEM–FEM simulation of tire–sand interaction based on improved contact model. Comput. Part. Mech. 2019, 7, 1–15. [Google Scholar] [CrossRef]
- Shaikh, S.A.; Li, Y.; Ma, Z.; Chandio, F.A.; Tunio, M.H.; Liang, Z.; Solangi, K.A. Discrete element method (DEM) simulation of single grouser shoe-soil interaction at varied moisture contents. Comput. Electron. Agric. 2021, 191, 106538. [Google Scholar] [CrossRef]
- Shaikh, S.A.; Li, Y.; Zheng, M.; Chandio, F.A.; Ahmad, F.; Tunio, M.H.; Abbas, I. Effect of Grouser Height on the Tractive Performance of Single Grouser Shoe under Different Soil Moisture Contents in Clay Loam Terrain. Sustainability 2021, 13, 1156. [Google Scholar] [CrossRef]
- He, D.; Si, Q.; Meng, X.; Li, Y. Effect of track shoes structural parameters on traction performance of unmanned underwater tracked bulldozer. Ocean. Eng. 2021, 237, 109655. [Google Scholar]
- Kim, J.T.; Choi, H.J.; Oh, Y.J. Optimization of grouser shape ratio for coastal terrain driving device using discrete element method. Terramechanics 2023, 110, 27–37. [Google Scholar] [CrossRef]
- Xie, D.; He, J.; Liu, T.; Liu, C.; Zhao, G.; Chen, L. Establishment and validation the DEM-MBD coupling model of flexible straw-Shajiang black soil-walking mechanism interactions. Comput. Electron. Agric. 2024, 224, 16. [Google Scholar] [CrossRef]
- Fu, J.; Li, J.; Tang, X.; Wang, R.; Chen, Z. Optimization of Structure Parameters of the Grouser Shoes for Adhesion Reduction under Black Soil. Agriculture 2021, 11, 795. [Google Scholar] [CrossRef]
- Wei, D.; Yang, Q.; Cao, H.; Xia, J.; Liu, G. Parameter optimization and tractive performance evaluation of tracked miner. Mar. Georesources Geotechnol. 2025, 43, 168–182. [Google Scholar] [CrossRef]
- Xueyuan, L. Optimal Design of the Track Shoe for Tracked Vehicle; Beijing Institute of Technology: Beijing, China, 2016. (In Chinese) [Google Scholar]
- Linxuan, Z. Theory and Simulation Research on Sandy Tractive Performance of Tracked Vehicle under Multi-Operation Conditions; National University of Defense Technology: Changsha, China, 2020. (In Chinese) [Google Scholar]
- Wang, W.H.; Chen, Y.Y.; Li, Y.F.; Liu, J.W. Tractive performance evaluation for unmanned amphibious traction vehicles on beach areas. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2025, 09544070251337210. [Google Scholar] [CrossRef]
- Yang, W.; Xia, K.; Fan, S.; Wang, L.; Li, T.; Zhang, J.; Feng, Y.A. Multi-Strategy Whale Optimization Algorithm and Its Application. Eng. Appl. Artif. Intell. 2022, 108, 104558. [Google Scholar] [CrossRef]
- Kalita, K.; Ramesh, J.V.N.; Čep, R.; Jangir, P.; Pandya, S.B.; Ghadai, R.K.; Abualigah, L. Many-Objective Whale Optimization Algorithm for Engineering Design and Large-Scale Many-Objective Optimization Problems. Int. J. Comput. Intell. Syst. 2024, 17, 171. [Google Scholar] [CrossRef]
- Wei, J.; Gu, Y.; Yan, Y.; Li, Z.; Lu, B.; Pan, S.; Cheong, N. LSEWOA: An Enhanced Whale Optimization Algorithm with Multi-Strategy for Numerical and Engineering Design Optimization Problems. Sensors 2025, 25, 2054. [Google Scholar] [CrossRef]
- Wei, J.; Gu, Y.; Lu, B.; Cheong, N. RWOA: A novel enhanced whale optimization algorithm with multi-strategy for numerical optimization and engineering design problems. PLoS ONE 2025, 20, e0320913. [Google Scholar] [CrossRef]
- Punia, P.; Raj, A.; Kumar, P. An Enhanced Beluga Whale Optimization Algorithm for Engineering Optimization Problems. J. Syst. Sci. Syst. Eng. 2024, 1–38. [Google Scholar] [CrossRef]
- Yuan, S. Analysis of the Contact Mechanics Characteristics of the Track of Digging and Bolting Machine Based on DEM-MBD Coupling; Liaoning Technical University: Fuxin, China, 2021. [Google Scholar]
- Giulio, B.M. The Revenge of the Tracks: Promising developments in rubber tracks. Mil. Technol. 2023, 47, 43–48. [Google Scholar]
- Hawkes, J. Continuous revolution: The rise of Composite Rubber Track technology. Jane’s Int. Def. Rev. IHS Jane’s Int. Def. Rev. 2021, 54, 36–43. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).