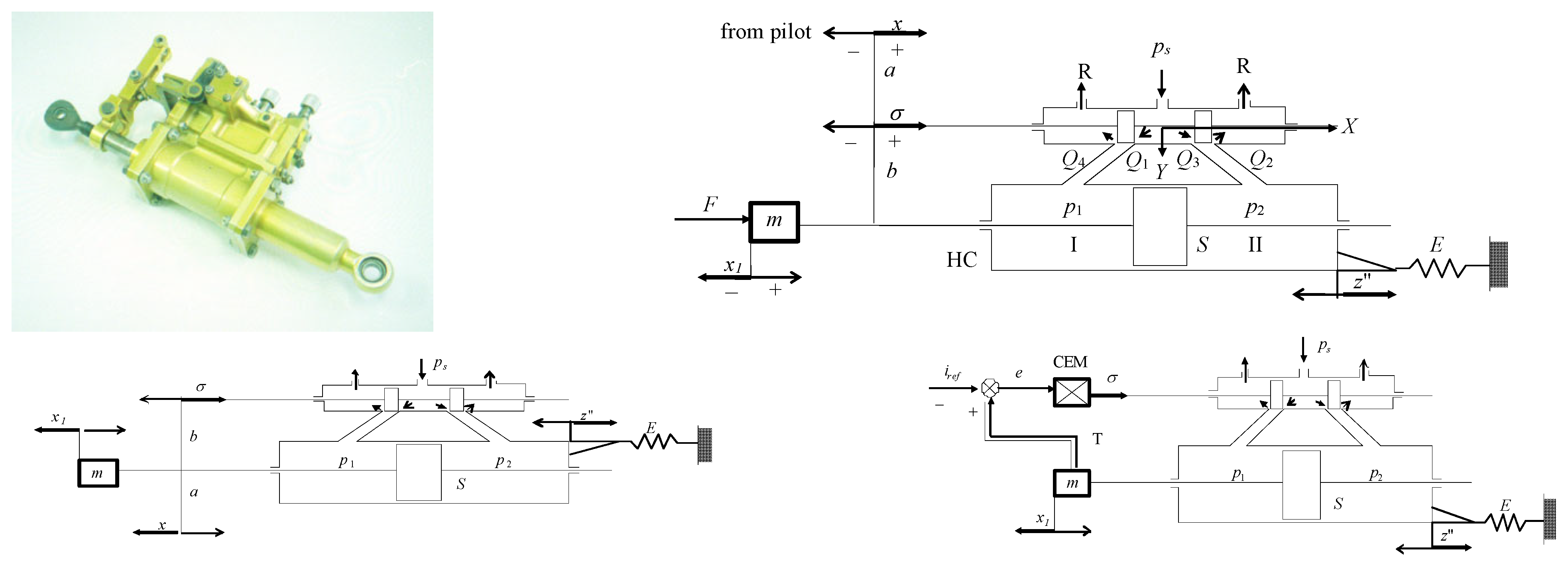
On Control Synthesis of Hydraulic Servomechanisms in Flight Controls Applications
Abstract
1. Introduction
Historical Comments
2. The Absolute Stability of the Loaded Electrohydraulic Servomechanism
2.1. Lurie–Lefschetz Approach with Indirect Control
- -
- the control signal equation
- -
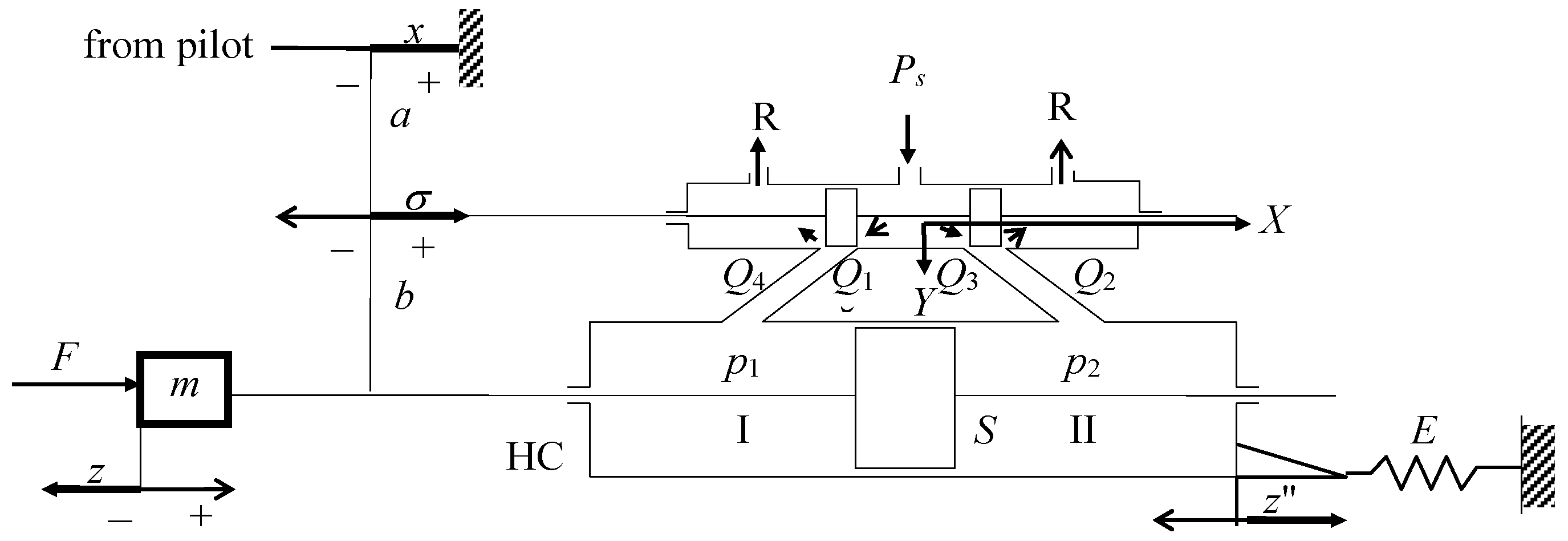
- the nonlinear equation of the servo-valve or distributor flow rate Q [28]
- -
- the flow rate balance equation in cylinder
- -
- the dynamic equilibrium equation of forces at the rod of the piston
2.2. Compromise MM Versus MI. The Absolute Stability Cone in the Feedback Vector Space
2.3. Absolute Stability and the Frequency Criterion of V. M. Popov. Extension in the Stochastic Domain
3. The Kinematics of the Rigid Feedback Linkage, the Impedance of the Mechano-Hydraulic Servomechanism and the Flutter Occurrence
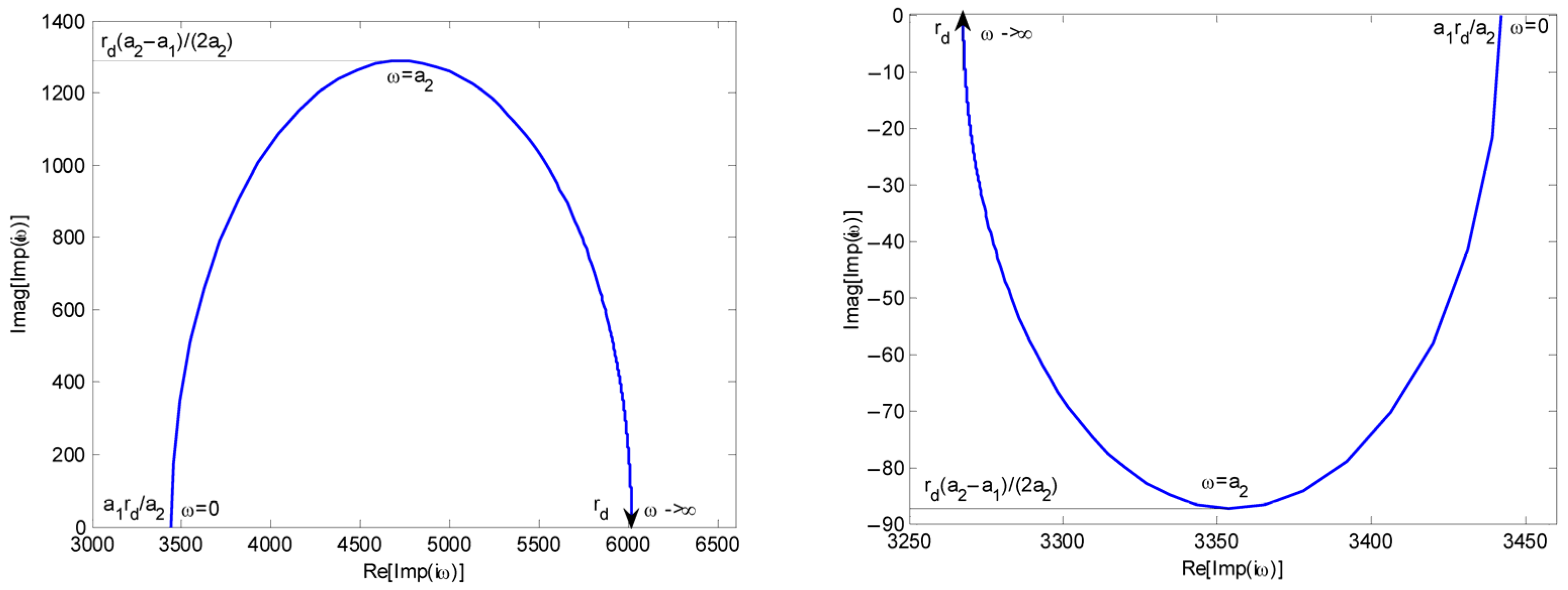
3.1. Impedance Mathematical Model
3.2. Main Result
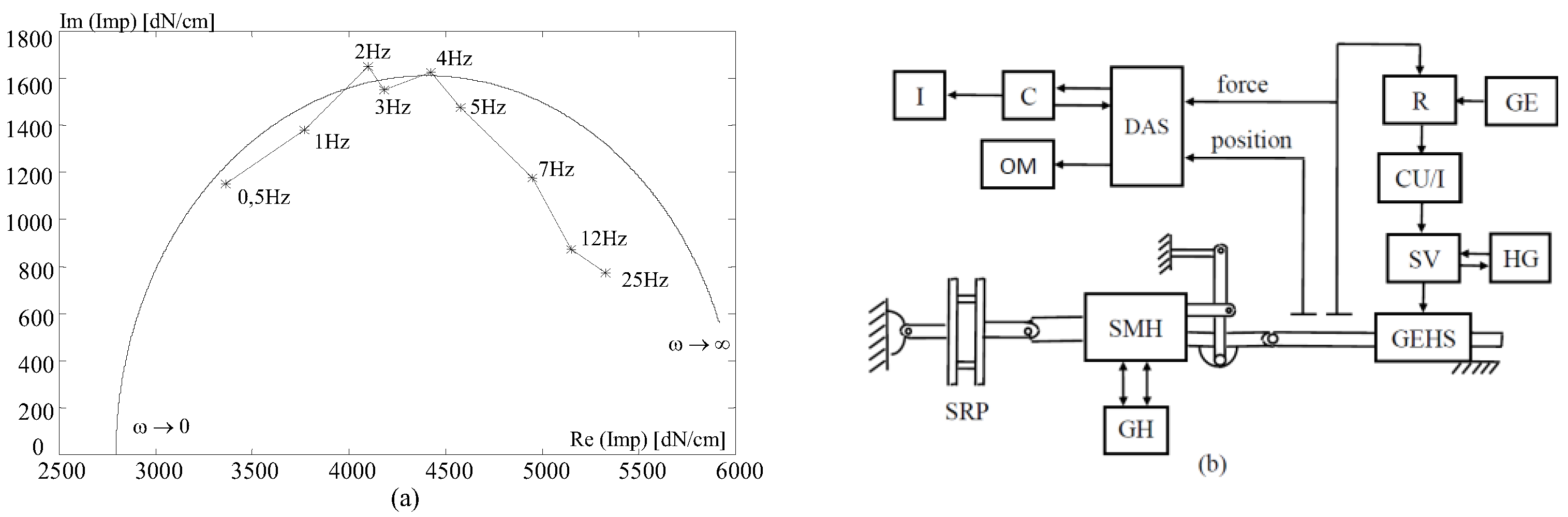
3.3. Impedance Function Measuring in Laboratory
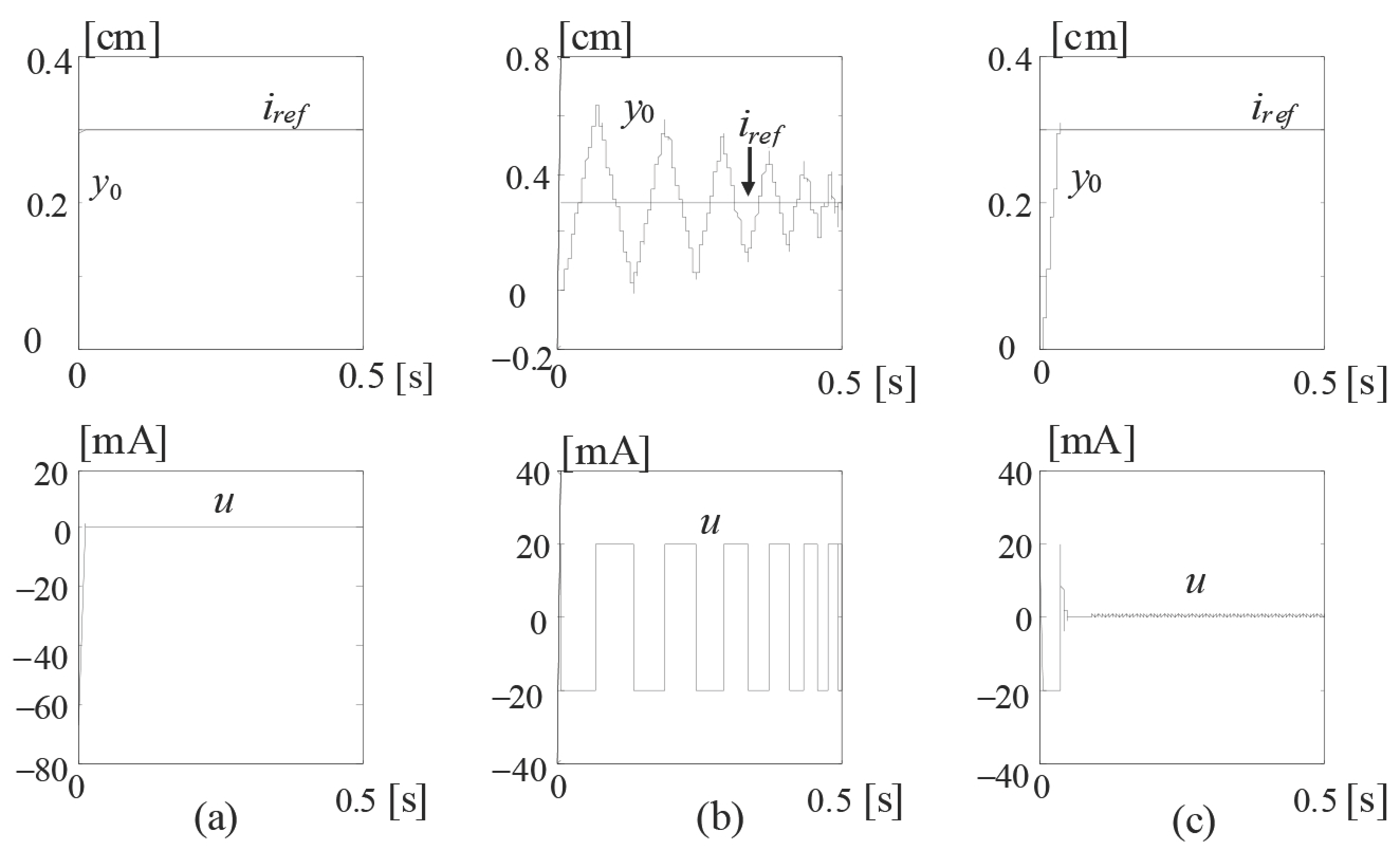
4. Robust Synthesis with Anti-Windup Compensation for Electrohydraulic Servomechanisms
4.1. Introduction
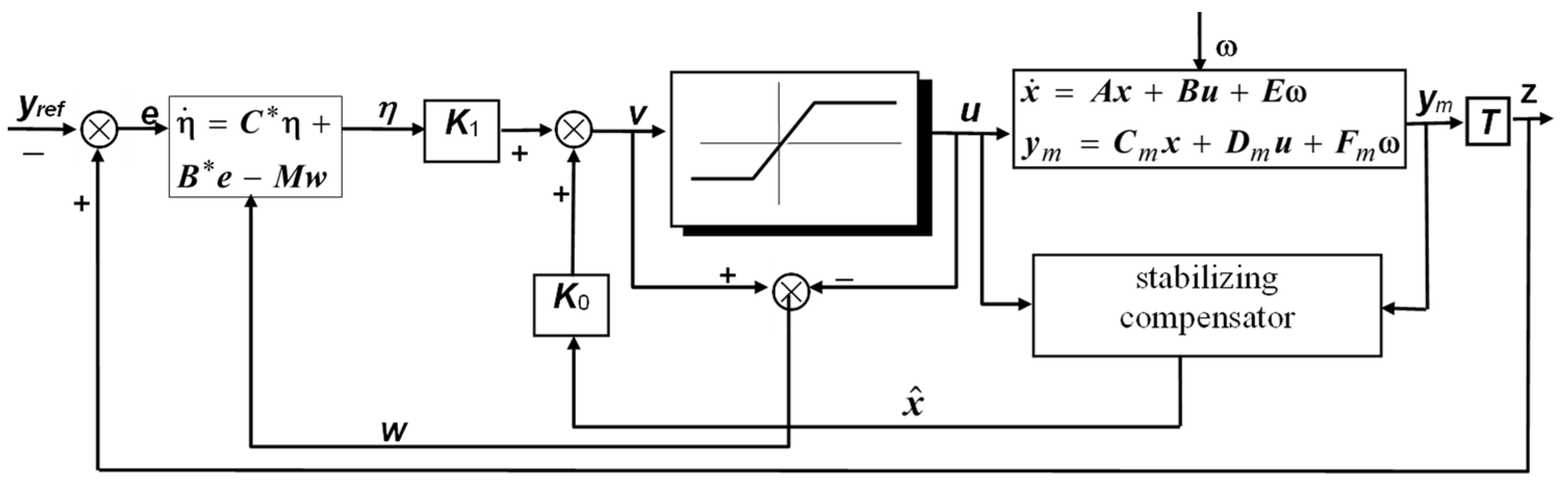
4.2. Robust Servomechanism Problem
4.3. Contributions to Servo-Compensator and Stabilizing Compensator Choices in the Case of Electrohydraulic Servo
4.4. Anti-Windup Compensation of the Saturating Electrohydraulic Servo
4.5. Numerical Application
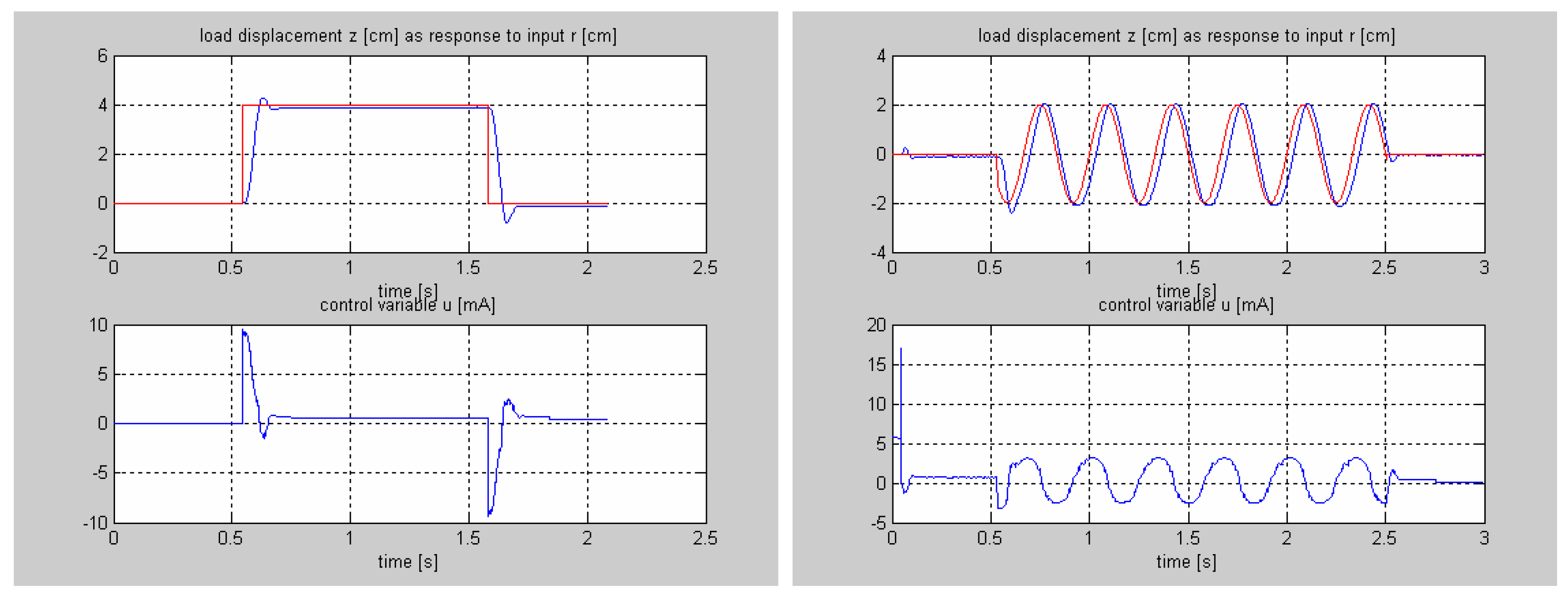
5. Neuro-Fuzzy Synthesis of Electrohydraulic Servo for Motion Control—Experimental Validation
5.1. Introduction
5.2. FSNC Description
5.3. Numerical Application
6. A Brief Overview of Some Recent Results in Hydraulic Servomechanisms
7. Some Final Remarks
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| the n-dimensional vector representing the state variables of the plant and the control (scalar) variable [mm] for mechano-hydraulic servomechanism | |
| A | a constant non-singular, n × n-dimensional matrix |
| b, c | n-dimensional vectors |
| h(σ) | the nonlinear, admissible characteristic of the actuator |
| r | a scalar |
| S | the active area of the piston |
| Vc | the cylinder chamber volume in mean position of the piston |
| kl | the internal leakage coefficient, including the flow rate-pressure gain |
| flow gain | |
| B | the bulk modulus of hydraulic oil |
| the displacement of the inertial load reduced at the piston rod | |
| the reference signal | |
| the control variable, for electro-hydraulic servomechanism | |
| the amplification of the spool displacement voltage | |
| the components of the feedback vector furnished by a system of position, velocity and acceleration transducers and processed in a regulator | |
| ksv | the velocity coefficient of the servo-valve [m/s], |
| cd | the flow rate coefficient |
| ps [daNcm−2] | the supply pressure |
| ρ | the fluid density [kgcm-3] |
| a() [cm2] | the admissible function of the control variable which determines the surface exposed to the fluid flow through the servo-valve orifices |
| the load pressure drop on the hydro-cylinder | |
| impedance function | |
| kinematic coefficients involving the values a, b (see Figure 5) | |
| the mounting structure stiffness | |
| the state of the system | |
| the control | |
| the regulated output | |
| the measurable output | |
| the disturbance | |
| the reference input | |
| the error in the system | |
| k | the equivalent spring stiffness |
| f | the equivalent damper coefficient |
| where V is the cylinder semi-volume and Bu is the bulk modulus of the used hydraulic fluid | |
| measured in cm3/(smA), is the derivative of the flow characteristic with respect to the input (control) electrical current of the servo-valve | |
| ku = ksvkVmA; kp, | measured in V/cm, is the gain of the position transducer |
| FSNC | fuzzy supervised neurocontrol |
| EHMCS | electrohydraulic motion control system |
| AW | anti-windup |
| LEHSM | loaded electrohydraulic servomechanism |
| EHMCS | Electro-Hydraulic Motion Control System |
| RSP | robust servomechanism problem |
| MI | mathematical instruments |
| MM | mathematical models |
| PHM | physical model |
| CS | controlled system |
| PHO | physical object |
References
- INCAS Bulletin. Available online: https://bulletin.incas.ro/files/cv__ursu-i__2024.pdf (accessed on 15 May 2025).
- Ursu, I.; Ursu, F.; Sireteanu, T. About absolute stable synthesis of electrohydraulic servo; Technical Papers of AIAA (AIAA-99-4090). In Proceedings of the Guidance, Navigation and Control Conference, Portland, OR, USA, 9–11 August 1999; Volume 2, pp. 848–858. [Google Scholar]
- Ursu, I. The kinematics of the rigid feedback linkage, the impedance of the hydraulic servomechanism and the flutter occurrence. INCAS Bull. 2012, 4, 63. [Google Scholar] [CrossRef]
- Ursu, I.; Tecuceanu, G.; Ursu, F.; Sireteanu, T.; Vladimirescu, M. From robust control to anti-windup compensation of electrohydraulic servo actuators. Aircr. Eng. Aerosp. Technol. 1998, 70, 259–264. [Google Scholar] [CrossRef]
- Ursu, I.; Ursu, F.; Tecuceanu, G.; Cristea, R. Fuzzy supervised neurocontrol of electrohydraulic servos. Proc. Appl. Math. Mech. 2006, 6, 851–852. [Google Scholar] [CrossRef]
- Ursu, I.; Ursu, F.; Popescu, F. Backstepping design for controlling electrohydraulic servos. J. Frankl. Inst. 2006, 343, 94–110. [Google Scholar] [CrossRef]
- Ursu, I. Dealing with mathematical modeling in applied control. INCAS Bull. 2011, 3, 87–93. [Google Scholar] [CrossRef]
- Popper, K.R. The Logic of Scientific Discovery; Eight impression; Hutchinson & Co. Publishers Ltd.: London, UK, 1975. [Google Scholar]
- Astrom, K.J.; Hagglund, T. PID Control. In The Control Handbook; Levine, W.S., Ed.; CRC Press: Piscataway, NJ, USA, 1996; pp. 198–209. [Google Scholar]
- Ursu, I.; Tecuceanu, G.; Ursu, F.; Cristea, R. Neuro-fuzzy control is better than crisp control. Acta Univ. Apulensis 2006, 11, 259–269. [Google Scholar]
- Toader, A.; Ursu, I. Pilot modeling based on time delay synthesis. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2014, 228, 740–754. [Google Scholar] [CrossRef]
- Ursu, I.; Ursu, F.; Sireteanu, T.; Stammers, C.W. Artificial intelligence-based synthesis of semiactive suspension systems. Shock Vib. Dig. 2000, 32, 3–10. [Google Scholar] [CrossRef]
- Ursu, I.; Ursu, F. Airplane ABS control synthesis using fuzzy logic. J. Intell. Fuzzy Syst. 2005, 16, 23–32. [Google Scholar] [CrossRef]
- Ursu, I.; Tecuceanu, G.; Toader, A.; Călinoiu, C.; Ursu, F.; Berar, V. Neuro-fuzzy control synthesis for hydrostatic type servoactuators. Experimental results. INCAS Bull. 2009, 1, 136–150. [Google Scholar] [CrossRef]
- Ion-Guţă, D.D.; Ursu, I.; Toader, A.; Enciu, D.; Dancă, P.A.; Nastase, I.; Croitoru, C.V.; Bode, F.I.; Sandu, M. Advanced thermal manikin for thermal comfort assessment in vehicles and buildings. Appl. Sci. 2022, 12, 1826. [Google Scholar] [CrossRef]
- Ursu, I.; Toader, A.; Enciu, D.; Guţă, D.D.I.; Stoica, C. Towards the artificial intelligent control applied on damping turbulence vibrations of an airplane wing. In Proceedings of the AIAA SciTech 2025 Forum, Orlando, FL, USA, 6–10 January 2025. [Google Scholar] [CrossRef]
- Han, J.-Q. Robustness of Control Systems and the Godel’s Incomplete Theorem. Control Theory Appl. 1999, 16, 149–155. [Google Scholar]
- Han, J.-Q. Control theory: It is a theory of model or control? Syst. Sci. Math. Sci. 1989, 9, 328–335. [Google Scholar]
- Zhang, R.J.; Zhigang, W.; Chao, Y. Dynamic stiffness testing-based flutter analysis of a fin with an actuator. Chin. J. Aeronaut. 2015, 28, 1400–1407. [Google Scholar] [CrossRef]
- IAR-93 Vultur. Available online: https://en.wikipedia.org/wiki/IAR-93_Vultur (accessed on 15 May 2025).
- Ursu, I. Study of the Stability and Compatibility of the Hydraulic Servomechanisms from the Primary Flight Controls; Report No. 34125; IMFCA: Bucharest, Romania, 1974. (In Romanian)
- Dowty Group. Available online: https://en.wikipedia.org/wiki/DowtyGroup (accessed on 15 May 2025).
- Ursu, I.; Vladimirescu, M.; Ursu, F. About Aeroservoelasticity Criteria for Electrohydraulic Servomechanisms Synthesis. In Proceedings of the 20th Congress of the International Council of the Aeronautical Sciences, Sorrento, Napoli, Italy, 8–13 September 1996; Volume 2, pp. 2335–2344. [Google Scholar]
- Letov, A.M. Stability of Nonlinear Control Systems, 1st ed.; Princeton University Press: Moskva, Russia, 1962. (In Russian) [Google Scholar]
- Aizerman, M.A.; Gantmaher, F.R. The Absolute Stability of Control Systems; Holden-Day: Moskva, Russia, 1963. (In Russian) [Google Scholar]
- Lefschetz, S. Stability of Nonlinear Control Systems; Academic Press: Cambridge, MA, USA, 1965. [Google Scholar]
- Hsu, J.C.; Meyer, A.U. Modern Control Principles and Applications; McGraw-Hill: New York, NY, USA, 1968. [Google Scholar]
- Merritt, H.E. Hydraulic Control Systems; John Wiley & Sons., Inc.: New York, NY, USA, 1966. [Google Scholar]
- Halanay, A.; Safta, C.A.; Ursu, I.; Ursu, F. Stability of equilibria in a four–dimensional nonlinear model of a hydraulic servomechanism. J. Eng. Math. 2004, 49, 391–406. [Google Scholar] [CrossRef]
- Ursu, I.; Ursu, F. Active and Semiactive Control; Romanian Academy Publishing House: Bucharest, Romania, 2002. (In Romanian) [Google Scholar]
- Morozan, T. The Method of V. M. Popov for Control Systems with Random Parameters. J. Math. Anal. Appl. 1966, 16, 201–215. [Google Scholar] [CrossRef]
- INCAS and Dowty Group. Collaboration Report with INCAS Elie Carafoli; Dowty Boulton Paul Ltd.: Wolverhampton, UK, 1979. [Google Scholar]
- Ursu, I.; Ursu, F. Some absolute stability restrictions in output feedback synthesis of electrohydraulic servos. In Proceedings of the International Conference on Recent Advances in Aerospace Actuation Systems and Components, Toulouse, France, 24–26 November 2004; pp. 173–182. [Google Scholar]
- De la Sen, M. Hyperstability of Linear Feed-Forward Time-Invariant Systems Subject to Internal and External Point Delays and Impulsive Nonlinear Time-Varying Feedback Controls. Computation 2023, 11, 134. [Google Scholar] [CrossRef]
- IAR 99. Available online: https://en.wikipedia.org/wiki/IAR_99 (accessed on 10 April 2025).
- Ursu, I.; Toader, A.; Balea, S.; Halanay, A. New stabilization and tracking control laws for electrohydraulic servomechanisms. Eur. J. Control 2013, 19, 65–80. [Google Scholar] [CrossRef]
- Davison, E.J. The robust control of a servomechanism problem for linear time-invariant multivariable system. IEEE Trans. Autom. Control 1976, 21, 25–34. [Google Scholar] [CrossRef]
- Krikelis, N.J.; Barkas, S.K. Design of tracking systems subject to actuator saturation. Int. J. Control 1984, 39, 667–682. [Google Scholar] [CrossRef]
- Park, J.K.; Choi, C.-H. A compensation method for improving the performance of multivariable control systems with saturating actuators. Control Theory Adv. Technol. 1993, 9, 305–322. [Google Scholar]
- Ursu, I.; Popescu, F.; Vladimirescu, M.; Costin, R. On some linearization methods of the generalized flow rate characteristic of the hydraulic servomechanism. Rev. Roum. Des Sci. Tech. Série Mécanique Appliquée 1994, 39, 207–217. [Google Scholar]
- Davison, E.J.; Goldenberg, A. Robust control of a general servomechanism problem: The servo-compensator. Automatica 1975, 11, 461–471. [Google Scholar] [CrossRef]
- Davison, E.J.; Ferguson, J. The design of controllers for the multivariable robust servomechanism problem using parameter optimization methods. IEEE Trans. Autom. Control 1981, 26, 93–110. [Google Scholar] [CrossRef]
- Shearer, J.L. Dynamic characteristics of valve-controlled hydraulic servomotors. Trans. ASME 1954, 76, 895–903. [Google Scholar] [CrossRef]
- Scherzinger, B.M. The design of servomechanism controllers for uncertain plants and input signals. Int. J. Control 1986, 44, 1587–1602. [Google Scholar] [CrossRef]
- Bucy, R.S. Lectures on Discrete Time Filtering; Springer: Berlin/Heidelberg, Germany, 1994. [Google Scholar]
- Ursu, I.; Ursu, F. New results in control synthesis for electrohydraulic servos. Int. J. Fluid Power 2004, 5, 25–38. [Google Scholar] [CrossRef]
- Wang, P.K.C. Analytical design of electrohydraulic servomechanism with near time-optimal response. IEEE Trans. Autom. Control 1963, 8, 15–27. [Google Scholar] [CrossRef]
- Tapkir, A. A Comprehensive Overview of Gradient Descent and its Optimization Algorithms. Int. Adv. Res. J. Sci. Eng. Technol. 2023, 10, 37–45. [Google Scholar] [CrossRef]
- Tyan, F.; Bernstein, S. Anti-windup compensator synthesis for systems with saturating actuators. In Proceedings of the 33rd Conference on Decision and Control, Lake Buena Vista, FL, USA, 14–16 December 1994; pp. 150–155. [Google Scholar]
- Ghazi Zadeh, A.; Fahim, A.; El-Gindy, M. Neural network and fuzzy logic applications to vehicle systems: Literature survey. Int. J. Veh. Des. 1997, 18, 132–193. [Google Scholar]
- Tzes, A.; Peng, P.-Y. Fuzzy Neural Network Control for DC-Motor Micromaneuvering; Transactions of the ASME. J. Dyn. Syst. Meas. Control 1997, 119, 312–315. [Google Scholar] [CrossRef]
- Wang, L.-X.; Kong, H. Combining mathematical model and heuristics into controllers: An adaptive fuzzy control approach. In Proceedings of the 33rd IEEE Conference on Decision and Control, Lake Buena Vista, FL, USA, 14–16 December 1994; Volume 4, pp. 4122–4127. [Google Scholar]
- Halanay, A.; Safta, C.A.; Ursu, F.; Ursu, I. Stability analysis for a nonlinear model of a hydraulic servo in a servoelastic framework. Nonlinear Anal. Real World Appl. 2009, 10, 1197–1209. [Google Scholar] [CrossRef]
- Ursu, I.; Enciu, D.; Tecuceanu, G. Equilibrium stability of a nonlinear structural switching system with actuator delay. J. Frankl. Inst. 2019, 357, 3680–3701. [Google Scholar] [CrossRef]
- Enciu, D.; Halanay, A. Stability for a delayed switched nonlinear system of differential equations in a critical case. Int. J. Control 2021, 95, 1543–1550. [Google Scholar] [CrossRef]
- Enciu, D.; Halanay, A.; Toader, A.; Ursu, I. Lyapunov-Malkin type approach of equilibrium stability in a critical case applied to a switched model of a servomechanism with state delay. Int. J. Control 2024, 97, 520–531. [Google Scholar] [CrossRef]
- Li, X.; Chen, X.; Zhou, C. Combined Observer-Controller Synthesis for Electro-Hydraulic Servo System with Modeling Uncertainties and Partial State Feedback. J. Frankl. Inst. 2018, 355, 5893–5911. [Google Scholar] [CrossRef]
- Wan, Z.; Yue, L.; Fu, Y. Neural Network Based Adaptive Backstepping Control forElectro-Hydraulic Servo System Position Tracking. Int. J. Aerosp. Eng. 2022, 2022, 3069092. [Google Scholar] [CrossRef]
- Yao, Y. Model-based nonlinear control of hydraulic servosystems: Challenges, developments and perspectives. Front. Mech. Eng. 2018, 13, 179–210. [Google Scholar] [CrossRef]
- Feng, L.; Yan, H. Nonlinear Adaptive Robust Control of the Electro-Hydraulic Servo System. Appl. Sci. 2020, 10, 4494. [Google Scholar] [CrossRef]
- Ursu, I.; Giurgiutiu, V.; Toader, A. Towards spacecraft applications of structural health monitoring. INCAS Bull. 2012, 4, 111–124. [Google Scholar] [CrossRef]
- Enciu, D.; Ursu, I.; Toader, A. New Results Concerning SHM Technology Qualification for Transfer on Space Vehicles. Struct. Control Health Monit. 2017, 24, e1992. [Google Scholar] [CrossRef]
 , upper bound ------, lower bound -·-·-·-·-·-. = 0.1 mm; = 1 mm. Sources: Refs. [21,30,33].
, upper bound ------, lower bound -·-·-·-·-·-. = 0.1 mm; = 1 mm. Sources: Refs. [21,30,33].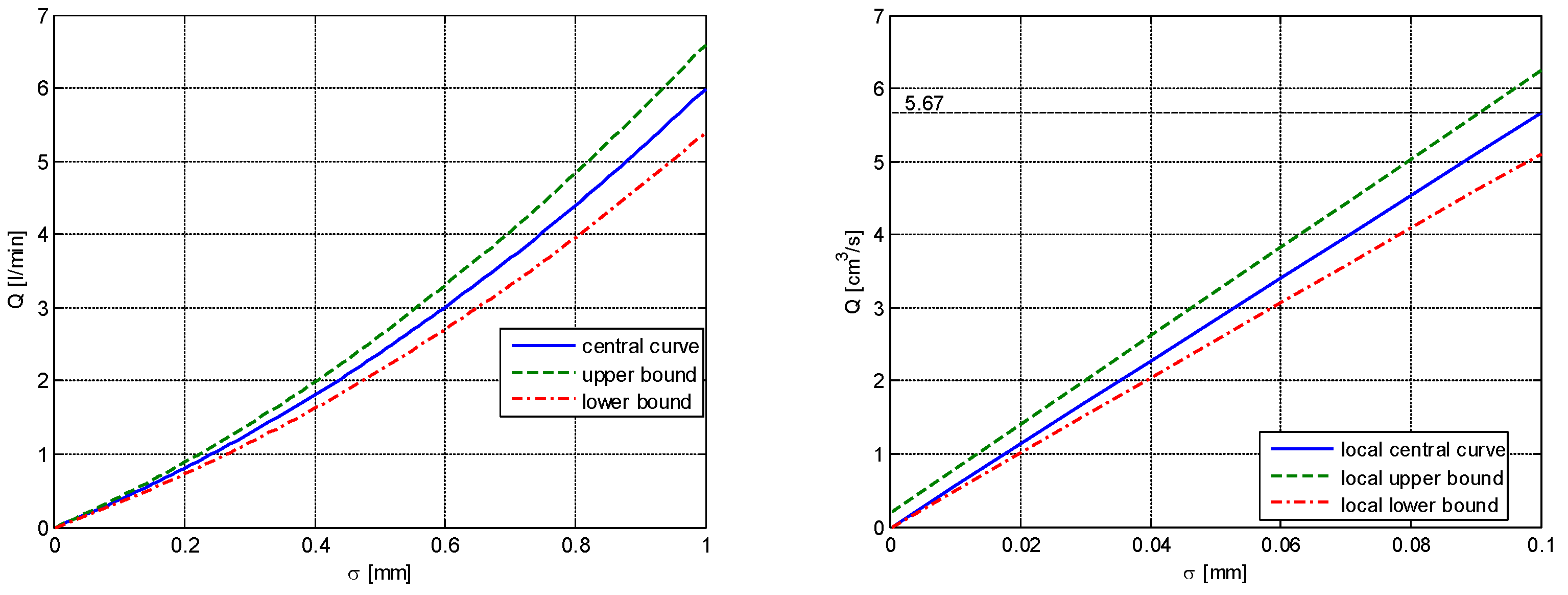

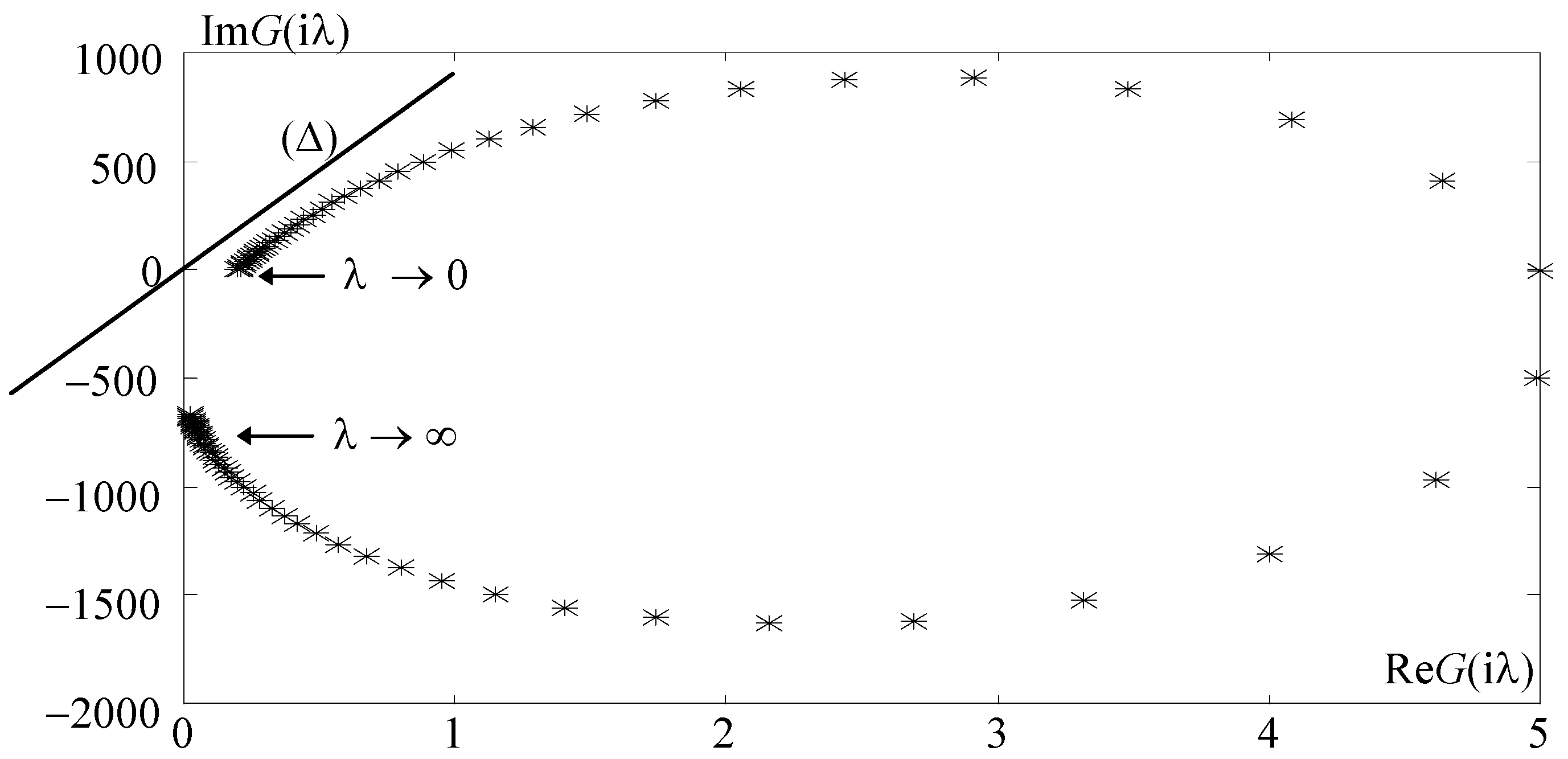
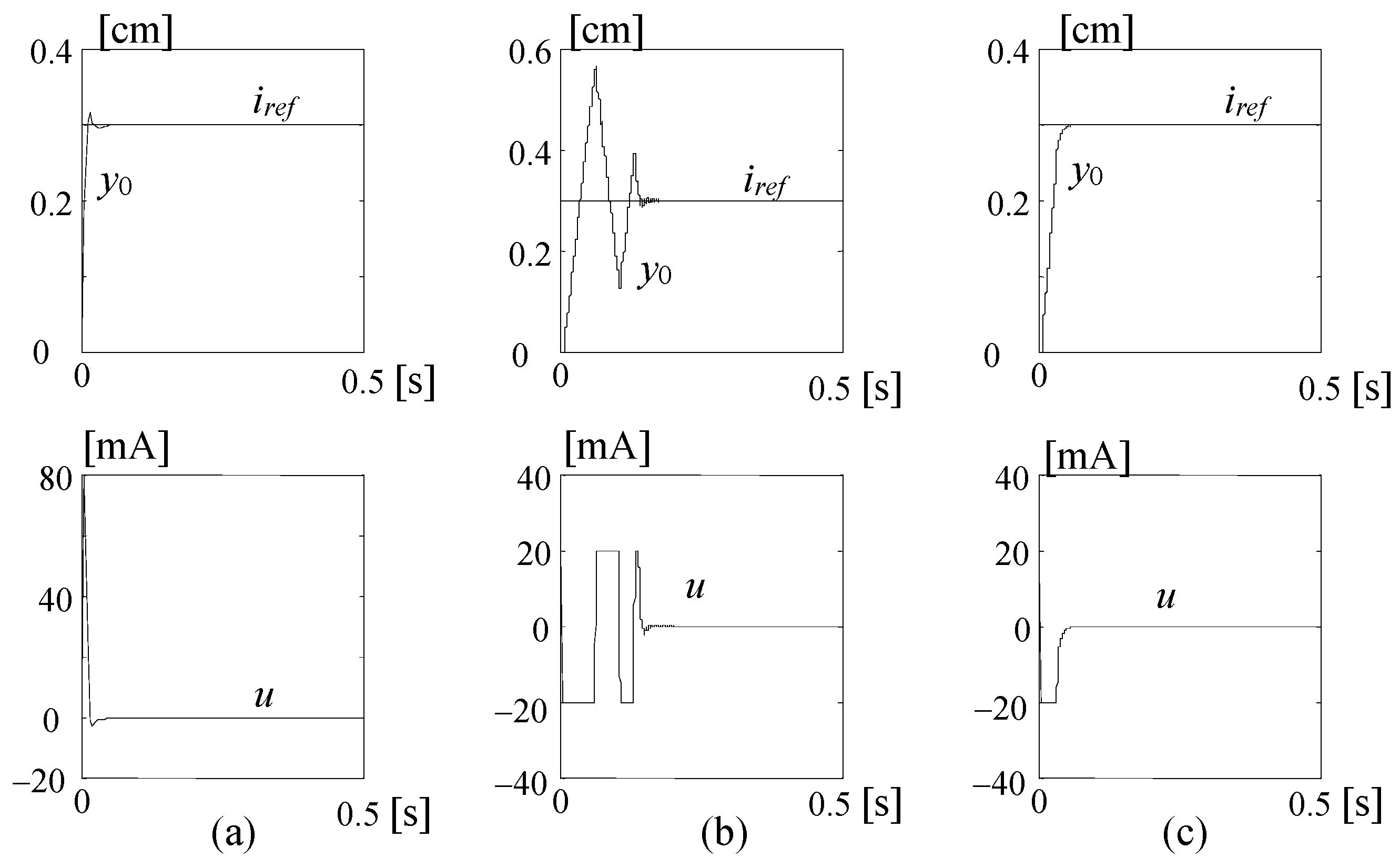


| Overall Control Valve Characteristics Flow [L/min]—Control [mm] | Local Control Valve Characteristics Flow —Control [mm] |
|---|---|
| central: | central: |
| upper bound: | upper bound: |
| lower bound: | lower bound: |
| choice of components inside the quadric of absolute stability (23); see Figure 1 for other notations; condition derived from Barbashin–Krasovskii theorem | |
| condition derived from V.M. Popov theorem |
| impedance definition, see (43), see Figure 5 | |
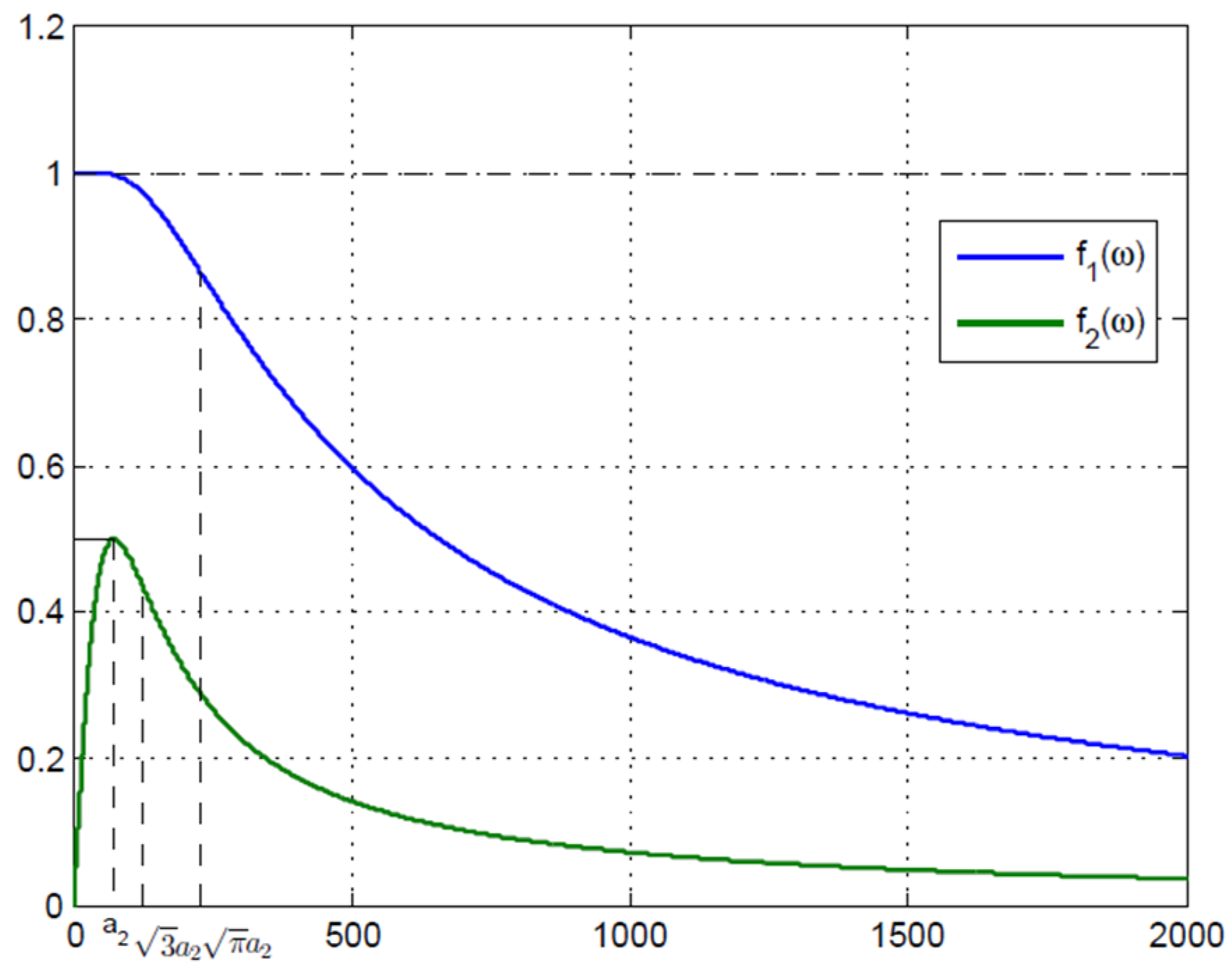
| Proposition 1 note: impedance can also be defined for the electrohydraulic servomechanism [30]. | see proof, see (48) see graphs of the impedance function in the two cases |
| 1 | 1 | 1 | 1 | |
| 0.0585 | 0.0037 | 0.2480 | 0.0155 | |
| 0 | 0 | 0.0169 | 0 | |
| 0 | 0 | 0 | 0 | |
| … | … | … | … | … |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ursu, I.; Enciu, D.; Toader, A. On Control Synthesis of Hydraulic Servomechanisms in Flight Controls Applications. Actuators 2025, 14, 346. https://doi.org/10.3390/act14070346
Ursu I, Enciu D, Toader A. On Control Synthesis of Hydraulic Servomechanisms in Flight Controls Applications. Actuators. 2025; 14(7):346. https://doi.org/10.3390/act14070346
Chicago/Turabian StyleUrsu, Ioan, Daniela Enciu, and Adrian Toader. 2025. "On Control Synthesis of Hydraulic Servomechanisms in Flight Controls Applications" Actuators 14, no. 7: 346. https://doi.org/10.3390/act14070346
APA StyleUrsu, I., Enciu, D., & Toader, A. (2025). On Control Synthesis of Hydraulic Servomechanisms in Flight Controls Applications. Actuators, 14(7), 346. https://doi.org/10.3390/act14070346