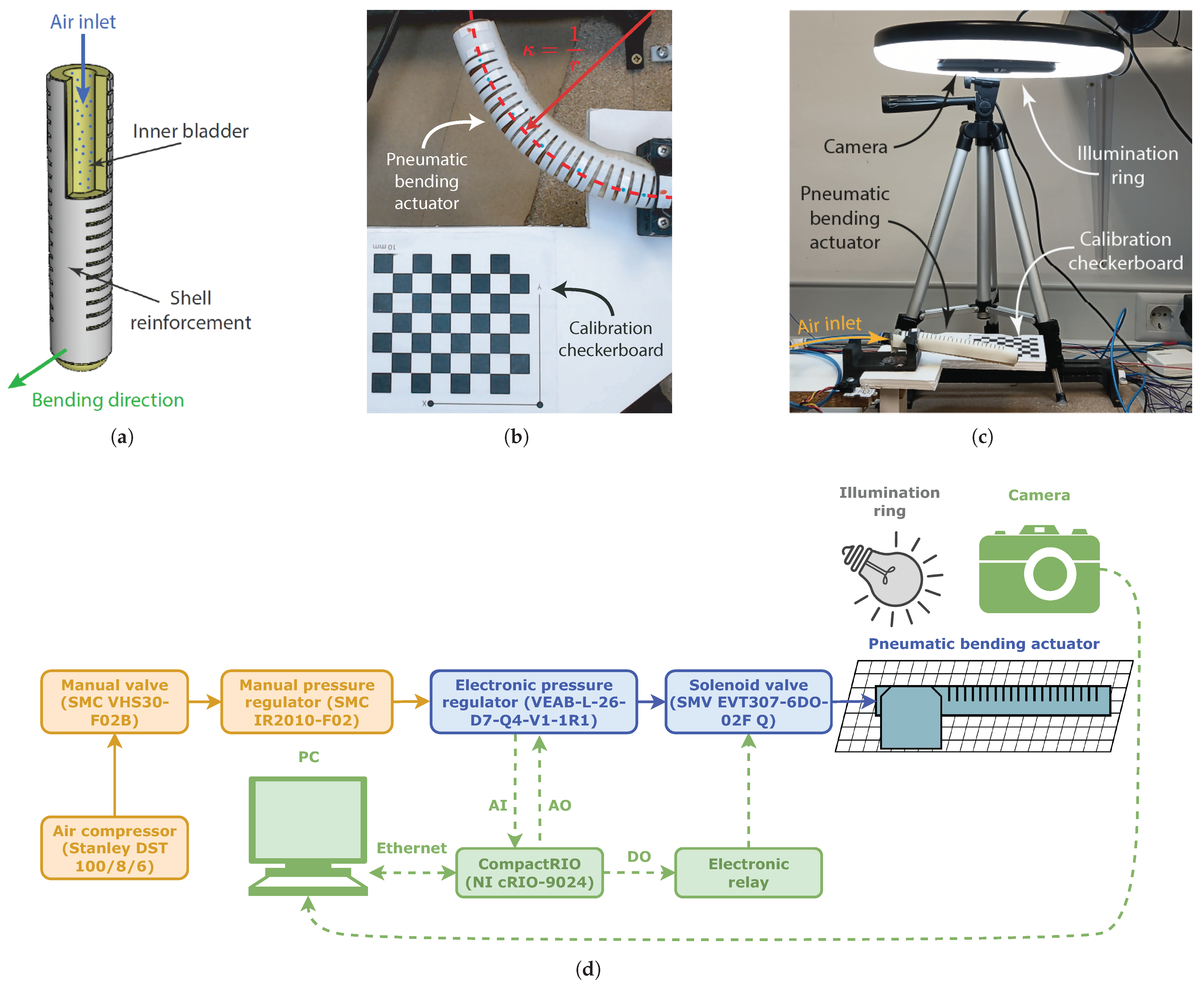
1. Introduction
As soft robotics advances toward a range of applications—such as assistive and wearable devices [
1,
2], surgical assistance [
3,
4,
5], collaborative robots [
6], rescue missions [
7,
8] and exploration [
9]—the development of compliant and robust actuators becomes essential. However, inherent nonlinear characteristics of soft actuators, such as hysteresis, can limit their performance [
10,
11].
Hysteresis arises naturally in a wide range of disciplines, from material science to mechanics, magnetism and even biological systems. Notably, smart materials, which are extensively used in soft robotics, ubiquitously exhibit hysteresis [
12,
13].
In soft pneumatic actuators, hysteresis appears due to multiple factors: energy dissipation during deformation in viscoelastic materials [
14,
15]; frictional losses between the surfaces of pneumatic chambers and other components added to guide deformations, such as braided shells [
16,
17] and even from nonlinearities coming from the pneumatic system itself [
18,
19]. Therefore, a thorough study and modeling of the hysteretic characteristics of soft actuators and their materials is an essential step toward their optimal design and control.
As [
20] remarks, the definition of hysteresis varies across different fields, papers and authors. Commonly, a hysteretic behavior is defined as a nonlinear phenomenon in which the response of a system depends not only on the current input but also on its past inputs, resulting in different paths during loading and unloading. Sometimes, the word hysteresis connotes lag, although this definition is misleading, since delay, per se, is not the mechanism that produces hysteresis. In fact, most dynamical systems (even linear) exhibit lag or phase shift with high enough frequencies, obtaining closed loops that behave as Lissajous-type loops [
21]. In contrast, a pure hysteretic behavior appears even when input signals become slower and slower, producing a nontrivial input–output loop that persists in the static limit and that is unrelated with phase shifts [
12,
21,
22].
Hysteresis models are categorized into three main groups: physics-based, data-driven and phenomenological. Physics-based models are derived using first principles along with particular material properties to capture the hysteresis within a system. One example is the Jiles–Atherton model, used to describe ferromagnetic hysteresis [
23]. However, physics-based models are usually too complex to be used in practical applications. In general, engineering practice seeks simpler models that keep relevant input–output features and are useful for characterization, design and control purposes [
24].
Data-driven methods have also been widely applied to characterize hysteretic behavior in dynamical systems. Among these approaches, there are regression-based techniques, such as the Auto-Regressive model with Exogenous inputs (ARX) and the Auto-Regressive Moving Average (ARMA) model [
25]. More recently, deep learning algorithms have gained attraction. For example, Recurrent Neural Networks (RNNs) have been trained to model and compensate hysteresis loops [
26]. Gaussian processes offer another powerful probabilistic approach, enabling both output representation and uncertainty quantification in hysteretic systems [
27]. In addition to these, a broad spectrum of other data-driven strategies has also been explored [
28].
However, while powerful, data-driven methods typically require large amounts of hysteresis data for accurate modeling. Moreover, their general black-box structure complicates both the interpretability and the adaptation of these models across different systems.
Phenomenological models, on the other hand, aim to describe hysteresis through explicit mathematical mappings between inputs and outputs. These models are classified into two types:
Models that use differential equations to characterize hysteresis, for instance, the Bouc–Wen model, which employs a nonlinear differential equation to represent hysteretic systems with a wide range of shapes [
29].
Models that use a composition of weighted hysteresis-like operators, such as the Maxwell-Slip model, a dynamic friction model commonly represented as a parallel connection of frictional sliders and springs [
30], the Preisach model, which has been mainly used for describing static magnetic behavior [
31], and the Prandtl–Ishlinskii model, which has been very popular in a wide range of systems for its simplicity and flexibility [
32].
Because phenomenological models capture intrinsic hysteretic properties, they are easier to identify. Also, their general and explicit mathematical formulation facilitates their integration with other systems and methods. For example, in [
33] a Nonlinear Auto-Regressive Moving Average model with Exogenous inputs (NARMAX) is combined with an improved Bouc–Wen model to model and control a magnetic shape memory alloy actuator.
Given the wide variety of phenomenological hysteresis models, and the fact that most works focus on only one or two, it can be challenging for researchers new to hysteresis modeling to determine which one is most relevant to their work. Furthermore, most of the review works on hysteresis, for example, [
28,
34,
35,
36], do not offer practical, side-by-side comparisons of the models.
Based on the above, the objectives of this work are as follows:
To describe the key features and variants of various widely used phenomenological models, providing a clearer understanding of their underlying ideas.
To serve as a tutorial for engineers and researchers interested in modeling hysteretic soft actuators by relating various commonly observed phenomena in hysteresis loops—such as asymmetry, the loading curve and the direction of hysteresis—to the mathematical structures and underlying concepts of each model.
To present a direct comparison of the models after fitting them with real experimental data from a soft pneumatic bending actuator. Through this comparison, we aim to provide insights into the strengths and limitations of each model, while evaluating the accuracy, complexity (e.g., number of parameters) and computational efficiency.
To assess which hysteresis models perform better or worse when applied to similar soft pneumatic bending actuators, thereby helping in the identification of trends across comparable systems.
The remainder of the paper is organized as follows.
Section 2 outlines the methodology, including the experimental setup, data acquisition and preprocessing, optimization algorithms and performance metrics.
Section 3,
Section 4,
Section 5 and
Section 6 present and evaluate the Preisach, Prandtl–Ishlinskii, Maxwell-Slip and Bouc–Wen models, respectively, including notable variations.
Section 7 discusses the conclusions derived through a comparative analysis of the models, and
Section 8 provides a final discussion.
3. The Preisach Model
The
Preisach model (PR) is one of the most popular operator-based models used to represent the nonlinear hysteretic behavior of systems. Originally, it was developed to represent magnetic hysteresis, which has been its main field of application [
13,
31]. However, because PR models can be specified purely in terms of mathematical formulations, they can be applied to a wide range of systems where the underlying physics are unknown. For example, they have been used to represent and compensate hysteresis in shape memory alloys [
38] and pneumatic artificial muscles [
39], to model piezoceramic [
40] and piezoelectric actuators [
41], to design robust and adaptive controllers [
42] and even to characterize the seismic response of structures [
43]. As a result, PR models have become a widely accepted mathematical tool for the description of hysteresis phenomena.
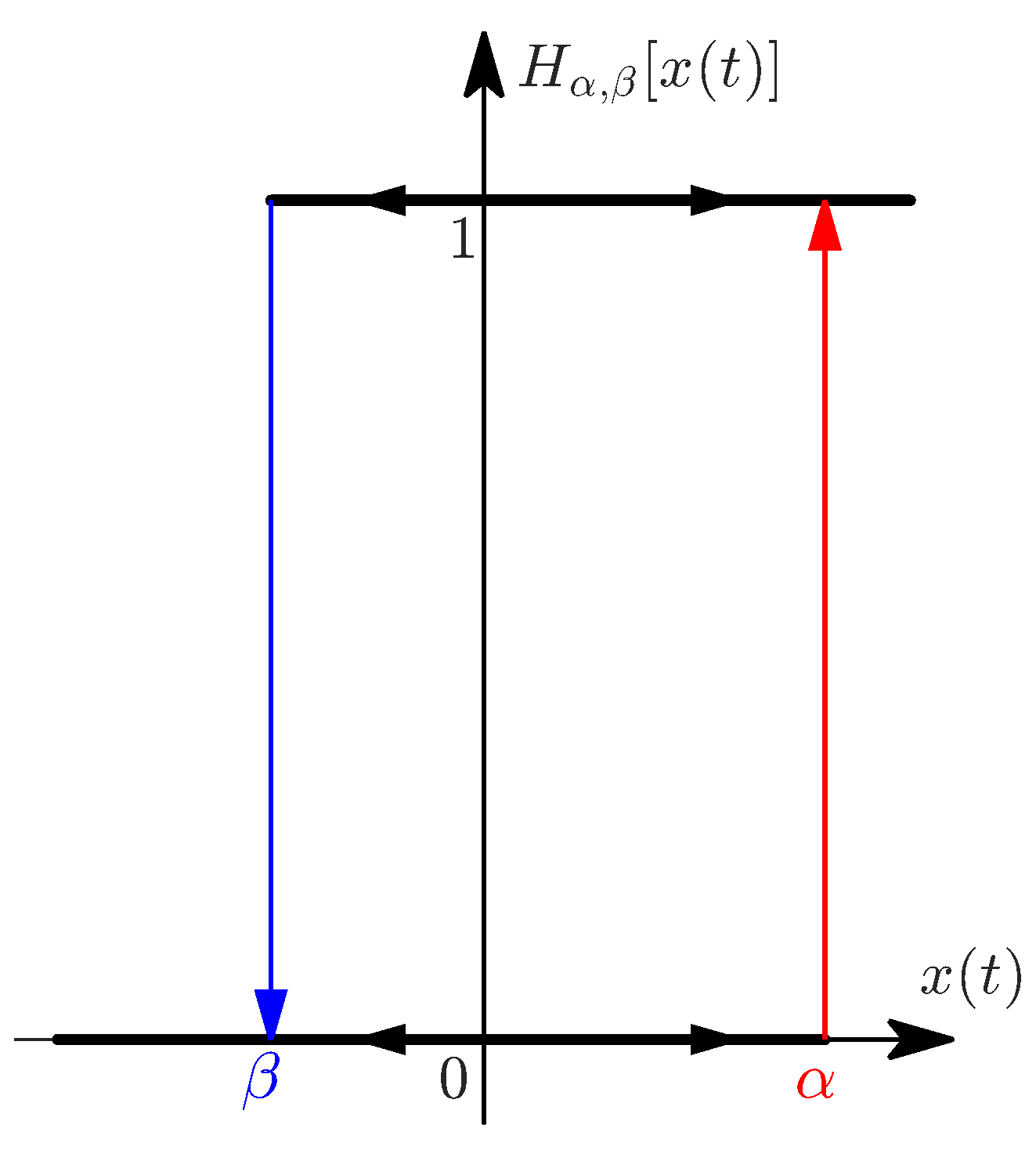
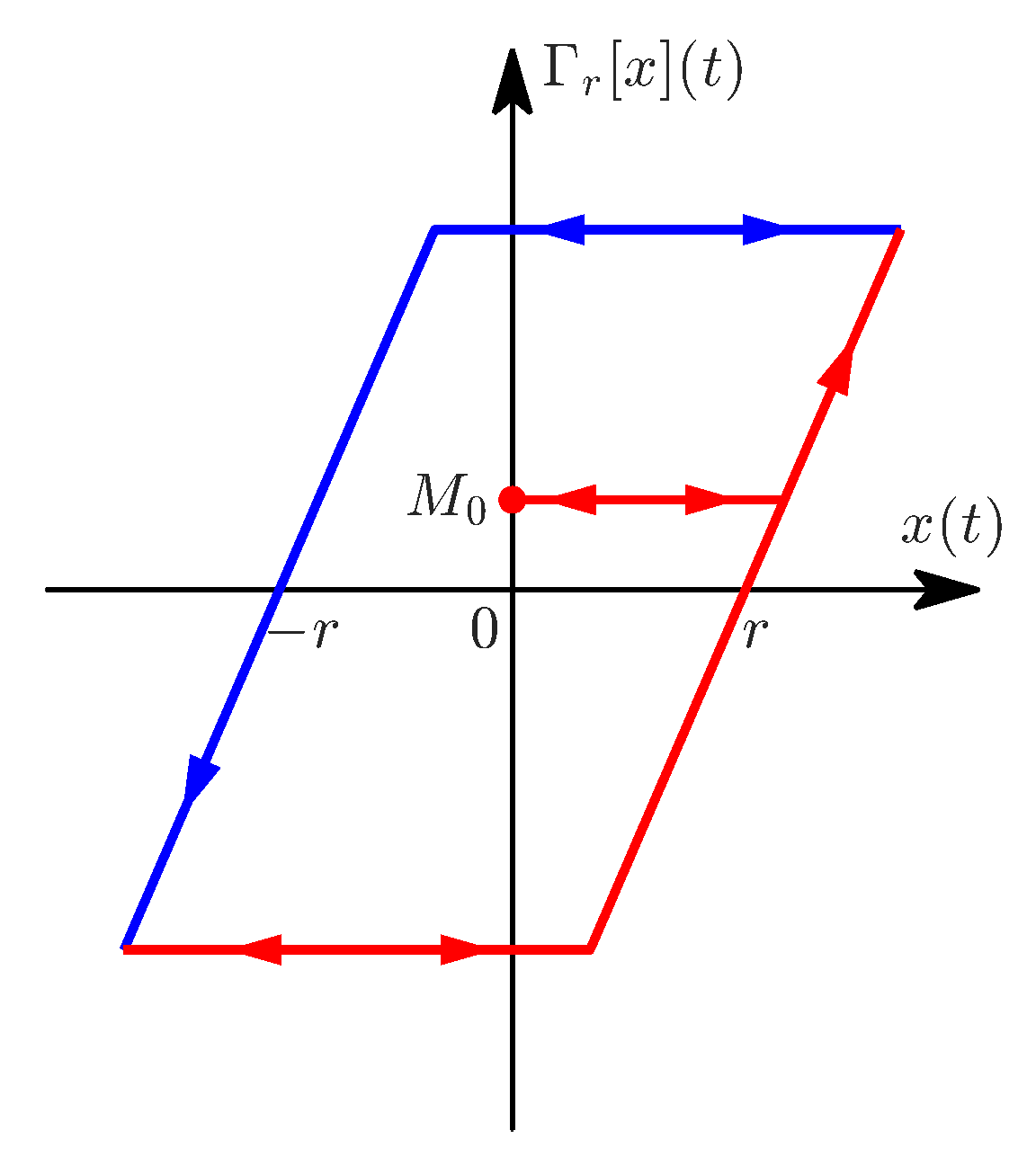
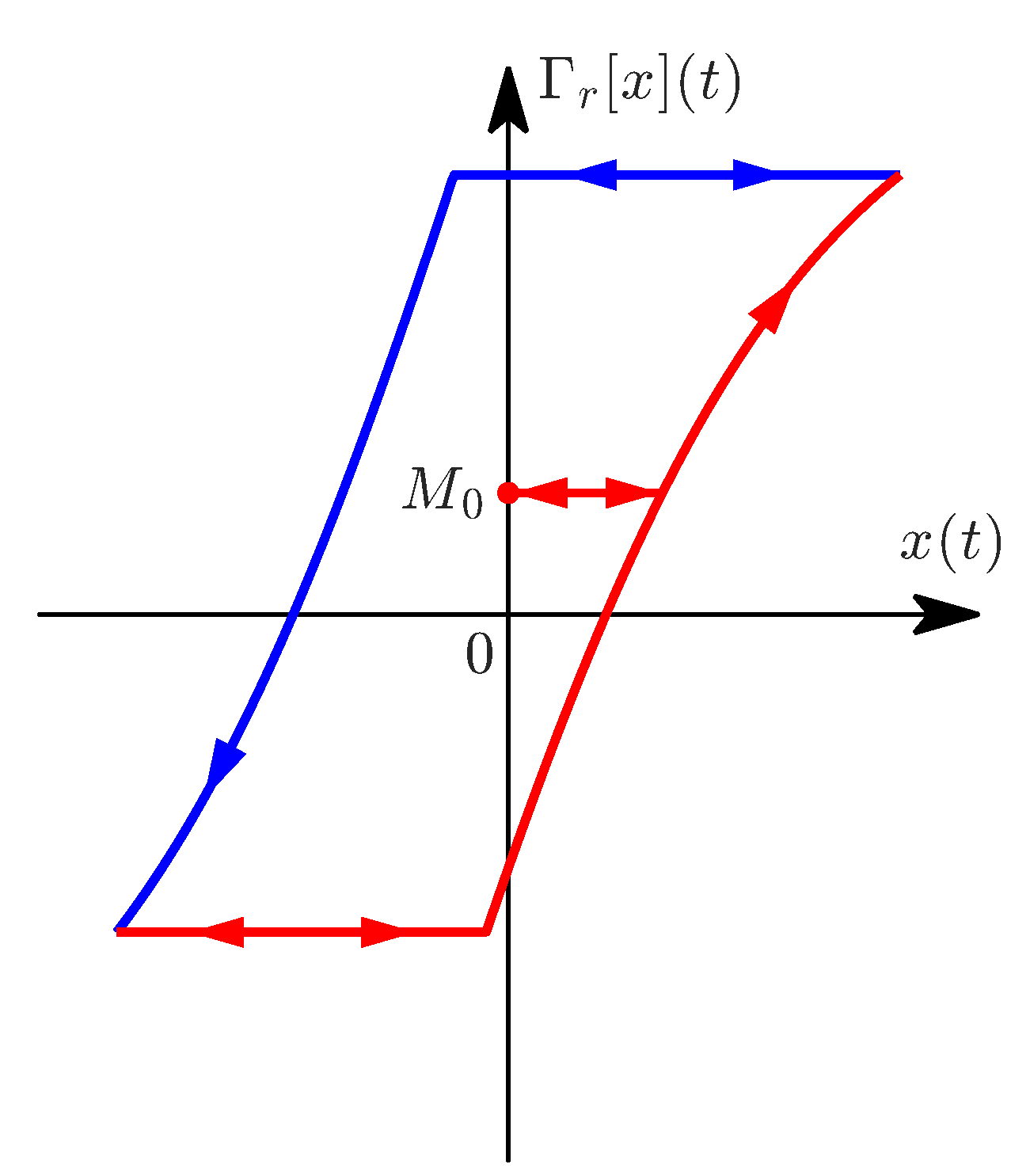
The PR model is based on the delayed relay operator
given by
where
is a time discretization of the input signal with a fixed step size
h. The initial condition is
, and
are, respectively, the upper and lower thresholds of the relay operator, shown in
Figure 4. In this work,
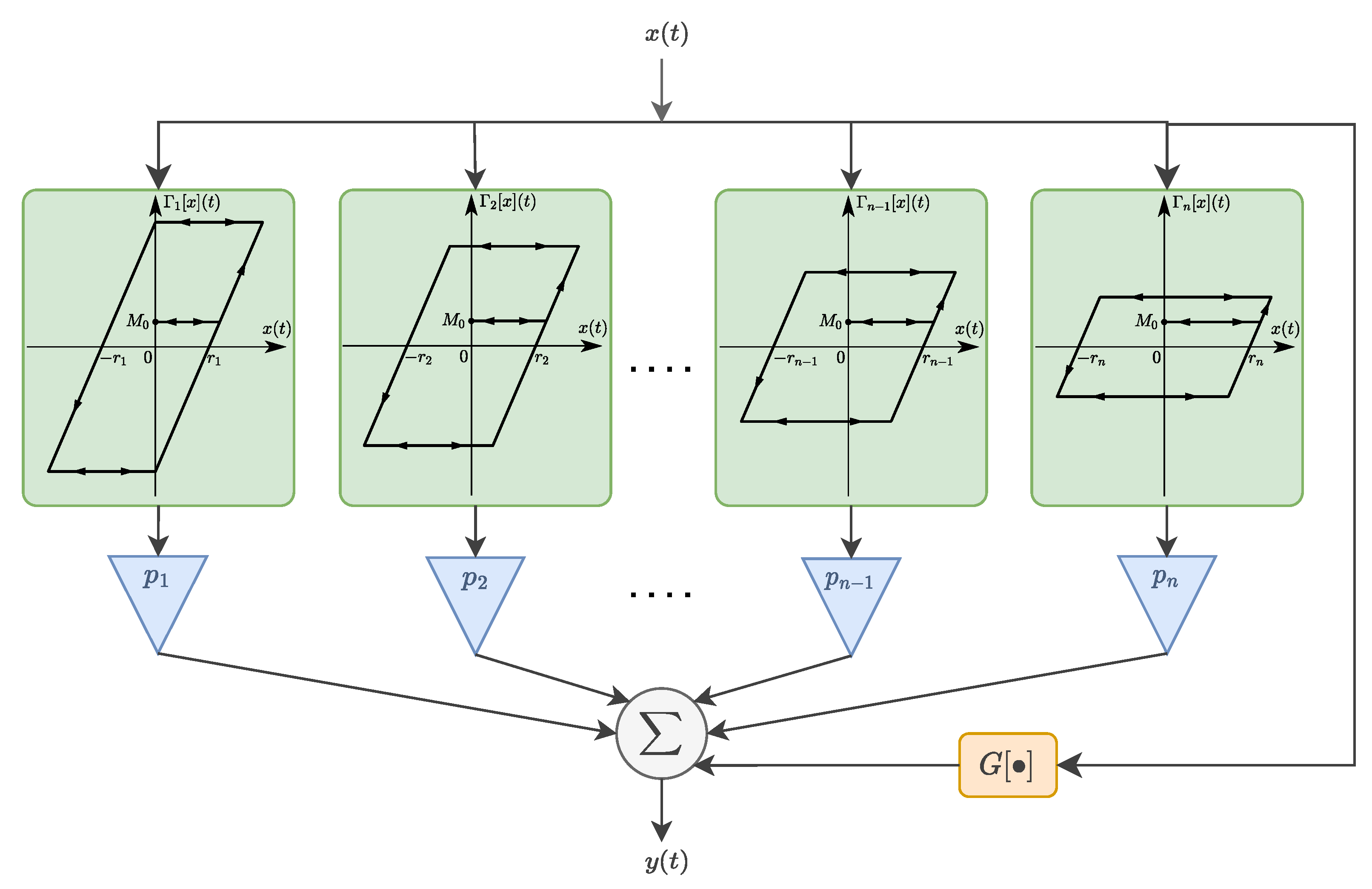
, as we use normalized data. The output of the PR model is obtained by summing many weighted relay operators connected in parallel, as illustrated in
Figure 5. When the number of operators approaches infinity, the continuous PR model is obtained:
in which
is the Preisach density function.
However, estimating the PR density function from hysteresis loops is a nontrivial task, and several methods have been developed to obtain it. Common approaches involve taking numerical derivatives of measurements. However, that can lead to significant errors if the data is noisy or poorly treated [
44].
Another common approach is to approximate the PR density function by some analytical probability density function [
45]. In this regard, some works aim to further simplify the identification of the density function. In this work, we adopt the solution of [
46], where the PR function is assumed to be the product of two independent general probability distributions:
where
and
are two distributions with variables
and
. These distributions are well-known continuous statistical distributions, such as the Gaussian
and Cauchy
distributions:
where the variable
k represents
or
, depending on the desired combination;
is the center of the distribution and
its standard deviation. If, instead of the continuous PR model,
N equally spaced thresholds for
and
between
and
are considered, Equation (
5) becomes
where the limits of the summation
are set to satisfy the condition
. Additionally, the term
is added to account for the offset in the experimental data.
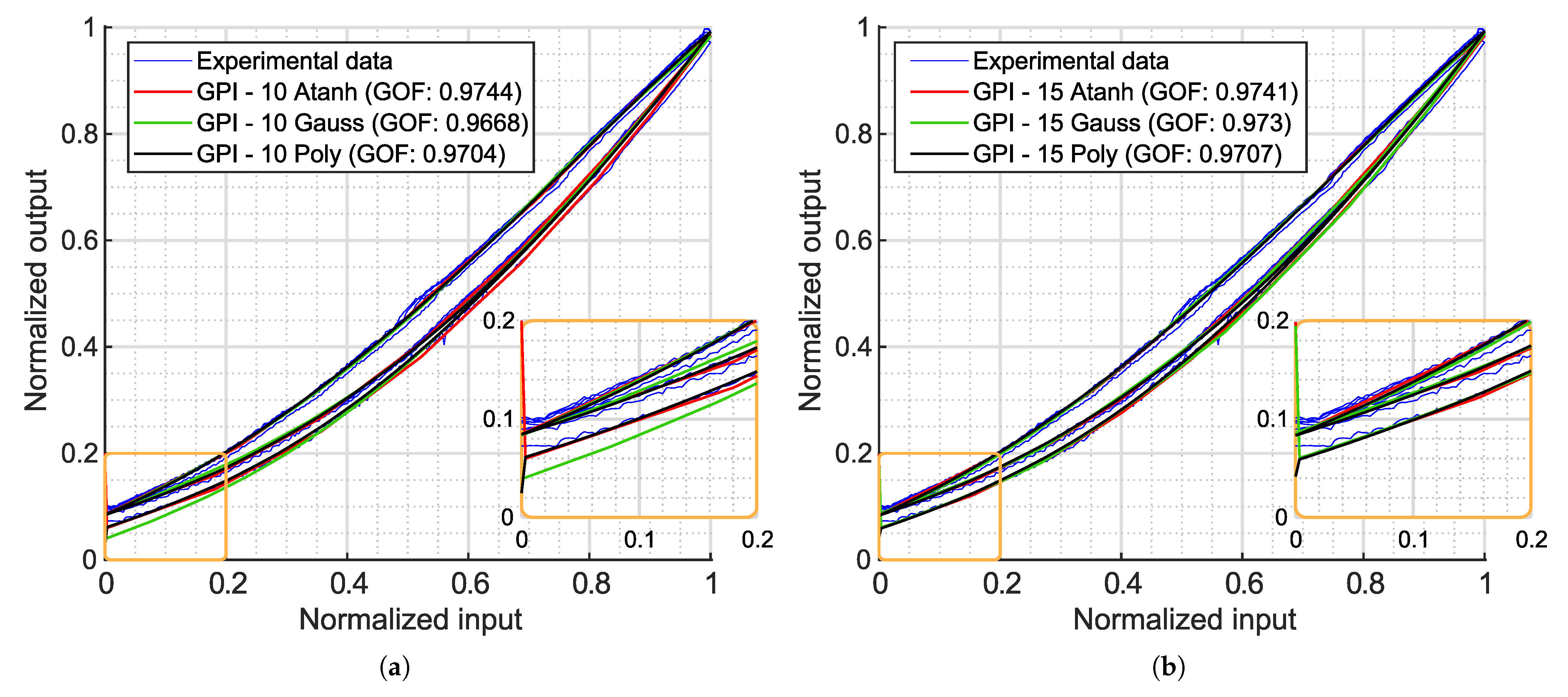
Fitting Results
In this section, the results of fitting the formulation of the PR model (
9) are presented. This model was fitted with the GA explained in
Section 2.3, applying two different combinations of the introduced probabilistic density functions (
7) and (
8) with 10, 50 and 100 operators.
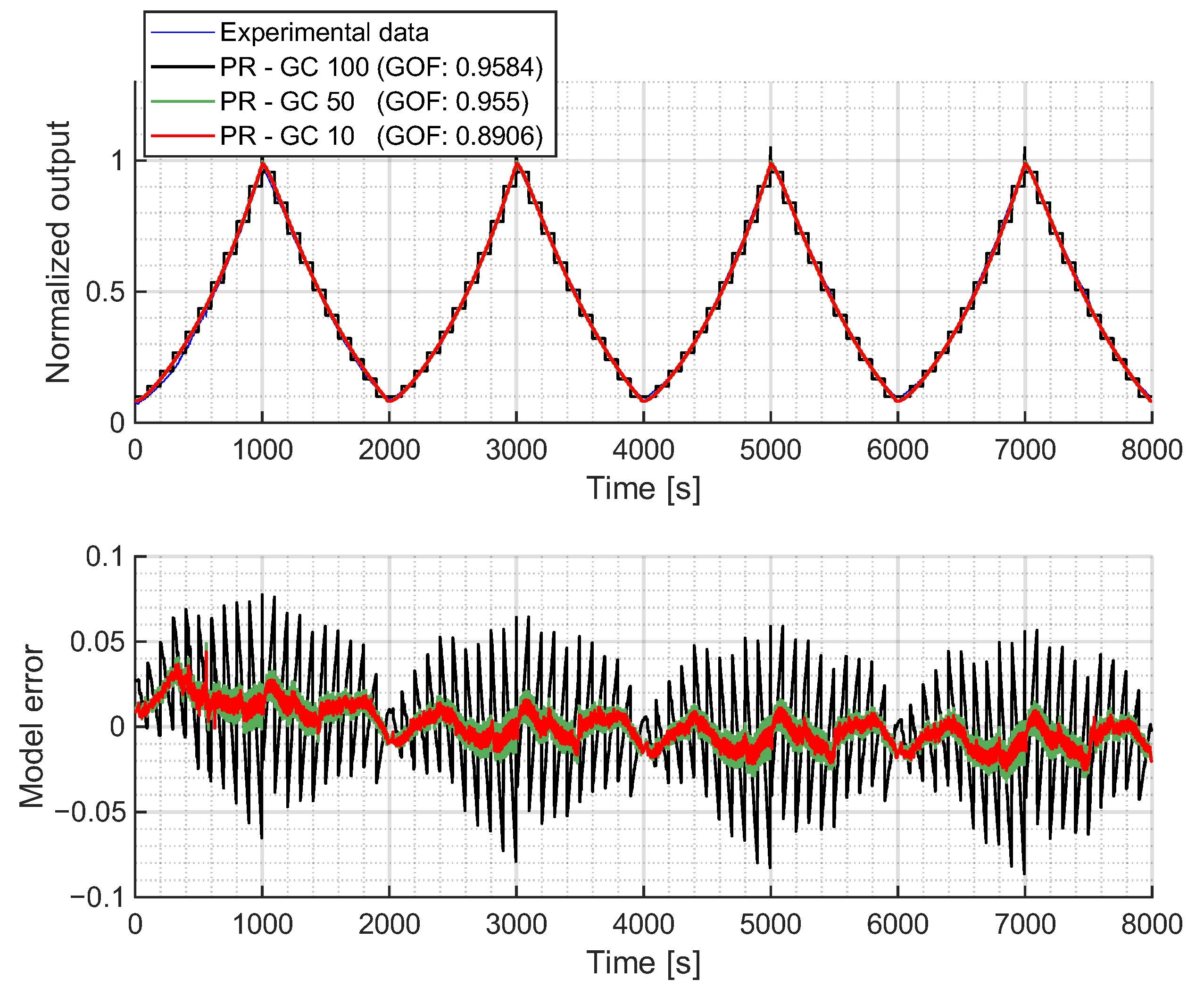
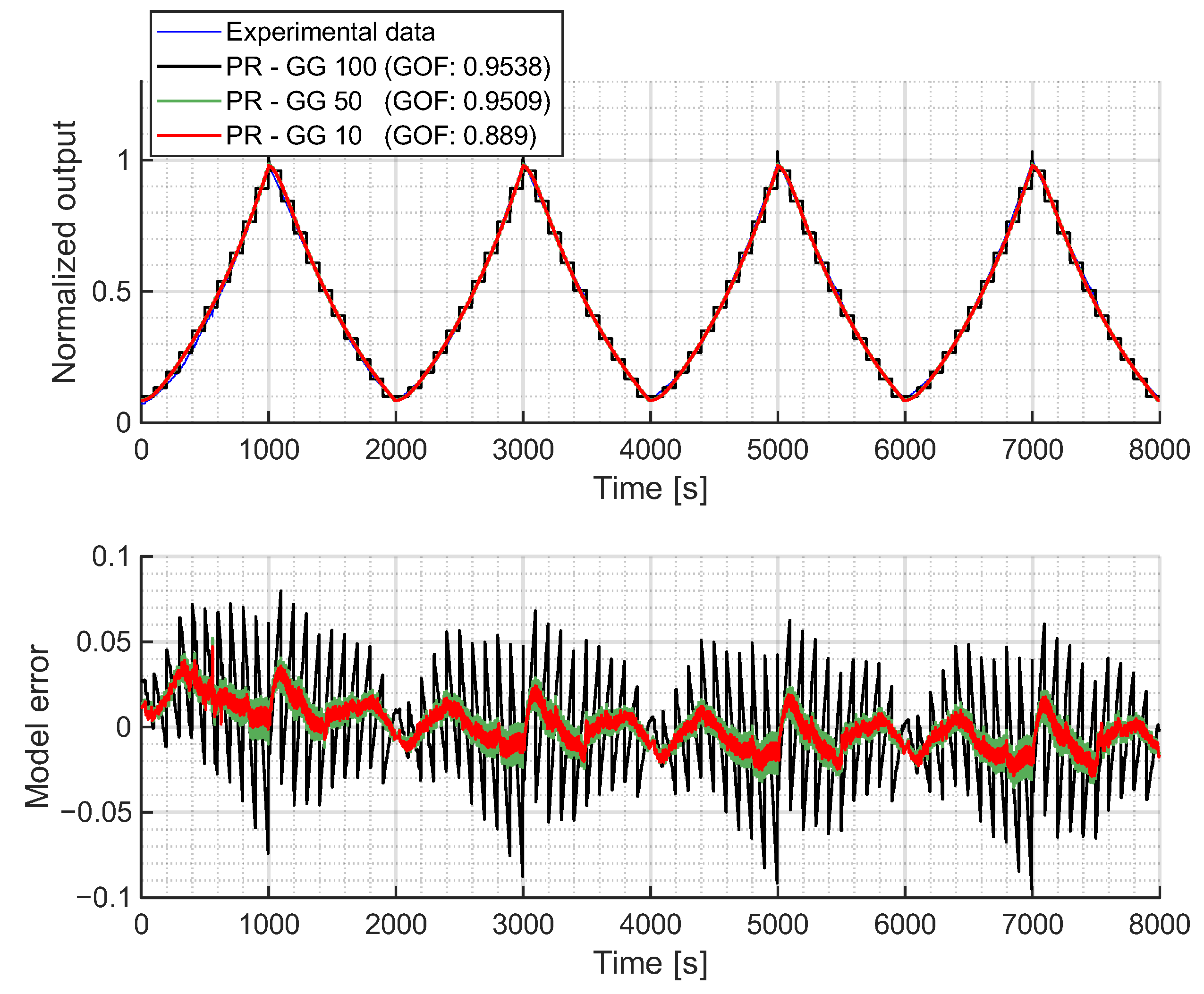
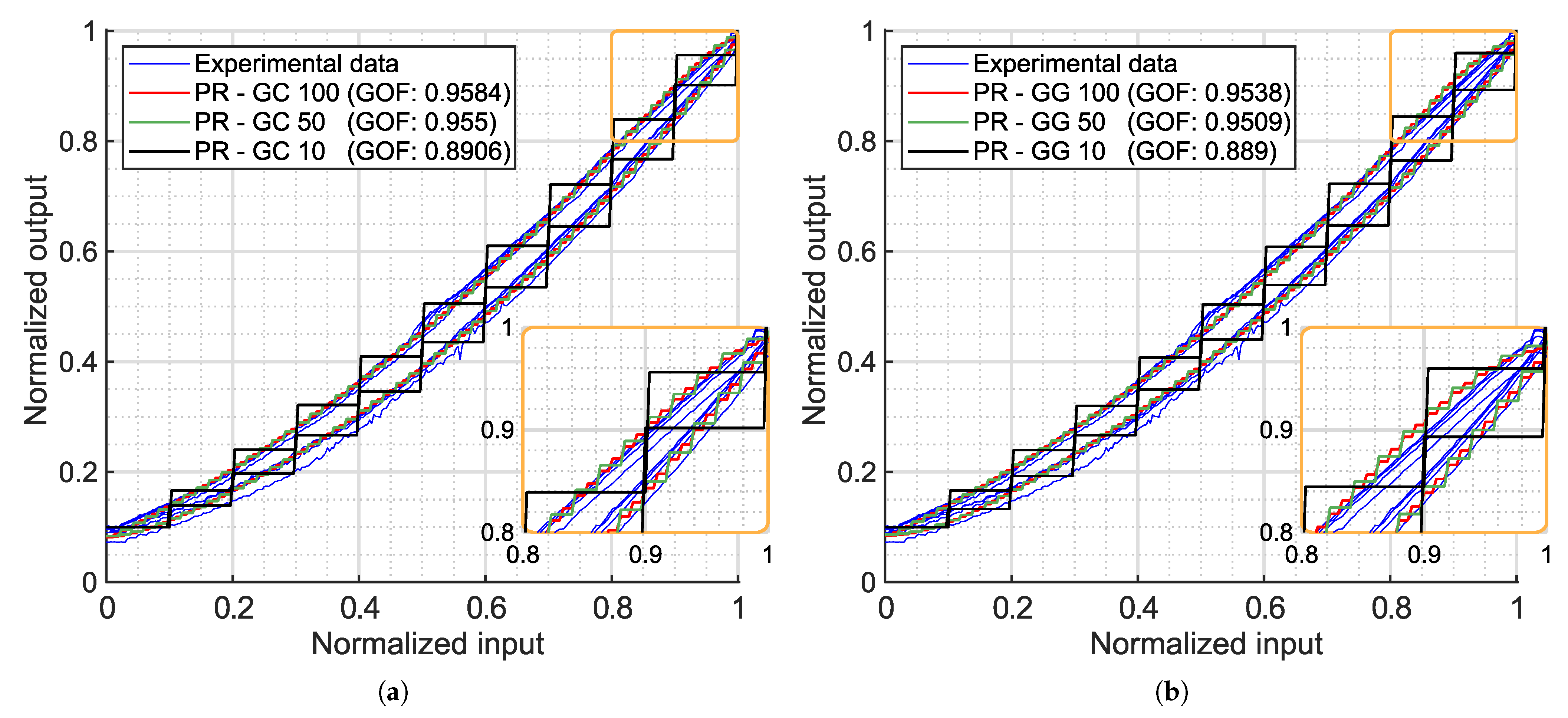
In the first case, 10 operators were selected to capture the general shape of the hysteresis model with a high level of discretization. Increasing the number of operators to 50 allowed for a better continuous approximation of the hysteresis loop, corresponding to a resolution of 0.02 of the normalized input signal. Finally, 100 operators were used to confirm if further increasing the number of operators did not improve the accuracy of the model. In all cases, the GA identified five different parameters: , , , and .
Figure 6a shows the fitted PR model using a Gaussian distribution for
and a Cauchy distribution for
, while
Figure 6b presents the results with Gaussian distributions for both
and
. In both cases, the PR model accurately captures the hysteretic behavior of the experimental data. With just 10 operators, the model achieves a GOF close to 0.90, and with 50 operators, it exceeds 0.95. Beyond this point, further increasing the number of operators does not significantly improve the GOF, as the discretization error no longer decreases sufficiently to outweigh the error introduced by the assumed shape of the density functions. In other words, once the discretization is sufficiently fine, the residual error is dominated by the mismatch between the chosen density function and the actual shape of the hysteresis. This effect is more clearly illustrated in the error plots shown in
Figure A1 and
Figure A2. Therefore, the marginal improvement in the GOF obtained by adding more operators does not sufficiently justify the increased computational cost (see
Table A1,
Table A2,
Table A3,
Table A4,
Table A5 and
Table A6).
The biggest difference between the two fitted combinations is that the Gaussian–Gaussian model slightly separates outward from the measured loop at the upper end (
Figure 6b, orange zoom) of the loop. Although this difference is not significant enough to have a major impact on the fitted results (as can be seen comparing the GOF values), the shape change highlights the necessity of finding proper combinations of distribution functions for each particular case.
Finally, the success of the PR model in representing the experimental data is attributed to its ability to capture the asymmetric shape through its density function, which depends on both the upward and downward thresholds. This allows for different paths on each side of the hysteresis loop. The main drawback of this formulation is that the initial loading curve is not modeled. However, it is worth noting that if the loading curve of the experimental data starts in a middle point of the loop and the relay operator takes the value of for , the PR model should be able to represent loading curves lying within the hysteresis loop.
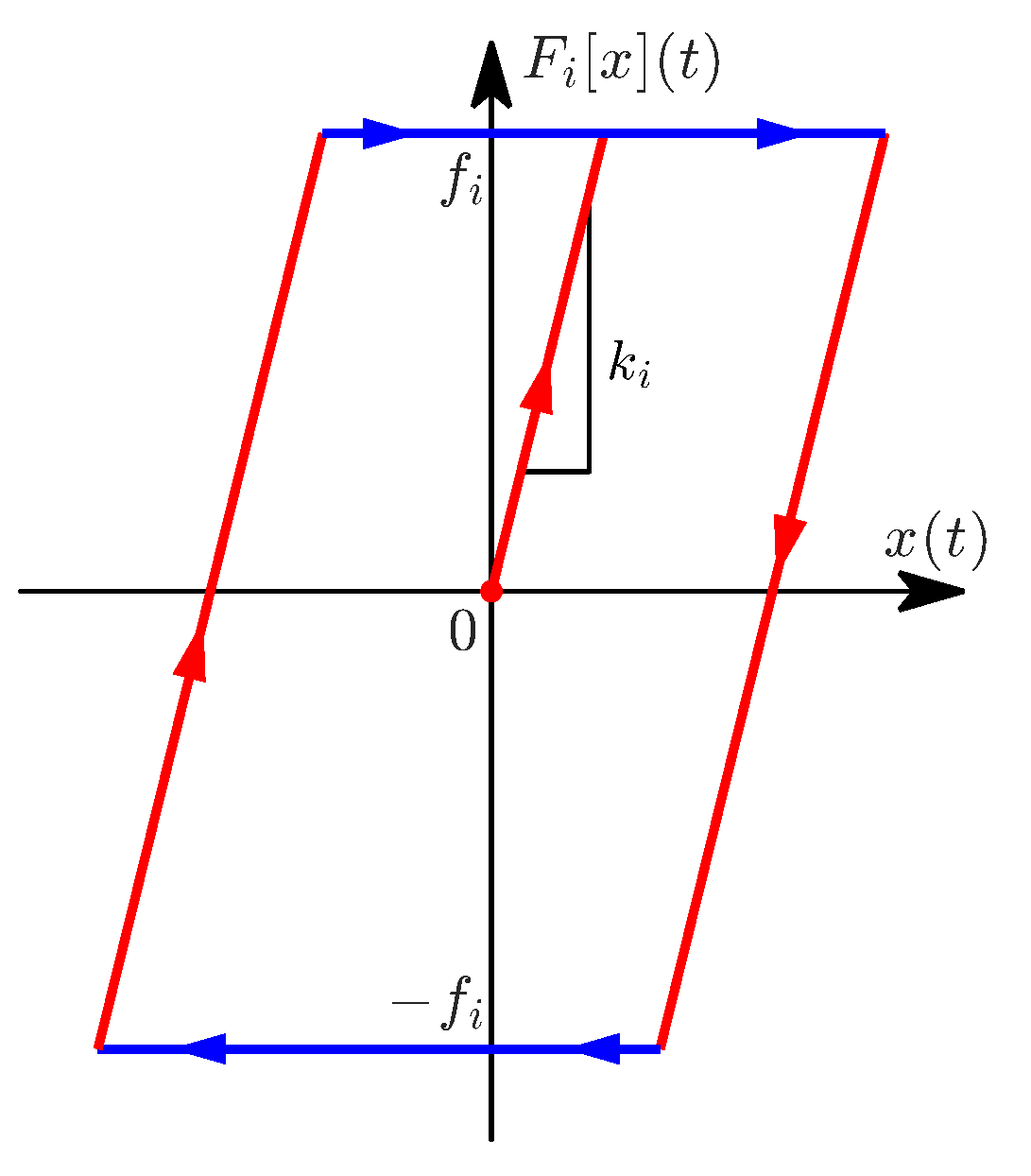
5. The Maxwell-Slip Model
The
Maxwell-Slip model (MS) is a hysteresis model originally proposed to describe the behavior of friction in mechanical systems. Nowadays, due to its simplicity and facility of computation, it has been used to model hysteresis in a wide range of actuators [
56,
57,
58,
59]. The MS model is based on the elasto-slide operator
, shown in
Figure 13:
Here,
denotes the time derivative of
. The elasto-slide operator is normally represented as a massless linear spring in combination with a massless block subject to Coulomb friction, where
is the stiffness of each spring,
is the breakaway friction force and
is position of each block. In addition,
is the sign function defined as
Sometimes, the elasto-slide operator is interpreted as an elasto-plastic operator that acts elastically until the force threshold
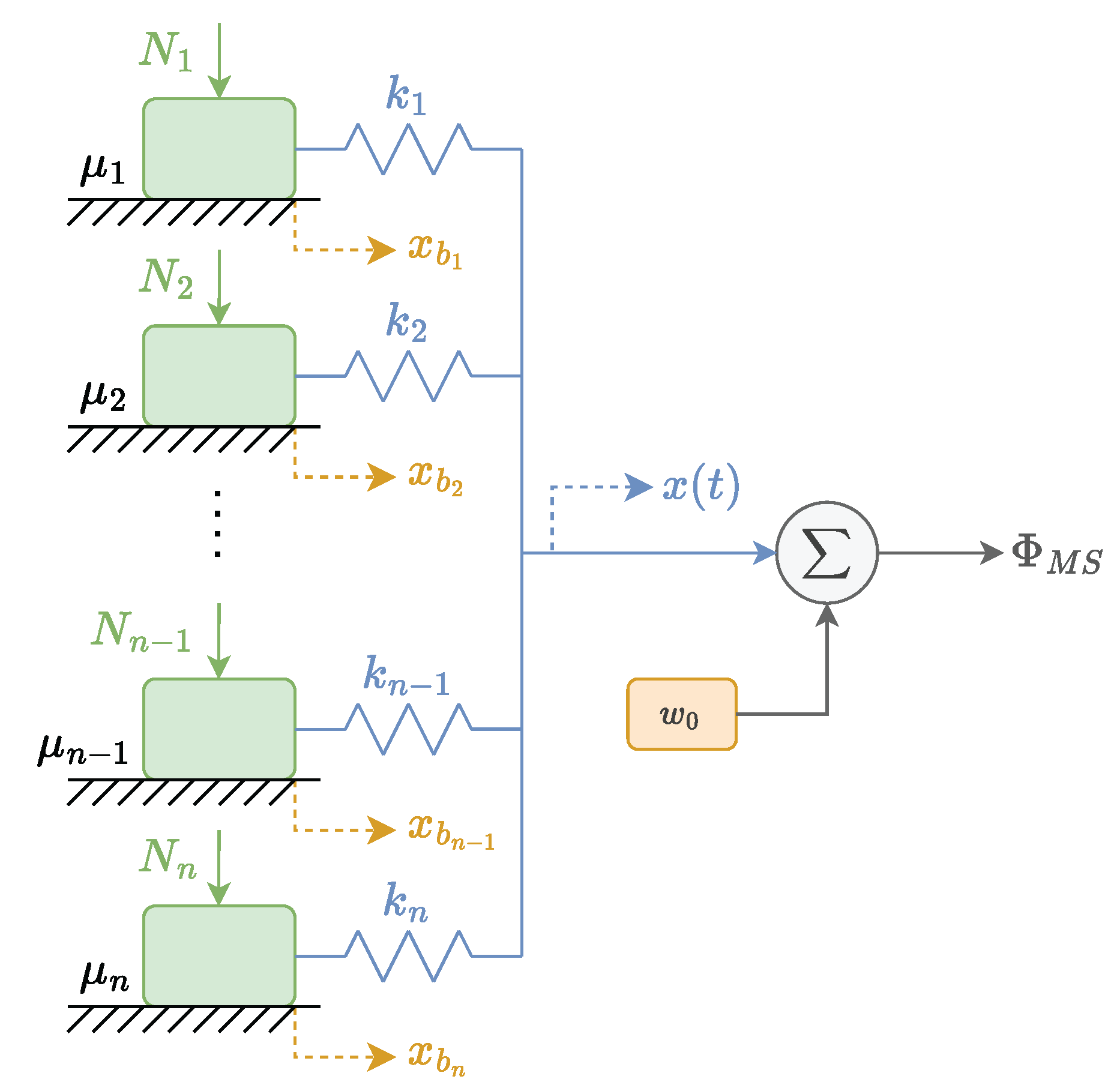
is surpassed, where the plastic behavior takes control. This plastic or sliding behavior is responsible for capturing the memory effects of the hysteresis. The output of the MS model is the summation of multiple parallel elasto-slide elements (
Figure 14) with an initial value
:
It is worth noting that the shape of the elasto-slide operator is similar to that of the stop operator in the PI model (
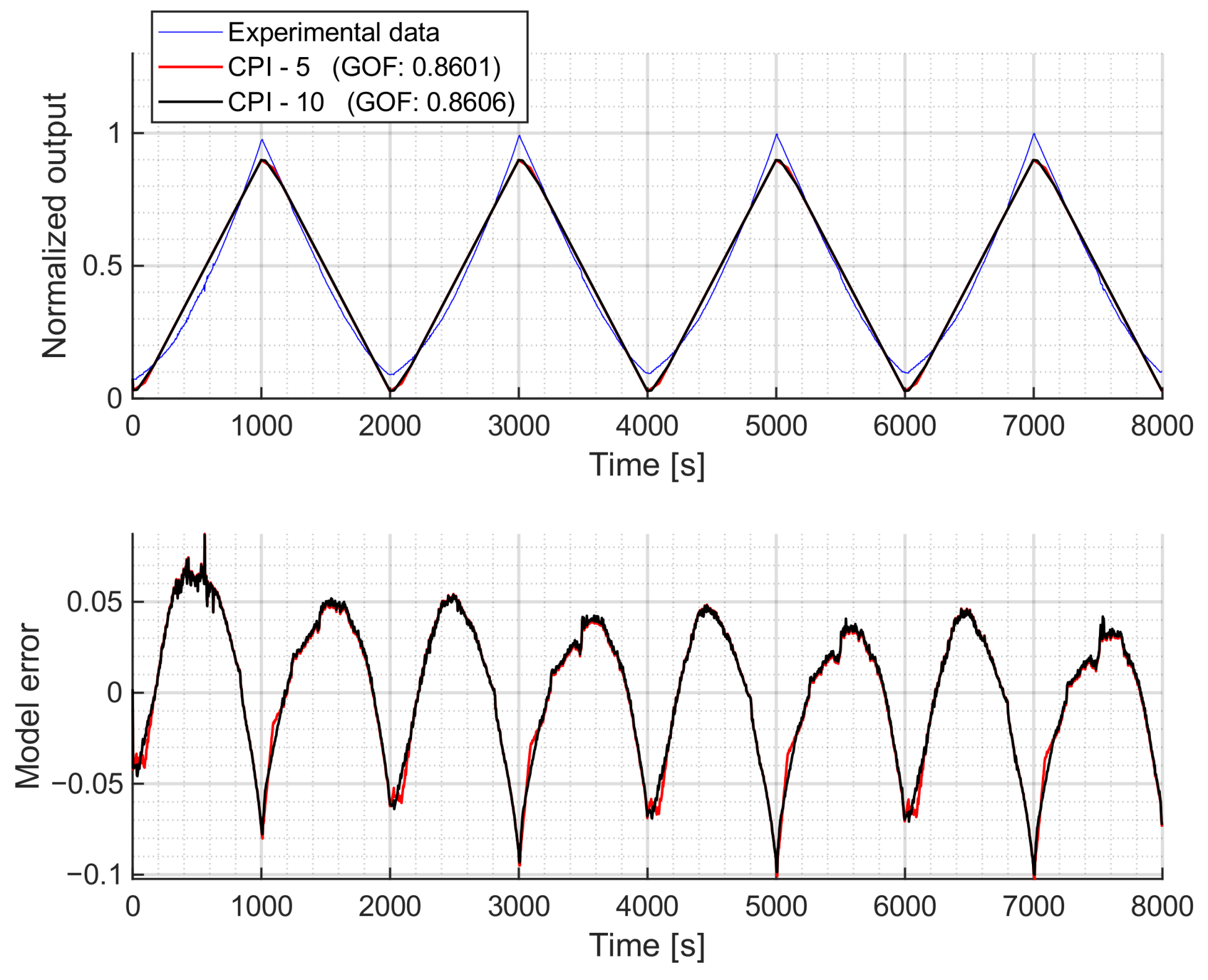
Figure 8). Consequently, the results obtained with this model would be similar to those of the stop operator-based CPI model.
Fitting Results
The fitted MS model with operators is presented in this section. As will be explained later, the number of operators does not affect the outcome. Similar to the CPI model, the threshold and stiffness coefficients were treated as free parameters, without any constraining functions. Thus, different parameters were identified: , and .
The results of the fitted MS model can be found in
Figure 15. As shown in the figure, the obtained model represents a straight line, failing to capture the nonlinear dynamics of the measured data. This behavior is also clearly observable in the upper plot (the simulation output) of
Figure A6.
Regardless of the number of operators, the results will remain the same. This is because the behavior of the fitted model is effectively reproduced by fitting the slope k of a single elasto-slide operator, ensuring that, over the input signal range, it never reaches the breakaway friction force f. This limitation arises because the elasto-slide operator represents loops that move clockwise, while the experimental data moves counterclockwise. Thus, this formulation of the MS model is not suitable for modeling the hysteretic behavior of the proposed soft pneumatic actuator.
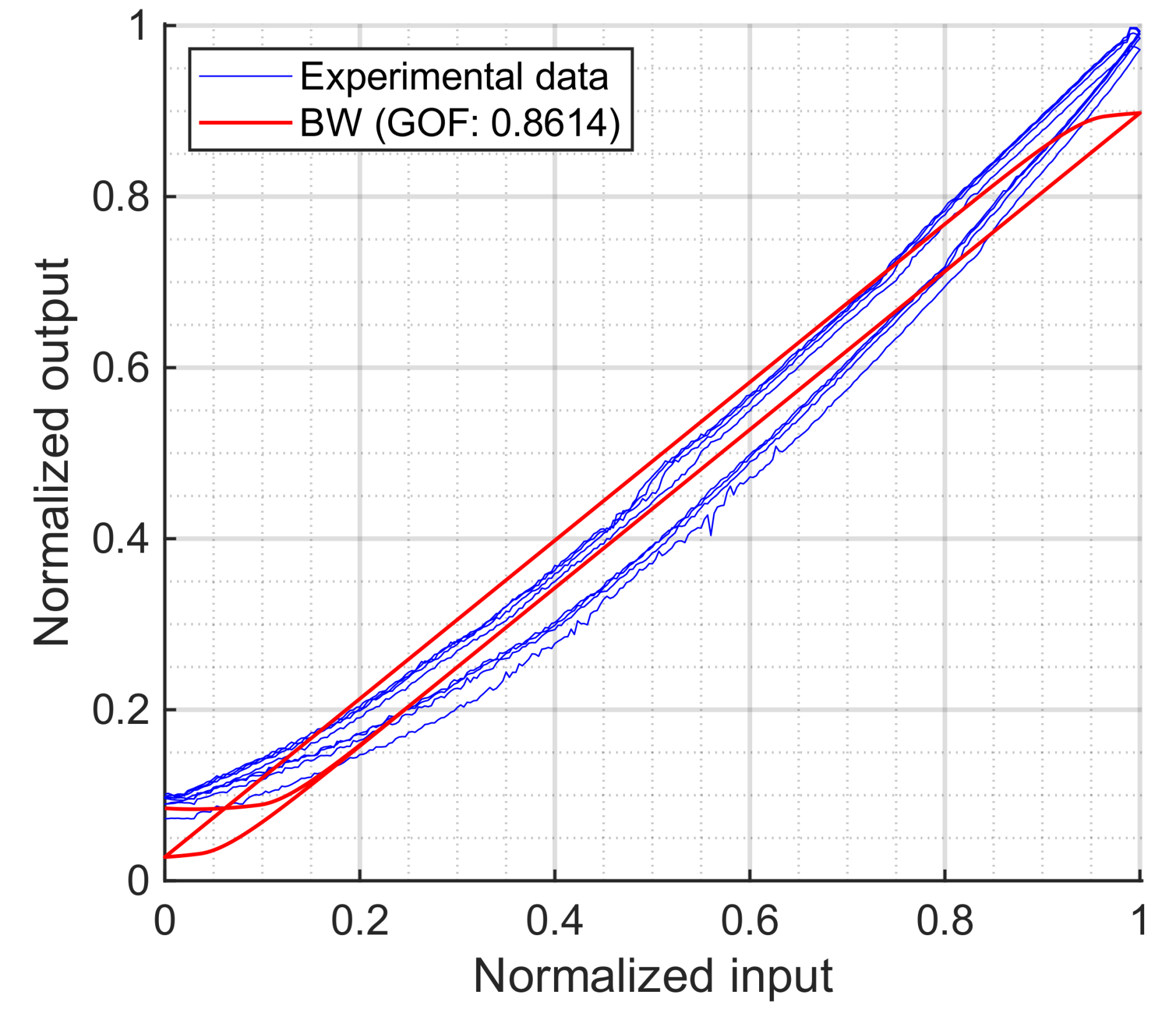
7. Comparative Analysis and Conclusions
This section presents a comparative analysis of the models fitted to the experimental data.
Table 1 summarizes the GOF values, simulation times and number of adjusted parameters for each model, along with a brief overview of the key results for each formulation.
The first conclusion is that the CPI and CBW models are discarded, as they fail to capture the asymmetric behavior of the actuator. The MS model (also unable to represent asymmetry) performs the worst with our experimental data. As discussed in its corresponding results section, the elasto-slide operator produces loops in the opposite direction to those observed experimentally. These shortcomings highlight the importance of selecting models and operators that align with the shape and direction of the experimental loop.
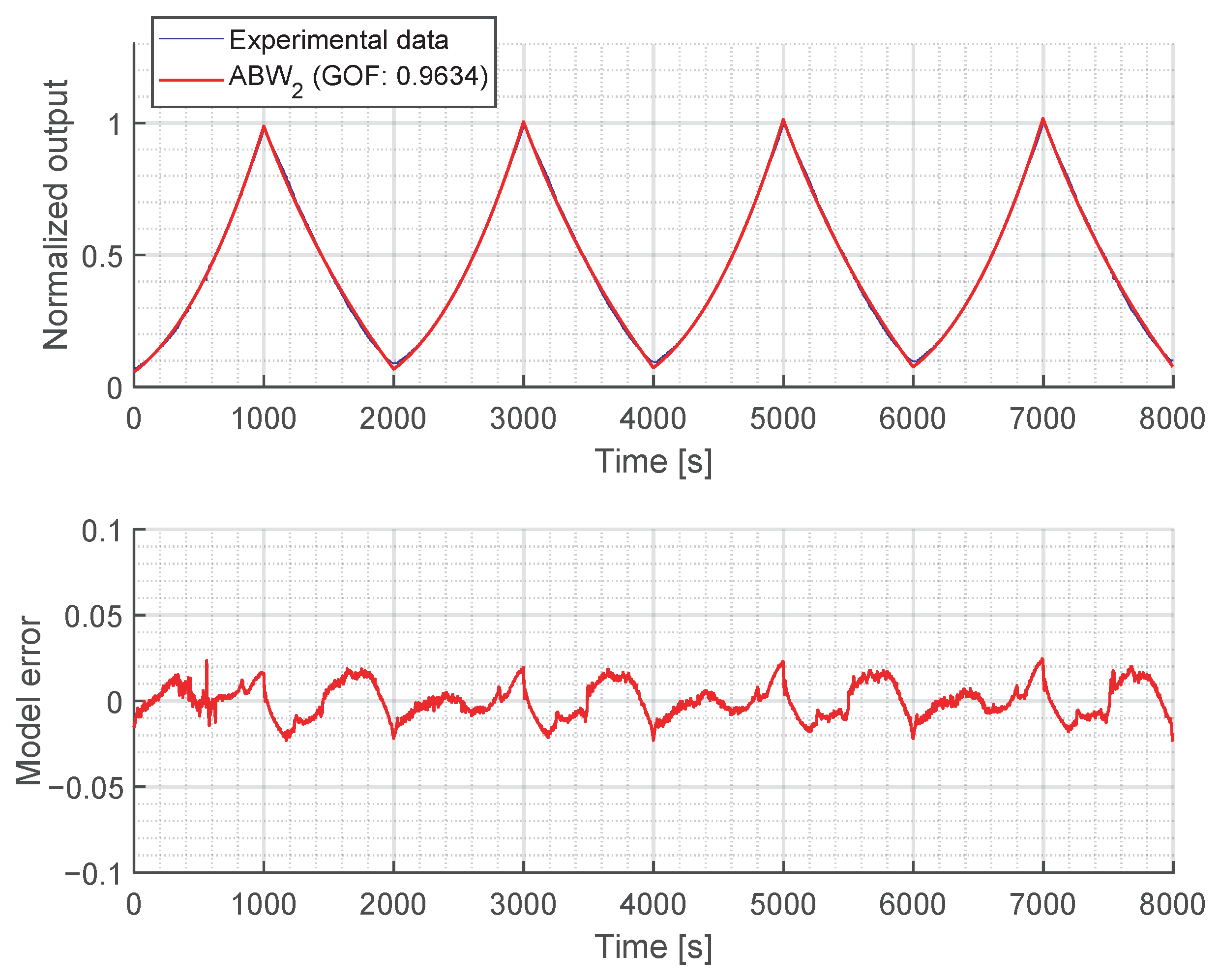
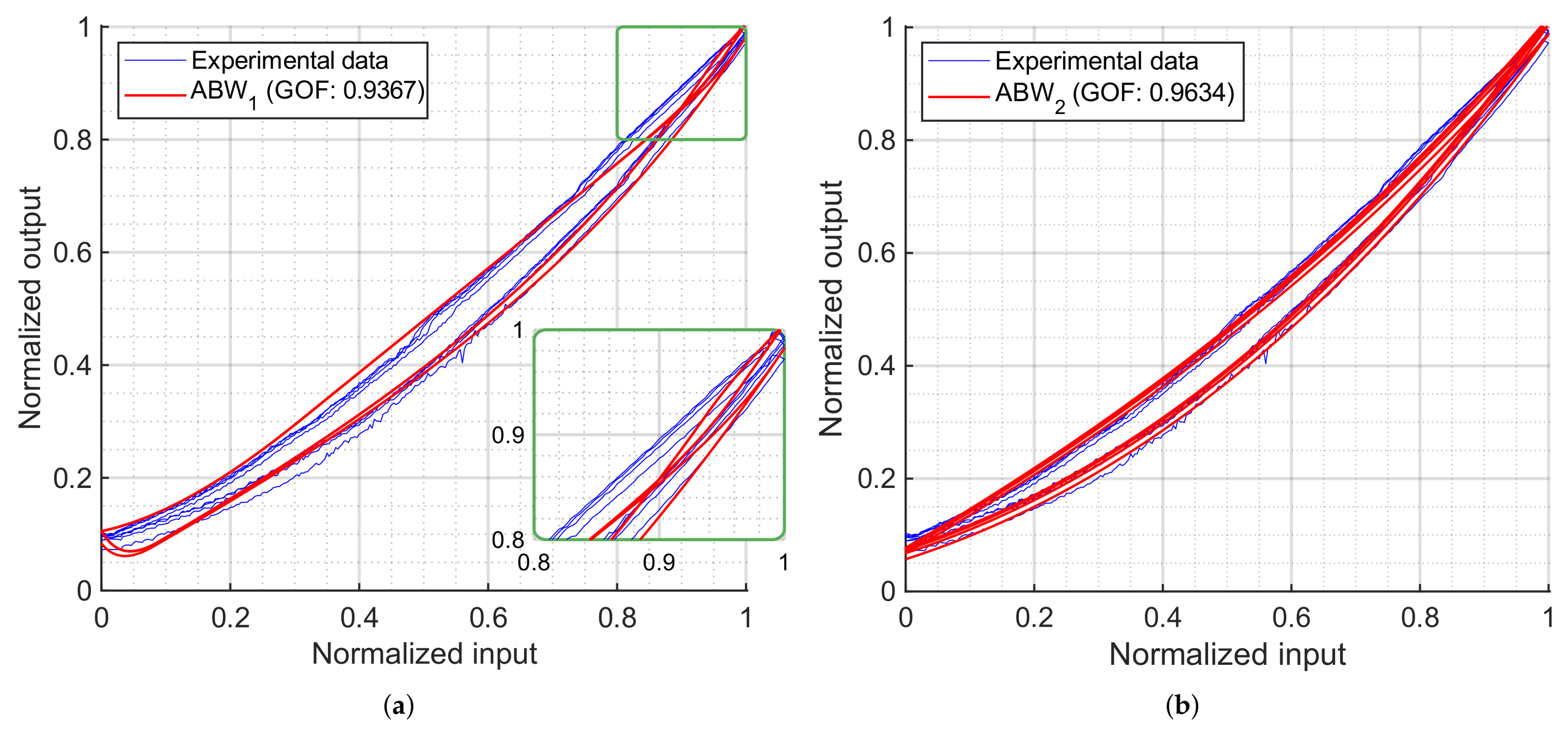
Among the asymmetric models analyzed, all achieved good fits, but the ABW is the most questionable: depending on the chosen asymmetry functions, it can produce hysteresis loops that are not physically consistent with the experimental data, as with the case of Equation (
30). However, with appropriately selected functions, it can yield continuous and feasible representations of all the key features of the hysteresis loop (i.e., the loading curve, the asymmetric shape, etc.), as demonstrated by the formulation shown in Equation (
31).
The PR model has the advantage of requiring the fewest parameters. With only five parameters, it successfully captures the asymmetry of the hysteresis loop. Nevertheless, it has two main limitations. First, the presented formulation does not reproduce the loading curve, although, as discussed in its section, alternative formulations may overcome this. Second, at least 50 operators are required to represent the hysteresis loop with low discretization, resulting in a longer computation time compared to the other models. This is the only model which exceeds the 10 ms barrier, which may be critical in some real-time control loops. Reducing the number of operators could shorten computation time but would increase discretization error, which may be problematic in precision applications.
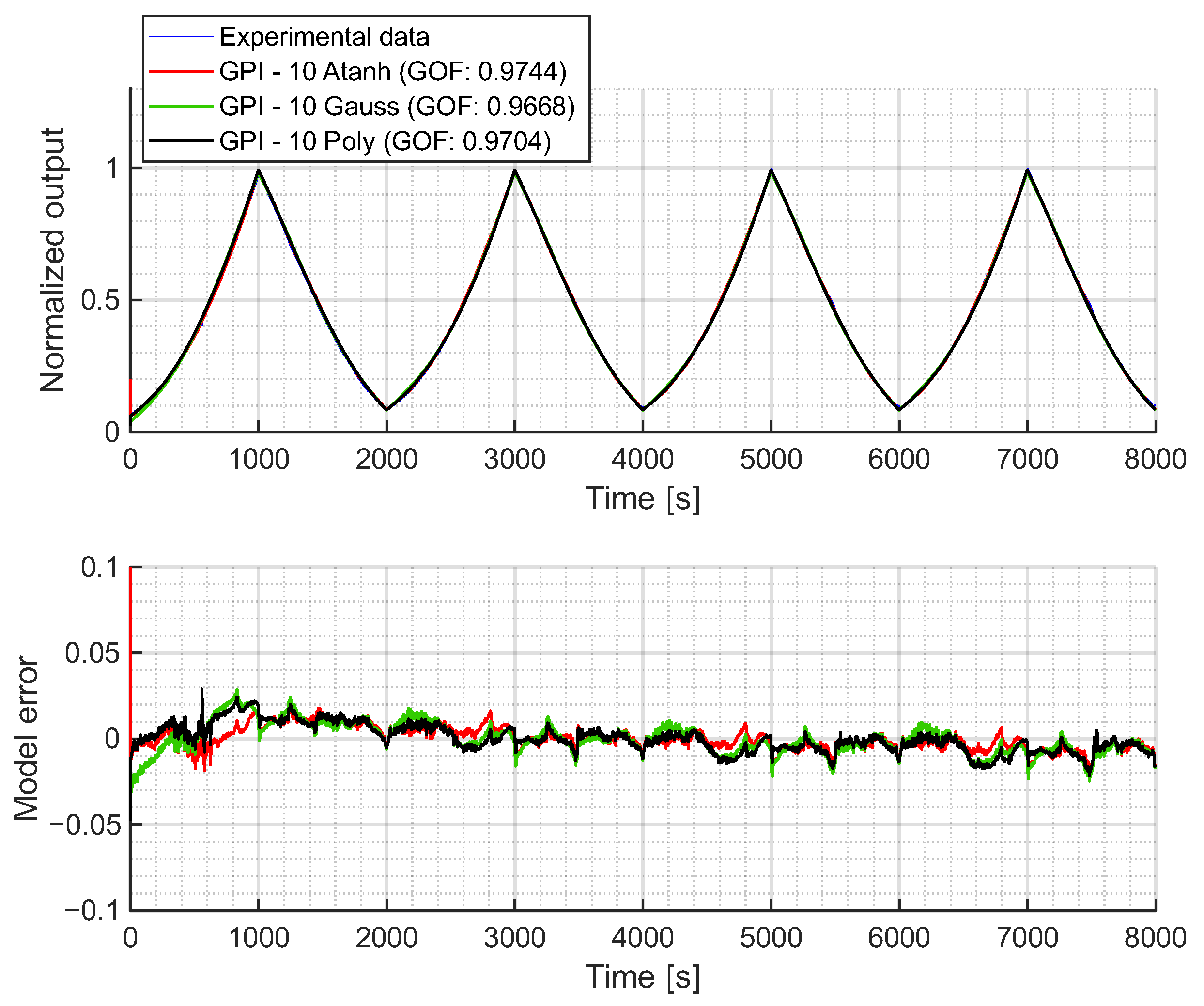
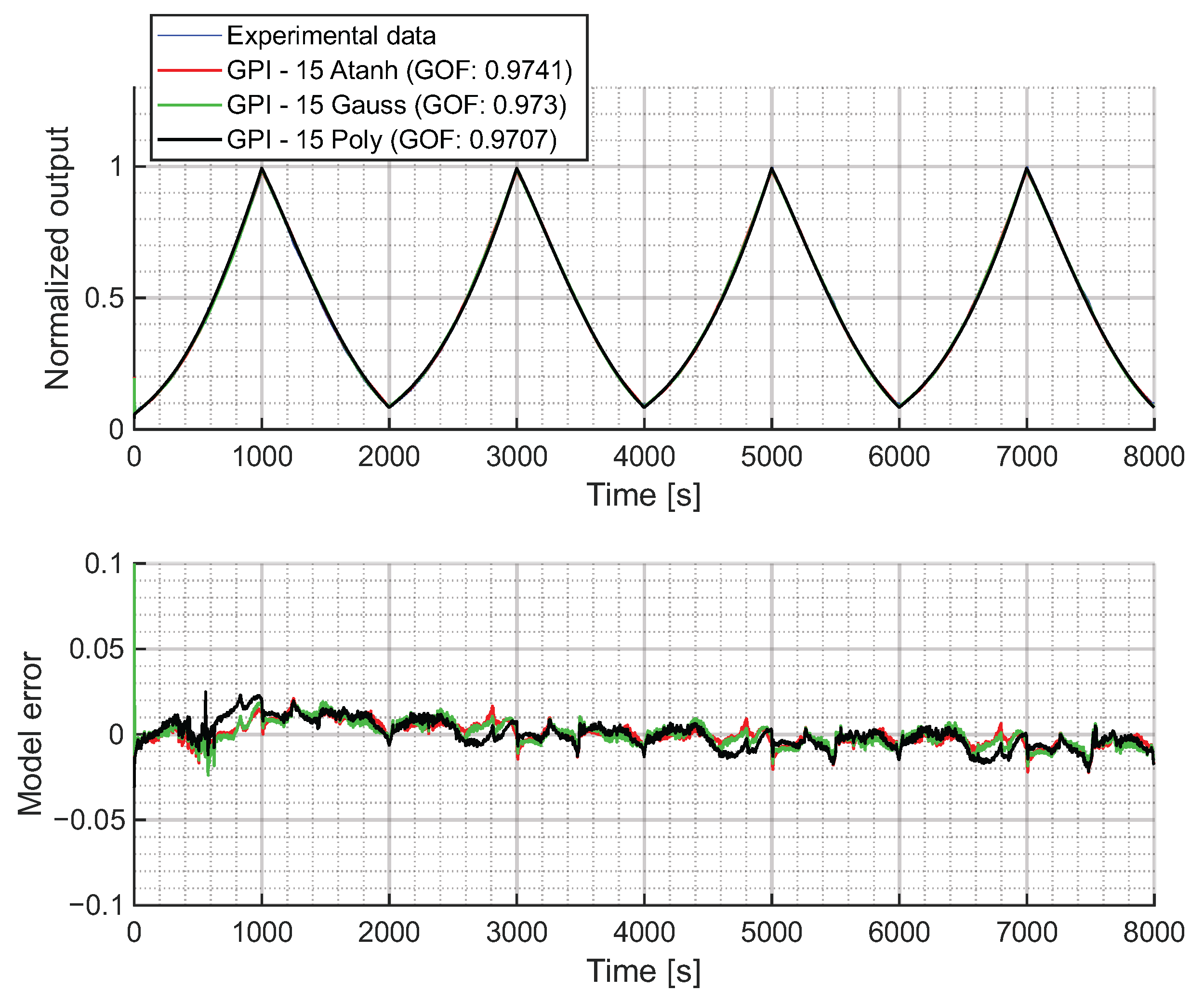
In any case, balancing accuracy, physical consistency, complexity and computational efficiency, the GPI model is likely the best choice for these soft pneumatic actuators. Even with 10 operators, it achieves a GOF above 0.96 in every case. Its explicit mapping, analytical invertibility and high GOF make it particularly well suited for both characterization and feedforward control implementation in applications requiring precise, real-time hysteresis compensation. Its only minor drawback is that the estimated initial value deviates from that of the experimental data. However, this can be easily corrected even in control loops. Within the envelope functions tested, the hyperbolic tangent achieves the highest GOF. However, the use of polynomial envelope functions is likely the best option: they capture the hysteretic behavior accounting for all the key dynamical properties of the system, with minimal loss in accuracy (approximately 0.974 with hyperbolic tangent vs. 0.97 with polynomial envelope functions) and reducing the number of parameters from 10 to 8.
8. Discussion
This work presents a direct comparative evaluation of different phenomenological hysteresis models, applying them to experimental data obtained from a hydrogel-based pneumatic bending actuator. The key concepts of each model are examined, highlighting the trade-offs between modeling fidelity, physical consistency, computational cost and implementation. Operator-based models, such as PR, CPI, GPI and MS, have been compared, emphasizing the importance of a careful selection of operators and the implementation of appropriate density functions.
Moreover, the pronounced asymmetrical behavior in the experimental data underlines the necessity of using asymmetric hysteresis models, such as PR, GPI or ABW models. As shown in the section on the ABW model (
Section 6.2), careful attention must be paid to model implementation, since not all asymmetric formulations yield feasible or accurate solutions.
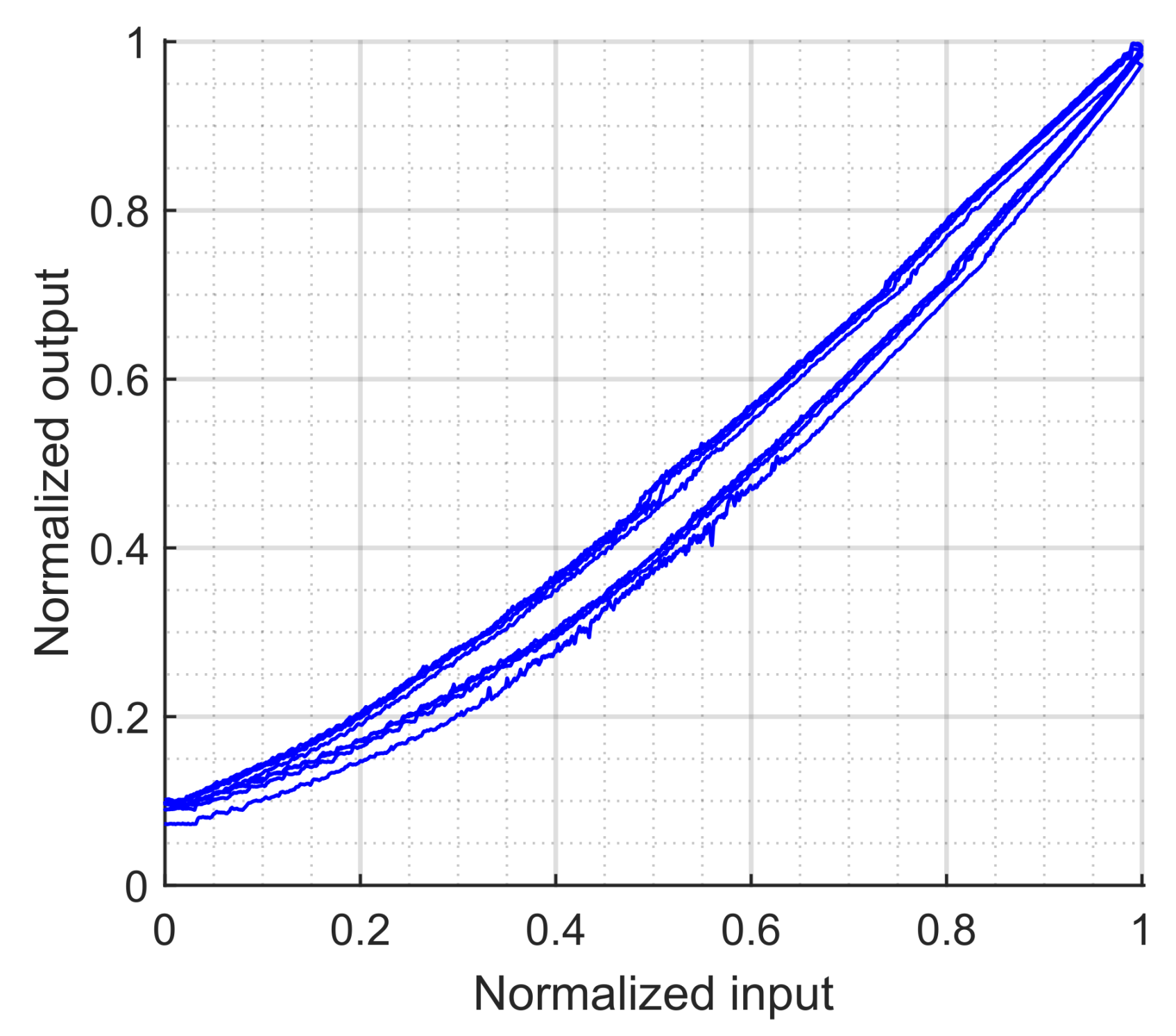
The experimental procedure has been designed to isolate the pure hysteretic behavior of the actuator using low-frequency (0.05 Hz) triangular input signals, effectively decoupling it from other dynamic effects. This analysis, however, was not designed to assess how the models perform under more dynamic operating conditions (e.g., rapid actuation or complex multi-frequency inputs), where viscoelastic and pneumatic dynamics may interact more strongly. Also, all experiments were conducted using a single amplitude (2 V) input signal, without exploring variations in actuation range. As a result, the formation and modeling of minor hysteresis loops have not been studied.
Future work can be built on these limitations by incorporating amplitude and frequency sweeps to evaluate model performance across a broader operational space. Doing so would enable a more complete understanding of hysteresis, using the present results as a reference for the static hysteretic behavior of the actuator and allowing for a clearer decoupling between hysteresis and other phenomena.
Undoubtedly, accurate modeling of actuator hysteresis can inform decisions during the design process, allowing for the development of soft actuators that exhibit reduced hysteresis based on their structural configuration or the materials used. Moreover, precise modeling can support the design of control strategies, as discussed in this work. This aligns with existing research, where various control strategies have been proposed to compensate for hysteresis effects and thereby enhance the tracking and positioning performance of smart actuators. These approaches underscore the necessity of advanced control methodologies to overcome the inherent nonlinearities of soft actuators, thereby ensuring reliable performance in sensitive and dynamic environments.
Therefore, the analysis and insights presented in this work aim to offer a clear guidance for researchers and engineers in the hysteresis modeling of actuators.