1. Introduction
When robots grasp fragile objects, it is necessary not only to consider the dropping and bruising caused by insufficient grasping firmness, as well as compression damage from excessive normal grasping forces, but also to pay attention to slip-induced damage during grasping with delicate surfaces. Therefore, it is not only necessary to consider the calculation of grasping force, but also to consider the calculation of grasping displacement. Due to the nonlinearity of frictional contact, some researchers have formulated the dexterous hand grasping problem as an optimization problem with nonlinear complementary constraints and solved it using the Alternating Direction Method of Multipliers (ADMM). For example, Carpentier [
1] proposed a solution method combining ADMM with the Proximal Method, and Kim [
2] introduced a GPU-friendly ADMM solution approach. However, these methods require solving a sub-problem each time that they are implemented. Analysis shows that the grasping is characterized by a set of variational inequalities [
3]. Under finite element or finite difference discretization, these variational inequalities generate complementarity problems [
4]. Due to the complementarity relationship between the parameters related to the slippage displacement and the grasping force, modeling the grasping problem as a complementarity model allows for the analysis of stable grasping, crushing damage, and slippage damage during the grasping based on the numerical solution of the complementary problem. There are two primary tasks here: establishing the complementarity-based mathematical model for dexterous grasping problems and developing the efficient numerical algorithm for this model. When the dexterous grasping problem is formulated as a Linear Complementarity Problem (LCP), incorporating unilateral contact and Coulomb friction constraints yields LCP with a saddle-point matrix structure characterized by asymmetric coefficients. This modeling framework effectively captures the intricate interactions between contact forces and frictional constraints during the grasping process.
Numerical approaches are presented to enable high-speed computation in dexterous robotic grasping modeled by LCPs. There are two main computational methods for LCPs arising from the field of dexterous robotic grasping: direct methods and projection methods. The Pivot method is a direct method. For example, Panagiotopoulos, Al-Fahed, and their colleagues [
5,
6,
7,
8,
9,
10] employed the Pivot method for solving such problems. When it is capable of solving the problem, the Pivot method can yield an exact solution. However, this method is limited to small-to-medium-scale systems and is only applicable to specific grasping scenarios. Bai [
11] and Werling [
12] adopted the Projected Gauss–Seidel (PGS) method for solving the problem. This method is easy to implement and allows for early termination. However, the linearization of friction cones can cause friction forces to bias towards the edges of the cones. While increasing the number of facets can reduce this error, it also leads to a rapid increase in the computational load. Significantly, many methods, such as the modulus-based method [
13], projection method [
14], and smoothing equation method [
15], have been proposed for solving large-scale LCPs. These foundational methods have inspired numerous modified variants in recent years, such as accelerated schemes [
16], hybrid strategies [
17,
18], and unified frameworks [
19]. However, when applied to grasping problems, modulus-based matrix splitting iteration methods and projection methods fail to converge due to the asymmetric or antisymmetric saddle-point structure of the coefficient matrix in the LCP, rendering them inapplicable to practical grasping scenarios. However, reformulating LCPs as smooth systems for solution purposes typically leads to strongly nonlinear formulations—even in basic problem instances—which introduce both theoretical challenges and computational complexities. Therefore, to effectively solve key parameters such as grasping forces and displacements, there is an urgent need to develop a dexterous robotic grasping complementarity problem solver with strong adaptability and the capability to handle large-scale problems. The development of such algorithms holds significant importance for advancing the application of complementarity problem methods in multi-fingered grasping analysis.
The non-smooth equations-based methodology effectively overcomes the shortcomings of previous approaches [
20]. Merit functions have been employed to reformulate the saddle-point-type LCP in dexterous grasping as a non-smooth system of equations [
21,
22], thereby transforming the original problem into one that requires solving this class of non-smooth formulations. There are numerous methods for solving such systems [
23,
24]. For dexterous grasping problems, the minimum grasping force that satisfies the required conditions is undoubtedly what we seek. Based on this characteristic, we choose to employ the Kaczmarz method for solving the problem. This method obtains the numerical solution that meets the conditions by continuously projecting onto hyperplanes. The Kaczmarz method was originally conceived as a solution strategy for both linear and nonlinear equation systems. Strohmer and Vershynin [
25] pioneered the stochastic enhancement of this classical iterative scheme, establishing the Randomized Kaczmarz (RK) approach for addressing linear systems. To improve convergence performance in such contexts, Bai developed two variants, the Greedy Randomized Kaczmarz (GRK) [
26] and the multi-step randomized extended Kaczmarz (MREK) [
27], by refining the RK framework through greedy selection mechanisms. Wang and Li [
28] later expanded this methodology to nonlinear scenarios by formulating the Nonlinear Randomized Kaczmarz (NRK) method. Liu and Li [
29] further innovated by combining principles from NRK and GRK to create two novel frameworks: the Nonlinear Greedy Deterministic Kaczmarz (NGDK) and the Nonlinear Greedy Randomized Kaczmarz (NGRK).
Applying the Kaczmarz framework to non-smooth equation solving, we introduced the Newton-Subgradient Non-smooth Greedy Randomized Kaczmarz (NSNGRK) algorithm in prior research [
30]. This approach exhibits strong performance in addressing LCPs arising from dexterous robotic grasping scenarios. However, two key limitations are observed: the method involves computationally intensive Jacobian evaluations at each iteration, and it employs the stochastic selection of a single constraint row among candidates satisfying the greedy criteria. When the scale of the non-smooth system of equations is large, this approach leads to a significant increase in computational cost. Additionally, the random selection of working rows results in an unpredictable number of iterations, further reducing efficiency. Based on these observations, we propose an improved method—the Newton-Subgradient Non-smooth Multi-step Greedy Kaczmarz (NSNMGK) method. In this new approach, during each iteration, the algorithm sequentially projects onto all rows that satisfy the greedy condition. By doing so, the generalized Jacobian matrix is computed only once per iteration, allowing all rows within the greedy set that meet the condition to participate in the computation. This not only addresses the issue of uncontrollable iteration counts caused by random row selection in the original method but also reduces the time overhead associated with multiple Jacobian computations. This is of great significance for improving the computational efficiency of dexterous robotic grasping complementarity problem solvers that are both highly adaptable and capable of handling large-scale problems.
This paper is organized as follows. The key notations, concepts, and foundational results required for subsequent analysis are systematically introduced in
Section 2. The proposed NSNMGK algorithm and rigorous theoretical analysis regarding its convergence properties are provided in
Section 3. Numerical dexterous grasping experiments validating the algorithm’s effectiveness are presented in
Section 4. The manuscript concludes with concluding remarks in
Section 5.
2. Preliminaries and Notation
The dexterous robotic grasping is essentially a highly nonlinear problem, coupling friction and contact. By linearizing friction cone and leveraging the complementarity relationships between variables in grasping process, the dexterous robotic grasping problem can be written as an LCP:
where matrix
is a non-symmetric saddle-point matrix with the form
,
is a vector, and
and
are complementarity variable pairs.
, which is defined by the grasping configuration, is a symmetric matrix with the same dimension as the number of contact points.
is a zero matrix.
and
are matrices determined by the grasping configurations and additional max grasping force constraints. In two-dimensional grasping problems, there exists
. In three-dimensional grasping problems, the above equation no longer holds. The irregularity of the matrix
presents challenges for solving the problem. By using a merit function
, the LCP(
b,
) can be transformed into a non-smooth system of equations. If merit function
with the property that
then the corresponding non-smooth system of equations of the LCP(
q,
) can be equivalently represented in the following non-smooth system of equations:
The NSNGRK method, as outlined in Algorithm 1, is proposed to solve Equation (
3) in our early work [
30]. Parameters required during the solution process, such as the generalized Jacobian matrix
, the threshold
, and the active index set
in Algorithm 1, is set as follows:
| Algorithm 1 Newton-Subgradient Non-smooth Greedy Randomized Kaczmarz [30]. |
- Require:
Matrix , vector , tolerance , initial value - Ensure:
Approximate solution - 1:
Initialize residual - 2:
for to n do - 3:
Compute constraint functions - 4:
end for - 5:
while do - 6:
Calculate the generalized Jacobian matrix - 7:
Compute adaptive threshold - 8:
Identify candidate set - 9:
Construct sampling distribution - 10:
Update solution - 11:
Refresh residual r and iteration count k - 12:
end while
|
When applying this method to grasping problems, we encountered several challenges. On the one hand, the NSNGRK method requires computing the generalized Jacobian matrix at each iteration and randomly selects only one active constraint row satisfying the greedy condition, which becomes computationally prohibitive for large-scale non-smooth systems. On the other hand, the random selection of projection rows each time leads to uncontrollable problems in the number of iterations, iteration time, and residuals during the solution process. Motivated by this observation, we develop the NSNMGK method, where all eligible rows meeting the greedy condition are incorporated into the computation during every iteration. The convergence analysis of the developed method framework necessitates the formalization of fundamental mathematical constructs, which we systematically organize as prerequisites for the subsequent theoretical investigation.
Definition 1 ([
31])
. In convex analysis, a subgradient of a convex function at a point in its domain is a vector such that, for all in the domain of ϕ, the following inequality holds: Definition 2 ([
28])
. A real matrix is said to be row-bounded below when there exists a positive constant ε satisfying . Definition 3 ([
28])
. A mapping is said to satisfy the local tangential cone condition when there exists a uniformity constant such that, for every index and any pair of points , one can find parameters satisfying the approximation inequalitywhere the uniformity constant satisfies . Lemma 1 ([
30])
. For convex functions that locally satisfy the tangential condition at point with within a neighborhood surrounding point , there exists subgradient at point and , satisfying Lemma 2 ([
30])
. For functions satisfying the local tangential cone condition with , the following inequality holds for all : Lemma 3. [30] For nonlinear mapping satisfying the local tangent cone condition with , it follows from the iterative formula that Lemma 4. [28] For a full column rank matrix , there exists . 4. Numerical Experiments
To validate the efficacy of the NSNGRK method and the NSNMGK method in dexterous robotic grasping tasks, we conduct several numerical experiments under four scenarios: (I) constrained planar grasping, (II) spatial grasping with partial force information, (III) unconstrained 3D grasping with fully unknown contact dynamics, (IV) five-finger grasping.
Our experimental analysis reveals that the NSNMGK method demonstrates superior computational efficiency compared to the NSNGRK method in three key metrics: iteration count (denoted as “IT”), final residual (denoted as “FRES”), and execution time (denoted as “TIME”). Quantitative comparisons further indicate a speed-up factor defined by the ratio of their execution times, mathematically expressed as
When speed-up is great than 1, the execution time of the NSNMGK method is less than the execution time of the NSNGRK method. The larger the value of speed-up, the less execution time consumbed by the NSNMGK method. All numerical experiments are executed on a computing platform equipped with an Intel CORE i7 processor operating at 2.3 GHz and 16 GB DDR4 RAM. A consistent initialization protocol
is adopted for all computational trials. The termination condition is once the IT exceed 20,000, or the residual error norm (denoted as “RES”), defined by
at the current iterate
, satisfies
1.0 × 10
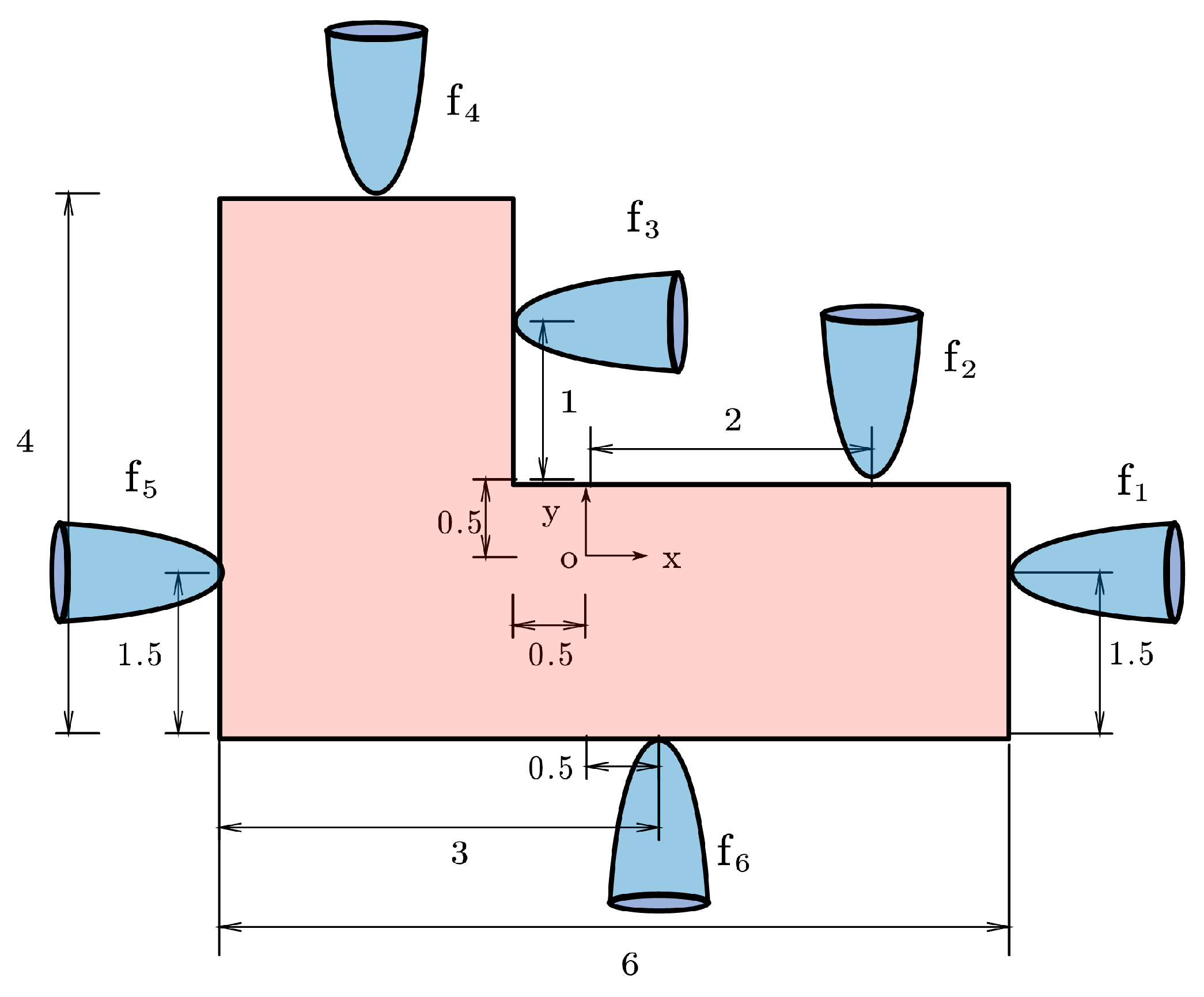
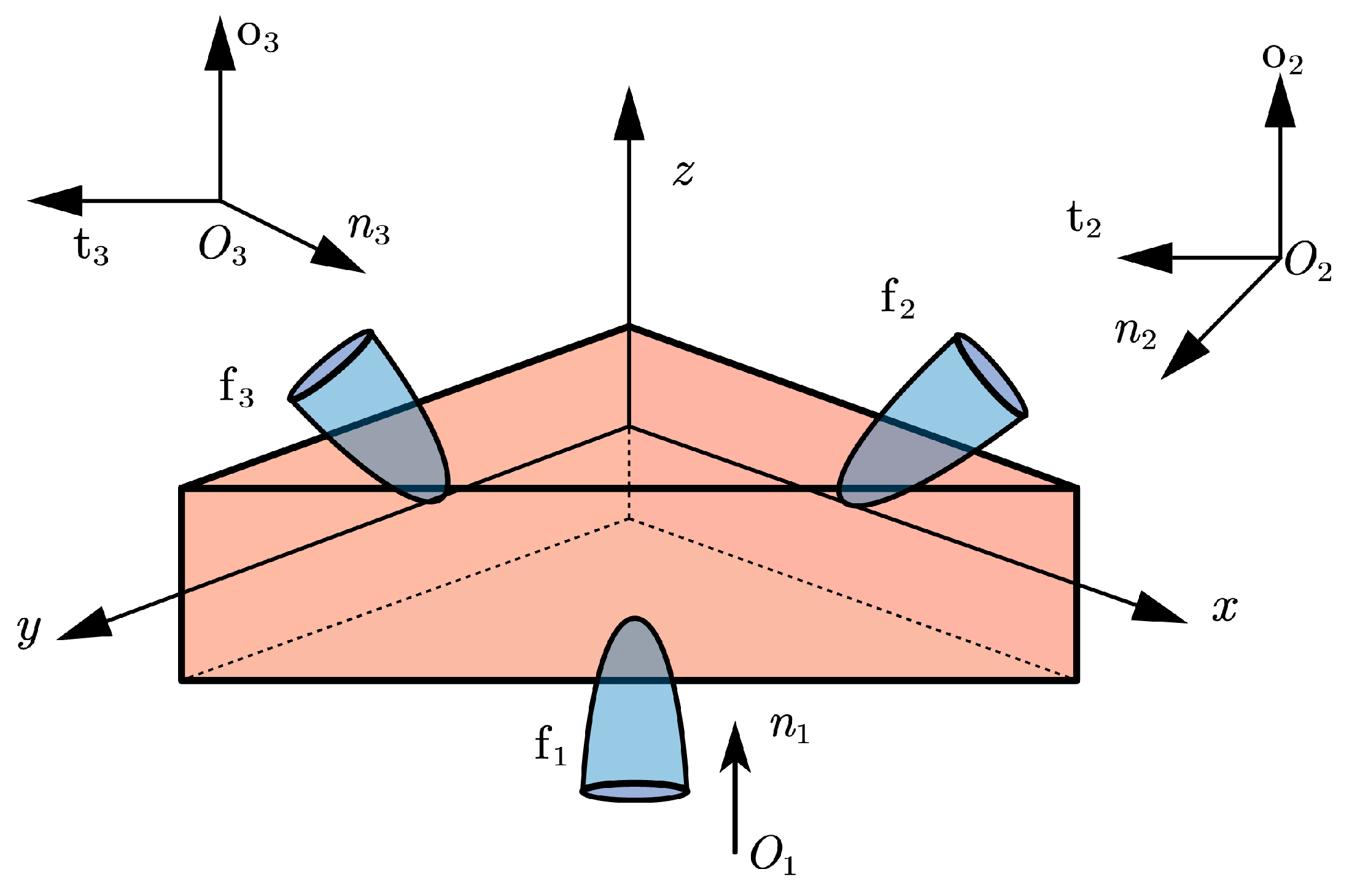
−4Example 1 ([
6])
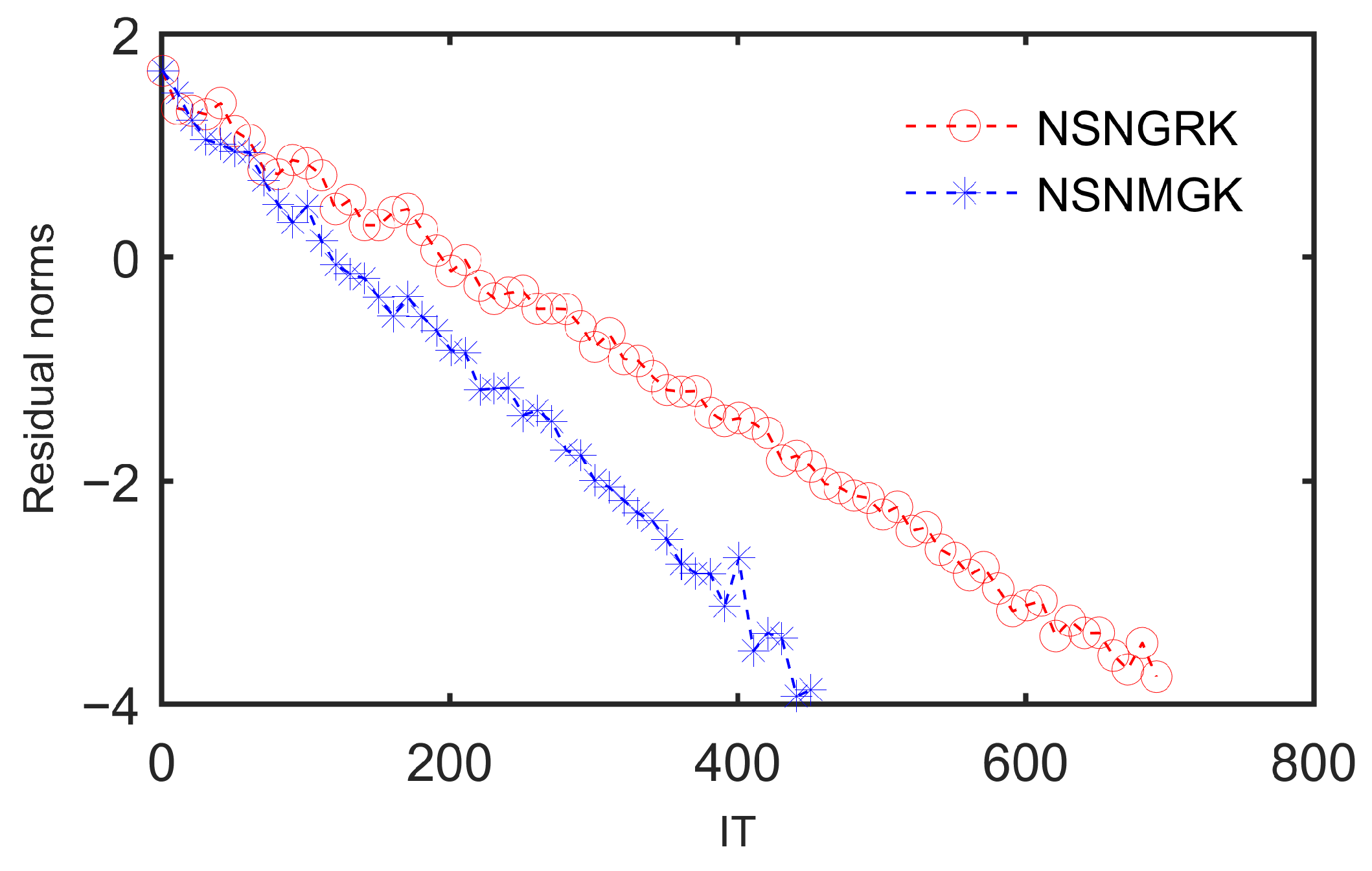
. Consider a planar rigid object grasped by six elastic compliant fingers, as illustrated in Figure 1. The global coordinate frame is established at the object’s geometric center, with specified contact points for each finger. Elastic properties of Finger are characterized by stiffness . An external resultant wrench is imposed on the object. Figure 2 presents the RES curves (logarithmic scale, base-10) plotted against the IT. As demonstrated, the NSNMGK method exhibits significantly improved convergence behavior compared to the NSNGRK method, achieving lower residual magnitudes within fewer iterations. The execution time of NSNGRK is shown to be 0.26563 s, with that of NSNMGK being demonstrated as 0.23438 s, and a speed-up ratio of 1.13333 is evidenced.
Table 1 reports the IT and FRES of two methods. The NSNGRK method employs a stochastic selection of working rows during each iteration, resulting in varying IT and FRES across different experimental trials. To provide a more comprehensive assessment of its overall performance, we conducted 50 independent experiments with the NSNGRK method and adopted the average values of IT and FRES as representative metrics. The quantitative indicators derived from the NSNGRK and NSNMGK algorithms, including grasping forces, fingertip displacements, and object displacements, are systematically presented in
Table 2 and
Table 3. As can be seen in
Table 1, the NSNGRK method exhibits an average iteration count of 703 with a final residual value of 9.1901 × 10
−5. In contrast, the NSNMGK method demonstrates deterministic solution characteristics, achieving a fixed iteration count of 458 and a final residual value of 8.7787 × 10
−5. Quantitative comparison demonstrates that the NSNMGK method outperforms the NSNGRK method in both iteration efficiency (reduced by 20.6%) and numerical accuracy (improved by 4.5%), while its deterministic output provides enhanced statistical stability and predictability. It can also be seen from the tables that fingers
,
, and
do not exert gripping forces on the object.
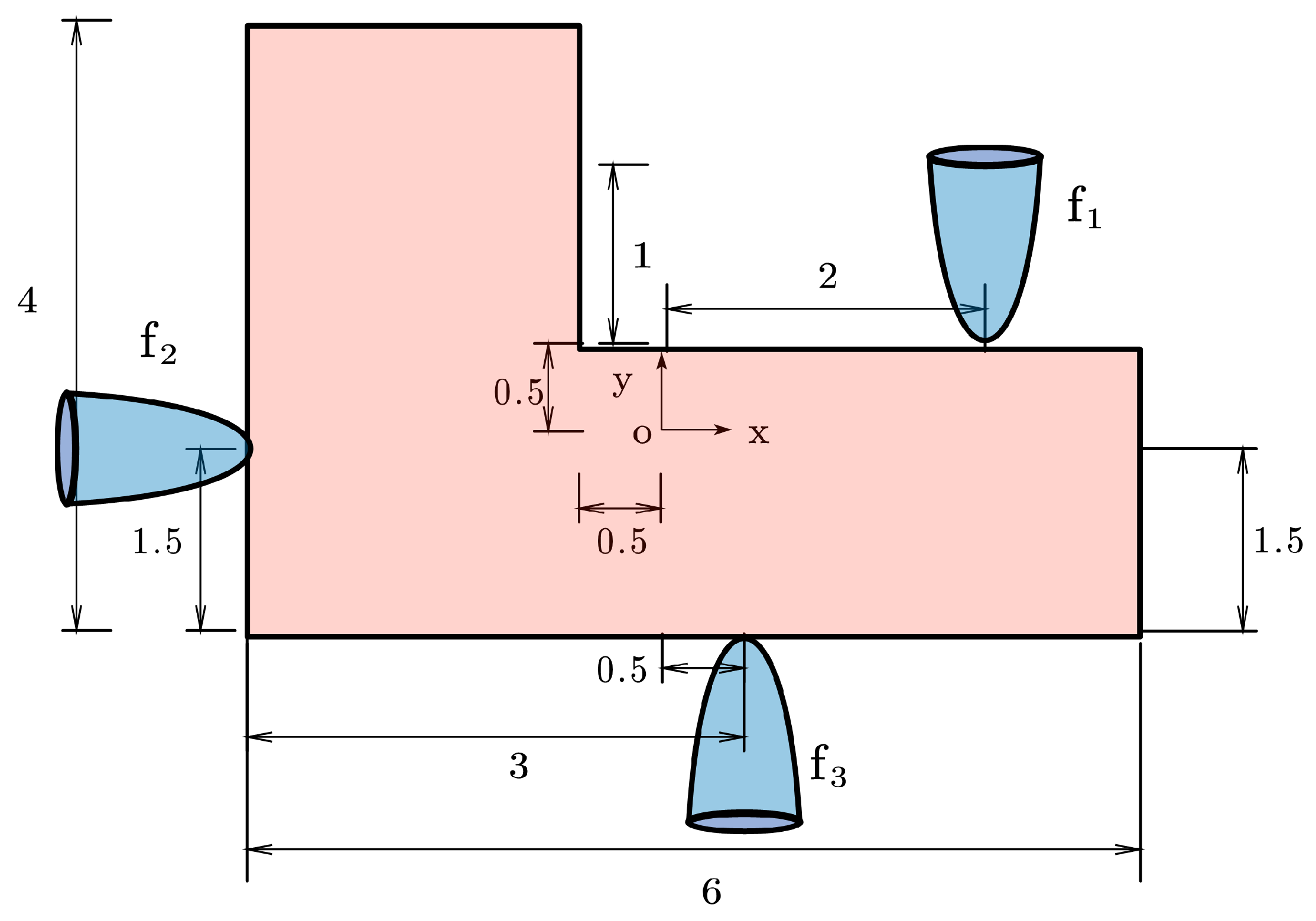
Below, we remove fingers
and
and change the grasping configuration, as shown in
Figure 3.
Table 4 reports the IT and FRES of two methods. As shown in
Table 4, under the current experimental configuration, the NSNGRK method exhibits an average iteration count of 3088 with a final residual value of 9.7665 × 10
−5. In contrast, the NSNMGK method demonstrates deterministic solution characteristics, achieving a constant iteration count of 1637 and a final residual value of 8.7375 × 10
−5. Quantitative analysis demonstrates that, under the given parameter settings, the NSNMGK method outperforms the NSNGRK method by 47.0% in iteration efficiency and 10.6% in numerical accuracy across these two key performance metrics, thereby confirming its enhanced stability and reliability for large-scale problem solving.
The resulting force–displacement distributions computed via both methods are systematically documented in
Table 5 and
Table 6, encompassing grasping forces, fingertip displacements, and object displacements profiles. As can be seen from the tables, the grasping forces and displacements calculated by the two methods are basically the same. But, compared with the former configuration, it can be observed that, although the grasping forces under the two configurations are the same, there are significant differences in the displacements generated during grasping. This indicates that fingers not generating grasping force constraints during the grasping process also generate grasping displacement constraints, which affect the final fingertip and object displacements.
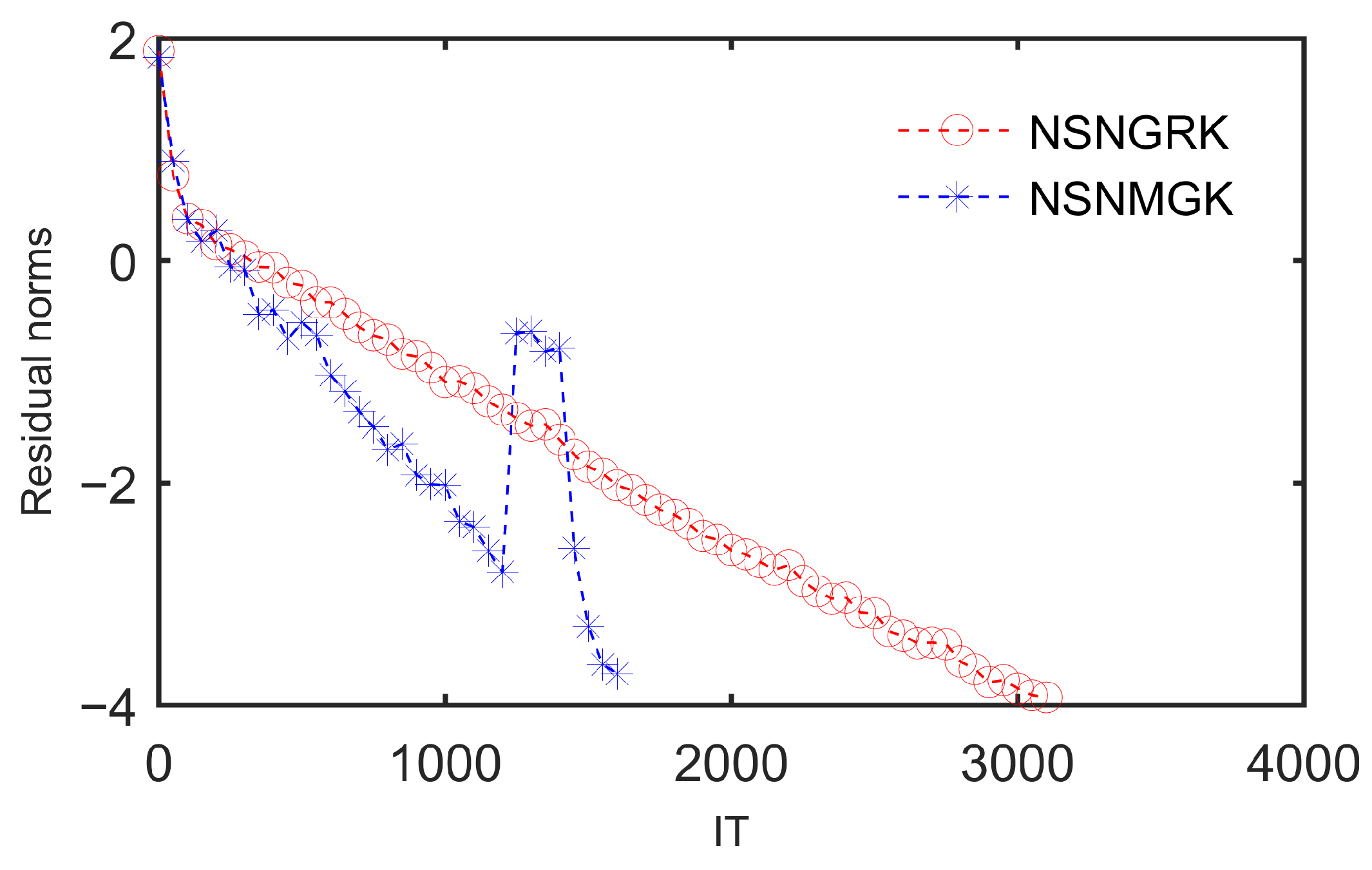
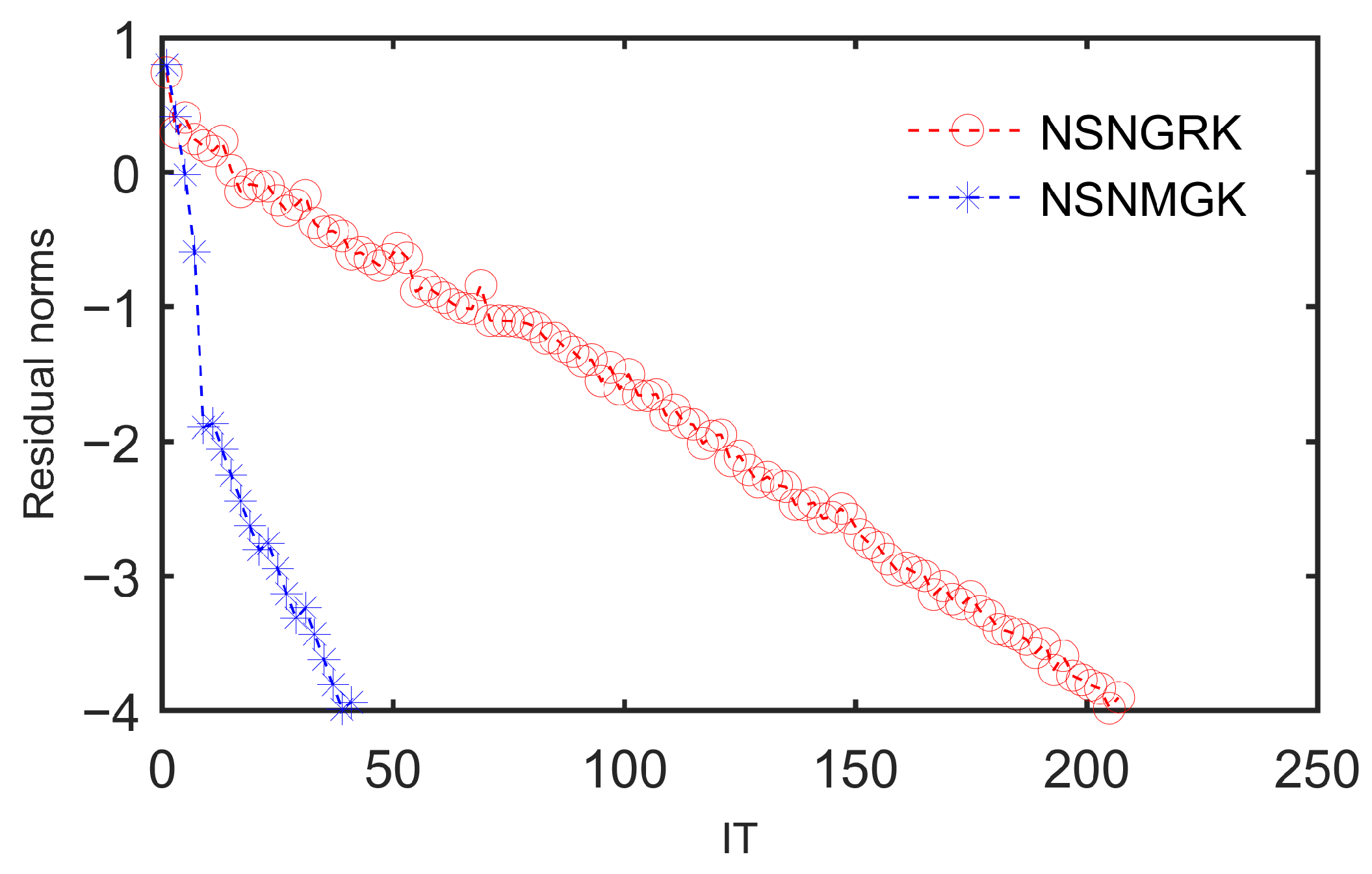
The curves of RES in base-10 logarithm versus the IT for the two methods are presented in
Figure 4. As demonstrated, the NSNMGK method also exhibits significantly improved convergence behavior compared to the NSNGRK method, achieving lower residual magnitudes within fewer iterations.The execution time of NSNGRK is shown to be 0.89063 s, with that of NSNMGK being demonstrated as 0.45313 s, and a speed-up ratio of 1.9655 is evidenced.
Example 2 ([
7])
. Consider a three-dimensional isosceles right-angled triangular prism grasped by three robotic fingers, as illustrated in Figure 5. The object’s centroid is aligned with the global coordinate system’s origin. Contact point coordinates are defined as , , . A Coulomb friction coefficient governs interfacial interactions. The compliance characteristics of the contact springs are parameterized as follows: normal stiffness , and tangential stiffness . Finger exerts a normal force on the prism. When constructing the linear complementarity model for dexterous robotic grasping, a polyhedral cone discretization is required to approximate the friction cone. As the number of pyramid faces increases, the approximation accuracy in capturing the true characteristics of the friction cone also improves.
Table 7 shows the IT, TIME, and FRES of Example 2 for both NSNGRK and NSNMGK method with different pyramid faces. The comparative analysis of
Table 7 reveals that the NSNMGK method demonstrates superior performance over the NSNGRK approach in three key metrics. Specifically, the NSNMGK algorithm achieves a speed-up of 3.0000 and 5.0000 for 4- and 8-face configurations, respectively, demonstrating a consistent enhancement in computational efficiency as the problem scale increases. This scalability advantage highlights the NSNMGK method’s inherent superiority in handling large-scale problems compared to the NSNGRK counterpart.
As illustrated in
Figure 6, the curves of the RES in base-10 logarithm versus IT for the 5-face pyramid configuration further substantiate this claim: the NSNMGK method exhibits significantly faster convergence behavior, reducing the required iteration count at an accelerated rate relative to the NSNGRK implementation.
Based on the configuration, the forces, slippage displacements and object displacements of two methods are given in
Table 8 and
Table 9. According to
Table 8, the NSNGRK method computes a normal force of 5.3318 and a tangential force of 1.3106 for finger
, while the normal force for finger
is 5.9732 and the tangential force is 1.5244. Notably, there are significant discrepancies in the grasping forces between the two fingers. In contrast, as shown in
Table 9, the NSNMGK method yields identical values for both fingers: a normal force of 5.6596 and a tangential force of 1.4104. The experimental results demonstrate that, under low-facet discretization conditions, although the NSNGRK method achieves numerical convergence, its solutions exhibit significant deviations from the physical ground truth. In contrast, the NSNMGK method yields results in both magnitude distribution and spatial consistency that align closely with the actual grasping scenario. This performance disparity directly validates the superior numerical robustness and algorithmic reliability of the NSNMGK method in multi-contact point mechanics analysis, particularly maintaining physical plausibility even under low-precision geometric approximations.
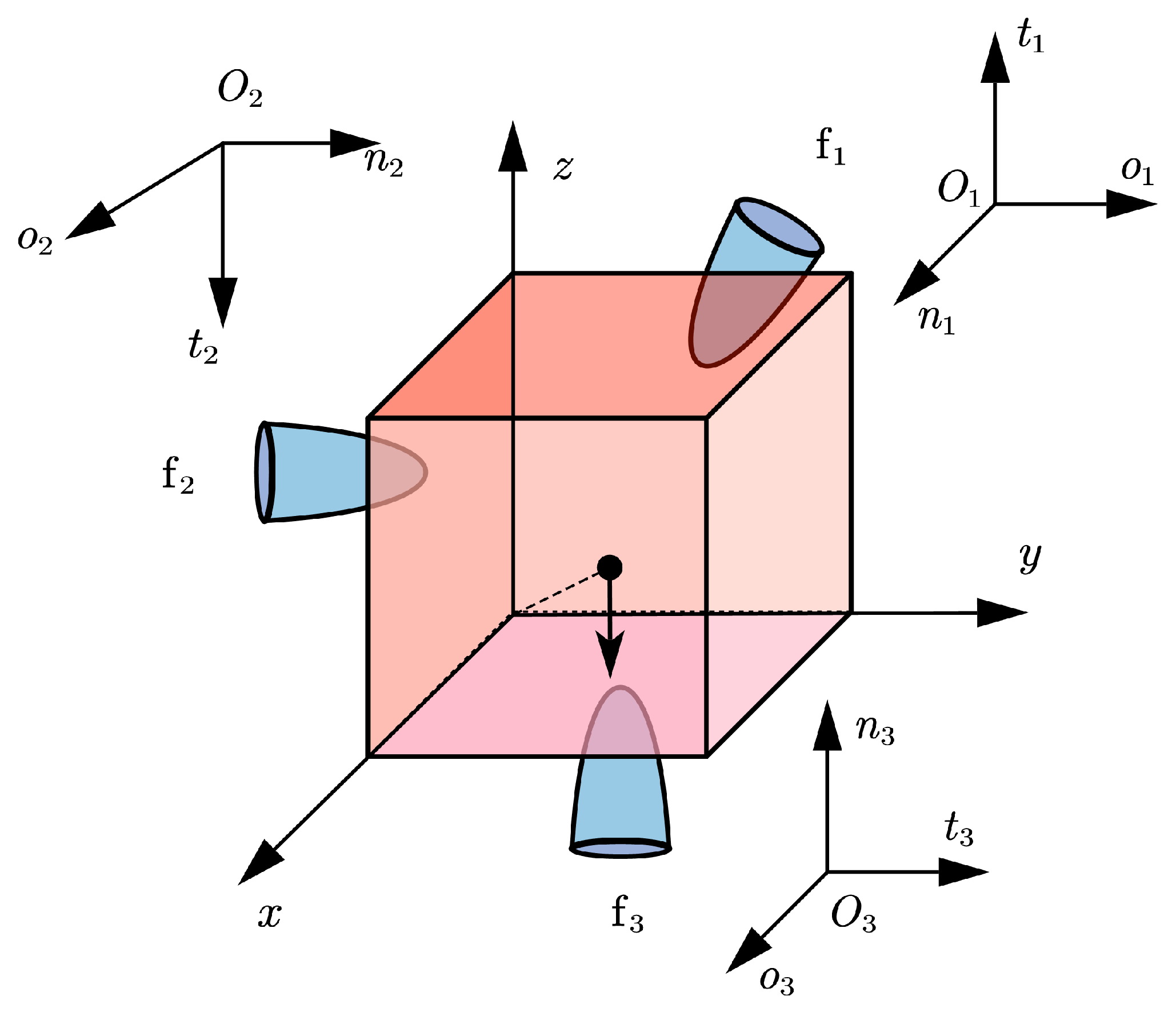
Example 3 ([
10])
. Consider a unit cube grasped by three hard fingers, as depicted in Figure 7; the global coordinate system is fixed at the left angle point of the bottom surface. The gravity of the cube is 5. The contact points with reference to the global coordinate system are , , . The compliance characteristics of the contact springs are parameterized as follows: normal stiffness , and tangential stiffness . A Coulomb friction coefficient governs interfacial interactions. Table 10 shows the IT, TIME, and FRES of Example 3 for both NSNGRK and NSNMGK methods with different pyramid faces. The comparative analysis in
Table 10 reveals that the NSNMGK method also demonstrates superior performance over the NSNGRK approach in three key metrics in this grasping problem. Specifically, the NSNMGK algorithm achieves a speed-up of 1.8182 and 3.9231 for 4- and 8-face configurations, respectively, demonstrating a consistent enhancement in computational efficiency as the problem scale increases. This scalability advantage also highlights the NSNMGK method’s inherent superiority in handling large-scale problems compared to the NSNGRK counterpart.
The forces, slippage displacements, and object displacements of two methods with five pyramid faces are given in
Table 11 and
Table 12. The results in these tables and figures once again demonstrate the superiority of the NSNMGK method compared with the NSNGRK method. The data presented in the table demonstrate that the grasping forces and displacements obtained by both methods accurately reflect the physical reality of the grasping scenario.
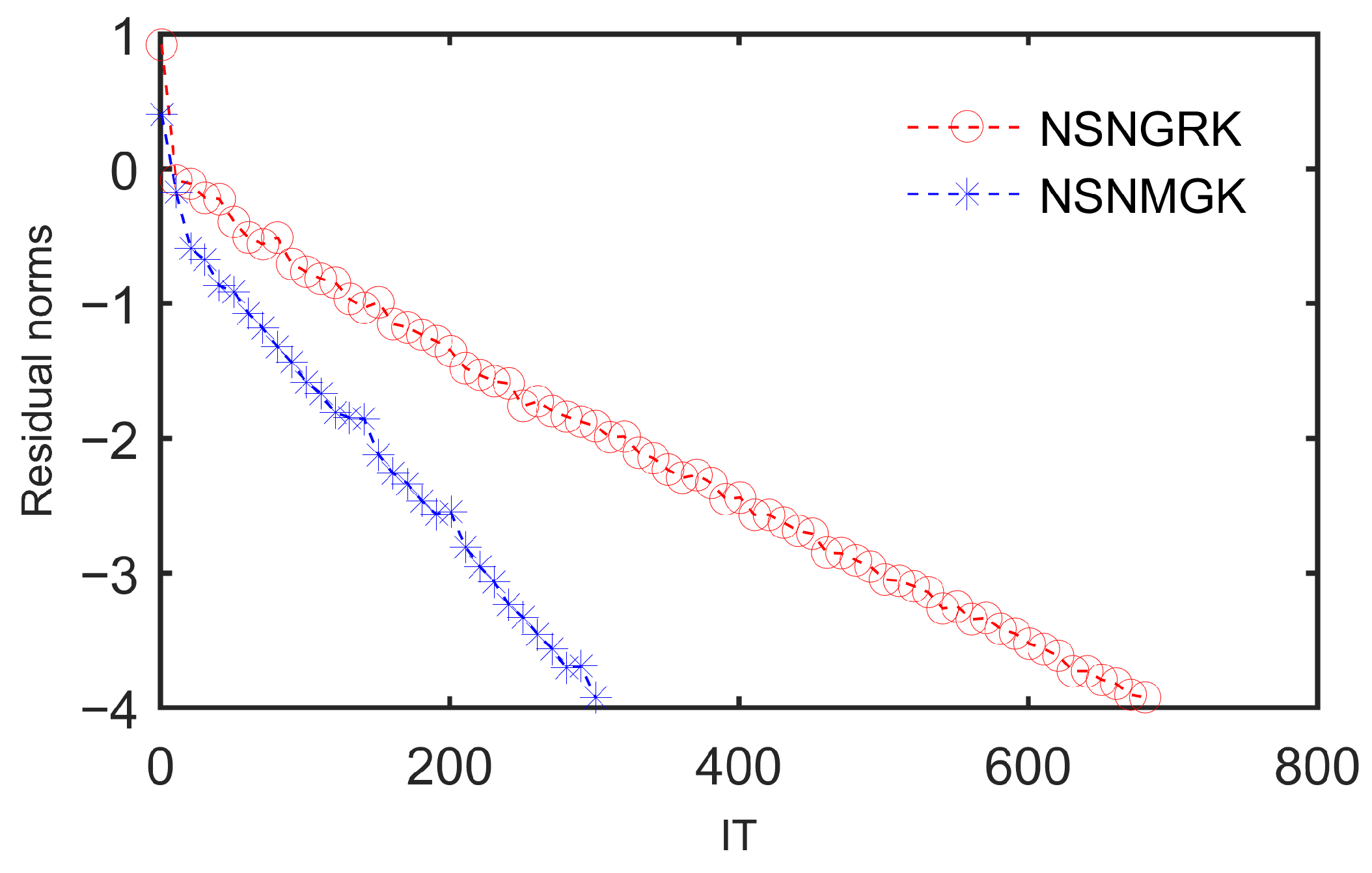
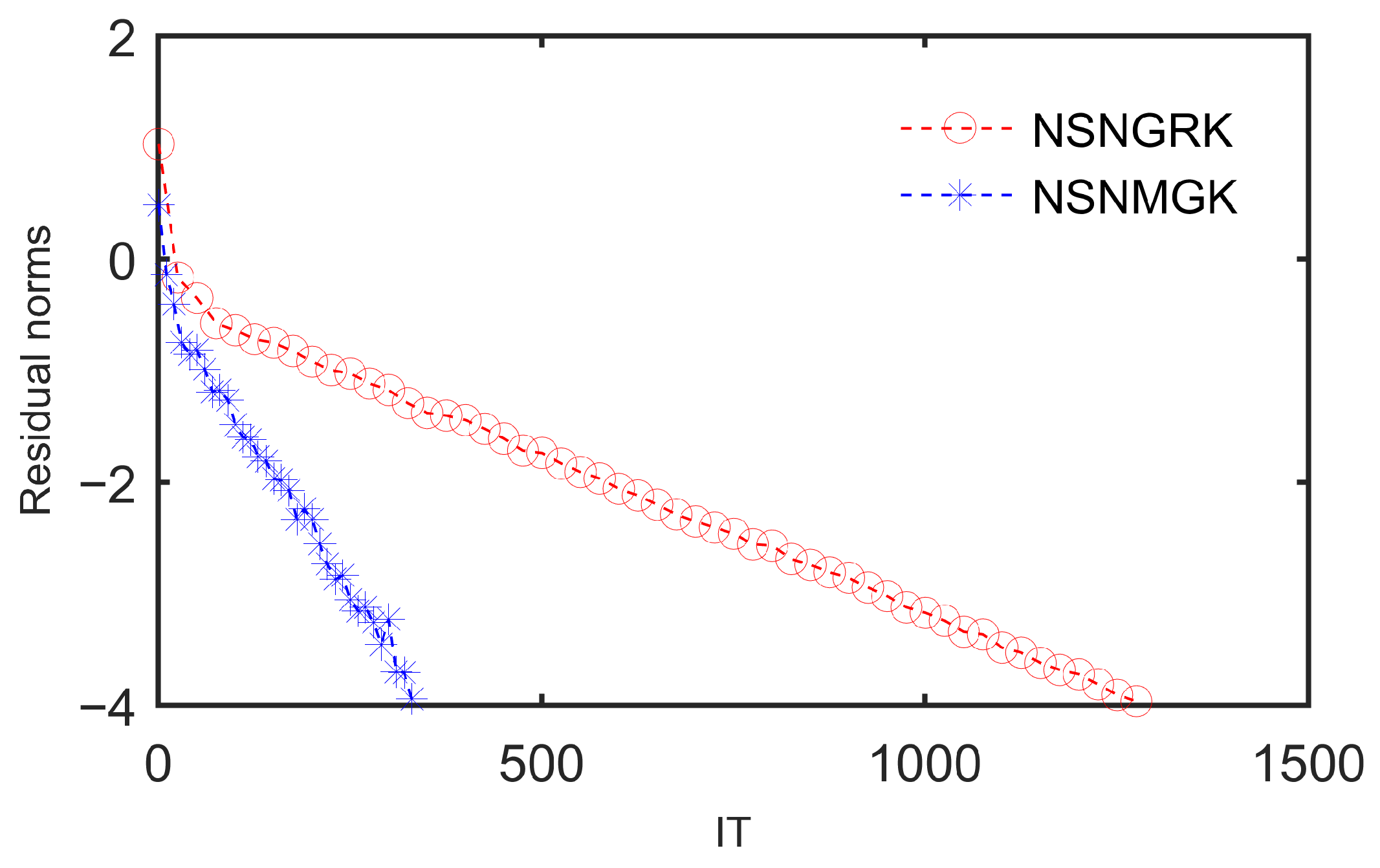
In
Figure 8, we depict the curves of the RES in base-10 logarithm versus the IT with five pyramid faces. It can also be seen that the NSNMGK method reduces the required iteration count at an accelerated rate relative to the NSNGRK implementation.
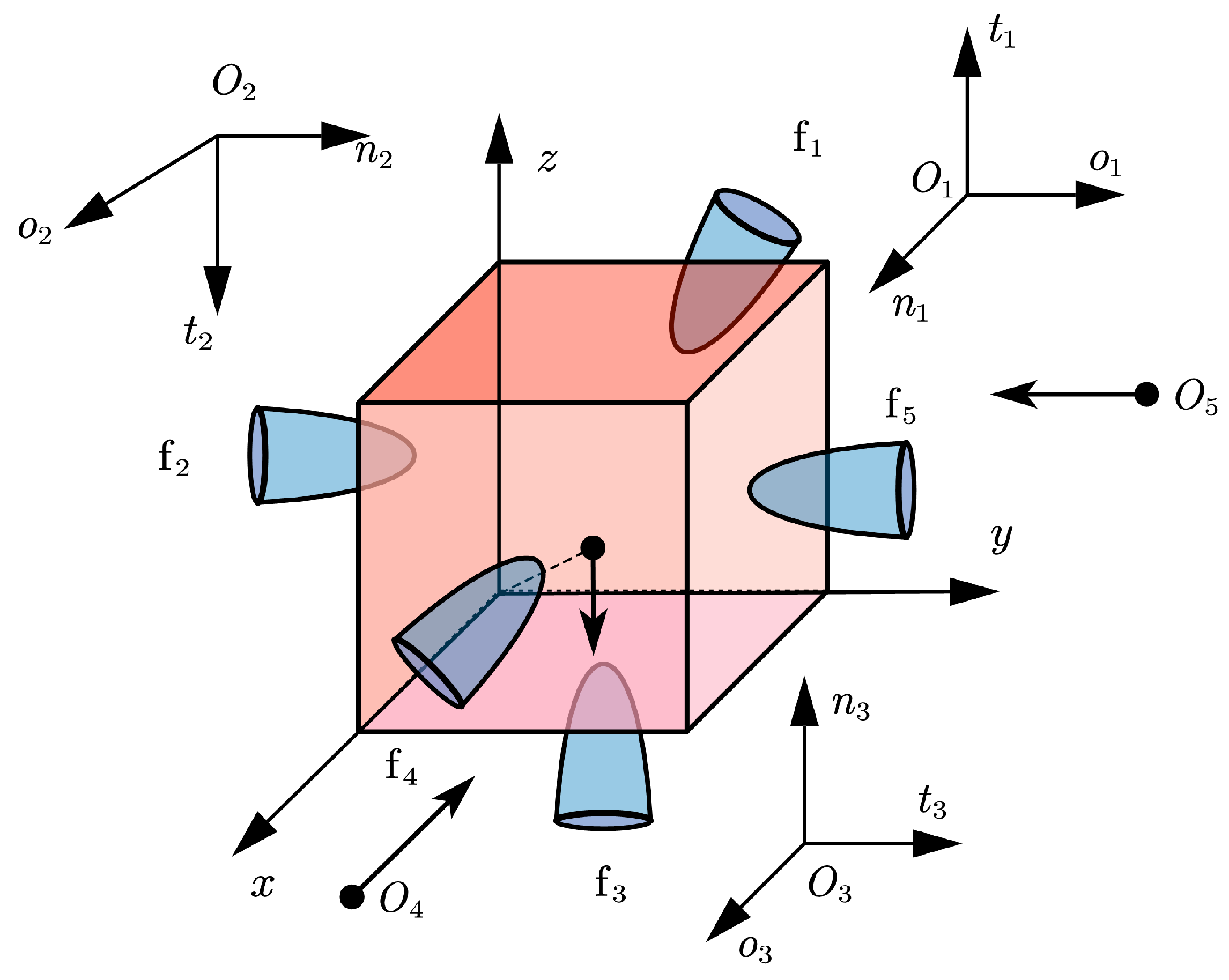
Example 4 ([
30])
. Consider a five-fingered grasping problem, which is built upon the framework of Example 3 by introducing two additional frictionless finger contact constraints to the original three-fingered model, as depicted in Figure 9. The contact points of the newly added fingers are defined at positions , on the object’s surface, while the remaining parameter configurations follow those in Example 3. Table 13 shows the IT and TIME of Example 4 for both NSNGRK and NSNMGK methods with different pyramid faces. The forces, five slippage displacements, and object displacements of two methods with five pyramid faces are given in
Table 14 and
Table 15. The curves of the RES in base-10 logarithm versus the IT with eight pyramid faces are depicted in
Figure 10. The results in these tables and figures once again demonstrate the superiority of the NSNMGK method compared with the NSNGRK method in the five-fingered grasping problem.
5. Discussion
The NSNMGK method demonstrates significant performance advantages in solving linear complementarity problems related to grasping. First, it employs a deterministic strategy for selecting working rows, eliminating the variability in experimental results caused by random sampling and ensuring the stability and reproducibility of the algorithm’s output. Second, compared to the NSNGRK method, NSNMGK exhibits superior iterative efficiency and numerical accuracy. Under identical experimental configurations (e.g.,
Table 4), it achieves fewer iterations (1637 vs. 3088) and lower final residuals (8.7375 × 10
−5 vs. 9.7665 × 10
−5). Moreover, the speedup increases with the problem scale (e.g., a 3× speedup for 4-facet pyramid configurations and a 5.0× speedup for 8-facet configurations—
Table 7). Additionally, under low-facet discretization conditions, the NSNMGK method yields grasping forces and displacements that align closely with physical reality, whereas the NSNGRK method shows significant deviations, demonstrating stronger numerical robustness and engineering applicability. Although physical experimental validation has not yet been conducted, the numerical experiments in this study are rigorously based on typical scenarios from the existing literature on multi-fingered grasping problems, thereby effectively ensuring the interpretability and reliability of the numerical results in practical applications.
Despite these advantages, the NSNMGK method faces certain limitations. Its deterministic mechanism introduces challenges in parallel implementation, which may hinder its efficiency in high-performance computing environments. It should be noted that the current method’s performance is evaluated primarily in static grasping scenarios within simulation environments, and its robustness under highly dynamic conditions or significant model uncertainties requires further investigation.
Overall, the NSNMGK method provides a more efficient and reliable numerical tool for real-time precise dexterous grasping. Future work will focus on the following directions: extending the NSNMGK framework to handle dynamic grasping scenarios and online adaptation to object uncertainties, and investigating the integration of this solver with real-time trajectory planning and control loops by using virtual prototyping technology for closed-loop dexterous manipulation.