Study on the Vibration Characteristics of Separated Armature Assembly in an Electro-Hydraulic Servo Valve Under Interference Fit

Abstract

The electro-hydraulic servo valve is a critical component that transforms electrical signals into hydraulic signals, thereby controlling the hydraulic system. It finds extensive application in precision control systems. The stability of the electro-hydraulic servo valve is primarily influenced by the armature assembly. Unlike integral armature assembly, the separated armature assembly, comprising the armature, spring tube, flapper, and feedback spring, is joined through an interference fit, which introduces prestress within the assembly. The existence of prestress may affect the operational mode of the armature assembly. Consequently, this paper investigates the vibration characteristics of the separated armature assembly under interference fit conditions. Comparative analysis reveals that interference fit indeed generates prestress, which cannot be overlooked. To further validate the reliability of the simulation results, the natural frequency of the separated armature assembly is determined by applying a sweeping frequency signal to the torque motor using an electric drive, thereby verifying the feasibility of the simulation analysis. Additionally, the impact of interference on the vibration characteristics of the separated armature assembly is examined, confirming the accuracy of the simulation analysis method based on the interference fit. The research on vibration characteristics of a separated armature assembly provides technical support for the structural optimization design of the electro-hydraulic servo valve, thereby enhancing its performance.

1. Introduction

The nozzle flapper servo valve has the advantages of fast response, high precision, and high sensitivity, and is widely used in hydraulic servo control systems. The occasional whistling during the operation of the servo valve [1], causes the spring tube rupture, resulting in servo valve failure, and even affects the function of the hydraulic system. The whistling is caused by the phenomenon of self-excited oscillations. The reported research shows that the self-excited oscillations are not only related to the pressure pulsation of the pilot-stage flow field [2,3] but also to the vibration characteristics of the armature assembly [4].

Mode is the inherent vibration characteristic of the structure, so the mode of the armature assembly is studied in this paper. As shown in Figure 1, the separated armature assembly is composed of four parts: armature, spring tube, flapper, and feedback spring. The characteristic of the separated armature assembly is that the flapper and feedback spring are two independent parts, while in the integral armature assembly, the flapper and feedback spring are integrated. Many researchers have studied the modal analysis of components. Zhang [5] used a modified transfer matrix method to calculate the modal calculation of the rotor in the turbomolecular pump, and the experiment proved that the method could calculate the modal of the rotor assembly with high accuracy. Kim [6] carried out natural frequency and Campbell diagram analysis of the turbine blades according to their assembly conditions, and verified the modal characteristics and resonance stability. Zhai [7] calculated the natural frequency and mode shape of the rotor assembly without a thrust disk through the transfer matrix method according to the actual assembly relationship, and verified the results by using the finite element method and a new modal experiment method, the interference fit and clearance fit between the parts were also considered in FEM. Daouk [8] studied the relationship between the number of bolts, the position of the bolts, and the pre-loaded torque value on the modal damping of the assembly. Yang [9] conducted modal analysis experiments using the force hammer excitation method and obtained the natural frequency and modal modes of stacked chip components.

The modal analysis of components cannot be simplified in some cases, and the influence of external conditions on the stiffness needs to be considered [10,11,12]. Orlowska [13] studied the effect of prestress on the natural frequency and dynamic characteristics of eccentric prestressed glass fiber reinforced polymer composite beams. The results show that prestress increases the first bending frequency and decreases the second bending frequency, and a comparison of the numerical and experimental data confirmed this effect. Hu [14] studied the effect of prestress on the dynamic characteristics of rail transit gearboxes and compared it with the model without prestress; the results showed that prestress has a significant effect on the modal characteristics of the gearbox. Through finite element analysis, Wang [15] constructed a prestressed modal module to obtain the strength and modal characteristics of the steering device. Li [16] studied the sealing interface of the ultra-high pressure diaphragm compressor cylinder head, and found that some modal frequencies changed transition with bolt loosening. Liu [17] analyzed the dynamic behavior of the printed circuit board assembly (PCBA) and the reliability of the board-level solder joints under thermal–vibration combined load. The results showed that when the temperature changes from 22 °C to 60 °C, the natural frequencies of PCBA decreases, resulting in a decrease in the fatigue life of solder joints. Therefore, in some cases, external conditions have an effect on the dynamic characteristics of components.

Different from the general components, the separated armature assembly is composed of four parts connected by interference fit. Interference fit usually occurs under the condition of shaft and hole fit, and the magnitude of interference has an effect on the modes of the components [18,19]. Fan [20] used Ansys Workbench software to study and analyze the modes of the rotor assembly connected by the interference fit between the elastic shaft and the rigid thick disk and obtained the natural frequency of the component.

In this paper, in order to explore the vibration characteristics of the separated armature assembly and provide technical support for the structural design and optimization of the servo valve, the influence of bonded, friction contact type, and contact surface nodes coupling or not on the modes of armature assembly is studied, and the influence of interference on the modes of armature assembly is further studied.

2. Armature Assembly

2.1. Geometry Model of Armature Assembly

There are two types of armature assembly: integral and separated, the separated armature assembly is composed of four parts: armature, spring tube, flapper, and feedback spring, and the four parts are assembled together by interference fit. As shown in Figure 1, armature and spring tube interference assembly, spring tube and flapper interference assembly, flapper, and feedback spring interference assembly. Therefore, there is prestress in the armature assembly under normal working conditions. The research shows that the existence of prestress has an effect on the modes of the structure [13,14,15].

Figure 1. Separated armature assembly.

2.2. Dynamic Model of Armature Assembly Under Prestressed Condition

For armature assembly, the free vibration differential equation without damping can be described as follows [21]:

$$[M]\left\{\ddot{u}\right\}+[K]\left\{u\right\}=\left\{0\right\}$$

(1)

where $[M]$ is the mass matrix of the armature assembly, $[K]$ is the stiffness matrix of the armature assembly, $\left\{\ddot{u}\right\}$ is the vibration acceleration matrix, and $\left\{u\right\}$ is the displacement matrix.

Under certain initial conditions, armature assembly move at the same frequency according to simple harmonic vibration.

$$\left\{u\right\}=\left\{\varphi \right\}\sin (\omega t+\theta )$$

(2)

Then, the equation can be simplified as

$$([K]-{\omega }_i^2[M])\{{\varphi }_i\}=0$$

(3)

$${\omega }_i^2={\displaystyle \frac{{\{{\varphi }_i\}}^{\mathrm{T}}[K]\{{\varphi }_i\}}{{\{{\varphi }_i\}}^{\mathrm{T}}[M]\{{\varphi }_i\}}}$$

(4)

where $\left\{{\varphi }_i\right\}$ and ${\omega }_i$ are modal shape and natural frequency of the ith mode, respectively.

Due to the interference fit of the armature assembly, the assembly prestress $[\sigma ]$ is generated, which generates a stress stiffness matrix $[S]$. The stress stiffness effect can be realized by superimposing the stress stiffness matrix into the elastic stiffness matrix of the structure.

$$[K_s]=[K]+[S]$$

(5)

where $[S]$ represents the stress stiffness matrix that accounts for assembly prestress, $[K_s]$ represents the stiffness matrix of the armature assembly considering the assembly prestress. This result is derived by substituting Equation (5) into Equation (3).

$$([K_s]-{\omega }_{is}^2[M])\{{\varphi }_i\}=0$$

(6)

$${\omega }_{is}^2={\displaystyle \frac{{\{{\varphi }_i\}}^{\mathrm{T}}[K_s]\{{\varphi }_i\}}{{\{{\varphi }_i\}}^{\mathrm{T}}[M]\{{\varphi }_i\}}}$$

(7)

where ${\omega }_{is}$ is the natural frequency of the ith mode considering the assembly prestress.

Thus, the ${\omega }_{is}$ can be described as

$${\omega }_s^2={\omega }_i^2+{\displaystyle \frac{{\{{\varphi }_i\}}^{\mathrm{T}}[S]\{{\varphi }_i\}}{{\{{\varphi }_i\}}^{\mathrm{T}}[M]\{{\varphi }_i\}}}$$

(8)

3. Modal Analysis of Interference Connected Assembly

In general, in the modal analysis of the assembly, the connection relationship between the two parts is simplified. For the interference fit assembly, there is prestress in the contact surface, which cannot be simplified according to the above method. For the modal analysis of armature assembly, previous studies [22,23] have used the direct-bonded method for the integrated armature assembly, but this method ignores the existence of prestress, therefore this type of contact is not suitable for separated armature assemblies. In order to simulate more closely to the real state, four schemes are used for comparative analysis and research.

Scheme A: Bonded contact; Scheme B: Friction contact; Scheme C: Bonded contact under node coupling condition; Scheme D: Frictional contact under node coupling conditions. The modal simulation analysis is completed by Ansys Workbench 2021 software, the geometric model is drawn by NX10.0 software, the size is referred to the real structure, the interference between each part is 0, and the interference is completed by the contact setting in the software. Constraints are set based on actual application scenarios, the bottom surface of the spring tube is set as a fixed constraint. The armature assembly is securely connected to the valve body through two holes in the spring tube base. The ambient temperature is configured to the default setting as specified by the software. Each part and the corresponding material parameters are shown in Table 1.

Table 1. Part name and corresponding material parameters.

Part	Armature	Spring Tube	Flapper	Feedback Spring
Materials	1J50	QBe1.9	3J1	3J1
Density (kg/m3)	8200	8230	8000	8000
Young’s Modulus (GPa)	157	125	190	190
Poisson’s Ratio	0.3	0.35	0.3	0.3
Yield strength (MPa)	685	1035	882	882

3.1. Scheme A: Setting of Bonded Contact

The contact modes between the armature and spring tube, spring tube and flapper, flapper and feedback spring are all set as bonded contact. Tetrahedral mesh is used to draw the whole components, in which the mesh size of the armature is 0.4 mm, the spring tube is 0.3 mm, the flapper is 0.2 mm, and the feedback spring is 0.2 mm. The thin wall of the spring tube is sealed. From the perspective of directions E and F in Figure 2, the armature assembly grid is shown in Figure 2a, and as shown in the figure, the nodes on each contact surface do not coincide. The results of the first-order mode to the fourth-order mode are analyzed.

Figure 2. Meshing. (a) Node coupling is not considered in meshing; (b) node coupling is considered in meshing.

3.2. Scheme B: Setting of Friction Contact

When friction contact is set, the flexible body is generally selected as the contact surface. In interference fit, the hole has a radial deviation and produces interference. Therefore, when the friction contact is set in this paper, the hole is the contact surface and the shaft is the target surface. Friction contact is made between the armature and spring tube. The surface belonging to the spring tube in the contact pair is the target surface, as shown in Figure 3. While the surface belonging to the armature is the contact surface. The friction coefficient is 0.1 and the value of the interference is 0.012 mm. Tetrahedral mesh is used in the whole assembly during mesh division, in which the mesh size of the armature is 0.4 mm, the spring tube is 0.3 mm, the flapper is 0.2 mm, and the feedback spring is 0.2 mm, and the thin wall of the spring tube is sealed. The frictional contact of interference fit is a nonlinear problem. During the simulation analysis, the error limits of grid control are set to aggressive mechanical. Shape inspection can ensure the prediction of unit distortion in the process of large strain analysis, so as to improve the quality of the unit, element order is set to quadratic when the cells are divided, and the grid is divided by quadratic higher-order cells. For large deformation of the model, the stiffness matrix needs to be adjusted in multi-step iterations to adapt to the influence of stress hardening, and the large deflection in solver controls is set to on during the analysis setting, which illustrates the difference between prestressed modal analysis and conventional modal analysis. Augmented lagrange contact equation is used at the contact pair to perform forced contact coordination. In the simulation analysis, the static stress analysis is carried out first, then the modal analysis is carried out, and the results of the first-order mode to the fourth-order mode are analyzed.

Figure 3. Contact setting.

3.3. Scheme C: Setting of Bonded Contacts with the Condition of Node Coupling

Node coupling refers to the sharing of grid nodes between different parts, ensuring a continuous grid. The shared topology function in Workbench allows for common node functionality across different parts but does not allow for contact between parts to be set. Therefore, node coupling is achieved through HyperMesh software 2021, and Scheme C is carried out through co-simulation of HyperMesh and Workbench software 2021R1.

(1)

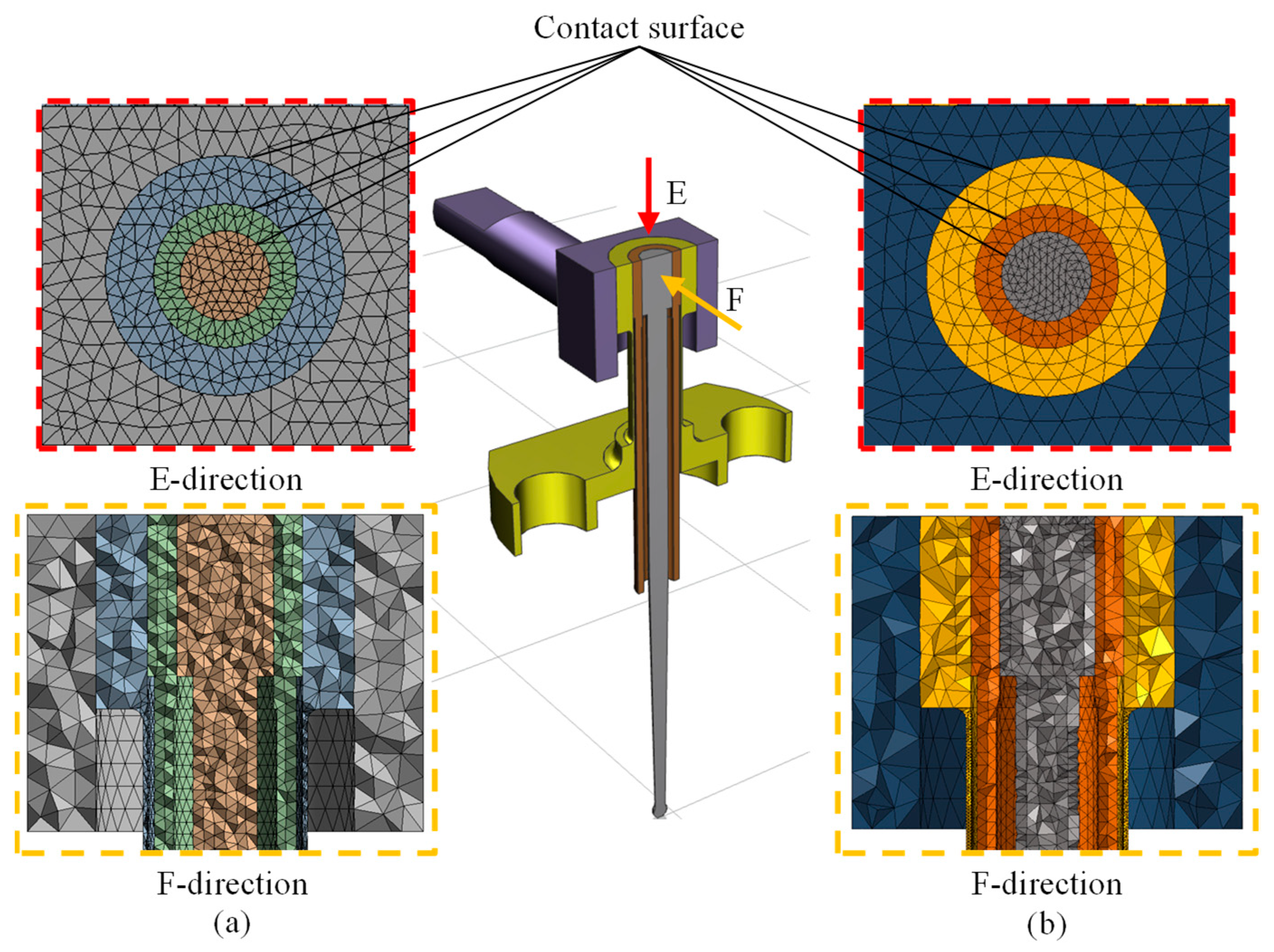
Modeling: The model is created using NX10.0 software and imported into HyperMesh software 2021 in stp format.

(2)

Unit type and material properties definition: The unit type is set as solid186, and the material properties are set according to Table 1.

(3)

Operation of armature assembly geometry model: Boolean operations are performed between the armature and spring tube, the spring tube and flapper, as well as the flapper and feedback spring. These operations serve a similar purpose as the shared topology function in Workbench.

(4)

Tetrahedral mesh division is used throughout the component. The mesh size for the armature is set as 0.4 mm; spring tube mesh size is 0.3 mm with thin wall encryption applied; flapper mesh size is 0.2 mm; feedback spring mesh size is also 0.2 mm.

(5)

Shared nodes separation: Using the detach function, boolean parts are separated into two so that shared nodes belong to two different parts while maintaining their original positions. This allows for node sharing while keeping both parts independent. If the contact surface nodes are not separated, they default to being part of a whole entity which prevents proper contact setting from being achieved, the meshed result is shown in Figure 2b.

(6)

Format conversion: Mesh generated by HyperMesh software 2021 is exported then converted into Mechanical APDL Product format before importing it back into Workbench software 2021R1.

(7)

The solver continues to utilize the Workbench software 2021R1. Bonded contact is employed for the interaction between the armature, spring tube, flapper, and feedback spring. A fixed constraint is applied to the bottom surface of the spring tube, and results of first-order mode to fourth-order mode are analyzed.

3.4. Scheme D: Frictional Contact Under Node Coupling Conditions

The node coupling treatment is the same as in (1)–(6) in Section 3.3. The frictional contact settings are the same as in Section 3.2, except for meshing.

4. Modal Analysis Results and Comparative Analysis

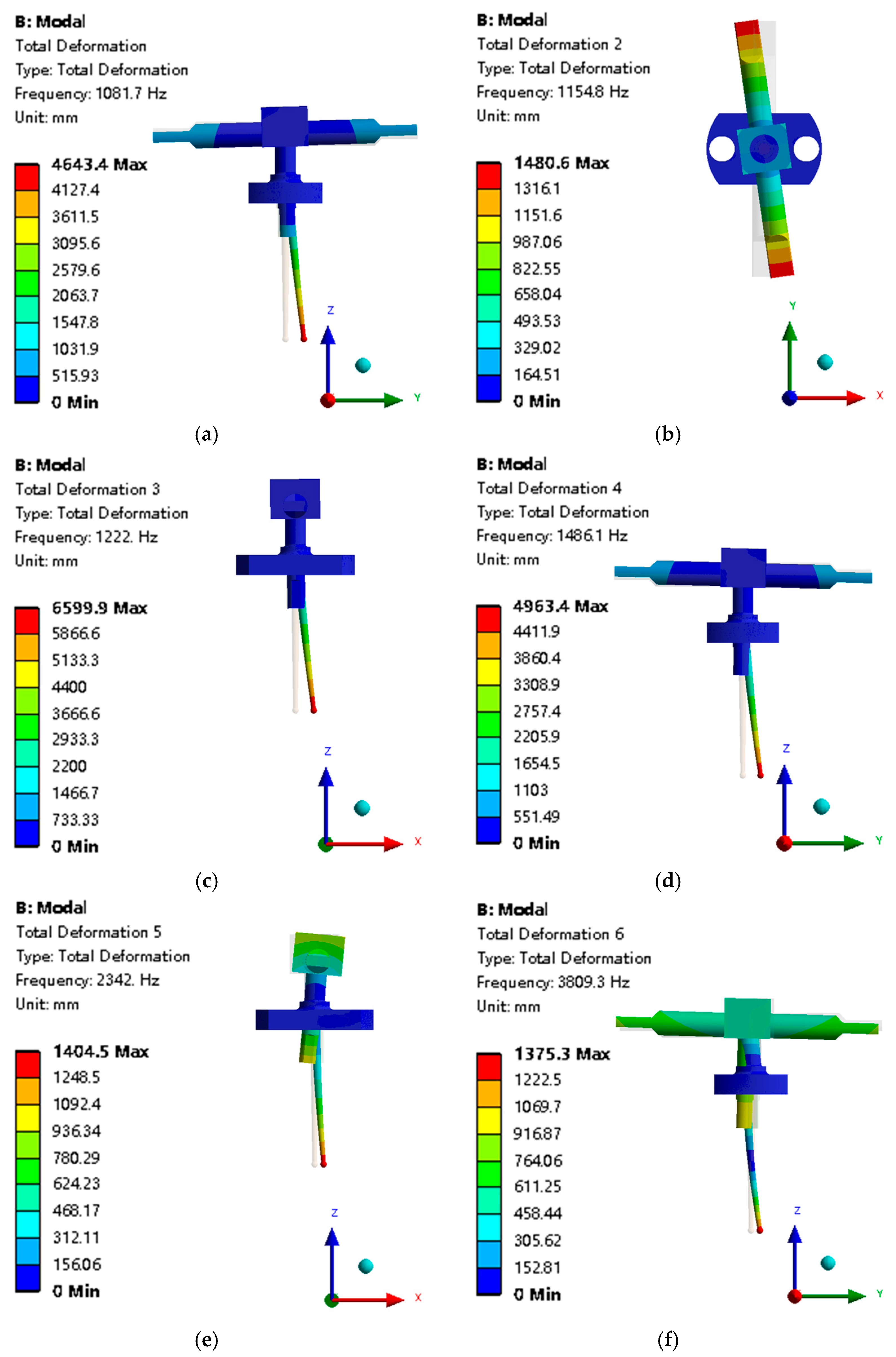
4.1. Modal Analysis Results of Different Schemes

The simulation analysis is carried out according to the four ABCD schemes, respectively, and the results of the first-order mode to the fourth-order mode are analyzed. The deformation direction of the same mode of different schemes is the same, but the natural frequencies are different.

Figure 4 shows the natural frequencies of the first to fourth modes of the armature assembly obtained by simulation analysis of different schemes. The figure shows that the results obtained by the second scheme are basically consistent. The results of the second mode are quite different. The natural frequencies of Schemes A and C are close to each other, and those of Schemes B and D are close to each other. The choice of contact type has a significant influence on the natural frequency of the armature assembly, while node coupling has little influence. Therefore, it is necessary to consider the interference fit when conducting a modal analysis of the interference fit armature assembly.

Figure 4. Calculation results.

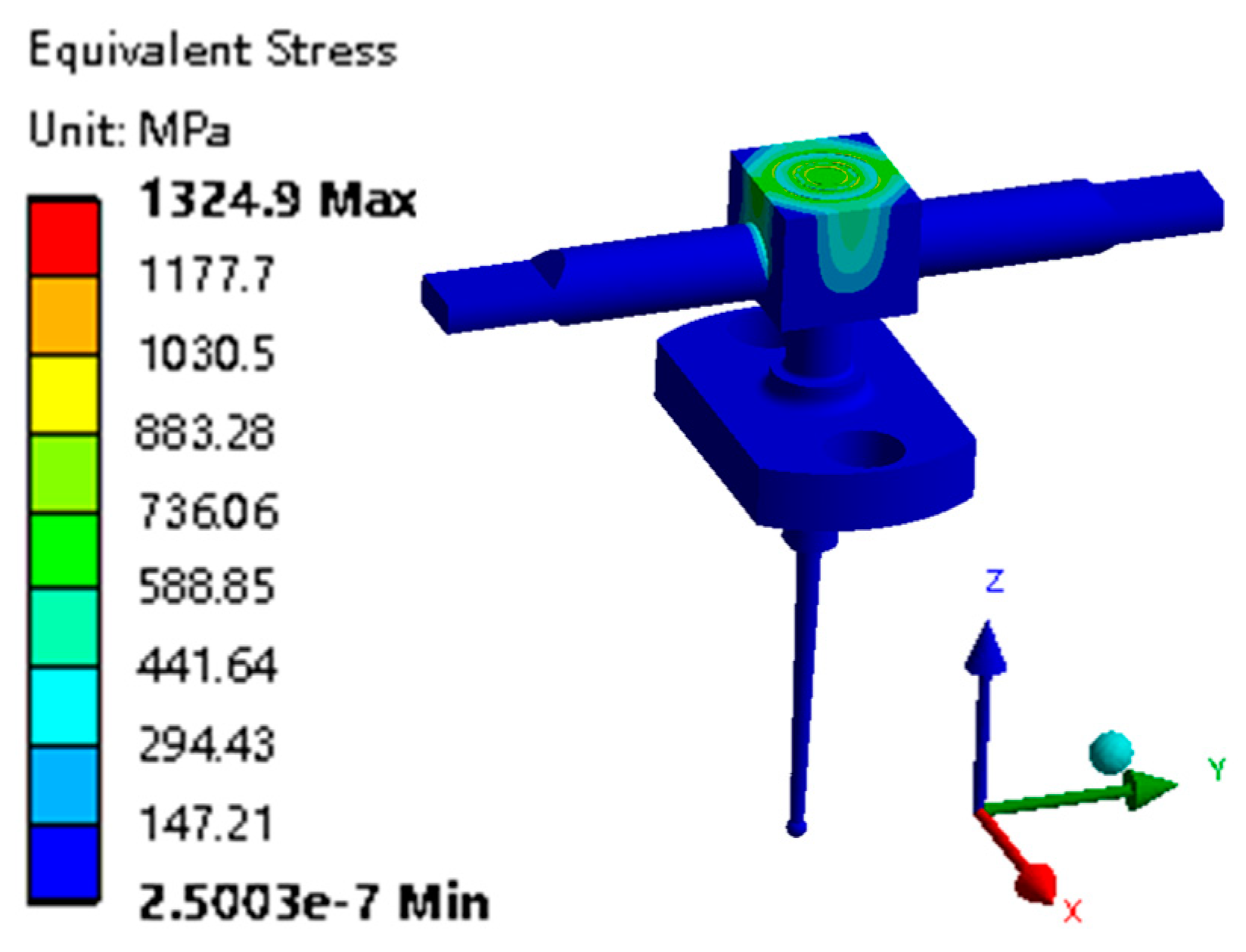
4.2. Static Structural Analysis of Armature Assembly

In order to further explore the impact of the interference fit on modes of the armature assembly, static structure analysis was carried out according to Scheme B, and the specific parameters were set by referring to Section 3.2. The strain diagram and stress diagram of the armature assembly under interference fit conditions were obtained and shown in Figure 5 and Figure 6, respectively. The figures show that under the action of the interference fit, there is prestress in the armature assembly, which leads to a certain amount of deformation, and the maximum value of deformation occurs at both ends of the armature, as shown in Figure 5. As shown in Figure 6, the stress of the armature assembly is mainly concentrated in the contact area of the armature assembly parts, the stress value is around 500 MPa, and the yield strength of the armature is 685 Mpa, indicating that the stress formed by the interference fit is relatively large. In addition, the maximum stress value is 1324.9 MPa. Although the value is relatively large, it appears at the corners and has little impact on the overall component, so it can be ignored.

Figure 5. Deformation nephogram.

Figure 6. Stress nephogram.

4.3. Modal Analysis of Armature Assembly

After the structural statics analysis, the modes of the prestressed armature assembly were analyzed. The first four modes of the armature assembly were obtained, referring to Section 3.2. for parameter setting, as shown in Figure 7. The natural frequency of the first mode is 1081.7 Hz, and the deformation form is the swing of the armature and the feedback spring in the ZOY plane. The natural frequency of the second mode is 1154.8 Hz, and the deformation form is the rotation of the armature around the Z axis. The natural frequency of the third mode is 1222 Hz, and the deformation form is the swing of the feedback spring in the ZOX plane. The natural frequency of the fourth mode is 1486.1 Hz, and the deformation form is the swing of the feedback spring in the ZOY plane. The natural frequency of the fifth mode is 2342 Hz, and the deformation form is the swing of the armature and the feedback spring in the ZOX plane. The natural frequency of the sixth mode is 3809.3 Hz, and the deformation form is a translation of the armature in the ZOY plane and the swing of the feedback spring in the ZOY plane.

Figure 7. Modal analysis results under interference fit. (a) First-order vibration mode. (b) Second-order vibration mode. (c) Third-order vibration mode. (d) Fourth-order vibration mode. (e) Fifth-order vibration mode. (f) Sixth-order vibration mode.

4.4. Verification of Modal Experiments

The mode test of the conventional parts is carried out using the hammering method [9], but the size of the armature assembly is small and precise, so the hammering method cannot be used, and a softer electric driving method is used in combination with its actual working characteristics. In order to verify the results of the simulation analysis, the armature assembly is installed in the torque motor, and the modes of the armature assembly are tested. The principle of the test system is shown in Figure 8a. The signal generator provides the input signal of the sweeping frequency to the torque motor. Driven by the input signal, the armature assembly has a bias, and the displacement of the bias will be detected by the laser displacement sensor. In order to detect the amplitude of the armature deflection, a plastic sheet is pasted on the end of the armature. When the frequency of the sweep signal is close to the natural frequency of the armature assembly, the armature assembly has a resonance phenomenon, and the vibration amplitude of the armature assembly increases significantly. Therefore, the natural frequency of the armature assembly can be identified by detecting the displacement of the armature assembly under the sweep signal.

Figure 8. Modal test of armature assembly. (a) Schematic diagram of the experimental system. (b) Data acquisition system.

The measured armature assembly is a separate armature assembly. The interference between the armature and the spring tube is 0.012 mm, the interference between the spring tube and the flapper is 0.015 mm, and the interference between the flapper and the feedback spring is 0.01 mm. The actual interference is the same as that in the simulation model. As shown in Figure 8b, the two coils in the torque motor are powered in parallel, the resistance of the coils in parallel is 25 Ω, and the rated current is 40 mA. The input signal is the frequency sweep signal provided by the signal generator. The voltage of the frequency sweep signal is 0 to 1 V, the frequency sweep time is 10 s, and the frequency sweep range is 1 to 4000 Hz. The model of the signal generator is SIGLENT, SDG 1022X, manufactured by Shenzhen Siglent Technology Co., Ltd., China, the sampling frequency is 150 MSa/s, and the maximum frequency of the signal generator is 25 MHz. The torque motor is installed on the valve body, and the valve body is fixed by a vise. The probe of the laser displacement sensor is adsorbed on the vice through the magnetic base. The model of the laser displacement sensor is KEYENCE LK-G150, made in Japan, the sampling rate is 100 μs, and the repetition accuracy is 0.5 μm. The D/A connection terminal is mainly used to collect data and transfer it to the computer. The model of the D/A connection terminal is ADVANTECH USB-4716, and the sampling frequency is 200 kS/s. A computer is used to observe, record, and analyze data.

The voltage data detected by the laser displacement sensor in the test is converted into displacement data for the Fourier transform as the longitudinal coordinate, and the frequency as the horizontal coordinate, as shown in Figure 9. The extreme values appear when the frequency is 991 Hz and 1572.4 Hz, indicating that the resonance phenomenon occurs in the armature assembly under the action of this frequency, and the frequency value can be considered as the natural frequency of the mode. As shown in Figure 8, the displacement detected by the laser displacement sensor is the deflection of the armature end in the ZOY plane, corresponding to the deflection direction of the armature in Figure 7a,d. The signal frequency ranges from 0 to 4000 Hz, and the natural frequency corresponding to the first six modes of the armature assembly is 3809.3 Hz, the highest natural frequency of the sixth mode. Thus, the two extremes correspond to the natural frequencies of the first and fourth modes, respectively.

Figure 9. Frequency domain analysis of armature end displacement under sweep signal.

The natural frequency value obtained from the test is compared with the results obtained from the simulation, as shown in Table 2 and Table 3. As shown in Table 2, the difference between the measured natural frequency of the first mode of the armature assembly and the simulation results is about 10%, among which the difference in Scheme B is the smallest, which is 9.15%. As shown in Table 3, the difference between the measured natural frequency of the fourth mode of the armature assembly and the simulation results is about 5.5%, in which the difference is the smallest in Scheme D, which is 5.28%. From the overall data, the error between the simulation results and the experimental results is less than 12%, indicating that the simulation results have a certain reliability, and the error may be caused by the plastic sheet at the top of the armature which is easy to measure. On the other hand, because the simulation results are close, the experimental results cannot judge which scheme is best, so further study is required.

Table 2. Simulation and experimental results analysis of first-order modes.

Simulation Plan	Plan A	Plan B	Plan C	Plan D
Calculated f1 (Hz)	1093.8	1081.7	1104.7	1090.4
Measured f1 (Hz)	991	991	991	991
Error (%)	10.37%	9.15%	11.47%	10.03%

Table 3. Simulation and experimental results analysis of fourth-order modes.

Simulation Plan	Plan A	Plan B	Plan C	Plan D
Calculated f4 (Hz)	1479.2	1486.1	1483.6	1489.4
Measured f4 (Hz)	1572.4	1572.4	1572.4	1572.4
Error (%)	5.93%	5.49%	5.65%	5.28%

4.5. Influence of Interference on Modal Analysis Results

It can be seen from Figure 1 that the armature assembly is composed of armature, spring tube, flapper and feedback spring through interference fit. In order to explore the influence of interference on the modes of armature assembly, the modal analysis of armature assembly is carried out according to scheme B, with interference as a variable, as shown in Figure 10. The influence of interference between the armature and the spring tube on the modes of the armature assembly is shown in Figure 10a. The influence of interference between the spring tube and the flapper on the modes of the armature assembly is Figure 10b. The influence of the interference between the flapper and the feedback rod on the modes of the armature assembly is shown in Figure 10c. As can be seen from the figure, among the first four modes, the corresponding natural frequencies of the first, third and fourth modes all decrease with the increase in interference, but the change is little; while the corresponding natural frequencies of the second mode decrease with the increase in interference, and the change is more obvious. Therefore, the change in interference has an effect on the modes of armature assembly, and the bonded contact setting in scheme A and scheme C is unscientific.

Figure 10. The influence of interference on the modes of armature assembly. (a) The influence of interference between the armature and the spring tube on the modes. (b) The influence of interference between the spring tube and the flapper on the modes. (c) The influence of interference between the flapper and the feedback spring on the modes.

In addition, Figure 4 shows that the simulation results of Scheme B and Scheme D are very close. Although common nodes on the contact surface can make the simulation results more accurate, the mesh needs to be divided by HyperMesh software 2021 and the operation is very complicated. The deviation of the calculation results between the two is negligible, so Scheme B is the optimal scheme for the modal analysis of armature assembly.

5. Precautions for the Design of Servo Valves

In the case of either integral or separated armature assembly, the mechanism of self-excited oscillation is similar. The natural frequency of the armature assembly is coupled with the pressure pulsation in the pilot stage flow field. The problem of internal stress caused by the interference fit of the separated armature assembly is relatively prominent, which cannot be simplified as the integral armature assembly.

The stiffness of the armature assembly is critical to the function and performance of the servo valve and must be prioritized as the primary consideration. In terms of vibration characteristics, the vibration source is mainly the pressure pulsation of the pilot valve, it is recommended to adopt the following schemes to reduce the probability of self-excited oscillation of the servo valve.

(1)

For a separated armature assembly, while ensuring compliance with the assembly’s stiffness requirements, the natural frequency of the armature assembly can be altered by modifying the structure or adjusting the interference fit.

(2)

While ensuring the fundamental functionality of the pilot stage of the servo valve, it is possible to modify the flow field structure to alter the frequency and amplitude of pressure pulsations. This adjustment helps to prevent the coupling of the pressure pulsation frequency with the natural frequency of the armature assembly, thereby reducing the likelihood of self-excited oscillations in the servo valve and enhancing its overall performance.

6. Conclusions

In this paper, the vibration characteristics of the separated armature assembly based on the interference fit are studied. Four different simulation methods are used to analyze the modes of the armature assembly, and the feasibility of the simulation analysis is verified by experiments. The following conclusions were obtained:

(1)

Due to the interference connection between the parts of the separated armature assembly, prestress is present and cannot be ignored. The method of bonded contact simplification in modal simulation analysis is unscientific. Whether the contact surface has common nodes or not has little influence on the modal simulation results.

(2)

The electric drive method is used to provide sweeping frequency signals to the armature assembly, and the natural frequencies of first-order and fourth-order modes of the armature assembly are obtained by the resonance principle, which verifies the feasibility of the simulation.

(3)

Interference has an effect on the modes of the armature assembly. With the increase in interference, the natural frequency corresponding to the first, third, and fourth modes of the armature assembly, all decrease with increasing interference, but the change is little, while the natural frequency corresponding to the second mode gradually decreases.

(4)

In the design of a servo valve with a separable armature assembly, while ensuring the fundamental functionality of the servo valve, it is possible to enhance its performance through two approaches. On the one hand, the natural frequency of the armature assembly can be modified by altering its structure or adjusting the interference fit. On the other hand, the frequency and amplitude of pressure pulsations can be changed by modifying the flow field structure. These adjustments help to prevent the coupling of the pressure pulsation frequency with the natural frequency of the armature assembly, thereby reducing the likelihood of self-excited oscillations in the servo valve and improving its overall performance.