A Servo Control Algorithm Based on an Explicit Model Predictive Control and Extended State Observer with a Differential Compensator

Abstract

Positioning servo systems utilizing permanent magnet synchronous linear motors (PMSLMs) are conventionally governed by cascaded P-PI controllers, which, despite their simplicity and robustness, suffer from limited tracking and anti-disturbance performance due to their single-degree-of-freedom (1-DOF) structure. This paper introduces a novel two-degree-of-freedom (2-DOF) control algorithm that integrates explicit model predictive control (EMPC) with a differential-compensated extended state observer (DCESO). The EMPC framework leverages position and velocity as state variables, eliminating the need for integral terms and thereby enhancing dynamic response. By employing an offline optimization approach, a control law is explicitly formulated to handle system constraints while minimizing online computational overhead. Additionally, a velocity feedforward term derived from the MPC framework is incorporated to further reduce tracking errors. To bolster disturbance rejection, the proposed DCESO introduces a differential compensator that mitigates the low-pass effects inherent in traditional ESOs, thereby improving estimation dynamics. Experimental results demonstrate that the proposed method significantly outperforms the conventional P-PI controller, increasing the position loop bandwidth from 147 Hz to 208 Hz and markedly enhancing anti-disturbance performance. The algorithm’s low online computational demand makes it highly suitable for industrial applications.

1. Introduction

Permanent magnet synchronous linear motors (PMSLMs) have emerged as pivotal actuators in high-precision industrial scenarios, such as semiconductor wafer inspection systems requiring sub-micron positioning accuracy and multi-axis CNC machine tools demanding rapid trajectory tracking for complex machining tasks [1]. In these applications, servo systems must simultaneously achieve high bandwidth to suppress vibration-induced positioning errors and a strong disturbance rejection capability to maintain stability under load variations and external shocks [2]. However, traditional control makes it difficult to meet both needs. It is necessary to find a new control solution to further improve the performance of PMSLM.

For positioning servo systems, the cascade P-PI controller shown in Figure 1 and its supplement [3] have been widely studied and applied due to their simple structure, easy tuning, and high robustness. However, in high-dynamic applications, the integral controller increases the time constant of the internal control loop, which deteriorates the system’s dynamic performance. Consequently, extensive research has focused on developing new control methods to enhance servo performance. Sliding mode control (SMC) has been applied in linear motors due to its excellent dynamic performance [4,5,6]. It achieves good tracking performance, but the chattering phenomenon inherent in SMC is inevitable. In addition, robust bounded control [7] and reinforcement learning [8] have been investigated and implemented. However, the structural complexity of these methods remains a primary limitation for practical applications.

Model predictive control (MPC) has a powerful ability to handle constraints. Its main process involves predicting the future states of the system based on the current system state and constraints, building a reasonable cost function, solving an optimal control sequence, applying the first control output of the sequence to the system, and repeating the above process at the next moment using the updated system state. Initially, the application of MPC was limited to slow process control industries such as chemical manufacturing [9]. With the improvement of computing performance, MPC has been increasingly used for high-frequency control applications such as servo motors [10]. Jiang et al. [11] proposed an improved implicit model predictive current control method to minimize the cost function while considering constraints, using an incremental model to estimate permanent magnet flux. Xu et al. [12] introduced the Laguerre function parameterization to reduce the computational burden and improve stability and speed-tracking performance. He et al. [13] proposed a simplified method based on geometric boundaries to solve the optimization problem in MPC. These methods, which require an online iteration to solve the optimal value, belong to implicit model predictive control (IMPC). However, the increased online computing burden of IMPC, caused by the demand for a higher control frequency, limits its promotion and application.

Bemporad used multiparameter quadratic programming (mp-QP) to provide an explicit solution to IMPC [14] and piecewise affine (PWA) functions to describe the offline solution of the optimization problem [15], which is known as explicit model predictive control (EMPC). By employing an efficient search tree algorithm, the online calculation time can be significantly reduced, meeting the requirements of real-time high-sampling control. Building on this, Lin et al. [16] proposed an active disturbance EMPC to enhance servo speed robustness against parameter perturbation and model mismatch. Guo et al. [17] introduced a constrained explicit controller with a load torque observer. Furthermore, studies have demonstrated that optimizing equality constraints can enhance the EMPC rule table and reduce computing costs [18,19]. However, despite its advantages, the EMPC has seen limited application in positioning servo systems.

The two-degrees-of-freedom (2-DOF) control scheme was proposed to address the compromise between stable dynamic performance and disturbance rejection, traditionally handled by an integral controller in conventional control structures. The concept of a 2-DOF controller involves the separate treatment of tracking performance and disturbance rejection. As a key component of 2-DOF schemes, the feedforward structure plays a crucial role in reducing tracking errors, particularly for ramp signals. Wang et al. [20] proposed an iterative feedforward tuning algorithm using the least squares method to decompose the feedback signal, thereby enhancing tracking accuracy. Lino et al. [21] introduced a feedforward structure into the fractional-order position and speed dual-loop system with a PI controller to improve trajectory tracking performance. In existing studies, research on feedforward controllers for MPC remains limited.

The disturbance estimation typically employs a disturbance observer (DOB) [22] or an extended state observer (ESO) [23]. In control schemes with DOB, the sensitivity to noise caused by the inverse of the model should be low-pass-filtered according to the robust stability criterion, which increases the difficulty of controller design. Therefore, control schemes with an ESO have been widely studied and applied. The scheme based on fractional-order PD control and an ESO can effectively improve the tracking accuracy and disturbance rejection performance of typical servo systems [24,25]. However, the low-pass effect of a traditional ESO negatively affects the convergence speed of disturbance estimation. Therefore, some studies have employed phase compensation to enhance the convergence speed of disturbance estimation [26,27].

To address the high computational cost of MPC and the trade-off between stability and disturbance estimation dynamics, this paper proposes a 2-DOF control scheme. The scheme integrates explicit model predictive control (EMPC) and an extended state observer with a differential compensator (DCESO) for PMSLM-based positioning servo systems. The control structure is shown in Figure 2.

The main contributions of this paper are summarized as follows:

• The application of EMPC to PMSLM-based positioning servo systems: By utilizing position and velocity as state variables, the adverse effects of integral terms on dynamic performance are avoided, resulting in a higher closed-loop bandwidth.
• The introduction of an MPC-based velocity feedforward term: By incorporating an MPC-based velocity feedforward term within the MPC structure, tracking accuracy for ramp signals is enhanced.
• The enhancement of ESO with a differential compensator (DCESO): The proposed DCESO incorporates a disturbance increment term to mitigate the inherent low-pass filtering limitations of traditional ESOs, thereby increasing the bandwidth of disturbance estimation and improving servo stiffness.
• The development of a 2-DOF control architecture (EMPC + DCESO): This integrated approach decouples tracking performance and disturbance rejection, enabling straightforward parameter tuning and low online computational consumption. Its modular design makes it ideal for deployment in embedded systems and industrial environments.

The rest of this paper is organized as follows: In Section 2, the EMPC controller is presented, the explicit process is analyzed, and the velocity feedforward term is derived. The structure of DCESO is presented in Section 3. Section 4 shows the experimental verification of the proposed method. The results in the time domain and frequency domain are compared with the commonly used P-PI controller, respectively. Section 5 concludes the paper with a summary of the key findings and future research directions.

2. Explicit Model Predictive Control

2.1. State Model of a Linear Motor

If the disturbance force of a linear motor is ignored, its force equilibrium equation can be expressed as follows:

$$m·\ddot{x}=u-\eta ·\dot{x}$$

(1)

where $m$ is the mass; $x$ is the displacement; $u$ is the control output; and $\eta$ is the viscous damping coefficient. It can also be formulated in the form of a state matrix.

$$\begin{array}{c} \dot{X}=A_{c}X+B_c·u\\ with A_c=\left[\begin{array}{cc}0& 1\\ 0& {\displaystyle \raisebox{1ex}{$-\eta $}\!\left/ \!\raisebox{-1ex}{$m$}\right.}\end{array}\right] B_c=\left[\begin{array}{c}0\\ {\displaystyle \raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$m$}\right.}\end{array}\right] X=\left[\begin{array}{c}x\\ \dot{x}\end{array}\right]\end{array}$$

(2)

The second-order Taylor approximation with the servo control period $T_s$ is applied to discretize this continuous system. The discrete state space equation can be expressed as follows:

$$\begin{array}{c} X_{k+1}=A{X}_k+B{u}_k\\ with A=\left[\begin{array}{cc}1& T_s-{\displaystyle \frac{\eta T_s^2}{2m}}\\ 0& 1-{\displaystyle \frac{\eta T_s}{m}}+{\displaystyle \frac{{\eta }^2{T}_s^2}{2m^2}}\end{array}\right] B=\left[\begin{array}{c}{\displaystyle \frac{T_s^2}{2m}}\\ {\displaystyle \frac{T_s}{m}}-{\displaystyle \frac{\eta T_s^2}{2m^2}}\end{array}\right]\end{array}$$

(3)

2.2. Derivation of MPC with Constraints

Based on the current system state of the motor, the states after multiple moments are predicted as follows:

$$\begin{array}{l}{X}_{k+1}=A{X}_k+B{u}_k\\ X_{k+2}=A\left(A{X}_k+B{u}_k\right)+B{u}_{k+1}=A^2{X}_k+AB{u}_k+B{u}_{k+1}\\ \dots \\ X_{k+n}=A^n{X}_k+{\displaystyle \sum _{i=1}^n{A}^{i-1}B{u}_{k+n-i}}\end{array}$$

(4)

The prediction can also be summarized in a matrix form.

$$\begin{array}{c}Z=M·X_k+\Pi ·U \\ with M={\left[\begin{array}{c}A\\ A^2\\ ⋮\\ A^{n_p}\end{array}\right]}_{2n_p\times 2} \Pi ={\left[\begin{array}{ccc}B& \dots & 0\\ AB& \dots & 0\\ ⋮& \ddots & ⋮\\ A^{n_p-1}B& \dots & A^{n_p-n_c}B\end{array}\right]}_{2n_p\times n_c} \\ Z={\left[\begin{array}{ccc}{X}_{k+1}& \dots & X_{k+n_p}\end{array}\right]}_{2n_p\times 1}^T U={\left[\begin{array}{ccc}{u}_k& \dots & u_{k+n_c-1}\end{array}\right]}_{n_c\times 1}^T\end{array}$$

(5)

The prediction step $n_p$ is larger than the control step $n_c$.

A quadratic cost function can be constructed as follows:

$$\begin{array}{c}J={\displaystyle \frac{1}{2}}{\left(Z-Z^{ref}\right)}^{T}Q\left(Z-Z^{ref}\right)+{\displaystyle \frac{1}{2}}{U}^{T}RU \\ U=\arg \underset{U}{\min }J \\ \mathrm{with} Z^{ref}={\left[\begin{array}{ccc}{X}_{k+1}^{ref}& \dots & X_{k+n_p}^{ref}\end{array}\right]}_{2n_p\times 1}^{T}Q={\left[\begin{array}{ccc}{w}_x& & 0\\ & w_v& \\ 0& & \ddots \end{array}\right]}_{2n_p\times 2n_p}R={\left[w_u\right]}_{n_c\times n_c}\end{array}$$

(6)

where $w_x$, $w_v$, and $w_u$ are the weight of position, speed, and the control output, respectively.

Substituting (5) into (6) and ignoring the terms unrelated to $U$, the following can be obtained:

$$\begin{array}{l}J={\displaystyle \frac{1}{2}}{U}^{T}HU+{(M{X}_k-Z^{ref})}^{T}Q\Pi U\\ with H={\Pi }^{T}Q\Pi +R\end{array}$$

(7)

When the motor works, there are inevitably state constraints and control output constraints. The constraints can be described in matrix form.

$$\begin{array}{c} \mathrm{N}{X}_k+\Gamma u_k\le \beta \\ \begin{array}{cccc}\hfill with& \mathrm{N}=\left[\begin{array}{c}{0}_{1\times 2}\\ 0_{1\times 2}\\ -I_{2\times 2}\\ I_{2\times 2}\end{array}\right]& \Gamma =\left[\begin{array}{c}-I_{1\times 1}\\ I_{1\times 1}\\ 0_{2\times 1}\\ 0_{2\times 1}\end{array}\right]& \beta =\left[\begin{array}{c}-u_{\min }\\ u_{\max }\\ -X_{\min }\\ X_{\max }\end{array}\right]\end{array}\end{array}$$

(8)

The constraints are normally unchanged by the running of motors, so Equation (8) can be extended to every predicted state.

$$\begin{array}{c}\overline{\mathrm{N}}Z+\overline{\Gamma }U\le b\\ \begin{array}{cccc}\hfill with& \overline{\mathrm{N}}={\left[\begin{array}{ccc}\mathrm{N}& & \\ & \ddots & \\ & & \mathrm{N}\end{array}\right]}_{6n_p\times 2n_p}& \overline{\Gamma }={\left[\begin{array}{ccc}\Gamma & & \\ & \ddots & \\ & & \Gamma \end{array}\right]}_{6n_p\times n_c}& {b=\left[\begin{array}{c}\beta \\ ⋮\\ \beta \end{array}\right]}_{6n_p\times 1}\hfill \end{array}\end{array}$$

(9)

Substituting Equation (5) into Equation (9), the problem can be converted into an inequality constraint of quadratic programming.

$$(\overline{\mathrm{N}}\Pi +\overline{\Gamma })U\le b-\overline{\mathrm{N}}M{X}_k$$

(10)

Combining Equations (7) and (10), the following equation can be obtained:

$$\begin{array}{l}J={\displaystyle \frac{1}{2}}{U}^{T}HU+{(M{X}_k-Z^{ref})}^{T}Q\Pi U\\ U=\arg \underset{U}{\min }J\\ s.t. (\overline{\mathrm{N}}\Pi +\overline{\Gamma })U\le b-\overline{\mathrm{N}}M{X}_k\end{array}$$

(11)

It is an optimization problem subject to the constraints of an IMPC. Such problems typically cannot be solved analytically and require online iterations for a numerical solution, where the iterative process becomes unacceptable for real-time control with a high control frequency.

2.3. Explicating MPC with Constraints

To bridge the aforementioned gap, the IMPC should be explicated. According to the constraints, the parameter space can be mapped to a set of convex polyhedral regions, and the quadratic programming (QP) problem is solved in each convex polyhedral region. The optimal control law is a piecewise representation of the parameter vector, converting the complex online solution into an offline solution. In real-time processing, the controller queries the control law lookup table based on the system state and reference values. This process requires only a simple online search, which greatly reduces the computational burden of the controller.

The reference vector and state vector can be extracted, and Equation (11) can be rewritten as follows:

$$\begin{array}{l}{J}_{\overline{X}}={\displaystyle \frac{1}{2}}{U}^{T}HU+{\overline{X}}^T\overline{F}U\\ U=\arg \underset{U}{\min }{J}_{\overline{X}}\\ s.t. (\overline{\mathrm{N}}\Pi +\overline{\Gamma })U\le b+\overline{E}\overline{X}\\ with \overline{F}=\left[\begin{array}{c}M\\ -{\overline{I}}_{2n_p\times 1}\end{array}\right]Q\Pi \overline{E}={\left[\begin{array}{c}-\overline{\mathrm{N}}M\\ 0_{2n_p\times 1}\end{array}\right]}^T\overline{X}={\left[\begin{array}{c}{X}_k\\ Z^{ref}\end{array}\right]}^T\end{array}$$

(12)

We can further define the following:

$$\begin{array}{l}z=U+H^{-1}{\overline{F}}^T\overline{X}\\ S=\overline{E}+\left(\overline{N}\Pi +\overline{\Gamma }\right)H^{-1}{\overline{F}}^T\overline{X}\end{array}$$

(13)

As such, the optimization of $U$ can be equivalent to the optimization of $z$.

$$\begin{array}{l}{J}_z={\displaystyle \frac{1}{2}}{z}^{T}Hz=J_{\overline{X}}+{\displaystyle \frac{1}{2}}{\overline{X}}^T\overline{F}{H}^{-1}{\overline{F}}^T\overline{X}\\ z=\arg \underset{z}{\min }{J}_z\\ s.t. (\overline{\mathrm{N}}\Pi +\overline{\Gamma })z\le b+S\overline{X}\end{array}$$

(14)

where z is called the piecewise affine (PWA) function [17] of the augmented parameter $\overline{X}$, and the constraint can be converted into a linear inequality of the parameter vector. The parameter vector space can be divided into a set of convex polyhedral regions, which are called critical regions.

$$C{R}_i=\left\{\overline{X}\in {\mathfrak{R}}^n|H_i\overline{X}\le K_i\right\}$$

(15)

The optimal solution can be expressed as the following PWA function:

$$u=f_i\overline{X}+g_i$$

(16)

where $f_i$ and $g_i$ are the coefficients of the PWA function. Based on the system state and reference value at each sampling moment, the optimal control quantity is obtained using Equation (16) and applied to the current loop.

2.4. Derivation of Velocity Feedforward Controller

The zero steady-state tracking error for constant speed is usually achieved by utilizing the speed feedforward structure. Currently, the feedforward controller for MPC is seldom studied in research. In this paper, the speed feedforward controller is analyzed and designed inspired by the MPC framework, while constraints are not considered in this analysis. Ideally, the analytical solution $U$ can be obtained through the differentiation of Equation (7).

$$\begin{array}{l}{\displaystyle \frac{\partial J}{\partial U}}=2{\Pi }^{T}Q\left(M{X}_k+\Pi U-Z^{ref}\right)+2RU=0\\ \Rightarrow U={\left({\Pi }^{T}Q\Pi +R\right)}^{-1}{\Pi }^{T}Q\left(Z^{ref}-M{X}_k\right)\end{array}$$

(17)

The first element of the optimal control output sequence is the following:

$$\begin{array}{c}{u}_k=K_{mpc}\left(Z^{ref}-M{X}_k\right) \\ with K_{mpc}={\left(\begin{array}{cccc}1& 0& \dots & 0\end{array}\right)}_{1\times n_c}{\left({\Pi }^{T}Q\Pi +R\right)}^{-1}{\Pi }^{T}Q={\left[\begin{array}{cccc}{k}_1& k_2& \dots & k_{n_p}\end{array}\right]}_{1\times 2n_p}\end{array}$$

(18)

where $K_{MPC}$ is a coefficient matrix and its element, $k_i$, is not always 0. In Equation (18), $\left(Z^{ref}-M{X}_k\right)$ can be expressed as follows:

$$\begin{array}{c}{Z}^{ref}-M{X}_k=\left[\begin{array}{l}{x}_1^{ref}\\ k_{v,MPC}^{ref}{v}_1^{ref}\\ ⋮\\ x_{n_p}^{ref}\\ k_{v,MPC}^{ref}{v}_{n_p}^{ref}\end{array}\right]-\left[\begin{array}{cc}1& q\\ 0& p\\ ⋮& ⋮\\ 1& q+qp+\dots q{p}^{n_p-1}\\ 0& p^{n_p}\end{array}\right]\left[\begin{array}{c}{x}_k\\ v_k\end{array}\right]=\left[\begin{array}{l}{x}_1^{ref}-x_k-q{v}_k\\ k_{v,MPC}^{ref}{v}_1^{ref}-p{v}_k\\ ⋮\\ x_{n_p}^{ref}-x_k-(q+qp+\dots q{p}^{n_p-1})v_k\\ k_{v,MPC}^{ref}{v}_{n_p}^{ref}-p^{n_p}{v}_k\end{array}\right]\\ with q=T_s-{\displaystyle \frac{\eta T_s^2}{2m}} p=1-{\displaystyle \frac{\eta T_s}{m}}+{\displaystyle \frac{{\eta }^2{T}_s^2}{2m^2}} \hfill \end{array}$$

(19)

As such, the $u_k$ in Equation (18) can be expressed as follows:

$$\begin{array}{c}{u}_k=k_1(x_1^{ref}-x_k)-(k_{1}q+k_{2}p)v_k+k_{v,MPC}^{ref}{k}_2{v}_1^{ref}+\dots \\ +k_{n_p-1}(x_{n_p}^{ref}-x_k)-(k_{n_p-1}(q+qp+\dots q{p}^{n_p-1})+k_{n_p}{p}^{n_p})v_k+k_{v,MPC}^{ref}{k}_{n_p}{v}_{n_p}^{ref}\\ ={\displaystyle \sum _i{k}_{x,i}\left(x_i^{ref}-x_k\right)-k_{v,i}{v}_k+k_{v,MPC}^{ref}{k}_{v,i}^{ref}{v}_i^{ref}} \end{array}$$

(20)

where $k_{v,i}^{ref}$ is calculated by MPC, and $k_{v,MPC}^{ref}$ is a newly defined velocity feedforward coefficient that exclusively influences the coefficients preceding the velocity reference $v_i^{ref}$, thereby enabling the independent tuning of the velocity feedforward component.

In the offline optimal control law of EMPC, the augmented matrix $\overline{X}$ also introduces a speed reference term $v_i^{ref}$ in the control law, which can also be regarded as a speed feedforward term.

In the time domain, when $k_{v,MPC}^{ref}=0$, the system lacks speed feedforward, meaning it tracks the reference signal without speed information. This configuration reduces position overshoot by allowing the system to respond more conservatively to reference changes. Gradually increasing $k_{v,MPC}^{ref}$ until the position tracking error approaches 0 at a constant speed can effectively improve the tracking accuracy of the position servo system for the ramp signal.

3. Extended State Observer with Differential Compensator

3.1. The Principle of ESO

The dynamic equation of the linear motor with unknown disturbances can be summarized as follows:

$$m\ddot{x}=u+d$$

(21)

where $d$ is the lumped disturbance, and the viscous damper is included. By introducing $d$ as a new system state, the extended state equation can be formulated in the matrix form.

$$\begin{array}{c}{\dot{X}}_e=A_e{X}_e+B_{e}u+D\dot{d} \\ with A_e=\left[\begin{array}{ccc}0& 1& 0\\ 0& 0& {\displaystyle \raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$m$}\right.}\\ 0& 0& 0\end{array}\right] B_e=\left[\begin{array}{c}0\\ {\displaystyle \raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$m$}\right.}\\ 0\end{array}\right] D=\left[\begin{array}{c}0\\ 0\\ 1\end{array}\right] X_e=\left[\begin{array}{c}x\\ \dot{x}\\ d\end{array}\right]\end{array}$$

(22)

By observing and comparing the position, the lumped disturbance force is estimated. The observation equation is constructed as follows:

$$\begin{array}{c}{\dot{\widehat{X}}}_e=A_e{\widehat{X}}_e+B_{e}u+LC\left(X_e-{\widehat{X}}_e\right)\\ with L=\left[\begin{array}{c}{l}_1\\ l_2\\ l_3\end{array}\right]=\left[\begin{array}{c}3{\omega }_0\\ 3{\omega }_0^2\\ m{\omega }_0^3\end{array}\right] C=\left[\begin{array}{ccc}1& 0& 0\end{array}\right]\end{array}$$

(23)

where the value with a hut means an estimated value and ${\omega }_0$ is a triple pole of the observer, describing the cut-off frequency of the observer, and should be placed on the left half plane of the S-plane to ensure stability.

3.2. Design of DCESO

From Equations (21) and (23), the transfer function from the actual disturbance $d$ to the estimated disturbance $\widehat{d}$ can be formulated.

$${\displaystyle \frac{\widehat{d}}{d}}={\displaystyle \frac{{\omega }_0^3}{s^3+3{\omega }_0{s}^2+3{\omega }_0^{2}s+{\omega }_0^3}}$$

(24)

It is a typical low-pass filter. The value ${\omega }_0$ determines the bandwidth of the filter. It is necessary to strike a balance between noise suppression and estimation dynamics. To address this challenge, this study proposes an ESO with an additional disturbance increment to predict the disturbance in the next moment and compensate for it, thereby enhancing the disturbance rejection of the servo system.

As shown in Figure 3, the estimated disturbance is differentiated to obtain the increment, which is then added to the compensation loop to raise the phase and increase the phase reverse. The noise amplification caused by the differentiation is mitigated by an additional second-order low-pass filter, which is defined as follows.

$$Q={\displaystyle \frac{{\omega }_n^2}{s^2+2\xi {\omega }_{n}s+{\omega }_n^2}}$$

(25)

After the modification, the transfer function of the estimation process can be obtained as follows:

$${\displaystyle \frac{{\widehat{d}}_A}{d}}={\displaystyle \frac{{\omega }_0^3\left(s^2+2\left(\xi +\frac{k_{\Delta \widehat{d}}{\omega }_n}{2}\right){\omega }_{n}s+{\omega }_n^2\right)}{(s^2+2\xi {\omega }_{n}s+{\omega }_n^2){(s+{\omega }_0)}^3}}$$

(26)

The original ESO exhibits a three-order low-pass effect, which limits the bandwidth and dynamic response of the observer. By introducing the disturbance increment, an additional second-order term appears in the numerator of Equation (26), the cut-off frequency, ${\omega }_n$, of which exceeds ${\omega }_0$. When the gain, $k_{\Delta \widehat{d}}$, increases, the underdamped system transitions into an overdamped system, which can be regarded as the product of two first-order systems. We can set a specific $k_{\Delta \widehat{d}}$, such that the cut-off frequency of one first-order system equals ${\omega }_0$, allowing it to cancel out with the denominator. So, Equation (26) can be simplified as follows:

$${\displaystyle \frac{{\widehat{d}}_A}{d}}={\displaystyle \frac{{\omega }_0^3\left(s+{\omega }_{\tilde{n}}\right)}{(s^2+2\xi {\omega }_{n}s+{\omega }_n^2){(s+{\omega }_0)}^2}}$$

(27)

where ${\omega }_n>{\omega }_0$. The decreasing order of the denominator wins the 90° phase and increases the estimation dynamic.

The effectiveness of the modification can be verified in the simulation, with the results shown in Figure 4. When ${\omega }_0=2000 \mathrm{r}\mathrm{a}\mathrm{d}/\mathrm{s}$, ${\omega }_n=3000 \mathrm{r}\mathrm{a}\mathrm{d}/\mathrm{s}$, and $\xi =0.707$, increasing $k_{\Delta \widehat{d}}$ effectively enhances the bandwidth of the estimation process. However, excessive $k_{\Delta \widehat{d}}$ increases the magnitude–frequency response, causing oscillation in the estimation. Therefore, $k_{\Delta \widehat{d}}$ in DCESO must be set appropriately. In addition, ${\omega }_n$ and $\xi$ should also be configured according to environmental noise and equipment characteristics.

4. Experimental Verification

4.1. Setup of Test Bench

The verification platform is shown in Figure 5. The linear servo system, manufactured by CNBHC Co., Ltd. (Chengdu, China) (Model No.: AFL210M-200), is air-floating-guided to eliminate coulomb friction, while viscous damping is also negligible. The linear motor, supplied by TM Motion (Kunshan, China) (Model No.: TMCP0100-195-200), has parameters listed in

Table 1. Motor parameters.

Parameters	Parameter Value	Parameters	Parameter Value
$R/\Omega$	6.2	$L_d,L_q/mH$	2.4
$I_{max}/A$	9.5	$I_N/A$	2.5
$U_{dc}/V$	160	$K_m/V·s·m^{-1}$	21.4
$K_e/N·A^{-1}$	18.5	$m/\mathrm{k}\mathrm{g}$	4.5

.

The servo controller is based on the PMAC CK3M-CPU11 from OMRON (Kyoto, Japan). The position is measured by a grating with a pitch of 20 μm. Through interpolation by the ADC with a 14-bit effective resolution, the system achieves a final positional resolution of 1.2 nm. The PI current controller and PWM algorithm are implemented in CK3M at a control frequency of 16 kHz.

The driver from Servotronix (Petah Tikva, Israel) (Model No.: CDHD-006-AP-B0) is connected to the PMAC and functions as an inverter to generate a voltage with a frequency of 16 kHz, matching the current control frequency. The drive employs three IGBT modules arranged in a three-phase inverter topology. Current sensing achieves 0.1% full-scale accuracy. The DC bus voltage connected to the driver is 48 V, with a rated current of 6 A and a maximum current of 18 A. The current closed-loop bandwidth is over 1.5 kHz.

Additionally, the set of convex polyhedral regions for the EMPC is calculated using the MPT3 toolbox [28] and implemented in CK3M via PowerPMAC IDE at a control frequency of 8 kHz.

As a type of 2-DOF control scheme, the tracking performance of the proposed controller, including the feedforward structure and the disturbance rejection, can be adjusted separately. Therefore, the parameters should be tuned in the following order:

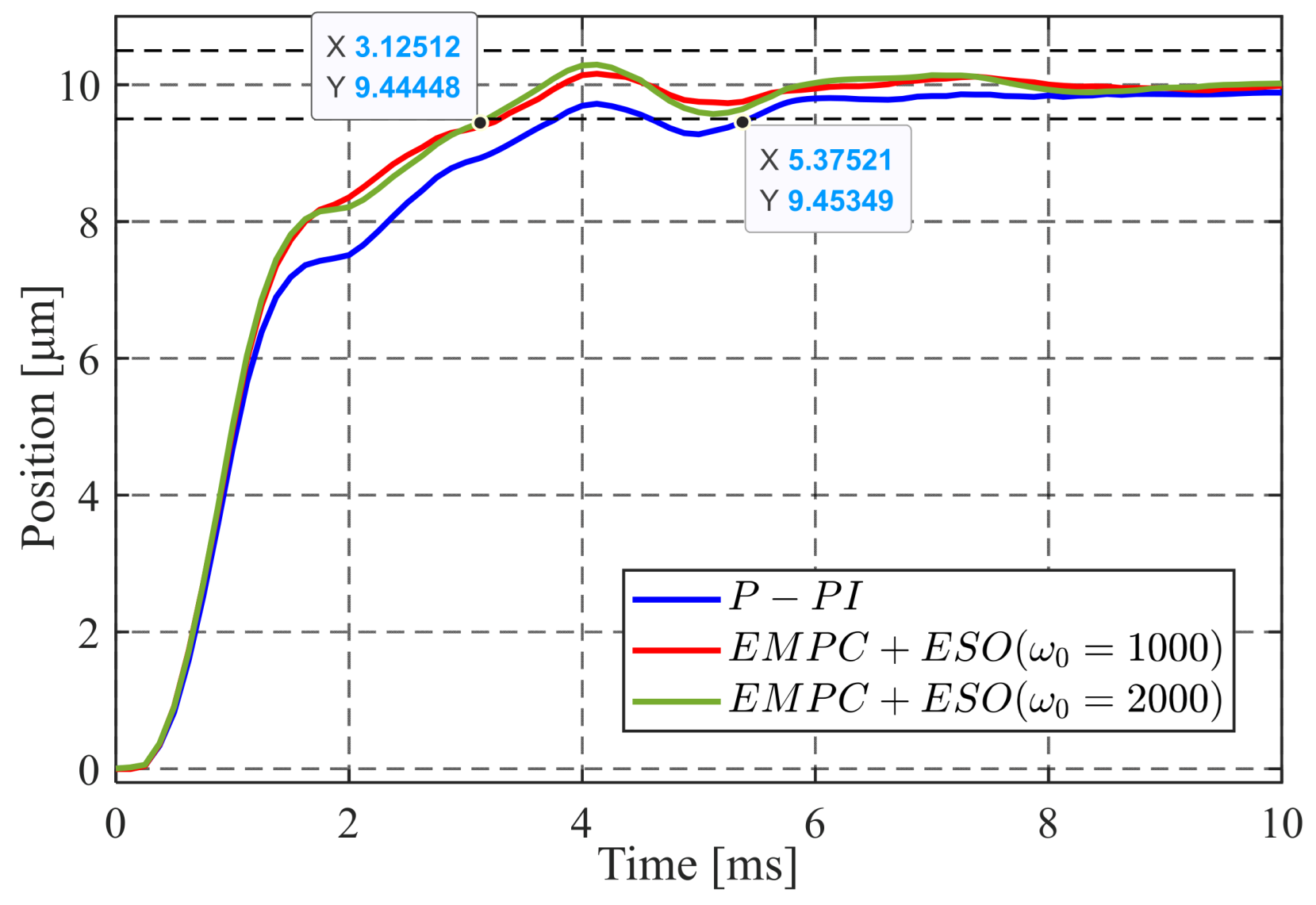
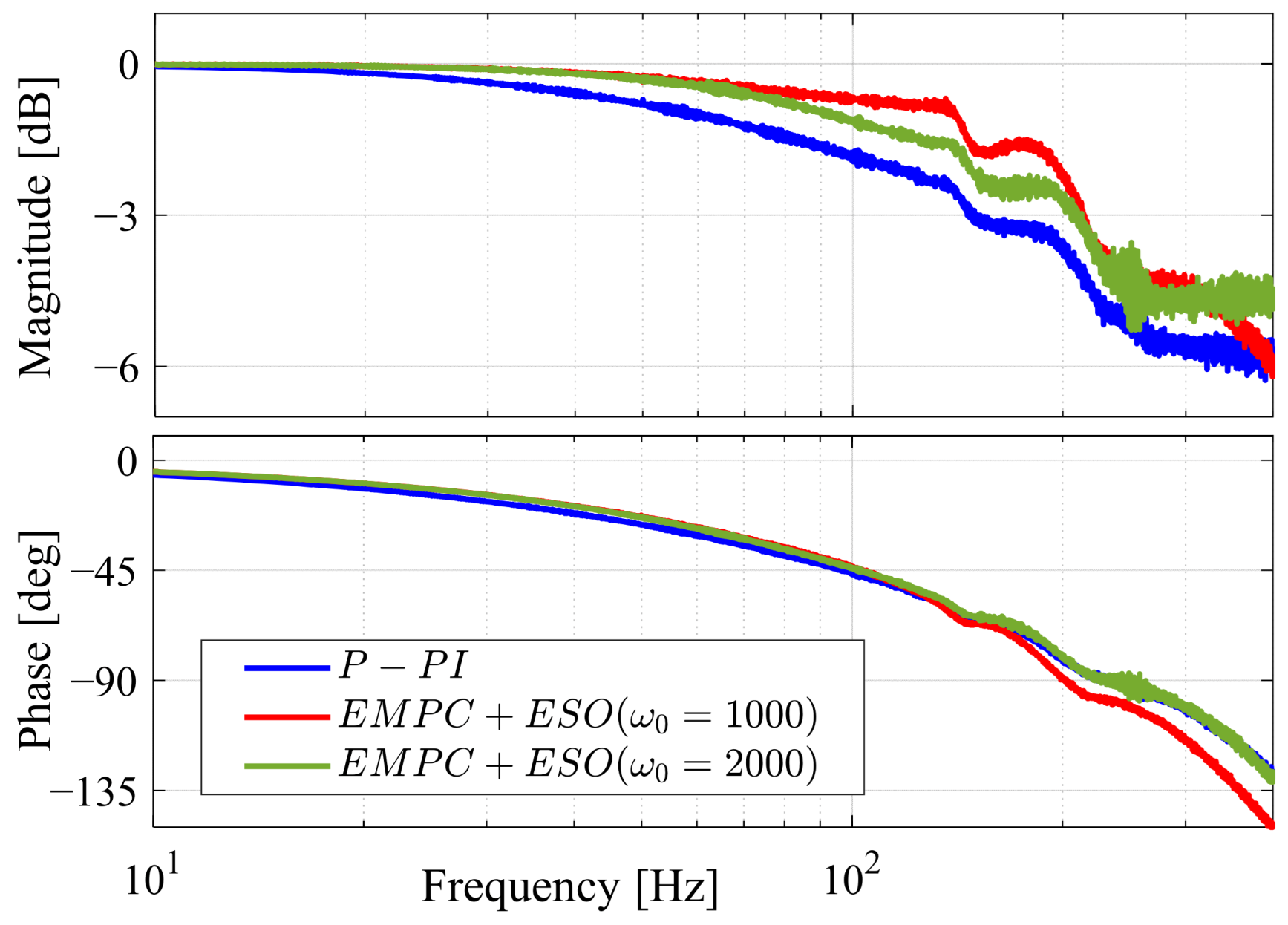
• Tune the position and velocity weights in the EMPC ($k_{v,MPC}^{ref}=0$) to achieve the maximal position loop bandwidth with an open-loop magnitude reserve of −10 dB.
• Increase the velocity feedforward coefficient in the EMPC until the steady-state tracking error for the ramp signal is 0.
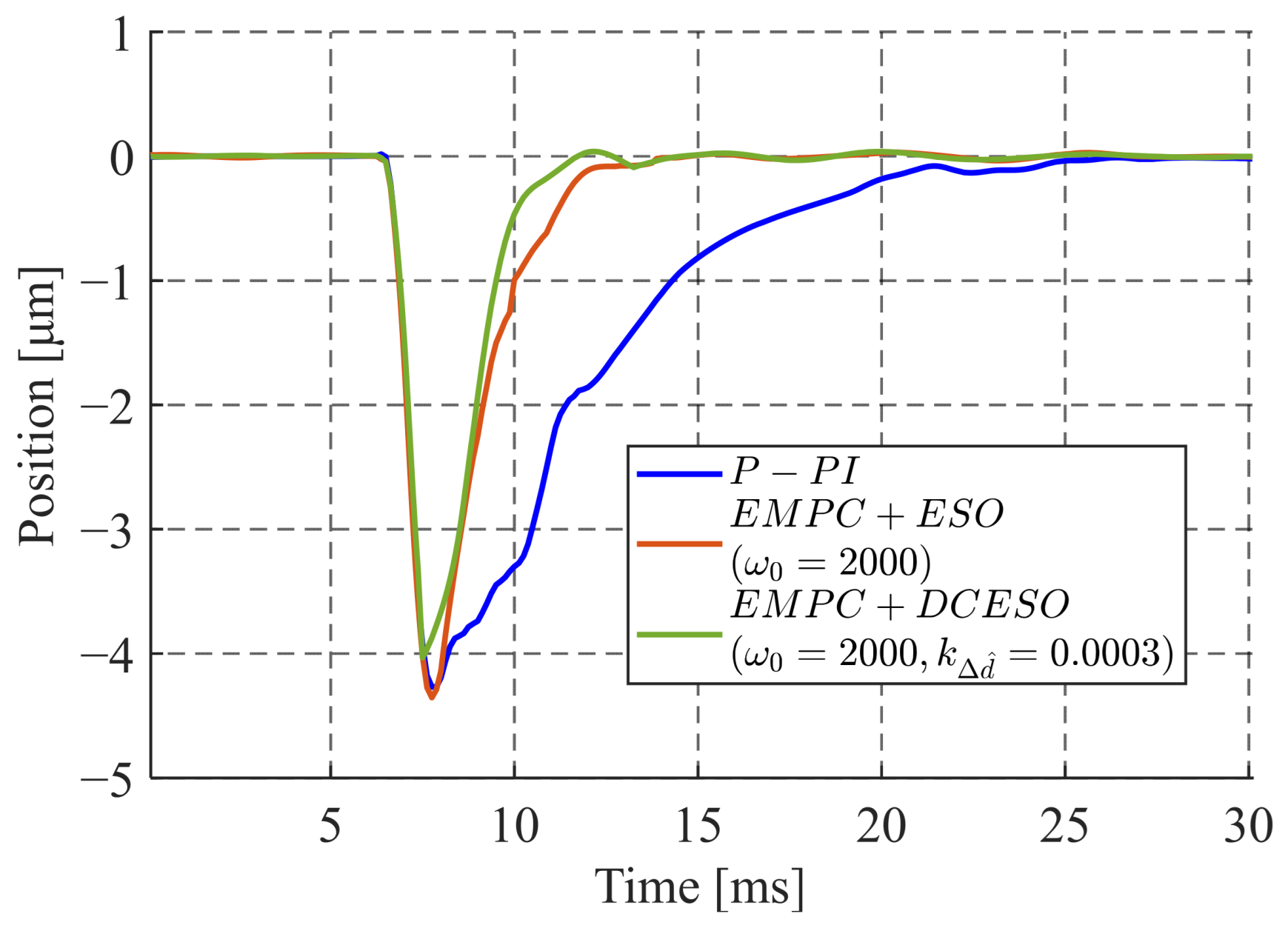
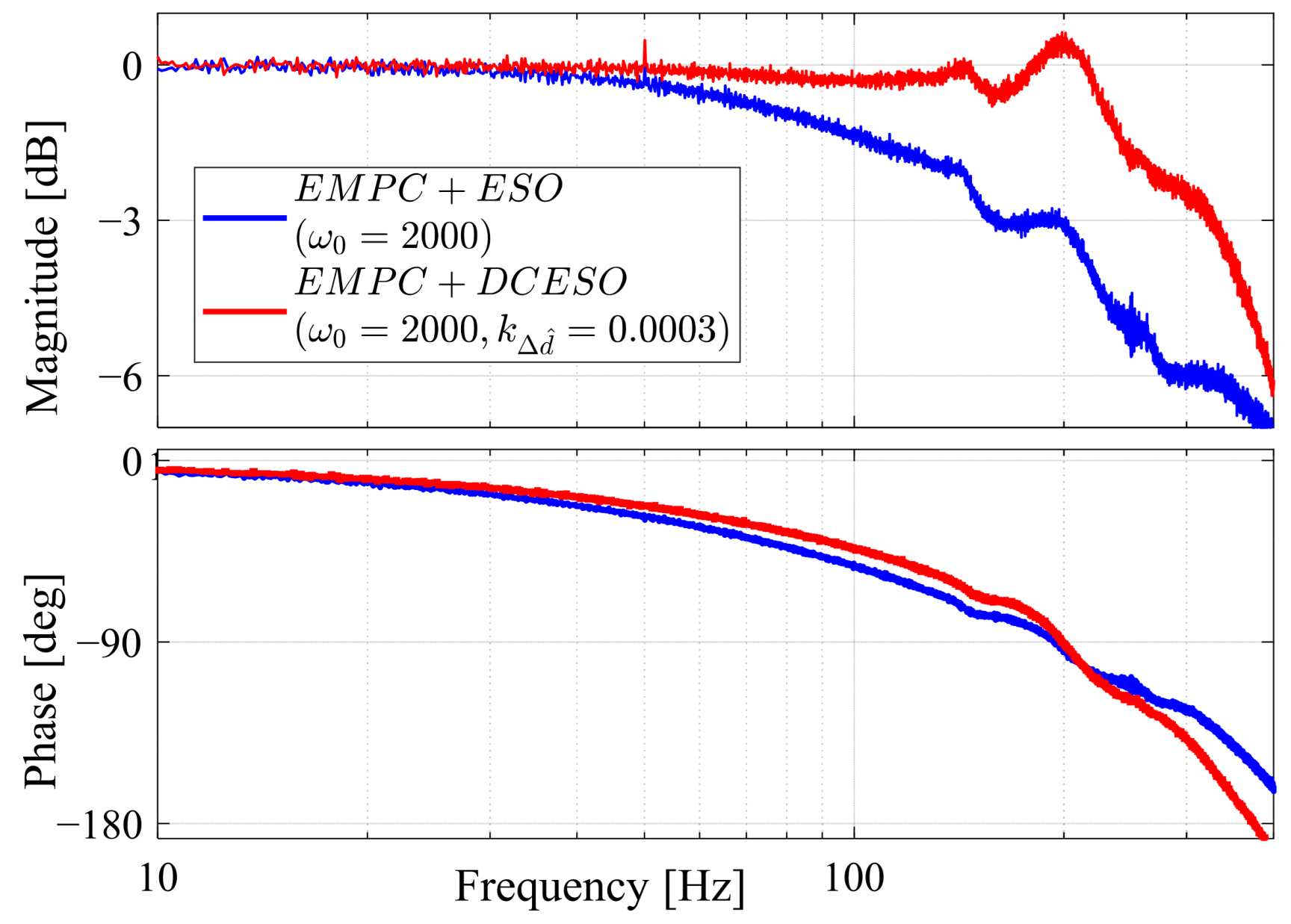
• Tune the poles of ESO and gradually increase the weights of the DCESO to enhance its anti-disturbance performance.

The control horizon $n_c$ and prediction horizon $n_p$ are both set to 6 steps. The system constraints are defined as follows: control output ($u$) within ±175 N, position ($x$) within ±100 mm, and velocity ($v$) within ±500 mm/s. The final weight parameters of EMPC are $w_x=2.9\times {10}^{14}$, $w_v=0.9\times {10}^8$, and $w_u=1$.

4.2. Experimental Results

To verify the effectiveness of the proposed servo control principle, experiments were conducted in both time and frequency domains, focusing on dynamic tracking performance and the disturbance rejection of the closed-loop system.

As shown in Figure 6, the step response illustrates the dynamic tracking performance. The reference position initially steps up to 10 μm. For comparison, the results of the traditional P-PI controller (with control gains $k_{x,P}=600$, $k_{v,P}=600$, $k_{v,I}=300$) are also included. These parameters ensure that the system achieves a maximum position-loop bandwidth with an open-loop gain margin of −10 dB (the control structure shown is in Figure 1).

Figure 6 demonstrates how increasing the observer pole has minimal impact on the step response. In this 2-DOF scheme, tracking performance and disturbance rejection are decoupled. Specifically, the settling time is used to evaluate the dynamic performance of the closed-loop system. It is defined as the time for the step response to reach and remain within ±5% of the reference position. The proposed controller reduces the settling time from 5.38 ms (P-PI controller) to 3.13 ms, representing a 41.8% improvement.

To compare the bandwidth, a sinusoidal sweep signal with an amplitude of 5 μm and a frequency range of 1 Hz to 600 Hz is given. The results for the closed-loop system are shown in Figure 7. The presented method increases the bandwidth from 147 Hz (P-PI) to 208 Hz, achieving a 41% improvement. Furthermore, increasing the poles of the ESO indicates that the bandwidth of the EMPC + ESO system remains stable at 208 Hz without significant variation. This demonstrates that ESO pole adjustments do not notably affect the system’s bandwidth, confirming the inherent parameter-tuning decoupling characteristic of the 2-DOF control architecture.

To further eliminate the tracking error at a constant speed, the feedforward control parameter of EMPC is tuned, and the results are presented in Figure 8. The experiment was conducted using a ramp reference with a speed of 20 mm/s. Without feedforward, the tracking error of the EMPC + DCESO remains at about 26 μm, and the settling time is about 5 ms. By gradually increasing the feedforward coefficient, the steady-state tracking error can be reduced to near 0 μm. This significantly improves tracking performance.

To verify the disturbance rejection, a disturbance current of 2.5 A was applied while the reference position was maintained at 0. The results are shown in Figure 9. For the P-PI controller, the servo lag is about 4.29 μm, and the settling time is about 15.13 ms. In contrast, in the EMPC + ESO control scheme, as the pole increases to 2000 rad/s, the servo lag decreases to 4.35 μm, and the settling time decreases to 5.87 ms, representing a 61.2% improvement.

The disturbance increment introduced in the compensation loop can further improve the disturbance rejection of the system. The filter parameters are configured as ${\omega }_n=3000 \mathrm{r}\mathrm{a}\mathrm{d}/\mathrm{s}$, and $\xi =0.71$, and the disturbance increment coefficient is $k_{\Delta \widehat{d}}=0.0003$. As demonstrated in Figure 9 and

Table 2. Servo lag and settling time with different control methods.

Controller	Servo Lag/μm	Settling Time/ms
P-PI	4.29	15.13
EMPC + ESO (${\omega }_0 =2000$)	4.35	5.87
EMPC + IPESO (${\omega }_0 =2000, k_{\Delta \widehat{d}}=0.0003$)	4	4.75

, due to the introduction of the disturbance increment, the servo lag of the EMPC + DCESO control scheme is reduced to 4 μm, and the settling time is reduced to 4.75 ms.

The effectiveness of the disturbance estimation can also be observed in the frequency domain. Figure 10 illustrates the bandwidth of the ESO + DCESO in a Bode diagram. A current sweep signal from 1 Hz to 600 Hz with an amplitude of 0.5 A is provided as the disturbance input, while the output represents the estimated disturbance.

From the magnitude–frequency bandwidth characteristics, it is evident that within the mid-to-low frequency range (100–200 Hz), the ESO exhibits rapid bandwidth attenuation, leading to a limited disturbance estimation bandwidth of merely 197 Hz. However, the DCESO, by incorporating differential compensation, maintains its magnitude–frequency characteristics near 0 dB within this frequency range, allowing the system to accurately estimate mid-to-low frequency disturbances without significant attenuation. The maximum disturbance estimation bandwidth of the DCESO reaches 336 Hz, indicating a 71% improvement over the ESO and significantly enhancing disturbance estimation performance.

5. Conclusions

This paper presents a novel 2-DOF control framework integrating EMPC and DCESO for PMSLM-based positioning servo systems. The proposed method addresses the limitations of conventional P-PI controllers by decoupling tracking performance and disturbance rejection. The EMPC module leverages position and velocity states to optimize the control inputs, eliminating integral terms for enhanced dynamic response, while the DCESO introduces a disturbance increment compensation mechanism to improve the estimation bandwidth. The experimental results demonstrate that the proposed controller achieves a 41% increase in the position loop bandwidth (from 147 Hz to 208 Hz) and a 68.6% reduction in the disturbance rejection settling time compared to the P-PI baseline. The DCESO effectively suppresses mid-to-low-frequency disturbances, achieving a 71% wider estimation bandwidth (336 Hz) through the phase compensation. The modular design enables straightforward parameter tuning and low online computational demands, making it highly suitable for industrial deployments.

This paper validates the performance of the proposed control method using a single-axis servo system. In the future, this control approach could be extended to gantry-type coplanar air-floating systems, which are widely used in semiconductor manufacturing equipment requiring high dynamic performance. The synchronization error between the two gantry sides could be regarded as a special type of disturbance and compensated through DCESO.