Design of a Longitudinal-Bending Elliptical Vibration Ultrasonic Transducer with a Bent Horn

Abstract

The thin and straight horn of the ultrasonic transducer is located in the center of the thick transducer, so that the tool tip of the ultrasonic vibration turning tool holder cannot be located on the outermost side of the entire tool holder, which leads to the structural interference between the tool holder and the part during turning. In order to solve this problem, this paper proposes a longitudinal-bending elliptical vibration ultrasonic transducer with a bending horn for ultrasonic vibration-assisted cutting (UVAC). The designed transducer can be used for the partial separation continuous high-speed elliptic ultrasonic vibration cutting (HEUVC) of external surface and internal cavity. The ultrasonic vibration amplitude of the transducer can meet the needs of HEUVC. When using an ultrasonic transducer with a bending horn for HEUVC, compared with conventional cutting (CC), HEUVC can improve the tool life by about 50%.

1. Introduction

UVAC can reduce cutting temperature and cutting force and improve tool life and surface integrity by separation effect, so it is widely used in cutting difficult-to-machine materials [1,2,3,4]. However, the application of ultrasonic vibration-assisted turning in practical production is limited because the ultrasonic vibration turning tool holder will interfere with the parts in structure [5,6]. The thin and straight horn of the ultrasonic transducer is located in the center of the thick transducer, so that the tool tip of the ultrasonic vibration turning tool holder cannot be located on the outermost side of the entire tool holder, which leads to the structural interference between the tool holder and the part during turning. In order to solve this problem, an ultrasonic vibration transducer with a bending horn must be designed for ultrasonic vibration-assisted turning. In traditional ultrasonic vibration cutting (UVC), the tool vibrates along the cutting speed direction, in elliptic ultrasonic vibration cutting (EUVC), the tool has vibration components along cutting speed and cutting depth. There is a critical cutting speed limit in UVC and EUVC, and the material removal rate (MRR) is low [7,8]. Zhang et al. proposed high-speed ultrasonic vibration cutting (HUVC), which improved the cutting speed several times [9]. However, due to the limitation of critical feed, the MRR is also low. Zhang et al. [10] proposed partial separation continuous high-speed ultrasonic vibration cutting (C-HUVC), which solved the problem of low MRR in UVAC. UVAC methods include UVC, EUVC, and HUVC. When the tool vibrates along the cutting depth direction, the tool impacts the workpiece radially, which leads to a large impact force, so the tool wear is intensified. When the tool vibrates along the cutting speed direction or the feeding direction, the tool impacts the metal of the cutting layer, and the impact force is small. In UVC, the tool is prone to chip when it retreats. In EUVC, the impact on the tool is great. In HUVC and C-HUVC, the tool vibrates along the feed direction. However, when cutting complex parts, the vibration direction of the tool changes between the cutting depth and the feed direction. None of the above UVAC methods can be used for turning complex parts. It is necessary to develop an elliptic ultrasonic vibration cutting method in tool base surfaces with a relatively small impact force on the tool. Therefore, it is necessary to design a longitudinal-bending elliptical vibration ultrasonic transducer with a bending horn for HEUVC.

Since 1975, HORTON et al. [11] introduced the concept of using piezosurgery for treating oral diseases. Today, piezosurgery with bending horns has become widely adopted in clinical practice [12,13,14,15]. Piezosurgery uses the principle of high-intensity focused ultrasound to cut biological tissues [16,17]. The strength of biological tissues is low, so the cutting force of cutting biological tissues is small. The diameter of the horn of the piezosurgery is only a few mm, so the stiffness is small. To solve the problem of changing the direction of longitudinal vibration when ultrasonic cleaning the inner surface of bending pipes, He et al. [18] proposed a design method of longitudinal vibration horn with included angle structure in 2017. In their design, two straight horns with a radius of 7.5 mm are assembled together by threads to form a bending horn. The stiffness of the horn of the transducer is too small to be used for UVAC, and the vibration direction of the horn is the simplest longitudinal vibration.

It is difficult to adjust the shape of ellipse for a single-drive transducer, so this paper adopts double-drive elliptical ultrasonic vibration mode [19,20]. Elliptical vibration ultrasonic transducers are usually designed by simulation method [21,22,23] and analytical method [24,25,26]. The matching of the frequencies of longitudinal vibration and bending vibration in the elliptical vibration ultrasonic transducer is mainly realized by adjusting the structural size [27,28,29]. The transducer is capacitive, which requires matching inductance to increase the amplitude of the transducer. According to the impedance matching theory put forward by Jiang et al. [30], the transducer can still obtain 70% of the maximum amplitude when it vibrates within the range of 0.4 kHz above and below the optimal resonance frequency. This theory can be used to match the frequencies of transducers with two different resonant frequencies so that the frequencies of longitudinal vibration and bending vibration are the same.

An ultrasonic transducer with a bending horn has been applied in cutting biological tissues and ultrasonic cleaning of bent pipes, but it has not been studied and applied in UVAC. The cutting force for cutting difficult-to-machine materials is usually several hundred newtons, and the cross section of the conventional turning tool holder is usually 25 cm × 25 cm or 32 cm × 32 cm, and the horn of the above transducer is too thin to meet the use. It is an unknown problem whether the transducer can produce the amplitude required by turning when the stiffness of the transducer is improved. Whether the transducer can be matched into an elliptical vibration transducer by matching the frequencies of longitudinal vibration and bending vibration is the second problem. The bending angle of the horn will affect the direction of vibration propagation, and whether the transducer can be matched into a transducer with a circular trajectory by matching the directions of longitudinal vibration and bending vibration is the third problem. This paper aims to solve the above three problems.

In this paper, first, a brief theoretical analysis is conducted to determine the relationship between the resonant angular frequency of longitudinal and bending vibrations in a beam and its structural dimensions. This provides a basis for adjusting the horn’s structural parameters during the simulation design of ultrasonic transducers. Second, through induction and summarization, a simulation design flowchart is proposed for longitudinal-bending elliptical vibration ultrasonic transducers with bending horns, enabling the acquisition of the transducer’s structural dimensions via simulation. Finally, the accuracy of the simulation design is verified through vibration testing, while cutting tests confirm the adaptability of the ultrasonic transducer and the feasibility of the cutting process.

2. Transducer and Application

Figure 1 shows problems and solutions of structural interference in ultrasonic vibration turning. As shown in Figure 1a, there is a problem of structural interference when turning with a conventional ultrasonic turning tool holder. To increase the output amplitude of the transducer, the horn is usually thinner than the transducer. The transducer is generally a revolving body, and the horn is located in the revolving center of the transducer, which makes the tool tip of the ultrasonic vibration turning tool holder unable to be located at the outermost side of the whole tool holder, which leads to the structural interference between the transducer and the part during turning. To solve this problem, an ultrasonic transducer with a bending horn can be adopted, as shown in Figure 1b. It is also possible to rotate the tool holder without bending the horn so that the tool tip is at the outermost side, but this method will make the tool holder larger and less feasible. An elliptical ultrasonic vibration transducer with a bending horn completely solves the problem of structural interference, and is suitable for the UVAC of external surface of parts.

UVAC can periodically open the cutting area, allowing coolant to enter and lubricate both the tool and the machined surface. This reduces cutting temperature and force, ultimately improving tool life and surface integrity. As a result, it is widely used for cutting difficult-to-machine materials. Given the prevalence of such materials in the aerospace field, UVAC holds broad application prospects. Figure 1c is a schematic diagram of turning the internal cavity in an aero-engine turbine disk with a conventional tool holder. There are many cavity structures in aero-engine parts, and the straight turning tool holder cannot enter them, so it can only be designed into various bending structure. To apply the UVAC method to the turning of aero-engine parts, it is necessary to design an ultrasonic transducer with a bending horn. Due to the complex structure of the cavity, the design range of the tool front end is limited. The tool front end of the ultrasonic tool holder should be basically the same as that of the conventional tool holder. Figure 1d is a schematic diagram of an elliptical ultrasonic vibration transducer with a bending horn turning the internal cavity of a turbine disk.

3. Finite Element Design

3.1. Theoretical Analysis

This part mainly determines the relationship between the resonant angular frequency of the bending wave and longitudinal wave in the beam and the structural size of the beam through a brief theoretical analysis, which provides a basis for the structural parameter adjustment of a horn in a simulation design.

A beam with two free ends satisfies the following Equation (1) at resonance:

$$L=n{\displaystyle \frac{\lambda }{2}}$$

(1)

where $L$ is the length of the beam, $\lambda$ is the wavelength, and $n$ is the number of half wavelengths in the beam at resonance.

The wavelength $\lambda$, frequency f, and sound velocity c satisfy the following Equation (2):

$$c=f\lambda$$

(2)

Equation (3) can be obtained from Equations (1) and (2):

$$\omega ={\displaystyle \frac{n\pi c}{L}}$$

(3)

where $\omega$ is the angular frequency of vibration.

The longitudinal wave velocity in the beam is

$$c_l=\sqrt{{\displaystyle \frac{E}{\rho }}}$$

(4)

where $E$ is elastic modulus and $\rho$ is density.

The sound velocity of bending wave in the beam is

$$c_b=\sqrt[4]{{\displaystyle \frac{{\omega }^{2}E{R}^2}{\rho }}}$$

(5)

where $R$ is the radius of gyration of the section.

$$R=\sqrt{{\displaystyle \frac{I}{A}}}$$

(6)

$$I={\displaystyle \frac{h{d}^3}{12}}$$

(7)

$$A=dh$$

(8)

where $I$ is the moment of inertia of section, $A$ is the area of section, $d$ is the width of section, and $h$ is the height of section.

Substituting Equation (4) into Equation (3) can obtain the angular frequency equation of longitudinal wave resonance in the beam:

$${\omega }_l=n\pi \sqrt{{\displaystyle \frac{E}{\rho }}}\times {\displaystyle \frac{1}{L}}$$

(9)

Substituting Equation (5) into Equation (3) can obtain the angular frequency equation of bending wave resonance in the beam:

$${\omega }_b={\displaystyle \frac{{\left(n\pi \right)}^2}{2\sqrt{3}}}\sqrt{{\displaystyle \frac{E}{\rho }}}\times {\displaystyle \frac{d}{L^2}}$$

(10)

According to Equation (9), the resonant frequency of longitudinal vibration in a beam is inversely proportional to its length. According to Equation (10), the resonant frequency of bending vibration in a beam is inversely proportional to the square of its length and directly proportional to the width of the beam section. Therefore, when matching the frequencies of longitudinal vibration and bending vibration in an elliptical vibration ultrasonic transducer, firstly, the length of the horn is designed properly, so that there is a small difference between the frequencies of longitudinal vibration and bending vibration, and then the frequency of bending vibration is close to the frequency of longitudinal vibration by adjusting the section width of the horn. Finally, the longitudinal vibration and bending vibration are matched to one frequency by impedance matching.

3.2. Simulation Design

Figure 2 shows two kinds of elliptical vibration ultrasonic transducer with a bending horn. An a-type transducer can be used for the ultrasonic vibration-assisted turning of external surfaces, and a B-type transducer can be used for the ultrasonic vibration-assisted turning of internal cavities. In the designed transducer, the horn, the flange, the front cap, and the bolt are a part, and the piezoelectric ceramic piece and the copper electrode are strung on the bolt and pressed by the end cap. Four half-piece piezoelectric ceramic plates near the front cap are used to generate bending vibration, and two complete piezoelectric ceramic plates near the end cap are used to generate longitudinal vibration. Two half-piece piezoelectric ceramic plates are spliced into one plate according to the opposite polarity. The polarity of the piezoelectric ceramic plate is shown by the blue arrow in Figure 2a,b. The diameter of the piezoelectric ceramic plate is required to be less than a quarter of the wavelength of sound waves in ceramic materials, and ceramic pieces with larger diameters should be selected to carry enough energy. In this paper, the piezoelectric ceramic plates with an outer diameter of 45 mm, an inner diameter of 15 mm, and a thickness of 5 mm are selected.

In Figure 2c, there are bolt holes for fixing the transducer and fixture, sealing groove for installing O-ring, and arc-shaped damping groove on the flange. The arc-shaped damping groove is formed by removing excess metal after the flange has a margin of 0.7 mm, and its function is to weaken the restraint of the flange on the transducer. The flange size is minimized with sufficient rigidity, and measurements of $D_2=71 \mathrm{m}\mathrm{m}$ and $L_3=8 \mathrm{m}\mathrm{m}$ are used. According to the experiment, the resonance effect of the transducer is good when the length of the end cap is $L_1=20 \mathrm{m}\mathrm{m}$. For the bending vibration, the front cap should be designed as thin as possible. In this paper, the front cap is 4 mm thicker than the flange. The wavelength of the beam (made of 42CrMo) is 258 cm when it resonates at 20 kHz. In order to ensure the transducer has sufficient stiffness, the longitudinal vibration of the elliptical vibration ultrasonic transducer with the bending horn designed in this paper is half wavelength. Figure 2d is a schematic diagram of the horn of a B-type transducer, and the tool is clamped and fixed on the horn. As shown in Figure 2a,b, θ and γ are the included angles between the vibration direction of point A and the axis of the transducer in bending vibration and longitudinal vibration, respectively. In Figure 3, θ-γ is set in the range from 60° to 120° in order to keep the included angle between the directions of longitudinal vibration and bending vibration at 60–90°. The closer the included angle between the directions of longitudinal vibration and bending vibration is to 90°, the smaller the amplitude loss is when the oblique oblate ellipse is turned into a circular trajectory by adjusting the phase difference. When the included angle between the directions of longitudinal vibration and bending vibration is equal to 60°, the amplitude loss is small when the oblique oblate ellipse is turned into a circular trajectory by adjusting the phase difference.

For the A-type transducer, the known parameters and the parameters to be solved are listed in

Table 1. Structural parameters of A-type transducers.

${\mathit{L}}_{\mathbf{1}}$	${\mathit{L}}_{\mathbf{2}}$	${\mathit{L}}_{\mathbf{3}}$	${\mathit{L}}_{\mathbf{4}}$	${\mathit{L}}_{\mathbf{5}}$	${\mathit{D}}_{\mathbf{1}}$	${\mathit{D}}_{\mathbf{2}}$	d	h	m	α	${\mathit{f}}_{\mathbf{1}}$	${\mathit{f}}_{\mathbf{2}}$	$\mathsf{\theta }\mathbf{-}\mathsf{\gamma }$
20	5	8	12		45	71			≥5

. Here, m is the distance difference between the outside of the front end of the horn and the outside of the flange in the axial direction of the transducer. $f_1$ is the frequency of the longitudinal vibration and $f_2$ is the frequency of the bending vibration. The units of $f_1$ and $f_2$ are kHz, the units of α and $\theta \text{-}\gamma$ are °, and the units of other parameters are mm. Figure 3a shows the flow chart of a simulation design for an A-type transducer. The general design idea is as follows: The first step is to design a half-wavelength longitudinal vibration transducer with a straight horn. Firstly, the section size of the horn is estimated, and then the length $L_5$ of the horn is calculated in a certain frequency range. The calculation here is based on the principle of half-wavelength longitudinal vibration, that is, the length of the horn should be the half-wavelength length of the sound wave in the material at the working frequency. The second step is to match the half-wavelength longitudinal vibration transducer with a straight horn into a longitudinal-bending hybrid elliptical vibration ultrasonic transducer. By adjusting the section size of the horn, the resonance frequencies of longitudinal vibration and bending vibration are close. The third step is to design an elliptical vibration ultrasonic transducer with a bending horn. Bending the horn makes the axis of the horn and the axis of the transducer form a certain included angle α. By adjusting the value of α, the directions of longitudinal vibration and bending vibration can be nearly perpendicular to each other. Further, the distance m from the front end of the horn to the outermost side of the transducer is adjusted by adjusting the length $L_5$ of the horn. The fourth step is to perform a final check of the designed elliptical vibration ultrasonic transducer with a bending horn. The ultimate goal of the design is to make the two paths of vibration (longitudinal vibration and bending vibration) nearly the same in frequency and nearly perpendicular to each other in vibration direction. At the same time, the front end of the horn extends out of the outermost side of the transducer for a certain distance to ensure that the tool holder does not interfere with the workpiece during ultrasonic vibration-assisted turning.

For the A-type transducer, in order to make the front end of the horn extend out of the transducer laterally, its horn is longer than that of the 20 kHz transducer, so the frequency of the A-type transducer is lower. At the same time, in order to ensure that the transducer has enough stiffness, its horn should not be designed too long, and the horn of the A-type transducer can be designed in the range of 16–20 kHz. Although the frequency below 20 kHz is not ultrasonic, the vibration cutting effect of vibration close to 20 kHz is similar to that of ultrasonic vibration cutting. According to the impedance matching theory put forward by Jiang et al. [30], the transducer can still obtain 70% of the maximum amplitude when it vibrates within the range of 0.4 kHz above and below the optimal resonance frequency. Therefore, the difference between $f_1$ and $f_2$ is in the range of 0.8 kHz, and 70% of the maximum amplitude can be obtained for both longitudinal vibration and bending vibration. In order to make the amplitude of longitudinal vibration and bending vibration as large as possible, the difference between $f_1$ and $f_2$ is in the range of 0.4 kHz.

For the B-type transducer, the known parameters and the parameters to be solved are listed in

Table 2. Structural parameters of B-type transducers.

${\mathit{L}}_{\mathbf{1}}$	${\mathit{L}}_{\mathbf{2}}$	${\mathit{L}}_{\mathbf{3}}$	${\mathit{L}}_{\mathbf{4}}$	${\mathit{L}}_{\mathbf{5}}$	${\mathit{D}}_{\mathbf{1}}$	${\mathit{D}}_{\mathbf{2}}$	d	e	h	n	α	${\mathit{f}}_{\mathbf{1}}$	${\mathit{f}}_{\mathbf{2}}$	$\mathsf{\theta }\mathbf{-}\mathsf{\gamma }$
20	5	8	12	≥20	45	71	≤32	5.2	24	34	90

. Here, $f_1$ is the frequency of the longitudinal vibration and $f_2$ is the frequency of the bending vibration. The units of $f_1$ and $f_2$ are kHz, the units of α and $\mathsf{\theta }\text{-}\mathsf{\gamma }$ are °, and the units of other parameters are mm. To avoid the structural interference between the horn and the turbine disk, the front structure of the horn is kept consistent with that of the conventional turning tool holder. The frequency matching and vibration direction matching of the elliptical vibration ultrasonic transducer are carried out by adjusting the structural size of the straight part of the horn. Figure 3b is the flow chart of a simulation design for a B-type transducer. The general design idea is as follows: The first step is to design a half-wavelength longitudinal vibration transducer with a bending horn. Firstly, the section size of the horn is estimated, and then the length $L_5$ of the straight part of the horn is calculated within a certain frequency range. The second step is to match a half-wavelength longitudinal vibration transducer with a bending horn into a longitudinal-bending hybrid elliptical vibration ultrasonic transducer. By adjusting the section size of the straight part of the horn, the resonance frequencies of the longitudinal vibration and bending vibration are close, and the vibration directions of the longitudinal vibration and bending vibration are nearly perpendicular to each other. The third step is to perform a final check of the designed elliptical vibration ultrasonic transducer with the bending horn. The ultimate goal of the design is to make the longitudinal vibration and bending vibration nearly the same in frequency and nearly perpendicular to each other in vibration direction. At the same time, it is ensured that the ultrasonic tool holder does not interfere with the turbine disk during ultrasonic vibration-assisted turning.

According to the finite element simulation flow chart in Figure 3, the A-type transducer and B-type transducer can be simulated and designed. The material parameters used in the finite element simulation are shown in

Table 3. Material parameters used in finite element simulation.

Part	Material	Density (kg/m3)	Elastic Modulus (GPa)	Poisson Ratio
Horn	42CrMo	7850	212	0.28
Piezoceramics	PZT-8	7600	86	0.3
Electrode plate	Red copper	8300	110	0.34
End cap	AISI 1045 Steel	7800	209	0.269
Tool	YT15	14,000	600	0.22

. The modal analysis module in Ansys Workbench is used for the finite element simulation.

4. Results and Discussion

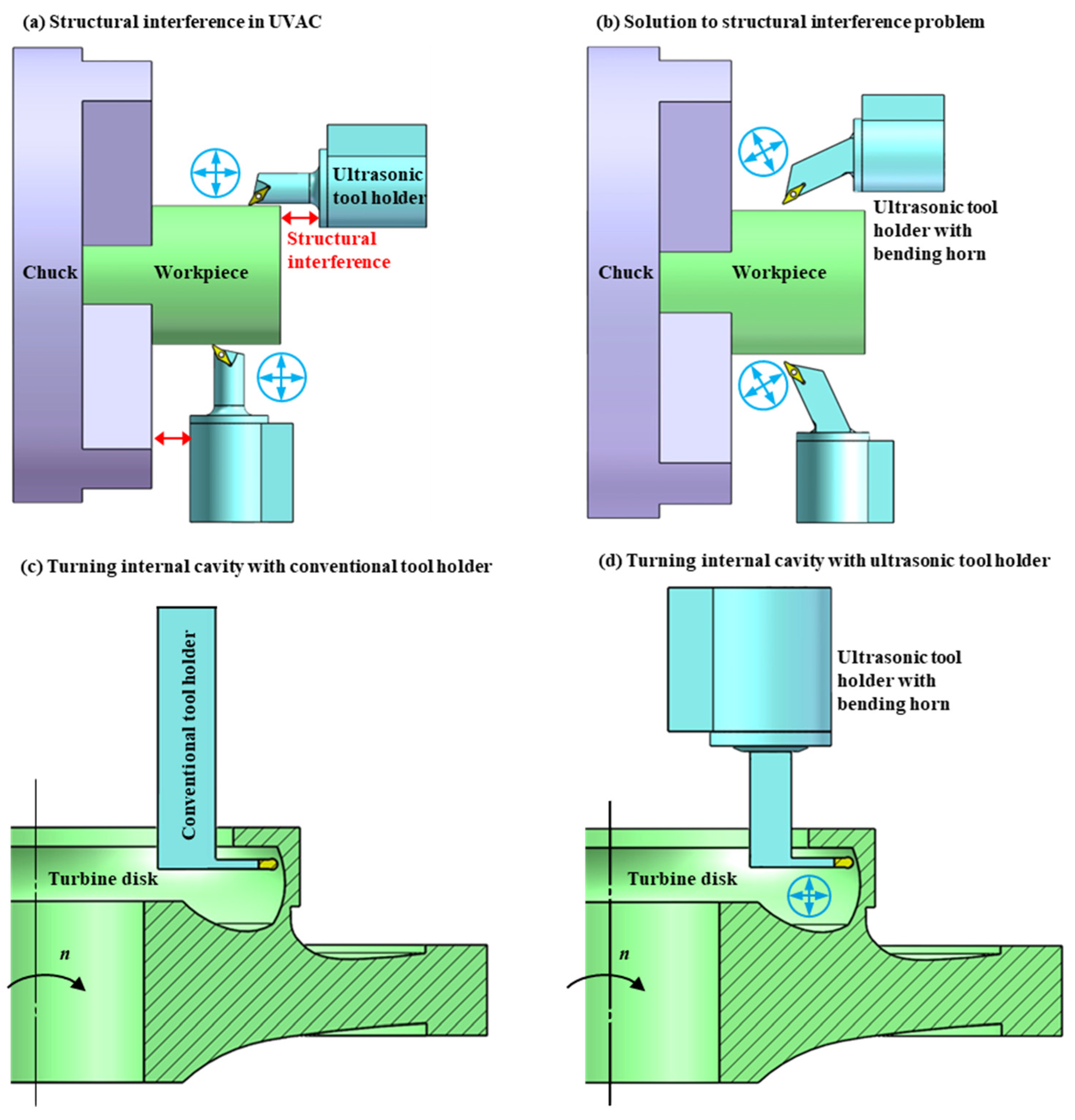
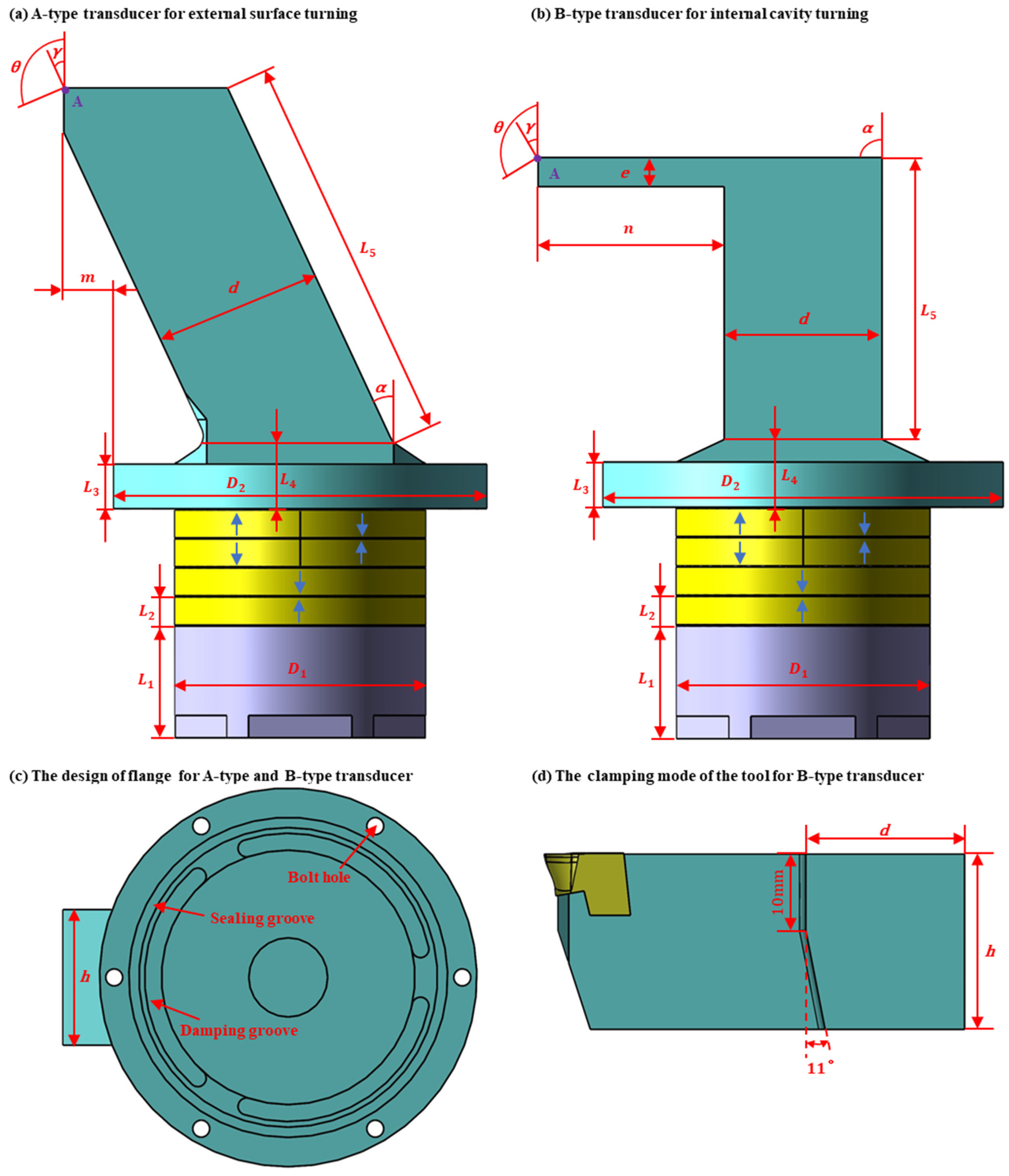
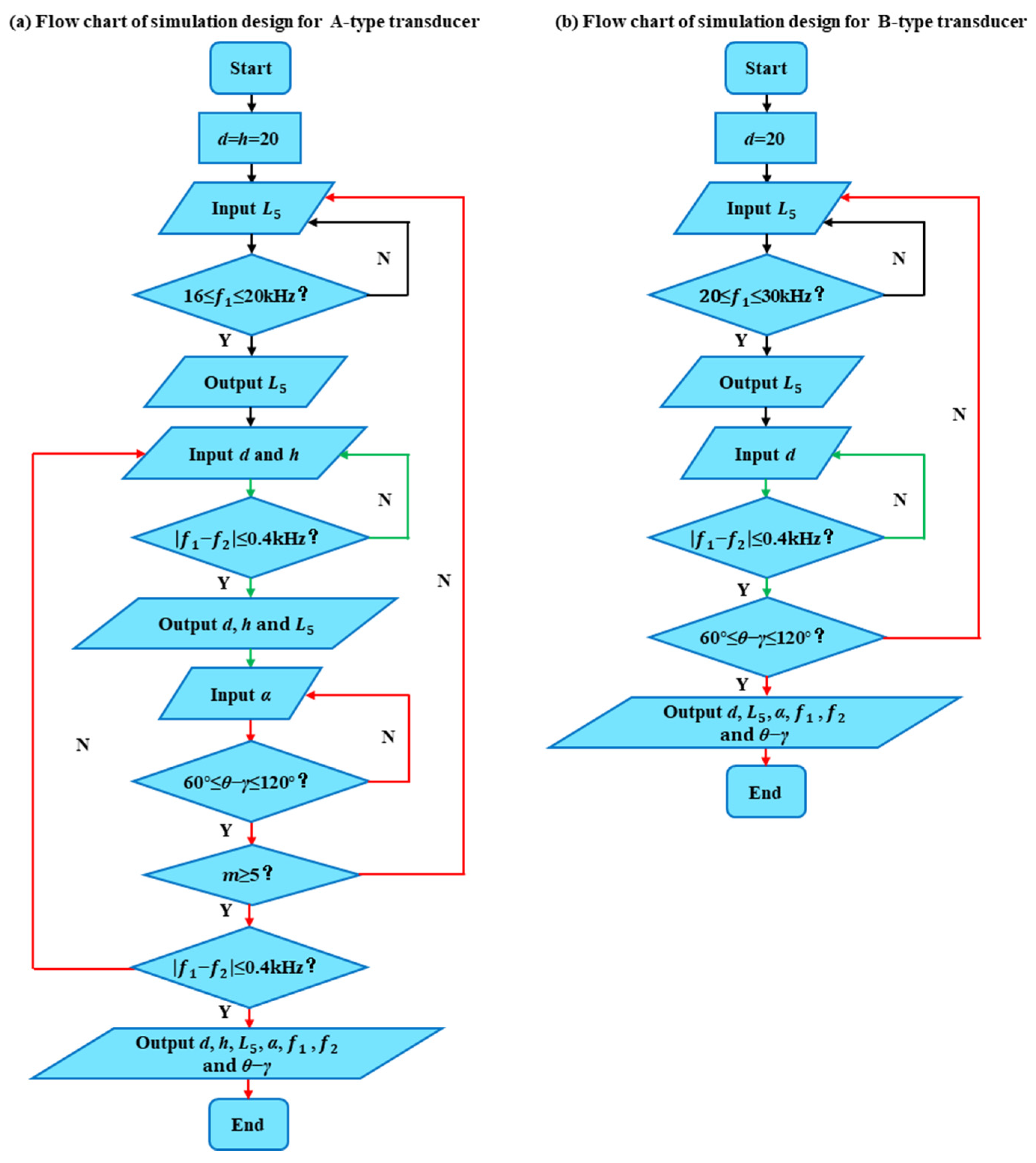
4.1. Simulation Design Results

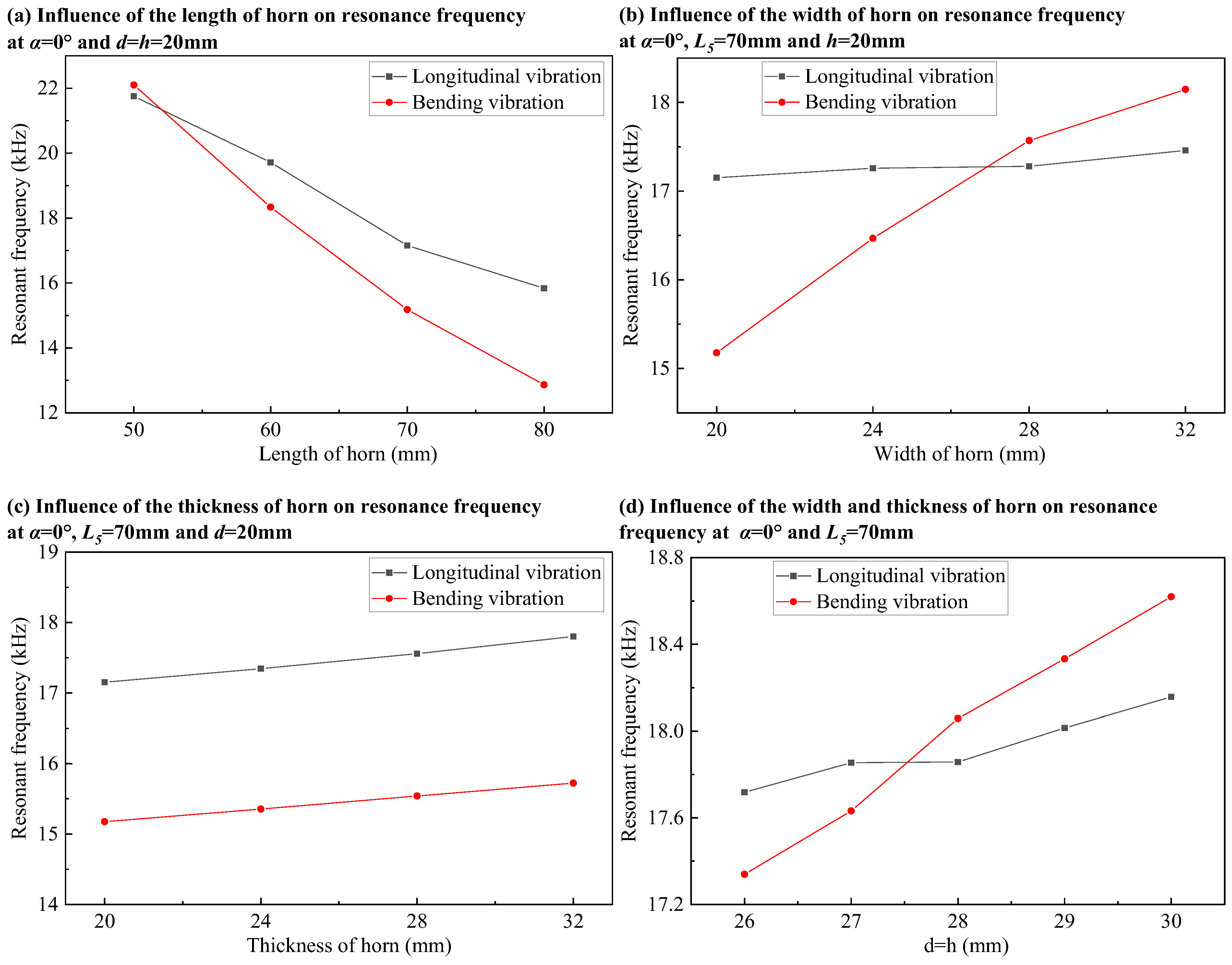
Figure 4 and Figure 5 are the simulation results of the A-type transducer. Figure 4 shows the influence of structural dimensions of the A-type transducer on the resonance frequency. The initial section size is estimated to be $d=h=20 \mathrm{m}\mathrm{m}$ according to the required stiffness and size requirements of the horn, and then the influence of the length of horn $L_5$ on the resonance frequency of longitudinal vibration and bending vibration is analyzed. As can be seen from Figure 4a, with the shortening of the length of horn, the resonant frequencies of the bending vibration and longitudinal vibration increase, and the frequency of the bending vibration increases faster so that the resonant frequencies of the bending vibration and longitudinal vibration can be equal. In order to ensure that the horn can extend out of the side of the transducer after bending, and at the same time consider the influence of the length of horn on the stiffness, $L_5=70 \mathrm{m}\mathrm{m}$ is determined.

Based on obtaining the length of the horn, the influence of the horn’s width d on the resonance frequencies of longitudinal and bending vibrations is investigated. As shown in Figure 4b, as the horn’s width increases, the resonant frequency of the bending vibration rises significantly, whereas the resonant frequency of the longitudinal vibration increases only slightly. Consequently, by adjusting the horn’s width, the resonant frequencies of the bending and longitudinal vibrations can be brought closer together.

On the basis of obtaining the length of the horn, the influence of the thickness of horn h on the resonance frequency of longitudinal vibration and bending vibration is studied. It can be found from Figure 4c that with the increase in thickness of the horn, the resonant frequencies of the bending vibration and longitudinal vibration have the same changing trend, so it is impossible to make the resonant frequencies of the bending vibration and longitudinal vibration close by changing the horn thickness. The horn thickness has little influence on the resonant frequency, but it has great influence on the stiffness of the horn, so that the thickness and width of the horn are equal in order to meet the requirements of frequency matching and stiffness at the same time. In Figure 4d, with the increase in the section size d and h of the horn, the resonance frequencies of the bending vibration and longitudinal vibration increase, and the resonance frequencies of the bending vibration increase faster so that the resonance frequencies of the bending vibration and longitudinal vibration can be equal.

The influence of the length, width, and thickness of the horn in Figure 4 on the resonant frequency of the bending vibration and longitudinal vibration corresponds to Equations (9) and (10). Equations (9) and (10) are obtained under the condition of a pure bending beam. From Equations (9) and (10), it can be seen that the angular frequency of longitudinal vibration is inversely proportional to the length of the horn, and the angular frequency of the bending vibration is inversely proportional to the square of the length of the horn. In Figure 4a, as the length of the horn decreases, the resonant frequency of the bending vibration increases faster than that of the longitudinal vibration. Equation (9) is independent of the width of the horn, and the angular frequency of the bending vibration in Equation (10) is proportional to the width of the horn. In Figure 4b, the resonant frequency of the longitudinal vibration does not change much with the increase in the width of the horn, while the resonant frequency of the bending vibration increases with the increase in the width of the horn. Equations (9) and (10) are independent of the thickness of the horn. In Figure 4c, the resonant frequencies of the longitudinal vibration and bending vibration do not change much with the increase in the thickness of the horn.

The transducer with $L_5=70 \mathrm{m}\mathrm{m}$ and $d=h=28 \mathrm{m}\mathrm{m}$ is selected as an elliptical vibration ultrasonic transducer with a straight horn. The resonance frequencies of the longitudinal vibration and bending vibration are 17.858 kHz and 18.058 kHz, respectively. After bending the horn for a certain angle, an elliptical vibration ultrasonic transducer with a bending horn can be obtained. Considering that the difference between 17.858 kHz and 18.058 kHz is only 0.2 kHz, and the resonant frequency of the transducer will change after the horn is bent to a certain angle, it is only required that the resonant frequencies of the longitudinal vibration and bending vibration are close, but not equal.

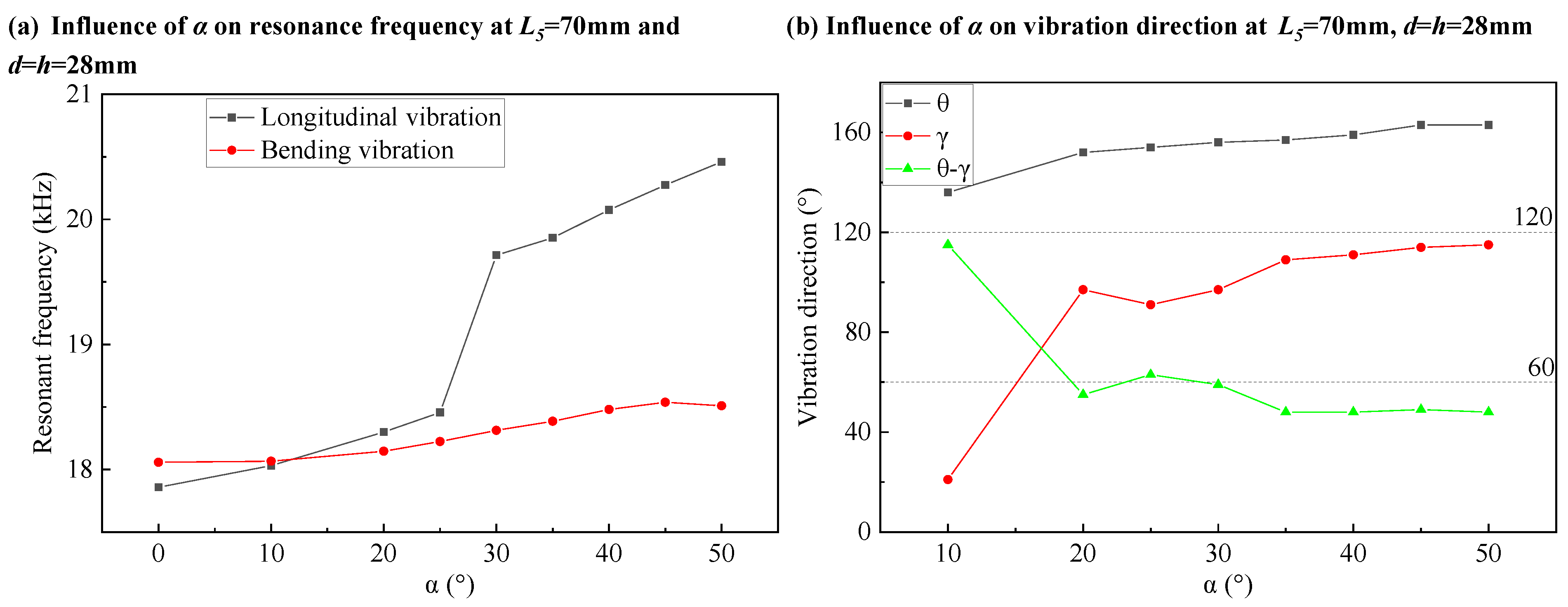
Figure 5 shows the influence of the bending angle α of the horn on the resonance characteristics of the transducer. Figure 5a studies the influence of the bending angle α on the resonance frequency. In Figure 5a, when α increases from 0° to 50°, the resonant frequency of the bending vibration increases slowly. The resonant frequency of the longitudinal vibration increases slowly with α increasing from 0° to 25°, and increases rapidly with α increasing from 25° to 50°. In the case of small α, the influence of the bending angle α of the horn on the frequency matching can be ignored, and in the case of large α, it is not conducive to the frequency matching. Figure 5b studies the influence of the bending angle α on the vibration direction. In Figure 5b, when α increases from 10° to 50°, the angle θ of the vibration direction of the bending vibration slowly increases. The angle γ of the vibration direction of the longitudinal vibration increases rapidly with α increasing from 10° to 20°, and slowly increases with α increasing from 20° to 50°.

The bending of the horn causes the asymmetry of the structure, which makes the vibration directions of the bending vibration and longitudinal vibration incline to the bending direction of the horn. Because of the different inclination degrees of the vibration directions of the bending vibration and longitudinal vibration, the vibration directions of the bending vibration and longitudinal vibration are not vertical. Considering the influence of the bending angle α of the horn on the resonant frequency and vibration direction of the transducer, $\alpha =25°$ is determined as the appropriate bending angle of the horn. After the optimization design, the structural parameters of the A-type transducer satisfying Figure 3a are shown in

Table 4. Structural parameters obtained by simulation for an A-type transducer.

${\mathit{L}}_{\mathbf{1}}$	${\mathit{L}}_{\mathbf{2}}$	${\mathit{L}}_{\mathbf{3}}$	${\mathit{L}}_{\mathbf{4}}$	${\mathit{L}}_{\mathbf{5}}$	${\mathit{D}}_{\mathbf{1}}$	${\mathit{D}}_{\mathbf{2}}$	d	h	m	α	${\mathit{f}}_{\mathbf{1}}$	${\mathit{f}}_{\mathbf{2}}$	$\mathit{\theta }\mathbf{\text{-}}\mathit{\gamma }$
20	5	8	12	70	45	71	28	28	6	25	18.473	18.326	63

.

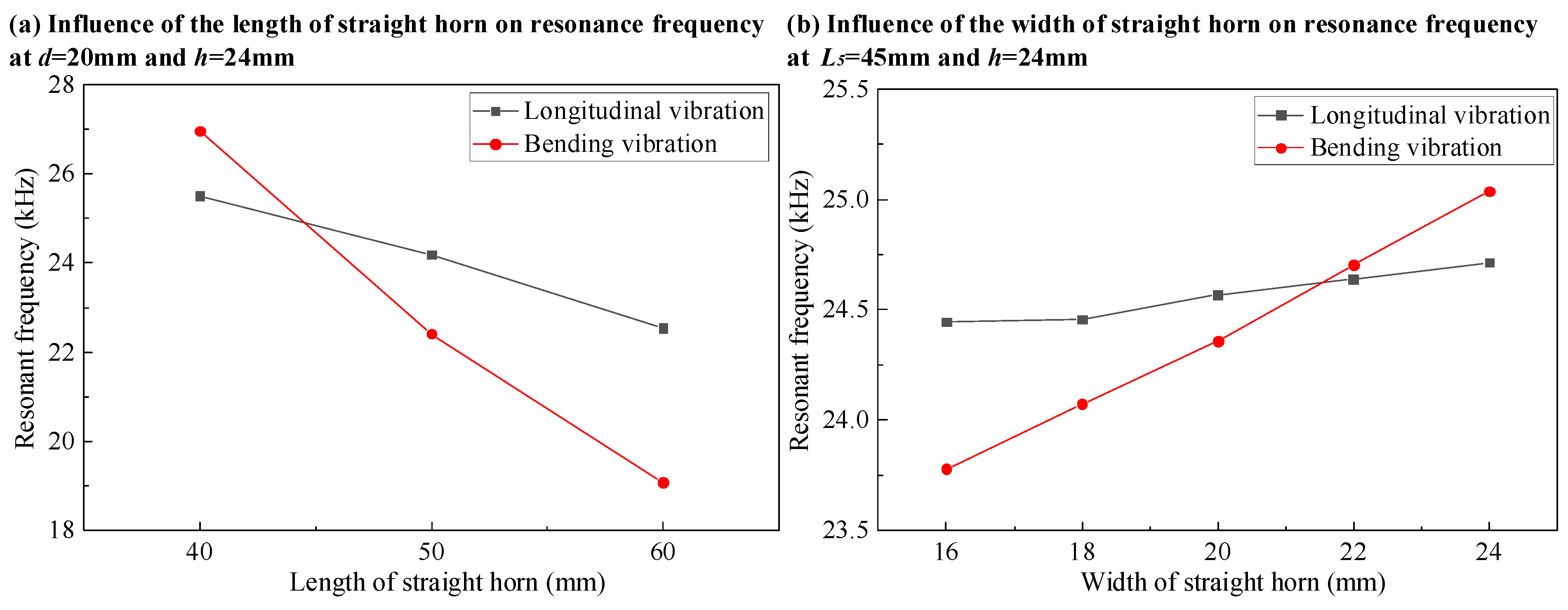
Figure 6 shows the simulation results of the B-type transducer. Figure 6 shows the influence of the structural dimensions of the B-type transducer on the resonance frequency. The initial width of the straight horn is estimated to be $d=20 \mathrm{m}\mathrm{m}$ according to the required stiffness and size requirements of the horn, and then the influence of the length of the straight horn $L_5$ on the resonance frequency of the longitudinal vibration and bending vibration is analyzed. As can be seen from Figure 6a, with the shortening of the length of the straight horn, the resonant frequencies of the bending vibration and longitudinal vibration increase, and the frequency of bending vibration increases faster so that the resonant frequencies of the bending vibration and longitudinal vibration can be equal.

On the basis of obtaining the length of the horn, the influence of the width of horn d on the resonance frequency of the longitudinal vibration and bending vibration is studied. As can be seen from Figure 6b, with the increase in the width of the horn, the resonant frequency of the bending vibration noticeably increases, while the resonant frequency of the longitudinal vibration increases slightly. Therefore, the resonant frequencies of the bending vibration and longitudinal vibration can be close by changing the width of the horn. The influence of the length and width of the straight horn in Figure 6 on the resonant frequency of the bending vibration and longitudinal vibration corresponds to Equations (9) and (10). The front structure of the horn of the B-type transducer is too thin, which will amplify the local vibration, and it is difficult to judge the direction of the vibration, so the influence of the structural size of the horn on the direction of the vibration is not discussed here. Reducing the value of parameter e will reduce the stiffness of the transducer, while increasing the value of parameter e will cause structural interference between the horn and the workpiece. The value of e of the ultrasonic transducer is kept the same as that of the conventional tool holder, so the influence of parameter e on the resonant frequency and vibration mode is not discussed in this paper. After the optimization design, the structural parameters of the B-type transducer satisfying Figure 3b are shown in

Table 5. Structural parameters obtained by simulation for a B-type transducer.

${\mathit{L}}_{\mathbf{1}}$	${\mathit{L}}_{\mathbf{2}}$	${\mathit{L}}_{\mathbf{3}}$	${\mathit{L}}_{\mathbf{4}}$	${\mathit{L}}_{\mathbf{5}}$	${\mathit{D}}_{\mathbf{1}}$	${\mathit{D}}_{\mathbf{2}}$	d	e	h	n	α	${\mathit{f}}_{\mathbf{1}}$	${\mathit{f}}_{\mathbf{2}}$	$\mathit{\theta }\mathbf{\text{-}}\mathit{\gamma }$
20	5	8	12	43	45	71	20	5.2	24	34	90	24.677	24.319	72

.

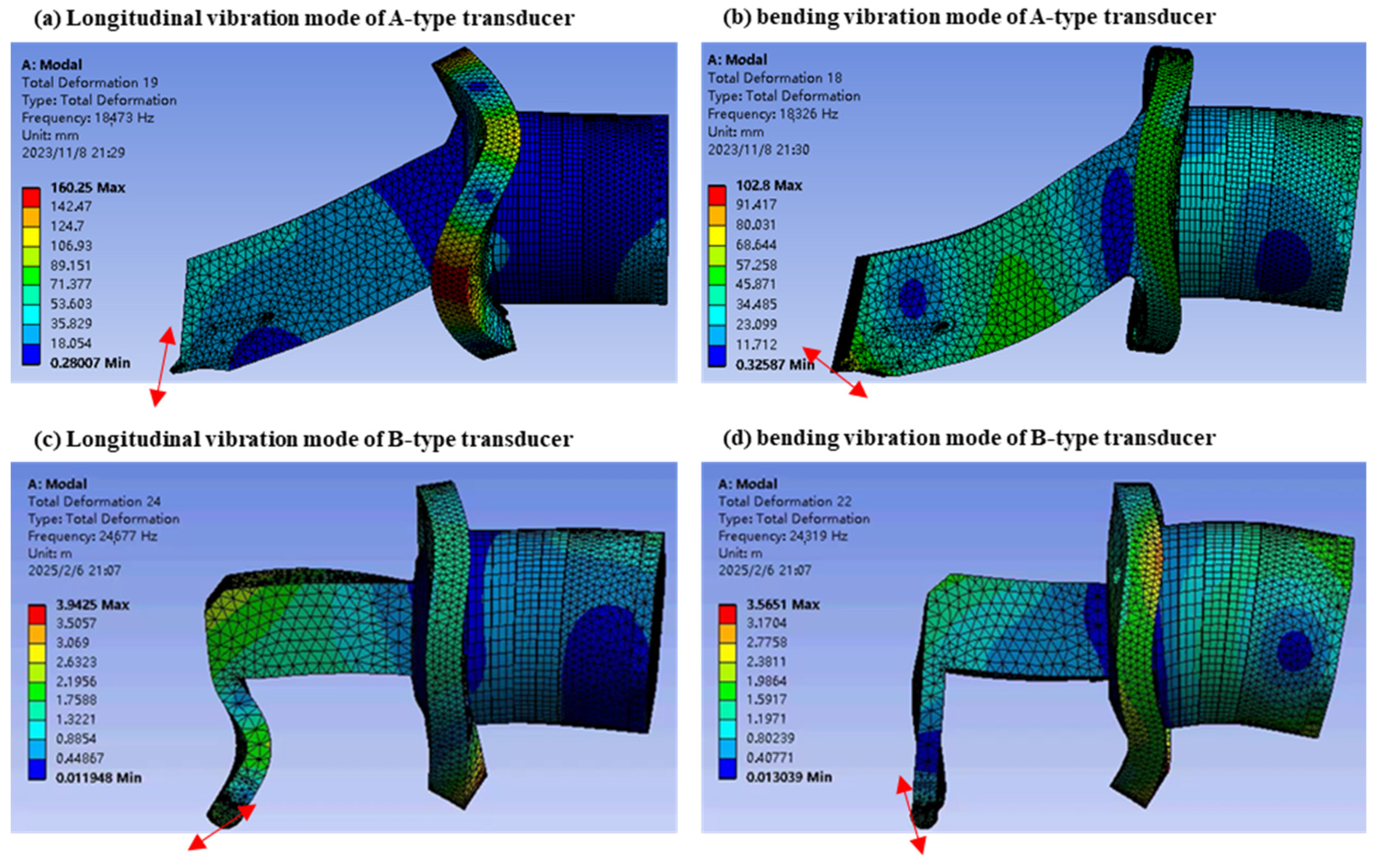
The modal analysis results of the optimized longitudinal-bending elliptical vibration ultrasonic transducer with a bending horn are shown in Figure 7. Figure 7a,c show the first longitudinal vibration mode, and the node is located in the flange. The mode shows that the vibration of the end cap is small, and it can also be used as a clamping point. In practice, clamping the end cap has little effect on the resonance characteristics. Figure 7b,d show the second bending vibration mode, and the nodes are located in the flange and the end cap. Therefore, the transducer can be fixed by the flange and the end cap. The size of the transducer in the second-order bending vibration mode is close to that in the first-order longitudinal vibration mode, so the bending vibration mode adopts the higher-order mode. The modes of the longitudinal vibration and bending vibration can be excited in practical use, and the amplitude is twice the amplitude required for UVAC, so the vibration efficiency of the transducer can meet the needs of use. The direction of the modal vibration is indicated by a red arrow in Figure 7. In Figure 7a,c, it can be clearly seen that the transducer part is vibrating longitudinally, while the longitudinal vibration of the horn deflects in the bending direction of the horn, which is caused by structural asymmetry.

4.2. Vibration Test

The transducers corresponding to the structural parameters in Table 4 and Table 5 are manufactured and assembled together according to the assembly relationship in Figure 2. The resonant frequency of the transducer is measured by PV520A impedance analyzer developed by Tsinghua University. The resonant frequencies of the longitudinal vibration and bending vibration of the A-type transducer are 18.332 kHz and 18.290 kHz, respectively, and the difference between the designed and measured resonant frequencies of the longitudinal vibration and bending vibration is 0.76% and 0.19%, respectively. The resonance frequencies of longitudinal vibration and bending vibration of the B-type transducer are 22.328 kHz and 22.678 kHz, respectively, and the difference between the designed and measured resonance frequencies of longitudinal vibration and bending vibration is 9.51% and 6.74%, respectively. According to the literature research on the modal simulation of transducers, the error between the designed frequency and the measured frequency needs to be within 10%, and the design error in this paper meets the requirements. When there is a design error, it will not adversely affect the frequency matching of the transducer, because the measured frequencies of the longitudinal vibration and bending vibration are all lower than the design frequency, and the decreased values are close.

Figure 8 shows the measuring device for the vibration amplitude and vibration direction. A Keyence LK-Navigator 2 laser micrometer is used to measure the amplitude and vibration direction of ultrasonic tool holders. The transducer is excited by applying voltage from an ultrasonic power supply, and the vibration amplitude is measured simultaneously in horizontal and vertical directions by a laser micrometer. When the vibration in a single direction is excited (exciting longitudinal vibration or bending vibration), the vibration amplitude and vibration direction can be obtained by synthesizing the amplitude measured in the horizontal and vertical directions. When the longitudinal vibration and bending vibration are excited at the same time, the elliptical vibration trajectory of the tool tip can be obtained by synthesizing the amplitudes measured in the horizontal and vertical directions.

For the A-type transducer, the direction angle of the longitudinal vibration is $\mathsf{\gamma }=82°$, the direction angle of the bending vibration is $\mathsf{\theta }=150°$, and the included angle between the directions of longitudinal vibration and bending vibration is $\mathsf{\theta }\text{-}\mathsf{\gamma }=68°$. The difference between the designed and the measured included angle between the directions of longitudinal vibration and bending vibration is 7.93%. For the B-type transducer, the direction angle of longitudinal vibration is $\mathsf{\gamma }=32°$, the direction angle of bending vibration is $\mathsf{\theta }=111°$, and the included angle between the directions of the longitudinal vibration and bending vibration is $\mathsf{\theta }\text{-}\mathsf{\gamma }=79°$. The difference between the designed and the measured included angle between the directions of the longitudinal vibration and bending vibration is 9.72%.

The transducer is capacitive, which requires matching the inductance to make the circuit resonate and thus increase the amplitude of the transducer. The appropriate matching inductance can be determined by debugging the transducer. When debugging, a sinusoidal voltage of 360 V is applied to the ultrasonic transducer, and the frequency of the output voltage can be changed by adjusting the output of the ultrasonic power supply. 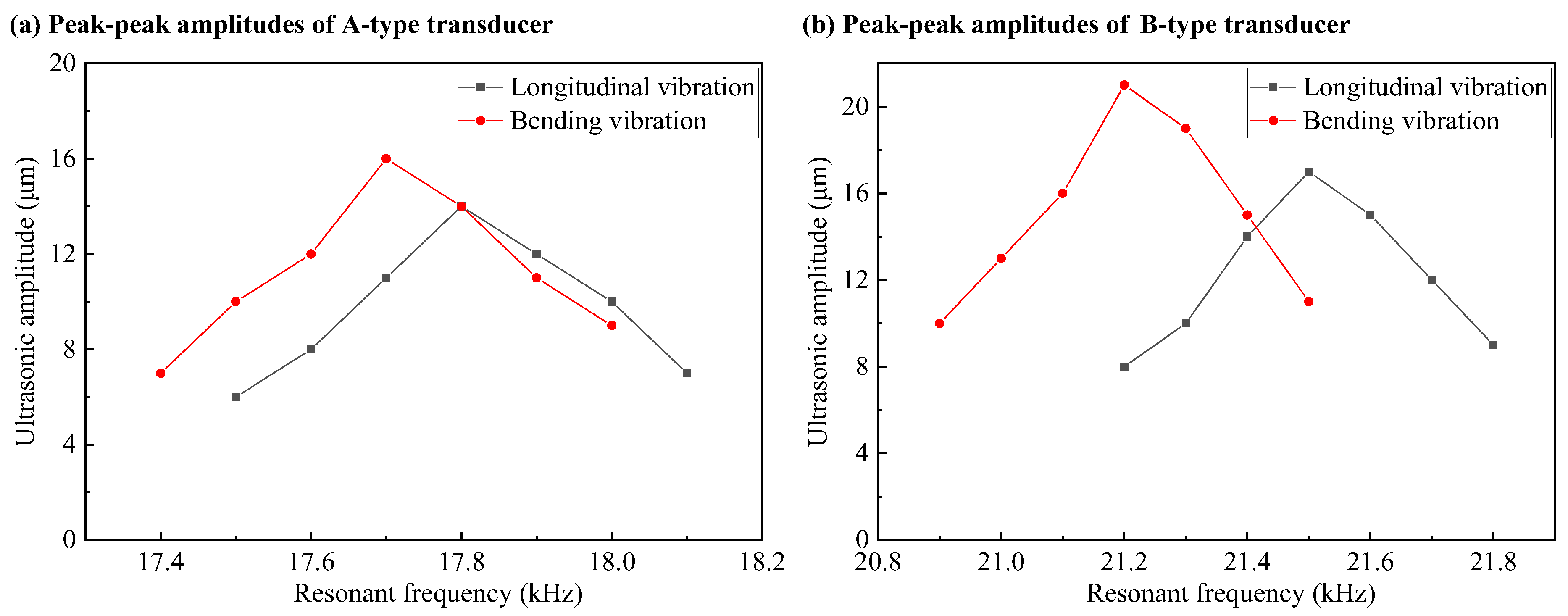Figure 9 shows the peak–peak amplitudes of transducers at different resonant frequencies with inductance $L=15 \mathrm{m}\mathrm{H}$. As can be seen from Figure 9, there is a resonance frequency with the largest amplitude for both the longitudinal vibration and bending vibration, which is lower than the mechanical resonance frequency measured by the impedance analyzer. The maximum peak–peak amplitudes of longitudinal vibration and bending vibration for the A-type transducer are 14 μm and 16 μm, respectively. The maximum peak–peak amplitudes of the longitudinal vibration and bending vibration for the B-type transducer are 17 μm and 21 μm, respectively. In order to make the resonance frequencies of the longitudinal vibration and bending vibration equal and their amplitudes as large as possible, 17.8 kHz is selected as the resonance frequency of the elliptical vibration ultrasonic transducer for the A-type transducer and 21.4 kHz is selected as the resonance frequency of the elliptical vibration ultrasonic transducer for the B-type transducer.

Let the longitudinal vibration of the elliptical vibration ultrasonic transducer vibrate along the x axis, and its bending vibration vibrates in the xOy plane, so the vibration equation of the tool tip can be obtained as follows:

$$\left\{\begin{array}{c}x=Bsin\left(2\pi Ft\right)+Csin\left(2\pi Ft+\phi \right)cos\left(\theta \text{-}\gamma \right)\\ y=Csin\left(2\pi Ft+\phi \right)sin\left(\theta \text{-}\gamma \right)\end{array}\right.$$

(11)

where B is the amplitude of the longitudinal vibration, μm; C is the amplitude of the bending vibration, μm; F is the frequency of the longitudinal vibration and bending vibration, Hz; t is time, s; $\phi$ is the phase difference of bending vibration compared with the longitudinal vibration.

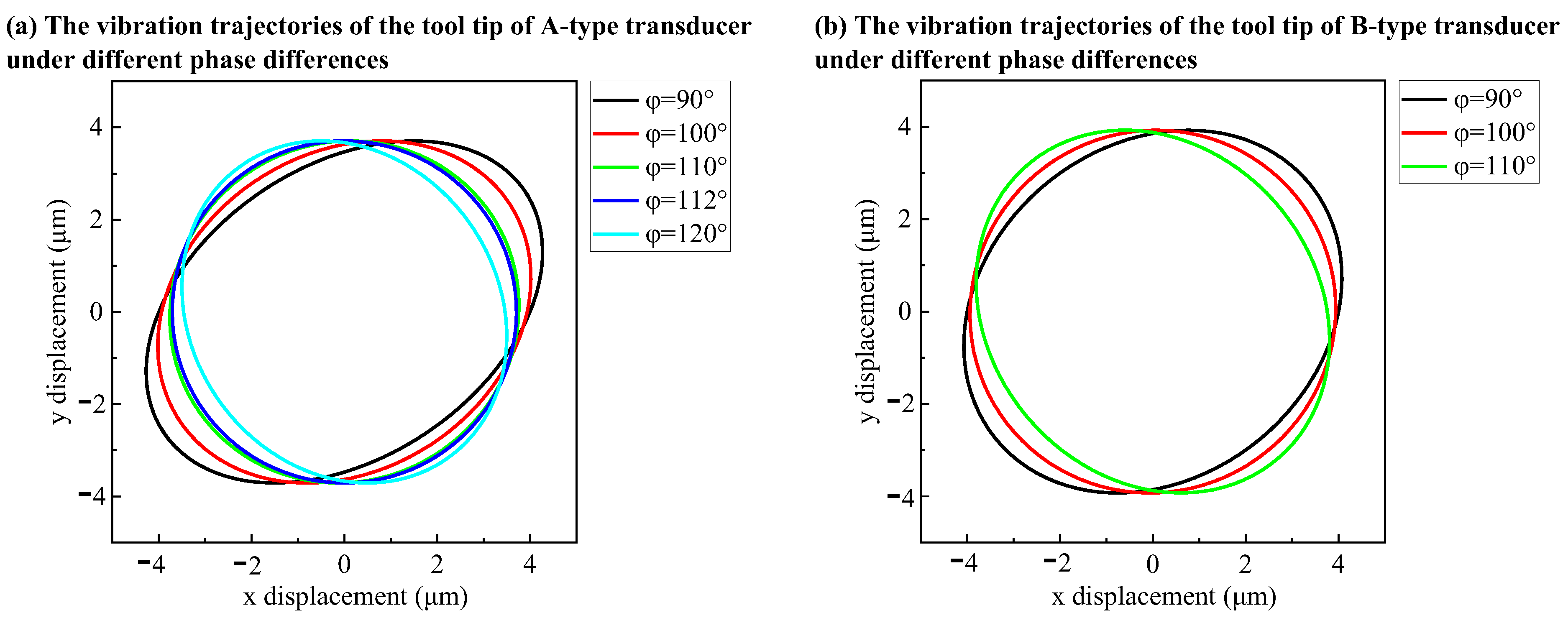
Figure 9 shows the maximum amplitude of the transducer at resonance, and the amplitude commonly used in elliptical vibration ultrasonic machining is 6–8 μm from peak to peak. Therefore, the study in Figure 10, Figure 11 and Figure 12 is carried out by adjusting the output of the ultrasonic power supply so that the amplitude of the transducer is 8 μm. Figure 10a shows the vibration trajectories of the tool tip under different phase differences for an A-type transducer at $B=C=4 \mathsf{\mu }\mathrm{m}$ and $F=17.8 \mathrm{k}\mathrm{H}\mathrm{z}$. Because there is an included angle of $68°$ between the directions of longitudinal vibration and bending vibration, the trajectory of the tool tip is an oblique oblate ellipse when the phase difference $\phi$ is $90°$, but it is approximately circular when the phase difference $\phi$ is $112°$. Figure 10b shows the vibration trajectories of the tool tip under different phase differences for a B-type transducer at $B=C=4 \mathsf{\mu }\mathrm{m}$ and $F=21.4 \mathrm{k}\mathrm{H}\mathrm{z}$. Because there is an included angle of $79°$ between the directions of longitudinal vibration and bending vibration, the trajectory of the tool tip is an oblique oblate ellipse when the phase difference $\phi$ is $90°$, but it is approximately circular when the phase difference $\phi$ is $100°$.

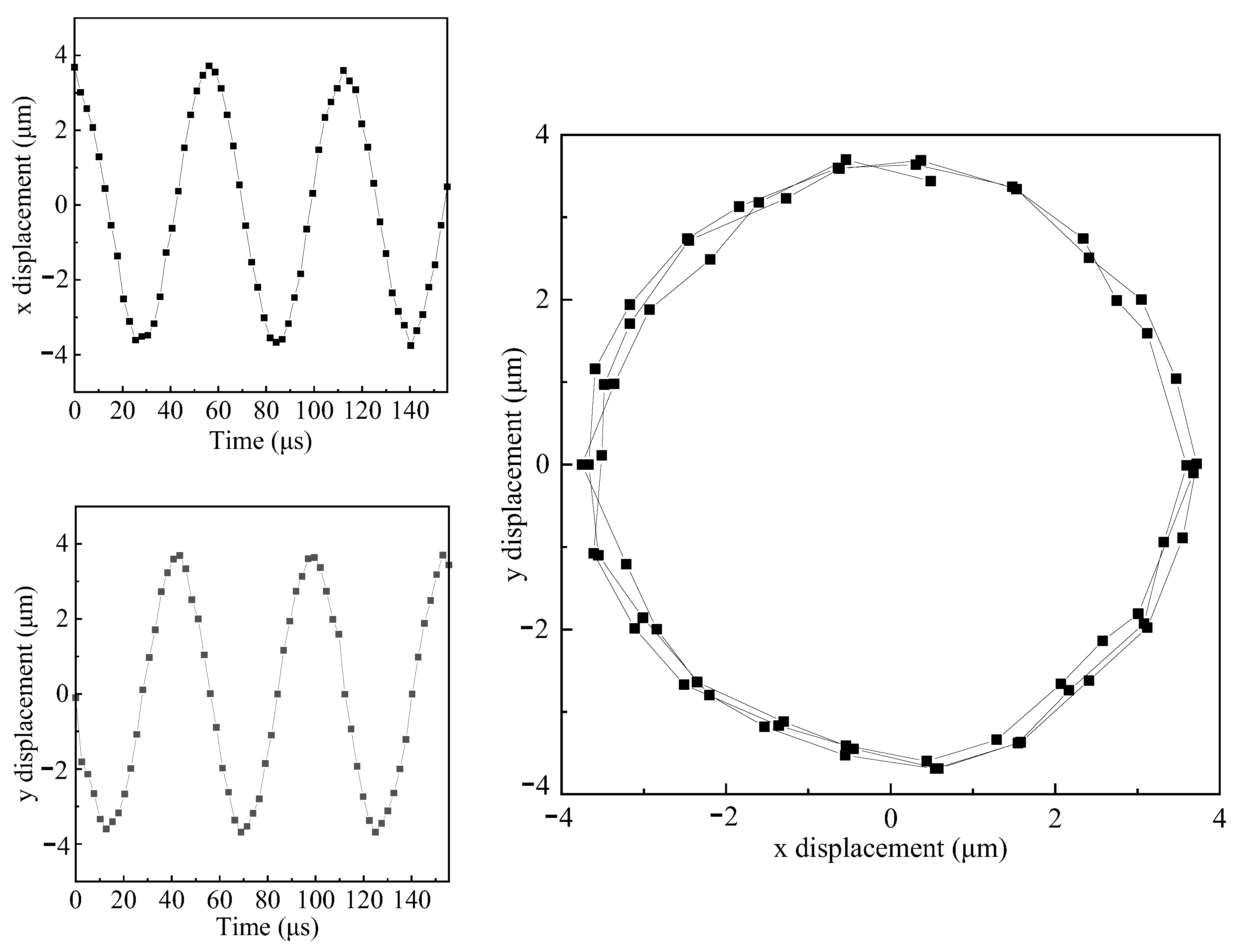
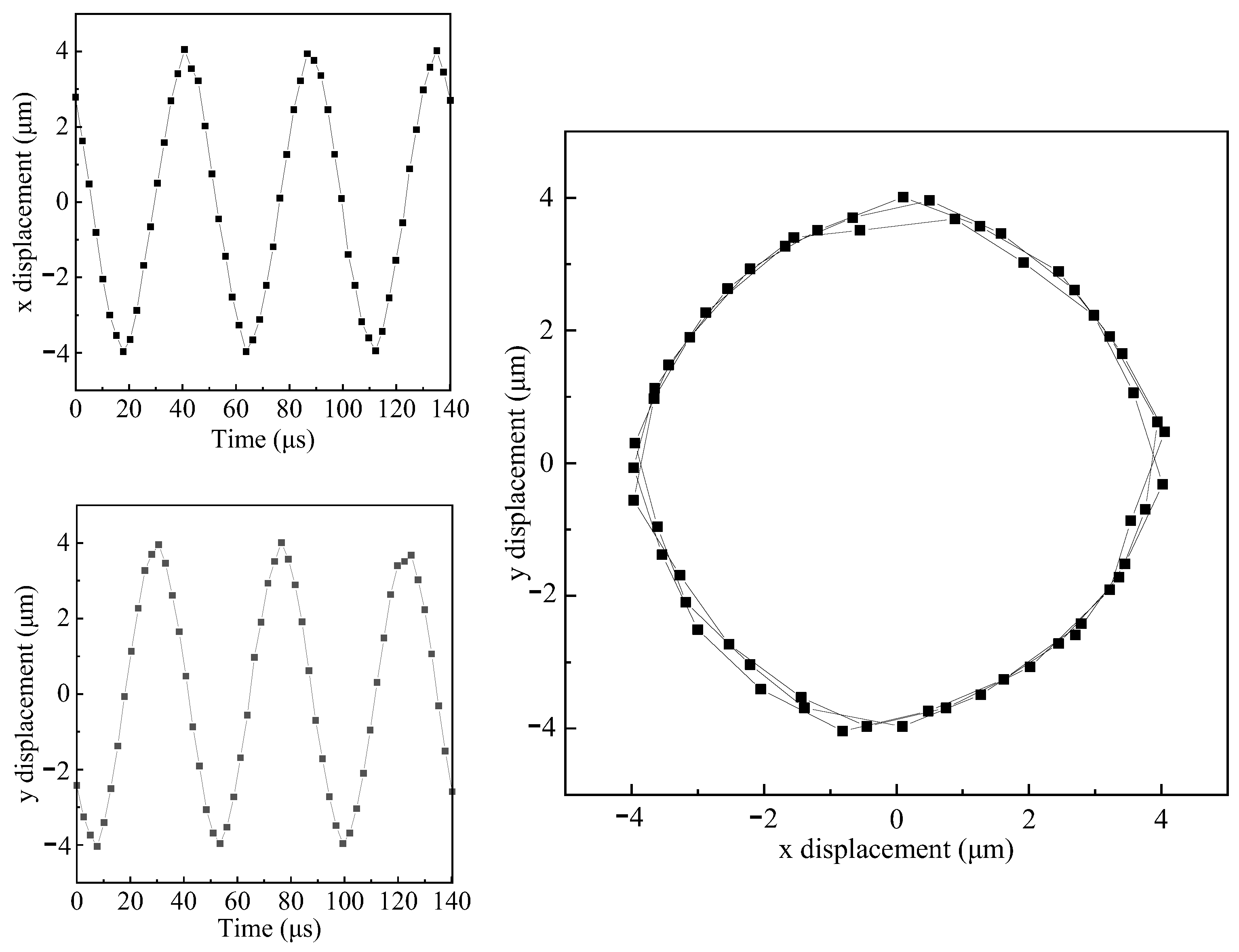
Figure 11 shows the measured vibration trajectory of the tool tip for an A-type transducer at $B=C=4 \mathsf{\mu }\mathrm{m}$ and $F=17.8 \mathrm{k}\mathrm{H}\mathrm{z}$. Figure 12 shows the measured vibration trajectory of the tool tip for a B-type transducer at $B=C=4 \mathsf{\mu }\mathrm{m}$ and $F=21.4 \mathrm{k}\mathrm{H}\mathrm{z}$. The elliptical trajectories in Figure 11 and Figure 12 are all approximately circular. Due to the frequency difference between the longitudinal vibration and the bending vibration, after the frequency matching of the transducer, both the longitudinal vibration and the bending vibration do not work at the resonance frequency with the maximum amplitude. However, due to the small difference and the low amplitude adopted, the transducer does not overheat during processing. During the continuous monitoring for two hours, the resonant frequency, output current, and amplitude of the transducer are relatively stable.

4.3. Machining Test

It is challenging to open the cutting zone during continuous cutting, which results in high cutting temperatures and forces that significantly limit tool life when machining difficult-to-machine materials. Intermittent UVAC can decrease cutting temperature and force by opening the cutting area, thereby enhancing tool life and making it a popular choice for machining such materials. However, intermittent cutting makes the MRR of UVAC low. Zhang et al. [10] put forward the partial separation continuous high-speed ultrasonic vibration cutting method, which can open the cutting area while cutting continuously, greatly improving the tool life and MRR. In this paper, we propose a partial separation continuous high-speed elliptical ultrasonic vibration cutting (HEUVC) method for cutting Inconel 718.

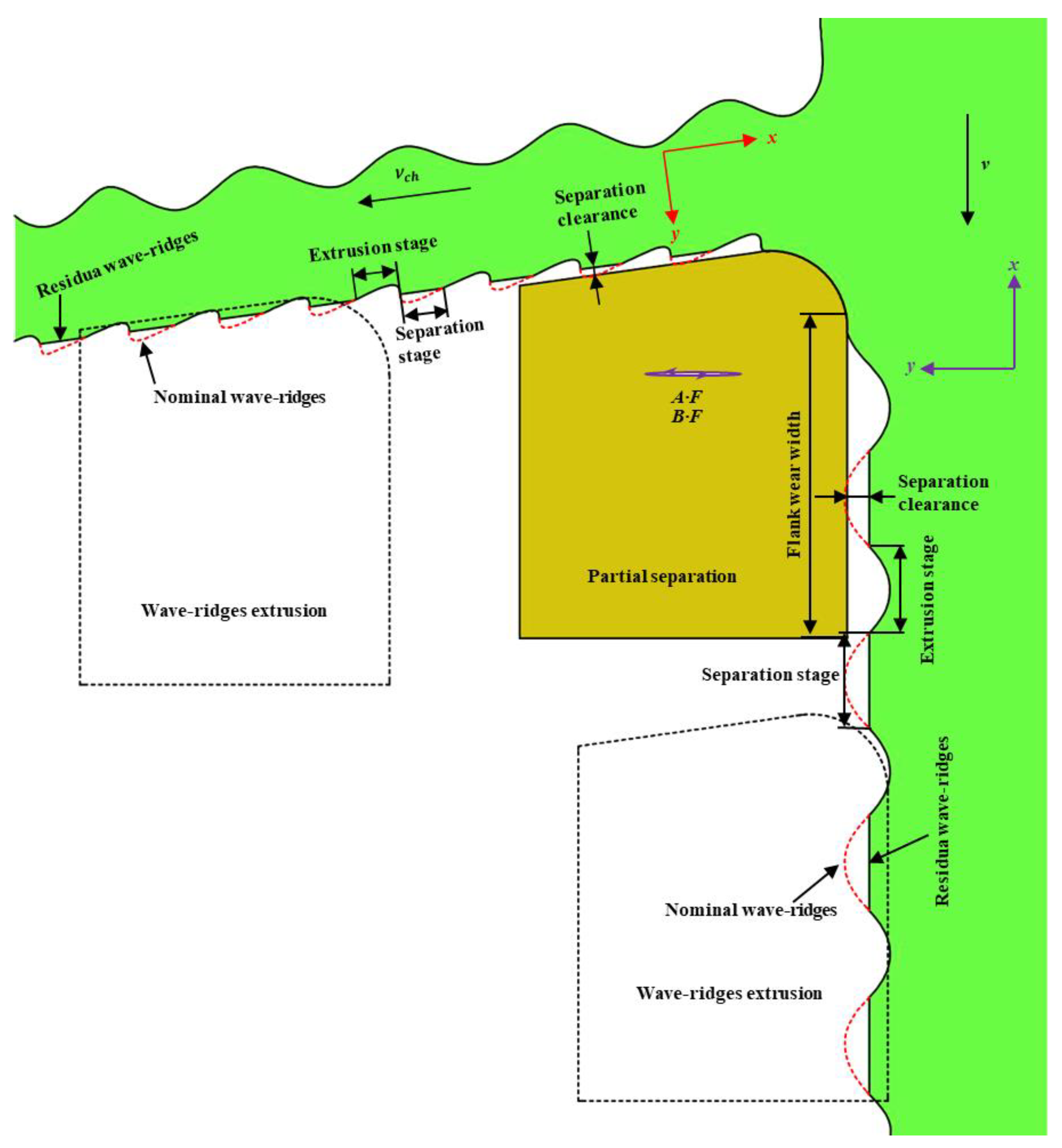
Figure 13 is a schematic diagram of a dynamic process of wave-ridges extrusion and partial separation on rake face and flank face in an orthogonal plane. Wave-ridges are periodic undulating structures generated in the direction of chip thickness or cutting thickness, including peaks and valleys. In a generation cycle of wave-ridges structure, there are two processes: wave-ridges extrusion and partial separation. In the process of wave-ridges extrusion, the tool extrudes the generated wave ridges. In the process of partial separation, a separation gap is generated between the tool and the previously extruded wave ridges.

Figure 14 shows experimental setup in HEUVC. In Figure 14a, a rhombic-type AlTiN-coated cemented carbide insert from Iscar (VCMT 160408-SM IC804) was mounted on the A-type transducer. The tool tip of the A-type transducer vibrates elliptically at the frequency of 17.8 kHz in the tool base. In Figure 14b, a TiAlN+AlTiN+TiN-coated cemented carbide insert from Iscar (TAGB 630Y IC808) was mounted on the B-type transducer. The tool tip of the B-type transducer vibrates elliptically at the frequency of 21.4 kHz in the tool base. A water-soluble emulsion is applied as a coolant on the rake face.

The comparative experiments of HEUVC and CC were carried out on a CNC lathe.

Table 6. Machining parameters.

Parameter Type	Parameter (unit)	Value
Vibration parameters	Vibration frequency (kHz)	17.8, 21.4
	phase difference (°)	112, 100
	Peak–peak amplitude (μm)	8
Process parameters	Cutting speed (m/min)	80
	Depth of cut (mm)	0.4
	Feed rate (mm/r)	0.2
Cooling parameters	Coolant pressure (bar)	50

contains all the machining parameters. In this paper, the finishing experiment of Inconel 718 is carried out, and the cutting parameters are set according to the requirements of finishing. An Olympus BX51M microscope is used to measure tool wear. When the maximum flank wear VBmax = 0.3 mm, the cutting experiment is stopped, and the cutting distance at this time is the tool life under this cutting condition. Three experiments were carried out to obtain the average of the experimental results.

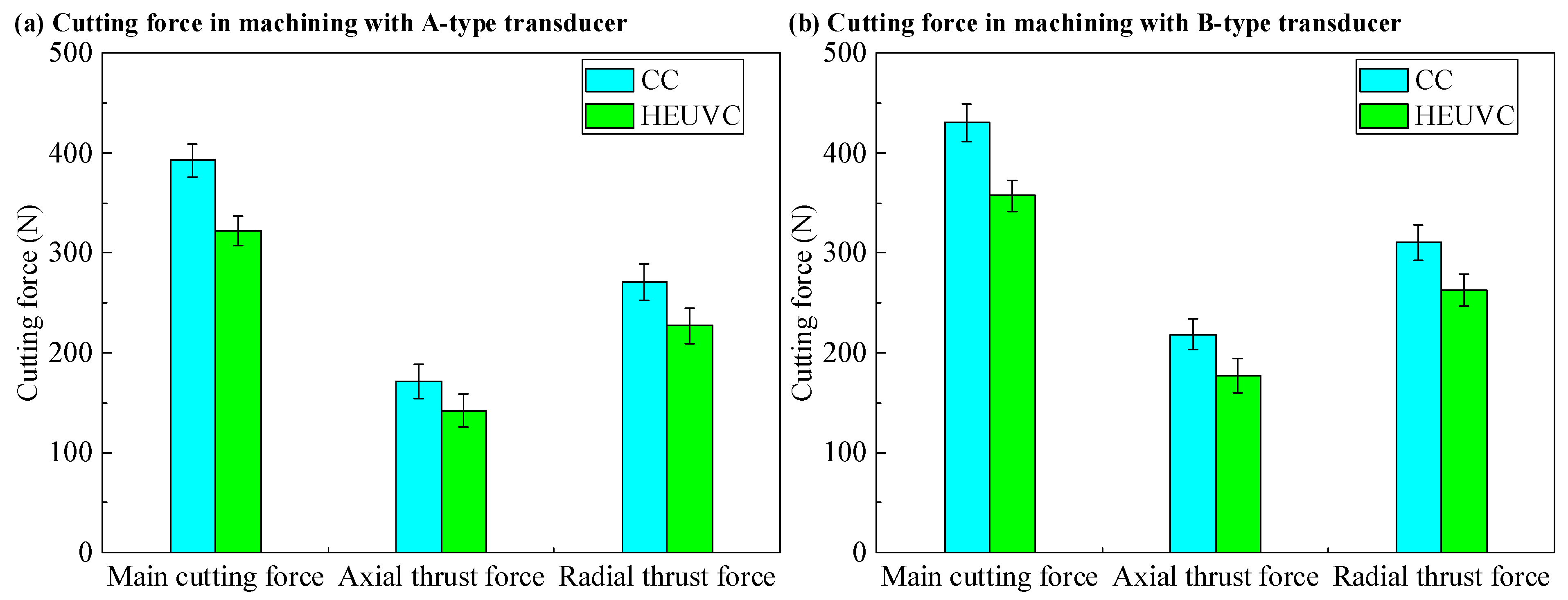
The HEUVC method can partially open the cutting area in the process of continuous cutting, so that the coolant can enter the cutting area to cool and lubricate the tool and workpiece, reduce the cutting temperature and cutting force, and thus prolong the tool life. As shown in Figure 15, compared with CC, the main cutting force, axial thrust force, and radial thrust force of HEUVC are reduced by 17.96%, 17.25%, and 16.24%, respectively, when cutting with the A-type transducer. Compared with CC, the main cutting force, axial thrust force, and radial thrust force of HEUVC are reduced by 16.95%, 18.93%, and 15.36%, respectively, when cutting with the B-type transducer.

Figure 16 shows the effect of cutting distance on flank wear when an elliptical vibration ultrasonic transducer with a bending horn is used to study the partial separation continuous high-speed elliptical ultrasonic vibration cutting Inconel 718. Compared with CC, HEUVC can improve the tool life by 65.74% when cutting with an A-type transducer. Compared with CC, HEUVC can improve the tool life by 44.62% when cutting with a B-type transducer. The rhombic-type tool is used in an A-type transducer, while the ball-end tool is used in a B-type transducer. Compared with the rhombic-type tool, the length of the cutting edge in which the ball-end tool participates in cutting is increased, which makes the cutting heat relatively dispersed, so the tool life of the ball-end tool is longer than that of the rhombic-type tool. Because the rhombic-type tool used in the A-type transducer has a short tool life, HEUVC can improve tool life more than CC. In other words, the smaller the base, the higher the improvement.

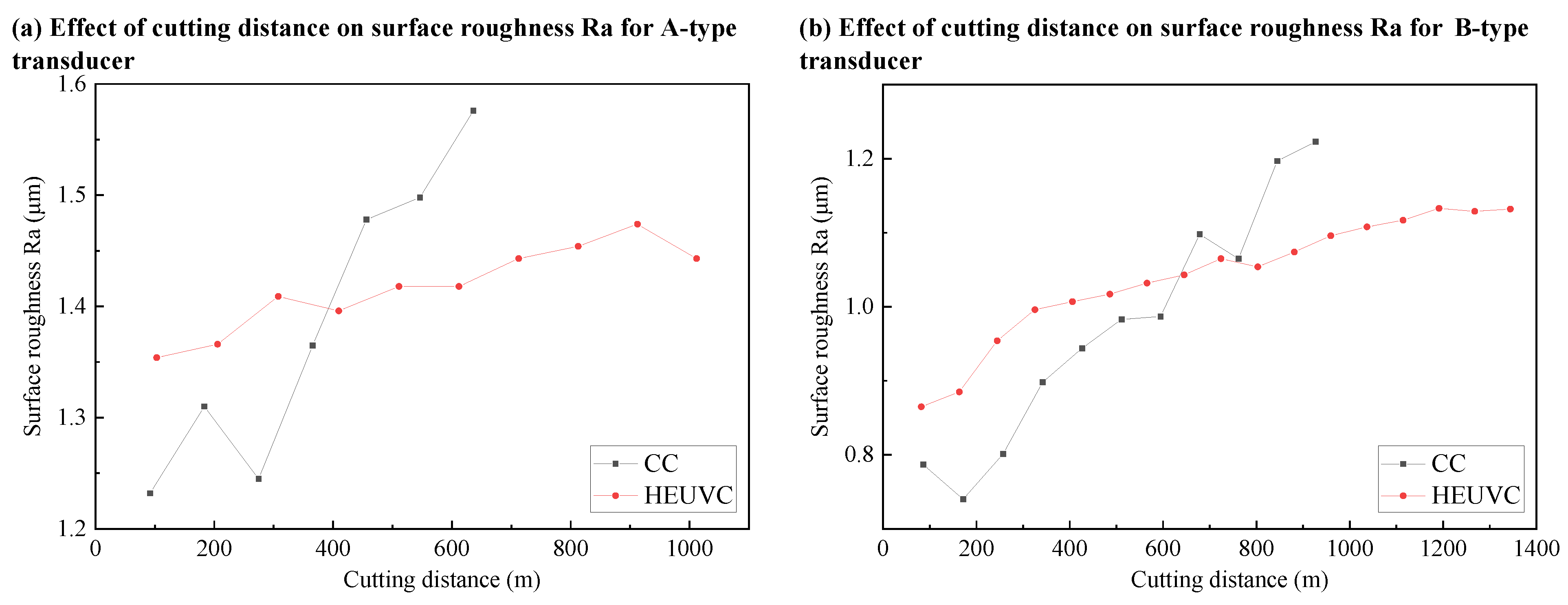
As shown in Figure 17, the roughness meets the finishing requirement that Ra is less than 1.6 μm. The vibration marks on the machined surface of HEUVC slightly increase the roughness, which can be seen from the roughness value at the initial stage of cutting. With the progress of cutting, the effect of HEUVC reducing cutting temperature and cutting force will reduce the deterioration of the machined surface by tools, thus achieving a lower surface roughness than CC. Figure 18 shows topographies of the machined surface of Inconel 718. Figure 18a,b are topographies of machined surface in CC. The existence of chatter marks is not observed in Figure 18a,b, which indicates that the designed ultrasonic vibration tool holder has sufficient rigidity. Figure c,d are topographies of machined surfaces in HEUVC. In Figure 18c,d, the stable ultrasonic vibration trace on the workpiece surface shows that the ultrasonic turning tool holder has a stable resonance characteristic, which shows that the design of elliptical vibration ultrasonic turning tool holder with a bending horn is successful. The wavelength ${\lambda }_s$ of ultrasonic vibration in Figure 18c is 73 μm, which is close to the theoretical calculation of 75 μm. The wavelength ${\lambda }_s$ of ultrasonic vibration in Figure 18d is 63 μm, which is close to the theoretical calculation of 62 μm.

5. Conclusions

In this paper, a longitudinal-bending elliptical vibration ultrasonic transducer with a bending horn and its design method are proposed. The application of the transducer solves the structural interference problem between the conventional ultrasonic tool holder and the workpiece in the process of UVAC. When matching the frequencies of longitudinal vibration and bending vibration in an elliptical vibration ultrasonic transducer, firstly, the length of the horn is designed properly, so that there is a small difference between the frequencies of longitudinal vibration and bending vibration, and then the frequency of the bending vibration is close to the frequency of the longitudinal vibration by adjusting the section width of the horn. Finally, the longitudinal vibration and bending vibration are matched to one frequency by impedance matching. The proposed frequency matching theory can be well applied to the simulation design of transducers. The bending of the horn causes the asymmetry of the structure, which makes the vibration directions of the bending vibration and longitudinal vibration incline to the bending direction of the horn. By adjusting the phase difference, the circular vibration trajectory of the tool tip can be obtained. The HEUVC method can partially open the cutting area in the process of continuous cutting, so that the coolant can enter the cutting area to cool and lubricate the tool and workpiece, reduce the cutting temperature and cutting force, and thus prolong the tool life. Compared with CC, the main cutting force, axial thrust force, and radial thrust force of HEUVC are reduced by 17.96%, 17.25%, and 16.24%, respectively, when cutting with an A-type transducer. Compared with CC, the main cutting force, axial thrust force, and radial thrust force of HEUVC are reduced by 16.95%, 18.93%, and 15.36%, respectively, when cutting with a B-type transducer. Compared with CC, HEUVC can improve the tool life by 65.74% when cutting with an A-type transducer. Compared with CC, HEUVC can improve the tool life by 44.62% when cutting with a B-type transducer.