Optimal Realtime Toolpath Planning for Industrial Robots with Sparse Sensing
Abstract
1. Introduction
2. Materials and Methods
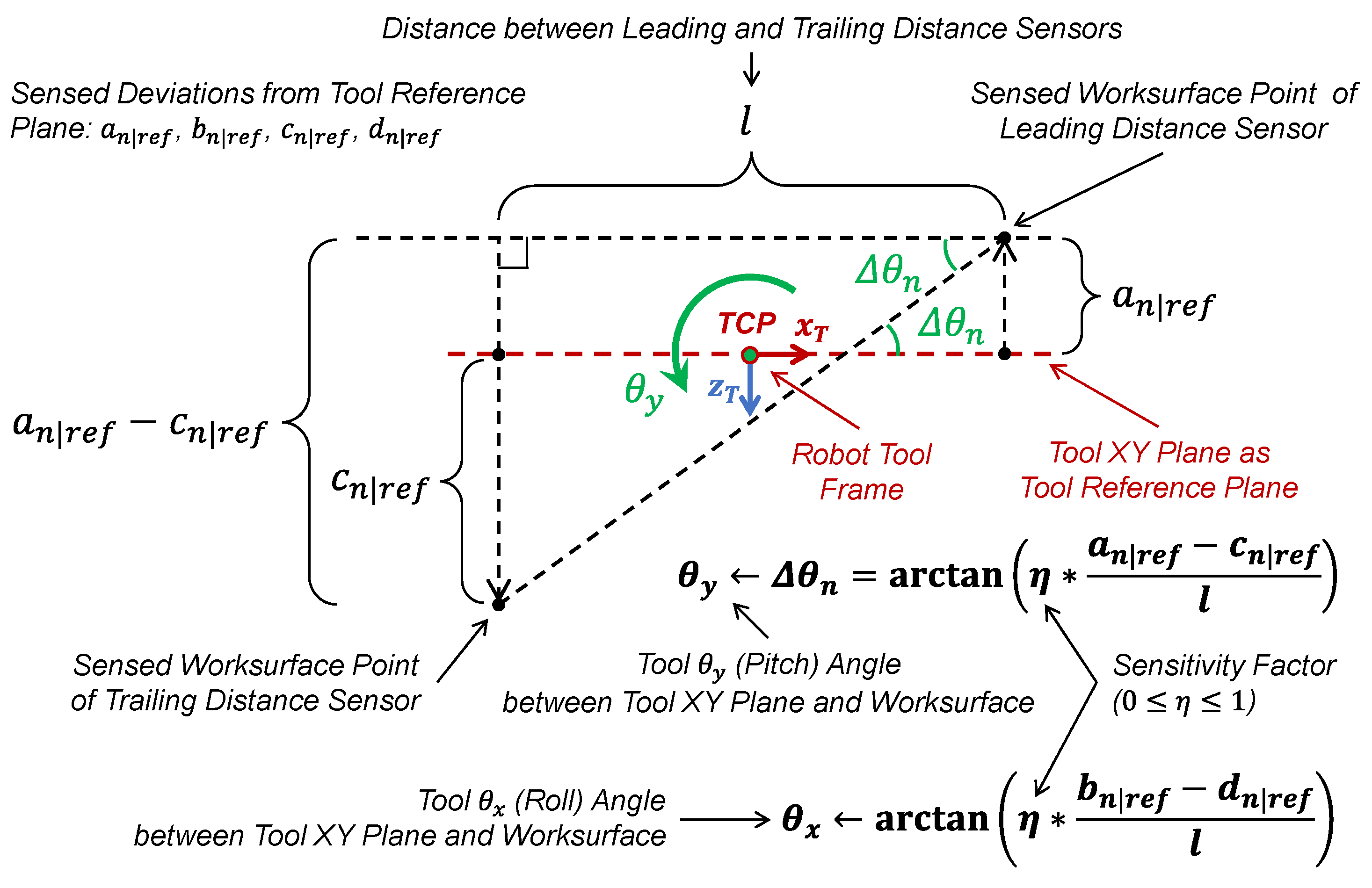
2.1. Problem Formulation
2.2. Realtime Error Tracking with Linear Quadratic Regulation
2.3. Experimental Settings
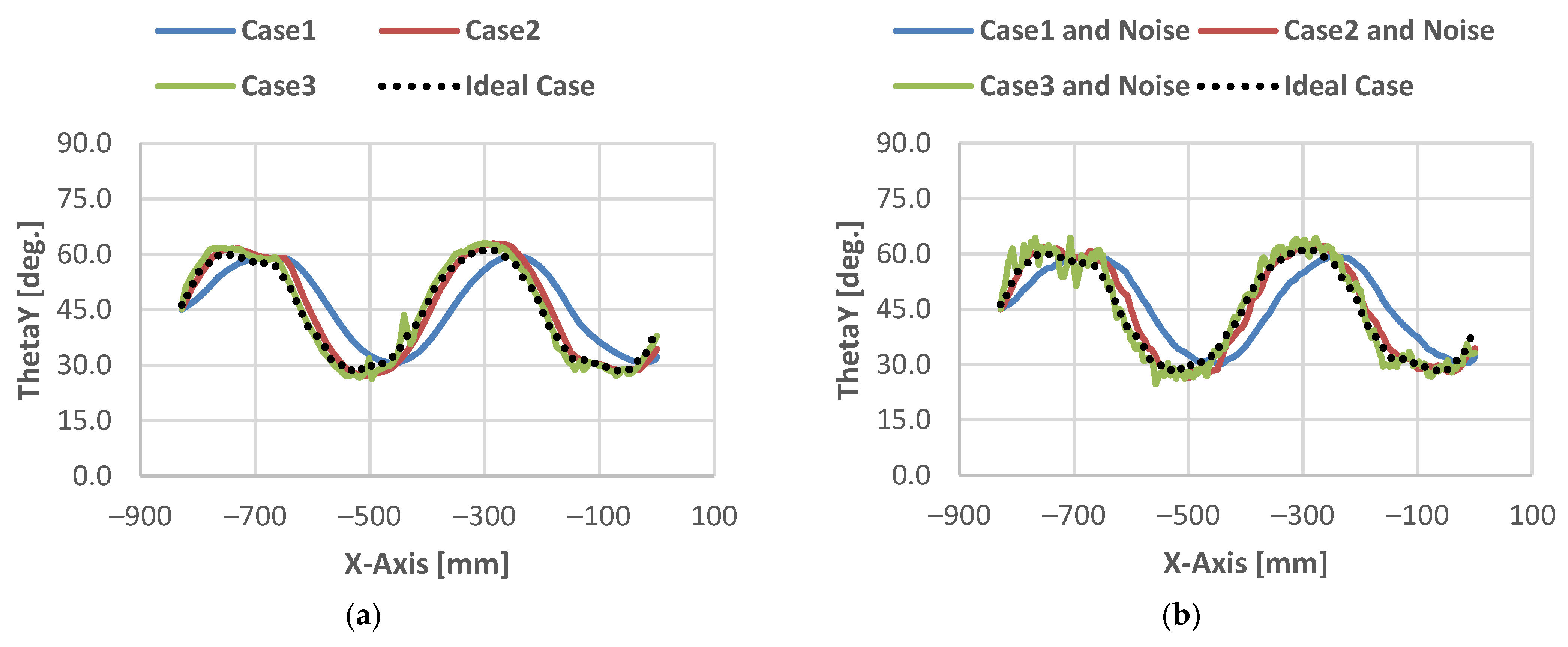
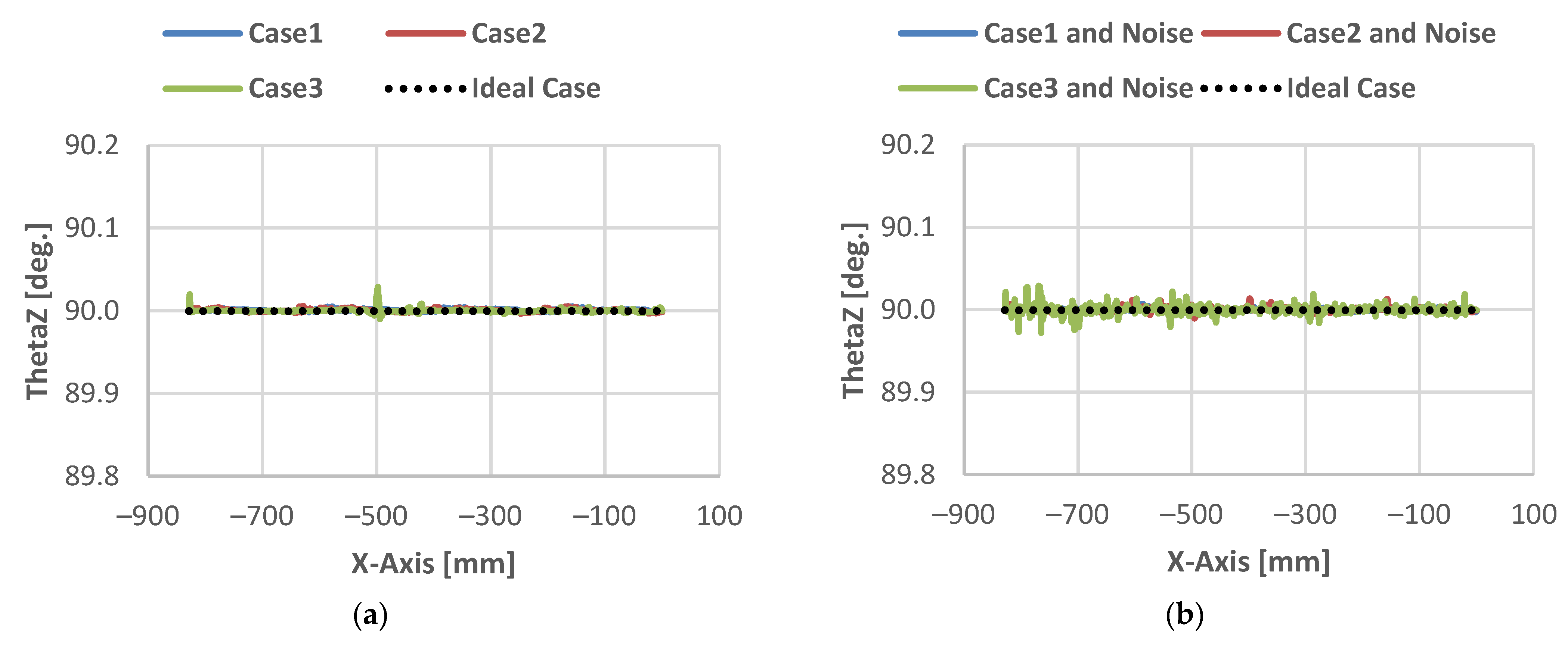
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| TCP | Tool Center Point |
| LQR | Linear Quadratic Regulation |
| RMS | Root Mean Square |
| ThetaX | Angle |
| ThetaY | Angle |
| ThetaZ | Angle |
| MPC | Model Predictive Control |
References
- Landscheidt, S.; Kans, M.; Winroth, M.; Wester, H. The future of industrial robot business: Product or performance based? Procedia Manuf. 2018, 25, 495–502. [Google Scholar] [CrossRef]
- Sanneman, L.; Fourie, C.; Shah, J.A. The State of Industrial Robotics: Emerging Technologies, Challenges, and Key Research Directions. Found. Trends® Robot. 2021, 8, 225–306. [Google Scholar] [CrossRef]
- Bartoš, M.; Bulej, V.; Bohušík, M.; Stanček, J.; Ivanov, V.; Macek, P. An overview of robot applications in automotive industry. Transp. Res. Procedia 2021, 55, 837–844. [Google Scholar] [CrossRef]
- ISO 8373:2012; Robots and Robotic Devices—Vocabulary. International Organization for Standardization: Geneva, Switzerland, 2012.
- ISO/TS 15066:2016; Robots and Robotic Devices—Collaborative Robots. International Organization for Standardization: Geneva, Switzerland, 2016.
- Ajoudani, A.; Tsagarakis, N.G.; Bicchi, A. Choosing Poses for Force and Stiffness Control. IEEE Trans. Robot. 2017, 33, 1483–1490. [Google Scholar] [CrossRef]
- Dachang, Z.; Baolin, D.; Puchen, Z.; Shouyan, C. Constant Force PID Control for Robotic Manipulator Based on Fuzzy Neural Network Algorithm. Complexity 2020, 2020, 3491845. [Google Scholar] [CrossRef]
- Shen, H.; Xie, W.F.; Tang, J.; Zhou, T. Adaptive Manipulability-Based Path Planning Strategy for Industrial Robot Manipulators. IEEE/ASME Trans. Mechatron. 2023, 28, 1742–1753. [Google Scholar] [CrossRef]
- Wang, G.; Li, W.; Jiang, C.; Zhu, D.; Li, Z.; Xu, W.; Zhao, H.; Ding, H. Trajectory Planning and Optimization for Robotic Machining Based On Measured Point Cloud. IEEE Trans. Robot. 2022, 38, 1621–1637. [Google Scholar] [CrossRef]
- Xie, H.; Wang, Y.; Zhang, H.; Tang, Y. Iterative Fine Point-Set Matching of a Free-Form Surface Based on the Point-to-Sphere Distance. IEEE/ASME Trans. Mechatron. 2022, 27, 5668–5678. [Google Scholar] [CrossRef]
- Yao, H.; Laha, R.; Figueredo, L.F.C.; Haddadin, S. Enhanced Dexterity Maps (EDM): A New Map for Manipulator Capability Analysis. IEEE Robot. Autom. Lett. 2024, 9, 1628–1635. [Google Scholar] [CrossRef]
- Angerer, A.; Hoffmann, A.; Larsen, L.; Vistein, M.; Kim, J.; Kupke, M.; Reif, W. Planning and Execution of Collision-free Multi-robot Trajectories in Industrial Applications. In Proceedings of the ISR 2016: 47st International Symposium on Robotics, Munich, Germany, 21–22 June 2016; pp. 1–7. [Google Scholar]
- Ayyad, A.; Halwani, M.; Swart, D.; Muthusamy, R.; Almaskari, F.; Zweiri, Y. Neuromorphic vision based control for the precise positioning of robotic drilling systems. Robot. Comput.-Integr. Manuf. 2023, 79, 102419. [Google Scholar] [CrossRef]
- Chen, C.; Peng, F.; Yan, R.; Li, Y.; Wei, D.; Fan, Z.; Tang, X.; Zhu, Z. Stiffness performance index based posture and feed orientation optimization in robotic milling process. Robot. Comput.-Integr. Manuf. 2019, 55, 29–40. [Google Scholar] [CrossRef]
- Erdős, G.; Kovács, A.; Váncza, J. Optimized joint motion planning for redundant industrial robots. CIRP Ann. 2016, 65, 451–454. [Google Scholar] [CrossRef]
- Heping, C.; Fuhlbrigge, T.; Xiongzi, L. Automated industrial robot path planning for spray painting process: A review. In Proceedings of the 2008 IEEE International Conference on Automation Science and Engineering, Washington, DC, USA, 23–26 August 2008; pp. 522–527. [Google Scholar]
- Larsen, L.; Kim, J.; Kupke, M.; Schuster, A. Automatic Path Planning of Industrial Robots Comparing Sampling-based and Computational Intelligence Methods. Procedia Manuf. 2017, 11, 241–248. [Google Scholar] [CrossRef]
- Lin, Y.; Zhao, H.; Ding, H. Posture optimization methodology of 6R industrial robots for machining using performance evaluation indexes. Robot. Comput.-Integr. Manuf. 2017, 48, 59–72. [Google Scholar] [CrossRef]
- Lu, Y.-A.; Tang, K.; Wang, C.-Y. Collision-free and smooth joint motion planning for six-axis industrial robots by redundancy optimization. Robot. Comput.-Integr. Manuf. 2021, 68, 102091. [Google Scholar] [CrossRef]
- Veeraraghavan, V.K. Auto-Normalization of Robot End-Effector. Master’s Thesis, Industrial Systems and Manufacturing Engineering, Wichita State University, Wichita, KS, USA, 2021. [Google Scholar]
- Reinhold, J.; Heilemann, L.L.; Lippross, S.; Meurer, T. Optimal path, orientation and trajectory planning along arbitrarily shaped surfaces for image-based robot-automated medical procedures. Control Eng. Pract. 2023, 139, 105656. [Google Scholar] [CrossRef]
- Zanchettin, A.M.; Rocco, P. Motion planning for robotic manipulators using robust constrained control. Control Eng. Pract. 2017, 59, 127–136. [Google Scholar] [CrossRef]
- Boldsaikhan, E.; Milhon, M.; Fukada, S.; Fujimoto, M.; Kamimuki, K. Metrology of Sheet Metal Distortion and Effects of Spot-Welding Sequences on Sheet Metal Distortion. J. Manuf. Mater. Process. 2023, 7, 109. [Google Scholar] [CrossRef]
- Boldsaikhan, E. Measuring and Estimating Rotary Joint Axes of an Articulated Robot. IEEE Trans. Instrum. Meas. 2020, 69, 8279–8287. [Google Scholar] [CrossRef]
- Ambaye, G.; Boldsaikhan, E.; Krishnan, K. Robot arm damage detection using vibration data and deep learning. Neural Comput. Appl. 2024, 36, 1727–1739. [Google Scholar] [CrossRef]
- Ambaye, G.; Boldsaikhan, E.; Krishnan, K. Soft Robot Design, Manufacturing, and Operation Challenges: A Review. J. Manuf. Mater. Process. 2024, 8, 79. [Google Scholar] [CrossRef]
- Moll, M.; Kavraki, L.E. Path planning for deformable linear objects. IEEE Trans. Robot. 2006, 22, 625–636. [Google Scholar] [CrossRef]
- Papageorgiou, D.; Sigurðardóttir, G.Þ.; Falotico, E.; Tolu, S. Sliding-mode control of a soft robot based on data-driven sparse identification. Control Eng. Pract. 2024, 144, 105836. [Google Scholar] [CrossRef]
- Ambaye, G.; Boldsaikhan, E.; Krishnan, K. Soft Robot Workspace Estimation via Finite Element Analysis and Machine Learning. Actuators 2025, 14, 110. [Google Scholar] [CrossRef]
- Desouza, G.N.; Kak, A.C. Vision for mobile robot navigation: A survey. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 237–267. [Google Scholar] [CrossRef]
- Răileanu, S.; Borangiu, T.; Anton, F.; Anton, S. Open source machine vision platform for manufacturing and robotics. IFAC-Pap. 2021, 54, 522–527. [Google Scholar] [CrossRef]
- Zhu, K.; Zhang, T. Deep reinforcement learning based mobile robot navigation: A review. Tsinghua Sci. Technol. 2021, 26, 674–691. [Google Scholar] [CrossRef]
- Ab Rashid, M.Z.; Mohd Yakub, M.F.; Zaki bin Shaikh Salim, S.A.; Mamat, N.; Syed Mohd Putra, S.M.; Roslan, S.A. Modeling of the in-pipe inspection robot: A comprehensive review. Ocean Eng. 2020, 203, 107206. [Google Scholar] [CrossRef]
- Hossain, S.; Lee, D.-j. Deep Learning-Based Real-Time Multiple-Object Detection and Tracking from Aerial Imagery via a Flying Robot with GPU-Based Embedded Devices. Sensors 2019, 19, 3371. [Google Scholar] [CrossRef]
- Mišeikis, J.; Brijačak, I.; Yahyanejad, S.; Glette, K.; Elle, O.J.; Torresen, J. Two-Stage Transfer Learning for Heterogeneous Robot Detection and 3D Joint Position Estimation in a 2D Camera Image Using CNN. In Proceedings of the 2019 International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019; pp. 8883–8889. [Google Scholar]
- Palleschi, A.; Hamad, M.; Abdolshah, S.; Garabini, M.; Haddadin, S.; Pallottino, L. Fast and Safe Trajectory Planning: Solving the Cobot Performance/Safety Trade-Off in Human-Robot Shared Environments. IEEE Robot. Autom. Lett. 2021, 6, 5445–5452. [Google Scholar] [CrossRef]
- Liu, Q.; Liu, Z.; Xu, W.; Tang, Q.; Zhou, Z.; Pham, D.T. Human-robot collaboration in disassembly for sustainable manufacturing. Int. J. Prod. Res. 2019, 57, 4027–4044. [Google Scholar] [CrossRef]
- Zacharia, P.; Aspragathos, N.; Mariolis, I.; Dermatas, E. A robotic system based on fuzzy visual servoing for handling flexible sheets lying on a table. Ind. Robot: Int. J. 2009, 36, 489–496. [Google Scholar] [CrossRef]
- Zhu, J.; Navarro-Alarcon, D.; Passama, R.; Cherubini, A. Vision-based manipulation of deformable and rigid objects using subspace projections of 2D contours. Robot. Auton. Syst. 2021, 142, 103798. [Google Scholar] [CrossRef]
- Slater, P.A.; Downey, J.M.; Piasecki, M.T.; Schoenholz, B.L. Portable Laser Guided Robotic Metrology System. In Proceedings of the 2019 Antenna Measurement Techniques Association Symposium (AMTA), San Diego, CA, USA, 6–11 October 2019; pp. 1–6. [Google Scholar]
- Gul, F.; Rahiman, W.; Nazli Alhady, S.S. A comprehensive study for robot navigation techniques. Cogent Eng. 2019, 6, 1632046. [Google Scholar] [CrossRef]
- Liu, B.; Xiao, X.; Stone, P. A Lifelong Learning Approach to Mobile Robot Navigation. IEEE Robot. Autom. Lett. 2021, 6, 1090–1096. [Google Scholar] [CrossRef]
- Yang, Y.; Cai, Y.; Jung Yoon, Y.; Zhao, H.; Gupta, S.K. Sensor-Based Planning and Control for Conformal Deposition on a Deformable Surface Using an Articulated Industrial Robot. J. Manuf. Sci. Eng. 2023, 146, 011008. [Google Scholar] [CrossRef]
- Huang, S.; Bergström, N.; Yamakawa, Y.; Senoo, T.; Ishikawa, M. High-performance robotic contour tracking based on the dynamic compensation concept. In Proceedings of the 2016 IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden, 16–21 May 2016; pp. 3886–3893. [Google Scholar]
- Ravankar, A.; Ravankar, A.A.; Kobayashi, Y.; Hoshino, Y.; Peng, C.-C. Path Smoothing Techniques in Robot Navigation: State-of-the-Art, Current and Future Challenges. Sensors 2018, 18, 3170. [Google Scholar] [CrossRef]
- Yang, H.; Qi, J.; Miao, Y.; Sun, H.; Li, J. A New Robot Navigation Algorithm Based on a Double-Layer Ant Algorithm and Trajectory Optimization. IEEE Trans. Ind. Electron. 2019, 66, 8557–8566. [Google Scholar] [CrossRef]
- Ollero, A.; Heredia, G.; Franchi, A.; Antonelli, G.; Kondak, K.; Sanfeliu, A.; Viguria, A.; Dios, J.R.M.-D.; Pierri, F.; Cortes, J.; et al. The AEROARMS Project: Aerial Robots with Advanced Manipulation Capabilities for Inspection and Maintenance. IEEE Robot. Autom. Mag. 2018, 25, 12–23. [Google Scholar] [CrossRef]
- Eskandaripour, H.; Boldsaikhan, E. Last-Mile Drone Delivery: Past, Present, and Future. Drones 2023, 7, 77. [Google Scholar] [CrossRef]
- Yuan, J.; Szydlowski, M.; Wang, X. An optimal sparse sensing approach for scanning point selection and response reconstruction in full-field structural vibration testing. Mech. Syst. Signal Process. 2024, 212, 111298. [Google Scholar] [CrossRef]
- Al-Tamimi, A.; Lewis, F.L.; Abu-Khalaf, M. Discrete-Time Nonlinear HJB Solution Using Approximate Dynamic Programming: Convergence Proof. IEEE Trans. Syst. Man Cybern. Part B 2008, 38, 943–949. [Google Scholar] [CrossRef] [PubMed]
- Rawlings, J.B.; Muske, K.R. The stability of constrained receding horizon control. IEEE Trans. Autom. Control 1993, 38, 1512–1516. [Google Scholar] [CrossRef]
- Scokaert, P.O.M.; Rawlings, J.B. Constrained linear quadratic regulation. IEEE Trans. Autom. Control 1998, 43, 1163–1169. [Google Scholar] [CrossRef]
- ABB. ABB RobotStudio Software. Available online: https://new.abb.com/products/robotics/robotstudio (accessed on 10 May 2024).



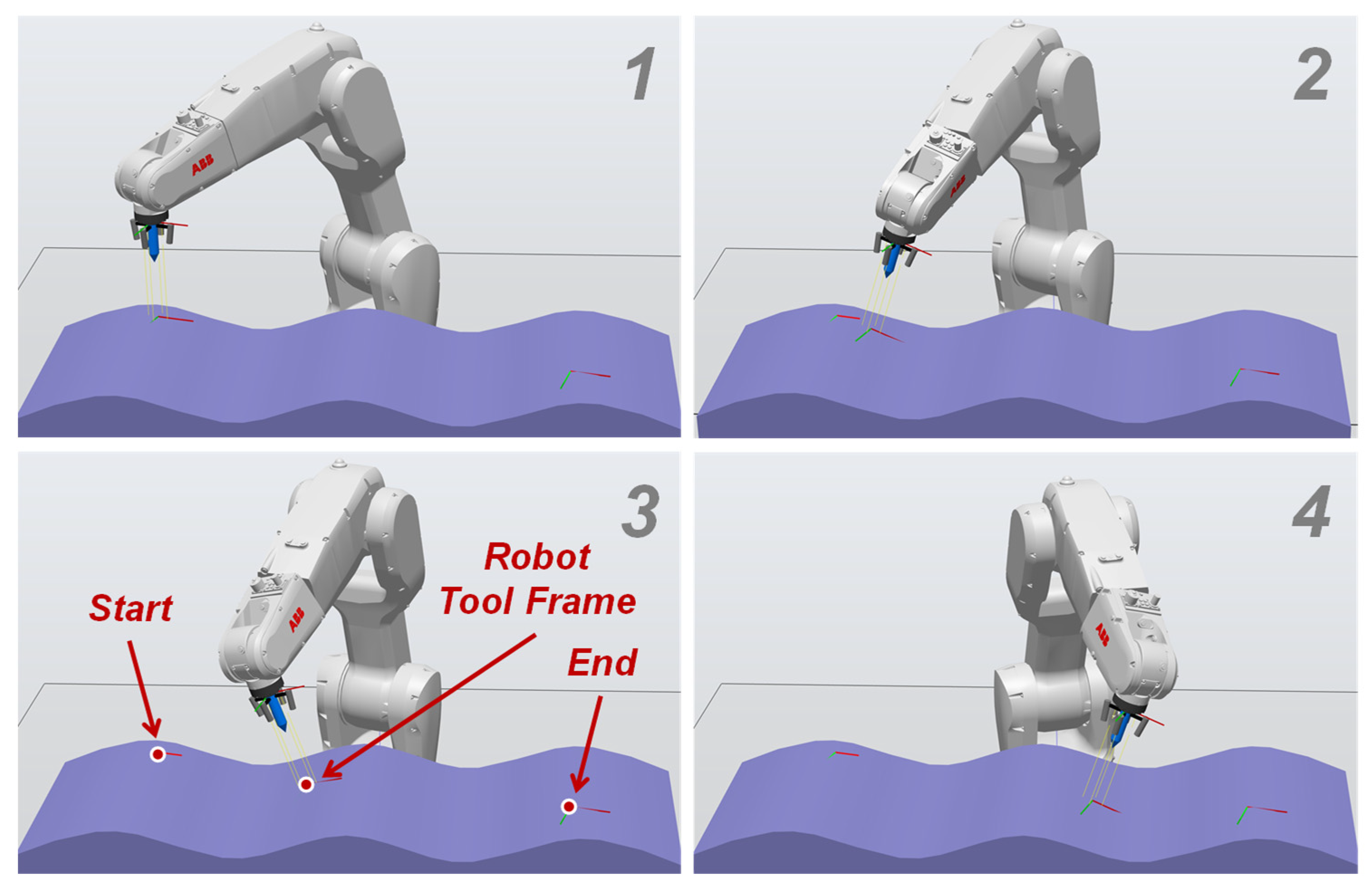

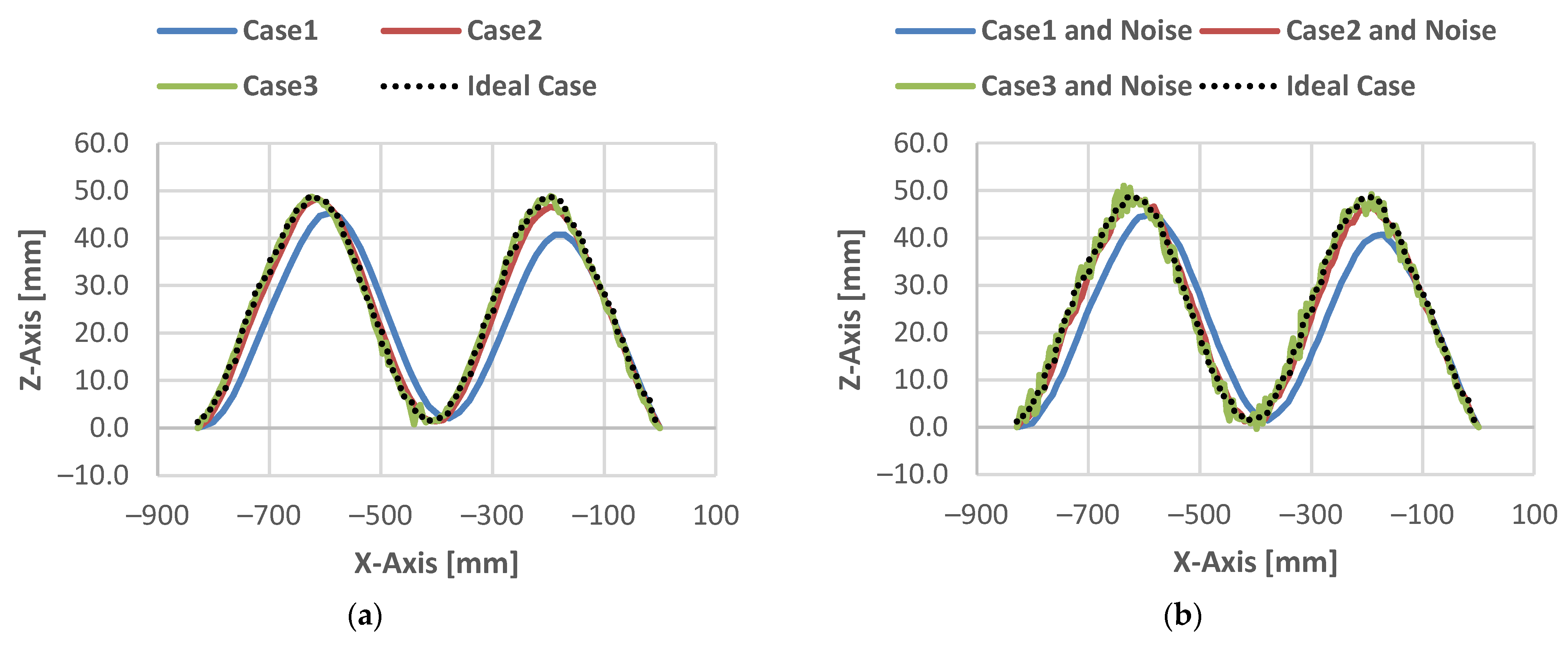

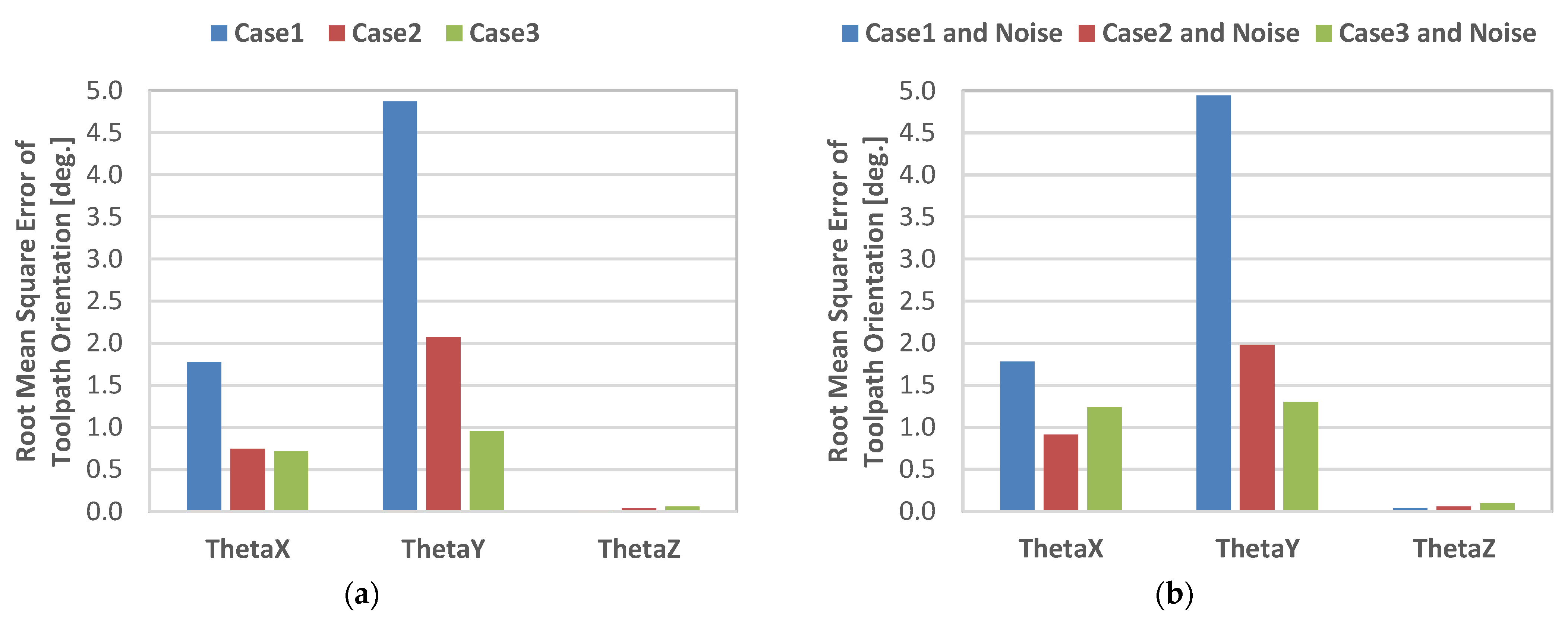
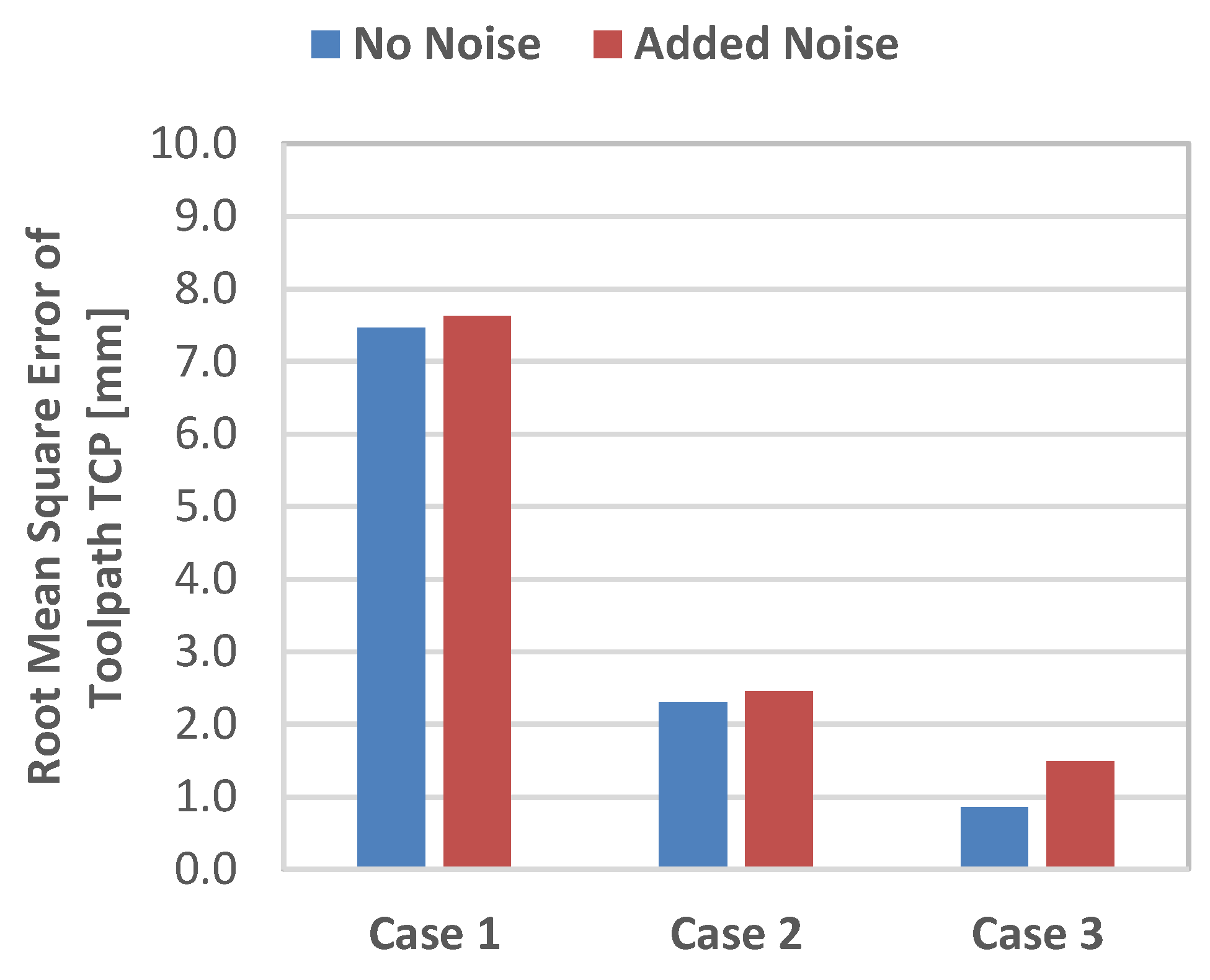

| Cases | ||
|---|---|---|
| Case 1: Reaching the known toolpath target is priority. | ||
| Case 2: Balancing the Case 1 and Case 3 goals is priority. | ||
| Case 3: Following sensed surface variations is priority. |
| Cases | ||
|---|---|---|
| Case 1: Reaching the known toolpath target is priority. | 0.27 | 0.92 |
| Case 2: Balancing the Case 1 and Case 3 goals is priority. | 0.62 | 0.62 |
| Case 3: Following sensed surface variations is priority. | 0.92 | 0.27 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Boldsaikhan, E.; Birney, C. Optimal Realtime Toolpath Planning for Industrial Robots with Sparse Sensing. Actuators 2025, 14, 279. https://doi.org/10.3390/act14060279
Boldsaikhan E, Birney C. Optimal Realtime Toolpath Planning for Industrial Robots with Sparse Sensing. Actuators. 2025; 14(6):279. https://doi.org/10.3390/act14060279
Chicago/Turabian StyleBoldsaikhan, Enkhsaikhan, and Cole Birney. 2025. "Optimal Realtime Toolpath Planning for Industrial Robots with Sparse Sensing" Actuators 14, no. 6: 279. https://doi.org/10.3390/act14060279
APA StyleBoldsaikhan, E., & Birney, C. (2025). Optimal Realtime Toolpath Planning for Industrial Robots with Sparse Sensing. Actuators, 14(6), 279. https://doi.org/10.3390/act14060279







