Drill-String Vibration Suppression Using Hybrid Magnetorheological Elastomer-Fluid Absorbers
Abstract
1. Introduction
2. Mathematical Modeling
2.1. Axial and Torsional Equations of Motion
2.2. Bit–Rock Interactions
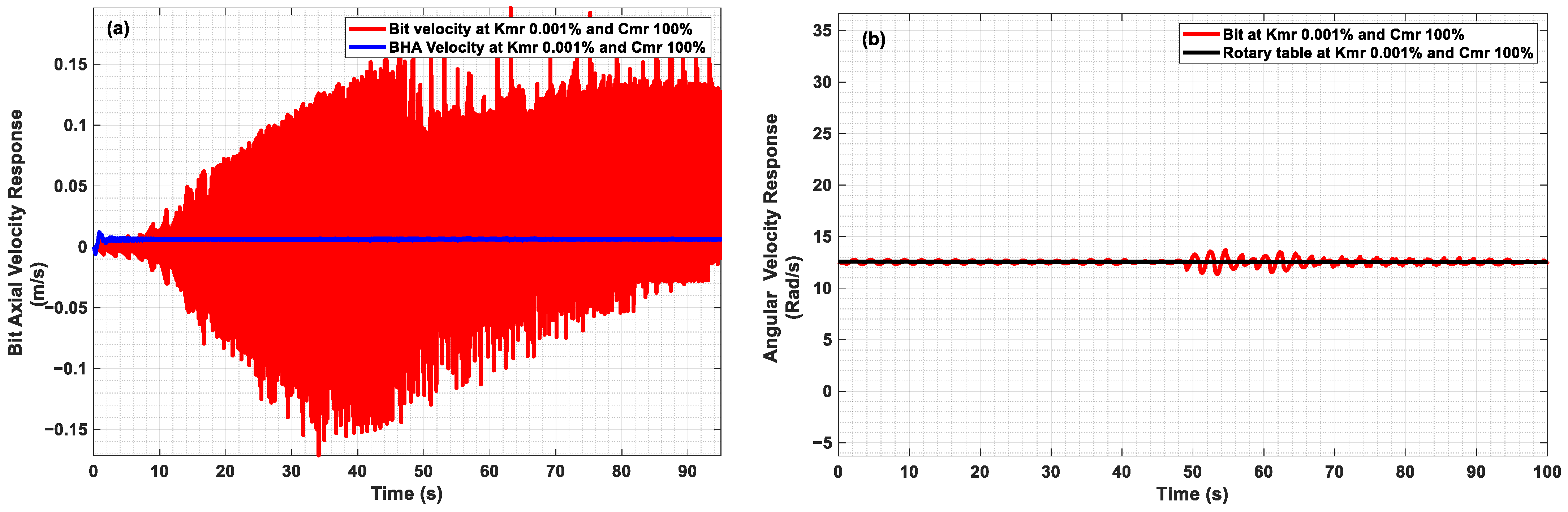
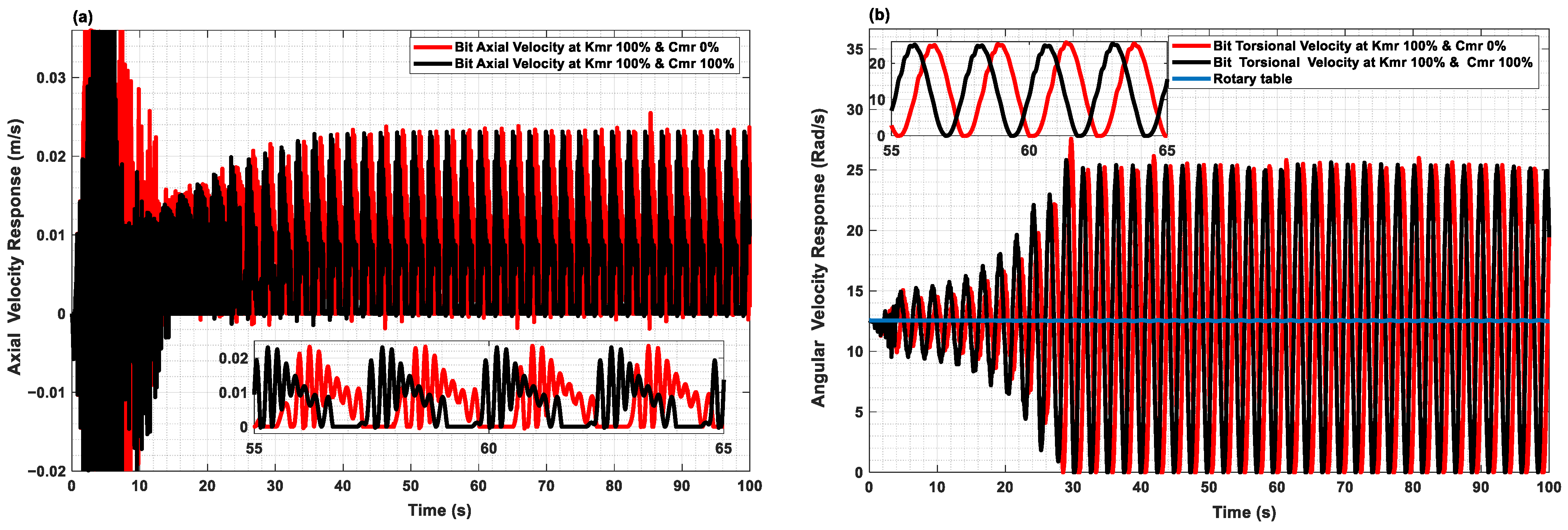
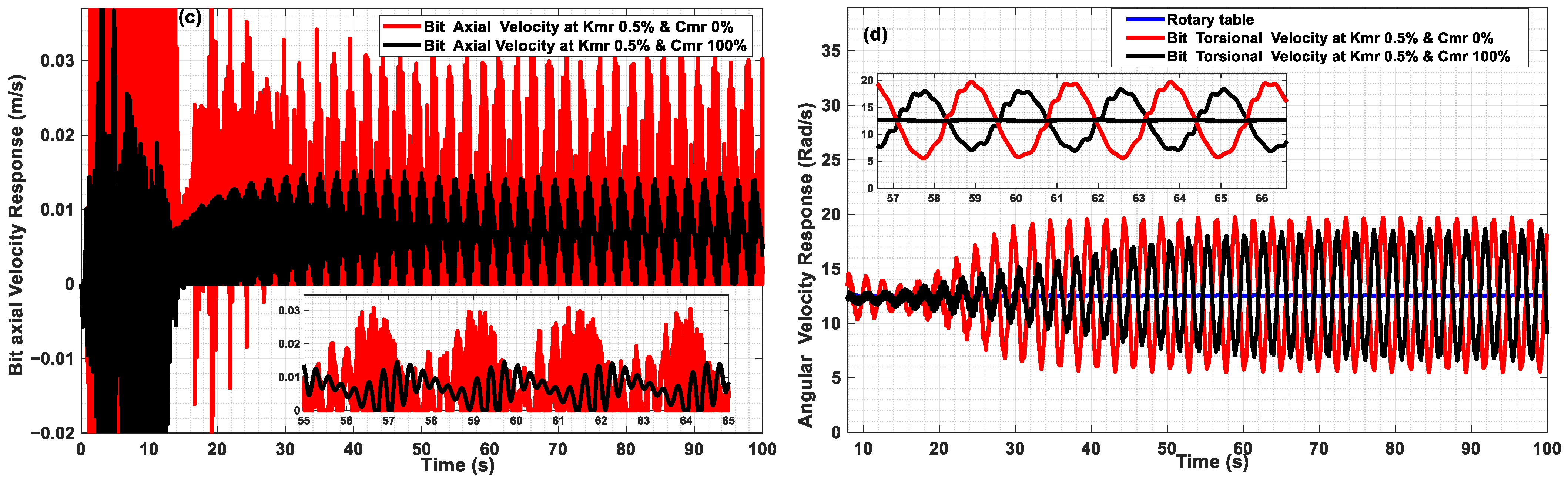
3. Results and Discussion
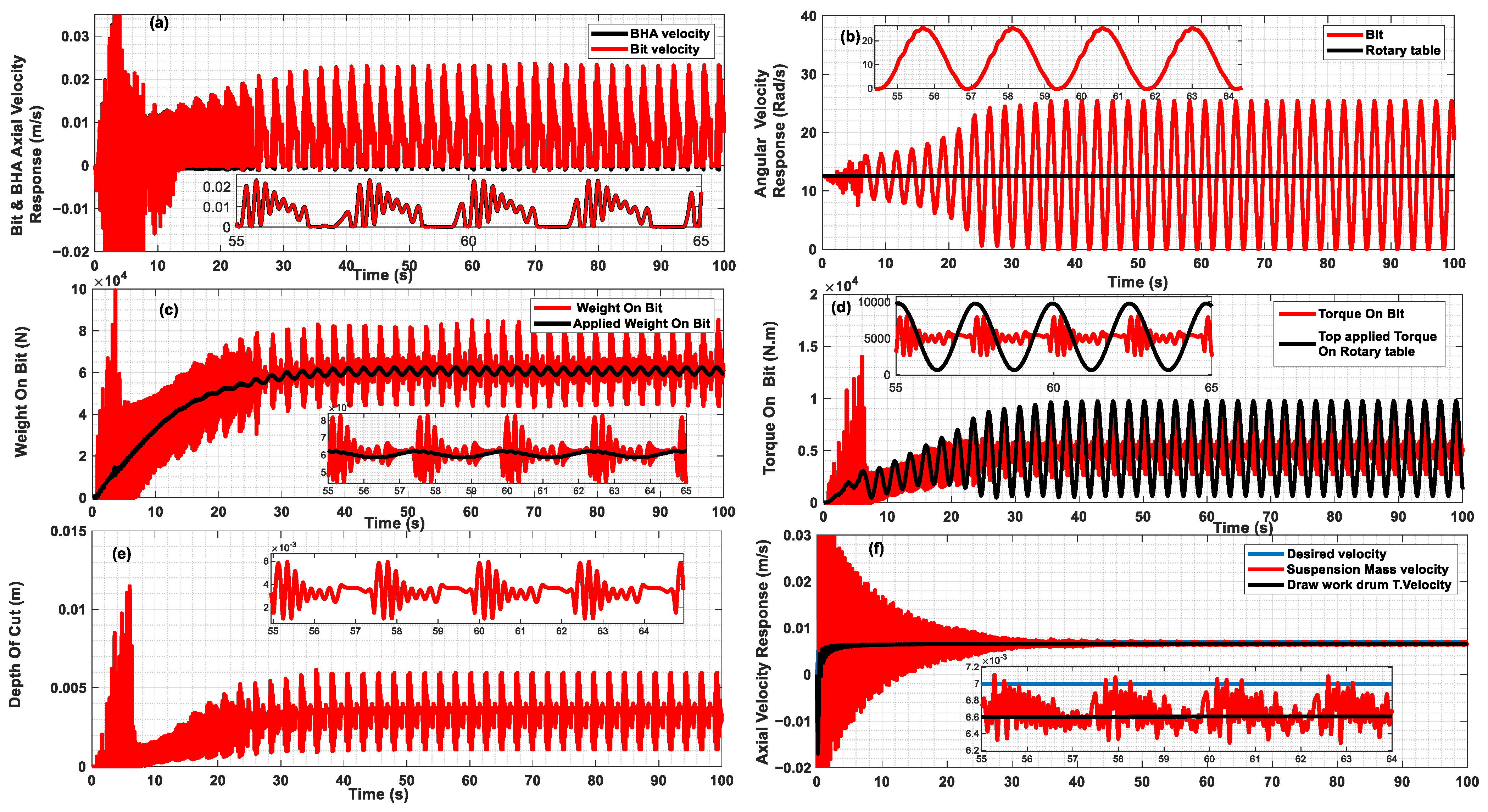
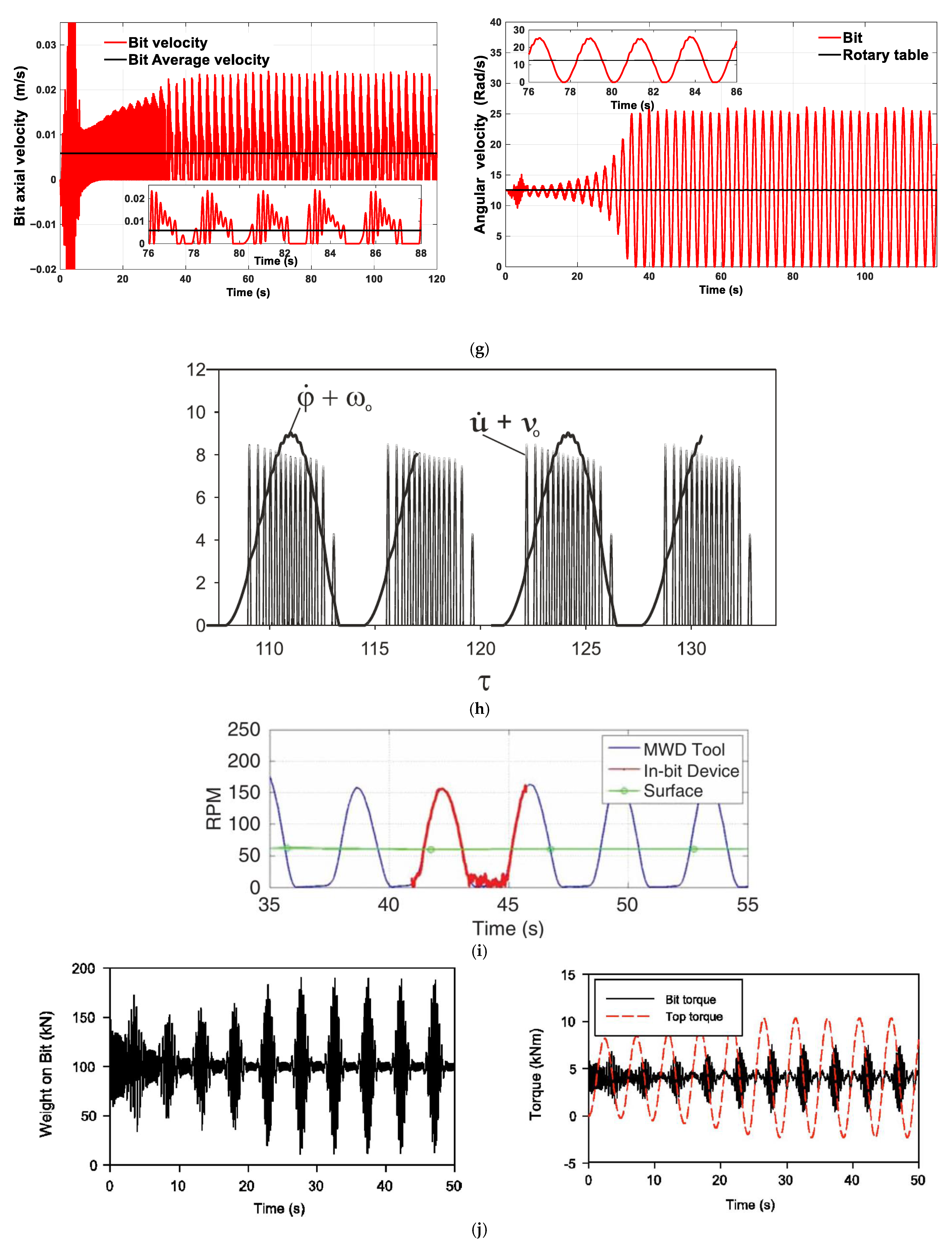
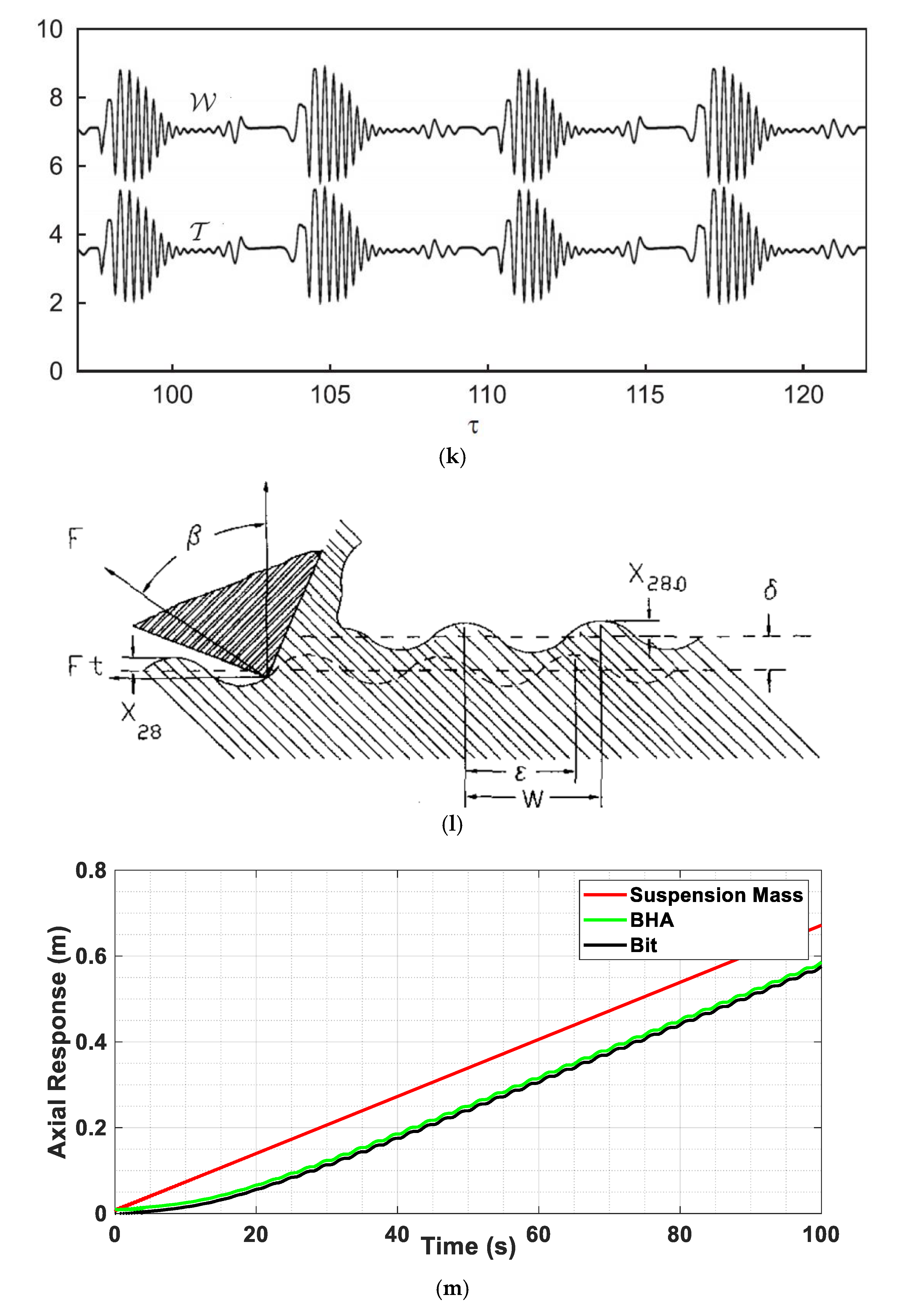
4. Axial Absorber Coefficients’ Optimal Values
5. Conclusions and Future Recommendations
- Developing a semi-active control method for the proposed absorber, enabling it to promptly adapt the axial MRE-F absorber’s coefficients over a wide range of values and operating conditions, including those involving nonlinear deformation behavior. This will enhance its applicability across various operational parameters and lithological variations, thereby extending the safe operation range.
- Improving the accuracy of the bit–rock interaction model. Phase III [30], which was not considered in this study based on the assumption of perfect cleaning of rock fragments from the bottom hole during cutting, should be included in future works to capture the whole rock-cutting process.
- Additionally, factors such as high-temperature effects in harsh environments, drill-pipe eccentricity, derrick flexibility, and lateral vibrations should be incorporated into future research.
- Enhancing the model: The current study employs a lumped-parameter model with limited degrees of freedom, focusing on axial and torsional dynamics. Future work should extend this model to incorporate higher-order vibration modes and lateral vibrations, which become significant in deviated wells and more complex drilling environments. This will allow for a more comprehensive representation of dynamic behavior along the entire drill string across a wider range of operating conditions.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Global Oil & Gas Exploration & Production—Market Size|IBISWorld. Available online: https://www.ibisworld.com/global/market-size/global-oil-gas-exploration-production/ (accessed on 23 May 2022).
- Li, Y.; Wang, J.; Shan, Y.; Wang, C.; Hu, Y. Measurement and Analysis of Downhole Drill String Vibration Signal. Appl. Sci. 2021, 11, 11484. [Google Scholar] [CrossRef]
- Ledgerwood, L.W.W.; Jain, J.R.; Hoffmann, O.J.; Spencer, R.W. Downhole Measurement and Monitoring Lead to an Enhanced Understanding of Drilling Vibrations and Polycrystalline Diamond Compact Bit Damage. SPE Drill. Complet. 2013, 28, 254–262. [Google Scholar] [CrossRef]
- Pavone, D.R.; Desplans, J.P. Application of High Sampling Rate Downhole Measurements for Analysis and Cure of Stick-Slip in Drilling. In Proceedings of the SPE Annual Technical Conference and Exhibition, New Orleans, LA, USA, 25–28 September 1994; pp. 335–345. [Google Scholar] [CrossRef]
- Wise, J.L.; Mansure, A.J.; Blankenship, D.A. Hard-Rock Field Performance of Drag Bits and a Downhole Diagnostics-While-Drilling (DWD) Tool. In Proceedings of the World Geothermal Congress, Antalya, Turkey, 24–29 April 2005; pp. 24–29. [Google Scholar]
- Tang, L.; Zhu, X.; Shi, C.; Tang, J.; Xu, D. Study of the Influences of Rotary Table Speed on Stick-Slip Vibration of the Drilling System. Petroleum 2015, 1, 382–387. [Google Scholar] [CrossRef]
- Jogi, P.N.; Macpherson, J.D.; Neubert, M. Field Verification of Model-Derived Natural Frequencies of a Drill String. J. Energy Resour. Technol. 2002, 124, 154–162. [Google Scholar] [CrossRef]
- Brett, J.F. The Genesis of Torsional Drillstring Vibrations. SPE Drill. Eng. 1992, 7, 168–174. [Google Scholar] [CrossRef]
- Challamel, N. Rock destruction effect on the stability of a drilling structure. J. Sound Vib. 2000, 233, 235–254. [Google Scholar] [CrossRef]
- Germay, C. Modeling and Analysis of Self-Excited Drill Bit Vibrations. Ph.D. Thesis, The University of Liège, Liège, Belgium, 2009. [Google Scholar]
- Baryshnikov, A.; Calderoni, A.; Ligrone, A.; Ferrara, P. A New Approach to the Analysis of Drillstring Fatigue Behavior. SPE Drill. Complet. 1997, 12, 77–84. [Google Scholar] [CrossRef]
- Zhu, Q.; Zou, Z.; Huang, B.; Ma, L.; Xia, J. Downhole Vibration Causing a Drill Collar Failure and Solutions. Nat. Gas Ind. B 2017, 4, 73–80. [Google Scholar] [CrossRef]
- Dong, G.; Chen, P. A Review of the Evaluation, Control, and Application Technologies for Drill String Vibrations and Shocks in Oil and Gas Well 2016. Shock Vib. 2016, 2016, 7418635. [Google Scholar] [CrossRef]
- Real, F.F.; Lobo, D.M.; Ritto, T.G.; Pinto, F.A.N.C. Experimental Analysis of Stick-Slip in Drilling Dynamics in a Laboratory Test-Rig. J. Pet. Sci. Eng. 2018, 170, 755–762. [Google Scholar] [CrossRef]
- Roohi, A.; Ashena, R.; Thonhauser, G.; Finkbeiner, T.; Gerbaud, L.; Rasouli, V. An Experimental Investigation of Drilling Performance Improvement Using Reaming While Drilling. J. Energy Resour. Technol. 2022, 144, 013202. [Google Scholar] [CrossRef]
- Sassi, S.; Renno, J.; Zhou, H.; Baz, A. Experimental Investigation of the Vibration Control of Nonrotating Periodic Drill Strings. J. Vib. Acoust. 2021, 143, 061004. [Google Scholar] [CrossRef]
- Tian, J.; Deng, Z.; He, H. Dynamic Research and Experimental Analysis of a Longitudinal–Torsional Coupled Impactor. Proc. Inst. Mech. Eng. C J. Mech. Eng. Sci. 2022, 236, 5223–5237. [Google Scholar] [CrossRef]
- Khulief, Y.A.; Al-Naser, H. Finite Element Dynamic Analysis of Drillstrings. Finite Elem. Anal. Des. 2005, 41, 1270–1288. [Google Scholar] [CrossRef]
- Spanos, P.D.; Sengupta, A.K.; Cunningham, R.A.; Paslay, P.R. Modeling of Roller Cone Bit Lift-Off Dynamics in Rotary Drilling. J. Energy Resour. Technol. 1995, 117, 197–207. [Google Scholar] [CrossRef]
- Tran, Q.-T.; Nguyen, K.-L.; Manin, L.; Andrianoely, M.-A.; Dufour, R.; Mahjoub, M.; Menand, S. Nonlinear Dynamics of Directional Drilling with Fluid and Borehole Interactions. J. Sound Vib. 2019, 462, 114924. [Google Scholar] [CrossRef]
- Kamel, J.M.; Yigit, A.S. Modeling and Analysis of Stick-Slip and Bit Bounce in Oil Well Drillstrings Equipped with Drag Bits. J. Sound Vib. 2014, 333, 6885–6899. [Google Scholar] [CrossRef]
- Christoforou, A.P.; Yigit, A.S. Fully Coupled Vibrations of Actively Controlled Drillstrings. J. Sound Vib. 2003, 267, 1029–1045. [Google Scholar] [CrossRef]
- de Moraes, L.P.P.; Savi, M.A. Drill-String Vibration Analysis Considering an Axial-Torsional-Lateral Nonsmooth Model. J. Sound Vib. 2019, 438, 220–237. [Google Scholar] [CrossRef]
- Aarsnes, U.J.F.; van de Wouw, N. Axial and Torsional Self-Excited Vibrations of a Distributed Drill-String. J. Sound Vib. 2019, 444, 127–151. [Google Scholar] [CrossRef]
- Christoforou, A.P.; Yigit, A.S. Dynamic modelling of rotating drillstrings with borehole interactions. J. Sound Vib. 1997, 206, 243–260. [Google Scholar] [CrossRef]
- Tucker, W.R.; Wang, C. An Integrated Model for Drill-String Dynamics. J. Sound Vib. 1999, 224, 123–165. [Google Scholar] [CrossRef]
- Li, X.; Yu, T.; Zhang, L.; Zeng, H.; Duan, C. Theoretical and Numerical Analysis of Coupled Axial-Torsional Nonlinear Vibration of Drill Strings. Shock Vib. 2021, 2021, 8046635. [Google Scholar] [CrossRef]
- Liu, X.; Vlajic, N.; Long, X.; Meng, G.; Balachandran, B. Coupled Axial-Torsional Dynamics in Rotary Drilling with State-Dependent Delay: Stability and Control. Nonlinear Dyn. 2014, 78, 1891–1906. [Google Scholar] [CrossRef]
- Yigit, A.S.; Christoforou, A.P. Stick-Slip and Bit-Bounce Interaction in Oil-Well Drillstrings. J. Energy Resour. Technol. 2006, 128, 268–274. [Google Scholar] [CrossRef]
- Detournay, E.; Defourny, P. A Phenomenological Model for the Drilling Action of Drag Bits. Int. J. Rock. Mech. Min. Sci. Geomech. Abstr. 1992, 29, 13–23. [Google Scholar] [CrossRef]
- Besselink, B.; van de Wouw, N.; Nijmeijer, H. A Semi-Analytical Study of Stick-Slip Oscillations in Drilling Systems. J. Comput. Nonlinear Dyn. 2011, 6, 021006. [Google Scholar] [CrossRef]
- Vaziri, V.; Kapitaniak, M.; Wiercigroch, M. Suppression of Drill-String Stick–Slip Vibration by Sliding Mode Control: Numerical and Experimental Studies. Eur. J. Appl. Math. 2018, 29, 805–825. [Google Scholar] [CrossRef]
- Petrovskii, A.; Bashmur, K.A.; Nashivanov, I.S. Adaptive Control of Drill String Vibrations. Chem. Pet. Eng. 2019, 54, 711–716. [Google Scholar] [CrossRef]
- Cheng, J.; Wu, M.; Wu, F.; Lu, C.; Chen, X.; Cao, W. Modeling and Control of Drill-String System with Stick-Slip Vibrations Using LPV Technique. IEEE Trans. Control Syst. Technol. 2021, 29, 718–730. [Google Scholar] [CrossRef]
- Lin, W.; Páez Chávez, J.; Liu, Y.; Yang, Y.; Kuang, Y. Stick-Slip Suppression and Speed Tuning for a Drill-String System via Proportional-Derivative Control. Appl. Math. Model. 2020, 82, 487–502. [Google Scholar] [CrossRef]
- Ali, A.; Salem, A.M.H.; Muthalif, A.G.A.; Ramli, R.B.; Julai, S. Development of a Performance-Enhanced Hybrid Magnetorheological Elastomer-Fluid for Semi-Active Vibration Isolation: Static and Dynamic Experimental Characterization. Materials 2022, 15, 3238. [Google Scholar] [CrossRef] [PubMed]
- Salem, A.M.H.; Ali, A.; Ramli, R.B.; Muthalif, A.G.A.; Julai, S. Effect of Carbonyl Iron Particle Types on the Structure and Performance of Magnetorheological Elastomers: A Frequency and Strain Dependent Study. Polymers 2022, 14, 4193. [Google Scholar] [CrossRef]
- Ashtiani, M.; Hashemabadi, S.H.; Ghaffari, A. A Review on the Magnetorheological Fluid Preparation and Stabilization. J. Magn. Magn. Mater. 2015, 374, 716–730. [Google Scholar] [CrossRef]
- Alias, N.F.; Muthalif, A.G.A.; Arpan, K.A.M.; Diyana Nordin, N.H. Experimental Investigation of Static Properties of Magnetorheological Elastomer. Iran. J. Sci. Technol. Trans. Mech. Eng. 2018, 42, 185–197. [Google Scholar] [CrossRef]
- Kubík, M.; Válek, J.; Žáček, J.; Jeniš, F.; Borin, D.; Strecker, Z.; Mazůrek, I. Transient Response of Magnetorheological Fluid on Rapid Change of Magnetic Field in Shear Mode. Sci. Rep. 2022, 12, 10612. [Google Scholar] [CrossRef]
- Bastola, A.K.; Paudel, M.; Li, L. Development of Hybrid Magnetorheological Elastomers by 3D Printing. Polymer 2018, 149, 213–228. [Google Scholar] [CrossRef]
- Qi, S.; Guo, H.; Fu, J.; Xie, Y.; Zhu, M.; Yu, M. 3D Printed Shape-Programmable Magneto-Active Soft Matter for Biomimetic Applications. Compos. Sci. Technol. 2020, 188, 107973. [Google Scholar] [CrossRef]
- Ananzeh, H.M.; Ramli, R.; Julai, S.; Muthalif, A.G.A. Mechanical Properties Comparison of Isotropic vs. Anisotropic Hybrid Magnetorheological Elastomer-Fluid. Polymers 2024, 16, 1215. [Google Scholar] [CrossRef]
- Skalski, P.; Kalita, K. Role of Magnetorheological Fluids and Elastomers in Today’s World. Acta Mech. Autom. 2017, 11, 267–274. [Google Scholar] [CrossRef]
- Xing, Z.; Yu, M.; Sun, S.; Fu, J.; Li, W. A Hybrid Magnetorheological Elastomer-Fluid (MRE-F) Isolation Mount: Development and Experimental Validation. Fac. Eng. Inf. Sci. Pap. Part. A 2016, 25, 015026. [Google Scholar] [CrossRef]
- Sun, S.S.; Yang, J.; Li, W.H.; Du, H.; Alici, G.; Yan, T.H.; Nakano, M. Development of an Isolator Working with Magnetorheological Elastomers and Fluids. Mech. Syst. Signal Process 2017, 83, 371–384. [Google Scholar] [CrossRef]
- Meirovitch, L. Fundamentals of Vibrations; McGraw-Hill: New York, NY, USA, 2001; ISBN 0070413452. [Google Scholar]
- Yigit, A.S.; Christoforou, A.P. Coupled torsional and bending vibrations of drillstrings subject to impact with friction. J. Sound Vib. 1998, 215, 167–181. [Google Scholar] [CrossRef]
- Yigit, A.S.; Christoforou, A.P. Coupled axial and transverse vibrations of oilwell drillstrings. J. Sound Vib. 1996, 195, 617–627. [Google Scholar] [CrossRef]
- Aarrestad, T.V.; Kyllingstad, A. Rig Suspension Measurements and Theoretical Models and the Effect on Drillstring Vibrations. SPE Drill. Complet. 1993, 8, 201–206. [Google Scholar] [CrossRef]
- Kallio, M. The Elastic and Damping Properties of Magnetorheological Elastomers. Ph.D. Thesis, Tampere University of Technology (TUT), Tampere, Finland, 2005. [Google Scholar]
- Elliott, S.J.; Tehrani, M.G.; Langley, R.S. Nonlinear Damping and Quasi-Linear Modelling. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2015, 373, 20140402. [Google Scholar] [CrossRef]
- Jiffri, S.; Paoletti, P.; Cooper, J.E.; Mottershead, J.E. Feedback Linearisation for Nonlinear Vibration Problems. Shock. Vib. 2014, 2014, 106531. [Google Scholar] [CrossRef]
- Detournay, E.; Richard, T.; Shepherd, M. Drilling Response of Drag Bits: Theory and Experiment. Int. J. Rock. Mech. Min. Sci. 2008, 45, 1347–1360. [Google Scholar] [CrossRef]
- Richard, T.; Germay, C.; Detournay, E. Self-Excited Stick–Slip Oscillations of Drill Bits. Comptes Rendus Mécanique 2004, 332, 619–626. [Google Scholar] [CrossRef]
- Richard, T. Determination of Rock Strength from Cutting Tests. Ph.D. Thesis, University of Minnesota, Minneapolis, MN, USA, 1999. [Google Scholar]
- Richard, T.; Germay, C.; Detournay, E. A Simplified Model to Explore the Root Cause of Stick–Slip Vibrations in Drilling Systems with Drag Bits. J. Sound Vib. 2007, 305, 432–456. [Google Scholar] [CrossRef]
- Germay, C.; Van de Wouw, N.; Nijmeijer, H.; Sepulchre, R. Nonlinear Drillstring Dynamics Analysis. SIAM J. Appl. Dyn. Syst. 2009, 8, 527–553. [Google Scholar] [CrossRef]
- Macdonald, K.A.; Bjune, J.V. Failure Analysis of Drillstrings. Eng. Fail. Anal. 2007, 14, 1641–1666. [Google Scholar] [CrossRef]
- Christoforou, A.; Yigit, A. Active Control of Stick-Slip Vibrations: The Role of Fully Coupled Dynamics. In Proceedings of the SPE Middle East Oil Show, Manama, Bahrain, 17–20 March 2001. [Google Scholar]
- Elsayed, M.A.; Dareing, D.W.; Vonderheide, M.A. Effect of Torsion on Stability, Dynamic Forces, and Vibration Characteristics in Drillstrings. J. Energy Resour. Technol. 1997, 119, 11–19. [Google Scholar] [CrossRef]
- Schwefe, T.; Ledgerwood, L.W.; Jain, J.R.; Fuselier, D.M.; Oueslati, H.; Endres, L. Development and Testing of Stick/Slip-Resistant PDC Bits. SPE/IADC Drill. Conf. Proc. 2014, 2, 974–984. [Google Scholar] [CrossRef]
- Elsayed, M.A.; Raymond, D.W. Analysis of Coupling Between Axial and Torsional Vibration in a Compliant Model of a Drillstring Equipped with a PDC Bit. In Proceedings of the Engineering Technology Conference on Energy, Parts A and B, Houston, TX, USA, 4–5 February 2002; pp. 897–904. [Google Scholar]
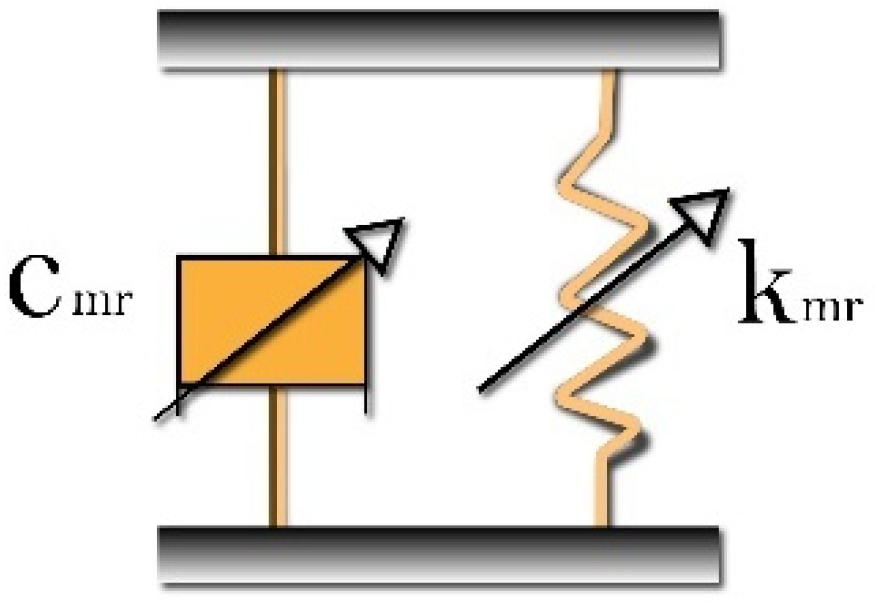
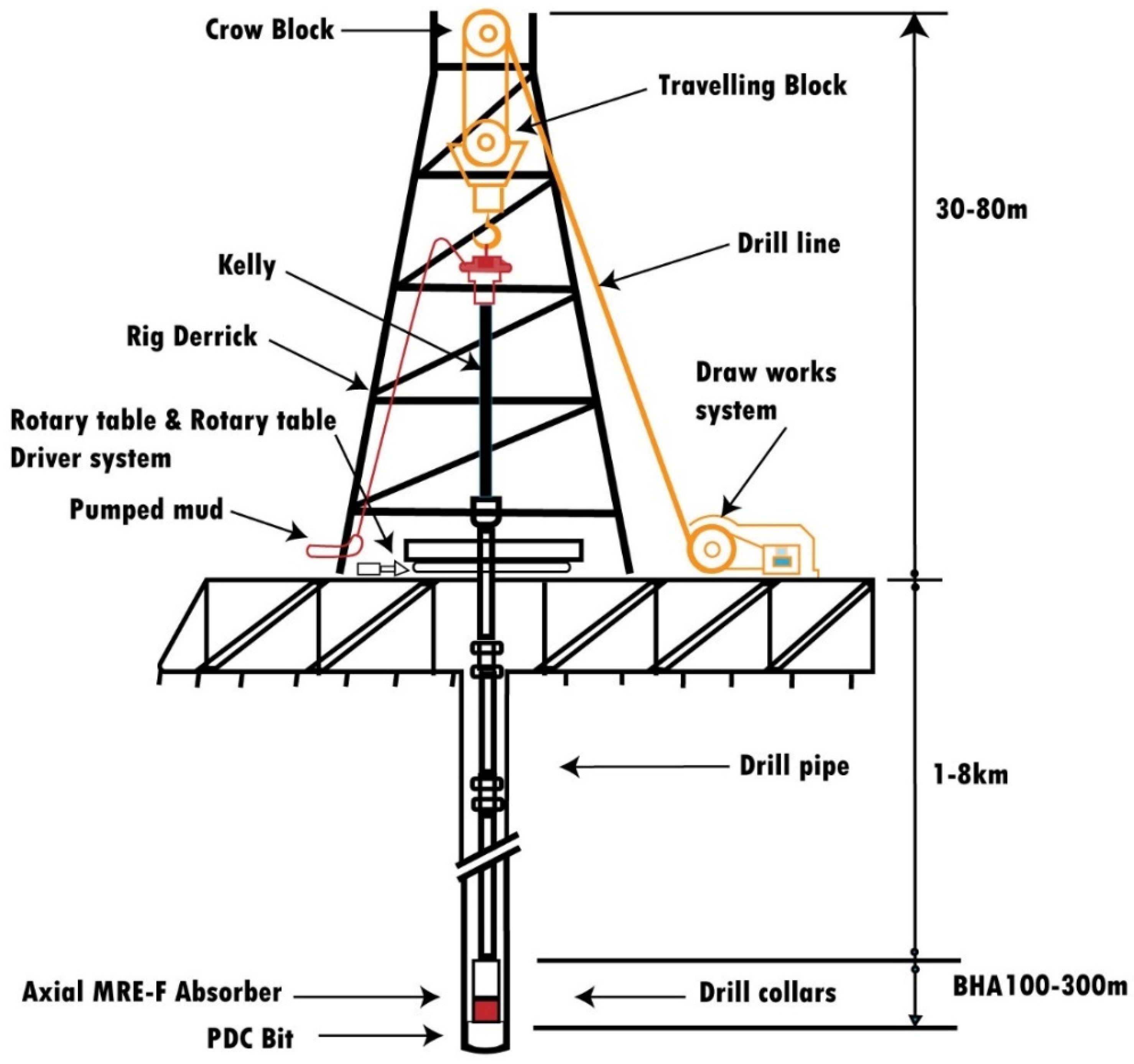



| Parameter | Description | Values |
|---|---|---|
| Axial absorber stiffness coefficient initial value | 7.54 × 109 N/m | |
| Axial absorber damping coefficient initial value | 5.13 × 104 N s/m |
| Parameters | Descriptions | Values |
|---|---|---|
| Cross section area of drill pipes | 3.5 × 10−3 m2 | |
| bo | Term of acceleration in a hyperbolic tangent function | 5.0 |
| CV | Effective damping due to fluid motion around the BHA | 3.75 N m s |
| Cds | Axial-direction damping of drill string | 18,753 N s/m |
| Crt | Gearbox internal torsional damping | 0 N m s |
| Do | Diameter of the drill line | 25 mm |
| BHA outer diameter | 16 cm | |
| BHA inner diameter | 4 cm | |
| EP | Elasticity modulus of drill pipe | 200 Gpa |
| Es | Elasticity modulus of drill line | 200 Gpa |
| Fbrake | Friction force controlling the drawworks’ drum movement | 130 kN |
| G | Acceleration due to gravity | 9.81 m/s2 |
| Drill pipes polar moment of inertia | 1.23 × 105 m4 | |
| JDW | Drawworks drum inertia | 930 kg·m2 |
| Jms | Drawworks motor shaft inertia | 23 kg m2 |
| Jrt | Rotary table inertia | 930 kg m2 |
| Jm | Rotary table motor shaft inertia | 23 kg m2 |
| JBHA | Bottom-hole assembly inertia | 102.5 kg m2 |
| Jpipe | Drill pipes’ inertia | 97.5 kg m2 |
| J | Drill string’s lumped inertia () | 135 kg m2 |
| kc | Contact stiffness of the rock linear | 37.5 M·N/m |
| Km | Motor constant of the drawworks system | 6 Vs |
| Kmo | Motor constant of the rotary table drive motor | 6 Vs |
| kds | Drill string’s effective axial stiffness () | 701.4 kN/m |
| K | Drill string’s effective torsional stiffness () | 937.2 N m/rad |
| Lp | Length of the drill pipes | 1000 m |
| Lb | Length of the bottom-hole assembly | 200 m |
| Lo | Drill lines’ initial length | 20 m |
| Lc | Armature inductance of the drawworks | 0.005 H |
| Li | Armature inductance of the rotary table | 0.005 H |
| Wear-flat length beneath each blade | 1.2 mm | |
| mTop | Suspension mass | 20,000 kg |
| mf | Mass of the fluid | 10,631 kg |
| mBHA | Mass of the BHA | 30,159.3 kg |
| mpipe | Mass of the drill pipes | 28,054.5 kg |
| ma | Effective mass of the drill string () | 50,142 kg |
| mbit | Mass of the bit | 120 Kg |
| n | Number of blades | 3.0 |
| Gearbox ratio of the drawworks’ motor | 14.30 | |
| N | Number of cycles during which the drill line moves between the traveling block and the crown block | 14 |
| Gearbox ratio of the rotary table motor | 7.2 | |
| Rb | Radius of the bit | 22 cm |
| RDW | Radius of the drawworks drum | 1050 mm |
| Rm | Armature resistance of the drawworks | 0.001 Ω |
| Rmo | Rotary table armature resistance | 0.001 Ω |
| The kinematic friction torque applied on drawworks drum through hand arm brake ( | 40.95 KN·m | |
| Supply voltage to the rotary table DC motor () | 542.9 V | |
| Desired top mass axial velocity | 7 mm/s | |
| Supply voltage to the drawworks drum DC motor () | 7.42 V | |
| Desired rotary table speed | 120 RPM | |
| Desired rotary table torsional velocity measured based on desired top mass axial veloc-ity () | 5.35 RPM | |
| Spatial orientation of wear-flats | 1.3 | |
| ε | Intrinsic specific energy | 45 MPa |
| ζ | Inclination of cutting force on cutting face | 0.8 |
| μ | Friction coefficient | 0.3 |
| μp | Drawworks brake-pad friction coefficient | 0.3 |
| Drill-string material density | 8000 kg/m3 | |
| Mud density | 1500 kg/m3 | |
| σ | Rock normal contact stress | 45 Mpa |
| A | Cross section area of drill lines | m2 |
| The values of the axial MRE-F absorber damping coefficient | N·s/m | |
| The Hook load () | N | |
| Heaviside function used to capture the Boundary condition of WOBf that depends on axial velocity in Phase II. | - | |
| Heaviside function used to capture the TOB friction component sing variations during reverse the angular velocity in Phase II | - | |
| The values of the axial MRE-F absorberthe stiffness coefficient | N/m | |
| The stiffness of the drill line () [50]. | N/m | |
| L | The length of drill lines from the crown block till the traveling Block ) | m |
| MR | Magnetorheological materials belong to the category of smart materials | - |
| MRFs | magnetorheological fluids material | - |
| MREs | magnetorheological elastomers material | - |
| MRE-F | hybrid magnetorheological elastomer-fluid | - |
| PDC | Polycrystalline diamond compact drill bits | - |
| Smoothness Index Value | An objective function can be established using the root mean square (RMS), which is a weighted function calculated from the percentage variation in both axial and torsional velocities with respect to their desired velocities | - |
| The torque at the motor shaft driving the rotary table () | N·m | |
| The torque applied on draw works drum from suspended weight () | N·m | |
| The torque transformed from the motor shaft to the draw works drum () | N·m | |
| tn | The time required for the bit to rotate by an angle of | s |
| T | is the total drilling time | s |
| TOB | Torque On Bit | N·m |
| TOBf | Torque On Bit friction component | N·m |
| TOBc | Torque On Bit cutting component | N·m |
| WOB | Weight On Bit | N |
| WOBf | Weight On Bit friction component | N |
| WOBc | Weight On Bit cutting component | N |
| The Axial displacement and velocity of the suspension mass | m,m/s | |
| The Axial displacement and velocity of the Bottom-Hole Assembly (BHA) | m,m/s | |
| The Axial displacement and velocity of the PDC bit | m,m/s | |
| the weight factor () used in the Smoothness Index Value equation for both bit velocities’ responses | - | |
| The angular displacement and velocity of draw works drum | Rad,Rad/s | |
| The angular displacement and velocity of bit | Rad,Rad/s | |
| , | The angular displacement and velocity of the rotary table. | Rad,Rad/s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kamel, J.M.; Muthalif, A.G.A.; Falah, A.H. Drill-String Vibration Suppression Using Hybrid Magnetorheological Elastomer-Fluid Absorbers. Actuators 2025, 14, 273. https://doi.org/10.3390/act14060273
Kamel JM, Muthalif AGA, Falah AH. Drill-String Vibration Suppression Using Hybrid Magnetorheological Elastomer-Fluid Absorbers. Actuators. 2025; 14(6):273. https://doi.org/10.3390/act14060273
Chicago/Turabian StyleKamel, Jasem M., Asan G. A. Muthalif, and Abdulazim H. Falah. 2025. "Drill-String Vibration Suppression Using Hybrid Magnetorheological Elastomer-Fluid Absorbers" Actuators 14, no. 6: 273. https://doi.org/10.3390/act14060273
APA StyleKamel, J. M., Muthalif, A. G. A., & Falah, A. H. (2025). Drill-String Vibration Suppression Using Hybrid Magnetorheological Elastomer-Fluid Absorbers. Actuators, 14(6), 273. https://doi.org/10.3390/act14060273





