Pressure Control in the Pump-Controlled Hydraulic Die Cushion Pressure-Building Phase Using Enhanced Model Predictive Control with Extended State Observer-Genetic Algorithm Optimization
Abstract
1. Introduction
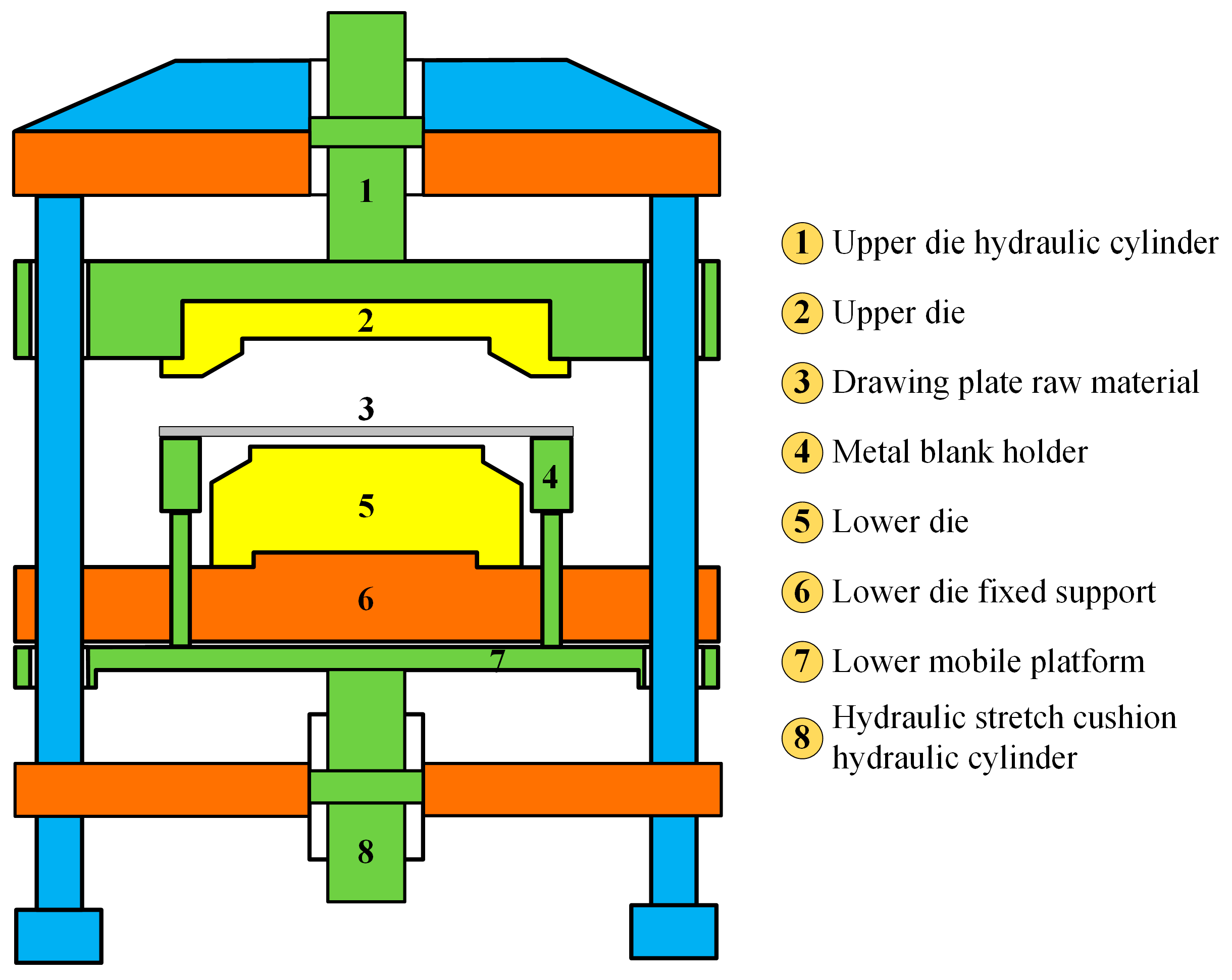
2. System Modeling
2.1. Mathematical Modeling of Swashplate Axial Piston Pumps
2.2. Mathematical Model of the Servo Motor
2.3. Mathematical Modeling of the Hydraulic Cylinder
2.4. State-Space Model
3. Control Scheme
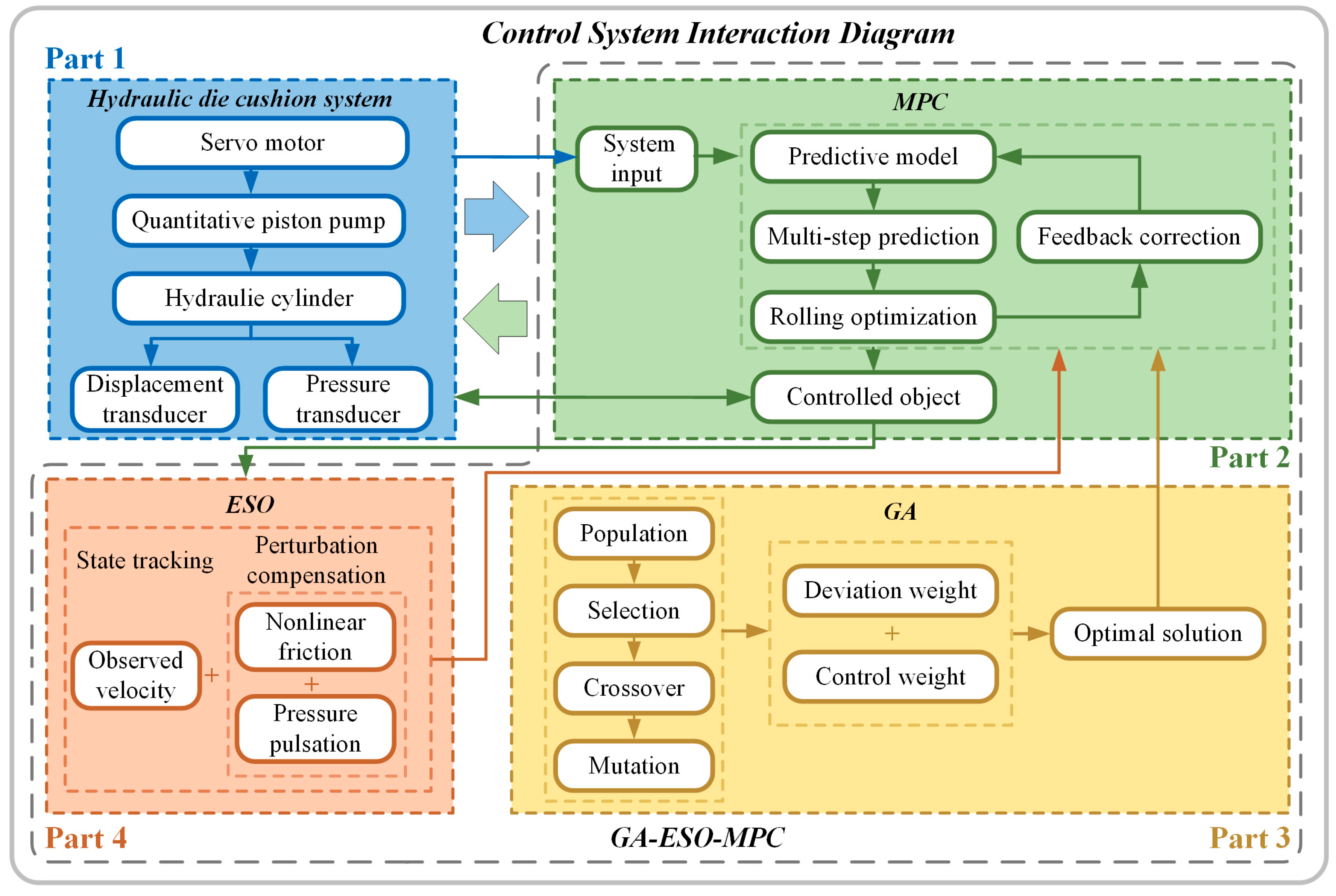
3.1. Algorithmic Architecture
- (1)
- The MPC algorithm is adopted to address upper and lower limit constraints essential for the effective pressure control of the hydraulic die cushion during the pressure-building process. This control strategy designs the corresponding output prediction equation based on the system model, expresses the constraints as a quadratic programming problem, and dynamically updates control policies in response to environmental disturbances, demonstrating enhanced robustness.
- (2)
- The ESO was designed to tackle internal disturbances and challenges in observing the velocity signal. This observer estimates and compensates for nonlinear friction and piston pump pulsation and observes the velocity information of the hydraulic cylinders required by the MPC algorithm.
- (3)
- The GA is used for parameter optimization within the complex context of MPC, which necessitates the configuration of numerous parameters. The GA optimizes the output volume deviation weight matrix Q and the system control volume weight matrix S through iterative processes, ensuring that MPC achieves optimal control effect.
3.2. Control Program Design
3.2.1. Incremental Prediction Model Design
3.2.2. Objective Function Design
3.2.3. Working Condition Constraints
3.2.4. ESO Design
3.2.5. Parameter Optimization Based on the GA
4. Experimental Validation
4.1. System Setup
4.2. Analysis of Experimental Results
4.2.1. Uniform Tensile Test
4.2.2. Sinusoidal Tensile Test
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wen, T.; Liu, L.; Wang, X.; Zheng, Y.; Yang, F.; Zhou, Y. Zinc-based alloy rapid tooling for sheet metal forming reinforced by SLM steel inlays. Int. J. Adv. Manuf. Technol. 2022, 122, 761–771. [Google Scholar] [CrossRef]
- Song, T.U.; Shin, J.S.; Jeong, C.Y. Fatigue Properties of Rolled Steel Sheets for Automotive Structure. J. Mater. Eng. Perform. 2022, 31, 8304–8313. [Google Scholar] [CrossRef]
- Zhang, J.R.; Pan, X.N.; Guo, J.C.; Bian, J.X.; Kang, J. Analysis of the static and dynamic characteristics of the electro-hydraulic pressure servo valve of robot. Sci. Rep. 2023, 13, 15553. [Google Scholar] [CrossRef] [PubMed]
- Li, J.Y.; Li, W.D.; Du, X.Y. Research on the Characteristics of Electro-hydraulic Position Servo System of RBF Neural Network Under Fuzzy Rules. Sci. Rep. 2024, 14, 15332. [Google Scholar] [CrossRef]
- Helian, B.; Chen, Z.; Yao, B.; Lyu, L.T.; Li, C. Accurate Motion Control of a Direct-driveHydraulic System with an Adaptive Nonlinear Pump Flow Compensation. IEEE-ASME Trans. Mechatron. 2020, 26, 2593–2603. [Google Scholar] [CrossRef]
- Zhang, T.G.; Yan, G.S.; Liu, X.H.; Ding, B.C.; Feng, G.D.; Ai, C. Hydrostatic bearing groove multi-objective optimization of the gear ring housing interface in a straight-line conjugate internal meshing gear pump. Sci. Rep. 2024, 14, 12172. [Google Scholar] [CrossRef]
- Zeng, X.; Zhang, X.; Yang, D.; Song, D.; Qian, Q.; Wu, Q. Dynamic coordination control for hydraulic hub-motor auxiliary system based on nmpc algorithm. Measurement 2022, 191, 110795. [Google Scholar] [CrossRef]
- Jiang, W.G.; Jia, P.S.; Yan, G.S.; Chen, G.S.; Ai, C.; Zhang, T.G.; Liu, K.Y.; Jia, C.Y.; Shen, W. Dynamic Response Analysis of Control Loops in an Electro-Hydraulic Servo Pump Control System. Processes 2022, 10, 1647. [Google Scholar] [CrossRef]
- Gao, B.; Li, X.; Zeng, X.; Chen, H. Nonlinear control of direct-drive pump-controlled clutch actuator in consideration of pump efficiency map. Control Eng. Pract. 2019, 91, 104110. [Google Scholar] [CrossRef]
- Chen, Z.; Helian, B.; Zhou, Y.; Geimer, M. An Integrated Trajectory Planning and Motion Control Strategy of a Variable Rotational Speed Pump-Controlled Electro-Hydraulic Actuator. IEEE-ASME Trans. Mechatron. 2023, 28, 588–597. [Google Scholar] [CrossRef]
- Huang, Z.; Xu, Y.; Ren, W.; Fu, C.; Cao, R.; Kong, X.; Li, W. Design of Position Control Method for Pump-Controlled Hydraulic Presses via Adaptive Integral Robust Control. Processes 2022, 10, 14. [Google Scholar] [CrossRef]
- Palmieri, M.E.; Lorusso, V.D.; Tricarico, L. Robust Optimization and Kriging Metamodeling of Deep-Drawing Process to Obtain a Regulation Curve of Blank Holder Force. Metals 2021, 11, 319. [Google Scholar] [CrossRef]
- Cavone, G.; Bozza, A.; Carli, R.; Dotoli, M. MPC-Based Process Control of Deep Drawing: An Industry 4.0 Case Study in Automotive. IEEE Trans. Autom. Sci. Eng. 2022, 19, 1586–1598. [Google Scholar] [CrossRef]
- Li, R.Y.; Jin, L.C. Analysis of Nonlinear Characteristics of Milling Force in Processing Splicing Joint Area of Automobile Mold. Ferroelectrics 2021, 578, 113–125. [Google Scholar]
- Xu, T.; Wu, H.; Xue, F.; Guo, J.W.; Ran, J.Q.; Gong, F. Structural design of stamping die of advanced high-strength steel part for automobile based on topology optimization with variable density method. Int. J. Adv. Manuf. Technol. 2022, 121, 8115–8125. [Google Scholar] [CrossRef]
- Sun, C.G.; Li, J.P.; Tan, Y.; Duan, Z.J. Proposed Feedback-Linearized Integral Sliding Mode Control for an Electro-Hydraulic Servo Material Testing Machine. Machines 2024, 12, 164. [Google Scholar] [CrossRef]
- Trojaola, I.; Elorza, I.; Irigoyen, E.; Pujana-Arrese, A.; Calleja, C. The Effect of Iterative Learning Control on the Force Control of a Hydraulic Cushion. Log. J. IGPL 2022, 30, 214–226. [Google Scholar] [CrossRef]
- Sun, Y.; Wan, Y.; Ma, H.F.; Liang, X.C. Real-Time Force Control of Hydraulic Manipulator Arms Without Force or Pressure Feedback Using a Nonlinear Algorithm. IEEE Robot. Autom. Lett. 2023, 8, 7146–7153. [Google Scholar] [CrossRef]
- Li, C.; Ding, R.Q.; Cheng, M.; Chen, Z.; Yao, B. Accurate Motion Control of an Independent Metering Actuator with Adaptive Robust Compensation of Uncertainties in Pressure Dynamics. IEEE Robot. Autom. Lett. 2024, 29, 3877–3889. [Google Scholar] [CrossRef]
- Ji, Y.; Zhang, J.Z.; He, C.K.; Hou, X.H.; Liu, W.L.; Han, J. Wheel Braking Pressure Control Based on Central Booster Electrohydraulic Brake-by-Wire System. IEEE Trans. Transp. Electrif. 2023, 9, 222–235. [Google Scholar] [CrossRef]
- Kim, S.-W.; Cho, B.Y.; Shin, S.H.; Oh, J.-H.; Hwangbo, J.M.; Park, H.-W. Force Control of a Hydraulic Actuator with a Neural Network Inverse Model. IEEE Robot. Autom. Lett. 2021, 6, 2814–2821. [Google Scholar] [CrossRef]
- Shang, Y.X.; Li, R.J.; Wu, S.; Liu, X.C.; Wang, Y.; Jiao, Z.X. A Research of High-Precision Pressure Regulation Algorithm Based on ON/OFF Valves for Aircraft Braking System. IEEE Trans. Ind. Electron. 2022, 69, 7797–7806. [Google Scholar] [CrossRef]
- Helian, B.; Mustalahti, P.; Mattila, J.; Chen, Z.; Yao, B. Adaptive robust pressure control of variable displacement axial piston pumps with a modified reduced-order dynamic model. Mechatronics 2022, 87, 102879. [Google Scholar] [CrossRef]
- Seo, G.; Yoon, S.; Kim, M.; Mun, C.; Hwang, E. Deep Reinforcement Learning-Based Smart Joint Control Scheme for On/Off Pumping Systems in Wastewater Treatment Plants. IEEE Access 2021, 9, 95360–95371. [Google Scholar] [CrossRef]
- Du, H.; Ding, K.Y.; Shi, J.J.; Feng, X.Y.; Guo, K.; Fang, J.H. High-gain observer-based pump/valve combined control for heavy vehicle electro-hydraulic servo steering system. Mechatronics 2022, 85, 102815. [Google Scholar] [CrossRef]
- Gan, X.C.; Pei, J.; Pavesi, G.; Yuan, S.Q.; Wang, W.J. Application of intelligent methods in energy efficiency enhancement of pump system: A review. Energy Rep. 2022, 8, 11592–11606. [Google Scholar] [CrossRef]
- Hao, Y.X.; Quan, L.; Qiao, S.F.; Xia, L.P.; Wang, X.Y. Coordinated Control and Characteristics of an Integrated Hydraulic–Electric Hybrid Linear Drive System. IEEE-ASME Trans. Mechatron. 2022, 27, 1138–1149. [Google Scholar] [CrossRef]
- Pfizenmaier, M.; Pippes, T.; Bohr, A.; Falkenstein, J. Load Emulation with Independent Metering for a Pump Test Bench. Actuators 2023, 12, 413. [Google Scholar] [CrossRef]
- Zhao, W.; Ebbesen, M.K.; Hansen, M.R.; Andersen, T.O. Enabling Passive Load-Holding Function and System Pressures Control in a One-Motor-One-Pump Motor-Controlled Hydraulic Cylinder: Simulation Study. Energies 2024, 17, 2484. [Google Scholar] [CrossRef]
- Cao, W.; Chen, Z.; Cheng, A.; Zhao, Q.; Tan, H. Multi-bandwidth observer-based adaptive robust pressure control for electro-hydraulic brake system with uncertainties and measurement noise. Control Eng. Pract. 2024, 153, 106122. [Google Scholar] [CrossRef]
- Ba, K.X.; Wang, Y.; He, X.L.; Wang, C.Y.; Yu, B.; Liu, Y.L.; Kong, X.D. Force Compensation Control for Electro-Hydraulic Servo System with Pump–Valve Compound Drive via QFT–DTOC. Chin. J. Mech. Eng. 2024, 37, 27. [Google Scholar] [CrossRef]
- Yu, B.; Zhu, Q.X.; Yao, J.; Zhang, J.X.; Huang, Z.P.; Jin, Z.G.; Wang, X.J. Design, Mathematical Modeling and Force Control for Electro-Hydraulic Servo System with Pump-Valve Compound Drive. IEEE Access 2020, 8, 171988–172005. [Google Scholar] [CrossRef]
- Tan, C.; Yu, P.; Jiang, Y.; Li, X.; Wang, G. Improved adaptive robust control of direct-drive pump-valve cooperative brake-by-wire unit with disturbance compensation. Smart Mater. Struct. 2024, 33, 125003. [Google Scholar] [CrossRef]
- Cheng, M.; Zhang, J.; Xu, B.; Ding, R.; Wei, J. Decoupling Compensation for Damping Improvement of the Electrohydraulic Control System with Multiple Actuators. IEEE-ASME Trans. Mechatron. 2018, 23, 1383–1392. [Google Scholar] [CrossRef]
- Yang, G. State filtered disturbance rejection control. Nonlinear Dyn. 2025, 113, 6739–6755. [Google Scholar] [CrossRef]
- Yang, G.; Yao, J. Multilayer neurocontrol of high-order uncertain nonlinear systems with active disturbance rejection. Int. J. Robust Nonlinear Control 2024, 34, 2972–2987. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, B.; Yin, H. Constraint-based adaptive robust tracking control of uncertain articulating crane guaranteeing desired dynamic control performance. Nonlinear Dyn. 2023, 111, 11261–11274. [Google Scholar] [CrossRef]
- Jing, C.; Zhang, H.; Yan, B.S.; Hui, Y.B.; Xu, H.G. State and disturbance observer based robust disturbance rejection control for friction electro-hydraulic load simulator. Nonlinear Dyn. 2024, 112, 17241–17255. [Google Scholar] [CrossRef]
- Liu, K.F.; Jin, T.; Shang, Z.T.; Wang, H. Neural adaptive dynamic surface control of an electro-hydraulic loading system for rail grinders. Nonlinear Dyn. 2024, 112, 14191–14213. [Google Scholar] [CrossRef]
- Han, J. From PID to Active Disturbance Rejection Control. IEEE Trans. Ind. Electron. 2009, 56, 900–906. [Google Scholar] [CrossRef]
- Gao, Z. Scaling and bandwidth-parameterization based controller tuning. In Proceedings of the 2003 American Control Conference, Denver, CO, USA, 4–6 June 2003; pp. 4989–4996. [Google Scholar]























| Parameters | Description |
|---|---|
| State variables | |
| Control variables | |
| Output variables | |
| Total leakage coefficient | |
| Internal dynamics of the system | |
| Input impact | |
| Output relationship | |
| Time-varying disturbance | |
| Jacobian matrix of f over x | |
| Jacobian matrix of f over u | |
| Sampling time | |
| Unit matrix |
| Name of Constraint | Constraint | Limitations |
|---|---|---|
| Control volume | Servo motor speed | [0, 1500] |
| Control increments | Servo motor speed increment | [−100, 100] |
| Hard constraints on output | System pressure | [0.95, 1.075] |
| Soft constraints on output volume | System pressure | [0.975, 1.025] |
| Parameters | Function |
|---|---|
| Bandwidths | Bandwidth of the ESO |
| Control horizon | Control step size for system inputs |
| Predictive horizon | System prediction horizon |
| Weighting matrix | Weighting matrix for output deviations |
| Weighting matrix | Weighting matrix for control increments |
| Weighting matrix | Weighting matrix for system control quantity |
| Weighting factor | Weighting coefficient for the system slack factor |
| Serial Number | Name | Model Number | Parameters |
|---|---|---|---|
| 1 | Pressure transducer | GEMS160S05ER001 | Test range: 0–25 MPa |
| 2 | Displacement transducer | KH10MB0060MC | Test range: 0–500 mm |
| 3 | Motion controllers | HIC3700 | Max main frequency: 480 MHz |
| 4 | AIO | HIC3700-AIO | 8 inputs/4 outputs |
| 5 | Servo drive | HI360-47P5A02 | EtherCAT Bus |
| 6 | Servo motor | HP11318-G152A-R1P7 | Rated torque: 21 Nm |
| 7 | Embedded controller | NI cRIO-9038 | 1.33 GHz CPU, 2 GB DRAM |
| 8 | Voltage acquisition card | NI 9201 | ±10 V AI channels |
| 9 | Current acquisition card | NI 9203 | ±20 mA AI channels |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, Z.; He, S.; Liao, Y.; Wang, H.; Song, M.; Jiang, J.; Chen, G. Pressure Control in the Pump-Controlled Hydraulic Die Cushion Pressure-Building Phase Using Enhanced Model Predictive Control with Extended State Observer-Genetic Algorithm Optimization. Actuators 2025, 14, 261. https://doi.org/10.3390/act14060261
Dong Z, He S, Liao Y, Wang H, Song M, Jiang J, Chen G. Pressure Control in the Pump-Controlled Hydraulic Die Cushion Pressure-Building Phase Using Enhanced Model Predictive Control with Extended State Observer-Genetic Algorithm Optimization. Actuators. 2025; 14(6):261. https://doi.org/10.3390/act14060261
Chicago/Turabian StyleDong, Zhikui, Song He, Yi Liao, Heng Wang, Mingxing Song, Jinpei Jiang, and Gexin Chen. 2025. "Pressure Control in the Pump-Controlled Hydraulic Die Cushion Pressure-Building Phase Using Enhanced Model Predictive Control with Extended State Observer-Genetic Algorithm Optimization" Actuators 14, no. 6: 261. https://doi.org/10.3390/act14060261
APA StyleDong, Z., He, S., Liao, Y., Wang, H., Song, M., Jiang, J., & Chen, G. (2025). Pressure Control in the Pump-Controlled Hydraulic Die Cushion Pressure-Building Phase Using Enhanced Model Predictive Control with Extended State Observer-Genetic Algorithm Optimization. Actuators, 14(6), 261. https://doi.org/10.3390/act14060261






