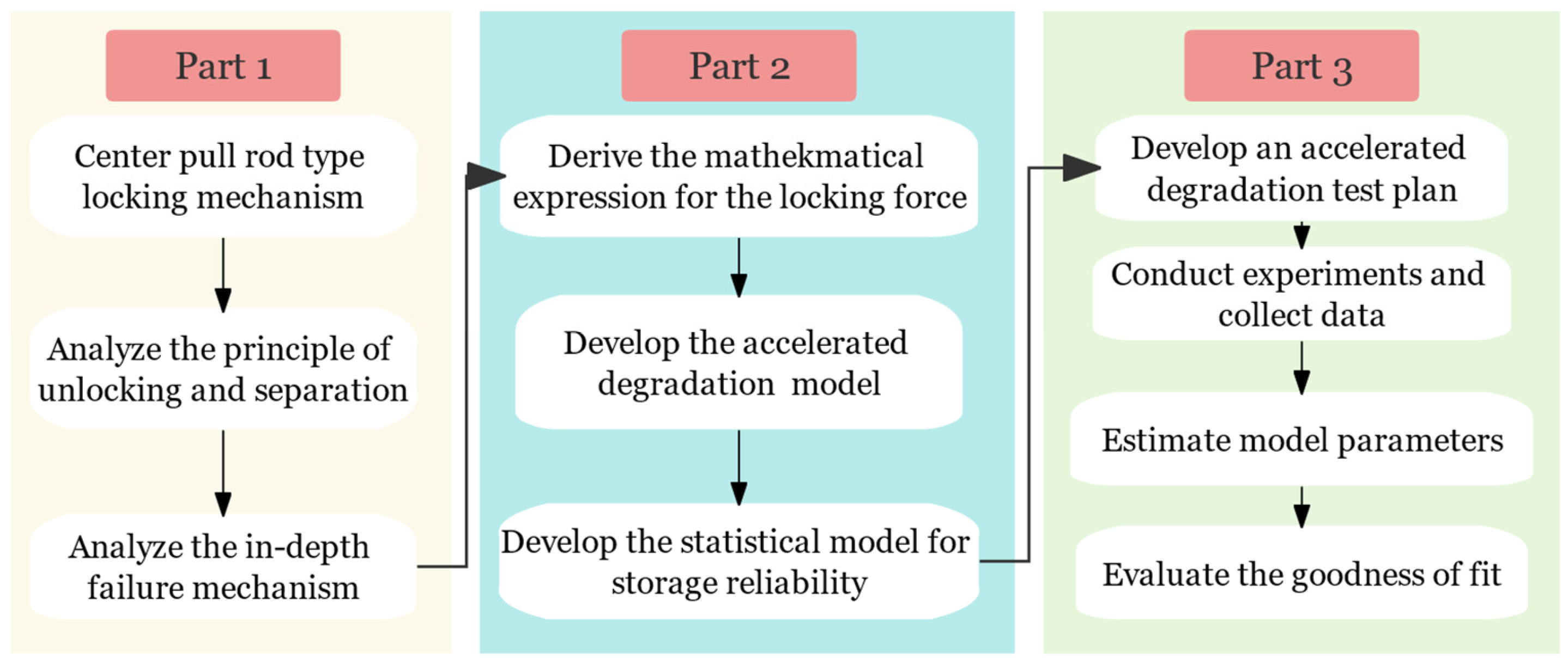
Reliability Modeling and Verification of Locking Mechanisms Based on Failure Mechanisms
Abstract
1. Introduction
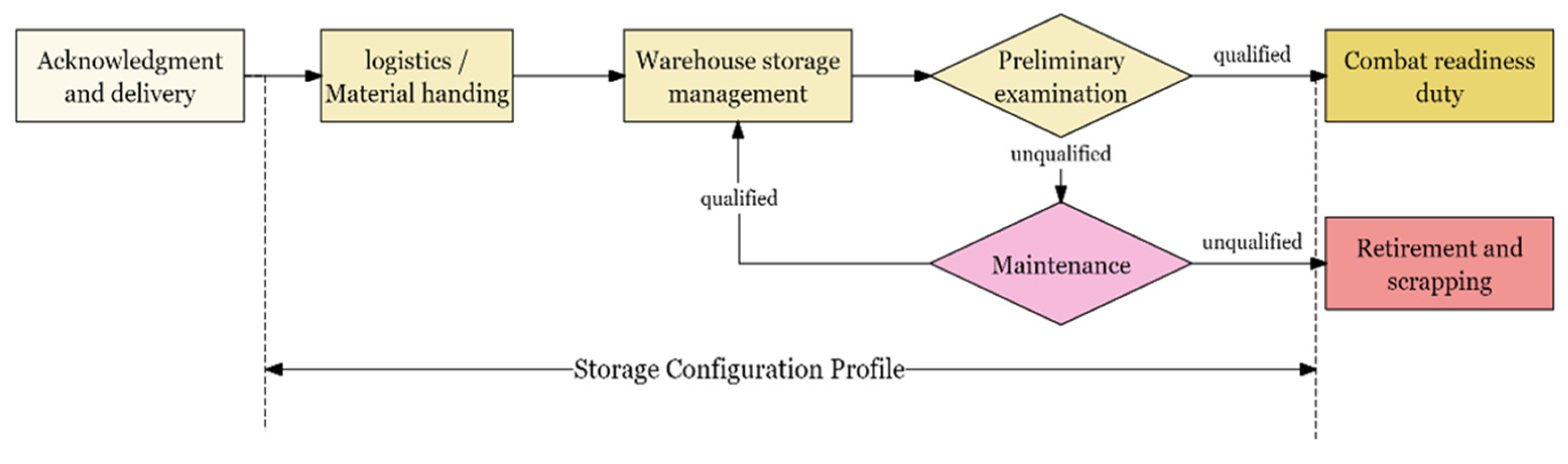
2. Failure Mechanism in the Storage Environment
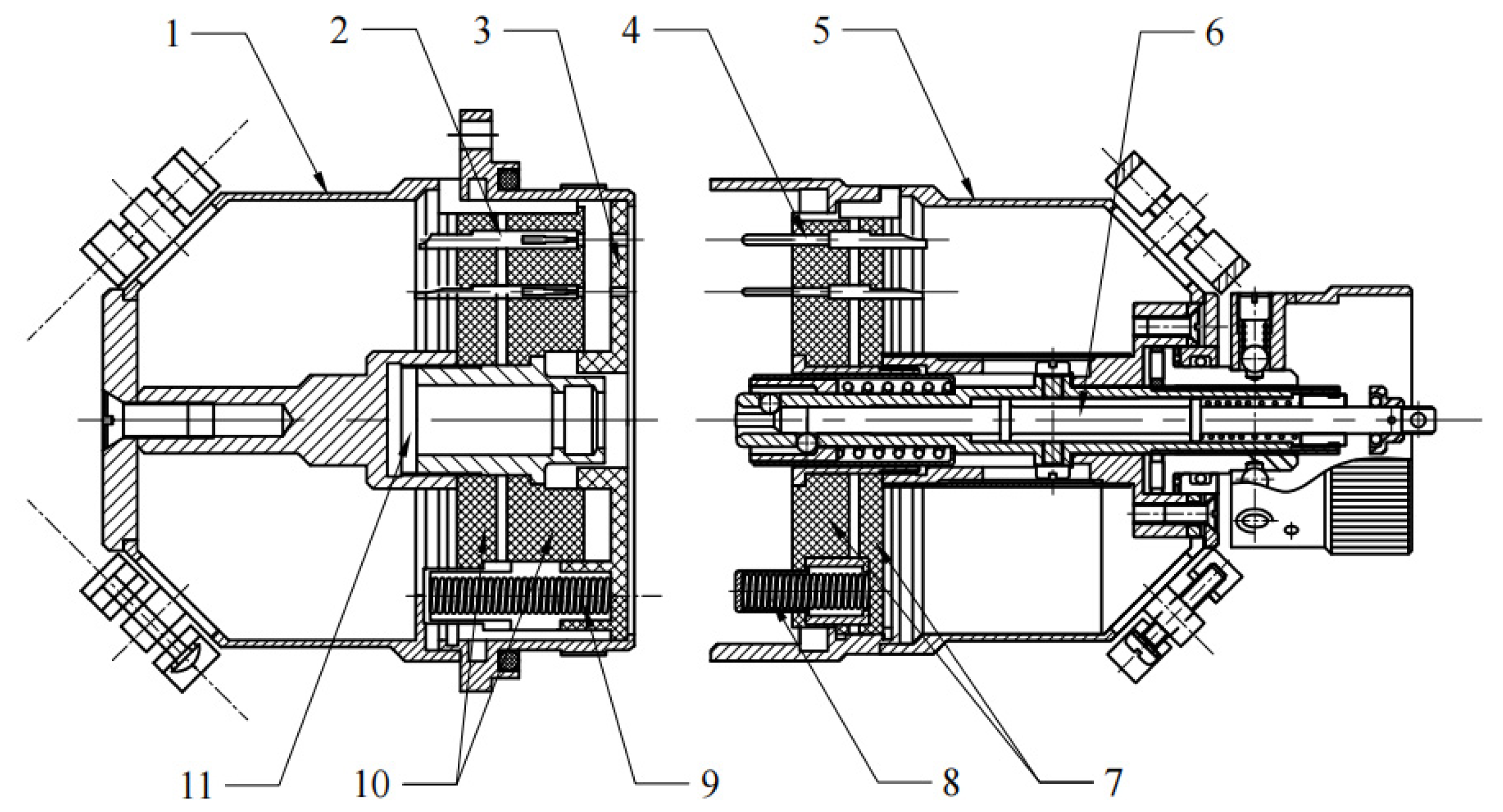
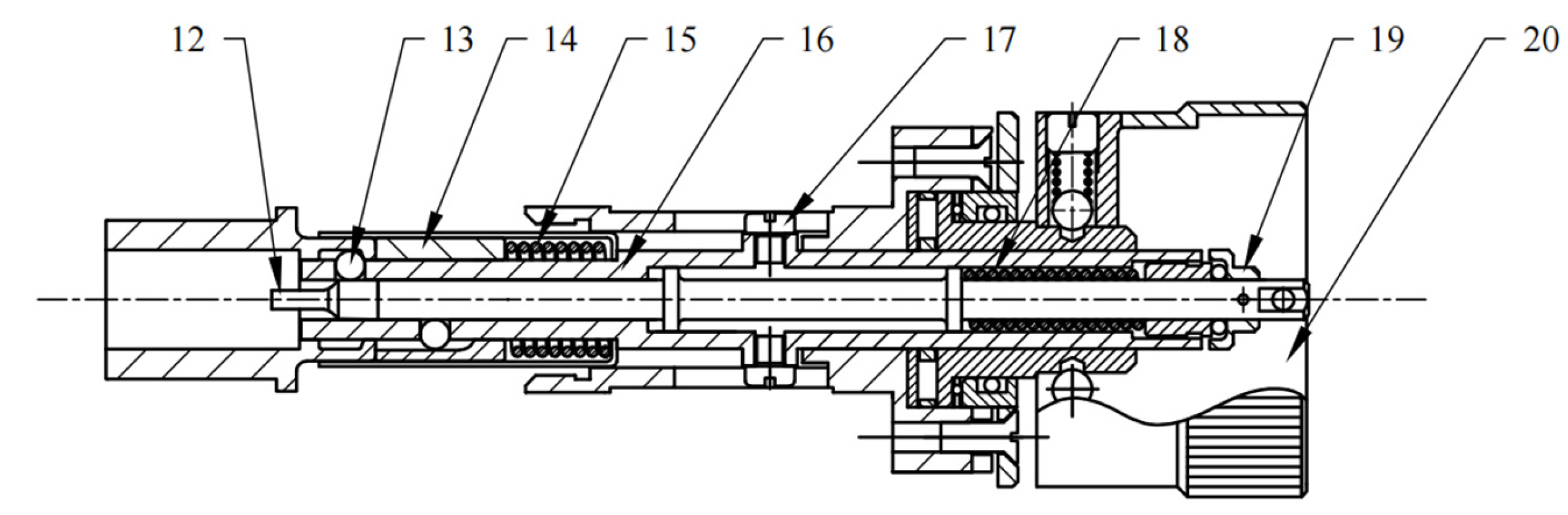
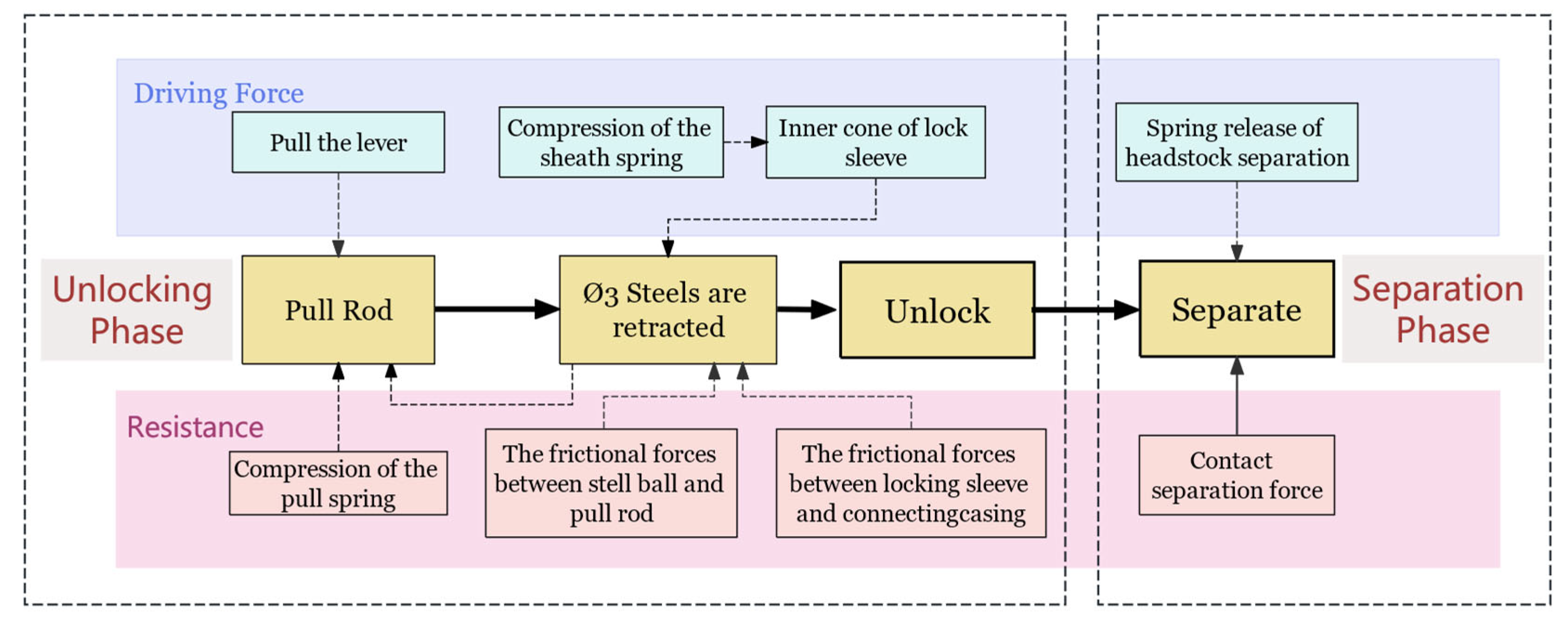
2.1. Structure and Operational Mechanism
2.2. Failure Mechanism Analysis
2.2.1. Deformation of the Pull Rod
2.2.2. Stress Relaxation of the Spring
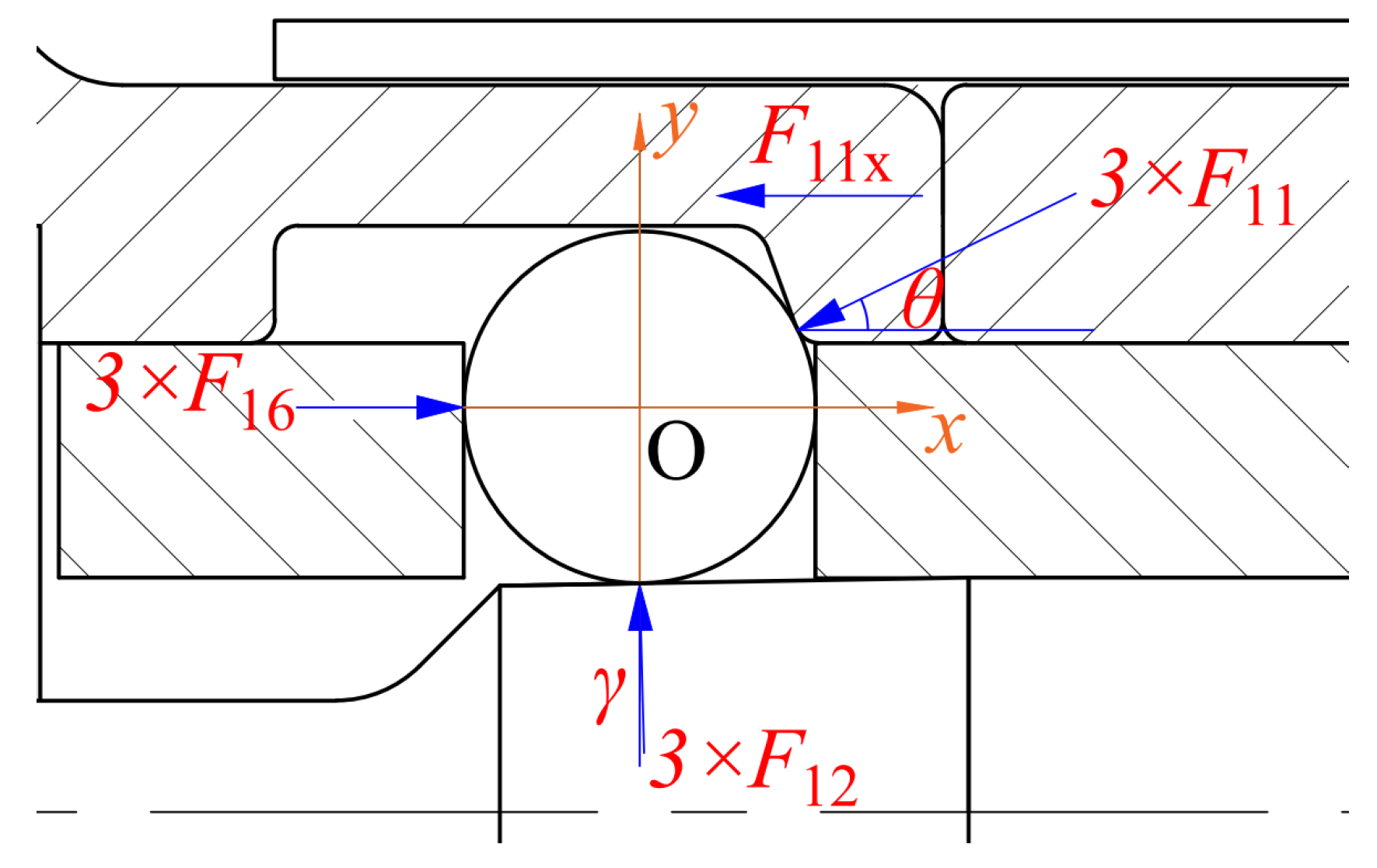
3. Static Model
4. Accelerated Degradation Modeling of the Unlocking Stage
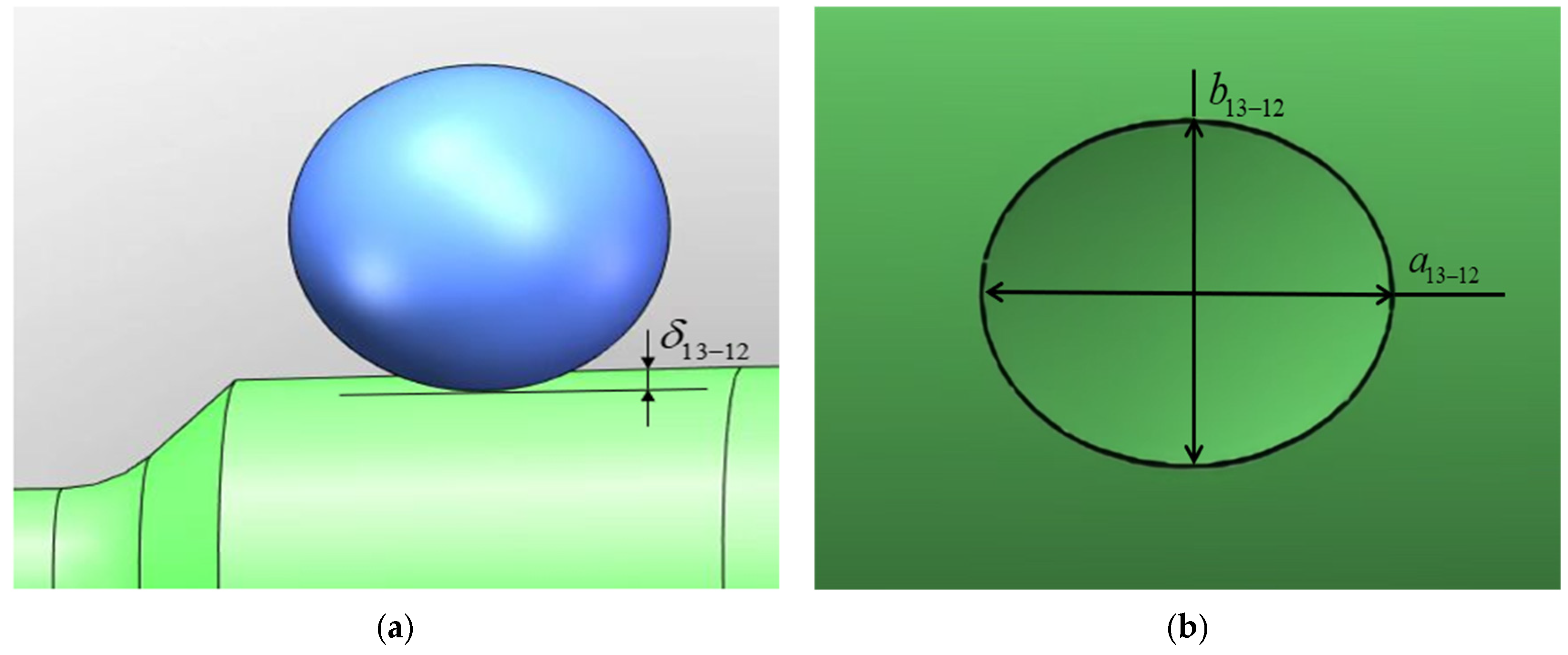
4.1. Accelerated Degradation Modeling of the Steel Ball to Pull-Rod Friction
4.2. Accelerated Degradation Modeling of the Spring Force
4.3. Reliability Model of the Unlocking Stage
5. Validation of the Accelerated Degradation Model
5.1. Accelerated Test Protocol
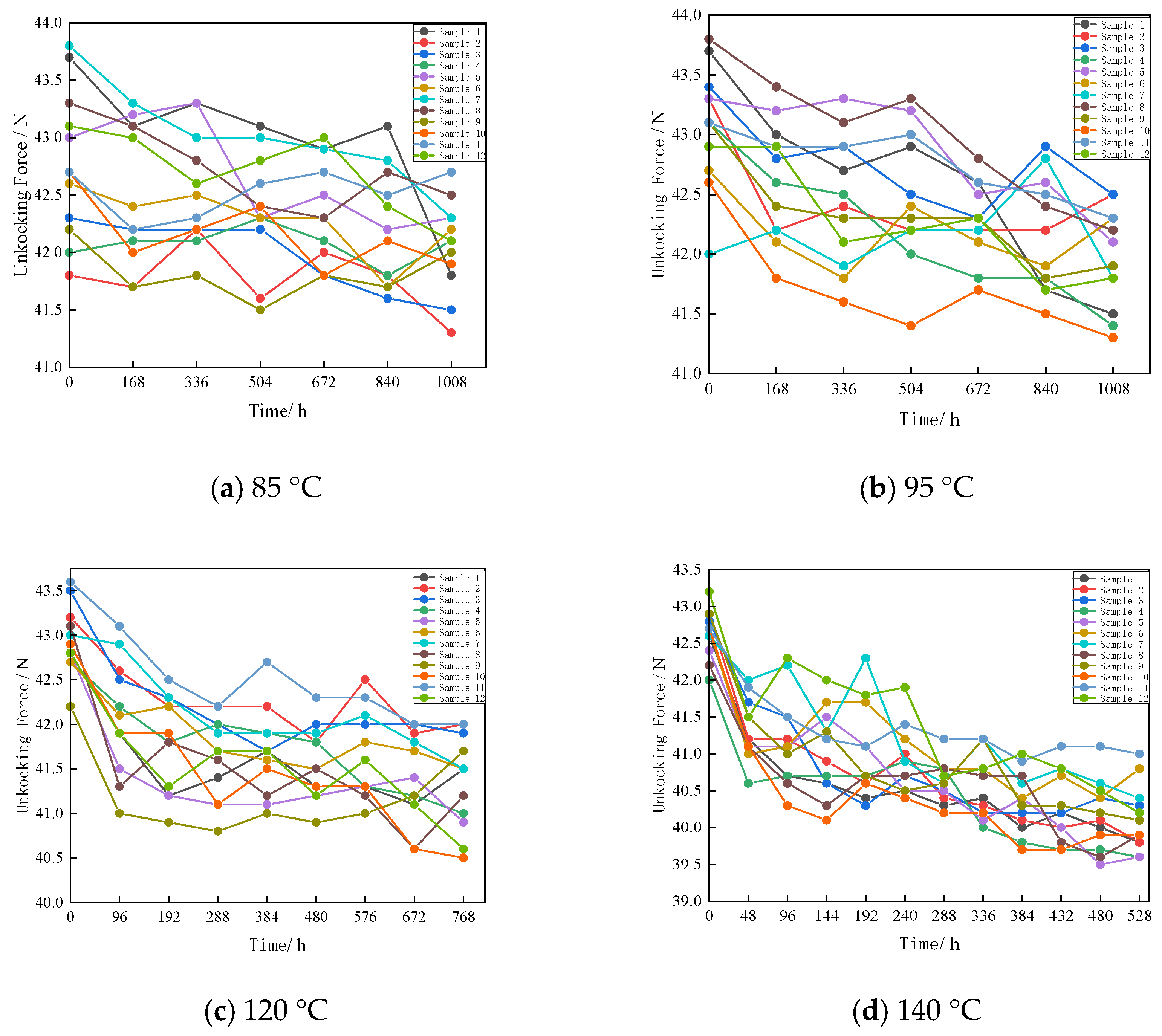
5.2. Statistical Analysis of Accelerated Test Data
5.3. Parameter Estimation
5.4. Verification of the Degradation Trajectory Model
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| cumulative dislocation strength within the crystal lattice of the spring | |
| cumulative product of various design and material parameters | |
| major axes of the elliptical projection | |
| parameters dependent on temperature | |
| minor axes of the elliptical projection | |
| spring index | |
| the mean diameter of the spring | |
| diameter of the spring wire | |
| activation energy | |
| elastic modulus | |
| crystal scale parameter | |
| force | |
| axial force generated by the φ3 steel ball on the pull rod | |
| friction force exerted by the steel ball on the pull rod | |
| friction coefficient | |
| material’s shear modulus | |
| strength of dislocations in the crystal | |
| height | |
| correction coefficient | |
| Boltzmann constant | |
| width of the crystal | |
| parameter associated with temperature | |
| parameters dependent on hardness | |
| sample size of the test | |
| degree of dislocation accumulation | |
| parameter associated with the material | |
| correlation coefficient | |
| unlocking reliability at time t | |
| distance of single-crystal dislocation movement | |
| displacement of the pull-rod movement | |
| absolute temperature | |
| time | |
| logarithmic mean | |
| volume of a single crystal | |
| Poisson’s ratio of the material | |
| speed of the slip movement of the dislocation of the crystal | |
| degradation rate of the spring | |
| deformation rate of the pull rod | |
| parameters to be estimated | |
| distances of the subsequent piled-up dislocations from the leading dislocation | |
| parameters to be estimated | |
| logarithmic standard deviation | |
| contact stress | |
| The cone angle of the pull rod | |
| magnitude of deformation | |
| plastic deformation amount of the crystal | |
| the dislocation density per unit crystal | |
| parameter related to material properties | |
| the frequency factor | |
| plastic strain | |
| applied shear stress on the material | |
| effective shear stress | |
| contact angle between the lock sleeve and the steel ball |
References
- Xin, L.; Feng, C.; Lv, W.; Zhou, Y.; Xiong, C.; Gao, Y.; Zhu, F. Electrical contact reliability investigation of high-speed electrical connectors under fretting wear behavior. Microelectron. Reliab. 2024, 115, 115510. [Google Scholar]
- Lin, M. Study on the Influence of Closing Quantity and Plating Thickness on the Storage Life of Contact Parts. Master’s Thesis, Zhejiang University of Science and Technology, Hangzhou, China, 2023. [Google Scholar]
- Wu, Y.J. Research on the Influence Law of Shell Nosing of Contact on the Storage Life. Master’s Thesis, Zhejiang University of Science and Technology, Hangzhou, China, 2022. [Google Scholar]
- Xie, S.W. Research on the Effects of Gold-Plated Thickness on the Storage Life of Cylindrical Slot Contacts. Master’s Thesis, Zhejiang University of Science and Technology, Hangzhou, China, 2022. [Google Scholar]
- Qin, B.; Zhang, Y. Comprehensive analysis of electro-mechanical characteristics and new regression models of a novel slanted groove electrical connector. Int. J. Non-Linear Mech. 2024, 104, 104863. [Google Scholar] [CrossRef]
- Liang, S.Y. Research on the Effects of Wire-Spring Angleon the Reliability of Electrical Connector Contacts. Master’s Thesis, Zhejiang University of Science and Technology, Hangzhou, China, 2023. [Google Scholar]
- Guo, H.J.; Liang, S.Y.; Chen, W.H.; Zhong, L.; Chen, Z.; Yan, J. Research on influence of wire spring inclination angle on storage life of wire spring hole electrical connector. Chin. J. Eng. Des. 2023, 30, 390–398. [Google Scholar]
- Qian, P.; Ma, Z.; Chen, W.; Zhang, T.; Wang, Z. Contact reliability modeling and assessment of electrical connectors with multi-aperture slotted leaf spring contacts. Adv. Mech. Eng. 2023, 15, 168781322311807. [Google Scholar] [CrossRef]
- He, W.; Feng, Y.; Wu, S.; Wang, W. Numerical study on thermal-electrical-mechanical coupling mechanism of electrical connectors considering contact resistance. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2024, 5, 1699–1712. [Google Scholar] [CrossRef]
- Shukla, A.; Martin, R.; Probst, R.; Song, J. Comparison of different statistical methods for prediction of lifetime of electrical connectors with short term tests. Microelectron. Reliab. 2023, 150, 115216. [Google Scholar] [CrossRef]
- Siddaiah, A.; Kasar, A.K.; Khosla, V.; Menezes, P.L. In-situ fretting wear analysis of electrical connectors for real system applications. J. Manuf. Mater. Process. 2019, 3, 47. [Google Scholar] [CrossRef]
- Wang, Y. Study on Reliability Modeling and Test Evaluation of G100 Silicone Rubber Insulator for Electrical Connectors. Master’s Thesis, Zhejiang University of Science and Technology, Hangzhou, China, 2023. [Google Scholar]
- Liu, X. Study on the Influence of Temperature and Humidity on the Insulation Performance of Polyurethane Adhesive for Electrical Connectors. Master’s Thesis, Zhejiang University of Science and Technology, Hangzhou, China, 2023. [Google Scholar]
- Jiang, H. The effect of environmental temperature and insulation materials on the insulation resistance of electrical connectors. Electron. Technol. Softw. Eng. 2021, 10, 222–223. [Google Scholar]
- Qian, P.; Liu, X.; Chen, W.; Wang, Z.; Guo, M. Storage reliability modeling of polyurethane seals for electrical connectors. J. Mech. Eng. 2024, 20, 361–371. [Google Scholar]
- Chen, T. Research on the Storage Life Assessment of 771 Silicone Seals for Electric Connectors. Master’s Thesis, Zhejiang Sci-Tech University, Hangzhou, China, 2022. [Google Scholar]
- Angadi, S.V.; Jackson, R.L.; Pujar, V.; Tushar, M.R. A comprehensive review of the finite element modeling of electrical connectors including their contacts. IEEE Trans. Compon. Packag. Manuf. Technol. 2020, 10, 836–844. [Google Scholar] [CrossRef]
- Hilmert, D.; Yuan, H.; Song, J. The analysis of failure mechanisms of electrical connectors in long-term use field vehicles. In Proceedings of the 2022 IEEE 67th Holm Conference on Electrical Contacts (HLM), Tampa, FL, USA, 23–26 October 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 1–8. [Google Scholar]
- Krüger, K.; Song, J. The influence of thermal cycling test parameters on the failure rate of electrical connectors. Microelectron. Reliab. 2022, 138, 114633. [Google Scholar] [CrossRef]
- Song, J.; Shukla, A.; Probst, R. The state of health of electrical connectors. Machines 2024, 12, 474. [Google Scholar] [CrossRef]
- Liu, S. Motion Reliability Analysis and Optimization Design of Planar Linkage Mechanisms Under Hybrid Uncertainty. Doctoral Dissertation, Wuhan University of Science and Technology, Wuhan, China, 2023. [Google Scholar]
- Liu, S.; Wang, X.; Kong, J.; Zeng, T.; Tang, W. Kinematic reliability analysis of planar metamorphic mechanisms with multi-source uncertainties. J. Mech. Eng. 2021, 17, 64–75. [Google Scholar]
- Feng, Y.S. Research on mechanism reliability theory. China Mech. Eng. 1992, 3, 4–6. [Google Scholar]
- Feng, Y.S. Wear reliability of mechanism. Acta Aeronaut. Astronaut. Sin. 1993, 12, 642–644. [Google Scholar]
- Xue, Z.; Feng, W.; Wang, W.; Xiong, X.; Wang, S. Motion reliability analysis of a folding arm mechanism based on the first-order second-moment method. Hoisting Transp. Mach. 2022, 19, 8–13. [Google Scholar]
- Li, Y.; Shang, D.; Fan, X.; Liu, Y. Motion reliability analysis of the delta parallel robot considering mechanism errors. Math. Probl. Eng. 2019, 2019, 3501921. [Google Scholar] [CrossRef]
- Yao, Q.; Zhang, Q.; Tang, J.; Wang, X.; Hu, M. Time-variant reliability analysis method for uncertain motion mechanisms based on stochastic process discretization. IEEE Access 2022, 10, 49040–49049. [Google Scholar] [CrossRef]
- Chen, X.; Gao, S. Dynamic accuracy reliability modeling and analysis of planar multi-link mechanism with revolute clearances. Eur. J. Mech. A-Solids 2021, 90, 104317. [Google Scholar] [CrossRef]
- Chen, X.; Gao, S. Dynamic response and dynamic accuracy reliability of planar mechanism with multiple lubricated clearances. Multibody Syst. Dyn. 2023, 57, 1–23. [Google Scholar] [CrossRef]
- Yang, Y.; Wang, M. Modeling and analysis of position accuracy reliability of R(RPS&RP) & 2-UPS parallel mechanism. J. Mech. Eng. 2023, 59, 62–72. [Google Scholar]
- Gao, Y.; Xiao, F.; Liu, J.; Wang, R. Distributed soft fault detection for interval type-2 fuzzy-model-based stochastic systems with wireless sensor networks. IEEE Trans. Ind. Inform. 2019, 15, 334–347. [Google Scholar] [CrossRef]
- Lv, J.; Yu, Z.; Zhang, H.; Sun, G.; Muhl, P.; Liu, J. Transformer based long–term prognostics for dynamic operating PEM fuel cells. IEEE Trans. Transp. Electrif. 2024, 10, 1747–1757. [Google Scholar] [CrossRef]
- Lv, J.; Kuang, J.; Yu, Z.; Sun, G.; Liu, J.; Leon, J.I. Diagnosis of PEM fuel cell system based on electrochemical impedance spectroscopy and deep learning method. IEEE Trans. Ind. Electron. 2024, 71, 657–666. [Google Scholar] [CrossRef]
- Chang, X.; Zhang, Z.; Yang, Z.; Zhen, E.; Wang, J. Technical discussion on the locking and unlocking scheme of the gas-liquid connector of the launch vehicle. Missiles Space Veh. 2021, 5, 99–103. [Google Scholar]
- Yang, F. Reliability Design Method of Locking Mechanism for Electric Connectors. Doctoral Dissertation, Zhejiang Sci-Tech University, Hangzhou, China, 2017. [Google Scholar]
- Chen, W.H.; Du, S.L.; Yang, F.; Pan, J.; Qian, P. Unlocking reliability analysis of the ball locking mechanism for separating electrical connectors. Chin. J. Eng. Des. 2017, 24, 280–285. [Google Scholar]
- Mealier, N.; Dau, F.; Guillaumat, L.; Arnoux, P. Reliability assessment of locking systems. Probabilistic Eng. Mech. 2010, 25, 67–74. [Google Scholar] [CrossRef]
- Tan, Z.Q.; Wang, S.J.; Zhao, M.Y. Movement function reliability of limit-locking mechanism of space cable-strut deployable articulated mast. Appl. Mech. Mater. 2013, 365–366, 344–350. [Google Scholar] [CrossRef]
- Hao, S. Reliability Analysis and Optimum Design of Key Component of the Locking Separation Mechanism of Electrical Connector. Master’s Thesis, Zhejiang Sci-Tech University, Hangzhou, China, 2016. [Google Scholar]
- Zhuang, Y.; Xie, Z.; Wang, B.; Wang, W.; Li, W.; Wang, Y. Design and analysis for a novel docking mechanism with T-type locking structure in space. In Proceedings of the 2019 IEEE 9th Annual International Conference on Cyber Technology in Automation, Control, and Intelligent Systems (CYBER), Suzhou, China, 29 July–2 August 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1085–1090. [Google Scholar]
- Wang, D.; Zhang, C.; Deng, J.; Cao, Y. Structure design of high-precision small theodolite shaft locking mechanism. Dev. Innov. Mach. Electr. Prod. 2024, 4, 34–36. [Google Scholar]
- Zhang, Q.; Zhang, L.; Zhang, W.; Xu, J.; Yang, Y.; Rao, W. Rapid Locking Mechanism for Electrical Connectors and Electrical Connectors. China Patent No. 201810562963, 3 July 2021. [Google Scholar]
- Chen, S.; Li, S.; Sun, J. Construction and evaluation method of fuzzy reliability life model for spherical joints based on accuracy, (Engineering Edition). J. Zhejiang Univ. 2025, 59, 626–634. [Google Scholar]
- Huang, L.; Li, X.; Zhang, W. Design and experimental research of electromagnetic hold down and release mechanism. J. Mach. Des. 2024, 4, 102–109. [Google Scholar]
- Popov, V.L. Contact Mechanics and Friction: Physical Principles and Applications; Tsinghua University Press: Beijing, China, 2010. [Google Scholar]
- Qian, L. A historical review of the study of crystal defects. Physics 1980, 9. [Google Scholar]
- He, X.; He, L.; Tang, M.; Xu, M. Effects of the vacancy point defect on electronic structure and optical properties of LiF under high pressure: A first-principles investigation. Acta Phys. Sin. 2011, 60, 547–551. [Google Scholar]
- Shi, D. Fundamentals of Materials Science; China Machine Press: Beijing, China, 2021. [Google Scholar]
- Liu, Q. Research progress on plastic deformation mechanism of Mg alloys. Acta Metall. Sin. 2010, 46, 1458–1472. [Google Scholar] [CrossRef]
- Zhang, S. Creep property and mechanism of AZ31 magnesium alloy under high temperature and low stress. J. Mech. Eng. 2009, 45, 291–295. [Google Scholar] [CrossRef]
- Li, J. Research on the Behavior and Mechanism of Short-Time High-Temperature Creep and Stress Relaxation of Fine Grain TC21 Titanium alloy; Harbin Institute of Technology: Harbin, China, 2014. [Google Scholar]
- Mu, X. Creep Mechanics; Xi’an Jiaotong University Press: Xi’an, China, 1990. [Google Scholar]
- Sadeghi, B.; Shabani, A.; Heidarinejad, A.; Laska, A.; Szkodo, M.; Cavaliere, P. A quantitative investigation of dislocation density in an Al matrix composite produced by a combination of micro-/macro-rolling. J. Compos. Sci. 2022, 6, 199. [Google Scholar] [CrossRef]
- Hariharan, K.; Majidi, O.; Kim, C.; Lee, M.; Barlat, F. Stress relaxation and its effect on tensile deformation of steels. Mater. Des. 2013, 52, 284–288. [Google Scholar] [CrossRef]
- Johnston, W.G.; Gilman, J.J. Dislocation velocities, dislocation densities, and plastic flow in lithium fluoride crystals. J. Appl. Phys. 1959, 30, 764–775. [Google Scholar] [CrossRef]
- Wen, B. Manual of Mechanical Design, 5th ed.; China Machine Press: Beijing, China, 2010. [Google Scholar]
- Zhao, J. Fundamentals of Materials Science, 3rd ed.; Higher Education Press: Beijing, China, 2021. [Google Scholar]
- Zhang, X. A continuum model for dislocation pile-up problems. Acta Mater. 2017, 128, 428–439. [Google Scholar] [CrossRef]
- Anderson, P.H.; Lothe, J. Theory of Dislocations, 3rd ed.; Cambridge University Press: Cambridge, UK, 2017. [Google Scholar]
- Xiao, L. Study on Stress Relaxation Properties and Microstructure Changes of Copper Alloys; Tianjin University: Tianjin, China, 1990. [Google Scholar]
- Hangzhou Aerospace Electronics Technology Co., Ltd. Electrical Connector Product Manual; Hangzhou Aerospace Electronics Technology, Co., Ltd.: Hangzhou, China, 2015. [Google Scholar]
- GB 26891-81; General Rules for Constant Stress Life Testing and Accelerated Life Testing. Ministry of Fourth Machinery Industry of the People’s Republic of China, National Standardization Administration: Beijing, China, 1981.
- GB/T 43368-2023; National Standardization Management Committee: General Specifications for Aerospace Separation and Dropping Connectors. China Standards Press: Beijing, China, 2023.
- Ji, Z. Particle Swarm Algorithm and Its Applications; Science Press: Beijing, China, 2009. [Google Scholar]
- Zhang, S.Q. Approach on the Fitting Optimization Index of Curve Regression. Chin. J. Health Stat. 2002, 1, 9–11. [Google Scholar]




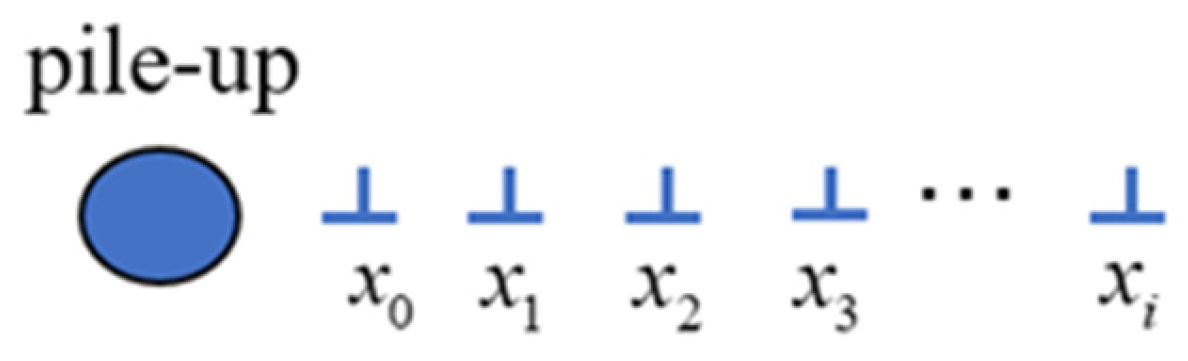



| Number | Name | Shear Modulus G (MPa) | Wire Diameter d (mm) | Mean Diameter D (mm) | Effective Laps n | Free Height H0 (mm) | Assembly Height H1 (mm) |
|---|---|---|---|---|---|---|---|
| 8 | Plug | 79,800 | 0.7 | 4.6 | 10 | 21.4 | 19 |
| 9 | Spring Socket Spring | 79,800 | 1.2 | 5.3 | 13 | 29.7 | 26.2 |
| 15 | Sheath Spring | 79,800 | 1 | 9.5 | 5.75 | 28.5 | 14.7 |
| 18 | Pull-Rod Spring | 79,800 | 0.9 | 5.1 | 13 | 27.8 | 17.2 |
| Number | Name | Material | Elastic Modulus E/MPa | Poisson’s Ratio v | (Equivalent) Radius r/mm | Melting Point Tm/°C | Hardness HRC |
|---|---|---|---|---|---|---|---|
| 12 | Pull Rod | CrWMn | 220 × 103 | 0.29 | 1.93 | 1370 | 40–60 |
| 13 | φ3 Steel Balls | 9Cr18 | 232 × 103 | 0.28 | 1.5 | 1400 | 61–66 |
| Parameter | ||||
|---|---|---|---|---|
| Estimated value | 0.6 | −0.7 | −10.8 | 44.42 |
| Parameter | ||
|---|---|---|
| Computed value | 0.62 | 0.1 |
| Parameter | ||
|---|---|---|
| Estimated value | 3.09 | 944.07 |
| Parameter | ||||||||
|---|---|---|---|---|---|---|---|---|
| Estimated value | 6.05 | 2215 | 7.51 | 2215 | 6.44 | 2215 | 6.78 | 2215 |
| Stress Level | 85 °C | 95 °C | 120 °C | 140 °C |
|---|---|---|---|---|
| 0.96 | 0.96 | 0.98 | 0.96 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qian, P.; Tu, T.; Chen, W.; Yang, F.; Chen, C.; Zhu, Y. Reliability Modeling and Verification of Locking Mechanisms Based on Failure Mechanisms. Actuators 2025, 14, 205. https://doi.org/10.3390/act14050205
Qian P, Tu T, Chen W, Yang F, Chen C, Zhu Y. Reliability Modeling and Verification of Locking Mechanisms Based on Failure Mechanisms. Actuators. 2025; 14(5):205. https://doi.org/10.3390/act14050205
Chicago/Turabian StyleQian, Ping, Tianying Tu, Wenhua Chen, Fan Yang, Chi Chen, and Yucheng Zhu. 2025. "Reliability Modeling and Verification of Locking Mechanisms Based on Failure Mechanisms" Actuators 14, no. 5: 205. https://doi.org/10.3390/act14050205
APA StyleQian, P., Tu, T., Chen, W., Yang, F., Chen, C., & Zhu, Y. (2025). Reliability Modeling and Verification of Locking Mechanisms Based on Failure Mechanisms. Actuators, 14(5), 205. https://doi.org/10.3390/act14050205






