Design of Automatic Landing System for Carrier-Based Aircraft Based on Adaptive Fuzzy Sliding-Mode Control
Abstract
1. Introduction
- Complex external disturbances. Disturbances such as carrier air wake and constant wind affect CBA landing. In addition, because the CBA exhibits heightened sensitivity to wind disturbances due to its flight conditions, which are characterized by a high angle of attack and low dynamic pressure, its controller must exhibit a strong capacity to prevent wind disturbance.
- Nonlinear coupling and parameter uncertainty. The controller must be able to overcome matching uncertainty and nonlinear coupling, particularly when the CBA exhibits a strong nonlinear coupling feature amid considerable alterations in flight conditions.
- Weak self-stabilization of velocity. During landing, the CBA stays in the instability domain in terms of its velocity and maintains continuous instability without any control action, causing inaccurate tracking of its landing trajectory. Therefore, the power compensation system must be studied to compensate for velocity deviation via thrust adjustment.
- Sliding-Mode Surface: A predefined trajectory in the state space that the system state is driven towards. Once the system state reaches this surface, it is forced to remain on it, ensuring the desired system behavior.
- Fuzzy Controller: Reduces the complexity of the control system by minimizing the number of fuzzy rules required. The fuzzy controller processes the sliding-mode switching function to produce smooth control actions.
- Adaptive Mechanism: Continuously adjusts control parameters in real-time based on the current state of the system and external disturbances. This ensures that the controller remains effective even as system parameters change, enhancing robustness and performance.
2. Problem Formulation
2.1. Nonlinear Dynamic Model of CBA
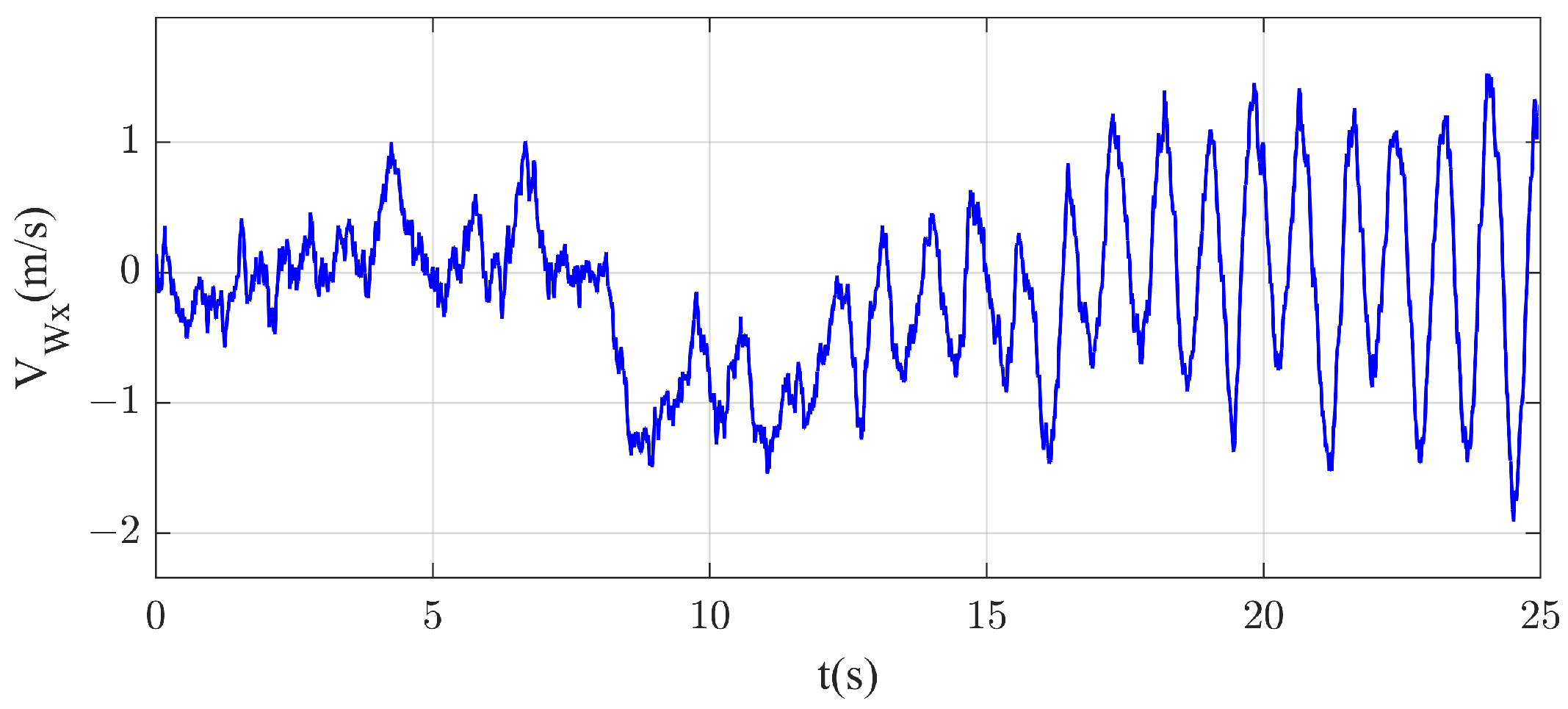
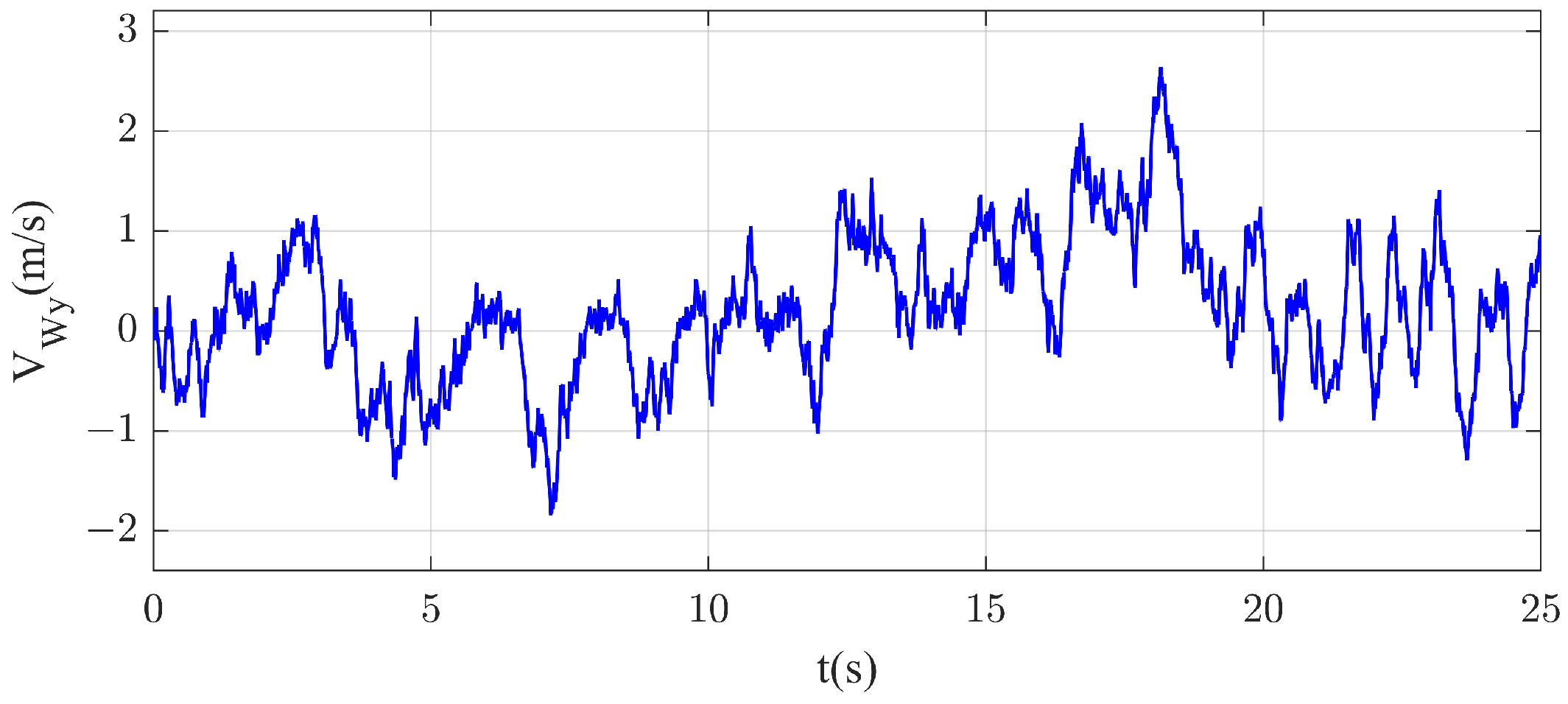
2.2. Carrier Air-Wake Model
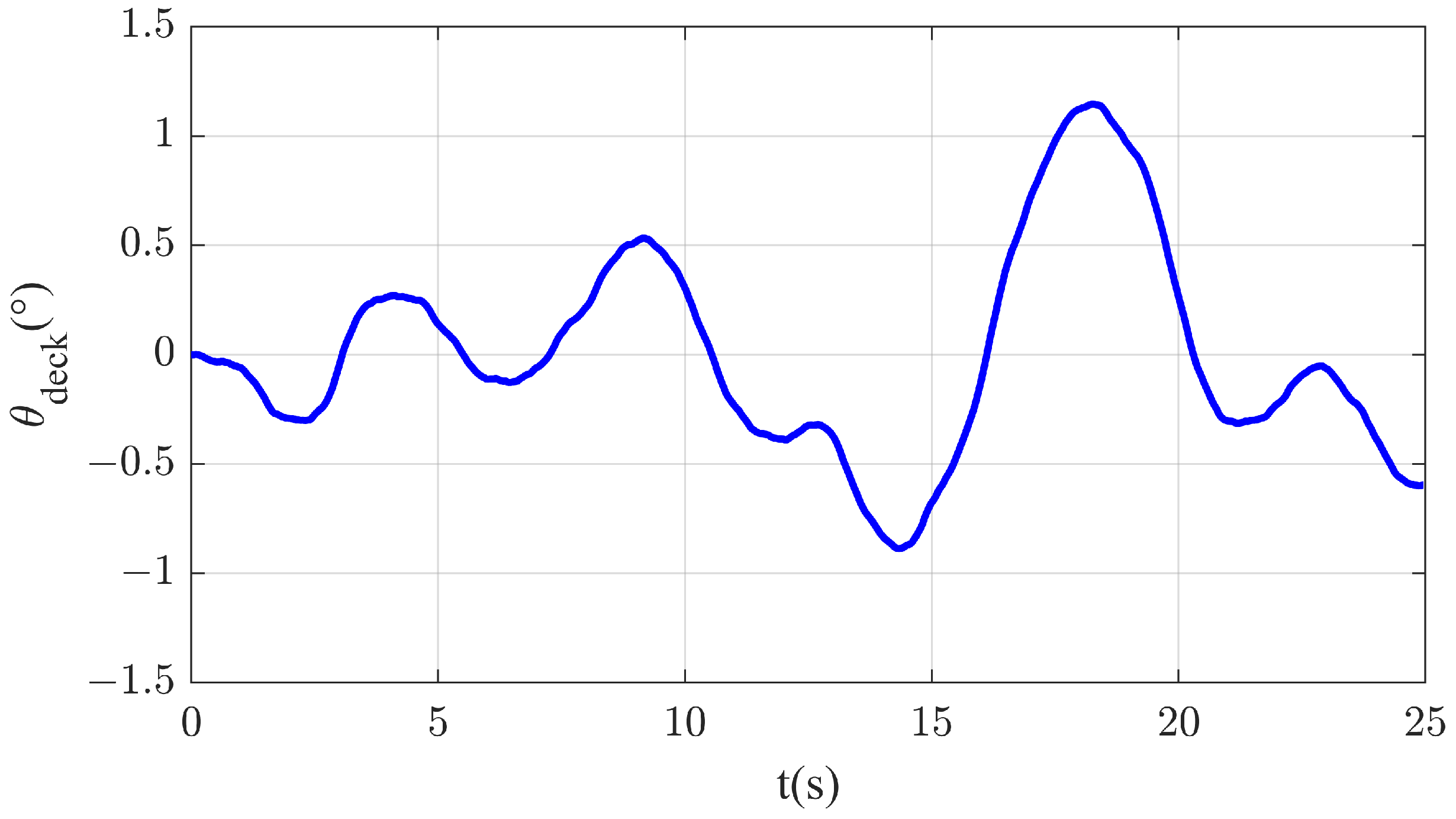
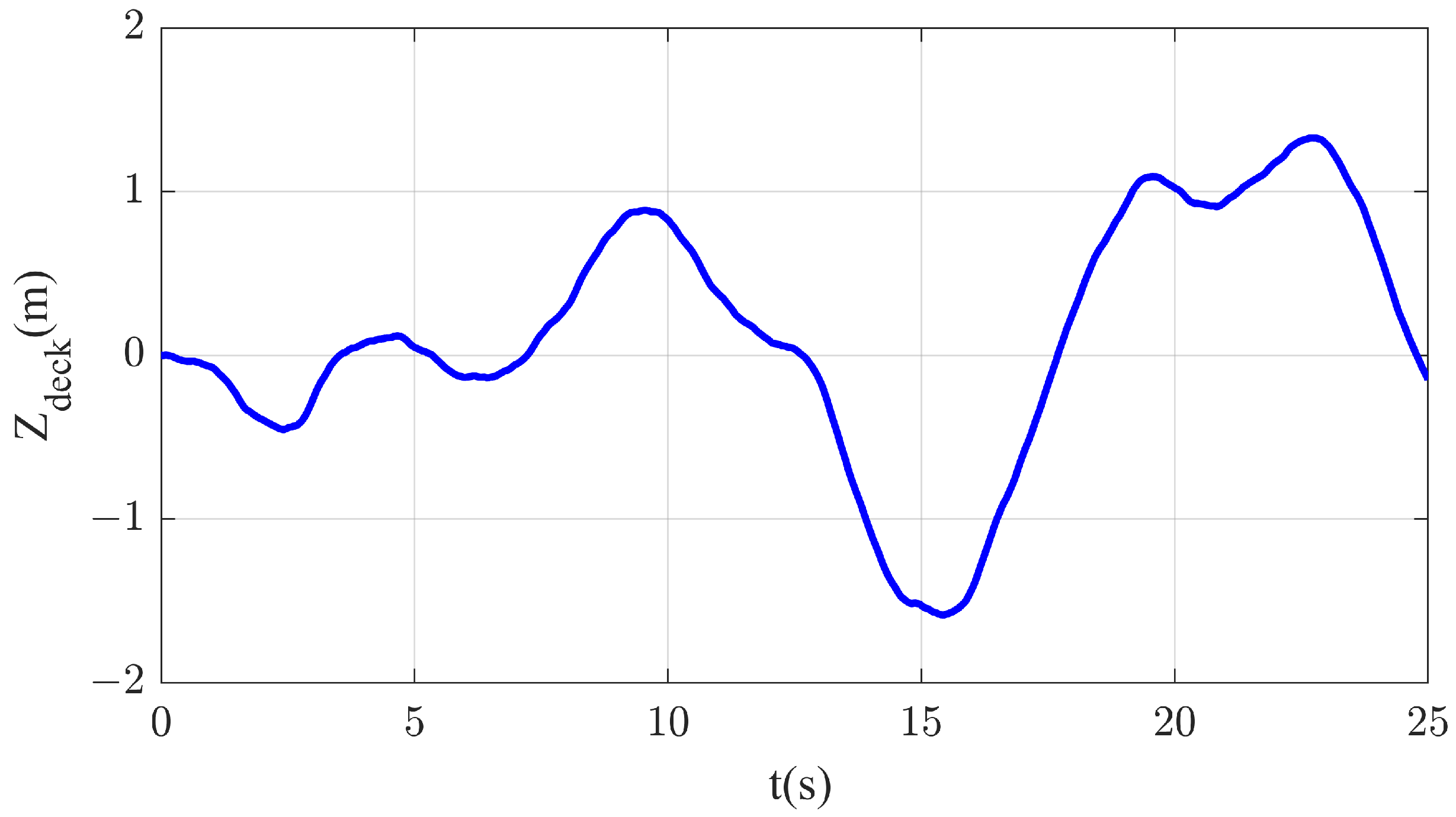
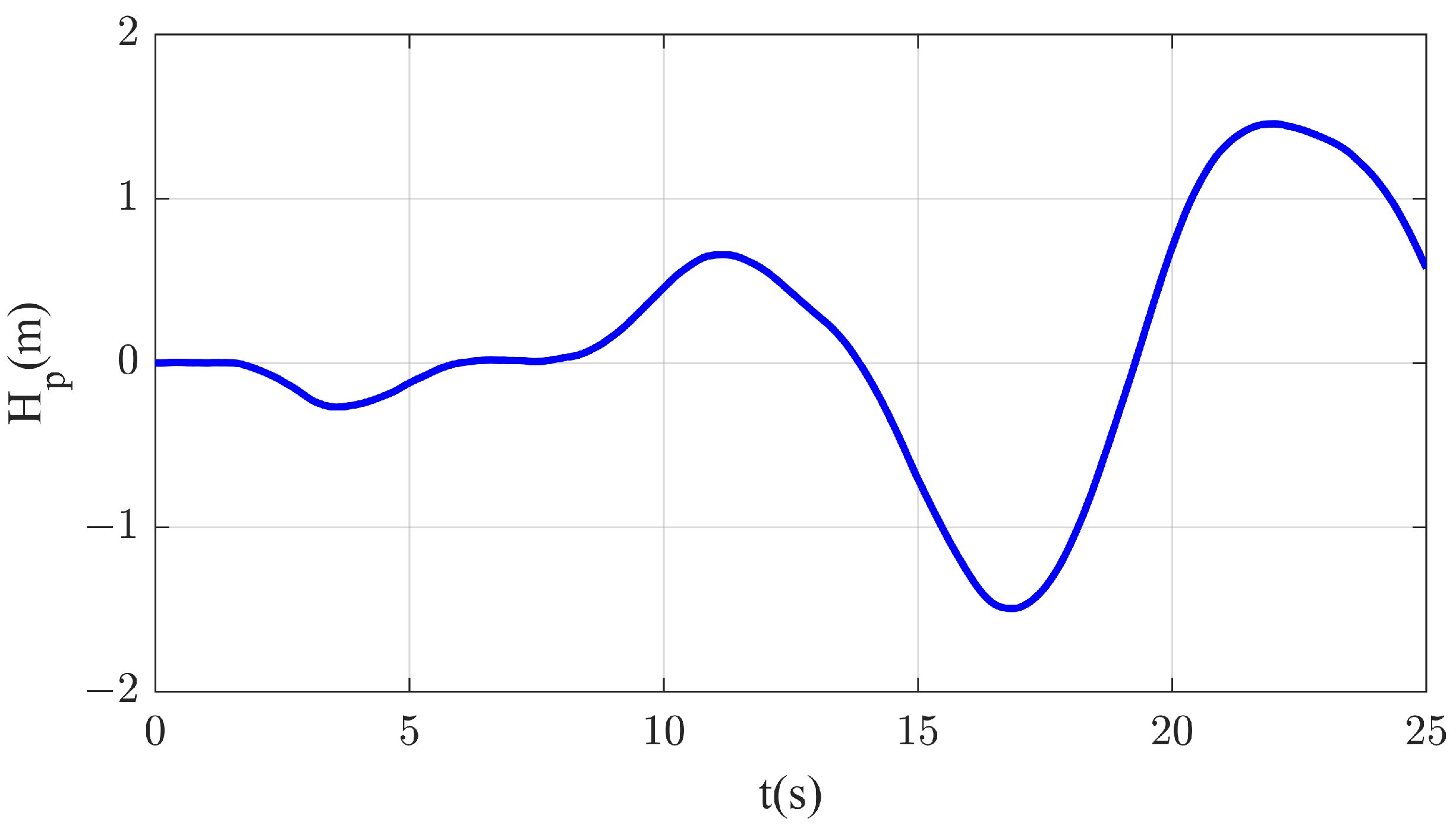
2.3. Motion Model of the Carrier Deck
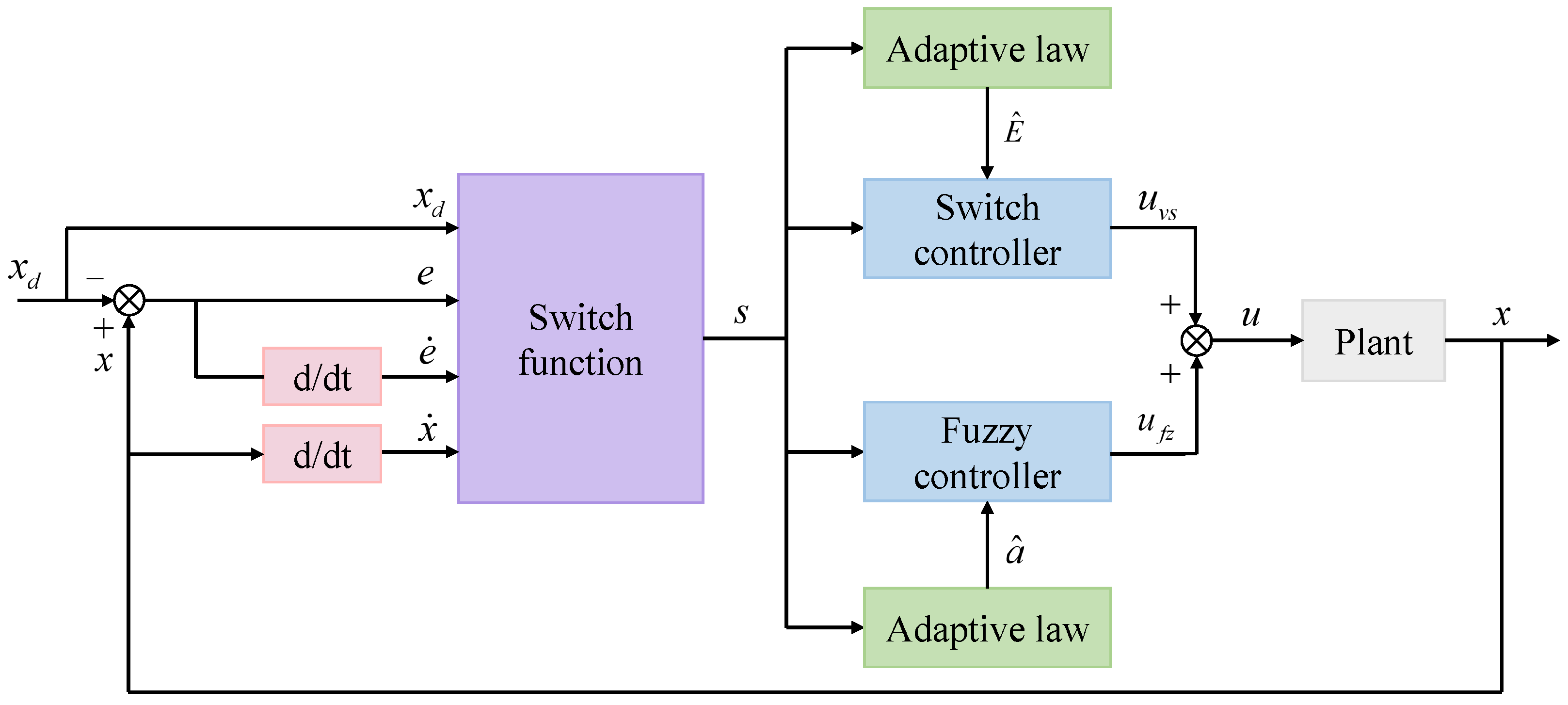
3. Design of the Adaptive Fuzzy Sliding-Mode Controller
3.1. Fuzzy Approximation Theorem
3.2. Design of the Controller
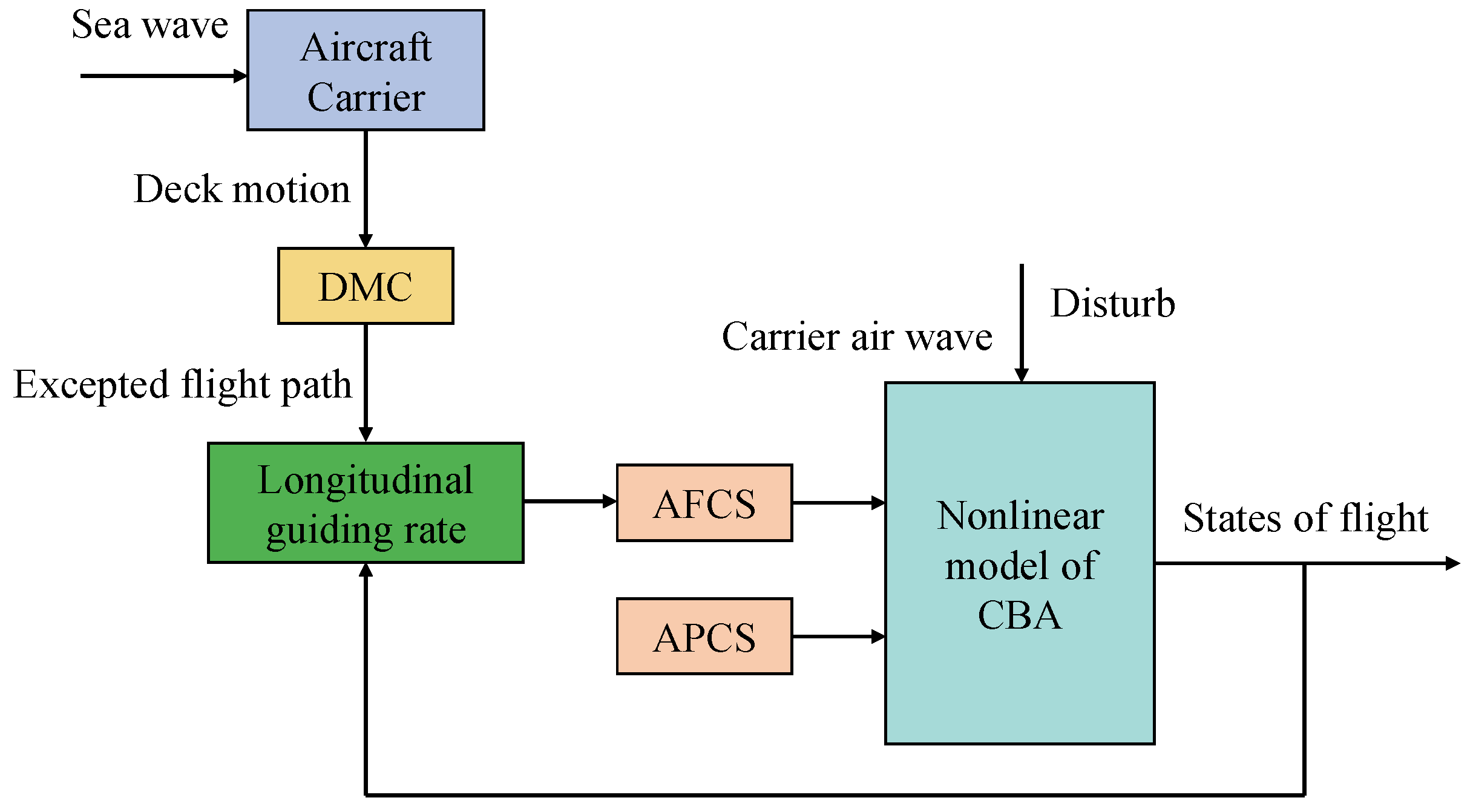
4. Design of the Longitudinal Automatic Landing System
4.1. Design of the AFCS
4.2. Design of the APCS
4.3. Design of the Longitudinal Guidance Law
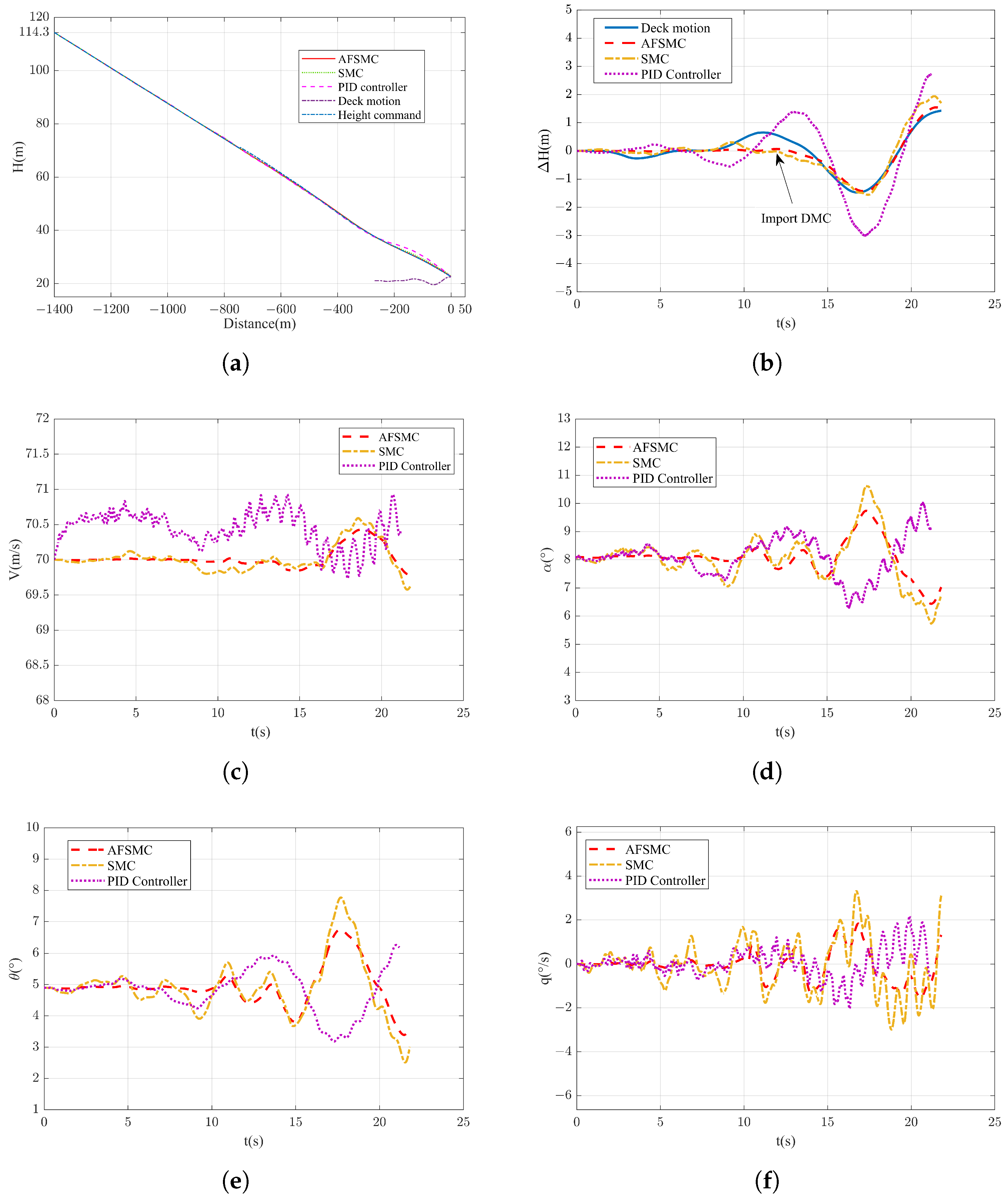
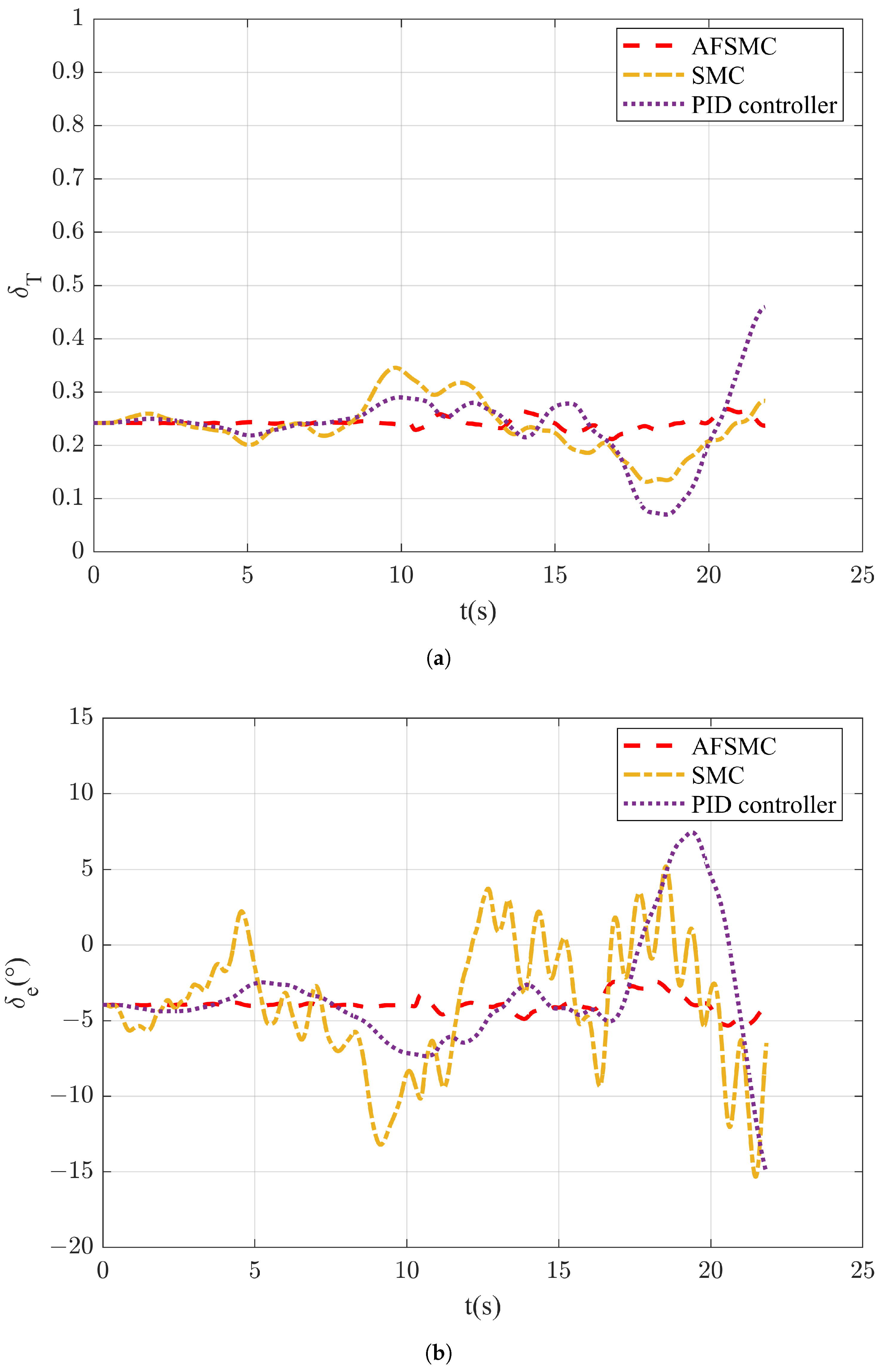
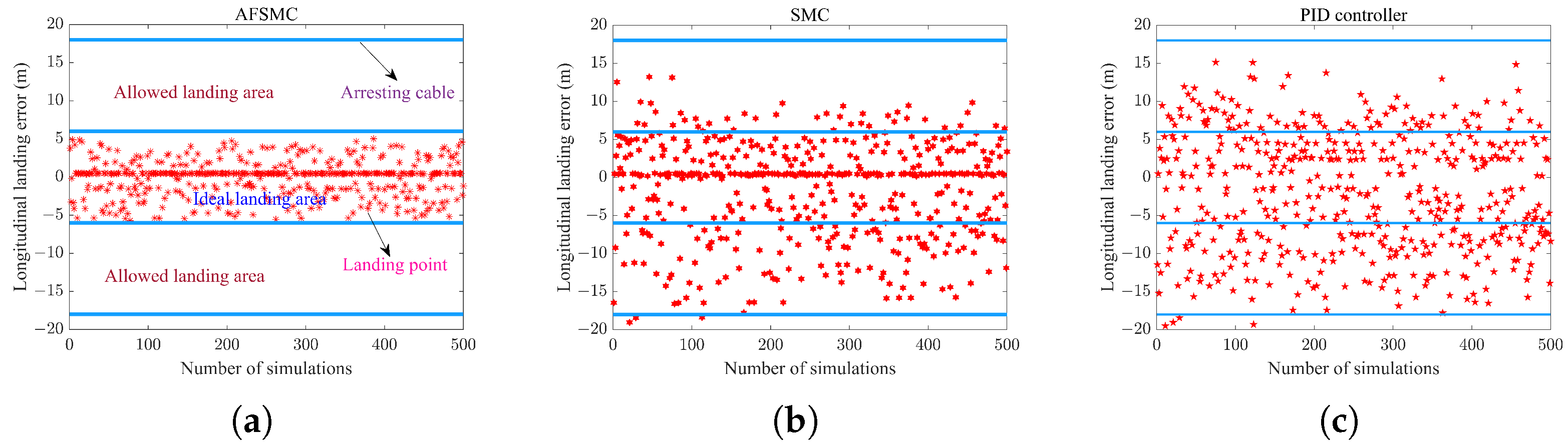
5. Simulations
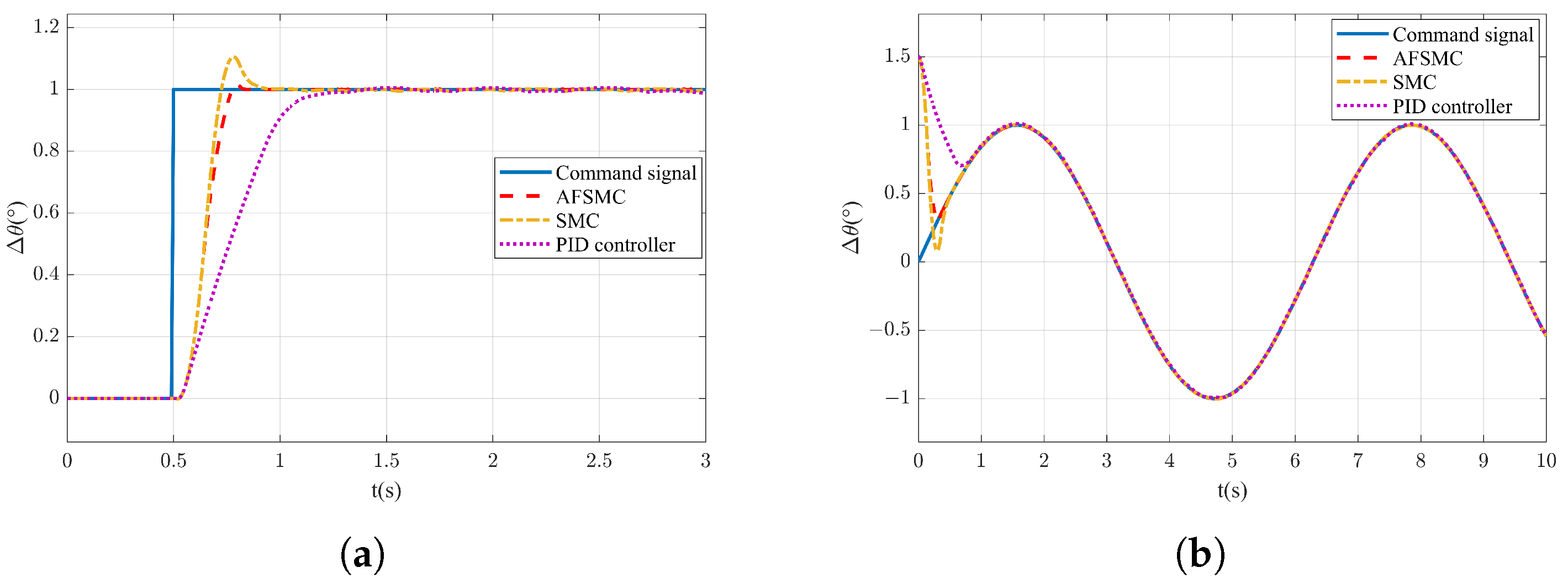
5.1. Parameter Settings and System Dynamic Response
5.2. Carrier Landing Simulation and Monte Carlo Target Shooting Testing
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liu, D.; Wu, J.; Zhou, Y.; Liu, Z.; Li, Y.; Wang, M. Practice and prospects of comprehensive support technologies of carrier-based aircraft. Hang Kong Xue Bao 2021, 42, 1. [Google Scholar]
- Johnson, G.; Peterson, B.; Taylor, J.; McCarthy, C. Test results of F/A-18 autoland trials for aircraft carrier operations. In Proceedings of the 2001 IEEE Aerospace Conference Proceedings (Cat. No. 01TH8542), Big Sky, MT, USA, 10–17 March 2001; Volume 3, pp. 3–1283. [Google Scholar]
- Zhang, W.; Zhang, Z.; Zhu, Q.; Xu, S. Dynamics model of carrier-based aircraft landing gears landed on dynamic deck. Chin. J. Aeronaut. 2009, 22, 371–379. [Google Scholar]
- Zhou, J.; Zeng, J.; Chen, J.; Tong, M. Analysis of Global Sensitivity of Landing Variables on Landing Loads and Extreme Values of the Loads in Carrier-Based Aircrafts. Int. J. Aerosp. Eng. 2018, 2018, 2105682. [Google Scholar] [CrossRef]
- Yang, X.; Yang, J.; Zhang, Z.; Ma, J.; Sun, Y.; Liu, H. A review of civil aircraft arresting system for runway overruns. Prog. Aerosp. Sci. 2018, 102, 99–121. [Google Scholar] [CrossRef]
- Yue, L.; Liu, G.; Hong, G. Design and simulation of F/A-18A automatic carrier landing guidance controller. In Proceedings of the AIAA Modeling and Simulation Technologies Conference, Washington, DC, USA, 13–17 June 2016; p. 3527. [Google Scholar]
- Urnes, J.; Hess, R. Development of the F/A-18A automatic carrier landing system. J. Guid. Control Dyn. 1985, 8, 289–295. [Google Scholar] [CrossRef]
- Sweger, J.F. Design Specifications Development for Unmanned Aircraft Carrier Landings: A Simulation Approach; US Naval Academy: Naval Academy, MD, USA, 2003. [Google Scholar]
- Mariano, I. Autonomous Landing System for a UAV. Master’s Thesis, Monterey California, Naval Post Graduate School, Monterey, CA, USA, 2004. [Google Scholar]
- JM Urnes, R.H.; Moomaw, R.; Huff, R. H-dot automatic carrier landing system for approach control in turbulence. J. Guid. Control 1981, 4, 177–183. [Google Scholar] [CrossRef]
- Misra, G.; Bai, X. Output-feedback stochastic model predictive control for glideslope tracking during aircraft carrier landing. J. Guid. Control Dyn. 2019, 42, 2098–2105. [Google Scholar] [CrossRef]
- Deng, J.; Yan, Z.; Ai, J. Application of fuzzy control technology to automatic carrier landing system. J. Syst. Simul. 2012, 24, 645–650. [Google Scholar]
- Yu, Y.; Wang, H.; Li, N.; Su, Z.; Wu, J. Automatic carrier landing system based on active disturbance rejection control with a novel parameters optimizer. Aerosp. Sci. Technol. 2017, 69, 149–160. [Google Scholar] [CrossRef]
- Wu, Z.; Ni, J.; Qian, W.; Bu, X.; Liu, B. Composite prescribed performance control of small unmanned aerial vehicles using modified nonlinear disturbance observer. ISA Trans. 2021, 116, 30–45. [Google Scholar] [CrossRef]
- Zhen, Z.; Jiang, S.; Ma, K. Automatic carrier landing control for unmanned aerial vehicles based on preview control and particle filtering. Aerosp. Sci. Technol. 2018, 81, 99–107. [Google Scholar] [CrossRef]
- Geng, J.; Yao, H.; Zhang, H. Studies on effect of air wake on slope and landing property of carrier aircraft. J. Syst. Simul. 2009, 21, 5940–5943. [Google Scholar]
- Luo, F.; Zhang, J.; Lyu, P.; Liu, Z.; Tang, W. Carrier-based aircraft precision landing using direct lift control based on incremental nonlinear dynamic inversion. IEEE Access 2022, 10, 55709–55725. [Google Scholar] [CrossRef]
- Guan, Z.; Ma, Y.; Zheng, Z.; Guo, N. Prescribed performance control for automatic carrier landing with disturbance. Nonlinear Dyn. 2018, 94, 1335–1349. [Google Scholar] [CrossRef]
- Subrahmanyam, M.B. H-infinity design of F/A-18A automatic carrier landing system. J. Guid. Control Dyn. 1994, 17, 187–191. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, J.; He, W. Adaptive fault-tolerant control for a nonlinear flexible aircraft wing system. Asian J. Control 2019, 21, 2340–2351. [Google Scholar] [CrossRef]
- Lungu, M.; Chen, M.; Vîlcică, D.A. Backstepping-and sliding mode-based automatic carrier landing system with deck motion estimation and compensation. Aerospace 2022, 9, 644. [Google Scholar] [CrossRef]
- Moulay, E.; Léchappé, V.; Bernuau, E.; Defoort, M.; Plestan, F. Fixed-time sliding-mode control with mismatched disturbances. Automatica 2022, 136, 110009. [Google Scholar] [CrossRef]
- Xiao, H.; Zhen, Z.; Xue, Y. Fault-tolerant attitude tracking control for carrier-based aircraft using RBFNN-based adaptive second-order sliding-mode control. Aerosp. Sci. Technol. 2023, 139, 108408. [Google Scholar] [CrossRef]
- Mofid, O.; Mobayen, S. Adaptive finite-time backstepping global sliding mode tracker of quad-rotor UAVs under model uncertainty, wind perturbation, and input saturation. IEEE Trans. Aerosp. Electron. Syst. 2021, 58, 140–151. [Google Scholar] [CrossRef]
- Dilmi, S. Enhancing flight envelope for a nonlinear aeroelastic wing-section using adaptive fuzzy sliding-mode control law. J. Aerosp. Eng. 2022, 35, 04022009. [Google Scholar] [CrossRef]
- Tian, Y.; Hu, Q.; Shao, X. Adaptive fault-tolerant control for attitude reorientation under complex attitude constraints. Aerosp. Sci. Technol. 2022, 121, 107332. [Google Scholar] [CrossRef]
- Xue, Y.; Zhen, Z.; Zhang, Z.; Cao, T.; Wan, T. Automatic carrier landing for UAV based on integrated disturbance observer and fault-tolerant control. Aircr. Eng. Aerosp. Technol. 2023, 95, 1247–1256. [Google Scholar] [CrossRef]
- Zhu, Q.; Yang, Z. Dynamic recurrent fuzzy neural network-based adaptive sliding control for longitudinal automatic carrier landing system. J. Intell. Fuzzy Syst. 2019, 37, 53–62. [Google Scholar] [CrossRef]
- Yao, Z.; Kan, Z.; Zhen, C.; Shao, H.; Li, D. Fault-Tolerant control for carrier-based UAV based on sliding mode method. Drones 2023, 7, 194. [Google Scholar] [CrossRef]
- Xu, D.; Liu, X.; Wang, L. Influence of carrier motion on landing safety for carrier-based airplanes. J. Beijing Univ. Aeronaut. Astronaut. 2011, 37, 289–294. [Google Scholar]
- Moorhouse, D.J.; Woodcock, R.J. Background Information and User Guide for MIL-F-8785C, Military Specification-Flying Qualities of Piloted Airplanes; Flight Dynamics Laboratory: Wright-Patterson AFB, OH, USA, 1982. [Google Scholar]
- Beal, T. Digital simulation of atmospheric turbulence for Dryden and von Karman models. J. Guid. Control Dyn. 1993, 16, 132–138. [Google Scholar] [CrossRef]
- Higgins, C.W.; Froidevaux, M.; Simeonov, V.; Vercauteren, N.; Barry, C.; Parlange, M.B. The effect of scale on the applicability of Taylor’s frozen turbulence hypothesis in the atmospheric boundary layer. Bound.-Layer Meteorol. 2012, 143, 379–391. [Google Scholar] [CrossRef]
- Deng, J. Research on the Theory and Simulation of Longitudinal Control System Design for Carrier-Based Aircraft Automatic Landing. Ph.D. Thesis, Fudan University, Shanghai, China, 2010. [Google Scholar]
- Li, A.; Liu, M.; Cao, X.; Liu, R. Adaptive quantized sliding mode attitude tracking control for flexible spacecraft with input dead-zone via Takagi-Sugeno fuzzy approach. Inf. Sci. 2022, 587, 746–773. [Google Scholar] [CrossRef]
- Van, M.; Ge, S.S. Adaptive fuzzy integral sliding-mode control for robust fault-tolerant control of robot manipulators with disturbance observer. IEEE Trans. Fuzzy Syst. 2020, 29, 1284–1296. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Ma, R.; Xing, Z.; Ai, J. Design of Automatic Landing System for Carrier-Based Aircraft Based on Adaptive Fuzzy Sliding-Mode Control. Actuators 2025, 14, 114. https://doi.org/10.3390/act14030114
Zhang H, Ma R, Xing Z, Ai J. Design of Automatic Landing System for Carrier-Based Aircraft Based on Adaptive Fuzzy Sliding-Mode Control. Actuators. 2025; 14(3):114. https://doi.org/10.3390/act14030114
Chicago/Turabian StyleZhang, Haotian, Ruoheng Ma, Zhenlin Xing, and Jianliang Ai. 2025. "Design of Automatic Landing System for Carrier-Based Aircraft Based on Adaptive Fuzzy Sliding-Mode Control" Actuators 14, no. 3: 114. https://doi.org/10.3390/act14030114
APA StyleZhang, H., Ma, R., Xing, Z., & Ai, J. (2025). Design of Automatic Landing System for Carrier-Based Aircraft Based on Adaptive Fuzzy Sliding-Mode Control. Actuators, 14(3), 114. https://doi.org/10.3390/act14030114




