1. Introduction
Rate integrating resonator gyroscopes (RIRGs) represent a kind of resonant gyroscope that has been adequately discussed and extensively applied within the inertial navigation community. These gyroscopes exhibit characteristics such as direct angular measurement and unlimited dynamic range [
1,
2]. The accuracy of the RIRG does not depend on the dimensions of the resonator, but rather on the material mechanism and manufacturing process, which can lead to two major types of errors in vibration: damping asymmetry and frequency mismatch [
3]. The requirements for suppressing instability in high-precision applications are necessary, encompassing more demands on the complexity of the control system and the accuracy of the error analysis.
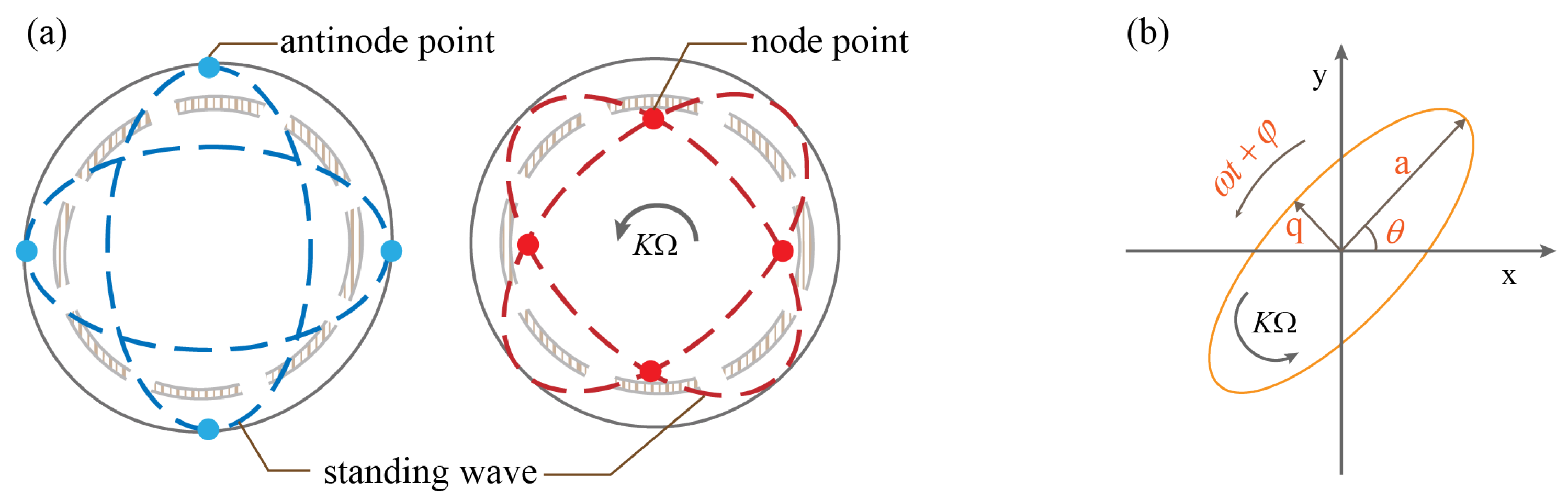
The relationship between the control strategy and the characteristic variables of the resonator could be described by the dynamic model equations related to damping asymmetry and frequency mismatch. Due to these errors, the output of the angle measurement contains multiple harmonic error terms correlated with the standing wave pattern angle [
4,
5].
For the purpose of reducing angular drifts, sophisticated control algorithms and imperfections compensation approaches have attracted lots of research interest. V. Apostolyuk [
6] presented a synthesis of a feedback controller aimed at reducing measurement drifts. Ryunosuke Gando [
7] and Kechen Guo [
8] utilized a feed-forward damper to adjust the resistance and voltage for compensating damping asymmetry. Siamak Zargari [
9] proposed an additional feedback path to decrease the quadrature error in the readout circuit. Parsa Taheri-Tehrani [
10] and Jiangkun Sun [
11] paid more attention to the relationship between the actuation gain and angular errors resulting from the electrode misalignment and the gap asymmetry. Ruan [
12] manipulated a proportional-integral resonance controller instead of traditional proportional-integral controllers to automatically eliminate frequency mismatch.
All of the above studies were conducted based on a linear dynamic model. However, it has been shown in the literature [
13,
14,
15] that there may exist fourth harmonic components present in the drift error. To comprehensively explore the dynamics of the RIRG system when operating beyond the linear region, it is essential to adopt a model including the nonlinear damping and stiffness contributions.
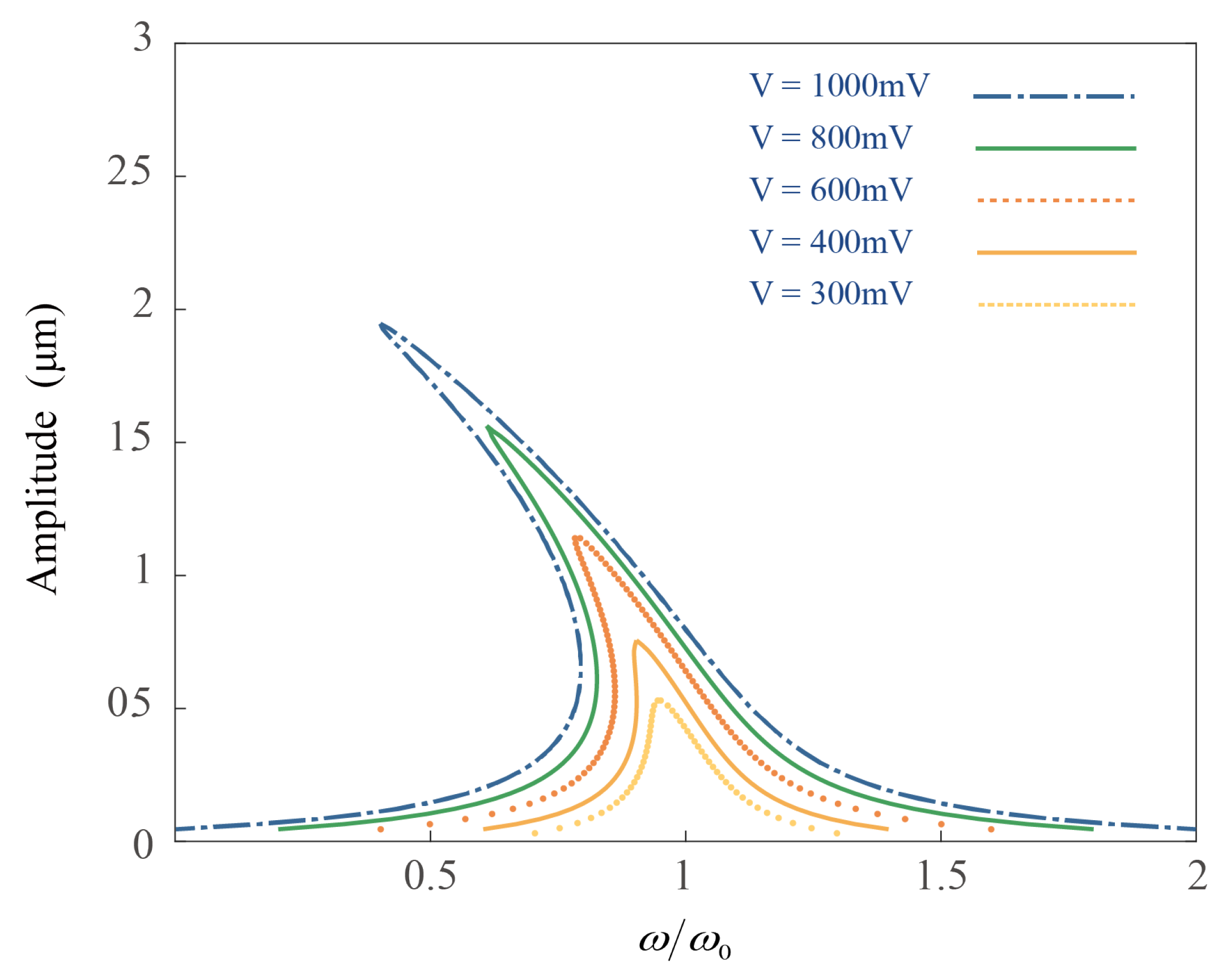
The nonlinear errors in RIRGs arise from multiple sources. Firstly, the use of flat electrodes for detection and actuation induces electrostatic spring-softening nonlinearity, leading to cubic nonlinearities. Additionally, the mechanical nonlinearity of the structure itself results in the Duffing nonlinearity. Extensive studies have documented the nonlinear response and bifurcation phenomena of resonators due to elastic and damping nonlinearities [
16,
17,
18]. Among the most commonly reported nonlinear effects is the amplitude–frequency response induced by Duffing nonlinearity. Several innovative techniques have been proposed to mitigate these effects, including the application of tuning voltages to adjust frequency mismatches dependent on bifurcation thresholds [
16], the use of capacitance corrections based on linearization factors [
18,
19], and the identification of amplitude-dependent correction gains to counteract nonlinearities in capacitive detection [
20]. Furthermore, nonlinearity originating from electrostatic transduction and capacitance gap nonuniformity complicates the relationship between the RIRG input and output [
21]. Given the correlation between harmonic errors and the standing wave pattern angle, an effective approach for precise angular measurement involves establishing a high-accuracy dynamic output compensation model for the RIRG. Therefore, the accuracy of parameter identification is crucial for the implementation of the nonlinearity harmonic error compensation.
Artificial intelligence has been gradually applied to various fields, including resonator gyroscopes. Xia et al. integrated a Fuzzy-PID controller with a BP neural network for the temperature control system of micro-gyroscopes, ensuring temperature stability [
22]. H. Yu et al. developed a capacitance-pose inverse model using a BP neural network to enhance the capacitance uniformity of RIRGs [
23]. Y. Li et al. proposed a genetic algorithm to optimize the dynamic output decomposition of resonator gyroscopes [
24].
Particle swarm optimization (PSO) is one of the intelligent swarm optimization algorithms which has good nonlinear optimization ability and variable recognizing ability [
25]. An improved PSO algorithm introduces chaos mapping which is used to enhance the distribution diversity of population particles, enabling more efficient and accurate parameter identification.
In this paper, considering the nonlinearities of the resonator, we develop a resonator motion model to analyze the effects of these errors on the threshold range of RIRG angular velocity and establish the relationship between the vibration pattern angle and the dynamic output drift errors of the RIRG. To denoise the RIRG output, we propose an improved particle swarm optimization (IPSO) algorithm based on chaos mapping for harmonic parameter identification aimed at compensating for the RIRG output drift. The effectiveness of the proposed IPSO-based parameter identification and drift compensation is validated through the simulation of the entire nonlinear RIRG control system. The performance of the compensation is evaluated by comparing the original drift error of the RIRG with the drift error corrected using the harmonic parameters identified by IPSO.
The following sections of this paper are organized as follows:
Section 2 presents an analysis of the dynamic model of the RIRG system containing nonlinear coefficient terms.
Section 3 discusses the threshold obstacle and the angle output distortion problem of RIRG in the nonlinear region based on the angular error equation.
Section 4 details the use of the IPSO algorithm to estimate the parameters. The results of the simulation and experimental studies on closed-loop control are presented in
Section 5.
Section 6 provides a summary of the findings of the study.
4. Harmonic Error Parameter Intelligent Identification and Compensation Method
In order to eliminate the error induced by the damping relevant error terms, a signal varying with the pattern angle is generated as compensation. The key to the compensation method is to estimate the RIRG’s damping asymmetry and damping nonlinearity parameters and exert the angle-dependent signal into the angular output loop. Equation (
10) explains that linear error induces second harmonic drifts, whereas nonlinear error leads to fourth harmonic changes. Therefore, the output form of the resonant standing wave motion is a superposition of multiple harmonics. Since whichever drifts discussed in this chapter are angle-dependent, for inertial measurement devices such as RIRG, which have a periodic pattern of their errors, the locomotor position of the standing wave can be utilized to achieve the identification of the error parameter of the RIRG. The physical significance of the error parameters to be identified indicates the dominance of the output angular error. The angle-dependent signal to be recognized can be written as
where vector
represents the harmonic error components.
For minimizing multiple harmonics variations caused by angle drift, it is significant to set the right amount of compensation signal. After the measurements of the RIRG are made as described previously, these angle output data are used to evaluate the parameters in the nonlinearity harmonic model.
4.1. LSM-Based Identification of Parameters for the Nonlinear Harmonic Model
The most widely used estimation method in the field of parameter identification is the least squares method (LSM). The advantage of LSM is the simplicity of the algorithm, and theoretically, the accuracy of its parameter estimates increases with the increase of observed data.
To reflect the time-varying characteristics of the parameters during the identification period, a forgetting factor is further introduced, which is to ensure that the influence of the previous data on parameter identification is smaller than that of the current data, so that the time-varying parameters can be better tracked. In addition, a damping factor is introduced to avoid the bursting phenomenon of the recognized parameters.
where
and
are the damping coefficient and forgetting factor.
However, the optimal metric for the LSM is the minimization of the sum of the estimated mean square errors of the measurement-based and does not ensure that the parameter identification errors are optimal, so the identification accuracy is not enough. In this paper, we propose an IPSO method to identify the harmonic parameters based on chaos mapping. This method eliminates the linear and nonlinear distribution of the angular velocity drift signals without affecting the feedback control parameters. IPSO can identify the unknown parameters so that we can set a virtual angle output loop with the estimate of the parameter vector and generate the compensation signal based on the identification. The IPSO method does not replace the PID control loops for the control of the major axis, minor axis, and resonance tracking.
4.2. IPSO-Based Identification of Parameters for the Nonlinear Harmonic Model
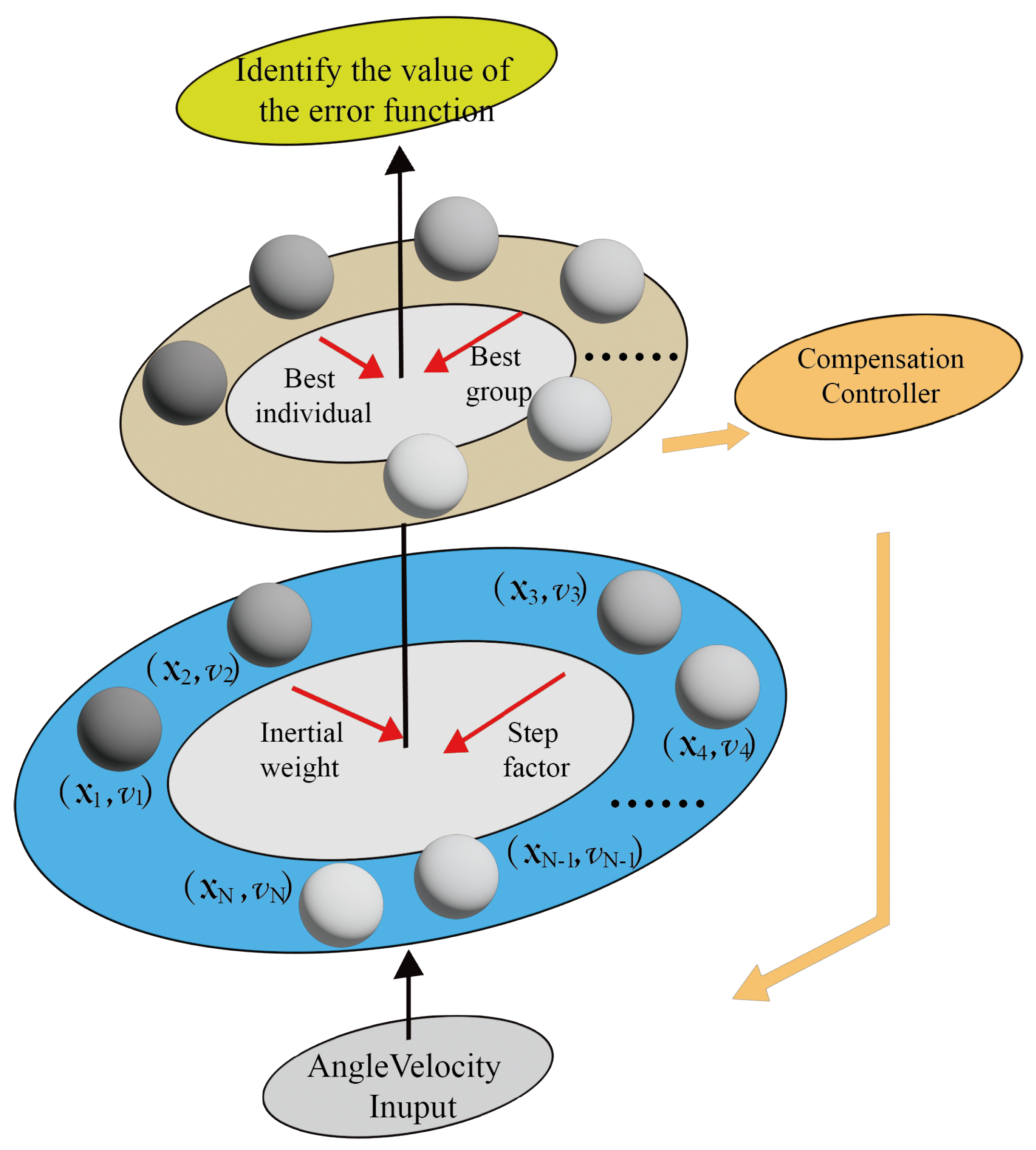
From the optimization theory, an intelligent identification algorithm is further used to identify the error parameters of the RIRG system. The PSO algorithm has the advantages of small computation, high accuracy, and fast convergence among many optimization algorithms. PSO is a swarm optimization algorithm inspired by the foraging process of flock birds, which is widely used to solve constraint optimization problems and find the optimal solution through simulating social behavior like cooperation and information sharing. The route decision of the flock while searching consists of three parts, spontaneous random search direction, its own searching experience, and the searching experience of the entire population. For the PSO algorithm, the foraging behavior of individual birds can be seen as the spontaneous random search of particles, and the optimal solution is the result of the optimal solution trend of the particle itself united with the best solution trend of the particle swarm. Each particle updates its properties of position and velocity according to the optimal fitness of itself and the optimal particle in the population so that the iteration direction of each particle is toward the region of the optimal solution.
The position of individual particles represents a trial solution for the search problem. The PSO is designed with time-varying inertia weights to enable it to consider the search performance, and its velocity and position update equations are as follows:
where
is the globally optimal particle and
is the locally optimal particle.
is the velocity attained by the particle after iterative search.
represents the position reached by the particle after iterative calculation.
denotes the inertia weight.
and
are the learning factors of the particle and the population, respectively.
and
are the random search coefficient of the particle and the population, respectively.
Comparing the fitness of each particle with , if the current value exceeds , then the value is set equal to the current location in the solution space. The fitness is compared with the best fitness observed previously in the overall population. If the current value exceeds , then is reset to the value of the current particle and the current particle position is recorded as the best solution.
- (1)
Adaptive inertia weight
The traditional PSO algorithm has the disadvantage of poor balance between search and evolution. Since the inertia weight reflects the dependable degree of the particles on the previous update rate, the variable weight is more adaptive to the change in optimization requirements than the constant weight. At the beginning of the iteration, the search strategy focused on the search domain broadening to find as many local optimal solutions as possible. In order to locate the region where the potential globally optimal solution exists as soon as possible, the step size of each search by the particle is to be appropriately enlarged. In the later stages of the iteration, the population requires search property for precise localization in the range of existing optimal solutions. Therefore, the search step size should be appropriately reduced. In addition, the process of random movement and then precise localization of the particle population is not a linear transition, so linearly varying inertia weight is unable to respond to changes in individual learning rates. To meet the tasks of these two search phases, nonlinear inertia weights are introduced to adapt to this situation. The adaptive weights are calculated as
where
and
denote the minimum inertia weight and maximum weight of particles when the population is initialized.
usually takes 0.1 and
usually takes 0.9,
t is the current number of iterations, and
T is the utmost number of iterations.
- (2)
IPSO based on chaotic variables
The diversity of population particles represents searching accuracy and convergence precision. If the distribution of initial values is too narrow, it may lead to a lack of diversity in the early population and affect the global search ability. There is a need for greater initial distribution diversity to mitigate the effects of uneven individual distribution during the population iteration. Benefiting from the stochastic and ergodic characteristics, the chaos technology has the ability out of the local optimal solution to overcome the defect of the PSO algorithm that is easy to fall into the local extreme point and thus has better performance of global optimization. To obtain a stronger chaotic traversal, we choose the Cubic chaotic mapping which is constructed by raising the degree of Logistic mapping. the Cubic chaotic mapping is appropriate and defined by the following equation:
where
for an unimodal surjection and ergodic enough in the range
[
26].
The Cubic chaotic mapping is used to design the initial search speed and position of particles for improving the uniformity of particle distribution:
where
and
are generated by Cubic chaos mapping.
Figure 5 is the flowchart of the IPSO. The process of parameter identification is to inversely obtain the corresponding model parameters from the measurement output so that the simulation result under those parameters can be as close as possible to the actual measured response curve. The optimization function is introduced as the IPSO algorithm fitness function to obtain the optimization parameters. Therefore, the parameter identification problem can be transformed into a set of optimization problems. Based on a set of optimal parameter vectors, the error between the simulation response result and the actual measurement reaches the minimum thus obtaining the identification result of error parameters. The target function is established according to the minimum sum of squares of errors, as shown in Equation (
22):
The harmonic parameters are evaluated using the IPSO, and the optimal solution is obtained. Each particle represents a different set of vector u and these particles are conceptual entities that travel through the multidimensional search space. At any iteration, each particle has a position and a velocity. The identification error function is designed to evaluate the compensation model performance. The identification error function is also the objective function of the particle swarm update, which ultimately reflects the accuracy of the identification. Then, the intelligent controller compares the gyroscope output with the fitting angular output by identification and updates the parameter vector by using the IPSO method. The individuals with the smallest fitness function are found by following the current search best value. When the minimum of the function is reached, the RIRG output is decomposed optimally.
5. Simulation Results and Performance Evaluation
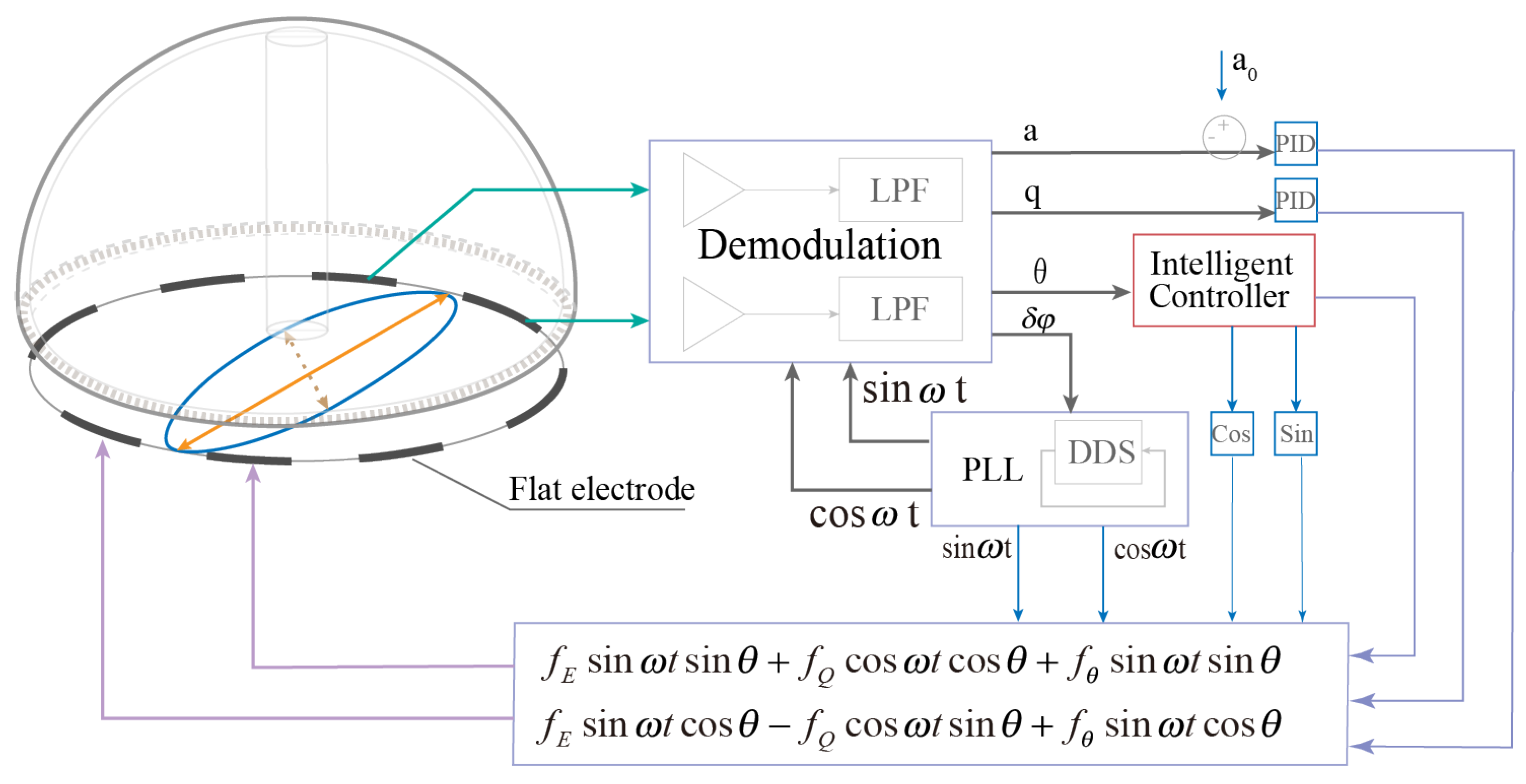
In order to validate the effectiveness and accuracy of error compensation using the IPSO parameter identification method, a series of tests were conducted on a self-built simulated dynamic system. The simulation validation system is shown in
Figure 6.
The proposed parameter identification method is validated through a comprehensive numerical simulation of the RIRG system, which incorporates the dynamics model of the gyroscope, the phase-locked loop for resonance tracking, the energy compensation loop for amplitude maintenance, and the motion feedback for quadrature nulling. The training set for the prediction model is constructed using the output of standing wave pattern angle simulations and the corresponding angular velocity input data. The performance of error parameters identification and compensation was compared based on LSM, PSO, and IPSO methods. The parameters used in the simulation related to the real RIRG device are presented in
Table 1.
The LSM-based parameter identification process is shown in
Figure 7. The forgetting factor is chosen to be 0.92 to improve the tracking accuracy and the damping factor is 0.9 to adapt to the nonlinearity of the system. Since the initial value of LSM is selected blindly, the estimation error jumps drastically in the early stage of identification, and as the number of measurements increases, the unreliability of the initial value gradually disappears, and the identification result tends to be stable. In addition to the problem of insufficient accuracy, LSM has the disadvantage of not being able to be implemented in real-time systems, where it cannot dynamically identify the error parameters based on the current error and system state to achieve optimal compensation.
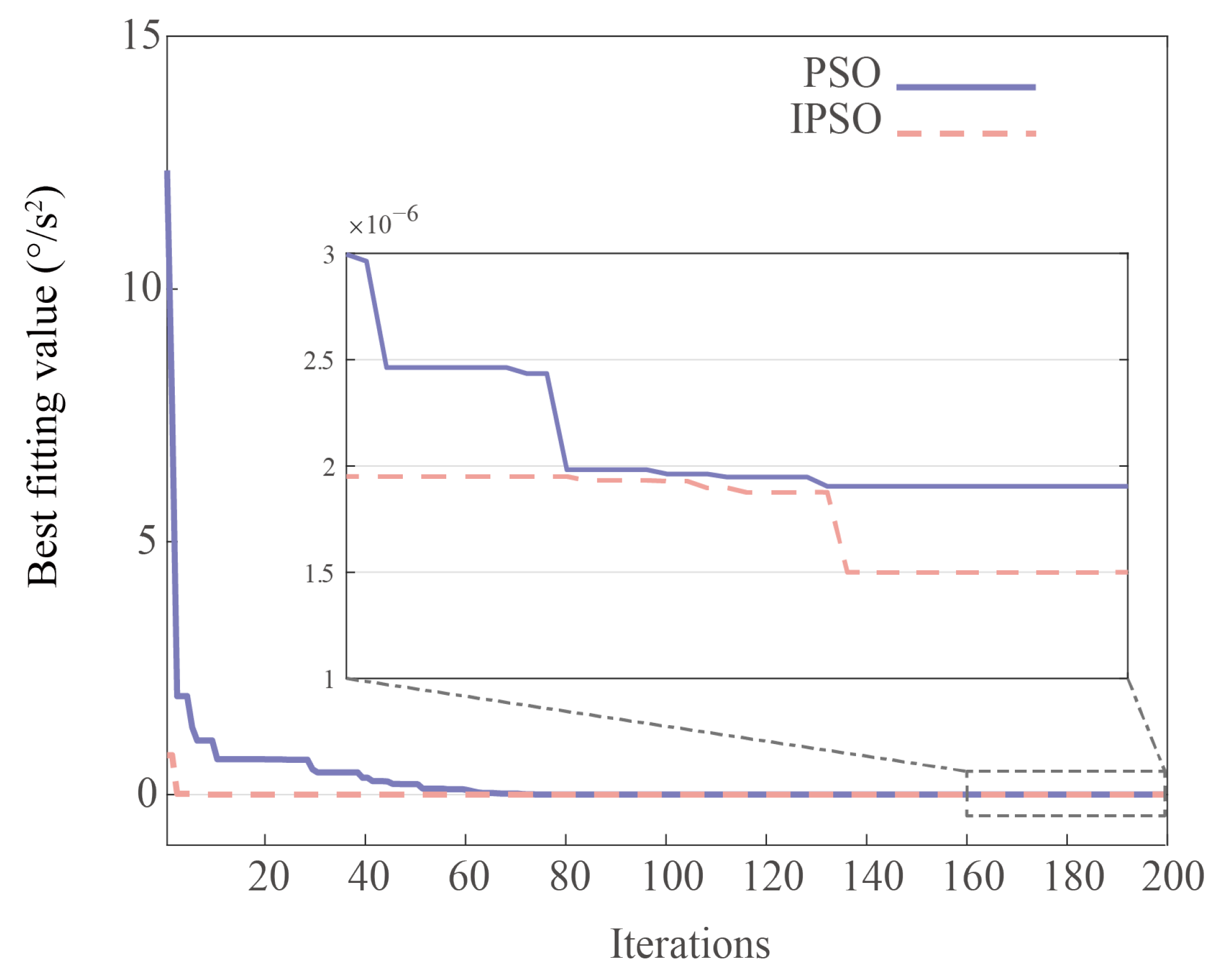
The core of the IPSO algorithm is to find a particle’s position that can satisfy the population’s optimal solution, and the investigation index is the objective function value as small as possible. The range of particle motion velocity is set within
and the range of
u is set within
, the population particle number is set as 150 and the number of iterations is set as 200. And then, the PSO and IPSO parameter initialization are set, respectively, to generate the random population. As shown in
Figure 8, the individuals with the smallest fitness function are found through iterations in the population. When the number of iterations reaches 160, the IPSO algorithm has converged, while the PSO has not yet fully converged.
The stability and the optimal rate of convergence of the PSO and IPSO are shown in
Figure 9, which means the number of iterations required to reach the optimal solution is reduced. This can be a critical factor in real-time system implementation where computational efficiency is important. By visualizing the optimization performance of the two algorithms under the same conditions, it can be intuitively seen that IPSO outperforms PSO in terms of convergence speed and global search capability.
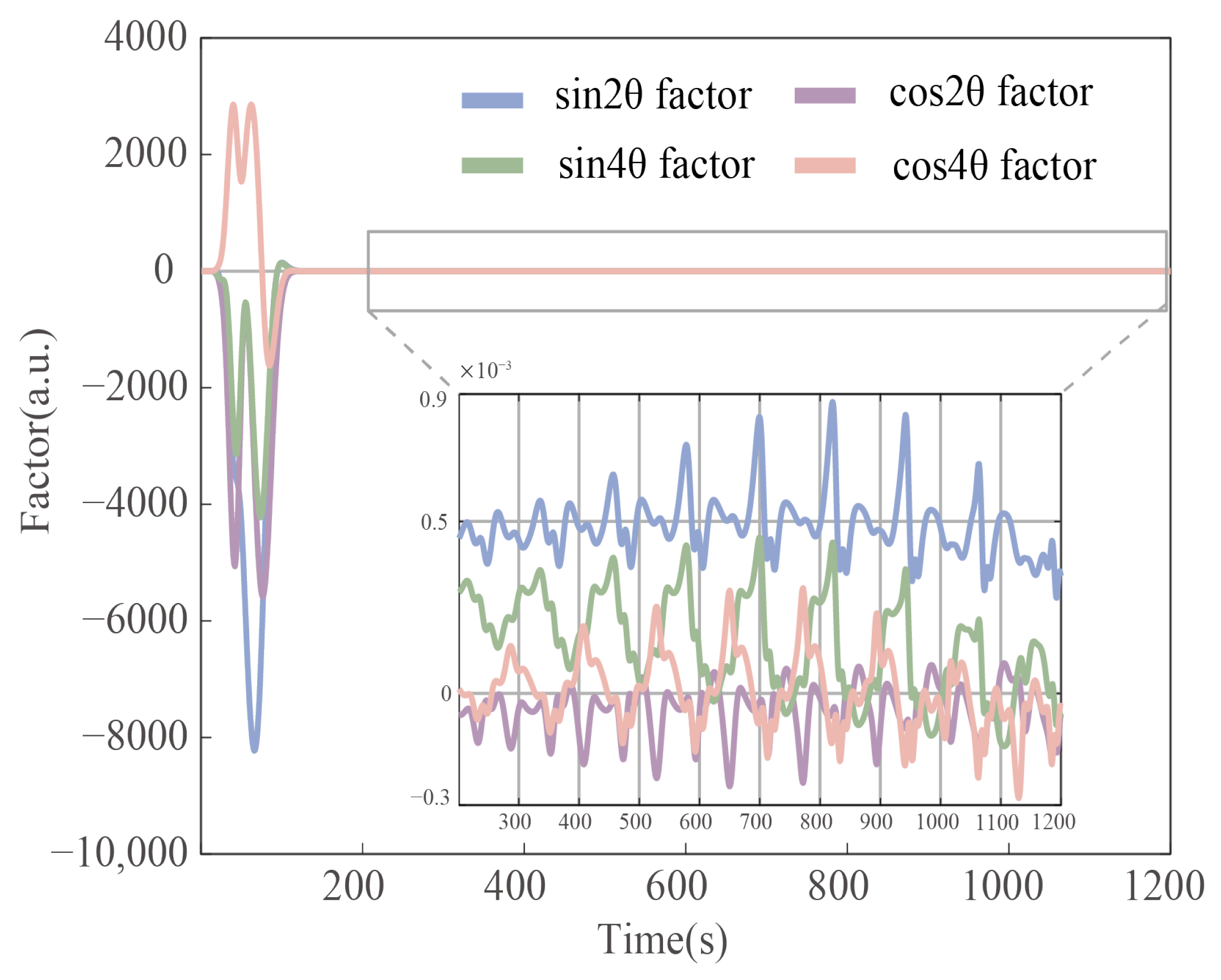
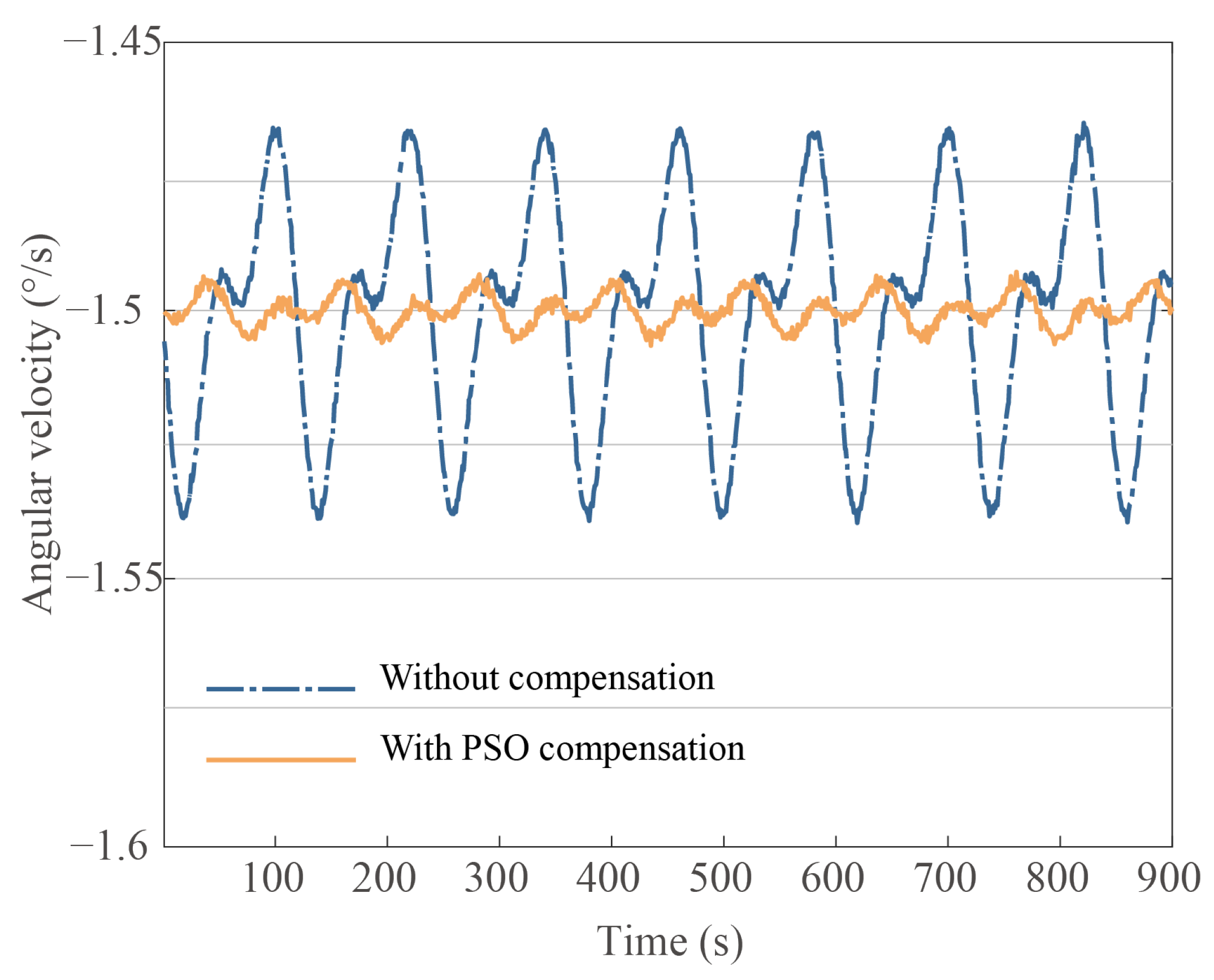
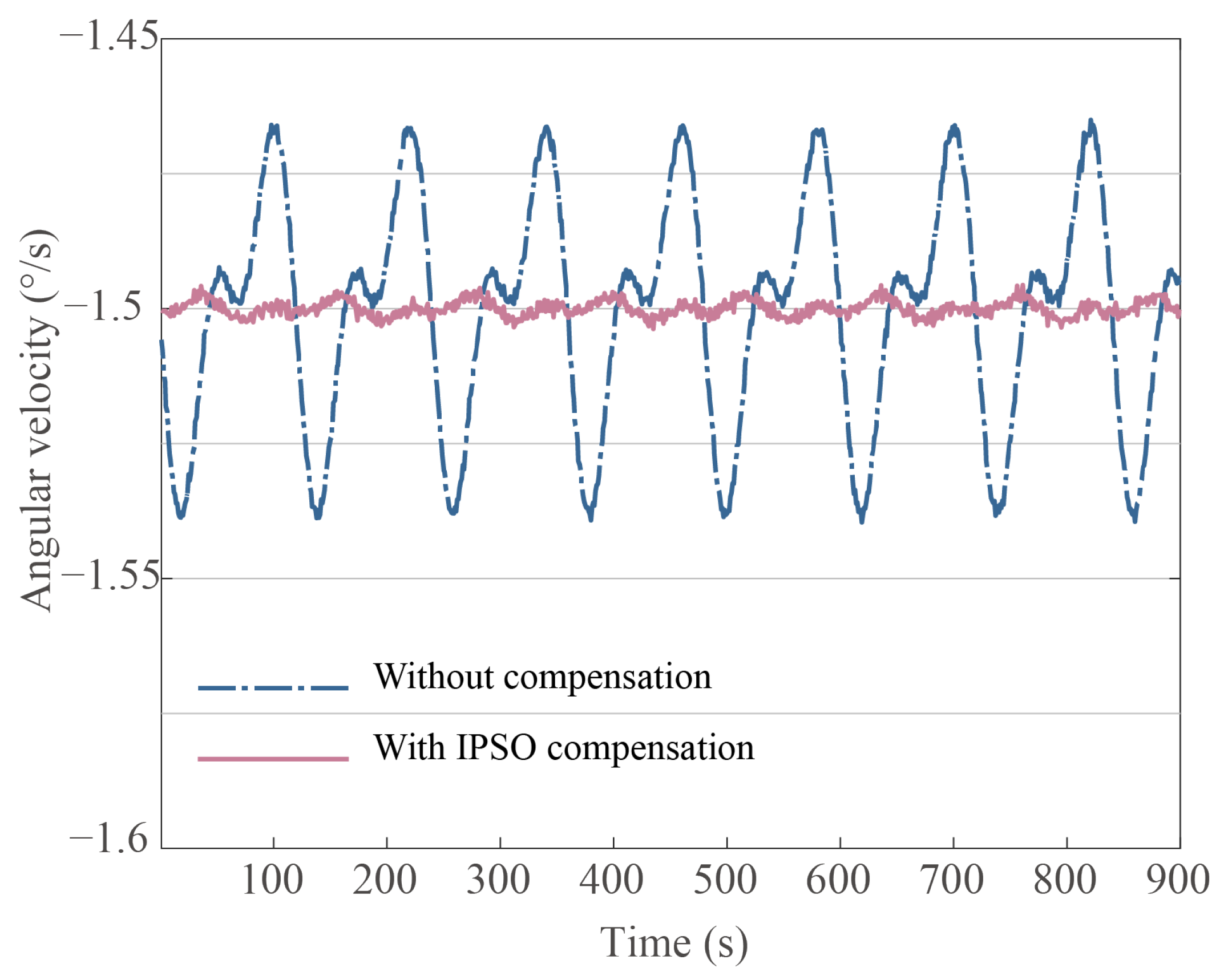
The error parameter identification and compensation experiments were conducted to verify the identification model’s effectiveness and the identification method’s feasibility. This paper analyzes and simulates gyroscope bias drift compensation under three identification methods with a standard deviation of 1 × 10−5 sampling noise added to the simulation model. The results from the IPSO-based parameter identification were successfully used in the feedback control to minimize angle drift error. Other methods were used for the comparison to prove the effectiveness, including LSM and PSO.
When the gyroscope is under constant rate input, the fluctuation magnitude of the standing wave rotation rate indicates the maximum angle drift.
Figure 9,
Figure 10 and
Figure 11 show the compensation results after minimizing the harmonic errors under diverse parameter identification methods and demonstrates the effectiveness of the IPSO as a powerful tool in the process of reducing bias drift error caused by damping anisotropy and damping nonlinearity. In
Figure 9,
Figure 10 and
Figure 11, the input rate condition is kept consistent. Following the IPSO-based compensation, the bias drift decreased from 2.1046 ×
°/s to 1.4722 ×
°/s. In comparison, other identification methods, including the traditional PSO and LSM, bias drift compensated values of 2.4533 ×
°/s and 9.8372 ×
°/s, respectively.
The standard deviations and the mean of measurements based on LSM, PSO, and IPSO identification are summarized in
Table 2. It can be seen that the LSM is lower than the intelligent algorithm in terms of recognition accuracy, the PSO has improved recognition accuracy but has a lower convergence rate, and the error compensation results using the improved PSO intelligent algorithm are much better than the other two algorithms.
In summary, the nonlinear error analysis and compensation method proposed in this paper can be successfully applied to RIRG and achieve high accuracy identification and compensation of the error parameters.
6. Conclusions
This paper presents a novel method for achieving high-precision identification and compensation of bias drift in RIRG dynamic output, which establishes the relationship between standing wave pattern angle and RIRG harmonic errors by introducing a nonlinearity component. Initially, the RIRG nonlinear error model reveals the propagation of damping-dependent elements in the RIRG system, including damping anisotropy error and damping nonlinearity error, leading to threshold regions, distortions, and periodic vibrations in measurements. Subsequently, a model for identifying harmonic parameters, which considers both damping anisotropy and nonlinear errors, is developed based on the dynamic drift model of the RIRG. Parameter identification of RIRG is an essential prerequisite for any adaptive control and state feedback compensation to minimize output errors. An IPSO method based on the slow varying averaged dynamic model is applied to harmonic error parameter identification in this paper. With the help of adaptive inertia weight and a richer initial distribution diversity of the population through chaos-based technique, it leads to IPSO for RIRG identification with improved accuracy, stability, and suitability. Compared with the LSM-based method and PSO-based identification methods, the measurement accuracy and the effect of harmonic components compensation are significantly enhanced. Numeric simulation validates the proposed algorithms with fast convergence and great accuracy. Estimated nonlinear damping parameters from the IPSO are effectively used for setting the correct amount of feedback to compensate for the nonlinear error in the angular drift. Based on the identification result, the compensation for the RIRG dynamic output error is realized. The dynamic experiment verifies the effectiveness of the proposed method, and the bias drift of the RIRG dynamic is reduced from 2.1046 × °/s to 1.4722 × °/s, the bias drift error is reduced by 93%, and accuracy is improved by an order of magnitude.