Almost Disturbance Decoupling Control Strategy for a Class of Underactuated Nonlinear Systems with Disturbances

Abstract

This paper introduces an almost disturbance decoupling approach to address the disturbance problem for a class of underactuated nonlinear systems. First, a residual system is constructed using a virtual controller and partial differential equations. Next, the unknown disturbances are addressed using an almost disturbance decoupling approach, where Young’s inequality is applied to handle the disturbance terms in the residual system. An almost disturbance decoupling controller is designed for the residual system. The locally asymptotic stability of the closed-loop system is rigorously proven using Lyapunov’s theorem. Finally, simulation results on an IWP system with unknown disturbances and experimental results on an overhead crane are presented to validate the effectiveness of the proposed almost disturbance decoupling control method.

1. Introduction

Many of the commonly used pieces of equipment, such as tower cranes and gantry cranes, in production and construction are affected by factors such as air turbulence and wind, which can bring challenges to control systems; so, disturbance control becomes an urgent problem to be solved. The type of equipment is underactuated systems. In this paper, the almost disturbance decoupling (ADD) method is used to design a nonlinear controller to solve the disturbance attenuation problem. The disturbance term is handled by Young’s inequality and backstepping is used to design an ADD controller for underactuated systems. The stability of the closed-loop control system is theoretically proven based on the Lyapunov stability theory.

The ADD problem was originally proposed by [1] for linear systems. The problem of ADD for linear systems is revisited by placing the maximum number of poles in the closed-loop solution [2]. Linearization methods are applied to address ADD control problems for nonlinear systems. In [3], stochastic equivalent linearization methods are used to deal with nonlinear hysteresis dynamics, but such methods may not adequately capture the dynamic properties of complex nonlinear systems. In [4], a piezoelectric dual-chip nonlinear actuator is first linearized using a stochastic equivalent linearization method and a robust controller is designed for solving a standard ADD problem. In [5], the linear ADD design method is applied to investigate a satellite attitude control problem by using an input/output feedback linearization method. For single-input single-output (SISO) nonlinear systems, the $L_2$ gain ADD problem is established and a parameterized state feedback controller is constructed such that the $L_e$ gain from the disturbance to the output is arbitrarily small by increasing its gain [6]. The problem of ADD for SISO nonlinear systems is also investigated by using the singular perturbation method and high-gain feedback in [7]. A new set of ADD results is obtained for SISO nonlinear systems with unstable zero dynamics [8]. Ref. [9] designs an ADD strategy to suppress the external position disturbance and attenuate oscillations caused by discontinuous mechanical gaps for an electrohydraulic load simulator with mechanical backlash. In [10], for lateral motion of electric vehicles with uncertain disturbances, ADD sampled state feedback is developed to attenuate the effect of the disturbance on the output with arbitrary accuracy. The adaptive stabilization control problem of uncertain high-order fully actuated (HOFA) nonlinear systems with disturbances is studied, an ADD method is employed to handle unknown disturbances, and a novel adaptive ADD controller is proposed in [11]. In [12], an HOFA design method is proposed to control HOFA systems with disturbances, and a weak disturbance decoupling controller is designed for HOFA nonlinear systems to ensure the stability of the closed-loop system and the desired output tracking performance while mitigating the effects of disturbances. The study in [13] proposes a nonsingular terminal sliding mode active disturbance rejection decoupling controller for a three-dimensional autonomous underwater vehicle to achieve efficient trajectory tracking and enhance the disturbance rejection capability. In [14], for nonlinear systems with normal form, a fixed-time ADD controller is constructed to attenuate the impact of disturbances on the states of the closed-loop system. For nonlinear systems with unknown disturbances, by using the backstepping design technique, an ADD state feedback controller is designed to ensure the internal stability of the closed-loop system and boundness of the $L_2$ gain from disturbance to output [15]. In [16,17], the concept of fuzzy approximate disturbance decoupling is introduced for multiple-input multiple-output (MIMO) uncertain nonlinear systems, and a fuzzy adaptive ADD controller is proposed. It is worth noting that the publications mentioned above address the ADD control problem for actuated systems. ADD control for underactuated systems has not been investigated so far.

Commonly used nonlinear control methods for real systems include backstepping, block backstepping, predictive control, fuzzy logic, neural networks, sliding mode control, output tracking, adaptive control, and so on. In this paper, the backstepping method is primarily employed to handle the impact of disturbances for uncertain underactuated nonlinear systems.

The paper in [18] designs two nonlinear control laws for ships with asymmetric inertia, addressing the limitations of conventional assumptions like symmetric inertia and positive damping. In [19], a backstepping sliding mode control law is designed for uncertain nonlinear flight control systems expressed in the form of parametric strict feedback, for avoiding the over-parameterization problem and improving the system’s robustness and control performance. In [20], an adaptive backstepping controller is designed with state feedback and an associated Lyapunov function in order to solve the control problem for a class of chaotic systems. In [21], an adaptive robust controller based on the backstepping method is designed for a class of nonlinear systems with unknown parameters, successfully solving the stability problem in classical strict feedback form with sufficiently small non-triangular structured disturbances. A mathematical model of a pump-controlled electrohydraulic actuator was developed, and position control was formulated using a modified backstepping technique with a special Lyapunov function to address uncertainties [22]. In [23], a controller combining backstepping and online parameter updating rules is proposed for a class of unmanned helicopters with parameter uncertainty. In [24], a kinematic model of an automated guided vehicle is proposed and an adaptive backstepping trajectory tracking controller is designed to ensure stability when the slip parameters are unknown. Adaptive backstepping is applied to control the longitudinal dynamics of an unmanned aerial vehicle, with a nonlinear controller designed using elevator deflection and thrust as actuators, aiming to make the closed-loop system follow aerodynamic velocity and flight path angle references [25]. In [26], a finite-time observer-based interactive trajectory tracking controller is designed for an asymmetric underactuated surface vessel system, with the aim of rigorously proving that the kinematic and dynamic tracking errors globally asymptotically converge to zero. Backstepping methods are widely acknowledged and extensively applied in feedback control of fully driven systems, with their theoretical foundation well supported by Lyapunov’s theorem. In recent years, the advancement of finite-time control has led to the proposal of adaptive methods for uncertain nonlinear systems, which represent a further extension of backstepping methods [27]. A feedback linearization method is utilized to control an inertia wheel pendulum (IWP), which is an underactuated system [28].

The backstepping method has not been effectively generalized to underactuated systems, primarily due to the unique characteristics of the system’s input matrix. So far, boundary-stabilized backstepping schemes have been explored for novel underactuated partial differential equation (PDE) systems [29]. Moreover, methods such as block backstepping [30,31] and underactuated backstepping [32,33], derived from the backstepping concept, address the stability of underactuated systems. However, the backstepping method has not been applied to handling underactuated systems with disturbances.

Inspired by the above work, this paper proposes an underactuated ADD backstepping method for a class of underactuated nonlinear systems with disturbances. The stability of the proposed scheme is rigorously analyzed and proven using Lyapunov-based theoretical methods. The proposed controller is applied to an IWP and an overhead crane with disturbances to validate its effectiveness. Simulation and experimental results demonstrate that the proposed scheme successfully addresses the control challenges of underactuated systems with unknown disturbances.

The contributions of this work are as follows:

(1) A novel disturbance control scheme, termed ADD, is proposed for a class of underactuated systems with disturbances. Firstly, a virtual controller is designed using PDE to construct a residual system. Subsequently, the backstepping method is further applied to develop an ADD controller for the residual system.

(2) To address unknown disturbance terms, disturbance coefficients are scaled using Young’s inequality, effectively canceling their impact. The effectiveness of the proposed scheme is validated by simulation on an IWP and an experiment on an overhead crane. Compared to the backstepping methods in [30,31], which rely on variable transformations to reduce the original system to a lower-order form followed by backstepping-based design and analysis, the proposed method demonstrates significant advantages. It is not limited to simple stabilization tasks but also achieves ADD control and eliminates the need for zero-dynamics analysis. As a result, it avoids the complexities typically associated with solving zero dynamics.

The remainder of the paper is structured as follows: Section 2 introduces a class of underactuated nonlinear systems with disturbances and some fundamental concepts. Section 3 presents an ADD design approach and conducts the stability analysis for the closed-loop system. The simulation results for an IWP system are discussed in Section 4. The experimental results for an overhead crane are discussed in Section 5. Section 6 concludes the paper.

2. Problem Formulation

A class of underactuated nonlinear disturbed systems in a non-strict feedback form is described as follows:

$$\begin{array}{ccc}\hfill {\dot{x}}_1& =& z_1\hfill \\ \hfill {\dot{x}}_2& =& z_2\hfill \\ \hfill {\dot{z}}_1& =& f_1\left(x,z_1\right)+p_1^T\left(x,z_1\right)w\hfill \\ \hfill {\dot{z}}_2& =& s\left(x,z\right)u+f_2\left(x,z\right)+p_2^T\left(x,z\right)w\hfill \\ \hfill y& =& x_1,\hfill \end{array}$$

(1)

where $x={\left[x_1,x_2\right]}^T\in {\mathbb{R}}^{2\times 1}$ and $z={\left[z_1,z_2\right]}^T\in {\mathbb{R}}^{2\times 1}$ are the system states; $u\in \mathbb{R}$ is the control input; $w\in {\mathbb{R}}^{r\times 1}$ is the disturbance input that is square-integrable; $y\in \mathbb{R}$ is the output; and $p_1\left(x,z_1\right)\in {\mathbb{R}}^{r\times 1}$, $p_2\left(x,z\right)\in {\mathbb{R}}^{r\times 1}$, $f_1\left(x,z_1\right)\in \mathbb{R}$, $f_2\left(x,z\right)\in \mathbb{R}$, and $s\left(x,z\right)\in \mathbb{R}$ are known nonlinear $C^1$ functions with $s\left(x,z\right)\ne 0$, $f_1\left(0,0\right)=0$, $f_2\left(0,0\right)=0$, $p_1\left(0,0\right)=0$, and $p_2\left(0,0\right)=0$.

Assumption 1.

There exist positive constants $F_1$ and $P_1$ so that

$$\begin{array}{ccc}\hfill ∥f\left(x,z_1+{\Delta }_1\right)-f\left(x,z_1\right)∥& \le & F_1∥{\Delta }_1∥\hfill \end{array}$$

(2)

$$\begin{array}{ccc}\hfill ∥p_1\left(x,z_1\right)∥& \le & P_1\hfill \end{array}$$

(3)

Lemma 1.

(Young’s inequality) [34]: For any positive constant γ, the following inequality is true:

$$a^{T}b\le {\displaystyle \frac{\gamma }{2}}{a}^{T}a+{\displaystyle \frac{1}{2\gamma }}{b}^{T}b$$

(4)

The purpose of this paper is to design an ADD controller for (1) so that the closed-loop system have the following properties:

(a) When $w=0$, the origin of the closed-loop system is locally asymptotically stable.

(b) For given $\varphi >0$ and zero initial conditions, the following inequality is true:

$${\int }_0^t{y}^T\left(u\right)y\left(u\right)du\le \varphi {\int }_0^t{w}^T\left(u\right)w\left(u\right)du$$

(5)

for any $t<\infty$ and w satisfying ${\int }_0^{\infty }{w}^T\left(u\right)w\left(u\right)du<\infty$.

Remark 1.

The non-strict feedback characteristic of system (1) is evident in both the absence of a standard triangular structure and the characteristics of the residual system, which can be considered as a pure feedback form. Therefore, system (1) is categorized as having a non-strict feedback structure in this study.

3. Design of Almost Disturbance Decoupling Controller and Stability Proof

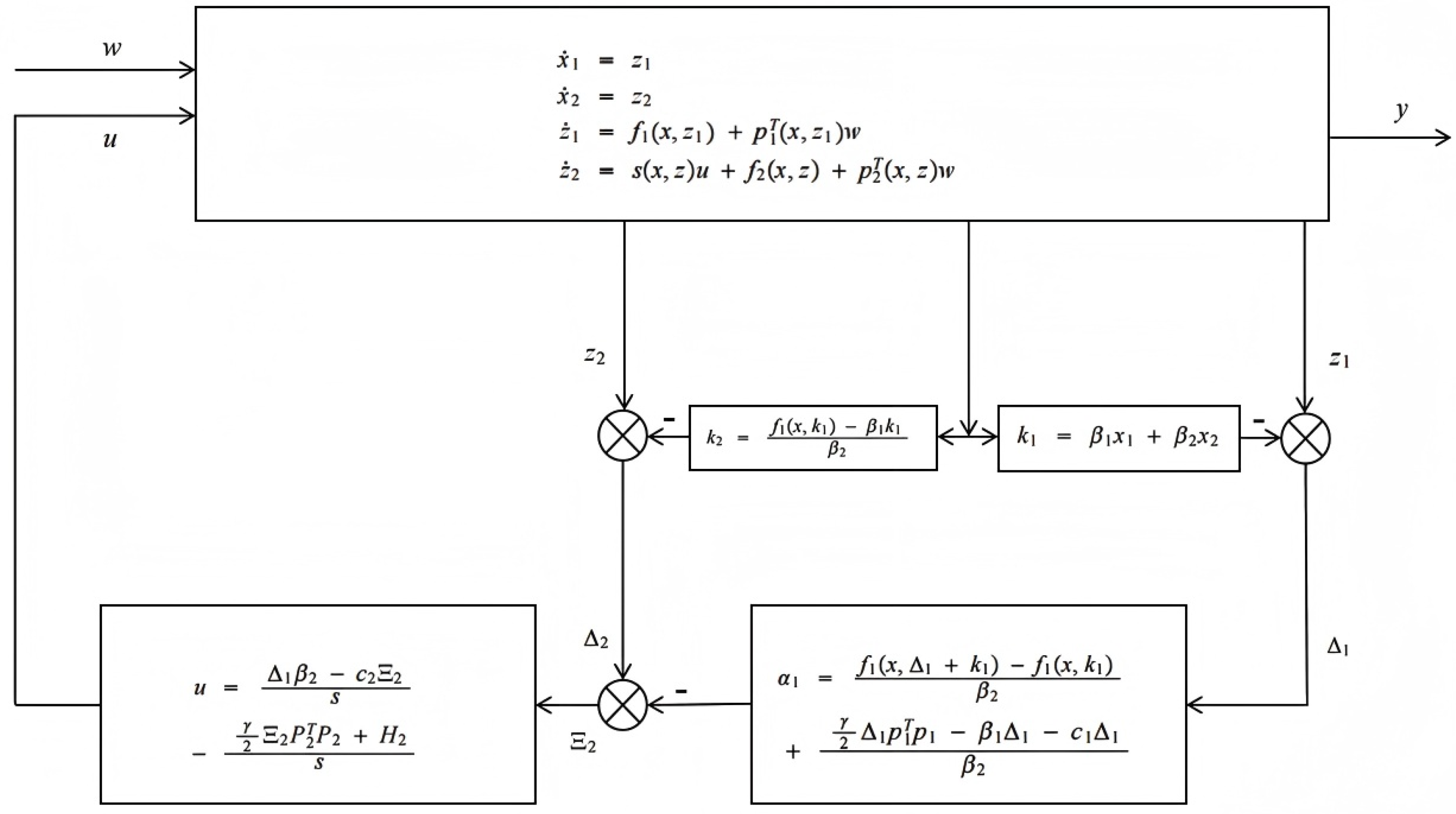
This section is devoted to designing an ADD controller for (1). To this end, a design algorithm is proposed, which is composed of three steps. The first step is to construct a virtual controller $z=k\left(x\right)$ so that $\dot{x}=k\left(x\right)$ is stable and $k\left(x\right)$ satisfies partial differential Equation (7). The second step is to construct a virtual controller ${\alpha }_1$ to make the derivative of Lyapunov function $V_1$ negative-definite. The third step is to design a controller u. Finally, the local stability of the closed-loop system is theoretically proved based on Lyapunov stability theory. The specific design steps of the controller are given as follows.

Step 1. The following coordinate transformation is introduced.

$$\begin{array}{ccc}\hfill {\Delta }_1& =& z_1-k_1\left(x\right)\hfill \end{array}$$

$$\begin{array}{ccc}\hfill {\Delta }_2& =& z_2-k_2\left(x\right)\hfill \end{array}$$

(6)

A virtual controller $k\left(x\right)={\left[k_1\left(x\right),k_2\left(x\right)\right]}^T$ is designed such that $\dot{x}=k\left(x\right)$ is stabilized. In order to eliminate ${\left({\displaystyle \frac{\partial k_1\left(x\right)}{\partial x}}\right)}^{T}k\left(x\right)$ in ${\dot{\Delta }}_1$, $k\left(x\right)$ satisfies the following PDE:

$$f_1\left(x,k_1\left(x\right)\right)=\left[\begin{array}{cc}{\displaystyle \frac{\partial k_1\left(x\right)}{\partial x_1}}& {\displaystyle \frac{\partial k_1\left(x\right)}{\partial x_2}}\end{array}\right]\left[\begin{array}{c}{k}_1\left(x\right)\\ k_2\left(x\right)\end{array}\right]$$

(7)

For simplicity, suppose a solution $k_1$ satisfies

$$k_1\left(x\right)={\beta }_1{x}_1+{\beta }_2{x}_2$$

(8)

where β₁ and β₂ are design parameters.

Then, the PDE becomes

$$f_1(x,k_1\left(x\right))={\beta }_1{k}_1\left(x\right)+{\beta }_2{k}_2\left(x\right)$$

(9)

which implies that

$$k_2\left(x\right)={\displaystyle \frac{f_1(x,k_1\left(x\right))-{\beta }_1{k}_1\left(x\right)}{{\beta }_2}}$$

(10)

Then, with (6), the subsystem about x can be rewritten as

$$\begin{array}{ccc}\hfill {\dot{x}}_1& =& {\Delta }_1+k_1\left(x\right)\hfill \end{array}$$

$$\begin{array}{ccc}\hfill {\dot{x}}_2& =& {\Delta }_2+k_2\left(x\right)\hfill \end{array}$$

(11)

In order to guarantee the stability of (11) with ${\Delta }_1={\Delta }_2=0$, the following assumption is introduced.

Assumption 2.

There exists a $C^1$ function $k\left(x\right)$ with $k\left(0\right)=0$ so that (8) and (9) are satisfied and the origin of (11) with ${\Delta }_1={\Delta }_2=0$ is locally exponentially stable.

Remark 2.

According to the converse Lyapunov theorem [35], Assumption 2 implies that there exists a Lyapunov function candidate $V_k\left(x\right)$ for subsystem (11) such that

$$\begin{array}{ccc}\hfill W_1{∥x∥}^2& \le & V_k\left(x\right)\le W_2{∥x∥}^2\hfill \end{array}$$

(12)

$$\begin{array}{ccc}\hfill {\left({\displaystyle \frac{\partial V_k\left(x\right)}{\partial x}}\right)}^{T}k\left(x\right)& \le & -L_1{∥x∥}^2\hfill \end{array}$$

(13)

$$\begin{array}{ccc}\hfill {∥{\displaystyle \frac{\partial V_k\left(x\right)}{\partial x}}∥}^2& \le & L_2{∥x∥}^2,\hfill \end{array}$$

(14)

where $W_1$, $W_2$, $L_1$, and $L_2$ are positive constants.

Step 2. Differentiating (6) yields

$$\begin{array}{ccc}\hfill {\dot{\Delta }}_1& =& {\dot{z}}_1-{\left({\displaystyle \frac{\partial k_1\left(x\right)}{\partial x}}\right)}^T\dot{x}\hfill \\ & =& f_1\left(x,z_1\right)+p_1^T\left(x,z_1\right)w\hfill \\ & & -{\left({\displaystyle \frac{\partial k_1\left(x\right)}{\partial x}}\right)}^T(\Delta +k\left(x\right))\hfill \\ & =& f_1(x,{\Delta }_1+k_1\left(x\right))+p_1^T\left(x,z_1\right)w\hfill \\ & & -{\left({\displaystyle \frac{\partial k_1\left(x\right)}{\partial x}}\right)}^T\Delta -{\left({\displaystyle \frac{\partial k_1\left(x\right)}{\partial x}}\right)}^{T}k\left(x\right)\hfill \\ & =& f_1(x,{\Delta }_1+k_1\left(x\right))-f_1(x,k_1\left(x\right))\hfill \end{array}$$

$$\begin{array}{ccc}& & -{\beta }_1{\Delta }_1-{\beta }_2{\mathsf{\Xi }}_2-{\beta }_2{\alpha }_1+p_1^T\left(x,z_1\right)w\hfill \end{array}$$

(15)

$$\begin{array}{ccc}\hfill {\dot{\Delta }}_2& =& {\dot{z}}_2-{\left({\displaystyle \frac{\partial k_2\left(x\right)}{\partial x}}\right)}^T\dot{x}\hfill \\ & =& su+f_2\left(x,z\right)+p_2^T\left(x,z\right)w\hfill \\ & & -{\left({\displaystyle \frac{\partial k_2\left(x\right)}{\partial x}}\right)}^T(\Delta +k\left(x\right))\hfill \end{array}$$

$$\begin{array}{cc}& =su+p_2^T\left(x,z\right)w+v\end{array}$$

(16)

where $\Delta ={\left[{\Delta }_1,{\Delta }_2\right]}^T$, $v=f_2(x,z)-{\left({\displaystyle \frac{\partial k_2\left(x\right)}{\partial x}}\right)}^T(\Delta +k\left(x\right))$, ${\alpha }_1$ is a virtual controller, and

$${\mathsf{\Xi }}_2={\Delta }_2-{\alpha }_1$$

(17)

The stability of the closed-loop system is analyzed using Lyapunov’s theorem. A Lyapunov candidate function can be constructed as

$$V_1={\displaystyle \frac{1}{2}}{\Delta }_1^2$$

(18)

Differentiating (18) yields

$$\begin{array}{ccc}\hfill {\dot{V}}_1& =& {\Delta }_1{\dot{\Delta }}_1\hfill \\ & =& {\Delta }_1\left(f_1(x,{\Delta }_1+k_1\left(x\right))-f_1(x,k_1\left(x\right))\right)\hfill \end{array}$$

$$\begin{array}{ccc}& & +{\Delta }_1\left(-{\beta }_1{\Delta }_1-{\beta }_2{\mathsf{\Xi }}_2-{\beta }_2{\alpha }_1+p_1^T\left(x,z_1\right)w\right)\hfill \end{array}$$

(19)

It follows from Lemma 1 that

$${\Delta }_1{p}_1^T\left(x,z_1\right)w\le {\displaystyle \frac{\gamma }{2}}{\Delta }_1^2{p}_1^T\left(x,z_1\right)p_1\left(x,z_1\right)+{\displaystyle \frac{1}{2\gamma }}{w}^{T}w$$

(20)

Substituting (20) into (19) produces

$$\begin{array}{ccc}\hfill {\dot{V}}_1& \le & {\Delta }_1\left(f_1(x,{\Delta }_1+k_1\left(x\right))-f_1(x,k_1\left(x\right))\right)\hfill \\ & & +{\Delta }_1\left(-{\beta }_1{\Delta }_1-{\beta }_2{\mathsf{\Xi }}_2-{\beta }_2{\alpha }_1\right)\hfill \\ & & +{\displaystyle \frac{\gamma }{2}}{\Delta }_1^2{p}_1^T\left(x,z_1\right)p_1\left(x,z_1\right)+{\displaystyle \frac{1}{2\gamma }}{w}^{T}w\hfill \\ & =& {\Delta }_1\left(f_1(x,{\Delta }_1+k_1\left(x\right))-f_1(x,k_1\left(x\right))\right)\hfill \\ & & +{\Delta }_1\left(-{\beta }_1{\Delta }_1-{\beta }_2{\alpha }_1+{\displaystyle \frac{\gamma }{2}}{\Delta }_1{p}_1^T\left(x,z_1\right)p_1\left(x,z_1\right)\right)\hfill \end{array}$$

$$\begin{array}{ccc}& & +{\displaystyle \frac{1}{2\gamma }}{w}^{T}w-{\Delta }_1{\beta }_2{\mathsf{\Xi }}_2\hfill \end{array}$$

(21)

Therefore, ${\alpha }_1$ can be designed as

$$\begin{array}{ccc}\hfill {\alpha }_1& =& -{\displaystyle \frac{1}{{\beta }_2}}\left(-f_1(x,{\Delta }_1+k_1\left(x\right))+f_1(x,k_1\left(x\right))\right)\hfill \end{array}$$

$$\begin{array}{ccc}& & -{\displaystyle \frac{1}{{\beta }_2}}\left(-{\displaystyle \frac{\gamma }{2}}{\Delta }_1{p}_1^T\left(x,z_1\right)p_1\left(x,z_1\right)+{\beta }_1{\Delta }_1-c_1{\Delta }_1\right).\hfill \end{array}$$

(22)

where c₁ > 0 is a design parameter.

Combining (21) with (22), it can be derived that

$${\dot{V}}_1\le -c_1{\Delta }_1^2+{\displaystyle \frac{1}{2\gamma }}{w}^{T}w-{\Delta }_1{\beta }_2{\mathsf{\Xi }}_2$$

(23)

With ${\alpha }_1$ in (22), (15) can be rewritten as

$${\dot{\Delta }}_1=-c_1{\Delta }_1-{\beta }_2{\mathsf{\Xi }}_2-{\displaystyle \frac{\gamma }{2}}{\Delta }_1{p}_1^T{p}_1+p_1^{T}w$$

(24)

Step 3. According to (22) and (17), ${\dot{\mathsf{\Xi }}}_2$ can be obtained as

$$\begin{array}{ccc}\hfill {\dot{\mathsf{\Xi }}}_2& =& {\dot{\Delta }}_2-{\dot{\alpha }}_1\hfill \\ & =& {\dot{\Delta }}_2-{\displaystyle \frac{\partial {\alpha }_1}{\partial x_1}}{z}_1-{\displaystyle \frac{\partial {\alpha }_1}{\partial x_2}}{z}_2-{\displaystyle \frac{\partial {\alpha }_1}{\partial {\Delta }_1}}{\dot{\Delta }}_1\hfill \\ & =& su+p_2^T\left(x,z\right)w+v-{\displaystyle \frac{\partial {\alpha }_1}{\partial x_1}}{z}_1-{\displaystyle \frac{\partial {\alpha }_1}{\partial x_2}}{z}_2\hfill \\ & & -{\displaystyle \frac{\partial {\alpha }_1}{\partial {\Delta }_1}}\left(f_1(x,z_1)+p_1^T\left(x,z_1\right)w-{\left({\displaystyle \frac{\partial k\left(x\right)}{\partial x}}\right)}^{T}z\right)\hfill \\ & =& su+v-{\displaystyle \frac{\partial {\alpha }_1}{\partial x_1}}{z}_1-{\displaystyle \frac{\partial {\alpha }_1}{\partial x_2}}{z}_2\hfill \\ & & -{\displaystyle \frac{\partial {\alpha }_1}{\partial {\Delta }_1}}\left(f_1(x,z_1)-{\left({\displaystyle \frac{\partial k\left(x\right)}{\partial x}}\right)}^{T}z\right)\hfill \\ & & +\left(p_2^T\left(x,z\right)-{\displaystyle \frac{\partial {\alpha }_1}{\partial {\Delta }_1}}{p}_1^T\left(x,z_1\right)\right)w\hfill \end{array}$$

$$\begin{array}{cc}& =su+H_2+P_2^{T}w\end{array}$$

(25)

where

$$\begin{array}{ccc}\hfill P_2^T& =& p_2^T\left(x,z\right)-{\displaystyle \frac{\partial {\alpha }_1}{\partial {\Delta }_1}}{p}_1^T\left(x,z_1\right)\hfill \end{array}$$

(26)

$$\begin{array}{ccc}\hfill H_2& =& v-{\displaystyle \frac{\partial {\alpha }_1}{\partial x_1}}{z}_1-{\displaystyle \frac{\partial {\alpha }_1}{\partial x_2}}{z}_2\hfill \end{array}$$

$$\begin{array}{ccc}& & -{\displaystyle \frac{\partial {\alpha }_1}{\partial {\Delta }_1}}\left(f_1(x,z_1)-{\left({\displaystyle \frac{\partial k\left(x\right)}{\partial x}}\right)}^{T}z\right)\hfill \end{array}$$

(27)

A Lyapunov candidate $V_2$ can be introduced as

$$V_2=V_1+{\displaystyle \frac{1}{2}}{\mathsf{\Xi }}_2^2$$

(28)

Differentiating $V_2$ gives

$${\dot{V}}_2={\dot{V}}_1+{\mathsf{\Xi }}_2{\dot{\mathsf{\Xi }}}_2$$

(29)

According to Lemma 1 and (23), Equation (29) can be written as

$$\begin{array}{ccc}\hfill {\dot{V}}_2& \le & -c_1{\Delta }_1^2+{\displaystyle \frac{1}{2\gamma }}{w}^{T}w-{\Delta }_1{\beta }_2{\mathsf{\Xi }}_2+{\mathsf{\Xi }}_2\left(su+H_2+P_2^{T}w\right)\hfill \\ & =& -c_1{\Delta }_1^2+{\displaystyle \frac{1}{2\gamma }}{w}^{T}w-{\Delta }_1{\beta }_2{\mathsf{\Xi }}_2\hfill \\ & & +{\mathsf{\Xi }}_2\left(su+H_2\right)+{\displaystyle \frac{\gamma }{2}}{\mathsf{\Xi }}_2^2{P}_2^T{P}_2+{\displaystyle \frac{1}{2\gamma }}{w}^{T}w\hfill \\ & =& -c_1{\Delta }_1^2+{\displaystyle \frac{1}{\gamma }}{w}^{T}w\hfill \end{array}$$

$$\begin{array}{ccc}& & +{\mathsf{\Xi }}_2\left(su+H_2-{\Delta }_1{\beta }_2+{\displaystyle \frac{\gamma }{2}}{\mathsf{\Xi }}_2{P}_2^T{P}_2\right)\hfill \end{array}$$

(30)

The controller is shown as follows:

$$u=s^{-1}\left(-H_2+{\Delta }_1{\beta }_2-{\displaystyle \frac{\gamma }{2}}{\mathsf{\Xi }}_2{P}_2^T{P}_2-c_2{\mathsf{\Xi }}_2\right)$$

(31)

where c₂ > 0 is a design parameter.

Substituting (31) into (30) results in

$${\dot{V}}_2\le -c_1{\Delta }_1^2-c_2{\mathsf{\Xi }}_2^2+{\displaystyle \frac{1}{\gamma }}{w}^{T}w$$

(32)

With u in (31), (25) can be changed to

$${\dot{\mathsf{\Xi }}}_2={\beta }_2{\Delta }_1-c_2{\mathsf{\Xi }}_2-{\displaystyle \frac{\gamma }{2}}{P}_2^T{P}_2{\mathsf{\Xi }}_2+P_2^{T}w$$

(33)

The design procedure given above can be intuitively visualized with the block diagram in Figure 1.

Theorem 1.

If Assumptions 1 and 2 are satisfied and ${\beta }_1$, ${\beta }_2$, $c_1$, $c_2$, λ, and γ are chosen so that

$$\begin{array}{ccc}\hfill {\displaystyle \frac{\gamma }{2}}{L}_2-L_1+{\displaystyle \frac{L_2}{\left|{\beta }_2\right|}}\left(F_1+{\displaystyle \frac{\gamma P_1^2}{2}}+\left|{\beta }_1+c_1\right|\right){\displaystyle \frac{\gamma }{2}}& <& 0\hfill \end{array}$$

(34)

$$\begin{array}{ccc}\hfill {\displaystyle \frac{1}{2\gamma }}-\lambda c_1+{\displaystyle \frac{L_2}{\left|{\beta }_2\right|}}\left(F_1+{\displaystyle \frac{\gamma P_1^2}{2}}+\left|{\beta }_1+c_1\right|\right){\displaystyle \frac{1}{2\gamma }}& <& 0\hfill \end{array}$$

(35)

$$\begin{array}{ccc}\hfill {\displaystyle \frac{1}{2\gamma }}-\lambda c_2& <& 0\hfill \end{array}$$

(36)

with the proposed controller (31), the closed-loop system has the following properties:

(a) When $w=0$, the origin of the closed-loop system is locally asymptotically stable.

(b) The following inequality is true:

$${\int }_0^t{y}^T\left(u\right)y\left(u\right)du\le \varphi {\int }_0^t{w}^T\left(u\right)w\left(u\right)du$$

(37)

for given $\varphi >0$ and zero initial conditions, $t<\infty$, and w satisfying ${\int }_0^{\infty }{w}^T\left(u\right)w\left(u\right)du<\infty$.

Proof. 

Inspired by the proof of Lemma 13.1 in [36], a Lyapunov function candidate is considered as

$$V=V_k+\lambda V_2$$

(38)

where $\lambda >0$ is a constant. □

The time derivative of V can be easily expressed as

$$\begin{array}{ccc}\hfill \dot{V}& =& {\dot{V}}_k+\lambda {\dot{V}}_2\hfill \\ & =& {\left({\displaystyle \frac{\partial V_k}{\partial x}}\right)}^T\left(\Delta +k\left(x\right)\right)\hfill \\ & & -\lambda \left(c_1{\Delta }_1^2+c_2{\mathsf{\Xi }}_2^2-{\displaystyle \frac{1}{\gamma }}{w}^{T}w\right)\hfill \\ & =& {\left({\displaystyle \frac{\partial V_k}{\partial x}}\right)}^T\left[\begin{array}{c}{\Delta }_1\\ {\mathsf{\Xi }}_2+{\alpha }_1\end{array}\right]+{\left({\displaystyle \frac{\partial V_k}{\partial x}}\right)}^{T}k\left(x\right)\hfill \\ & & -\lambda \left(c_1{\Delta }_1^2+c_2{\mathsf{\Xi }}_2^2-{\displaystyle \frac{1}{\gamma }}{w}^{T}w\right)\hfill \\ & =& {\left({\displaystyle \frac{\partial V_k}{\partial x}}\right)}^T\left[\begin{array}{c}{\Delta }_1\\ {\mathsf{\Xi }}_2\end{array}\right]+{\left({\displaystyle \frac{\partial V_k}{\partial x}}\right)}^T\left[\begin{array}{c}0\\ {\alpha }_1\end{array}\right]\hfill \\ & & -L_1{∥x∥}^2-\lambda \left(c_1{\Delta }_1^2+c_2{\mathsf{\Xi }}_2^2-{\displaystyle \frac{1}{\gamma }}{w}^{T}w\right)\hfill \end{array}$$

$$\begin{array}{ccc}& & +{\left({\displaystyle \frac{\partial V_k}{\partial x}}\right)}^{T}k\left(x\right)+L_1{∥x∥}^2\hfill \end{array}$$

(39)

It follows from Assumption 1 and (22) that

$$\begin{array}{ccc}\hfill ∥{\alpha }_1∥& \le & ∥-{\displaystyle \frac{1}{{\beta }_2}}[-f_1(x,{\Delta }_1+k_1\left(x\right))+f_1(x,k_1\left(x\right))]∥\hfill \\ & & +∥-{\displaystyle \frac{1}{{\beta }_2}}[-{\displaystyle \frac{\gamma }{2}}{\Delta }_1{p}_1^T\left(x,z_1\right)p_1\left(x,z_1\right)]∥\hfill \\ & & +∥-{\displaystyle \frac{1}{{\beta }_2}}[{\beta }_1{\Delta }_1+c_1{\Delta }_1]∥\hfill \\ & \le & {\displaystyle \frac{1}{\left|{\beta }_2\right|}}{F}_1∥{\Delta }_1∥+{\displaystyle \frac{\gamma }{2\left|{\beta }_2\right|}}{P}_1^2∥{\Delta }_1∥+\left|{\displaystyle \frac{{\beta }_1+c_1}{{\beta }_2}}\right|∥{\Delta }_1∥\hfill \end{array}$$

$$\begin{array}{cc}& ={\displaystyle \frac{1}{\left|{\beta }_2\right|}}\left(F_1+{\displaystyle \frac{\gamma }{2}}{P}_1^2+\left|{\beta }_1+c_1\right|\right)∥{\Delta }_1∥\end{array}$$

(40)

Using Lemma 1 and (14), it follows that

$$\begin{array}{ccc}\hfill {\left({\displaystyle \frac{\partial V_k}{\partial x}}\right)}^T\left[\begin{array}{c}{\Delta }_1\\ {\mathsf{\Xi }}_2\end{array}\right]& \le & {\displaystyle \frac{\gamma }{2}}{∥{\displaystyle \frac{\partial V_k}{\partial x}}∥}^2+{\displaystyle \frac{1}{2\gamma }}{∥\left[\begin{array}{c}{\Delta }_1\\ {\mathsf{\Xi }}_2\end{array}\right]∥}^2\hfill \end{array}$$

$$\begin{array}{cc}& \le {\displaystyle \frac{\gamma }{2}}{L}_2{∥x∥}^2+{\displaystyle \frac{1}{2\gamma }}{∥{\Delta }_1∥}^2+{\displaystyle \frac{1}{2\gamma }}{∥{\mathsf{\Xi }}_2∥}^2\end{array}$$

(41)

In addition, according to (14) and (40), the following inequality can be easily verified.

$$\begin{array}{ccc}\hfill {\left({\displaystyle \frac{\partial V_k}{\partial x}}\right)}^T\left[\begin{array}{c}0\\ {\alpha }_1\end{array}\right]& \le & ∥{\displaystyle \frac{\partial V_k}{\partial x}}∥∥{\alpha }_1∥\hfill \\ & \le & L_2∥x∥∥{\alpha }_1∥\hfill \\ & \le & L_2{\displaystyle \frac{1}{\left|{\beta }_2\right|}}\left(F_1+{\displaystyle \frac{\gamma }{2}}{P}_1^2+\left|{\beta }_1+c_1\right|\right)∥x∥∥{\Delta }_1∥\hfill \end{array}$$

$$\begin{array}{cc}& \le {\displaystyle \frac{L_2}{\left|{\beta }_2\right|}}\left(F_1+{\displaystyle \frac{\gamma P_1^2}{2}}+\left|{\beta }_1+c_1\right|\right)\left({\displaystyle \frac{\gamma }{2}}{∥x∥}^2+{\displaystyle \frac{1}{2\gamma }}{∥{\Delta }_1∥}^2\right)\end{array}$$

(42)

Substituting (41) and (42) into (39) produces

$$\begin{array}{ccc}\hfill \dot{V}& \le & {\left({\displaystyle \frac{\partial V_k}{\partial x}}\right)}^T\left[\begin{array}{c}{\Delta }_1\\ {\mathsf{\Xi }}_2\end{array}\right]+{\left({\displaystyle \frac{\partial V_k}{\partial x}}\right)}^T\left[\begin{array}{c}0\\ {\alpha }_1\end{array}\right]-L_1{∥x∥}^2\hfill \\ & & -\lambda \left(c_1{\Delta }_1^2+c_2{\mathsf{\Xi }}_2^2-{\displaystyle \frac{1}{\gamma }}{w}^{T}w\right)+{\left({\displaystyle \frac{\partial V_k}{\partial x}}\right)}^{T}k\left(x\right)+L_1{∥x∥}^2\hfill \end{array}$$

$$\begin{array}{cc}& \le {\displaystyle \frac{\gamma }{2}}{L}_2{∥x∥}^2+{\displaystyle \frac{1}{2\gamma }}{∥{\Delta }_1∥}^2+{\displaystyle \frac{1}{2\gamma }}{∥{\mathsf{\Xi }}_2∥}^2\end{array}$$

(43)

$$\begin{array}{ccc}& & +{\displaystyle \frac{L_2}{\left|{\beta }_2\right|}}\left(F_1+{\displaystyle \frac{\gamma P_1^2}{2}}+\left|{\beta }_1+c_1\right|\right)\left({\displaystyle \frac{\gamma }{2}}{∥x∥}^2+{\displaystyle \frac{1}{2\gamma }}{∥{\Delta }_1∥}^2\right)\hfill \\ & & -L_1{∥x∥}^2-\lambda \left(c_1{\Delta }_1^2+c_2{\mathsf{\Xi }}_2^2-{\displaystyle \frac{1}{\gamma }}{w}^{T}w\right)+{\left({\displaystyle \frac{\partial V_k}{\partial x}}\right)}^{T}k\left(x\right)+L_1{∥x∥}^2\hfill \\ & \le & {\displaystyle \frac{\gamma }{2}}{L}_2{∥x∥}^2-L_1{∥x∥}^2+{\displaystyle \frac{L_2}{\left|{\beta }_2\right|}}\left(F_1+{\displaystyle \frac{\gamma P_1^2}{2}}+\left|{\beta }_1+c_1\right|\right){\displaystyle \frac{\gamma }{2}}{∥x∥}^2\hfill \\ & & +{\displaystyle \frac{1}{2\gamma }}{\Delta }_1^2-\lambda c_1{\Delta }_1^2+{\displaystyle \frac{L_2}{\left|{\beta }_2\right|}}\left(F_1+{\displaystyle \frac{\gamma P_1^2}{2}}+\left|{\beta }_1+c_1\right|\right){\displaystyle \frac{1}{2\gamma }}{\Delta }_1^2\hfill \\ & & +{\displaystyle \frac{1}{2\gamma }}{\mathsf{\Xi }}_2^2-\lambda c_2{\mathsf{\Xi }}_2^2+{\displaystyle \frac{\lambda }{\gamma }}{w}^{T}w+{\left({\displaystyle \frac{\partial V_k}{\partial x}}\right)}^{T}k\left(x\right)+L_1{∥x∥}^2\hfill \\ & \le & \left({\displaystyle \frac{\gamma }{2}}{L}_2-L_1+{\displaystyle \frac{L_2}{\left|{\beta }_2\right|}}\left(F_1+{\displaystyle \frac{\gamma P_1^2}{2}}+\left|{\beta }_1+c_1\right|\right){\displaystyle \frac{\gamma }{2}}\right){∥x∥}^2\hfill \\ & & +\left({\displaystyle \frac{1}{2\gamma }}-\lambda c_1+{\displaystyle \frac{L_2}{\left|{\beta }_2\right|}}\left(F_1+{\displaystyle \frac{\gamma P_1^2}{2}}+\left|{\beta }_1+c_1\right|\right){\displaystyle \frac{1}{2\gamma }}\right){\Delta }_1^2\hfill \end{array}$$

$$\begin{array}{ccc}& & +\left({\displaystyle \frac{1}{2\gamma }}-\lambda c_2\right){\mathsf{\Xi }}_2^2+{\displaystyle \frac{\lambda }{\gamma }}{w}^{T}w+{\left({\displaystyle \frac{\partial V_k}{\partial x}}\right)}^{T}k\left(x\right)+L_1{∥x∥}^2\hfill \end{array}$$

(44)

According to (13) and (34)–(36), it can be seen that $\dot{V}$ is negative-definite for $w=0$, which implies that property (a) is true.

To prove the property (b), (46) is rewritten as

$$\dot{V}\le \left({\displaystyle \frac{\gamma }{2}}{L}_2-L_1+{\displaystyle \frac{L_2}{\left|{\beta }_2\right|}}\left(F_1+{\displaystyle \frac{\gamma P_1^2}{2}}+\left|{\beta }_1+c_1\right|\right){\displaystyle \frac{\gamma }{2}}\right)x_1^2+{\displaystyle \frac{\lambda }{\gamma }}{w}^{T}w$$

(45)

Integrating (45) with $V\left(0\right)=0$ gives

$$\begin{array}{ccc}\hfill 0& \le & V\left(t\right)\le \left({\displaystyle \frac{\gamma }{2}}{L}_2-L_1+{\displaystyle \frac{L_2}{\left|{\beta }_2\right|}}\left(F_1+{\displaystyle \frac{\gamma P_1^2}{2}}+\left|{\beta }_1+c_1\right|\right){\displaystyle \frac{\gamma }{2}}\right){\int }_0^t{x}_1^2\left(u\right)du\hfill \end{array}$$

$$\begin{array}{ccc}& & +{\displaystyle \frac{\lambda }{\gamma }}{\int }_0^t{w}^T\left(u\right)w\left(u\right)du\hfill \end{array}$$

(46)

which is equivalent to (37) with $\varphi ={\displaystyle \frac{\lambda }{-\gamma \left(\frac{\gamma }{2}{L}_2-L_1+\frac{L_2}{\left|{\beta }_2\right|}\left(F_1+\frac{\gamma P_1^2}{2}+\left|{\beta }_1+c_1\right|\right)\frac{\gamma }{2}\right)}}$.

Remark 3.

Note that $V_k$ is the Lyapunov function candidate for subsystem (11) and $V_2$ for subsystem (15) and (25). Therefore, $V=V_k+\lambda V_2$ is the Lyapunov function candidate for the whole system composed of two subsystems (11), and (15) and (25).

Remark 4.

The challenge of the ADD controller design lies in handling the indefinite term $x^T\Delta$ in ${\dot{V}}_k$. Its impact on $\dot{V}$ has to be canceled out by other negative-definite terms through several inequality amplification steps.

4. Simulation Results: Inertia Wheel Pendulum

In this part, the underactuated nonlinear model defined in [37] for the IWP with a physical damping term satisfying the matching condition is considered to demonstrate the effectiveness of the proposed underactuated ADD backstepping method, which is given by

$$\begin{array}{ccc}& & \left(I_1+I_2+m_1{l}_1^2+m_2{l}_2^2\right){\ddot{q}}_1+I_2{\ddot{q}}_2\hfill \\ & =& \left(m_1{l}_1+m_2{l}_2\right)gsin{q}_1+w_1\hfill \end{array}$$

$$\begin{array}{ccc}\hfill I_2{\ddot{q}}_1+I_2{\ddot{q}}_2& =& \delta {\dot{q}}_2+u+w_2,\hfill \end{array}$$

(47)

where $q_1$ and $q_2$ stand for the pendulum angle and the disk angle, $m_1$ and $m_2$ are the pendulum mass and the wheel mass, $l_1$ is the distance from the origin to the center of mass of the pendulum, $l_2$ is the pendulum length, $I_1$ and $I_2$ denote the moments of inertia of the pendulum and wheel, u represents the torque input, g is the gravity coefficient, $\delta$ is the damping coefficient, and $w_1$ and $w_2$ are disturbances. The IWP system (47) can be rewritten as

$$\begin{array}{ccc}\hfill {\ddot{q}}_1& =& M\left(sin{q}_1\right)-\delta b_1{\dot{q}}_2-b_{1}u+\left[b_1,-b_1\right]W\hfill \end{array}$$

$$\begin{array}{ccc}\hfill {\ddot{q}}_2& =& M\left(sin{q}_1\right)-\delta b_1{\dot{q}}_2-b_{1}u+\left[-b_1,b_2\right]W,\hfill \end{array}$$

(48)

where $b_1={\displaystyle \frac{1}{m_1{l}_1^2+m_2{l}_2^2+I_1}}$, $b_2={\displaystyle \frac{1}{I_2}}+b_1$, $M=(m_1{l}_1+m_2{l}_2)g{b}_1$, and $W={\left[w_1,w_2\right]}^T$.

A new set of variables is defined as

$$\begin{array}{ccc}\hfill x_1& =& b_2{q}_1+b_1{q}_2\hfill \\ \hfill x_2& =& q_1\hfill \\ \hfill z_1& =& b_2{\dot{q}}_1+b_1{\dot{q}}_2\hfill \end{array}$$

$$\begin{array}{ccc}\hfill z_2& =& {\dot{q}}_1\hfill \end{array}$$

(49)

Then, system (48) is changed to (1) with $f_1=\overline{M}\left(sin{x}_2\right)$, $f_2=Msin{x}_2+\left(b_2{z}_2-z_1\right)\delta$, $p_1^T=\left[(b_2-b_1)b_1,0\right]$, $p_2^T=\left[b_1,-b_1\right]$, and $s=-b_1$ with $\overline{M}=M(b_2-b_1)$.

The ADD controller for the IWP system is composed of $k\left(x\right)$ in (8)–(10), ${\alpha }_1$ in (22), and u in (31).

Remark 5.

For this system, $V_k={\displaystyle \frac{1}{2}}{x}^{T}x$ can be used so that (12)–(14) are satisfied with $W_1={\displaystyle \frac{1}{3}}$, $W_2=1$, $L_1=0.5$, $L_2=2$, ${\beta }_1=-1$, and ${\beta }_2=-1$ due to the following relation.

$$\begin{array}{ccc}& & {\left({\displaystyle \frac{\partial V_k\left(x\right)}{\partial x}}\right)}^{T}k\left(x\right)\hfill \\ & =& x^{T}k\left(x\right)={\beta }_1{x}_1^2+{\beta }_2{x}_1{x}_2+{\displaystyle \frac{\overline{M}{x}_{2}sin{x}_2-{\beta }_1^2{x}_1{x}_2-{\beta }_1{\beta }_2{x}_2^2}{{\beta }_2}}\hfill \\ & \le & {\beta }_1{x}_1^2+{\displaystyle \frac{\left({\beta }_2^2-{\beta }_1^2\right)}{{\beta }_2}}{x}_1{x}_2+{\displaystyle \frac{\overline{M}{x}_2^2-{\beta }_1{\beta }_2{x}_2^2}{{\beta }_2}}\hfill \\ & \le & {\beta }_1{x}_1^2+\left|{\displaystyle \frac{\left({\beta }_2^2-{\beta }_1^2\right)}{2{\beta }_2}}\right|x_1^2+\left|{\displaystyle \frac{\left({\beta }_2^2-{\beta }_1^2\right)}{2{\beta }_2}}\right|x_2^2+{\displaystyle \frac{\overline{M}{x}_2^2-{\beta }_1{\beta }_2{x}_2^2}{{\beta }_2}}\hfill \\ & \le & \left({\beta }_1+\left|{\displaystyle \frac{\left({\beta }_2^2-{\beta }_1^2\right)}{2{\beta }_2}}\right|\right)x_1^2+\left(\left|{\displaystyle \frac{\left({\beta }_2^2-{\beta }_1^2\right)}{2{\beta }_2}}\right|+{\displaystyle \frac{\overline{M}-{\beta }_1{\beta }_2}{{\beta }_2}}\right)x_2^2\hfill \end{array}$$

$$\begin{array}{cc}& \le -x_1^2-1.352x_2^2\le -0.5\left(x_1^2+x_2^2\right)\end{array}$$

(50)

Remark 6.

The region of attraction can be determined by applying the analysis method given in Section 8.2 of the book in [36] to the closed-loop system composed of (11), (24), and (33) with V defined in (38) and $V_k={\displaystyle \frac{1}{2}}{x}^{T}x$.

The IWP model parameters taken from [33] are $m_1=0.01$ kg, $m_2=0.1$ kg, $l_1=0.35$ m, $l_2=0.5$ m, $I_1=3.5\times {10}^{-3}\mathrm{kg}·{\mathrm{m}}^2$, $I_1=1.4\times {10}^{-2}\mathrm{kg}·{\mathrm{m}}^2$, $g=9.8$, and $\delta =0.02$. The initial conditions are selected as $q_1\left(0\right)=0.3$ rad, $q_2\left(0\right)=0$, $\dot{q_1}\left(0\right)=0$, and $\dot{q_2}\left(0\right)=0$. In addition, the controller gains are $c_1=0.6096$, $c_2=1$, $\gamma =2$, ${\beta }_1=-1$, and ${\beta }_2=-1$.

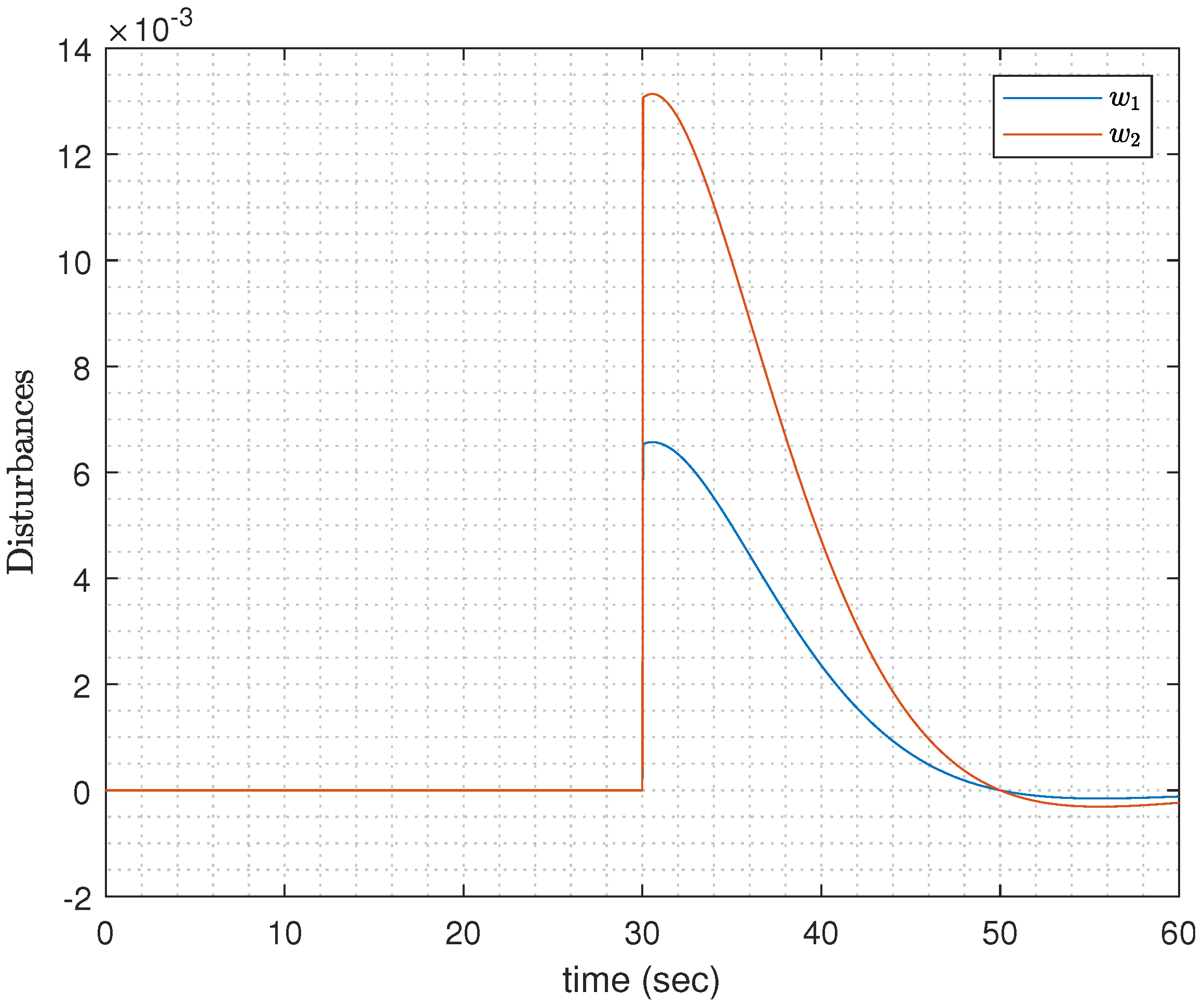
The following disturbances are used in the simulation.

$$w_i=\left\{\begin{array}{cc}0,& \mathrm{if}t\le 30\\ -iexp\left(-0.15t\right)sin\left(2\pi ft\right)& \mathrm{if}t>30\end{array}\right.$$

(51)

with $i=1, 2$ and $f=0.02$.

In order to show the superiority of the proposed control method, the feedback linearization method developed in [28] is simulated on the IWP as well.

The controller in [28] is given by

$$u={\displaystyle \frac{-{\Delta }_1{\dot{e}}_1-{\Delta }_2{\dot{e}}_2+{\Delta }_3{f}_{z_1}-{\Delta }_4{\ddot{q}}_{d_2}+{\Delta }_4{f}_{z_2}-k_{p}y}{-\left({\Delta }_3{g}_{z_1}+{\Delta }_4{g}_{z_2}\right)}}$$

where $q_{d_1}=0$ and

$$\begin{array}{ccc}\hfill y& =& {\Delta }_1{e}_1+{\Delta }_2{e}_2+{\Delta }_3{\dot{e}}_1+{\Delta }_4{\dot{e}}_2\hfill \\ \hfill \left[\begin{array}{c}{f}_{z_1}\\ f_{z_2}\end{array}\right]& =& M_x\left[\begin{array}{c}\left(m_1{l}_1+m_2{l}_2\right)gsin{q}_1\\ \delta {\dot{q}}_2\end{array}\right]\hfill \\ \hfill \left[\begin{array}{c}{g}_{z_1}\\ g_{z_2}\end{array}\right]& =& M_x\left[\begin{array}{c}0\\ 1\end{array}\right]\hfill \end{array}$$

with $e_1=q_{d_1}-q_1$, $e_2=-q_2$, $M_x={\left[\begin{array}{cc}\left(I_1+I_2+m_1{l}_1^2+m_2{l}_2^2\right)& I_2\\ I_2& I_2\end{array}\right]}^{-1}$, ${\Delta }_1=0.5$, ${\Delta }_2=0.002$, ${\Delta }_3=0.1$, ${\Delta }_4=0.001$, and $k_p=1$.

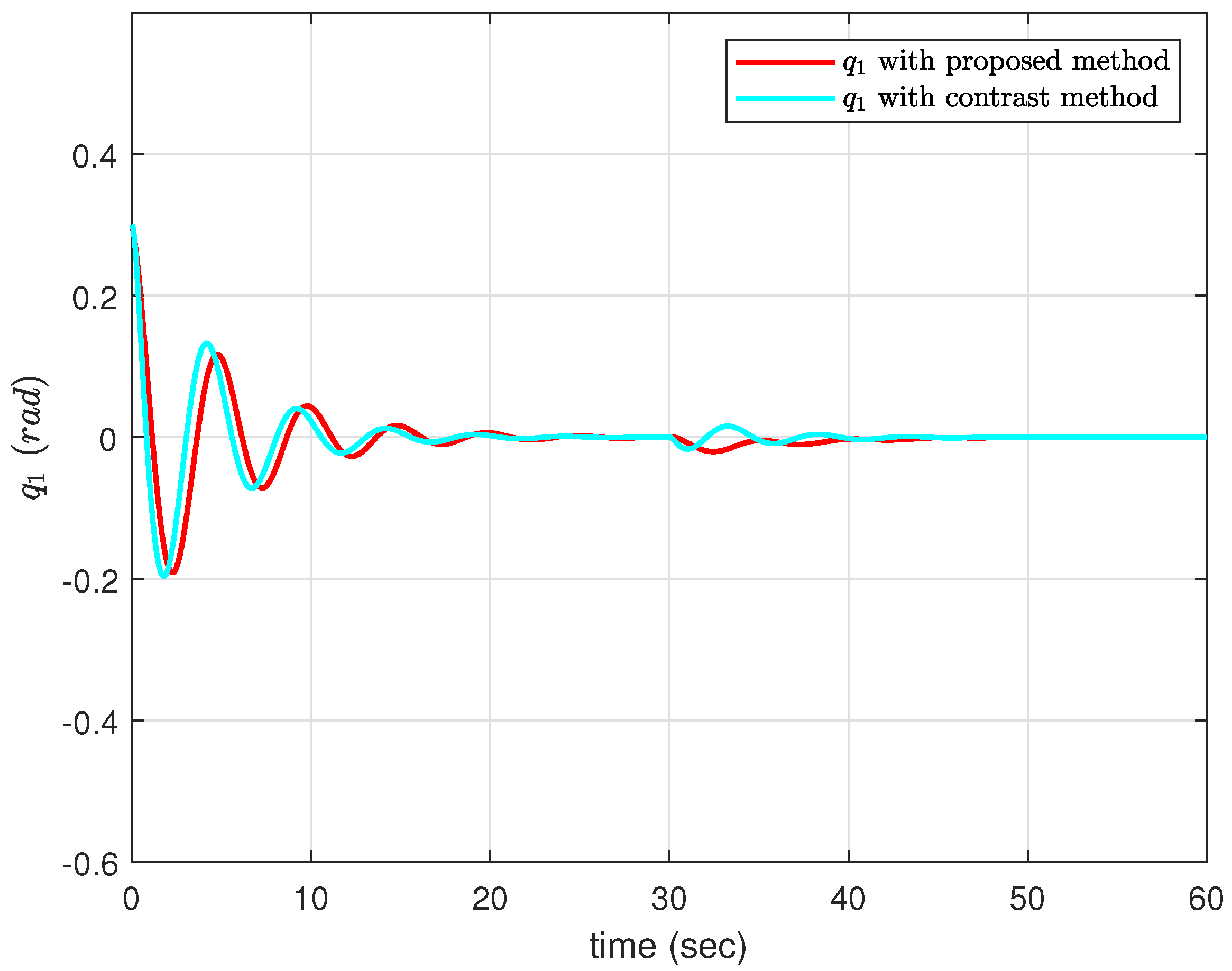
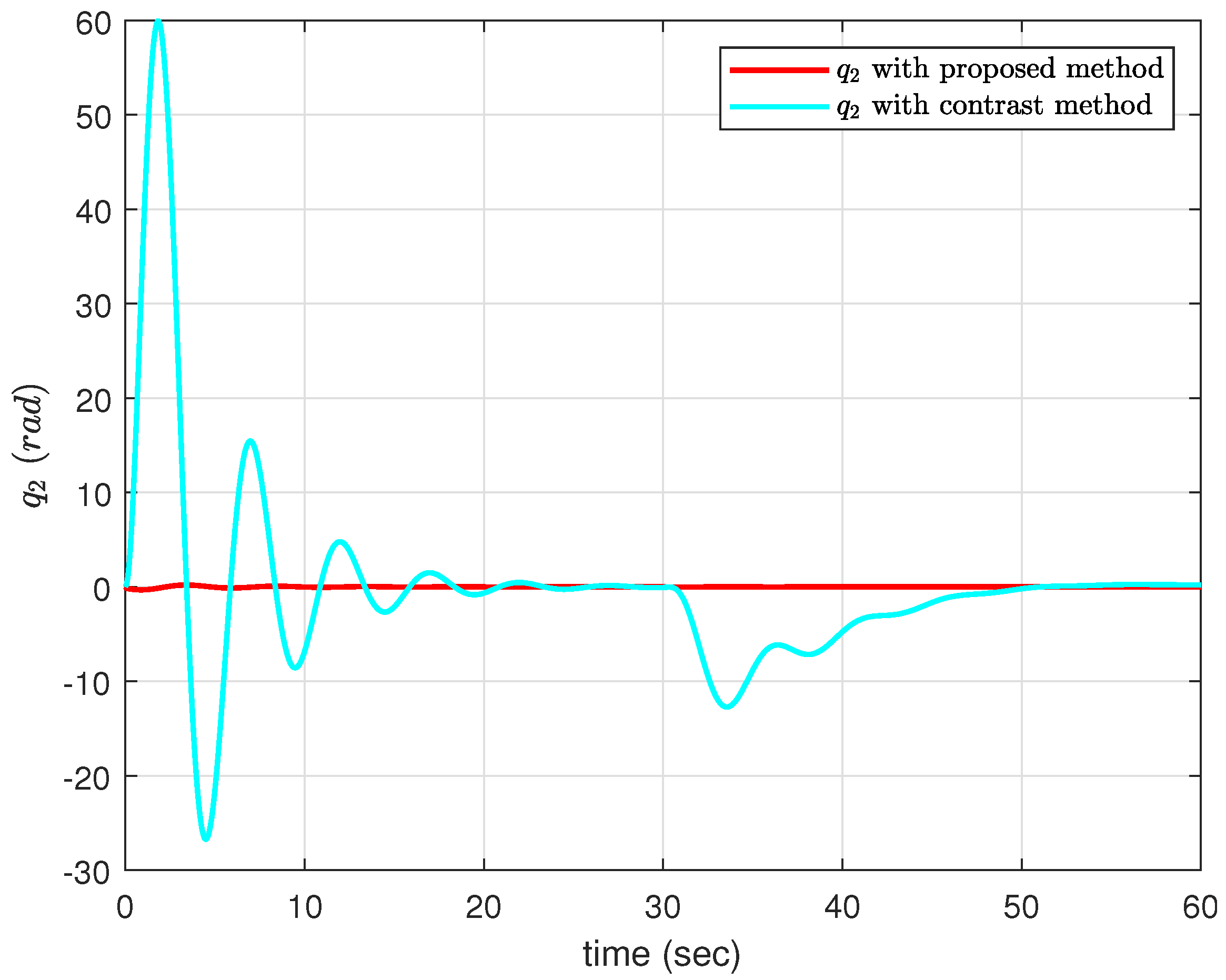
Figure 2, Figure 3, Figure 4 and Figure 5 show the simulation results on the IWP system. As shown in Figure 2 and Figure 3, with the proposed method, it takes a shorter time for the IWP to stabilize. After introducing the disturbances (51) at the 30 s mark, which is shown in Figure 4, the deviation in $q_1$ with the proposed method is slightly greater than the feedback linearization, while the deviation in $q_2$ is much smaller compared with the feedback linearization. Furthermore, compared with the proposed method, the feedback linearization experiences much greater oscillation. 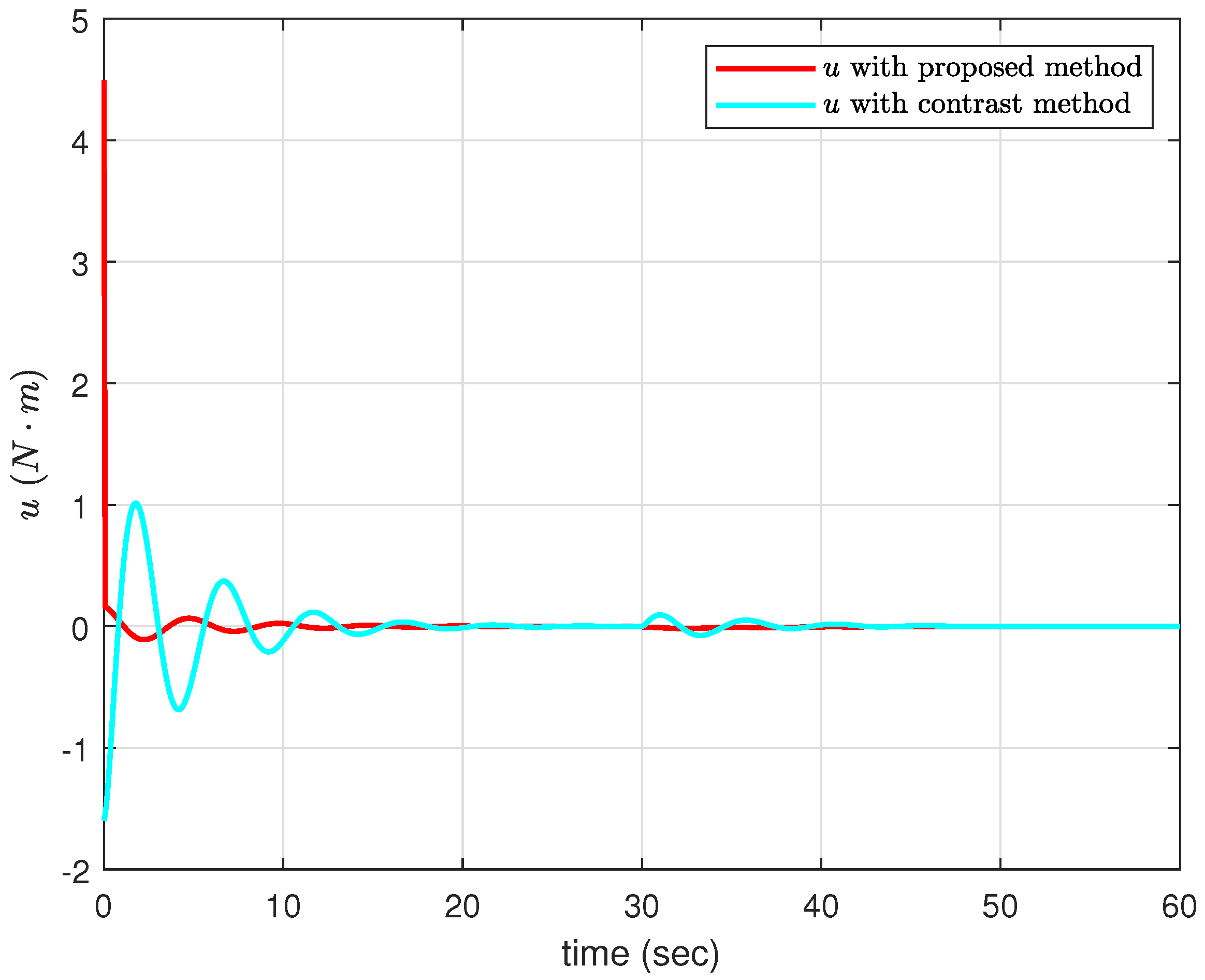Figure 5 displays the control signals u. The simulation results of the IWP model validate that the proposed underactuated ADD controller can achieve better control performance compared with the feedback linearization method.

5. Experimental Results: Overhead Crane

This section applies the proposed ADD control algorithm to an overhead crane. The overhead crane can be modeled as

$$\begin{array}{ccc}\hfill \left(m_c+m_p\right){\ddot{q}}_1+\left(m_{p}Lcos{q}_2\right){\ddot{q}}_2-m_{p}L{\dot{q}}_2^{2}sin{q}_2& =& u+w_1\hfill \end{array}$$

$$\begin{array}{ccc}\hfill \left(m_{p}Lcos{q}_2\right){\ddot{q}}_1+m_p{L}^2{\ddot{q}}_2+m_{p}gLsin{q}_2& =& w_2\hfill \end{array}$$

(52)

where $q_1$ and $q_2$ stand for the trolley displacement and the payload swing angle, respectively; $m_c$ is the weight of the trolley; $m_p$ is the weight of the payload; L is the length of the rope; g is the gravity coefficient; and $w_1$ and $w_2$ are disturbances.

Then, (52) can be linearized at the point $q_2=0$ as follows.

$$\begin{array}{ccc}\hfill {\ddot{q}}_1& =& {\displaystyle \frac{1}{m_c}}u+{\displaystyle \frac{1}{m_c}}{w}_1-{\displaystyle \frac{1}{D_1}}{w}_2+{\displaystyle \frac{M_g}{D_1}}{q}_2\hfill \end{array}$$

$$\begin{array}{ccc}\hfill {\ddot{q}}_2& =& -{\displaystyle \frac{1}{D_1}}u-{\displaystyle \frac{1}{D_1}}{w}_1+{\displaystyle \frac{M_1}{E}}{w}_2-{\displaystyle \frac{M_1{M}_g}{E}}{q}_2\hfill \end{array}$$

(53)

where $D=L^2{m}_c$, $D_1=L{m}_c$, $E=L^2{m}_c{m}_p$, $M_1=m_c+m_p$, and $M_g=m_{p}gL$.

Define $e_1=q_{d1}-q_1$ and $e_2=q_{d2}-q_2$. Then, ${\ddot{e}}_1$ and ${\ddot{e}}_2$ can be expressed as

$$\begin{array}{ccc}\hfill {\ddot{e}}_1& =& {\ddot{q}}_{d1}-{\ddot{q}}_1\hfill \end{array}$$

$$\begin{array}{ccc}\hfill {\ddot{e}}_2& =& {\ddot{q}}_{d2}-{\ddot{q}}_2\hfill \end{array}$$

(54)

where $q_{d1}$ is a desired trolley trajectory and $q_{d2}=0$ is a desired swing angle.

A new set of variables is introduced as

$$\begin{array}{ccc}\hfill x_1& =& {\displaystyle \frac{e_1}{L}}+e_2\hfill \\ \hfill x_2& =& e_2\hfill \\ \hfill z_1& =& {\displaystyle \frac{{\dot{e}}_1}{L}}+{\dot{e}}_2\hfill \end{array}$$

$$\begin{array}{ccc}\hfill z_2& =& {\dot{e}}_2\hfill \end{array}$$

(55)

Then, by differentiating these variables, system (53) can be changed to (1) with $s={\displaystyle \frac{1}{D_1}}$ and

$$\begin{array}{ccc}\hfill f_1& =& \left(-{\displaystyle \frac{M_g}{D}}+{\displaystyle \frac{M_1{M}_g}{E}}\right)q_{d2}+{\displaystyle \frac{{\ddot{q}}_{d1}}{L}}+{\ddot{q}}_{d2}+\left({\displaystyle \frac{M_g}{D}}-{\displaystyle \frac{M_1{M}_g}{E}}\right)x_2\hfill \\ \hfill f_2& =& {\displaystyle \frac{M_1{M}_g}{E}}{q}_{d2}+{\ddot{q}}_{d2}-{\displaystyle \frac{M_1{M}_g}{E}}{x}_2\hfill \\ \hfill p_1& =& {\left[\begin{array}{cc}0& {\displaystyle \frac{1}{D}}-{\displaystyle \frac{M_1}{E}}\end{array}\right]}^T\hfill \\ \hfill p_2& =& {\left[\begin{array}{cc}{\displaystyle \frac{1}{D_1}}& -{\displaystyle \frac{M_1}{E}}\end{array}\right]}^T\hfill \end{array}$$

The ADD controller for this overhead crane is composed of $k\left(x\right)$ in (8) and (10) and ${\alpha }_1$ in (22) and u in (31).

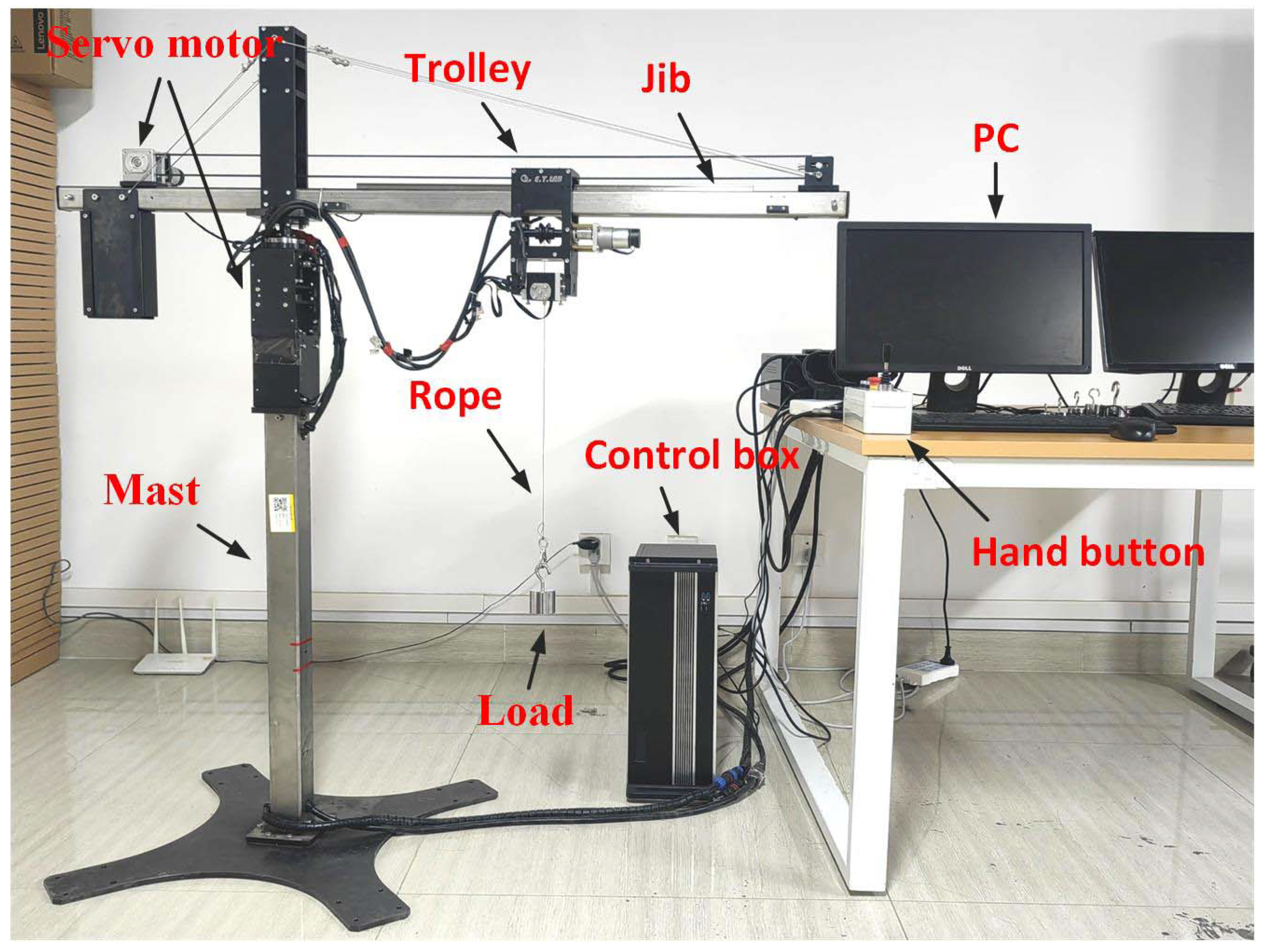
The overhead crane platform is mainly composed of a jib, a trolley, a rope, and a load, as shown in Figure 6. The platform parameters are $m_c=1.852$ kg, $m_p=0.5$ kg, $L=0.5$ m, and $g=9.8{\mathrm{m}/\mathrm{s}}^2$. The controller gains are given below: $c_1=1$, $c_2=5$, $\gamma =0.01$, ${\beta }_1=-1.2$, and ${\beta }_2=10$. The initial conditions are chosen as $q_1\left(0\right)=-0.17$ m, $q_2\left(0\right)=0$ rad, ${\dot{q}}_1\left(0\right)=0$ m/s, and ${\dot{q}}_2\left(0\right)=0$ rad/s.

The proposed ADD controller is applied to control the trolley to track the following reference signal:

$$q_{d1}=\left\{\begin{array}{cc}{M}_a^{T}T& 0<t<t_1\\ A_{\eta }sin\left(2\pi f_{\eta }\left(t-t_1\right)\right)+{\eta }_{t1}& t_1\le t<t_2\\ M_b^{T}T& t_2\le t<t_3\\ {\eta }_0& t_3\le t\end{array}\right.$$

(56)

where $M_a=M_{t1}^{-1}{M}_{st1}$, $M_b=M_{t1}^{-1}{M}_{st2}$, $A_{\eta }=-0.2$, $f_{\eta }={\displaystyle \frac{1}{40}}$, $t_1=10$, $t_2=t_1+2.5T_{\eta }$, $t_3=t_2+10$, ${\eta }_0=-0.17$, ${\eta }_{t1}=-0.47$, $T_{\eta }={\displaystyle \frac{1}{f_{\eta }}}$, $T={\left[\begin{array}{cccccc}1& t& t^2& t^3& t^4& t^5\end{array}\right]}^T$,

$$M_{t1}=\left[\begin{array}{cccccc}1& t_0& t_0^2& t_0^3& t_0^4& t_0^5\\ 0& 1& 2t_0& 3t_0^2& 4t_0^3& 5t_0^4\\ 0& 0& 2& 6t_0& 12t_0^2& 20t_0^3\\ 1& t_1& t_1^2& t_1^3& t_1^4& t_1^5\\ 0& 1& 2t_1& 3t_1^2& 4t_1^3& 5t_1^4\\ 0& 0& 2& 6t_1& 12t_1^2& 20t_1^3\end{array}\right],M_{t2}=\left[\begin{array}{cccccc}1& t_2& t_2^2& t_2^3& t_2^4& t_2^5\\ 0& 1& 2t_2& 3t_2^2& 4t_2^3& 5t_2^4\\ 0& 0& 2& 6t_2& 12t_2^2& 20t_2^3\\ 1& t_3& t_3^2& t_3^3& t_3^4& t_3^5\\ 0& 1& 2t_3& 3t_3^2& 4t_3^3& 5t_3^4\\ 0& 0& 2& 6t_3& 12t_3^2& 20t_3^3\end{array}\right]$$

$$M_{st1}=\left[\begin{array}{c}{\eta }_0\\ 0\\ 0\\ A_{\eta }sin\left(2\pi f_{\eta }\left(t_1-t_1\right)\right)+c_{\eta }\\ 2A_{\eta }\pi f_{\eta }cos\left(2\pi f_{\eta }\left(t_1-t_1\right)\right)\\ -4A_{\eta }{\pi }^2{f}_{\eta }^{2}sin\left(2\pi f_{\eta }\left(t_1-t_1\right)\right)\end{array}\right],M_{st2}=\left[\begin{array}{c}{A}_{\eta }sin\left(2\pi f_{\eta }\left(t_2-t_1\right)\right)+c_{\eta }\\ 2A_{\eta }\pi f_{\eta }cos\left(2\pi f_{\eta }\left(t_2-t_1\right)\right)\\ -4A_{\eta }{\pi }^2{f}_{\eta }^{2}sin\left(2\pi f_{\eta }\left(t_2-t_1\right)\right)\\ {\eta }_0\\ 0\\ 0\end{array}\right]$$

with $t_0=0$, $c_{\eta }=-0.47$.

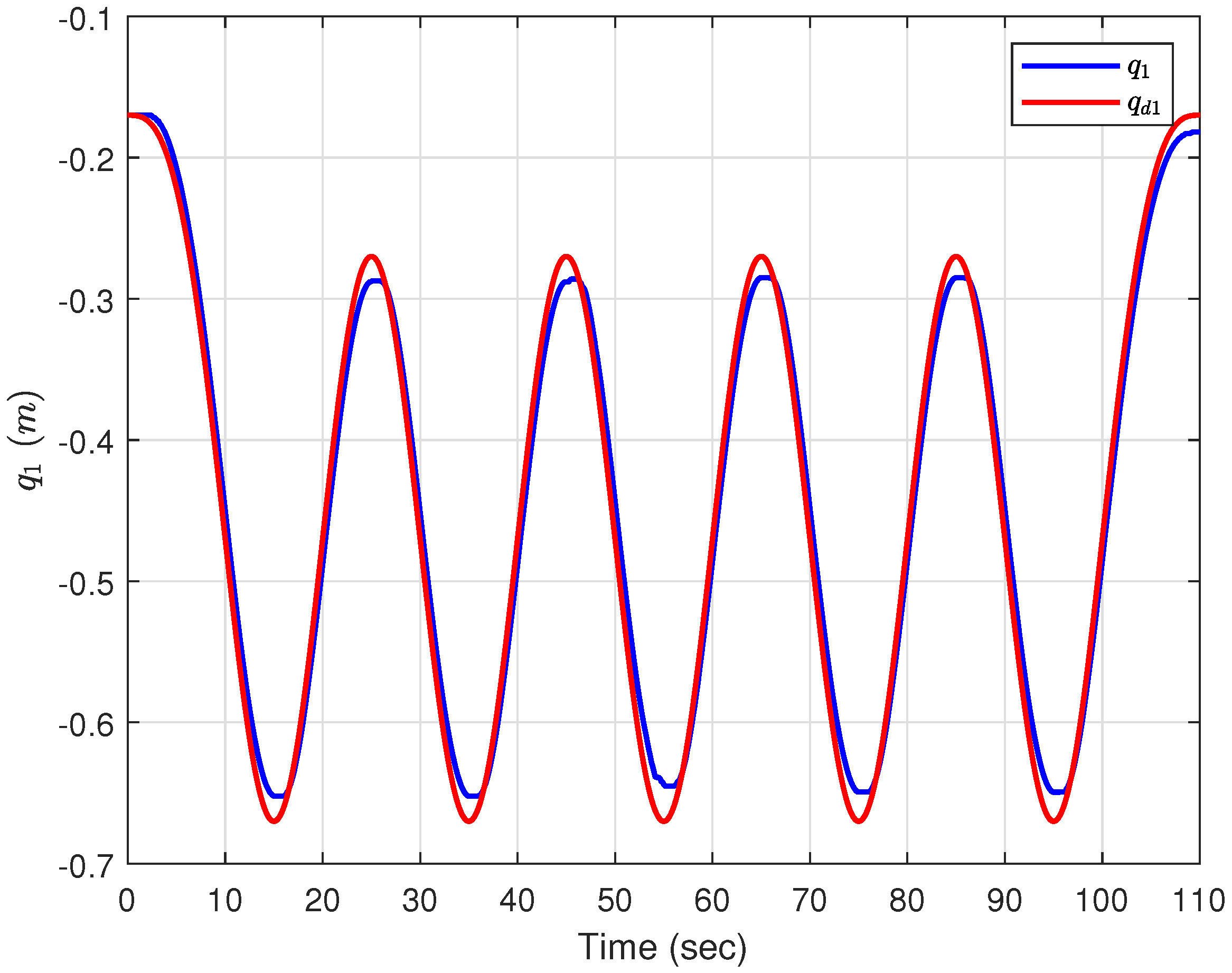
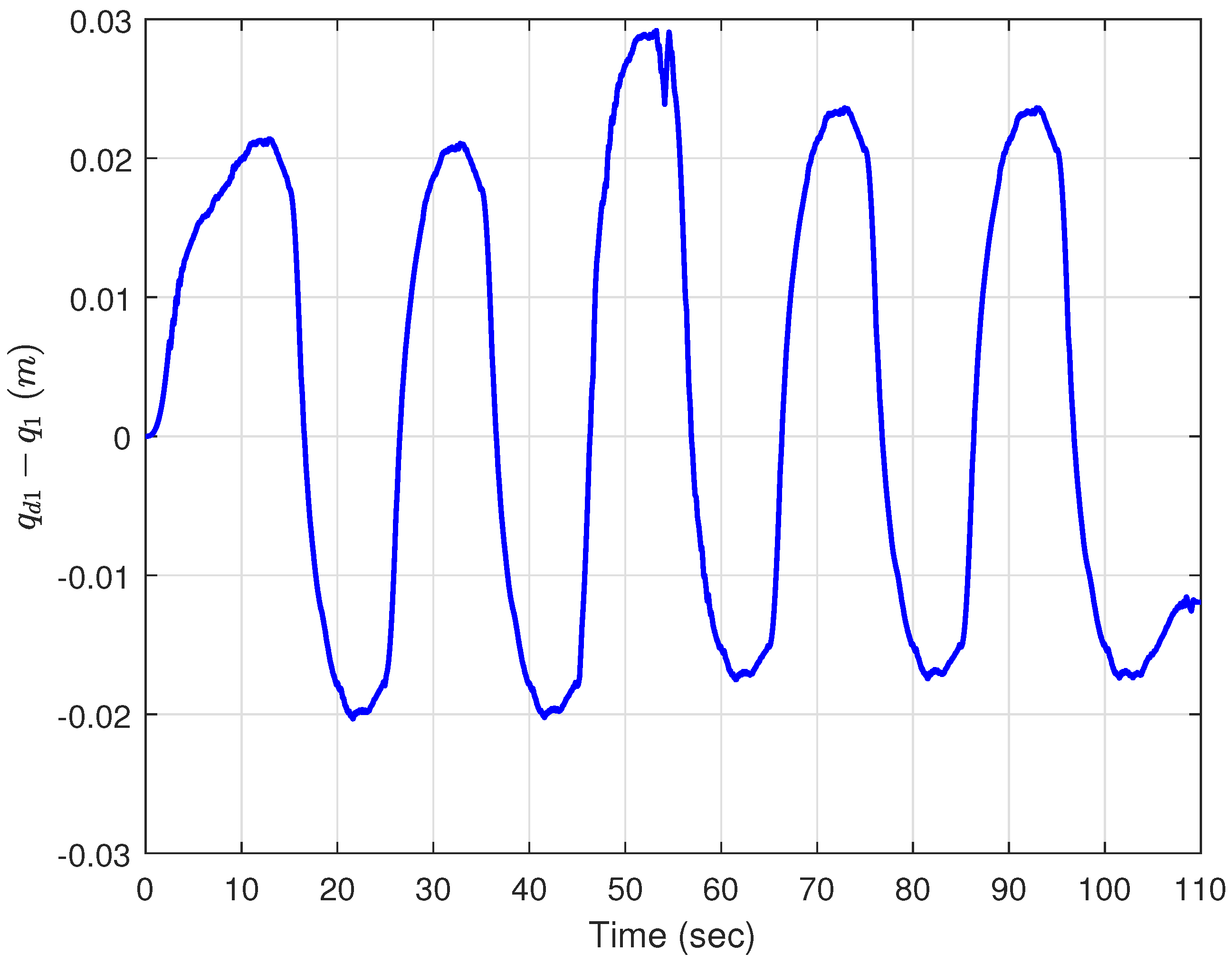
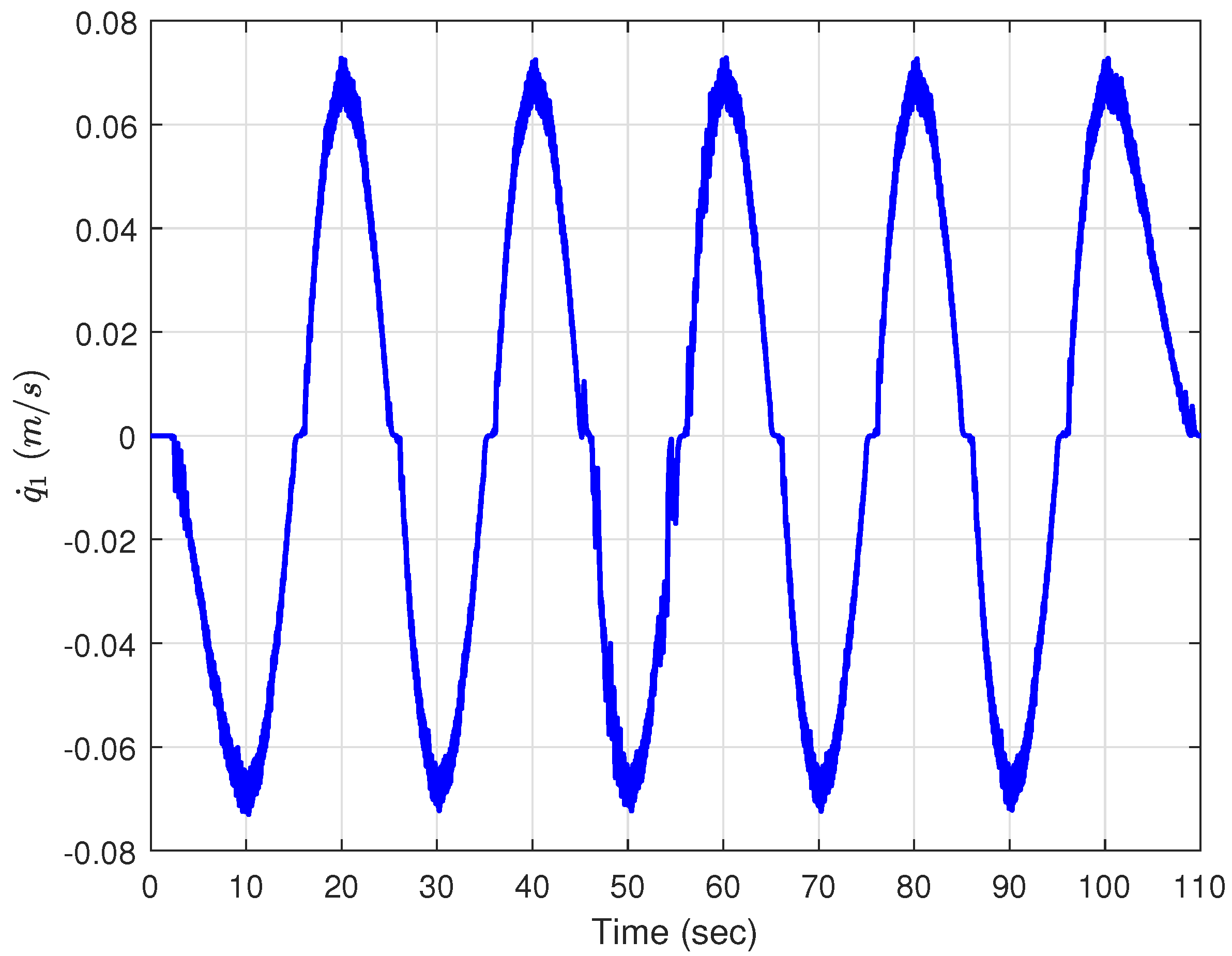
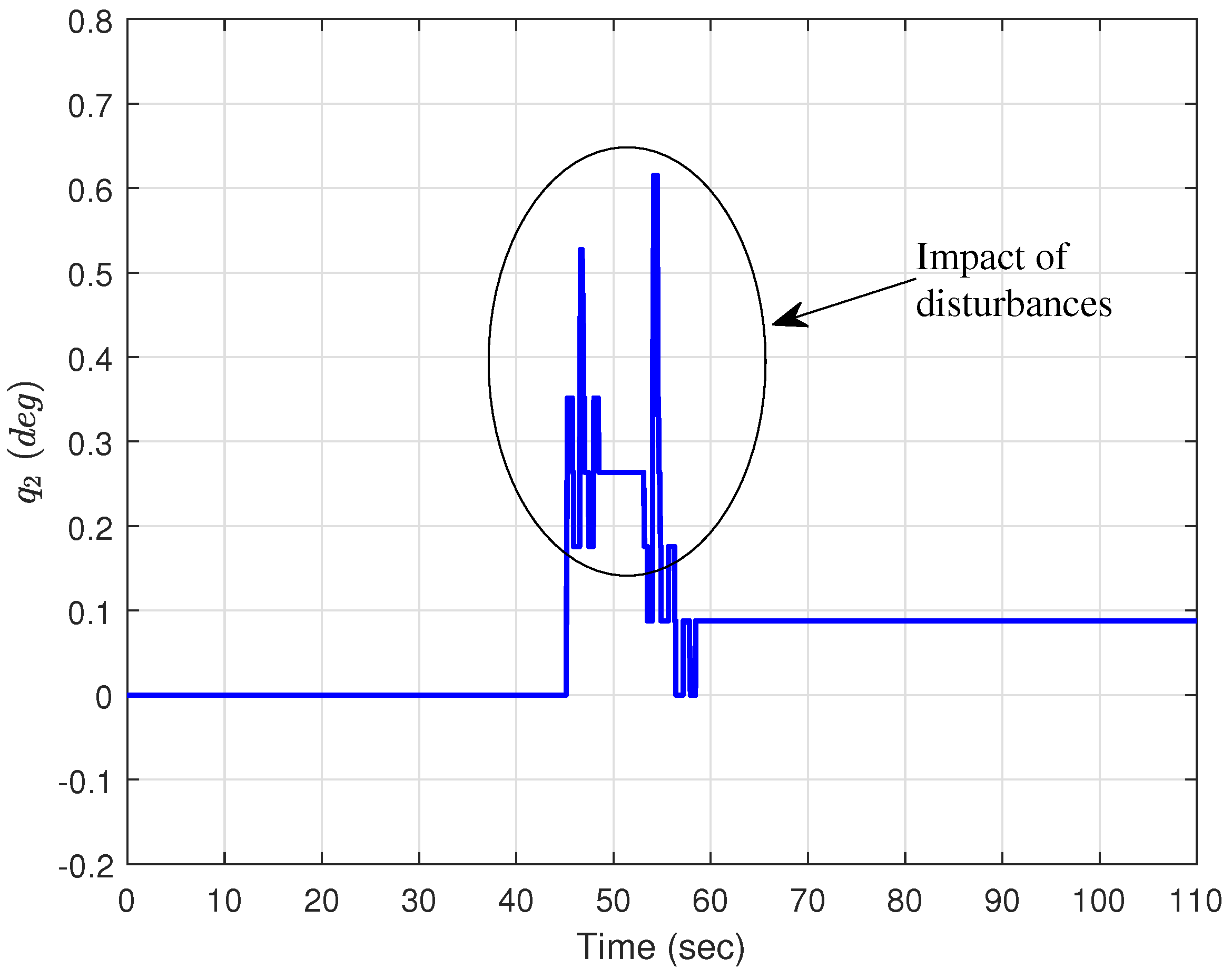
The experimental results are presented in Figure 7, Figure 8, Figure 9, Figure 10 and Figure 11. Figure 7 shows the reference and actual trajectories for the trolley, from which it can be observed that the trolley is able to follow the reference trajectory. The tracking error for the trolley is shown in Figure 8. Figure 9 displays the velocity of the trolley. Figure 10 depicts the swinging angle of the payload in the direction of the trolley movement. When disturbances are applied with strong wind from a hairdryer between 45 and 55 s, it can be observed from Figure 7 and Figure 10 that the payload experiences some oscillation and quickly returns to its steady-state value and the trolley trajectory is almost unaffected. 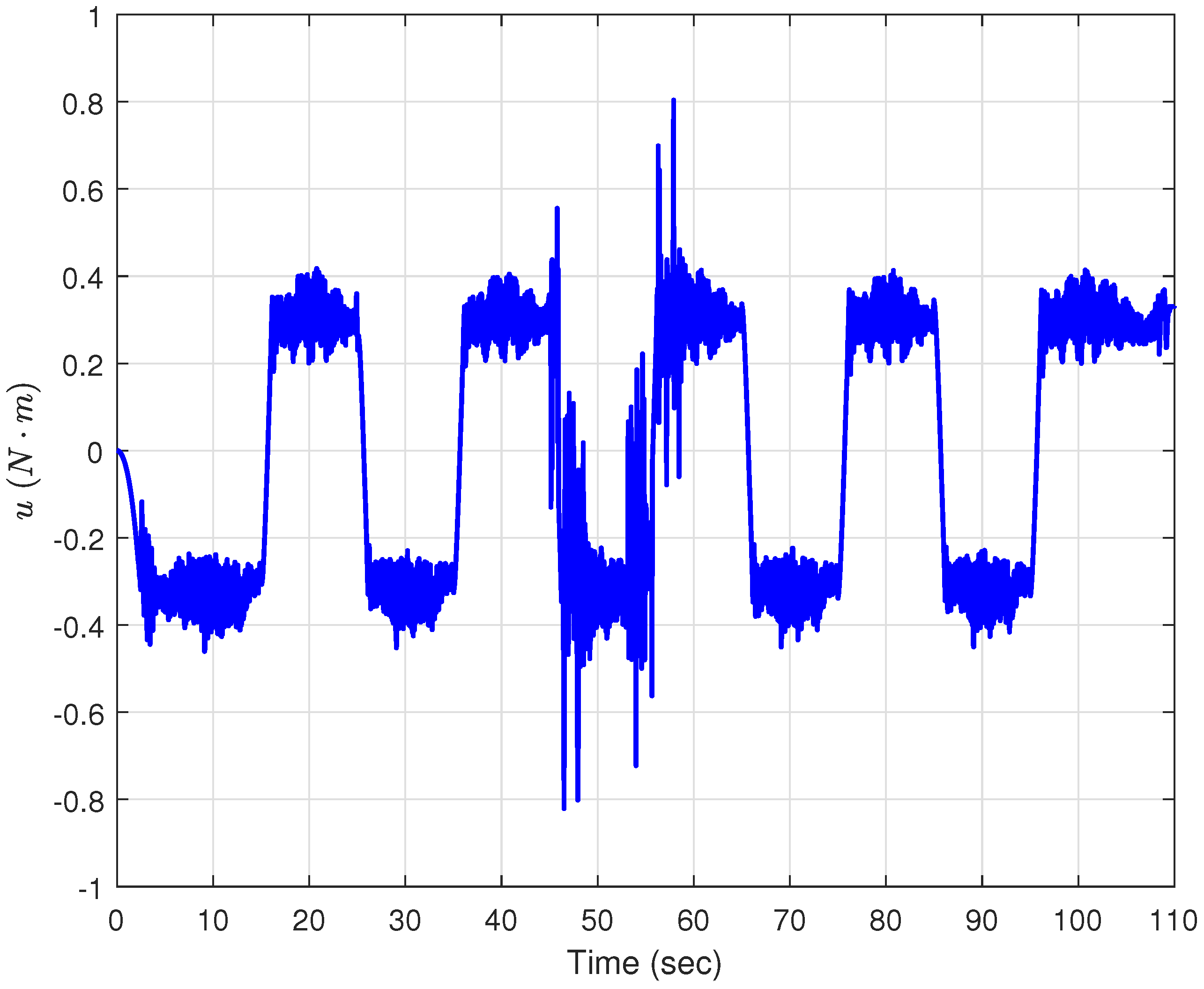Figure 11 shows that u is within a reasonable range. Based on the experimental results, it can be concluded that the proposed method is feasible and has a strong disturbance rejection capability.

6. Conclusions

An ADD problem for a class of underactuated nonlinear systems with disturbances has been addressed using the backstepping method. First, a virtual controller is designed using PDEs to construct a residual system. Then, the backstepping method is further applied to develop an ADD controller for the residual system. To address the unknown disturbance terms, Young’s inequality is employed to scale the disturbance coefficients, effectively counteracting their influence. The effectiveness of the proposed scheme is validated with simulation on the IWP system and an experiment on the overhead crane subject to unknown disturbances. The main limitation is the lack of proof for the global stability of the closed-loop system, which inspires us to conduct research work on the global stability of the closed-loop system with an ADD controller. It is worth noting that the proposed controller design is conducted under the assumption that there is no input saturation. One of the focuses of future studies will be to investigate the impact of input saturation on the ADD control performance. Another focus of future work will be to extend the proposed control method to more general underactuated systems.