1. Introduction
With the advancement of robotic technology, interactions among humans, robots, and environments have become increasingly frequent, such as zero-force dragging teachers [
1]. In most industrial scenarios, robotic arms typically carry unknown dynamic payloads during dragging operations. These uncertain loads alter the dynamic parameters of the manipulator and degrade the estimation accuracy of end-effector contact forces. Therefore, accurate load force estimation of the robotic end-effector is crucial to achieve safe and stable physical interaction, especially when the robot must quickly grasp and assemble components of varying weights while accurately detecting external contacts with human operators and the environment [
2].
To address this, numerous methods have been proposed to mitigate errors caused by varying payloads. Conventional payload compensation typically relies on pre-calibration, where load parameters are updated upon payload replacement. These approaches are broadly categorized into two main types: model-free and model-based.
Model-based methods rely on an explicit analytical dynamics model derived from physics principles, where payload parameters are directly incorporated into the model equations.
Model-free methods bypass the need for a physics-based model and instead use data-driven techniques (e.g., machine learning) to compensate for payload-induced errors directly from data.
In the former, Shareef et al. [
3] gave a detailed comparison among various learning-based techniques. To reduce the time consumption associated with online fine-tuning data collection across the joint space, Shan et al. [
4] proposed a learning-based calibration scheme that leverages pre-trained neural network models to learn calibrated dynamic characteristics across a wide joint space in advance. Taie et al. [
5] put forward a new online identification method that employs a bagging ensemble machine learning approach to estimate payload inertial parameters. While data-driven methods excel in handling complex dynamics, they often lack interpretability and require substantial computational resources for training and inference.
Conversely, model-based calibration methods are designed to achieve rapid calibration by compensating for variations in the end-effector payload. In [
6], it is demonstrated that rapid calibration can be achieved when force/torque measurements are available and the payload geometry is known. Common ways for payload identification can be broadly classified into four categories [
7]: (1) Wrench-based estimation using external sensors: this approach employs a wrist-mounted 6D force/torque sensor to measure the interaction wrench between the end-effector and the payload, combined with an inertial measurement unit (IMU) to capture accelerations. As this technique relies solely on external sensing, it imposes no additional requirements on the robot [
8,
9]. (2) Model-based estimation with joint torque sensing: if joint torque sensors and an accurate dynamic model of the robot are available, the external joint torques can be estimated, and payload forces can thereby be deduced [
10]. It is worth noting the advances in sensor technology, including the development of highly sensitive integrated unidirectional pressure sensors [
11]. (3) Differential torque measurement: If the system repeatedly executes the same trajectory, the inertial parameters of the payload can be determined by analyzing the difference in joint torque measurements between loaded and unloaded motions. This approach is illustrated in [
12,
13]. (4) Combined dynamics–payload identification: Given the similarity between payload identification and robot dynamics identification, it is feasible to estimate both simultaneously within a unified formulation, as demonstrated in [
14,
15]. The least squares fitting methods used in the aforementioned methods assume that all measurement errors originate solely from torque measurements and that the data matrix that includes joint accelerations is error-free. However, the double-time differentiation of position data obtained from encoders to compute joint accelerations results in highly noisy acceleration signals and multiple outliers [
5]. Moreover, force/torque-sensor-based methods are costly and susceptible to drift and external influence. To eliminate the need for prior knowledge of the payload and to enable intuitive online payload identification, Kurdas et al. [
16] presented a momentum-observer-based online payload identification method utilizing proprioceptive sensors from tactile robots and a novel filter design for kinematic measurements. However, fixed-gain first-order filter architectures often fail to meet the requirements of systems subject to unknown payload variations, and the accuracy of an observer is largely determined by the precision of the dynamic model of robots, particularly the modeling of joint friction.
Motivated by the challenges outlined above, this paper proposes a novel sensorless payload estimation scheme of serial robots using a disturbance Kalman filter with the variable-parameter noise model to enhance the robustness of the algorithm to process noise and model uncertainty. The major contributions can be summarized as follows:
(1) We give an accurate dynamic model with the nonlinear friction related to the velocity load; the dynamic model-based disturbance observer is integrated in an online payload estimation process.
(2) We establish a variable-parameter noise model via considering the influence of friction and velocity on the noise parameters in the Kalman filter, thus modifying the Kalman filter algorithm.
The remainder of this article is structured as follows.
Section 2 introduces the modeling of robot dynamics involving velocity- and load-dependent friction and the establishment of a generalized momentum-based dynamic model.
Section 3 designs the disturbance Kalman filter with a variable-parameter noise model. Later, the experimental results, analysis, and discussion are provided in
Section 4. Finally,
Section 5 gives the conclusion and future work of this paper.
2. Generalized Momentum-Based Dynamic Model
The inverse dynamics model of an n-DOFs serial robot, accounting for external torques induced by payload, can be expressed as follows [
17]:
where
,
, and
denote the vectors of joint angular position, velocity, and acceleration, respectively;
,
, and
are inertial dynamic parameter matrices that characterize the inertia force/torque, centrifugal and Coriolis force/torque, and the gravity, respectively;
denotes the torque matrix related to inertial dynamics;
captures the friction torque vector of the joint side;
is called the external disturbance from external payload applied to the robotic manipulator system;
is a diagonal matrix of the joint reduction ratio; the matrix
represents the joint torque; and the motor output torque vector
is expressed as a function of the motor current matrix
and torque constant matrix
;
is the external force/torque acting on the end-effector of the robot;
is the Jacobian matrix.
In previous studies, friction has been shown to exhibit nonlinear characteristics that depend on joint velocity and load torque. For the
j-th joint, the friction model can be written as follows [
18]:
where
and
are the coefficients of the quadratic term for the viscous friction;
is the static friction coefficient;
is the Coulomb friction coefficient; the parameters
denotes the Stribeck velocity characterizing static friction and Coulomb friction;
,
, and
are the load-dependent friction coefficients; and
indicates the load torque. Note that the friction model (2) resists direct linearization due to its inherent nonlinear characteristics. For dynamic parameter identification methods involving velocity- and load-dependent friction, refer to literatures [
18,
19].
Since joint accelerations are obtained through second-order numerical differentiation of joint positions, which induce significant noise, we formulate the generalized momentum equation to circumvent this issue, the generalized momentum
and its derivative
are defined as follows [
20]:
Based on the skew-symmetric nature of the matrix
and the symmetric structure of the inertia matrix
[
21], the following property can be derived:
By substituting Equations (
1a), (
1b) and (
4) into Equation (
3b), we can obtain the following momentum-based dynamic model:
4. Experimental Results
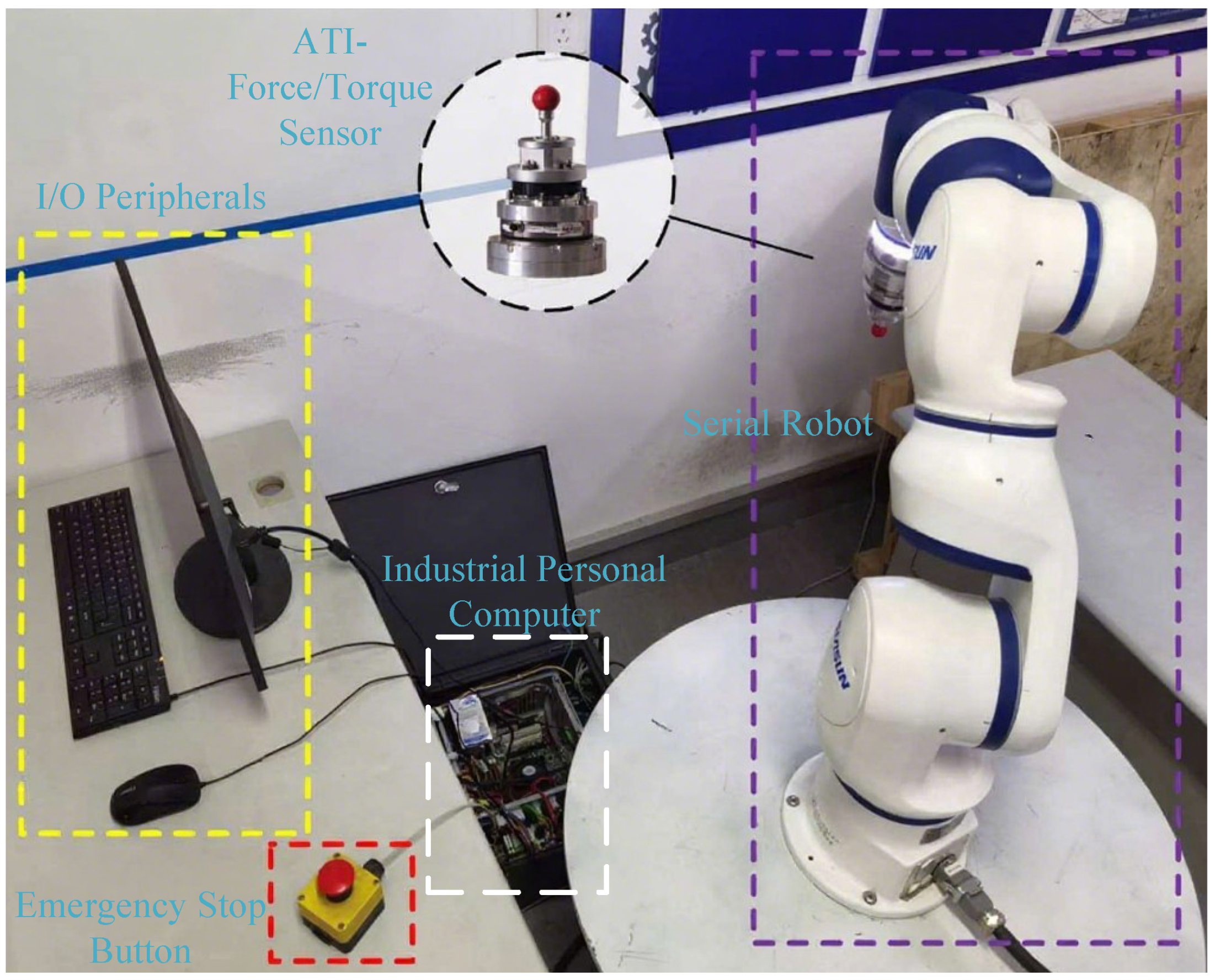
In this section, we employ a seven-DOF SIASUN collaborative robot (SIASUN Robot & Automation Co., Ltd., Shenyang, China) equipped with a six-axis force/torque sensor
(ATI Industrial Automation, USA), as shown in
Figure 1, to accomplish the comparative experimental study of unknown constant load estimation for the performance of different payload estimation approaches such as force sensor measurements, direct current estimation, generalized momentum observers, and Kalman-filter-based observers. The hardware of the control system for the robotic arm is a Beckhoff C6320-30 industrial computer (Beckhoff Automation GmbH & Co. KG., Weilburg, Germany) running on the Windows platform. To achieve real-time industrial control, the industrial computer is also equipped with TwinCAT3 automation motion control software based on the TwinCAT NC runtime core, thus transforming the industrial computer into a control system that integrates a logic controller (PLC), motion controller (NC) and I/O. Communication with the Elmo drives of each joint of the robotic arm is achieved through the EtherCAT bus. It should be noted that the inertial parameters (masses, centers of mass, and inertia tensors) for all links of the 7-DOF manipulator were extracted from a high-fidelity computer-aided design (CAD) model of the robot; see
Table 1.
4.1. Payload Estimation
To evaluate the performance of the external load observer with the optimized noise model, we designate the Kalman filter (KF)-based observers employing fixed- and variable-parameter noise models as the base Kalman filter observer and optimized Kalman filter observer, respectively. Among the compared methods, the direct current estimation and generalized momentum observer first estimate the external joint torques and then compute the resultant end-effector load. In contrast, the force sensor method, BKF observer, and OKF observer directly measure or estimate the external load. The experimental procedure is structured as follows:
(1) Following a one-hour warm-up period, the manipulator is positioned into the initial configuration depicted in
Figure 2a under position control mode, with the payload resting stationary on the table and connected to the end-effector via a cable.
(2) As illustrated in
Figure 2b, the end-effector is then commanded to move vertically upward at a velocity of 10 mm/s for 10 seconds until the payload is fully lifted. Force sensor data and observer outputs are recorded throughout the motion. Four payload masses
are tested. Although forces and torques in other directions are also influenced by the payload variation, the dominant change manifests primarily in the gravitational direction, and the results are shown in
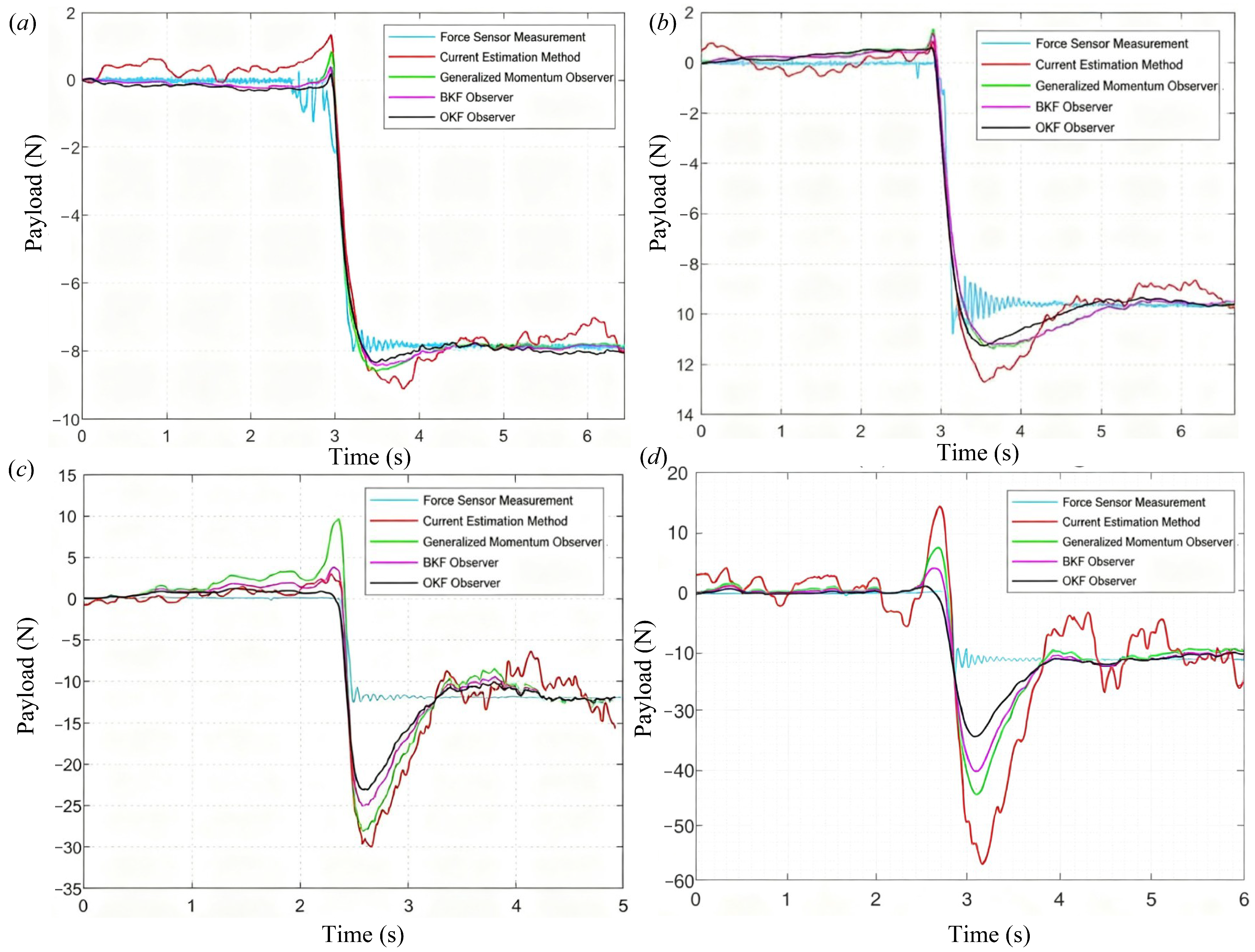
Figure 3. It should be noted that this experiment was designed to compare the performance of different load observers; thus, the analysis focuses exclusively on the response speed and convergence performance during payload lifting. Accordingly,
Figure 3 presents only the data segments immediately before and after the payload is lifted.
As shown in
Figure 3, aside from the substantial noise in the current-based method that impairs its convergence, the steady-state performance of the three observers is quite similar. Given the presence of certain unmodeled dynamics in the observers, the deviation between their steady-state values and the actual measurements from the force sensor remains within an acceptable range. Therefore, the performance analysis focuses primarily on dynamic characteristics. The unknown constant load can be treated as a step input, and common step response metrics, including rise time, peak time, overshoot, and settling time, are used for evaluation. Additionally, a noticeable reverse peak is observed in the observers at the onset of load variation, likely caused by current noise during contact transition. This contact-induced peak is also considered as a dynamic performance metric. Although the peak emerges from the initial zero baseline, it correlates positively with the overshoot, as seen in
Figure 3. We define the contact peak as the percentage ratio of the difference between the peak value and the initial value relative to the steady-state value. The commonly used step response performance metrics are summarized in
Table 2,
Table 3,
Table 4 and
Table 5.
A cross-experimental comparison of the dynamic parameters of the four observation methods reveals that, apart from the nearly identical rise times across all methods, the OKF observer consistently achieves the minimum values in all other metrics. Under most operating conditions, the contact peak and overshoot are reduced by at least 20%, while improvements in peak time and settling time remain below 10%. These results demonstrate that the OKF observer exhibits superior dynamic performance compared to alternative methods, characterized by faster response and convergence, reduced overshoot, and diminished contact peaks. This validates the effectiveness and advantages of the OKF-based external load observer. A longitudinal comparison of the dynamic parameters across experimental groups reveals that as the external load mass increases, the observer exhibits faster response speeds but also introduces larger overshoot. Since the observer fundamentally relies on current information, this indicates that the dynamic performance of current-based observation methods is influenced by the load magnitude. Although reducing the observer gain can mitigate overshoot, it concurrently diminishes response speed. Thus, in practical applications, parameter tuning is essential to achieve an optimal balance between response rapidity and overshoot suppression.
4.2. Direct Teaching for Unknown Payload
To bridge the gap between theory and validation and verify the effectiveness of the drag-to-demonstrate strategy based on unknown load compensation at variable speeds
, we designed two experimental scenarios: linear drag demonstration and curved drag demonstration, as shown in
Figure 4. These were conducted under three experimental conditions: end-effector without load (“no-load condition”), end-effector with load but without load compensation (“load condition”), and end-effector with load and load compensation (“load compensation condition”). During the experiments, the robot arm’s end-effector was dragged to move along the trajectory. A six-axis force sensor was installed at the end-effector, with the drag force primarily manifested as the resultant force in the X and Y directions of the sensor. The force exerted by the load itself on the force sensor was subsequently subtracted from the measurements.
The experimental results of drag forces under various conditions are presented in
Table 6. The magnitude of the drag force is characterized by its mean and peak values, while the compliance of the dragging motion is represented by the maximum mean square error. The data in parentheses indicates the percentage difference between the drag force values after load compensation and those before compensation, relative to the difference between the drag forces under loaded and no-load conditions. A negative symbol and a larger absolute value indicate more complete load compensation. It can be observed that for linear drag teaching, the reduction in drag force after load compensation is significant, with the compensated values being very close to those under the no-load condition. For curved-path drag teaching, due to the complexity of the task, the overall compensation effect is slightly inferior to that of linear dragging. Nevertheless, the results still validate the effectiveness of the load compensation strategy during dragging operations.
5. Conclusions
In the paper, we present a novel sensorless disturbance Kalman filter for accurately estimating the different payload exerted on the end-effector of serial robots. The DKF employs a generalized momentum-based dynamic model of robots that incorporates velocity- and load-dependent nonlinear friction, achieving superior performance in external force estimation. A classic Kalman filter framework is adopted to effectively implement the approach. Furthermore, the influence of load, friction, and velocities on noise parameters within the Kalman filtering algorithm is explicitly considered through a variable-parameter modeling of the noise term, thereby enhancing the overall performance and adaptability of the DKF. Comparative experimental results of multiple external load observations for the robotic end-effector demonstrate that the proposed OKF observer achieves significant improvements in dynamic performance, such as response speed and overshoot, over both the BKF observer and other existing methods.
In the design of the external load observer for robotic end-effectors, our study only addresses loads with constant or slowly varying mass, which limits application to highly dynamic scenarios. In practice, loads may change unpredictably in more complex ways. In future work, we will extend this research to more complex and dynamic loading conditions. Moreover, we plan to integrate unidirectional pressure sensors, which could assist in integrating the DKF into a force controller, enabling tasks like collision detection with payloads and assembly.