1. Introduction
The term transport vehicles refers to vehicles, rail trains, airplanes, ships, etc. Low-voltage electrical appliances are widely used in the electrical control systems of these vehicles, playing a role in controlling, switching on–off, protecting, and regulating circuits. The working environment of these appliances is much harsher than that of general indoor environments, and includes vibrations, high temperatures, and electromagnetic radiation [
1]. Variable loads may also be generated. A sudden change in load intensifies the impact of the arc on the low-voltage electrical contact system, potentially for a long time, resulting in failure or malfunction [
2,
3]. Passive components in low-voltage electrical appliances typically exhibit good reliability data, but they still cause most electronic device failures [
4]. However, research on the reliability of these appliances for transportation vehicles has encountered difficulties such as complex load changes, temperature effects, vibration and shock, and limitations in evaluation and prediction models and testing. Therefore, with the advancement of transport technology and the increasing demand for reliability, research in this field is urgently needed.
At present, traditional reliability theory is still used to evaluate the reliability of low-voltage electrical appliances, generally using the truncated method of fixed number tests, taking the final failure time of the samples obtained from the test as the statistical data object, and then using the optimal distribution type to evaluate the reliability of the product. The methods commonly used for determining failure distribution types are generally graphical estimation, optimal linear unbiased estimation, and maximum likelihood estimation. This study analyzes in-depth the failure mechanism of low-voltage electrical appliances used in transport vehicles under variable-load conditions, establishing a model for reliability evaluation and prediction based on data-driven variable load. By building a simulation test platform for the operation of transport vehicles, variable-load test data was collected. After processing this data, a complete evaluation dataset was constructed, which was then input into the evaluation prediction model to predict the remaining life of these appliances used in transport vehicles. The accuracy of this model was verified by comparing the remaining life value of these appliances obtained based on the prediction model with the actual measured value on the test platform. This research provides a theoretical basis for assessing the reliability of low-voltage electrical appliances used in transport vehicles. By predicting the remaining life of these appliances in advance, safety accidents caused by failure of these appliances can be effectively avoided, especially in the field of transport vehicles that require extremely high safety requirements.
2. Analysis of Failure Mechanisms of Low-Voltage Electrical Appliances Used in Transport Vehicles
There are three failure modes for low-voltage electrical appliances used in transport vehicles: mechanical system failure, electromagnetic system failure, and contact system failure.
Figure 1 shows the tested low-voltage electrical appliances, where the contact system has the highest probability of failure. Therefore, the focus of this study is on the reliability of the contact system under variable-load conditions.
During the operation of transport vehicles, if the internal low-voltage electrical appliances are subjected to continuous vibration impact or the impact frequency matches the natural frequency, it will have adverse effects on the structural and functional integrity of the appliances. Vibration shock is often accompanied by vibration variable load, temperature rise variable load, and electromagnetic variable load. Variable load can lead to arcs, and failure of the contact system is mainly due to the impact of electrical arcing on the damage mechanisms of the contacts and the resulting microstructural characteristics of the ablated surfaces [
5].
2.1. Failure Mechanism of Contact Systems with a Rise in Temperature
When the transport vehicle is in operation, there is minimal mutual friction between the surface layers of the moving and static contact bimetallic sheets of low-voltage electrical appliances in the electronic control system. This friction will cause tiny protrusions on the contact surface to squeeze and rub against each other, resulting in energy loss and temperature rise during this squeezing and rubbing process. This increase in temperature leads to material expansion, and thermal expansion of the contacts may change the contact pressure and contact resistance, resulting in variable loads. This change in load can also cause a rise in temperature, during which the contact system may experience fatigue due to mechanical vibration or arc effects, where the accumulation of fatigue can lead to the failure of low-voltage electrical contact systems. Here, the failure mechanism of the contact system is analyzed by introducing the fatigue damage theory model. This model incorporates a fatigue life degradation function to characterize the cumulative damage effect of load cycles [
6]. The motion state of the transport vehicle can be simulated through a vibration test bench, and the functional relationship between the vibration stress and fatigue life cycles of the test bench is described by the S-N curve [
7], which is the number of stress cycles to failure. Its expression is provided and can directly be used in fatigue analysis without needing to run a nonlinear optimization [
8]. This curve shown in
Figure 2 describes the average value of a series of tests. In Formula (1), S is the amplitude of vibration stress and N is the number of vibration stress actions that cause contact failure. The effective range in the S-N curve approximates a straight line in double logarithmic coordinates.
As shown in
Figure 1, once the slope is determined, the approximate algebraic relationship of S-N is
where
b represents the correlation with the properties of metal materials, and
Hc is a constant value. The model of the relationship between the electrical life of low-voltage electrical appliances used in transport vehicles and their exposure to vibration stress based on the principle of cumulative loss is derived as follows:
where
LS represents electrical lifespan. Vibration stress causes an increase in temperature of low-voltage electrical contacts, which then causes cumulative damage to the contact. The damage model is represented as follows:
where
V represents the damage rate,
represents the vibration stress, and
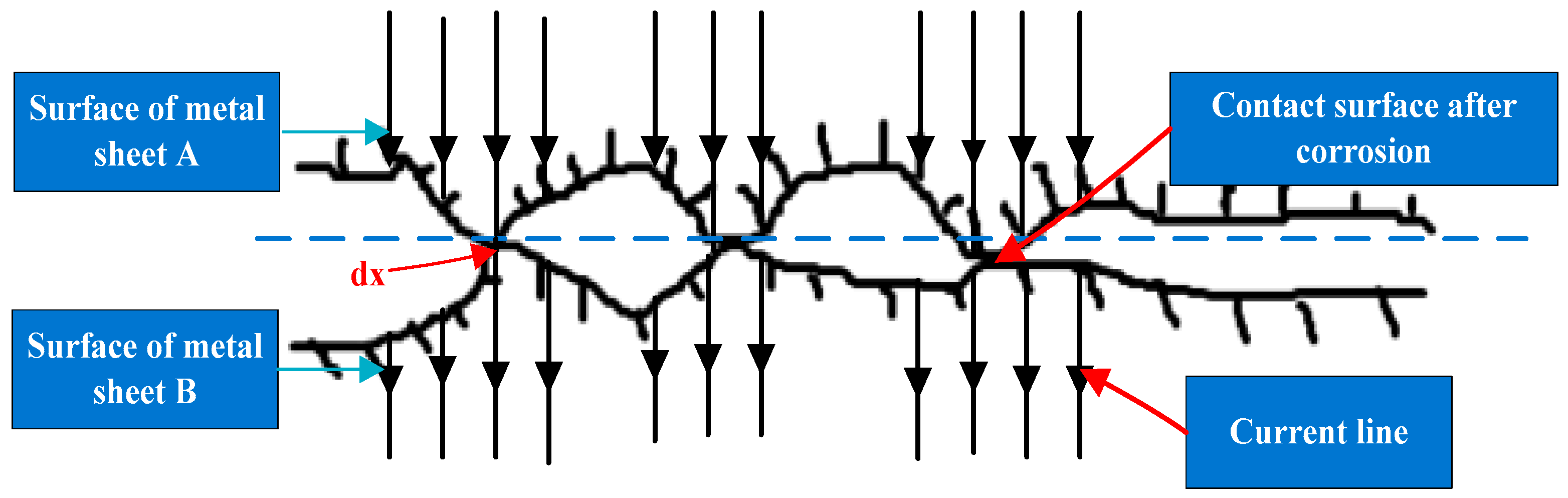
n is a constant. This indicates that the remaining life of the permanent low-voltage electrical equipment of the carrier is closely related to the vibration stress it is subjected to. The temperature rise in the contact part of low-voltage electrical appliances may lead to variable-load generation, and arcs may occur under these variable-load conditions. The surface condition of the bimetallic contact layer of low-voltage electrical appliance contacts under the action of arcs is shown in
Figure 3.
The main reasons for the rise in temperature of bimetallic contacts in low-voltage electrical appliances are the heat generated by current and the frictional heat generated by vibration. During the operation of these appliances used in transport vehicles, there will be energy loss when the current passes through the contact resistor of the appliances. Almost all these losses are converted into thermal energy, which can cause an increase in the temperature of low-voltage electrical contacts used in transportation vehicles. The consequences of temperature rise are as follows:
This may lead to an increase in contact resistance, thereby generating more heat, forming a vicious cycle, further accelerating the aging and damage of contacts;
Under high-temperature conditions, the material of low-voltage electrical contacts may melt or burn, leading to contact failure;
High-temperature environments may accelerate the oxidation process of the contact surface, form an oxide film, and affect conductivity;
The reaction rate of certain chemicals increases at high temperatures, which may corrode the contact material.
Due to the influence of the above factors, the reliability of the contacts in high-temperature environments is reduced, increasing the risk of faults occurring. To quantitatively analyze the impact of temperature rises on the reliability of low-voltage electrical contacts used in transport vehicles, a thermal equilibrium equation is established based on the surface condition of the contact layer of the bimetallic strip in
Figure 2.
where the contact point area is
A, the thermal conductivity is
λ, the contact point resistivity is
ρ, the contact point surface circumference is
g, the heat dissipation coefficient is
CT, the contact point resistance temperature rise is
τ, and
x is related to the shape of the contact point area. By solving the second-order differential of the thermal equilibrium equation,
when
x→∞, the rise in low-voltage electrical temperature is
τw. The heat generation of the narrow part of the contact point is
ρA1l, where
ρ is the thermal conductivity,
A1 is the area of the heating conductor, l is the length of the heating conductor, and the heat dissipation of low-voltage electrical appliances is
CTgl τmax. When
x→0, the maximum temperature rise
τmax can be obtained:
where
. Therefore,
Due to the uneven surface of the contact point, the interface of the contact layer is actually a series of concave–convex contacts, resulting in a rough contact surface. Due to the presence of vibration stress and contact pressure, sliding friction will occur during the closing process of the contacts, especially in the contact layer of low-voltage electrical appliances inside high-speed trains, which will generate relative motion friction during the vibration process. Friction will generate heat, and under the continuous friction between friction points, the temperature will rise, represented by
τf.
where
is a constant,
L is the normal length of the load, μ is the friction coefficient,
v1 and
v2 are the velocities of the two surfaces,
k1 and
k2 are the material constants of the two surfaces, and
h is the width of the contact zone. During the closing process, the contact will generate heat through friction. Let
tc be the time when the contact undergoes displacement and an instantaneous temperature rise. The temperature rise generated during the friction process is calculated and integrated in Formula (8):
where
N is the number of experiments, the height of the surface contact point is represented by
Az, and the material constant is represented by
c.
f(
δ) is the relevant friction correction factor and is approximately equal to the height value
Az in the calculation. The temperature rise generated by dynamic friction and that generated by the thermal equilibrium of contact resistance are fused together to obtain the temperature rise
Tf:
Under the action of temperature rise and vibration load stress, the corrosion and oxidation of contact bimetallic strips are the main reasons for the failure of low-voltage electrical contacts used in transport vehicles, while under vibration load, the reason for failure is micro-motion wear on concave and convex areas. Under the combined action of vibration, friction, and temperature changes, the heat generated by friction intensifies the corrosion and oxidation of the contact bimetallic strip. At the same time, the relative motion of friction leads to the rupture of the oxide film, exposing the metal contact material and continuing the oxidation reaction, shortening the contact life. The process of contact point failure caused by temperature and vibration is shown in
Figure 4.
There is a complex mutual coupling effect between vibration stress and temperature stress, and it is difficult to quantitatively analyze the impact of these two stresses on contact failure. Under the combined effects of temperature changes and vibration friction stress, the failure mechanism of low-voltage electrical appliances used in transport vehicles is the same. Statistical analysis of their electrical life shows that they comply with the principle of mutual independence and follow a two-parameter Weibull distribution. Combined with the temperature rise effects caused by vibration and temperature, the functional relationship model between the electrical life of low-voltage electrical appliances used in transport vehicles and the temperature and vibration stress caused by variable loads satisfies Formula (11):
where
L represents the electrical life of the contact,
α represents the temperature rise sensitivity coefficient,
β represents the vibration sensitivity coefficient,
η represents the Boltzmann constant,
Tf represents the temperature rise,
E represents the thermal sensitivity of the bimetallic strip,
N represents the vibration stress,
δ represents the cumulative damage constant, and
γ represents the correlation with the properties of the metal material.
2.2. Failure Mechanism of Contact System Under Arc Conditions
When the static and moving contacts of the contact system are disconnected, if the conditions for generating an arc are reached between the contacts, these arcs occur naturally even at low voltage when the roughness is in the micron range [
9]. An arc is a gas with strong light and extremely high temperature. This arc, accompanied by high temperature, melts the surface material of the contact metal sheet, with the resulting molten liquid being sprayed and dispersed under the action of airflow and a magnetic field, which leads to electrical wear of the contacts during the disconnection process. The mechanism of electrical wear involves the loss of quality of the contact metal sheet caused by the energy and time of arc ignition. This arc ignition causes cumulative damage to the contact system, ultimately leading to the failure of low-voltage electrical appliances. This damage mainly occurs in three stages: connection, the closed state, and disconnection.
When the contact passes through higher voltage and current in the process of making, closing, and breaking, the facial mask on the contact metal sheet may be broken down by the circuit voltage or burned by the circuit current. Due to heat dissipation caused by the current passing through the contact resistor, there is an increase in the temperature of the conductive spots on the metal sheet that the contact connects with, leading to local melting and even fusion welding on the surface of the metal sheet. When the contact resistance current is high, it is likely that the arc breaks through the surface facial mask at the contact metal sheet when the contact opens. When the contact closes, this contact resistance may generate a lot of joule heat, removing the organic matter at the contact and decreasing the size of the film resistance on the metal sheet. At this point, the main reason for the failure of the contact system is no longer the resistance of the contact film but is arc generation and the subsequent welding problems. When the contact is close to closing, a line voltage is generated and may break down, forming an arc. The current becomes connected when the contact is closed, and the arc is extinguished. When the contacts collide, kinetic energy is generated, and the electric repulsion may cause the contacts to bounce, resulting in the formation of an arc when the contacts break, melting and vaporizing the metal surface of the contacts. When the contact bounces to the maximum distance, the contact connects and closes again, the arc is extinguished, the metal material on the surface of the metal sheet melts, and after dispersing, it cools down to produce welding. When the contact is disconnected or repelled by electric force, the formation of an instantaneous arc will melt and vaporize the metal surface of the contact. When the contact is closed again, the molten liquid on the surface of the metal sheet will quickly cool down, causing the metal to solidify and form a fusion weld. From the above analysis, it can be concluded that the failure modes vary depending on the process of contact connection, closure, and disconnection.
Systems usually suffer from failures due to internal degradation (e.g., corrosion, fatigue, or wear) and external shocks [
10]. Because arcing can cause changes in the contact gap of low-voltage electrical contacts, the damage model is an effective way to resolve contradictions in lifetime prediction [
11] and the degradation rate model of contact bimetallic strips [
12]:
where the erosion coefficient
K reflects the relationship between the arc energy and the change in contact gap and is influenced by the contact area, contact material, arc motion, and other environmental factors such as humidity, temperature, and air pressure, which collectively affect the change in the contact metal gap. m is the degradation index, reflecting the degradation rate and randomness of the contact gap. When
m < 0, the change function
W (
N) of the arc energy reflects the factors that affect this energy, such as the breaking rate and load type.
N is the operating life of the low-voltage electrical contact. The degradation model of the contact gap is obtained by integrating the model of Formula (12):
when
m < 0, the accumulated energy of the arc is
. In practical situations, due to the influence of the initial value of the contact surface gap, it is necessary to modify the parameters of the degradation model in Formula (13):
where
m < 0. The initial value of the contact surface gap between the contacts is
. The arc energy generated during a single disconnection process
E is
where the sampling parameters are voltage value
un, current value
in, frequency
n, time interval
, and frequency
.
Taking a circuit breaker as an example, the mechanism of arc energy generation in the contact system under arc conditions is analyzed. The arc initiation phase angle of AC power is divided into three zones: [0,
π/3), [
π/3, 2
π/3), and [2
π/3,
π). When the initial arc phase angle is in the [0,
π/3) zone, the expression of arc current is
where
. When the C-phase current is disconnected, the A-phase and B-phase currents form a loop, and their arc currents are represented as follows:
where
tf is the moment the arc extinguishes when the current begins to disconnect, and
tx is the moment the arc extinguishes when the current ends. The initial value
can be calculated according to Formula (17), and the constant
n value can be obtained. When
φ in the range of [
π/3, 2
π/3), the A-phase arc current can be expressed as
At the moment the arc extinguishes when the B-phase current is disconnected, the A-phase and C-phase currents form a loop, and the current
iAC is calculated as follows:
when
φ is in the [2π/3, π) interval, the arc of the A phase-disconnected current begins to extinguish. In this case, the current
iA is calculated as follows:
In summary, the Joule integral of the A-phase contact is calculated as follows:
where
φf is the initial extinguishing phase angle when the current is turned on, and
φx is the final arc extinguishing phase angle when the current is disconnected.
3. Reliability Assessment Modeling Based on Variable-Load Data-Driven Approach
Due to the greatly improved reliability and lifespan of low-voltage electrical appliances used in transport vehicles, it is generally difficult to obtain data on their failure time [
13]. Therefore, residual life prediction methods based on failure time are in a dilemma. Data-driven and machine learning methods provide efficient and accurate approaches for solving impact problems [
14], so this study adopts a data-driven approach to evaluate the reliability and predict the electrical life of these appliances. The key to data-driven methods is to use performance degradation data to establish degradation models without the need for failure time, which is very suitable for reliability assessment and prediction of the appliances. If traditional reliability life assessment methods are used, a large number of vehicles would need to use low-voltage electrical test samples for fatigue testing, which is impossible; instead, Bayesian models [
15] are used to solve the problem. The Bayesian evaluation method can comprehensively utilize historical information and overcome the limitations caused by small sample sizes [
16]. Data-driven policies can be used in a more intelligent way to achieve anomaly detection and effectively avoid the introduction of expert experience, thus having a broader scope of application [
17].
Take
n (
n ≤ 2) pieces from low-voltage electrical products used in transport vehicles as samples for timed truncation tests [
18], and conduct a total of
k tests on this group of samples, with each test lasting
ti (0 <
t1 <
t2 <
t3 <
tk) and the number of samples that have not failed at time
ti being
ni. The number of samples without failure after testing is
i =1, 2, 3, …
k. If
, then the sample has no failures:
i = 1, 2, 3, …
k. The cumulative failure probabilities obtained from conducting
k tests on the samples are
The cumulative failure probability is
pi at time
ti. There are two types of test results, invalid or not invalid, which follow a binomial distribution. Therefore, the probability of
ri failure in the total number of samples
si is
where
represents the combination of failure probabilities, and the sample has a normal probability of no failure:
In Bayes statistical inference, selecting an appropriate prior distribution is crucial for parameter estimation. It is very reasonable to use the Beta distribution as a prior distribution for cumulative failure probability, especially when dealing with small sample situations [
19]. Therefore, the prior distribution Beta is changed to an incomplete Beta distribution, and its probability density function is
where
is the Beta function,
α > 0,
β > 0, and
. From the above analysis, it can be seen that under the aforementioned conditions, the prior function of
p1 is
According to Bayes’ theorem, the posterior distribution of cumulative failure probability
p1 is
The point estimate of cumulative failure probability
p1 is the mean of the posterior distribution, which is
where
is the cumulative failure probability of posterior mean
.
Due to
p1 ≤
p2 ≤⋯≤
pk, take the prior distribution of
p2 as Beta (
, 1, 0.5,
β). The hyperparameter
β follows a uniform distribution of (1,
c), and the prior distribution of cumulative failure probability
p2 is
According to Bayes’ theorem, the posterior distribution of the cumulative failure probability
p2 is
The Bayes point estimate of cumulative failure probability
p2 is
According to mathematical induction, the prior distribution [
20] of cumulative failure probability
pi is known as
Similarly, the posterior distribution of cumulative failure probability
pi is
Therefore, based on the Bayes model, the general form of cumulative failure probability
is obtained:
After obtaining
pi through the above method, it can be concluded from the above formula that the scale parameter
η and shape parameter
β in the Weibull model [
21] can be obtained through the weighted least squares method. The two-parameter classical Weibull distribution is commonly implemented to cater for the product’s reliability, model the failure rates, and analyze lifetime phenomena [
22].
η is a scale parameter that is related to the lowest contact failure rate, and β is a shape parameter that is related to the trend of contact failure rate.
By combining Bayes’ method with the weighted least squares method [
23], one of the most commonly used methods in producing the Weibull distribution is the ordinary least squares technique, which is useful in reliability and lifetime modeling [
24]. Prior information and data features can be effectively utilized in parameter estimation, thereby improving the accuracy and reliability of the estimation. First, take the weight as
wi, and then calculate
using Bayes’ method and substitute it into Formula (37):
Consider the following:
is obtained, where
In an actual operation process, the failure rate of low-voltage electrical appliances used in transport vehicles is often affected by various factors, resulting in their time-varying and non-uniform failure characteristics. To effectively simulate this complex performance degradation process, a stochastic process with nonlinear drift can be used for modeling the stochastic nonlinear degradation process, which can more flexibly and accurately describe the nonlinearity of the degradation process [
25]. If the initial value of the random process is 0, the model of the random process with nonlinear drift is as follows:
where
X(
t) represents the actual performance degradation degree of low-voltage electrical appliances used in the transport vehicle at time t in the random process. The cumulative effect of the performance degradation failure process is represented by
. The drift coefficient and diffusion coefficient represent the impact of uncertain factors on the performance of low-voltage electrical equipment.
W(
t) is a standard stochastic process.
To reflect the individual differences in the evaluation prediction model, the parameters are treated as random variables. If they follow the same distribution, they are denoted as
=
D. Since
D > 0, and thus
> 0, assuming they follow the Gamma function distribution, then D follows the inverse Gamma model [
26] function distribution.
where
determines the shape of the distribution,
determines the degree of expansion of the distribution,
x > 0,
> 0, and
> 0, further assuming that under given conditions of
,
μ follows a normal distributions:
After determining the prior distribution,
D follows the inverse Gamma function distribution Ga(
v(
τ − t),
u) as shown in Formula (40). When
D is given and
μ follows a normal distribution, the estimated value of parameters
is calculated according to
where
N is the total number of samples and
Mi is the total number of
i-th detections. At time
ti1, the
i-th degradation quantity of
tim is
Xi1,
Xim, and
are the
i-th degradation increments at time
.
is the time interval,
j is the number of detections, and
μ and
σ are calculated according to the above formula.
When
X(
t) reaches the failure threshold L for the first time, the low-voltage electrical equipment used in the transport vehicle fails, and the probability density function of the remaining life is as follows:
In general, the expected value of the probability density function of the remaining life distribution can be used as the predicted value. This expected value can be obtained from the above equation:
In formulas (42) and (43), N represents the remaining number of operations, L represents the number of failures, and L0 is the cumulative number of operations.
Based on the aforementioned Bayesian non-parametric uncertainty inference model, assuming that the reliability of low-voltage electrical equipment used in transport vehicles follows a two-parameter Weibull distribution [
27], the reliability calculation function is
where
F(
t) is the cumulative distribution function CDF of the fault distribution of low-voltage electrical appliances used in transport vehicles, and
T is the fault-free operating time of these appliances. The estimated CDF has a lower spread, higher reliability, and sharper probabilistic forecasts with better accuracy [
28].
4. Validation of Reliability Evaluation Model Based on Variable-Load Data-Driven Approach
4.1. Construction of a Reliability Testing Platform
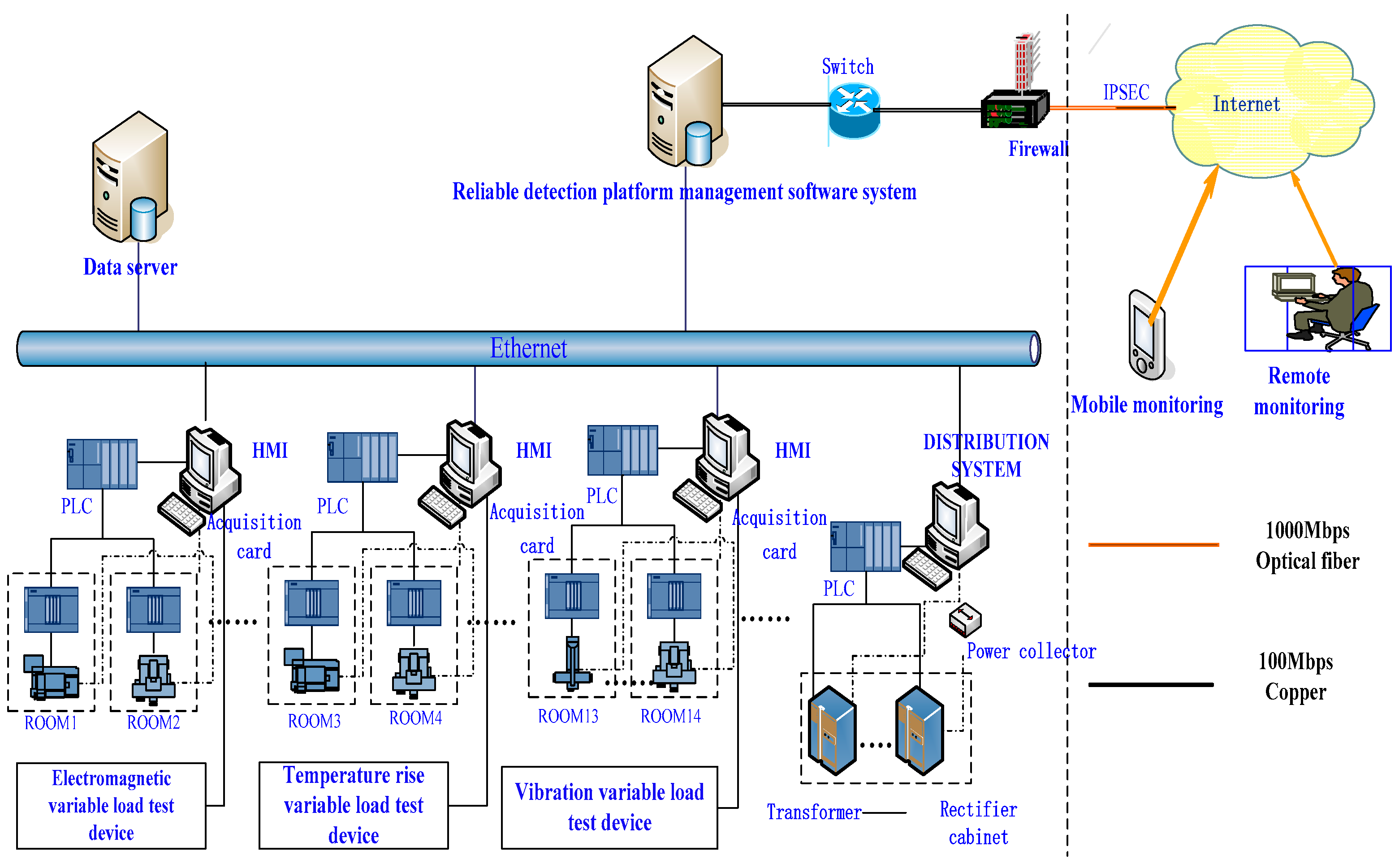
The research and design of a reliability testing platform for low-voltage electrical appliances used in transport vehicles mainly aim to evaluate and verify the performance and reliability of these appliances. The reliability testing platform is integrated with a management software system and a variable-load testing device. The overall plan of the testing platform is shown in
Figure 5. The platform management software system includes a series of functions such as test parameter setting, test process control, test data collection, storage, query, printing, remote monitoring, fault alarm, and reliability evaluation. The variable-load test device includes a vibration variable-load test device, an electromagnetic variable-load test device, a temperature rise variable-load test device, etc., where vibration variable load is the main influencing factor on the reliability of low-voltage electrical appliances used in transport vehicles.
The vibration variable-load test device was used to simulate transport vehicles and generate variable excitation vibrations with different vibration intensity characteristics. The dynamic response signals of the tested low-voltage electrical contact system are captured by sensors, and the upper computer software system processes, analyzes, evaluates, and visualizes the collected signals.
Taking circuit breaker detection as an example, its contact current and voltage data contain rich electrical performance characteristic information, which can be used to evaluate and predict the remaining life of the circuit breaker. The electrical life of circuit breakers is generally long, so their failure tests take a long time. In order to quickly collect failure test data, the accelerated life method is adopted to shorten the failure test schedule. Detection parameters are set according to the national standard GB/T14048.1-2023 [
29] “Low voltage switchgear and control equipment”, and the parameter settings for the accelerated test are shown in
Table 1. The circuit breaker is installed on the vibration table as shown in
Figure 6a. During the test, the management software system collects variable-load current and voltage data as shown in
Figure 6b. The data collected during the experiment includes action time, bounce frequency, bounce time, contact pressure, arc time, coil voltage, coil current, arc time, breaking current, contact resistance, arc energy, pull-in time, cumulative arc energy, trigger time, release voltage, contact voltage drop, release time, rebound time, over travel time, and the power factor, a total of 20 characteristic parameter data categories.
The reliability of low-voltage electrical appliances used in transport vehicles is affected by various environmental factors, and some parameters have significant interference, with no discernible trend in their changes. In addition, some parameters have a high correlation with each other, resulting in consistent trends in their changes, due to the large number of feature parameters that consume computer resources and affect the evaluation effect. Using the Spearman index to define the Spearman matrix, which is a mathematical object expressing the pattern of dependence among the components of a multivariate functional dataset [
30], the Spearman rank correlation coefficient method was used to analyze and study the top seven feature parameters in terms of weight ranking, which are cumulative arc energy, contact voltage drop, contact resistance, release voltage, arc time, suction time, and arc energy. These seven feature parameters constitute the evaluation feature dataset.
4.2. Construction of Reliability Assessment Feature Parameter Set
(1) Reliability characteristic parameter calculation
The calculation method for evaluating feature parameters is as follows:
① Adhesion time
tx: The interval time from the initial state to the suction state, excluding bounce time.
where
t1 is the starting time of the coil current and
t2 is the first closing time of the contact.
② Arcing time
tr: The entire process from the formation of the arc to its final extinction, which refers to the time when the current passes through the contact point and the arc discharge phenomenon occurs.
where
t3 is the moment of starting the arc and
t4 is the moment of extinguishing the arc.
③ Arc energy: The energy released by arc combustion during the arc time.
where
u (
t) is the arc voltage and
i (
t) is the arc current.
④ Accumulated arc energy: As the data collected in the experiment is discrete, the values of voltage and current sampling points are, respectively, recorded as
un and
in. Calculation of arc energy:
where is the interval time between adjacent two samples, and
fs is the sampling frequency.
⑤ Contact resistance refers to the resistance between two conductors at the contact point, which may cause an increase in temperature at the contact point. The formula for calculating the relationship between contact resistance
R and temperature is
When the temperature is 0, the contact resistance is, the temperature coefficient of resistivity is, and the calculation formula in the above equation is
where the resistivity
ρ, thermal conductivity
λ, and the integrated median calculated from
are
.
⑥ Contact voltage drop refers to the voltage decrease caused by contact resistance when current passes through a contact point. Calculation formula for contact pressure drop:
where
Ud is the contact pressure drop (unit: V);
I is the current passing through the contact point (unit: A); and
Rc represents contact resistance (unit: Ω).
⑦ Release voltage refers to the voltage drop at both ends of the contact during 40% of the breaking process, which can be collected by sensors.
⑧ Kernel principal component analysis can handle the nonlinearity and the dynamic features simultaneously [
31]. Due to the nonlinear nature of the variable loads generated by low-voltage electrical appliances used in transport vehicles, the analysis and evaluation of nonlinear high-dimensional data require efficient algorithms and models that can capture nonlinear features in high-dimensional space. The process of processing raw data to obtain kernel principal components is as follows:
Standardize the collected feature parameter data to form a feature parameter set
xi (
i = 1, …,
n,
xi ∈
R), and map
xi to a high-dimensional space using a nonlinear function
ξ. If
xi meets the centralization condition, then the covariance matrix [
32] of the samples in high-dimensional space is
The eigenvalues and eigenvectors of matrix
Cm can be obtained according to the above formula. In
,
λ is the eigenvalue of matrix
Cm, and
v is the eigenvector corresponding to λ. There are
where
h = 1, …,
n. Given that
λ = 0 and
wi = (1, …,
n) exists, let
According to formulas (53) and (54),
Define an
n ×
n matrix
h such that
According to Equation (56), we have
where
w = (
w1, …,
wn), and the eigenvalues and eigenvectors are obtained by solving the characteristic equation
nλw = hw. The
h-th
(h = 1, 2,...,
n) principal component
th in the feature space can be obtained from the feature vector
vh.
The selection of
th is based on Formula (59), where
E is a predetermined constant. When
xi does not meet the centralization criteria, use
fij instead of
hij:
where
lij = 1,
hij is the kernel principal component function.
(2) Evaluate the process of constructing feature parameter sets
Constructing the initial feature parameter vector
X0 includes contact voltage drop, contact resistance, release voltage, arc time, pull-in time, arc energy, and cumulative arc energy. Due to the differences in magnitude and dimension between the feature parameters in the feature parameter vector
X0, normalization of
X0 is required [
33] to alleviate the adverse impact of handling effects in the setting of differential expression analysis [
34], and the large weight may mask the decimal changes in the weight. Therefore, the deviation normalization method is adopted:
where
x is the original data, min (
x) is the minimum value in the data, max (
x) is the maximum value in the data, and
is the normalized data. Using kernel principal component analysis to reduce the dimensionality of feature parameter
X0, kernel principal component
X2 is obtained. The feature quantity
X1 =
and the kernel principal component
X2 are merged to construct the full feature quantity
X, that is,
. The construction process of parameter set
X for reliability evaluation of low-voltage electrical appliances based on variable-load operation tools is shown in
Figure 7:
4.3. Verification of Reliability Assessment Model Evaluation
(1) Construction of Variable-Load Feature Dataset
Taking the variable-load test of circuit breaker model NDM3-15 as an example, seven samples from the same manufacturer and batch are selected for the variable-load test, and any one sample is chosen as the validation sample. The evaluation data obtained through experiments are shown in
Table 2.
(2) Screening of strongly correlated feature data
Due to the nonlinear nature of the characteristic data collected during variable-load testing, the correlation between reliability evaluation characteristic parameters is evaluated and screened using the Spearman correlation coefficient method. The Spearman correlation coefficient method [
35] ranks two variables
X and
Y, with a ranking difference of
:
Among them,
R (
Xi) and
R (
Yi) are the rankings of variables
X and
Y, respectively.
where
is the correlation coefficient,
n is the number of feature parameters, and
is the sum of the squares of all ranking differences.
The range of correlation coefficient values is . The closer approaches 0, the weaker the correlation. When approaches 1 or −1, the stronger the correlation. When , the degradation feature quantity is completely negatively correlated with contact failure. When , the degradation feature quantity is completely positively correlated with contact failure. Judging the strength of correlation based on the range of , indicates extremely weak correlation or no correlation, indicates weak correlation, indicates moderate correlation, indicates strong correlation, and indicates strong correlation.
According to the variable-load test data in
Table 2, the correlation between the failure characteristic parameters shown in
Table 3 and the electrical life is calculated. From
Table 3, it can be intuitively seen that the cumulative arc energy has a strong correlation with the electrical life, and the other related strengths are ranked in order of nuclear principal component, contact resistance, and contact voltage drop.
(3) Evaluation and validation of predictive applications based on variable-load data-driven models
Methods based on data-driven models are widely used in the field of dynamic evaluation and prediction [
36,
37]. Through these methods, prior information is obtained through simulation experiments and prior and posterior failure information is integrated. Based on this prior and posterior information, a data-driven model is used to construct a probability distribution of the remaining lifespan and then determine the reliability of the tested sample from the probability distribution of the remaining lifespan.
Table 4 shows the correspondence between the number of circuit breaker test operations and accumulated arc energy obtained through simulation experiments. The table shows that the number of operations (electrical lifetime) for samples 1, 2, and 3 is 35,700, 35,870, and 36,100, respectively. The average accumulated arc energy of three samples is taken as the failure threshold [
38], which is ω = 1,076,392.
The analysis of experimental data shows that the optimal evaluation parameters are the cumulative arc energy, nuclear principal components, contact resistance, and contact voltage drop, with a cumulative arc energy failure threshold of ω = 1,076,392. The evaluation and prediction process based on the variable-load data-driven model is shown in
Figure 8. Experiments are conducted on any selected validation sample; accumulated arc energy, nuclear principal components, contact resistance, and contact voltage drop test data are collected and processed using a reliability testing platform; and the constructed evaluation dataset is input into the reliability evaluation model. The evaluation prediction results are shown in
Table 5.
According to
Table 5, the relative error RE of the predicted values is mostly less than 6%, indicating that the evaluation of the prediction effect based on the variable-load data-driven model can meet the engineering needs.
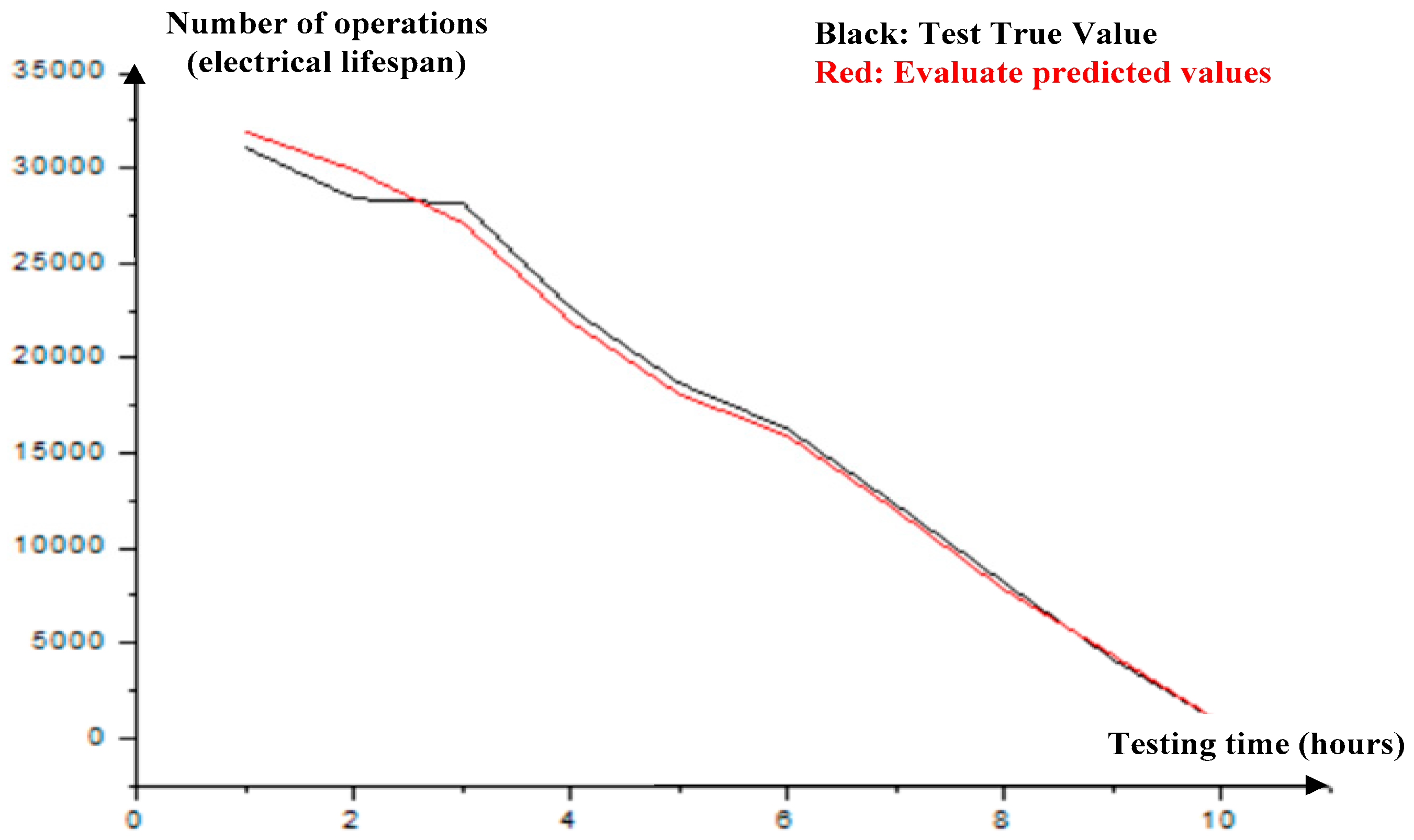
Based on the data in
Table 5, the predicted values of the model evaluation are compared with the actual test values as shown in
Figure 9. The black and red curves in
Figure 9 represent the actual test value and the model evaluation prediction value, respectively. The black and red curves are close, indicating that the model evaluation prediction value is consistent with the actual test value, which verifies the high reliability of the evaluation results based on variable-load data-driven models.
The reliability assessment model is applied to the reliability testing platform management software system, 32 samples of circuit breakers are randomly selected for transport vehicles, and their remaining operation times are predicted through experiments. The prediction results are shown in
Table 6, and the reliability is calculated according to Formula (44). According to the table, there are 1000 remaining operations for the predicted sample, and the reliability is close to 0, indicating that the sample has failed. The remaining number of operations for the predicted sample is around 14,000, with a reliability of approximately 60%. If this remaining number of operations is around 30,000, and the reliability of the sample is close to 100%, the product reliability can fully meet user needs.
The remaining operation times and reliability curves are drawn based on the predicted remaining number of operations (lifespan) and reliability in
Table 6, as shown in
Figure 10.
Figure 10 indicates that the higher the remaining lifespan of the predicted sample, the higher the reliability of the sample.
In summary, based on the variable-load data-driven reliability evaluation model, the input feature parameters such as cumulative arc energy, nuclear principal components, contact resistance, contact voltage drop, and threshold parameter values have high accuracy and good performance in outputting evaluation prediction values. Therefore, data-driven models based on variable loads meet the evaluation and prediction needs of low-voltage electrical appliances for transport vehicles.