Restoring Model of a Pneumatic Artificial Muscle with Structure Parameters: Analysis and Identification
Abstract
1. Introduction
2. Model of the PAM
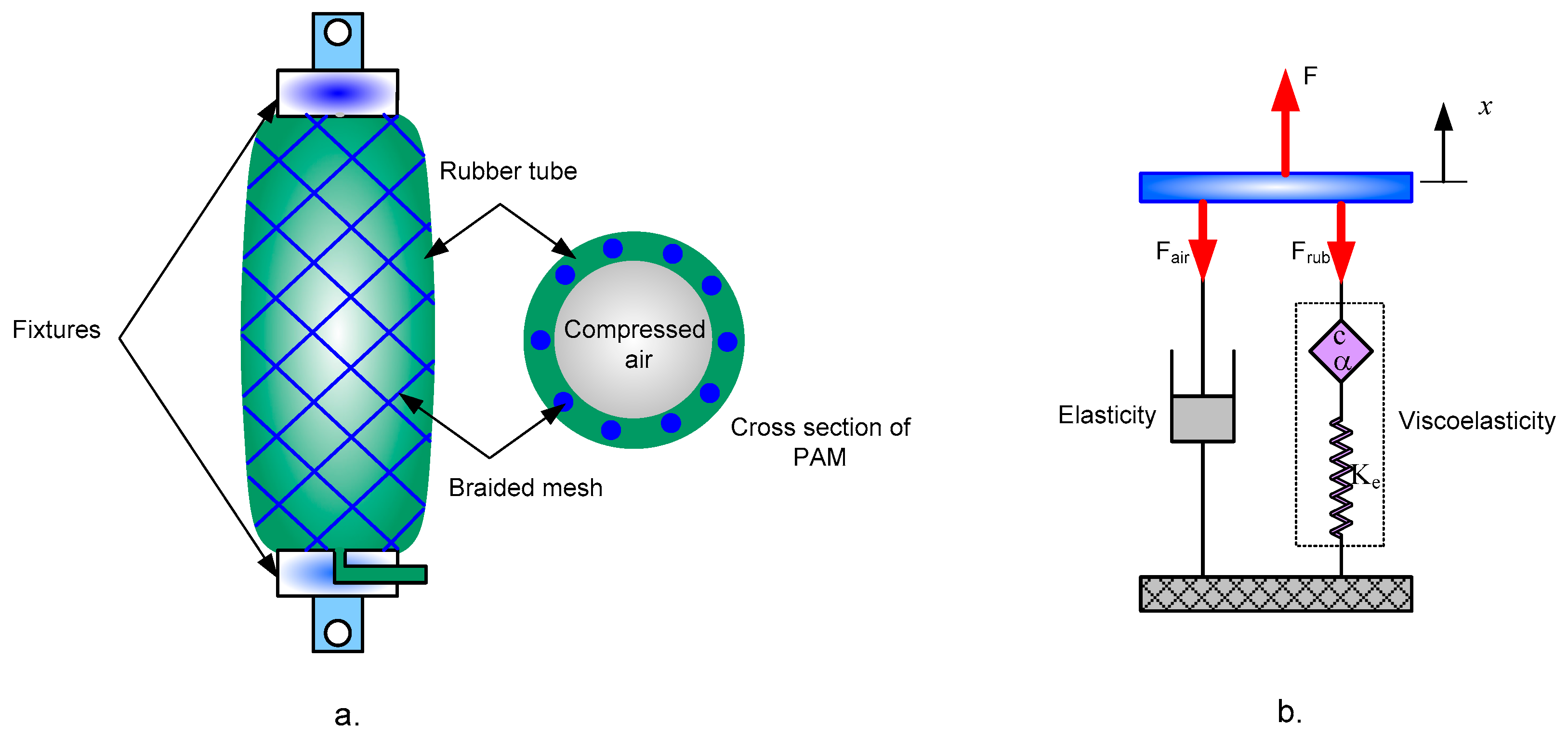
2.1. Physical Model
2.2. Elastic Model
2.3. Viscoelastic Model
3. Algorithm of Parameter Identification
3.1. Cost Function
3.2. Water Cycle Algorithm
4. Experimental Results and Evaluation
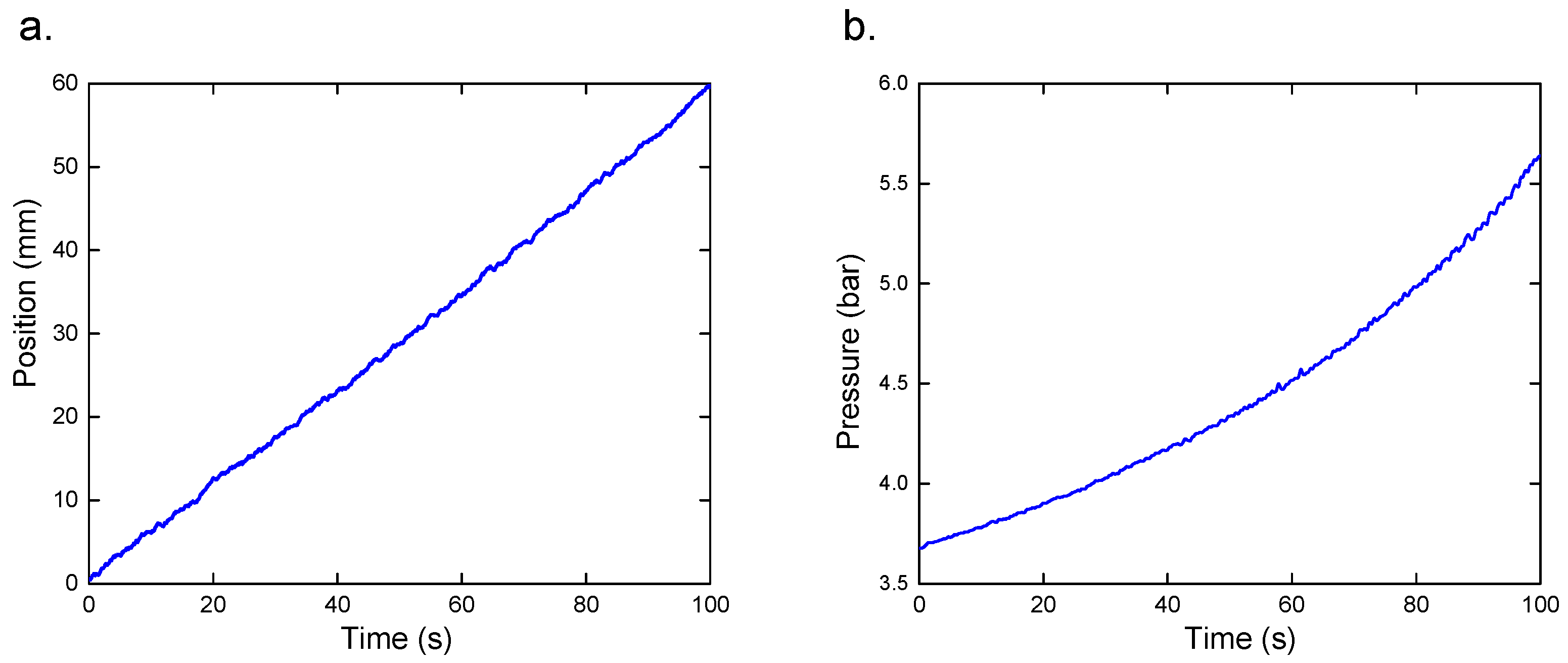
4.1. Experimental Apparatus
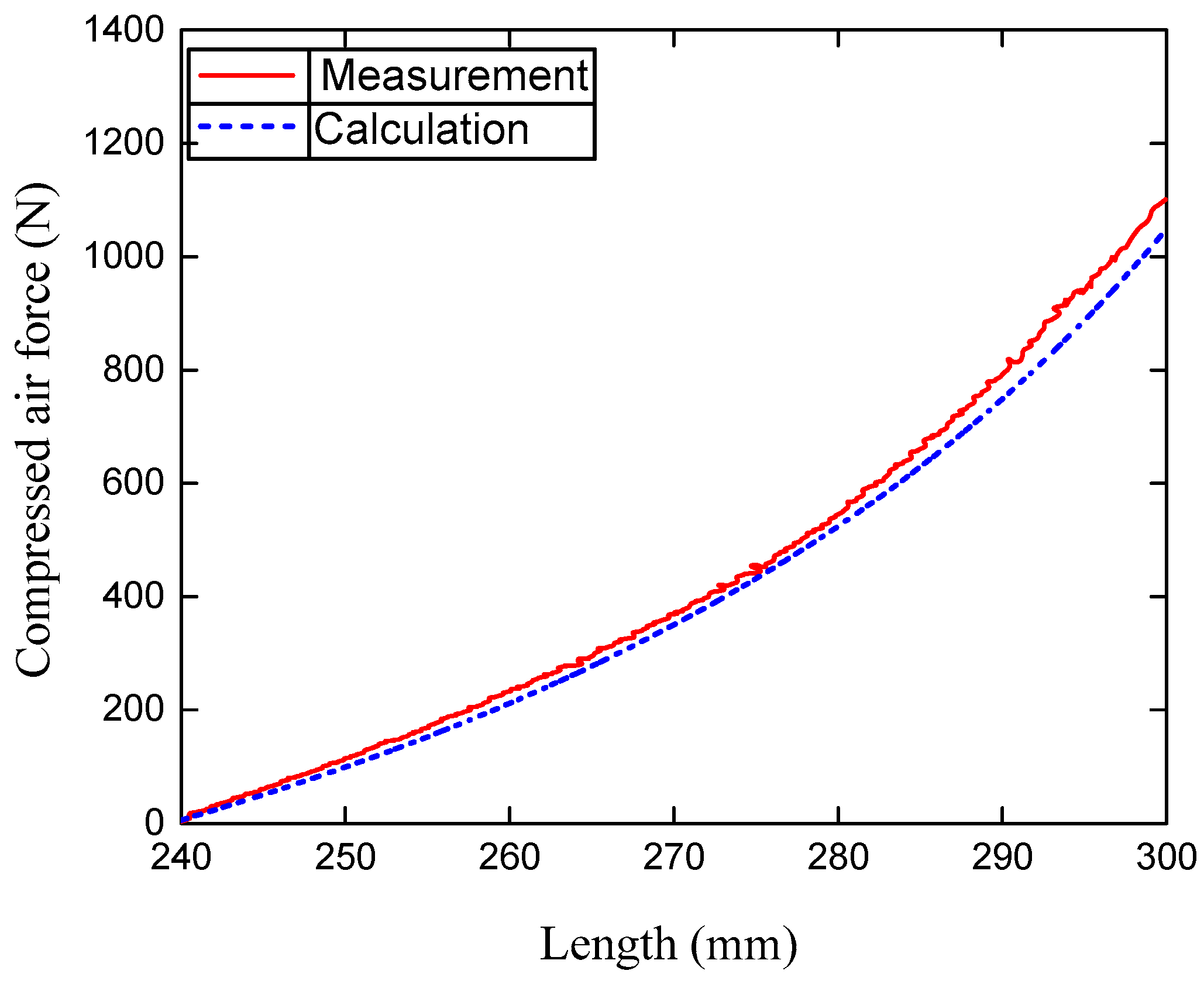
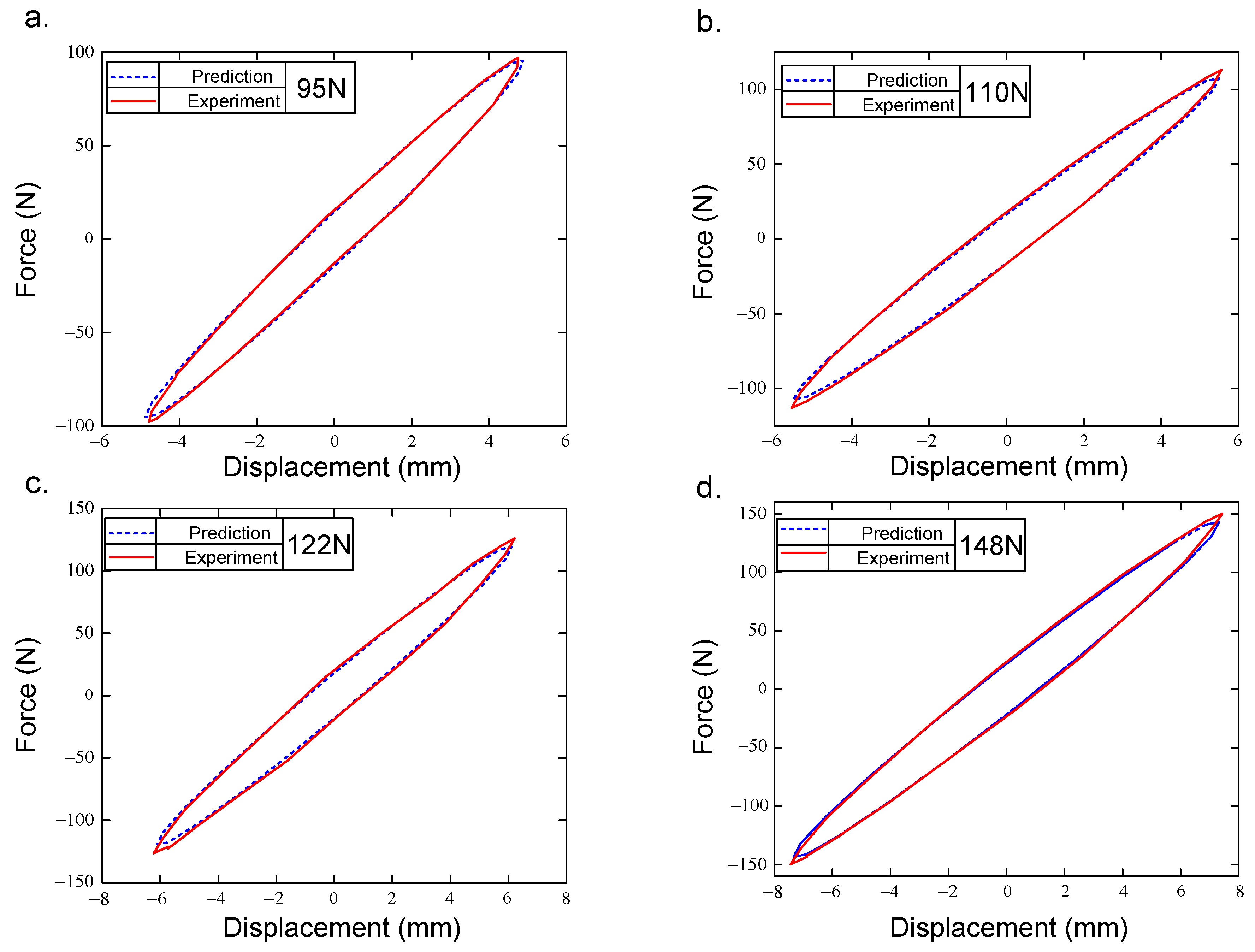
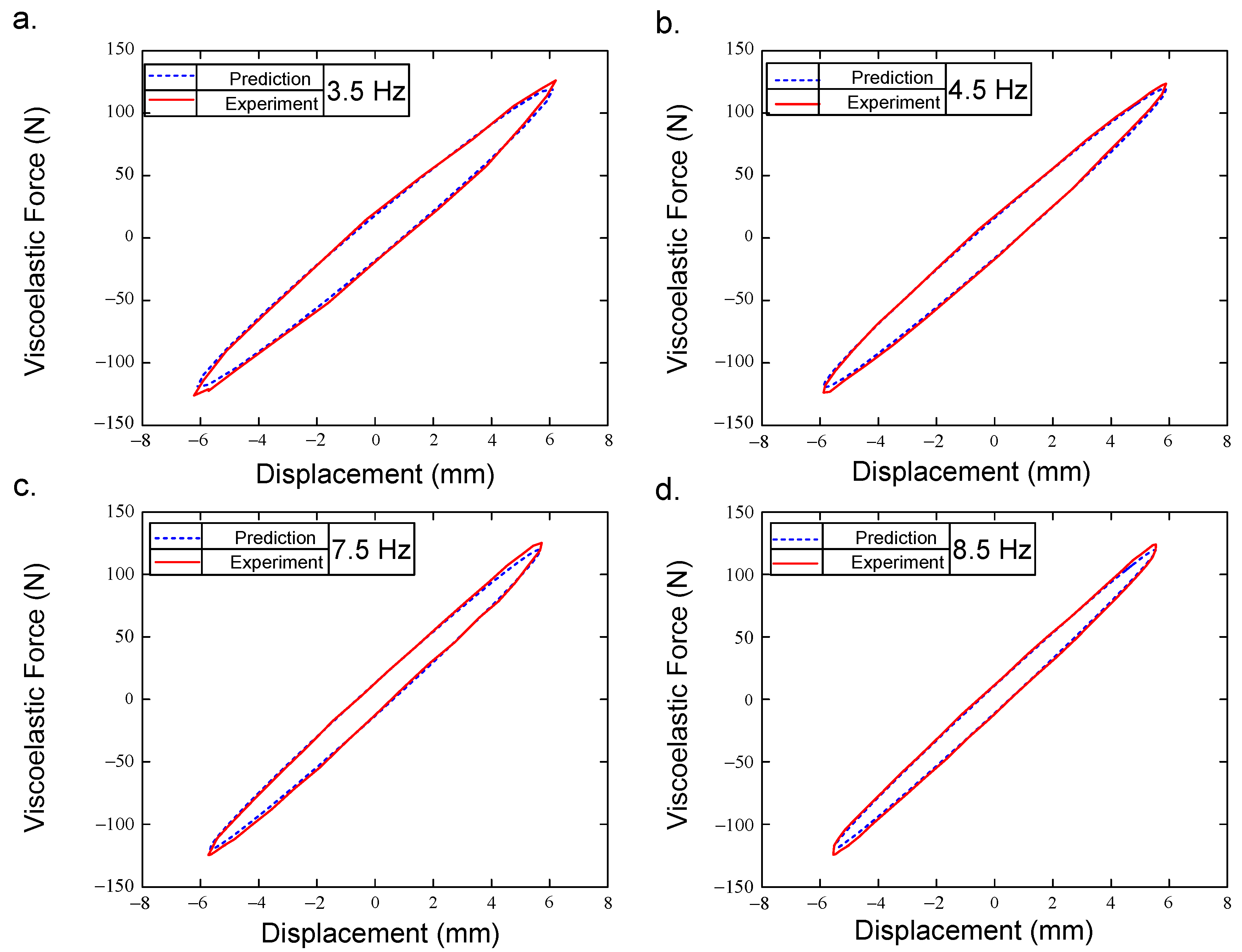
4.2. Results and Discussion
- Elastic model due to compressed air
- b.
- Restoring model of the PAM
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Xiao, W.; Hu, D.; Chen, W.; Yang, G.; Han, X. Modeling and analysis of bending pneumatic artificial muscle with multi-degree of freedom. Smart Mater. Struct. 2021, 30, 095018. [Google Scholar] [CrossRef]
- Lin, C.-J.; Sie, T.-Y.; Chu, W.-L.; Yau, H.-T.; Ding, C.-H. Tracking control of pneumatic artificial muscle-activated robot arm based on sliding-mode control. Actuators 2021, 10, 66. [Google Scholar] [CrossRef]
- Zhang, Y.; Cheng, Q.; Chen, W.; Xiao, J.; Hao, L.; Li, Z. Dynamic modeling and inverse compensation for coupled hysteresis in pneumatic artificial muscle-actuated soft manipulator with variable stiffness. ISA Trans. 2024, 145, 468–478. [Google Scholar] [CrossRef]
- Xie, S.Q.; Jamwal, P.K. An iterative fuzzy controller for pneumatic muscle driven rehabilitation robot. Expert Syst. Appl. 2011, 38, 8128–8137. [Google Scholar] [CrossRef]
- Liu, Q.; Zuo, J.; Zhu, C.; Xie, S.Q. Design and control of soft rehabilitation robots actuated by pneumatic muscles: State of the art. Future Gener. Comput. Syst. 2020, 113, 620–634. [Google Scholar] [CrossRef]
- Nguyen, H.T.; Trinh, V.C.; Le, T.D. An Adaptive Fast Terminal Sliding Mode Controller of Exercise-Assisted Robotic Arm for Elbow Joint Rehabilitation Featuring Pneumatic Artificial Muscle Actuator. Actuators 2020, 9, 118. [Google Scholar] [CrossRef]
- Tomori, H.; Midorikawa, Y.; Nakamura, T. Vibration control of an artificial muscle manipulator with a magnetorheological fluid brake. In Proceedings of the 13th International Conference on Electrorheological Fluids and Magnetorheological Suspensions, Ankara, Turkey, 2–6 July 2012. [Google Scholar]
- Kalita, B.; Leonessa, A.; Dwivedy, S.K. A Review on the Development of Pneumatic Artificial Muscle Actuators: Force Model and Application. Actuators 2022, 11, 288. [Google Scholar] [CrossRef]
- Lin, C.J.; Lin, C.R.; Yu, S.K.; Chen, C.T. Hysteresis model and tracking control for a dual pneumatic artificial muscle systems using Prandtl-Ishlinskii model. Mechatronics 2014, 28, 35–45. [Google Scholar] [CrossRef]
- Xie, S.L.; Liu, H.T.; Mei, J.P.; Gu, G.Y. Modeling and compensation of asymmetric hysteresis for pneumatic artificial muscles with a modified generalized Prandtl-Ishlinskii model. Mechatronics 2018, 52, 49–57. [Google Scholar] [CrossRef]
- Tri, V.N.; Kamers, B.; Romon, H.; Brussel, H.V. Characterization of hysteresis in a pneumatic muscle manipulatot with accounting for the creep effect. IFAC Proc. Vol. 2010, 43, 296–302. [Google Scholar] [CrossRef]
- Sarosi, J. Elimination of the hysteresis effect of PAM actuator: Modeling and experimental studies. Teh. Vjesn.-Tech. Gaz. 2015, 22, 1489–1494. [Google Scholar]
- Mohareb, S.A.; Alsharkawi, A.; Zgoul, M. Hysteresis modeling of a PAM system using ANFIS. Actuators 2021, 10, 280. [Google Scholar] [CrossRef]
- Luo, X.; Xia, M.; Ding, Y.; Ding, H. Hysteresis modeling and compensation of a pneumatic end-effector based on Gaussian process regression. Sens. Actuators A Phys. 2020, 315, 112227. [Google Scholar] [CrossRef]
- Shakiba, S.; Ourak, M.; Poorten, E.V.; Ayati, M.; Yousefi-Koma, A. Modeling and compensation of asymmetric rate-dependent hysteresis of a miniature pneumatic artificial muscle-based catheter. Mech. Syst. Signal Process. 2021, 154, 107532. [Google Scholar] [CrossRef]
- Kalita, B.; Dwivedy, S.K. Nonlinear dynamics of a parametrically excited pneumatic artificial muscle (PAM) actuator with simultaneous resonance condition. Mech. Mach. Theory 2019, 135, 281–297. [Google Scholar] [CrossRef]
- Srosi, J.; Biro, I.; Nemeth, J.; Cveticanin, L. Dynamic modeling of a pneumatic muscle actuator with two-direction motion. Mech. Mach. Theory 2015, 85, 281–297. [Google Scholar] [CrossRef]
- Doumit, M.; Leclair, J. Development and testing of stiffness model for pneumatic. Int. J. Mech. Sci. 2017, 120, 30–41. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, H.; Ma, T.; Hao, L.; Li, Z. A comprehensive dynamic model for pneumatic artificial muscles considering different input frequencies and mechanical loads. Mech. Syst. Signal Process. 2021, 148, 107133. [Google Scholar] [CrossRef]
- Guan, Q.; Sun, J.; Liu, Y.; Wereley, N.M.; Leng, J. Characterization and nonlinear models of bending extensile/contractile pneumatic artificial muscles. Smart. Mater. Struct. 2021, 30, 025024. [Google Scholar] [CrossRef]
- Saito, N.; Satoh, T.; Saga, N. Double Air Chambers Pneumatic Artificial Muscle and Non-Hysteresis Position Control. Actuators 2024, 13, 282. [Google Scholar] [CrossRef]
- Dunn, L. Introduction to viscoelasticity in polymers and its impact on rolling resistance in pneumatic tyres. Int. J. Squiggly Wobbly Mater. 2019, 23, 1–8. [Google Scholar]
- Shitikova, M.V.; Krusser, A.I. Models of viscoelastic materials: A review on historical development and formulation. In Theoretical Analyses, Computations, and Experiments of Multiscale Materials; Springer: Cham, Switzerland, 2022. [Google Scholar]
- Perkins, J.N.; Lach, T.M. Viscoelasticity: Theories, Types and Models; Nova Science Publishers: Hauppauge, NY, USA, 2011. [Google Scholar]
- Fatima, I.D.; Shafi, N.; Anjum, H. Viscoelastic properties of rubber material modeling. In Proceedings of the 2019 International Conference on Applied and Engineering Mathematics (ICAEM), Taxila, Pakistan, 27–29 August 2019. [Google Scholar]
- Berg, M. A model for rubber springs in the dynamic analysis of rail vehicles. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 1997, 211, 95–108. [Google Scholar] [CrossRef]
- Podlubny, I. Practional Differential Equations; Academic Press: Cambridge, MA, USA, 1999. [Google Scholar]
- Eskandar, H.; Sadollah, A.; Bahreininejad, A.; Hamdi, M. Water cycle algorithm—A novel metaheuristic optimization method for solving constrained engineering optimization problems. Comput. Struct. 2012, 110–111, 151–166. [Google Scholar] [CrossRef]







|
Step 1: Select the initial parameters including: Nriver—number of rivers; dmax—a small number (close to zero); Npop—population size. Step 2: Generate random initial population (Npop) and number of initial streams (Nstream), rivers(Nriver) and sea. |
| Step 3: Calculate the value of the fitness function for each stream by using Equation (16). Step 4: Determine the intensity calculation of flow for sea and river. |
| Step 5: Streams flow to river and rivers flow to sea |
| Step 6: Exchange the position of the stream and river and the position of the river and sea
If the fitness function of the stream is lower than that of the river Exchange position of stream and river end If the fitness function of the river lower than that of the sea Exchange position of river and sea end Step 7: Check evaporation condition among sea and river |
| If the evaporation condition is satisfied Creation of clouds and rain by |
| end with a coefficient showing the range of the searching region near the sea. Step 8: Check evaporation condition among sea and stream |
| If the evaporation condition is satisfied Creation of clouds and rain by: |
| end Step 9: Reduce the value of by using |
| Step 10: Check the convergence condition. If the convergence condition is satisfied, the algorithm will be stopped to obtain the optimal solution; otherwise return to step 5. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nguyen, M.K.; Trinh, V.C.; Vo, N.Y.P.; Le, T.D. Restoring Model of a Pneumatic Artificial Muscle with Structure Parameters: Analysis and Identification. Actuators 2024, 13, 355. https://doi.org/10.3390/act13090355
Nguyen MK, Trinh VC, Vo NYP, Le TD. Restoring Model of a Pneumatic Artificial Muscle with Structure Parameters: Analysis and Identification. Actuators. 2024; 13(9):355. https://doi.org/10.3390/act13090355
Chicago/Turabian StyleNguyen, Minh Ky, Van Chon Trinh, Ngoc Yen Phuong Vo, and Thanh Danh Le. 2024. "Restoring Model of a Pneumatic Artificial Muscle with Structure Parameters: Analysis and Identification" Actuators 13, no. 9: 355. https://doi.org/10.3390/act13090355
APA StyleNguyen, M. K., Trinh, V. C., Vo, N. Y. P., & Le, T. D. (2024). Restoring Model of a Pneumatic Artificial Muscle with Structure Parameters: Analysis and Identification. Actuators, 13(9), 355. https://doi.org/10.3390/act13090355






